Смежные вертикальные односторонние накрест лежащие углы: Углы при параллельных прямых и секущей

Углы смежные вертикальные. Н.Никитин Геометрия

Геометрия — это весьма многогранная наука. Она развивает логику, воображение и интеллект. Конечно, из-за своей сложности и огромного количества теорем и аксиом, она не всегда нравится школьникам. Кроме этого, существует необходимость постоянно доказывать свои выводы, используя общепринятые стандарты и правила.

Смежные и вертикальные углы — это неотъемлемая составляющая геометрии. Наверняка многие школьники просто обожают их по той причине, что их свойства понятны и просты в доказательстве.

Образование углов

Любой угол образуется путем пересечения двух прямых или проведения двух лучей из одной точки. Они могут называться либо одной буквой, либо тремя, которые последовательно обозначают точки построения угла.

Углы измеряются в градусах и могут (в зависимости от их значения) по-разному называться. Так, существует прямой угол, острый, тупой и развернутый. Каждому из названий соответствует определенная градусная мера или ее промежуток.

Острым называется угол, мера которого не превышает 90 градусов.

Тупым является угол, превышающий 90 градусов.

Угол называется прямым в том случае, когда его градусная мера равна 90.

В том случае, когда он образован одной сплошной прямой, и его градусная мера равна 180, его называют развернутым.

Углы, имеющие общую сторону, вторая сторона которых продолжает друг друга, называются смежными. Они могут быть как острыми, так и тупыми. Пересечение линией образует смежные углы. Свойства их следующие:

1. Сумма таких углов будет равна 180 градусам (существует теорема, доказывающая это). Поэтому можно легко вычислить один из них, если известен другой.
2. Из первого пункта следует, что смежные углы не могут быть образованы двумя тупыми или двумя острыми углами.

Благодаря этим свойствам, можно всегда вычислить градусную меру угла, имея значение другого угла или, по крайней мере, отношение между ними.

Вертикальные углы

Углы, стороны которых являются продолжением друг друга, называются вертикальными.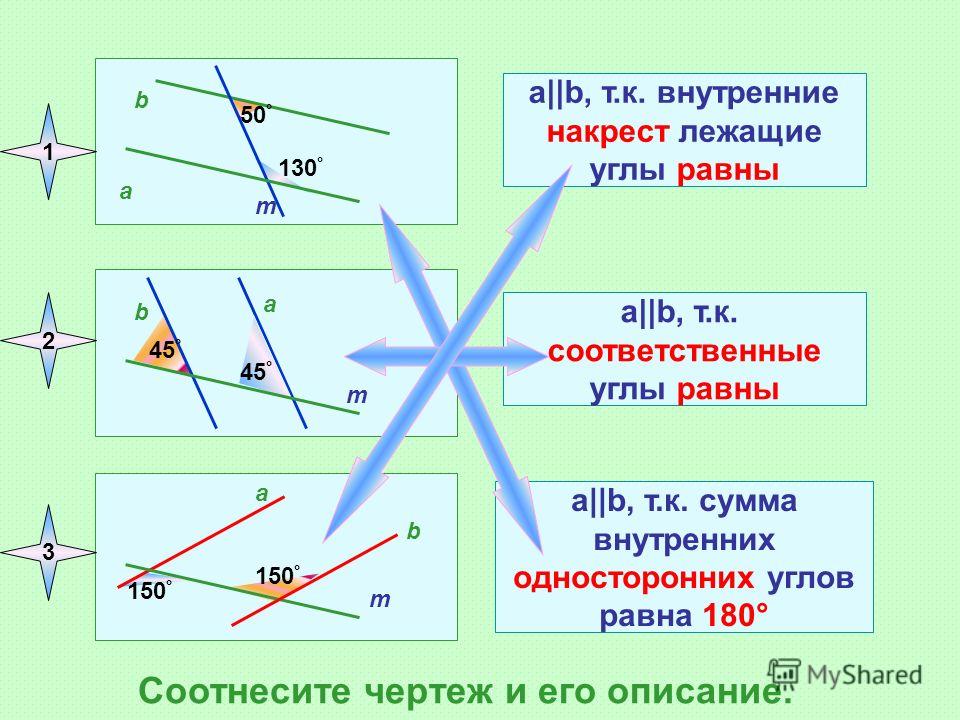 В качестве такой пары могут выступать любые их разновидности. Вертикальные углы всегда равны между собой.

Они образуются при пересечении прямых. Совместно с ними всегда присутствуют и смежные углы. Угол может быть одновременно смежным для одного и вертикальным для другого.

При пересечении произвольной линией также рассматривают еще несколько видов углов. Такая линия называется секущей, она и образует соответственные, односторонние и накрест лежащие углы. Они равны между собой. Их можно рассматривать в свете свойств, которые имеют вертикальные и смежные углы.

Таким образом, тема углов представляется довольно простой и понятной. Все их свойства легко запомнить и доказать. Решение задач не представляется сложным до тех пор, пока углам соответствует числовое значение. Уже дальше, когда начнется изучение sin и cos, придется запоминать множество сложных формул, их выводов и следствий. А до того времени можно просто наслаждаться легкими задачками, в которых необходимо найти смежные углы.

Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными лучами. На рисунке 20 углы АОВ и ВОС смежные.

Сумма смежных углов равна 180°

Теорема 1. Сумма смежных углов равна 180°.

Доказательство. Луч ОВ (см. рис.1) проходит между сторонами развернутого угла. Поэтому ∠ АОВ + ∠ ВОС = 180° .

Из теоремы 1 следует, что если два угла равны, то смежные с ними углы равны.

Вертикальные углы равны

Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами сторон другого. Углы АОВ и COD, BOD и АОС, образованные при пересечении двух прямых, являются вертикальными (рис. 2).

Теорема 2. Вертикальные углы равны.

Доказательство. Рассмотрим вертикальные углы АОВ и COD (см. рис. 2). Угол BOD является смежным для каждого из углов АОВ и COD. По теореме 1 ∠ АОВ + ∠ BOD = 180°, ∠ COD + ∠ BOD = 180°.

Отсюда заключаем, что ∠ АОВ = ∠ COD.

Следствие 1. Угол, смежный с прямым углом, есть прямой угол.

Рассмотрим две пересекающиеся прямые АС и BD (рис.3). Они образуют четыре угла. Если один из них прямой (угол 1 на рис.3), то остальные углы также прямые (углы 1 и 2, 1 и 4 — смежные, углы 1 и 3 — вертикальные). В этом случае говорят, что эти прямые пересекаются под прямым углом и называются перпендикулярными (или взаимно перпендикулярными). Перпендикулярность прямых АС и BD обозначается так: AC ⊥ BD.

Серединным перпендикуляром к отрезку называется прямая, перпендикулярная к этому отрезку и проходящая через его середину.

АН — перпендикуляр к прямой

Рассмотрим прямую а и точку А, не лежащую на ней (рис.4). Соединим точку А отрезком с точкой Н прямой а. Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а, если прямые АН и а перпендикулярны. Точка Н называется основанием перпендикуляра.

Чертежный угольник

Справедлива следующая теорема.

Теорема 3. Из всякой точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.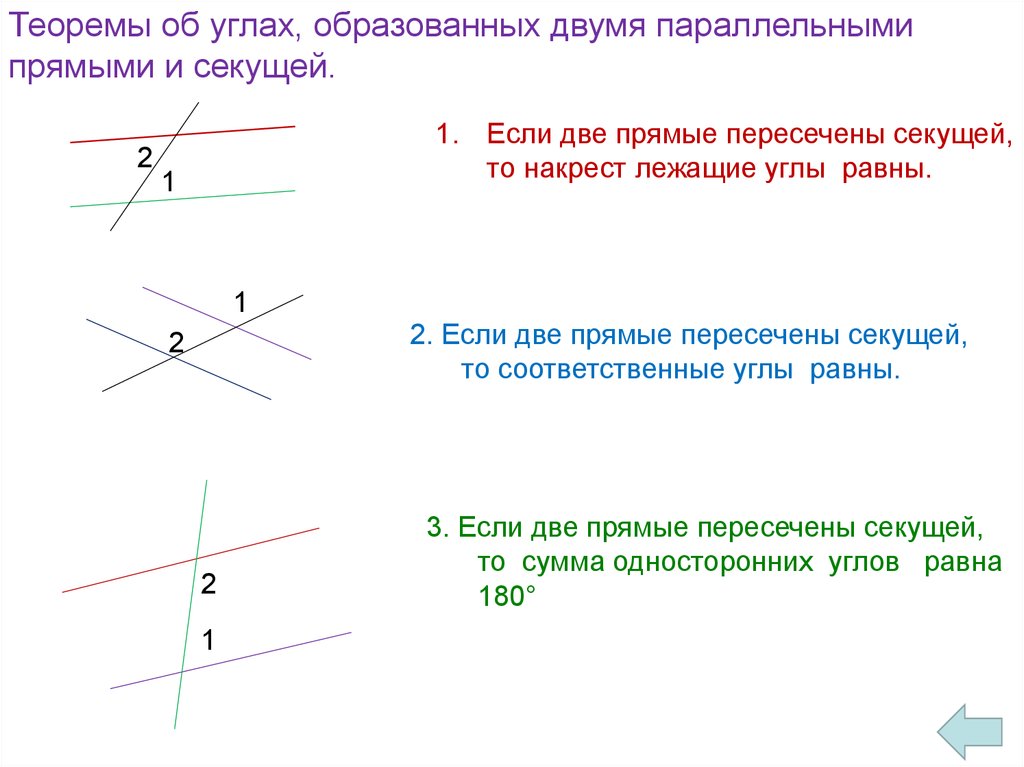

Для проведения на чертеже перпендикуляра из точки к прямой используют чертежный угольник (рис.5).

Замечание. Формулировка теоремы обычно состоит из двух частей. В одной части говорится о том, что дано. Эта часть называется условием теоремы. В другой части говорится о том, что должно быть доказано. Эта часть называется заключением теоремы. Например, условие теоремы 2 — углы вертикальные; заключение — эти углы равны.

Всякую теорему можно подробно выразить словами так, что ее условие будет начинаться словом «если», а заключение — словом «то». Например, теорему 2 можно подробно высказать так: «Если два угла вертикальные, то они равны».

Пример 1. Один из смежных углов равен 44°. Чему равен другой?

Решение. Обозначим градусную меру другого угла через x , тогда согласно теореме 1.
44° + х = 180°.
Решая полученное уравнение, находим, что х = 136°. Следовательно, другой угол равен 136°.

Пример 2. Пусть на рисунке 21 угол COD равен 45°.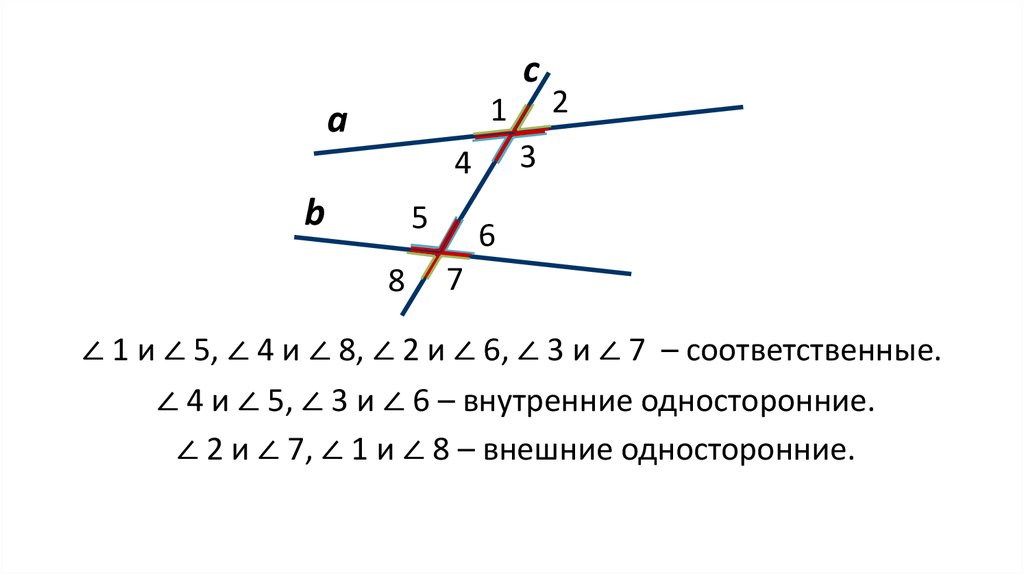 Чему равны углы АОВ и АОС?

Решение. Углы COD и АОВ вертикальные, следовательно, по теореме 1.2 они равны, т. е. ∠ АОВ = 45°. Угол АОС смежный с углом COD, значит, по теореме 1.
∠ АОС = 180° — ∠ COD = 180° — 45° = 135°.

Пример 3. Найти смежные углы, если один из них в 3 раза больше другого.

Решение. Обозначим градусную меру меньшего угла через х. Тогда градусная мера большего угла будет Зх. Так как сумма смежных углов равна 180° (теорема 1), то х + Зх = 180°, откуда х = 45°.
Значит, смежные углы равны 45° и 135°.

Пример 4. Сумма двух вертикальных углов равна 100°. Найти величину каждого из четырех углов.

Решение. Пусть условию задачи отвечает рисунок 2. Вертикальные углы COD к АОВ равны (теорема 2), значит, равны и их градусные меры. Поэтому ∠ COD = ∠ АОВ = 50° (их сумма по условию 100°). Угол BOD (также и угол АОС) смежный с углом COD, и, значит, по теореме 1
∠ BOD = ∠ АОС = 180° — 50° = 130°.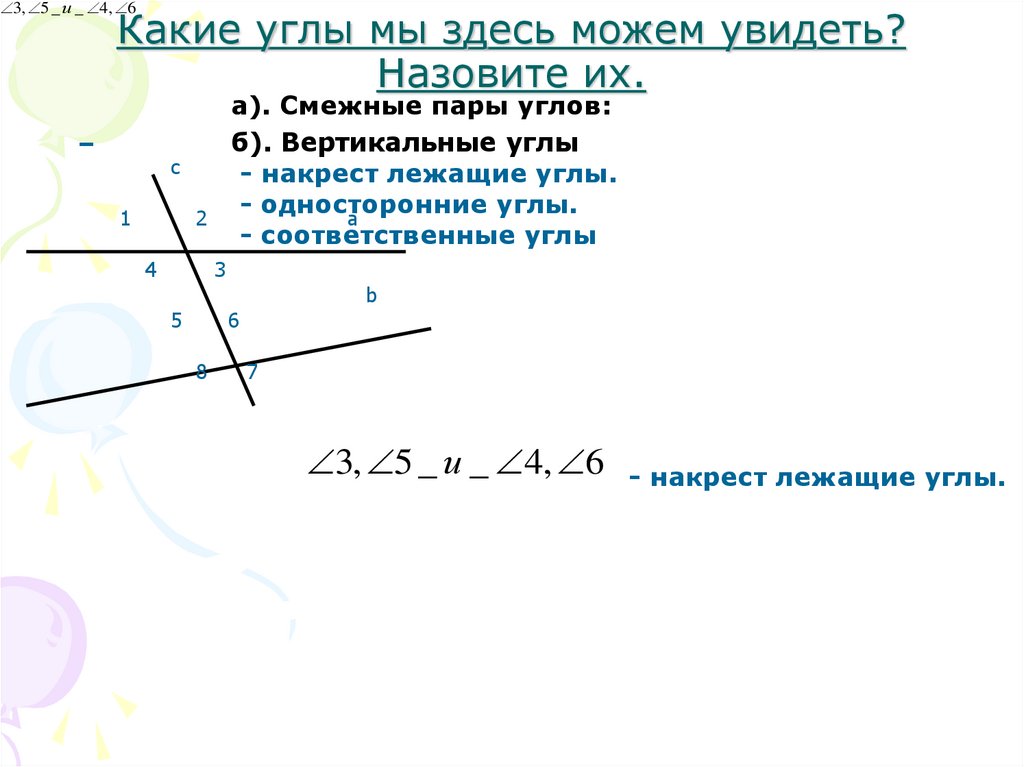

Смежные углы – два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой.

Сумма смежных углов равна 180°

Вертикальные углы — это два угла, у которых стороны одного угла являются продолжение сторон другого.

Вертикальные углы равны.

2. Признаки равенства треугольников:

I признак : Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

II признак : Если стороны и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

III признак : Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны

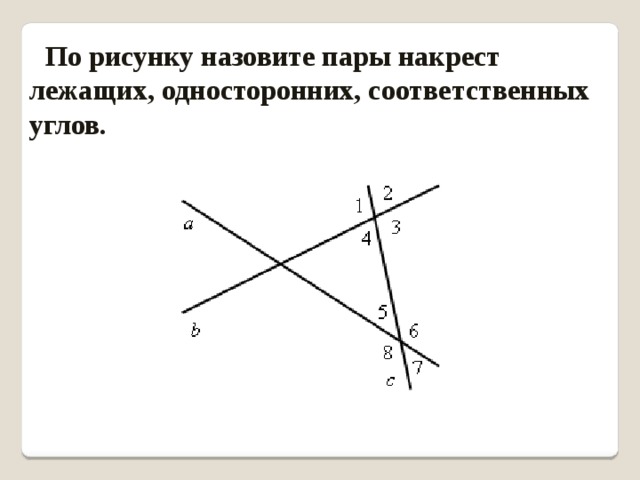
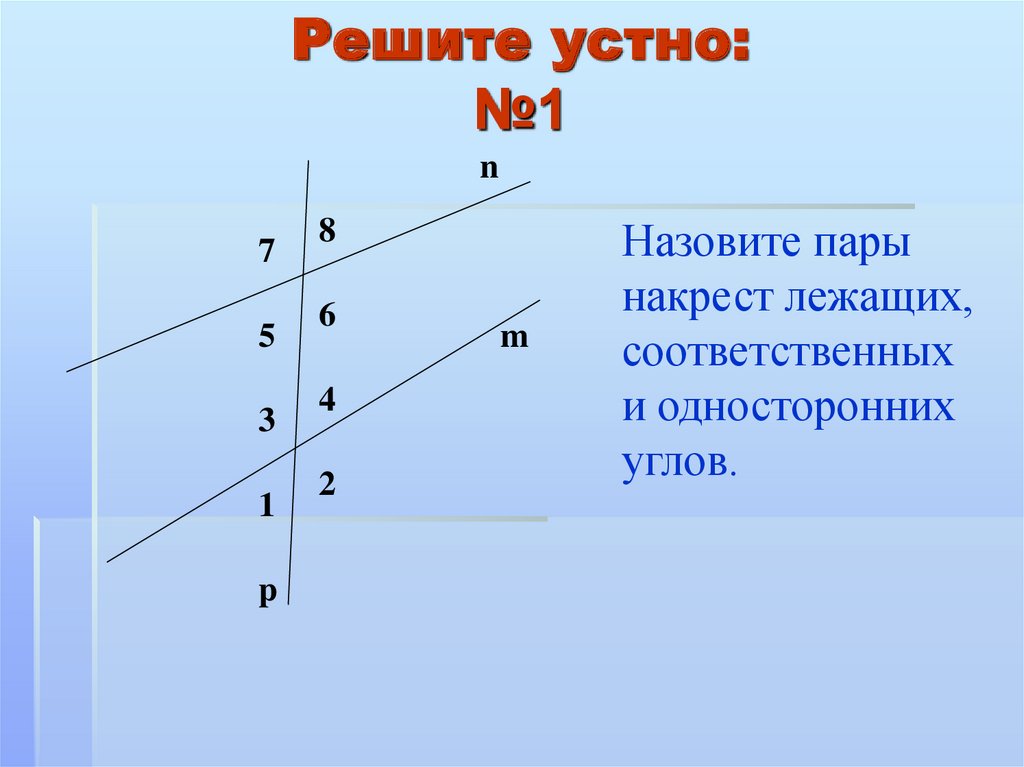
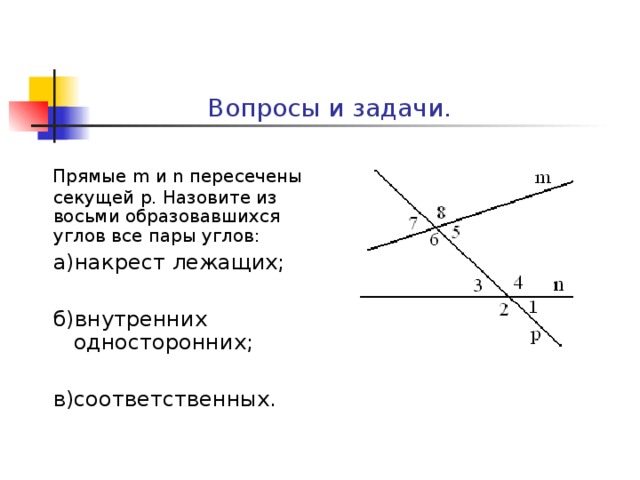
3. Признаки параллельности двух прямых: односторонние углы, накрест лежащие и соответственные:

Две прямые на плоскости называются параллельными , если они не пересекаются.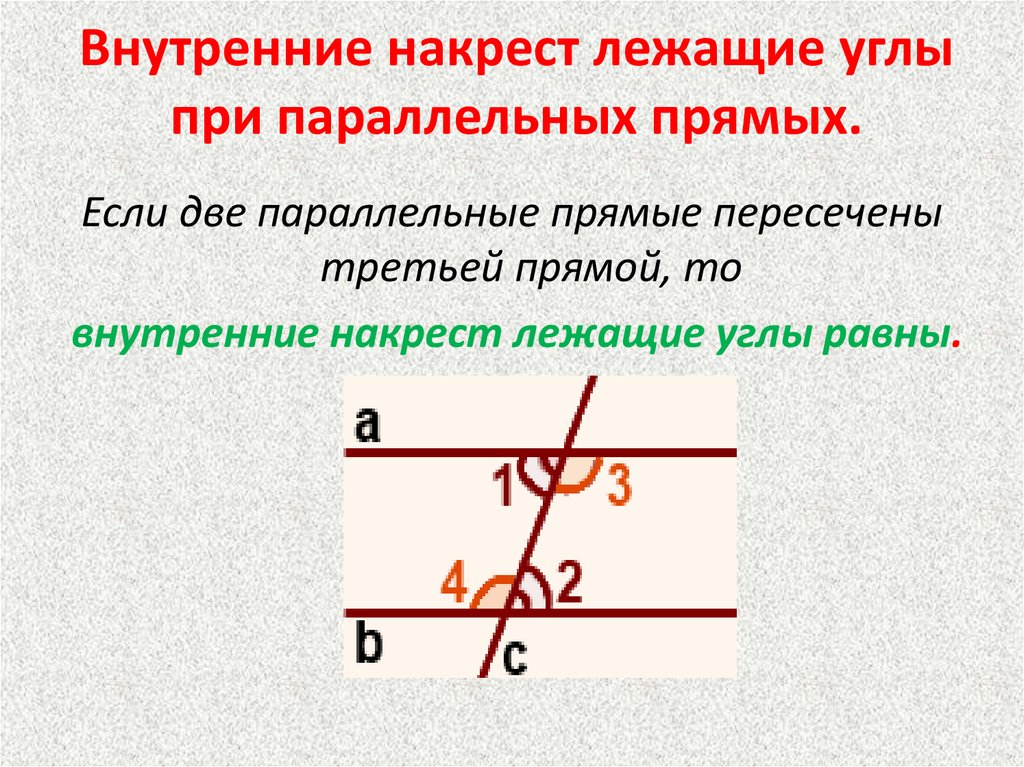

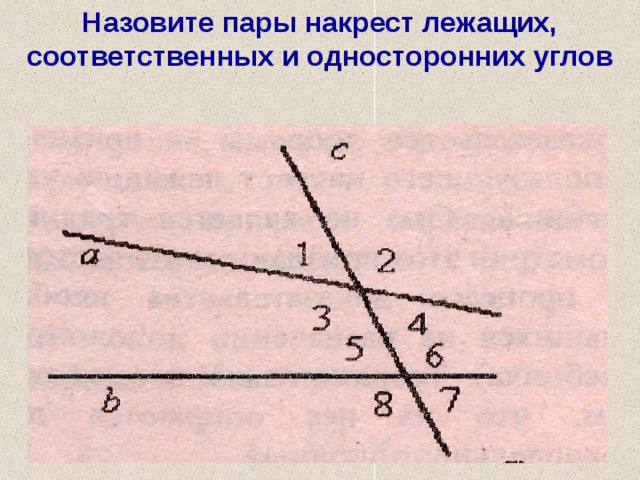
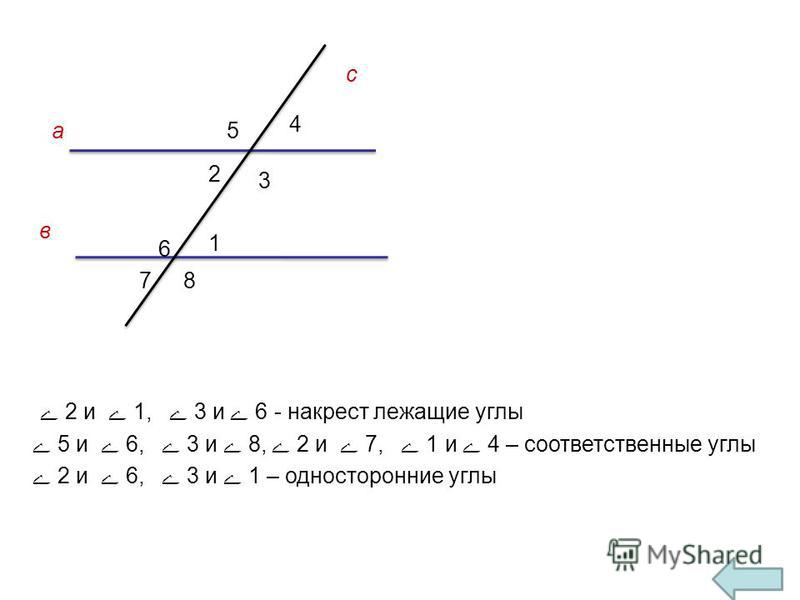
Накрест лежащие углы: 3 и 5, 4 и 6;

Односторонние углы: 4 и 5, 3 и 6; рис. Стр55

Соответственные углы: 1 и 5, 4 и 8, 2 и 6, 3 и 7;

Теорема : Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

Теорема : Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

Теорема : Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.

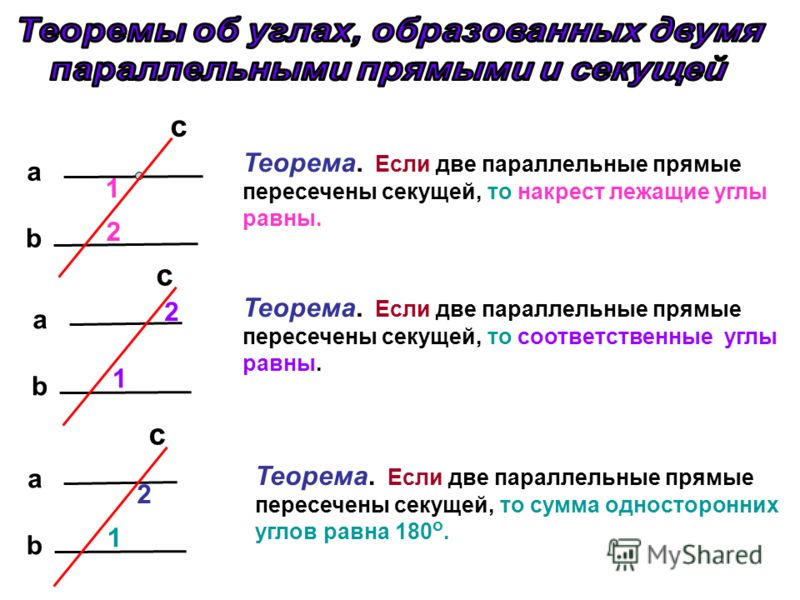
Теорема : если две параллельные прямые пересечены секущей, то накрест лежащие углы равны

Теорема : если две параллельные прямые пересечены секущей, то соответственные углы равны

Теорема : если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°

4. Сумма углов треугольника:

Сумма углов треугольника равна 180°

5. Свойства равнобедренного треугольника:

Теорема: В равнобедренном треугольнике углы при основании равны.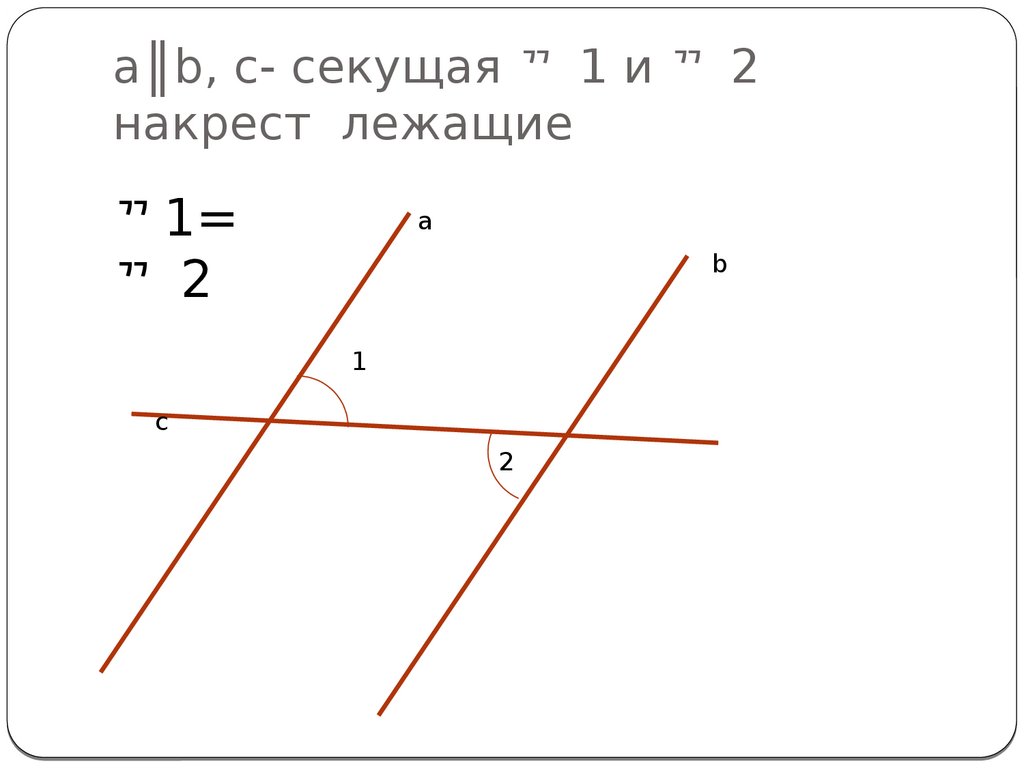

Теорема: В равнобедренном треугольнике биссектриса, проведенная к основанию, являетсямедианой и высотой (медиана наоборот), (биссектриса делит угол пополам, медиана делит сторону пополам, высота образует угол 90°)

Признак: Если два угла треугольника равны, то треугольник равнобедренный.

6. Прямоугольный треугольник:

Прямоугольный треугольник — это треугольник, в котором один угол прямой (то есть составляет 90 градусов)

В прямоугольном треугольнике гипотенуза больше катета

1. Сумма двух острых углов прямоугольного треугольника равна 90°

2. Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы

3. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°

7. Равносторонний треугольник:

РАВНОСТОРОННИЙ ТРЕУГОЛЬНИК, плоская фигура, имеющая три стороны равной длины; три внутренних угла, образуемых сторонами, также равны и составляют 60 °С.

Сумма углов четырёхугольника равна 2 π = 360°.

Четырёхугольник можно вписать в окружность тогда и только тогда, сумма противоположных углов равна 180°

10. Признаки подобия треугольников:

I признак : если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны

II признак : если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.

III признак : если три стороны одного треугольника порциональны трем сторонам другого, то такие треугольники подобны

11. Формулы:

· Теорема Пифагора: a 2 +b 2 =c 2

· Теорема sin:

· Теорема cos:

· 3 формулы площади треугольника:

· Площадь прямоугольного треугольника: S= S=

· Площадь равностороннего треугольника:

· Площадь параллелограмма: S = ah

· Площадь квадрата: S = a2

· Площадь трапеции:

· Площадь ромба:

· Площадь прямоугольника: S=ab

· Равносторонний треугольник. Высота: h=

· Тригонометрическая единица: sin 2 a+cos 2 a=1

· Средняя линия треугольника: S=

· Средняя линия трапеции : МК=

©2015-2019 сайт
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2017-12-12

Г Л А В А I.

ОСНОВНЫЕ ПОНЯТИЯ.

§11. СМЕЖНЫЕ И ВЕРТИКАЛЬНЫЕ УГЛЫ.

1. Смежные углы.

Если мы продолжим сторону какого-нибудь угла за его вершину, то получим два угла (черт. 72): / А ВС и / СВD, у которых одна сторона ВС общая, а две другие АВи ВD составляют прямую линию.

Два угла, у которых одна сторона общая, а две другие составляют прямую линию, называются смежными углами.

Смежные углы можно получить и таким образом: если из какой-нибудь точки прямой проведём луч (не лежащий на данной прямой), то получим смежные углы.
Например, / АDF и / FDВ — углы смежные (черт. 73).

Смежные углы могут иметь самые разнообразные положения (черт. 74).

Смежные углы в сумме составляют развёрнутый угол, поэтому сумма двух смежных углов равна 2d.

Отсюда прямой угол можно определить как угол, равный своему смежному углу.

Зная величину одного из смежных углов, мы можем найти величину другого смежного с ним угла.

Например, если один из смежных углов равен 3 / 5 d , то второй угол будет равен:

2d — 3 / 5 d = l 2 / 5 d .

2. Вертикальные углы.

Если мы продолжим стороны угла за его вершину, то получим вертикальные углы. На чертеже 75 углы EOF и АОС- вертикальные; углы АОЕ и СОF — также вертикальные.

Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого угла.

Пусть / 1 = 7 / 8 d (черт. 76). Смежный с ним / 2 будет равен 2d — 7 / 8 d , т. е. 1 1 / 8 d .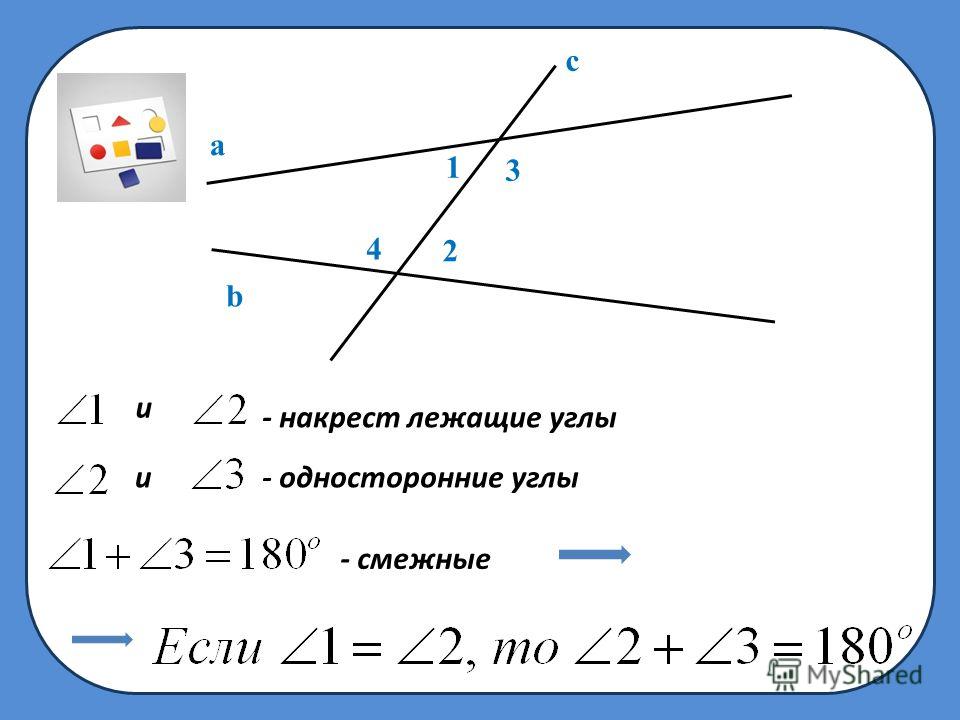

Таким же образом можно вычислить, чему равны / 3 и / 4.
/ 3 = 2d — 1 1 / 8 d = 7 / 8 d ; / 4 = 2d — 7 / 8 d = 1 1 / 8 d (черт. 77).

Мы видим, что / 1 = / 3 и / 2 = / 4.

Можно решить ещё несколько таких же задач, и каждый раз будет получаться один и тот же результат: вертикальные углы равны между собой.

Однако, чтобы убедиться в том, что вертикальные углы всегда равны между собой, недостаточно рассмотреть отдельные числовые примеры, так как выводы, сделанные на основе частных примеров, иногда могут быть и ошибочными.

Убедиться в справедливости свойства вертикальных углов необходимо путём рассуждения, путём доказательства.

Доказательство можно провести следующим образом (черт. 78):

/ a + / c = 2d ;
/ b + / c = 2d ;

(так как сумма смежных углов равна 2d ).

/ a + / c = / b + / c

(так как и левая часть этого равенства равна 2d , и правая его часть тоже равна 2d ).

В это равенство входит один и тот же угол с .

Если мы от равных величин отнимем поровну, то и останется поровну. В результате получится: / a = / b , т. е. вертикальные углы равны между собой.

При рассмотрении вопроса о вертикальных углах мы сначала объяснили, какие углы называются вертикальными, т. е. дали определение вертикальных углов.

Затем мы высказали суждение (утверждение) о равенстве вертикальных углов и в справедливости этого суждения убедились путём доказательства. Такие суждения, справедливость которых надо доказывать, называются теоремами . Таким образом, в данном параграфе мы дали определение вертикальных углов, а также высказали и доказали теорему об их свойстве.

В дальнейшем при изучении геометрии нам постоянно придётся встречаться с определениями и доказательствами теорем.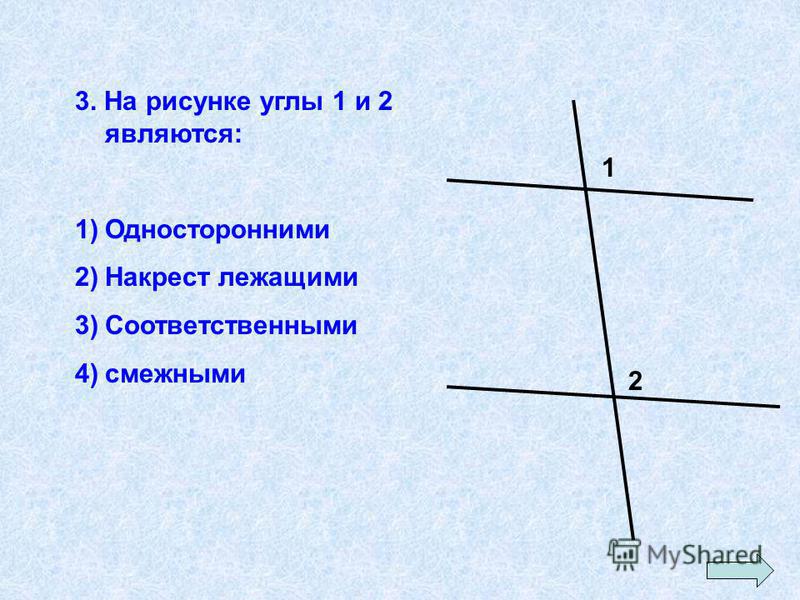

3. Сумма углов, имеющих общую вершину.

На чертеже 79 / 1, / 2, / 3 и / 4 расположены по одну сторону прямой и имеют общую вершину на этой прямой. В сумме эти углы составляют развёрнутый угол, т. е.
/ 1+ / 2+/ 3+ / 4 = 2d .

На чертеже 80 / 1, / 2, / 3, / 4 и / 5 имеют общую вершину. В сумме эти углы составляют полный угол, т. е. / 1 + / 2 + / 3 + / 4 + / 5 = 4d .

Упражнения.

1. Один из смежных углов равен 0,72 d. Вычислить угол, составленный биссектрисами этих смежных углов.

2. Доказать, что биссектрисы двух смежных углов образуют прямой угол.

3. Доказать, что если два угла равны, то равны и их смежные углы.

4. Сколько пар смежных углов на чертеже 81?

5. Может ли пара смежных углов состоять из двух острых углов? из двух тупых углов? из прямого и тупого угла? из прямого и острого угла?

6.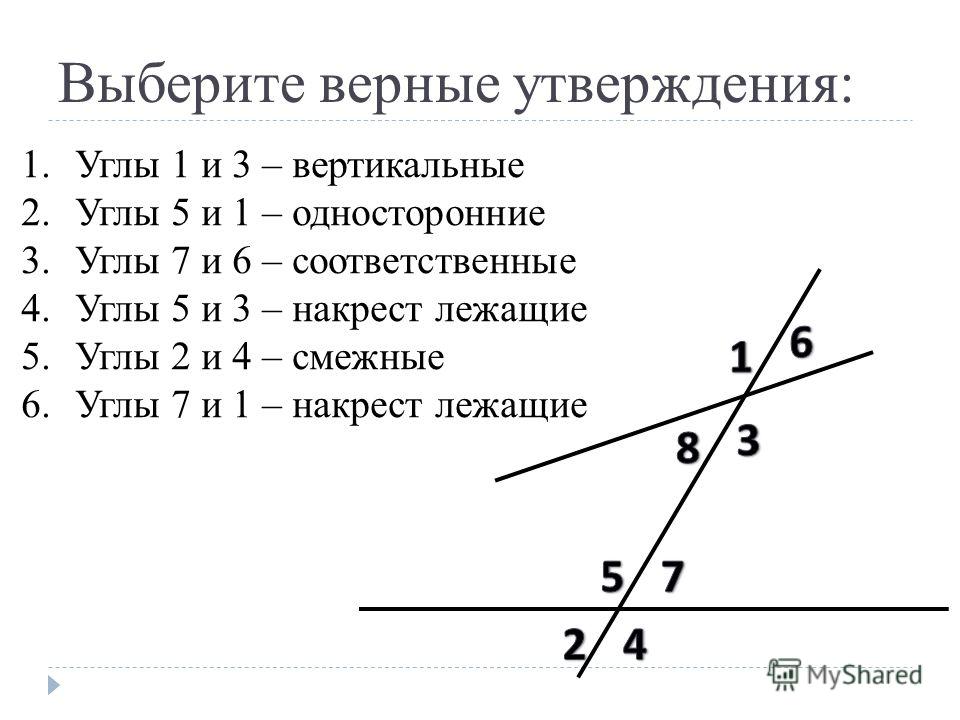 Если один из смежных углов прямой, то что можно сказать о величине смежного с ним угла?

7. Если при пересечении двух прямых линий один угол прямой, то что можно сказать о величине остальных трёх углов?

СМЕЖНЫЕ И ВЕРТИКАЛЬНЫЕ УГЛЫ — Без Сменки

30 июня, 2022

1 мин

Мтмт 📈

Геометрия начинается не с точек или прямых, а с углов. Когда две прямые пересекаются в одной точке появляются углы. И они обладают определёнными названиями и свойствами.

🔸 Углы лежащие по одну сторону от какой-то прямой называются смежными и равны в сумме 180 градусам. А углы, которые лежат друг напротив друга называются вертикальными и равны друг другу.

🔹 Если у нас внезапно есть две параллельные прямые, и мы каким-то магическим образом пересекаем их третьей, то получаются знаменитые углы при параллельных прямых. В школе было важно не запутаться в их названиях, а в ЕГЭ важно вспомнить какие из них равны, а какие в сумме дают 180 градусов. Есть один простой способ запомнить это раз и навсег… ну как получится, попытка не пытка.

❗️ Посмотрите на углы сверху и снизу, это ведь 2 случая углов при пересечении прямых. Вот у нас повыше был один случай, а тут целых два. То есть с половиной углов мы уже разобрались, теперь решаем, как они связаны между собой. Попробуем наложить верхний угол на нижний и, о чудо, смотрите они сошлись идеально. Углы которое совместились и равны между собой. Вот и все. 😌

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!

Редакция Без Сменки

Честно. Понятно. С душой.

44 подписчиков

+ Подписаться

Редакция Без Сменки

01 июля, 2022

1 мин

Хим 🧪

Химические свойства фенола

Фенол обладает слабыми кислотными свойствами! 1️⃣ Взаимодействие с щелочными металлами 2С₆H₅OH. ..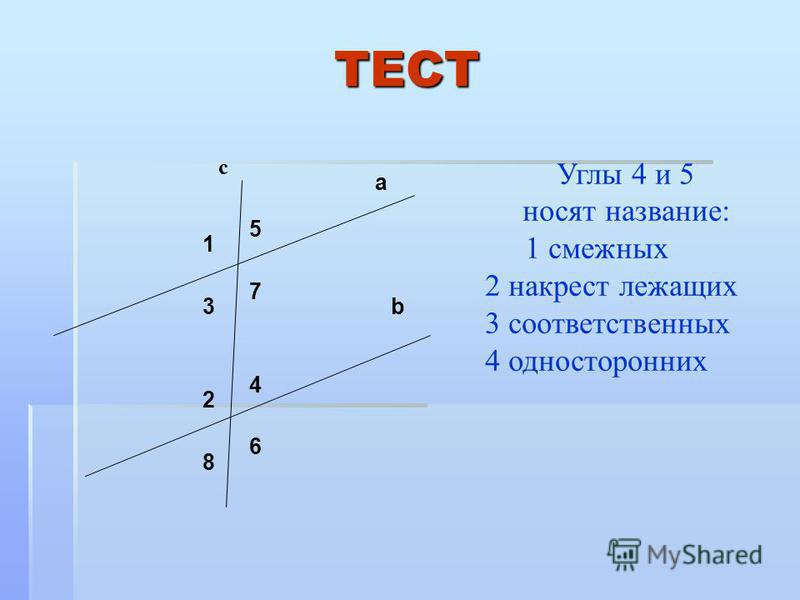

Редакция Без Сменки

30 июня, 2022

1 мин

Мтмт 📈

Виды углов

Каждый угол, в зависимости от его величины, имеет своё название: 🔺Острый — Меньше 90°. 🔺Прямой…

Редакция Без Сменки

29 июня, 2022

1 мин

Физ 🔬

Средняя квадратичная скорость

👀 Принято считать, что все молекулы идеального газа двигаются с одинаковой скоростью, которую…

Редакция Без Сменки

28 мая, 2022

1 мин

Общ 👨‍👩‍👧

Федеративное устройство РФ

В области государственно-территориального устройства Россия является федерацией и состоит из 85. ..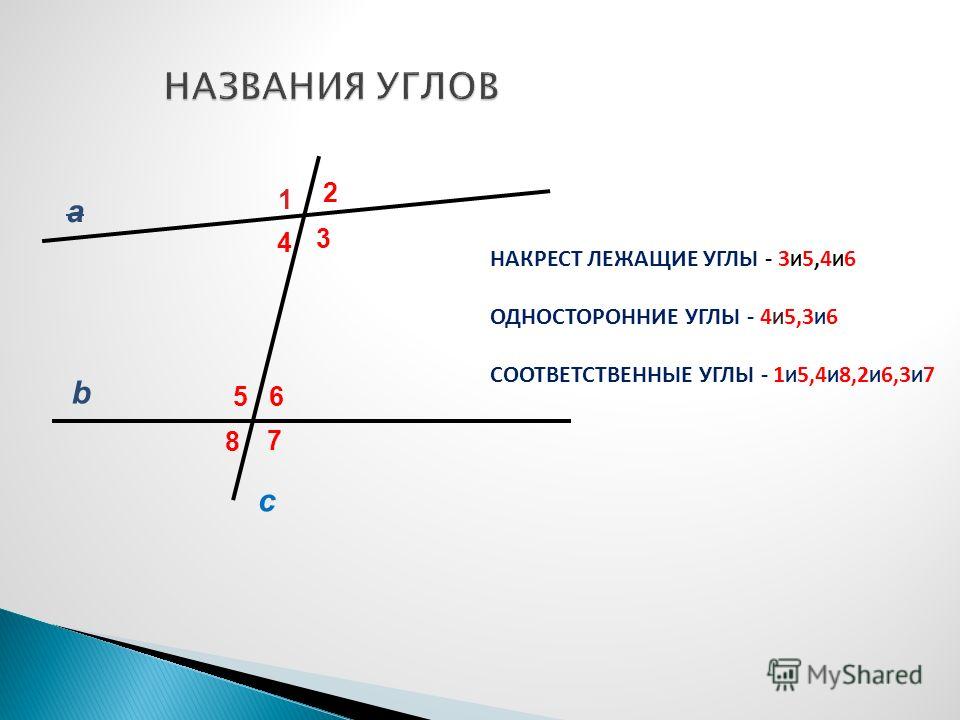

---

Альтернативные внутренние углы — ChiliMath

Пара несмежных углов, которые лежат между двумя прямыми, но находятся на противоположных сторонах поперечной, называются альтернативными внутренними углами .

Чередующиеся внутренние углы образуются при пересечении секущей двух параллельных или непараллельных прямых. Один из способов помочь вам идентифицировать эту пару углов — внимательно посмотреть на слова «альтернативный» и «внутренний».

Альтернативный говорит вам, что углы лежат на противоположные стороны поперечной. Внутренняя , с другой стороны, означает, что углы лежат на внутренней стороне двух линий.

На приведенной выше диаграмме угол 3 и угол 6 расположены с внутренней стороны или между линиями k и m. Они также находятся на противоположных сторонах трансверсали и не примыкают друг к другу. Следовательно, \угол 3 и \угол 6 являются парой альтернативных внутренних углов. Другая пара — \угол 5 и \угол 4.

СОВЕТ: Вы можете легко определить пару чередующихся внутренних углов, потому что они образуют Z-образную форму или обратную Z-образную форму, как вы можете видеть на рисунках ниже.

---

Альтернативные внутренние углы Теорема

Если две параллельные прямые пересечены секущей, то пары альтернативных внутренних углов равны .

Здесь у нас есть поперечная t, пересекающая прямые c и w. Так как противоположные внутренние углы равны, оба угла имеют одинаковую меру.

Однако, если секущая пересекает две непараллельные прямые, образующиеся пары чередующихся внутренних углов не равны и не имеют никакого отношения друг к другу.

---

Примеры задач с альтернативными внутренними углами

Пример 1 : Перечислите все пары альтернативных внутренних углов.

Сразу видно, что углы \angle 1, \angle 8, \angle 5 и \angle 4 расположены на внутренней стороне наших двух линий, линий h и s.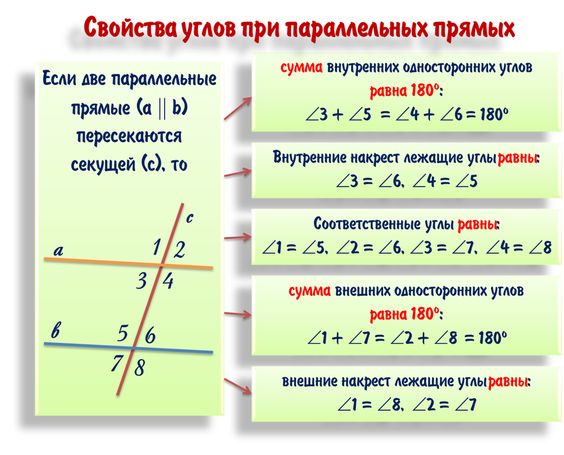 Это наши внутренние углы.

Но так как нас просят определить пары чередующихся внутренних углов, давайте рассмотрим пары внутренних углов, несмежных и находящихся по разные стороны от трансверсали, т.е. Итак, мы имеем

• \угол 1 и \угол 4
• \угол 8 и \угол 5

---

Пример 2: Заполните пропуски, чтобы сделать следующие утверждения верными.

• При пересечении секущей двух ___________ прямых образующиеся параллельные внутренние углы равны. 9\circ , какова мера угла 3?

  Когда вас просят определить угловые меры, полезно сначала определить особое отношение заданных углов. В этом примере нам предоставляют измерение угла 6, а затем спрашивают, каково измерение угла 3. Оба угла лежат между прямыми n и e, что сразу делает их внутренними углами. Тогда мы видим, что они расположены по разные стороны от трансверсали. Следовательно, \угол 6 и \угол 3 являются альтернативными внутренними углами. 9\ циркуляр .

  ---

  Вас также могут заинтересовать:

  Альтернативные внешние углы

  Дополнительные углы

  Соответствующие углы

  Дополнительные вертикальные углы

  2

  Что такое горизонтальная линия? Определение, уравнение, примеры, факты

  Что такое горизонталь?

  Что ты видишь?

  В наличии стояк линейка , стоячая отвертка и вертикальный термометр.

  Что ты сейчас видишь?

  На полу лежит спальная веревка, отвертка и термометр лежат на полу.

  То, что вы видите, описывается как ГОРИЗОНТАЛЬНОЕ положение или объекты, расположенные горизонтально.

  Спящая линия — это не что иное, как горизонтальная линия.

  A отвертка горизонтальное положение аналогично лестнице, лежащей горизонтально.

  A термометр лежать на полу — то же самое, что человек, лежащий горизонтально на полу.

  Горизонтальность противоположна вертикали. В геометрии мы используем слова «вертикальный» и «горизонтальный» для обозначения стояния и сна соответственно.

  Линия, на которой кажется, что земная поверхность встречается с небом, называется горизонтом. Все, что параллельно горизонту, называется горизонтальным.

  Поскольку вертикаль противоположна горизонтали, все, что образует угол 90 градусов (прямой угол) с горизонталью или горизонтом, называется вертикальным.

  Итак, горизонтальная линия проходит слева направо.

  Использование горизонтали и вертикали в математике

  • Складываем и вычитаем по горизонтали и вертикали.

  Пример 1:

  Добавьте 24 и 33 по горизонтали и вертикали.

  Горизонтальный	Вертикальный
  $ 24 + 33 = 57 $	$ = 53 = 57 $	$ = 53 = 57 $	$ = 53 = 57 $	$ 243 33 = 53 = 57 $	. и вертикальные гистограммы. Горизонтальная гистограмма Пример 3: Вертикальная гистограмма Пример 4: Мы используем горизонтальные и вертикальные линии в геометрии и искусстве. Что такое горизонтальная линия? Представьте, что у вас есть лист бумаги, и кто-то просит вас нарисовать линию. Как вы думаете, какие все возможности придут вам в голову? Хорошо; есть несколько способов сделать это. Если вам было скучно; вы, скорее всего, просто нарисуете такое случайное движение; называется наклонной линией . А если бы вы хотели думать как математик или художник; вы бы представили дерево или что-то стоящее и нарисовали бы линию сверху вниз вот так; называется вертикальной линией . Или вы можете представить автомобиль или что-то лежащее и начертить свою линию от слева направо вот так; называется горизонтальной линией . Горизонтальная линия — это спящая линия. Это прямая линия, идущая слева направо или справа налево. Слово «горизонтальный» происходит от слова «горизонт», которое представляет собой линию, где земля и небо встречаются далеко-далеко. Родственные рабочие листы Горизонтальные линии вокруг нас Мы видим горизонтальные линии повсюду вокруг нас в фигурах, предметах, фигурах и рисунках. Вот несколько примеров горизонтальных линий. Горизонтальные линии в объектах: Горизонтальные линии в математике: Горизонтальные линии являются строительными блоками очень многих 2D и 3D форм в элементарной геометрии. Квадраты, треугольники, прямоугольники, кубы, трапеции, призмы — это лишь некоторые основные примеры форм, в которых мы можем наблюдать горизонтальные линии. Горизонтальные линии в координатной плоскости В координатной геометрии горизонтальные линии определяются как линии, параллельные оси x . Если две точки на прямой имеют одинаковые координаты по оси Y и точек, то говорят, что линия горизонтальна. На данном изображении AB представляет собой горизонтальную линию, параллельную оси x , и если вы внимательно наблюдаете, координата y обеих точек A и B совпадают. Еще одно интересное замечание относительно горизонтальных линий заключается в том, что они всегда перпендикулярны вертикальным линиям. Рисование горизонтальной линии Использование линейки: Чтобы провести горизонтальную линию с помощью линейки, держите линейку в нерабочем положении параллельно краю страницы и проводите линию слева направо или справа налево. левый. Чтобы нарисовать горизонтальную линию на координатной плоскости Выполните следующие действия. Нанесите любую точку на координатную плоскость, например (1, 2). Определите координату Y отмеченной точки. Здесь 2, Нанесите на координатную плоскость еще одну точку, чтобы ее координата y совпадала с координатой предыдущей точки. Например, (–5, 2). Соедините две точки, нанесенные линейкой, чтобы получить горизонтальную линию. Использование горизонтальных линий Горизонтальные линии используются в симметрии и фотографии. Горизонтальная линия симметрии проходит через изображение слева направо (или наоборот) и делит изображение на одинаковые половины. Фотокамеры предназначены для фотосъемки в альбомном (горизонтальном) или портретном (вертикальном) режиме. В горизонтальном режиме фотографии шире, чем в высоту. В вертикальном режиме фотографии в высоту больше, чем в ширину. Наши глаза видят окружающее горизонтально, давая более широкий обзор, а не выше. Горизонтальная линия и вертикальная линия Горизонтальная линия Вертикальная линия Это спящая линия, которая идет слева направо или наоборот. Это прямая линия, идущая сверху вниз или наоборот. Он параллелен оси x. Он параллелен оси Y. Перпендикулярно оси Y. Перпендикулярно оси x. Забавные факты Слово «горизонтальный» произошло в середине 16 века от современного латинского «горизонтальный», от позднего латинского горизонта. Решенные примеры  Пример 1. Какие отрезки представляют собой горизонтальные линии? Решение: Прямые BC и AD горизонтальные. Пример 2: Определите линии, указанные стрелками в каждой из следующих фигур. Решение: Горизонтальная линия Вертикальная линия Горизонтальная линия Вертикальная линия Пример 3: Определите горизонтальные линии в заданной форме. Решение: AB, EF и CD — горизонтальные линии данных фигур. Пример 4: Назовите пять букв английского алфавита, в которых есть горизонтальные линии. Решение: E, F, H, L, T Практические задачи 1 Что из следующего является горизонтальной линией? a b c d Правильный ответ: a Горизонтальная линия — это спящая линия. 2 Сколько горизонтальных линий имеет данная фигура? 1 2 3 4 Правильный ответ: 3 Есть 3 прямые линии, которые идут слева направо или справа налево 3 В какое время минутная стрелка часов станет горизонтальной? 12 часов Четверть 12-го Половина 12-го 12:40 Правильный ответ: Четверть 12-го быть горизонтальным. Часто задаваемые вопросы Что такое горизонтальная линия в координатной геометрии? Горизонтальная линия – это прямая линия, параллельная ось x и где все точки на линии имеют одну и ту же y- координату . Все ли горизонтальные линии в двумерных фигурах параллельны? Да, все горизонтальные линии параллельны друг другу. Горизонтальные линии при продолжении также никогда не пересекаются друг с другом. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт