Вертикальные и смежные углы
Углы, у которых одна сторона общая, а другие стороны лежат на одной прямой (на рис. углы 1 и 2 смежные). Рис. к ст. Смежные углы … Большая советская энциклопедия
СМЕЖНЫЕ УГЛЫ — углы, имеющие общую вершину и одну общую сторону, а две др. их стороны лежат на одной прямой … Большая политехническая энциклопедия
См. Угол … Большой Энциклопедический словарь
СМЕЖНЫЕ УГЛЫ, два угла, сумма которых равна 180°. Каждый из этих углов дополняет другой до развернутого угла … Научно-технический энциклопедический словарь
См. Угол. * * * СМЕЖНЫЕ УГЛЫ СМЕЖНЫЕ УГЛЫ, см. Угол (см. УГОЛ) … Энциклопедический словарь
— (Angles adjacents) такие, которые имеют общую вершину и общую сторону. Преимущественно под этим именем подразумеваются такие С. углы, которых остальные две стороны лежат по противоположным направлениям одной прямой, проведенной через вершину … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
См. Угол … Естествознание.
Две прямые пересекаются, создавая пару вертикальных углов. Одна пара состоит из углов A и B, другая из C и D. В геометрии, два угла называются вертикальными, если они созданы пересечением двух … Википедия
Пара комплементарных углов, дополняющих друг друга до 90 градусов Комплементарные углы это пара углов, которые дополняют друг друга до 90 градусов. Если два комплементарных угла являются соседними (т.е. имеют общую вершину и разделяются только… … Википедия
Пара дополнительных углов, дополняющих друг друга до 90 градусов Дополнительные углы это пара углов, которые дополняют друг друга до 90 градусов. Если два дополнительных угла являются с … Википедия
Книги
- О доказательстве в геометрии , Фетисов А.И.. Эта книга будет изготовлена в соответствии с Вашим заказом по технологии Print-on-Demand. Однажды, в самом начале учебного года, мне пришлось услышать разговор двух девочек. Старшая из них…
- Комплексная тетрадь для контроля знаний.
 Геометрия. 7 класс. ФГОС , Бабенко Светлана Павловна, Маркова Ирина Сергеевна. В пособии представлены контрольно-измерительные материалы (КИМы) по геометрии для проведения текущего, тематического и итогового контроля качества знаний учащихся 7 класса. Содержание пособия…
Геометрия. 7 класс. ФГОС , Бабенко Светлана Павловна, Маркова Ирина Сергеевна. В пособии представлены контрольно-измерительные материалы (КИМы) по геометрии для проведения текущего, тематического и итогового контроля качества знаний учащихся 7 класса. Содержание пособия…
угол до развернутого, то есть равного 180°, поэтому для их нахождения вычтите из этого известную величину основного угла α₁ = α₂ = 180°-α.
Из этого имеются . Если два угла одновременно являются и смежными, и равными, то они прямые. Если один из смежных углов является прямым, то есть составляет 90 градусов, то другой угол тоже прямой. Если один из смежных углов острый, то другой будет тупым. Аналогично, если один из углов тупой, то второй, соответственно, будет острым.
Острый угол – это такой, градусная мера которого меньше 90 градусов, но больше 0. Тупой угол имеет градусную меру больше 90 градусов, но меньше 180.
Другое свойство смежных углов формулируется так: если два угла равны, то углы, смежные с ними, также равны. Это , что если есть два угла, градусная мера для которых совпадает (например, она составляет 50 градусов) и при этом из них имеет смежный угол, то значения этих смежных углов тоже совпадают (в примере их градусная мера будет равна 130 градусам).
Это , что если есть два угла, градусная мера для которых совпадает (например, она составляет 50 градусов) и при этом из них имеет смежный угол, то значения этих смежных углов тоже совпадают (в примере их градусная мера будет равна 130 градусам).
Источники:
- Большой Энциклопедический Словарь — Смежные углы
- угол 180 градусов
Слово « » имеет различные толкования. В геометрии угол – это часть плоскости, ограниченная двумя лучами, выходящими из одной точки – вершины. Когда речь идет о прямых, острых, развернутых углах, то подразумеваются именно геометрические углы.
Как и любые фигуры в геометрии, углы можно сравнивать. Равенство углов определяется с помощью движения. Угол нетрудно разделить на две равные части. Разделить на три части немного сложнее, но все же это можно сделать с помощью линейки и циркуля. Кстати, эта задача казалась довольно трудной. Описать, что один угол больше или меньше другого, геометрически несложно.
В качестве единицы измерения углов принят – 1/180
Что такое смежный угол
Угол – это геометрическая фигура (рис. 1), образованная двумя лучами OA и OB (стороны угла), исходящими из одной точки O (вершина угла).
1), образованная двумя лучами OA и OB (стороны угла), исходящими из одной точки O (вершина угла).
СМЕЖНЫЕ УГЛЫ — два угла, сумма которых равна 180°. Каждый из этих углов дополняет другой до развернутого угла.
Смежные углы — (Agles adjacets) такие, которые имеют общую вершину и общую сторону. Преимущественно под этим именем подразумеваются такие углы, которых остальные две стороны лежат по противоположным направлениям одной прямой, проведенной через.
Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.
рис. 2
На рисунке 2 углы a1b и a2b смежные. У них общая сторона b, а стороны a1, a2 — дополнительные полупрямые.
рис. 3
На рисунке 3 изображена прямая AB, точка C расположена между точками A и B. Точка D — точка не лежащая на прямой AB. Получается, что углы BCD и ACD смежные. У них общая сторона CD, а стороны CA и CB дополнительные полупрямые прямой AB, так как точки A, B разделены начальной точкой C.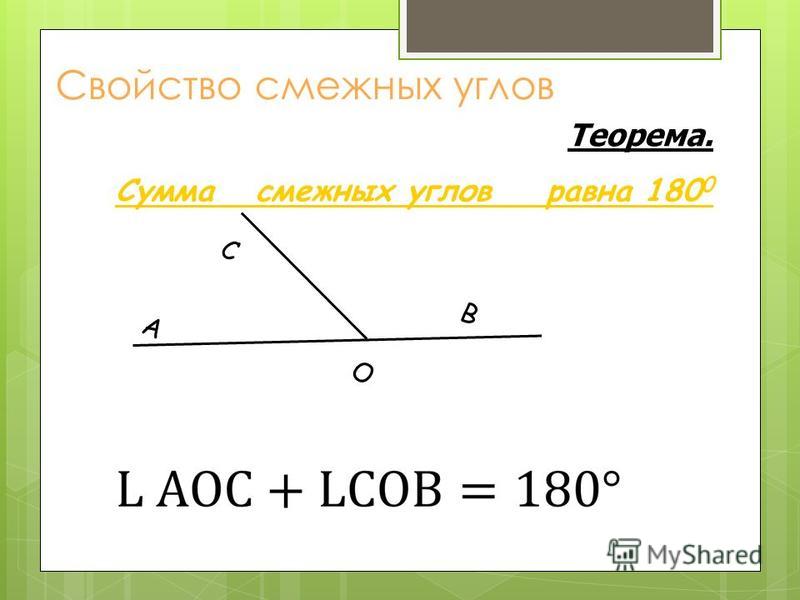
Теорема о смежных углах
Теорема: сумма смежных углов равна 180°
Доказательство:
Углы a1b и a2b смежные (см. рис. 2) Луч b проходит между сторонами a1, и a2 развернутого угла. Следовательно, сумма углов a1b и a2b равна развернутому углу, то есть 180°. Теорема доказана.
Угол, равный 90° называется прямым. Из теоремы о сумме смежных углов следует, что угол, смежный с прямым углом также прямой угол. Угол, меньший 90° называется острым, а угол больше 90° — тупым. Так как сумма смежных углов равна 180°, значит угол, смежный с острым углом — тупой угол. А угол смежный с тупым углом — острый угол.
Смежные углы — два угла с общей вершиной, одна из сторон которых — общая, а оставшиеся стороны лежат на одной прямой (не совпадая). Сумма смежных углов равна 180°.
Определение 1. Углом называется часть плоскости, ограниченная двумя лучами с общим началом.
Определение 1.1. Углом называют фигуру, состоящую из точки — вершины угла — и двух различных полупрямых, исходящих из этой точки, — сторон угла.
Например, угол ВОС на рис1 Рассмотрим сначала две пересекающиеся прямые. При пересечении прямые образуют углы. Есть частные случаи:
Определение 2. Если стороны угла являются дополнительными полупрямыми одной прямой, то угол называется развернутым.
Определение 3. Прямой угол — это угол величиной в 90 градусов.
Определение 4. Угол, меньший 90 градусов, называется острым углом.
Определение 5. Угол, больший 90 градусов и меньший 180 градусов, называется тупым углом.
пересекающиеся прямые.
Определение 6. Два угла, одна сторона которых общая, а другие стороны лежат на одной прямой, называются смежными.
Определение 7. Углы, стороны которых продолжают друг друга, называются вертикальными углами.
На рисунке 1:
смежные: 1 и 2; 2 и 3; 3 и 4; 4 и 1
вертикальные: 1 и 3; 2 и 4
Теорема 1. Сумма смежных углов равна 180 градусов.
Для доказательства рассмотрим на рис. 4 смежные углы АОВ и ВОС.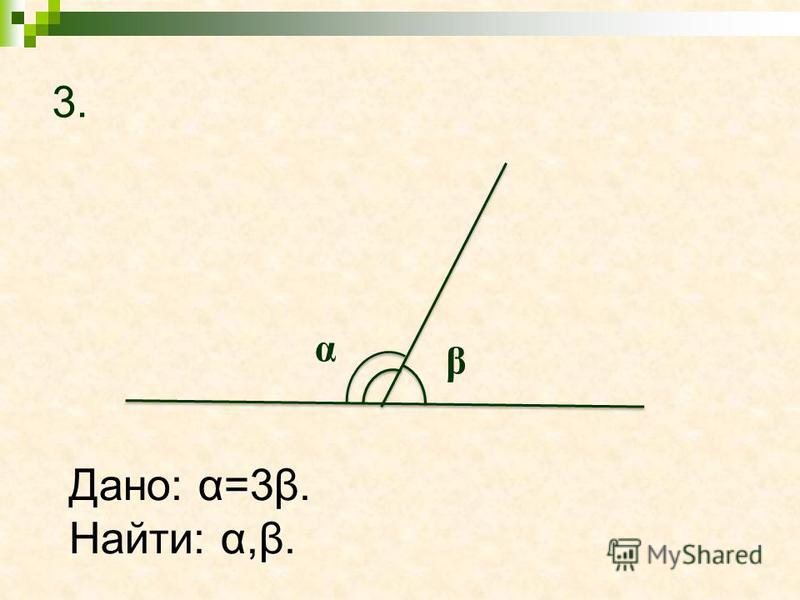
рис. 4
Связь математики с музыкой
«Раздумывая об искусстве и науке, об их взаимных связях и противоречиях, я пришел к выводу, что математика и музыка находятся на крайних полюсах человеческого духа, что этими двумя антиподами ограничивается и определяется вся творческая духовная деятельность человека и, что между ними размещается все, что человечество создало в области науки и искусства.»
Г. Нейгауз
Казалось бы, искусство — весьма отвлеченная от математики область. Однако связь математики и музыки обусловлена как исторически, так и внутренне, несмотря на то, что математика — самая абстрактная из наук, а музыка — наиболее отвлеченный вид искусства.
Консонанс определяет приятное для слуха звучание струны
В основе этой музыкальной системы были два закона, которые носят имена двух великих ученых — Пифагора и Архита. Вот эти законы:
 е. как 1:2, 2:3, 3:4. Причем, чем меньше число n в отношении n:(n+1) (n=1,2,3), тем созвучнее получающийся интервал.
е. как 1:2, 2:3, 3:4. Причем, чем меньше число n в отношении n:(n+1) (n=1,2,3), тем созвучнее получающийся интервал.2. Частота колебания w звучащей струны обратно пропорциональна ее длине l .
w = a: l ,
где а — коэффициент, характеризующий физические свойства струны.
Так же предложу вашему внимаю забавную пародию про спор двух математиков =)
Геометрия вокруг нас
Геометрия в нашей жизни имеет немаловажное значение. Ввиду того, что когда оглядеться вокруг, то не сложно будет заметить, что нас окружают различные геометрические фигуры. Мы с ними сталкиваемся повсюду: на улице, в классе, дома, в парке, в спортивном зале, в школьной столовой, в принципе везде, где бы мы с вами не находились.
Но темой сегодняшнего урока являются смежные угли. Поэтому давайте оглянемся вокруг и попытаемся в этом окружении найти углы. Если вы внимательно посмотрите в окно, то можете увидеть, что некоторые ветки дерева образуют смежные углы, а в перегородках на воротах можно заметить множество вертикальных углов.
Задание 1.
1. Вот на столе на книжной подставке стоит книга. Какой угол она образует?
2. А вот ученик работает за ноутбуком. Какой угол вы видите здесь?
3. Какой угол образует фото рамка на подставке?
4. Как вы думаете, возможно ли, чтобы два смежных угла были равными?
Задание 2.
Перед вами изображена геометрическая фигура. Что это за фигура, назовите ее? А теперь назовите все смежные углы, которые вы можете увидеть на этой геометрической фигуре.
Задание 3.
Перед вами изображение рисунка и картины. Рассмотрите их внимательно и скажите, какие виды улов вы видите на картине, а какие углы на рисунке.
Решение задач
1) Даны два угла, относящиеся друг к другу как 1: 2, а смежные с ними — как 7: 5. Нужно найти эти углы.
2) Известно, что один из смежных углов больше другого в 4 раза. Чему равны смежные углы?
Чему равны смежные углы?
3) Необходимо найти смежные углы, при условии, что один из них на 10 градусов больше от второго.
Математический диктант на повторение ранее выученного материала
1) Выполните рисунок: прямые a I b пересекаются в точке А. Отметьте меньший из образованных углов цифрой 1, а остальные углы – последовательно цифрами 2,3,4; дополняющие лучи прямой а — через а1 и а2, а прямой b — через b1 i b2.
2) Пользуясь выполненным рисунком, впишите нужные значения и объяснения в места пропусков в тексте:
а) угол 1 и угол …. смежные, поскольку…
б) угол 1 и угол …. вертикальные, поскольку…
в) если угол 1 = 60°, то угол 2 = …, потому что…
г) если угол 1 = 60°, то угол 3 = …, потому что…
Решите задачи:
1. Может ли сумма 3-х углов, образованных при пересечении 2-х прямых, равняться 100°? 370°?
2. На рисунке найдите все пары смежных углов. А теперь вертикальных углов. Назовите эти углы.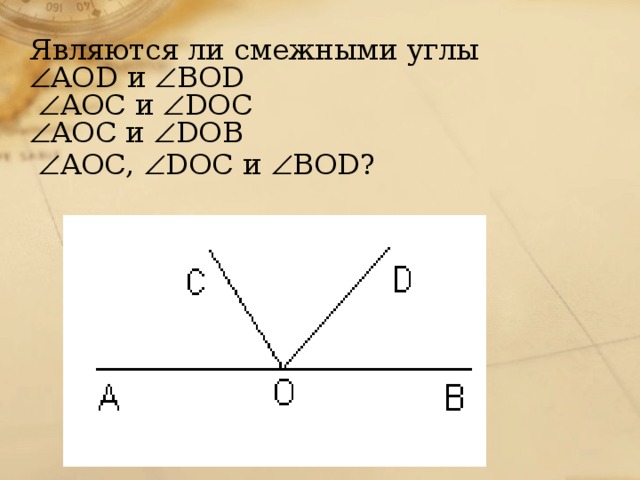
3. Нужно найти угол, когда он втрое больше, чем смежный с ним.
4. Две прямые пересеклись между собой. В результате этого пересечения образовались четыре угла. Определите величину любого из них, при условии что:
а) сумма 2-х углов из четырех 84°;
б) разность 2-х углов из них равна 45°;
в) один угол в 4 раза меньше чем второй;
г) сумма трех из данных углов равна 290°.
Итог урока
1. назовите углы, которые образуются при пересечении 2-х прямых?
2. Назовите все возможные пары углов, находящихся на рисунке, и определите их вид.
Домашнее задание:
1. Найдите отношение градусных мер смежных углов, когда один из них на 54° больше второго.
2. Найдите углы, которые образуются при пересечении 2-х прямых, при условии, что один из углов равняется сумме 2-х других углов, смежных с ним.
3. Необходимо найти смежные углы, когда биссектриса одного из них образует со стороной второго угол, который больше чем второй угол на 60°.
4. Разница 2-х смежных углов равна трети от суммы этих двух углов. Определите величины 2-х смежных углов.
5. Разница и сумма 2-х смежных углов относятся как 1: 5 соответственно. Найдите смежные углы.
6. Разница двух смежных составляет 25% от их суммы. Как относятся величины 2-х смежных углов? Определите величины 2-х смежных углов.
Вопросы:
- Что такое угол?
- Какие бывают типы углов?
- Какая особенность смежных углов?
Предмети > Математика > Математика 7 класс
Вопрос 1. Какие углы называются смежными?
Ответ. Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.
На рисунке 31 углы (a 1 b) и (a 2 b) смежные. У них сторона b общая, а стороны a 1 и a 2 являются дополнительными полупрямыми.
Вопрос 2. Докажите, что сумма смежных углов равна 180°.
Ответ. Теорема 2.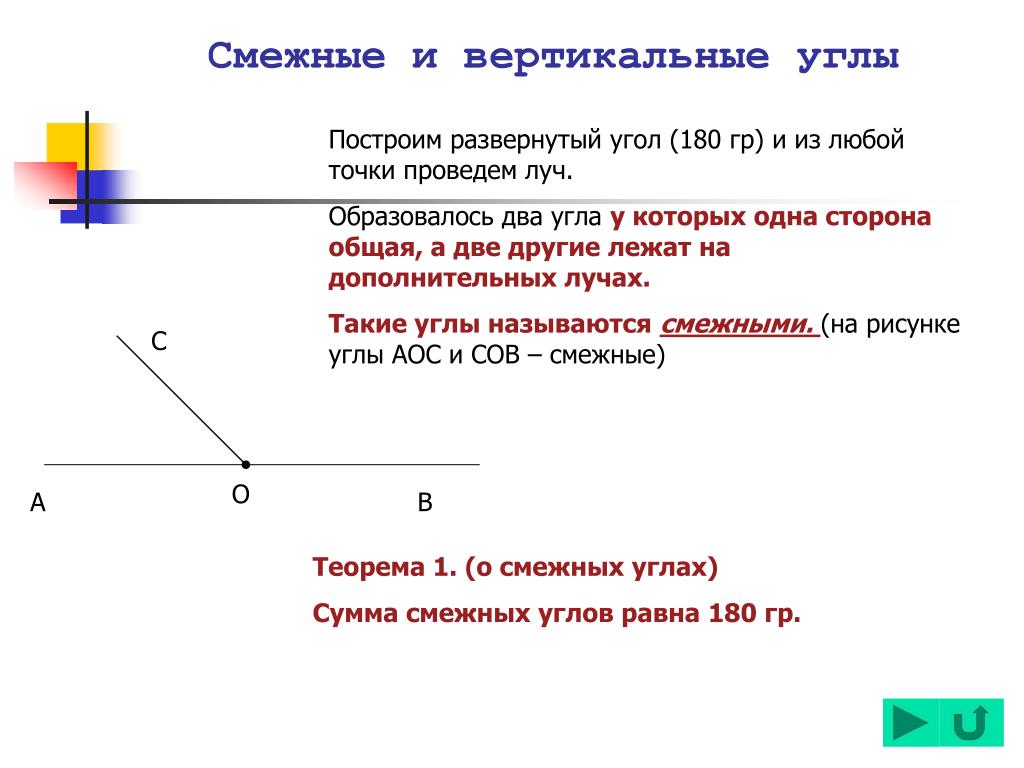 1. Сумма смежных углов равна 180°.
1. Сумма смежных углов равна 180°.
Доказательство. Пусть угол (a 1 b) и угол (a 2 b) — данные смежные углы (см. рис.31). Луч b проходит между сторонами a 1 и a 2 развёрнутого угла. Поэтому сумма углов (a 1 b) и (a 2 b) равна развёрнутому углу, т. е. 180°. Что и требовалось доказать.
Вопрос 3. Докажите, что если два угла равны, то смежные с ними углы также равны.
Ответ.
Из теоремы 2.1 следует, что если два угла равны, то смежные с ними углы равны.
Допустим, углы (a 1 b) и (c 1 d) равны. Нам нужно доказать, что углы (a 2 b) и (c 2 d) тоже равны.
Сумма смежных углов равна 180°. Из этого следует, что a 1 b + a 2 b = 180° и c 1 d + c 2 d = 180°. Отсюда, a 2 b = 180° — a 1 b и c 2 d = 180° — c 1 d. Так как углы (a 1 b) и (c 1 d) равны, то мы получаем, что a 2 b = 180° — a 1 b = c 2 d. По свойству транзитивности знака равенства следует, что a 2 b = c 2 d. Что и требовалось доказать.
Вопрос 4. Какой угол называется прямым (острым, тупым)?
Ответ.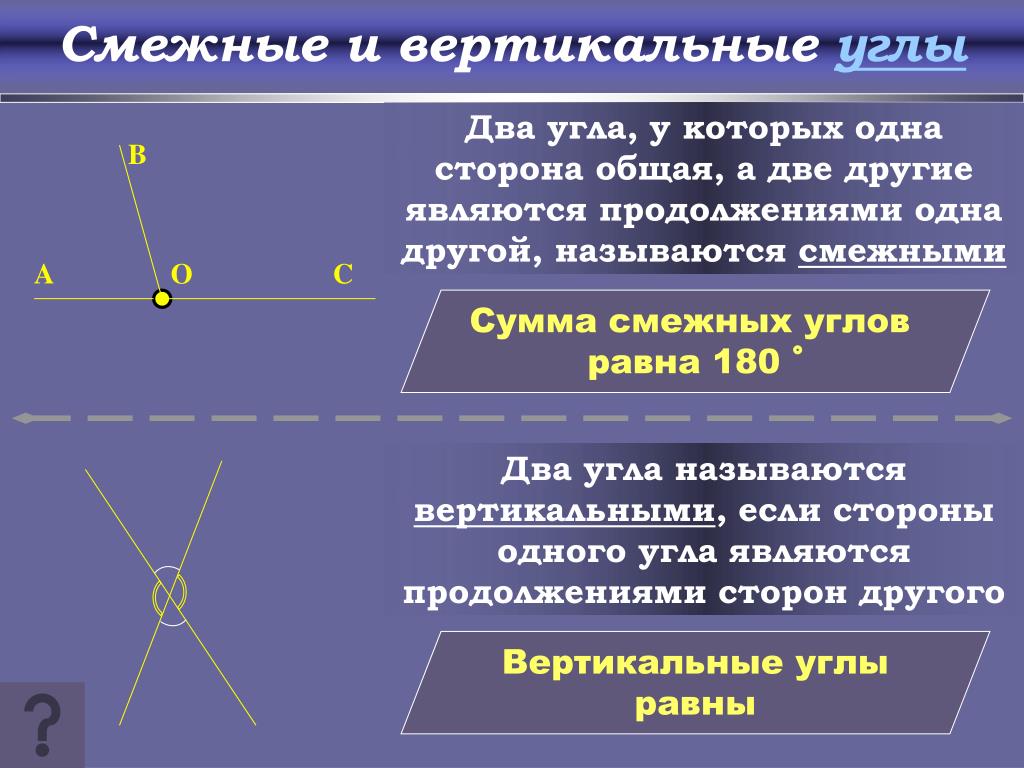 Угол, равный 90°, называется прямым углом.
Угол, равный 90°, называется прямым углом.
Угол, меньший 90°, называется острым углом.
Угол, больший 90° и меньший 180°, называется тупым.
Вопрос 5. Докажите, что угол, смежный с прямым, есть прямой угол.
Ответ. Из теоремы о сумме смежных углов следует, что угол, смежный с прямым углом, есть прямой угол: x + 90° = 180°, x= 180° — 90°, x = 90°.
Вопрос 6. Какие углы называются вертикальными?
Ответ. Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого.
Вопрос 7. Докажите, что вертикальные углы равны.
Ответ. Теорема 2.2. Вертикальные углы равны.
Доказательство. Пусть (a 1 b 1) и (a 2 b 2)- данные вертикальные углы (рис. 34). Угол (a 1 b 2) является смежным с углом (a 1 b 1) и с углом (a 2 b 2). Отсюда по теореме о сумме смежных углов заключаем, что каждый из углов (a 1 b 1) и (a 2 b 2) дополняет угол (a 1 b 2) до 180°, т.е. углы (a 1 b 1) и (a 2 b 2) равны. Что и требовалось доказать.
Что и требовалось доказать.
Вопрос 8. Докажите, что если при пересечении двух прямых один из углов прямой, то остальные три угла тоже прямые.
Ответ. Предположим, что прямые AB и CD пересекают друг друга в точке O. Предположим, что угол AOD равен 90°. Так как сумма смежных углов равна 180°, то получаем, что AOC = 180°-AOD = 180°- 90°=90°. Угол COB вертикален углу AOD, поэтому они равны. То есть угол COB = 90°. Угол COA вертикален углу BOD, поэтому они равны. То есть угол BOD = 90°. Таким образом, все углы равны 90°, то есть они все – прямые. Что и требовалось доказать.
Вопрос 9. Какие прямые называются перпендикулярными? Какой знак используется для обозначения перпендикулярности прямых?
Ответ. Две прямые называются перпендикулярными, если они пересекаются под прямым углом.
Перпендикулярность прямых обозначается знаком \(\perp\). Запись \(a\perp b\) читается: «Прямая a перпендикулярна прямой b».
Вопрос 10. Докажите, что через любую точку прямой можно провести перпендикулярную ей прямую, и только одну.
Ответ. Теорема 2.3. Через каждую прямую можно провести перпендикулярную ей прямую, и только одну.
Доказательство. Пусть a — данная прямая и A — данная точка на ней. Обозначим через a 1 одну из полупрямых прямой a с начальной точкой A (рис. 38). Отложим от полупрямой a 1 угол (a 1 b 1), равный 90°. Тогда прямая, содержащая луч b 1 , будет перпендикулярна прямой a.
Допустим, что существует другая прямая, тоже проходящая через точку A и перпендикулярная прямой a. Обозначим через c 1 полупрямую этой прямой, лежащую в одной полуплоскости с лучом b 1 .
Углы (a 1 b 1) и (a 1 c 1), равные каждый 90°, отложены в одну полуплоскость от полупрямой a 1 . Но от полупрямой a 1 в данную полуплоскость можно отложить только один угол, равный 90°. Поэтому не быть другой прямой, проходящей через точку A и перпендикулярной прямой a. Теорема доказана.
Вопрос 11. Что такое перпендикуляр к прямой?
Ответ. Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной данной, который имеет одним из своих концов их точку пересечения. Этот конец отрезка называется основанием перпендикуляра.
Этот конец отрезка называется основанием перпендикуляра.
Вопрос 12. Объясните, в чём состоит доказательство от противного.
Ответ. Способ доказательства, который мы применили в теореме 2.3, называется доказательством от противного. Этот способ доказательства состоит в том, что мы cначала делаем предположение, противоположное тому, что утверждается теоремой. Затем путем рассуждений, опираясь на аксиомы и доказанные теоремы, приходим к выводу, противоречащему либо условию теоремы, либо одной из аксиом, либо доказанной ранее теореме. На этом основании заключаем, что наше предположение было неверным, а значит, верно утверждение теоремы.
Вопрос 13. Что называется биссектрисой угла?
Ответ. Биссектрисой угла называется луч, который исходит из вершины угла, проходит между его сторонами и делит угол пополам.
Как найти смежный угол?
Математика — древнейшая точная наука, которую в обязательном порядке изучают в школах, колледжах, институтах и университетах. Однако, базовые знания всегда закладываются еще в школе. Порой, ребенку задают достаточно сложные задания, а родители не в силах помочь, потому что просто забыли некоторые вещи из математики. Например, как найти смежный угол по величине основного угла и т.п. Задача проста, но может вызвать затруднения при решении из-за незнания того, какие углы называются смежными и как их найти.
Однако, базовые знания всегда закладываются еще в школе. Порой, ребенку задают достаточно сложные задания, а родители не в силах помочь, потому что просто забыли некоторые вещи из математики. Например, как найти смежный угол по величине основного угла и т.п. Задача проста, но может вызвать затруднения при решении из-за незнания того, какие углы называются смежными и как их найти.
Рассмотрим подробнее определение и свойства смежных углов, а также как их вычислить по данным в задаче.
Определение и свойства смежных углов
Два луча, исходящие из одной точки образуют фигуру под названием «плоский угол». При этом эта точка именуется вершиной угла, а лучи являются его сторонами. Если продолжить один из лучей дальше начальной точки по прямой, то образуется еще один угол, который и называется смежным. У каждого угла в этом случае есть два смежных угла, так как стороны угла равнозначны. То есть всегда присутствует еще смежный угол в 180 градусов.
К основным свойствам смежных углов относят
- Смежные углы имеют общую вершину и одну сторону;
- Сумма смежных углов равна всегда 180 градусам или числу Пи, если вычисление ведется в радианах;
- Синусы смежных углов всегда равны;
- Косинусы и тангенсы смежных углов равны, но имеют противоположные знаки.

Как найти смежные углы
Обычно даются три вариации задач на нахождение величины смежных углов
- Дана величина основного угла;
- Дано соотношение основного и смежного угла;
- Дана величина вертикального угла.
Каждый вариант задачи имеет свое решение. Рассмотрим их.
Дана величина основного угла
Если в задаче указана величина основного угла, то найти смежный угол очень просто. Для этого достаточно из 180 градусов вычесть величину основного угла, и вы получите величину смежного угла. Данное решение исходит из свойства смежного угла — сумма смежных углов равна всегда 180 градусам.
Если же величина основного угла дана в радианах и в задаче требуется найти смежный угол в радианах, то необходимо вычесть из числа Пи величину основного угла, так как величина полного развернутого угла в 180 градусов равна числу Пи.
Дано соотношение основного и смежного угла
В задаче может быть дано соотношение основного и смежного угла вместо градусов и радиан величины основного угла. В этом случае решение будет выглядеть, как уравнение пропорции:
В этом случае решение будет выглядеть, как уравнение пропорции:
- Обозначаем долю пропорции основного угла, как переменную «Y».
- Долю относящуюся к смежному углу обозначаем, как переменную «Х».
- Количество градусов, которые приходятся на каждую пропорцию, обозначим, например, «a».
- Общая формула будет выглядеть так — a*X+a*Y=180 или a*(X+Y)=180.
- Находим общий множитель уравнения «a» по формуле a=180/(X+Y).
- Затем полученное значение общего множителя «а» умножаем на долю угла, который необходимо определить.
Таким образом мы можем найти величину смежного угла в градусах. Однако, если необходимо найти величину в радианах, то нужно просто перевести градусы в радианы. Для этого умножаем угол в градусах на число Пи и делим все на 180 градусов. Полученное значение будет в радианах.
Дана величина вертикального угла
Если в задаче не дана величина основного угла, но дана величина вертикального угла, то вычислить смежный угол можно по такой же формуле, что и в первом пункте, где дана величина основного угла.
Вертикальный угол — это угол, который исходит из той же точки, что и основной, но при этом он направлен в строго противоположном направлении. Тем самым получается зеркальное отражение. Это значит, что вертикальный угол по величине равен основному. В свою очередь, смежный угол вертикального угла равен смежному углу основного угла. Благодаря этому можно вычислить смежный угол основного угла. Для этого просто вычитаем из 180 градусов величину вертикального и получаем значение смежного угла основного угла в градусах.
Если же величина дана в радианах, то необходимо вычесть из числа Пи величину вертикального угла, так как величина полного развернутого угла в 180 градусов равна числу Пи.
Также вы можете прочесть наши полезные статьи и .
Определение смежных. Смежные и вертикальные углы
Как найти смежный угол?
Математика — древнейшая точная наука, которую в обязательном порядке изучают в школах, колледжах, институтах и университетах. Однако, базовые знания всегда закладываются еще в школе. Порой, ребенку задают достаточно сложные задания, а родители не в силах помочь, потому что просто забыли некоторые вещи из математики. Например, как найти смежный угол по величине основного угла и т.п. Задача проста, но может вызвать затруднения при решении из-за незнания того, какие углы называются смежными и как их найти.
Порой, ребенку задают достаточно сложные задания, а родители не в силах помочь, потому что просто забыли некоторые вещи из математики. Например, как найти смежный угол по величине основного угла и т.п. Задача проста, но может вызвать затруднения при решении из-за незнания того, какие углы называются смежными и как их найти.
Рассмотрим подробнее определение и свойства смежных углов, а также как их вычислить по данным в задаче.
Определение и свойства смежных углов
Два луча, исходящие из одной точки образуют фигуру под названием «плоский угол». При этом эта точка именуется вершиной угла, а лучи являются его сторонами. Если продолжить один из лучей дальше начальной точки по прямой, то образуется еще один угол, который и называется смежным. У каждого угла в этом случае есть два смежных угла, так как стороны угла равнозначны. То есть всегда присутствует еще смежный угол в 180 градусов.
К основным свойствам смежных углов относят
- Смежные углы имеют общую вершину и одну сторону;
- Сумма смежных углов равна всегда 180 градусам или числу Пи, если вычисление ведется в радианах;
- Синусы смежных углов всегда равны;
- Косинусы и тангенсы смежных углов равны, но имеют противоположные знаки.

Как найти смежные углы
Обычно даются три вариации задач на нахождение величины смежных углов
- Дана величина основного угла;
- Дано соотношение основного и смежного угла;
- Дана величина вертикального угла.
Каждый вариант задачи имеет свое решение. Рассмотрим их.
Дана величина основного угла
Если в задаче указана величина основного угла, то найти смежный угол очень просто. Для этого достаточно из 180 градусов вычесть величину основного угла, и вы получите величину смежного угла. Данное решение исходит из свойства смежного угла — сумма смежных углов равна всегда 180 градусам.
Если же величина основного угла дана в радианах и в задаче требуется найти смежный угол в радианах, то необходимо вычесть из числа Пи величину основного угла, так как величина полного развернутого угла в 180 градусов равна числу Пи.
Дано соотношение основного и смежного угла
В задаче может быть дано соотношение основного и смежного угла вместо градусов и радиан величины основного угла. В этом случае решение будет выглядеть, как уравнение пропорции:
В этом случае решение будет выглядеть, как уравнение пропорции:
- Обозначаем долю пропорции основного угла, как переменную «Y».
- Долю относящуюся к смежному углу обозначаем, как переменную «Х».
- Количество градусов, которые приходятся на каждую пропорцию, обозначим, например, «a».
- Общая формула будет выглядеть так — a*X+a*Y=180 или a*(X+Y)=180.
- Находим общий множитель уравнения «a» по формуле a=180/(X+Y).
- Затем полученное значение общего множителя «а» умножаем на долю угла, который необходимо определить.
Таким образом мы можем найти величину смежного угла в градусах. Однако, если необходимо найти величину в радианах, то нужно просто перевести градусы в радианы. Для этого умножаем угол в градусах на число Пи и делим все на 180 градусов. Полученное значение будет в радианах.
Дана величина вертикального угла
Если в задаче не дана величина основного угла, но дана величина вертикального угла, то вычислить смежный угол можно по такой же формуле, что и в первом пункте, где дана величина основного угла.
Вертикальный угол — это угол, который исходит из той же точки, что и основной, но при этом он направлен в строго противоположном направлении. Тем самым получается зеркальное отражение. Это значит, что вертикальный угол по величине равен основному. В свою очередь, смежный угол вертикального угла равен смежному углу основного угла. Благодаря этому можно вычислить смежный угол основного угла. Для этого просто вычитаем из 180 градусов величину вертикального и получаем значение смежного угла основного угла в градусах.
Если же величина дана в радианах, то необходимо вычесть из числа Пи величину вертикального угла, так как величина полного развернутого угла в 180 градусов равна числу Пи.
Также вы можете прочесть наши полезные статьи и .
Что такое смежный угол
Угол – это геометрическая фигура (рис.1), образованная двумя лучами OA и OB (стороны угла), исходящими из одной точки O (вершина угла).
СМЕЖНЫЕ УГЛЫ — два угла, сумма которых равна 180°. Каждый из этих углов дополняет другой до развернутого угла.
Каждый из этих углов дополняет другой до развернутого угла.
Смежные углы — (Agles adjacets) такие, которые имеют общую вершину и общую сторону. Преимущественно под этим именем подразумеваются такие углы, которых остальные две стороны лежат по противоположным направлениям одной прямой, проведенной через.
Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.
рис. 2
На рисунке 2 углы a1b и a2b смежные. У них общая сторона b, а стороны a1, a2 — дополнительные полупрямые.
рис. 3
На рисунке 3 изображена прямая AB, точка C расположена между точками A и B. Точка D — точка не лежащая на прямой AB. Получается, что углы BCD и ACD смежные. У них общая сторона CD, а стороны CA и CB дополнительные полупрямые прямой AB, так как точки A, B разделены начальной точкой C.
Теорема о смежных углах
Теорема: сумма смежных углов равна 180°
Доказательство:
Углы a1b и a2b смежные (см. рис. 2) Луч b проходит между сторонами a1, и a2 развернутого угла. Следовательно, сумма углов a1b и a2b равна развернутому углу, то есть 180°. Теорема доказана.
рис. 2) Луч b проходит между сторонами a1, и a2 развернутого угла. Следовательно, сумма углов a1b и a2b равна развернутому углу, то есть 180°. Теорема доказана.
Угол, равный 90° называется прямым. Из теоремы о сумме смежных углов следует, что угол, смежный с прямым углом также прямой угол. Угол, меньший 90° называется острым, а угол больше 90° — тупым. Так как сумма смежных углов равна 180°, значит угол, смежный с острым углом — тупой угол. А угол смежный с тупым углом — острый угол.
Смежные углы — два угла с общей вершиной, одна из сторон которых — общая, а оставшиеся стороны лежат на одной прямой (не совпадая). Сумма смежных углов равна 180°.
Определение 1. Углом называется часть плоскости, ограниченная двумя лучами с общим началом.
Определение 1.1. Углом называют фигуру, состоящую из точки — вершины угла — и двух различных полупрямых, исходящих из этой точки, — сторон угла.
Например, угол ВОС на рис1 Рассмотрим сначала две пересекающиеся прямые. При пересечении прямые образуют углы. Есть частные случаи:
При пересечении прямые образуют углы. Есть частные случаи:
Определение 2. Если стороны угла являются дополнительными полупрямыми одной прямой, то угол называется развернутым.
Определение 3. Прямой угол — это угол величиной в 90 градусов.
Определение 4. Угол, меньший 90 градусов, называется острым углом.
Определение 5. Угол, больший 90 градусов и меньший 180 градусов, называется тупым углом.
пересекающиеся прямые.
Определение 6. Два угла, одна сторона которых общая, а другие стороны лежат на одной прямой, называются смежными.
Определение 7. Углы, стороны которых продолжают друг друга, называются вертикальными углами.
На рисунке 1:
смежные: 1 и 2; 2 и 3; 3 и 4; 4 и 1
вертикальные: 1 и 3; 2 и 4
Теорема 1. Сумма смежных углов равна 180 градусов.
Для доказательства рассмотрим на рис. 4 смежные углы АОВ и ВОС. Их суммой является развернутый угол АОС. Поэтому сумма данных смежных углов равна 180 градусов.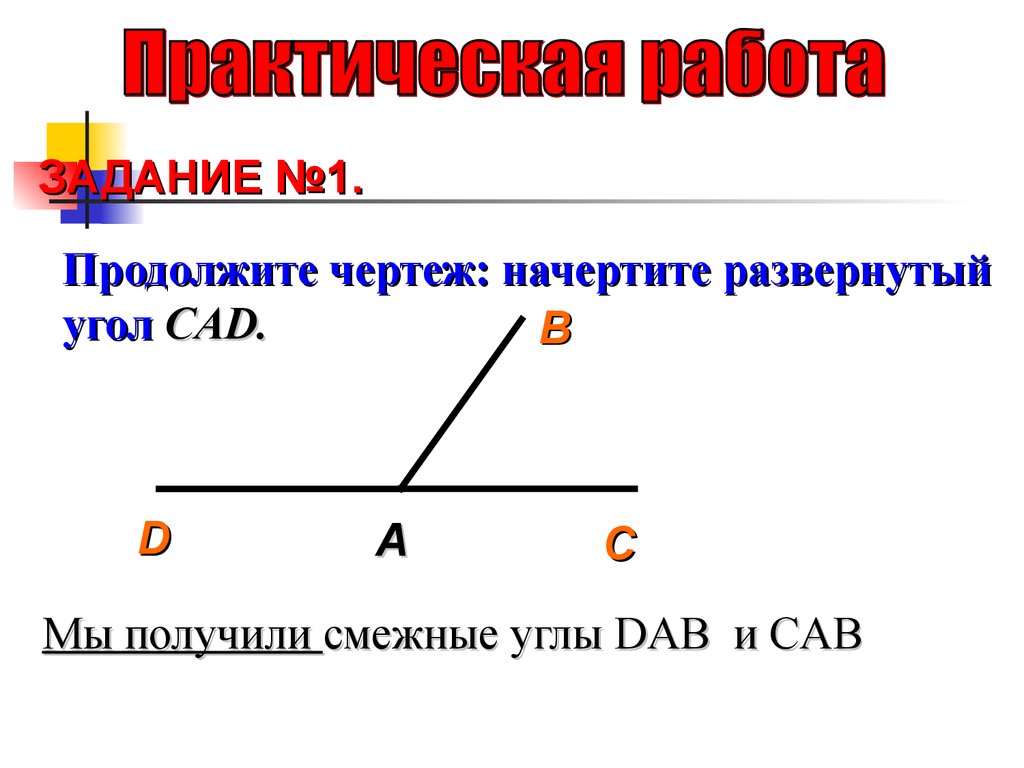
рис. 4
Связь математики с музыкой
«Раздумывая об искусстве и науке, об их взаимных связях и противоречиях, я пришел к выводу, что математика и музыка находятся на крайних полюсах человеческого духа, что этими двумя антиподами ограничивается и определяется вся творческая духовная деятельность человека и, что между ними размещается все, что человечество создало в области науки и искусства.»
Г. Нейгауз
Казалось бы, искусство — весьма отвлеченная от математики область. Однако связь математики и музыки обусловлена как исторически, так и внутренне, несмотря на то, что математика — самая абстрактная из наук, а музыка — наиболее отвлеченный вид искусства.
Консонанс определяет приятное для слуха звучание струны
В основе этой музыкальной системы были два закона, которые носят имена двух великих ученых — Пифагора и Архита. Вот эти законы:
1. Две звучащие струны определяют консонанс, если их длины относятся как целые числа, образующие треугольное число 10=1+2+3+4, т. е. как 1:2, 2:3, 3:4. Причем, чем меньше число n в отношении n:(n+1) (n=1,2,3), тем созвучнее получающийся интервал.
е. как 1:2, 2:3, 3:4. Причем, чем меньше число n в отношении n:(n+1) (n=1,2,3), тем созвучнее получающийся интервал.
2. Частота колебания w звучащей струны обратно пропорциональна ее длине l .
w = a: l ,
где а — коэффициент, характеризующий физические свойства струны.
Так же предложу вашему внимаю забавную пародию про спор двух математиков =)
Геометрия вокруг нас
Геометрия в нашей жизни имеет немаловажное значение. Ввиду того, что когда оглядеться вокруг, то не сложно будет заметить, что нас окружают различные геометрические фигуры. Мы с ними сталкиваемся повсюду: на улице, в классе, дома, в парке, в спортивном зале, в школьной столовой, в принципе везде, где бы мы с вами не находились.
Но темой сегодняшнего урока являются смежные угли. Поэтому давайте оглянемся вокруг и попытаемся в этом окружении найти углы. Если вы внимательно посмотрите в окно, то можете увидеть, что некоторые ветки дерева образуют смежные углы, а в перегородках на воротах можно заметить множество вертикальных углов.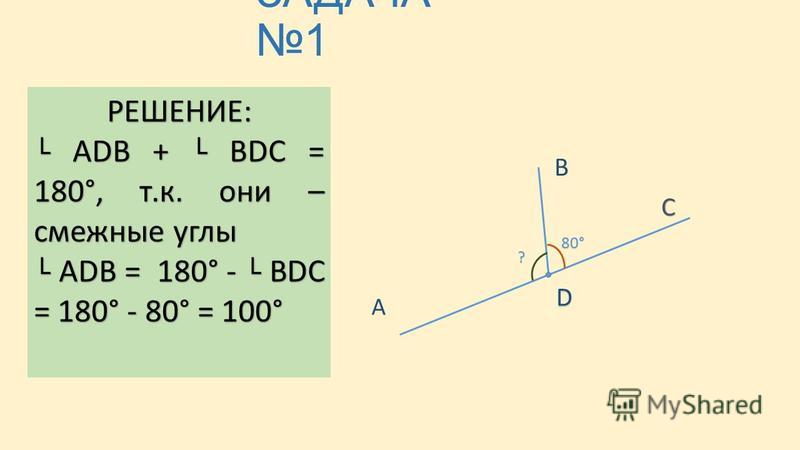 Приведите свои примеры смежных углов, которые вы наблюдаете в окружающей обстановке.
Приведите свои примеры смежных углов, которые вы наблюдаете в окружающей обстановке.
Задание 1.
1. Вот на столе на книжной подставке стоит книга. Какой угол она образует?
2. А вот ученик работает за ноутбуком. Какой угол вы видите здесь?
3. Какой угол образует фото рамка на подставке?
4. Как вы думаете, возможно ли, чтобы два смежных угла были равными?
Задание 2.
Перед вами изображена геометрическая фигура. Что это за фигура, назовите ее? А теперь назовите все смежные углы, которые вы можете увидеть на этой геометрической фигуре.
Задание 3.
Перед вами изображение рисунка и картины. Рассмотрите их внимательно и скажите, какие виды улов вы видите на картине, а какие углы на рисунке.
Решение задач
1) Даны два угла, относящиеся друг к другу как 1: 2, а смежные с ними — как 7: 5. Нужно найти эти углы.2) Известно, что один из смежных углов больше другого в 4 раза. Чему равны смежные углы?
3) Необходимо найти смежные углы, при условии, что один из них на 10 градусов больше от второго.
Математический диктант на повторение ранее выученного материала
1) Выполните рисунок: прямые a I b пересекаются в точке А. Отметьте меньший из образованных углов цифрой 1, а остальные углы – последовательно цифрами 2,3,4; дополняющие лучи прямой а — через а1 и а2, а прямой b — через b1 i b2.2) Пользуясь выполненным рисунком, впишите нужные значения и объяснения в места пропусков в тексте:
а) угол 1 и угол …. смежные, поскольку…
б) угол 1 и угол …. вертикальные, поскольку…
в) если угол 1 = 60°, то угол 2 = …, потому что…
г) если угол 1 = 60°, то угол 3 = …, потому что…
Решите задачи:
1. Может ли сумма 3-х углов, образованных при пересечении 2-х прямых, равняться 100°? 370°?
2. На рисунке найдите все пары смежных углов. А теперь вертикальных углов. Назовите эти углы.
3. Нужно найти угол, когда он втрое больше, чем смежный с ним.
4. Две прямые пересеклись между собой. В результате этого пересечения образовались четыре угла. Определите величину любого из них, при условии что:
Определите величину любого из них, при условии что:
а) сумма 2-х углов из четырех 84°;
б) разность 2-х углов из них равна 45°;
в) один угол в 4 раза меньше чем второй;
г) сумма трех из данных углов равна 290°.
Итог урока
1. назовите углы, которые образуются при пересечении 2-х прямых?
2. Назовите все возможные пары углов, находящихся на рисунке, и определите их вид.
Домашнее задание:
1. Найдите отношение градусных мер смежных углов, когда один из них на 54° больше второго.
2. Найдите углы, которые образуются при пересечении 2-х прямых, при условии, что один из углов равняется сумме 2-х других углов, смежных с ним.
3. Необходимо найти смежные углы, когда биссектриса одного из них образует со стороной второго угол, который больше чем второй угол на 60°.
4. Разница 2-х смежных углов равна трети от суммы этих двух углов. Определите величины 2-х смежных углов.
5. Разница и сумма 2-х смежных углов относятся как 1: 5 соответственно. Найдите смежные углы.
Найдите смежные углы.
6. Разница двух смежных составляет 25% от их суммы. Как относятся величины 2-х смежных углов? Определите величины 2-х смежных углов.
Вопросы:
- Что такое угол?
- Какие бывают типы углов?
- Какая особенность смежных углов?
Два угла размещнные на одной прямой и имеющие одну вершину называются смежными.
Иначе — если сумма двух углов на одной прямой равна 180 градусам и одна сторона у них общая, то это смежные углы.
1 смежный угол + 1 смежный угол = 180 градусов.
Смежные углы -это два угла, у которых одна сторона общая, а две другие стороны в целом образуют прямую линию.
Сумма двух смежных углов всегда равна 180 градусам. К примеру, если один угол 60 градусов, то второй обязательно будет равен 120 градусам (180-60).
Углы АОС и ВОС являются смежными углами, потому что соблюдается все условия характеристики смежных углов:
1. ОС -общая сторона двух углов
ОС -общая сторона двух углов
2.АО -сторона угла АОС, ОВ -сторона угла ВОС. Вместе эти стороны образуют прямую линию АОВ.
3.Угла два и сумма их равна 180 градусов.
Вспоминая школьный курс геометрии, про смежные углы мы можем сказать следующее:
у смежных углов — одна сторона общая, а другие две стороны принадлежат одной прямой, то есть находятся на одной прямой. Если по рисунку, то углы СОВ и ВОА — это смежные углы, сумма которых всегда равна 180 , так как они разделяют развернутый угол, а развернутый угол всегда равен 180 .
Смежные углы понятие легкое в геометрии. Смежные углы, угол плюс угол дают 180 градусов в общей сумме.
Два смежных угла — это будет один развернутый угол.
Есть еще несколько свойств. Со смежными углами задачи решать и теоремы доказывать легко.
Смежные углы образуются при проведении луча из произвольной точки прямой. Тогда эта произвольная точка оказывается вершиной угла, луч — общей стороной смежных углов, а прямая от которой проведен луч — двумя оставшимися сторонами смежных углов. Смежные углы могут быть как одинаковыми в случае перпендикуляра, так и отличатся при наклонном луче. Легко понять, что сумма смежных углов равна 180 градусов или попросту прямой линии. По другому этот угол можно объяснить простым примером — вы сперва шли в одном направлении по прямой, потом передумали, решили вернуться назад и развернувшись на 180 градусов отправились по той же прямой в обратном направлении.
Смежные углы могут быть как одинаковыми в случае перпендикуляра, так и отличатся при наклонном луче. Легко понять, что сумма смежных углов равна 180 градусов или попросту прямой линии. По другому этот угол можно объяснить простым примером — вы сперва шли в одном направлении по прямой, потом передумали, решили вернуться назад и развернувшись на 180 градусов отправились по той же прямой в обратном направлении.
Итак, что же такое смежный угол? Определение:
Смежными называются два угла с общей вершиной и одной общей стороной, причем две другие стороны этих углов лежат на одной прямой.
И небольшой видео урок, где толково показано про смежные углы, вертикальные углы, плюс про перпендикулярные прямые, которые являются частным случаем смежных и вертикальных углов
Смежные углы — это углы, у которых одна сторона общая, а вторая является одной линией.
Смежные углы — это углы, зависящие друг от друга. То есть если общую строну слегка повернуть, то один угол уменьшится на сколько-то градусов и автоматически второй угол увеличится на столько же градусов.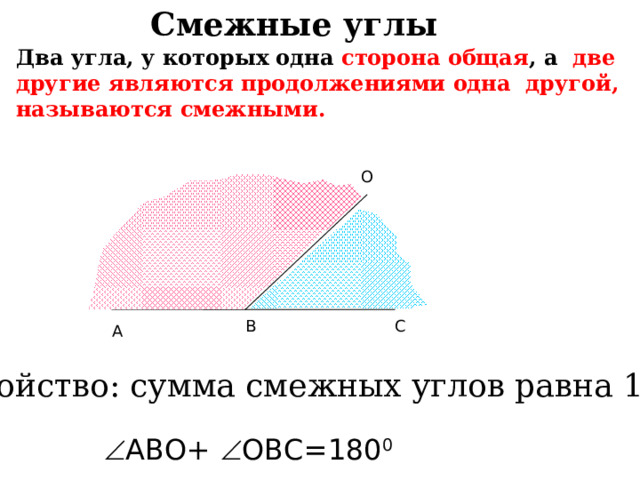 Это свойство смежных углов позволяет в Геометрии решать различные задачи и осуществлять доказательства различных теорем.
Это свойство смежных углов позволяет в Геометрии решать различные задачи и осуществлять доказательства различных теорем.
Общая же сумма смежных углов всегда равна 180 градусов.
Из курса геометрии, (насколько я помню за 6 класс) смежными называются два угла, у которых одна сторона общая, а другие стороны являются дополнительными лучами, сумма смежных углов равна 180. Каждый из двух смежных углов, дополняет другой до развернутого угла. Пример смежных углов:
Смежные углы это два угла с общей вершиной, одна из сторон которых общая, а оставшиеся стороны лежат на одной прямой (не совпадая). Сумма смежных углов равна ста восьмидесяти градусам. А вообще все это очень легко находится в гугле или учебнике геометрии.
Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными лучами. На рисунке 20 углы АОВ и ВОС смежные.
Сумма смежных углов равна 180°
Теорема 1. Сумма смежных углов равна 180°.
Доказательство. Луч ОВ (см. рис.1) проходит между сторонами развернутого угла. Поэтому ∠ АОВ + ∠ ВОС = 180° .
Из теоремы 1 следует, что если два угла равны, то смежные с ними углы равны.
Вертикальные углы равны
Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами сторон другого. Углы АОВ и COD, BOD и АОС, образованные при пересечении двух прямых, являются вертикальными (рис. 2).
Теорема 2. Вертикальные углы равны.
Доказательство. Рассмотрим вертикальные углы АОВ и COD (см. рис. 2). Угол BOD является смежным для каждого из углов АОВ и COD. По теореме 1 ∠ АОВ + ∠ BOD = 180°, ∠ COD + ∠ BOD = 180°.
Отсюда заключаем, что ∠ АОВ = ∠ COD.
Следствие 1. Угол, смежный с прямым углом, есть прямой угол.
Рассмотрим две пересекающиеся прямые АС и BD (рис.3). Они образуют четыре угла. Если один из них прямой (угол 1 на рис.3), то остальные углы также прямые (углы 1 и 2, 1 и 4 — смежные, углы 1 и 3 — вертикальные). В этом случае говорят, что эти прямые пересекаются под прямым углом и называются перпендикулярными (или взаимно перпендикулярными). Перпендикулярность прямых АС и BD обозначается так: AC ⊥ BD.
В этом случае говорят, что эти прямые пересекаются под прямым углом и называются перпендикулярными (или взаимно перпендикулярными). Перпендикулярность прямых АС и BD обозначается так: AC ⊥ BD.
Серединным перпендикуляром к отрезку называется прямая, перпендикулярная к этому отрезку и проходящая через его середину.
АН — перпендикуляр к прямой
Рассмотрим прямую а и точку А, не лежащую на ней (рис.4). Соединим точку А отрезком с точкой Н прямой а. Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а, если прямые АН и а перпендикулярны. Точка Н называется основанием перпендикуляра.
Чертежный угольник
Справедлива следующая теорема.
Теорема 3. Из всякой точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.
Для проведения на чертеже перпендикуляра из точки к прямой используют чертежный угольник (рис.5).
Замечание. Формулировка теоремы обычно состоит из двух частей. В одной части говорится о том, что дано.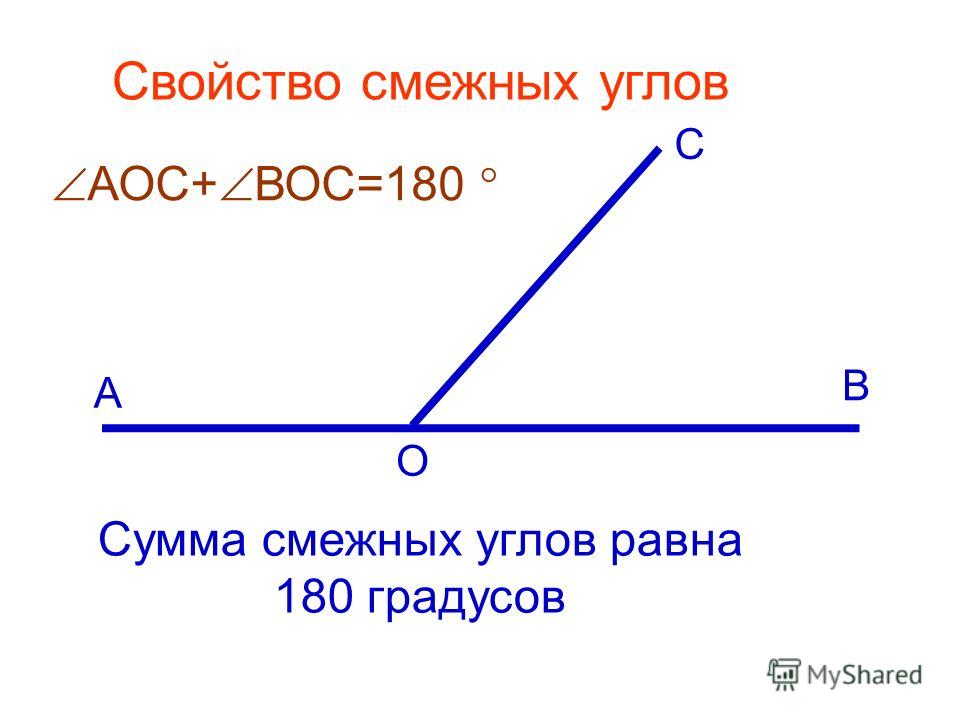 Эта часть называется условием теоремы. В другой части говорится о том, что должно быть доказано. Эта часть называется заключением теоремы. Например, условие теоремы 2 — углы вертикальные; заключение — эти углы равны.
Эта часть называется условием теоремы. В другой части говорится о том, что должно быть доказано. Эта часть называется заключением теоремы. Например, условие теоремы 2 — углы вертикальные; заключение — эти углы равны.
Всякую теорему можно подробно выразить словами так, что ее условие будет начинаться словом «если», а заключение — словом «то». Например, теорему 2 можно подробно высказать так: «Если два угла вертикальные, то они равны».
Пример 1. Один из смежных углов равен 44°. Чему равен другой?
Решение. Обозначим градусную меру другого угла через x , тогда согласно теореме 1.
44° + х = 180°.
Решая полученное уравнение, находим, что х = 136°. Следовательно, другой угол равен 136°.
Пример 2. Пусть на рисунке 21 угол COD равен 45°. Чему равны углы АОВ и АОС?
Решение. Углы COD и АОВ вертикальные, следовательно, по теореме 1.2 они равны, т. е. ∠ АОВ = 45°. Угол АОС смежный с углом COD, значит, по теореме 1.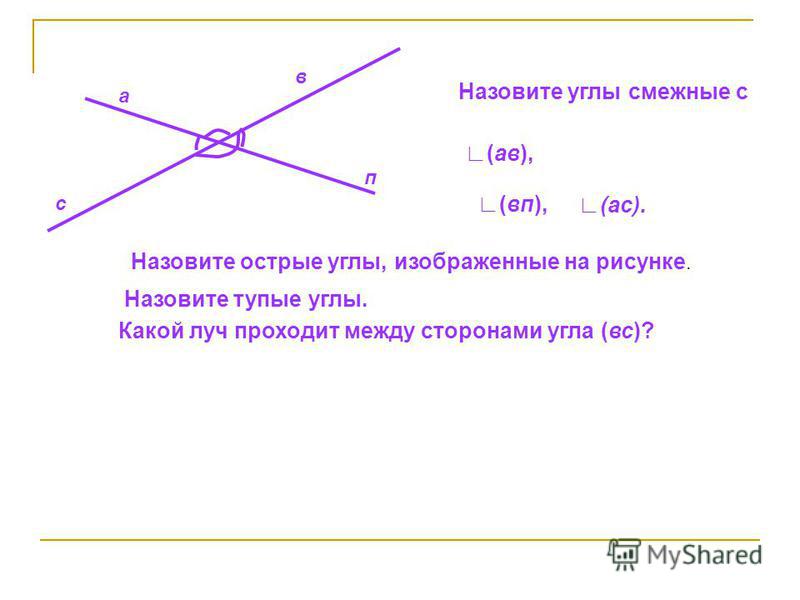
∠ АОС = 180° — ∠ COD = 180° — 45° = 135°.
Пример 3. Найти смежные углы, если один из них в 3 раза больше другого.
Решение. Обозначим градусную меру меньшего угла через х. Тогда градусная мера большего угла будет Зх. Так как сумма смежных углов равна 180° (теорема 1), то х + Зх = 180°, откуда х = 45°.
Значит, смежные углы равны 45° и 135°.
Пример 4. Сумма двух вертикальных углов равна 100°. Найти величину каждого из четырех углов.
Решение. Пусть условию задачи отвечает рисунок 2. Вертикальные углы COD к АОВ равны (теорема 2), значит, равны и их градусные меры. Поэтому ∠ COD = ∠ АОВ = 50° (их сумма по условию 100°). Угол BOD (также и угол
АОС) смежный с углом COD, и, значит, по теореме 1
∠ BOD = ∠ АОС = 180° — 50° = 130°.
Вопрос 1. Какие углы называются смежными?
Ответ. Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.
На рисунке 31 углы (a 1 b) и (a 2 b) смежные. У них сторона b общая, а стороны a 1 и a 2 являются дополнительными полупрямыми.
Вопрос 2. Докажите, что сумма смежных углов равна 180°.
Ответ. Теорема 2.1. Сумма смежных углов равна 180°.
Доказательство. Пусть угол (a 1 b) и угол (a 2 b) — данные смежные углы (см. рис.31). Луч b проходит между сторонами a 1 и a 2 развёрнутого угла. Поэтому сумма углов (a 1 b) и (a 2 b) равна развёрнутому углу, т. е. 180°. Что и требовалось доказать.
Вопрос 3. Докажите, что если два угла равны, то смежные с ними углы также равны.
Ответ.
Из теоремы 2.1 следует, что если два угла равны, то смежные с ними углы равны.
Допустим, углы (a 1 b) и (c 1 d) равны. Нам нужно доказать, что углы (a 2 b) и (c 2 d) тоже равны.
Сумма смежных углов равна 180°. Из этого следует, что a 1 b + a 2 b = 180° и c 1 d + c 2 d = 180°. Отсюда, a 2 b = 180° — a 1 b и c 2 d = 180° — c 1 d.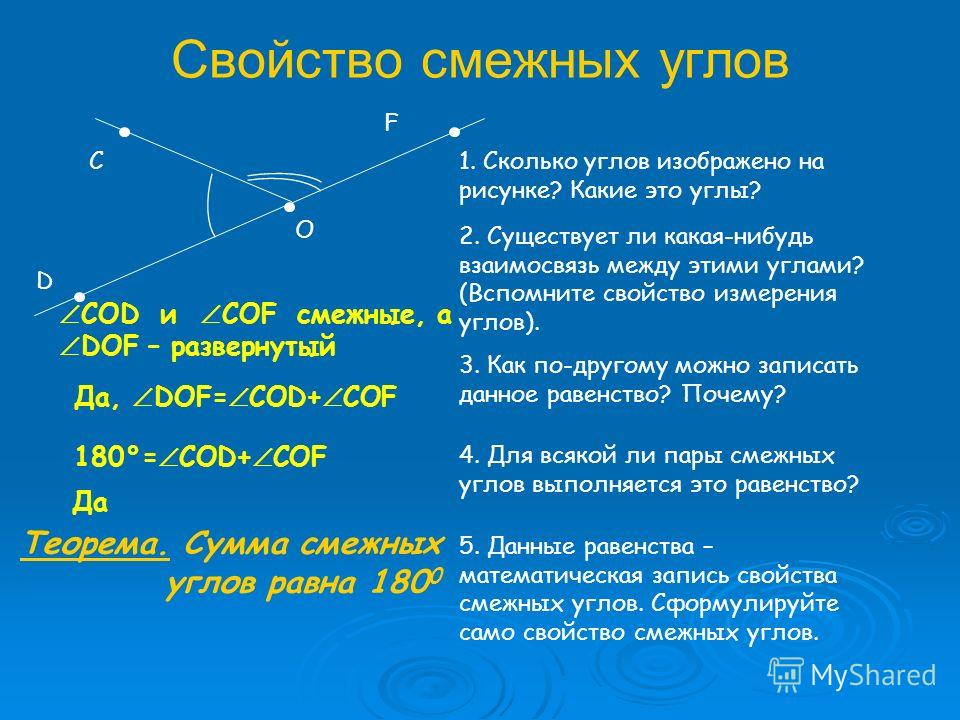 Так как углы (a 1 b) и (c 1 d) равны, то мы получаем, что a 2 b = 180° — a 1 b = c 2 d. По свойству транзитивности знака равенства следует, что a 2 b = c 2 d. Что и требовалось доказать.
Так как углы (a 1 b) и (c 1 d) равны, то мы получаем, что a 2 b = 180° — a 1 b = c 2 d. По свойству транзитивности знака равенства следует, что a 2 b = c 2 d. Что и требовалось доказать.
Вопрос 4. Какой угол называется прямым (острым, тупым)?
Ответ. Угол, равный 90°, называется прямым углом.
Угол, меньший 90°, называется острым углом.
Угол, больший 90° и меньший 180°, называется тупым.
Вопрос 5. Докажите, что угол, смежный с прямым, есть прямой угол.
Ответ. Из теоремы о сумме смежных углов следует, что угол, смежный с прямым углом, есть прямой угол: x + 90° = 180°, x= 180° — 90°, x = 90°.
Вопрос 6. Какие углы называются вертикальными?
Ответ. Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого.
Вопрос 7. Докажите, что вертикальные углы равны.
Ответ. Теорема 2.2. Вертикальные углы равны.
Доказательство. Пусть (a 1 b 1) и (a 2 b 2)- данные вертикальные углы (рис.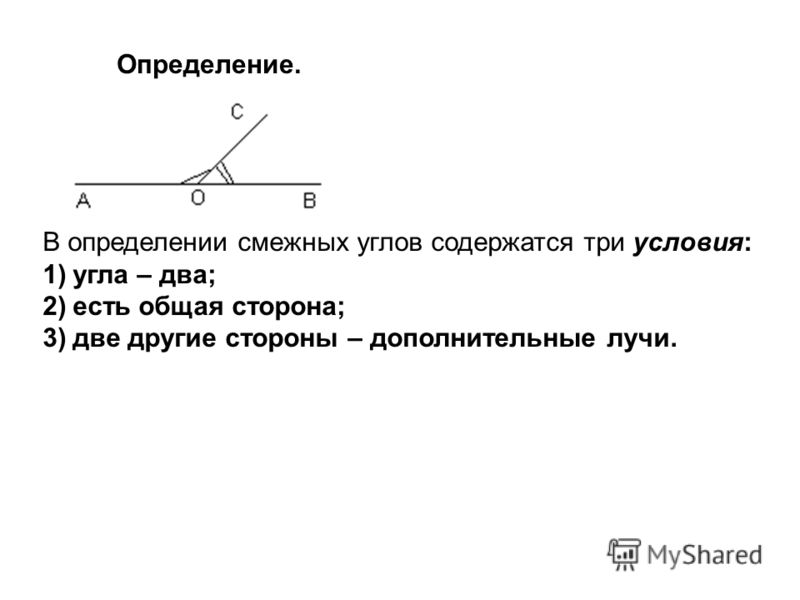 34). Угол (a 1 b 2) является смежным с углом (a 1 b 1) и с углом (a 2 b 2). Отсюда по теореме о сумме смежных углов заключаем, что каждый из углов (a 1 b 1) и (a 2 b 2) дополняет угол (a 1 b 2) до 180°, т.е. углы (a 1 b 1) и (a 2 b 2) равны. Что и требовалось доказать.
34). Угол (a 1 b 2) является смежным с углом (a 1 b 1) и с углом (a 2 b 2). Отсюда по теореме о сумме смежных углов заключаем, что каждый из углов (a 1 b 1) и (a 2 b 2) дополняет угол (a 1 b 2) до 180°, т.е. углы (a 1 b 1) и (a 2 b 2) равны. Что и требовалось доказать.
Вопрос 8. Докажите, что если при пересечении двух прямых один из углов прямой, то остальные три угла тоже прямые.
Ответ. Предположим, что прямые AB и CD пересекают друг друга в точке O. Предположим, что угол AOD равен 90°. Так как сумма смежных углов равна 180°, то получаем, что AOC = 180°-AOD = 180°- 90°=90°. Угол COB вертикален углу AOD, поэтому они равны. То есть угол COB = 90°. Угол COA вертикален углу BOD, поэтому они равны. То есть угол BOD = 90°. Таким образом, все углы равны 90°, то есть они все – прямые. Что и требовалось доказать.
Вопрос 9. Какие прямые называются перпендикулярными? Какой знак используется для обозначения перпендикулярности прямых?
Ответ. Две прямые называются перпендикулярными, если они пересекаются под прямым углом.
Две прямые называются перпендикулярными, если они пересекаются под прямым углом.
Перпендикулярность прямых обозначается знаком \(\perp\). Запись \(a\perp b\) читается: «Прямая a перпендикулярна прямой b».
Вопрос 10. Докажите, что через любую точку прямой можно провести перпендикулярную ей прямую, и только одну.
Ответ. Теорема 2.3. Через каждую прямую можно провести перпендикулярную ей прямую, и только одну.
Доказательство. Пусть a — данная прямая и A — данная точка на ней. Обозначим через a 1 одну из полупрямых прямой a с начальной точкой A (рис. 38). Отложим от полупрямой a 1 угол (a 1 b 1), равный 90°. Тогда прямая, содержащая луч b 1 , будет перпендикулярна прямой a.
Допустим, что существует другая прямая, тоже проходящая через точку A и перпендикулярная прямой a. Обозначим через c 1 полупрямую этой прямой, лежащую в одной полуплоскости с лучом b 1 .
Углы (a 1 b 1) и (a 1 c 1), равные каждый 90°, отложены в одну полуплоскость от полупрямой a 1 . Но от полупрямой a 1 в данную полуплоскость можно отложить только один угол, равный 90°. Поэтому не быть другой прямой, проходящей через точку A и перпендикулярной прямой a. Теорема доказана.
Но от полупрямой a 1 в данную полуплоскость можно отложить только один угол, равный 90°. Поэтому не быть другой прямой, проходящей через точку A и перпендикулярной прямой a. Теорема доказана.
Вопрос 11. Что такое перпендикуляр к прямой?
Ответ. Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной данной, который имеет одним из своих концов их точку пересечения. Этот конец отрезка называется основанием перпендикуляра.
Вопрос 12. Объясните, в чём состоит доказательство от противного.
Ответ. Способ доказательства, который мы применили в теореме 2.3, называется доказательством от противного. Этот способ доказательства состоит в том, что мы cначала делаем предположение, противоположное тому, что утверждается теоремой. Затем путем рассуждений, опираясь на аксиомы и доказанные теоремы, приходим к выводу, противоречащему либо условию теоремы, либо одной из аксиом, либо доказанной ранее теореме. На этом основании заключаем, что наше предположение было неверным, а значит, верно утверждение теоремы.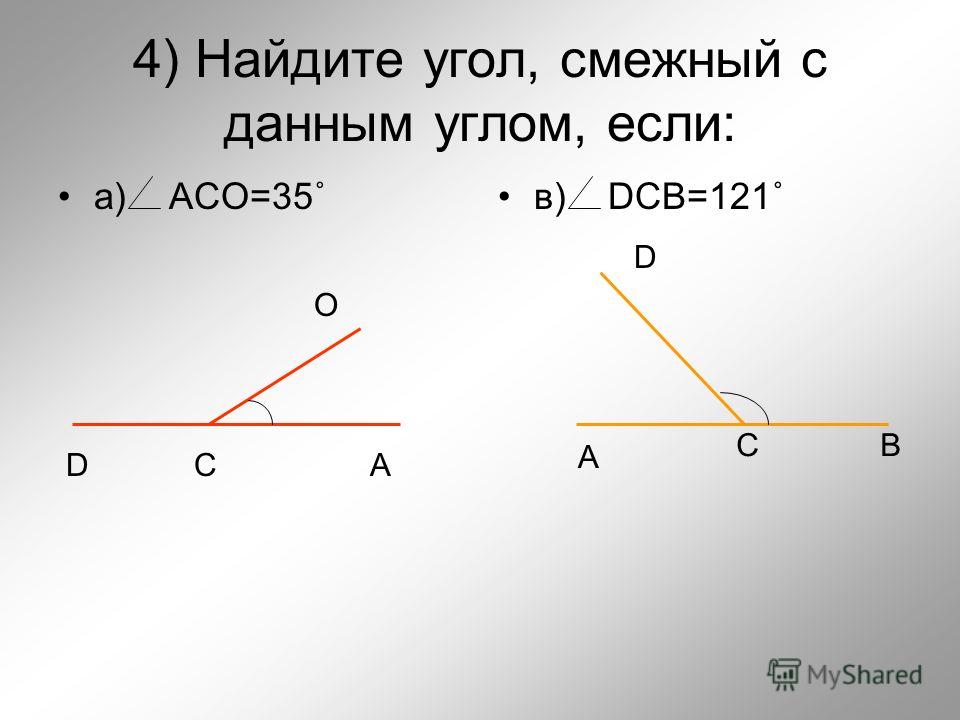
Вопрос 13. Что называется биссектрисой угла?
Ответ. Биссектрисой угла называется луч, который исходит из вершины угла, проходит между его сторонами и делит угол пополам.
Угол вертикальные и смежные углы их свойства. Угол
Г Л А В А I.
ОСНОВНЫЕ ПОНЯТИЯ.
§11. СМЕЖНЫЕ И ВЕРТИКАЛЬНЫЕ УГЛЫ.
1. Смежные углы.
Если мы продолжим сторону какого-нибудь угла за его вершину, то получим два угла (черт. 72): / А ВС и / СВD, у которых одна сторона ВС общая, а две другие АВи ВD составляют прямую линию.
Два угла, у которых одна сторона общая, а две другие составляют прямую линию, называются смежными углами.
Смежные углы можно получить и таким образом: если из какой-нибудь точки прямой проведём луч (не лежащий на данной прямой), то получим смежные углы.
Например, / АDF и / FDВ — углы смежные (черт. 73).
Смежные углы могут иметь самые разнообразные положения (черт. 74).
Смежные углы в сумме составляют развёрнутый угол, поэтому сумма двух смежных углов равна 2d.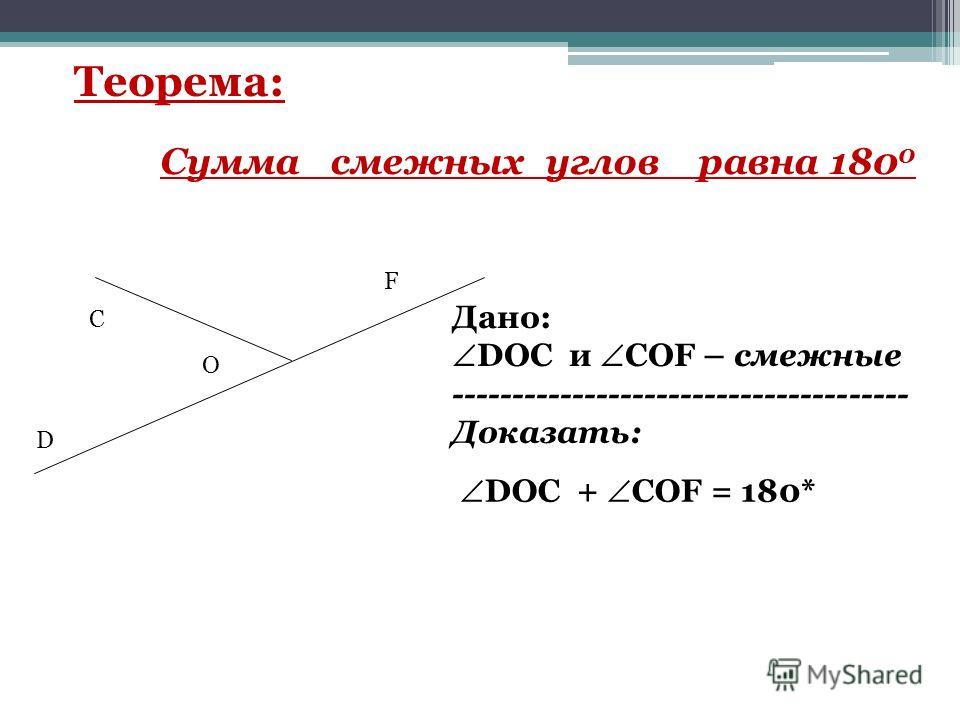
Отсюда прямой угол можно определить как угол, равный своему смежному углу.
Зная величину одного из смежных углов, мы можем найти величину другого смежного с ним угла.
Например, если один из смежных углов равен 3 / 5 d , то второй угол будет равен:
2d — 3 / 5 d = l 2 / 5 d .
2. Вертикальные углы.
Если мы продолжим стороны угла за его вершину, то получим вертикальные углы. На чертеже 75 углы EOF и АОС- вертикальные; углы АОЕ и СОF — также вертикальные.
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого угла.
Пусть / 1 = 7 / 8 d (черт. 76). Смежный с ним / 2 будет равен 2d — 7 / 8 d , т. е. 1 1 / 8 d .
Таким же образом можно вычислить, чему равны / 3 и / 4.
/ 3 = 2d — 1 1 / 8 d = 7 / 8 d ; / 4 = 2d — 7 / 8 d = 1 1 / 8 d (черт.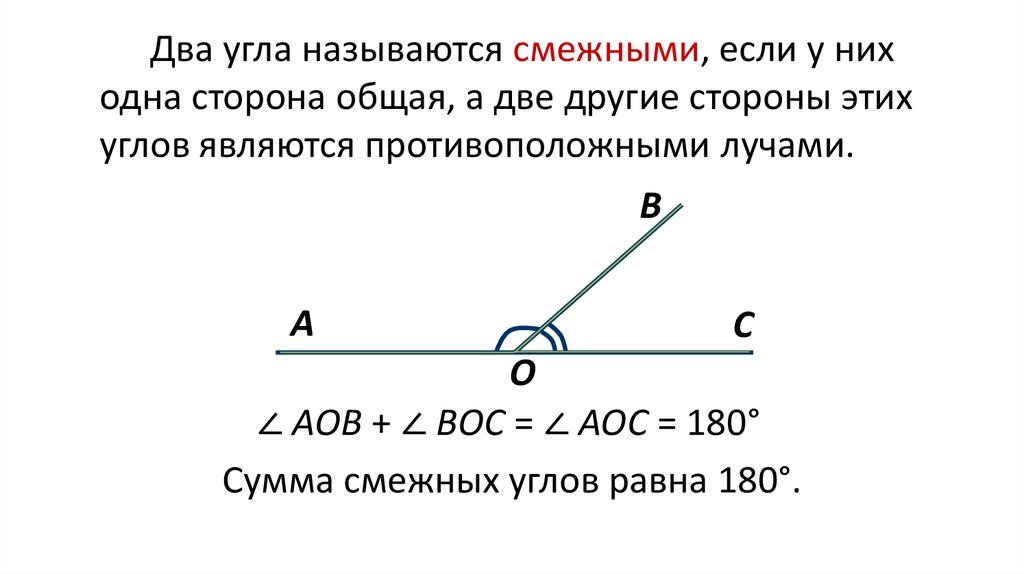 77).
77).
Мы видим, что / 1 = / 3 и / 2 = / 4.
Можно решить ещё несколько таких же задач, и каждый раз будет получаться один и тот же результат: вертикальные углы равны между собой.
Однако, чтобы убедиться в том, что вертикальные углы всегда равны между собой, недостаточно рассмотреть отдельные числовые примеры, так как выводы, сделанные на основе частных примеров, иногда могут быть и ошибочными.
Убедиться в справедливости свойства вертикальных углов необходимо путём рассуждения, путём доказательства.
Доказательство можно провести следующим образом (черт. 78):
/ a + / c = 2d ;
/ b + / c = 2d ;
(так как сумма смежных углов равна 2d ).
/ a + / c = / b + / c
(так как и левая часть этого равенства равна 2d , и правая его часть тоже равна 2d ).
В это равенство входит один и тот же угол с .
Если мы от равных величин отнимем поровну, то и останется поровну. В результате получится: / a = / b , т. е. вертикальные углы равны между собой.
При рассмотрении вопроса о вертикальных углах мы сначала объяснили, какие углы называются вертикальными, т. е. дали определение вертикальных углов.
Затем мы высказали суждение (утверждение) о равенстве вертикальных углов и в справедливости этого суждения убедились путём доказательства. Такие суждения, справедливость которых надо доказывать, называются теоремами . Таким образом, в данном параграфе мы дали определение вертикальных углов, а также высказали и доказали теорему об их свойстве.
В дальнейшем при изучении геометрии нам постоянно придётся встречаться с определениями и доказательствами теорем.
3. Сумма углов, имеющих общую вершину.
На чертеже 79 / 1, / 2, / 3 и / 4 расположены по одну сторону прямой и имеют общую вершину на этой прямой.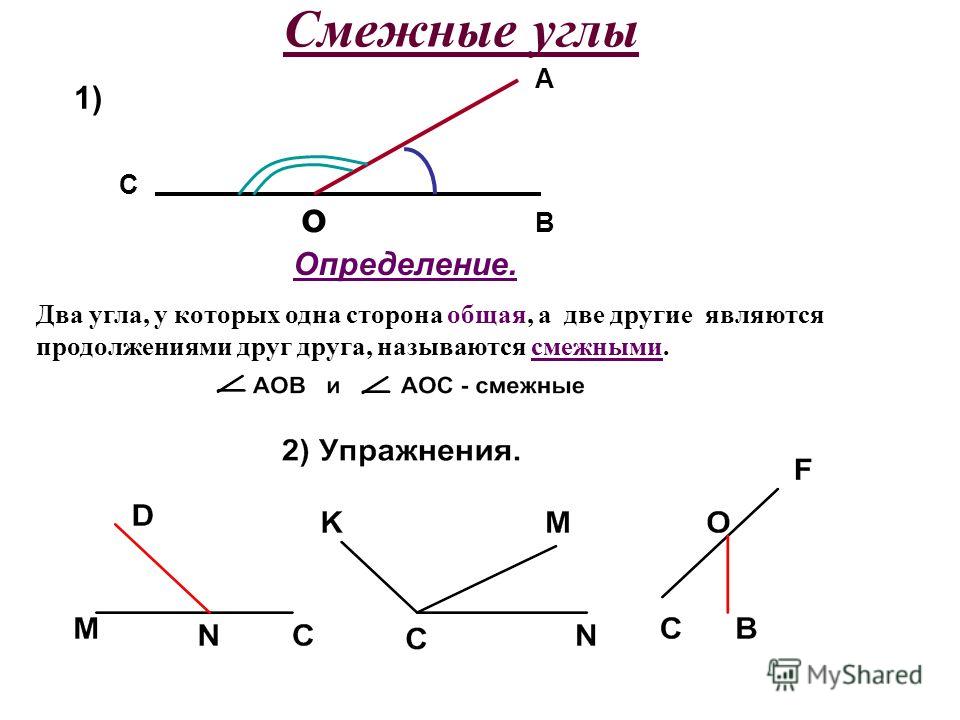 В сумме эти углы составляют развёрнутый угол, т. е.
В сумме эти углы составляют развёрнутый угол, т. е.
/ 1+ / 2+/ 3+ / 4 = 2d .
На чертеже 80 / 1, / 2, / 3, / 4 и / 5 имеют общую вершину. В сумме эти углы составляют полный угол, т. е. / 1 + / 2 + / 3 + / 4 + / 5 = 4d .
Упражнения.
1. Один из смежных углов равен 0,72 d. Вычислить угол, составленный биссектрисами этих смежных углов.
2. Доказать, что биссектрисы двух смежных углов образуют прямой угол.
3. Доказать, что если два угла равны, то равны и их смежные углы.
4. Сколько пар смежных углов на чертеже 81?
5. Может ли пара смежных углов состоять из двух острых углов? из двух тупых углов? из прямого и тупого угла? из прямого и острого угла?
6. Если один из смежных углов прямой, то что можно сказать о величине смежного с ним угла?
7. Если при пересечении двух прямых линий один угол прямой, то что можно сказать о величине остальных трёх углов?
по теме: Смежные и вертикальные углы, их свойства.
(3 занятия)
В результате изучения темы нужно:
УМЕТЬ:
Понятия: смежных и вертикальных углов, перпендикулярных прямых
Различать понятия смежные и вертикальные углы
Теоремы смежных и вертикальных углов
Решать задачи с использованием свойств смежных и вертикальных углов
Свойства смежных и вертикальных углов
Строить смежные и вертикальные углы, перпендикулярные прямые
ЛИТЕРАТУРА:
1. Геометрия. 7 класс. Ж. Кайдасов, Г. Досмагамбетова, В. Абдиев. Алматы «Мектеп». 2012
2. Геометрия. 7 класс. К.О.Букубаева, А.Т. Миразова. Алматы « Атамұра ». 2012
3. Геометрия. 7 класс. Методическое руководство. К.О.Букубаева. Алматы « Атамұра ». 2012
4. Геометрия. 7 класс. Дидактический материал. А.Н.Шыныбеков. Алматы « Атамұра ». 2012
5. Геометрия. 7 класс. Сборник задач и упражнений. К.О.Букубаева, А.Т.Миразова. Алматы « Атамұра ». 2012
Помни, что работать нужно по алгоритму!
Не забывай проходить проверку, делать пометки на полях,
Пожалуйста, не оставляй без ответа, возникшие у тебя вопросы.
Будь объективен во время взаимопроверки, это поможет и тебе, и тому,
кого ты проверяешь.
ЖЕЛАЮ УСПЕХА!
ЗАДАНИЕ №1.
Прочитай определение и выучи (2б):
Определение. Углы, у которых одна сторона общая, а две другие стороны являются дополнительными лучами, называются смежными.
2) Выучи и запиши в тетрадь теорему: (2б)
Сумма смежных углов равна 180.
Дано:
∠ АОД и ∠ ДОВ –данные смежные углы
ОД — общая сторона
Доказать:
∠ АОД + ∠ ДОВ = 180
Доказательство:
На основе аксиомы III 4:
∠ АОД + ∠ ДОВ = ∠ АОВ.
∠ АОВ — развернутый. Следовательно,
∠ АОД + ∠ ДОВ = 180
Теорема доказана.
3) Из теоремы следует: (2б)
1) Если два угла равны, то смежные с ними углы равны;
2) если смежные углы равны, то градусная мера каждого из них равна 90°.
Запомни!
Угол, равный 90°, называется прямым углом.
Угол, меньше 90°, называется острым углом.
Угол, больше 90° и меньше 180°, называется тупым углом.
Прямой угол Острый угол Тупой угол
Так как сумма смежных углов равна 180°, то
1) угол, смежный с прямым углом, прямой;
2) угол, смежный с острым углом, тупой;
3) угол, смежный с тупым углом, острый.
4) Рассмотри образец решения з адачи:
а) Дано: ∠ h k и ∠ kl — смежные; ∠ h k больше ∠ kl на 50° .
Найти: ∠ h k и ∠ kl .
Решение: Пусть ∠ kl = х, тогда ∠ h k = х + 50°. По свойству о сумме смежных углов ∠ kl + ∠ h k = 180°.
х + х + 50° = 180°;
2х = 180° — 50°;
2х = 130°;
х = 65°.
∠ kl = 65°; ∠ h k = 65°+ 50° = 115°.
Ответ: 115° и 65°.
б) Пусть ∠ kl = х, тогда ∠ h k = 3х
х + 3х = 180°; 4х = 180°; х = 45°; ∠ kl = 45°; ∠ hk = 135°.
Ответ: 135° и 45°.
5) Работа с определением смежных углов: (2 б)
6) Найди ошибки в определениях: (2б)
Пройди проверку №1
Задание №2
1)Построй 2 смежных угла так, чтобы их общая сторона проходила через точку C и сторона одного из углов совпадала с лучом AB. (2б)
(2б)
2). Практическая работа на открытие свойства смежных углов: (5б)
Ход работы
1. Построй угол смежный углу а , если а : острый, прямой, тупой.
2. Измерь величины углов.
3.Данные измерений занеси в таблицу.
4. Найди соотношение между величинами углов а и .
5. Сделай вывод о свойстве смежных углов.
Пройди проверку №2
Задание №3
Начертите неразвернутый ∠ АОВ и назовите лучи, являющиеся сторонами этого угла.
Проведите луч О, являющийся продолжение луча ОА, и луч ОД, являющийся продолжение луча ОВ.
Запишите в тетради: углы ∠ АОВ и ∠ СОД называются вертикальными. (3б)
Выучи и запиши в тетрадь: (4б)
Определение: Углы, у которых стороны одного из них являются дополнительными лучами другого, называются вертикальными углами.
1 и
Лучи
OF
и
OA
,
OC
и
OE
являются попарно дополнительными лучами.
Теорема: Вертикальные углы равны.
Доказательство.
Вертикальные углы образуются при пересечении двух прямых. Пусть прямые а и b пересекаются в точке О. ∠ 1 и ∠ 2 –вертикальные углы.
∠ АОС-развернутый, значит ∠ АОС= 180°. Однако ∠ 1+ ∠ 2= ∠ АОС, т.е.
∠ 3+ ∠ 1= 180°, отсюда имеем:
∠ 1= 180 — ∠ 3. (1)
Также имеем, что ∠ ДОВ= 180°, отсюда ∠ 2+ ∠ 3= 180°, или ∠ 2= 180°- ∠ 3. (2)
Так как в равенствах (1) и (2) прямые части равны, то ∠ 1= ∠ 2.
Теорема доказана.
5). Работа с определением вертикальных углов:(2б)
6) Найди ошибку в определении:(2б).
Пройди проверку №3
Задание №4
1)Практическая работа на открытие свойства вертикальных углов:(5б)
Ход работы:
1.Построй угол β вертикальный углу α , если α :
острый, прямой, тупой.
2.Измерь величины углов.
3.Данные измерений занеси в таблицу
4.Найди соотношение между величинами углов α и β.
5.Сделай вывод о свойстве вертикальных углов.
2)Доказательство свойств смежных и вертикальных углов. (3б)
2) Рассмотри образец решения з адачи.
Задача. Прямые АВ и СД пересекаются в точке О так, что ∠ AOД = 35°. Найдите углы АОС и ВОС.
Решение:
1) Углы АОД и АОС смежные, поэтому ∠ BOC = 180° — 35° = 145°.
2) Углы АОС и ВОС также смежные, поэтому ∠ BOC = 180° — 145° = 35°.
Значит, ∠ BOC = ∠ АОД = 35°, причем эти углы являются вертикальными. Вопрос: верно ли утверждение, что любые вертикальные углы равны?
3) Решение задач на готовых чертежах: (3б)
1. Найти углы АОВ, АОD, COD.
3) Найти углы BOC, FOA.: (3б)
3. Найди на рисунке смежные и вертикальные углы. Пусть известны величины двух углов, отмеченных на чертеже, 28? и 90?. Можно ли найти величины остальных углов, не выполняя измерений (2б)
Пройди проверку №4
Задание №5
Проверь свои знания, выполнив проверочную работу №1
Задание №6
1) Самостоятельно докажи свойства вертикальных углов и запиши эти доказательства в тетрадь.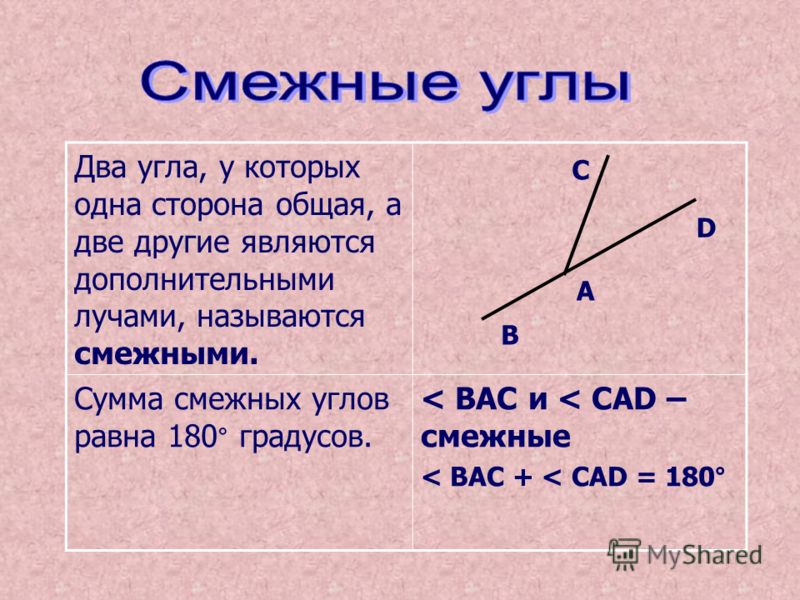 (3б)
(3б)
Учащиеся самостоятельно, используя свойства вертикальных и смежных углов, должны обосновать тот факт, что если при пересечении двух прямых один из образовавшихся углов прямой, то остальные углы также прямые.
2) Реши на выбор две задачи:
1.Градусные меры смежных углов относятся как 7:2. Найдите эти углы.(2б)
2.Один из углов, образовавшихся при пересечении двух прямых, в 11 раз меньше другого.Найдите каждый из углов.(3б)
3.Найдите смежные углы,если их разность и их сумма относятся как 2:9.(3б)
Задание №7
Молодец! Можешь приступать к проверочной работе №2.
Проверочная работа №1.
Реши на выбор любой из вариантов (10б)
Вариант 1
г)
Смежные
д) Начертите (на глаз) угол в 30° и
е) Какие углы называются вертикальными?
Два угла называются вертикальными, если орни равны.
ж) Из точки А провести две прямые, перпендикулярные прямой а
Можно провести только одну прямую.
Вариант 2
1.Ученик, отвечая на вопросы учителя, дал соответствующие ответы. Проверьте, верны ли они, пометив в третьем столбике словом «ДА», «НЕТ», «НЕ ЗНАЮ». В случает «НЕТ» запишите там же верный ответ или добавьте недостающее.
Д)
Нет. Они вертикальные
Е) Какие прямые называются перпендикулярными?
Две прямые называются перпендикулярными, если они пересекаются под прямым углом
Ж) Начертите вертикальные углы так, чтобы их стороны были перпендикулярными прямыми.
2. Назовите вертикальные углы на данном рисунке.
Итого:10 баллов
«5»-10баллов;
«4»-8-9 баллов;
«3»-5-7 баллов.
Проверочная работа №2.
Реши на выбор любой вариант
Вариант I
Найдите смежные углы, если их разность и их сумма относятся как 2:9. (4б)
Найдите все неразвернутые углы, образованные при пересечении двух прямых, если один из них на 240°, меньше суммы двух других. (6б)
(6б)
Вариант II
1) Найдите смежные углы, если их разность и их сумма относятся как 5:8(4б)
2) Найдите все неразвернутые углы, образованные при пересечении двух прямых, если один из них на 60°, больше суммы двух других.(6б)
Итого:10 баллов
«5»-10баллов;
«4»-8-9 баллов;
«3»-5-7 баллов.
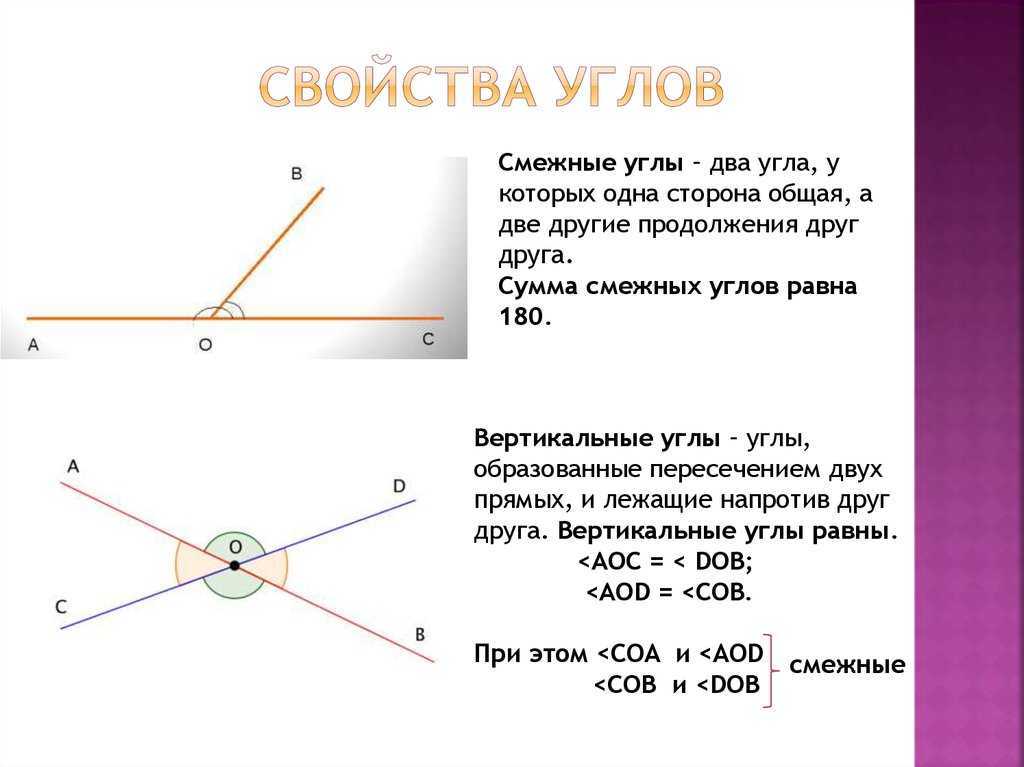
Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными лучами. На рисунке 20 углы АОВ и ВОС смежные.
Сумма смежных углов равна 180°
Теорема 1. Сумма смежных углов равна 180°.
Доказательство. Луч ОВ (см. рис.1) проходит между сторонами развернутого угла. Поэтому ∠ АОВ + ∠ ВОС = 180° .
Из теоремы 1 следует, что если два угла равны, то смежные с ними углы равны.
Вертикальные углы равны
Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами сторон другого. Углы АОВ и COD, BOD и АОС, образованные при пересечении двух прямых, являются вертикальными (рис.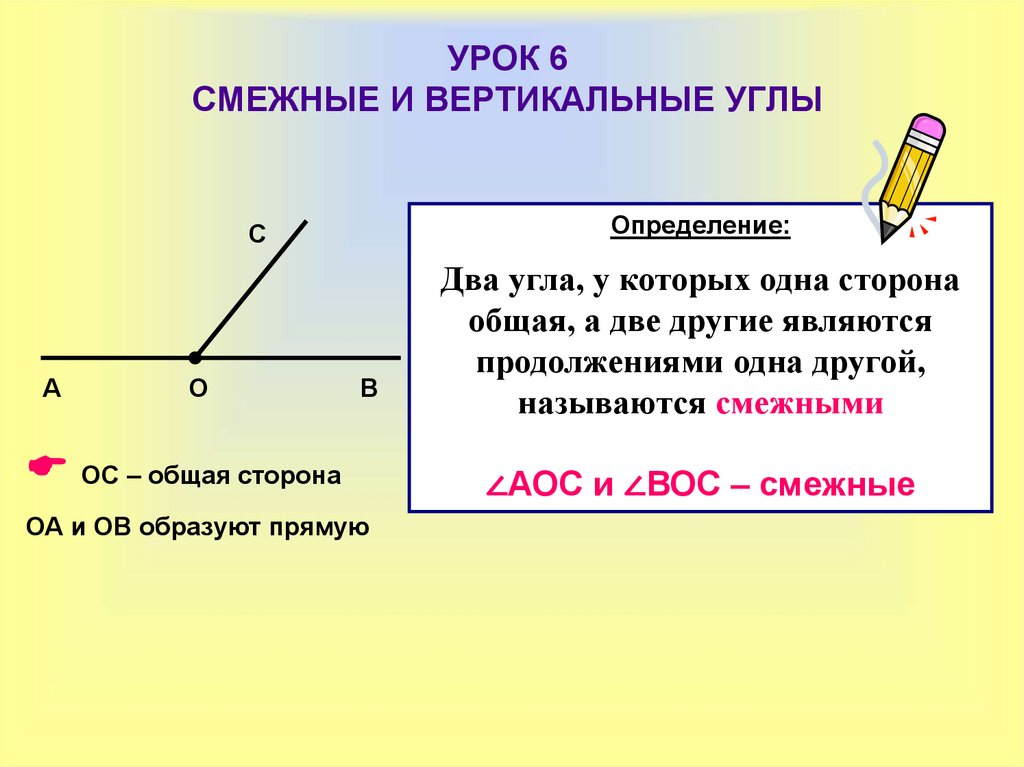 2).
2).
Теорема 2. Вертикальные углы равны.
Доказательство. Рассмотрим вертикальные углы АОВ и COD (см. рис. 2). Угол BOD является смежным для каждого из углов АОВ и COD. По теореме 1 ∠ АОВ + ∠ BOD = 180°, ∠ COD + ∠ BOD = 180°.
Отсюда заключаем, что ∠ АОВ = ∠ COD.
Следствие 1. Угол, смежный с прямым углом, есть прямой угол.
Рассмотрим две пересекающиеся прямые АС и BD (рис.3). Они образуют четыре угла. Если один из них прямой (угол 1 на рис.3), то остальные углы также прямые (углы 1 и 2, 1 и 4 — смежные, углы 1 и 3 — вертикальные). В этом случае говорят, что эти прямые пересекаются под прямым углом и называются перпендикулярными (или взаимно перпендикулярными). Перпендикулярность прямых АС и BD обозначается так: AC ⊥ BD.
Серединным перпендикуляром к отрезку называется прямая, перпендикулярная к этому отрезку и проходящая через его середину.
АН — перпендикуляр к прямой
Рассмотрим прямую а и точку А, не лежащую на ней (рис.4). Соединим точку А отрезком с точкой Н прямой а. Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а, если прямые АН и а перпендикулярны. Точка Н называется основанием перпендикуляра.
Соединим точку А отрезком с точкой Н прямой а. Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а, если прямые АН и а перпендикулярны. Точка Н называется основанием перпендикуляра.
Чертежный угольник
Справедлива следующая теорема.
Теорема 3. Из всякой точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.
Для проведения на чертеже перпендикуляра из точки к прямой используют чертежный угольник (рис.5).
Замечание. Формулировка теоремы обычно состоит из двух частей. В одной части говорится о том, что дано. Эта часть называется условием теоремы. В другой части говорится о том, что должно быть доказано. Эта часть называется заключением теоремы. Например, условие теоремы 2 — углы вертикальные; заключение — эти углы равны.
Всякую теорему можно подробно выразить словами так, что ее условие будет начинаться словом «если», а заключение — словом «то». Например, теорему 2 можно подробно высказать так: «Если два угла вертикальные, то они равны».
Пример 1. Один из смежных углов равен 44°. Чему равен другой?
Решение. Обозначим градусную меру другого угла через x , тогда согласно теореме 1.
44° + х = 180°.
Решая полученное уравнение, находим, что х = 136°. Следовательно, другой угол равен 136°.
Пример 2. Пусть на рисунке 21 угол COD равен 45°. Чему равны углы АОВ и АОС?
Решение. Углы COD и АОВ вертикальные, следовательно, по теореме 1.2 они равны, т. е. ∠ АОВ = 45°. Угол АОС смежный с углом COD, значит, по теореме 1.
∠ АОС = 180° — ∠ COD = 180° — 45° = 135°.
Пример 3. Найти смежные углы, если один из них в 3 раза больше другого.
Решение. Обозначим градусную меру меньшего угла через х. Тогда градусная мера большего угла будет Зх. Так как сумма смежных углов равна 180° (теорема 1), то х + Зх = 180°, откуда х = 45°.
Значит, смежные углы равны 45° и 135°.
Пример 4. Сумма двух вертикальных углов равна 100°. Найти величину каждого из четырех углов.
Найти величину каждого из четырех углов.
Решение. Пусть условию задачи отвечает рисунок 2. Вертикальные углы COD к АОВ равны (теорема 2), значит, равны и их градусные меры. Поэтому ∠ COD = ∠ АОВ = 50° (их сумма по условию 100°). Угол BOD (также и угол
АОС) смежный с углом COD, и, значит, по теореме 1
∠ BOD = ∠ АОС = 180° — 50° = 130°.
На данном уроке мы рассмотрим и уясним для себя понятие смежные углы. Рассмотрим теорему, которая их касается. Введем понятие «вертикальные углы». Рассмотрим опорные факты, касающиеся этих углов. Далее сформулируем и докажем два следствия об угле между биссектрисами вертикальных углов. В конце занятия рассмотрим несколько задач, посвященных этой теме.
Начнем наш урок с понятия «смежные углы». На рисунке 1 изображен развернутый угол ∠АОС и луч ОВ, который делит данный угол на 2 угла.
Рис. 1. Угол ∠АОС
Рассмотрим углы ∠АОВ и ∠ВОС. Вполне очевидно, что они имеют общую сторону ВО, а стороны АО и ОС являются противолежащими. Лучи ОА и ОС дополняют друг друга, а значит, они лежат на одной прямой. Углы ∠АОВ и ∠ВОС являются смежными.
Лучи ОА и ОС дополняют друг друга, а значит, они лежат на одной прямой. Углы ∠АОВ и ∠ВОС являются смежными.
Определение: Если два угла имеют общую сторону, а две другие стороны являются дополняющими лучами, то данные углы называются смежными .
Теорема 1: Сумма смежных углов — 180 о.
Рис. 2. Чертеж к теореме 1
∠МОL + ∠LON = 180 o . Данное утверждение является верным, так как луч OL делит развернутый угол ∠MON на два смежных угла. То есть мы не знаем градусных мер ни одного из смежных углов, а знаем лишь их сумму — 180 о.
Рассмотрим пересечение двух прямых. На рисунке изображено пересечение двух прямых в точке О.
Рис. 3. Вертикальные углы ∠ВОА и ∠СОD
Определение: Если стороны одного угла являются продолжением второго угла, то такие углы называются вертикальными. Именно поэтому на рисунке изображено две пары вертикальных углов: ∠АОВ и ∠СОD, а также ∠AOD и ∠ВОС.
Теорема 2: Вертикальные углы равны.
Используем рисунок 3.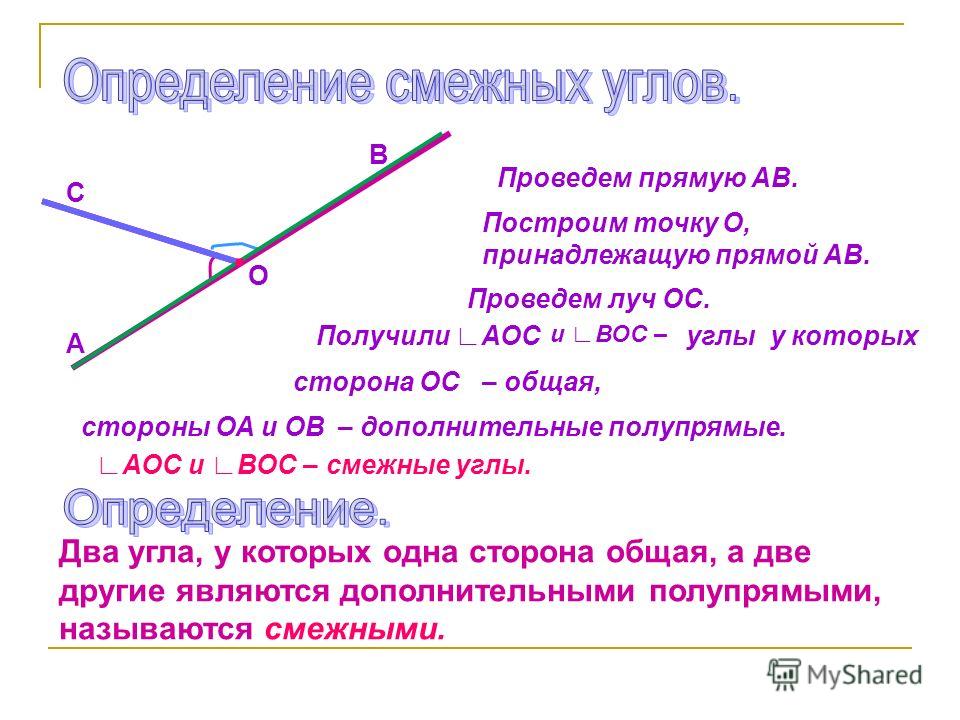 Рассмотрим развернутый угол ∠АОС. ∠АОВ = ∠АОС — ∠ВОС = 180 о — β. Рассмотрим развернутый угол ∠ВОD. ∠CОD = ∠BОD — ∠BОС = 180 о — β.
Рассмотрим развернутый угол ∠АОС. ∠АОВ = ∠АОС — ∠ВОС = 180 о — β. Рассмотрим развернутый угол ∠ВОD. ∠CОD = ∠BОD — ∠BОС = 180 о — β.
Из этих соображений мы делаем вывод, что ∠АОВ = ∠СОD = α. Аналогично, ∠AOD = ∠ВОС = β.
Следствие 1: Угол между биссектрисами смежных углов равен 90 о.
Рис. 4. Чертеж к следствию 1
Поскольку ОL — биссектриса угла ∠ВОА, то угол ∠LOB = , аналогично ∠ВОК = . ∠LOK = ∠LOB + ∠BOK = + = . Сумма углов α + β равна 180 о, поскольку данные углы — смежные.
Следствие 2: Угол между биссектрисами вертикальных углов равен 180 о.
Рис. 5. Чертеж к следствию 2
KO — биссектриса ∠AOB, LO — биссектриса ∠COD. Очевидно, что ∠KOL = ∠KOB + ∠BOC + ∠COL = o . Сумма углов α + β равна 180 о, так как данные углы — смежные.
Рассмотрим некоторые задачи:
Найдите угол, смежный с ∠АOС, если ∠АOС = 111 о.
Выполним чертеж к задаче:
Рис. 6. Чертеж к примеру 1
Поскольку ∠АОС = β и ∠СOD = α смежные углы, то α + β = 180 о. То есть 111 о + β = 180 о.
То есть 111 о + β = 180 о.
Значит, β = 69 о.
Этот тип задач эксплуатирует теорему о сумме смежных углов.
Один из смежных углов прямой, каким (острым, тупым или прямым) является другой угол?
Если один из углов прямой, а сумма двух углов 180 о, то и другой угол тоже прямой. Эта задача проверяет знания о сумме смежных углов.
Верно ли, что если смежные углы равны, то они прямые?
Составим уравнение: α + β = 180 о, но поскольку α = β, то β + β = 180 о, значит, β = 90 о.
Ответ: Да, утверждение верно.
Даны два равных угла. Верно ли, что и смежные им углы тоже будут равны?
Рис. 7. Чертеж к примеру 4
Если два угла равны α, то соответствующие им смежные углы будут 180 о — α. То есть они будут равны между собой.
Ответ: Утверждение верно.
- Александров А.Д., Вернер А.Л., Рыжик В.И. и др. Геометрия 7. — М.: Просвещение.
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия 7. 5-е изд. — М.: Просвещение.
- \Бутузов В.
 Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузова, С.Б. Кадомцев, В.В. Прасолова, под редакцией В.А. Садовничего. — М.: Просвещение, 2010.
Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузова, С.Б. Кадомцев, В.В. Прасолова, под редакцией В.А. Садовничего. — М.: Просвещение, 2010.
- Измерение отрезков ().
- Обобщающий урок по геометрии в 7-м классе ().
- Прямая линия, отрезок ().
- № 13, 14. Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузова, С.Б. Кадомцев, В.В. Прасолова, под редакцией В.А. Садовничего. — М.: Просвещение, 2010.
- Найдите два смежных угла, если один из них в 4 раза больше другого.
- Дан угол. Постройте для него смежный и вертикальный углы. Сколько таких углов можно построить?
- * В каком случае получается больше пар вертикальных углов: при пересечении трех прямых в одной точке или в трех точках?
1. Смежные углы.
Если мы продолжим сторону какого-нибудь угла за его вершину, то получим два угла (рис. 72): ∠АВС и ∠СВD, у которых одна сторона ВС общая, а две другие, АВ и ВD, составляют прямую линию.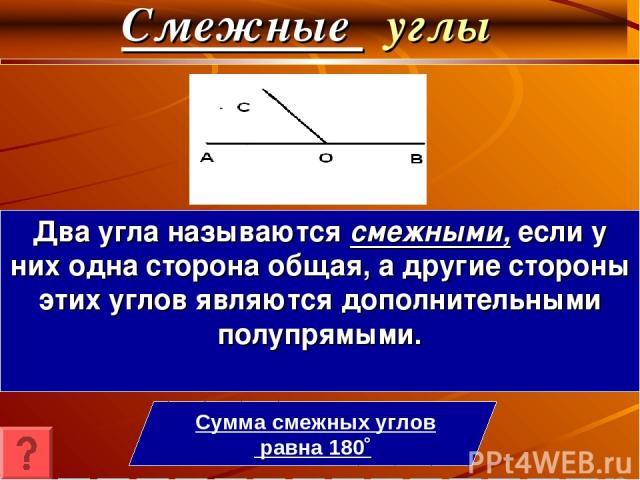
Два угла, у которых одна сторона общая, а две другие составляют прямую линию, называются смежными углами.
Смежные углы можно получить и таким образом: если из какой-нибудь точки прямой проведём луч (не лежащий на данной прямой), то получим смежные углы.
Например, ∠АDF и ∠FDВ — углы смежные (рис. 73).
Смежные углы могут иметь самые разнообразные положения (рис. 74).
Смежные углы в сумме составляют развёрнутый угол, поэтому сумма двух смежных углов равна 180°
Отсюда прямой угол можно определить как угол, равный своему смежному углу.
Зная величину одного из смежных углов, мы можем найти величину другого смежного с ним угла.
Например, если один из смежных углов равен 54°, то второй угол будет равен:
180° — 54° = l26°.
2. Вертикальные углы.
Если мы продолжим стороны угла за его вершину, то получим вертикальные углы. На рисунке 75 углы EOF и АОС- вертикальные; углы АОЕ и СОF — также вертикальные.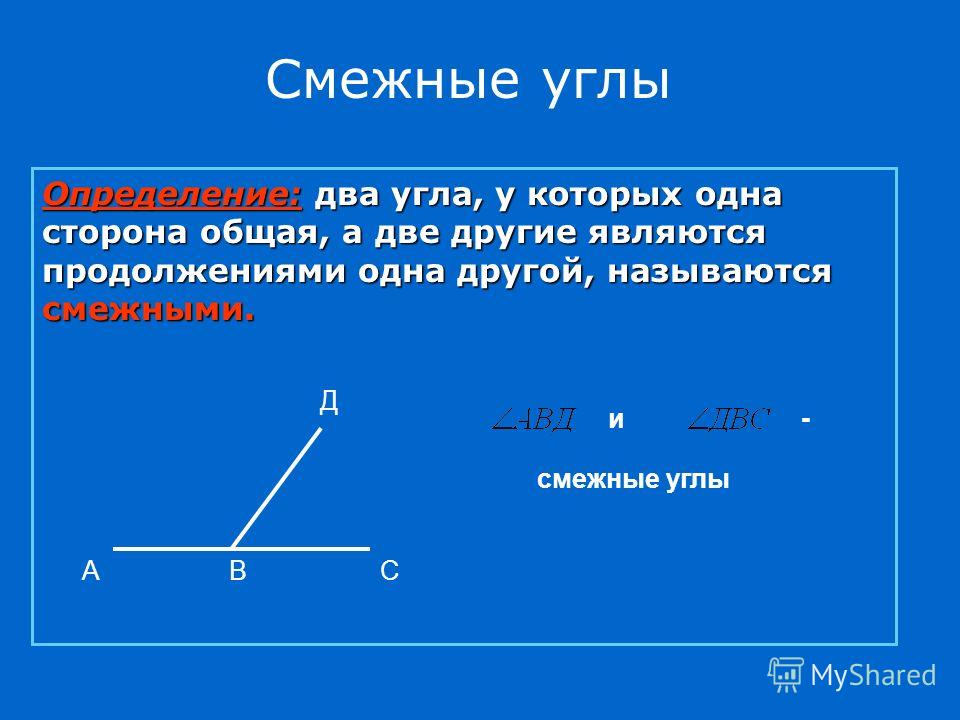
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого угла.
Пусть ∠1 = \(\frac{7}{8}\) ⋅ 90°(рис. 76). Смежный с ним ∠2 будет равен 180° — \(\frac{7}{8}\) ⋅ 90°, т. е. 1\(\frac{1}{8}\) ⋅ 90°.
Таким же образом можно вычислить, чему равны ∠3 и ∠4.
∠3 = 180° — 1\(\frac{1}{8}\) ⋅ 90° = \(\frac{7}{8}\) ⋅ 90°;
∠4 = 180° — \(\frac{7}{8}\) ⋅ 90° = 1\(\frac{1}{8}\) ⋅ 90° (рис. 77).
Мы видим, что ∠1 = ∠3 и ∠2 = ∠4.
Можно решить ещё несколько таких же задач, и каждый раз будет получаться один и тот же результат: вертикальные углы равны между собой.
Однако, чтобы убедиться в том, что вертикальные углы всегда равны между собой, недостаточно рассмотреть отдельные числовые примеры, так как выводы, сделанные на основе частных примеров, иногда могут быть и ошибочными.
Убедиться в справедливости свойства вертикальных углов необходимо путём доказательства.
Доказательство можно провести следующим образом (рис.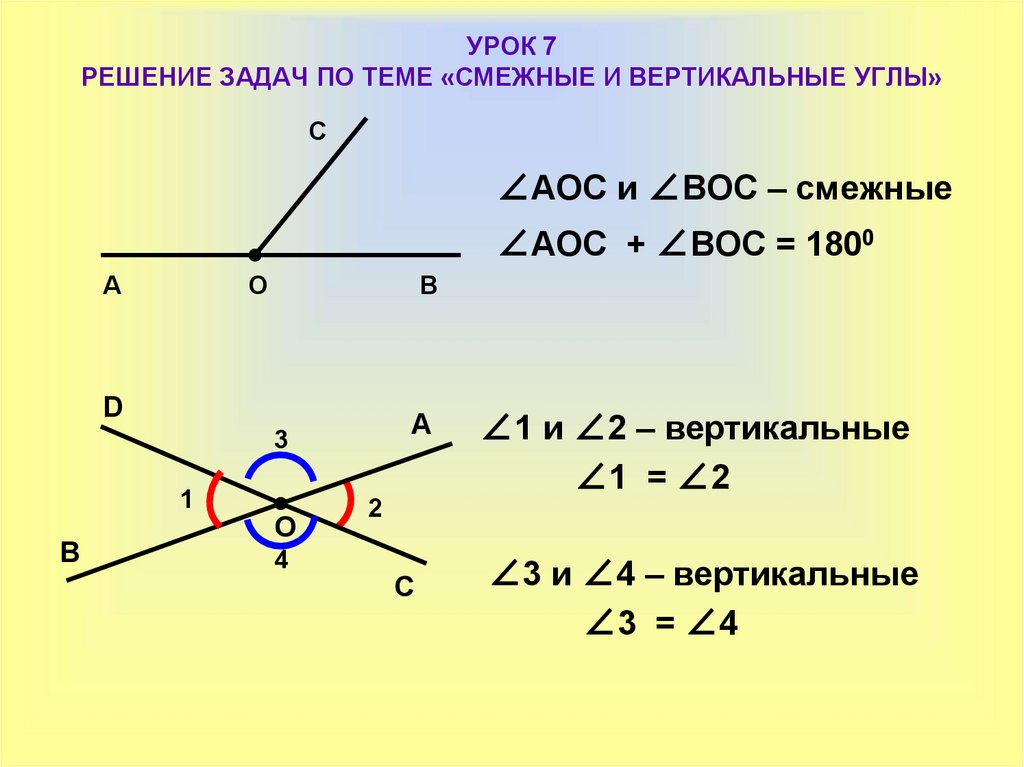 78):
78):
∠a + ∠c = 180°;
∠b + ∠c = 180°;
(так как сумма смежных углов равна 180°).
∠a + ∠c = ∠b + ∠c
(так как и левая часть этого равенства равна 180°, и правая его часть тоже равна 180°).
В это равенство входит один и тот же угол с .
Если мы от равных величин отнимем поровну, то и останется поровну. В результате получится: ∠a = ∠b , т. е. вертикальные углы равны между собой.
3. Сумма углов, имеющих общую вершину.
На чертеже 79 ∠1, ∠2, ∠3 и ∠4 расположены по одну сторону прямой и имеют общую вершину на этой прямой. В сумме эти углы составляют развёрнутый угол, т. е.
∠1 + ∠2 + ∠3 + ∠4 = 180°.
На чертеже 80 ∠1, ∠2, ∠3, ∠4 и ∠5 имеют общую вершину. В сумме эти углы составляют полный угол, т. е. ∠1 + ∠2 + ∠3 + ∠4 + ∠5 = 360°.
Другие материалы
Обрезать изображение по форме
Excel для Microsoft 365 Word для Microsoft 365 Outlook для Microsoft 365 PowerPoint для Microsoft 365 Excel для Microsoft 365 для Mac Word для Microsoft 365 для Mac PowerPoint для Microsoft 365 для Mac Word для Интернета PowerPoint для Интернета Excel 2021 Word 2021 Outlook 2021 PowerPoint 2021 Excel 2021 для Mac Word 2021 для Mac PowerPoint 2021 для Mac Excel 2019 Word 2019 Outlook 2019 PowerPoint 2019 Excel 2019 для Mac Word 2019для Mac PowerPoint 2019 для Mac Excel 2016 Word 2016 Outlook 2016 PowerPoint 2016 Excel 2016 для Mac Word 2016 для Mac PowerPoint 2016 для Mac Excel 2013 Word 2013 Outlook 2013 Excel 2010 Word 2010 Outlook 2010 PowerPoint 2010 Excel для Mac 2011 Word для Mac 2011 PowerPoint для Mac 2011 Больше. ..Меньше
..Меньше
Если вы хотите изменить контур фотографии, чтобы придать ей форму (например, круг или прямоугольник со скругленными углами), используйте инструмент обрезки на ленте с Опция Обрезать по форме .
Вы можете обрезать фигуру в Word, PowerPoint, Outlook или Excel.
Обрезать изображение до формы, например круга
Вы можете быстро изменить форму изображения, обрезав его до определенной формы. Изображение автоматически обрезается, чтобы заполнить геометрию выбранной формы с сохранением ее пропорций.
(Если вы хотите обрезать одно и то же изображение более чем по одной форме, сделайте копии изображения и обрежьте каждое изображение до нужной формы по отдельности.)
- org/ListItem»>
Нажмите на картинку.
Вы можете обрезать несколько изображений одновременно, но вы должны обрезать их до одинаковой формы. (Но в Word это сложно, потому что вы не можете выбрать несколько изображений, которые по умолчанию имеют В строке с опцией раскладки Text .)
Щелкните Инструменты для рисования > Формат и в группе Размер щелкните стрелку под Обрезка .
org/ListItem»>Затем используйте Crop > Fit или Crop > Fill , чтобы изменить, какая часть изображения вписывается в форму, которую вы применили:
Fill Заполняет всю форму изображением. Некоторые внешние края изображения могут быть обрезаны. На полях формы не должно быть пустого пространства.
org/ListItem»>
Fit Помещает все изображение в форму, сохраняя при этом исходное соотношение сторон изображения. На полях фигуры может быть пустое пространство.
(Черные маркеры обрезки появляются по краям и углам изображения, когда вы выбираете параметр «По размеру или заливке».)
Вы можете настроить положение изображения в рамке, выбрав изображение и перетащив его в нужное место. Например, это может помочь вам отцентрировать самую важную часть изображения в фигуре, которую вы применили к изображению.
Обрежьте поля изображения, перетащив черный маркер обрезки следующим образом:
Описание
Действие
Обрезать одну сторону
Перетащите внутрь боковой маркер обрезки
Обрезать две смежные стороны одновременно
Перетащите внутрь угловой маркер обрезки
Обрезать одинаково с двух параллельных сторон одновременно
Нажмите и удерживайте клавишу Ctrl при перетаскивании внутрь бокового маркера обрезки
org/ListItem»>
Используйте Insert > Picture , чтобы добавить изображение в файл Office (например, документ Word, презентацию PowerPoint или сообщение электронной почты Outlook).
В появившемся меню выберите Обрезать до формы , а затем щелкните фигуру, до которой нужно обрезать.
Форма немедленно применяется к изображению.
Нажмите кнопку Crop еще раз, когда закончите.
Начните с фигуры и добавьте к ней изображение
Вы можете добавить изображение в качестве заливки для фигуры, а затем отредактировать или обрезать фигуру.
Добавление рисунка к фигуре
Добавьте фигуру в документ (инструкции см. в разделе Добавление фигур) и щелкните фигуру, чтобы выбрать ее.
Щелкните Инструменты рисования > Формат и в группе Стили фигур щелкните Заливка формы > Рисунок .

Выберите нужный тип изображения (например, Из файла или Онлайн-изображения ), а затем перейдите к нужному изображению и вставьте его.
Изменение размера фигуры
Чтобы изменить размеры заполненной фигуры, сохранив ее основной формат, выберите ее и перетащите любой из маркеров изменения размера.
Выберите, как изображение вписывается в фигуру
Если ваше изображение перекошено, обрезано или не заполняет форму так, как вы хотите, используйте Инструменты Fit и Fill в меню Crop для тонкой настройки:
Щелкните фигуру, созданную с помощью Заливка фигуры > Изображение .
Щелкните Инструменты для работы с рисунками > Формат и в группе Размер щелкните стрелку под Урожай . Появится меню с параметрами обрезки.
Выберите Вписать , если вы хотите, чтобы как можно большая часть изображения помещалась в форму; исходное соотношение сторон изображения будет сохранено, но внутри фигуры может остаться пустое пространство.

Выберите Заливка , чтобы фигура соответствовала границам изображения, обрезая все, что находится за пределами фигуры. Вы можете перетащить изображение, чтобы изменить его часть, отображаемую внутри фигуры.
При желании вы можете отрегулировать область обрезки с помощью маркеров обрезки, как описано в разделе «Обрезка изображения».
Когда вы закончите, нажмите клавишу ESC или щелкните в любом месте документа за пределами изображения.
Используйте точки редактирования для редактирования или обрезки фигуры
Хотя инструменты обрезки недоступны для фигур, вы можете использовать инструмент Edit Points для настройки фигуры.
Выберите фигуру, которую хотите изменить.
Нажмите Формат фигуры и в группе Вставить фигуры выберите Редактировать фигуру > Редактировать точки .
org/ListItem»>Чтобы удалить точку вершины, удерживайте Ctrl и щелкните ее. Чтобы добавить точку вершины, удерживайте клавишу Ctrl и щелкните в любом месте периметра фигуры, где еще нет точки вершины.
Перетащите вершины фигуры (которые отображаются в виде черных точек по периметру фигуры), пока фигура не примет желаемый вид.
См. также
Обрезать картинку в Office
Вырезать или закрыть часть изображения
Если вы хотите изменить контур фотографии, чтобы придать ей форму (например, круг или прямоугольник со скругленными углами), используйте инструмент обрезки на ленте.
Вы можете обрезать фигуру в Word, PowerPoint или Excel.
Новые версии
- Какую версию Office для Mac вы используете?
- Новые версии
- 2011
Обрезка до определенной формы
Быстро изменить форму изображения, обрезав его до определенной формы. Изображение автоматически обрезается, чтобы заполнить геометрию выбранной формы с сохранением ее пропорций.
Если вы хотите обрезать одно и то же изображение более чем по одной форме, сделайте копии изображения и обрежьте каждое изображение до нужной формы по отдельности.
Используйте Insert > Picture , чтобы добавить изображение в файл Office (например, документ Word, презентацию PowerPoint или книгу Excel).
В вашем файле выберите изображение, которое вы хотите обрезать.
На вкладке Picture Format щелкните стрелку рядом с Crop .
(Если вы не видите вкладку Формат изображения , убедитесь, что вы выбрали изображение (а не фигуру). )
)
Укажите на Обрезать до фигуры и затем щелкните фигуру, до которой вы хотите обрезать.
Форма немедленно применяется к изображению.
Если вы хотите изменить форму, снова нажмите кнопку Crop на ленте.
Черные маркеры обрезки появляются по краям и углам изображения.
Обрежьте изображение, перетащив любой маркер обрезки внутрь. Если вы перетащите один из угловых маркеров, он обрежет две смежные стороны одновременно.
Если вы перетащите один из угловых маркеров, он обрежет две смежные стороны одновременно.
Обрезка по размеру или заполнению формы
После того, как вы добавили изображение к фигуре, вы можете выбрать, как изображение вписывается в фигуру, используя инструменты Fit и Fill для тонкой настройки.
В вашем файле выберите изображение, которое вы хотите внутри формы.
На вкладке Picture Format щелкните стрелку рядом с Crop .

Если вы не видите вкладку Формат изображения , убедитесь, что вы выбрали изображение (а не фигуру).
Щелкните Fill или Fit , а затем щелкните за пределами рисунка.
Опция
Описание
Заполнить
Удаляет (или «обрезает») часть изображения, но по-прежнему заполняет всю фигуру.

Подходит для
Подгоняет все изображение под фигуру. Исходное соотношение сторон изображения сохраняется, но внутри фигуры может быть пустое пространство.
Обрезка до определенной формы
Быстрый способ изменить форму изображения — обрезать его до определенной формы. Когда вы обрезаете до определенной формы, изображение автоматически обрезается, чтобы заполнить геометрию формы. Пропорции изображения соблюдены.
Пропорции изображения соблюдены.
В вашем файле выберите изображение, которое вы хотите обрезать до определенной формы.
Перейдите на вкладку Формат изображения .
(Если вы не видите вкладку Формат изображения , убедитесь, что вы выбрали изображение (а не фигуру).)
В разделе Adjust щелкните стрелку рядом с Crop , выберите Mask to Shape , укажите тип фигуры, а затем щелкните фигуру, до которой вы хотите обрезать изображение.

Форма немедленно применяется к изображению.
Если вы хотите изменить форму, снова нажмите кнопку Crop на ленте.
Черные маркеры обрезки появляются по краям и углам изображения.
Перетащите маркеры обрезки, чтобы обрезать поля изображения, а затем щелкните за пределами изображения.
Когда вы закончите, щелкните за пределами изображения.
Обрезка по размеру или заполнению формы
После того, как вы добавили изображение к фигуре, вы можете выбрать, как изображение будет вписываться в фигуру, используя инструменты Crop to Fit и Crop to Fill для точной настройки.
Щелкните изображение, которое вы хотите внутри фигуры.
Перейдите на вкладку Формат изображения .
(Если вы не видите вкладку Формат изображения , убедитесь, что вы выбрали свое изображение.)
В разделе Adjust щелкните стрелку рядом с Crop , щелкните Crop to Fill или Crop to Fit , а затем щелкните за пределами изображения:
Опция
Описание
Обрезать до заполнения
Удаляет (или «обрезает») часть изображения, но по-прежнему заполняет всю фигуру.

Обрезать по размеру
Подгоняет все изображение под фигуру. Исходное соотношение сторон изображения сохраняется, но внутри фигуры может быть пустое пространство.
Когда закончите, нажмите ESC.
Какое приложение вы используете?
Слово | PowerPoint
Word: вписать изображение в фигуру
Веб-приложение Word не имеет функции «обрезать по фигуре», которая есть в настольном приложении, но вы по-прежнему можете использовать быстрые стили изображений, чтобы применить к изображению некоторые основные фигуры, как описано здесь:
Вставьте изображение в документ. (Выберите Вставить > Изображение , а затем перейдите к изображению, которое хотите использовать.)
Выбрав изображение на холсте, выберите вкладку Изображение на ленте, а затем откройте галерею Стили изображения :
Выберите фигуру, чтобы применить ее к изображению.
После применения формы вы можете изменить ее размер по мере необходимости.
PowerPoint: обрезка изображения по фигуре
Выберите изображение на слайде, чтобы обрезать его до формы.
На вкладке Изображение справа выберите стрелку рядом с Кадрирование .
Совет: Если вы не видите вкладку Изображение , обязательно выберите изображение.
Выберите Обрезать по форме , затем выберите форму, которую нужно применить к границе изображения.

Если вы хотите обрезать поля изображения, снова выберите Обрезать , а затем перетащите маркер внутрь по мере необходимости. Перетащите другие маркеры по мере необходимости.
Чтобы сохранить изменения, нажмите кнопку Crop еще раз или нажмите клавишу Esc.
Обрезать картинку в Office
Силовая установка
Рисунки, диаграммы и таблицы
Диаграммы и картинки
Диаграммы и картинки
Обрезать картинку в Office
Excel для Microsoft 365 Word для Microsoft 365 Outlook для Microsoft 365 PowerPoint для Microsoft 365 Project Online Desktop Client Excel для Microsoft 365 для Mac Word для Microsoft 365 для Mac PowerPoint для Microsoft 365 для Mac Word для Интернета OneNote для Интернета PowerPoint для Интернет Excel 2021 Word 2021 Outlook 2021 PowerPoint 2021 Project Professional 2021 Project Standard 2021 Excel 2021 для Mac Word 2021 для Mac PowerPoint 2021 для Mac Excel 2019Word 2019 Outlook 2019 PowerPoint 2019 Project профессиональный 2019 Project Standard 2019 Excel 2019 для Mac Word 2019 для Mac PowerPoint 2019 для Mac Excel 2016 Word 2016 Outlook 2016 PowerPoint 2016 Project профессиональный 2016 Project Standard 2016 Excel 2016 для Mac Excel 2013 Word 2013 Outlook 2013 PowerPoint 2013 Project профессиональный 2013 Project стандартный 2013 Excel 2010 Word 2010 Outlook 2010 PowerPoint 2010 Дополнительно. ..Меньше
..Меньше
Обрежьте изображение, чтобы обрезать ненужные внешние края.
Если вместо этого вы хотите удалить фон изображения, см. раздел Удаление фона изображения.
Если вы хотите увеличить или уменьшить изображение , см. Изменение размера изображения.
Важно: Обрезанные части изображения не удаляются из файла и потенциально могут быть видны другим; включая поисковые системы, если обрезанное изображение размещено в Интернете. Если в области, которую вы обрезаете, есть конфиденциальная информация, убедитесь, что вы удалили обрезанные области (см. ниже), а затем сохраните файл.
В дополнение к базовой обрезке полей вы также можете обрезать изображения до определенных форм и соотношений сторон или обрезать заливку изображения внутри фигуры (в Office для Mac и в Office 2010 и более поздних версиях).
1:32
Office может помочь вам с базовым редактированием изображений, как показано в видео выше, но для более сложных задач вам может понадобиться специальное приложение для редактирования изображений. У Digital Trends есть рекомендации по бесплатному программному обеспечению для редактирования фотографий.
Обрезать поля изображения
Используйте Insert > Picture , чтобы добавить изображение в файл Office (например, в документ Word, презентацию PowerPoint или книгу Excel).
Щелкните изображение правой кнопкой мыши.
 Появится всплывающее меню с двумя кнопками непосредственно над или под меню. Crop это одна из кнопок.
Появится всплывающее меню с двумя кнопками непосредственно над или под меню. Crop это одна из кнопок.Нажмите кнопку Обрезать .
Черные маркеры обрезки появляются по краям и углам изображения.
Обрежьте изображение одним из следующих способов:
Описание
Действие
Обрезать одну сторону
Перетащите внутрь боковой маркер обрезки
Обрезать две смежные стороны одновременно
Перетащите внутрь угловой маркер обрезки
Обрезать одинаково с двух параллельных сторон одновременно
Нажмите и удерживайте клавишу Ctrl при перетаскивании внутрь бокового маркера обрезки
Вы также можете обрезать или добавить поля вокруг изображения, перетащив маркеры обрезки наружу, а не внутрь.

(Необязательно) Чтобы изменить положение области обрезки, либо измените область обрезки, перетащив края или углы прямоугольника обрезки, либо переместите изображение.
Когда вы закончите, нажмите клавишу ESC или щелкните в любом месте документа за пределами изображения.
Примечание. Инструменты обрезки недоступны для фигур, но в Office 2010 и более поздних версиях можно изменить размер фигуры и использовать инструмент Edit Points для достижения эффекта, аналогичного обрезке, или для настройки формы. Дополнительную информацию см. в разделе Использование точек редактирования для редактирования или обрезки фигуры.
Обрезать до формы, например круга
См. Обрезка изображения по фигуре.
Прочие культуры
Выберите заголовок ниже, чтобы открыть его и просмотреть подробные инструкции.
Обрезка изображения до обычного размера фотографии или соотношения сторон позволяет легко поместить его в стандартную рамку изображения. Вы также можете использовать этот инструмент для предварительного просмотра того, как изображение будет соответствовать определенному соотношению сторон перед кадрированием.
Используйте Insert > Picture , чтобы добавить изображение в файл Office (например, документ Word, презентацию PowerPoint или книгу Excel).

Нажмите на картинку.
Нажмите Инструменты для работы с рисунками > Format и в группе Size щелкните стрелку под Crop .
В появившемся меню выберите Соотношение сторон , затем щелкните нужное соотношение.
Появится прямоугольник обрезки, показывающий, как будет выглядеть изображение, обрезанное до выбранного соотношения сторон.
org/ListItem»>Когда вы закончите, нажмите клавишу ESC или щелкните в любом месте документа за пределами изображения.
При желании отрегулируйте область обрезки с помощью маркеров обрезки, как описано в разделе «Обрезка изображения».
См. Начните с фигуры и добавьте к ней изображение.
Приложения Paint (в некоторых версиях Windows) и Paint 3D (в Windows 10) помогают обрезать изображение. Откройте свое изображение в приложении, и вы увидите кнопку Crop на панели инструментов. Посмотрите этот краткий видеообзор о некоторых функциях приложения Paint 3D.
По умолчанию после обрезки изображения обрезанные области остаются частью файла, скрытыми от просмотра. Однако вы можете уменьшить размер файла, удалив обрезанные области из файла изображения. Это также помогает предотвратить просмотр удаленных вами частей изображения другими людьми.
Однако вы можете уменьшить размер файла, удалив обрезанные области из файла изображения. Это также помогает предотвратить просмотр удаленных вами частей изображения другими людьми.
Важно: Если вы удалили обрезанные области, а затем передумали, вы можете нажать кнопку Отменить , чтобы восстановить их. Удаление можно отменить до тех пор, пока файл не будет сохранен.
Чтобы удалить обрезанные области из файла изображения:
Выберите изображение или изображения, из которых вы хотите удалить обрезанные области.
Щелкните Работа с рисунками > Формат и в группе Настройка щелкните Сжатие изображений .
 Появится диалоговое окно с параметрами сжатия.
Появится диалоговое окно с параметрами сжатия.Если вы не видите вкладки Picture Tools и Format , убедитесь, что вы выбрали фото. Возможно, вам придется дважды щелкнуть изображение, чтобы выбрать его и открыть вкладку Format . Кроме того, если размер экрана уменьшен, вы можете увидеть только значок Compress Pictures .
В разделе Параметры сжатия убедитесь, что Удалить обрезанные области изображений 9Флажок 0006 установлен.
Чтобы удалить кадрирование только для выбранного изображения или изображений, а не для всех изображений в файле, установите флажок Применить только к этому изображению .

При необходимости выберите параметр Разрешение .
Нажмите OK .
Совет: Дополнительные сведения об уменьшении размера файла изображений и сжатии изображений см. в разделе Уменьшение размера файла изображения.
См. также
Вырезать или закрыть часть изображения
Вставить картинки
Добавление рисунка в документ Word
Уменьшить размер файла изображения
Используйте параметры макета Word для перемещения изображений
Обтекание изображения текстом в Word
Обрезать поля изображения
Используйте Insert > Pictures , чтобы добавить изображение в файл Office (например, документ Word, презентацию PowerPoint или книгу Excel).
Нажмите на картинку, затем нажмите кнопку Формат изображения вкладка на ленте панели инструментов.
На вкладке Picture Format выберите Crop .
Черные маркеры обрезки появляются по краям и углам изображения.
Обрежьте изображение, перетащив любой маркер обрезки внутрь. Если вы перетащите один из угловых маркеров, он обрежет две смежные стороны одновременно.
Щелкните вдали от изображения, чтобы увидеть обрезанное изображение.
Примечание. После обрезки изображения обрезанные части скрываются, но остаются частью файла изображения. Чтобы окончательно удалить обрезанную часть и уменьшить размер изображения, см. раздел ниже на этой странице под названием «Удалить обрезанные области изображения».
Обрезать до определенной формы
См. Обрезка изображения по фигуре.
Удалить обрезанные области изображения
По умолчанию даже после обрезки части изображения обрезанные части остаются частью файла изображения. Однако вы можете уменьшить размер файла, удалив обрезки из файла изображения. Это также помогает предотвратить просмотр удаленных вами частей изображения другими людьми.
Однако вы можете уменьшить размер файла, удалив обрезки из файла изображения. Это также помогает предотвратить просмотр удаленных вами частей изображения другими людьми.
Важно: Удаление обрезанных областей изображения нельзя отменить. Поэтому делать это следует только после того, как вы уверены, что сделали все обрезки и изменения, которые хотите.
Чтобы удалить обрезанные области файла изображения:
Щелкните изображение или изображения, из которых вы хотите удалить обрезанные области.
На вкладке Формат изображения нажмите Сжать изображения .

(Если вы не видите вкладку Формат изображения , убедитесь, что вы выбрали изображение.)
Установите флажок Удалить обрезанные области изображений .
Чтобы удалить кадрирование только для выбранного изображения или изображений, а не для всех изображений в файле, выберите Только выбранные изображения .
См. также
Вставка изображений в Office для Mac
Перемещение, поворот или группировка изображения, текстового поля или другого объекта в Office для Mac
Изменение размера изображения, фигуры, текстового поля или объекта WordArt
Управление обтеканием объектов текстом в Word для Mac
В Word для Интернета и PowerPoint для Интернета вы можете выполнить базовую обрезку изображения — обрезать ненужные поля изображения. Однако только настольные приложения могут удалять обрезанные области с изображения.
Однако только настольные приложения могут удалять обрезанные области с изображения.
Обрезать картинку
Выберите изображение, которое хотите обрезать.
На ленте выберите вкладку Изображение .
Выберите стрелку вниз рядом с Crop , затем выберите Crop .
Черные маркеры обрезки появляются по краям изображения.
org/ListItem»>Когда вы закончите обрезку полей, щелкните за границей изображения, чтобы сохранить изменения.
Наведите указатель мыши на маркер обрезки, затем щелкните и перетащите внутрь, чтобы обрезать поля изображения.
Важно: Обрезанные части изображения не удаляются из файла и потенциально могут быть видны другим; включая поисковые системы, если обрезанное изображение размещено в Интернете. Только настольные приложения Office могут удалять обрезанные области из базового файла изображения.
Обрезать изображение по форме
Подробные сведения см. в разделе Поместить изображение внутри фигуры.
Просмотр фотографий по местоположению в программе «Фото» на Mac
Искать в этом руководстве
- Добро пожаловать
- Обзор импорта
- Из фотографий iCloud
- С камеры или телефона
- С запоминающих устройств, DVD-дисков и т.
 д.
д. - Из почты, Safari и других приложений
- Импорт фотографий из другой библиотеки
- Где фотографии, которые я импортировал?
- Просмотрите свои фотографии
- Просмотр отдельных фотографий
- Добавьте заголовки, подписи и многое другое
- Взаимодействуйте с текстом на фотографии с помощью Live Text
- Используйте визуальный поиск, чтобы узнать о фотографии
- Просмотр фотографий, которыми с вами поделились другие
- Удалить фотографии или восстановить удаленные
- Скрыть фотографии от просмотра
- Просмотр серий фотографий
- Воспроизведение видеоклипов
- Просмотр воспоминаний
- Персонализируйте воспоминания
- Просмотр фотографий по тому, кто на них изображен
- Просмотр фотографий по местоположению
- Показать определенные типы элементов
- Поиск фотографий по тексту, содержанию или дате
- Поиск фотографий по ключевому слову
- Что такое альбомы?
- Создание альбомов
- Создание смарт-альбомов
- Группировать альбомы в папки
- Основы редактирования
- Обрезайте и выпрямляйте фотографии
- Используйте фильтр, чтобы изменить фотографию
- Настройте свет, экспозицию и другие параметры фотографии
- Ретушь фотографий
- Убрать эффект красных глаз
- Отрегулируйте баланс белого фотографии
- Применение корректировок кривых
- Применить настройки уровней
- Изменить определение
- Применение изменений к определенным цветам
- Снизить уровень шума
- Повышение резкости фотографии
- Изменение освещения фотографии в портретном режиме
- Применить виньетку
- Напишите или нарисуйте на фотографии
- Используйте другие приложения при редактировании в Фото
- Изменить живое фото
- Изменить видео
- Редактировать видео в кинематографическом режиме
- Что такое общие альбомы?
- Включите общие альбомы
- Создать общий альбом
- Добавляйте, удаляйте и редактируйте фотографии в общем альбоме
- Добавить или удалить подписчиков
- Подпишитесь на общие альбомы
- Используйте сообщения и почту для обмена фотографиями
- Используйте AirDrop для обмена фотографиями
- Делитесь фотографиями с помощью других приложений и веб-сайтов
- Экспорт фотографий, видео, слайд-шоу и воспоминаний
- Создавайте слайд-шоу
- Создавайте проекты с помощью сторонних приложений
- Закажите профессиональную печать
- Распечатайте свои фотографии
- Обзор системной библиотеки фотографий
- Создайте дополнительные библиотеки
- Резервное копирование библиотеки фотографий
- Восстановить из Time Machine
- Восстановить библиотеку
- Изменить место хранения фотографий и видео
- Изменить настройки фотографий
- Сочетания клавиш и жесты
- Авторские права
Если ваша камера поддерживает GPS (как iPhone) или вы добавили информацию GPS к своим фотографиям, приложение «Фото» может автоматически отображать ваши фотографии на карте.

 Геометрия. 7 класс. ФГОС , Бабенко Светлана Павловна, Маркова Ирина Сергеевна. В пособии представлены контрольно-измерительные материалы (КИМы) по геометрии для проведения текущего, тематического и итогового контроля качества знаний учащихся 7 класса. Содержание пособия…
Геометрия. 7 класс. ФГОС , Бабенко Светлана Павловна, Маркова Ирина Сергеевна. В пособии представлены контрольно-измерительные материалы (КИМы) по геометрии для проведения текущего, тематического и итогового контроля качества знаний учащихся 7 класса. Содержание пособия…

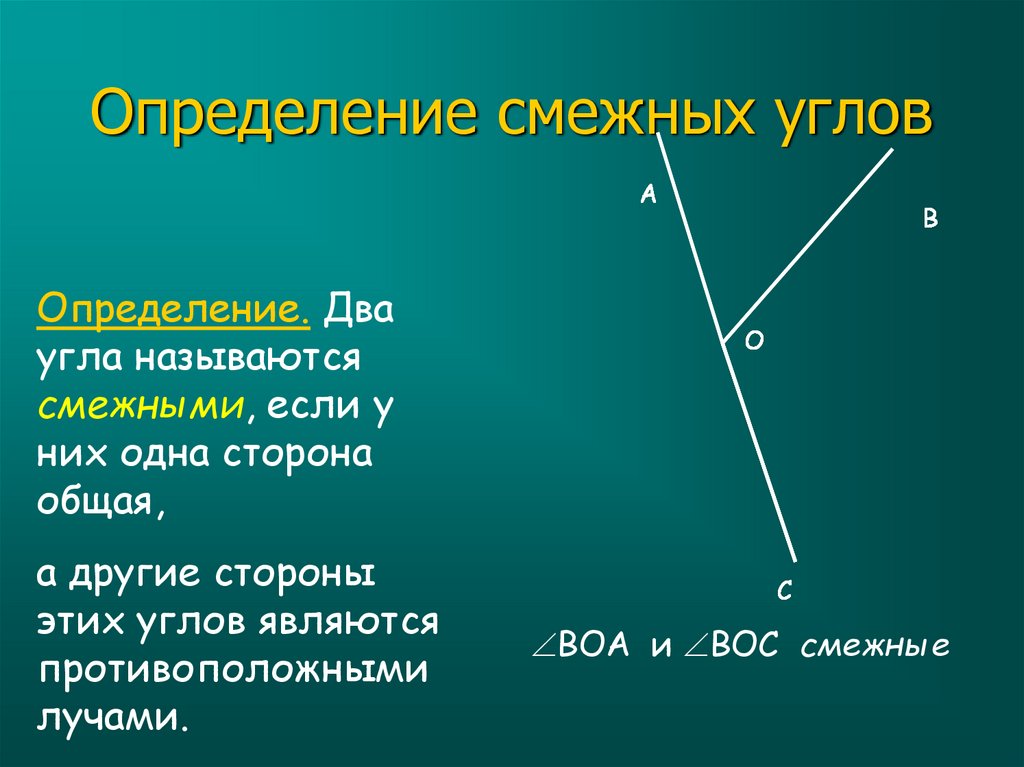 Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузова, С.Б. Кадомцев, В.В. Прасолова, под редакцией В.А. Садовничего. — М.: Просвещение, 2010.
Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузова, С.Б. Кадомцев, В.В. Прасолова, под редакцией В.А. Садовничего. — М.: Просвещение, 2010.