Собственная скорость катера 12,8 километров час скорость … -reshimne.ru
Новые вопросы
Ответы
12,8 + 1,7= 13,5 скорость по теч, 12,8 — 1,7 = 11,1 скорость против
Похожие вопросы
Помогите пж это важно к завтрашниму дню надо…
Найти значение m и n, при которых векторы ā(2;1;-2) и b (-4;m;n) есть колинеарными….
СРОЧНО!
два равных круга касаются друг друга и внутренним образом касаются некоторого третьего круга. Найдите радиус третьего круга, если периметр треугольника, вершинами которого являются центры указанных кругов ,равен 24см….
Вычисли уменьшаемое 80+20 вычитаемое 12 разность?. ..
..
Запишите все правильные несократимые дроби со знаменателем 20…
Напишите сумму 265 минус 16 и 3 плюс 14 плюс 98 плюс 49 Икс плюс 32 и игрек плюс 13 минус 98 и 5 плюс 56…
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский язык
Химия
Физика
Биология
Другие предметы
История
Обществознание
Окружающий мир
География
Українська мова
Українська література
Қазақ тiлi
Беларуская мова
Информатика
Экономика
МузыкаПраво
Французский язык
Немецкий язык
МХК
ОБЖ
Психология
Задачи для 5-6 классов — Движение по воде
1.
2. Собственная скорость катера 12,4 км/ч. Скорость течения реки 3,6 км/ч. Найдите скорость катера по течению реки.
3. Собственная скорость теплохода 32,8 км/ч. Скорость течения реки 3,7 км/ч. Найдите скорость теплохода против течения реки.
4. Скорость катера в стоячей воде 12,3 км/ч. Скорость течения реки 2,8 км/ч. Найдите скорость катера против течения реки.
5. Собственная скорость катера 12,3 км/ч. Скорость течения реки 3,8 км/ч. Найдите скорость катера по течению и против течения реки.
6. Собственная скорость моторной лодки 23,6 км/ч. Скорость течения реки 2,9 км/ч. Найдите скорость моторной лодки по течению и против течения реки.
7. Скорость катера в стоячей воде 11,9 км/ч, а по течению реки -14,7 км/ч. Найдите скорость течения реки.
8. Скорость лодки по течению реки 8,2 км/ч. Собственная скорость лодки 5,8 км/ч. Найдите скорость течения реки.
Собственная скорость лодки 5,8 км/ч. Найдите скорость течения реки.
9. По течению реки катер за 1 ч проходит 32,3 км. Найдите скорость катера против течения, если скорость течения реки 4,5 км/ч.
10. Против течения реки теплоход за 1 ч проходит 26,7 км. Найдите скорость теплохода по течению, если скорость течения реки 3,8 км/ч.
11. Скорость моторной лодки по течению реки 25,5 км/ч. Скорость течения реки 3,7 км/ч. Найдите собственную скорость моторной лодки.
12. Скорость теплохода по течению реки 33,1 км/ч. Скорость течения реки 2,9 км/ч. Найдите собственную скорость теплохода.
13. Скорость катера против течения реки 21,2 км/ч. Скорость течения реки 4,8 км/ч. Найдите собственную скорость катера.
14. Скорость лодки против течения реки 9,1 км/ч. Скорость течения реки 2,7 км/ч. Найдите собственную скорость лодки.
15. Собственная скорость катера 21,7 км/ч, а его скорость по течению реки — 24,2 км/ч. Найдите скорость катера против течения реки.
Найдите скорость катера против течения реки.
16. Собственная скорость теплохода 47,5 км/ч, а его скорость по течению реки — 51,3 км/ч. Найдите скорость теплохода против течения реки.
17. Собственная скорость теплохода 41,2 км/ч, а его скорость против течения реки — 37,6 км/ч. Найдите скорость теплохода по течению реки.
18. Собственная скорость лодки 4,5 км/ч, а ее скорость против течения — 3,8 км/ч. Найдите скорость лодки по течению реки.
19. Скорость катера по течению реки 28,4 км/ч. Скорость течения реки 3,9 км/ч. Найдите собственную скорость катера и его скорость против течения реки.
20. Скорость теплохода по течению реки 53,1 км/ч. Скорость течения реки 3,6 км/ч. Найдите собственную скорость теплохода и его скорость против течения реки.
21. Скорость лодки против течения реки 3,8 км/ч. Скорость течения реки 1,7 км/ч. Найдите собственную скорость лодки и ее скорость по течению реки.
22. Скорость катера против течения реки 23,6 км/ч. Скорость течения реки 2,8 км/ч. Найдите собственную скорость катера и его скорость по течению реки.
Скорость течения реки 2,8 км/ч. Найдите собственную скорость катера и его скорость по течению реки.
23. Скорость катера по течению реки 19,2 км/ч, а против течения -14,8 км/ч. Найдите скорость течения реки.
24. Скорость лодки по течению реки 5,4 км/ч, а против течения -3,6 км/ч. Найдите скорость течения реки.
25. Скорость теплохода по течению реки 48,6 км/ч, а против течения — 42,4 км/ч. Найдите собственную скорость теплохода.
26. Скорость моторной лодки по течению реки 7,1 км/ч, а против течения — 3,5 км/ч. Найдите собственную скорость моторной лодки.
27. Скорость катера по течению реки 18,2 км/ч, а против течения -12,4 км/ч. Какой путь по этой реке преодолеет плот за 4 ч?
28. Скорость теплохода по течению реки 24,4 км/ч, а против течения — 18,8 км/ч. Какой путь по этой реке преодолеет плот за 6 ч?
29. Собственная скорость теплохода 48,2 км/ч, а его скорость против течения реки — 45,5 км/ч. Какое расстояние пройдет теплоход по течению реки за 5 ч?
Какое расстояние пройдет теплоход по течению реки за 5 ч?
30. Собственная скорость теплохода 57,3 км/ч, а его скорость против течения реки — 43,7 км/ч. Какое расстояние пройдет теплоход по течению реки за 3 ч?
31. Моторная лодка, собственная скорость которой 12,6 км/ч, прошла за 3 ч по течению реки 46,2 км. Найдите скорость течения реки.
32. Катер, собственная скорость которого 8,4 км/ч, прошел за 2 ч по течению реки 20,2 км. Найдите скорость течения реки.
33. Скорость течения реки 4,6 км/ч. Теплоход за 4 ч прошел против течения 154,4 км. Какова собственная скорость теплохода?
34. Скорость течения реки 2,9 км/ч. Катер за 5 ч прошел против течения 35,5 км. Какова собственная скорость катера?
35. Туристы проплыли на лодке 24 км вниз по реке до острова и, побыв там, вернулись в лагерь. Скорость течения реки 2 км/ч, собственная скорость лодки 8 км/ч. Сколько времени туристы были в пути?
36. До места рыбалки вверх по реке 12 км. Скорость течения реки 2 км/ч. Собственная скорость лодки, в которой друзья отправились на рыбалку, — 8 км/ч. Сколько времени будет потрачено на то, чтобы добраться к месту рыбалки, и сколько времени уйдет на обратный путь?
Скорость течения реки 2 км/ч. Собственная скорость лодки, в которой друзья отправились на рыбалку, — 8 км/ч. Сколько времени будет потрачено на то, чтобы добраться к месту рыбалки, и сколько времени уйдет на обратный путь?
37. Собственная скорость лодки 9 км/ч. Скорость течения реки 3 км/ч. Сколько времени понадобится, чтобы на этой лодке проплыть 48 км по реке и вернуться обратно? 5 38. Собственная скорость лодки 15 км/ч. Скорость течения реки 3 км/ч. Сколько времени понадобится, чтобы на этой лодке проплыть 36 км по реке и вернуться обратно?
39. Расстояние между двумя причалами 24 км. Сколько времени потратит катер на путь от одного причала до другого и обратно, если его собственная скорость 12 км/ч, а скорость течения реки — 4 км/ч?
40. Расстояние между двумя городами 240 км. Сколько времени потратит теплоход на путь от одного города до другого и обратно, если его собственная скорость 54 км/ч, а скорость течения реки — 6 км/ч?
41. Лодка проплывает по течению реки 36,6 км за 6 ч. Скорость лодки против течения реки 2,5 км/ч. Найдите собственную скорость лодки и скорость течения реки.
Скорость лодки против течения реки 2,5 км/ч. Найдите собственную скорость лодки и скорость течения реки.
42. Катер проплывает против течения реки 24 км за 5 ч. Его скорость по течению реки — 8,2 км/ч. Найдите собственную скорость катера и скорость течения реки.
43. Собственная скорость катера 11,6 км/ч. Скорость течения реки 4,9 км/ч. Сначала катер плыл 2,4 ч против течения реки, а потом 1,5 ч — по озеру. Какое расстояние прошел катер за это время?
44. Собственная скорость моторной лодки 17,2 км/ч. Скорость течения реки 2,7 км/ч. Сначала лодка плыла 1,5 ч против течения реки, а потом 3,2 ч — по озеру. Какое расстояние прошла моторная лодка за это время?
45. Катер проплыл 1,3 ч по озеру, а потом 2,5 ч — вниз по реке. Какое расстояние преодолел катер за это время, если его собственная скорость 24,6 км/ч, а скорость течения реки 3,8 км/ч?
46. Теплоход плыл 4,2 ч по озеру, а потом 3,4 ч — вниз по реке. Какое расстояние проплыл теплоход за это время, если его собственная скорость 52,3 км/ч, а скорость течения реки 4,6 км/ч?
47. По течению реки теплоход прошел 84 км за 4 ч, а 45 км против течения — за 3 ч. Найдите скорость течения реки.
По течению реки теплоход прошел 84 км за 4 ч, а 45 км против течения — за 3 ч. Найдите скорость течения реки.
48. По течению реки катер прошел 64 км за 8 ч, а 12 км против течения — за 2 ч. Найдите скорость течения реки.
49. По течению реки лодка проходит 72 км за 6 ч, а 56 км против течения — за 8 ч. Найдите собственную скорость лодки.
50. По течению реки теплоход прошел 65 км за 5 ч, а 24 км против течения — за 3 ч. Найдите собственную скорость теплохода.
Как находится собственная скорость. Задачи на движение по воде
Данный материал представляет собой систему задач по теме “Движение”.
Цель: помочь учащимся более полно овладеть технологиями решения задач по данной теме.
Задачи на движение по воде.
Очень часто человеку приходится совершать движения по воде: реке, озеру, морю.
Сначала он это делал сам, потом появились плоты,
лодки, парусные корабли. С развитием техники
пароходы, теплоходы, атомоходы пришли на помощь
человеку.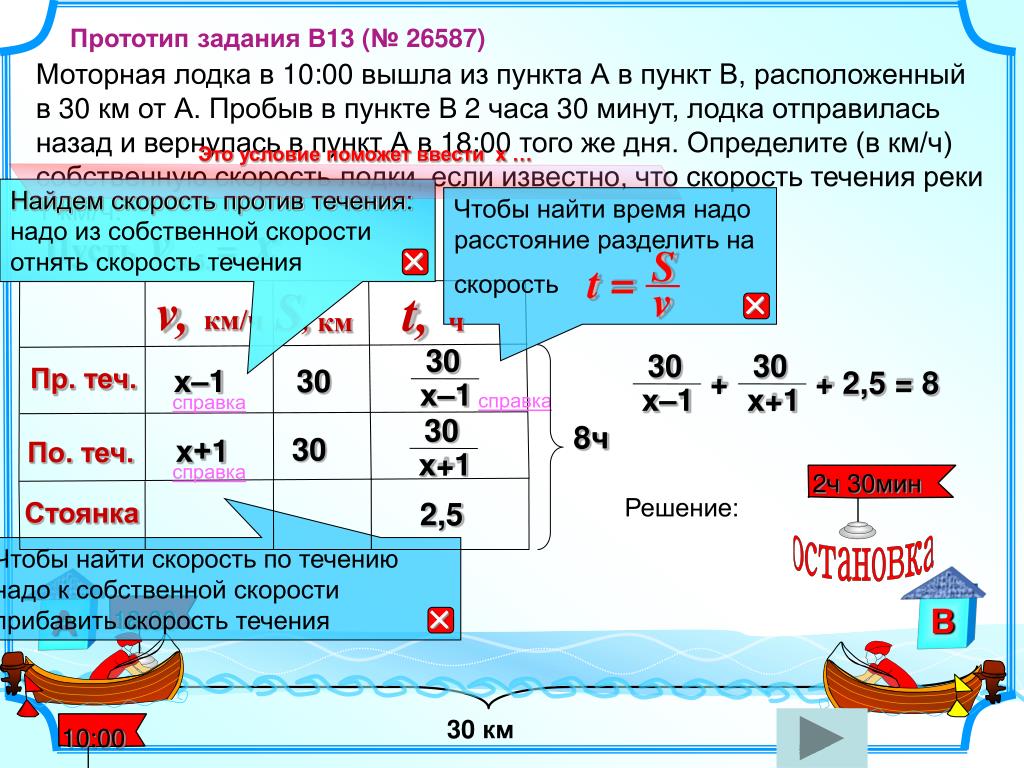 И всегда его интересовали длина пути и
время, затраченное на его преодоление.
И всегда его интересовали длина пути и
время, затраченное на его преодоление.
Представим себе, что на улице весна. Солнце растопило снег. Появились лужицы и побежали ручьи. Сделаем два бумажных кораблика и пустим один из них в лужу, а второй — в ручей. Что же произойдет с каждым из корабликов?
В луже кораблик будет стоять на месте, а в ручейке — поплывет, так как вода в нем «бежит» к более низкому месту и несет его с собой. То же самое будет происходить с плотом или лодкой.
В озере они будут стоять на месте, а в реке – плыть.
Рассмотрим первый вариант: лужа и озеро. Вода в них не движется и называется стоячей .
Кораблик поплывет по луже только в том случае, если мы его подтолкнем или если подует ветер. А лодка начнет двигаться в озере при помощи весел или если она оснащена мотором, то есть за счет своей скорости. Такое движение называют движением в стоячей воде .
Отличается ли оно от движения по дороге? Ответ:
нет. А это значит, что мы с вами знаем как
действовать в этом случае.
Задача 1. Скорость катера по озеру равна 16 км/ч.
Какой путь пройдет катер за 3 часа?
Ответ: 48 км.
Следует запомнить, что скорость катера в стоячей воде называют собственной скоростью .
Задача 2. Моторная лодка за 4 часа проплыла по озеру 60 км.
Найдите собственную скорость моторной лодки.
Ответ: 15 км/ч.
Задача 3. Сколько времени потребуется лодке, собственная скорость которой
равна 28 км/ч, чтобы проплыть по озеру 84 км?
Ответ: 3 часа.
Итак, чтобы найти длину пройденного пути, необходимо скорость умножить на время.
Чтобы найти скорость, необходимо длину пути разделить на время.
Чтобы найти время, необходимо длину пути разделить на скорость.
Чем же отличается движение по озеру от
движения по реке?
Вспомним бумажный кораблик в ручье. Он плыл, потому что вода в нем движется.
Такое движение называют движением по течению .
А в обратную сторону – движением против
течения .
Итак, вода в реке движется, а значит имеет свою скорость. И называют ее скоростью течения реки . (Как ее измерить?)
Задача 4. Скорость течения реки равна 2 км/ч. На сколько километров река относит
любой предмет (щепку, плот, лодку) за 1час, за 4 часа?
Ответ: 2 км/ч, 8 км/ч.
Каждый из вас плавал в реке и помнит, что по течению плыть гораздо легче, чем против течения. Почему? Потому, что в одну сторону река «помогает» плыть, а в другую — «мешает».
Те же, кто не умеет плавать, могут представить себе ситуацию, когда дует сильный ветер. Рассмотрим два случая:
1) ветер дует в спину,
2) ветер дует в лицо.
И в том и в другом случае идти сложно. Ветер в спину заставляет бежать, а значит, скорость нашего движения увеличивается. Ветер в лицо сбивает нас, притормаживает. Скорость при этом уменьшается.
Остановимся на движении по течению реки. Мы уже
говорили о бумажном кораблике в весеннем ручье.
Вода понесет его вместе с собой.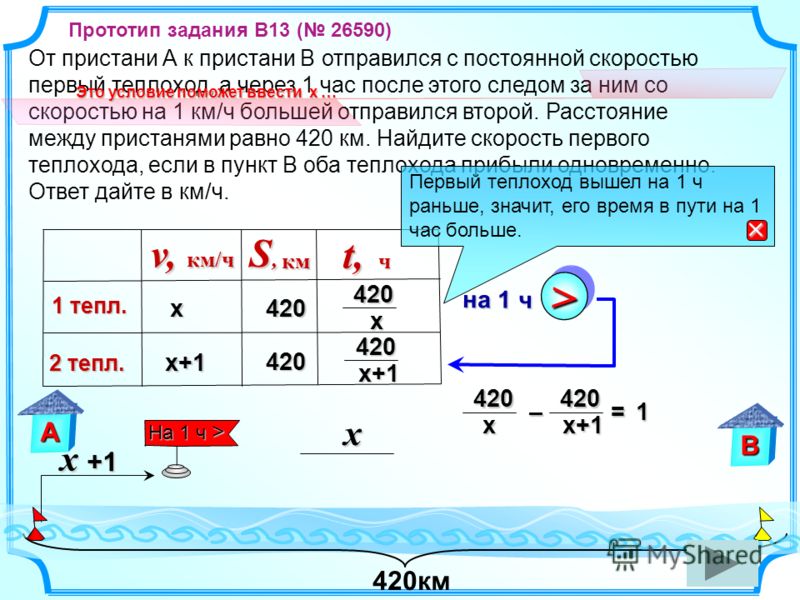 И лодка,
спущенная на воду, поплывет со скоростью течения.
Но если у нее есть собственная скорость, то она
поплывет еще быстрее.
И лодка,
спущенная на воду, поплывет со скоростью течения.
Но если у нее есть собственная скорость, то она
поплывет еще быстрее.
Следовательно, чтобы найти скорость движения по течению реки, необходимо сложить собственную скорость лодки и скорость течения.
Задача 5. Собственная скорость катера равна 21 км/ч, а скорость течения реки 4 км/ч. Найдите скорость катера по течению реки.
Ответ: 25км/ч.
Теперь представим себе, что лодка должна плыть против течения реки. Без мотора или хотя бы весел, течение отнесет ее в обратную сторону. Но, если придать лодке собственную скорость (завести мотор или посадить гребца), течение будет продолжать отталкивать ее назад и мешать двигаться вперед со своей скоростью.
Поэтому, чтобы найти скорость лодки против течения, необходимо из собственной скорости вычесть скорость течения.
Задача 6. Скорость течения реки равна 3 км/ч, а собственная скорость катера 17 км/ч.
Найдите скорость катера против течения.
Ответ: 14 км/ч.
Задача 7. Собственная скорость теплохода равна 47,2 км/ч, а скорость течения реки 4,7 км/ч. Найдите скорость теплохода по течению и против течения.
Ответ: 51,9 км/ч; 42,5 км/ч.
Задача 8. Скорость моторной лодки по течению равна12,4 км/ч. Найдите собственную скорость лодки, если скорость течения реки 2,8 км/ч.
Ответ: 9,6 км/ч.
Задача 9. Скорость катера против течения равна 10,6 км/ч. Найдите собственную скорость катера и скорость по течению, если скорость течения реки 2,7 км/ч.
Ответ: 13,3 км/ч; 16 км/ч.
Связь между скоростью по течению и
скоростью против течения.
Введем следующие обозначения:
V с. — собственная скорость,
V теч. — скорость течения,
V по теч. — скорость по течению,
V пр.теч. — скорость против течения.
Тогда можно записать следующие формулы:
V no теч = V c + V теч;
V np. теч = V c — V теч.;
Попытаемся изобразить это графически:
Вывод: разность скоростей по течению
и против течения равна удвоенной скорости
течения.
Vno теч — Vnp. теч = 2 Vтеч.
Vтеч = (V по теч — Vnp. теч): 2
1) Скорость катера против течения равна 23 км/ч, а скорость течения 4 км/ч.
Найдите скорость катера по течению.
Ответ: 31 км/ч.
2) Скорость моторной лодки по течению реки равна 14 км/ч/ а скорость течения 3 км/ч. Найдите скорость лодки против течения
Ответ: 8 км/ч.
Задача 10. Определите скорости и заполните таблицу:
* — при решении п.6 смотри рис.2.
Ответ: 1) 15 и 9; 2) 2 и 21; 3) 4 и 28; 4) 13 и 9; 5)23 и 28; 6) 38 и 4.
Решение задач на «движение по воде» многим дается с трудом. В них существует несколько видов скоростей, поэтому решающие начинаю путаться. Чтобы научиться решать задачи такого типа, надо знать определения и формулы. Умение составлять схемы очень облегчает понимание задачи, способствует правильному составлению уравнения. А правильно составленное уравнение — самое главное в решении любого типа задач.
Инструкция
В задачах «на движение по реке» присутствуют скорости: собственная скорость (Vс), скорость по течению (Vпо теч. ), скорость против течения (Vпр. теч.), скорость течения (Vтеч.). Необходимо отметить, что собственная скорость водного суда – это скорость в стоячей воде. Чтобы найти скорость по течению, надо к скорости течения прибавить собственную. Для того чтобы найти скорость против течения, надо из собственной скорости вычесть скорость течения.
), скорость против течения (Vпр. теч.), скорость течения (Vтеч.). Необходимо отметить, что собственная скорость водного суда – это скорость в стоячей воде. Чтобы найти скорость по течению, надо к скорости течения прибавить собственную. Для того чтобы найти скорость против течения, надо из собственной скорости вычесть скорость течения.
Первое, что необходимо выучить и знать «на зубок» — формулы. Запишите и запомните:
Vпо теч=Vс+Vтеч.
Vпр. теч.=Vс-Vтеч.
Vпр. теч=Vпо теч. — 2Vтеч.
Vпо теч.=Vпр. теч+2Vтеч.
Vтеч.=(Vпо теч. — Vпр. теч)/2
Vс=(Vпо теч.+Vпр теч.)/2 или Vс=Vпо теч.+Vтеч.
На примере разберем, как находить собственную скорость и решать задачи такого типа.
Пример 1.Скорость лодки по течению 21,8км/ч, а против течения 17,2 км/ч. Найти собственную скорость лодки и скорость течения реки.
Решение: Согласно формулам: Vс=(Vпо теч.+Vпр теч.)/2 и Vтеч.=(Vпо теч. — Vпр. теч)/2, найдем:
Vтеч = (21,8 — 17,2)/2=4,62=2,3 (км/ч)
Vс = Vпр теч. +Vтеч=17,2+2,3=19,5 (км/ч)
+Vтеч=17,2+2,3=19,5 (км/ч)
Ответ: Vc=19,5 (км/ч), Vтеч=2,3 (км/ч).
Пример 2. Пароход прошел против течения 24 км и вернулся обратно, затратив на обратный путь на 20 мин меньше, чем при движении против течения. Найдите его собственную скорость в неподвижной воде, если скорость течения равна 3 км/ч.
За Х примем собственную скорость парохода. Составим таблицу, куда занесем все данные.
Против теч. По течению
Расстояние 24 24
Скорость Х-3 Х+3
время 24/ (Х-3) 24/ (Х+3)
Зная, что на обратный путь пароход затратил на 20 минут времени меньше, чем на путь по течению, составим и решим уравнение.
20 мин=1/3 часа.
24/ (Х-3) – 24/ (Х+3) = 1/3
24*3(Х+3) – (24*3(Х-3)) – ((Х-3)(Х+3))=0
72Х+216-72Х+216-Х2+9=0
Х=21(км/ч) – собственная скорость парохода.
Ответ: 21 км/ч.
Обратите внимание
Скорость плота считается равной скорости водоема.
Согласно учебной программе по математике дети обязаны обучиться решать задачи на движение еще в исходной школе. Впрочем задачи такого вида зачастую вызывают у учащихся затруднение. Значимо,чтоб ребенок осознал, что такое собственная скорость , скорость течения, скорость по течению и скорость вопреки течения. Только при этом условии школьник сумеет легко решать задачи на движение.
Впрочем задачи такого вида зачастую вызывают у учащихся затруднение. Значимо,чтоб ребенок осознал, что такое собственная скорость , скорость течения, скорость по течению и скорость вопреки течения. Только при этом условии школьник сумеет легко решать задачи на движение.
Вам понадобится
- Калькулятор, ручка
Инструкция
1. Собственная скорость – это скорость катера либо иного средства передвижения в статичной воде. Обозначьте ее – V собств.Вода в реке находится в движении. Значит она имеет свою скорость , которая именуется скорость ю течения (V теч.)Скорость катера по течению реки обозначьте – V по теч., а скорость супротив течения – V пр. теч.
2. Сейчас запомните формулы, нужные для решения задач на движение:V пр. теч.= V собств. – V теч.V по теч.= V собств. + V теч.
3. Выходит, исходя из этих формул, дозволено сделать следующие итоги.Если катер движется вопреки течения реки, то V собств. = V пр. теч. + V теч.Если катер движется по течению, то V собств. = V по теч. – V теч.
= V пр. теч. + V теч.Если катер движется по течению, то V собств. = V по теч. – V теч.
4. Решим несколько задач на движение по реке.Задача 1. Скорость катера вопреки течения реки 12,1 км/ч. Обнаружьте собственную скорость катера, зная, что скорость течения реки 2 км/ч.Решение: 12,1 + 2 = 14, 1 (км/ч) – собственная скорость катера.Задача 2. Скорость катера по течению реки 16,3 км/ч, скорость течения реки 1,9 км/ч. Сколько метров прошел бы это катер за 1 мин., если находился в стоячей воде?Решение: 16,3 – 1,9 = 14,4 (км/ч) – собственная скорость катера. Переведем км/ч в м/мин: 14,4 / 0,06 = 240 (м/мин.). Значит, за 1 минуту катер прошел бы 240 м.Задача 3. Два катера отправились единовременно насупротив друг другу из 2-х пунктов. 1-й катер двигался по течению реки, а 2-й – вопреки течения. Встретились они через три часа. За это время 1-й катер прошел 42 км, а 2-й – 39 км.Обнаружьте собственную скорость всякого катера, если вестимо, что скорость течения реки 2 км/ч.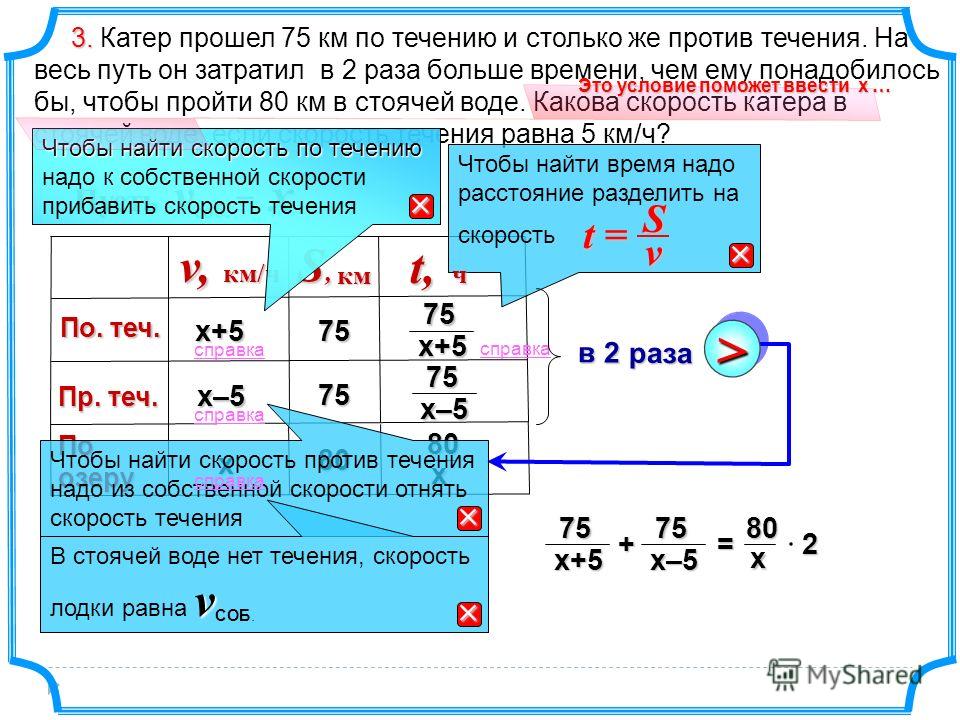 Решение: 1) 42 / 3 = 14 (км/ч) – скорость движения по течению реки первого катера. 2) 39 / 3 = 13 (км/ч) – скорость движения вопреки течения реки второго катера. 3) 14 – 2 = 12 (км/ч) – собственная скорость первого катера. 4) 13 + 2 = 15 (км/ч) – собственная скорость второго катера.
Решение: 1) 42 / 3 = 14 (км/ч) – скорость движения по течению реки первого катера. 2) 39 / 3 = 13 (км/ч) – скорость движения вопреки течения реки второго катера. 3) 14 – 2 = 12 (км/ч) – собственная скорость первого катера. 4) 13 + 2 = 15 (км/ч) – собственная скорость второго катера.
Задачи на движение кажутся трудными только на 1-й взор. Дабы обнаружить, скажем, скорость движения судна вопреки течения , довольно представить высказанную в задаче обстановку. Возьмите ребёнка в малое путешествие по реке, и школьник обучится “щелкать такие задачки, как орешки”.
Вам понадобится
- Калькулятор, ручка.
Инструкция
1. Согласно нынешней энциклопедии (dic.academic.ru), скорость – это колляция поступательного движения точки (тела), численно равная при равномерном движении отношению пройденного пути S к промежуточному времени t, т.е. V = S / t.
2. Для того дабы обнаружить скорость движения какого-нибудь судна супротив течения, надобно знать собственную скорость судна и скорость течения. Собственная скорость – это скорость движения судна в стоячей воде, скажем, в озере. Обозначим ее – V собств.Скорость течения определяется по тому, на какое расстояние река относит предмет за единицу времени. Обозначим ее – V теч.
Собственная скорость – это скорость движения судна в стоячей воде, скажем, в озере. Обозначим ее – V собств.Скорость течения определяется по тому, на какое расстояние река относит предмет за единицу времени. Обозначим ее – V теч.
3. Дабы обнаружить скорость движения судна супротив течения (V пр. теч.), надобно из собственной скорости судна вычесть скорость течения.Выходит, получили формулу: V пр. теч.= V собств. – V теч.
4. Обнаружим скорость движения судна вопреки течения реки, если знаменито, что собственная скорость судна равна 15,4 км/ч, а скорость течения реки – 3,2 км/ч.15,4 – 3,2 = 12,2 (км/ч) – скорость движения судна супротив течения реки.
5. В задачах на движение зачастую требуется перевести км/ч в м/с. Дабы это сделать, необходимо припомнить, что 1 км = 1000 м, 1 ч = 3600 с. Следственно, х км/ч = х * 1000 м / 3600 с = х / 3,6 м/с. Выходит, дабы перевести км/ч в м/с необходимо поделить на 3,6.Скажем, 72 км/ч = 72:3,6 = 20 м/с.Дабы перевести м/с в км/ч необходимо умножить на 3,6. Скажем, 30 м/с = 30 * 3,6 = 108 км/ч.
Скажем, 30 м/с = 30 * 3,6 = 108 км/ч.
6. Переведем х км/ч в м/мин. Для этого припомним, что 1 км = 1000 м, 1 ч = 60 мин. Значит, х км/ч = 1000 м / 60 мин. = х / 0,06 м/мин. Следственно, дабы перевести км/ч в м/мин. необходимо поделить на 0,06.Скажем, 12 км/ч = 200 м/мин.Дабы перевести м/мин. в км/ч нужно умножить на 0,06.Скажем, 250 м/мин. = 15 км/ч
Полезный совет
Не забывайте о том, в каких единицах вы измеряете скорость.
Обратите внимание!
Не позабудьте о том, в каких единицах вы измеряете скорость.Дабы перевести км/ч в м/с необходимо поделить на 3,6.Дабы перевести м/с в км/ч надобно умножить на 3,6.Дабы перевести км/ч в м/мин. необходимо поделить на 0,06.Дабы перевести м/мин. в км/ч нужно умножить на 0,06.
Полезный совет
Решить задачу на движение помогает рисунок.
Согласно учебной программе по математике дети должны научиться решать задачи на движение еще в начальной школе. Однако задачи такого вида часто вызывают у учащихся затруднение. Важно,чтоб ребенок понял, что такое собственная скорость , скорость течения, скорость по течению и скорость против течения. Только при этом условии школьник сможет легко решать задачи на движение.
Важно,чтоб ребенок понял, что такое собственная скорость , скорость течения, скорость по течению и скорость против течения. Только при этом условии школьник сможет легко решать задачи на движение.
Вам понадобится
- Калькулятор, ручка
Инструкция
Собственная скорость — это скорость катера или другого средства передвижения в неподвижной воде. Обозначьте ее — V собств.
Вода в реке находится в движении. Значит она имеет свою скорость , которая называется скорость ю течения (V теч.)
Скорость катера по течению реки обозначьте — V по теч., а скорость против течения — V пр. теч.
Теперь запомните формулы, необходимые для решения задач на движение:
V пр. теч.= V собств. — V теч.
V по теч.= V собств. + V теч.
Итак, исходя из этих формул, можно сделать следующие выводы.
Если катер движется против течения реки, то V собств. = V пр. теч. + V теч.
Если катер движется по течению, то V собств. = V по теч. — V теч.
= V по теч. — V теч.
Решим несколько задач на движение по реке.
Задача 1. Скорость катера против течения реки 12,1 км/ч. Найдите собственную скорость катера, зная, что скорость течения реки 2 км/ч.
Решение: 12,1 + 2 = 14, 1 (км/ч) — собственная скорость катера.
Задача 2. Скорость катера по течению реки 16,3 км/ч, скорость течения реки 1,9 км/ч. Сколько метров прошел бы это катер за 1 мин., если находился в стоячей воде?
Решение: 16,3 — 1,9 = 14,4 (км/ч) — собственная скорость катера. Переведем км/ч в м/мин: 14,4 / 0,06 = 240 (м/мин.). Значит, за 1 минуту катер прошел бы 240 м.
Задача 3. Два катера отправились одновременно навстречу друг другу из двух пунктов. Первый катер двигался по течению реки, а второй — против течения. Встретились они через три часа. За это время первый катер прошел 42 км, а второй — 39 км.Найдите собственную скорость каждого катера, если известно, что скорость течения реки 2 км/ч.
Решение: 1) 42 / 3 = 14 (км/ч) — скорость движения по течению реки первого катера.
2) 39 / 3 = 13 (км/ч) — скорость движения против течения реки второго катера.
3) 14 — 2 = 12 (км/ч) — собственная скорость первого катера.
4) 13 + 2 = 15 (км/ч) — собственная скорость второго катера.
Это скорость катера или другого средства передвижения в неподвижной воде. Обозначьте ее — V собств.
Вода в реке находится в движении. Значит она имеет свою скорость , которая скорость ю (V теч.)
Скорость катера по течению реки обозначьте — V по теч., а скорость против течения — V пр. теч.
Решим несколько задач на движение по реке.
Задача 1. Скорость катера против течения реки 12,1 км/ч. Найдите собственную скорость катера, зная, что скорость течения реки 2 км/ч.
Решение: 12,1 + 2 = 14, 1 (км/ч) — собственная скорость катера.
Задача 2. Скорость катера по течению реки 16,3 км/ч, скорость течения реки 1,9 км/ч. Сколько прошел бы это катер за 1 мин., если находился в стоячей воде?
Решение: 16,3 — 1,9 = 14,4 (км/ч) — собственная скорость катера. Переведем км/ч в м/мин: 14,4 / 0,06 = 240 (м/мин.). Значит, за 1 минуту катер прошел бы 240 м.
Переведем км/ч в м/мин: 14,4 / 0,06 = 240 (м/мин.). Значит, за 1 минуту катер прошел бы 240 м.
Задача 3. Два катера отправились одновременно навстречу друг другу из двух . Первый катер двигался по течению реки, а второй — против течения. Встретились они три часа. За это время первый катер прошел 42 км, а второй — 39 км.Найдите собственную скорость каждого катера, если известно, что скорость течения реки 2 км/ч.
Решение: 1) 42 / 3 = 14 (км/ч) — скорость движения по течению реки первого катера.
2) 39 / 3 = 13 (км/ч) — скорость движения против течения реки второго катера.
3) 14 — 2 = 12 (км/ч) — собственная скорость первого катера.
4) 13 + 2 = 15 (км/ч) — собственная скорость второго катера.
Обратите внимание
Не забудьте о том, в каких единицах вы измеряете скорость.
Чтобы перевести км/ч в м/с нужно разделить на 3,6.
Чтобы перевести м/с в км/ч нужно умножить на 3,6.
Чтобы перевести км/ч в м/мин. нужно разделить на 0,06.
Чтобы перевести м/мин. в км/ч надо умножить на 0,06.
Полезный совет
Решить задачу на движение помогает рисунок.
Задачи на движение кажутся сложными только на первый взгляд. Чтобы найти, например, скорость движения судна против течения , достаточно представить изложенную в задаче ситуацию. Возьмите ребёнка в небольшое путешествие по реке, и школьник научится «щелкать такие задачки, как орешки».
Вам понадобится
- Калькулятор, ручка.
Инструкция
Для того чтобы найти скорость движения какого-либо , нужно собственную скорость судна и скорость течения.Собственная скорость — это скорость движения судна в стоячей воде, например, в озере. Обозначим ее — V собств.Скорость течения определяется по тому, на расстояние река относит за единицу времени. Обозначим ее — V теч.
Чтобы найти скорость движения судна против течения (V пр. теч.), нужно из собственной скорости судна вычесть скорость течения.Итак, получили формулу: V пр. теч.= V собств. — V теч.
теч.= V собств. — V теч.
Собственная скорость и скорость течения. Задачи на движение по воде
Данный материал представляет собой систему задач по теме “Движение”.
Цель: помочь учащимся более полно овладеть технологиями решения задач по данной теме.
Задачи на движение по воде.
Очень часто человеку приходится совершать движения по воде: реке, озеру, морю.
Сначала он это делал сам, потом появились плоты, лодки, парусные корабли. С развитием техники пароходы, теплоходы, атомоходы пришли на помощь человеку. И всегда его интересовали длина пути и время, затраченное на его преодоление.
Представим себе, что на улице весна. Солнце растопило снег. Появились лужицы и побежали ручьи. Сделаем два бумажных кораблика и пустим один из них в лужу, а второй — в ручей. Что же произойдет с каждым из корабликов?
В луже кораблик будет стоять на месте, а в
ручейке — поплывет, так как вода в нем «бежит»
к более низкому месту и несет его с собой. То же
самое будет происходить с плотом или лодкой.
В озере они будут стоять на месте, а в реке – плыть.
Рассмотрим первый вариант: лужа и озеро. Вода в них не движется и называется стоячей .
Кораблик поплывет по луже только в том случае, если мы его подтолкнем или если подует ветер. А лодка начнет двигаться в озере при помощи весел или если она оснащена мотором, то есть за счет своей скорости. Такое движение называют движением в стоячей воде .
Отличается ли оно от движения по дороге? Ответ: нет. А это значит, что мы с вами знаем как действовать в этом случае.
Задача 1. Скорость катера по озеру равна 16 км/ч.
Какой путь пройдет катер за 3 часа?
Ответ: 48 км.
Следует запомнить, что скорость катера в стоячей воде называют собственной скоростью .
Задача 2. Моторная лодка за 4 часа проплыла по озеру 60 км.
Найдите собственную скорость моторной лодки.
Ответ: 15 км/ч.
Задача 3. Сколько времени потребуется лодке, собственная скорость которой
равна 28 км/ч, чтобы проплыть по озеру 84 км?
Ответ: 3 часа.
Итак, чтобы найти длину пройденного пути, необходимо скорость умножить на время.
Чтобы найти скорость, необходимо длину пути разделить на время.
Чтобы найти время, необходимо длину пути разделить на скорость.
Чем же отличается движение по озеру от
движения по реке?
Вспомним бумажный кораблик в ручье. Он плыл, потому что вода в нем движется.
Такое движение называют движением по течению . А в обратную сторону – движением против течения .
Итак, вода в реке движется, а значит имеет свою скорость. И называют ее скоростью течения реки . (Как ее измерить?)
Задача 4. Скорость течения реки равна 2 км/ч. На сколько километров река относит
любой предмет (щепку, плот, лодку) за 1час, за 4 часа?
Ответ: 2 км/ч, 8 км/ч.
Каждый из вас плавал в реке и помнит, что по
течению плыть гораздо легче, чем против течения.
Почему? Потому, что в одну сторону река
«помогает» плыть, а в другую — «мешает».
Те же, кто не умеет плавать, могут представить себе ситуацию, когда дует сильный ветер. Рассмотрим два случая:
1) ветер дует в спину,
2) ветер дует в лицо.
И в том и в другом случае идти сложно. Ветер в спину заставляет бежать, а значит, скорость нашего движения увеличивается. Ветер в лицо сбивает нас, притормаживает. Скорость при этом уменьшается.
Остановимся на движении по течению реки. Мы уже говорили о бумажном кораблике в весеннем ручье. Вода понесет его вместе с собой. И лодка, спущенная на воду, поплывет со скоростью течения. Но если у нее есть собственная скорость, то она поплывет еще быстрее.
Следовательно, чтобы найти скорость движения по течению реки, необходимо сложить собственную скорость лодки и скорость течения.
Задача 5. Собственная скорость катера равна 21 км/ч, а скорость течения реки 4 км/ч. Найдите скорость катера по течению реки.
Ответ: 25км/ч.
Теперь представим себе, что лодка должна плыть
против течения реки. Без мотора или хотя бы весел,
течение отнесет ее в обратную сторону. Но, если
придать лодке собственную скорость (завести
мотор или посадить гребца), течение будет
продолжать отталкивать ее назад и мешать
двигаться вперед со своей скоростью.
Без мотора или хотя бы весел,
течение отнесет ее в обратную сторону. Но, если
придать лодке собственную скорость (завести
мотор или посадить гребца), течение будет
продолжать отталкивать ее назад и мешать
двигаться вперед со своей скоростью.
Поэтому, чтобы найти скорость лодки против течения, необходимо из собственной скорости вычесть скорость течения.
Задача 6. Скорость течения реки равна 3 км/ч, а собственная скорость катера 17 км/ч.
Найдите скорость катера против течения.
Ответ: 14 км/ч.
Задача 7. Собственная скорость теплохода равна 47,2 км/ч, а скорость течения реки 4,7 км/ч. Найдите скорость теплохода по течению и против течения.
Ответ: 51,9 км/ч; 42,5 км/ч.
Задача 8. Скорость моторной лодки по течению равна12,4 км/ч. Найдите собственную скорость лодки, если скорость течения реки 2,8 км/ч.
Ответ: 9,6 км/ч.
Задача 9. Скорость катера против течения равна
10,6 км/ч. Найдите собственную скорость катера и
скорость по течению, если скорость течения реки
2,7 км/ч.
Ответ: 13,3 км/ч; 16 км/ч.
Связь между скоростью по течению и
скоростью против течения.
Введем следующие обозначения:
V с. — собственная скорость,
V теч. — скорость течения,
V по теч. — скорость по течению,
V пр.теч. — скорость против течения.
Тогда можно записать следующие формулы:
V no теч = V c + V теч;
V np. теч = V c — V теч.;
Попытаемся изобразить это графически:
Вывод: разность скоростей по течению и против течения равна удвоенной скорости течения.
Vno теч — Vnp. теч = 2 Vтеч.
Vтеч = (V по теч — Vnp. теч): 2
1) Скорость катера против течения равна 23 км/ч, а скорость течения 4 км/ч.
Найдите скорость катера по течению.
Ответ: 31 км/ч.
2) Скорость моторной лодки по течению реки равна 14 км/ч/ а скорость течения 3 км/ч. Найдите скорость лодки против течения
Ответ: 8 км/ч.
Задача 10. Определите скорости и заполните таблицу:
* — при решении п. 6 смотри рис.2.
6 смотри рис.2.
Ответ: 1) 15 и 9; 2) 2 и 21; 3) 4 и 28; 4) 13 и 9; 5)23 и 28; 6) 38 и 4.
Согласно учебной программе по математике дети должны научиться решать задачи на движение еще в начальной школе. Однако задачи такого вида часто вызывают у учащихся затруднение. Важно,чтоб ребенок понял, что такое собственная скорость , скорость течения, скорость по течению и скорость против течения. Только при этом условии школьник сможет легко решать задачи на движение.
Вам понадобится
- Калькулятор, ручка
Инструкция
Собственная скорость — это скорость катера или другого средства передвижения в неподвижной воде. Обозначьте ее — V собств.
Вода в реке находится в движении. Значит она имеет свою скорость , которая называется скорость ю течения (V теч.)
Скорость катера по течению реки обозначьте — V по теч., а скорость против течения — V пр. теч.
Теперь запомните формулы, необходимые для решения задач на движение:
V пр. теч.= V собств. — V теч.
теч.= V собств. — V теч.
V по теч.= V собств. + V теч.
Итак, исходя из этих формул, можно сделать следующие выводы.
Если катер движется против течения реки, то V собств. = V пр. теч. + V теч.
Если катер движется по течению, то V собств. = V по теч. — V теч.
Решим несколько задач на движение по реке.
Задача 1. Скорость катера против течения реки 12,1 км/ч. Найдите собственную скорость катера, зная, что скорость течения реки 2 км/ч.
Решение: 12,1 + 2 = 14, 1 (км/ч) — собственная скорость катера.
Задача 2. Скорость катера по течению реки 16,3 км/ч, скорость течения реки 1,9 км/ч. Сколько метров прошел бы это катер за 1 мин., если находился в стоячей воде?
Решение: 16,3 — 1,9 = 14,4 (км/ч) — собственная скорость катера. Переведем км/ч в м/мин: 14,4 / 0,06 = 240 (м/мин.). Значит, за 1 минуту катер прошел бы 240 м.
Задача 3. Два катера отправились одновременно навстречу друг другу из двух пунктов. Первый катер двигался по течению реки, а второй — против течения. Встретились они через три часа. За это время первый катер прошел 42 км, а второй — 39 км.Найдите собственную скорость каждого катера, если известно, что скорость течения реки 2 км/ч.
Встретились они через три часа. За это время первый катер прошел 42 км, а второй — 39 км.Найдите собственную скорость каждого катера, если известно, что скорость течения реки 2 км/ч.
Решение: 1) 42 / 3 = 14 (км/ч) — скорость движения по течению реки первого катера.
2) 39 / 3 = 13 (км/ч) — скорость движения против течения реки второго катера.
3) 14 — 2 = 12 (км/ч) — собственная скорость первого катера.
4) 13 + 2 = 15 (км/ч) — собственная скорость второго катера.
Итак, допустим, наши тела двигаются в одном направлении. Как ты думаешь, сколько случаев может быть для такого условия? Правильно, два.
Почему так получается? Уверена, что после всех примеров ты с легкостью сам разберешься, как вывести данные формулы.
Разобрался? Молодец! Пришло время решить задачу.
Четвертая задача
Коля едет на работу на машине со скоростью км/ч. Коллега Коли Вова едет со скоростью км/ч. Коля от Вовы живет на расстоянии км.
Через сколько времени Вова догонит Колю, если из дома они выехали одновременно?
Посчитал? Сравним ответы — у меня получилось, что Вова догонит Колю через часа или через минут.
Сравним наши решения…
Рисунок выглядит вот таким образом:
Похож на твой? Молодец!
Так как в задаче спрашивается, через сколько ребята встретились, а выехали они одновременно, то время, которое они ехали, будет одинаковым, так же как место встречи (на рисунке оно обозначено точкой). Составляя уравнения, возьмем время за.
Итак, Вова до места встречи проделал путь. Коля до места встречи проделал путь. Это понятно. Теперь разбираемся с осью передвижения.
Начнем с пути, который проделал Коля. Его путь () на рисунке изображен как отрезок. А из чего состоит путь Вовы ()? Правильно, из суммы отрезков и, где — изначальное расстояние между ребятами, а равен пути, который проделал Коля.
Исходя из этих выводов, получаем уравнение:
Разобрался? Если нет, просто прочти это уравнение еще раз и посмотри на точки, отмеченные на оси. Рисунок помогает, не правда ли?
Рисунок помогает, не правда ли?
часа или минут минут.
Надеюсь, на этом примере ты понял, насколько важную роль играет грамотно составленный рисунок!
А мы плавно переходим, точнее, уже перешли к следующему пункту нашего алгоритма — приведение всех величин к одинаковой размерности.
Правило трех «Р» — размерность, разумность, расчет.
Размерность.
Далеко не всегда в задачах дается одинаковая размерность для каждого участника движения (как это было в наших легких задачках).
Например, можно встретить задачи, где сказано, что тела двигались определенное количество минут, а скорость их передвижения указана в км/ч.
Мы не можем просто взять и подставить значения в формулу — ответ получится неверный. Даже по единицам измерения наш ответ «не пройдет» проверку на разумность. Сравни:
Видишь? При грамотном перемножении у нас также сокращаются единицы измерения, и, соответственно, получается разумный и верный результат.
А что происходит, если мы не переводим в одну систему измерения? Странная размерность у ответа и % неверный результат.
Итак, напомню тебе на всякий случай значения основных единиц измерения длины и времени.
сантиметр = миллиметров
дециметр = сантиметров = миллиметров
метр = дециметров = сантиметров = миллиметров
километр = метров
минута = секунд
час = минут = секунд
сутки = часа = минут = секунд
Совет: Переводя единицы измерения, связанные с временем (минуты в часы, часы в секунды и т.д.) представь в голове циферблат часов. Невооруженным глазом видно, что минут это четверть циферблата, т.е. часа, минут это треть циферблата, т.е. часа, а минута это часа.
А теперь совсем простенькая задача:
Маша ехала на велосипеде из дома в деревню со скоростью км/ч на протяжении минут. Какое расстояние между машиным домом и деревней?
Посчитал? Правильный ответ — км.
минут — это час, и еще минут от часа (мысленно представил себе циферблат часов, и сказал, что минут — четверть часа), соответственно — мин = ч.
Разумность.Ты же понимаешь, что скорость машины не может быть км/ч, если речь, конечно, идет не о спортивном болиде? И уж тем более, она не может быть отрицательной, верно? Так вот, разумность, это об этом)
Расчет.
Посмотри, «проходит» ли твое решение на размерность и разумность, и только потом проверяй расчеты. Логично же — если с размерностью и разумностью получается несостыковочка, то проще все зачеркнуть и начать искать логические и математические ошибки.
«Любовь к таблицам» или «когда рисунка недостаточно»Далеко не всегда задачи на движение такие простые, как мы решали раньше. Очень часто, для того, чтобы правильно решить задачу, нужно не просто нарисовать грамотный рисунок, но и составить таблицу со всеми данными нам условиями.
Первая задача
Из пункта в пункт, расстояние между которыми км, одновременно выехал велосипедист и мотоциклист. Известно, что в час мотоциклист проезжает на км больше, чем велосипедист.
Определите скорость велосипедиста, если известно, что он прибыл в пункт на минут позже, чем мотоциклист.
Вот такая вот задача. Соберись, и прочитай ее несколько раз. Прочитал? Начинай рисовать — прямая, пункт, пункт, две стрелочки…
В общем рисуй, и сейчас сравним, что у тебя получилось.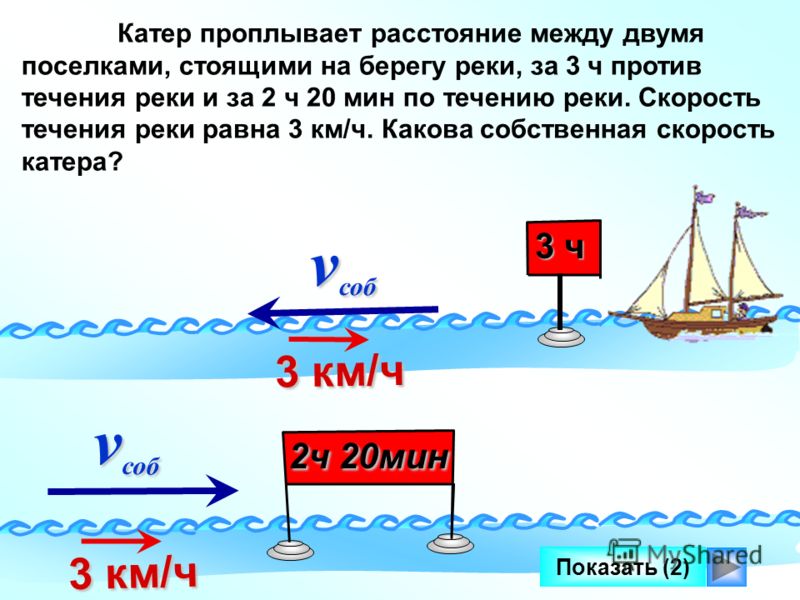
Пустовато как-то, правда? Рисуем таблицу.
Как ты помнишь, все задачи на движения состоят из компонентов: скорость, время и путь . Именно из этих граф и будет состоять любая таблица в подобных задачах.
Правда, мы добавим еще один столбец — имя , про кого мы пишем информацию — мотоциклист и велосипедист.
Так же в шапке укажи размерность , в какой ты будешь вписывать туда величины. Ты же помнишь, как это важно, правда?
У тебя получилась вот такая таблица?
Теперь давай анализировать все, что у нас есть, и параллельно заносить данные в таблицу и на рисунок.
Первое, что мы имеем — это путь, который проделали велосипедист и мотоциклист. Он одинаков и равен км. Вносим!
Возьмем скорость велосипедиста за, тогда скорость мотоциклиста будет …
Если с такой переменной решение задачи не пойдет — ничего страшного, возьмем другую, пока не дойдем до победного. Такое бывает, главное не нервничать!
Таблица преобразилась. У нас осталась не заполнена только одна графа — время. Как найти время, когда есть путь и скорость?
У нас осталась не заполнена только одна графа — время. Как найти время, когда есть путь и скорость?
Правильно, разделить путь на скорость. Вноси это в таблицу.
Вот и заполнилась наша таблица, теперь можно внести данные на рисунок.
Что мы можем на нем отразить?
Молодец. Скорость передвижения мотоциклиста и велосипедиста.
Еще раз перечитаем задачу, посмотрим на рисунок и заполненную таблицу.
Какие данные не отражены ни в таблице, ни на рисунке?
Верно. Время, на которое мотоциклист приехал раньше, чем велосипедист. Мы знаем, что разница во времени — минут.
Что мы должны сделать следующим шагом? Правильно, перевести данное нам время из минут в часы, ведь скорость дана нам в км/ч.
Магия формул: составление и решение уравнений — манипуляции, приводящие к единственно верному ответу.
Итак, как ты уже догадался, сейчас мы будем составлять уравнение .
Составление уравнения:
Взгляни на свою таблицу, на последнее условие, которое в нее не вошло и подумай, зависимость между чем и чем мы можем вынести в уравнение?
Правильно.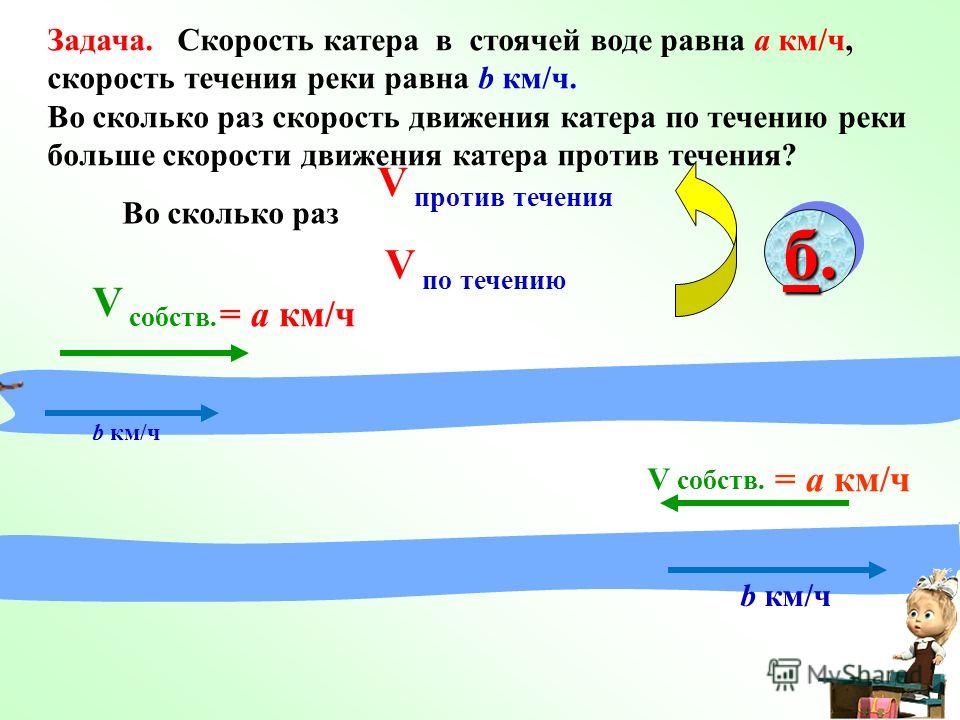 Мы можем составить уравнение, основываясь на разнице во времени!
Мы можем составить уравнение, основываясь на разнице во времени!
Логично? Велосипедист ехал больше, если мы из его времени вычтем время движения мотоциклиста, мы как раз получим данную нам разницу.
Это уравнение — рациональное. Если не знаешь, что это такое, прочти тему « ».
Приводим слагаемые к общему знаменателю:
Раскроем скобки и приведем подобные слагаемые:Уф! Усвоил? Попробуй свои силы на следующей задаче.
Решение уравнения:
Из этого уравнения мы получаем следующее:
Раскроем скобки и перенесем все в левую часть уравнения:
Вуаля! У нас простое квадратное уравнение. Решаем!
Мы получили два варианта ответа. Смотрим, что мы взяли за? Правильно, скорость велосипедиста.
Вспоминаем правило «3Р», конкретнее «разумность». Понимаешь о чем я? Именно! Скорость не может быть отрицательной, следовательно, наш ответ — км/ч.
Вторая задача
Два велосипедиста одновременно отправились в -километровый пробег. Первый ехал со скоростью, на км/ч большей, чем скорость второго, и прибыл к финишу на часов раньше второго. Найти скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч.
Найти скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч.
Напоминаю алгоритм решения:
- Прочитай задачу пару раз — усвой все-все детали. Усвоил?
- Начинай рисовать рисунок — в каком направлении они двигаются? какое расстояние они прошли? Нарисовал?
- Проверь, все ли величины у тебя одинаковой размерности и начинай выписывать кратко условие задачи, составляя табличку (ты же помнишь какие там графы?).
- Пока все это пишешь, думай, что взять за? Выбрал? Записывай в таблицу! Ну а теперь просто: составляем уравнение и решаем. Да, и напоследок — помни о «3Р»!
- Все сделал? Молодец! У меня получилось, что скорость велосипедиста — км/ч.
-«Какого цвета твоя машина?» — «Она красивая!» Правильные ответы на поставленные вопросы
Продолжим наш разговор. Так какая там скорость у первого велосипедиста? км/ч? Очень надеюсь, что ты сейчас не киваешь утвердительно!
Внимательно прочти вопрос: «Какая скорость у первого велосипедиста?»
Понял, о чем я?
Именно! Полученный — это не всегда ответ на поставленный вопрос!
Вдумчиво читай вопросы — возможно, после нахождения тебе нужно будет произвести еще некоторые манипуляции, например, прибавить км/ч, как в нашей задаче.
Еще один момент — часто в задачах все указывается в часах, а ответ просят выразить в минутах, или же все данные даны в км, а ответ просят записать в метрах.
Смотри за размерностью не только в ходе самого решения, но и когда записываешь ответы.
Задачи на движение по кругу
Тела в задачах могут двигаться не обязательно прямо, но и по кругу, например, велосипедисты могут ехать по круговой трассе. Разберем такую задачу.
Задача №1
Из пункта круговой трассы выехал велосипедист. Через минут он еще не вернулся в пункт и из пункта следом за ним отправился мотоциклист. Через минут после отправления он догнал велосипедиста в первый раз, а еще через минут после этого догнал его во второй раз.
Найдите скорость велосипедиста, если длина трассы равна км. Ответ дайте в км/ч.
Решение задачи №1
Попробуй нарисовать рисунок к этой задаче и заполнить для нее таблицу. Вот что получилось у меня:
Между встречами велосипедист проехал расстояние, а мотоциклист — .
Но при этом мотоциклист проехал ровно на один круг больше, это видно из рисунка:
Надеюсь, ты понимаешь, что по спирали они на самом деле не ездили — спираль просто схематически показывает, что они ездят по кругу, несколько раз проезжая одни и те же точки трассы.
Разобрался? Попробуй решить самостоятельно следующие задачи:
Задачи для самостоятельной работы:
- Два мо-то-цик-ли-ста стар-ту-ют од-но-вре-мен-но в одном на-прав-ле-нии из двух диа-мет-раль-но про-ти-во-по-лож-ных точек кру-го-вой трас-сы, длина ко-то-рой равна км. Через сколь-ко минут мо-то-цик-ли-сты по-рав-ня-ют-ся в пер-вый раз, если ско-рость од-но-го из них на км/ч боль-ше скорости дру-го-го?
- Из одной точки кру-го-вой трас-сы, длина ко-то-рой равна км, од-н-времен-но в одном на-прав-ле-нии стар-то-ва-ли два мотоциклиста. Ско-рость пер-во-го мотоцикла равна км/ч, и через минут после стар-та он опе-ре-дил вто-рой мотоцикл на один круг. Най-ди-те ско-рость вто-ро-го мотоцикла.
 Ответ дайте в км/ч.
Ответ дайте в км/ч.
- Пусть км/ч — ско-рость пер-во-го мо-то-цик-ли-ста, тогда ско-рость вто-ро-го мо-то-цик-ли-ста равна км/ч. Пусть пер-вый раз мо-то-цик-ли-сты по-рав-ня-ют-ся через часов. Для того, чтобы мо-то-цик-ли-сты по-рав-ня-лись, более быст-рый дол-жен пре-одо-леть из-на-чаль-но раз-де-ля-ю-щее их рас-сто-я-ние, рав-ное по-ло-ви-не длины трас-сы.
Получаем, что время равно часа = минут.
- Пусть ско-рость вто-ро-го мотоцикла равна км/ч. За часа пер-вый мотоцикл про-шел на км боль-ше, чем вто-рой, соответственно, получаем уравнение:
Скорость второго мотоциклиста равна км/ч.
Задачи на течение
Теперь, когда ты отлично решаешь задачи «на суше», перейдем в воду, и рассмотрим страаашные задачи, связанные с течением.
Представь, что у тебя есть плот, и ты спустил его в озеро. Что с ним происходит? Правильно. Он стоит, потому что озеро, пруд, лужа, в конце концов, — это стоячая вода.
Скорость течения в озере равна .
Плот поедет, только если ты сам начнешь грести. Та скорость, которую он приобретет, будет собственной скоростью плота. Неважно куда ты поплывешь — налево, направо, плот будет двигаться с той скоростью, с которой ты будешь грести. Это понятно? Логично же.
А сейчас представь, что ты спускаешь плот на реку, отворачиваешься, чтобы взять веревку…, поворачиваешься, а он … уплыл…
Это происходит потому что у реки есть скорость течения , которая относит твой плот по направлению течения.
Его скорость при этом равна нулю (ты же стоишь в шоке на берегу и не гребешь) — он движется со скоростью течения.
Разобрался?
Тогда ответь вот на какой вопрос — «С какой скоростью будет плыть плот по реке, если ты сидишь и гребешь?» Задумался?
Здесь возможно два варианта.
1-й вариант — ты плывешь по течению.
И тогда ты плывешь с собственной скоростью + скорость течения. Течение как бы помогает тебе двигаться вперед.
2-й вариант — ты плывешь против течения.
Тяжело? Правильно, потому что течение пытается «откинуть» тебя назад. Ты прилагаешь все больше усилий, чтобы проплыть хотя бы метров, соответственно скорость, с которой ты передвигаешься, равна собственная скорость — скорость течения.
Допустим, тебе надо проплыть км. Когда ты преодолеешь это расстояние быстрее? Когда ты будешь двигаться по течению или против?
Решим задачку и проверим.
Добавим к нашему пути данные о скорости течения — км/ч и о собственной скорости плота — км/ч. Какое время ты затратишь, двигаясь по течению и против него?
Конечно, ты без труда справился с этой задачей! По течению — час, а против течения аж часа!
В этом и есть вся суть задач на движение с течением .
Несколько усложним задачу.
Задача №1
Лодка с моторчиком плыла из пункта в пункт часа, а обратно — часа.
Найдите скорость течения, если скорость лодки в стоячей воде — км/ч
Решение задачи №1
Обозначим расстояние между пунктами, как, а скорость течения — как.
| Путь S | Скорость v, км/ч | Время t, часов | |
| A -> B (против течения) | 3 | ||
| B -> A (по течению) | 2 |
Мы видим, что лодка проделывает один и тот же путь, соответственно:
Что мы брали за?
Скорость течения. Тогда это и будет являться ответом:)
Скорость течения равна км/ч.
Задача №2
Байдарка в вышла из пункта в пункт, расположенный в км от. Пробыв в пункте час минут, байдарка отправилась назад и вернулась в пункт в.
Определите (в км/ч) собственную скорость байдарки, если известно, что скорость течения реки км/ч.
Решение задачи №2
Итак, приступим. Прочитай задачу несколько раз и сделай рисунок. Думаю, ты без труда сможешь решить это самостоятельно.
Все величины у нас выражены в одном виде? Нет. Время отдыха у нас указано и в часах, и в минутах.
Переведем это в часы:
час минут = ч.
Теперь все величины у нас выражены в одном виде. Приступим к заполнению таблицы и поиску того, что мы возьмем за.
Пусть — собственная скорость байдарки. Тогда, скорость байдарки по течению равна, а против течения равна.
Запишем эти данные, а так же путь (он, как ты понимаешь, одинаков) и время, выраженное через путь и скорость, в таблицу:
| Путь S | Скорость v, км/ч | Время t, часов | |
| Против течения | 26 | ||
| По течению | 26 |
Посчитаем, сколько времени байдарка затратила на свое путешествие:
Все ли часов она плыла? Перечитываем задачу.
Нет, не все. У нее был отдых час минут, соответственно, из часов мы вычитаем время отдыха, которое, мы уже перевели в часы:
ч байдарка действительно плыла.
Приведем все слагаемые к общему знаменателю:
Раскроем скобки и приведем подобные слагаемые. Далее решаем получившееся квадратное уравнение.
Далее решаем получившееся квадратное уравнение.
С этим, я думаю, ты тоже справишься самостоятельно. Какой ответ у тебя получился? У меня км/ч.
Подведем итоги
ПРОДВИНУТЫЙ УРОВЕНЬ
Задачи на движение. Примеры
Рассмотрим примеры с решениями для каждого типа задач.
Движение с течением
Одни из самых простых задач — задачи на движение по реке . Вся их суть в следующем:
- если движемся по течению, к нашей скорости прибавляется скорость течения;
- если движемся против течения, из нашей скорости вычитается скорость течения.
Пример №1:
Катер плыл из пункта A в пункт B часов а обратно — часа. Найдите скорость течения, если скорость катера в стоячей воде км/ч.
Решение №1:
Обозначим расстояние между пунктами, как AB, а скорость течения — как.
Все данные из условия занесем в таблицу:
| Путь S | Скорость v, км/ч | Время t, часов | |
| A -> B (против течения) | AB | 50-x | 5 |
| B -> A (по течению) | AB | 50+x | 3 |
Для каждой строки этой таблицы нужно записать формулу:
На самом деле, можно не писать уравнения для каждой из строк таблицы. Мы ведь видим, что расстояние, пройденное катером туда и обратно одинаково.
Мы ведь видим, что расстояние, пройденное катером туда и обратно одинаково.
Значит, расстояние мы можем приравнять. Для этого используем сразу формулу для расстояния:
Часто приходится использовать и формулу для времени:
Пример №2:
Против течения лодка проплывает расстояние в км на час дольше, чем по течению. Найдите скорость лодки в стоячей воде, если скорость течения равна км/ч.
Решение №2:
Попробуем сразу составить уравнение. Время против течения на час больше, чем время по течению.
Это записывается так:
Теперь вместо каждого времени подставим формулу:
Получили обычное рациональное уравнение, решим его:
Очевидно, что скорость не может быть отрицательным числом, значит, ответ: км/ч.
Относительное движение
Если какие-то тела движутся друг относительно друга, часто бывает полезно посчитать их относительную скорость. Она равна:
- сумме скоростей, если тела движутся навстречу друг другу;
- разности скоростей, если тела движутся в одном направлении.

Пример №1
Из пунктов A и B одновременно навстречу друг другу выехали два автомобиля со скоростями км/ч и км/ч. Через сколько минут они встретятся. Если расстояние между пунктами км?
I способ решения:
Относительная скорость автомобилей км/ч. Это значит, что если мы сидим в первом автомобиле, то он нам кажется неподвижным, но второй автомобиль приближается к нам со скоростью км/ч. Так как между автомобилями изначально расстояние км, время, через которое второй автомобиль проедет мимо первого:
II способ решения:
Время от начала движения до встречи у автомобилей, очевидно, одинаковое. Обозначим его. Тогда первый автомобиль проехал путь, а второй — .
В сумме они проехали все км. Значит,
Другие задачи на движение
Пример №1:
Из пункта А в пункт В выехал автомобиль. Одновременно с ним выехал другой автомобиль, который ровно половину пути ехал со скоростью на км/ч меньшей, чем первый, а вторую половину пути он проехал со скоростью км/ч.
В результате автомобили прибыли в пункт В одновременно.
Найдите скорость первого автомобиля, если известно, что она больше км/ч.
Решение №1:
Слева от знака равно запишем время первого автомобиля, а справа — второго:
Упростим выражение в правой части:
Поделим каждое слагаемое на АВ:
Получилось обычное рациональное уравнение. Решив его, получим два корня:
Из них только один больше.
Ответ: км/ч.
Пример №2
Из пункта A круговой трассы выехал велосипедист. Через минут он еще не вернулся в пункт А и из пункта А следом за ним отправился мотоциклист. Через минут после отправления он догнал велосипедиста в первый раз, а еще через минут после этого догнал его во второй раз. Найдите скорость велосипедиста, если длина трассы равна км. Ответ дайте в км/ч.
Решение:
Здесь будем приравнивать расстояние.
Пусть скорость велосипедиста будет, а мотоциклиста — . До момента первой встречи велосипедист был в пути минут, а мотоциклист — .
При этом они проехали равные расстояния:
Между встречами велосипедист проехал расстояние, а мотоциклист — . Но при этом мотоциклист проехал ровно на один круг больше, это видно из рисунка:
Надеюсь, ты понимаешь, что по спирали они на самом деле не ездили- спираль просто схематически показывает, что они ездят по кругу, несколько раз проезжая одни и те же точки трассы.
Полученные уравнения решаем в системе:
КРАТКОЕ ИЗЛОЖЕНИЕ И ОСНОВНЫЕ ФОРМУЛЫ
1. Основная формула
2. Относительное движение
- Это сумма скоростей, если тела движутся навстречу друг другу;
- разность скоростей, если тела движутся в одном направлении.
3. Движение с течением :
- Если движемся по течению, к нашей скорости прибавляется скорость течения;
- если движемся против течения, из скорости вычитается скорость течения.
Мы помогли тебе разобраться с задачами на движение…
Теперь твой ход…Если ты внимательно прочитал текст и прорешал самостоятельно все примеры, готовы спорить, что ты все понял.
И это уже половина пути.
Напиши внизу в комментариях разобрался ли ты с задачами на движение?
Какие вызывают наибольшие трудности?
Понимаешь ли ты, что задачи на «работу» — это почти тоже самое?
Напиши нам и удачи на экзаменах!
Решение задач на «движение по воде» многим дается с трудом. В них существует несколько видов скоростей, поэтому решающие начинаю путаться. Чтобы научиться решать задачи такого типа, надо знать определения и формулы. Умение составлять схемы очень облегчает понимание задачи, способствует правильному составлению уравнения. А правильно составленное уравнение — самое главное в решении любого типа задач.
Инструкция
В задачах «на движение по реке» присутствуют скорости: собственная скорость (Vс), скорость по течению (Vпо теч.), скорость против течения (Vпр. теч.), скорость течения (Vтеч.). Необходимо отметить, что собственная скорость водного суда – это скорость в стоячей воде. Чтобы найти скорость по течению, надо к скорости течения прибавить собственную. Для того чтобы найти скорость против течения, надо из собственной скорости вычесть скорость течения.
Для того чтобы найти скорость против течения, надо из собственной скорости вычесть скорость течения.
Первое, что необходимо выучить и знать «на зубок» — формулы. Запишите и запомните:
Vпо теч=Vс+Vтеч.
Vпр. теч.=Vс-Vтеч.
Vпр. теч=Vпо теч. — 2Vтеч.
Vпо теч.=Vпр. теч+2Vтеч.
Vтеч.=(Vпо теч. — Vпр. теч)/2
Vс=(Vпо теч.+Vпр теч.)/2 или Vс=Vпо теч.+Vтеч.
На примере разберем, как находить собственную скорость и решать задачи такого типа.
Пример 1.Скорость лодки по течению 21,8км/ч, а против течения 17,2 км/ч. Найти собственную скорость лодки и скорость течения реки.
Решение: Согласно формулам: Vс=(Vпо теч.+Vпр теч.)/2 и Vтеч.=(Vпо теч. — Vпр. теч)/2, найдем:
Vтеч = (21,8 — 17,2)/2=4,62=2,3 (км/ч)
Vс = Vпр теч.+Vтеч=17,2+2,3=19,5 (км/ч)
Ответ: Vc=19,5 (км/ч), Vтеч=2,3 (км/ч).
Пример 2. Пароход прошел против течения 24 км и вернулся обратно, затратив на обратный путь на 20 мин меньше, чем при движении против течения. Найдите его собственную скорость в неподвижной воде, если скорость течения равна 3 км/ч.
Найдите его собственную скорость в неподвижной воде, если скорость течения равна 3 км/ч.
За Х примем собственную скорость парохода. Составим таблицу, куда занесем все данные.
Против теч. По течению
Расстояние 24 24
Скорость Х-3 Х+3
время 24/ (Х-3) 24/ (Х+3)
Зная, что на обратный путь пароход затратил на 20 минут времени меньше, чем на путь по течению, составим и решим уравнение.
20 мин=1/3 часа.
24/ (Х-3) – 24/ (Х+3) = 1/3
24*3(Х+3) – (24*3(Х-3)) – ((Х-3)(Х+3))=0
72Х+216-72Х+216-Х2+9=0
Х=21(км/ч) – собственная скорость парохода.
Ответ: 21 км/ч.
Обратите внимание
Скорость плота считается равной скорости водоема.
Внимание, только СЕГОДНЯ!
Все интересное
Скорость течения реки нужно знать, например, чтобы рассчитать надежность паромной переправы или определить безопасность купания. Скорость течения может различаться на разных участках. Вам понадобитсяДлинная прочная веревка, секундомер, плавучий…
Движение различных тел в окружающей среде характеризуется рядом величин, одна из которых – средняя скорость. Этот обобщенный показатель определяет скорость тела на всем перемещении. Зная зависимость модуля мгновенной скорости от времени, среднюю…
Этот обобщенный показатель определяет скорость тела на всем перемещении. Зная зависимость модуля мгновенной скорости от времени, среднюю…
В курсе физики помимо обычной скорости, знакомой всем из алгебры, существует понятие «нулевая скорость». Нулевая скорость или, как ее еще называют, – начальная находится другим способом, отличным от формулы нахождения обычной скорости. …
Согласно первому закону механики, всякое тело стремится сохранять состояние покоя или равномерного прямолинейного движения, что по сути одно и то же. Но такая безмятежность возможна разве что в космосе.
Возможна скорость без ускорения, но…
Задачи на кинематику, в которых необходимо вычислить скорость, время или путь равномерно и прямолинейно движущихся тел, встречаются в школьном курсе алгебры и физики. Для их решения найдите в условии величины, которые можно между собой уравнять.…
По городу шагает турист, мчится автомобиль, в воздухе летит самолет. Одни тела движутся быстрее других. Автомобиль движется быстрее пешехода, а самолет летит быстрее автомобиля. В физике величиной, характеризующей быстроту движения тел, является…
В физике величиной, характеризующей быстроту движения тел, является…
Движение тел принято делить по траектории на прямолинейное и криволинейное, а также по скорости – на равномерное и неравномерное. Даже не зная теории физики можно понять, что прямолинейное движение – это движение тела по прямой линии, а…
Согласно учебной программе по математике дети должны научиться решать задачи на движение еще в начальной школе. Однако задачи такого вида часто вызывают у учащихся затруднение. Важно,чтоб ребенок понял, что такое собственная скорость, скорость…
В 7 классе курс алгебры усложняется. В программе появляется много интересных тем. В 7 классе решают задачи на разные темы, например: «на скорость (на движение)», «движение по реке», «на дроби», «на сравнение…
Задачи на движение кажутся сложными только на первый взгляд. Чтобы найти, например, скорость движения судна против течения, достаточно представить изложенную в задаче ситуацию. Возьмите ребёнка в небольшое путешествие по реке, и школьник научится…
Решение дробных задач в курсе школьной математике – это начальная подготовка учеников к изучению математического моделирования, являющегося более сложным, но имеющим широкое приложение понятием. Инструкция 1Дробными являются задачи, которые…
Инструкция 1Дробными являются задачи, которые…
Скорость, время и расстояние – физические величины, взаимосвязанные процессом движения. Различают равномерное и равноускоренное (равнозамедленное движение) тела. При равномерном движении скорость тела постоянна и не меняется с течением времени. При…
Согласно учебной программе по математике дети обязаны обучиться решать задачи на движение еще в исходной школе. Впрочем задачи такого вида зачастую вызывают у учащихся затруднение. Значимо,чтоб ребенок осознал, что такое собственная скорость , скорость течения, скорость по течению и скорость вопреки течения. Только при этом условии школьник сумеет легко решать задачи на движение.
Вам понадобится
- Калькулятор, ручка
Инструкция
1. Собственная скорость – это скорость катера либо иного средства передвижения в статичной воде. Обозначьте ее – V собств.Вода в реке находится в движении. Значит она имеет свою скорость , которая именуется скорость ю течения (V теч. )Скорость катера по течению реки обозначьте – V по теч., а скорость супротив течения – V пр. теч.
)Скорость катера по течению реки обозначьте – V по теч., а скорость супротив течения – V пр. теч.
2. Сейчас запомните формулы, нужные для решения задач на движение:V пр. теч.= V собств. – V теч.V по теч.= V собств. + V теч.
3. Выходит, исходя из этих формул, дозволено сделать следующие итоги.Если катер движется вопреки течения реки, то V собств. = V пр. теч. + V теч.Если катер движется по течению, то V собств. = V по теч. – V теч.
4. Решим несколько задач на движение по реке.Задача 1. Скорость катера вопреки течения реки 12,1 км/ч. Обнаружьте собственную скорость катера, зная, что скорость течения реки 2 км/ч.Решение: 12,1 + 2 = 14, 1 (км/ч) – собственная скорость катера.Задача 2. Скорость катера по течению реки 16,3 км/ч, скорость течения реки 1,9 км/ч. Сколько метров прошел бы это катер за 1 мин., если находился в стоячей воде?Решение: 16,3 – 1,9 = 14,4 (км/ч) – собственная скорость катера. Переведем км/ч в м/мин: 14,4 / 0,06 = 240 (м/мин. ). Значит, за 1 минуту катер прошел бы 240 м.Задача 3. Два катера отправились единовременно насупротив друг другу из 2-х пунктов. 1-й катер двигался по течению реки, а 2-й – вопреки течения. Встретились они через три часа. За это время 1-й катер прошел 42 км, а 2-й – 39 км.Обнаружьте собственную скорость всякого катера, если вестимо, что скорость течения реки 2 км/ч.Решение: 1) 42 / 3 = 14 (км/ч) – скорость движения по течению реки первого катера. 2) 39 / 3 = 13 (км/ч) – скорость движения вопреки течения реки второго катера. 3) 14 – 2 = 12 (км/ч) – собственная скорость первого катера. 4) 13 + 2 = 15 (км/ч) – собственная скорость второго катера.
). Значит, за 1 минуту катер прошел бы 240 м.Задача 3. Два катера отправились единовременно насупротив друг другу из 2-х пунктов. 1-й катер двигался по течению реки, а 2-й – вопреки течения. Встретились они через три часа. За это время 1-й катер прошел 42 км, а 2-й – 39 км.Обнаружьте собственную скорость всякого катера, если вестимо, что скорость течения реки 2 км/ч.Решение: 1) 42 / 3 = 14 (км/ч) – скорость движения по течению реки первого катера. 2) 39 / 3 = 13 (км/ч) – скорость движения вопреки течения реки второго катера. 3) 14 – 2 = 12 (км/ч) – собственная скорость первого катера. 4) 13 + 2 = 15 (км/ч) – собственная скорость второго катера.
Задачи на движение кажутся трудными только на 1-й взор. Дабы обнаружить, скажем, скорость движения судна вопреки течения , довольно представить высказанную в задаче обстановку. Возьмите ребёнка в малое путешествие по реке, и школьник обучится “щелкать такие задачки, как орешки”.
Вам понадобится
- Калькулятор, ручка.
Инструкция
1. Согласно нынешней энциклопедии (dic.academic.ru), скорость – это колляция поступательного движения точки (тела), численно равная при равномерном движении отношению пройденного пути S к промежуточному времени t, т.е. V = S / t.
2. Для того дабы обнаружить скорость движения какого-нибудь судна супротив течения, надобно знать собственную скорость судна и скорость течения.Собственная скорость – это скорость движения судна в стоячей воде, скажем, в озере. Обозначим ее – V собств.Скорость течения определяется по тому, на какое расстояние река относит предмет за единицу времени. Обозначим ее – V теч.
3. Дабы обнаружить скорость движения судна супротив течения (V пр. теч.), надобно из собственной скорости судна вычесть скорость течения.Выходит, получили формулу: V пр. теч.= V собств. – V теч.
4. Обнаружим скорость движения судна вопреки течения реки, если знаменито, что собственная скорость судна равна 15,4 км/ч, а скорость течения реки – 3,2 км/ч. 15,4 – 3,2 = 12,2 (км/ч) – скорость движения судна супротив течения реки.
15,4 – 3,2 = 12,2 (км/ч) – скорость движения судна супротив течения реки.
5. В задачах на движение зачастую требуется перевести км/ч в м/с. Дабы это сделать, необходимо припомнить, что 1 км = 1000 м, 1 ч = 3600 с. Следственно, х км/ч = х * 1000 м / 3600 с = х / 3,6 м/с. Выходит, дабы перевести км/ч в м/с необходимо поделить на 3,6.Скажем, 72 км/ч = 72:3,6 = 20 м/с.Дабы перевести м/с в км/ч необходимо умножить на 3,6.Скажем, 30 м/с = 30 * 3,6 = 108 км/ч.
6. Переведем х км/ч в м/мин. Для этого припомним, что 1 км = 1000 м, 1 ч = 60 мин. Значит, х км/ч = 1000 м / 60 мин. = х / 0,06 м/мин. Следственно, дабы перевести км/ч в м/мин. необходимо поделить на 0,06.Скажем, 12 км/ч = 200 м/мин.Дабы перевести м/мин. в км/ч нужно умножить на 0,06.Скажем, 250 м/мин. = 15 км/ч
Полезный совет
Не забывайте о том, в каких единицах вы измеряете скорость.
Обратите внимание!
Не позабудьте о том, в каких единицах вы измеряете скорость.Дабы перевести км/ч в м/с необходимо поделить на 3,6. Дабы перевести м/с в км/ч надобно умножить на 3,6.Дабы перевести км/ч в м/мин. необходимо поделить на 0,06.Дабы перевести м/мин. в км/ч нужно умножить на 0,06.
Дабы перевести м/с в км/ч надобно умножить на 3,6.Дабы перевести км/ч в м/мин. необходимо поделить на 0,06.Дабы перевести м/мин. в км/ч нужно умножить на 0,06.
Полезный совет
Решить задачу на движение помогает рисунок.
5 класс. Математика. Никольский. Учебник. Ответы к стр. 122
Измерение величин
Задачи на движение
Ответы к стр. 122
542. Катер, имеющий собственную скорость 15 км/ч, проплыл 2 ч по течению реки и 3 ч против течения. Какое расстояние проплыл катер за все время, если скорость течения реки 2 км/ч?
1) 15 + 2 = 17 (км/ч) — скорость катера по течению реки
2) 15 — 2 = 13 (км/ч) — скорость катера против течения реки
3) 17 • 2 = 34 (км) — проплыл катер по течению
4) 13 • 3 = 39 (км) — проплыл катер против течения
5) 34 + 39 = 73 (км) — проплыл катер за все время
О т в е т: катер проплыл 73 км.
543. а) Расстояние между причалами 24 км. Сколько времени потратит моторная лодка на путь между причалами туда и обратно, если собственная скорость моторной лодки 10 км/ч, а скорость течения 2 км/ч?
б) Расстояние между двумя причалами 36 км. Сколько времени потратит на путь от одного причала до другого и обратно катер, если его собственная скорость 15 км/ч, а скорость течения реки 3 км/ч?
Сколько времени потратит на путь от одного причала до другого и обратно катер, если его собственная скорость 15 км/ч, а скорость течения реки 3 км/ч?
а) 1) 10 + 2 = 12 (км/ч) — скорость лодки по течению
2) 10 — 2 = 8 (км/ч) — скорость лодки против течения
3) 24 : 12 = 2 (ч) — будет плыть лодка между причалами по течению
4) 24 : 8 = 3 (ч) — будет плыть лодка между причалами против течения
5) 2 + 3 = 5 (ч) — потратит моторная лодка на путь между причалами
О т в е т: лодка потратит 5 ч.
б) 1) 15 + 3 = 18 (км/ч) — скорость катера по течению
2) 15 — 3 = 12 (км/ч) — скорость катера против течения
3) 36 : 18 = 2 (ч) — будет плыть катер между причалами по течению
4) 36 : 12 = 3 (ч) — будет плыть катер между причалами против течения
5) 2 + 3 = 5 (ч) — потратит катер на путь между причалами
О т в е т: катер потратит 5 ч.
544. Определив скорости, заполните таблицу:
Ʋсобств. | Ʋтечения | Ʋпо теч. | Ʋпр. теч. | |
| 1 | 12 км/ч | 4 км/ч | 16 км/ч | 8 км/ч |
| 2 | 25 км/ч | 3 км/ч | 28 км/ч | 22 км/ч |
| 3 | 24 км/ч | 4 км/ч | 28 км/ч | 20 км/ч |
| 4 | 12 км/ч | 5 км/ч | 17 км/ч | 7 км/ч |
| 5 | 19 км/ч | 3 км/ч | 22 км/ч | 16 км/ч |
| 6 | 42 км/ч | 3 км/ч | 45 км/ч | 39 км/ч |
545. Определите, какая скорость получится следующим действием:
Определите, какая скорость получится следующим действием:
а) Ʋс.+ Ʋт.; б) Ʋс. — Ʋт.; в) Ʋпр. т. + Ʋт.;
г) Ʋпр. т. + 2Ʋт.; д) Ʋпо т. — Ʋт.; е) Ʋпо т. — Ʋпр. т.
а) Ʋс.+Ʋт. = Ʋпо т.;
б) Ʋс. − Ʋт. = Ʋпр. т.;
в) Ʋпр. т. + Ʋт. = Ʋс.;
г) Ʋпр. т. + 2Ʋт. = Ʋпо т.;
д) Ʋпо т. — Ʋт. = Ʋс.;
е) Ʋпо т. — Ʋпр. т. = 2Ʋт..
546. а) По течению моторная лодка проплыла 48 км за 3 ч, а против течения − за 4 ч. Найдите скорость течения.
а) По течению моторная лодка проплыла 48 км за 3 ч, а против течения − за 4 ч. Найдите скорость течения.
б) Катер проплыл 72 км по течению за 2 ч, а против течения за 3 ч. За сколько часов это расстояние проплывут плоты?
а) 1) 48 : 3 = 16 (км/ч) − скорость лодки по течению
2) 48 : 4 = 12 (км/ч) − скорость лодки против течения
3) 16 — 12 = 4 (км/ч) − удвоенная скорость течения
4) 4 : 2 = 2 (км/ч) − скорость течения
О т в е т: скорость течения 2 км/ч.
б) 1) 72 : 2 = 36 (км/ч) — скорость катера по течению реки
2) 72 : 3 = 24 (км/ч) — скорость катера против течения реки
3) 36 — 24 = 12 (км/ч) — удвоенная скорость течения
4) 12 : 2 = 6 (км/ч) — скорость течения
5) 72 : 6 = 12 (ч) — будут плыть плоты
О т в е т: за 12 ч.
547. Скорость течения равна 3 км/ч. На сколько километров в час скорость катера по течению больше скорости против течения?
Ʋпо т. − Ʋпр. т. = 2Ʋт. = 2 • 3 = 6 (км/ч) − скорость катера по течению больше скорости катера против течения
− Ʋпр. т. = 2Ʋт. = 2 • 3 = 6 (км/ч) − скорость катера по течению больше скорости катера против течения
О т в е т: на 6 км/ч.
548. 5 июля 1923 года из Москвы в Нижний Новгород вылетел аэроплан «Ультиматум». Так была открыта первая трасса Аэрофлота длиной 420 км. Аэроплан шёл на высоте 250 м и преодолел всё расстояние за 3 ч 30 мин. Найдите скорость аэроплана. Какие условия в задаче являются лишними?
3 ч 30 мин = 210 мин
420 : 210 = 2 (км/мин) = 120 (км/ч) — скорость аэроплана
О т в е т: скорость аэроплана 120 км/ч, лишние условия в задаче — высота и дата полета.
Ответы по математике. 5 класс. Учебник. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В.
Математика. 5 класс
Страница 75 №291-297 ГДЗ к учебнику «Математика» 5 класс Дорофеев, Шарыгин, Суворова
ГДЗ 1 класс
ГДЗ 10 класс
- Категория: ГДЗ Математика учебник 5 класс Дорофеев, Шарыгин, Суворова
Задание № 291. а) Мальчик заметил, что на путь по течению реки было затрачено меньше времени, чем на тот же путь против течения. Чем это можно объяснить, если учесть, что мотор лодки работал одинаково хорошо во время все поездки?
а) Мальчик заметил, что на путь по течению реки было затрачено меньше времени, чем на тот же путь против течения. Чем это можно объяснить, если учесть, что мотор лодки работал одинаково хорошо во время все поездки?
б) На путь из пункта A в пункт B теплоход затратил 1 ч 40 мин, а на обратный путь − 2 ч. В каком направлении течет река?
Ответы 7 гуру
а) При движении по течению реки, собственная скорость лодки увеличивается на скорость течения реки, а при движении против течении, реки скорость лодки уменьшается на скорость течения реки. Поэтому скорость лодки по течению больше скорости лодки против течения.
б) Река течет в направлении из пункта A в пункт B, так как в этом направлении теплоход затратил меньше времени, а значит его скорость была больше.
Задание № 292. Скорость катера в стоячей воде равна 12 км/ч, а скорость течения реки равна 3 км/ч. Определите:
а) скорость катера по течению реки;
б) скорость катера против течения реки;
в) путь катера по течению реки за 3 ч;
г) путь катера против течения реки за 5 ч.
Ответы
а) 12 + 3 = 15 (км/ч) − скорость катера по течению реки.
б) 12 − 3 = 9 (км/ч) − скорость катера против течения реки.
в) 15 * 3 = 45 (км) − путь катера по течению реки за 3 ч.
г) 9 * 5 = 45 (км) − путь катера против течения реки за 5 ч.
Задание № 293. Смоделируйте ситуацию с помощью рисунка и заполните таблицу:
Подсказка. Рассмотрите рисунок 3. 13. Какую скорость изображает отрезок AC? отрезки CB и CD? отрезок AB? отрезок AD?
Для каждой ситуации, описанной в таблице, установите, какие отрезки на этом рисунке даны и какие надо найти.
Ответы
AC − собственная скорость лодки,
CB − скорость течения реки,
CD − скорость течения реки,
AB − скорость лодки против течения,
AD − скорость лодки по течению.
Задача № 294. Катер, имеющий скорость 15 км/ч, проплыл 2 ч по течению реки и 3 ч против течения. Какое расстояние проплыл катер за это время, если скорость течения реки 2 км/ч?
Решение с объяснением
Найдем скорость катера по течению.
Для этого сложим собственную скорость катера и скорость течения:
1) 15 + 2 = 17 (км/ч) − скорость катера по течению;
Найдем расстояние, которое проплыл катер по течению. Для этого умножим скорость катера по течению на время:
2) 17 * 2 = 34 (км) − проплыл катер по течению;
Найдем скорость катера против течения. Для этого из собственной скорости катера вычтем скорость течения:
3) 15 − 2 = 13 (км/ч) − скорость катера против течения;
Найдем расстояние, которое проплыл катер против течения. Для этого умножим скорость катера против течения на время:
4) 13 * 3 = 39 (км) − проплыл катер против течения;
Найдем суммарное расстояние, которое проплыл катер. Для этого сложим расстояние, которое проплыл катер по течению и против течения:
5) 34 + 39 = 73 (км) − проплыл катер всего.
Ответ: 73 км.Запись в тетради:
1) 15 + 2 = 17 (км/ч) − скорость катера по течению.
2) 17 * 2 = 34 (км) − проплыл катер по течению.
3) 15 − 2 = 13 (км/ч) − скорость катера против течения.
4) 13 * 3 = 39 (км) − проплыл катер против течения.
5) 34 + 39 = 73 (км) − проплыл катер всего.
Ответ: 73 км.
Задание № 295. Собственная скорость теплохода равна 27 км/ч, скорость течения реки − 3 км/ч. Сколько времени затратит теплоход на путь между двумя пристанями, расстояние между которыми 120 км, если он будет плыть:
а) по течению реки;
б) против течения реки?
Решение с пояснениями
а) Найдем скорость теплохода по течению. Для этого сложим собственную скорость теплохода и скорость течения:
1) 27 + 3 = 30 (км/ч) − скорость теплохода по течению;
Найдем, сколько времени затратит теплоход на путь между двумя пристанями. Для этого расстояние разделим на скорость:
2) 120 : 30 = 4 (ч) затратит теплоход на путь между двумя пристанями.
Ответ: 4 часа.б) Найдем скорость теплохода против течения. Для этого из собственной скорости теплохода вычтем скорость течения:
1) 27 − 3 = 24 (км/ч) − скорость теплохода против течения;
Найдем, сколько времени затратит теплоход на путь между двумя пристанями.Для этого расстояние разделим на скорость:
2) 120 : 24 = 5 (ч) затратит теплоход на путь между двумя пристанями.
Ответ: 5 часов.Пишем:
а) 1) 27 + 3 = 30 (км/ч) − скорость теплохода по течению.
2) 120 : 30 = 4 (ч) затратит теплоход на путь между двумя пристанями.
Ответ: 4 часа.б) 1) 27 − 3 = 24 (км/ч) − скорость теплохода против течения.
2) 120 : 24 = 5 (ч) затратит теплоход на путь между двумя пристанями.
Ответ: 5 часов.
Задача № 296. Катер проплыл 72 км по течению реки и вернулся обратно. Какой путь занял у него больше времени и на сколько, если собственная скорость катера 21 км/ч, а скорость течения реки 3 км/ч?
Решение задачи с объяснением
Найдем скорость катера по течению. Для этого сложим собственную скорость катера и скорость течения:
1) 21 + 3 = 24 (км/ч) − скорость катера по течению;
Найдем время движения катера по течению. Для этого разделим расстояние на скорость:
2) 72 : 24 = 3 (ч) − двигался катер по течению;
Найдем скорость катера против течения.Для этого из собственной скорости катера вычтем скорость течения:
3) 21 − 3 = 18 (км/ч) − скорость катера против течения;
Найдем время движения катера против течения. Для этого разделим расстояние на скорость:
4) 72 : 18 = 4 (ч) − двигался катер против течения;
Найдем разницу затраченного катером времени при движении против течения и по течению. Для этого из большего времени вычтем меньшее:
5) 4 − 3 = 1 (ч) − разница во времени между временем движения катера против течения и по течению.
Ответ: катер затратил на 1 час больше при движении против течения реки, чем по течению.Записываем в тетрадь:
1) 21 + 3 = 24 (км/ч) − скорость катера по течению.
2) 72 : 24 = 3 (ч) − двигался катер по течению.
3) 21 − 3 = 18 (км/ч) − скорость катера против течения.
4) 72 : 18 = 4 (ч) − двигался катер против течения.
5) 4 − 3 = на 1 (ч) − больше времени занял путь против течения реки.
Ответ: на 1 час больше занял путь против течения реки, чем по течению.
Задача № 297. Расстояние между причалами 24 км. Сколько времени потратит моторная лодка на путь от одного причала до другого и обратно, если собственная скорость моторной лодки 100 км/ч, а скорость течения 2 км/ч?
Решение задачи
Найдем скорость лодки по течению. Для этого сложим собственную скорость лодки и скорость течения:
1) 10 + 2 = 12 (км/ч) − скорость лодки по течению;
Найдем время движения лодки по течению. Для этого разделим расстояние на скорость:
2) 24 : 12 = 2 (ч) − двигалась лодка по течению;
Найдем скорость лодки против течения. Для этого из собственной скорости лодки вычтем скорость течения:
3) 10 − 2 = 8 (км/ч) − скорость лодки против течения;
Найдем время движения лодки против течения. Для этого разделим расстояние на скорость:
4) 24 : 8 = 3 (ч) − двигалась лодка против течения;
Найдем общее время, потраченное лодкой на путь. Для этого сложим время движения по и против течения:
5) 2 + 3 = 5 (ч) − потратила моторная лодка на путь от одного причала до другого и обратно.
Ответ: 5 часов.Запись задачи в тетради:
1) 10 + 2 = 12 (км/ч) − скорость лодки по течению.
2) 24 : 12 = 2 (ч) − двигалась лодка по течению.
3) 10 − 2 = 8 (км/ч) − скорость лодки против течения.
4) 24 : 8 = 3 (ч) − двигалась лодка против течения.
5) 2 + 3 = 5 (ч) − потратила моторная лодка на путь от одного причала до другого и обратно.
Ответ: 5 часов.
- Назад
- Вперед
умножить наподелить на
Ответы к учебнику за пятый класс «Математика», авторы учебника: Г.В.Дорофеев, Шарыгин, С.Б.Суворова. Мы ни на минуту не сомневаемся, что вы и самостоятельно можете с легкостью выполнить все эти задания, найти ответы и решить все задачи без нашего решебника. Но ГДЗ на 7 гуру поможет вам очень быстро проверить, правильно ли выполнено домашнее задание.
ПЕРЕЙТИ К СПИСКУ ВСЕХ СТРАНИЦ УЧЕБНИКА МАТЕМАТИКА 5 КЛАСС ДОРОФЕЕВ >>
Вам может пригодиться:
Boat Speed Calculator
Boat Safe — сайт, поддерживаемый сообществом. Мы можем получать комиссию за ссылки на этой странице, но мы уверены во всех рекомендуемых продуктах.
Большинство из нас хочет знать максимальную скорость лодки, но не знает, как ее рассчитать. И, скорее всего, мы не думаем, что нам это нужно. GPS — это хороший способ определить скорость вашего судна без особых усилий. Он делает всю работу за вас одним взглядом. Но он не всегда будет доступен, особенно если есть перебои в обслуживании или проблемы с питанием. Кроме того, что, если вы хотите знать, прежде чем войти в воду? К счастью, рассчитать скорость лодки не так сложно. Давайте посмотрим, что вам нужно знать.
Но он не всегда будет доступен, особенно если есть перебои в обслуживании или проблемы с питанием. Кроме того, что, если вы хотите знать, прежде чем войти в воду? К счастью, рассчитать скорость лодки не так сложно. Давайте посмотрим, что вам нужно знать.
Основы расчета скорости лодки
При расчете скорости лодки вам необходимо знать несколько факторов. Вот почему большинство из нас не любит вычислять его самостоятельно. И почему инструмент калькулятора намного полезнее. Тем не менее, мы считаем, что знание основ того, как и почему работает калькулятор, также важно. Даже если вам никогда не придется писать его от руки.
Вам необходимо знать мощность вала вашей лодки, а также ее водоизмещение. Вам также нужно будет включить постоянную Крауча, которая зависит от типа лодки, о которой мы говорим. Это число используется конструкторами лодок при проектировании типов корпуса. Например, средние малолитражки имеют константу Крауча 150. Гоночный катамаран может иметь до 230. Высокоскоростные малолитражки будут иметь константу Крауча 19.0.
Высокоскоростные малолитражки будут иметь константу Крауча 19.0.
Лошадиная сила
Лошадиная сила составляет 550 футо-фунтов в секунду. Это равняется 746 ваттам энергии. Ряд факторов влияет на то, какая мощность в лошадиных силах идеальна для вашей лодки. Это относится к размеру и форме корпуса так же, как и ко всему остальному. Общее эмпирическое правило для лошадиных сил заключается в том, что на каждую лошадиную силу вам нужно от 5 до 40 фунтов веса. Слишком мало лошадиных сил, и вы можете сжечь свой двигатель слишком быстро. Слишком большая мощность может быть опасна. На самом деле каждая лодка должна иметь максимальную мощность в лошадиных силах. Если вы замените свой подвесной мотор на более мощный, вы рискуете повредить лодку, потерять управление и что-то похуже. Когда дело доходит до HP, больше не всегда значит лучше.
Водоизмещение
Водоизмещение — это объем воды, вытесняемый вашей лодкой. Затем это преобразуется в вес, чтобы, с практической точки зрения, вы могли считать водоизмещение веса лодки. Например, гоночный гидросамолет может иметь водоизмещение 6700 фунтов.
Например, гоночный гидросамолет может иметь водоизмещение 6700 фунтов.
A Пример расчета скорости
Скорость = квадратный корень из (лошадиные силы/водоизмещение) X Постоянная наклона
Давайте рассмотрим пример, чтобы получить лучшее представление о меньшей лодке.
Скорость = квадратный корень из (50 л.с./800 фунтов) X 150
Скорость = 37,5 миль в час
В крайнем случае вы можете решить это самостоятельно с ручкой и бумагой. Или, что более вероятно, калькулятор в вашем телефоне. Инструмент калькулятора, конечно, делает это очень простым. Но если вы когда-нибудь окажетесь в затруднительном положении без под рукой, полезно знать математику, стоящую за этим.
Расчет лошадиных сил
Другая важная проблема для многих яхтсменов связана с лошадиными силами. Как мы уже говорили ранее, у вашей лодки должно быть достаточное количество лошадиных сил. Слишком мало — это борьба, которая может сжечь ваш двигатель. Слишком много может повредить лодку и привести к несчастным случаям.
Помните, что при проектировании вашей лодки учитывались эти расчеты. Корпус и транец рассчитаны на то, чтобы выдерживать только определенное давление и вес. Даже небольшое увеличение мощности может резко увеличить нагрузку на корпус. Это также увеличит крутящий момент на транце. Если это выходит за рамки рекомендаций производителя, вы можете полностью разрушить корпус.
Означает ли это, что вы никогда не сможете превысить номинальную мощность своего корпуса? Не совсем. Необходимо сделать размещение. Вам придется усилить корпус и транец, чтобы справиться с более высокой мощностью. Очевидно, что на данный момент у нас тяжелая работа. Если вы не уверены прямо сейчас, как усилить корпус лодки, вы можете остаться в установленных пределах. Еще одна вещь, которую следует учитывать, — это наличие самоотливной кабины. Новый двигатель может нарушить баланс вашей лодки. Это может привести к тому, что вода попадет в шпигаты и замочит лодку.
Если вам нужно купить новый двигатель, вы можете рассчитать мощность по той же формуле. В этом прелесть любой математической формулы: вы можете найти любое число в уравнении, если знаете остальные. Итак, если вы хотите узнать количество лошадиных сил для достижения желаемой максимальной скорости, сделайте обратный расчет. Допустим, в этом случае вы хотите, чтобы ваша лодка разгонялась до 50 миль в час.
В этом прелесть любой математической формулы: вы можете найти любое число в уравнении, если знаете остальные. Итак, если вы хотите узнать количество лошадиных сил для достижения желаемой максимальной скорости, сделайте обратный расчет. Допустим, в этом случае вы хотите, чтобы ваша лодка разгонялась до 50 миль в час.
Мощность = (скорость/приседание) в квадрате x рабочий объем
HP = (50/150) в квадрате x 800
л.с. = 88,89
В этом случае, если ваша маленькая лодка водоизмещением 800 фунтов, если вы хотите развить скорость 50 миль в час, вам нужен двигатель мощностью 90 л.с.
При обновлении двигателя следует помнить о весе. Как правило, более мощный двигатель также будет тяжелее. Изменение смещения, очевидно, меняет фигуры. Тем не менее, это не всегда так. Многие современные двигатели очень хорошо справляются с задачей снижения веса.
А как насчет скорости корпуса?
Еще одна формула для расчета скорости водоизмещающего корпуса, которую вы можете увидеть, довольно проста.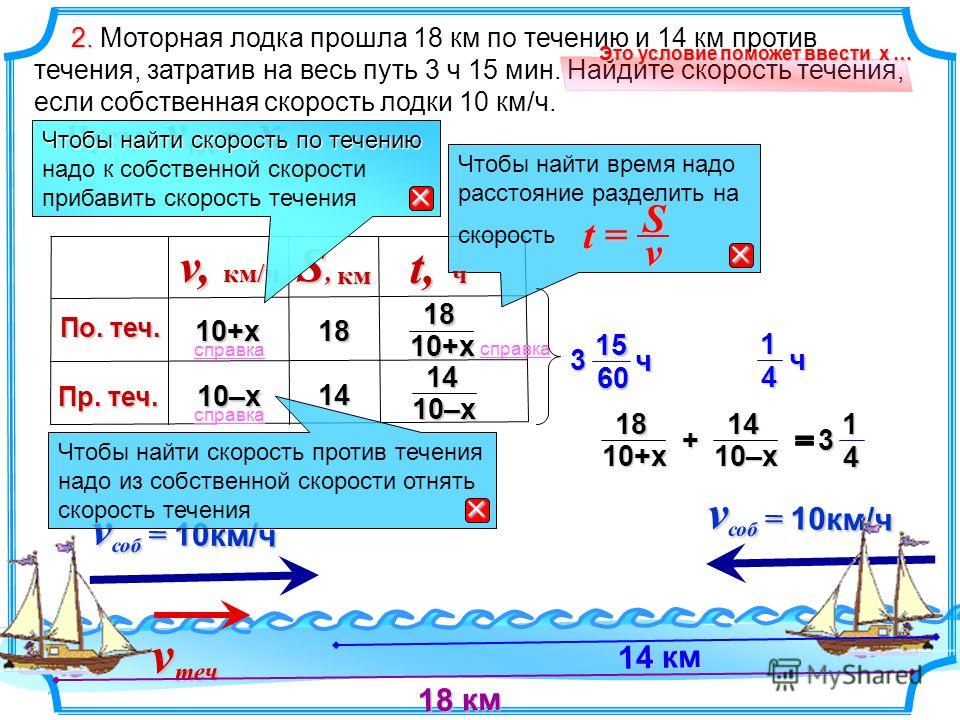 Для этого не требуется столько цифр, но он также не дает наиболее точного ответа. Формула
Для этого не требуется столько цифр, но он также не дает наиболее точного ответа. Формула
1,34 x квадратный корень из длины ватерлинии в футах или
2,43 x квадратный корень из длины ватерлинии в метрах.
Например, если у вас есть 16-футовая лодка, квадратный корень равен 4. Таким образом, формула будет 1,34 X 4 = 5,46 узлов.
1 узел равен примерно 1,15 мили в час, так что вы можете пересчитать это в мили в час, если вам так проще. Это приведет вас к скорости 6,3 мили в час, плюс-минус.
Теоретическая максимальная скорость судна. Тем не менее, многие факторы могут помешать вам. То, сколько у вас лошадиных сил, проскальзывание гребного винта, состояние вашей лодки и многое другое, влияет на это. Даже состояние воды и чистота корпуса могут повлиять на максимальную скорость.
Длина ватерлинии не меняется?
Почему существует эта формула, а также другая формула? Этот расчет более старый и не такой точный. Например, длина вашей ватерлинии может меняться по мере увеличения скорости. Таким образом, точность очень сомнительна. Кроме того, когда вы добавляете мощность, достаточную для преодоления сопротивления корпуса, это число больше не применяется. Это означает, что когда вы используете свой двигатель для движения, наше исходное уравнение гораздо полезнее. Это здесь действительно то, о чем вы должны знать. Вы можете найти его, когда загуглите скорость лодки и удивитесь, почему существуют разные формулы. Сегодня даже производители лодок игнорируют этот расчет. Это просто никоим образом не применимо к современному судостроению.
Например, длина вашей ватерлинии может меняться по мере увеличения скорости. Таким образом, точность очень сомнительна. Кроме того, когда вы добавляете мощность, достаточную для преодоления сопротивления корпуса, это число больше не применяется. Это означает, что когда вы используете свой двигатель для движения, наше исходное уравнение гораздо полезнее. Это здесь действительно то, о чем вы должны знать. Вы можете найти его, когда загуглите скорость лодки и удивитесь, почему существуют разные формулы. Сегодня даже производители лодок игнорируют этот расчет. Это просто никоим образом не применимо к современному судостроению.
Проблемы со страховкой
Последнее замечание, которое вы, возможно, захотите учесть, если хотите улучшить свою лодку. Допустим, вы можете получить более мощный двигатель и действительно увеличить общую скорость. Это может быть весело, если вы делаете это безопасно, и, конечно же, безопасность является проблемой номер один. Но есть еще одна проблема, которая может заставить вас дважды подумать.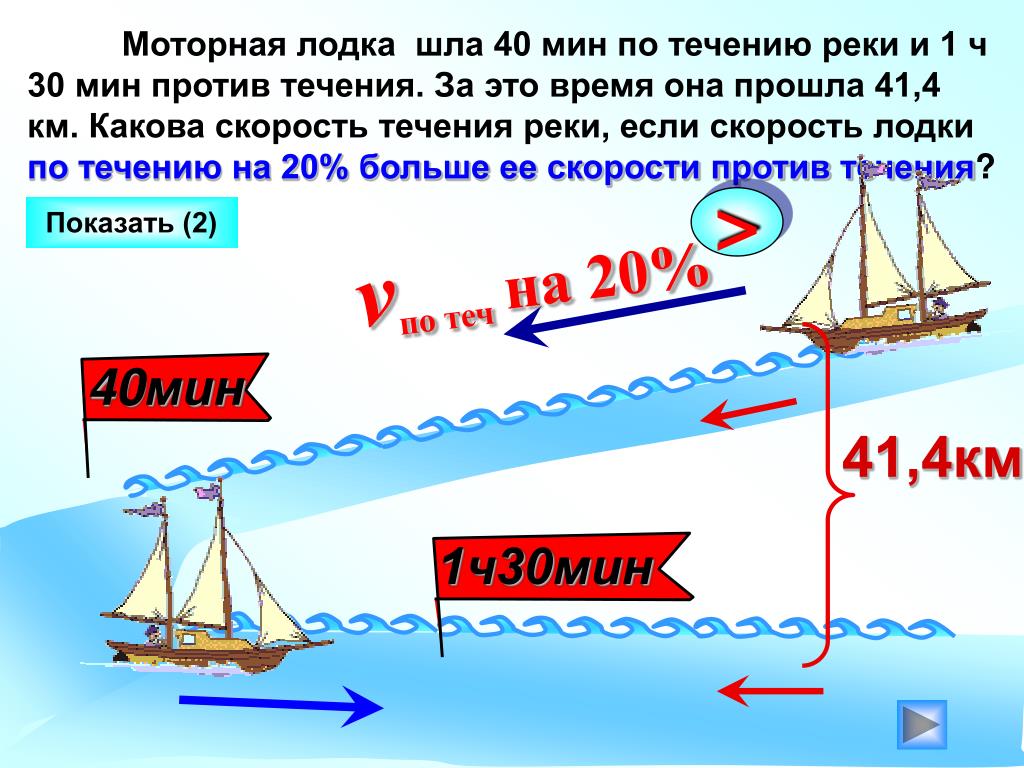 По крайней мере, вы захотите изучить его дальше, чтобы убедиться, что это не проблема. Страхование.
По крайней мере, вы захотите изучить его дальше, чтобы убедиться, что это не проблема. Страхование.
Перед установкой нового двигателя проконсультируйтесь со своей страховой компанией, особенно если он увеличивает мощность. Если вы превысите рекомендации производителя, у вас могут возникнуть проблемы. Если произойдет несчастный случай, ваша страховая компания может отказать в выплате.
Хуже того, если вы попали в аварию с двигателем повышенной мощности, вина может автоматически стать вашей. Вы можете быть признаны ответственными или небрежными за ущерб, причиненный в результате. Ваша страховка не покроет вас, и результатом могут стать судебные иски. Таким образом, перед тем, как что-либо предпринимать, ознакомьтесь с любыми государственными правилами катания на лодках. Нет смысла тратить время и деньги на то, что вы не можете или не должны делать.
Итог
Умение рассчитывать мощность и скорость лодки — очень полезный навык. Наличие удобного калькулятора также стоит. Это позволяет вам лучше понять, сколько времени займет любое путешествие, какой вес может нести ваше судно и многое другое. Плюс, будем честными, это круто.
Это позволяет вам лучше понять, сколько времени займет любое путешествие, какой вес может нести ваше судно и многое другое. Плюс, будем честными, это круто.
Какова средняя скорость парусника?
Когда я пытаюсь вычислить продолжительность того плавания, которое у меня есть в планах, мне всегда нужно сначала узнать одну вещь: среднюю скорость парусника, особенно в дальних путешествиях. Если у вас такая же проблема, эта статья для вас.
Так какова средняя скорость парусника? Большинство парусников курсируют со скоростью 4–6 узлов (4,5–7 миль в час) с максимальной скоростью 7 узлов (8 миль в час или 13 км/ч). Более крупные гоночные яхты могут легко развивать скорость до 15 узлов (17 миль в час или 28 км/ч) со средней крейсерской скоростью 6-8 узлов (7-9 км/ч).миль/ч). Крейсерская скорость более 8 узлов встречается редко.
Различные типы парусников развивают очень разную скорость. Конечно, все зависит от ветровых условий, течения и многих других факторов. Знаете ли вы, что скорость лодки напрямую связана с ее длиной? Чем больше лодка, тем быстрее она идет. Я объясню это вам позже, но сначала подробнее о средней скорости.
Знаете ли вы, что скорость лодки напрямую связана с ее длиной? Чем больше лодка, тем быстрее она идет. Я объясню это вам позже, но сначала подробнее о средней скорости.
В этой статье:
- Факторы, определяющие скорость
- Преобразование и расчет скорости плавания
- Расчет скорости корпуса собственной лодки
- Превышение скорости корпуса
- Количество морских миль
- Связанные вопросы
Факторы, определяющие скорость
Итак, давайте немного подробнее остановимся на скорости парусника. Наиболее важным фактором в определении скорости является тип корпуса. У меня есть для вас два основных правила. Первый: чем меньше лодка находится под водой, тем быстрее она идет.
Вот средние крейсерские скорости для разных типов корпусов:
- Однокорпусник — 6-8 узлов
- Катамараны и тримараны — 9-10 узлов
- Самый быстрый однокорпусник (мировой рекорд кругосветки) — 15,43 узла
- Самый быстрый тримаран (мировой рекорд кругосветки) — 27 узлов
Однокорпусный — Обычный парусник — однокорпусный. Почти все однокорпусные суда водоизмещающие. Водоизмещающий корпус находится под водой, отталкивая воду. Это позволяет лодке более плавно рассекать воду; это стабилизирует лодку. Если вы хотите, чтобы он ехал быстрее, вам придется поднять весь корпус над водой. Позже я покажу вам, как рассчитать максимальную скорость корпуса вашей лодки.
Почти все однокорпусные суда водоизмещающие. Водоизмещающий корпус находится под водой, отталкивая воду. Это позволяет лодке более плавно рассекать воду; это стабилизирует лодку. Если вы хотите, чтобы он ехал быстрее, вам придется поднять весь корпус над водой. Позже я покажу вам, как рассчитать максимальную скорость корпуса вашей лодки.
Катамараны и тримараны — это глиссирующие корпуса, то есть они находятся на поверхности воды. Они вытесняют меньше воды, поэтому они быстрее. Но глиссирующий корпус менее стабилен, чем водоизмещающий. Чтобы компенсировать это, катамараны и тримараны имеют два или три корпуса, что делает их чрезвычайно плавучими. Поскольку это не обычная парусная лодка, я не буду о них рассказывать в этой статье.
Второй фактор — длина лодки. Это второе практическое правило: чем длиннее лодка, тем быстрее она движется. У каждого парусника есть максимальная скорость корпуса, которую он не может превысить (теоретически). Скорость корпуса определяется длиной лодки.
Вот максимальные скорости корпуса для различных длин однокорпусных судов:
| длина | метра | узла | миль в час | км/ч |
|---|---|---|---|---|
| 16 футов | 5 м | 5 | 5,8 | 9,3 |
| 26 футов | 8 м | 6,8 | 7,8 | 12,6 |
| 36 футов | 11 м | 8 | 9,2 | 14,8 |
| 40 футов | 12 м | 8,5 | 9,8 | 15,7 |
| 65 футов | 20 м | 10,8 | 12,4 | 20 |
| 80 футов | 24 м | 12 | 13,8 | 22,2 |
| 100 футов | 30 м | 13,4 | 15,4 | 24,8 |
| 144 фута | 44 м | 16 | 18,4 | 29,6 |
Обратите внимание: максимальная скорость корпуса не является средней скоростью движения. Это верхний предел (теоретически — читайте дальше, чтобы узнать больше).
Это верхний предел (теоретически — читайте дальше, чтобы узнать больше).
Третий и, пожалуй, самый очевидный фактор — это направление и скорость ветра. Если вы планируете большое путешествие, например, переход через океан, обязательно проверьте господствующий ветер и направление для вашего времени года. Вы хотите убедиться, что у вас есть как можно больше подветренной стороны, а также благоприятное течение. Вот почему большинство моряков предпочитают идти на восток, а не на запад, путешествуя по миру.
Если вы хотите знать, почему идти на восток разумно, я рекомендую вам прочитать мою предыдущую статью о кругосветном плавании здесь.
Преобразование и вычисление скорости плавания
Как рассчитать необходимую скорость плавания
Итак, представьте, что вам нужно вовремя добраться до дока. Это в 50 милях отсюда. Вам нужно прибыть в 21:00. На данный момент 1500 часов. Было бы удобно знать, с какой скоростью нужно плыть, чтобы успеть.
Формула проста:
морских миль/время = необходимая средняя скорость
2100 — 1500 = 360 минут
360/60 = 6 часовВаша средняя скорость должна быть: 50 морских миль / 6 = 8,3 узла
Преобразование узлов в мили в час и км/ч
Чтобы преобразовать узлы в мили в час или км/ч, просто умножьте количество узлов на приведенное ниже соотношение.
1 узел = 1,151 миль/ч
1 узел = 1,852 км/ч
Расчет скорости корпуса собственной лодки
Отлично, у нас есть хорошее общее представление о том, чего ожидать от наших надежных судов. Если вы хотите пойти глубже, вы можете попытаться рассчитать максимальную скорость корпуса собственной лодки. Рассчитать максимальную скорость на самом деле очень просто. Пришло время достать свой калькулятор.
Вы вычисляете максимальную скорость корпуса (HS), взяв длину в футах (lwl), извлеките квадратный корень и умножьте его на 1,34.
ГС = √ лвл * 1,34
HS = скорость корпуса
lwl = длина по ватерлинии
Таким образом, 80-футовая лодка имеет максимальную скорость корпуса:
√ 80 * 1,34 = 12 узлов
Превышение скорости корпуса
Водоизмещающий корпус имеет максимальную скорость корпуса. Скорость корпуса — это теоретическая скорость, которая говорит нам, какая максимальная эффективная скорость есть. Все, что выше этой скорости, требует гораздо больше энергии. Если вы приводите свою лодку в движение двигателем, вы можете превысить скорость, толкая корпус через собственную носовую волну (хотя для этого требуется много лошадиных сил, и это не очень хорошо для вашего двигателя).
Если вместо этого вы плывете, вы можете превысить скорость своего корпуса с помощью погоды. Давайте назовем эти условия серфинга (звучит хорошо).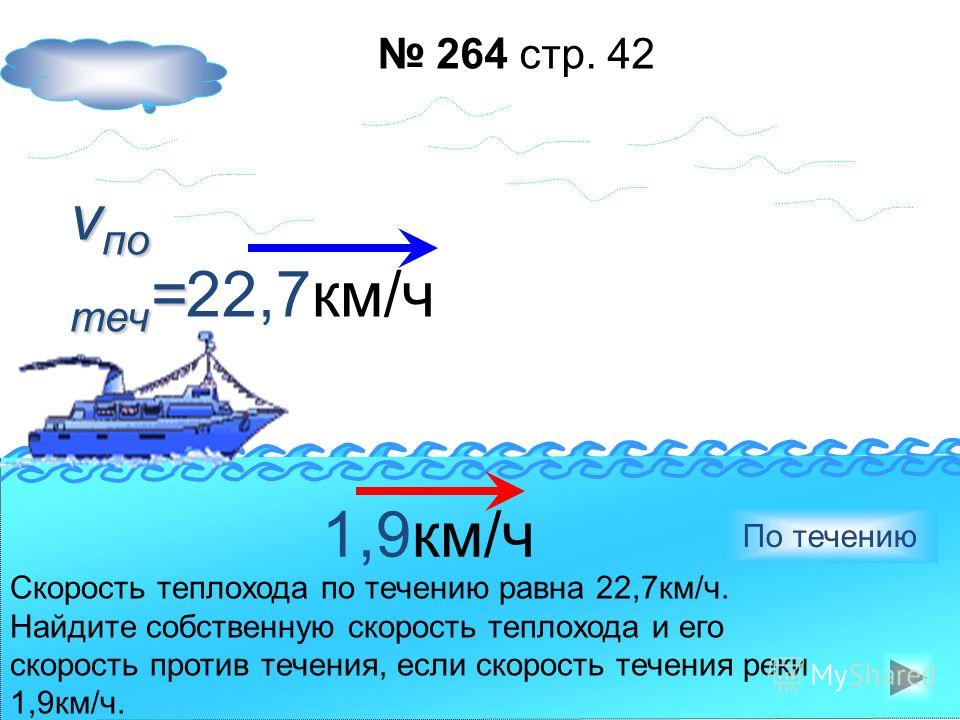 Это может случиться с вами, когда вы плывете по ветру, и течение одновременно толкает вас вперед. Это поможет вам обогнать собственную волну. Если это происходит, длина волны становится больше, чем длина корпуса: вода не может уйти с пути достаточно быстро. В результате лодка начинает глиссировать, увеличивая сопротивление воды в передней части. Поздравляю: вы катаетесь на собственной носовой волне.
Это может случиться с вами, когда вы плывете по ветру, и течение одновременно толкает вас вперед. Это поможет вам обогнать собственную волну. Если это происходит, длина волны становится больше, чем длина корпуса: вода не может уйти с пути достаточно быстро. В результате лодка начинает глиссировать, увеличивая сопротивление воды в передней части. Поздравляю: вы катаетесь на собственной носовой волне.
Однако увеличение скорости не будет ошеломляющим (около 1 узла). Правда в том, что водоизмещающий корпус привязан к своей скорости. Просто для того, чтобы продвинуть его по воде, требуется много энергии. Он создан для того, чтобы резать, а не катить воду.
Количество морских миль
Парусники не ходят молниеносно, но ходят круглосуточно и без выходных. Из-за этого они могут преодолевать довольно большое расстояние. Какое расстояние мы на самом деле можем преодолеть с консервативной скоростью?
Средняя парусная яхта покрывает расстояние примерно 100 морских миль (NM) , на скорости около 4,5 узлов. Это равно 115 милям или 185 км.
Это равно 115 милям или 185 км.
1 морская миля равна 1,852 км или 1,151 мили
Вы можете рассчитать расстояние в день, просто умножив скорость в узлах на 24 часа:
м. миль = узлы * 24
Большинство парусников преодолевают от 100 до 180 морских миль в день. Это означает, что быстроходный парусник в идеальных условиях может пройти более 200 миль. Впечатляющий. Однако все, что превышает 180 морских миль, встречается редко. Обычно мы видим такие высокие крейсерские скорости только в гонках.
Вот расстояния в день (мили) для различных крейсерских скоростей:
| скорость корпуса | НМ | мили | км |
|---|---|---|---|
| 4 | 96 | 111 | 178 |
| 5 | 120 | 115 | 222 |
| 6 | 144 | 166 | 267 |
| 7 | 168 | 190 | 311 |
| 8 | 192 | 221 | 356 |
| 9 | 216 | 249 | 400 |
С какой скоростью может двигаться парусник? Средняя скорость парусника под двигателем составляет 4-5 узлов (5 миль в час или 8 км/ч). Большинство моряков переключаются на двигатель при скорости хода менее 6 узлов, особенно во время перехода.
Большинство моряков переключаются на двигатель при скорости хода менее 6 узлов, особенно во время перехода.
Как быстро ходят гоночные парусники? Гоночные парусники могут развивать скорость от 30 до 50 узлов (35-58 миль в час или 55-92 км/ч). Рекорд установлен на скорости 65,45 узла (75 миль в час или 121 км/ч). Они могут превзойти скорость ветра, потому что у них глиссирующий корпус вместо водоизмещающего, что делает их намного быстрее обычных парусников
Может ли парусник плыть быстрее ветра? Парусники с глиссирующим корпусом (многокорпусные) могут двигаться быстрее ветра. Водоизмещающие корпуса (средний парусник) не могут противостоять ветру или немного в условиях серфинга.
Вы нашли ответ на свой конкретный вопрос?
👍 92
👎 5
Оценочные задачи (системы уравнений с двумя переменными)
Оценочные задачи (системы уравнений с двумя переменными) Лодка может пройти 16 миль вверх по реке за 2 часа. Та же лодка может пройти 36 миль вниз по течению за 3 часа. Что такое
скорость лодки в стоячей воде? Какова скорость течения?
Та же лодка может пройти 36 миль вниз по течению за 3 часа. Что такое
скорость лодки в стоячей воде? Какова скорость течения?
Что мы пытаемся найти в этой задаче?
Мы хотим найти две вещи: скорость лодки в
стоячая вода и скорость течения. Каждая из этих вещей будет
быть представлено другой переменной:
C = скорость тока
Поскольку у нас есть две переменные, нам нужно будет найти систему из двух уравнений, которые нужно решить.
Как найти два нужных уравнения?
Проблемы скорости основаны на отношениях Расстояние
= (Ставка)(Время) .
Для организации работы мы составим карту расстояний, скорость и время, за которое лодка движется как против течения, так и против течения. Диаграмма даст нам информацию о расстоянии, скорости и времени, которое нам нужно написать наши два уравнения.
Вот как выглядит диаграмма до того, как мы поместим любой из
наша информация в нем:
Давайте посмотрим на слова задачи.
Лодка может пройти 16 миль вверх по реке за 2 часа. Мы поместим 16 в нашу диаграмму для расстояния вверх по течению, и мы поставим 2 в график времени вверх по течению.
Та же лодка может пройти 36 миль вниз по течению за 3 часа. Мы поместим 36 на нашу диаграмму для расстояния вниз по течению, и мы поставим 3 на графике для времени вниз по течению.
Теперь наша диаграмма выглядит так:
Теперь давайте подумаем о скорости движения лодки.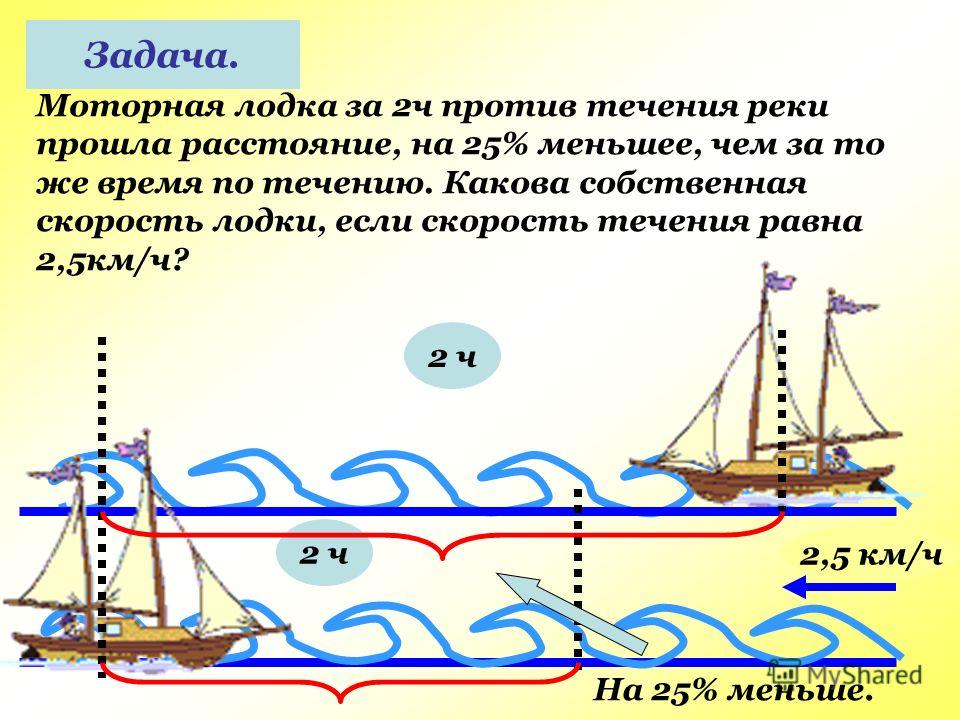 Мы знаем, что если бы лодка стояла на тихом озере, ее мотор двигал бы ее.
со скоростью В миль в час. Но лодка не на тихом озере;
он движется вверх и вниз по течению реки. Если лодка плывет
вверх по течению, течение (которое составляет C миль в час) будет давить на
катер, и скорость катера уменьшится на С миль в час.
Результирующая скорость лодки (движущейся против течения) равна B-C миль в час.
С другой стороны, если лодка движется вниз по течению, течение
толкать лодку быстрее, и скорость лодки увеличится на С миль
в час. Результирующая скорость лодки (плывущей по течению)
составляет B+C миль в час. Мы поместим эту информацию в нашу диаграмму:
Мы знаем, что если бы лодка стояла на тихом озере, ее мотор двигал бы ее.
со скоростью В миль в час. Но лодка не на тихом озере;
он движется вверх и вниз по течению реки. Если лодка плывет
вверх по течению, течение (которое составляет C миль в час) будет давить на
катер, и скорость катера уменьшится на С миль в час.
Результирующая скорость лодки (движущейся против течения) равна B-C миль в час.
С другой стороны, если лодка движется вниз по течению, течение
толкать лодку быстрее, и скорость лодки увеличится на С миль
в час. Результирующая скорость лодки (плывущей по течению)
составляет B+C миль в час. Мы поместим эту информацию в нашу диаграмму:
Каждая строка диаграммы даст нам уравнение.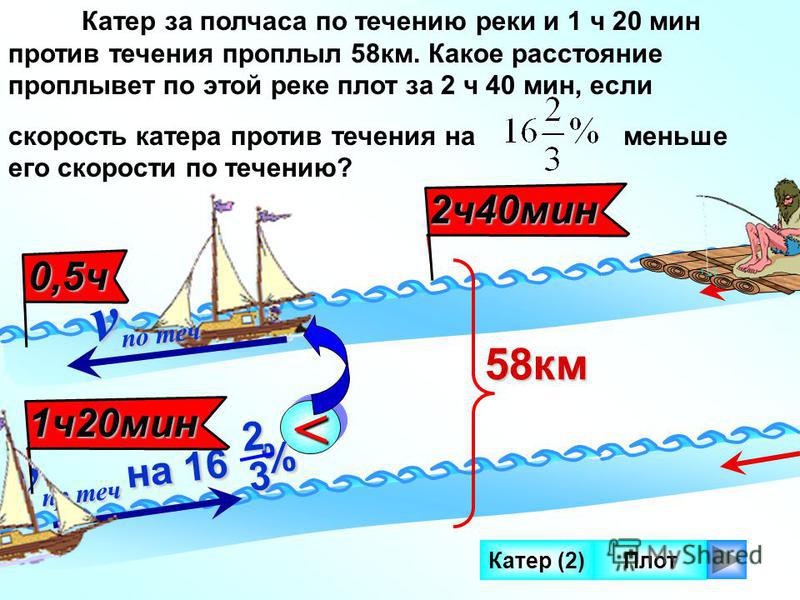
Движение вверх по течению, Расстояние = (Скорость)(Время), поэтому 16 = (B-C)(2)
Движение вниз по течению, Расстояние = (Скорость) (Время), поэтому 36 = (B+C)(3)
Теперь решим систему уравнений:
36 = 3(В+С)
Если мы разделим обе части первого уравнения на 2, то
станет 8 = B-C.
Если мы разделим обе части второго уравнения на 3,
это станет 12 = B+C.
Сложим эти уравнения, чтобы найти решение:
12 = Б+В
20 = 2В
10 = В
Скорость лодки в стоячей воде 10 миль в час.
Чтобы найти скорость течения, мы можем подставить 10 для B в любом из наших уравнений. Мы выберем самое простое уравнение работать с:
12 = 10+С
2 = С
Скорость течения 2 мили в час.
Гонконгские джонки: ваш путеводитель по лучшим чартерным лодкам
Гонконг (CNN) — В одну минуту вы садитесь на гонконгскую джонку, окруженную глянцевыми небоскребами, их стеклянные и стальные фасады отражаются в воде.
Всего через 45 минут вы оказываетесь в отдаленной бухте, наслаждаетесь свежими закусками и готовыми окунуться в лазурные воды для купания.
К счастью, вам не нужно быть владельцем яхты, чтобы насладиться этим типично гонконгским приключением.
Совершите визуальную экскурсию по самым красивым местам Гонконга.
Хотя слово «джонка» традиционно относится к китайским деревянным парусникам времен династии Хань, которые до сих пор используются в естественных гаванях и на островах Гонконга, в наши дни это универсальное выражение, которое относится к любой гонконгской чартерной лодке.
Сегодняшние джонки поставляются с современной роскошью, а в Гонконге еда и напитки занимают центральное место.
Мы связались с несколькими ведущими операторами барахла, чтобы узнать больше о многочисленных пакетах и лодках, которые предлагают все, от вейкбординга до спа-процедур на борту.
Самые живописные дороги Гонконга
Для классического барахла
Микеланджело
В главной спальне установлена мягкая мебель Ralph Lauren.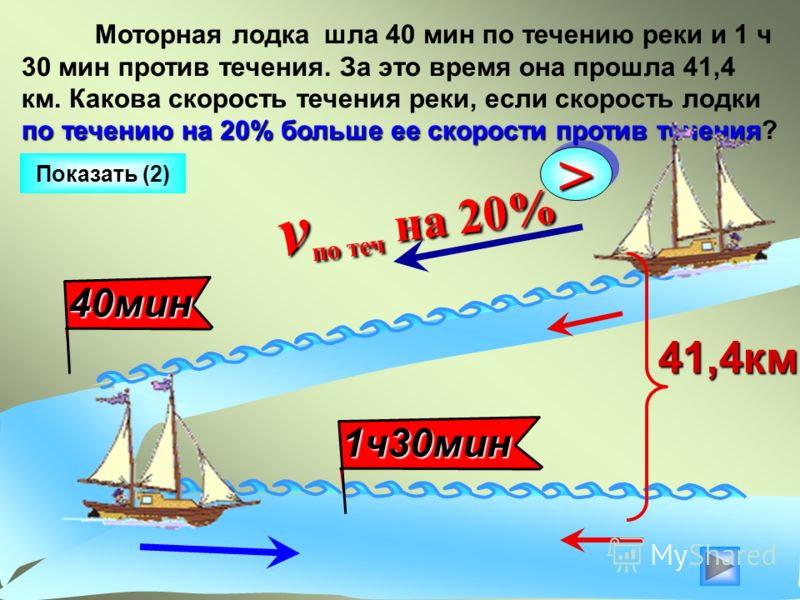
Courtesy Michelangelo
Классическая гонконгская джонка имеет сложную конструкцию, изобретенную много веков назад, чтобы выдерживать трудности морских путешествий.
Сегодняшние версии с двигателем для отдыха сохранили этот традиционный вид, но оснащены встроенными элементами роскоши и удобствами.
Например, 80-футовый Микеланджело опрятный, олдскульный шарм.
Эта роскошная трехпалубная яхта с отделкой из тика, латуни и красного дерева включает в себя роскошные спальни, ванные комнаты, столовую, гостиную и кухню с собственным поваром.
Wi-Fi, кондиционер, караоке, аудиосистема Bose и камера на крыше напоминают вам, что вы все еще в 21 веке.
Вместительная верхняя палуба может быть превращена в танцпол, а за обеденным столом могут разместиться от 10 до 12 человек для морской трапезы.
Куда плыть?
Дао Те Лаггер Микеланджело рекомендует залив Джосс-Хаус, недалеко от залива Клируотер, недалеко от гавани Виктория, откуда «открывается потрясающий панорамный вид на побережье и острова Гонконга».
«В группе Ninepin (или на островах Кво-Чау) одни из самых чистых вод, которые я видел в Гонконге, и на островах вокруг, которые вы можете исследовать», — добавляет Лаггер.
Для тех, кто хочет путешествовать дальше, Лаггер говорит, что Двойная Гавань, отдаленная гавань на северо-востоке Новых Территорий, является еще одной жемчужиной.
Aqua Luna
Если вам нужна классическая джонка с красными парусами, попробуйте Aqua Luna.
Он предлагает все, от 45-минутных обзорных экскурсий по гавани Гонконга до вечерних круизов Symphony of Light, где вы можете насладиться ужином из десяти блюд, наблюдая ночное лазерное шоу.
Коктейли и димсам в деревянном интерьере с кондиционером.
Посетите www.luxuryjunk.com.hk и aqualuna.com.hk/flash для получения дополнительной информации. Цены доступны по запросу.
Гонконг: путеводитель Insider Travel Guide
Для чистой роскоши
Lazydays
Lazydays предлагает альтернативу обычным тусовкам.
Courtesy Lazydays
Это для тех, кто действительно хочет побаловать себя.
Стандартные пакеты Lazydays включают просекко, крафтовое пиво и водные игрушки.
Меню и кейтеринг можно настроить по индивидуальному заказу — есть даже вариант палео.
Детский детский бассейн гарантирует, что малыши не упустят возможности повеселиться, а на борту также могут играть ди-джеи и музыкальные группы.
Когда вы уезжаете, уход за телом не прекращается: компания объединила усилия со «специалистами по гидратации и оздоровлению для восстановления сил после круиза», предложив спа, маникюр и услуги дворецкого.
«Если вы можете уйти, поездка в будний день — это фантастика», — говорит Ирэн Мур из Lazydays.
«Лучшие месяцы для лодочных прогулок — сентябрь и октябрь, когда погода немного прохладнее, но все же приятная, а вода все еще теплая — гораздо лучший способ насладиться прогулкой на свежем воздухе, чем в очень влажные месяцы», — добавляет Мур.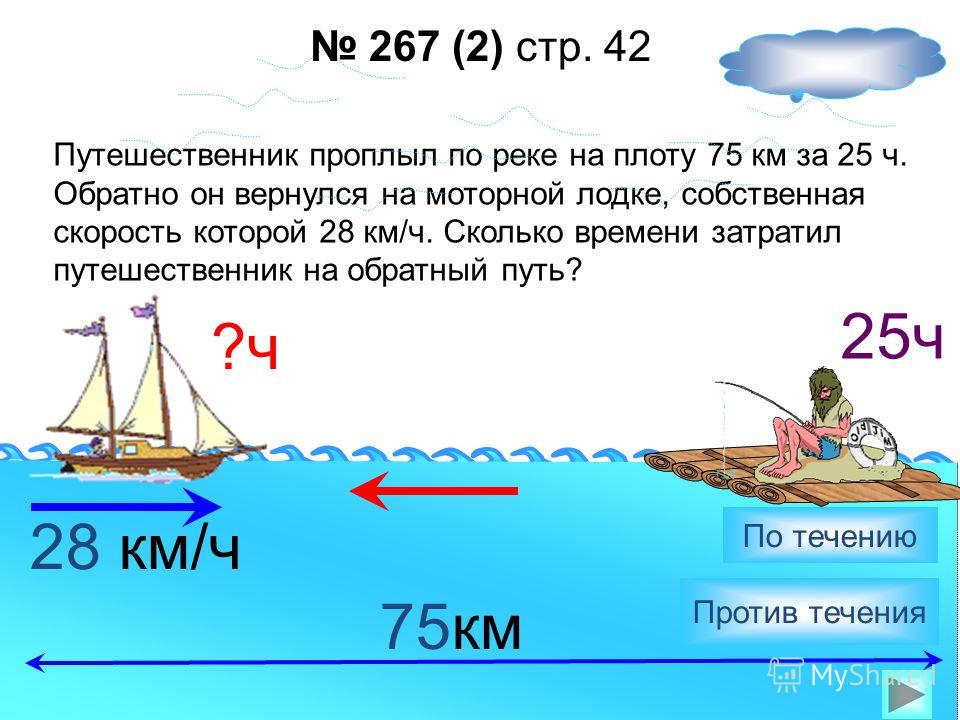
Посетите www.lazydays.com.hk для получения дополнительной информации. Для взрослых цены на пакеты варьируются от 940 гонконгских долларов (121 доллар США) до 1175 долларов США. Минимальная плата за их лодки составляет от 14 100 гонконгских долларов (1 818 долларов США) до 17 625 гонконгских долларов для 15 взрослых и от 23 500 до 29 гонконгских долларов.,375 на 25 взрослых.
Hong Kong Yachting
Удобства на борту Jungle Jane and Tarzan включают надувную горку и бар.
гонконгские джонки hk Yachting 01
Лодки-близнецы Jungle Jane и Tarzan — жемчужины короны этой австралийской компании.
Их открытые палубы переходят в специально разработанные плавательные платформы шириной 22 фута.
«Мы проплыли на них более 4000 морских миль от Австралии, — говорит Джесс Харрис из Hong Kong Yachting.
В джонках есть «надувная горка, надувная гостиная, бар с официантками, королевский шезлонг и кресла-мешки с первоклассной звуковой системой Fusion».
Вместимостью до 100 человек они являются популярным выбором для проведения корпоративных мероприятий, свадеб и больших вечеринок.
Советы от владельца?
«Если вам нужна выгодная сделка, попробуйте запросить праздничный или будний день или взять напрокат барахло в марте и апреле или октябре и ноябре, в преддверии жарких летних месяцев», — говорит Харрис. «Часто можно подобрать лодку за полцены».
Hong Kong Yachting Экскурсии на джонках начинаются от 8500 гонконгских долларов (1096 долларов США) на 30 человек в течение одного дня.
Проверьте www.hongkongyachting.com для получения дополнительной информации. Цены на пакеты нежелательной поездки, включая еду и напитки, начинаются от 650 гонконгских долларов на человека. Цена однодневного чартера на Jungle Jane составляет 25 000 гонконгских долларов, а на Tarzan — 27 000 гонконгских долларов. Для вечернего чартера цены на две лодки составляют 23 000 и 24 000 гонконгских долларов соответственно.
Отрыв
Breakaway предлагает пикап на следующий день для походов.
Courtesy Breakaway
В зависимости от вашего уровня энергии, с Breakaway вы можете провести целый день, провести романтический ужин на двоих или просто позавтракать или пообедать у воды.
Идеально подходит для тех, кто ищет более интимную поездку или не хочет собирать большую вечеринку.
Хочешь остаться еще немного? Забронируйте поход на пляж с ночевкой и трансфером на следующий день.
Этот оператор роскошных яхт предлагает пакеты «все включено» с широким выбором индивидуальных вариантов.
Организатор частных мероприятий доступен для консультации.
Дженни Куо из Breakaway выбрала Тай Лонг Ван, где песок и вода мягкие и чистые.
«Когда вы попадаете в Тай Лонг Ван, у вас создается иллюзия, что вы были где-то еще, кроме Гонконга», — говорит Куо.
Для получения дополнительной информации посетите сайт www. breakawayhk.com . 14 850 гонконгских долларов (1 915 долларов США) покрывают еду и напитки для 15 человек в течение всего дня.
breakawayhk.com . 14 850 гонконгских долларов (1 915 долларов США) покрывают еду и напитки для 15 человек в течение всего дня.
Как быть местным жителем Гонконга: 10 советов
Для вечеринок, праздников и приключений
Вкусно
Основатели Деннис и Анушка Вильянуэва – давние гурманы.
Courtresy Nextwave Charters
Для домашних блюд с большими порциями выбирайте Delicious.
Основатель Деннис Вильянуэва говорит нам, что он обслуживал знаменитостей, включая Наоми Кэмпбелл, Мэйси Грей и Джека Блэка.
«Анушка, моя жена и я всегда мечтали о собственном небольшом продовольственном бизнесе, — говорит Вильянуэва, приехавшая из Филиппин.
«Мы всегда любили нашу еду. Работая в лучших ресторанах и барах Гонконга, мы попробовали хорошую еду и захотели создать свой собственный бренд.»
В качестве поставщика питания Delicious использует лодки, предоставленные Nextwave Charters.
Вильянуэва обещает, что просекко, крафтовое пиво, вино и сангрия будут литься рекой.
А как насчет его фирменных фаст-фудов?
«Жареный цыпленок с лемонграссом и чесноком, свежеприготовленные пироги с овощами, руккола с инжиром, салат из артишоков и тертого пармезана [и] наш знаменитый шоколадный торт» — вот лишь некоторые из предлагаемых угощений.
Что касается пейзажей, то он рекомендует Черепашью бухту Ламмы и Тай Лонг Ван.
Дополнительные услуги включают скоростные катера и лодки-бананы для занятий водными видами спорта.
Посетите www.delicious-hk.com для получения дополнительной информации. Цены: от 5500 гонконгских долларов (709 долларов США) до 8500 гонконгских долларов за китайский хлам. От 6000 до 8700 гонконгских долларов за Western White Cruiser, вмещающий 38 человек.
Jaspa’s Junks
Кухня — неотъемлемая часть нездоровой пищи в Jaspa’s.
Предоставлено castelo concept
Когда дело доходит до еды, Jaspa’s Junks не мешкает.
«Мы предлагаем приветственные закуски, приготовленные на борту, а затем обед или ужин в форме шведского стола, приготовленные нашим шеф-поваром на борту каждого чартера», — говорит Брайан Парфитт из Jaspa’s Junks.
Он также уверяет нас, что, бездельничая ли вы, или в воде, или на плотах весь день, на обратном пути вас встретят «горячей пиццей и декадентским шоколадным тортом».
Все это идет на традиционном китайском барахле с «полностью загруженным iPod отличной музыки для вечеринок».
Также можно заняться водными видами спорта.
Посетите www.casteloconcepts.com для получения дополнительной информации. 2500 гонконгских долларов (322 доллара США) за однодневную поездку.
Лучший димсам в Гонконге: как попробовать ням-ча по-кантонски
Съешьте свой путь через историю Гонконга
Примечание редактора: эта статья была первоначально опубликована в 2011 году. Она была переформатирована и переиздана в 2017 году.
3
ГлавнаяПерейти к содержимому
ПЕРВОЕ ПРЕДУПРЕЖДЕНИЕ: Приятное свежее осеннее утро!
Этим вечером быстро упасть в 60-е и 50-е, а завтра начать в верхнем 40-м и нижнем 50-м. Завтра мы должны увидеть много солнечного света с низким уровнем влажности.
Завтра мы должны увидеть много солнечного света с низким уровнем влажности.
Заключенные Алабамы бастуют за улучшение условий содержания в тюрьмах
Энергетические бригады Алабамы готовятся к урагану Ян
BJCTA ищет операторов MAX, Birmingham Xpress
0952 Центр борьбы с преступностью в Алабаме сотрудничает с Алабамской коалицией против изнасилований
Обновлено: 6 часов назад
|
Автор Tristan Ruppert
Центральная Алабама CrimeStoppers объявляет о новом партнерстве с Алабамской коалицией против изнасилований.
Закон о ферме истекает в следующем году, фермеры сталкиваются с новыми проблемами
Обновлено: 6 часов назад
|
Автор Aajene Robinson
Предыдущий пятилетний законопроект о фермерских хозяйствах истекает в следующем году, и в настоящее время правительственные чиновники путешествуют по стране, изучая проблемы, с которыми фермеры столкнулись с 2020 года по настоящее время.
Преступники Центральной Алабамы ищут информацию по делу об убийстве
Обновлено: 6 часов назад
|
Автор: WBRC Staff
25 сентября около 20:00 заместители шерифа округа Талладега были отправлены в 100-й квартал Семинол-авеню в связи с сообщением о застреленном человеке, по данным Central Alabama Crime Stoppers.
Жилищные управления Бирмингема и Бессемера получают по 1,5 миллиона долларов на развитие молодежной рабочей силы
Обновлено: 6 часов назад
|
By Chasity Maxie
Конгрессмен Терри Сьюэлл была в городе в понедельник, чтобы объявить о миллионах на обучение молодых людей.
Представитель Терри Сьюэлл отреагировала на возвращение Алекса Дрюке и Энди Хьюна домой
Обновлено: 6 часов назад
|
By Chasity Maxie
Новая реакция члена Конгресса Терри Сьюэлл на освобождение двух ветеранов вооруженных сил США, которые были взяты в плен три месяца назад во время боевых действий на стороне украинских войск против России.
Тело найдено в корзине для пожертвований одежды на предприятии
Обновлено: 12 часов назад
|
By WSFA 12 News Staff
Полиция Южной Алабамы сообщила, что в понедельник в мусорной корзине для пожертвований одежды было найдено тело.
Спутниковые и радары
Особенности
Последнее видео
Хорошие вещи: Crossville HS Homecoming Королева, ее Crown
Редка Greepy Born Born Born a Alabama
Rare Green Puppy Born Born a Alabama
0941
Организация наставничества в Tuscaloosa Co.
Веставия Хиллз Подозреваемый в церкви в суде
Больше новостей
Собаки, найденные с человеческим Skull в Birmingham
Dogs.
Автор WBRC Staff
Коронер сказал, что мужчина нашел своих собак с черепом в 400-м квартале Олбани-плейс.
36-летний мужчина погиб в результате аварии на мотоцикле в Бирмингеме
Обновлено: 13 часов назад
|
Автор WBRC Staff
Коронер сообщил, что пострадавший ехал на пересечении Хайленд-авеню и 21-й площади Саут, когда не справился с управлением мотоциклом и врезался в бордюр.
6 Расследование на вашей стороне
Государство требует смертной казни по делу о стрельбе в церкви Веставии
Обновлено: 14 часов назад
|
Дженнифер Хортон
Штат будет добиваться смертной казни по делу о стрельбе в Епископальной церкви Святого Стефана, что было подтверждено в понедельник. 70-летнему Роберту Финдли Смиту предъявлено обвинение в убийстве двух или более человек.
Восточная Алабама
Полиция Силакоги: Алабама. Мужчина, обвиняемый в сексуальных преступлениях, бежит на Аляску, арестован в аэропорту
Обновлено: 15 часов назад
|
Автор WBRC Staff
По данным полиции, мужчина из Силакоги вернулся в Алабаму, где ему предъявлены многочисленные обвинения в сексуальном насилии после побега на Аляску в начале этого года.
The Good Stuff
Алабамский щенок французского бульдога родился зеленым
Обновлено: 13 часов назад
|
Автор WBRC Staff
Владелец собаки в Хелене празднует появление своего французского бульдога в помете. У французского бульдога родился зеленый щенок!
Хорошие вещи
Хорошие вещи: Crossville HS Королева возвращения на родину делится своей короной
Обновлено: 10 часов назад
|
Автор WBRC Staff
В пятницу вечером в средней школе Кроссвилля в графстве Декалб молодая женщина была коронована как королева возвращения на родину, но она отдала свою корону другой молодой женщине, которая живет с церебральным параличом.
Новости Таскалуса
Медицинский центр Таскалуса VA предлагает услуги по предотвращению самоубийств
Обновлено: 20 часов назад
|
Кельвин Рейнольдс
В 2020 году 152 ветерана Алабамы покончили жизнь самоубийством.
Родители школ города Трассвилл обеспокоены безопасностью в школах
Обновлено: 12 часов назад
|
Лорен Харксен
Родители говорят, что около года назад ученица создала так называемую тетрадь смерти с именами 37 учеников. Они говорят, что узнали об инциденте только после того, как сотрудник школьного ресурса услышал, что совсем недавно другому ученику угрожали.
CrimeStoppers предлагает советы жертвам нападения
Обновлено: 25 сентября 2022 г., 18:24 CDT
|
Автор Brady Talbert
Моменты после автомобильной аварии могут быть беспокойными, но это только усиливается, когда другой водитель убегает.
19-летний подросток погиб в результате опрокидывания в округе Ли
Обновлено: 25 сентября 2022 г., 10:20 CDT
|
Автор: WSFA 12 News Staff
Мужчина из Opelika погиб в результате автомобильной аварии в округе Ли.
Округ Шелби
Тело пропавшего лодочника найдено на озере Лэй
Обновлено: 25 сентября 2022 г., 21:43 CDT
|
Автор WBRC Staff
Около 8:00 утра в воскресенье, 25 сентября, тело 51-летнего Дэвида Этериджа было найдено и опознано недалеко от того же места, где он пропал без вести.
Авария двух автомобилей на бульваре Пинсон-Вэлли в Тарранте
Обновлено: 25 сентября 2022 г., 10:08 CDT
|
Автор WBRC Staff
Полицейское управление Тарранта отреагировало на аварию с двумя автомобилями в воскресенье, 25 сентября, на Пинсон-Вэлли-Паркуэй и Пайн-Хилл-роуд.
ДОПОЛНИТЕЛЬНЫЕ НОВОСТИ
Стрельба расследуется в жилом комплексе в Таскалусе
Обновлено: 25 сентября 2022 г., 21:32 CDT
|
Автор WBRC Staff
Отдел по расследованию насильственных преступлений Таскалуса расследует убийство в квартале 400 на 8-й авеню, северо-восток, апартаменты Ривер-Роуд.
National
«Мы получили наше чудо»: освобожденные американцы вернулись домой в Алабаме
Обновлено: 24 сентября 2022 г., 16:12 CDT
|
Ассошиэйтед Пресс
Два ветерана вооруженных сил США, пропавшие без вести три месяца назад во время боевых действий с украинскими войсками против России, прибыли домой в Алабаму в субботу, встреченные объятиями, аплодисментами и слезами радости в главном аэропорту штата.
Новости Таскалуса
Новая программа наставничества для молодых заключенных округа Таскалуса
Обновлено: 13 часов назад
|
Келвин Рейнольдс
У детей, задержанных по уголовным обвинениям в Таскалузе, появилась новая возможность поделиться своими мыслями и чувствами.
Национальный
ГРАФИКА: Женщина сбита поездом, когда она находилась в полицейском крейсере, припаркованном на путях
Обновлено: 24 сентября 2022 г. , 1:55 CDT
, 1:55 CDT
|
От сотрудников КМГХ
Примерно через 1 минуту и 9 секунд после того, как Риос-Гонсалес был помещен сзади, впервые вдали слышен гудок поезда.
Мужчина получил опасные для жизни травмы после стрельбы с участием офицера в Бирмингеме
Обновлено: 25 сентября 2022 г., 16:49 CDT
|
Автор WBRC Staff
Полиция Бирмингема заявила, что в настоящее время расследует стрельбу, произошедшую 24 сентября с участием офицера. 25, 2022 в 22:08 CDT
|
Лорен Харксен
По данным AAA, в 2021 году средняя годовая стоимость владения и эксплуатации нового автомобиля составляла 9 666 долларов или 805,50 долларов в месяц. В этом году он подскочил до 10 728 долларов или 894 долларов в месяц.
Алекс Друке и Энди Хьюн прибывают в Бирмингем после трех месяцев пребывания в русском плену
Обновлено: 24 сентября 2022 г. , 23:05 CDT
, 23:05 CDT
|
Лорен Харксен
Влюбленные обменивались улыбками, объятиями и даже смехом, когда они, наконец, воссоединились в международном аэропорту Бирмингем-Шаттлсуорт субботним днем.
Семья высказалась после того, как изображения заключенного из Алабамы стали вирусными
Обновлено: 15 часов назад
|
Эшли Бауэрман
Распространенные в Интернете изображения заключенного в тюрьме Алабамы вызвали общественный резонанс в социальных сетях.
Саудовская Аравия помогает выступить посредником Алекс Друке, Энди Хюин выпускают
Обновлено: 24 сентября 2022 г., 23:11 CDT
|
Лорен Харксен
Посольство США в Саудовской Аравии сообщило близким Алекса Дрюке и Энди Хьюна об их освобождении в среду. В посольстве говорят, что это были лишь двое из десяти заключенных, освобожденных на этой неделе из пяти разных стран.
Крушение пассажирского самолета в Онеонте, 2 человека
Обновлено: 24 сентября 2022 г., 12:21 CDT
|
Автор: WBRC Staff
По сообщению администрации города Онеонта, к северу от взлетно-посадочной полосы муниципального аэропорта Онеонта в Роббинс-Филд разбился самолет с двумя пассажирами.
Gamecock Struts МакКленнена на чемпионате Северной Америки IC37
Год напряженной работы — три серии зимних регат в Форт-Лодердейле и целое лето парусного спорта в Ньюпорте — окупились для команды Gamecock Питера МакКленнена (вверху), когда они одержали победу в соревновании 20 — флот лодок, чтобы выиграть чемпионат Северной Америки IC37 2022 года. Команда настолько доминировала в первых шести гонках регаты, что смогла насладиться неторопливым круизом к причалу, в то время как оставшиеся 19лодки участвовали в финальной гонке, чтобы определить второстепенные места. «Отмычка» Питера Вагнера заняла второе место, а «Новая волна» Стива Либеля — третье.
«Огромно», — сказал МакКленнен о победе. «Я думаю об одном дизайне этого клуба, восходящем к New York 30 [построенному в 1905 году]. Как энтузиаст классических яхт, я думаю, что это одна из самых особенных вещей в клубе, большие гонки на больших лодках с одним дизайном. Чтобы, наконец, прорваться и стать чемпионом Северной Америки в этом году, он еще не полностью реализован. Мы были на подиуме раньше, [на IC37 North Americans 2021 года] мы были вторыми, в Melges 20 мы были третьими, но никогда не выигрывал [чемпионат Северной Америки или страны]».
Североамериканский чемпионат IC37 проходил с 23 по 25 сентября в Нью-Йоркском яхт-клубе Harbour Court в Ньюпорте, штат Род-Айленд. Регата стала заключительным событием летнего календаря регат IC37 2022 года, в котором 20 коринфских команд боролись за высшие награды. более восьми гонок на проливе Род-Айленд и заливе Наррагансетт. Класс IC37 был создан нью-йоркским яхт-клубом для продвижения конкурса одного дизайна среди яхтсменов-любителей. Высокопроизводительная 37-футовая килевая лодка была разработана Марком Миллсом, а строгие правила класса обеспечивают самые равные условия в парусном спорте на больших лодках. Второй чемпионат Северной Америки в этом классе спонсировали Hammetts Hotel, Safe Harbour Marinas и Helly Hansen.
Высокопроизводительная 37-футовая килевая лодка была разработана Марком Миллсом, а строгие правила класса обеспечивают самые равные условия в парусном спорте на больших лодках. Второй чемпионат Северной Америки в этом классе спонсировали Hammetts Hotel, Safe Harbour Marinas и Helly Hansen.
Коллективное время в IC37 для 20-сильного флота за лето было очевидно в эти выходные в многолюдных обгонах и близких финишах. Ошибки наказывались быстро, а откатиться назад после неудачного старта было чрезвычайно тяжело. Однако МакКленнен и его команда были на другом уровне, во многом благодаря почти 40 дням, проведенным этим летом на корабле. Экипаж Gamecock начал регату вторым, выиграл следующую гонку — и еще две на всякий случай — и ни в одной гонке не финишировал хуже четвертого. МакКленнен объяснил их преимущество обширной практикой этим летом и стремлением как можно больше участвовать в своей гонке.
«[Нам] пришлось держаться подальше [от других лодок]», — сказал он. «Эти лодки не любят плыть рядом друг с другом. Всякий раз, когда вы находитесь в скомпрометированной ситуации, и есть две лодки, пытающиеся занять позицию друг против друга, обе лодки всегда проигрывают. Целью № 1 для нас в оба дня было освободиться, даже если вы находитесь на неблагоприятной стороне. Как только мы освободимся, мы сможем плыть с заданной скоростью весь день».
Всякий раз, когда вы находитесь в скомпрометированной ситуации, и есть две лодки, пытающиеся занять позицию друг против друга, обе лодки всегда проигрывают. Целью № 1 для нас в оба дня было освободиться, даже если вы находитесь на неблагоприятной стороне. Как только мы освободимся, мы сможем плыть с заданной скоростью весь день».
Находясь вдали от других лодок, даже если это означало использование некоторых транцов, чтобы найти свободное место, также давало тактику Кэмерону Эпплтону свободу работать при колебаниях ветра, которые по разным причинам были значительными в оба дня.
«Вчера было так изменчиво, а сегодня так изменчиво», — сказал МакКленнен. «[Сегодня], если вы попадали не на ту сторону курса, с одной стороны дуло 20 узлов, а с другой стороны дуло восемь».
МакКленнен также отметил время, проведенное его командой в зимней серии IC37, которая проходила в течение последних двух зим из яхт-клуба Лодердейла в Форт-Лодердейле, штат Флорида. состояние моря было важным фактором в гонках.
«Мы очень привыкли к волнам, так как оба сезона участвовали во Флориде», — сказал МакКленнен. «Мне более комфортно на этих волнах, чем если бы мы плыли только внутри [бухты Наррагансетт]».
Чемпионат Северной Америки стал финальным событием Летней серии IC37 2022 года. В то время как Gamecock была лучшей командой на воде сегодня, чемпионство сезона досталось New Wave Стива Либеля.
Либель плавал в классе до этого года, но прошлой осенью приобрел собственную лодку. Чемпионство сезона было основной целью его команды на это лето. В чемпионате сезона учитывалось выступление команды в 168-й ежегодной регате; Национальный чемпионат, который проводился во время Недели гонок в Ньюпорте, представленный Rolex; и чемпионат Северной Америки. Кроме того, команда может засчитать результат либо регаты Sail Newport Regatta в июле, либо уик-энда Safe Harbour Race Weekend в августе.
«У нас была одна цель — выиграть лето, — говорит Либель. «Мы знали, что вы должны войти в пятерку лучших в крупных регатах, а затем в два лучших в регатах категории B. Мы думали, что если это произойдет, мы будем в хорошей форме. И, оказывается, это то, что мы сделали».
Мы думали, что если это произойдет, мы будем в хорошей форме. И, оказывается, это то, что мы сделали».
В общей сложности 15 лодок прошли квалификацию для участия в чемпионате сезона, что свидетельствует о силе класса.
Сегодняшние результаты «Новой волны» — пара шестых и одна восьмая — на первый взгляд были солидными, но не впечатляющими. Однако тот факт, что команда финишировала во всех трех гонках, впечатляет, учитывая трудности, которые им пришлось преодолеть.
«Мы сломали наш стаксель-фал на первом такте первой гонки, и нам пришлось использовать наш спинакерный фал для стакселя, так что обход наветренной отметки был немного медленным», — говорит Либель. «Затем, после первой гонки, мы привязали нашу стрелу, так что, по крайней мере, у нас была стрела для второй и третьей гонок. Наш лучник был звездой дня. Он трижды был буровой, привязывая стаксель».
2022 IC37 Чемпионат Северной Америки
New York Yacht Club Harbour Court
23–25 сентября 2022 г.
Окончательные результаты
Место, название яхты, владелец/шкипер, родной город, результаты, общее количество баллов 1-3-[21/DNS] ; 12
2. Отмычка, Питер Вагнер, Портола-Вэлли, Калифорния, США – 5-4-6-[10]-3-2-1 ; 21
3. Новая волна, Стив Либель, Тампа, Флорида, США – [12] -3 -1 -2 -6 -6 -8 ; 26
4. МО, Бен Кинни/Ханна Светт, Джеймстаун, Род-Айленд, США – 6–2–2–[11]–2–11–7; 30
5. Бдительный, Джон Хеле, Ньюпорт, Род-Айленд, США – 9-10 -3 -3 -[16] -4 -4 ; 33
6. Дас Блау Макс, Кори, Марк и Ник Сертл Сертл, Джеймстаун, Род-Айленд, США – 4-15-5-[16]-7-1-10; 42
7. Кубит, Крис Льюис, Остин, Техас, США – 11-6-[17]-6-5-8-6 ; 42
8. Йондер, Дуглас Ньюхаус, Ньюпорт, Род-Айленд, США – 3-11-8-4-[13]-7-12; 45
9. Кашмир, Майкл Майер, Стив Хендерсон, Теллурайд, Колорадо, США – 13–8–7–8–[14]–5–14; 55
10. Тикет, Эд Уитмор, Норфолк, Вирджиния, США – 14-7-[16]-12-12-12-2 ; 59
11. Аретуса, Фил Лотц, Ft. Лодердейл, Флорида, США – 15–5–14–5–18–[19] -3 ; 60
12. Старая школа, Гэнсон Эванс, Понте-Ведра-Бич, Флорида, США – 8–12–13–7–[19]–10–11; 61
Старая школа, Гэнсон Эванс, Понте-Ведра-Бич, Флорида, США – 8–12–13–7–[19]–10–11; 61
13. RAMROD, Rodrick Jabin, Аннаполис, Мэриленд, США – 1-[21/DSQ]-21/RET-18-4-13-9; 66
14. Махало, Чарльз Кенахан, Ньюпорт, Род-Айленд, США – 7–13–12–[19]–11–18–5; 66
15. Далее, Джон Десмонд, Кохассет, Массачусетс, США – 10 -14 -9 -13 -8 -14 -[15] ; 68
16. Midnight Blue, Alexis Michas, Нью-Йорк, штат Нью-Йорк, США – [18] -9 -11 -9 -10 -16 -13 ; 68
17. Вака Явака, Майкл Гольдфарб, Сиэтл, Вашингтон, США – 16–17–15–14–9-9 -[18] ; 80
18. Малая Медведица, Питер Каммиски, Гринвич, Коннектикут, США – [20] -19 -10 -17 -17 -17 -16 ; 96
19. WarBride, Ben duPont, Рокленд, Делавэр, США – 17–18–[21/RET]–15–15–15–19; 99
20. Рес Потенция, Томас Ньюман, МИДЛТАУН, Род-Айленд, США – 19–16–18–[20]–20–20–17; 110
Нравится Newport Buzz? Мы рассчитываем на щедрость таких читателей, как вы, которые поддерживают нас, чтобы помочь с нашей миссией держать вас в курсе и развлекать вас местными, независимыми новостями и контентом.

 Ответ дайте в км/ч.
Ответ дайте в км/ч.
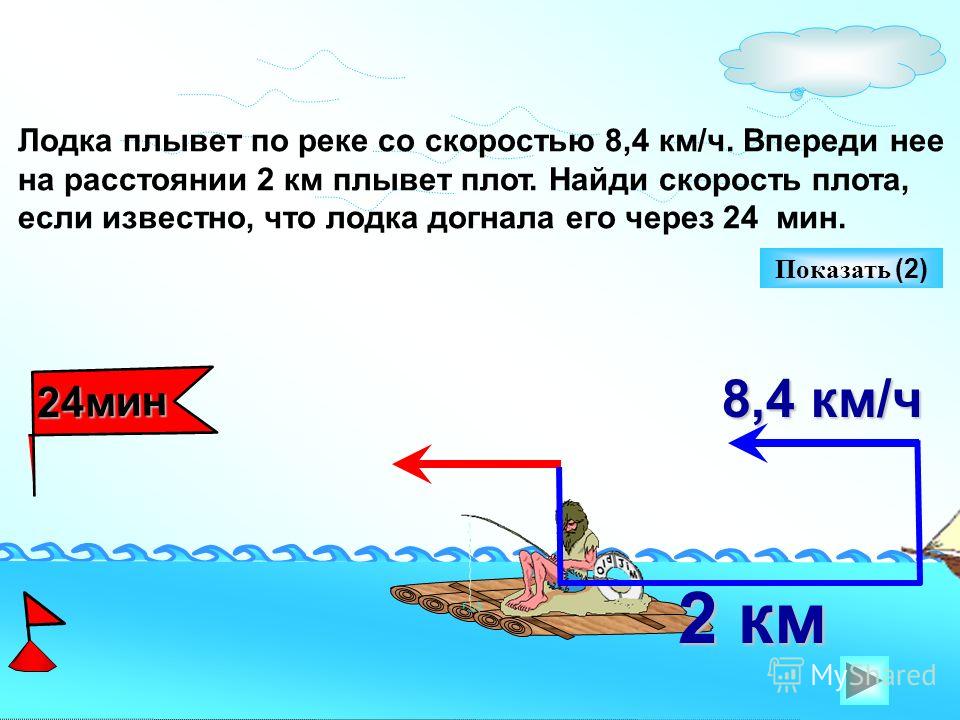 Для этого сложим собственную скорость катера и скорость течения:
Для этого сложим собственную скорость катера и скорость течения: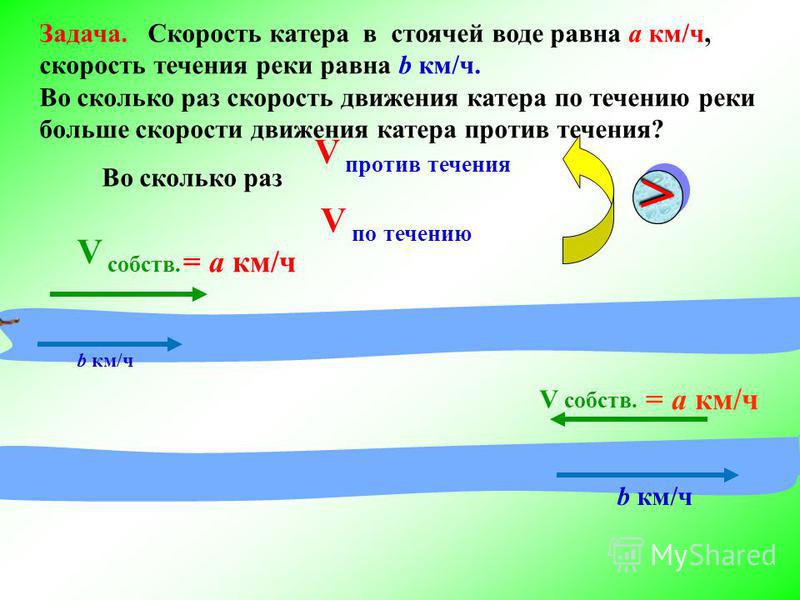
 Для этого расстояние разделим на скорость:
Для этого расстояние разделим на скорость: Для этого из собственной скорости катера вычтем скорость течения:
Для этого из собственной скорости катера вычтем скорость течения:
