Система нормальных уравнений: 13. Система нормальных уравнений и явный вид ее решения при оценивании методом наименьших квадратов линейной модели парной регрессии

Содержание

Система нормальных уравнений — Энциклопедия по экономике

Параметры уравнений регрессии находят решением системы нормальных уравнений, отвечающих требованию способа наименьших квадратов. [c.390]
Величины указанных параметров были рассчитаны решением системы нормальных уравнений, получаемых способом наименьших квадратов [c.24]

Это условие приводит к системе нормальных уравнений, решение которых позволяет определить параметры уравнения регрессии. Эти уравнения имеют вид [c.99]

Считая формулу связи линейной (Y = a0 + aiX ), определяем зависимость рентабельности производства плащей в зависимости от рентабельности выпуска зонтов. Для этого решается система нормальных уравнений [c.83]

Этап 3. Система нормальных уравнений для функции имеет вид [c.223]

Считая формулу связи линейной (у = а0 + щх), определим зависимость выпуска промышленных изделий от их запуска. Для этого решается система нормальных уравнений [c.160]

Для исчисления параметров я0 и я, используется система нормальных уравнений [c.

368]

В случае выравнивания по прямой способ наименьших квадратов приводит к следующей системе нормальных уравнений [c.322]

По такому же принципу рассчитываются и параметры криволинейного уравнения. Так, в случае параболической зависимости параметры а0, аь а2 находятся по следующей системе нормальных уравнений [c.322]

Вторым этапом является поиск значений параметров уравнения. Параметры трендовых моделей определяются с помощью системы нормальных уравнений. В случае применения линейного тренда используют следующую систему уравнений, которую решают способом наименьших квадратов [c.612]

Величина k определяет гармонику ряда Фурье и определяется целым числом, как правило, в пределах от 1 до 4. Параметры уравнения находят с помощью системы нормальных уравнений способом наименьших квадратов. [c.616]

Отсюда система нормальных уравнений имеет вид [c.239]

Коэффициенты регрессии для представления (4.16) находятся с помощью системы нормальных уравнений (чтобы не загромождать запись, индекс k, по которому идет суммирование у результативного и факторных признаков, подразумевается, но не приводится k — 1,2,.

.., п). [c.125]

Параметры уравнения OQ, а и а находим из системы нормальных уравнений, при ] / = 0 значения параметров рассчитываются по формулам [c.185]

Значения констант а0, а,, а2,. .. могут быть вычислены путем решения системы нормальных уравнений. [c.126]

Анализ зависимости между ценой продукта и его количеством в динамике позволяет выбрать для функции спроса линейную форму связи вида Р= а0 + а[ + a(Q. По методу наименьших квадратов определяются неизвестные параметры ай и а[ на основе составления и решения системы нормальных уравнений вида [c.74]

Анализ зависимости между издержками и количеством выпускаемой продукции в динамике позволяет для функции издержек выбрать также линейную форму связи вида С= Ь0 + b Q. Неизвестные параметры Ь0 и Ь( также находятся по методу наименьших квадратов на основе составления и решения системы нормальных уравнений вида [c.75]

Уравнение прямой имеет вид у, = а0 + а t. В связи с этим система нормальных уравнений для оценивания параметров прямой имеет вид [c.

81]

Упрощенный расчет параметров уравнений заключается в переносе начала координат в середину ряда динамики. В этом случае упрощаются сами нормальные уравнения, а кроме того, уменьшаются абсолютные значения величин, участвующих в расчете. В самом деле, если до переноса начала координат / было равно 1,2,3,. .., п, то после переноса — t=. .. —4, — 3, —2, -1,0,1,2,3,4…, если число члена ряда нечетное. Когда же число ряда четное, то f =… —5, —3, — 1, 1,3,5… Следовательно, /и все f, у которых р нечетное число, равны 0. Таким образом, все члены уравнений, содержащие /с такими степенями, могут быть исключены. Системы нормальных уравнений теперь упрощаются для прямой [c.82]

Система нормальных уравнений для нахождения параметров линейной парной регрессии методом наименьших квадратов имеет следующий вид [c.115]

В данном случае задача сводится к определению неизвестных параметров а0 а а2. Они определяются на основе системы нормальных уравнений [c.115]

А, а, р и у — параметры производственной функции, которые определяются в результате решения системы нормальных уравнений. [c.363]

При функциональной форме мультиколлинеарности по крайней мере одна из парных связей между объясняющими переменными является линейной функциональной зависимостью. В этом случае матрица Х Х особенная, так как содержит линейно зависимые векторы-столбцы и ее определитель равен нулю, т. е. нарушается предпосылка 6 регрессионного анализа. Это приводит к невозможности решения соответствующей системы нормальных уравнений и получения оценок параметров регрессионной модели. [c.108]

Система нормальных уравнений 54 ——в матричной форме 85 [c.304]

Определение зависимости изменения затрат от изменения технико-экономических параметров изделий включает следующие основные этапы объединение изделий в параметрические ряды отбор параметров, в наибольшей степени влияющих на себестоимость изделий установление формы связи зависимости изменения себестоимости от изменения параметров построение системы нормальных уравнений в соответствии с принятой функцией и расчет коэффициентов. [c.185]

Система нормальных уравнений будет выглядеть следующим образом [c.158]

По данным, приведенным в табл. 5.7 (итоги гр. 2-6), построена система нормальных уравнений [c.204]

Полученная система называется системой нормальных уравнений для нахождения параметров а0 и ах при выравнивании по прямой линии. - [c.47]

Для получения конкретного математического выражения функциональной связи между двумя переменными у» is. х при гиперболической их взаимозависимости составлена система нормальных уравнений [c.52]

Из системы нормальных уравнений находим параметры b и а [c.29]

Для оценки параметров уравнения множественной регрессии применяют метод наименьших квадратов (МНК). Для линейных уравнений и нелинейных уравнений, приводимых к линейным, строится следующая система нормальных уравнений, решение которой позволяет получить оценки параметров регрессии [c.49]

Система нормальных уравнений составит [c.115]

Для определения параметров а и Ь применяется МНК. Система нормальных уравнений следующая [c.146]

Система нормальных уравнений будет иметь вид [c.45]

Применение МНК для оценки параметров параболы второй степени приводит к следующей системе нормальных уравнений [c.63]

Напомним, что в математической статистике для получения несмещенной оценки дисперсии случайной величины соответствующую сумму квадратов отклонений от средней делят не на число наблюдений я, а на число степеней свободы (degress of freedom) я — т, равное разности между числом независимых наблюдений случайной величины п и числом связей, ограничивающих свободу их изменения, т. е. число т уравнений, связывающих эти наблюдения. Поэтому в знаменателе выражения (3.26) стоит число степеней свободы п — 2, так как две степени свободы теряются при определении двух параметров прямой из системы нормальных уравнений (3.5). [c.62]

Напомним, что согласно методу наименьших квадратов параметры прямой1 у, = /(0 = Ь0 + bit находятся из системы нормальных уравнений (3.

5), в которой в качестве х, берем t [c.141]

При применении метода наименьших квадратов для оценки параметров экспоненциальной, логистической функций или функции Гомперца возникают сложности с решением получаемой системы нормальных уравнений, поэтому предварительно, до получения соответствующей системы, прибегают к некоторым преобразованиям этих функций (например, логарифмированию и др.) (см. 5.5). [c.143]

В этом модуле реализовано решение системы нормальных уравнений методом наименьших квадратов. Прогноз с использованием модуля М107 осуществляется на базе небольшого числа данных (N > 10) по упрощенной схеме, т. е. по трем наиболее распространенным функциям [c.41]

На основе коэффициентов парной корреляции обра зуется система нормальных уравнений, однако, относящаяся ие к. самим коэффициентам уравнения О , а к таким же величинам в стандартизованном масштабе р [c.45]

Система нормальных уравнений и явный вид её решения при оценивании методом наименьших квадратов (МНК) линейной модели парной регрессии (на примере модели Оукена).

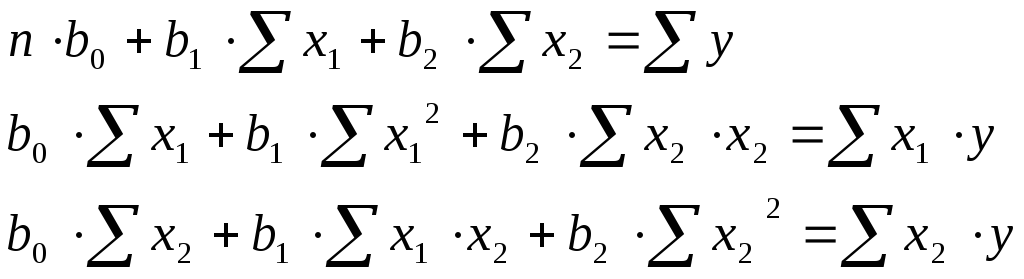
Системой линейный нормальных уравнений называется следующая система алгебраических уравнений:

, где — матрица весов (матрица — матрица обратных весов или весовых коэффициентов).

Модель Оукена:

t=1,2,…

где x_t — темп прироста безработицы в году t,

y_t — темп роста ВВП.

Обозначения:

, , , — число уравнений наблюдений.

Системой нормальных уравнений данной системы называется следующая система линейных уравнений (для данной модели ):

, где , (27.1)

Для ЛМПР (в частности, модели Оукена) система нормальных уравнений (27.1) имеет следующий вид:

, решая данную систему методом Гаусса, получаем явный вид её решения:

— будет лучше, если вы её проверите. Для удобства можно перейти к средним величинам, тогда формулы приобретают вид:

, обратите внимание на разницу в записи и .

Предыдущая форма приводится к следующей системе:

28. Ковариационная матрица оценок коэффициентов линейной модели парной регрессии: явные выражения .

Рассмотрим следующую ЛМПР:

Соответственно:

, . Используя исходные определения, получаем:

Матрица , . Таким образом, справедливы равенства:

;

Вывод формул (для романтиков):

, соответственно

Выведем :

, что преобразовываем как:

Выведем :

, знаменатель равен (см. предыдущ.), получаем .

Выведем :

Осталось только подставить их в формулы: , и .

Ч.Т.Д.

29.Свойства МНК-оценок параметров линейной модели множественной регрессии (ЛММР) при нормальном векторе случайных остатков: независимость случайных векторов

Рассмотрим с учётом схемы Гаусса-Маркова в компактной форме и случайный вектор истинной ошибки оценки : (1)

или в компактном виде

Видно, что вектор является выходом линейного преобразования вектора . Следовательно, вектор имеет нормальный закон распределения с числовыми характеристиками

Значит, и вектор является нормально распределённым случайным вектором с числовыми характеристиками .

Теперь рассмотрим вектор

Подставим в это выражение (1)

(2)

или в компактной записи

Согласно (2) вектор тоже является выходом линейного преобразования вектора . Следовательно, и вектор имеет нормальный закон распределения. Его числовые характеристики

Для доказательства независимости нормально распределенных случайных величин необходимо и достаточно доказать, что эти векторы некоррелированны, т.е. что их взаимная ковариационная матрица нулевая:

30.Свойства МНК-оценок параметров линейной модели множественной регрессии (ЛММР) при нормальном векторе случайных остатков: закон распределение оценки .

(Внимание: нумерация формул идёт не по порядку)

Так как вектор случайных остатков имеет нормальный закон распределения, то и нормально распределённым будет случайный вектор . (8.86) Компоненты этого вектора имеют количественные характеристики

Образуем из этих компонент независимые стандартные нормально распределённые случайные переменные (8.90)

Рассмотрим величину ( — это эффективная линейная несмещенная оценка, обладающая свойством наименьших квадратов), она зависит от выборки , а значит, является случайной переменной.

Начнем с оценки вектора случайных остатков (8,79)

Представим этот вектор как выход линейного преобразования вектора . Для этого подставим в правую часть 8,79 правую часть и приведем подобные члены:

Здесь приняли обозначение

Теперь, в правую часть предпоследнего равенства подставляем правую часть и, раскрывая скобки, получаем искомое преобразование:

(8,81)

В компактном виде получаем (8. 81’)

С учетом 8,81 находим значение квадратичной формы ( )

(8.82)

С учётом (8.82) и (8.86) получим

(8.89)

С учётом (8.89) и (8.90) получим:

(8.91)

Это значит, что при нормально распределённом векторе случайных остатков в схеме Гаусса-Маркова квадратичная форма (8.91) является случайной переменной, распределённой (с точностью до множителя ) по закону хи-квадрат с количеством степеней свободы К+1. Ч учётом этого утверждения, находим, что (8.92)

В силу (8.92) оценка дисперсии единицы веса тоже имеет с точностью до множителя закон распределения хи-квадрат с количеством степеней свободы n-(k+1):

31. Свойства МНК-оценок параметров линейной модели множественной регрессии (ЛММР) при нормальном векторе случайных остатков: закон распределения дроби .

— стандартная ошибка (оценка среднего квадратического отклонения) компоненты . Докажем, что случайная переменная (8.107)

имеет закон распределения Стьюдента с количеством степеней свободы n-(k+1), т.е.

(8.108)

Доказательство.

Разделим числитель и знаменатель дроби (8.107) на константу .

Учитывая (из 30-го вопроса), получим:

(8.109)

Здесь символом обозначена стандартная нормально распределённая случайная переменная.

— дробь Стьюдента с n степенями свободы (7.47)

С учётом (7.47) и (8.109) получим представление (8.108)

07. Метод наименьших квадратов (МНК). Свойства оценок на основе МНК

Возможны разные виды уравнений множественной регрессии: линейные и нелинейные.

Ввиду четкой интерпретации параметров наиболее широко используется линейная функция. В линейной множественной регрессии параметры при X называются Коэффициентами «чистой» Регрессии. Они характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизмененном значении других факторов, закрепленных на среднем уровне.

Рассмотрим линейную модель множественной регрессии

. (2.1)

Классический подход к оцениванию параметров линейной модели множественной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака Y от расчетных минимальна:

. (2.2)

Как известно из курса математического анализа, для того чтобы найти экстремум функции нескольких переменных, надо вычислить частные производные первого порядка по каждому из параметров и приравнять их к нулю.

Итак, имеем функцию аргумента:

Находим частные производные первого порядка:

После элементарных преобразований приходим к системе линейных нормальных уравнений для нахождения параметров линейного уравнения множественной регрессии (2. 1):

(2.3)

Для двухфакторной модели данная система будет иметь вид:

Метод наименьших квадратов применим и к Уравнению Множественной Регрессии В стандартизированном масштабе:

(2.4)

Где – Стандартизированные Переменные: , , для которых среднее значение равно нулю: , а среднее квадратическое отклонение равно единице: ; – Стандартизированные Коэффициенты Регрессии.

Стандартизованные коэффициенты регрессии показывают, на сколько единиц изменится в среднем результат, если соответствующий фактор изменится на одну единицу при неизменном среднем уровне других факторов. В силу того, что все переменные заданы как центрированные и нормированные, стандартизованные коэффициенты регрессии можно сравнивать между собой, ранжируя факторы по силе их воздействия на результат. В этом основное достоинство стандартизованных коэффициентов регрессии в отличие от коэффициентов «чистой» регрессии, которые несравнимы между собой.

Применяя МНК к уравнению множественной регрессии в стандартизированном масштабе, получим систему нормальных уравнений вида

(2.5)

Где и – коэффициенты парной и межфакторной корреляции.

Коэффициенты «чистой» регрессии связаны со стандартизованными коэффициентами регрессии следующим образом:

. (2.6)

Поэтому можно переходить от уравнения регрессии в стандартизованном масштабе (2.4) к уравнению регрессии в натуральном масштабе переменных (2.1), при этом параметр A определяется как .

Рассмотренный смысл стандартизованных коэффициентов регрессии позволяет их использовать при отсеве факторов – из модели исключаются факторы с наименьшим значением .

На основе линейного уравнения множественной регрессии

(2.7)

Могут быть найдены частные уравнения регрессии:

(2.8)

Т. е. уравнения регрессии, которые связывают результирующий показатель с соответствующим фактором при закреплении остальных факторов на среднем уровне. В развернутом виде систему (2.8) можно переписать в виде:

При подстановке в эти уравнения средних значений соответствующих факторов они принимают вид парных уравнений линейной регрессии, т. е. имеем

(2.9)

Где

В отличие от парной регрессии частные уравнения регрессии характеризуют изолированное влияние фактора на результат, ибо другие факторы закреплены на неизменном уровне. Эффекты влияния других факторов присоединены в них к свободному члену уравнения множественной регрессии. Это позволяет на основе частных уравнений регрессии определять Частные Коэффициенты Эластичности:

, (2.10)

Где – коэффициент регрессии для фактора в уравнении множественной регрессии, – частное уравнение регрессии.

Наряду с частными коэффициентами эластичности могут быть найдены Средние по совокупности показатели эластичности:

, (2.11)

Которые показывают, на сколько процентов в среднем изменится результат, при изменении соответствующего фактора на 1%. Средние показатели эластичности можно сравнивать друг с другом и соответственно ранжировать факторы по силе их воздействия на результат.

Рассмотрим Пример. Пусть имеются следующие данные (условные) о сменной добыче угля на одного рабочего Y (т), мощности пласта (м) и уровне механизации работ (%), характеризующие процесс добычи угля в 10 шахтах.

Таблица 2.2

№	1	2	3	4	5	6	7	8	9	10
	8	11	12	9	8	8	9	9	8	12
	5	8	8	5	7	8	6	4	5	7
Y	5	10	10	7	5	6	6	5	6	8

Предполагая, что между переменными Y, , существует линейная корреляционная зависимость, найдем уравнение регрессии Y по и .

Для дальнейших вычислений составляем таблицу ():

Таблица 2.3

№			Y
1	2	3	4	5	6	7	8	9	10	11	12
1	8	5	5	64	25	25	40	40	25	5,13	0,016
2	11	8	10	121	64	100	88	110	80	8,79	1,464
3	12	8	10	144	64	100	96	120	80	9,64	0,127
4	9	5	7	81	25	49	45	63	35	5,98	1,038
5	8	7	5	64	49	25	56	40	35	5,86	0,741
6	8	8	6	64	64	36	64	48	48	6,23	0,052
7	9	6	6	81	36	36	54	54	36	6,35	0,121
8	9	4	5	81	16	25	36	45	20	5,61	0,377
9	8	5	6	64	25	36	40	48	30	5,13	0,762
10	12	7	8	144	49	64	84	96	56	9,28	1,631
Сумма	94	63	68	908	417	496	603	664	445	68	6,329
Среднее Значение	9,4	6,3	6,8	90,8	41,7	49,6	60,3	66,4	44,5	–	–
	2,44	2,01	3,36	–	–	–	–	–	–	–	–
	1,56	1,42	1,83	–	–	–	–	–	–	–	–

Для нахождения параметров уравнения регрессии в данном случае необходимо решить следующую систему нормальных уравнений:

Откуда получаем, что , , .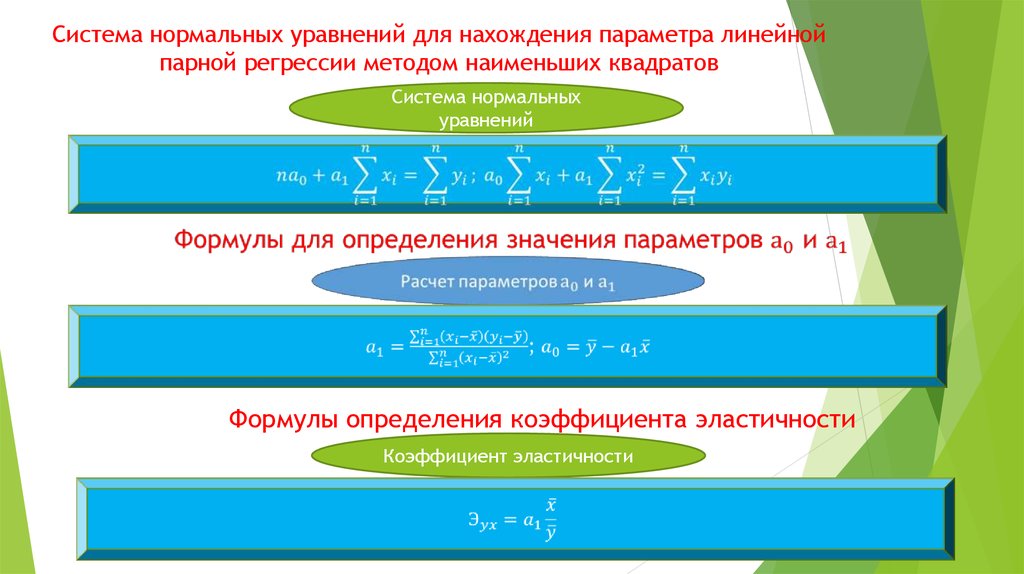 Т. е. получили следующее уравнение множественной регрессии:

Оно показывает, что при увеличении только мощности пласта (при неизменном ) на 1 м добыча угля на одного рабочего Y увеличится в среднем на 0,854 т, а при увеличении только уровня механизации работ (при неизменном ) на 1% – в среднем на 0,367 т.

Найдем уравнение множественной регрессии в стандартизованном масштабе:

При этом стандартизованные коэффициенты регрессии будут

Т. е. уравнение будет выглядеть следующим образом:

Так как стандартизованные коэффициенты регрессии можно сравнивать между собой, то можно сказать, что мощность пласта оказывает большее влияние на сменную добычу угля, чем уровень механизации работ.

Сравнивать влияние факторов на результат можно также при помощи средних коэффициентов эластичности (2.11):

Вычисляем:

, .

Т. е. увеличение только мощности пласта (от своего среднего значения) или только уровня механизации работ на 1% увеличивает в среднем сменную добычу угля на 1,18% или 0,34% соответственно. Таким образом, подтверждается большее влияние на результат Y фактора , чем фактора .

< Предыдущая		Следующая >

Особые случаи решения системы нормальных уравнений методом наименьших квадратов для уточнения орбит небесных тел

Цитировать:

Мирмахмудов Э.Р. Особые случаи решения системы нормальных уравнений методом наименьших квадратов для уточнения орбит небесных тел // Universum: технические науки : электрон. научн. журн. 2020. 11(80). URL: https://7universum.com/ru/tech/archive/item/10955 (дата обращения: 27.09.2022).

Прочитать статью:

АННОТАЦИЯ

В данной статье приведены результаты обработки оптических наблюдений космического тела методом наименьших квадратов. Получены формулы связывающие коэффициенты условных уравнений при особых случаях движения небесного тела. Разработаны формулы для вычисления ковариационной матрицы и средней квадратической ошибки результатов уточнения орбиты. Вычислены начальные координаты и компоненты скорости небесного тела по результатам наблюдений, выполненных в 25 обсерваториях. Произведен анализ точности уточняемых параметров орбиты при использовании результатов наблюдений двух обсерваторий. Предлагается использовать модифицированный метод наименьших квадратов для промежуточных орбит.

ABSTRACT

The results of processing optical observations of a space body by the least squares method are given in this paper. The coefficients of the conditional equations for special cases of motion of a celestial body were obtained here. Formulas for calculating the covariance matrix and the root mean square error of the orbit refinement results have been developed. The initial coordinates and velocity components of a celestial body are calculated based on the results of observations carried out at 25 observatories. An analysis of the accuracy of the improved orbital parameters using the results of observations of two observatories is carried out.

Ключевые слова: ковариационная матрица, условные уравнения, метод наименьших квадратов, изохронные производные, точность координат.

Keywords: covariance matrix, conditional equations, least square method, isochronous derivatives, coordinate accuracy.

Наблюдение космических тел обычно производится в период оппозиции и охватывает узкую дугу орбиты. Соответственно, фиксация интервала времени для такого отрезка орбиты будет незначительной по сравнению с периодом обращения вокруг центрального тела. Определение надежной орбиты по такой дуге и интервалу времени считается приближенной [11]. Поэтому предпочитают использовать измерения, выполненные в нескольких оппозициях, которые распределены равномерно по орбите с привлечением большего количества обсерваторий (рис.1).

Рисунок 1. Наблюдение космического тела (много станций)

На начальном этапе необходимо сравнить наблюдения, выполненные в оппозициях, с эфемеридными значениями, вычисленными на основе предварительных элементов орбиты. При этом следует учесть поправки за параллакс, аберрацию, прецессию и нутацию, а также за собственные движения опорных звезд [1]. Поскольку моменты наблюдений фиксируются во всемирном времени, то их следует редуцировать на эфемеридное время. Резкий скачок между наблюденными и вычисленными значениями говорит об ошибочных результатах наблюдений, которые отбрасывают или же вводят с уменьшенным весом. Данные, полученные в разных климатических условиях, представляют неравномерное распределение вдоль орбиты [6]. Например, когда неблагоприятные погодные условия не позволяют наблюдать на всех обсерваториях, тогда приходится иметь дело с наблюдениями одной или двух обсерваторий (рис.2).

Рисунок 2. Наблюдение спутника ( две станции)

Прежде всего, наблюдения должны охватывать по возможности большую дугу орбиты. При большом числе наблюдений целесообразно использовать нормальные места. Когда имеется длинный ряд наблюдений, то трудно решить, является ли изменение следствием ошибки наблюдений, неточности исходных координат или же вызвано реальным изменением этой величины с течением времени. В случае исследования ошибок звездных каталогов желательно использовать реальные наблюдения, дающие большую информацию об ошибках, когда же улучшают орбиту, то выгоднее использовать нормальные места [10]. В качестве нормальных мест можно применять и системы элементов, определенные по наблюдениям с коротким интервалом времени. Однако это может привести к плохой обусловленности системы нормальных уравнений. Для полной характеристики обусловленности системы необходимо произвести весьма громоздкие вычисления “собственных чисел” матрицы коэффициентов и найти “собственные решения”. Практически это неприемлемо. В таком случае плохую обусловленность системы нормальных уравнений можно решить, применив регуляризацию системы, что является не простой задачей [5].

Нахождение неизвестных параметров в задаче улучшения орбит сводится к решению избыточной системы линеаризованных условных уравнений вида

(1)

где А – матрица коэффициентов условных уравнений, Х — матрица неизвестных параметров, E — матрица ошибок или невязок измеренных величин, L — матрица поправок измеренных величин. Если n – число уточняемых параметров, а N – число измерений, то матрицы (1) будут иметь вид

, (2)

Если допустить, что e _k подчиняется нормальному закону, то система (1) решается методом наименьших квадратов. Согласно этому методу, решением максимального правдоподобия (1) будет Х, удостоверяющее условию минимума квадратичной формы.

, (2)

где Р – матрица весов измерений, знак «т» означает транспонирование. Условию минимума (2) дает нормальную систему уравнений [4]

, (3)

где , – симметричная n х n — матрица. Если определитель не нуль, то получаем решение

(4)

Далее находим матрицу ковариации – , и ошибку единицы веса — .

(5)

Для составления матрицы А достаточно знать частные производные от текущих значений параметров движения по их начальным значениям. При улучшении орбит космических тел. не имеющих тесных сближений с массивными телами, матрицу изохронных производных обычно вычисляют по формулам невозмущенного движения. В случае же тесных сближений с массивным телом, изохронные производные необходимо вычислить с учетом возмущений [3,7].

. (6)

В астрономической практике встречаются случаи, когда один или несколько из неизвестных параметров зависят от всех остальных параметров, в таких случаях используется метод наименьших квадратов при наличии связей. Рассмотрим решение системы нормальных уравнений в случае связи

(7)

где

, (8)

Составим функцию Лагранжа

(9)

Дифференцируем (9) по X

(10)

Находим X как функцию k

(11)

где

(12)

Получим окончательное выражение для k и X

(13)

, (14)

. (15)

. (16)

Матрица ковариации будет иметь вид

, (17)

где

, (18)

. (19)

Уточнение орбит малых тел на основе промежуточных орбит методом наименьших квадратов при учете связи делает результат более корректным, чем без такого учета [2].

Для оценки точности наблюдений, полученных в 25 и 2 обсерваториях, были использованы 198 наблюдения космического тела с 1963 по 1979 (Таб.1). Уточненные начальные координаты и компоненты скорости космического тела на эпоху Т = 1972 01 20.0 ЕТ (JD = 2 441 336.5) были вычислены методом численного интегрирования Эверхарта 19 порядка [8,9]. В качестве опорной орбиты использована промежуточная орбита, полученная на основе фиктивной массы центрального тела.

Таблица 1.

Начальные координаты и скорости

	25 обсерваторий	2 обсерватории
	-1. 68245079676	— 1.68245407315
	1.59202427231	1.59202132792
	1.09344607955	0.09344147227
	-0.00798591570	— 0.00798591014
	-0.00752703765	— 0.00752705069
	-0.00191836267	— 0.00191839919
	0. 877^//	0.709^//

Из таблицы 1 видно, что точность улучшения координат и компонент скоростей с использованием 2 наземных обсерваторий имеет почти близкое значение с точностью улучшения по 25 обсерваториям, что говорит о надежности наблюдений при ограниченном числе станций наблюдений.

Таким образом, использование метода наименьших квадратов при наличии связей для уточнения орбит небесных тел является наиболее приемлемым в случае тесного сближения космического тела с массивным телом. Критерием точности орбиты является ковариационная матрица и средняя квадратическая ошибка единицы веса.

Список литературы:

Абалакин В.К. и др. Справочное руководство по небесной механике и астродинамике. М.: Недра. 1971.- 584 с.
Batrakov Yu.V., Mirmakhmudov E.R. On effectiveness of using intermediate orbits for computing the perturbed motion / Proceedings of the 1 SPAIN-USSR Workshop on positional astronomy and celestial mechanics. Held at Valencia.Spain.March.11-15.1991, P.71-73.
Бахшиян Б.Ц. и Суханов А.А. Об изохронных производных первого и второго порядка в задаче двух тел / Космические исследования. 1978, т.16, №4. С.481.
Большаков В. Д., Гайдаев П.А. Теория математической обработки геодезических измерений. М.:Недра,1977. – 368с.
Линник Ю.В. Метод наименьших квадратов и основа теории обработки наблюдений. М.:Физматгиз, 1966. – 336c.
Мирмахмудов Э.Р. Анализ точности оптических методов наблюдений космических тел в Узбекистане. Вопросы науки и образования. Москва. 2020. №30 (114). С. 45-57.
Мирмахмудов Э.Р. О пригодности результатов наблюдений одной или двух обсерваторий для улучшения орбит малых планет. Материалы 2 -Всесоюзной Астрономической школы по программе «Орбита». Тираспольский ГПИ им. Шевченко. Тирасполь.1990,С.27.
Mirmakhmudov E. Summary report of the Astronomical Institute investigations on the small bodies during 1922-1995//Memoria della Societa ‘Astronomica Italiana‘. 2002.Vol.73, № 3. P.655-657.
Мирмахмудов Э.Р. Построение промежуточных орбит небесного тела с касаниями второго и третьего порядка. The scientific heritage. Budapest, Hungary. 2020. V.1, №53, P.36-41.
Никольская Т.К. Об одном способе составления нормальных мест. Бюлл. ИТА.1972,т.3,N4.С.220-224.
Субботин М. Ф. Введение в теоретическую астрономию. М.: Недра,1968. –800c.

Оценка параметров линейного регрессионного уравнения —

Теория

Для оценки параметров регрессионного уравнения наиболее часто используют метод наименьших квадратов (МНК), в основе которого лежит предположение о независимости наблюдений исследуемой совокупности. Сущность данного метода заключается в нахождении параметров модели (α, β), при которых минимизируется сумма квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических, полученных по выбранному уравнению регрессии:

В итоге получаем систему нормальных уравнений:

_₍₂₀₎

Эту систему можно записать в виде:

_₍₂₁₎

_{Решая данную систему линейных уравнений с двумя неизвестными получаем}_{оценки наименьших квадратов}_:

_{(22, 23)}

_{В уравнениях регрессии параметр α показывает усредненное влияние на результативный признак неучтенных факторов, а параметр β – коэффициент регрессии показывает, насколько изменяется в среднем значение результативного признака при увеличении факторного на единицу.}

_{Между линейным коэффициентом корреляции и коэффициентом регрессии существует определенная зависимость, выражаемая формулой:}

_₍₂₄₎

_где_{– коэффициент регрессии в уравнении связи;}

– среднее квадратическое отклонение соответствующего статистически существенного факторного признака.

_{Пример.}

_{Имеются следующие данные о размере страховой суммы и страховых возмещений на автотранспортные средства одной из страховых компаний.}

_{Таблица 4}

_{Зависимость между размером страховых возмещений и страховой суммой на автотранспорт}

_№	_{Объем страхового возмещения (тыс.долл.), Yi}	_{Стоимость застрахованного автомобиля (тыс. долл.), X}_i
₁	_0,1	_8,8
₂	_1,3	_9,4
₃	_0,1	_10,0
₄	_2,6	_10,6
₅	_0,1	_11,0
₆	_0,3	_11,9
₇	_4,6	_12,7
₈	_0,3	_13,5
₉	_0,4	_15,5
₁₀	_7,3	_16,7
_Итого	_17,1	_120,1

_{Предположим наличие линейной зависимости между рассматриваемыми признаками.}

_{Построим расчетную таблицу для определения параметров линейного уравнения регрессии объема страхового возмещения.}

_{Таблица 5}

_{Расчетная таблица для определения параметров уравнения регрессии}

_№	_{Объем страхового возмещения (тыс.долл.), Yi}	_{Стоимость застрахованного автомобиля (тыс.долл.), X}_i	_х2	_ху
₁	_0,1	_8,8	_77,44	_0,88	_0,052
₂	_1,3	_9,4	_88,36	_12,22	_0,362
₃	_0,1	_10,0	_100,00	_1,00	_0,672
₄	_2,6	_10,6	_112,36	_27,56	_0,982
₅	_0,1	_11,0	_121,00	_1,10	_1,188
₆	_0,3	_11,9	_141,61	_3,57	_1,653
₇	_4,6	_12,7	_161,29	_58,42	_2,066
₈	_0,3	_13,5	_182,25	_4,05	_2,479
₉	_0,4	_15,5	_240,25	_6,20	_3,513
₁₀	_7,3	_16,7	_278,89	_121,91	_4,133
_Итого	_17,1	_120,1	_1503,45	_236,91	_17,100

_{Система нормальных уравнений имеет вид:}

_{Отсюда:}_а₀_=-4,4944;_а₁_=0,5166.

_{Следовательно,}

_{Значения}_{в таблице получены путем подстановки значений факторного признака}_x_i_{(стоимость застрахованного автомобиля) в полученное уравнение регрессии.}

_{Коэффициент регрессии}_а₁_{=0,5166 означает, что при увеличении стоимости застрахованного автомобиля на 1 тыс.долл., объем страхового возмещения возрастает в среднем на 0,5166 тыс.долл.}

Метод наименьших квадратов с примером решения

Содержание:

Применение МНК
Рассмотрим пример с решением

Возможны различные типы уравнений множественной регрессии: линейные и нелинейные.

При четкой интерпретации параметров наиболее широко используются линейные функции. В линейной множественной регрессии параметры приназываются коэффициентами «чистой» регрессии. Они характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизмененном значении других факторов, закрепленных на среднем уровне.

Рассмотрим линейную модель множественной регрессии (2.1)

Классический подход к оценке параметров модели линейной множественной регрессии основан на методе наименьших квадратов (МНК). В случае МНК сумма квадратов отклонений фактического значения действующего знака равна от расчетныхминимальна: (2.2)

Как известно в ходе математического анализа, чтобы найти экстремумы функции некоторых переменных, необходимо вычислить первую производную каждого параметра и сделать их равными нулю.

Итак. Имеем функцию аргумента:

Находим частные производные первого порядка:

Для двухфакторной модели данная система будет иметь вид:

Метод наименьших квадратов применим и к уравнению множественной регрессии в стандартизированном масштабе:

(2.4)

где — стандартизированные переменные: для которых среднее значение равно нулю: а среднее квадратическое отклонение равно единице:

стандартизированные коэффициенты регрессии.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Высшая математика: лекции, формулы, теоремы, примеры задач с решением

Сравнивая их друг с другом, можно ранжировать факторы по силе их воздействия на результат. В этом основное достоинство стандартизованных коэффициентов регрессии в отличие от коэффициентов «чистой» регрессии, которые несравнимы между собой.

Применение МНК

где и — коэффициенты парной и межфакторной корреляции.

Коэффициенты «чистой» регрессии связаны со стандартизованными коэффициентами регрессии следующим образом:

Поэтому можно переходить от уравнения регрессии в стандартизованном масштабе (2.4) к уравнению регрессии в натуральном масштабе переменных (2.1), при этом параметр определяется как

Рассмотренный смысл стандартизованных коэффициентов регрессии позволяет их использовать при отсеве факторов — из модели исключаются факторы с наименьшим значением .

На основе линейного уравнения множественной регрессии

(2.7)

могут быть найдены частные уравнения регрессии:

т.е. уравнения регрессии, которые связывают результативный признак с соответствующим фактором при закреплении остальных факторов на среднем уровне. В развернутом виде систему (2.8) можно переписать в виде:

где

В отличие от парной регрессии частные уравнения регрессии характеризуют изолированное влияние фактора на результат, ибо другие факторы закреплены на неизменном уровне. Эффекты влияния других факторов присоединены в них к свободному члену уравнения множественной регрессии. Это позволяет на основе частных уравнений регрессии определять частные коэффициенты эластичности: (2.10)

где — коэффициент регрессии для фактора в уравнении множественной регрессии, — частное уравнение регрессии.

Наряду с частными коэффициентами эластичности могут быть найдены средние по совокупности показатели эластичности: (2.11) которые показывают на сколько процентов в среднем изменится результат, при изменении соответствующего фактора на 1%. Средние показатели эластичности можно сравнивать друг с другом и соответственно ранжировать факторы по силе их воздействия на результат.

Возможно вам будут полезны данные страницы:

Ряд тейлора примеры решения

Интеграл примеры решения

Векторное произведение примеры решения

Замечательные пределы примеры решения

(для сокращения объема вычислений ограничимся только десятью наблюдениями). Пусть имеются следующие данные (условные) о сменной добыче угля на одного рабочего (т),

мощности пласта (м) и уровне механизации работ (%), характеризующие процесс добычи угля в 10 шахтах.

Предполагая, что между переменными существует линейная корреляционная зависимость, найдем уравнение регрессии по и .

Для удобства дальнейших вычислений составляем таблицу

Откуда получаем, что. Т.е. получили следующее уравнение множественной регрессии:

Оно показывает, что при увеличении только мощности пласта (при неизменном ) на 1 м добыча угля на одного рабочего у увеличится в среднем на 0,854 т, а при увеличении только уровня механизации работ (при неизменном ) на 1%-в среднем на 0,367 т.

Найдем уравнение множественной регрессии в стандартизованном масштабе:

, при этом стандартизованные коэффициенты регрессии будут

Т. е. уравнение будет выглядеть следующим образом:

Сравнивать влияние факторов на результат можно также при помощи средних коэффициентов эластичности (2.11):

Вычисляем:

Т.е. увеличение только мощности пласта (от своего среднего значения) или только уровня механизации работ на 1% увеличивает в среднем сменную добычу угля на 1,18% или 0,34% соответственно. Таким образом, подтверждается большее влияние на результат фактора , чем фактора .

мл | Нормальное уравнение в линейной регрессии

Нормальное уравнение представляет собой аналитический подход к линейной регрессии с функцией стоимости наименьших квадратов. Мы можем напрямую узнать значение θ без использования градиентного спуска. Следование этому подходу является эффективным и экономящим время вариантом при работе с набором данных с небольшими функциями. Метод нормального уравнения основан на математической концепции максимума и минимума, в которой производная и частная производная любой функции будут равны нулю в точках минимума и максимума. Итак, в методе нормального уравнения мы получаем минимальное значение функции стоимости, находя ее частную производную по каждому весу и приравнивая ее к нулю.

Нормальное уравнение выглядит следующим образом:

В приведенном выше уравнении
θ: параметра гипотезы, которые определяют его лучше всего.
X: Введите значение функции для каждого экземпляра.
Y: Выходное значение каждого экземпляра.

Математика За уравнением:

Учитывая функцию гипотезы

где,
n: нет. функций в наборе данных.
х 9{2}

, где
x ⁱ : входное значение i ^ih обучающего примера.
м: № учебных экземпляров
n: нет. функций набора данных
y ⁱ : ожидаемый результат i ^th экземпляр

Представим функцию стоимости в векторной форме.

Здесь мы проигнорировали 1/2 м, так как это не повлияет на работу. Он использовался для математического удобства при расчете градиентного спуска. Но здесь он больше не нужен.

x ⁱ _j : значение j ^ih функция в i ^ih обучающий пример.

Далее можно сократить до

Но каждое остаточное значение возводится в квадрат. Мы не можем просто возвести приведенное выше выражение в квадрат. Поскольку квадрат вектора/матрицы не равен квадрату каждого из его значений. Таким образом, чтобы получить значение в квадрате, умножьте вектор/матрицу на ее транспонирование. Таким образом, окончательное полученное уравнение равно

Следовательно, функция стоимости составляет

, теперь, теперь получая значение θ с использованием частичной производной

SO, это, наконец, выработано

SO, это, наконец, получен

. Уравнение с θ, дающее минимальное значение стоимости.

Пример:

Python3

импорт numpy as np

import matplotlib.pyplot as plt

from sklearn. datasets import make_regression

x, y = make_regression( n_samples = 100 , N_FEATURES = 1 ,

67777777779 6677777777779 677777777 67770136 = 1 , noise = 10 , random_state = 10 )

plt.scatter(x, y, s = 30 , маркер = 'o' )

PLT. xlabel ( "Функция_1->" ) 6 ". ->" )

plt.title( 'Simple Linear Regression' )

plt.show()

y = y.reshape( 100 , 1 )

Output:

Let's implement the Normal Equation:

Python3

x_new = np.array([np.ones( len (x)), x.flatten()]).T

theta_best_values = np. linalg.inv(x_new.T.dot(x_new)).dot(x_new.T).dot(y)

print (theta_best_values)

 [[ 0,52804151]
 [30.65896337]]

Попробуйте предсказать новый экземпляр данных:

Python3

3 02:0279 3 02: [[-2] [4]] После добавления x0: [[ 1. -2.] [ 1. 4.]]
Python3

x_sample = np.array([[ - 2 ], [ 4 ]])

x_sample_new = np.array([np.ones( len (x_sample)), x_sample.flatten()]).T

print ( "Before adding х0:\n" , x_sample)

print ( "После добавления x0:\n" , x_sample_new)

predict_value = x_sample_new.dot(theta_best_values)

print (predict_value)

 [[-60.78988524]
 [123.16389501]]

Plot the output:

Python3

plt.scatter(x,y,s = 30 ,marker = 'o )

PLT.PLOT (X_SAMPLE, PRODICT_VALU0136 "feature_1 --->" )

Plt.ylabel ( "Target_variable --->" )

PLT. TITL

plt.show()

Verify the above using sklearn LinearRegression class:

Python3

from sklearn.linear_model import LinearRegression

lr = LinearRegression()

lr.fit(x,y)

print ( "Best value of theta :" ,lr.intercept_,lr.coef_,sep = '\n' )

print ( "predicted value:" 92\ge 0\), а равенство невозможно благодаря второй части теоремы. Т\mathbf{А}\). 9Т\mathbf{b}\).

Решите \(n\times n\) линейную систему \(\mathbf{N}\mathbf{x} = \mathbf{z}\) для \(\mathbf{x}\).

На последнем шаге мы можем использовать факт, доказанный в теореме AtA, что \(\mathbf{N}\) является симметричным и положительно определенным, и использовать факторизацию Холецкого, как в симметричных положительно определенных матрицах. (Команда обратной косой черты делает это автоматически.)

Функция 24 (нормальный)

 """
лнормальный(А,б)
Решите линейную задачу наименьших квадратов с помощью нормальных уравнений.
Возвращает минимизатор ||b-Ax||.
"""
функция lsnormal(A,b)
Н = А'*А; г = А'*б;
R = холецкий (N).U
w = forwardsub(R',z) # решить R'z=c
x = backsub(R,w) # решить Rx=z
вернуть х
конец

Обусловливание и стабильность

Мы уже использовали A\b как собственный способ решения линейной задачи наименьших квадратов \(\mathbf{A}\mathbf{x}\приблизительно\mathbf{b}\) в Юлии. {-1}\|\). 92\]

во 2-й норме. Если \(\kappa(\mathbf{A})\) велико, возведение его в квадрат может дестабилизировать нормальные уравнения: хотя решение задачи наименьших квадратов является чувствительным, нахождение его с помощью нормальных уравнений делает его вдвойне чувствительным.

Упражнения

✍ Вычислите решение методом наименьших квадратов, когда
\[\begin{split}\mathbf{A} = \begin{bmatrix} 2 & -1 \\ 0 и 1 \\ -2 и 2 \end{bmatrix}, \qquad \mathbf{b} = \begin{bmatrix} 1\\-5\\6 \end{bmatrix}.\end{split}\] 93\). (При нахождении асимптотического числа вы можете игнорировать такие термины, как \(mn\), общая степень которых меньше трех.)
⌨ Пусть \(t_1,\ldots,t_m\) будет \(m+1\) равноотстоящими точками в \([0,2\pi]\).
(a) Пусть \(\mathbf{A}_\beta\) будет матрицей в (58), которая соответствует подгонке данных функцией \(c_1 + c_2 \sin(t) + c_3 \cos(\ бета т)\). Используя тождество (66), составьте таблицу чисел условий \(\mathbf{A}_\beta\) для \(\beta = 2,1. {-8} \). 92(\бета т).\)
(c) Почему имеет смысл, что \(\kappa\bigl(\mathbf{A}_\beta\bigr)\to \infty\) as \(\beta\to 1\) в части (b ), но не в части (а)?
✍ ⌨ Когда \(\mathbf{A}\) равно \(m\times n\) с рангом меньше, чем \(n\), псевдоинверсия по-прежнему определена и может быть вычислена с помощью pinv из LinearAlgebra . Однако поведение в этом случае не всегда интуитивно понятно. Пусть
\[\begin{split}\mathbf{A}_s = \begin{bmatrix} 1&1\0&0\0&s \end{bmatrix}.\end{split}\] 9+\).

Выполнение линейной регрессии с использованием нормального уравнения | Роберт Квятковски

Не всегда необходимо запускать алгоритм оптимизации для выполнения линейной регрессии. Вы можете решить конкретное алгебраическое уравнение — нормальное уравнение — чтобы получить результаты напрямую. Хотя для больших наборов данных это даже близко не оптимально с вычислительной точки зрения, это все же один из вариантов, о котором стоит знать.

Фото Антуана Дотри на Unsplash

1. Введение

Линейная регрессия является одним из наиболее важных и популярных методов прогнозирования в анализе данных. Это также один из старейших - знаменитый C.F. Гаусс в начале 19-го века использовал его в астрономии для расчета орбит (подробнее).

Его цель состоит в том, чтобы подогнать наилучшую линию (или гипер-/плоскость) к набору заданных точек (наблюдений) путем вычисления параметров функции регрессии, которые минимизируют конкретную функцию стоимости (ошибку), например. среднеквадратическая ошибка (MSE).

Напоминаем, ниже приведено уравнение линейной регрессии в развернутом виде.

Уравнение 1: Уравнение линейной регрессии

В векторизованной форме оно выглядит так:

Ур. 2: Уравнение линейной регрессии в векторизованной форме

, где θ — вектор весов параметров.

Обычно нахождение наилучших параметров модели выполняется путем запуска какого-либо алгоритма оптимизации (например, градиентного спуска) для минимизации функции стоимости. Однако можно получить значения (веса) этих параметров, решив также алгебраическое уравнение, называемое нормальным уравнением. Он определяется, как показано ниже.

Уравнение 3: нормальное уравнение

2. Ручные вычисления

В этой статье мы выполним линейную регрессию для очень простого случая, чтобы избежать длительных ручных вычислений. Кстати, если вы считаете, что вам нужно освежить свои навыки линейной алгебры, в Интернете есть много хороших ресурсов (например, сериалы на YouTube, которые я рекомендую).

В этом примере есть только три точки (наблюдения) только с одной переменной (X₁). На графике они выглядят так, как показано ниже.

Точечная диаграмма, показывающая точки, использованные в этом примере

В этом случае уравнение линейной регрессии имеет вид:

Ур. 4: Уравнение линейной регрессии для этого примера

Признаки (X) и метки (y):

Матрицы признаков и меток

Обратите внимание, что мы добавляем член смещения по умолчанию, равный 1, — он будет обновлен во время наших расчетов. Отсутствие этого термина приведет к неправильному решению.

Шаг 1: Транспонирование матрицы X

Это относительно простая задача — строки становятся новыми столбцами.

Шаг 2: Умножение на транспонированную матрицу и матрицу X

Шаг 3: Инверсия результирующей матрицы

Для обращения простой матрицы 2x2 мы можем использовать формулу:

Следовательно, мы получаем:

Примечание: для больших матриц (больше, чем 3X3), их инвертирование становится гораздо более громоздкой задачей, и обычно используется алгоритмический подход — например, исключение Гаусса. Это важно помнить!

Шаг 4: Умножение инвертированной матрицы с транспонированным X

Шаг 5: Окончательное умножение для получения вектора наилучших параметров

Наконец, наши уравнения линейной регрессии принимают вид:

Ур. 5: Уравнение линейной регрессии с лучшими весами

Нанесение этой линии на предыдущий график выглядит так, как показано ниже.

Точечная диаграмма с исходными точками и линией регрессии (красная)

3. Реализация на Python

Те же вычисления можно реализовать на Python с помощью библиотеки Numpy, которая содержит набор функций линейной алгебры в коллекции numpy.linalg.

 import numpy as npX = np.c_[[1,1,1],[1,2,3]] # определяющие функции 
 y = np.c_[[1,3,2]] # определяющие метки 
 theta = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y) # нормальное уравнение 
 print(theta)

Результаты выполнения кода выше

Теперь мы можем определить новые функции, которые хотели бы предсказать значения для.

 X_new = np.c_[[1,1,1,1],[0, 0.5,1.5,4]] # новых функций

Применяя уравнение 2, мы получаем прогнозируемые значения.

 y_pred = X_new.dot(theta) # предсказания 
 print(y_pred)

Прогнозируемые значения

4. Комментарии

Как видите, использовать нормальное уравнение и реализовать его на Python довольно просто — это всего лишь одна строка кода. Так почему же он не используется повсеместно?

Проблема в его численной сложности. Решение этого уравнения требует инвертирования матрицы, а это вычислительно затратная операция — в зависимости от реализации, в большой нотации O это O(n³) или чуть меньше. Это означает ужасное масштабирование, что практически означает, что когда вы удваиваете количество функций, время вычислений увеличивается в 2³ = 8 раз. Также существует некоторая вероятность того, что результат шага 2 вообще необратим, что приведет к большим проблемам. Вот почему на практике такой подход встречается редко.

С другой стороны, этот подход рассчитывается всего за один шаг, и вам не нужно выбирать параметр скорости обучения. Кроме того, с точки зрения использования памяти этот подход является линейным O (m), что означает, что он эффективно хранит огромные наборы данных, если они помещаются только в память вашего компьютера.

Нормальное уравнение для линейной регрессии Учебное пособие

Содержание:

Что такое нормальное уравнение?
Нормальное уравнение против градиентного спуска
- Градиентный спуск
- Чем они отличаются?
Расшифровка, когда использовать нормальное уравнение
Нормальное уравнение с нуля в Python
Часто задаваемые вопросы

Большинство проблем, с которыми мы сталкиваемся, можно решить несколькими способами. Например, если мы хотим перейти с одной стороны комнаты на другую, мы можем решить пройтись по комнате, пока не дойдем до противоположной стороны, или мы можем просто пересечь ее.

Нормальное уравнение является лишь акцентом этой концепции. Это просто еще один способ решить проблему. Какую проблему вы задали? Мы расскажем об этом в оставшейся части этой статьи. На данный момент все, что вам нужно знать, это то, что это эффективный подход, который может помочь вам сэкономить много времени при реализации линейной регрессии при определенных условиях.

Давайте углубимся…

Что такое нормальное уравнение?

Нормальное уравнение представляет собой решение в замкнутой форме, используемое для нахождения значения θ, которое минимизирует функцию стоимости. Другой способ описать нормальное уравнение — использовать одношаговый алгоритм для аналитического нахождения коэффициентов, минимизирующих функцию потерь. Оба описания работают, но что именно они означают? Мы начнем с линейной регрессии.

Линейная регрессия делает прогноз, y_hat, вычисляя взвешенную сумму входных признаков плюс член смещения. Математически это можно представить следующим образом:

Где θ представляет параметры, а n — количество признаков.

По сути, все, что происходит в приведенном выше уравнении, является скалярным произведением θ, и x суммируется. Таким образом, более краткий способ представить это — использовать его векторизованную форму:

h(θ) — это функция гипотезы.

Учитывая эту приблизительную целевую функцию, мы можем использовать нашу модель для прогнозирования. Чтобы определить, хорошо ли наша модель научилась, важно измерить производительность нашей модели на обучающих данных. Для этого вычисляем функцию потерь. Цель процесса обучения — найти значения тета (θ), минимизирующие функцию потерь.

Вот как мы можем представить нашу функцию потерь математически:

В приведенном выше уравнении тета (θ) представляет собой n + 1-мерный вектор, а наша функция потерь является функцией значения вектора. Следовательно, частная производная функции потерь J должна быть взята по каждому параметру θ_j по очереди. Все они должны быть равны нулю. Выполнение этого процесса и решение для всех значений θ от θ_0 до θ_n приведет к значениям θ, которые минимизируют функцию потерь.

Работа над решением параметров от θ_0 до θ_n с использованием описанного выше процесса приводит к чрезвычайно сложной процедуре вывода. Действительно, есть более быстрое решение.

Взгляните на формулу нормального уравнения:

Где:

θ → Параметры, минимизирующие функцию потерь X → Значения входных признаков для каждого экземпляра y → Вектор выходных значений для каждого экземпляра

Нормальное уравнение против градиентного спуска

Хотя оба метода стремятся найти параметры тета (θ), которые минимизируют функцию потерь, метод подхода сильно различается между двумя решениями.

Поскольку мы уже рассмотрели, как работает нормальное уравнение в разделе «Что такое нормальное уравнение?», в этом разделе мы кратко коснемся градиентного спуска, а затем расскажем, чем эти два метода отличаются.

Градиентный спуск

Градиентный спуск — один из наиболее часто используемых алгоритмов машинного обучения в машинном обучении. Он развернут для итеративного поиска параметров тета (θ), которые минимизируют функцию потерь.

Процесс начинается с первой оценки производительности модели. Затем частная производная вычисляется из функции потерь, которая используется для ссылки на наклон в его текущей точке. Наконец, мы предпринимаем шаги, пропорциональные отрицательному градиенту, чтобы спуститься к минимуму функции потерь, обновив текущий набор параметров — см. формулу ниже.

Этот процесс повторяется до сходимости в минимуме функции потерь.

Чем они отличаются?

Наиболее очевидным отличием нормального уравнения от градиентного спуска является то, что оно аналитическое. Градиентный спуск использует итеративный подход, что означает, что наши параметры обновляются постепенно до сходимости. Еще одно тонкое отличие заключается в том, что градиентный спуск требует от нас определения скорости обучения, которая контролирует размер шагов, предпринимаемых для достижения минимума функции потерь. Нормальное уравнение не требует от нас определения скорости обучения, потому что мы не предпринимаем итерационных шагов — мы получаем результаты напрямую.

Кроме того, масштабирование признаков не требуется, когда мы используем метод нормального уравнения; мы обычно выполняем масштабирование функций, чтобы убедиться, что наши функции имеют аналогичный диапазон значений. Это связано с тем, что градиентный спуск чувствителен к диапазонам наших точек данных. Неспособность нормализовать наши функции при использовании градиентного спуска может привести к асимметрии в контурном графике функции потерь, но нормальное уравнение не страдает от этой проблемы.

Расшифровка, когда использовать нормальное уравнение 93) сложность времени выполнения, из-за которой нормальное уравнение работает очень медленно, когда n очень велико - узнайте больше о сложности времени.

Таким образом, лучше всего использовать градиентный спуск, когда количество признаков в наборе данных велико. Эндрю Нг, известный эксперт по машинному обучению и искусственному интеллекту, рекомендует рассмотреть возможность использования градиентного спуска, когда количество признаков n превышает 10 000. Для 10 000 функций или меньше вам может быть лучше использовать обычное уравнение, поскольку вам не требуется выбирать значение для скорости обучения, что означает, что вам нужно настроить на один гиперпараметр меньше.

Нормальное уравнение с нуля в Python

Давайте создадим регрессионную задачу для проверки этого уравнения:

 import numpy as np
импортировать matplotlib.pyplot как plt
из sklearn.datasets импортировать make_regression
# Генерация проблемы регрессии
X, y = make_regression(
    n_samples=100,
    n_features=2,
    п_информативный=2,
    шум = 10,
    случайное_состояние = 25
    )
# Визуализировать функцию по индексу 1 по сравнению с целью
plt.subplots (figsize = (8, 5))
plt.scatter(X[:, 1], y, маркер='o')
plt.xlabel("Функция в индексе 1")
plt.ylabel("Цель")
plt.show()

Здесь мы реализуем нормальное уравнение:

 # добавляет x0 = 1 к каждому экземпляру
X_b = np.concatenate([np.ones((len(X), 1)), X], ось=1)
# рассчитать нормальное уравнение
theta_best = np. linalg.inv (X_b.T.dot (X_b)).dot (X_b.T).dot (y)
# лучшие значения для тета
перехват, * coef = theta_best
print(f"Перехват: {перехват}\n\
Коэффициенты: {коэффициент}")
Перехват: 0,35921242677977794
Коэффициенты: [6,129199175400593, 96,44309685893134]

Давайте проверим нашу модель, сделав прогноз:

 # создание нового образца
new_sample = np.array([[-2, 0,25]])
# добавление термина смещения к экземпляру
new_sample_b = np.concatenate([np.ones((len(new_sample), 1)), new_sample], ось=1)
# предсказание значения нашего нового образца
new_sample_pred = new_sample_b.dot(theta_best)
print(f"Прогноз: {new_sample_pred}")
Прогноз: [12.21158829]

Всякий раз, когда вы реализуете алгоритм машинного обучения с нуля, всегда полезно иметь метод проверки вашего решения; Scikit-learn — одна из самых популярных библиотек машинного обучения на Python. Он включает несколько реализаций различных алгоритмов, включая линейную регрессию, которую мы будем использовать для проверки нашего нормального уравнения.

 из импорта sklearn.linear_model LinearRegression
лр = линейная регрессия ()
лр.фит(Х, у)
print(f"Перехват: {lr.intercept_}\n\
Коэффициенты: {lr.coef_}")
print(f"Прогноз: {lr.predict(new_sample)}")
Перехват: 0,3592124267797807
Коэффициенты: [6,12919918 96,44309686]
Прогноз: [12.21158829]

Решения примерно равны, поэтому мы можем подтвердить правильность нашего решения.

Часто задаваемые вопросы (FAQ)

Что такое нормальное уравнение в машинном обучении?

Нормальное уравнение представляет собой аналитический подход к нахождению значения θ, которое минимизирует функцию потерь без повторения.

Когда следует использовать нормальное уравнение вместо градиентного спуска?

Лучше использовать нормальное уравнение, когда у нас меньше функций. Вычисление нормального уравнения становится сложным с вычислительной точки зрения, когда количество признаков в нашем наборе данных велико.

Можно ли использовать нормальное уравнение для логистической регрессии?

К сожалению, нет. В теории классификации есть только одна условная модель, имеющая решение в закрытой форме, — линейная регрессия.

В чем разница между нормальным уравнением и градиентным спуском?

Очевидная разница между нормальным уравнением и градиентным спуском заключается в том, что в нормальном уравнении используется аналитический подход для нахождения минимума функции потерь, тогда как в градиентном спуске используется итеративный подход. Еще одно отличие состоит в том, что вам не нужно настраивать скорость обучения для вычисления нормального уравнения, поскольку для нахождения параметров θ требуется только один шаг.

Нормальное уравнение линейной регрессии | Адам Дхалла

Обоснование и линейная алгебра за нормальными уравнениями, а также исчисление.

Это продолжение моей серии по линейной алгебре, которую следует рассматривать как дополнительный ресурс при изучении класса 18.06 Гилберта Стрэнга на OCW. Это можно близко сопоставить с его серией.

Эта статья требует понимания четырех фундаментальных подпространств матрицы, проекции, проекции векторов на плоскости, проекционных матриц, ортогональности, ортогональности подпространств, исключения, транспонирования и инверсии. Я настоятельно рекомендую понять все в Лекция 15.

В предыдущей статье я писал о подгонке линии к точкам данных на двумерной плоскости в контексте линейной регрессии с градиентным спуском. В этом подходе использовалась идея [отрицательного] градиента, вектора, указывающего в направлении наискорейшего спуска, состоящего из частных производных функции стоимости, а именно параметров.

Мы обновляли каждый параметр отрицательным градиентом на каждой итерации, чтобы в конечном итоге минимизировать стоимость, которая нашла лучшие параметры для создания лучшей линии.

Математика машинного обучения I: градиентный спуск с одномерной линейной регрессией

Прямое обращение к математике в простейшем возможном варианте использования.

medium.com

Этот подход, мягко говоря, основан на вычислениях. Можем ли мы найти алгоритм (или набор уравнений), который также позволил бы нам наилучшим образом подогнать линию к набору данных, используя только линейную алгебру? Краткий ответ: да. Посмотрим, как.

Проблема

Я не буду здесь останавливаться на постановке задачи. У нас есть три точки — (1, 1), (2, 2) и (3, 2). Невозможно подобрать линейное уравнение (линию) к этому набору точек.

Но, на первый взгляд, все равно довольно неясно, как это выглядит на языке матриц и векторов. Что ж, эта последовательность из трех точек — это всего лишь три уравнения, включающие C и D. В частности,

Мы уже знакомы с представлением систем уравнений в виде матриц. Естественно, мы можем превратить это в систему уравнений, используя базовые знания линейной алгебры:

Как видите, эта система явно содержит противоречивую информацию — вторая и третья записи в b одинаковы, хотя левая часть отличается. Если бы мы продолжили с исключением (чего мы делать не будем), то увидели бы, что получили бы неудачное 1D = 2 И 2D = 2, которое невозможно удовлетворить.

Еще одно заключительное замечание: задачи линейной регрессии почти всегда включают системы, в которых уравнений на больше, чем переменных, что дает возможность уравнениям конфликтовать.

Итак, нам нужно найти «почти решение» для C и D, которое минимизирует ошибку между фактическими ответами и ответами в нашей строке.

Важность метода наименьших квадратов

Противоречивые системы уравнений встречаются в реальной жизни гораздо чаще, чем точные, разрешимые системы.

Неразрешимое уравнение.

Дело в том, что в реальной жизни наблюдения редко бывают абсолютно точными. При наблюдении за химической реакцией или анализом крови обязательно будет определенный уровень шума, который может повлиять на результат. Надеюсь, не намного, но помните — все, что нужно, это + или — 0,00000001 на ответ b , чтобы сделать всю систему неразрешимой. Короче говоря, идеально решаемые проблемы чрезвычайно трудно встретить в реальной жизни.

Но это не значит, что данные бесполезны вообще! Почти все данные, используемые в науке, не являются чисто верными, но достаточно близкими, чтобы обозначить тенденцию. Вот что мы можем делать с помощью метода наименьших квадратов — извлекать данные из несовершенных систем уравнений.

Как мы это делаем, является предметом этой статьи и включает в себя изменение b на p, проецируем наш вектор ответа b на что-то, расположенное в пространстве столбца A, так что он разрешим. Мы постараемся свести к минимуму ошибку e , которая исходит от каждой проекции.

Вопрос в том, как найти два нужных параметра (C и D) для линии, которые минимизируют стоимость (неточность между точками на линии и фактическими точками). Или, на языке линейной алгебры, почти ответ C, D, который минимизирует стоимость. Перед этим нам нужно вернуться к проекции и рассмотреть этот график как набор матриц и векторов.

Проекция и проекционные матрицы

Эта статья предназначена для людей, знакомых с проекцией и проекционными матрицами. Это только краткий обзор. Для получения дополнительной информации о проекциях и матрицах проекций, здесь является хорошим источником.

Проекция — это действие по взятию вектора и подпространства и разбиение вектора на компонент, лежащий в подпространстве. Другими словами, это проблема нахождения точки 9.0003 p на подпространстве или векторе S , ближайшем к внешнему вектору v , который вы хотите спроецировать на S. Обычно это визуально представляется метафорами с тенями.

После проецирования некоторого вектора w на v, наша проекция теперь лежит на прямой, проходящей через v. как xhat.

Ключом к проецированию вектора является нахождение этой xhat, на которую затем можно умножить на , чтобы получить длину новой проекции.

Мэтью Бретт.
Чтобы найти этот xhat, мы воспользуемся ортогональностью . Мы знаем, что ошибка, которая представляет собой разницу между нашим исходным и проецируемым вектором (здесь w - c v ), ортогональна нашему вектору, на который мы проецируем (здесь v ). С деталями не так уж сложно разобраться, но для их объяснения потребуется время, поэтому я буду обращаться к этому видео, чтобы объяснить остальное.
В любом случае, у нас есть две формулы для нахождения xhat. Один, когда мы имеем дело только с проецированием на векторы, и один, когда мы имеем дело с проецированием на подпространства (матрицы).
Мы можем использовать их, чтобы найти xhat, который является единственным значением при работе с двумя векторами, но вектором в задачах, где вы проецируете на подпространство, где длина вектора xhat совпадает с размерностью подпространства . Еще раз повторюсь — это должно быть переподготовкой.
Найдя xhat, мы можем найти значение нашей проекции p, которая является вектором, спроецированным либо на другой вектор, либо на подпространство, умножив xhat на — это работает в любой ситуации — просто размер xhat будет меняться в зависимости от на проблему.
Напомнить вам Ax = b? Так и должно быть — это точно то же самое, за исключением того, что теперь мы решаем приближение b с приближением x.
Предполагая, что вы знаете и понимаете проекцию, я не буду тратить много времени. Ниже я покажу один наглядный пример проекции на подпространство, чтобы еще раз представить идею проекционных матриц.
— проекция вектора v на пространство столбцов A. q — ошибка. Если вы понимаете этот образ, вы понимаете проекцию. Хоакин Гарсия-Альфаро.
Здесь мы проецируем вектор v на двумерную плоскость, представленную здесь как пространство столбца некоторой матрицы A. p — это наше проецирование v на пространство столбца, которое, как вы можете видеть, является просто произведением v и проекционная матрица А. Краткое освежение в матрицах проекций:
Любая такая линия или подпространство a имеет проекционную матрицу P, которую можно умножить на любой другой вектор b для проецирования на подпространство a. Формулы для проекционных матриц как для проецирования на подпространство, так и для прямой, следующие:
Конечно, это непохоже на то, чтобы я представил формулу, не пытаясь досконально объяснить ее, но это немного более сложная статья, и я оставьте интуицию до проф. Видео Гилберта Стрэнга на эту тему.
Регрессия методом наименьших квадратов
Примечание: «регрессия» — это красивое слово из статистики, обозначающее одну из этих проблем наилучшего соответствия.
Примечание II. Сначала я начну с линейной алгебры, а когда все это будет сделано и разобрано, посмотрим, как мы можем получить точно такой же ответ с помощью элементарного многомерного исчисления.
Возвращаясь к предыдущей картинке, мы видим, что нам нужно найти «близкий ответ», который мы назовем xhat , который минимизирует ошибку системы. Возвращаясь к нашему примеру, это означает найти C и D, которые минимизируют ошибку.
Здесь ошибку можно официально рассматривать как e = b - A*xhat. Этот xhat не будет ответом на эту проблему, но сведет к минимуму разницу между оценочным ответом и фактическим ответом .
Дело в том, что мы не можем это решить. Существует только способ найти C и D для системы, имеющей определенные решения. Алгебра так не работает — представьте, что вы пытаетесь решить неразрешимое уравнение, чтобы найти размер x 9.0624, что «достаточно близко» с использованием классической алгебры? Это было бы невозможно. Всякий раз, когда вы занимаетесь алгеброй, вы находите точные решения или их отсутствие.
Итак, мы можем найти обходной путь найти разрешимое уравнение Axhat = b , которое похоже на наше исходное уравнение, но на самом деле разрешимо. Вы можете видеть, к чему это идет.
Напомним, что система уравнений Ax = b разрешима, если b находится в пространстве столбцов A, , так как тогда мы можем просто найти правильную линейную комбинацию столбцов для решения для b.
Основываясь на этом знании, нам нужно изменить нашу неразрешимую b на что-то, что находится в пространстве столбца A.
Это именно то, для чего предназначена проекция. Проекция берет компонент некоторого вектора v , который лежит в подпространстве S , и возвращает этот компонент, который полностью находится в подпространстве S. Этот результирующий спроецированный вектор p находится в S.

Что нам нужно нужно найти способ спроецировать нашу неразрешимую b в пространство столбцов, чтобы найти некоторое p, разрешимое в Ax = p.

Текущее значение b находится вне пространства столбцов (неразрешимое), поэтому его необходимо спроецировать на пространство столбцов (p или Axhat), которое затем разрешимо, поскольку находится в пространстве столбцов A.
Вспомните, как мы нашли p в двумерной проекции нужно сначала найти p = xhat*a. Найдя xhat, мы можем умножить его на a, чтобы получить проекцию.
Затем мы могли бы найти этот xhat, используя формулы для проектирования, которые я описал в начале статьи. Поскольку мы проектируем на подпространство C(A), мы используем матричную версию формулы проекции для хат.
Все, что нам нужно сделать, это подставить A в эту формулу и найти xhat. Результатом этого будет множитель с подпространством A для создания нашей проекции p.
Я не буду показывать все расчеты, так как они основаны на базовой линейной алгебре для решения системы уравнений.
Наш первый шаг — подставить наши A и b в формулу и начать вычислять C и D. Вскоре это становится тривиальным вопросом на исключение Гаусса.
Выполнив несложное умножение матриц, мы подошли к задаче на исключение Гаусса, которую можно решить путем исключения.
Получается ответ:
Подождите, это все? Мы только что решили для нашего xhat, который сводит к минимуму стоимость! Нам не нужно , чтобы найти p, так как это не является целью линейной регрессии. Мы пытаемся найти только кратные. Возможно, вы это предвидели, но формула для проецирования вектора на матрицу и решения для xhat является нормальным уравнением.
Давайте подтвердим, что полученная линия хорошо подходит для нашего набора данных.
По-моему, это чертовски правильно. И, конечно же, это будет линия, которая сведет ошибку к минимуму. Вся идея проецирования вектора v на подпространстве S состоит в том, чтобы найти точку p на подпространстве, которая минимизирует расстояние между вектором и подпространством min (v-p). Итак, если мы используем проекцию, чтобы найти это, сама концепция использования проекции для решения проблемы гарантирует, что мы найдем минимум.
Еще одна важная вещь, о которой следует упомянуть — нормальное уравнение работает с гораздо более сложными задачами линейной регрессии. Например, проблема с 3 переменными (попытка найти наиболее подходящую плоскости) работают точно так же — поскольку нормальное уравнение — это просто набор матричных операций, мы делаем то же самое, за исключением того, что вместо этого A будет просто матрицей 3 x 3, а b будет вектором 3 x 1.
Мы можем сделать это для любого количества уравнений и переменных, если, как правило, количество переменных меньше, чем количество уравнений. Мы просто запускаем нормальное уравнение так же, как и раньше.
Таким образом, нормальное уравнение может найти наилучшую прямую/плоскость для любой системы уравнений без использования каких-либо концепций исчисления, алгоритмов итеративного градиентного спуска или даже истинной функции стоимости. Но как мы можем добиться тех же результатов для C и D, просто используя классическое исчисление?
Приходя к тем же выводам с исчислением
Если вы не знакомы с исчислением или просто не заинтересованы и были здесь только для части линейной алгебры, не стесняйтесь выйти. Но вот как мы можем подтвердить наш ответ с помощью исчисления.
То, что мы делали с нормальным уравнением, заключалось в том, чтобы минимизировать общую ошибку системы. Минимизация часто напоминает нам исчисление, и здесь эта связь не является неправильной. Если мы сможем найти функцию, которая дает нам ошибку, мы сможем найти минимум (правильные C и D) с помощью исчисления.
Во-первых, формула для общей ошибки — та, с которой мы столкнулись в начале статьи. Мы возводим в квадрат каждую ошибку, чтобы исключить любые негативы.
Это функция, которую мы хотим минимизировать — общая квадратичная ошибка E². Но как нам найти C и D, если их нет в этом? Что ж, и состоят из более мелких компонентов, которые мы можем разобрать. Помните, что каждая ошибка — это разница между ее предсказанием (значением в строке) и фактическим значением? Итак, взглянув на три уравнения, определяющие эту систему, мы можем:
Итак, мы можем заменить ошибки в нашей формуле E² этими парами прогноз-ответ, сделав нашу новую формулу E² чем-то, что мы можем дифференцировать относительно C и D.
Это уравнение имеет график в виде трехмерного параболического поверхности, с глобальным минимумом и без максимума. Это довольно интуитивно — глядя на это, нет предела тому, насколько большой мы можем сделать нашу стоимость, но есть наименьшее возможное значение.
Способ, которым мы находим локальные минимумы или максимумы функций с помощью исчисления, состоит в том, чтобы приравнять производную (производные) к нулю (найти, где функция имеет наклон 0, что означает максимум или минимум, но здесь только минимум, поскольку существует без максимума).
Поскольку эта функция имеет две входные переменные, C и D, мы должны найти частных производных по C и D и найти, где они обе равны 0. Другими словами, мы должны найти градиент.
Во-первых, нам нужно найти наши частные производные.
Используя правило сумм, правило степени и правило цепочки, мы можем привести их оба к более простому состоянию. Я не буду показывать расчеты здесь, но вот потрепанная фотография моей доски с расчетами на ней.
В любом случае, после упрощения обоих мы получаем две частные производные (вместе градиент). Это:
Затем мы должны найти значения C и D, при которых обе эти производные равны нулю. Если вам нужна геометрическая перспектива, вот какое значение C и D достигает основания параболы, как показано ниже:
Основание этой параболы имеет обе производные = 0
Это, конечно, простая система уравнений после установив оба значения в 0. Мы могли бы даже использовать исключение Гаусса для решения этой системы, но я буду придерживаться исключения нормального уравнения.
Решение этой системы дает, к счастью, точно такие же результаты, что и наш путь нормального уравнения, а именно:
Нормальное уравнение часто используется для задач линейной регрессии с меньшим количеством переменных. При вычислении нормального уравнения на компьютере с чем-то вроде NumPy или MATLAB следует соблюдать осторожность, и это вычислительная сложность (насколько медленно вычисляются).
При вычислении x, компьютер фактически делает то же самое с правой стороны, что эквивалентно (мы просто перенесли АТА на другую сторону). Но, как видите, для этого требуется инвертировать матрицу размера (n, n). Инверсия матриц хороша на небольшом уровне, но, как правило, это довольно сложная задача для вычислений, и ее вычислительная сложность близка к O (n³), где n количество переменных.
Итак, чаще всего советуют использовать градиентный спуск, когда количество переменных приближается к уровню n = 10 000. Большинство задач, предшествующих этому, должны решаться по нормальному уравнению.
Адам Дхалла учится в старшей школе из Ванкувера, Британская Колумбия. Он очарован внешним миром и в настоящее время изучает новые технологии для защиты окружающей среды.
Посетите его сайт здесь .
Подпишитесь на его I nstagram и его LinkedIn . Чтобы получить больше подобного контента, подпишитесь на его информационный бюллетень здесь.
Не решать нормальные уравнения – Итан Эпперли
(Обычная) линейная задача наименьших квадратов заключается в следующем: даны матрица и вектор длины , найти вектор, максимально близкий к , когда измеряется по двукратной норме. То есть мы стремимся к
(1)
Из этого уравнения название «наименьшие квадраты» говорит само за себя: мы ищем, что минимизирует сумму квадратов расхождений между элементами и .
Задача наименьших квадратов повсеместно используется в естественных науках, технике, математике и статистике. Если мы будем думать о каждой строке как о входе, а о соответствующей ей записи как о выходе, то решение модели наименьших квадратов дает коэффициенты линейной модели для отношения вход-выход. Учитывая новые ранее невидимые входные данные, наша модель предсказывает выход примерно равным . Вектор состоит из коэффициентов для этой линейной модели. Решение методом наименьших квадратов удовлетворяет тому свойству, что среднеквадратическая разница между выходными данными и предсказанием настолько мала, насколько это возможно для всех вариантов выбора векторов коэффициентов.
Как решить задачу наименьших квадратов? Классический подход к решению, повсеместно встречающийся в учебниках, заключается в решении системы линейных уравнений, известной как нормальных уравнения . Нормальные уравнения, связанные с задачей наименьших квадратов (1), имеют вид
(2)
Эта система уравнений всегда имеет решение. Если имеет полный ранг по столбцу, то обратим, и единственное решение методом наименьших квадратов для (1) определяется выражением . Мы предполагаем, что имеет полный column-rankQ для остальной части этого обсуждения. Чтобы решить нормальные уравнения в программном обеспечении, мы вычисляем и решаем (2) с помощью линейного решателя, такого как «\» в MATLAB. ¹ Более того, мы могли бы использовать разложение Холецкого, поскольку матрица положительно определена. (Как это обычно бывает при матричных вычислениях, почти никогда не бывает хорошей идеей явно формировать обратную матрицу или любую матрицу.) Мы также можем решать нормальные уравнения, используя итерационный метод, такой как (предварительно обусловленный) сопряженный градиент.
Цель статьи - выступить против использования нормальных уравнений для решения задач наименьших квадратов, по крайней мере, в большинстве случаев. Так что же не так с обычными уравнениями? Проблема не в том, что нормальные уравнения математически некорректны. Вместо этого проблема в том, что нормальные уравнения часто приводят к низкая точность для решения методом наименьших квадратов с использованием компьютерной арифметики.
Большую часть времени при использовании компьютеров мы храним действительные числа как числа с плавающей запятой . ² Рациональные числа можно представить на компьютере в виде целых чисел, и операции можно выполнять точно. Однако это чревато большой неэффективностью, поскольку количество цифр в рациональных числах может стать очень большим, что значительно удорожает память и время для решения задач линейной алгебры с рациональными числами. По этим причинам в подавляющем большинстве числовых вычислений используются числа с плавающей запятой, которые хранят только конечное число цифр для любого заданного действительного числа. В этой модели, за исключением крайне редких обстоятельств, ошибки округления при арифметических операциях — неотъемлемая часть жизни. На грубом уровне правильная модель, которую следует держать в голове, состоит в том, что действительные числа на компьютере хранятся в экспоненциальном представлении только с 16 десятичными цифрами после запятой. ³ Это упрощение во многих отношениях. Во-первых, компьютеры хранят числа в двоичном формате, и поэтому вместо 16 десятичных цифр после запятой они хранят 52 двоичные цифры. Это составляет примерно 16 десятичных цифр. Во-вторых, существуют разные форматы хранения действительных чисел в виде чисел с плавающей запятой на компьютере с разным количеством хранимых цифр. Широко используемый формат двойной точности IEEE имеет точность около 16 десятичных знаков; формат одинарной точности IEEE имеет примерно 8. При сложении, вычитании, умножении и делении двух чисел результат вычисляется, а затем округляется до 16 десятичных цифр; любые лишние цифры информации отбрасываются. Таким образом, результат нашей арифметики на компьютере — это верный ответ на арифметическую задачу плюс маленькая ошибка округления . Эти ошибки округления по отдельности малы, но для решения задачи линейной алгебры даже небольшого размера требуются тысячи таких операций. Убедиться, что множество мелких ошибок не накапливаются в большую ошибку, является частью тонкого искусства численных вычислений.
Чтобы сделать грубое упрощение, если решить систему линейных уравнений на компьютере с помощью хорошо разработанной части программного обеспечения, можно получить приближенное решение, которое после учета накопления ошибок округления близко к . Но то, насколько близко вычисленное решение и истинное решение, зависит от того, насколько «хорошей» является матрица. «Прекрасность» матрицы количественно определяется величиной, известной как число обусловленности , которую мы обозначаем . ⁴ На самом деле существует несколько определений числа обусловленности в зависимости от нормы, которая используется для измерения размеров векторов. Поскольку мы используем 2-норму, подходящим числом обусловленности 2-нормы является отношение наибольшего и наименьшего сингулярных значений . Грубо говоря, относительная ошибка между и примерно ограничена как
(3)
Знак «» соответствует тому факту, что у нас есть примерно 16 десятичных цифр точности в арифметике двойной точности с плавающей запятой. Таким образом, если число условий примерно равно , то мы должны ожидать около цифр точности в нашем вычисленном решении.
Точность задачи наименьших квадратов определяется ее собственным числом обусловленности. Мы надеемся, что сможем решить задачу наименьших квадратов с точностью, равной эмпирической оценке погрешности (3), которую мы получили для линейных систем уравнений, а именно с такой же точностью. Но это не та точность, которую мы получаем для задачи наименьших квадратов, когда решаем ее с помощью нормальных уравнений. Вместо этого мы получаем точность вроде
(4)
. Решая нормальные уравнения, мы эффективно возводим число обусловленности в квадрат! Возможно, это неудивительно, поскольку нормальные уравнения также более или менее возводят матрицу в квадрат, вычисляя . Это квадратичное число условий резко влияет на точность вычисляемого решения. Если число обусловленности равно , то нормальные уравнения дают нам абсолютную бессмыслицу для ; мы ожидаем, что не получим ни одной цифры правильного ответа. Сравните это с приведенным выше, где мы смогли получить правильные цифры в решении, несмотря на то, что число условия в раз больше, чем !
Все это было бы просто печальным фактом жизни для задачи наименьших квадратов, если бы нормальные уравнения и их плохие свойства точности были лучшим, что мы могли сделать для задачи наименьших квадратов. Но мы можем лучше! Можно решить линейную задачу наименьших квадратов, вычислив так называемую QR-факторизацию матрицы . ⁵ В MATLAB задачу наименьших квадратов можно решить с помощью QR-факторизации, вызвав «A\b». Не вдаваясь в подробности, вывод состоит в том, что решение по методу наименьших квадратов с помощью хорошо спроектированной ⁶ Одним из способов вычисления QR-факторизации является ортогонализация Грама–Шмидта, но точность этого способа также невелика. Золотой стандарт расчета QR-факторизации с помощью отражателей Хаусхолдера, обладающий превосходными свойствами точности. Для QR-факторизации требуется такое же количество времени, как и для решения нормальных уравнений, и она имеет значительно улучшенные свойства точности, достигая желаемого эмпирического поведения ⁷ Точнее, эмпирическое правило похоже на . Таким образом, даже если мы решим задачу наименьших квадратов с QR-факторизацией, мы все равно получим число условия в квадрате в нашей границе ошибки, но квадрат этого числа условий умножается на остаток , который мал, если подходит метод наименьших квадратов. Решение методом наименьших квадратов обычно интересно только тогда, когда невязка мала, что оправдывает исключение его из эмпирического правила.
(5)
Я не описал, как точно вычисляется QR-факторизация, ни как использовать QR-факторизацию для решения задач наименьших квадратов, ни даже что такое QR-факторизация. Все эти темы прекрасно объясняются в стандартных учебниках в этой области, а также в общедоступных ресурсах, таких как Википедия. Можно еще многое сказать о многочисленных преимуществах решения задачи наименьших квадратов с помощью QR-факторизации 9.1439 8 Например, он может работать с разреженными матрицами, в то время как нормальные уравнения часто не работают, он имеет более высокую точность, чем исключение Гаусса с частичным поворотом, даже для решения линейных систем, матрица «» в QR-факторизации может быть неявно представлена как произведение легко вычисляемых с помощью отражателей Хаусхолдера, которые намного эффективнее, когда и т. д., но в интересах краткости позвольте мне сказать следующее: TL; DR, когда представлены в дикой природе с задачей наименьших квадратов, метод решения один по умолчанию должно быть основано на хорошо реализованной QR-факторизации, а не на решении нормальных уравнений.
Предположим, по какой-то причине в нашем распоряжении нет высококачественного алгоритма QR-факторизации. Должны ли мы тогда прибегать к нормальным уравнениям? Даже в этом случае есть способ свести задачу решения задачи наименьших квадратов к линейной системе уравнений без возведения в квадрат числа обусловленности! (Для тех, кто заинтересован, для этого мы распознаем нормальные уравнения как дополнение Шура к несколько большей системе линейных уравнений, а затем решаем ее. См. уравнение (7) в этом посте для более подробного обсуждения этого подхода.)
Название поста Не решай нормальные уравнения намеренно завышено. Бывают случаи, когда решение нормальных уравнений уместно. Если он хорошо обусловлен с небольшим числом обусловленности, возведение числа обусловленности в квадрат может быть не таким уж плохим. Если матрица слишком велика для хранения в памяти, можно решить задачу наименьших квадратов, используя нормальные уравнения и метод сопряженных градиентов.
Однако резкое снижение точности решения нормальных уравнений должно лишить этот подход фактического способа решения задач наименьших квадратов.
No related posts.
Навигация по записям
Предыдущая статьяСложение и вычитание дробей с одинаковым знаменателем: Сложение и вычитание дробей с одинаковыми знаменателями
Следующая статьяСобственная скорость катера 12 8: Собственная скорость катера 12,8 км/ч. Скорость течения реки 1,7 км/ч. Найдите скорость катера по течению и против течения.
Добавить комментарий Отменить ответ
Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий *
Имя *
Email *
Сайт

Найти:
Рубрики
Геометрия
Математика
Физика
Химия
Школьная жизнь
Разное
© 2015 - 2019 Муниципальное казённое общеобразовательное учреждение «Таловская средняя школа»
Карта сайта