Собственное значение: Кафедра математики Физического факультета МГУ им. М.В.Ломоносова

Помогите решить / разобраться (М)

Сообщения без ответов | Активные темы | Избранное

Правила форума

Посмотреть правила форума

MrWorm	минимальное собственное значение матрицы 21.11.2017, 12:14
12/12/11 11	Здравствуйте, я хотел бы попросить вашей помощи в некоторой задаче в области численных методов. У меня есть большая матрица (100×100) квадратная, симметричная, действительная. Мне необходимо найти минимальное собственное значение (СЗ) этой матрицы. Я читал про разные методы и остановился на двух. 1) QR разложение, позволяет найти все СЗ матрицы. На этом методе я остановился. Однако он слишком медленный и не устраивает меня. 2) Степенной метод. Очень быстрый метод, по сравнению с QR, позволяет найти модуль максимального СЗ матрицы. Если обратить матрицу, то можно найти модуль минимального СЗ. Проблема с которой я столкнулся — не смог найти метод позволяющий найти обратную матрицу. Я делал две разные реализации, но они работают с небольшими матрицами, при этом с небольшими (4х4) эти методы работают. Если я не ошибаюсь, я использовал метод в лоб. Проблема с большими матрицами в том, что появляются очень большие числа, которые не помещаются даже в double precision. Можете подсказать, если ли какие-то другие эффективные методы нахождения минимального СЗ матрицы или её обращения? Спасибо.

ozheredov	Re: минимальное собственное значение матрицы 21.11.2017, 12:55
10/03/16 2619 Aeroport	MrWorm 100 х 100 это не большая матрица — это смехотворно маленькая матрица. Никакие реализации методов нахождения обратной матрицы и сз делать не нужно— для этого есть стандартные функции в R и Matlab, которые в вашем случае найдут обратную матрицу и минимальное сз примерно за 0.000001 секунды Если не секрет из какой области задача?

Евгений Машеров	Re: минимальное собственное значение матрицы 21.11.2017, 13:15
Заслуженный участник 11/03/08 8537 Москва	Присоединяясь к замечанию о том, что 100х100 это не очень большая матрица, разве что руками считать, отмечу, что для нахождения минимального С. З. степенным методом не обязательно использовать обратную матрицу, хотя это и даёт лучшую скорость сходимости. Если взять матрицу , то её собственные значения будут связаны с С.З. исходной матрицы, как и «последние будут первыми». В качестве k лучше взять величину, несколько большую максимального С.З. матрицы А. И на всякий случай напомню, что степенной метод даёт не максимальное, а максимальное по модулю С.З., и если там будут отрицательные — может быть интересно…

MrWorm	Re: минимальное собственное значение матрицы 21.11.2017, 13:32
12/12/11 11	Спасибо за ответы! ozheredov Согласен, что матрица не большая, я несколько не корректно написал. Большая в смысле того, что считать руками такие матрицы сложно. Это университетская задача не имеющая конкретного приложения. Так же я не указал этого, но я понимаю, что можно воспользоваться различными бибилиотеками которые дадут моментально результат. Меня интересует в данном случае код не использующий сторонние библиотеки. Евгений Машеров Спасибо, попробую этот метод!

ozheredov	Re: минимальное собственное значение матрицы 21.11.2017, 13:50
10/03/16 2619 Aeroport	MrWorm А, извините, я не понял что это просто у вас часть программы. Тогда подключите нормальную математическую библиотеку — они есть на с++, пайтон, джава и т.п. В любом случае библиотечная функция будет работать надёжнее и гораздо быстрее, поскольку их оптимизируют на уровне машинного кода

Евгений Машеров	Re: минимальное собственное значение матрицы 21.11.2017, 15:59
Заслуженный участник 11/03/08 8537 Москва	Ещё бы для хорошего совета было бы полезно знать, это упражнение по программированию, по вычислительной математике или часть проекта по какой-то прикладной дисциплине?

MrWorm	Re: минимальное собственное значение матрицы 21. 11.2017, 16:22
12/12/11 11	ozheredov Это был бы идеальный вариант, но меня интересует, как это запрограммировать самому. Евгений Машеров Совершенно верно, это упражнение по программированию.

MrWorm	Re: минимальное собственное значение матрицы 21. 11.2017, 19:19
12/12/11 11	Евгений Машеров Я попробовал написанный вами метод. Я тестировал его на простых матрицах (3х3) и получалось находить минимальные и максимальные СЗ. К сожалению на моей матрице он ведёт себя очень не стабильно, при увеличении числа итерраций на порядки и фиксированном приближении, СЗ на выходе имеют разброс на десятки.

ewert	Re: минимальное собственное значение матрицы 22. 11.2017, 19:41
Заслуженный участник 11/05/08 32132	MrWorm в сообщении #1267638 писал(а): увеличении числа итерраций на порядки и фиксированном приближении, СЗ на выходе имеют разброс на десятки. Непонятно, что все эти слова означают. Но, во всяком случае, следует иметь в виду, что метод простых итераций сходится очень медленно — со скоростью геометрической прогрессии, знаменатель которой более-менее равен отношению предпоследнего собственного числа к последнему. Для матрицы сто на сто типичным значением будет что-то вроде . И это не только медленно; надо ещё считаться с тем, что фактическая погрешность будет примерно в сотню раз больше, чем разность соседних приближений. Т.е. если стабилизировались три цифры, то достигнутая точность — лишь порядка десяти процентов. А ведь для матриц такого же размера (некоторого специального вида) и — тоже вполне типично…

Евгений Машеров	Re: минимальное собственное значение матрицы 23.11.2017, 10:05
Заслуженный участник 11/03/08 8537 Москва	Ну, собственно, для матрицы 100х100 степенной метод имеет одно достоинство — программировать его не просто, а очень просто. Хотя и тут можно нарваться. Помнится, один мой знакомый слишком буквально понял правило расчёта и, вычислив очередной элемент вектора, его сразу же помещал на место. И долго недоумевал. Скорость сходимости — да, может быть прискорбно низкой. И даже никакой Заратустра не запретил максимальному С.З. быть кратным. Хотя для некоторых матриц можно доказать факт отсутствия кратности и получить оценки скорости сходимости. (Оффтоп) Задача о рейтинге футбольных команд — матрица A содержит встреч команд меж собой, для расчёта рейтинга принимается, что победа над сильной командой даёт больший вклад в рейтинг, задача сводится к , и поскольку матрица A неразложима и имеет положительные элементы, по теореме Фробениуса-Перрона у неё одно максимальное действительное С.З. А при кратном С.З. собственный вектор в ходе вычислений вправе прыгать как угодно в пространстве, натянутом на соответствующие кратному значению собственные вектора. Для борьбы с этим в рамках степенного метода придумали одновременные итерации, когда берётся набор k ортогональных (для начала — можно просто случайных) векторов, их умножают на матрицу, полученные вектора ортогонализуют и запускают в цикл по новой. Работает, но не панацея. Скорость определяется отношением первого и (k+1) С.З., и тоже может быть невысока. Степенной метод и иже с ним не для доступной обычным образом матрицы, они для случая, когда матрица очень велика и разрежена, или велика и хранима во внешней памяти, или велика и её элементы не хранятся, а вычисляются по требованию, в общем, когда единственная доступная операция это умножить вектор на эту матрицу. Да и там степенной метод и его продвинутые версии не единственный вариант, но, по крайней мере, «препарат выбора». Хотя лично я испытываю нежные чувства к методу Якоби (вращений), но в данном случае его рекомендовать бы не стал. Его главное достоинство — гарантированная ортогональность всех собственных векторов — здесь явно излишне, да и «покупать корову ради одного бифштекса» в смысле считать все собственные значения и вектора, когда требуется одно минимальное — «половое излишество, паркетный пол линолеумом покрывать». Мне кажется, тут лучше QR найти трудно. Правда, программируется он двухэтапно. Сперва надо привести (отражениями) к трёхдиагональной форме, а уж потом QR. Причём без сдвигов сразу будет находиться наименьшее С.З. (Оффтоп) Силами студентов в подшефном колхозе был построен Q-рятник на 1024 QRместа Или можно, также приведя к трёхдиагональному виду, использовать бисекции.

ewert	Re: минимальное собственное значение матрицы 23.11.2017, 12:33
Заслуженный участник 11/05/08 32132	Евгений Машеров в сообщении #1268277 писал(а): И даже никакой Заратустра не запретил максимальному С. З. быть кратным. Речь шла вроде как о симметричных матрицах, а для них это не имеет значения. Т.е. Евгений Машеров в сообщении #1268277 писал(а): при кратном С.З. собственный вектор в ходе вычислений вправе прыгать как угодно в пространстве, натянутом на соответствующие кратному значению собственные вектора — соотв., не вправе. — Чт ноя 23, 2017 13:48:35 — Да, не обратил сначала внимания. Даже и кратность с.ч. не заставит с.в. скакать — разве что ползти, но для поиска с.ч. это не важно. Скакать он будет в другом случае — если есть разные максимальные по модулю с.ч. Но в симметричном случае и это не проблема — надо просто отслеживать по отдельности приближения к с.в., получаемые на чётных и на нечётных итерациях, проверяя их коллинеарность.

Евгений Машеров	Re: минимальное собственное значение матрицы 24. 11.2017, 09:30
Заслуженный участник 11/03/08 8537 Москва	Это да, пример, в котором наблюдается скакание, требует асимметричной матрицы…

Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию

Страница 1 из 1

[ Сообщений: 12 ]

Модераторы: Модераторы Математики, Супермодераторы

Кто сейчас на конференции

Сейчас этот форум просматривают: нет зарегистрированных пользователей

Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения

Найти:

Нулевое собственное значение — Большая Энциклопедия Нефти и Газа, статья, страница 1

Cтраница 1

Нулевое собственное значение может быть, вообще говоря, вырожденным.  [1]

Нулевое собственное значение эндоморфизма ad z по определению встречается только в подпространстве / Со — Положив с 0, видим, что gn r не является тождественным нулем на F.  [2]

Лишь нулевое собственное значение может иметь бесконечную кратность.  [3]

Помимо нулевых собственных значений, интересующий нас оператор [ — с У ( ь) ] имеет и ( одно) отрицательное собственное значение.  [4]

Помимо нулевых собственных значений, интересующий нас оператор [ — д2ц У ( фъ) ] имеет и одно отрицательное собственное значение.  [5]

Двум нулевым собственным значениям I z соответствуют два различных состояния рассматриваемой пары. Поэтому существуют четыре различных собственных состояния нашей системы.  [6]

А имеет нулевое собственное значение. В строго математическом смысле проблема обращения неразрешима лишь в том случае, когда какое-либо из собственных значений матрицы А в точности равно нулю.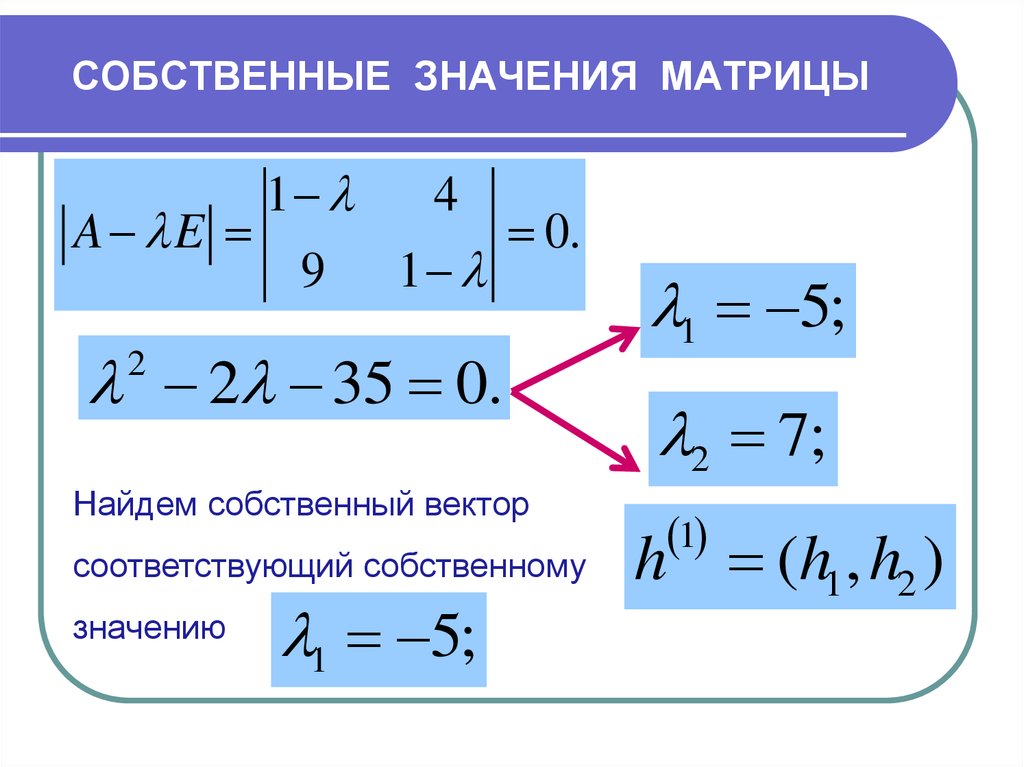 Но с практической точки зрения мы встречаемся с большими вычислительными трудностями не только когда А имеет нулевое собственное значение, но и тогда, когда А имеет одно или несколько весьма малых собственных, значении. Математический анализ таких почти особых систем заслуживает особо пристального внимания. Строго говоря, проблема обращения матрицы может быть рассмотрена без каких-либо сведений относительно проблемы собственных значений.  [7]

А имеет нулевое собственное значение. В строго математическом смысле проблема обращения неразрешима лишь в том случае, когда какое-либо из собственных значений матрицы А в точности равно нулю. Но с практической точки зрения мы встречаемся с большими вычислительными трудностями не только когда А имеет нулевое собственное значение, но и тогда, когда А имеет одно или несколько весьма малых собственных значений. Математический анализ таких почти особых систем заслуживает особо пристального внимания. Строго говоря, проблема обращения матрицы может быть рассмотрена без каких-либо сведений относительно проблемы собственных значений.  [8]

Поскольку число нулевых собственных значений матрицы равно р-г 1 и она неположительна, то матрица F имеет только отрицательные собственные значения.  [9]

А не имеет нулевого собственного значения.  [10]

А не имеет нулевого собственного значения.  [11]

Предположим, что нулевому собственному значению матрицы Q ( 9) соответствует инвариантное подпространство Е0, состоящее только из собственных векторов.  [12]

Первое множество соответствует нулевому собственному значению особой точки, второе — паре чисто мнимых. Деформации таких ростков в типичных однопараметрических семействах стабильно ( с точностью до надстройки седел) эквивалентны выписанным в таблице 1 главным деформациям и версальны.  [13]

Этим пяти функциям соответствуют нулевые собственные значения.  [14]

Если квадрат матрицы имеет только нулевые собственные значения, то она сама тоже имеет только нулевые собственные значения. Это означает, что матрица нильпотентна. А квадрат любой нильпотентной матрицы 2-го порядка равен нулю.  [15]

Страницы:      1    2    3    4

собственных векторов и собственных значений — как объяснить их 10-летнему ребенку | Сундареш Чандран

Делаем менее интуитивные понятия интуитивно понятными

Фото Бенджамина Лизардо на Unsplash

Собственные значения и собственные векторы занимают центральное место (но не ограничиваются) во многих известных алгоритмах машинного обучения. Такие алгоритмы, как SVD, PCA, спектральная кластеризация, сегментация изображений, трехмерная реконструкция, используют собственные значения и собственные векторы в качестве основной логики для работы.

Несмотря на их полезность, их критичность во многих известных приложениях и то, что они являются частью линейной алгебры 101, они часто считаются трудными для понимания и даже опасаются начинающих статистиков/специалистов по данным в первую очередь из-за того, насколько неинтуитивной может быть концепция .

Если вы впервые слышите слова «собственное значение и собственный вектор», эта история поможет вам понять основную концепцию, лежащую в основе собственных векторов и собственных значений. Если вы хорошо это знаете и, возможно, захотите объяснить это своей племяннице или племяннику (или тому, кто не разбирается в статистике), эта история поможет в этом 🙂

В параллельной вселенной жили две могущественные силы — матрицы и векторы. Матрицы были хулиганами, а векторы были робкими и легко пугаемыми. Всякий раз, когда вектор встречается с матрицей, он перенаправляет свой путь. Если бы вектор шел за продуктами и встретил на своем пути матрицу, он бы развернулся и пошел к дому своего друга. Если бы он шел в университет и встречал на своем пути матрицу, он бы пошел в торговый центр.

Как и в любой другой истории, среди векторов были и повстанцы. Они были названы собственными векторами . Они проповедовали ненасилие и были очень упрямы в своем деле. Независимо от матрицы, они всегда держались своего пути. Не беспокоясь о том, что над ними издеваются, они продолжали идти к месту назначения, потому что были ориентированы на цель. Да, временами было трудно, когда очень мощная матрица блокировала их путь и пыталась перенаправить их. Но это только замедлит их, а не перенаправит. Если бы слабая матрица преградила им путь, они ускорили бы дальнейшее сдувание матрицы. Этой способностью адаптироваться к сильной или слабой матрице обладали только собственные векторы, и они называются собственными значениями. У каждой матрицы есть свои особые нарушители спокойствия, также известные как собственные векторы.

что мы узнали: собственных векторов — это особые векторы, которые сохраняют свое направление, несмотря на запугивание со стороны матриц (в математике мы называем это матричным преобразованием). Эти векторы ускоряются (удлиняются) или замедляются (сжимаются/сжимаются) в зависимости от интенсивности издевательств (трансформации) с коэффициентом собственного значения.

В математических терминах уравнение собственного вектора и собственного значения обозначается как:

Уравнение собственного вектора и собственного значения

Где A — матрица, v — соответствующий собственный вектор матрицы, а лямбда — собственное значение. Другой способ прочесть уравнение (если хотите, чтобы это звучало умнее): всякий раз, когда матрица A умножается на специальный вектор v, вектор масштабируется с коэффициентом лямбда.

Теперь, если вы соблюдаете приведенное выше уравнение, лямбда (или коэффициент масштабирования) может быть любым числом (включая комплексное). Если он положительный, это означает, что он указывает в том же направлении, что и исходный вектор. Существуют также специальные матрицы-боссы, называемые сингулярными матрицами, где лямбда равна 0, а также есть матрицы с отрицательным значением лямбда, что означает, что собственный вектор меняет свое направление на противоположное, но остается на линии, на которую он опирается.

Важность и применение собственных векторов и собственных значений в большей степени зависят от изменения базиса и выходят за рамки этой статьи. Если вы хотите узнать больше о том, почему Eigen-вещи так широко используются в линейной алгебре и машинном обучении и как они упрощают определенные вычисления на порядок 100 или более (при определенных сценариях), оставьте комментарий 🙂

Понравилась моя статья? Купи мне кофе

Сундареш пишет статьи, связанные с наукой о данных, и любит преподавать

Привет 👋 Я только что создал здесь страницу.

Теперь ты можешь угостить меня кофе!

www.buymeacoffee.com

Определение и значение собственного значения — Merriam-Webster

собственное значение ˈī-gən-ˌval-(ˌ)yü

: скаляр, связанный с данным линейным преобразованием векторного пространства и обладающий тем свойством, что существует некоторый ненулевой вектор, который при умножении на скаляр равен вектору, полученному в результате выполнения преобразования над вектором

особенно : корень характеристического уравнения матрицы

Примеры предложений

Недавние примеры в Интернете Снова и снова, независимо от их специфических характеристик, случайные матрицы обнаруживают один и тот же хаотический, но регулярный характер распределения своих собственных значений . — Журнал Кванта , 5 февраля 2013 г. Паттерн включал второй слой чисел, называемый собственными значениями , которые подобны ДНК матрицы. — Журнал Quanta , 6 мая 2019 г. Напротив, кривая Трейси-Уидома, по-видимому, возникает из сильно коррелированных переменных, таких как взаимодействующие виды, цены акций и собственные значения матрицы . — Натали Волховер, 9 лет.0055 ПРОВОДНАЯ , 27 октября 2014 г.

Эти примеры предложений автоматически выбираются из различных онлайн-источников новостей, чтобы отразить текущее использование слова «собственное значение». Мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв.

История слов

Этимология

частичный перевод немецкого Eigenwert , от eigen собственный, своеобразный + Wert значение

Первое известное использование

1927, в значении, определенном выше

Путешественник во времени

Первое известное использование собственного значения было в 1927 году

Посмотреть другие слова того же года

Словарные статьи Около

собственное значение

собственный тон

собственное значение

собственный вектор

Посмотреть другие записи поблизости

Процитировать эту запись «Собственное значение».