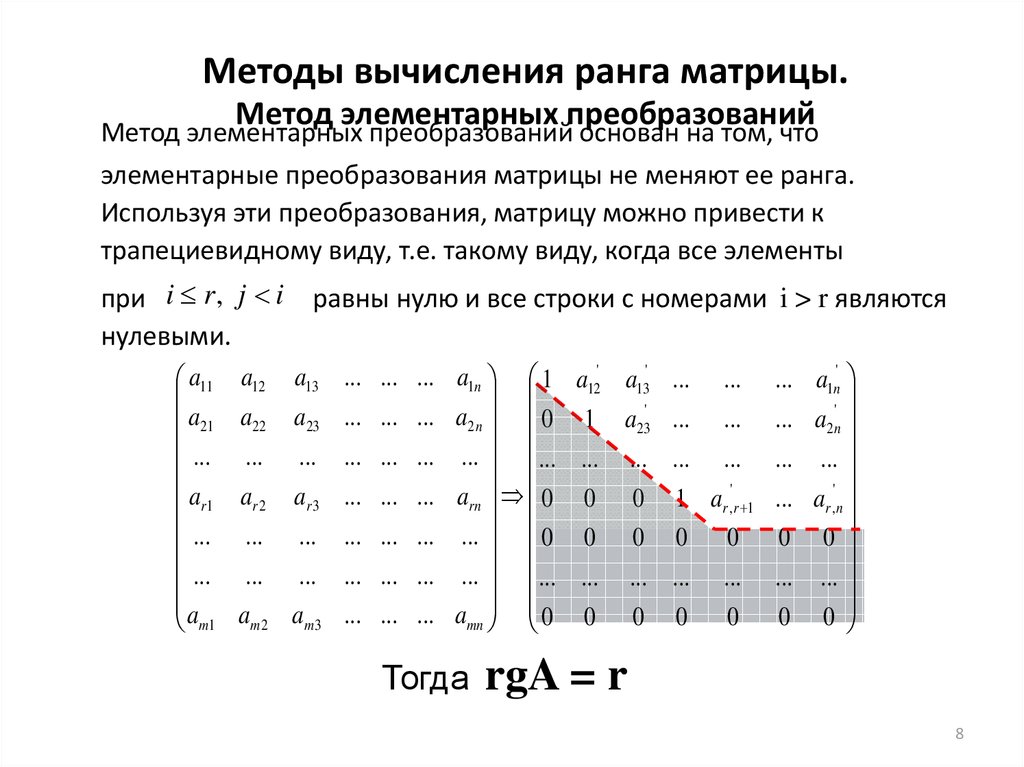
Собственные числа и вектора матриц. Методы их нахождения
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Пусть число $\lambda$ и вектор $x\in L, x\neq 0$ таковы, что $$Ax=\lambda x.\qquad\qquad\qquad\qquad\qquad(1)$$ Тогда число $\lambda$ называется собственным числом линейного оператора $A,$ а вектор $x$ собственным вектором этого оператора, соответствующим собственному числу $\lambda.$
В конечномерном пространстве $L_n$ векторное равенство (1) эквивалентно матричному равенству $$(A-\lambda E)X=0,\,\,\,\, X\neq 0.\qquad\qquad\quad\quad (2)$$
Отсюда следует, что число $\lambda$ есть собственное число оператора $A$ в том и только том случае, когда детерминант $det(A-\lambda E)=0,$ т. е. $\lambda$ есть корень многочлена $p(\lambda)=det(A-\lambda E),$ называемого характеристическим многочленом оператора $A.$ Столбец координат $X$ любого собственного вектора соответствующего собственному числу $\lambda$ есть нетривиальное решение однородной системы (2).
Примеры.
Найти собственные числа и собственные векторы линейных операторов, заданных своими матрицами.4.134. $A=\begin{pmatrix}2&-1&2\\5&-3&3\\-1&0&-2\end{pmatrix}.$
Решение.
Найдем собственные вектора заданного линейного оператора. Число $\lambda$ есть собственное число оператора $A$ в том и только том случае, когда $det(A-\lambda E)=0.$ Запишем характеристическое уравнение:
$$A-\lambda E=\begin{pmatrix}2&-1&2\\5&-3&3\\-1&0&-2\end{pmatrix}-\lambda\begin{pmatrix}1&0&0\\0&1&0\\0&0&1\end{pmatrix}=$$ $$=\begin{pmatrix}2-\lambda&-1&2\\5&-3-\lambda&3\\-1&0&-2-\lambda\end{pmatrix}.$$
$$det(A-\lambda E)=\begin{vmatrix}2-\lambda&-1&2\\5&-3-\lambda&3\\-1&0&-2-\lambda\end{vmatrix}=$$ $$=(2-\lambda)(-3-\lambda)(-2-\lambda)+3+2(-3-\lambda)+5(-2-\lambda)=$$ $$=-\lambda^3-3\lambda^2+4\lambda+12+3-6-2\lambda-10-5\lambda=-\lambda^3-3\lambda^2-3\lambda-1=0. 3=0\Rightarrow \lambda=-1.$$
3=0\Rightarrow \lambda=-1.$$
Собственный вектор для собственного числа $\lambda=-1$ найдем из системы $$(A-\lambda E)X=0, X\neq 0, \Rightarrow (A+E)X=0, X\neq 0$$
$$(A+E)X=\begin{pmatrix}2+1&-1&2\\5&-3+1&3\\-1&0&-2+1\end{pmatrix}\begin{pmatrix}x_1\\x_2\\x_3\end{pmatrix}=$$ $$=\begin{pmatrix}3x_1-x_2+2x_3\\5x_1-2x_2+3x_3\\-x_1-x_3\end{pmatrix}=0.$$
Решим однородную систему уравнений:
$$\left\{\begin{array}{lcl}3x_1-x_2+2x_3=0\\ 5x_1-2x_2+3x_3=0\\-x_1-x_3=0\end{array}\right.$$
Вычислим ранг матрицы коэффициентов $A=\begin{pmatrix}3&-1&2\\5&-2&3\\-1&0&-1\end{pmatrix}$ методом окаймляющих миноров:
Фиксируем минор отличный от нуля второго порядка $M_2=\begin{vmatrix}3&-1\\5&-2\end{vmatrix}=-6+5=-1\neq 0.$
Рассмотрим окаймляющий минор третьего порядка: $\begin{vmatrix}3&-1&2\\5&-2&3\\-1&0&-1\end{vmatrix}=6+3-4-5=0;$
Таким образом ранг матрицы $A$ равен двум.
Выберем в качестве базисного минор $M=\begin{vmatrix}3&-1\\5&-2\end{vmatrix}=-1\neq 0. $ Тогда, полагая $x_3=c,$ получаем: $$\left\{\begin{array}{lcl}3x_1-x_2+2с=0\\ 5x_1-2x_2+3с=0\end{array}\right.\Rightarrow\left\{\begin{array}{lcl}3x_1-x_2=-2c\\5x_1-2x_2=-3c\end{array}\right.$$
$ Тогда, полагая $x_3=c,$ получаем: $$\left\{\begin{array}{lcl}3x_1-x_2+2с=0\\ 5x_1-2x_2+3с=0\end{array}\right.\Rightarrow\left\{\begin{array}{lcl}3x_1-x_2=-2c\\5x_1-2x_2=-3c\end{array}\right.$$
По правилу Крамера находим $x_1$ и $x_2:$
$\Delta=\begin{vmatrix}3&-1\\5&-2\end{vmatrix}=-6+5=-1;$
$\Delta_1=\begin{vmatrix}-2c&-1\\-3c&-2\end{vmatrix}=4c-3c=c;$
$\Delta_2=\begin{vmatrix}3&-2c\\5&-3c\end{vmatrix}=-9c+10c=c;$
$x_1=\frac{\Delta_1}{\Delta}=\frac{c}{-1}=-c;$ $x_2=\frac{\Delta_2}{\Delta}=\frac{c}{-1}=-c.$
Таким образом, общее решение системы $X(c)=\begin{pmatrix}-c\\-c\\c\end{pmatrix}.$
Из общего решения находим фундаментальную систему решений: $E=X(1)=\begin{pmatrix}-1\\-1\\1\end{pmatrix}.$
С использованием фундаментальной системы решений, общее решение может быть записано в виде $X(c)=cE.$
Ответ: $\lambda=-1;$ $X=c\begin{pmatrix}-1\\-1\\1\end{pmatrix}, c\neq 0.$
{jumi[*3]}
4. 2-\lambda-1)=0\Rightarrow \lambda=2.$$
2-\lambda-1)=0\Rightarrow \lambda=2.$$
Собственный вектор для собственного числа $\lambda=2$ найдем из системы $$(A-\lambda E)X=0, X\neq 0, \Rightarrow (A-2E)X=0, X\neq 0$$
$$(A-2E)X=\begin{pmatrix}-2&-1&0\\1&-1&-2\\1&-1&-2\end{pmatrix}\begin{pmatrix}x_1\\x_2\\x_3\end{pmatrix}=$$ $$=\begin{pmatrix}-2x_1-x_2\\x_1-x_2-2x_3\\x_1-x_2-2x_3\end{pmatrix}=0.$$
Решим однородную систему уравнений:
$$\left\{\begin{array}{lcl}-2x_1-x_2=0\\ x_1-x_2-2x_3=0\\x_1-x_2-2x_3=0\end{array}\right.$$
Вычислим ранг матрицы коэффициентов $A=\begin{pmatrix}-2&-1&0\\1&-1&-2\\1&-1&-2\end{pmatrix}$ методом окаймляющих миноров:
Фиксируем минор отличный от нуля второго порядка $M_2=\begin{vmatrix}-2&-1\\1&-1\end{vmatrix}=2+1=3\neq 0.$
Рассмотрим окаймляющий минор третьего порядка: $\begin{vmatrix}-2&-1&0\\1&-1&-2\\1&-1&-2\end{vmatrix}=0;$
Таким образом ранг матрицы $A$ равен двум.
Выберем в качестве базисного минор $M=\begin{vmatrix}-2&-1\\1&-1\end{vmatrix}=3\neq 0. $ Тогда, полагая $x_3=c,$ получаем: $$\left\{\begin{array}{lcl}-2x_1-x_2=0\\ x_1-x_2-2с=0\end{array}\right.\Rightarrow\left\{\begin{array}{lcl}-2x_1-x_2=0\\x_1-x_2=2c\end{array}\right.$$
$ Тогда, полагая $x_3=c,$ получаем: $$\left\{\begin{array}{lcl}-2x_1-x_2=0\\ x_1-x_2-2с=0\end{array}\right.\Rightarrow\left\{\begin{array}{lcl}-2x_1-x_2=0\\x_1-x_2=2c\end{array}\right.$$
По правилу Крамера находим $x_1$ и $x_2:$
$\Delta=\begin{vmatrix}-2&-1\\1&-1\end{vmatrix}=2+1=3;$
$\Delta_1=\begin{vmatrix}0&-1\\2c&-1\end{vmatrix}=2c;$
$\Delta_2=\begin{vmatrix}-2&0\\1&2c\end{vmatrix}=-4c;$
$x_1=\frac{\Delta_1}{\Delta}=\frac{2c}{3};$ $x_2=\frac{\Delta_2}{\Delta}=\frac{-4c}{3}.$
Таким образом, общее решение системы $X(c)=\begin{pmatrix}\frac{2c}{3}\\-\frac{4c}{3}\\c\end{pmatrix}.$
Из общего решения находим фундаментальную систему решений: $E=X(1)=\begin{pmatrix}\frac{2}{3}\\-\frac{4}{3}\\1\end{pmatrix}.$
С использованием фундаментальной системы решений, общее решение может быть записано в виде $X(c)=cE.$ Переобозначив постоянную, $\alpha=3c,$ получаем собственный вектор $X=\alpha\begin{pmatrix}2\\-4\\3\end{pmatrix}, \alpha\neq 0. $
$
Ответ: $\lambda=2;$ $X=\alpha\begin{pmatrix}2\\-4\\3\end{pmatrix}, \alpha\neq 0.$
Домашнее задание.
Найти собственные числа и собственные векторы линейных операторов, заданных своими матрицами.
4.135. $A=\begin{pmatrix}0&1&0\\-4&4&0\\-2&1&2\end{pmatrix}.$
Ответ: $\lambda=2;$ $X=c_1\begin{pmatrix}1\\2\\0\end{pmatrix}+c_2\begin{pmatrix}0\\0\\1\end{pmatrix}, $c_1$ и $ c_2$ не равны одновременно нулю.
4.142. $A=\begin{pmatrix}1&-3&1\\3&-3&-1\\3&-5&1\end{pmatrix}.$
Ответ: $\lambda_1=-1,$ $X(\lambda_1)=c\begin{pmatrix}1\\1\\1\end{pmatrix};$ $\lambda_2=2,$ $X(\lambda_2)=c\begin{pmatrix}4\\1\\7\end{pmatrix};$ $\lambda_3=-2,$ $X(\lambda_3)=c\begin{pmatrix}2\\3\\3\end{pmatrix}, c\neq 0.$
{jumi[*4]}
Сообщество Экспонента
- Публикация
- 15.
 09.2022
09.2022
Системы управления, Другое
Видел видос на канале экспоненты по созданию топливной системы. Вопрос заключается в наличии более полного описания готового примера или соответсвующее документации. Я новичок в симулинке и ещё многого не знаю. Адекватных и раскрытых пособий по созданию гидрав…
Моделирование гидравлических систем в simulink
- Публикация
- 10.09.2022
Системы управления, Электропривод и силовая электроника, Другое
Планирую написать книгу про модельно-ориентированное программирование с автоматическим генерированием кода применительно к разработке разнообразных микропроцессорных систем управления электроприводов. В этой книге в научно-практическо-методической форме я план…
Планирую написать книгу про модельно-ориентированное программирование с автоматическим генерированием кода применительно к разработке разнообразных микропроцессорных систем управления электроприводов.
- Публикация
- 24.08.2022
Цифровая обработка сигналов, Системы связи, Математика и статистика
&…
Здесь собрана литература по комбинированным методам множественного доступа, в которых используется разделение пользователей в нескольких ресурсных пространствах.
- вопрос
- 23.08.2022
Математика и статистика, Радиолокация, Цифровая обработка сигналов
Есть записанный сигнал с датчика (синус с шумом). Как определить соотношение сигнал/шум?
Есть записанный сигнал с датчика (синус с шумом). Как определить соотношение сигнал/шум?
4 Ответа
- ЦОС
- цифровая обработка сигналов
23.08.2022
- Публикация
- 23.08.2022
Цифровая обработка сигналов, Системы связи, Математика и статистика
&. ..
..
Здесь соборана литература по методам множественного доступа с поляризационным разделением и разделением по орбитальном угловому моменту.
- Публикация
- 16.08.2022
Цифровая обработка сигналов, Системы связи, Математика и статистика
Здесь собрана литература по методам множественного доступа с пространственным разделением.
- вопрос
- 22.07.2022
Изображения и видео, Цифровая обработка сигналов, Математика и статистика, Биология, Встраиваемые системы, Глубокое и машинное обучение(ИИ), Автоматизация испытаний, ПЛИС и СнК, Системы управления, Другое
Здравствуйте. Мне нужно обработать большое количество файлов с похожими названиями, каждый блок файлов относится к отдельному объекту, например: file_1_1.txt file_1_2.txt file_1_3.txt file_1_4.txt fil…
Здравствуйте. Мне нужно обработать большое количество файлов с похожими названиями, каждый блок файлов относится к отдельному объекту, например:
file_1_1.txt
file_1_2.txt
file_1_3.txt
file_1_4.txt
fil…
Мне нужно обработать большое количество файлов с похожими названиями, каждый блок файлов относится к отдельному объекту, например:
file_1_1.txt
file_1_2.txt
file_1_3.txt
file_1_4.txt
fil…
2 Ответа
- чтение
22.07.2022
- вопрос
- 17.07.2022
Математика и статистика, Цифровая обработка сигналов
Уважаемые коллеги, добрый вечер! В общем, возникла проблема следующего характера. Имеется сигнал, достаточно большой объем точек, длительность порядка 35-40 секунд. Он представлят собой последовательн…
Уважаемые коллеги, добрый вечер! В общем, возникла проблема следующего характера. Имеется сигнал, достаточно большой объем точек, длительность порядка 35-40 секунд. Он представлят собой последовательн…
- MATLAB
- Signal Processing
17.07.2022
- вопрос
- 15.07.2022
Системы связи, Цифровая обработка сигналов
Здравствуйте! Сделала в симулинке модель сигнала с модуляцией QPSK. На входе сигнала подала последоватльномть с Генератора Бернули бинарного. Sample time: 1/8000. ПРи выводе сигнала на анализатор спек…
На входе сигнала подала последоватльномть с Генератора Бернули бинарного. Sample time: 1/8000. ПРи выводе сигнала на анализатор спек…
Здравствуйте! Сделала в симулинке модель сигнала с модуляцией QPSK. На входе сигнала подала последоватльномть с Генератора Бернули бинарного. Sample time: 1/8000. ПРи выводе сигнала на анализатор спек…
- сигнал
- модуляция
- qpsk
- скорость бита
- битрейт
- символьная скорость
- скорость передачи информации
- цифровая манипуляция
15.07.2022
- Публикация
- 13.07.2022
Цифровая обработка сигналов, Системы связи, Математика и статистика
&…
Здесь собрана литература по методам множественного доступа с кодовым разделением
Результаты поиска
Нет результатов поиска, попробуйте задать другие параметры.
Собственные числа и собственные векторы матрицы.
Определение 9.3. Вектор х называется собственным вектором матрицы А, если найдется такое число λ, что выполняется равенство: Ах = λх, то есть результатом применения к х линейного преобразования, задаваемого матрицей А, является умножение этого вектора на число λ. Само число λ называется собственным числом матрицы А.
Подставив в формулы (9.3) x`j = λxj, получим систему уравнений для определения координат собственного вектора:
.
Отсюда
. (9.5)
Эта линейная однородная система будет
иметь нетривиальное решение только в
случае, если ее главный определитель
равен 0 (правило Крамера).
получим уравнение для определения собственных чисел λ, называемое характеристическим уравнением. Кратко его можно представить так:
| A — λE | = 0, (9.6)
поскольку в его левой части стоит определитель матрицы А-λЕ. Многочлен относительно λ | A — λE| называется характеристическим многочленом матрицы А.
Свойства характеристического многочлена:
- Характеристический многочлен линейного
преобразования не зависит от выбора
базиса.
Доказательство.
(см.
(9.4)), но
следовательно,
.
 Таким образом,
не зависит от выбора базиса. Значит, и
|A-λE|
не изменяется при переходе к новому
базису.
Таким образом,
не зависит от выбора базиса. Значит, и
|A-λE|
не изменяется при переходе к новому
базису. Если матрица А линейного преобразования является симметрической (т.е. аij=aji), то все корни характеристического уравнения (9.6) – действительные числа.
Свойства собственных чисел и собственных векторов:
Если выбрать базис из собственных векторов х1, х2
(9.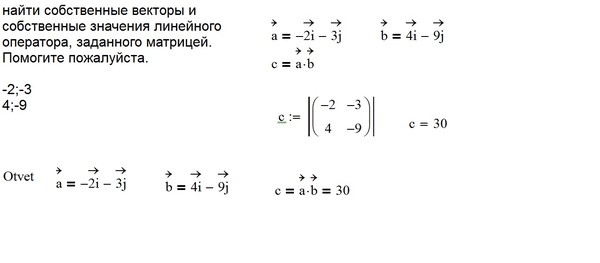 7)
Доказательство
этого свойства следует из определения
собственных векторов.
7)
Доказательство
этого свойства следует из определения
собственных векторов.
Если собственные значения преобразования А различны, то соответствующие им собственные векторы линейно независимы.
Если характеристический многочлен матрицы А имеет три различных корня, то в некотором базисе матрица А имеет диагональный вид.
Пример.
Найдем собственные числа и собственные векторы матрицы Составим характеристическое уравнение: (1- λ)(5 — λ)(1 — λ) + 6 — 9(5 — λ) — (1 — λ) — (1 — λ) = 0, λ³ — 7λ² + 36 = 0, λ1 = -2, λ2 = 3, λ3 = 6.
Найдем координаты собственных векторов,
соответствующих каждому найденному
значению λ.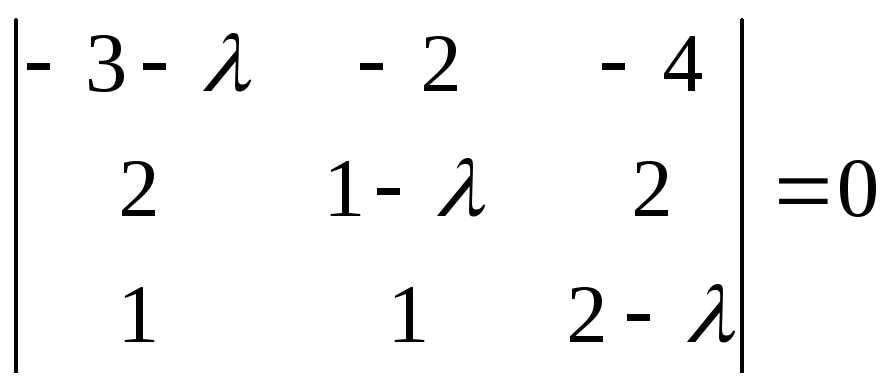 Из (9.5) следует, что если х(1)={x1,x2,x3}
– собственный вектор, соответствующий λ1=-2, то
Из (9.5) следует, что если х(1)={x1,x2,x3}
– собственный вектор, соответствующий λ1=-2, то
— совместная, но неопределенная система. Ее решение можно записать в виде
Подставив в систему (9.5) λ2=3, получим систему для определения координат второго собственного вектора — x(2)={y1,y2,y3}:
, откуда х(2)={b,-b,b} или, при условии |x(2)|=1, x(2)=
Для λ3 = 6 найдем собственный вектор x(3)={z1, z2, z3}:
, x(3)={c,2c,c} или в нормированном варианте
х(3) =
Можно
заметить, что х(1)х(2) = ab – ab = 0, x(1)x(3) = ac – ac = 0, x(2)x(3) = bc — 2bc + bc = 0. Таким
образом, собственные векторы этой
матрицы попарно ортогональны.
Таким
образом, собственные векторы этой
матрицы попарно ортогональны.
Лекция 10.
Квадратичные формы и их связь с симметричными матрицами. Свойства собственных векторов и собственных чисел симметричной матрицы. Приведение квадратичной формы к каноническому виду.
Определение 10.1. Квадратичной формой действительных переменных х1, х2,…,хn называется многочлен второй степени относительно этих переменных, не содержащий свободного члена и членов первой степени.
Примеры квадратичных форм:
(n = 2),
(n = 3). (10.1)
Напомним данное в прошлой лекции определение симметрической матрицы:
Определение 10.2. Квадратная матрица
называется симметрической, если
,
то есть если равны элементы матрицы,
симметричные относительно главной
диагонали.
Свойства собственных чисел и собственных векторов симметрической матрицы:
Все собственные числа симметрической матрицы действительные.
Доказательство (для n = 2).
Пусть матрица А имеет вид: . Составим характеристическое уравнение:
(10.2) Найдем дискриминант:
следовательно, уравнение имеет только действительные корни.
Собственные векторы симметрической матрицы ортогональны.
Доказательство (для n = 2).
Координаты собственных векторов и должны удовлетворять уравнениям:
Следовательно, их можно задать так:
. Скалярное произведение этих векторов имеет вид:
По теореме Виета из уравнения (10.2)
получим, что Подставим эти соотношения в предыдущее
равенство: Значит,
.
Замечание. В примере, рассмотренном в лекции 9, были найдены собственные векторы симметрической матрицы и обращено внимание на то, что они оказались попарно ортогональными.
Определение 10.3. Матрицей квадратичной формы (10.1) называется симметрическая матрица . (10.3)
Таким образом, все собственные числа матрицы квадратичной формы действительны, а все собственные векторы ортогональны. Если все собственные числа различны, то из трех нормированных собственных векторов матрицы (10.3) можно построить базис в трехмерном пространстве. В этом базисе квадратичная форма будет иметь особый вид, не содержащий произведений переменных.
Собственные числа и векторы — Энциклопедия по экономике
Собственные числа и векторы [c.496]Нахождение максимального собственного числа и соответствующего ему собственного вектора уравнения (С — т]21) X [c.136]
ЛА.
 5. Пусть А — п х п матрица А = (1 — а)1 + агг, где г — [1. .. 1] — п х 1 вектор. Найдите собственные числа и собственные векторы матрицы А.
[c.507]
5. Пусть А — п х п матрица А = (1 — а)1 + агг, где г — [1. .. 1] — п х 1 вектор. Найдите собственные числа и собственные векторы матрицы А.
[c.507]Собственные числа и собственные векторы. Характеристический многочлен, алгебраическая и геометрическая кратности собственного числа. Сохранение собственных чисел и их кратностей при преобразовании подобия. Неравенство между алгебраической и геометрической кратностями собственного числа. [c.11]
Показать, что МНК в ортогональной регрессии сводится к поиску собственных чисел и векторов ковариационной матрицы. Почему остаточная дисперсия равна минимальному собственному числу этой матрицы [c.17]
Как будет видно дальше, из теоремы 4, собственные значения вещественной симметрической матрицы будут вещественными. Однако в общем случае собственные значения (и собственные векторы) могут быть комплексными. В настоящей книге комплексные числа появляются только в связи с собственными значениями и собственными векторами несимметрических матриц (гл. 8). Поэтому подробное изучение комплексных матриц опускается. Все матрицы и векторы в дальнейшем будут предполагаться вещественными, за исключением тех случаев, когда специально оговорено, что они комплексные.
[c.34]
8). Поэтому подробное изучение комплексных матриц опускается. Все матрицы и векторы в дальнейшем будут предполагаться вещественными, за исключением тех случаев, когда специально оговорено, что они комплексные.
[c.34]
Пусть XQ — вещественная симметрическая матрица порядка n, a UQ — нормированный собственный вектор, соответствующий простому собственному значению АО матрицы XQ. Тогда, как известно из 8.8, для каждой матрицы X из окрестности N(XQ] матрицы XQ существуют и единственны число А = А(Х) и вектор и = и(Х), такие что [c.235]
Собственные векторы Ut (i = 1,р) матрицы S являются и собственными векторами матрицы S + kl с собственными числами ii — hi + k. Следовательно, матрица (S + kl)-1 = [c.269]
Затем проводится сравнение векторов структурной динамики актива и пассива баланса и оценка факторов, влияющих на соотношение собственных и заемных источников, а, следовательно, и на финансовую устойчивость организации. К числу важнейших факторов, обусловленных внутренними и внешними условиями работы организации, как правило, относят [c. 319]
319]
Так как собственные векторы известны, по формуле (7.29) можно определить главные компоненты. При этом обычно довольствуются меньшим, чем л, числом главных компонент, но достаточным, чтобы воспроизвести большую часть дисперсии. По мере выделения главных компонент доля общей дисперсии становится все меньше и меньше. Процедуру вычисления главных компонент прекращают в тот момент, когда собственные значения, соответствующие каждый раз наибольшим дисперсиям, становятся пренебрежимо малыми. Количество выделенных главных компонент г в общем случае значительно меньше числа объясняющих переменных т. По г главным компонентам строится матрица Z. С помощью главных компонент оцениваются параметры регрессии [c.317]
А-пих — наибольшее собственное значение (число) матрицы суждений, которое чаще всего вычисляется по следующему алгоритму сначала суммируется каждый столбец матрицы суждений, затем сумма первого столбца умножается на величину первой компоненты, рассчитанного вектора приоритетов, сумма второго столбца на вторую и т. д. затем полученные числа суммируются и получается зна-
[c.254]
д. затем полученные числа суммируются и получается зна-
[c.254]
Пусть х N(m, S). Поскольку матрица S симметрична и неотрицательно определена, то, как известно (приложение ЛА, п. 15), все ее собственные значения AJ, г = 1,…, п, неотрицательны и существует ортогональная матрица Р, такая что Л = Р ЛР, где Л — диагональная матрица, на главной диагонали которой стоят числа AJ, г = 1,…, п. Тогда вектор s = Р х — Р т в силу N5) является гауссовским, а из (МС.7) следует, что Es = 0 и V(s) = Л. Это означает, что компоненты вектора s некоррелированы, а в силу N4) и независимы. Таким образом, [c.525]
Если /= 0, то Ху == 0, а —столбец единиц. Забудем о том, что Xj = 0 и выберем наименьших характеристических корней, где k — число объясняющих переменных в модели (т. е. k = k — 1). Из k собственных векторов, соответствующих этим собственным значениям, построим матрицу [c.252]
МГК дает четкий показатель качества представления данных определенным числом главных компонент (первых собственных векторов). Аналогичный показатель можно определить и в случае нелинейного анализа. Рассмотрим отношение суммы квадратов расстоянии между входными данными слоя СОК и соответствующими нейронами слоя к общей дисперсии данных.
[c.125]
Аналогичный показатель можно определить и в случае нелинейного анализа. Рассмотрим отношение суммы квадратов расстоянии между входными данными слоя СОК и соответствующими нейронами слоя к общей дисперсии данных.
[c.125]
Структура и философия книги не изменилась. Кроме небольших изменений есть и два больших. Во-первых, мы переставили местами 12 и 13 гл. 1, поскольку необходимо обсудить комплексные числа перед собственными числами и собственными векторами, также исправлена ошибка в теореме 1.7. Во-вторых, в гл. 17 по психометрике мы переписали 8—10, относящиеся к теореме Э карта-Юн га. [c.18]
Пример 15. Найти собственные числа и обсшенные векторы матрицы [c.46]
Денежные потоки в любой организации, без преувеличения, можно назвать ее кровеносной системой. В то же время этот показатель, как никакой другой, труден для прогнозирования. Эта глава посвящена проблеме управления активами и пассивами Министерства финансов Голландии (далее — MoF). Особое внимание будет уделено оценке суммы ежемесячного валового сбора налогов. Мы рассмотрим и сравним различные методы, в том числе, и модель ARIMA — собственную разработку MoF. Так как нейронные сети превосходят другие методы по показателю среднеквадратичной ошибки (MSE) на вновь предъявляемых образцах, мы будем выделять различные типы индивидуального и совместного поведения переменных с помощью анализа первичных весов, тестов на чувствительность и выделения кластеров среди векторов весов-состояния.
[c.94]
Мы рассмотрим и сравним различные методы, в том числе, и модель ARIMA — собственную разработку MoF. Так как нейронные сети превосходят другие методы по показателю среднеквадратичной ошибки (MSE) на вновь предъявляемых образцах, мы будем выделять различные типы индивидуального и совместного поведения переменных с помощью анализа первичных весов, тестов на чувствительность и выделения кластеров среди векторов весов-состояния.
[c.94]
Третья часть является прикладным ядром книги. Она содержит правила работы с дифференциалами, список дифференциалов от важных скалярных, векторных и матричных функций (включая собственные числа, собственные векторы и обратные матрицы Мура—Пенроуза). Также приведены таблицы идентификации для матриц Гессе и Якоби. [c.16]
Проблема отыскания собственных значений и собственных векторов матриц составляет основу специального раздела алгебры далее мы еще вернемся к этому вопросу. Здесь лишь отметим один важный резу ч ьтат алгебры матриц- для симметрических матриц (1 2. 3) все и соб ственных значений являются деиствнге [ьными числами.
[c.26]
3) все и соб ственных значений являются деиствнге [ьными числами.
[c.26]
Если Аф1, то из (1.10) сдедует, что хп+ =0, в силу чего (1.9) примет вид Ах = Ах. Следовательно, Я — собственное значение матрицы А и, по нашему предположению, А собственным значением, следовательно, является числом Фробениуса. По теореме Фробениуса-Перрона у матрицы А существует неотрицательный собственный вектор хА = (хА, хп+1), соответствующий Я = 1. Очевидно, что хп+1 Ф 0, так как в противном случае из (1.9) следовало бы, что Ах = х А это противоречит тому, что число Фробениуса Ял [c.267]
ПРОИЗВОДСТВЕННЫЙ (ТЕХНОЛОГИЧЕСКИЙ) СПОСОБ — термин, обозначающий любой процесс производства того или иного продукта. Под производством, как и под обработкой, понимают здесь не только собственно производственные технологические процессы, но и хранение продуктов сырья, транспортировку, связанные с ними процессы управления и т. д. Словом, все. что превращает исходное сырье в продукт производства. Способ характеризуется набором ингредиентов, в частности нормами затрат и выпуска различных ресурсов. Это позволяет объяснить ЭВМ реальные различия между разными способами (литьем и штамповкой, перевозкой по воде и воздуху и т. Д.). ЭВМ не интересуется, какой именно технологический проаесс имеется в виду, какова температура печи или скорость резания на станке. Для нее все технологические способы различаются именно использованием затрат в разных соотношениях. Поэтому в экономико-математической модели способ производство, (иногда применяют и такой термин) характеризуется рядом присущих ему чисел (вектором) — нормами затрат и выпуска различных ресурсов в единицу времени, в том числе коэффициентами материалоемкости, трудоемкости, фондоемкости, капиталоемкости. В модель можно закладывать именно такие коэффициенты.
[c.49]
Это позволяет объяснить ЭВМ реальные различия между разными способами (литьем и штамповкой, перевозкой по воде и воздуху и т. Д.). ЭВМ не интересуется, какой именно технологический проаесс имеется в виду, какова температура печи или скорость резания на станке. Для нее все технологические способы различаются именно использованием затрат в разных соотношениях. Поэтому в экономико-математической модели способ производство, (иногда применяют и такой термин) характеризуется рядом присущих ему чисел (вектором) — нормами затрат и выпуска различных ресурсов в единицу времени, в том числе коэффициентами материалоемкости, трудоемкости, фондоемкости, капиталоемкости. В модель можно закладывать именно такие коэффициенты.
[c.49]
В соответствии с теоремой Фробениуса-Перрона максимальное по модулю собственное значение АА неотрицательной квадратной матрицы А > О неотрицательно, а среди собственных векторов, принадлежащих ЛА, имеется неотрицательный вектор. В случае А > О все неотрицательные собственные векторы матрицы А положительны и принадлежат только ее максимальному по модулю собственному значению ЛА. Кроме того, в этом случае любые два положительных собственных вектора у и х отличаются лишь числовым множителем, т.е. у= ах. Максимальное по модулю собственное значение ЛА неотрицательной матрицы А называется числом Фробениуса матрицы А, а соответствующий ему неотрицательный собственный вектор — вектором Фробениуса для матрицы А.
[c.11]
Кроме того, в этом случае любые два положительных собственных вектора у и х отличаются лишь числовым множителем, т.е. у= ах. Максимальное по модулю собственное значение ЛА неотрицательной матрицы А называется числом Фробениуса матрицы А, а соответствующий ему неотрицательный собственный вектор — вектором Фробениуса для матрицы А.
[c.11]
НАХОЖДЕНИЕ СОБСТВЕННЫХ ВЕКТОРОВ И СОБСТВЕННЫХ ЗНАЧЕНИЙ КВАДРАТНОЙ МАТРИЦЫ
НАХОЖДЕНИЕ СОБСТВЕННЫХ ВЕКТОРОВ И СОБСТВЕННЫХ ЗНАЧЕНИЙ КВАДРАТНОЙ МАТРИЦЫНа предыдущую страницу На главную На следующую страницу
НАХОЖДЕНИЕ СОБСТВЕННЫХ ВЕКТОРОВ И СОБСТВЕННЫХ ЗНАЧЕНИЙ КВАДРАТНОЙ МАТРИЦЫ
6.1 Собственные векторы и собственные значения квадратной матрицы
6.2 Встроенные функции MathCad для вычисления собственных векторов и собственных значений матриц
6.3 Частичные проблемы собственных значений
6.4 Задания
6.
 1 Собственные векторы и собственные значения квадратной матрицы
1 Собственные векторы и собственные значения квадратной матрицы
Большое число научно технических задач, а также некоторых исследований в области вычислительной математики требуют нахождения собственных значений и собственных векторов матриц.
Вектор x=(x1,x2…xn) ϵ En называется собственным вектором матрицы А=(aij)nn, если существует такое число λ ϵ R, что имеет место равенство:
(1)
Число λ называется собственным значением матрицы А.
Поскольку при умножении собственных векторов на скаляр он остается собственным вектором той же матрицы, его можно нормировать. В частности, каждую координату собственного вектора можно разделить на максимальную из них или на длину вектора. В последнем случае получится единичный собственный вектор.
Характеристической матрицей С данной матрицы А называется матрица вида:
(2)
где Е – единичная матрица.
Легко видеть, что равенство (1) можно записать в виде:
(3)
Если перейти к координатной форме записи вектора x, то
(4)
Системы (3) и (4) являются однородной системой n линейных уравнений c n неизвестными. Она имеет ненулевое решение лишь тогда, когда её определитель равен нулю.
(5)
Определитель матрицы С является многочленом n-ной степени относительно λ
(6)
называется характеристическим многочленом. Корни этого многочлена являются собственными значениями матрицы А.
Для нахождения собственных векторов матрицы требуется решить систему линейных алгебраических уравнений, решение которой не единственно.
Из линейной алгебры известно, что в этом случае структура общего решения системы имеет следующий вид: одно или несколько неизвестных, называемых свободными,
могут принимать любые значения, а общие неизвестные выражаются через свободные. Число свободных неизвестных равно числу уравнений системы являющихся следствием остальных уравнений, т.е.,
Число свободных неизвестных равно числу уравнений системы являющихся следствием остальных уравнений, т.е.,
(7)
где m – число свободных неизвестных; n – размерность системы.
На практике, если свободное неизвестное одно (что часто бывает), его полагают равным некоторому числу, например 1. После этого находят остальные неизвестные (компоненты вектора), которые определяются однозначно. Эта процедура не влияет на результат решения задачи, поскольку уже отмечалось, что собственные векторы находятся с точностью до постоянного множителя.
Пример. Вычислить собственные числа и собственные векторы матрицы А.
Решение. Составим характеристический многочлен:
Найдем корни этого многочлена:
Для нахождения собственных векторов f1 и f2, соответствующих собственным значениям λ1 и λ2, составим систему уравнений для каждого из них:
или в координатной форме:
Замечаем, что уравнения линейно зависимы. Поэтому оставляем лишь одно из них. Из первого уравнения следует, что
x2= – x1. Неизвестное x1 можно считать свободным. Полагаем
x1=1, тогда x2= – 1 и, собственный вектор, соответствующий собственному значению
λ1=2, имеет вид f1=(1, –1) или f1=l1 – l2, где
l1, l2 – единичные орты выбранной базисной системы.
Поэтому оставляем лишь одно из них. Из первого уравнения следует, что
x2= – x1. Неизвестное x1 можно считать свободным. Полагаем
x1=1, тогда x2= – 1 и, собственный вектор, соответствующий собственному значению
λ1=2, имеет вид f1=(1, –1) или f1=l1 – l2, где
l1, l2 – единичные орты выбранной базисной системы.
Аналогично находим второй собственный вектор, соответствующий собственному значению λ2 = 5
Отсюда x1=1; x2=2.
вектор f1 нормирован, нормируем также вектор f2, разделив его компоненты на большую из них. Получим:
Можно так же привести векторы к единичной длине, разделив их компоненты на значения модулей векторов:
,
Мы рассмотрели простейший пример вычисления собственных значений векторов для матрицы 2-го порядка. Нетрудно также привести подобное решение для матрицы 3-го порядка и для некоторых весьма специальных случаев.
Нетрудно также привести подобное решение для матрицы 3-го порядка и для некоторых весьма специальных случаев.
В общем случае, особенно для матриц высокого порядка, задача нахождения их собственных значений и собственных векторов, называемая полной проблемой собственных значений, значительно более сложная.
На первый взгляд может показаться, что вопрос сводится к вычислению корней многочлена (6). Однако эта задача осложнена тем, что среди собственных значений часто встречаются кратные. И, кроме того, для произвольной матрицы непросто вычислить сами коэффициенты характеристического многочлена.
6.2 Встроенные функции MathCad для вычисления собственных векторов и собственных значений матриц
Для решения задач на собственные векторы и собственные значения в Mathcad встроено несколько функций, реализующих довольно сложные вычислительные алгоритмы:
— eigenvals(A) – вычисляет вектор, элементами которого являются собственные значения матрицы А;
— eigenvecs(A)– вычисляет матрицу, содержащую нормированные собственные векторы, соответствующие собственным значениям матрицы А.
Пример. Найти собственные значения и собственные векторы матрицы с помощью MathCad.
1. Задаем системную переменную и матрицы А (исходную) и Е (единичную):
2. Находим собственные значения и собственные векторы матрицы А с помощью встроенных функций MathCad:
3. Находим собственные значения и собственные векторы матрицы А вручную. Для этого составляем характеристический определитель и вычисляем характеристический полином:
4. Приравниваем его нулю нажатием Ctrl+= (получаем характеристическое уравнение):
5. Находим корни характеристического уравнения с помощью символьных вычислений (подсвечиваем λ нажатием мыши и выбираем в меню Символы→Переменные→Вычислить, затем нажимаем символ =)
6. Присваиваем
Это и есть собственные значения матрицы А.
7. Далее найдем собственные векторы матрицы А вручную. Для этого запишем левую часть системы уравнений:
где x1, x2 – элементы собственных векторов, соответствующих собственным значениям λ.
8. Получим собственный вектор, соответствующий собственному значению λ1:
Запишем каждое уравнение системы отдельно (приравниваем их нулю нажатием Ctrl+=)
Из первого уравнения выразим x2 (подсвечиваем λ нажатием мыши и выбираем в меню Символы→Переменные→Вычислить)
Принимаем x1=0.869 (согласно пункту 2)
Тогда x2=0.5688×0.869=0.494
Собственный вектор, соответствующий собственному значению λ1:
9. Получим собственный вектор, соответствующий собственному значению λ2:
Запишем каждое уравнение системы отдельно (приравниваем их нулю нажатием Ctrl+=)
Из первого уравнения выразим x2 (подсвечиваем λ нажатием мыши и выбираем в меню Символы→Переменные→Вычислить)
Принимаем x1=-0. 604 (согласно пункту 2)
604 (согласно пункту 2)
Тогда x2= –1.319×(–0.604)=0.797
Собственный вектор, соответствующий собственному значению λ2:
Для собственных векторов матрицы справедливы следующие утверждения:
1. Собственные векторы матрицы, отвечающие различным собственным значениям, линейно независимы.
2. Если число различных корней матрицы n-го порядка равно n, то в пространстве En существует базис из собственных векторов матрицы А (непосредственно следует из свойства 1).
3. Базис из собственных векторов матрицы А существует в том и только в том случае, когда сумма размерностей собственных подпространств равна n. Такая матрица называется матрицей простой структуры. Если A – матрица простой структуры, то любой вектор из En является линейной комбинацией линейно независимой системы собственных векторов этой матрицы.
4. Матрица простой структуры подобна диагональной матрице, т. е.
, такая что
е.
, такая что
(8)
где – собственные значения матрицы .
5. Все корни характеристического многочлена симметрической матрицы действительны, т.е.
6. Собственные векторы симметрической матрицы, отвечающие различным собственным значениям, ортогональны.
7. Для симметрической матрицы A в пространстве En существует ортонормированный базис из собственных векторов.
Решим еще два примера на нахождение собственных векторов и собственных значений матрицы.
Пример 1. Найти собственные векторы и собственные значения матрицы
Решение. Находим корни характеристического многочлена
==
,
Ищем собственные векторы с собственным значением λ=1, как решение системы :
Общее решение системы . Фундаментальная система решений или базис пространства решений
,
Собственный вектор для λ=-2 находим из системы
Ответ.
, , – собственные векторы.
Пример 2. Найти ортонормированный базис из собственных векторов симметрической матрицы A
Находим характеристический многочлен матрицы A
Целые корни ищем среди делителей свободного члена:
Найдем собственные векторы с собственным значением λ= -1
Базис в пространстве решений
Так как мы ищем ортонормированный базис, то ортогонализуем систему f1, f2. Получаем , , , , , .
Нашли ортонормированный базис в собственном подпространстве с собственным значением λ= -1. Найдем собственный вектор для собственного значения λ=5
Решаем методом Гаусса, получим , ,
Ответ. Искомый ортонормированный базис
Преобразование подобия (8) можно использовать для упрощения исходной матрицы, а задачу вычисления её собственных значений свести к аналогичной задаче для более простой матрицы. Очевидно, самым лучшим упрощением исходной матрицы было бы приведение её к треугольному виду:
Очевидно, самым лучшим упрощением исходной матрицы было бы приведение её к треугольному виду:
Тогда характеристическая матрица С так же имела бы треугольный вид. Как известно, определитель треугольной матрицы равен произведению ее диагональных элементов, поэтому характеристический многочлен в этом случае имеет вид:
(9)
Собственные значения матрицы, равные корням этого многочлена, можно получить сразу.
, (10)
Таким образом, собственные значения треугольной матрицы равны её диагональным элементам.
Некоторые типы матриц удается привести к треугольному виду с помощью преобразований подобия. В частности, симметрическую матрицу можно привести к диагональному виду. На практике часто используется приведение симметрической матрицы к трехдиагональному виду.
Существует ряд методов, основанных на преобразовании подобия, позволяющие привести исходную матрицу к более простой структуре.
6.3 Частичные проблемы собственных значений
Часто в практических вычислениях нужны не все собственные значения, а лишь некоторые из них.
Для решения частичной проблемы собственных значений, состоящей в определении одного или нескольких собственных значений и соответствующих им собственных векторов, обычно используют итерационные методы. Строится такой итерационный процесс, который сходится к одному собственному значению и собственному вектору, причем используемые алгоритмы весьма экономичны.
Построим итерационный процесс, применяя метод итераций к решению систем уравнений
(11)
Представим (11) через вспомогательный вектор у:
(12)
Пусть х(0) – начальное приближение собственного вектора х, причем собственные векторы на каждой итерации нормированы, так что
Используя соотношение (12), получим:
или, применяя умножение обеих частей равенства скалярно на х(0), получим , учитывая, что , запишем
Следующие приближения можно вычислить, нормируя у(1). Окончательно итерационный процесс записывается в виде:
Окончательно итерационный процесс записывается в виде:
(13)
Процесс (13) продолжается до установления постоянных значений λ и х. При этом нужно учесть, что, применяя критерии завершения итераций, следует проверять близость векторов и .
Можно показать, что найденное значение λ является наибольшим по модулю собственным значением данной матрицы А, а х – соответствующим ему вектором.
Скорость сходимости этого итерационного процесса зависит от удачного выбора начального приближения.
Для решения системы (11) можно использовать и другие итерационные методы. В некоторых задач нужно искать не наибольшие, а наименьшие по модулю собственные значения матрицы А. В этом случае можно умножить (11) на матрицу А-1:
(14)
(15)
Следовательно, 1/λ является собственным значением обратной матрицы, и задача (15) отличается от ранее рассмотренной тем, что здесь будет вычисляться наибольшее
по модулю собственное значение1/λ матрицы А–1, что будет достигнуто при наименьшем по модулю λ.
6.4 Задания
1. Найти собственные числа и собственные векторы матрицы А (упражнение 1).
2. Доказать, что все собственные значения диагональной матрицы равны ее диагональным элементам.
3. Найти собственные значения треугольной матрицы.
4. Доказать, что нуль является собственным значением матрицы А тогда и только тогда, когда А – вырожденная матрица.
5. Доказать, что собственные значения матрицы А–1 обратны собственным значениям матрицы А.
6. Собственные значения матрицы А равны
. Найти все собственные значения матриц:
а) 3А, б) А-2Е.
Упражнение 1 выполняется по вариантам, остальные – без вариантов.
Таблица 6
7. В соответствии с выбранным вариантом (табл. 7) найти собственные значения и собственные вектора матриц A и B с использованием математического редактора MathCad. Осуществить проверку правильности нахождения собственных значений и собственных векторов матриц с помощью встроенных функций MathCad
eigenvals() и eigenvecs().
Таблица 7
Наверх
На предыдущую страницу На главную На следующую страницу
Физический смысл собственных векторов и собственных значений
Теги: Собственные значения Вектор признаков
Адрес перепечатки:http://blog.csdn.net/sunshine_in_moon/article/details/45749691
Эта статья переведена из Жиху Даниэля.
Из определения Ax = cx: A — матрица, c — собственное значение, а x — собственный вектор.
Матрица A, умноженная на x, означает, что вектор x преобразован (повернут или растянут) (линейное преобразование), и эффект этого преобразования — постоянная c, умноженная на вектор x ( То есть только растяжка).
Обычно мы находим собственные значения и собственные векторы, чтобы выяснить, какие векторы (конечно, собственные векторы) могут быть растянуты только матрицей и до какой степени (собственные значения) размер). Значение этого состоит в том, чтобы четко увидеть, в каких аспектах матрица может дать наибольший эффект (мощность), а также классифицировать, обсудить и изучить каждый сгенерированный собственный вектор (обычно изучаются те, которые имеют наибольшие собственные значения).
Обновление и 2015.12.02 Я случайно увидел это введение сегодня, и мне кажется, что оно очень ясное, и я поделюсь им с вами!
Подключиться:http://jingyan.baidu.com/article/3065b3b68c6bb6becff8a488.html
Я изучал матрицы в колледжах. Кажется ли матрица слишком абстрактной, неясной и трудной для понимания? Она не имеет ничего общего с реальной жизнью. Среди них матрица имеет свойство, называемое собственным вектором, если вы выучили матрицу , Я спрошу об этом, но то, что он делает, не сказано в книге, но это весьма полезно, но где это используется, каждый может только сказать, что я не знаю.Здесь я объясню вам геометрический смысл вектора признаков. Дайте всем знать с первого взгляда
Инструменты / материалы
бумага
ручка
Не забывайте использовать свой мозг
Метод / шаг
Если вектор v является собственным вектором квадратной матрицы A, он должен быть выражен в следующей форме:
В это время λ называется собственным значением, соответствующим собственному вектору v, а группа собственных векторов матрицы представляет собой группу ортогональных векторов. Разложение по собственным значениям состоит в разложении матрицы в следующую форму:
Разложение по собственным значениям состоит в разложении матрицы в следующую форму:
где Q — матрица, составленная из собственных векторов этой матрицы A, Σ — диагональная матрица, а каждый элемент на диагонали — собственное значение. Прежде всего, должно быть ясно, что матрица на самом деле является линейным преобразованием, потому что вектор, полученный путем умножения матрицы на вектор, фактически эквивалентен выполнению линейного преобразования этого вектора. Например, рассмотрим следующую матрицу:
Фактически это соответствует линейному преобразованию в следующей форме:
Потому что результат умножения этой матрицы M на вектор (x, y):
Вышеупомянутая матрица является симметричной, поэтому это преобразование является преобразованием растяжения в направлениях осей x и y (каждый диагональный элемент будет растянут и преобразован в одном измерении, когда значение> 1, он растягивается Длинная, укороченная, когда значение <1), когда матрица не симметрична, предположим, что матрица выглядит так:
Он описывает следующее преобразование:
Фактически это преобразование растяжения оси на плоскости (как показано синей стрелкой). На рисунке синяя стрелка является наиболее важным направлением изменения ( Может быть более одного направления изменения.) Если мы хотим описать трансформацию, мы можем описать основное направление изменения. Давайте посмотрим на предыдущую формулу разложения на собственные значения. Разложенная Σ-матрица представляет собой диагональную матрицу. Собственные значения упорядочены от больших к меньшим. Собственные векторы, соответствующие этим собственным значениям, описывают направление изменения матрицы. (От основных изменений к незначительным)
На рисунке синяя стрелка является наиболее важным направлением изменения ( Может быть более одного направления изменения.) Если мы хотим описать трансформацию, мы можем описать основное направление изменения. Давайте посмотрим на предыдущую формулу разложения на собственные значения. Разложенная Σ-матрица представляет собой диагональную матрицу. Собственные значения упорядочены от больших к меньшим. Собственные векторы, соответствующие этим собственным значениям, описывают направление изменения матрицы. (От основных изменений к незначительным)
Когда матрица является многомерной, тогда эта матрица представляет собой линейное преобразование в многомерном пространстве. Это линейное изменение не может быть представлено изображениями, но возможно, что это преобразование также имеет множество направлений преобразования. Мы используем функции Первые N собственных векторов, полученных разложением значений, соответствуют наиболее важным N направлениям изменения этой матрицы. Мы можем аппроксимировать эту матрицу (преобразование), используя первые N изменяющихся направлений. Это то, что я сказал ранее: извлеките из этой матрицы наиболее важные особенности. Подводя итог, можно сказать, что разложение по собственным значениям позволяет получить собственные значения и собственные векторы. Собственное значение указывает, насколько важен признак, а собственный вектор указывает, что это за признак. Каждый собственный вектор можно понимать как линейное подпространство. С этими линейными подпространствами можно многое сделать. Однако разложение по собственным значениям также имеет много ограничений: например, преобразованная матрица должна быть квадратной матрицей.
Это то, что я сказал ранее: извлеките из этой матрицы наиболее важные особенности. Подводя итог, можно сказать, что разложение по собственным значениям позволяет получить собственные значения и собственные векторы. Собственное значение указывает, насколько важен признак, а собственный вектор указывает, что это за признак. Каждый собственный вектор можно понимать как линейное подпространство. С этими линейными подпространствами можно многое сделать. Однако разложение по собственным значениям также имеет много ограничений: например, преобразованная матрица должна быть квадратной матрицей.
Примечания
Последняя полоса — это ключ, вы должны внимательно посмотреть
На этой основе понять PCA намного проще.
Интеллектуальная рекомендация
LeetCode — path-sum-ii
тема: Given a binary tree and a sum, find all root-to-leaf paths where each path’s sum equals the given sum. For example: Given the below binary tree andsum = 22, return Значение: Вот тот же путь к су. ..
..
Как использовать Ajax, как добиться асинхронного
layout: post title: Как использовать Ajax, как добиться асинхронного подзаголовок: как использовать ajax date: 2018-10-31 author: LY header-img: img/post-bg-debug.png catalog: true tags: — java -синхр…
Разверните приложение ASP.NET Core в производственной среде (CentOS7)
Прочтите содержание Описание окружающей среды Подготовьте приложение ASP.NET Core установкаCentOS7 Установите .NET Core SDK для CentOS7. Развертывание приложения ASP.NET Core Настроить Nginx Настроить…
Ubuntu 18.04 с (Гао) набор (джи) и украсить
1. Сначала установите систему (процесс пропущен) Сравните окончательные визуализации: 2. Украсить (1) Терминальное благоустройство Установите Zsh: Установите oh-my-zsh: Изменить предпочтения: Изменить…
Распределенный | Сравнительный анализ того, как MyCat мигрирует в алгоритм шардинга DBLE: хэширование
Об авторе Пользователь Zhong Yue-Senior DBLE Старший архитектор юниверской линии использует DBLE в крупных ключевых проектах. Вечный практикующий, который круглый год запутывается в MySQL и часто испо…
Вечный практикующий, который круглый год запутывается в MySQL и часто испо…
Вам также может понравиться
NunMPY (3) — Пользовательский тип данных: Структурированный массив
NunMPY (3) — Пользовательский тип данных: Структурированный массив Эта статья представляет метод типа данных в Нампах, чтобы решить эту проблему, что тип данных элемента должен быть последовательным в…
Oracle использует перестановку и комбинацию для расчета максимальной просадки
Что тебе нужно знать: Максимальная скорость восстановления: максимальное значение диапазона восстановления доходности, когда историческая стоимость продукта отодвигается назад в любой исторический мом…
Краткое изложение трехмерных проблем развития на основе мобильного телефона на основе цезия
Сейчас цезия становится более пожарным, на основе его веб-версий. Разработка очень, технология относительно зрелая, но разработка мобильного терминала намного меньше, поскольку потребности в проекте н. ..
..
Рамочная среда робота
Справочная документация:http://www.cnblogs.com/fnng/p/3871712.html Требуемая среда: 1、Python: https://www.python.org/ РЧ-каркас основан на Python, поэтому у вас должна быть среда Python. 2、Robot frame…
Система установки Android и яркость экрана приложений
…
7.1: Собственные значения и собственные векторы матрицы
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 14538
- Кен Каттлер
- Университет Бригама Янга via Lyryx
Результаты
- Описать собственные значения геометрически и алгебраически.
- Найдите собственные значения и собственные векторы для квадратной матрицы.

Спектральная теория относится к изучению собственных значений и собственных векторов матрицы. Он имеет фундаментальное значение во многих областях и является предметом нашего изучения в этой главе.
Определение собственных векторов и собственных значений
В этом разделе мы будем работать со всем набором комплексных чисел, обозначаемых \(\mathbb{C}\). Напомним, что действительные числа \(\mathbb{R}\) содержатся в комплексных числах, поэтому обсуждения в этом разделе применимы как к действительным, так и к комплексным числам.
Чтобы проиллюстрировать идею, лежащую в основе того, что будет обсуждаться, рассмотрим следующий пример.
Пример \(\PageIndex{1}\): собственные векторы и собственные значения
Пусть \[A = \left[ \begin{array}{rrr} 0 & 5 & -10 \\ 0 & 22 & 16 \\ 0 & -9 & -2 \end{array} \right]\nonumber\] Вычислить произведение \(AX\) для \[X = \left[ \begin{array}{r} 5 \\ -4 \\ 3 \end{array} \right], X = \left[ \begin{array}{r} 1 \\ 0 \\ 0 \end{array} \right]\nonumber\] Что вы заметили в \(AX\ ) в каждом из этих продуктов?
Решение
Сначала вычислите \(AX\) для \[X =\left[ \begin{array}{r} 5 \\ -4 \\ 3 \end{array} \right]\nonumber\]
Этот продукт задается \[AX = \left[ \begin{array}{rrr} 0 & 5 & -10 \\ 0 & 22 & 16 \\ 0 & -9 & -2 \end{array} \right ] \left[ \begin{array}{r} -5 \\ -4 \\ 3 \end{массив} \right] = \left[ \begin{array}{r} -50 \\ -40 \\ 30 \end{array} \right] =10\left[ \begin{array}{r} -5 \\ -4 \\ 3 \end{array} \right]\nonumber\]
В этом случае произведение \(AX\) привел к вектору, который равен \(10\), умноженному на вектор \(X\). Другими словами, \(AX=10X\).
Другими словами, \(AX=10X\).
Посмотрим, что будет в следующем продукте. Вычислить \(AX\) для вектора \[X = \left[ \begin{array}{r} 1 \\ 0 \\ 0 \end{array} \right]\nonumber\]
Этот продукт определяется выражением \[AX = \left[ \begin{array}{rrr} 0 & 5 & -10 \\ 0 & 22 & 16 \\ 0 & -9 & -2 \end{array} \right] \left[ \begin {array}{r} 1 \\ 0 \\ 0 \end{array} \right] = \left[ \begin{array}{r} 0 \\ 0 \\ 0 \end{array} \right] =0 \left[ \begin{array}{r} 1 \\ 0 \\ 0 \end{массив} \right]\nonnumber\]
В этом случае произведение \(AX\) дает вектор, равный \(0\), умноженному на вектор \(X\), \(AX=0X\).
Возможно, эта матрица такова, что \(AX\) приводит к \(kX\) для каждого вектора \(X\). Однако рассмотрим \[\left[ \begin{array}{rrr} 0 & 5 & -10 \\ 0 & 22 & 16 \\ 0 & -9 & -2 \end{array} \right] \left[ \ begin{array}{r} 1 \\ 1 \\ 1 \end{array} \right] = \left[ \begin{array}{r} -5 \\ 38 \\ -11 \end{array} \right ]\nonumber \] В этом случае \(AX\) не приводит к вектору формы \(kX\) для некоторого скаляра \(k\).
В первых двух продуктах, рассчитанных в примере \(\PageIndex{1}\), есть нечто особенное. Обратите внимание, что для каждого \(AX=kX\), где \(k\) — некоторый скаляр. Когда это уравнение выполняется для некоторых \(X\) и \(k\), мы называем скаляр \(k\) собственным значением оператора \(A\). Мы часто используем специальный символ \(\lambda\) вместо \(k\), когда говорим о собственных значениях. В примере \(\PageIndex{1}\) значения \(10\) и \(0\) являются собственными значениями матрицы \(A\), и мы можем пометить их как \(\lambda_1 = 10\) и \(\лямбда_2 = 0\).
Когда \(AX = \lambda X\) для некоторого \(X \neq 0\), мы называем такое \(X\) собственным вектором матрицы \(A\). Собственные векторы \(A\) связаны с собственным значением. Следовательно, если \(\lambda_1\) является собственным значением \(A\) и \(AX = \lambda_1 X\), мы можем пометить этот собственный вектор как \(X_1\). Заметим еще раз, что для того, чтобы быть собственным вектором, \(X\) должен быть ненулевым.
Собственные векторы также имеют геометрическое значение. Когда у вас есть ненулевой вектор , который при умножении на матрицу дает другой вектор, параллельный первому или равный 9{n}\) будет ненулевым вектором , для которого
\[AX=\lambda X \label{eigen1}\] для некоторого скаляра \(\lambda .\) Тогда \(\lambda\) называется собственное значение матрицы \(A\) и \(X\) называется собственным вектором матрицы \(A\), ассоциированным с \(\lambda\), или \(\lambda\)-собственным вектором \( А\).
Множество всех собственных значений \(n\times n\) матрицы \(A\) обозначается \(\sigma \left( A\right)\) и называется спектром \ (А.\)
Собственными векторами матрицы \(А\) являются те векторы \(Х\), для которых умножение на \(А\) дает вектор в том же или противоположном направлении, что и \(Х\). Поскольку нулевой вектор \(0\) не имеет направления, это не имеет смысла для нулевого вектора. Как отмечалось выше, \(0\) никогда не может быть собственным вектором.
Как отмечалось выше, \(0\) никогда не может быть собственным вектором.
Рассмотрим собственные векторы более подробно. Предположим, \(X\) удовлетворяет \(\eqref{eigen1}\). Тогда \[\begin{array}{c} AX — \lambda X = 0 \\ \mbox{or} \\ \left( A-\lambda I\right) X = 0 \end{array}\nonumber\] для некоторого \(X \neq 0.\) Эквивалентно вы можете написать \(\left( \lambda I-A\right)X = 0\), что используется чаще. Следовательно, когда мы ищем собственные векторы, мы ищем нетривиальные решения этой однородной системы уравнений!
Напомним, что решения однородной системы уравнений состоят из основных решений и линейных комбинаций этих основных решений. В этом контексте мы называем основные решения уравнения \(\left( \lambda I — A\right) X = 0\) основными собственными векторами . Отсюда следует, что любая (ненулевая) линейная комбинация основных собственных векторов снова является собственным вектором.
Предположим, что матрица \(\left(\lambda I — A\right)\) обратима, так что \(\left(\lambda I — A\right)^{-1}\) существует. {-1}0 \\ &= 0\end{aligned}\] Это утверждает, что \(X=0\). Однако мы потребовали, чтобы \(X \neq 0\). Поэтому \(\left(\lambda I — A\right)\) не может иметь обратного!
{-1}0 \\ &= 0\end{aligned}\] Это утверждает, что \(X=0\). Однако мы потребовали, чтобы \(X \neq 0\). Поэтому \(\left(\lambda I — A\right)\) не может иметь обратного!
Напомним, что если матрица необратима, то ее определитель равен \(0\). Следовательно, мы можем заключить, что \[\det \left( \lambda I — A\right) =0 \label{eigen2}\] Обратите внимание, что это эквивалентно \(\det \left(A- \lambda I \right) =0\).
Выражение \(\det \left( \lambda I-A\right)\) является многочленом (от переменной \(x\)) называемым характеристическим полиномом \(A\) , и \(\det \left( \lambda I-A\right) =0\) называется характеристическим уравнением . По этой причине мы можем также ссылаться на собственные значения \(A\) как на характеристических значений , но первое часто используется по историческим причинам.
Следующая теорема утверждает, что корни характеристического многочлена являются собственными значениями \(A\). Таким образом, когда выполняется [eigen2], \(A\) имеет ненулевой собственный вектор.
Теорема \(\PageIndex{1}\): существование собственного вектора
Пусть \(A\) — матрица \(n\times n\) и пусть \(\det \left( \lambda I — A\right) =0\) для некоторого \(\lambda \in \mathbb{C}\). 9{n}\) такое, что \(AX=\lambda X\).
- Доказательство
Для \(A\) матрицы \(n\times n\) метод разложения Лапласа показывает, что \(\det \left( \lambda I — A \right)\) является полиномом степени \(n .\) Таким образом, уравнение \(\eqref{eigen2}\) имеет решение \(\lambda \in \mathbb{C}\) по основной теореме алгебры. Тот факт, что \(\lambda\) является собственным значением, остается в качестве упражнения.
Нахождение собственных векторов и собственных значений
Теперь, когда собственные значения и собственные векторы определены, мы изучим, как их найти для матрицы \(A\).
Сначала рассмотрим следующее определение.
Определение \(\PageIndex{2}\): Кратность собственного значения
Пусть \(A\) будет матрицей \(n \times n\) с характеристическим полиномом, заданным выражением \(\det \left( \lambda Я — А\право)\). Тогда кратность собственного значения \(\lambda\) оператора \(A\) — это количество раз, когда \(\lambda\) встречается как корень этого характеристического многочлена. 92 = 0\) и найти \(\лямбда\). Мы находим, что \(\lambda = 2\) — это корень, который встречается дважды. Следовательно, в этом случае \(\lambda = 2\) является собственным значением \(A\) кратности, равной \(2\).
Тогда кратность собственного значения \(\lambda\) оператора \(A\) — это количество раз, когда \(\lambda\) встречается как корень этого характеристического многочлена. 92 = 0\) и найти \(\лямбда\). Мы находим, что \(\lambda = 2\) — это корень, который встречается дважды. Следовательно, в этом случае \(\lambda = 2\) является собственным значением \(A\) кратности, равной \(2\).
Теперь мы подробно рассмотрим, как найти собственные значения и собственные векторы для матрицы \(A\). Используемые шаги суммированы в следующей процедуре.
Процедура \(\PageIndex{1}\): нахождение собственных значений и собственных векторов
Пусть \(A\) — матрица \(n \times n\).
- Сначала найдите собственные значения \(\lambda\) оператора \(A\), решив уравнение \(\det \left( \lambda I -A \right) = 0\).
- Для каждого \(\lambda\) найти основные собственные векторы \(X \neq 0\), найдя основные решения \(\left( \lambda I — A \right) X = 0\).
Чтобы проверить свою работу, убедитесь, что \(AX=\lambda X\) для каждого \(\lambda\) и связанного с ним собственного вектора \(X\).
Мы рассмотрим эти шаги в следующем примере.
Пример \(\PageIndex{2}\): поиск собственных значений и собственных векторов
Пусть \(A = \left[ \begin{array}{rr} -5 & 2 \\ -7 & 4 \end{array} \right]\). Найдите его собственные значения и собственные векторы.
Решение
Мы будем использовать процедуру \(\PageIndex{1}\). Сначала мы находим собственные значения \(A\), решая уравнение \[\det \left( \lambda I — A \right) =0\nonumber \]
Это дает \[\begin{aligned} \det \ left( \lambda \left[ \begin{array}{rr} 1 & 0 \\ 0 & 1 \end{array} \right] — \left[ \begin{array}{rr} -5 & 2 \\ — 7 & 4 \end{array} \right] \right) &= 0 \\ \\ \det \left[ \begin{array}{cc} \lambda +5 & -2 \\ 7 & \lambda -4 \ конец{массив} \справа] &= 0 \конец{выровнено}\] 92 + \lambda — 6 = 0\nonnumber\]
Решая это уравнение, находим, что \(\lambda_1 = 2\) и \(\lambda_2 = -3\).
Теперь нам нужно найти основные собственные векторы для каждого \(\lambda\). Сначала найдем собственные векторы для \(\lambda_1 = 2\). Мы хотим найти все векторы \(X \neq 0\) такие, что \(AX = 2X\). Это решения \((2I — A)X = 0\). \[\begin{align} \left( 2 \left[ \begin{array}{rr} 1 & 0 \\ 0 & 1 \end{массив}\right] — \left[ \begin{array}{rr} -5 & 2 \\ -7 & 4 \end{массив}\right] \right) \left[ \begin{array}{c} x \\ y \end{массив}\right] &= \left[ \ begin{array}{r} 0 \\ 0 \end{array} \right] \\ \\ \left[ \begin{array}{rr} 7 & -2 \\ 7 & -2 \end{array}\ right] \left[ \begin{array}{c} x \\ y \end{array}\right] &= \left[ \begin{array}{r} 0 \\ 0 \end{array} \right] \конец{выровнено}\]
Мы хотим найти все векторы \(X \neq 0\) такие, что \(AX = 2X\). Это решения \((2I — A)X = 0\). \[\begin{align} \left( 2 \left[ \begin{array}{rr} 1 & 0 \\ 0 & 1 \end{массив}\right] — \left[ \begin{array}{rr} -5 & 2 \\ -7 & 4 \end{массив}\right] \right) \left[ \begin{array}{c} x \\ y \end{массив}\right] &= \left[ \ begin{array}{r} 0 \\ 0 \end{array} \right] \\ \\ \left[ \begin{array}{rr} 7 & -2 \\ 7 & -2 \end{array}\ right] \left[ \begin{array}{c} x \\ y \end{array}\right] &= \left[ \begin{array}{r} 0 \\ 0 \end{array} \right] \конец{выровнено}\]
Увеличенная матрица для этой системы и соответствующая уменьшенная форма строки-эшелона задаются как \[\left[ \begin{array}{rr|r} 7 & -2 & 0 \\ 7 & -2 & 0 \end{ array}\right] \rightarrow \cdots \rightarrow \left[ \begin{array}{rr|r} 1 & -\frac{2}{7} & 0 \\ 0 & 0 & 0 \end{array} \ right]\nonumber\]
Решением является любой вектор вида \[\left[ \begin{array}{c} \frac{2}{7}s \\ s \end{array} \right] = s \left[ \begin{array}{r} \frac{2}{7} \\ 1 \end{array} \right]\nonumber \]
Умножая этот вектор на \(7\), мы получаем более простое описание решения этой системы, заданное как \[t \left[ \begin{array}{r} 2 \\ 7 \end{array} \right ]\nonumber\]
Это дает базовый собственный вектор для \(\lambda_1 = 2\) как \[\left[ \begin{array}{r} 2\\ 7 \end{array} \right]\nonumber\ ]
Для проверки проверим, что \(AX = 2X\) для этого основного собственного вектора.
\[\left[ \begin{array}{rr} -5 и 2 \\ -7 & 4 \end{массив}\right] \left[ \begin{array}{r} 2 \\ 7 \end {массив} \right] = \left[ \begin{array}{r} 4 \\ 14 \end{массив}\right] = 2 \left[ \begin{array}{r} 2\\ 7 \end{ массив} \справа]\номер\]
Это то, что мы хотели, поэтому мы знаем, что этот базовый собственный вектор верен.
Далее мы повторим этот процесс, чтобы найти основной собственный вектор для \(\lambda_2 = -3\). Мы хотим найти все векторы \(X \neq 0\) такие, что \(AX = -3X\). Это решения \(((-3)I-A)X = 0\). \[\begin{align} \left( (-3) \left[ \begin{array}{rr} 1 & 0 \\ 0 & 1 \end{array}\right] — \left[ \begin{array} {rr} -5 и 2 \\ -7 и 4 \end{массив}\right] \right) \left[ \begin{array}{c} x \\ y \end{массив}\right] &= \ left[ \begin{array}{r} 0 \\ 0 \end{array} \right] \\ \left[ \begin{array}{rr} 2 & -2 \\ 7 & -7 \end{array} \right] \left[ \begin{array}{c} x \\ y \end{array}\right] &= \left[ \begin{array}{r} 0 \\ 0 \end{array} \right ] \end{выровнено}\]
Увеличенная матрица для этой системы и соответствующая сокращенная форма строки-эшелона задаются как \[\left[ \begin{array}{rr|r} 2 & -2 & 0 \\ 7 & -7 & 0 \end{ array}\right] \rightarrow \cdots \rightarrow \left[ \begin{array}{rr|r} 1 & -1 & 0 \\ 0 & 0 & 0 \end{array} \right]\nonumber \]
Решением является любой вектор вида \[\left[ \begin{array}{c} s \\ s \end{array} \right] = s \left[ \begin{array}{r} 1 \\ 1 \end{массив} \right]\nonumber\]
Это дает базовый собственный вектор для \(\lambda_2 = -3\) как \[\left[ \begin{array}{r} 1\\ 1 \end{array} \right]\nonumber\]
Проверить , мы проверяем, что \(AX = -3X\) для этого основного собственного вектора.
\[\left[ \begin{array}{rr} -5 и 2 \\ -7 & 4 \end{массив}\right] \left[ \begin{array}{r} 1 \\ 1 \end {массив} \right] = \left[ \begin{array}{r} -3 \\ -3 \end{массив}\right] = -3 \left[ \begin{array}{r} 1\\ 1 \end{array} \right]\nonumber\]
Это то, что мы хотели, поэтому мы знаем, что этот базовый собственный вектор верен.
Ниже приведен пример использования процедуры \(\PageIndex{1}\) для матрицы \(3 \times 3\).
Пример \(\PageIndex{3}\): поиск собственных значений и собственных секторов
поиск собственных значений и собственных векторов для матрицы \[A=\left[ \begin{array}{rrr} 5 & -10 & -5 \\ 2 & 14 & 2 \\ -4 & -8 & 6 \end{array} \right]\nonumber \]
Решение
Мы будем использовать процедуру \(\PageIndex{1}\). Сначала нам нужно найти собственные значения \(A\). Напомним, что они являются решениями уравнения \[\det \left( \lambda I — A \right) =0\nonnumber \]
В этом случае уравнение имеет вид \[\det \left( \lambda \left[ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{ array} \right] — \left[ \begin{array}{rrr} 5 & -10 & -5 \\ 2 & 14 & 2 \\ -4 & -8 & 6 \end{array} \right] \right ) =0\nonumber \], который становится \[\det \left[ \begin{array}{ccc} \lambda — 5 & 10 & 5 \\ -2 & \lambda — 14 & -2 \\ 4 & 8 & \lambda — 6 \end{array} \right] = 0\nonumber \]
Используя разложение Лапласа, вычислите этот определитель и упростите его. {2}-20\лямбда +100\вправо) =0\не число \] 9{2}\nonumber \] Следовательно, \(\lambda_2 = 10\) является собственным значением кратности два.
{2}-20\лямбда +100\вправо) =0\не число \] 9{2}\nonumber \] Следовательно, \(\lambda_2 = 10\) является собственным значением кратности два.
Теперь, когда мы нашли собственные значения для \(A\), мы можем вычислить собственные векторы.
Сначала мы найдем основные собственные векторы для \(\lambda_1 =5.\) Другими словами, мы хотим найти все ненулевые векторы \(X\) так, что \(AX = 5X\). Для этого необходимо решить уравнение \(\left( 5 I — A \right) X = 0\) для \(X\) следующим образом. \[\left( 5\left[ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right] — \left[ \begin {array}{rrr} 5 & -10 & -5 \\ 2 & 14 & 2 \\ -4 & -8 & 6 \end{array} \right] \right) \left[ \begin{array}{r } x \\ y \\ z \end{массив} \right] =\left[ \begin{array}{r} 0 \\ 0 \\ 0 \end{массив} \right]\nonumber \]
То есть вам нужно найти решение \[ \left[ \begin{array}{rrr} 0 & 10 & 5 \\ -2 & -9 & -2 \\ 4 & 8 & -1 \end{ array} \right] \left[ \begin{array}{r} x \\ y \\ z \end{array} \right] =\left[ \begin{array}{r} 0 \\ 0 \\ 0 \end{array} \right]\nonumber \]
Теперь это знакомая проблема. Вы настраиваете расширенную матрицу и сокращаете строку, чтобы получить решение. Таким образом, матрица, которую вы должны уменьшить по строке, равна \[\left[ \begin{array}{rrr|r} 0 & 10 & 5 & 0 \\ -2 & -9& -2 & 0 \\ 4 & 8 & -1 & 0 \end{array} \right]\nonumber \] Сокращенная форма строки-эшелона: \[\left[ \begin{array}{rrr|r} 1 & 0 & — \frac{5}{4} & 0 \\ 0 & 1 & \frac{1}{2} & 0 \\ 0 & 0 & 0 & 0 \end{array} \right]\nonumber \ ] и поэтому решением является любой вектор вида \[\left[ \begin{array}{c} \frac{5}{4}s \\ -\frac{1}{2}s \\ s \end {массив} \right] =s\left[ \begin{array}{r} \frac{5}{4} \\ -\frac{1}{2} \\ 1 \end{массив} \right]\ нечисло \] где \(s\in \mathbb{R}\). Если мы умножим этот вектор на \(4\), мы получим более простое описание решения этой системы, которое дается выражением \[t \left[ \begin{array}{r} 5 \\ -2 \\ 4 \ end{массив} \right] \label{basiceigenvect}\] где \(t\in \mathbb{R}\). Здесь основной собственный вектор задается как \[X_1 = \left[ \begin{array}{r} 5 \\ -2 \\ 4 \end{array} \right]\nonumber \]
Вы настраиваете расширенную матрицу и сокращаете строку, чтобы получить решение. Таким образом, матрица, которую вы должны уменьшить по строке, равна \[\left[ \begin{array}{rrr|r} 0 & 10 & 5 & 0 \\ -2 & -9& -2 & 0 \\ 4 & 8 & -1 & 0 \end{array} \right]\nonumber \] Сокращенная форма строки-эшелона: \[\left[ \begin{array}{rrr|r} 1 & 0 & — \frac{5}{4} & 0 \\ 0 & 1 & \frac{1}{2} & 0 \\ 0 & 0 & 0 & 0 \end{array} \right]\nonumber \ ] и поэтому решением является любой вектор вида \[\left[ \begin{array}{c} \frac{5}{4}s \\ -\frac{1}{2}s \\ s \end {массив} \right] =s\left[ \begin{array}{r} \frac{5}{4} \\ -\frac{1}{2} \\ 1 \end{массив} \right]\ нечисло \] где \(s\in \mathbb{R}\). Если мы умножим этот вектор на \(4\), мы получим более простое описание решения этой системы, которое дается выражением \[t \left[ \begin{array}{r} 5 \\ -2 \\ 4 \ end{массив} \right] \label{basiceigenvect}\] где \(t\in \mathbb{R}\). Здесь основной собственный вектор задается как \[X_1 = \left[ \begin{array}{r} 5 \\ -2 \\ 4 \end{array} \right]\nonumber \]
Обратите внимание, что здесь нельзя допустить \(t=0\), потому что это приведет к нулевому вектору, а собственные векторы никогда не равны 0! Кроме этого значения, любой другой выбор \(t\) в \(\eqref{basiceigenvect}\) приводит к собственному вектору.
Это хорошая идея, чтобы проверить свою работу! Для этого возьмем исходную матрицу и умножим на основной собственный вектор \(X_1\). Мы проверяем, получили ли мы \(5X_1\). \[\left[ \begin{array}{rrr} 5 & -10 & -5 \\ 2 & 14 & 2 \\ -4 & -8 & 6 \end{array} \right] \left[ \begin{ array}{r} 5 \\ -2 \\ 4 \end{array} \right] = \left[ \begin{array}{r} 25 \\ -10 \\ 20 \end{array} \right] = 5\left[ \begin{array}{r} 5 \\ -2 \\ 4 \end{array} \right]\nonumber \] Это то, что мы хотели, поэтому мы знаем, что наши вычисления были правильными.
Далее мы найдем основные собственные векторы для \(\lambda_2, \lambda_3=10.\) Эти векторы являются основными решениями уравнения \[\left( 10\left[ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right] — \left[ \begin{array}{rrr} 5 & -10 & -5 \\ 2 & 14 & 2 \\ -4 & -8 & 6 \end{array} \right] \right) \left[ \begin{array}{r} x \\ y \\ z \end{array} \right] =\ left[ \begin{array}{r} 0 \\ 0 \\ 0 \end{array} \right]\nonumber \] То есть вы должны найти решения для \[\left[ \begin{array}{rrr} 5 & 10 & 5 \\ -2 & -4 & -2 \\ 4 & 8 & 4 \end{массив} \right] \left[ \begin{массив}{c} x \\ y \\ z \end {массив} \right] =\left[ \begin{array}{r} 0 \\ 0 \\ 0 \end{массив} \right]\nonumber \]
Рассмотрим расширенную матрицу \[\left[ \begin{array}{rrr|r} 5 & 10 & 5 & 0 \\ -2 & -4 & -2 & 0 \\ 4 & 8 & 4 & 0 \ end{array} \right]\nonumber \] Сокращенная форма строки-эшелона для этой матрицы: \[\left[ \begin{array}{rrr|r} 1 & 2 & 1 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array} \right]\nonumber \] и поэтому собственные векторы имеют вид \[\left[ \begin{array}{c} -2s-t \\ s \\ t \end{array} \right] =s\left[ \begin{array}{r} -2 \\ 1 \\ 0 \end{array} \right] +t\left[ \begin{array }{r} -1 \\ 0 \\ 1 \end{array} \right]\nonumber \] Обратите внимание, что вы не можете выбрать \(t\) и \(s\) равными нулю, потому что это приведет к в нулевом векторе, а собственные векторы никогда не равны нулю.
Здесь есть два основных собственных вектора, заданные как \[X_2 = \left[ \begin{array}{r} -2 \\ 1\\ 0 \end{array} \right] , X_3 = \left[ \ begin{array}{r} -1 \\ 0 \\ 1 \end{array} \right]\nonumber \]
Любая (ненулевая) линейная комбинация \(X_2\) и \(X_3\) также будет приводит к собственному вектору для собственного значения \(\lambda =10.\) Как и в случае с \(\lambda =5\), всегда проверяйте свою работу! Для первого основного собственного вектора мы можем проверить \(AX_2 = 10 X_2\) следующим образом. \[\left[ \begin{array}{rrr} 5 & -10 & -5 \\ 2 & 14 & 2 \\ -4 & -8 & 6 \end{array} \right] \left[ \begin{ array}{r} -1 \\ 0 \\ 1 \end{array} \right] = \left[ \begin{array}{r} -10 \\ 0 \\ 10 \end{array} \right] = 10\left[ \begin{array}{r} -1 \\ 0 \\ 1 \end{array} \right]\nonnumber \] Это то, что мы хотели. Проверка второго базового собственного вектора \(X_3\) остается в качестве упражнения.
Важно помнить, что для любого собственного вектора \(X\), \(X \neq 0\). Однако возможно, что собственные значения равны нулю. Это показано в следующем примере.
Это показано в следующем примере.
Пример \(\PageIndex{4}\): нулевое собственное значение
Пусть \[A=\left[ \begin{array}{rrr} 2 & 2 & -2 \\ 1 & 3 & -1 \\ -1 & 1 & 1 \end{array} \right]\nonumber \] Найдите собственные значения и собственные векторы \(A\).
Решение
Сначала найдем собственные значения \(A\). Мы сделаем это с помощью определения \(\PageIndex{1}\). 9{2}+8\лямбда=0\). Вы можете убедиться, что решения равны \(\lambda_1 = 0, \lambda_2 = 2, \lambda_3 = 4\). Обратите внимание, что, хотя собственные векторы никогда не могут быть равны \(0\), возможно иметь собственное значение, равное \(0\).
Теперь найдем основные собственные векторы. Для \(\lambda_1=0\) нужно решить уравнение \(\left( 0 I — A \right) X = 0\). Это уравнение принимает вид \(-AX=0\), поэтому расширенная матрица для поиска решений имеет вид \[\left[ \begin{array}{rrr|r} -2 & -2 & 2 & 0 \\ -1 & -3 & 1 & 0 \\ 1 & -1 & -1 & 0 \end{array} \right]\nonumber \] Сокращенная форма строки-эшелона \[\left[ \begin{array}{ rrr|r} 1 & 0 & -1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array} \right]\nonumber \] Таким образом, собственные векторы имеют вид \(t\left[ \begin{array}{r} 1 \\ 0 \\ 1 \end{array} \right]\) где \(t\neq 0\) и основной собственный вектор задается \[X_1 = \left[ \begin{array}{r} 1 \\ 0 \\ 1 \end{массив} \right]\nonnumber \]
Мы можем проверить правильность этого собственного вектора, проверив, что выполняется уравнение \(AX_1 = 0 X_1\). Произведение \(AX_1\) равно \[AX_1=\left[ \begin{array}{rrr} 2 & 2 & -2 \\ 1 & 3 & -1 \\ -1 & 1 & 1 \end{ array} \right] \left[ \begin{array}{r} 1 \\ 0 \\ 1 \end{array} \right] = \left[ \begin{array}{r} 0 \\ 0 \\ 0 \end{array} \right]\nonumber \]
Произведение \(AX_1\) равно \[AX_1=\left[ \begin{array}{rrr} 2 & 2 & -2 \\ 1 & 3 & -1 \\ -1 & 1 & 1 \end{ array} \right] \left[ \begin{array}{r} 1 \\ 0 \\ 1 \end{array} \right] = \left[ \begin{array}{r} 0 \\ 0 \\ 0 \end{array} \right]\nonumber \]
Это явно равно \(0X_1\), так что уравнение выполняется. Следовательно, \(AX_1 = 0X_1\) и, таким образом, \(0\) является собственным значением \(A\).
Вычисление других основных собственных векторов остается в качестве упражнения.
В следующих разделах мы рассмотрим способы упрощения процесса нахождения собственных значений и собственных векторов с помощью свойств специальных типов матриц.
Собственные значения и собственные векторы для специальных типов матриц
Существует три специальных вида матриц, которые можно использовать для упрощения процесса нахождения собственных значений и собственных векторов. В этом разделе мы будем обсуждать подобные матрицы, элементарные матрицы, а также треугольные матрицы. 9{-1}BPX=\lambda X\nonumber \] и поэтому \[BPX=\lambda PX\nonumber \]
9{-1}BPX=\lambda X\nonumber \] и поэтому \[BPX=\lambda PX\nonumber \]
Поскольку \(P\) взаимно однозначно и \(X \neq 0\), отсюда следует, что \(PX \neq 0\). Здесь \(PX\) играет роль собственного вектора в этом уравнении. Таким образом, \(\lambda\) также является собственным значением \(B\). Аналогичным образом можно проверить, что любое собственное значение \(B\) также является собственным значением \(A\), и, таким образом, обе матрицы имеют желаемые собственные значения.
Доказательство второго утверждения аналогично и оставлено в качестве упражнения.
Обратите внимание, что это доказательство также демонстрирует, что собственные векторы \(A\) и \(B\) будут (обычно) различными . В доказательстве мы видим, что \(AX = \lambda X\), а \(B \left(PX\right)=\lambda \left(PX\right)\). Следовательно, для собственного значения \(\lambda\) \(A\) будет иметь собственный вектор \(X\), а \(B\) будет иметь собственный вектор \(PX\).
Второй специальный тип матриц, который мы обсуждаем в этом разделе, — это элементарные матрицы. Напомним из определения 2.8.1, что элементарная матрица \(E\) получается путем применения одной операции строки к единичной матрице.
Напомним из определения 2.8.1, что элементарная матрица \(E\) получается путем применения одной операции строки к единичной матрице.
Элементарные матрицы можно использовать для упрощения матрицы перед поиском ее собственных значений и собственных векторов. Это показано в следующем примере.
Пример \(\PageIndex{5}\): упрощение с использованием элементарных матриц
Найдите собственные значения для матрицы \[A = \left[ \begin{array}{rrr} 33 & 105 & 105 \\ 10 & 28 & 30 \\ -20 & -60 & -62 \end{array} \right]\nonumber \]
Решение
Эта матрица имеет большие числа, и поэтому мы хотели бы максимально упростить ее перед вычислением собственных значений.
Мы сделаем это, используя операции со строками. Во-первых, прибавьте \(2\) раз вторую строку к третьей строке. Для этого умножьте слева \(A\) на \(E \left(2,2\right)\). Затем вправо умножьте \(A\) на обратную \(E \left(2,2\right)\), как показано на рисунке. \[\left[ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 2 & 1 \end{array} \right] \left[ \begin{array}{rrr } 33 & 105 & 105 \\ 10 & 28 & 30 \\ -20 & -60 & -62 \end{array} \right] \left[ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & -2 & 1 \end{array} \right] =\left[ \begin{array}{rrr} 33 & -105 & 105 \\ 10 & -32 & 30 \\ 0 & 0 & -2 \end{array} \right]\nonumber \] По лемме \(\PageIndex{1}\) результирующая матрица имеет те же собственные значения, что и \(A\), где здесь матрица \(E \ left(2,2\right)\) играет роль \(P\).
Повторяем этот шаг следующим образом. На этом шаге мы используем элементарную матрицу, полученную путем прибавления \(-3\) второй строки к первой строке. \[\left[ \begin{array}{rrr} 1 & -3 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right] \left[ \begin{array}{ rrr} 33 & -105 & 105 \\ 10 & -32 & 30 \\ 0 & 0 & -2 \end{array} \right] \left[ \begin{array}{rrr} 1 & 3 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right] =\left[ \begin{array}{rrr} 3 & 0 & 15 \\ 10 & -2 & 30 \\ 0 & 0 & -2 \end{array} \right] \label{elemeigenvalue}\] Опять же по лемме \(\PageIndex{1}\), эта результирующая матрица имеет те же собственные значения, что и \(A\). На этом этапе мы можем легко найти собственные значения. Пусть \[B = \left[ \begin{array}{rrr} 3 & 0 & 15 \\ 10 & -2 & 30 \\ 0 & 0 & -2 \end{array} \right]\nonumber \] Тогда , мы находим собственные значения \(B\) (и, следовательно, \(A\)) путем решения уравнения \(\det \left( \lambda I — B \right) = 0\). Вы должны убедиться, что это уравнение становится \[\left(\lambda +2 \right) \left( \lambda +2 \right) \left( \lambda — 3 \right) =0\nonnumber \] Решение этого уравнения приводит к собственные значения \(\lambda_1 = -2, \lambda_2 = -2\) и \(\lambda_3 = 3\). Следовательно, это также собственные значения \(A\).
Следовательно, это также собственные значения \(A\).
Используя элементарные матрицы, мы смогли создать матрицу, для которой нахождение собственных значений было проще, чем для \(A\). В этот момент вы можете вернуться к исходной матрице \(A\) и решить \(\left(\lambda I — A \right) X = 0\), чтобы получить собственные векторы \(A\).
Обратите внимание, что при умножении справа на элементарную матрицу вы выполняете операцию столбца, определенную элементарной матрицей. В \(\eqref{elemeigenvalue}\) умножение на элементарную матрицу справа просто включает три умножения первого столбца и прибавление ко второму. Таким образом, не обращаясь к элементарным матрицам, переход к новой матрице в \(\eqref{elemeigenvalue}\) можно проиллюстрировать \[\left[ \begin{array}{rrr} 33 & -105 & 105 \\ 10 & -32 & 30 \\ 0 & 0 & -2 \end{array} \right] \rightarrow \left[ \begin{array}{rrr} 3 & -9& 15 \\ 10 & -32 & 30 \\ 0 & 0 & -2 \end{array} \right] \rightarrow \left[ \begin{array}{rrr} 3 & 0 & 15 \\ 10 & -2 & 30 \\ 0 & 0 & -2 \end{array} \right]\nonumber \]
Третий специальный тип матрицы, который мы рассмотрим в этом разделе, — это треугольная матрица. Напомним определение 3.1.6, в котором говорится, что верхняя (нижняя) треугольная матрица содержит все нули ниже (выше) главной диагонали. Помните, что нахождение определителя треугольной матрицы — это простая процедура взятия произведения элементов на главной диагонали. Оказывается, есть также простой способ найти собственные значения треугольной матрицы.
Напомним определение 3.1.6, в котором говорится, что верхняя (нижняя) треугольная матрица содержит все нули ниже (выше) главной диагонали. Помните, что нахождение определителя треугольной матрицы — это простая процедура взятия произведения элементов на главной диагонали. Оказывается, есть также простой способ найти собственные значения треугольной матрицы.
В следующем примере мы покажем, что собственными значениями треугольной матрицы являются элементы на главной диагонали.
Пример \(\PageIndex{6}\): собственные значения треугольной матрицы
Пусть \(A=\left[ \begin{array}{rrr} 1 & 2 & 4 \\ 0 & 4 & 7 \\ 0 & 0 & 6 \end{array} \right] .\) Найдите собственные значения \(A\).
Решение
Нам нужно решить уравнение \(\det \left( \lambda I — A \right) = 0\) следующим образом \[\begin{aligned} \det \left( \lambda I — A \ справа) = \det \left[ \begin{array}{ccc} \lambda -1 & -2 & -4 \\ 0 & \lambda -4 & -7 \\ 0 & 0 & \lambda -6 \end{ array} \right] =\left( \lambda -1 \right) \left( \lambda -4 \right) \left( \lambda -6 \right) =0\end{aligned}\]
Решение уравнения \(\left( \lambda -1 \right) \left( \lambda -4 \right) \left( \lambda -6 \right) = 0\) для \(\lambda \) приводит к собственные значения \(\lambda_1 = 1, \lambda_2 = 4\) и \(\lambda_3 = 6\). Таким образом, собственными значениями являются элементы на главной диагонали исходной матрицы.
Таким образом, собственными значениями являются элементы на главной диагонали исходной матрицы.
Тот же результат верен для нижних треугольных матриц. Для любой треугольной матрицы собственные значения равны элементам на главной диагонали. Чтобы найти собственные векторы треугольной матрицы, мы используем обычную процедуру.
В следующем разделе мы исследуем важный процесс, связанный с собственными значениями и собственными векторами матрицы.
Эта страница под названием 7.1: Собственные значения и собственные векторы матрицы распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована Кеном Каттлером (Lyryx) с помощью исходного содержимого, которое было отредактировано в соответствии со стилем и стандартами Платформа LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Кен Каттлер
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Показать страницу TOC
- нет
- Теги
- источник@https://lyryx.
 com/first-course-linear-алгебра
com/first-course-linear-алгебра
- источник@https://lyryx.
Собственный вектор и собственное значение
У них много применений!
Простой пример: собственный вектор не меняет направление при преобразовании:
Как найти этот вектор?
Математика этого
Для квадратной матрицы A собственный вектор и собственное значение делают это уравнение верным:
Посмотрим в действии:
Пример: Для этой матрицы
собственный вектор равен
с соответствующим собственным значением 6
Давайте сделаем несколько перемножений матриц, чтобы проверить, верно ли это.
Av дает нам:
=
−6×1+3×4
4×1+5×4
=
λv дает нам:
Да, они равны!
Итак, мы получаем Av = λv, как и обещали.
Обратите внимание, как мы умножаем -матрицу на -вектор и получаем тот же результат, что и при умножении скаляра (просто числа) на этот -вектор .
Как найти эти собственные вещи?
Начнем с нахождения собственного значения . Мы знаем, что это уравнение должно быть верным:
Av = λv
Затем мы вводим единичную матрицу, поэтому мы имеем дело с матрицей-против-матрицы:
Ср = λIv
Перенести все на левую сторону:
Av − λIv = 0
Если v не равно нулю, то мы можем (надеюсь) найти λ, используя только определитель:
| А — λI | = 0
Давайте попробуем это уравнение на нашем предыдущем примере:
Пример: Найдите λ
Начните с | А — λI | = 0
| | | | = 0 |
То есть:
−6−λ
3
4
5−λ
= 0
Вычисление определителя дает:
(−6−λ)(5−λ) − 3×4 = 0
, что упрощает это квадратное уравнение:
λ 2 + λ − 42 = 0
При решении получается:
λ = −7 или 6
И да, есть два возможных собственных значения.
Теперь, когда мы знаем собственных значений , найдем соответствующие им собственных векторов .
Пример (продолжение): Найдите собственный вектор для собственного значения
λ = 6 :Начните с:
Av = λv
Подставляем известные нам значения:
После умножения получаем два уравнения:
| −6x + 3y | = | 6x |
| 4x + 5y | = | 6 лет |
Перевести все на левую сторону:
| −12x + 3y | = | 0 |
| 4x − 1 год | = | 0 |
Любое уравнение показывает, что y = 4x , поэтому собственный вектор является любым ненулевым кратным этому:
И мы получаем решение, показанное вверху страницы:
=
−6×1+3×4
4×1+5×4
=
. .. а также …
.. а также …
Итак, Av = λv, и у нас получилось!
Теперь ваша очередь найти собственный вектор для другого собственного значения −7
Почему?
Для чего они?
Одна из замечательных вещей заключается в том, что мы можем использовать матрицы для преобразования пространства, что часто используется в компьютерной графике.
В этом случае собственный вектор — это «направление, которое не меняет направление» !
А собственное значение — это масштаб растяжения:
- 1 означает без изменений,
- 2 означает удвоение длины,
- −1 означает направление назад вдоль направления собственного значения
- и т. д.
Также много приложений в физике и т.д.
Почему «Айген»
Eigen — немецкое слово, означающее «собственный» или «типичный»
«das ist ihnen eigen » по немецки означает «то есть типичный из них»
Иногда в английском языке мы используем слово «характеристика», поэтому собственный вектор можно назвать «характеристическим вектором».
Не просто два измерения
Собственные векторы отлично работают в трех измерениях и выше.
Пример: найдите собственные значения для этой матрицы 3×3:
Первое вычисление A − λI:
− λ
=
2−λ
4−λ
5
4
3−λ
Now the determinant should equal zero:
2−λ
4−λ
5
4
3−λ
= 0
Что равно:
(2−λ) [ (4−λ)(3−λ) − 5×4 ] = 0
В итоге получается кубическое уравнение, но просто Глядя на это здесь, мы видим, что один из корней равен 2 (из-за 2−λ), а часть в квадратных скобках квадратична, с корнями из −1 и 8 .
Таким образом, собственные значения равны −1 , 2 и 8
Пример (продолжение): найти собственный вектор, соответствующий собственному значению
−1Подставить известные нам значения:
Перевести все на левую сторону:
| 3x | = | 0 |
| 5 лет + 5 лет | = | 0 |
| 4 года + 4 года | = | 0 |
Таким образом, x = 0 и y = −Z и таким образом, собственное вектор является любым ненулевым кратным:
Тест AV:
=
4–5
4–3
=
и λv:
39=
и λv:
39=
и λv:
4039=
и λv:
4039=
и λv:
4039=
и λv:
4039=
и λv:
4039=
. Av = λv, ура!
Av = λv, ура!
(Вы можете попробовать свои силы в собственных значениях 2 и 8 )
Вращение
Вернувшись снова в двухмерный мир, эта матрица совершит поворот на θ:
cos(θ)
−sin(θ)
sin(θ)
соз(θ)
Пример: Повернуть на 30°
cos(30°) = √3 2 и sin(30°) = 1 2 , поэтому:
9 дюймов (040°) 30°)
sin(30°)
cos(30°)
=
√3 2
−1 2
1 2
√ 3 2
Но если мы повернем все точки , что это за «направление, которое не меняет направление»?
Let us work through the mathematics to find out:
First calculate A − λI:
√3 2
−1 2
1 2
√3 2
− λ
=
√3 2 −λ
−1 2
1 2
√3 2 −λ
Now the determinant should equal zero:
√3 2 −λ
−1 2
1 2
√3 2 −λ
= 0
, который:
( √3 2 −λ) ( √3 2 — ( −1903 2 ) = 0
Что становится этим квадратным уравнением:
λ 2 − (√3)λ + 1 = 0
Whose roots are:
λ = √3 2 ± i 2
The eigenvalues are complex!
Я не знаю, как показать это на графике, но мы все равно получаем решение.
Собственный вектор
Итак, какой собственный вектор соответствует, скажем, корню √3 2 + i 2 2 2
Начните с:
Av = λv
Поместите значения, которые мы знаем:
√3 2
−1 2
1 2
a 2 + I 2 )
После умножения мы получаем эти два уравнения:
√3 2 x — 1 9043
6668 2 x — 1 9043668 2 x — 1 90439 2 2 x — 1 903Y = √3 2 x + I 2 x 1 2 x + √3 2 2 x + √3 68 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 . Which simplify to: −y = i x x = i y And the solution is any non-zero multiple of : или Ничего себе, такой простой ответ! Это только потому, что мы выбрали 30°? Или это работает для любой матрицы вращения? Я позволю вам решить это! Попробуйте другой угол, или еще лучше используйте «cos(θ)» и «sin(θ)». Oh, and let us check at least one of those solutions: √3 2 −1 2 1 2 √ 3 2 = i √3 2 − 1 2 i 2 + √3 2 Does it match this? ( √3 2 + i 2 ) = i √3 2 − 1 2 √ 3 2 + i 2 О, да! 17820, 17821, 17804, 17805, 17806, 17807, 17814, 17818, 17819, 17808, 17809, 17810, 17811, 17812, 17813, 17815, 17816, 17817, 17822, 17823 i 2 y
i 2 y
Собственные значения и собственные векторы
Цели
- Изучите определение собственного вектора и собственного значения.

- Научитесь находить собственные векторы и собственные значения геометрически.
- Научитесь решать, является ли число собственным значением матрицы, и если да, то как найти соответствующий собственный вектор.
- Рецепт: найти базис для λ-собственного пространства.
- Картинки: является ли вектор собственным вектором, собственные векторы стандартных матричных преобразований.
- Теорема: расширенная теорема об обратимой матрице.
- Словарное слово: собственное пространство .
- Основные словарные слова: собственный вектор , собственное значение .
В этом разделе мы определяем собственные значения и собственные векторы. Они составляют наиболее важный аспект структурной теории квадратных матриц. Таким образом, собственные значения и собственные векторы, как правило, играют ключевую роль в реальных приложениях линейной алгебры.
Вот самое важное определение в этом тексте.
Определение
Пусть A — матрица размера n × n.
- Собственный вектор оператора A — это ненулевой вектор v в Rn такой, что Av=λv для некоторого скаляра λ.
- собственное значение оператора A — это скаляр λ такой, что уравнение Av=λv имеет нетривиальное решение.
Если Av=λv для vA=0, мы говорим, что λ является собственным значением для v, и что v является собственный вектор для λ.
Немецкий префикс «eigen» примерно переводится как «я» или «собственный». Собственный вектор A — это вектор, кратный самому себе матричным преобразованием T(x)=Ax, что, возможно, объясняет терминологию. С другой стороны, «собственный» часто переводится как «характерный»; мы можем думать о собственном векторе как описывающем внутреннее или характеристическое свойство A.
Собственные векторы равны по определению ненулевым . Собственные значения могут быть равны нулю.
Собственные значения могут быть равны нулю.
Мы не считаем нулевой вектор собственным вектором: поскольку A0=0=λ0 для каждого скаляра λ, соответствующее собственное значение будет неопределенным.
Если кто-то передаст вам матрицу A и вектор v, легко проверить, является ли v собственным вектором A: просто умножьте v на A и посмотрите, является ли Av скалярным кратным v. матрица A, совершенно не очевидно, как найти собственные векторы. Мы узнаем, как это сделать, в Разделе 5.2.
Пример (проверка собственных векторов)
Пример (проверка собственных векторов)
Пример (собственный вектор с собственным значением 0)
Сказать, что Av=λv означает, что Av и λv коллинеарны с началом координат . Итак, собственный вектор оператора A — это ненулевой вектор v, такой что Av и v лежат на одной прямой, проходящей через начало координат. В этом случае Av является скалярным числом, кратным v; собственное значение является коэффициентом масштабирования.
Для матриц, возникающих как стандартная матрица линейного преобразования, часто лучше всего нарисовать рисунок, а затем геометрически найти собственные векторы и собственные значения, изучив, какие векторы не сдвинуты со своей линии. Для преобразования, заданного геометрически, нет необходимости даже вычислять его матрицу, чтобы найти собственные векторы и собственные значения.
Пример (Отражение)
Вот пример. Пусть T:R2→R2 будет линейным преобразованием, которое отражается на прямой L, определяемой y=−x, и пусть A будет матрицей для T. Мы найдем собственные значения и собственные векторы A без выполнения каких-либо вычислений.
Это преобразование определено геометрически, поэтому рисуем картинку.
Вектор u не является собственным вектором, потому что Au не коллинеарно u и началу координат.
Вектор z также не является собственным вектором.
Вектор v является собственным, поскольку Av коллинеарен вектору v и началу координат. Вектор Av имеет ту же длину, что и v, но имеет противоположное направление, поэтому соответствующее собственное значение равно −1.
Вектор Av имеет ту же длину, что и v, но имеет противоположное направление, поэтому соответствующее собственное значение равно −1.
Вектор w является собственным вектором, поскольку Aw коллинеарен w и началу координат: действительно, Aw равен w! Это означает, что w является собственным вектором с собственным значением 1.
Оказывается, что все собственные векторы лежат либо на L, либо на прямой, перпендикулярной L. Векторы на L имеют собственное значение 1, а векторы, перпендикулярные L, имеют собственное значение −1.
Рисунок 8. Собственный вектор A — это вектор x, такой что Ax коллинеарен с x и началом координат. Щелкните и перетащите головку x, чтобы убедиться, что все такие векторы лежат либо на L, либо на прямой, перпендикулярной L.Теперь мы приведем еще пять примеров такого рода
Пример (Проекция)
Пример (Идентификация)
Пример (Расширение)
Пример (сдвиг)
Пример (вращение)
Здесь мы упомянем один основной факт о собственных векторах.
Факт (собственные векторы с различными собственными значениями линейно независимы)
Пусть v1,v2,…,vk — собственные векторы матрицы A, и предположим, что соответствующие собственные значения λ1,λ2,…,λk различных (отличных друг от друга). Тогда {v1,v2,…,vk} линейно независима.
Когда k=2, это говорит о том, что если v1,v2 — собственные векторы с собственными значениями λ1A=λ2, то v2 не кратно v1. На самом деле любой ненулевой кратный cv1 вектора v1 также является собственным вектором с собственным значением λ1:
A(cv1)=cAv1=c(λ1v1)=λ1(cv1).
Как следствие изложенного факта имеем следующее.
Матрица размера n × n A имеет не более n собственных значений.
Предположим, что A — квадратная матрица. Мы уже знаем, как проверить, является ли заданный вектор собственным вектором A, и в этом случае найти собственное значение. Наша следующая цель — проверить, является ли данное действительное число собственным значением A, и в этом случае найти все соответствующие собственные векторы. Опять же, это будет просто, но более сложно. Таким образом, единственной недостающей частью будет поиск собственных значений A; это основное содержание Раздела 5.2.
Опять же, это будет просто, но более сложно. Таким образом, единственной недостающей частью будет поиск собственных значений A; это основное содержание Раздела 5.2.
Пусть A — матрица размера n × n, а λ — скаляр. Собственные векторы с собственным значением λ, если они есть, являются ненулевыми решениями уравнения Av=λv. Мы можем переписать это уравнение следующим образом:
Av=λv⇐⇒Av−λv=0⇐⇒Av−λInv=0⇐⇒(A−λIn)v=0.
Следовательно, собственные векторы A с собственным значением λ, если они есть, являются нетривиальными решениями матричного уравнения (A−λIn)v=0, т. е. ненулевыми векторами в Nul(A−λIn). Если это уравнение не имеет нетривиальных решений, то λ не является собственным вектором A.
Приведенное выше наблюдение важно, поскольку оно говорит о том, что нахождение собственных векторов для заданного собственного значения означает решение однородной системы уравнений. Например, если
А=С713-32-3-3-2-1Д,
, то собственный вектор с собственным значением λ является нетривиальным решением матричного уравнения
C713-32-3-3-2-1DCxyzD=λCxyzD.
Это переводится в систему уравнений
E7x+y+3z=λx−3x+2y−3z=λy−3x−2y−z=λz−−−→E(7−λ)x+y+3z=0−3x+(2−λ)y− 3z=0−3x−2y+(−1−λ)z=0.
То же, что и уравнение однородной матрицы
C7-λ13-32-λ-3-3-2-1-λDCxyzD=0,
, т. е. (A−λI3)v=0.
Определение
Пусть A — матрица размера n × n, и пусть λ — собственное значение A. λ-собственное пространство матрицы A — это множество решений уравнения (A−λIn)v=0, т. е. подпространство Nul(A−λIn ).
Собственное λ-пространство является подпространством, поскольку оно является нулевым пространством матрицы, а именно матрицы A−λIn. Это подпространство состоит из нулевого вектора и всех собственных векторов A с собственным значением λ.
Пример (вычисление собственных пространств)
Пример (вычисление собственных пространств)
Пример (Отражение)
Рецепты: собственные пространства
Пусть A — матрица размера n × n, а λ — число.
- λ является собственным значением A тогда и только тогда, когда (A−λIn)v=0 имеет нетривиальное решение, тогда и только тогда, когда Nul(A−λIn)A={0}.

- В этом случае найти базис для λ-собственного пространства A означает найти базис для Nul(A−λIn), что можно сделать, найдя параметрическую векторную форму решений однородной системы уравнений (A−λIn )v=0.
- Размерность собственного λ-пространства A равна количеству свободных переменных в системе уравнений (A−λIn)v=0, т. е. количеству столбцов A−λIn без точек опоры.
- Собственные векторы с собственным значением λ являются ненулевыми векторами в Nul(A−λIn) или, что то же самое, нетривиальными решениями (A−λIn)v=0.
В заключение мы сделаем наблюдение о 0-собственном пространстве матрицы.
Факт
Пусть A — матрица размера n × n.
- Число 0 является собственным значением A тогда и только тогда, когда A необратимо.
- В этом случае 0-собственное пространство A равно Nul(A).
Доказательство
Мы знаем, что 0 является собственным значением A тогда и только тогда, когда Nul(A−0In)=Nul(A) отличен от нуля, что эквивалентно необратимости A по теореме об обратимых матрицах в разделе 3. 6. В этом случае 0-собственное пространство по определению Nul(A−0In)=Nul(A).
6. В этом случае 0-собственное пространство по определению Nul(A−0In)=Nul(A).
Конкретно, собственный вектор с собственным значением 0 — это ненулевой вектор v, такой что Av=0v, т. е. такой, что Av=0. Это в точности ненулевые векторы в нуль-пространстве A.
Теперь у нас есть два новых способа сказать, что матрица обратима, поэтому мы добавляем их к теореме об обратимой матрице.
Теорема об обратимой матрице
Пусть A — матрица размера n×n, и пусть T:Rn→Rn — матричное преобразование T(x)=Ax. Следующие операторы эквивалентны:
- А обратим.
- A имеет n точек опоры.
- Нуль(А)={0}.
- Столбцы A линейно независимы.
- Колонны А пролета Рн.
- Ax=b имеет единственное решение для каждого b в Rn.
- Т обратим.
- Т один к одному.
- Т на.
- дет(А)А=0.
- 0 не является собственным значением A.
Комментарии, исправления или предложения? (Требуется бесплатная учетная запись GitHub)
Собственные значения и собственные векторы матриц 3 на 3
Собственные значения и собственные векторы матриц 3 на 3 Так же, как матрицы 2 на 2 могут представлять преобразования плоскости, матрицы 3 на 3 могут представлять преобразования трехмерного пространства.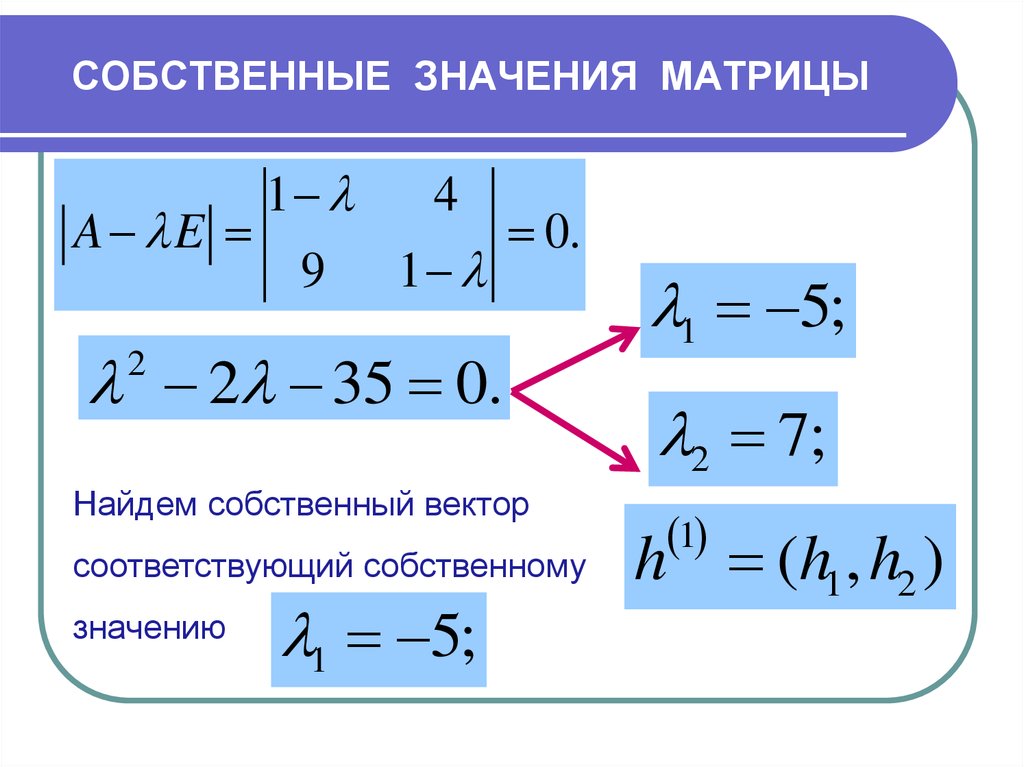 Картина более сложная, но, как и в случае 2 на 2, наши лучшие идеи приходят от нахождения собственных векторов матрицы: то есть тех векторов, направление которых преобразование оставляет неизменным.
Картина более сложная, но, как и в случае 2 на 2, наши лучшие идеи приходят от нахождения собственных векторов матрицы: то есть тех векторов, направление которых преобразование оставляет неизменным.
Если ненулевое {\bf e} является собственным вектором матрицы A 3 на 3, то
А\,{\bf е}=\лямбда \,{\bf е}
для некоторого скаляра \lambda . Этот скаляр называется собственным значением A.
Это может быть переписано
А\,{\bf е}=\лямбда \,I\,{\bf е},
и в свою очередь как
\влево(А\,-\лямбда \,I\вправо)\,{\bf e}={\bf 0}.
Как и в случае 2 на 2, матрица A-\lambda \,I должна быть вырожденной. Тогда мы еще раз спрашиваем: при каких значениях \lambda A-\lambda \,I является сингулярным? То есть значения, удовлетворяющие характеристическому уравнению
\text{det}\left(A-\lambda \,I\right)\,=\,0?
Рассмотрим пример
\left(\begin{array}{ccc}-2&-4&2\\-2&1&2\\4&2&5\end{массив}\right).
Характеристическое уравнение
\text{det}\left(\begin{array}{ccc}-2-\lambda &-4&2\\-2&1-\lambda &2\\4&2&5-\lambda \end{array}\right)=0 .
Раскрывая определитель,
\влево(-2-\лямбда\вправо)[\влево(1-\лямбда\вправо)\влево(5-\лямбда\вправо)-2\умножить на 2]+4[\влево(-2\вправо) )\times \left(5-\lambda\right)-4\times 2]+2[\left(-2\right)\times 2-4\left(1-\lambda\right)]=0. 9{2}-\лямбда-30\вправо)=\влево(\лямбда-3\вправо)\влево(\лямбда+5\вправо)\влево(\лямбда-6\вправо),
это означает, что собственные значения равны 3, -5 и 6.
Теперь приступаем к решению
\left(\begin{array}{ccc}-2-\lambda &-4&2\\-2&1-\lambda &2\\4&2&5-\lambda \end{array}\right)\left(\begin{array }{c}X\\Y\\Z\конец{массив}\right)=\left(\begin{массив}{c}0\\0\\0\end{массив}\right)
для каждого собственного значения \lambda . Теперь каждая такая система будет иметь бесконечно много решений, потому что если {\bf e} является собственным вектором, то и любой кратен {\bf e}. Таким образом, наша стратегия будет заключаться в том, чтобы попытаться найти собственный вектор с X = 1, а затем, при необходимости, увеличить его. (Если такого собственного вектора нет, мы знаем, что X на самом деле должно быть равно нулю, и вместо этого мы ищем собственный вектор с Y = 1 и так далее.)
(Если такого собственного вектора нет, мы знаем, что X на самом деле должно быть равно нулю, и вместо этого мы ищем собственный вектор с Y = 1 и так далее.)
Собственный вектор, соответствующий собственному значению 3
В случае \lambda =3 имеем
\left(\begin{array}{ccc}-5&-4&2\\-2&-2&2\\4&2&2\end{массив}\right)\left(\begin{array}{c}X\\Y\ \Z\end{массив}\right)=\left(\begin{array}{c}0\\0\\0\end{массив}\right).
Установка X=1 дает, как и наши первые два уравнения,
-5-4Y+2Z=0,
-2-2Y+2Z=0.
Вычитание первого из второго:
3+2Y=0,
и, таким образом, Y=-\frac{3}{2}.
Подставляя обратно во второе уравнение,
-2+3+2Z=0,
что дает Z=-\frac{1}{2}.
Проверяя третье уравнение,
4-3-1=0,
который работает. Это дает нам собственный вектор
\left(1,-\frac{3}{2},-\frac{1}{2}\right).
Для удобства мы можем увеличить масштаб в 2 раза, чтобы получить
\влево(2,-3,-1\вправо).
Собственный вектор, соответствующий собственному значению -5
В случае \lambda =-5 имеем
\left(\begin{array}{ccc}3&-4&2\\-2&6&2\\4&2&10\end{массив}\right)\left(\begin{array}{c}X\\Y\\Z\ конец {массив}\справа)=\влево(\начало{массив}{с}0\\0\\0\конец{массив}\справа).
Установка X=1 дает, как и наши первые два уравнения,
3-4Y+2Z=0,
-2+6Y+2Z=0.
Вычитание первого из второго:
-5+10Y=0,
и, таким образом, Y=\frac{1}{2}.
Подставляя обратно во второе уравнение,
-2+3+2Z=0,
что дает Z=-\frac{1}{2}.
Проверяя третье уравнение,
4+1-5=0,
который работает. Это дает нам собственный вектор
\left(1,-\frac{1}{2},\frac{1}{2}\right).
Еще раз, мы можем масштабироваться в 2 раза, чтобы получить
\влево(2,-1,1\вправо).
Собственный вектор, соответствующий собственному значению 6
В случае \lambda =6 имеем
\left(\begin{array}{ccc}-8&-4&2\\-2&-5&2\\4&2&-1\end{массив}\right)\left(\begin{array}{c}X\\ Y\\Z\end{массив}\right)=\left(\begin{array}{c}0\\0\\0\end{массив}\right).
Установка X=1 дает, как и наши первые два уравнения,
-8-4Y+2Z=0,
-2-5Y+2Z=0.
Вычитание первого из второго:
6-Y=0,
и, таким образом, Y=6.
Подставляя обратно во второе уравнение,
-2-30+2Z=0,
давая Z=16.
Проверяя третье уравнение,
4+12-16=0,
который работает. Это дает нам собственный вектор
\влево(1,6,16\вправо).
Общие Соображения
В общем, собственные значения реальной матрицы 3 на 3 могут быть
(i) три различных действительных числа, как здесь;
(ii) три действительных числа с повторениями;
(iii) одно действительное число и два сопряженных недействительных числа.
Геометрическая интерпретация преобразования зависит от того, что из вышеперечисленного верно: первое будет включать растяжение в трех направлениях собственного вектора, третье — вращение и растяжение вдоль своей оси, а второе — обычно один из нескольких типов трехмерного изображения. сдвиг. Однако мы оставляем эти детали на данный момент.
сдвиг. Однако мы оставляем эти детали на данный момент.
Еще одним важным применением собственных значений и собственных векторов является диагонализация, и именно к ней мы сейчас и обратимся.
Создано с помощью пакета ExportAsWebPage в Wolfram Mathematica 7.0
7. Собственные значения и собственные векторы
На этой странице
Определения
Нахождение собственных значений и собственных векторов (краткое описание)
Примеры 2×2
Сколько собственных значений и собственных векторов?
Примеры 3×3
Введение
На предыдущей странице, Собственные значения и собственные векторы — физический смысл и апплет геометрической интерпретации, мы видели пример растяжения эластичной мембраны и то, как это было представлено матричным умножением, а в особых случаях эквивалентно скалярным умножением.
Этот пример демонстрирует очень важную концепцию в технике и науке — собственных значений и собственных векторов — которая широко используется во многих приложениях, включая исчисление, поисковые системы, демографические исследования, аэронавтику и так далее.
Определение собственных значений и собственных векторов матрицы
Пусть A будет любой квадратной матрицей. Ненулевой вектор v является собственным вектором числа A , если
Av = λ v
для некоторого числа λ, называемого соответствующим собственным значением 9.
ПРИМЕЧАНИЕ: Немецкое слово « eigen » примерно переводится как «собственный» или «принадлежащий». Собственные значения и собственные векторы соответствуют друг другу (спарены) для любой конкретной матрицы А .
Решенные примеры ниже дают некоторое представление о том, что означают эти понятия. Во-первых, краткое изложение того, что мы собираемся сделать:
Как найти собственные значения и собственные векторы матрицы 2×2
- Настройте характеристическое уравнение , используя | А − λ I | = 0
- Решить характеристическое уравнение, получив собственных значений (2 собственных значения для системы 2×2)
- Заместитель собственные значения двух уравнений, заданных как A − λ I
- Выберите удобное значение для x 1 , затем найдите x 2
- Полученные значения образуют соответствующие собственных векторов из A (2 собственных вектора для системы 2×2)
Не существует единой формулы для собственных векторов как таковой — это скорее набор шагов, которые нам нужно выполнить, чтобы найти собственные значения и собственные векторы.
Давайте посмотрим на несколько примеров.
Пример 1
Начнем с системы двух уравнений, а именно:
y 1 = −5 x 1 + 2 x 2
y 2 = −9 x 1 + 6 x 2
Мы можем записать эти уравнения в матричной форме так:
`[(y_1),(y_2)]=[(-5,2), (-9,6)][(x_1),(x_2)]`
В общем случае мы можем записать приведенные выше матрицы как:
г = Ав
где
`bb(y) = [(y_1),(y_2)],`
`bb(A) = [(-5,2), (-9,6)]` и
`bb(v) = [(x_1),(x_2)]`
Шаг 1. Составьте характеристическое уравнение, используя |A − λI| = 0
Наша задача состоит в том, чтобы найти собственных значений λ и собственных векторов v, таких что:
у = λv
Ищем скалярных значений λ (числа, а не матрицы), которыми можно заменить матрицу A в выражении y = Av.
То есть мы хотим найти такое λ, что:
−5 x 1 + 2 x 2 = λ x 1
−9 x 1 + 6 x 2 = λ x 2
Перестановка дает:
— (5 — λ ) х 1 + 2 х 2 = 0
−9 x 1 + (6 − λ ) x 2 = 0 (1)
Это может быть записано с использованием матричной записи с единичной матрицей I как:
`(bb(A) — lambdabb(I))bb(v) = 0`, то есть:
`(bb(A) — лямбда[(1,0),(0,1)])bb(v) = 0`
`(bb(A) — [(лямбда,0),(0,лямбда)])bb(v) = 0`
Ясно, что у нас есть тривиальное решение `bb(v)=[(0),(0)]`, но для того, чтобы найти любые нетривиальные решения, мы применяем результат, следующий из правила Крамера, что это уравнение будет иметь нетривиальное (т. е. ненулевое) решение v , если его коэффициент-детерминант имеет значение 0.
е. ненулевое) решение v , если его коэффициент-детерминант имеет значение 0.
Полученное уравнение с использованием определителей `|bb(A) — lambdabb(I)| = 0` называется характеристическим уравнением .
Шаг 2. Решить характеристическое уравнение, получив собственные значения (2 собственных значения для системы 2×2) 92 — лямбда — 12`
`= (лямбда + 3)(лямбда — 4)`
Теперь это равно 0, когда:
`(лямбда + 3)(лямбда — 4) = 0`
То есть когда:
`лямбда = -3 или 4.`
Эти два значения являются собственными значениями для этой конкретной матрицы A .
Шаг 3. Подставьте собственные значения в два уравнения, заданные A − λI
Случай 1: `лямбда_1 = -3`
Когда `лямбда = лямбда_1 = -3`, уравнения (1) принимают вид:
`[-5-(-3)]x_1 + 2x_2 = 0`
`-9x_1 + [6-(-3)]x_2 = 0`
То есть:
`-2x_1 + 2x_2 = 0`
`-9x_1 + 9x_2 = 0` (2)
Разделив первую строку уравнений (2) на «-2» и вторую строку на «-9» (не обязательно, но помогает нам увидеть, что происходит), мы получим идентичные уравнения:
`x_1 — x_2 = 0`
`х_1 — х_2 = 0`
Шаг 4.
 Выберите удобное значение x 1 , затем найдите x 2
Выберите удобное значение x 1 , затем найдите x 2 Конечно, есть бесконечные решения, где `x_1 = x_2`. Мы выбираем удобное значение для `x_1`, скажем, `1`, что дает `x_2=1`.
Шаг 5. Полученные значения формируют соответствующие собственные векторы A (2 собственных вектора для системы 2×2)
Таким образом, соответствующий собственный вектор:
`бб(v_1)=[(1),(1)]`
ПРИМЕЧАНИЕ: Мы могли бы легко выбрать `x_1=3`, `x_2=3` или, если на то пошло, `x_1=-100`, `x_2=-100`. Эти значения по-прежнему будут «работать» в матричном уравнении.
В общем, мы могли бы написать наш ответ как «`x_1=t`, `x_2=t`, для любого значения t «, однако обычно имеет смысл выбрать удобное начальное значение (обычно для `x_1`) , а затем получить результирующие оставшиеся значения.
Это правильно?
Мы можем проверить, подставив:
`bb(Av)_1 = [(-5,2), (-9,6)][(1),(1)] `
`= [(-3),(-3)] `
`= -3[(1),(1)] `
`= лямбда_1bb(v)_1`
Мы нашли собственных значений `lambda_1=-3` и собственных векторов `bb(v)_1=[(1),(1)]` для матрицы
`bb(A) = [(-5,2), (-9,6)]` такое, что `bb(Av)_1 = lambda_1bb(v)_1. `
`
Графически мы можем видеть, что матрица `bb(A) = [(-5,2), (-9,6)]` действует на вектор `bb(v_1)=[(1),(1)]` эквивалентно умножению `bb(v_1)=[(1),(1)]` на скаляр `lambda_1 = -3.` В результате применяется шкала `-3.`
123-1-2-312-1-2-3xyОткрыть изображение на новой страницеГрафик, показывающий преобразование y 1 = Av 1
Случай 2: `лямбда_2 = 4`
Когда `лямбда = лямбда_2 = 4`, уравнения (1) принимают вид:
`(-5-(4))x_1 + 2x_2 = 0`
`-9x_1 + (6-(4))x_2 = 0`
То есть:
`-9x_1 + 2x_2 = 0`
`-9x_1 + 2x_2 = 0`
Мы выбираем удобное значение для `x_1` из `2`, давая `x_2=9`. Таким образом, соответствующий собственный вектор:
`bb(v)_2=[(2),(9)]`
Мы могли бы проверить это, умножив и заключив `[(-5,2), (-9,6)][(2),(9)] = 4[(2),(9)]`, то есть ` bb(Av)_2 = лямбда_2bb(v)_2. `
`
Мы нашли собственное значение `lambda_2=4` и собственный вектор `bb(v)_2=[(2),(9)]` для матрицы `bb(A) = [(-5,2), (-9,6)]` такое, что `bb(Av)_2 = lambda_2bb(v)_2.`
Графически мы можем видеть, что матрица `bb(A) = [(-5,2), (-9,6)]` действие на вектор `bb(v_2)=[(2),(9)]` эквивалентно умножению `bb(v_2)=[(2),(9)]` на скаляр `lambda_2 = 4. «Результат применения шкалы «4».
5101520510152025303540xyОткрыть изображение на новой страницеСколько собственных значений и собственных векторов?
В приведенном выше примере мы имели дело с системой `2xx2` и нашли 2 собственных значения и 2 соответствующих собственных вектора.
Если бы у нас была система `3xx3`, мы бы нашли 3 собственных значения и 3 соответствующих собственных вектора.
В общем, система `nxxn` будет производить `n` собственных значений и `n` соответствующих собственных векторов.
Пример 2
Найдите собственные значения и соответствующие собственные векторы для матрицы `[(2,3), (2,1)]. `
`
Ответить
Матрица `bb(A) = [(2,3), (2,1)]` соответствует линейным уравнениям:
`y_1 = 2x_1 + 3x_2`
`y_2 = 2x_1 + x_2`
Мы хотим найти такое λ, что:
`2x_1 + 3x_2 = лямбда x_1`
`2x_1 + x_2 = лямбда x_2`
Перестановка дает:
`(2-лямбда)x_1 + 3x_2 = 0`
`2x_1 + (1-лямбда)x_2 = 0` (3)
Характеристическое уравнение `|bb(A) — lambdabb(I)| = 0` для этого примера:
`|bb(A) — лямбдабб(I)| = | (2-лямбда, 3), (2, 1-лямбда) | ` 92 — 3лямбда — 4`
`=0`
Имеет значение `0`, когда `(лямбда — 4)(лямбда +1) = 0`.
Случай 1: `лямбда = 4`
При `лямбда_1 = 4` уравнения (3) принимают вид:
`(2-4)x_1 + 3x_2 = 0`
`2x_1 + (1-4)x_2 = 0`
То есть:
`-2x_1 + 3x_2 = 0`
`2x_1 -3x_2 = 0`
Мы выбираем удобное значение для `x_1` из `3`, что дает `x_2=2`. Таким образом, соответствующий собственный вектор:
Таким образом, соответствующий собственный вектор:
`бб(v_1)=[(3),(2)]`
Умножив, чтобы проверить наш ответ, мы найдем:
`[(2,3), (2,1)][(3),(2)] = 4[(3),(2)]`, то есть `bb(Av)_1 = lambda_1bb(v) _1.`
Графически мы можем видеть, что матрица `bb(A) = [(2,3), (2,1)]`, действующая на вектор `bb(v_1)=[(3),(2)]` эквивалентна к умножению `bb(v_1)=[(3),(2)]` на скаляр `lambda_1 = 4.` В результате применяется шкала `4.`
24681012246810xyОткрыть изображение на новой страницеГрафик, показывающий преобразование y 1 = Av 1 = λ 1 x 1
Случай 2: `lambda = -1`
При `lambda_2 = -1` уравнения (3) становятся:
`(2+1)x_1 + 3x_2 = 0`
`2x_1 + (1+1)x_2 = 0`
То есть:
`3x_1 + 3x_2 = 0`
`2x_1 + 2x_2 = 0`
Мы выбираем удобное значение `x_1 = 1`, что дает `x_2=-1`. Таким образом, соответствующий собственный вектор:
Таким образом, соответствующий собственный вектор:
`бб(v_2)=[(1),(-1)]`
Умножив, чтобы проверить наш ответ, мы найдем:
`[(2,3), (2,1)][(1),(-1)] = -1[(1),(-1)]`, то есть `bb(Av)_2 = lambda_2bb (в)_2.`
Графически мы можем видеть, что матрица `bb(A) = [(2,3), (2,1)]`, действующая на вектор `bb(v_2)=[(1),(-1)]`, равна эквивалентно умножению `bb(v_2)=[(1),(-1)]` на скаляр `lambda_2 = -1.` Мы масштабируем вектор `bb(v_2)` на `-1.`
1-11-1xyОткрыть изображение на новой страницеГрафик, показывающий преобразование y 2 = Av 2 = λ 2 x 2
Пример 3
Найдите собственные значения и соответствующие собственные векторы для матрицы `[(3,2), (1,4)].`
Ответить
Матрица `bb(A) = [(3,2), (1,4)]` соответствует линейным уравнениям:
`y_1 = 3x_1 + 2x_2`
`y_2 = x_1 + 4x_2`
Мы хотим найти такое λ, что:
`3x_1 + 2x_2 = лямбда x_1` 92 — 7лямбда +10`
`=0`
Имеет значение `0`, когда `(лямбда — 5)(лямбда — 2) = 0`.
Случай 1: `лямбда = 5`
При `лямбда_1 = 5` уравнения (4) принимают вид:
`(3-5)x_1 + 2x_2 = 0`
`x_1 + (4-5)x_2 = 0`
То есть:
`-2x_1 + 2x_2 = 0`
`x_1 — x_2 = 0`
Мы выбираем удобное значение `x_1 = 1`, что дает `x_2=1`. Таким образом, соответствующий собственный вектор:
`бб(v_1)=[(1),(1)]`
Умножив, чтобы проверить наш ответ, мы найдем:
`[(3,2), (1,4)][(1),(1)] = 5[(1),(1)]`, то есть `bb(Av)_1 = lambda_1bb(v) _1.`
Графически мы можем видеть, что матрица `bb(A) = [(3,2), (1,4)]`, действующая на вектор `bb(v_1)=[(1),(1)]` эквивалентна к умножению `bb(v_1)=[(1),(1)]` на скаляр `lambda_1 = 5.` В результате применяется шкала `5.`
12345-1123456-1xyОткрыть изображение на новой страницеГрафик, показывающий преобразование y 1 = Av 1 = λ 1 x 1
Случай 2: `lambda = 2`
С `lambda_2 = 2`, уравнения
`(3-2)x_1 + 2x_2 = 0`
`x_1 + (4-2)x_2 = 0`
То есть:
`x_1 + 2x_2 = 0`
`x_1 + 2x_2 = 0`
Мы выбираем удобное значение `x_1 = 2`, что дает `x_2=-1`. Таким образом, соответствующий собственный вектор:
Таким образом, соответствующий собственный вектор:
`бб(v_2)=[(2),(-1)]`
Умножив, чтобы проверить наш ответ, мы найдем:
`[(3,2), (1,4)][(2),(-1)] = 2[(2),(-1)]`, то есть `bb(Av)_2 = lambda_2bb( в)_2.`
Графически мы можем видеть, что матрица `bb(A) = [(3,2), (1,4)]`, действующая на вектор `bb(v_2)=[(2),(-1)]`, равна эквивалентно умножению bb(v_2) на скаляр lambda_2 = 5. Мы масштабируем вектор bb(v_2) на 5.
246810-2-4-6xyОткрыть изображение на новой страницеГрафик, показывающий преобразование y 2 = Av 2 = λ 2 x 2
Матрицы 3xx3, их собственные значения и собственные векторы
Процесс нахождения собственных значений и собственных векторов матрицы `3xx3` аналогичен процессу для случая `2xx2`.
Пример 4: случай `3xx3`
Найдите собственные значения и собственные векторы для матрицы `[(0,1,0),(1,-1,1),(0,1,0)]. `
`
Ответить
Мы хотим найти `лямбда` такую, что:
`x_2 = лямбда x_1` 92 + лямбда -2)`
`= -лямбда(лямбда + 2)(лямбда -1)`
`=0`
Это происходит, когда `лямбда_1 = 0`, `лямбда_2=-2` или `лямбда_3= 1.`
Случай 1: `лямбда=0`
Уравнения (5) становятся:
`x_2 = 0`
`x_1 — x_2 + x_3 = 0`
`x_2 = 0`
Очевидно, `x_2 = 0`, и мы выберем `x_1 = 1`, что дает `x_3 = -1`.
Таким образом, для собственного значения `lambda_1=0` соответствующий собственный вектор равен `bb(v)_1 =[(1),(0),(-1)].`
Случай 2: `лямбда=-2`
Уравнения (5) становятся:
`2 х_1 + х_2 = 0`
`x_1 + x_2 + x_3 = 0`
`x_2 + 2 x_3 = 0`
Выбор `x_1 = 1` дает `x_2 = -2`, а затем `x_3 = 1.` ),(-2),(1)].`
Случай 3: `лямбда=1`
Уравнения (5) принимают вид:
`- х_1 + х_2 = 0`
`x_1 — 2x_2 + x_3 = 0`
`x_2 — x_3 = 0`
Выбор «x_1 = 1» дает «x_2 = 1», а затем «x_3 = 1».
Таким образом, для собственного значения «lambda_3=1» соответствующий собственный вектор равен (1),(1)].`
Собственные векторы — Как найти?
Мы знаем, что векторы меняют свою величину и направление, когда к ним применяется некоторое линейное преобразование. Но некоторые векторы не сильно меняются (или, другими словами, меняются не более чем на свой масштабный коэффициент) даже после применения к ним преобразований. Такие векторы называются собственными векторами. Мы всегда должны находить собственные значения перед нахождением собственных векторов.
Вместе с примерами научимся находить собственные значения и собственные векторы для матриц 2 × 2 и 3 × 3.
| 1. | Что такое собственные векторы? |
| 2. | Собственные значения и собственные векторы |
| 3. | Как найти собственные векторы матрицы 2 × 2? |
4. | Как найти собственные векторы матрицы 3 × 3? |
| 5. | В поисках собственного пространства |
| 6. | Диагонализация матрицы с использованием собственных значений и собственных векторов |
| 7. | Часто задаваемые вопросы о собственных векторах |
Что такое собственные векторы?
В линейной алгебре собственных векторов квадратной матрицы являются ненулевыми векторами, которые при умножении на квадратную матрицу дадут только скалярное число векторов. т. е. вектор v называется собственным вектором квадратной матрицы A тогда и только тогда, когда A v = λ v для некоторого скаляра λ. Здесь v является собственным вектором, так как при его умножении на A получается λ v , что является скалярным числом, кратным v . Здесь скаляр λ называется собственным значением, которое соответствует собственному вектору v .
Здесь скаляр λ называется собственным значением, которое соответствует собственному вектору v .
Слово «eigen» означает «собственный», «характерный», «собственный», «типичный» и т. д. и происходит из немецкого языка. Таким образом, собственные векторы матрицы также известны как характеристические векторы матрицы.
В приведенной выше формуле, если A — квадратная матрица порядка n × n, тогда v — вектор-столбец порядка nx1. Здесь v является правым собственным вектором A, поскольку он умножается на правую часть A. В основном собственный вектор означает, что это правильный собственный вектор. Напротив, левый собственный вектор матрицы порядка n × n — это вектор-строка порядка 1xn, такая что v A = λ v .
Собственные значения и собственные векторы
В предыдущем разделе мы видели, что вектор-столбец v является собственным вектором квадратной матрицы A (порядка n × n) тогда и только тогда, когда A v = λ v . Мы можем записать это уравнение как A v = λI v , где I — единичная матрица того же порядка n × n. Уравнение можно записать как
Мы можем записать это уравнение как A v = λI v , где I — единичная матрица того же порядка n × n. Уравнение можно записать как
A v — λI v = O
Здесь O — нулевая матрица.
(А — λI) v = О … (1)
Чтобы эта однородная система имела нетривиальное решение, определитель должен быть равен 0.
|A — λI| = 0 … (2)
Мы можем завершить шаги по нахождению собственных значений и собственных векторов для любой квадратной матрицы A следующим образом:
- Чтобы найти собственные значения A, решите характеристическое уравнение |A — λI| = 0 (уравнение (2)) для λ, и все такие значения λ давали бы собственные значения.
- Чтобы найти собственные векторы A, подставьте каждое собственное значение (т. е. значение λ) в уравнение (1) (A — λI) v = O и найдите v , используя метод по вашему выбору.

(Это приведет к системе однородных линейных уравнений. Чтобы узнать, как решать такие системы, щелкните здесь.)
Давайте посмотрим, как найти собственные векторы матрицы 2 × 2 и матрицы 3 × 3, используя эти шаги.
Как найти собственные векторы матрицы 2 × 2?
Чтобы найти собственные векторы, мы сначала должны вычислить собственные значения, используя вышеупомянутые шаги. Разберем процесс на примере.
Пример: Найти собственные значения и собственные векторы матрицы A = \(\left[\begin{array}{ll}
5 и 4 \\\
1 и 2
\end{массив}\right]\).
Решение:
Пусть λ представляет собственное значение (значения) и v = \(\left[\begin{array}{l}
х\\
г
\end{массив}\right]\) представляют собственный вектор(ы).
Тогда уравнение характеристики:
|A — λI| = 0
\(\left|\begin{массив}{ll}
5- λ&4\\
1 и 2- λ
\end{массив}\right|\) = 0
(5 - λ) (2 — λ) — (4)(1) = 0
10 — 5λ — 2λ + λ 2 — 4 = 0
λ 2 — 7λ + 6 = 0
(λ — 6)(λ — 1) = 0
λ = 6, λ = 1.
Таким образом, собственные значения равны 1 и 6. Найдем соответствующий собственный вектор каждому собственному значению в каждом случае.
При λ = 1:
Подставьте λ = 1 в уравнение:
(A — λI) v = O
\(\left[\begin{array}{ll}
5- 1 и 4\\
1 и 2- 1
\end{массив}\right]\) \(\left[\begin{массив}{l}
х\\
г
\end{массив}\right]\) = \(\left[\begin{массив}{l}
0\\
0
\end{массив}\right]\)
\(\left[\begin{массив}{ll}
4& 4 \\\
1 и 1
\end{массив}\right]\) \(\left[\begin{массив}{l}
х\\
г
\end{массив}\right]\) = \(\left[\begin{массив}{l}
0\\
0
\end{array}\right]\)
Чтобы решить эту систему, мы применяем элементарные преобразования строк (в качестве альтернативы мы можем использовать правило Крамера) на матрице коэффициентов:
Apply R 2 → 4R 2 — R 1 ,
\(\left[\begin{array}{ll}
4& 4 \\\
0 и 0
\end{массив}\right]\) \(\left[\begin{массив}{l}
х\\
г
\end{массив}\right]\) = \(\left[\begin{массив}{l}
0\\
0
\end{array}\right]\)
Расширение в виде уравнений,
4x + 4y = 0
У нас есть одно уравнение с двумя переменными. Итак, предположим, что y = t. Тогда
Итак, предположим, что y = t. Тогда
4x + 4t = 0 ⇒ 4x = -4t ⇒ x = -t
Итак, решение: \(\left[\begin{array}{l}
х\\
г
\end{массив}\right]\) = \(\left[\begin{массив}{l}
-т\\
т
\end{массив}\right]\) = t \(\left[\begin{массив}{l}
-1\\
1
\end{array}\right]\)
Таким образом, собственный вектор равен \(\left[\begin{array}{l}
-1\\
1
\end{массив}\right]\).
Когда λ = 6:
Подставим λ = 1 в уравнение:
(A — λI) v = O
\(\left[\begin{array}{ll}
5- 6 и 4\\
1 и 2-6
\end{массив}\right]\) \(\left[\begin{массив}{l}
х\\
г
\end{массив}\right]\) = \(\left[\begin{массив}{l}
0\\
0
\end{массив}\right]\)
\(\left[\begin{массив}{ll}
-1&4\\
1 и -4
\end{массив}\right]\) \(\left[\begin{массив}{l}
х\\
г
\end{массив}\right]\) = \(\left[\begin{массив}{l}
0\\
0
\end{array}\right]\)
Чтобы решить эту систему, мы применяем элементарные преобразования строк (в качестве альтернативы мы также можем найти правило Крамера) на матрице коэффициентов:
Применить R 2 → R 2 + R 1 ,
\(\left[\begin{array}{ll}
-1&4\\
0 и 0
\end{массив}\right]\) \(\left[\begin{массив}{l}
х\\
г
\end{массив}\right]\) = \(\left[\begin{массив}{l}
0\\
0
\end{array}\right]\)
Разложение в виде уравнений,
-x + 4y = 0
Пусть y = t. Тогда -x + 4t = 0 ⇒ x = 4t.
Тогда -x + 4t = 0 ⇒ x = 4t.
Итак, решение: \(\left[\begin{array}{l}
х\\
г
\end{массив}\right]\) = \(\left[\begin{массив}{l}
4т\\
т
\end{массив}\right]\) = t \(\left[\begin{массив}{l}
4\\
1
\end{array}\right]\)
Таким образом, собственный вектор равен \(\left[\begin{array}{l}
4\\
1
\end{массив}\right]\).
Таким образом, собственные векторы данной матрицы 2 × 2 равны \(\left[\begin{array}{l}
-1\\
1
\end{массив}\right]\) и \(\left[\begin{массив}{l}
4\\
1
\end{массив}\right]\).
Как найти собственные векторы матрицы 3 × 3?
Выполняем те же шаги, что и выше, для матрицы 3 × 3. Вот пример.
Пример: Найти собственные векторы матрицы 3 × 3 A = \(\left[\begin{array}{lll}
1&1&1\
1 & 1 & 1 \
1 и 1 и 1
\end{массив}\right]\).
Решение:
Пусть λ будет собственным значением и v = \(\left[\begin{array}{l}
х\
у\\г
\end{array}\right]\) — собственный вектор A.
Нахождение собственных значений:
Характеристическое уравнение:
|A — λI| = 0
\(\left|\begin{массив}{lll}
1- λ&1&1\
1&1- λ&1\
1 и 1 и 1- λ
\end{array}\right|\) = 0
Вычисляя определитель, получаем
-λ 3 + 3λ 2 = 0
λ 2 (-λ+3) = 0 9
Таким образом, собственные значения равны 0 и 3. Найдем соответствующие собственные векторы.
Когда λ = 0:
(A — λI) v = 0
\(\left[\begin{array}{lll}
1- 0&1&1\
1&1- 0&1\
1 и 1 и 1- 0
\end{массив}\right]\) \(\left[\begin{массив}{l}
х\
г\\г
\end{массив}\right]\) = \(\left[\begin{массив}{l}
0\
0\\0
\end{массив}\right]\)
\(\left[\begin{array}{lll}
1&1&1\
1&1&1\
1 и 1 и 1
\end{массив}\right]\) \(\left[\begin{массив}{l}
х\
г\\г
\end{массив}\right]\) = \(\left[\begin{массив}{l}
0\
0\\0
\end{array}\right]\)
Применить R 2 → R 2 — R 1 и R 3 → R 3 — R 1 (\left,
\begin{массив}{lll}1&1&1\
0 & 0& 0\\
0 и 0 и 0
\end{массив}\right]\) \(\left[\begin{массив}{l}
х\
г\\г
\end{массив}\right]\) = \(\left[\begin{массив}{l}
0\
0\\0
\end{array}\right]\)
Разложив приведенную выше матрицу, мы получим
x + y + z = 0
У нас есть только одно уравнение с двумя неизвестными. Итак, предположим, что две переменные равны y = t 1 и z = t 2 . Тогда приведенное выше уравнение принимает вид:
Итак, предположим, что две переменные равны y = t 1 и z = t 2 . Тогда приведенное выше уравнение принимает вид:
x + t 1 + t 2 = 0 ⇒ x = — t 1 — t 2 .
Таким образом, собственный вектор равен:
\(\left[\begin{array}{l}
х\
у\\г
\end{массив}\right]\) = \(\left[\begin{массив}{l}
— т 1 — т 2 \
т 1 \т 2
\end{массив}\right]\) = t 1 \(\left[\begin{array}{l}
-1\
1\0
\end{массив}\right]\) + t 2 \(\left[\begin{массив}{l}
-1\
0\1
\end{массив}\right]\).
Таким образом, собственные векторы, соответствующие λ = 0, равны \(\left[\begin{array}{l}
-1\
1\0
\end{массив}\right]\) и \(\left[\begin{массив}{l}
-1\
0\1
\end{массив}\right]\).
Когда λ = 3:
(A — λI) v = 0
\(\left[\begin{array}{lll}
1- 3&1&1\
1&1- 3&1\
1 и 1 и 1-3
\end{массив}\right]\) \(\left[\begin{массив}{l}
х\
г\\г
\end{массив}\right]\) = \(\left[\begin{массив}{l}
0\
0\\0
\end{массив}\right]\)
\(\left[\begin{array}{lll}
-2&1&1\
1&-2&1\
1 и 1 и -2
\end{массив}\right]\) \(\left[\begin{массив}{l}
х\
г\\г
\end{массив}\right]\) = \(\left[\begin{массив}{l}
0\
0\\0
\end{array}\right]\)
Применить R 2 → 2R 2 + R 1 и R 3 → 2R 3 + R 1 ,
\(\left[\begin{array}{lll}
-2&1&1\
0&-3&3\\
0 и 3 и -3
\end{массив}\right]\) \(\left[\begin{массив}{l}
х\
г\\г
\end{массив}\right]\) = \(\left[\begin{массив}{l}
0\
0\\0
\end{array}\right]\)
Теперь примените R 3 → R 3 + R 2 ,
\(\left[\begin{массив}{lll}
-2&1&1\
0&-3&3\\
0 и 0 и 0
\end{массив}\right]\) \(\left[\begin{массив}{l}
х\
г\\г
\end{массив}\right]\) = \(\left[\begin{массив}{l}
0\
0\\0
\end{array}\right]\)
Разложив вышеприведенную матрицу, получим
-2x + y + z = 0
-3y + 3z = 0
Пусть z = t. Тогда
Тогда
-3y + 3z = 0 ⇒ z = y = t.
-2x + y + z = 0 ⇒ -2x + t + t = 0 ⇒ x = t.
Таким образом, собственный вектор равен:
\(\left[\begin{array}{l}
х\
у\\г
\end{массив}\right]\) = \(\left[\begin{массив}{l}
т\
т\т
\end{массив}\right]\) = t \(\left[\begin{массив}{l}
1\
1\1
\end{массив}\right]\).
Таким образом, собственный вектор, соответствующий λ = 3, равен \(\left[\begin{array}{l}
1\
1\1
\end{массив}\right]\).
Таким образом, собственные векторы данной матрицы 3 × 3 равны \(\left[\begin{array}{l}
-1\
1\0
\end{массив}\right]\), \(\left[\begin{массив}{l}
-1\
0\1
\end{массив}\right]\) и \(\left[\begin{массив}{l}
1\
1\1
\end{массив}\right]\).
Поиск собственного пространства
собственное пространство матрицы (линейное преобразование) представляет собой набор всех ее собственных векторов. т. е. найти собственное пространство:
т. е. найти собственное пространство:
- Сначала найти собственные значения.
- Затем найдите соответствующие собственные векторы.
- Просто заключите все собственные векторы в набор (порядок не имеет значения).
Из приведенного выше примера собственное пространство A равно \(\left\{\left[\begin{array}{l}
-1\
1\0
\end{массив}\right], \left[\begin{массив}{l}
-1\
0\1
\end{массив}\right], \left[\begin{массив}{l}
1\
1\1
\end{массив}\right]\right\}\).
Обратите внимание, что векторы в собственном пространстве линейно независимы.
Диагонализация матрицы с использованием собственных значений и собственных векторов
Диагонализация матрицы A — это процесс ее записи в виде произведения трех матриц, из которых средняя является диагональной матрицей, т. е. A = XDX -1 , где D — матрица собственных значений (чтобы найти D, возьмем единичная матрица того же порядка, что и A, замените в ней единицы собственными значениями), а X — матрица собственных векторов, записанных в том же порядке, что и собственные значения в D. Вот пример.
Вот пример.
Пример: Диагонализация матрицы \(=\left[\begin{array}{lll}
1&1&1\
1&1&1\
1 и 1 и 1
\end{массив}\right]\).
Решение:
Мы уже нашли, что собственные значения равны 0, 0 и 3. Соответствующие собственные векторы равны \(\left[\begin{array}{l}
-1\
1\0
\end{массив}\right]\), \(\left[\begin{массив}{l}
-1\
0\1
\end{массив}\right]\) и \(\left[\begin{массив}{l}
1\
1\1
\end{массив}\right]\). Таким образом,
D = \(\left[\begin{array}{lll}
0&0&0\
0&0&0\
0 и 0 и 3
\end{массив}\right]\) и X = \(\left[\begin{массив}{rcr}
-1&-1&1\
1&0&1\
0 и 1 и 1
\end{массив}\right]\).
Тогда обратная матрица X равна X -1 = \(\left[\begin{array}{rcr}
-1/3&2/3&-1/3\
-1/3&-1/3&2/3\
1/3 и 1/3 и 1/3
\end{массив}\right]\).

 09.2022
09.2022 Таким образом,
не зависит от выбора базиса. Значит, и
|A-λE|
не изменяется при переходе к новому
базису.
Таким образом,
не зависит от выбора базиса. Значит, и
|A-λE|
не изменяется при переходе к новому
базису.
 com/first-course-linear-алгебра
com/first-course-linear-алгебра
