Испытания и события. Виды случайных событий и операции над событиями. Общие правила комбинаторики. Классическое определение вероятности. Примеры непосредственного вычисления вероятностей. Элементы теории корреляции
1. Испытания и события. Виды случайных событий и операции над событиями.
Испытания – это опыт, эксперимент, наблюдение.
Например, подбрасывание игральной кости, монеты, выстрел из винтовки и.т.д.
Событие – это результат исход испытания.
Например, выпадение герба или решки.
Случайным событием называют любой исход опыта, который может произойти или не произойти, если будет осуществлена определенная совокупность условий.
Обозначаются события как А, В, С…
События прописываются:
А – выпадет 5 очков
В – выпадет 3 очка
Недостоверный исход элементарных событий обозначается через w.
Элементарные
события рассматриваются, как неразложимые и
взаимоисключаемые исходы опыта.
Множество всех элементов событий называется пространством элементов событий или пространством исходов и обозначается Ω.
Конечное пространство
Событие будет называться подмножеством множества Ω.
Событие называется достоверным, если оно обязательно наступит в результате данного опыта и обозначается через Ω.
Событие называется невозможным если оно заведомо не произойдет в результате опыта. Оно обозначается ø.
Два события называются несовместными, если появление одного из них исключает появление другого события в одном и том же опыте, т.е. не могут произойти в одном и том же опыте.
В противном случае события называются совместные, т.е. появление одного из них не исключает появление в одном и том же опыте.
События А1, А2, А3, … Аn называют попарно несовместными, если любые 2 из них не совместные.
Совокупность
событий образуют полную группу, если они попарно
несовместные и в результате каждого опыта происходит одно и только одно из них.
Событие называется равновозможное, если одно из них не является объективно более возможным, чем другие, т.е. все события имеют равные шансы.
Два события называются противоположными, если в данном опыте они несовместимы и одно из них обязательно произойдет: А – появление герба, Ã – появление решки.
2. Общие правила комбинаторики. Размещение, перестановки, сочетания с повторениями и без повторений.
Правило суммы:
Если некоторый объект А может быть выбран m способами, а некоторый объект В n, то либо объект А либо объект В может быть выбран m+n способами.
Правило произведений:
Если некоторый объект А может быть выбран m способами и после некоторого выбора объект В можно выбрать n способами, то пара объектов в указанном порядке можно выбрать m*n способами.
n — Количество всех вариантов
Перестановка без повторений:
Перестановкой
называются комиции, состоящие из одних и тех же n-различных
элементов и отличает их порядком расположения.
Число всевозможных перестановок: Pn=n!
Размещение без повторений:
Размещением называют комбинацию, состоящую из n-различными элементами по m элементов, которые отличаются либо составом элементов, либо их порядком.
Amn =
Сочетание без повторений:
Называется комбинация, состоящая из n-различных элементов по m, которая отличается хотя бы 1 элементом (порядок элементом не имеет значение)
Сmn =
Размещение и сочетание с повторениями:
Если в размещение или сочетании из n элементов по m некоторые из элементов или все, могут оказаться одинаковыми, то такие размещение или сочетания называются с повторениями.
Размещение с повторениями (порядок важен)
Ãmn = nm
Сочетание с повторениями (порядок не важен)
Čmn = Сmn+m-1 =
Перестановки с повторениями:
Если
в перестановках из общего числа n-элементов
есть k различных элементов,
при этом, если первый элемент повторяется n1
раз, второй n2 раз, k
повторяется nk раз. При чем n=сумме
всех элементов, то такие перестановки называются с повторением.
При чем n=сумме
всех элементов, то такие перестановки называются с повторением.
n=n1+n2+…+nk
Ãn(n1,n2,…nk) =
3. Классическое определение вероятности. Примеры непосредственного вычисления вероятностей.
Теория вероятности – это математическая наука изучающая закономерность, присущее массовым случайным явлениям.
В дискретном пространстве вероятность каждого элементарного исхода считается заданной и обозначается P(…)
Всегда вероятность события положительна, P=>0.
Сумма конечных или бесконечных вероятностей всех элементарных исходов – это элементарные события.
Вероятность события:
P(A)=
Вероятность события А называют относительные числа благоприятных данному событию (m) к числу всевозможных событий (n).
Свойства классической вероятности:
1) Достоверные события равна
P(А)=1, n=m
2) Вероятность невозможных событий
P(А)=P(ø)=0/n=0
m=0
3) Вероятность случайных событий
P(A)=m/n
m<n 0<=P(A)<=1
Вероятность любого
события удовлетворяет двойственному неравенству, которое находится в пределах
от 0 до 1.
Пример:
В урне находится 3 белых шара, 4 черных, 5 синих.
Какова вероятность появления белого шара
n=3б+4ч+5с=12
A – Извлечение белого шара
P(A)=m/n=3/12
4. Относительная частота. Устойчивость относительной частоты.
1 2 3 4
1 2 3 4 ©emirsaba. | Басты бет Lessons Curriculum vitae Documents |
Комбинированная формула, Комбинации без повторения
Содержание страницы
Комбинации и перестановки
Комбинированная формула
Комбинации без повторений Пример
Комбинации в математике похожи на перестановки, но это разные вещи.
При перестановках, как с повторением, так и без повторения, важен порядок.
Например, с номером телефона, который представляет собой перестановку чисел.
Комбинации и перестановки Перестановка
Номер телефона может быть таким: 034357698
Чтобы позвонить нужному человеку, необходимо набрать цифры в правильном порядке.
В лотерее могут быть следующие выигрышные номера: 23 45 31 52 03
Неважно, в каком порядке вы выбираете номера в своем билете, если они есть у вас. Выиграет.
Эта страница специально посвящена комбинациям БЕЗ повторения каких-либо чисел или объектов.
Комбинация против перестановкиКак правило, существует гораздо больше перестановок, чем комбинаций, которые можно составить из набора числа.
Рассмотрим числа: 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8
Это та же комбинация цифр, но другая перестановка.
С номерами от 1 до 8 ,
есть 8! возможные упорядоченные перестановки. 8! = 40320
8! = 40320
Таким образом, только 1 комбинация, но 40320 возможные перестановки без повторения.
Комбинация Формула
Существует формула комбинации, которую можно использовать для определения количества комбинаций, возможных при выбирая из группы. 9{11}}P_4} = \bf{\frac{11!}{(11 \space — \space 4)!}} = \bf{\frac{11!}{7!}} = \bf{\frac {39’916’800}{5’040}} = 7920
Поскольку порядок выгула собак в комбинации не имеет значения, количество комбинаций будет меньше числа перестановок.
Итак, нам нужно уменьшить 7920 на правильную величину.
Каким-то образом изменив исходную сумму перестановок \bf{\frac{11!}{(11 \space — \space 4)!}}.
Изменение Формула перестановки Нам нужно избавиться от упорядоченных перестановок, которые не подлежат подсчету.
Потому что 1 , 2 , 3 , 4 и 4 , 3 , 2 , 1
— это  2 перестановки, но они представляют собой одну и ту же  1 комбинацию.
Из 4 собак количество возможных перестановок равно 4! .
Разделим 7920 на это 4! , достаточно уменьшает 7920 ,
дает нам правильное количество возможных комбинаций выбора  4 собак из  11.
\bf{\frac{7920}{4!}} = \bf{\frac{7920}{24}} = 330
Умножение на \bf{\frac{1}{4!}} аналогично деление на 4! .
Здесь мы можем сделать \bf{\frac{11!}{(11 \space — \space 4)!}} × \bf{\frac{1}{4!}}, в результате \bf{\frac{11!}{4!(11 \space — \space 4)!}}.
\bf{\frac{11!}{4!(11 \пробел — \пробел 4)!}} = 330
Эта новая сумма фактически представляет собой формулу комбинации.
Обозначение комбинаций в математике похоже на обозначение перестановок в том смысле, что оно может быть представлено в несколько разных способов. 9п} ) все представляют выбор k комбинации из n .
Комбинация Пример формулы
(1.1)
В кондитерской есть 14 разных плиток шоколада.
Мальчик хочет купить 3 разные батончики из этой группы.
Сколько комбинаций 9{14}}C_3} = \bf{\frac{14!}{3!\space(14 \space — \space 3)!}} = \bf{\frac{87178291200}{239500800}} = 364
Существует 364 возможных комбинаций  3 различных плиток шоколада, которые можно приготовить
из группы  14 доступных на выбор.
- Дом ›
- Статистика/данные › Комбинированная формула
√ Перестановки и комбинации: определение, обозначения, примеры (определения и примеры)
by Sigma
Содержание
Определения- а Комбинация — это когда порядок не имеет значения.

- a Перестановка Когда порядок имеет значение.
Другими словами:
ПерестановкиПерестановка — это упорядоченная Комбинация.
Существует 2 типа перестановки:
- Перестановка с повторением: например, замок. Это может быть «444».
- Перестановка без повторения: например, первые три человека в забеге. Нельзя быть первым и вторым.
Формула написана:
N R
, где
- повторение разрешено
- порядок имеет значение
- N — это количество вещей на выбор
- R — число вещей, которые мы выбираем n
- .
1. Для PIN-кода моей учетной записи есть 10 номеров на выбор (0,1,2,3,4,5,6,7,8,9), и мы выбираем 6 из них.
 (Вы можете выбрать один и тот же номер дважды или более)
(Вы можете выбрать один и тот же номер дважды или более)n r = 10 × 10 × 10 × 10 × 10 × 10 = 1 000 000
Таким образом, для моего вывода существует 1 000 000 перестановок.
2. В каком порядке 7 бегунов могут оказаться в тройке лучших? (бегун на первом месте не может быть на втором месте)
Итак, есть 210 перестановок для трех лучших бегунов.
Обозначение перестановкиВместо записи всей формулы люди используют различные обозначения, такие как эти:0301 n P r = n P r =
P (7,3) = 210
CombinationsЕсть 2 типа комбинаций (помните порядок теперь не имеет значения):
- комбинация с повторением: например монеты в кармане (5,5,10,10,10)
- комбинация без повторения : например, номера лотереи (5,14,17,22,30,34)
Формула написана:
где,
- n — количество вещей на выбор
- r — количество вещей, которые мы можем выбрать
- r — количество вещей, которые мы можем выбрать из 9002 6 02952 порядок
- 0
- 0 не имеет значения
Формула написана:
где,
- n — количество вещей на выбор
- r — количество вещей, которые мы выбираем из n
- повторение НЕ разрешено
- порядок не имеет значения
1.
 В холодильнике есть клубника, виноград, бананы, ананасы и яблоки. Я хочу сделать 3 чашки сока. Сколько комбинаций я могу сделать? (повторение разрешено)
В холодильнике есть клубника, виноград, бананы, ананасы и яблоки. Я хочу сделать 3 чашки сока. Сколько комбинаций я могу сделать? (повторение разрешено)Итак, я могу сделать 420 комбинаций соков.
2. Мой учитель сказал мне выбрать 3 девочек из 7 девочек в моем классе. Сколько вариантов у меня есть? (повтор не допускается)
Комбинированная нотацияВместо написания всей формулы люди используют разные обозначения, такие как эти:
C ( N, R ) = 4
9000 2 =77977777777777777777777777777777777777777777777777777777777777777777777777777777777777797777
97797797797797797797797779. 9.9. ). = N C R =774 C =
9000 2 C = 9000 2 C = = . 0027
00271. У Грейс 4 юбки, 5 футболок, 4 туфельки. Можно комбинировать друг с другом. Определите, сколькими способами она может комбинировать юбку, футболку и туфли.
Ответ
Есть:
4 юбка
5 футболка
4 туфли
Тогда 4 x 5 x 4 = 80 способов.
2. Семья мистера Райта сделает совместное фото. У него две дочери и один сын. Он хочет, чтобы его ребенок всегда стоял между ним и его женой. Определите, сколько положений нужно сделать.
Ответить
Между мистером и миссис Райт всегда есть трое детей.
Итак, есть только изменение детской позиции 3! = 3.2.1 = 6
Тогда из-за того, что Мистер и Миссис Справа всегда находятся в крайнем левом-правом положении, поэтому есть только две возможности (Мистер Справа с левой стороны и Миссис Справа с правой стороны или наоборот) .
в заключение, есть 6 х 2 = 12 позиций.
3. В саду живут 3 мальчика и 4 девочки. Они будут смотреть шоу и сидеть на скамейке. Сколькими способами их расположить, если:
- Нет ограничений
- Мальчики и девочки чередуются
Ответ
3 мальчика
4 девочки
- Без ограничений = 7! = 7 P 7 = 5040 способов
- Мальчики и девочки чередуются = 4 x 3 x 3 x 2 x 2 x 1 x 1 = 144 способа.

Примечание: красные, как девушки.
4. В тесте по математике 10 вопросов. Студенты должны ответить на пять вопросов. Каждый ученик должен ответить на 8 вопросов. Сколько способов выбрать еще пять вопросов?
Ответ
Всего вопросов 10
5 необходимо выполнить
Необходимо ответить на три вопроса, и учащиеся должны выбрать его из других пяти вопросов.
Итак, здесь используется комбинированная концепция.
5 C 3 = 10 способов.
5. Сэнди отправляется в магазин за 5 разными закусками со вкусом барбекю и 4 разными бутылками диетической газировки. Если есть 10 различных вкусов барбекю и 6 различных видов диетической газировки на выбор, определите, сколько различных вариантов предлагает Сэнди.
Ответ
Закуски: 5 из 10 вариантов
Сода: 4 из 6 вариантов
затем
10 C 5 x 6 C 4 = 252 x 157801. Есть большая группа студентов, состоящая из 7 мужчин и 8 женщин.

, где
- . из п
, где

 Выясним их суть и формулы, по которым можно найти их количество.
Выясним их суть и формулы, по которым можно найти их количество. В отличие от элементов множеств, элементы выборки могут повторяться.
В отличие от элементов множеств, элементы выборки могут повторяться.
 Представьте, что мы наугад запускаем руку в корзинку с целью вытащить три конфеты. Вытащенные конфеты – это и есть выборка. Так как мы вытаскиваем 3 конфеты из 6, то получаем (6,3)-выборку. Порядок расположения конфет в ладони совершенно несущественен, поэтому эта выборка является неупорядоченной. Ну, и так как все конфеты различны, то выборка без повторений. Итак, в данной ситуации говорим о неупорядоченной (6,3)-выборке без повторений.
Представьте, что мы наугад запускаем руку в корзинку с целью вытащить три конфеты. Вытащенные конфеты – это и есть выборка. Так как мы вытаскиваем 3 конфеты из 6, то получаем (6,3)-выборку. Порядок расположения конфет в ладони совершенно несущественен, поэтому эта выборка является неупорядоченной. Ну, и так как все конфеты различны, то выборка без повторений. Итак, в данной ситуации говорим о неупорядоченной (6,3)-выборке без повторений.
 При этом выборки могут быть самыми различными: у нас даже могут оказаться все конфеты одного сорта. Следовательно, в этой ситуации мы имеем дело с неупорядоченной (4,20)-выборкой с повторениями.
При этом выборки могут быть самыми различными: у нас даже могут оказаться все конфеты одного сорта. Следовательно, в этой ситуации мы имеем дело с неупорядоченной (4,20)-выборкой с повторениями.
 Множество U таково: U={1,5,7,8}. Цифры каждого составленного числа образуют (4,8)-выборку. Порядок следования цифр в числе важен, т.е. выборка упорядоченная. Повторения допускаются, поэтому здесь мы имеем дело с упорядоченной (4,8)-выборкой с повторениями.
Множество U таково: U={1,5,7,8}. Цифры каждого составленного числа образуют (4,8)-выборку. Порядок следования цифр в числе важен, т.е. выборка упорядоченная. Повторения допускаются, поэтому здесь мы имеем дело с упорядоченной (4,8)-выборкой с повторениями.
 org 2023
org 2023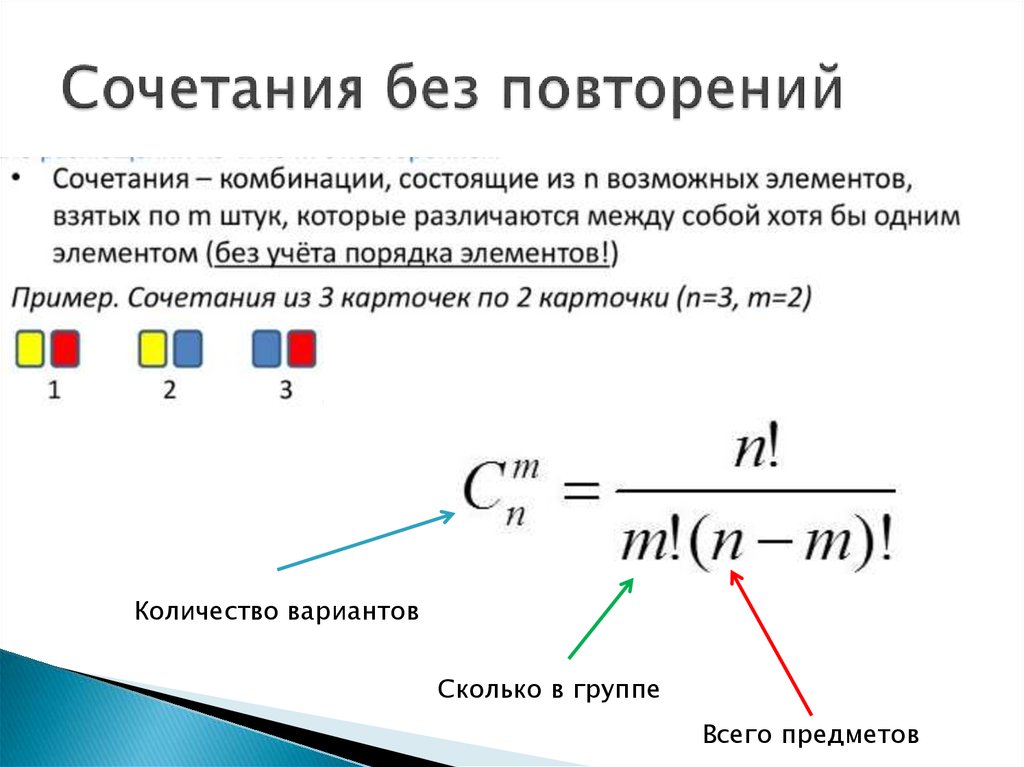
 (Вы можете выбрать один и тот же номер дважды или более)
(Вы можете выбрать один и тот же номер дважды или более) В холодильнике есть клубника, виноград, бананы, ананасы и яблоки. Я хочу сделать 3 чашки сока. Сколько комбинаций я могу сделать? (повторение разрешено)
В холодильнике есть клубника, виноград, бананы, ананасы и яблоки. Я хочу сделать 3 чашки сока. Сколько комбинаций я могу сделать? (повторение разрешено) 0027
0027
