Сочетание формула комбинаторики: Размещения, перестановки, сочетания с повторениями. Формула включения — исключения

Размещения, перестановки, сочетания с повторениями. Формула включения — исключения

Размещения с повторениями

Определение. Отображение множества первых натуральных чисел в данное множество , называется размещением с повторениями, составленным из данных элементов по .

Размещения с повторениями называются также конечными последовательностями.

Два размещения с повторениями одинаковы тогда и только тогда, когда на одинаковых местах находятся одни и те же элементы.

Если в размещении с повторениями некоторый элемент ставится в соответствие различным натуральным числам, т.е., иначе говоря, данный элемент занимает различных мест, то говорят, что этот элемент повторяется в размещении раз.

Пример. Всевозможные размещения с повторениями из трех элементов по 2:

   

Теорема. Число всевозможных размещений с повторениями из элементов по равно

   

Доказательство. По индукции. При теорема верна, так как сами элементы составляют всевозможные размещения элементов по одному, то число этих размещений равно .

Предположим, что число размещений с повторениями из элементов по равно . Составим из данных элементов всевозможные размещения с повторениями по элементу. Во всяком размещении с повторениями по элементу

   

первые элементов

   

образуют некоторое размещение с повторениями из по элементов. В качестве последнего -го элемента может быть взят любой из элементов. При различных выборах получаются различные размещения. Кроме того, два различные размещения -го порядка дают два различные размещения -го порядка.

Таким образом, число всех размещений -го порядка равно

   

Задача. Имеется различных книг, каждая в экземплярах. Сколькими способами может быть сделан выбор книг из числа данных?

Перестановки с повторениями

Всякое размещение с повторениями, в котором элемент повторяется раз, элемент повторяется раз и т.

д. элемент повторяется раз, где , , , — данные числа, называется перестановкой с повторениями порядка

   

в которой данные элементы повторяются соответственно , , раз.

Теорема. Число различных перестановок с повторениями из элементов , в которых элементы повторяются соответственно раз, равно

   

Доказательство. Если мы будем считать все элементов перестановки с повторениями различными, то всего различных вариантов перестановок элементов — . Однако среди этих перестановок не все различны. В самом деле, все элементы мы можем переставлять местами друг с другом, и от этого перестановка не изменится. Точно так же, можем переставлять элементы , , , . Таким образом, всякая перестановка может быть записана способами. Следовательно, число различных перестановок с повторениями равно

   

Задача. Дано различных предметов. Сколькими способами можно разбить эти предметы на 3 группы так, чтобы первая группа содержала предметов, вторая предметов, а третья предметов?

Показать решение

Сочетания с повторениями

Определение. Если каждому элементу некоторого конечного множества поставлено в соответствие целое неотрицательное число — кратность данного элемента, то говорят, что задано сочетание с повторениями. Сумма кратностей всех элементов называется порядком сочетания.

Всякое сочетание с повторениями -го порядка, составленное из множества, содержащего элементов, называется также сочетанием с повторением из элементов по .

Если — кратности элементов , то по определению есть порядок сочетания

   

Теорема. Число сочетаний с повторениями из элементов по выражается формулой

   

Пример. В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и картошка. Сколькими способами можно купить 7 пирожных?

Решение. Положим пирожные в коробку, а чтобы они не перепутались, разделим их картонными разделителями. Нужно 3 разделителя. Обозначения: 0 (картонки-разделители) и 1 — пирожные. Примерная покупка: 1110101101 — три наполеона, 1 эклер, 2 песочных и 1 картошка.

Итак два класса объектов 1 (7 штук) и 0 (3 штуки) — покупка — 10 объектов.

Два способа рассуждения:

(1) задача сводится к выбору мест для 7 пирожных (или для 3 разделителей) среди 10 объектов.

(2) другой способ рассуждения (эквивалентный). Надо разбить 10 мест на две группы: для 7 пирожных и 3 разделителей.

В чем особенность: объекты повторяются, причем один эклер на вкус неотличим от другого. Отсюда название: сочетания с повторениями. Можно представлять себе, что пирожные непрерывно пекут, так что они не переводятся, сколько ни ешь. Это совсем другая ситуация, чем в обычных сочетаниях!!!

Пусть заданы два числа: — число выбираемых элементов, и — число типов элементов, из которых производится выбор. Число сочетаний с повторениями порядка из элементов типов равно числу способов выбора мест для собственно выбираемых элементов различных классов, или, что то же: для разделителей между ними.

Итак, основная формула:

   

Задача.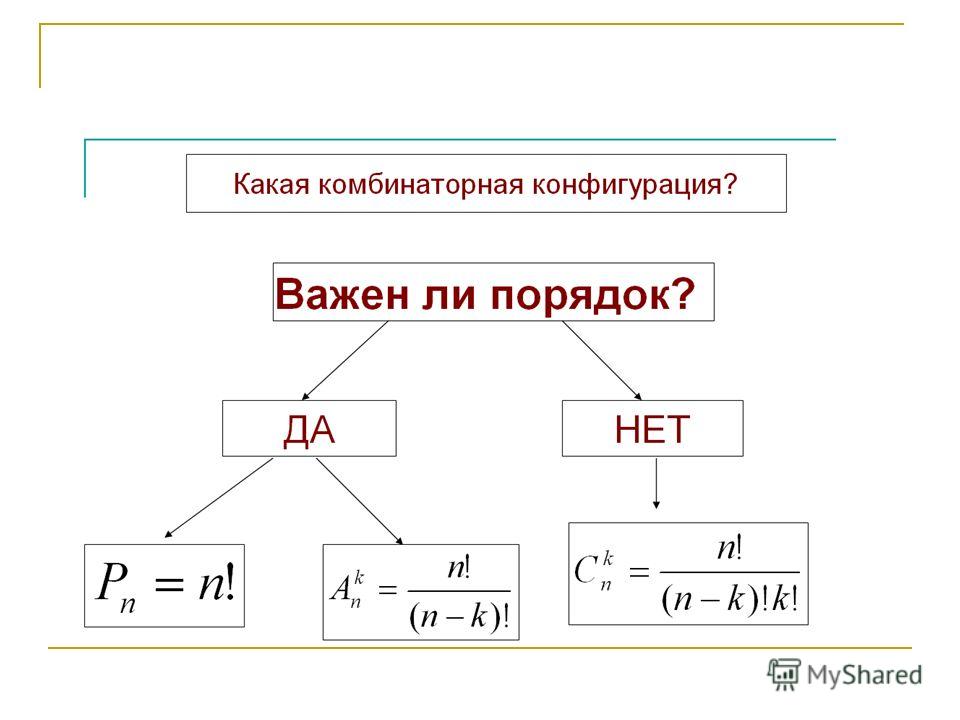 Имеется одинаковых предметов. Сколькими способами можно распределить эти предметы между лицами?

Сочетания с повторениями с дополнительными условиями

Сколько существует сочетания с повторениями таких, что в них обязательно входят элементы фиксированных типов?

Сразу возьмем по одному элементу указанного типа, и тогда уже сразу окажутся заняты мест. Остальные мест можно заполнять элементами прежних типов.

В частности, пусть число типов — числа выбранных элементов. Сколько существует сочетаний с повторениями, так что представлены хотя бы по одному все типы элементов?

Пример. шаров размещаются по ящикам. Сколько существует способов разместить их так, что пустых ящиков нет?

Решение. Пусть нолики — шарики, а единички — стенки ящиков (потребуется единичек). Две единички сразу кладем по краям.

Теперь положим между ними шарики-нолики, а далее нужно заполнить некоторые промежутки между ними так, чтобы между любыми двумя ноликами находилась не более одной единички. Значит, из промежутков между шариками нужно выбрать места для единичек. Всего таких способов .

Метод координат. Подсчет числа путей

Рассмотрим координатную сетку: двигаясь по ней, помечаем каждый перекресток — производим суммирование числа возможных путей, ведущих на каждый перекресток. Получаем известный треугольник Паскаля.

Поскольку на перекресток на уровне (считая сверху и принимая верхний уровень за нулевой) ведет путей (число способов выбрать движений направо вниз из общего числа движений вниз), то свойство суммирования путей на перекрестке можно записать как

   

По прежнему остается справедливым свойство симметрии .

Формула включения — исключения

Определение. Число элементов множества называется мощностью множества и обозначается .

Теорема. Пусть даны множества . Тогда количество элементов в объединении этих множеств можно найти по формуле:

   

Доказательство проводится по индукции. Пусть . Нужно доказать формулу

   

Действительно, множество состоит из всех элементов множества и тех элементов множества , которые не содержатся в множестве . Тогда, сложив количества элементов во множествах и , мы два раза посчитаем количество элементов, общих для множеств и .

Предположим, что формула включения — исключения справедлива для множеств.
Докажем ее для множеств. Множество можно представить в виде

   

Тогда получаем (первое равенство по формуле включения — исключения для двух множеств):

   

Используя формулу

   

и формулу включения — исключения для множеств, получаем

   

В эту формулу  подставляем выражение, полученное ранее, и теорема доказана.

Задачи.

1. Есть три билета в различные театры. Сколькими способами они могут быть распределены между 25 школьниками, если каждый школьник может получить только один билет?

2. Есть три билета на КВН 1 апреля. Сколькими способами они могут быть распределены между 25 школьниками (более одного билета в руки не давать!!!)?
3. Телефонный номер состоит из 7 цифр. Насколько легче угадать правильный номер, если знать, что все его цифры различны?

4. В буфете продаются 5 сортов пирожков: с яблоками, с капустой, картошкой, мясом и грибами (цена всех пирожков одинакова). Скольким числом способов можно сделать покупку из 10 пирожков?

5. (Продолжение). Скольким числом способов можно сделать покупку так, чтобы попробовать пирожков всех видов?

6. (Продолжение). Скольким числом способов можно сделать покупку так, чтобы в нее вошло не менее двух пирожков с мясом и хотя бы один пирожок с яблоками?

7. Скольким числом способов можно вывести на арену цирка 5 львов и 4 тигра так, чтобы никакие два тигра не шли друг за другом (оказавшись рядом, они начинают драться)?

8. За круглым столом короля Артура сидят 12 рыцарей. Из них каждый враждует со своими соседями. Для участия в спецоперации по освобождению заколдованной принцессы нужно выбрать 5 рыцарей, но при этом нельзя посылать вместе рыцарей, враждующих друг с другом. Скольким числом способов это можно сделать?

9. Докажите формулу

   

10. Докажите, что число различных решений уравнения

   

в неотрицательных целых числах равно .

11. Докажите, что число различных решений уравнения

   

в натуральных числах равно .

12.

Сколькими способами можно разложить 15 одинаковых шаров по 5 различным ящикам так, чтобы оказалось не более двух пустых ящиков?

13. Сколькими способами можно разложить 20 одинаковых шаров по 5 различным ящикам так, чтобы в каждом ящике оказалось не менее двух шаров?

14. Сколькими способами можно разложить 20 одинаковых шаров по 6 различным ящикам так, чтобы в каждом ящике оказалось не более 5 шаров?

15. Докажите, что число таких перестановок чисел , которые удовлетворяют условию при всех , равно

   

все формулы комбинаторики

Вы искали все формулы комбинаторики? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и задачи комбинаторика, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «все формулы комбинаторики».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как все формулы комбинаторики,задачи комбинаторика,как понять комбинаторику,комбинаторика,комбинаторика в математике,комбинаторика в математике это,комбинаторика для чайников,комбинаторика задачи,комбинаторика математика,комбинаторика матпрофи,комбинаторика определение,комбинаторика основные понятия и формулы комбинаторики,комбинаторика основные формулы,комбинаторика перестановка,комбинаторика перестановки,комбинаторика примеры,комбинаторика примеры решения задач,комбинаторика сочетание,комбинаторика сочетания,комбинаторика формула,комбинаторика формулы,комбинаторика это в математике,комбинаторики,комбинаторные формулы,математика комбинаторика,матпрофи комбинаторика,определение комбинаторика,основная формула комбинаторики,основные правила комбинаторики,основные формулы комбинаторика,основные формулы комбинаторики,основные формулы комбинаторики перестановки размещения сочетания,основные формулы комбинаторики размещения перестановки сочетания,основы комбинаторики,перестановки формула,правила комбинаторики,правило комбинаторики,примеры сочетания,сколько способов,сочетание комбинаторика,сочетание формула комбинаторики,сочетания в комбинаторике,сочетания комбинаторика,формула количества размещений,формула комбинаторика,формула комбинаторики,формула комбинаторики сочетание,формула нахождения перестановки,формула перестановки,формула перестановок,формула сочетания в комбинаторике,формулы комбинаторики,формулы комбинаторики все,формулы комбинаторики перестановки размещения сочетания примеры,формулы комбинаторики с примерами,формулы по комбинаторике,что такое комбинаторика,что такое комбинаторика в математике,элементы комбинаторики расчет количества вариантов. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и все формулы комбинаторики. Просто введите задачу в окошко и нажмите «решить» здесь (например, как понять комбинаторику).

Решить задачу все формулы комбинаторики вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Простые перестановки и комбинации

Содержание

Комбинаторика

Этот урок охватывает темы комбинаторики (комбинации, перестановки с повторениями и без них, круговые и вынужденные перестановки). Он предоставит вам все необходимые теоретические знания по теме и покажет, как они применяются в стандартных тестовых задачах.

Факториал

Факториал целого числа n определяется как последовательное произведение всех натуральных чисел от n до 1:

н! знак равно п × (п — 1) × (п — 2) × (п — 3) × . . . 1

По соглашению 0! = 1.

0! и 1! единственные два факториала, которые являются нечетными; остальные имеют коэффициент 2 в них.

• 1! = 1
• 2! = 2 × 1 = 2
• 3! = 3 × 2 × 1 = 6
• 4! = 4 × 3 × 2 × 1 = 24
• 5! = 5 × 4 × 3 × 2 × 1 = 120
• 6! = 6 × 5 × 4 × 3 × 2 × 1 = 720
• 7! = 7 × 6 × 5 × 4 × 3 × 2 × 1 = 5040

 

В большинстве тестов вам не нужно вычислять большие факториалы. В большинстве случаев вы сможете уменьшить их или упростить выражение.

Например: Найдите значение 23!/21!

1. 21
2. 23
3. 462
4. 506
5. 10626

 

Если вы запишете все коэффициенты, то увидите тенденцию:

(23 × 22 × 21 × 20 × 19 × 18…. .1) / (22 × 21 × 20 × 19 × 18…1 ).

Вы можете отменить все числа в числителе против тех же чисел в знаменателе, кроме 23×22 в числителе. Итак,

23!/21! = 23 × 22 = 506,

Комбинации

Комбинации означают группы элементов, в которых порядок элементов не имеет значения.

Основная формула для комбинаций:

, где nC _k — количество возможных комбинаций k элементов, взятых из более широкого набора n элементов.

Пример: В коробке семь кубиков разного цвета. Если вы достанете из коробки два кубика, сколько различных цветовых комбинаций возможно?

1. 12
2. 17
3. 21
4. 38
5. 42

Здесь

Подсказка: легко увидеть, что если вам нужно выбрать один элемент из множества n элементов, то есть n способов сделать это. (Например, выберите один день из 365 — есть 365 способов выбрать его). Если вам нужно выбрать два элемента, формула

Это та же формула, что и выше, только упрощенная для случая двух элементов. Вы можете запомнить его, а можете использовать общую формулу, как вам удобнее.

Перестановки

Перестановки — это упорядоченное расположение элементов. Количество возможных упорядоченных перестановок почти всегда больше, чем количество неупорядоченных комбинаций одного и того же набора элементов.

Формула перестановок:

, где nP _k — количество возможных упорядоченных расположений k элементов из большего набора из n элементов.

Пример: В коробке семь кубиков разного цвета. Если взять из коробки два кубика, один правой рукой, а другой левой, и важно место в одной или другой руке, сколько различных комбинаций можно составить?

1. 12
2. 17
3. 21
4. 38
5. 42

Здесь

Эти перестановки также называются перестановками без повторения.

Пример: Сколькими различными способами можно назначить четырех врачей четырем пациентам, если каждый врач принимает одного пациента? У первого врача есть четыре варианта, у второго — три, у третьего — два, а у четвертого — только один.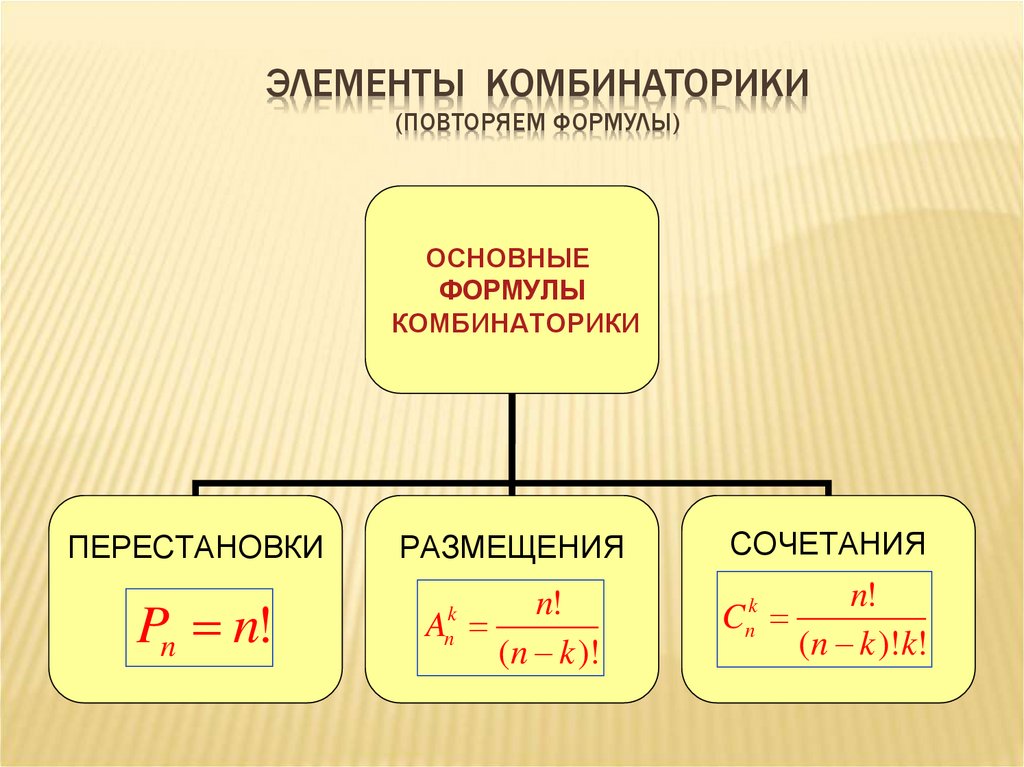 Тогда общее количество аранжировок равно 9.0003

4×3×2×1 = 4! = 24.

Если есть еще 4 пациента, но больше врачей, скажем, 6, то у вас есть перестановки подмножества. Найдем количество способов, которыми 6 врачей могут быть назначены к 4 пациентам. Первого пациента может получить любой из 6 врачей, так что вариантов 6. Второго пациента может лечить любой из 5 оставшихся врачей (поскольку у одного и того же 6-го врача не может быть 2 пациентов), поэтому есть 5 вариантов. Затем есть 4 варианта назначения врача третьему пациенту и 3 варианта для 4-го пациента. Общее количество вариантов равно произведению вариантов для каждого пациента

= 6 × 5 × 4 × 3 = 360 способов.

Другой пример: Каково количество возможных трехбуквенных сочетаний букв K, L, M, N.

Есть 4 варианта для первой буквы, 3 для второй и 2 для третьей,

Итак, всего 4 × 3 × 2 = 24 варианта.

Перестановки с повторениями

Если вам нужно переставить множество, содержащее повторяющиеся элементы, вам нужно скорректировать формулу для этих повторений.

Пример: Сколькими способами можно переставить буквы в слове SOLO?

Используемая формула:

, где n — количество элементов в исходном наборе, в котором имеется j различных повторяющихся элементов, а r — количество повторений каждого элемента.

 

Возвращаясь к примеру SOLO, всего 4 буквы, поэтому

n = 4,

и одна повторяющаяся буква, поэтому

j = 1.

Тогда количество повторений буква O равна 2, поэтому

r1 = 2,

 

Подставьте это в формулу:

Перестановки с комбинациями

Чтобы взглянуть на перестановки и комбинации шире, вам нужно понять, как они соотносятся друг с другом. Мы сказали, что перестановки в основном аналогичны комбинациям, но с учетом порядка элементов.

Это отражено дополнительным элементом в знаменателе в формуле комбинаций:

Вот пример, поясняющий это.

Вам нужно выбрать четыре группы для выступления на концерте из 8 доступных групп и определить порядок их выступления.

Обычный способ сделать это такой же, как и в приведенном выше примере с врачами и пациентами: 8 вариантов для первого слота в концерте, 7 вариантов для второго слота, 6 для третьего и 5 для последнего. Всего получается 8 × 7 × 6 × 5 = 1680 возможных вариантов.

Другой способ сделать это — применить формулу перестановок:

Здесь n = 8, так как всего 8 полос, k = 4, так как нужно выбрать 4. Тогда

Еще один способ сделать это — разбить задачу на две части. шаги:

Сначала вам нужно определить четыре полосы, а затем вам нужно расположить их в определенном порядке. Это менее удобный способ решения данной конкретной задачи, но вам нужно знать логику, так как она может понадобиться для более сложных задач.

Первый шаг — выбрать 4 полосы из 8, не принимая во внимание порядок. Это делается с помощью формулы комбинаций

Где, опять же, n=8 и k = 4.

Существует 4 × 3 × 2 × 1 = 24 способа упорядочить этот набор. Теперь у вас есть 70 способов выбрать группы и 24 способа заказать их. Это дает 70 × 24 = 1680 способов выбрать упорядоченную комбинацию полос. Вы достигли того же результата. Это должно дать вам представление о том, как связаны комбинации и перестановки, чтобы вы могли применить эту логику к задачам любого уровня сложности.

Круговые перестановки

В этом типе задач объекты располагаются по кругу. Отличие от линейных перестановок в том, что круг не имеет четкого начала и конца, как линия. Итак, хотя комбинации ABCD и BCDA — это два разных варианта линейной перестановки, они представляют собой одну и ту же комбинацию по кругу:

Итак, в круге имеет значение только различный порядок элементов по отношению друг к другу; неважно, с какой точки окружности мы начнем их отсчет. Мы можем начать с A, что приведет к ABCD, или мы можем начать с C, что приведет к CDAB — это одна и та же комбинация по кругу.

Если вы можете расположить четыре элемента в ряд за 4! способами (4 варианта на первое место, 3 на второе, 2 на третье, 1 на четвертое

= 4 × 3 × 2 × 1 = 4! = 24,

меньше вариантов расположения тех же четырех элементов вокруг круг. Мы должны исключить идентичные комбинации, которые были определены выше. Повторяющихся комбинаций столько, сколько слотов вокруг круга. Если ABCD является той же комбинацией, что и BCDA, CDAB и DABC, это дает четыре различных линейных варианта для каждого. круговая комбинация (существует четыре различных варианта размещения первого элемента А без изменения порядка элементов относительно друг друга.) Итак, чтобы найти количество круговых перестановок, мы должны разделить количество перестановки по количеству слотов вокруг круга (или количеству возможных способов размещения первого элемента), так что формула для круговых перестановок равна

где м количество слотов по кругу. В случае четырех элементов будет

Перестановки с ограничениями

Некоторые задачи перестановок могут иметь определенные ограничения, например, определенные два элемента не могут быть размещены рядом друг с другом. Возьмем пример: даны 5 элементов в порядке, A, B, C, D и E, с ограничением, что элементы A и E не могут быть размещены рядом друг с другом, сколько существует способов упорядочить элементы?

Есть два способа сделать это. Во-первых, это классический способ умножения вариантов: имеется

5 вариантов размещения первого элемента A. (Начнем с того, который участвует в ограничении.) Остается либо 3, либо 2 варианта размещения E (потому что если А поставить на первое или последнее место, то рядом с ним есть только одно место, недоступное для Е; но если А поставить на одно из средних мест, то рядом с А есть два места, закрытые для Е) .

Для A есть два «краевых» варианта, а для A три «средних». Это означает, что в 2/5 случаев у E будет 3 варианта, а в 3/5 случаях у E будет 2 варианта. После того, как мы разместили E, осталось 3 варианта для B, 2 для C и 1 для D. Умножьте варианты:

5 × (2/5 × 3 + 3/5 × 2) × 3 × 2 × 1 = 72.

Теперь есть еще один способ сделать это. Подсчитаем общее количество возможных комбинаций для 5 элементов:

5! = 5 × 4 × 3 × 2 × 1 = 120,

Теперь исключим варианты, где А и Е стоят вместе. Есть 4 пары мест, которые могут занимать A и E, и по 2 варианта на каждое место (AE или EA). Это дает 8 вариантов расположения А рядом с Е.

Если два места для А и Е определены, их 3! варианты размещения оставшихся элементов B, C и D. Таким образом, общее количество комбинаций из 5 элементов, в которых A и E размещены вместе, равно

8 × 3! = 8 × 3 × 2 × 1 = 48,

Таким образом, общее количество вариантов размещения 5 элементов так, чтобы A и E не располагались вместе, равно

120 – 48 = 72. комбинаторика для расчета вероятности.

Рассмотрим следующий пример. В коробке 6 разных кубиков: желтый, красный, зеленый, синий, оранжевый и фиолетовый. Какова вероятность того, что если вы вытащите из коробки 4 кубика, среди них окажется желтый и синий? Здесь удобно использовать формулу вероятности:

Общее количество комбинаций из 4-х кубиков

Количество комбинаций из 4-х кубиков, содержащих желтый кубик и синий кубик

Ищем комбинации из 4-х кубиков, в которых 2 кубика уже выбраны: желтый и синий. Нам нужно выбрать остальные 2 кубика из оставшихся 4 кубиков в коробке, и есть 4C ₂ способов сделать это.

Теперь посчитаем вероятность:

P = 6/15 = 2/5.

 

Ключевые советы урока

1. Используйте формулу для комбинаций, когда порядок не имеет значения, и формулу для перестановок, когда порядок имеет значение.
2. Иногда для ответа на вопрос удобнее вычислить вероятность того, что событие не произойдет.

Перестановки, комбинации, факториалы и биномиальные коэффициенты

Перестановки, комбинации, факториалы и биномиальные коэффициенты Биномиальный коэффициент

Большинство азартных игр хорошо изучены математически и сфальсифицированы так, что дом имеет небольшое преимущество. Клиенты казино играют в игры для развлечения и полагаются на удачу. Казино размещают игры, чтобы зарабатывать деньги, и полагаются на математику, чтобы добиться успеха.

Эти азартные игры и многие другие практические вопросы обсуждается с точки зрения вероятностей. Чтобы понять вероятности, нужно знать, как считать определенные виды событий. Удобно говорить в терминах различных привычных видов деятельности выбор предметов из набора, где событие будет результатом определенного вида отбора. В играх предметы могут быть картами или бросками костей, но принципы очень общие, и применимо ко многим ситуациям и видам предметов.

Существуют формулы для подсчета этих событий. Чтобы понять их полностью, и для их использования полезно понимать, как формулы производные, потому что производные обеспечивают решающее понимание вида мышления, которое можно применить к таким проблемам.

Вот выводы для трех наиболее важных формул. Первый концептуально самый сложный, но два других легко следуют за ним.

Выбор с заменой

Один из самых простых способов выбрать элементы из набора — заменить элемент каждый раз, когда он выбран.

Простым примером может служить n различных шаров в непрозрачном пакете. По одному из мешка вынимается мяч, отмечается и возвращается.

Каждый розыгрыш одинаковый: всего н шары, так просто n способов выбрать мяч.

Для каждого способа выбрать первый шар существует n способов нарисуйте его, а затем второй шар, поэтому количество способов нарисовать два шара n × n .

Повторение этого процесса k раз дает количество способов рисования к мячи из н в сумке как

н ^к .

Перестановки

n шт.

перестановка отдельных элементов представляет собой упорядочение, или последовательность, предметов.

Например

а, б, в
 

а также

такси
 

две разные перестановки букв a, b и c.

Число перестановок n элементов записывается символически как Р ( н ).

угадать формулу

все перестановки букв a, b и c

a	b	c
a	c	b
b	a	c
b	c	a
c	a	б
в	б	а

Сколько перестановок

1 шт?	1
2 шт?	2 (обратите внимание, что это 2 × 1)
3 шт. ?	6 (обратите внимание, что это 3 × 2 × 1)

Можно догадаться, что в общем случае количество перестановок n элементов будет дано по формуле

P ( n ) = n × ( n −1) × … × 1

Этот специальный продукт называется n факториал и пишется

n !

Но как можно утверждать, что эта формула верна?

вывод формулы

Предположим, вы подсчитали все способы упорядочить 90 349 n 90 350 -1 предметов, и назовем его P ( n −1). Можете ли вы найти формулу для н элементов исходя из чего?

904 14

добавление 4-го элемента к перестановке из 3-х элементов можно 4 способами

г	а	б	в
а	г	б	а
б	г	в
а	б	в	г

Подумайте, как вставить еще один элемент в каждую из этих аранжировок. из n −1 шт. Для каждой аранжировки другой элемент может быть вставлен в любой из н позиций: перед первым, между первым и вторым и т. д. и после последнего.

Таким образом, количество способов расположить n предметов равно

(количество способов расстановки n −1 шт.) × (количество способов вставить новый элемент среди n −1 элементов)

То есть,

P ( n −1) × n

Если формула верна для n −1 элементов, тогда формула для n предметов будет

= ( n −1)! × n
= n !

Отсюда по принципу «математической индукции» следует, что формула

P ( n ) = n !

выполняется для каждого n .

Перестановки

тыс. элементов, взятых из n элементов

Теперь рассмотрим различное расположение или порядок 90 349 000 90 350 предметов. взято из н шт.

Это количество способов выбрать k элементов из n различных элементы, где порядок элементов имеет значение. Это часто пишется

Р ( н , к ),

и читать «перестановки 90 349 n 90 350 элементов, взятых 90 349 k 90 350 одновременно».

вывод формулы

Предположим, что из мешка, состоящего из n предметов, вытащили тыс. предметов. Тогда в мешке осталось n − k предметов.

Теперь количество способов вытащить оставшиеся предметы равно количество перестановок остальных элементов, С ( н — к ) .

Для каждого из P ( n , k ) способов вытащить первый тыс. шт., есть P ( n − k ) способы вытаскивания оставшихся предметов. Это P ( n , k ) × P ( n − k ) вообще.

Но количество способов вытащить к предметов, затем вытащить остальные п − k , то же, что и количество способов вытащить все n предметов, то есть

P ( n , k ) P ( n − k ) = Р ( n ) .

Теперь применим формулу для P ( n ):

Р ( н , к ) ( н − к )! = n ! ,

и переставить, чтобы получить

P ( n , k ) = n ! ⁄ ( п — к )!

Комбинации из

k предметов, взятых из n предметов

Фраза «комбинации n отдельных элементов, взятых k одновременно» означает способы, которыми k из n элементов могут быть объединены, независимо от заказа .

Таким образом, вместо того, чтобы рассматривать заказов , в которых элементы выбраны, как и в случае с перестановками, комбинации учитывают , который устанавливает элементов.

Комбинации из 90 349 n 90 350 различных элементов, взятых 90 349 k 90 350 одновременно, часто пишется

С ( н , к )

или же

C в C ( n , k ) означает «комбинации» или «выборы». Также часто читается номер C ( n , k ). « n выберите k ».

вывод формулы

Чтобы вывести формулу для C ( n ,  k ), разделите проблему заказ , в котором выбраны предметы, из выпуска , из которых выбраны следующим образом.

Количество перестановок k элементов, взятых из n элементов, равно

(количество комплектов к шт. взято из n ) × (количество способов заказать тыс. шт.).

То есть:

P ( n , k ) = C ( n , k ) × P ( )

Переставьте это, чтобы получить:

C ( n ,  k )	= P ( n ,  k ) ⁄ P ( k ,  k )
	= ( п ! ⁄ ( n − k )! ) ⁄ к !
	= n ! ⁄ ( к ! ( п — к )! ) ,

и это ваш «биномиальный коэффициент»

C ( н , к ) = n ! ⁄ ( к ! ( п — к )! ) .