Гид по сочетанию декоров ЭГГЕР
Откройте для себя новые декоры и варианты сочетаний
Гид по сочетанию декоров ЭГГЕР —
Характер и эмоции Вашего интерьера
Коллекция декоров ЭГГЕР 2020 предлагает широкий выбор дизайнерских решений для воплощения любых ваших идей. Новый онлайн инструмент, подготовленный декор менеджерами нашей компании, поможет Вам при создании новых образов в мебели и дизайне интерьера.
Все представленные в нем декоры входят в складскую программу в плитах, бумажно-слоистых пластиках и кромках.
—>
h2710 ST10
Каштан Кентукки песочный
ПодробнееВарианты сочетаний
-
h2122 ST22
Древесина белая
ПодробнееВарианты сочетаний
-
h2250 ST36
Ясень Наварра
ПодробнееВарианты сочетаний
h4450 ST22
Флитвуд белый
ПодробнееВарианты сочетаний
-
h2176 ST37
Дуб Галифакс белый
ПодробнееВарианты сочетаний
-
h4326 ST28
Дуб Гладстоун серо-бежевый
ПодробнееВарианты сочетаний
-
h4433 ST22
Сосна Аланд полярная
ПодробнееВарианты сочетаний
-
Клён сахарный шампань
ПодробнееВарианты сочетаний
h2401 ST22
Сосна Касцина
ПодробнееВарианты сочетаний
-
h2180 ST37
Дуб Галифакс натуральный
ПодробнееВарианты сочетаний
-
h2318 ST10
Дикий дуб натуральный
ПодробнееВарианты сочетаний
-
1251 ST22
Робиния Брэнсон натуральная коричневая
ПодробнееВарианты сочетаний
-
h4157 ST12
Дуб Винченца
ПодробнееВарианты сочетаний
-
h2344 ST32
Дуб Шерман коньяк коричневый
ПодробнееВарианты сочетаний
-
h4303 ST10
Дуб Гамильтон натуральный
ПодробнееВарианты сочетаний
-
h4700 ST10
Орех Пацифик натуральный
ПодробнееВарианты сочетаний
-
h4330 ST36
Дуб Антор натуральный
ПодробнееВарианты сочетаний
-
h4730 ST10
Гикори натуральный
ПодробнееВарианты сочетаний
-
h2346 ST32
Дуб Шерман антрацит
ПодробнееВарианты сочетаний
-
h2714 ST19
Орех Линкольн
ПодробнееВарианты сочетаний
-
h4325 ST28
Дуб Гладстоун табак
ПодробнееВарианты сочетаний
-
h4408 ST38
Лиственница горная коричневая термо
ПодробнееВарианты сочетаний
-
h2253 ST19
Робиния Брэнсон трюфель коричневый
ПодробнееВарианты сочетаний
-
h4178 ST37
Дуб Галифакс глазурованный чёрный
ПодробнееВарианты сочетаний
-
h3033 ST10
Дуб Хантон тёмный
ПодробнееВарианты сочетаний
-
h4176 ST37
Дуб Галифакс олово
ПодробнееВарианты сочетаний
-
h2330 ST10
Дуб Санта-Фе винтаж
ПодробнееВарианты сочетаний
-
h4146 ST19
Дуб Лоренцо бежево-серый
ПодробнееВарианты сочетаний
-
h2345 ST32
Дуб Шерман серый
ПодробнееВарианты сочетаний
-
h4430 ST22
Сосна Аланд белая
ПодробнееВарианты сочетаний
-
h2313 ST10
Дуб Уайт-Ривер серо-коричневый
ПодробнееВарианты сочетаний
-
h4190 ST19
Металлик Файнлайн антрацит
ПодробнееВарианты сочетаний
-
h4453 ST22
Флитвуд серая лава
ПодробнееВарианты сочетаний
-
h2312 ST10
Дуб Уайт-Ривер песочно-бежевый
ПодробнееВарианты сочетаний
-
h2486 ST36
Сосна Пасадена
ПодробнееВарианты сочетаний
-
h4156 ST12
Дуб Корбридж серый
ПодробнееВарианты сочетаний
Эта статья предназначена для людей с нарушениями зрения или с когнитивными нарушениями, использующих программы чтения с экрана, например Экранный диктор корпорации Microsoft, JAWS или NVDA с продуктами Microsoft 365. Эта статья входит в набор содержимого поддержки средства чтения с экрана Microsoft 365, где содержатся дополнительные сведения о специальных возможностях в наших приложениях. Общие справочные сведения доступны на главной странице службы поддержки Майкрософт.
Эта статья входит в набор содержимого поддержки средства чтения с экрана Microsoft 365, где содержатся дополнительные сведения о специальных возможностях в наших приложениях. Общие справочные сведения доступны на главной странице службы поддержки Майкрософт.
С помощью SharePoint в Microsoft 365 клавиатуры и чтения с экрана можно создавать новые документы в библиотеке документов, где вы можете легко делиться документами со своей командой. Мы проверили эту функцию с использованием экранного диктора и приложения JAWS, но она может работать и с другими средствами чтения с экрана, если они соответствуют общепринятым стандартам и методам для специальных возможностей.
Примечания:
-
Новые возможности Microsoft 365 становятся доступны подписчикам Microsoft 365 по мере выхода, поэтому в вашем приложении эти возможности пока могут отсутствовать. Чтобы узнать о том, как можно быстрее получать новые возможности, станьте участником программы предварительной оценки Office.

-
Дополнительные сведения о средствах чтения с экрана см. в статье о работе средств чтения с экрана в Microsoft Office.
-
Рекомендуем использовать SharePoint в Microsoft 365 в веб-браузере Microsoft Edge. Поскольку SharePoint в Microsoft 365 работает в браузере, в сочетаниях клавиш есть некоторые отличия от классической программы. Например, для перехода в область команд и выхода из нее вместо F6 используются клавиши CTRL+F6. Кроме того, такие распространенные сочетания клавиш, как F1 (справка) и CTRL+O (открыть), относятся к командам веб-браузера, а не SharePoint в Microsoft 365.
Создание нового документа
Войдите в учетную запись Microsoft 365 для своей организации, запустите приложение SharePoint, а затем откройте библиотеку документов.
Совет: В SharePoint Online для библиотек документов предусмотрены два представления: классическое и SharePoint в Microsoft 365. Для большинства пользователей по умолчанию используется представление SharePoint в Microsoft 365. Но если при перемещении по библиотеке документов вы слышите фразу «Кнопка Извлечь», то у вас классическое представление. Чтобы просматривать библиотеки документов в представлении SharePoint в Microsoft 365, когда услышите фразу «Кнопка Извлечь», нажмите клавишу ВВОД. Когда представление библиотеки документов изменится на SharePoint в Microsoft 365, и фокус переместится с кнопки «Извлечь» на ссылку «Создать», прозвучит название вашей библиотеки документов, а затем — слово «Создать».
Когда вы открываете библиотеку в SharePoint в Microsoft 365, фокус находится на кнопке «Новое». Вы услышите «Создать, создать папку или документ Office в этом расположении, используйте клавиши СТРЕЛКА ВЛЕВО и СТРЕЛКА ВПРАВО для навигации и клавишу ВВОД для активации, подменю, для перемещения между элементами, нажимая клавишу СТРЕЛКА ВВЕРХ или СТРЕЛКА ВНИЗ». (В экранный диктор вы услышите «Элемент меню, состояние».)
Совет: Если фокус находится не на кнопке Создать, нажимая клавишу TAB, пока не услышите имя библиотеки и «Выход из меню» или «Меню, создать, Создать, создать папку или документ Office в этом расположении, используйте клавиши СТРЕЛКА ВЛЕВО и СТРЕЛКА ВПРАВО для навигации и клавишу ВВОД для активации подменю, для перемещения между элементами нажимая клавишу СТРЕЛКА ВВЕРХ или СТРЕЛКА ВНИЗ». (В экранный диктор вы услышите «Элемент меню, состояние».)
(В экранный диктор вы услышите «Элемент меню, состояние».)
Чтобы открыть меню, нажмите ВВОД.
Нажимайте клавишу СТРЕЛКА ВНИЗ, пока не услышите имя приложения Office, а затем нажмите клавишу ВВОД.
Откроется новый документ. Вы услышите «Создать, создать папку или Office документ в этом расположении, используйте клавиши СТРЕЛКА ВЛЕВО и СТРЕЛКА ВПРАВО для навигации и клавишу ВВОД, чтобы активировать подменю». (В экранный диктор вы услышите «Элемент меню, состояние»)
Создайте документ. Документы Office сохраняются автоматически. Именем документа является его номер.
Для выхода нажмите клавиши ALT+Г, а затем нажимайте клавишу СТРЕЛКА ВНИЗ, пока не услышите «Выход». Нажмите клавишу ВВОД. Если вы используете JAWS, окно закроется.
Если вы используете экранный диктор, откроется диалоговое окно Вы хотите закрыть все вкладки или текущую вкладку?.
Нажмите клавишу СТРЕЛКА ВПРАВО. Вы услышите сообщение «Закрыть текущую вкладку».
Нажмите клавишу ВВОД. Документ закрывается, а фокус возвращается в библиотеку.
См. также
Извлечение и возврат файлов в библиотеке документов SharePoint Online с помощью средства чтения с экрана
Редактирование документа в библиотеке документов SharePoint Online с помощью средства чтения с экрана
Сочетания клавиш в SharePoint Online
Выполнение основных задач в SharePoint Online с помощью средства чтения с экрана
Использование чтения с экрана для изучения и навигации по SharePoint Online
Создавайте SharePoint в Microsoft 365 в библиотеке документов с помощью клавиатуры и чтения с экрана, чтобы легко делиться документами со своей командой. Мы проверили эту функцию с использованием экранного диктора и приложения JAWS, но она может работать и с другими средствами чтения с экрана, если они соответствуют общепринятым стандартам и методам для специальных возможностей. Вы также узнаете, как переименовать документ.
Мы проверили эту функцию с использованием экранного диктора и приложения JAWS, но она может работать и с другими средствами чтения с экрана, если они соответствуют общепринятым стандартам и методам для специальных возможностей. Вы также узнаете, как переименовать документ.
Примечания:
-
Новые возможности Microsoft 365 становятся доступны подписчикам Microsoft 365 по мере выхода, поэтому в вашем приложении эти возможности пока могут отсутствовать. Чтобы узнать о том, как можно быстрее получать новые возможности, станьте участником программы предварительной оценки Office.
-
Дополнительные сведения о средствах чтения с экрана см. в статье о работе средств чтения с экрана в Microsoft Office.
org/ListItem»>
Рекомендуем использовать SharePoint в Microsoft 365 в веб-браузере Microsoft Edge. Поскольку SharePoint в Microsoft 365 работает в браузере, в сочетаниях клавиш есть некоторые отличия от классической программы. Например, для перехода в область команд и выхода из нее вместо F6 используются клавиши CTRL+F6. Кроме того, такие распространенные сочетания клавиш, как F1 (справка) и CTRL+O (открыть), относятся к командам веб-браузера, а не SharePoint в Microsoft 365.
В этом разделе
-
Создание документа
-
Переименование документа
Создание нового документа
Откройте библиотеку SharePoint в Microsoft 365, в которой вы хотите создать документ.
Нажимая клавишу TAB, пока не услышите «Панели команд» и текущий элемент.
Нажимая клавишу СТРЕЛКА ВЛЕВО, пока не услышите «Новый, элемент меню», а затем нажмите клавишу ВВОД.
Нажимая клавишу СТРЕЛКА ВНИЗ, пока не услышите тип документа, который вы хотите создать, например «Документ Word». Нажмите клавишу ВВОД, чтобы выбрать ее.
Нажмите клавишу ВВОД, чтобы выбрать ее.
В выбранном приложении откроется Office в Интернете документ. Например, если вы создаете документWord,Word в Интернете в режиме редактирования.
Создайте содержимое документа в приложенииOffice в Интернете. Документ автоматически будет сохранен с именем по умолчанию, например Document.docx.
Когда содержимое документа будет довольным, нажмите CTRL+W, чтобы закрыть текущую вкладкуMicrosoft Edge, на которой вы создаете документ. ПриложениеOffice в Интернете и документ закрыты.
Новый документ появится в списке документов библиотеки документов.
Переименование документа
Например, можно переименовать документ, чтобы изменить стандартное имя нового документа на более описательное.
-
Перейдите к документу, который вы хотите переименовать.
-
Когда документ будет открыт, нажмите shift+F10, чтобы открыть контекстное меню.
-
Нажимая клавишу СТРЕЛКА ВНИЗ, пока не услышите слово «Переименовать», затем нажмите клавишу ВВОД.
 Откроется диалоговое окно Переименовать. Фокус будет в поле «Имя документа».
Откроется диалоговое окно Переименовать. Фокус будет в поле «Имя документа». -
Введите новое имя документа и нажмите ввод.
Диалоговое окно закроется, а фокус вернется в документ с обновленным именем.
См. также
Извлечение и возврат файлов в библиотеке документов SharePoint Online с помощью средства чтения с экрана
Редактирование документа в библиотеке документов SharePoint Online с помощью средства чтения с экрана
Сочетания клавиш в SharePoint Online
Выполнение основных задач в SharePoint Online с помощью средства чтения с экрана
Использование чтения с экрана для изучения и навигации по SharePoint Online
Техническая поддержка пользователей с ограниченными возможностями
Корпорация Майкрософт стремится к тому, чтобы все наши клиенты получали наилучшие продукты и обслуживание. Если у вас ограниченные возможности или вас интересуют вопросы, связанные со специальными возможностями, обратитесь в службу Microsoft Disability Answer Desk для получения технической поддержки. Специалисты Microsoft Disability Answer Desk знакомы со многими популярными специальными возможностями и могут оказывать поддержку на английском, испанском, французском языках, а также на американском жестовом языке. Перейдите на сайт Microsoft Disability Answer Desk, чтобы узнать контактные сведения для вашего региона.
Если у вас ограниченные возможности или вас интересуют вопросы, связанные со специальными возможностями, обратитесь в службу Microsoft Disability Answer Desk для получения технической поддержки. Специалисты Microsoft Disability Answer Desk знакомы со многими популярными специальными возможностями и могут оказывать поддержку на английском, испанском, французском языках, а также на американском жестовом языке. Перейдите на сайт Microsoft Disability Answer Desk, чтобы узнать контактные сведения для вашего региона.
Если вы представитель государственного учреждения или коммерческой организации, обратитесь в службу Disability Answer Desk для предприятий.
Подбор цвета в интерьере онлайн: как найти сочетания цветов для интерьера онлайн с помощью программы
Руководствуйтесь собственными эмоциями — они не подведут. Остальную работу сделает за вас программа для раскладки цветов
Профи в своих интервью в один голос утверждают: главное в интерьере дома — это ощущение счастья его хозяев. И что в декораторских силах это ощущение создать и в дом привнести.
И что в декораторских силах это ощущение создать и в дом привнести.
Что правда, то правда: декораторы действительно умеют решать сложные задачи простыми способами. Один из них — виртуозная работа с цветом. Но прежде чем начать что-либо делать и предлагать заказчику, декоратор должен сам выявить эту «канву счастья» для каждого заказчика. Поверьте, каждый клиент мучается проблемой выбора: «а действительно ли это «мое»? Не подогнанное под удачный концепт, не привнесенное извне, пусть даже очень талантливым профи, а именно мое?
Jakobsdals
Обычно, когда в моей работе дело доходит до этого момента, я предлагаю несколько разных отправных точек, с каждой из которых мы можем начать проектирование абсолютно индивидуального интерьера. Но вот недавно к этим точкам добавилась еще одна: подбор цвета в интерьере онлайн при помощи довольно простого приложения. Оно очень мне нравится. А мои заказчики, которым я предлагала в него «поиграть» — в совершенном восторге.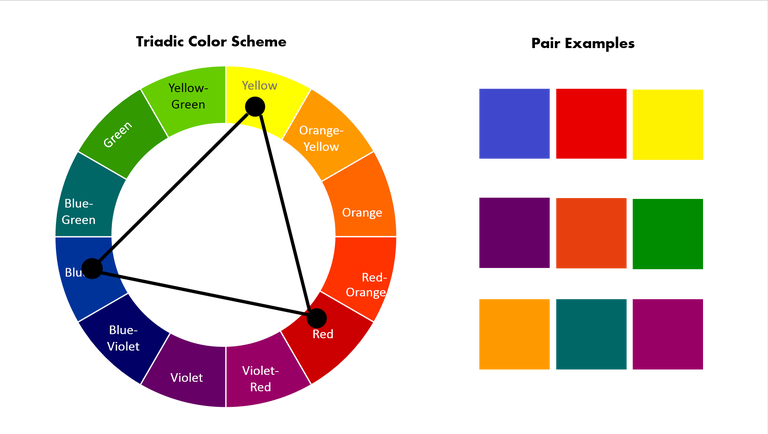
ЧИТАЙТЕ ПО ТЕМЕ…
- Способ Люшера: Как выбрать цвет для интерьера
- Как выбрать правильные цвета, руководствуясь сезонным методом
Яшина Мария | Different Rooms
Представьте такую историю: вы вернулись из отпуска и готовы на волне ярких эмоций, отдохнувшие, погрузиться в тему дизайна и ремонта с головой. Перебираете отпускные фотографии: вас согревают пережитые эмоции, вам нравится картинка и то ощущение гармонии, которое в вас откликается при взгляде на фото.
Яшина Мария | Different Rooms
Подбор цветов в интерьере онлайн
Смело берите и загружайте ту самую отпускную фотографию в приложение. Программа проанализирует ее и подскажет подходящее сочетание цветов в интерьере — онлайн подбор разложит все по полочкам: покажет основной цвет, пару дополнительных и акцентные нюансы.
Приложение Voice of color, о котором я говорю, разработано компанией-продавцом красок
PPG Paints. Продаются они, к сожалению, только на территории США и Канады. Но это не мешает нам (дизайнерам) активно пользоваться их цветовыми раскладками. Программа по подбору цвета в интерьере дает конкретную палитру, с которой довольно просто работать. Начнем с самого начала.
Продаются они, к сожалению, только на территории США и Канады. Но это не мешает нам (дизайнерам) активно пользоваться их цветовыми раскладками. Программа по подбору цвета в интерьере дает конкретную палитру, с которой довольно просто работать. Начнем с самого начала.
Как работает программа для подбора цвета стен в комнате
Один пример всегда лучше большого количества самых правильных слов. Давайте попробуем сделать подбор цветов онлайн для комнаты, исходя из этого фото. А затем проанализируем процесс.
Яшина Мария | Different Rooms
Программа не русифицирована, потому буду рассказывать и переводить основные пункты меню. Раздел, который нас интересует — это Grab color from photo. В него мы и будем загружать наши отпускные фотографии. Приложение покажет набор основных цветов на картинке (Main colors in this image). Еще две вкладки — Shades и Harmony — демонстрируют соответствующие линейки.
Факт: Может случиться так, что вам нравится не вся картинка целиком, а какое-то конкретное сочетание цветов на фотографии. Приятный момент — если ткнуть пальчиком в любое место на фото, подбор цветов интерьера онлайн делается для выбранной зоны. То есть линейка превратится в набор из нескольких оттенков, расположенных именно в этой области. Разобравшись со всем функционалом, можно подобрать и сохранить несколько особенно вдохновляющих вариантов цветовых раскладок. Что дальше?
Приятный момент — если ткнуть пальчиком в любое место на фото, подбор цветов интерьера онлайн делается для выбранной зоны. То есть линейка превратится в набор из нескольких оттенков, расположенных именно в этой области. Разобравшись со всем функционалом, можно подобрать и сохранить несколько особенно вдохновляющих вариантов цветовых раскладок. Что дальше?
Alvhem Mäkleri & Interiör
Итак, у нас получились довольно симпатичные сочетания из основных цветов с картинки с закатом. Очень подходящие для любителей серых интерьеров с вкраплениями теплых оттенков.
- Основной цвет — серо-голубой. Совершенно нейтральный, фоновый цвет для стен.
- Следующий, болотный цвет Plunge Pool — в нем хорошо будут смотреться добротные кухонные фасады.
- Графитово-серым, который здесь очень красиво называется Mountain Pine, стоит выделить габаритную мебель и добавить его, например, в виде мраморного панно в отделку камина.

- Следующие два оттенка, на несколько тонов темнее фонового, прекрасно подойдут для дверей, плинтусов и штор.
- Золотисто бежевый — паркетная доска французской елочкой на пол.
- Красивый пудровый в самом конце используем для аксессуаров и негабаритной мебели. Складывается очень красивая картинка, правда?
Desenio
Своим клиентам я предлагаю «играть с фото» самостоятельно, при этом сохраняя способом PrintScrin любые понравившиеся сочетания. То есть цветовые предложения изначально исходят не от меня — заказчик сам проводит подбор цветов интерьера онлайн, а мне дает «вводные» для работы.
Дальше я уже слушаю эмоции, рассуждения клиента о том, какой вариант ему кажется самым жизнеспособным в долгой перспективе. Но в конечном итоге нести ответственность за «счастливую» цветовую гамму в доме нести именно мне. Потому варианты «из программы» я всегда немного корректирую — иной раз отдаю предпочтение более нейтральному фону или подбираю чуть более выразительные акцентные пары цветов.
Leroy Merlin OFFICIEL
Совет: Точное следование алгоритму совершенно не обязательно — вы можете экспериментировать, добавлять в интерьер цвета не «по убывающей», а в равных пропорциях. Пытайтесь делать рекомендованные программой оттенки более или менее насыщенными.
Henrik Nero
Важно понимать: главное, что делает профессиональный дизайнер с цветовой палитрой — он помогает вам сохранить и перенести ваши ощущения счастья и гармонии, ваши эмоции в интерьер. И что немаловажно, только вы и он будете знать, с чего все начиналось. А правильный storyteling в интерьере ничуть не менее важен, чем хорошо подобранный цвет стен.
ВАША ОЧЕРЕДЬ…
Пробовали ли вы когда-нибудь подбирать цвета для комнаты онлайн? Какими сервисами? Насколько довольны результатом? Расскажите нам об этом в разделе комментариев!
Спонсируемые
Zwickau bis Gera I Wir machen Ihren Garten zum perfekten Erholungsraum
Спонсируемые
Zwickau bis Gera I Wir machen Ihren Garten zum perfekten Erholungsraum
Топ 13 генераторов цветовых схем
Natalia Shpitula
Обновлено
Loading. ..
..
Содержание:
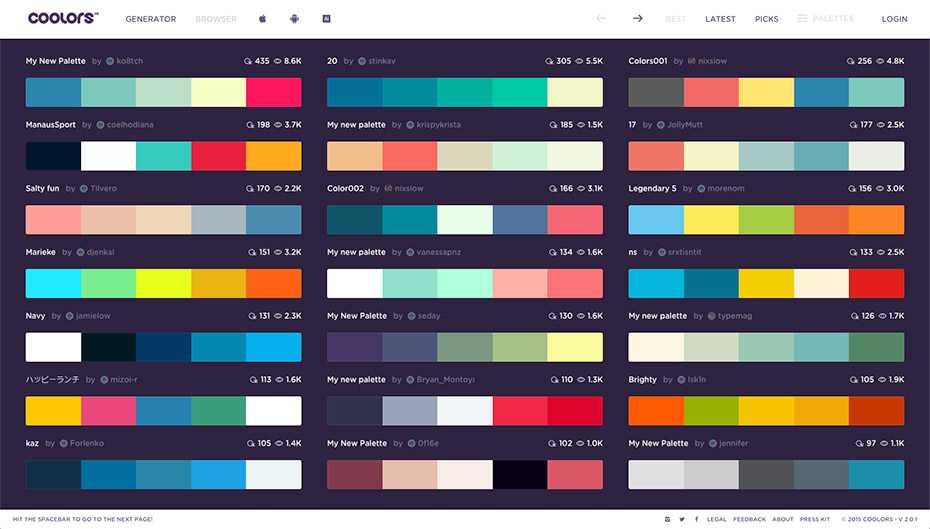
1.Coolors
2.Colorsafe
3.Color.Hailpixel
4.Colorhunt
5.Galactic.Ink
6.Colrd
7.Sipapp
8.Flatuicolors
9.Paletton
10.Colr
11.Javier.Xyz
12.Colourco
Фирменный цвет поможет повысить узнаваемость бренда на 80%, выделить вас среди конкурентов и завоевать доверие покупателей. Как подобрать цветовую гамму, если у вас нет опыта в дизайне? Использовать онлайн-генераторы, которые профессионально сочетают оттенки. Составили список лучших сервисов — сайтов и мобильных приложений.
Палитру можно создать за считанные секунды. Просто выберите любой цвет — и автоматически получите идеальную комбинацию. Отрегулируйте оттенки по температуре, насыщенности, яркости и экспортируйте в удобный формат (PNG, PDF, SCSS, SVG). Нужно вдохновение? Используйте раздел с готовыми схемами и сохраняйте их для своих проектов. Для удобства работы загрузите приложения программы для iOS или Android.
2. Colorsafe
Оптимизирует сайт в соответствии с принципами международного руководства по веб-доступности (Web content accessibility guidelines). Укажите цвет фона и шрифта — и инструмент сгенерирует палитру, которая будет комфортна для людей с нарушениями зрения. Отсортируйте полученные варианты и сохраните избранные в библиотеке — в ней есть функция совместной работы над проектами.
Укажите цвет фона и шрифта — и инструмент сгенерирует палитру, которая будет комфортна для людей с нарушениями зрения. Отсортируйте полученные варианты и сохраните избранные в библиотеке — в ней есть функция совместной работы над проектами.
Этот сервис работает онлайн, но удобнее всего использовать его как мобильное приложение для iOS. Процесс понятен интуитивно. В один клик выберите цвет, проведите пальцем (или мышкой) влево или вправо для изменения оттенка, а вверх или вниз — для яркости. В мобильной версии есть полезная опция распознавания. Понравился цвет, который конкуренты использовали в наружной рекламе? Просто наведите на него камеру — и приложение подскажет номер и название оттенка.
Открытая коллекция нескольких тысяч готовых палитр для вдохновения. Их используют графические дизайнеры, иллюстраторы, веб-разработчики, маркетологи. Палитры можно отсортировать по новым, трендовым, популярным, смотреть все подряд или в случайном порядке. Сохраняйте любимые сочетания, управляйте личной коллекцией и копируйте понравившиеся цветовые коды.
Генератор с «умным» цветовым кругом подойдет опытным пользователям. Здесь собраны все профессиональные инструменты для работы с цветом. Выбирайте цветовые схемы (аналоговые, комплиментарные, триады, тетрады и другие), модели (RGB или RYB), светлый или темный фон сайта. Полученную комбинацию можно сразу скачать в Illustrator или Photoshop.
6. Colrd
Ресурс понравится и тем, кто ищет вдохновения, и тем, кто хочет создать свою палитру. Интерфейс прост и интуитивно понятен. В разделе «Исследовать» собраны фото и иллюстрации, разложенные на цветовые схемы. Здесь можно найти картины Ван Гога и работы современных фотографов, смотреть все подряд или отсортировать по разным критериям. А раздел «Создать» предлагает сгенерировать один цвет, палитру или градиент.
Платный инструмент для компьютеров или телефонов на системе iOS позволяет быстро создавать, систематизировать и редактировать сочетания, а также делиться результатами с командой. Созданные палитры все время остаются видимыми сбоку экрана — это удобно для сравнения в процессе работы. Есть также онлайн-конвертер, который переводит схемы в 24 формата — как для печати, так и для использования в интернете.
Есть также онлайн-конвертер, который переводит схемы в 24 формата — как для печати, так и для использования в интернете.
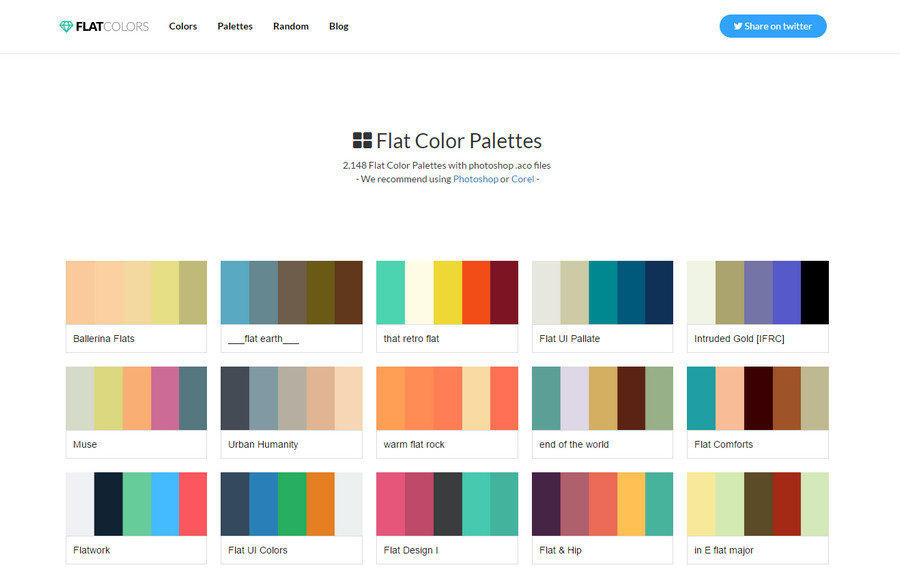
8. Flatuicolors
Лаконичный сервис, где собраны всего 14 палитр от дизайнеров. Используйте 280 цветов для брендинга, презентаций или рекламы. Название и код любого оттенка можно узнать и скопировать для дальнейшей работы.
Мощный онлайн-генератор с классическим цветовым кругом и множеством функций подойдет опытным пользователям. Выбирайте варианты цветовых схем и настраивайте их при помощи различных инструментов. Получив результат, запустите проверку и посмотрите, как цвета будут выглядеть для дальтоников и на различных экранах.
10. Colr
Ресурс предлагает «играть с цветами и схемами». Для этого здесь собраны креативные инструменты. Одна из самых полезных функций — возможность добавить любое изображение и разложить его на оттенки. Также можно ввести название цвета и получить на его основе карту ассоциаций.
Простой инструмент для создания гармоничных цветовых схем.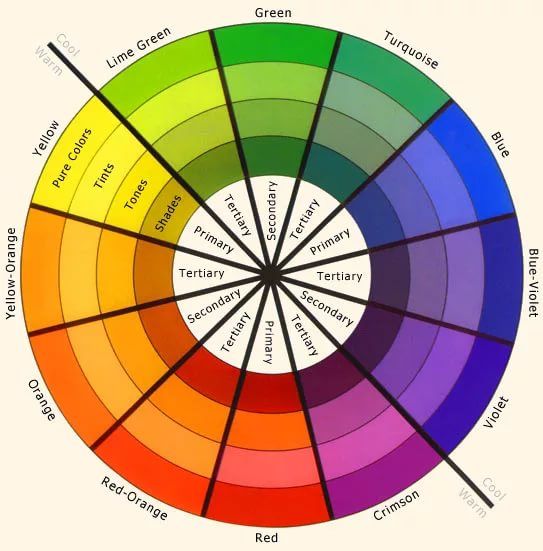 Укажите основные и оттеночные краски, способ их смешивания, степень прозрачности — и редактируйте, пока не получите нужный результат.
Укажите основные и оттеночные краски, способ их смешивания, степень прозрачности — и редактируйте, пока не получите нужный результат.
Управляйте цветами одним движением мышки или пальца на тачскрине. Просто выберите в меню нужную схему: от монохрома до тетрады. Сайт покажет вам все варианты сочетаний. Возможности сортировки по цветам нет, зато понравившуюся комбинацию можно сохранить.
Выбрали желаемый цвет для вашего бренда?
Создайте соответственный фирменный стиль на Logaster!
Заключение
Чтобы брендировать бизнес, не обязательно обращаться к дизайнеру — современные онлайн-инструменты помогут вам вдохновиться и профессионально подобрать цветовую палитру. Не знаете, с чего начать? Создайте главный визуальный символ бренда — логотип. Сгенерировать его в несколько кликов можно на сайте Logaster. После этого приступайте к другим элементам фирменного стиля — цветам, шрифтам и стилеобразующей графике.
Цветовая подборка. Сочетание цвета и подбор цвета онлайн
Выбор цветовой схемы для сайта является одним из важных моментов в процессе дизайна. Подбор сочетания цветов — достаточно сложный и творческий процесс. К счастью, существует достаточно много сервисов, которые могут оказать существенную поддержку для правильного выбора.
Подбор сочетания цветов — достаточно сложный и творческий процесс. К счастью, существует достаточно много сервисов, которые могут оказать существенную поддержку для правильного выбора.
Некоторые ресурсы, упомянутые в данном обзоре, предоставляют возможность выбора из большого количества уже готовых цветовых схем, а другие позволяют в интерактивном режиме построить собственную схему.
Kuler
Adobe Kuler содержит большую библиотеку готовых цветовых схем. Вы можете просмотреть схему онлайн и загрузить ее для использования в продуктах серии Adobe Creative Suite.
Colour Lovers в текущий момент имеет почти 2 миллиона созданных пользователями цветовых схем. Вы можете просматривать их, сортируя по дате, рейтингу, количеству просмотров.
ColoRotate имеет библиотеку готовых цветовых схем. Также вы можете создать свою собственную схему с помощью уникального 3D инструмента. Цветовую схему можно использовать напрямую в Photoshop и Fireworks с помощью плагина ColoRotate .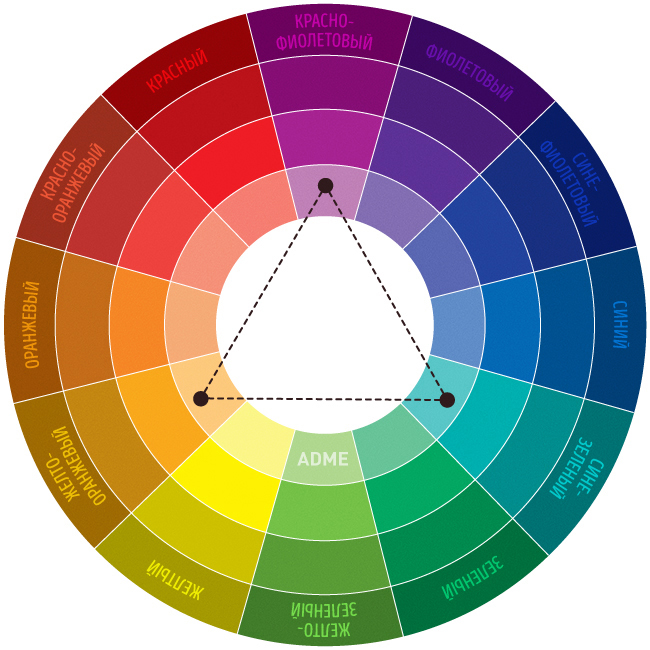
Color Scheme Designer позволяет выбрать тип цветовой схемы (моно, комплиментарную, триада, тетрада, аналоговая). Затем можно будет настроить цвета и посмотреть действие схемы на примере.
ColorSchemer Gallery
ColorSchemer располагает большой библиотекой созданной пользователями цветовых схем. Вы можете сортировать их по дате размещения, рейтингу или количеству загрузок.
Как же правильно сочетать цвета? Ведь от выбранной палитры будет зависеть общий настрой вашего интерьера и ваше настроение. Ниже представлены десять типов цветовых комбинаций, которые помогут вам составить гармоничную цветовую гамму для вашего дома и не только.
АхроматическиеЗдесь используются только оттенки серого, от белого до черного. Ахроматические цвета – это цвета, отсутствующие в спектре. Чистые ахроматические цвета (без примесей оттенков цвета) в природе практически не существуют. Всегда черный (или серый) будет иметь тот или иной оттенок. К черному стремится любой цвет при снижении яркости (например, при уменьшении освещенности до полной темноты). При увеличении яркости любой цвет стремится к белому.
При увеличении яркости любой цвет стремится к белому.
Использование только одних ахроматических цветов дает возможность создать невероятно оригинальный интерьер. Здесь как нигде в других случаях может быть выражена сама фактура используемого материала: блеск, матовость, прозрачность, бархатистость, структура поверхности необычных видов. Если добавить к ахроматическим цветам один яркий цвет, часто это красный, то получается очень стильное помещение. Такие сочетания могут быть использованы в минимализме с намеком на японский стиль. Если добавить нежные, еле заметные оттенки, то такое сочетание можно использовать как основу под дизайн в таких современных стилях, как хай-тек.
ОсновныеГлавные, основные, цвета на цветовом круге: красный, желтый, синий. На то они и основные, что составляют основу цветового круга. Имея в руках краски только этих цветов плюс белый и черный, опытный художник создаст все остальные цвета (при условии, что три основных цвета будут радужной чистоты, без примесей).
Цвета второго порядка: зеленый, фиолетовый, оранжевый. Получаются путем смешивания попарно трех основных цветов: красного, желтого и синего. Например, при смешении желтого и синего – получается зеленый. Составных цветов всего три: оранжевый, зеленый и фиолетовый.
Сложные цвета получаются путем смешивания трех составных цветов с рядом лежащими основными. Например: оранжевый плюс желтый: получается желто-оранжевый. Таких цветов уже шесть. Триада сложных цветов может быть одной из этих комбинаций: красно-оранжевый, желто-зеленый и сине-фиолетовый; сине-зеленый, желто-оранжевый и красно-фиолетовый. На цветовом круге все они находятся на одинаковом расстоянии друг от друга, занимая промежуточное положение между составными цветами. Затемняя или осветляя эти цвета в той или иной степени, мы получаем всю возможную гамму цветов. На основном цветовом круге сложные цвета представлены (насколько это возможно) без осветления или затемнения, путем смешивания цветов в равной пропорции. Если же пропорции цветов для смешивания менять по своему усмотрению и дополнительно еще и осветлять либо затемнять цвета, то в итоге мы получим всю градацию цветов, представленную на полном цветовом круге и даже более того. Как пример некоторых сложных цветов:
Если же пропорции цветов для смешивания менять по своему усмотрению и дополнительно еще и осветлять либо затемнять цвета, то в итоге мы получим всю градацию цветов, представленную на полном цветовом круге и даже более того. Как пример некоторых сложных цветов:
До сих пор мы рассматривали цвета по принципам их получения путем смешивания трех основных цветов, затем сложных и составных. В итоге можно получить все возможные чистые хроматические цвета. Палитру можно значительно расширить, добавляя в хроматические цвета – ахроматические. Но это лишь начало игры в цвета. Теперь перейдем к типам взаимоотношений между цветами, рассматривая их расположение на цветовом круге. Это уже – руководство к действию. От расположения комбинации выбранных цветов на цветовом круге зависит их влияние на наше восприятие. В зависимости от того, выбрали ли мы рядом стоящие цвета или противоположно расположенные цвета на цветовом круге – будет меняться и воздействие этой комбинации цветов на наше восприятие. Теперь есть смысл обратиться к полному цветовому кругу.
Теперь есть смысл обратиться к полному цветовому кругу.
Контрастными по отношению друг к другу считаются два цвета, между которыми на цветовом круге находятся три промежуточных цвета (эти пары выборок часто путают с дополнительными цветами). Таких пар цветов шесть, по количеству пар цветов в основном цветовом круге.
Подобные пары цветов очень часто использовались в одежде скоморохов, эти сочетания максимально броски и навязчивы. Надо помнить, что использование насыщенных контрастных цветов – это очень жесткое сочетание, его нельзя использовать в равных по объему плоскостях и массах в интерьере. Но, используя контрастный цвет как небольшой акцент, например, голубые тарелки и полотенца в желтой кухне, мы достигнем ярких, эффектных сочетаний. Они будоражат и повышают жизненный тонус. Использование контрастных точек и штрихов в интерьере способно придать жизнь и шарм скучному помещению, наподобие тому, как капля перца способна изменить вкус пресного блюда. Но надо помнить, что стоит только переборщить с перцем, и блюдо становится несъедобным. Совсем иное впечатление возникнет при использовании разбеленных контрастных сочетаний (с добавлением ахроматических цветов), например, таких как кремово-желтый и серо-голубой. Чем более разбелены контрастные цвета, тем меньше ограничений в их использовании в одном пространстве. Вообще ахроматические цвета способны спасти любую выборку цветов, даже контрастную. Об этом речь пойдет далее.
Но надо помнить, что стоит только переборщить с перцем, и блюдо становится несъедобным. Совсем иное впечатление возникнет при использовании разбеленных контрастных сочетаний (с добавлением ахроматических цветов), например, таких как кремово-желтый и серо-голубой. Чем более разбелены контрастные цвета, тем меньше ограничений в их использовании в одном пространстве. Вообще ахроматические цвета способны спасти любую выборку цветов, даже контрастную. Об этом речь пойдет далее.
Прямо противоположные цвета на цветовом круге называются дополнительными. С дополнительными цветами можно провести один любопытный фокус. Если мы разделим спектр на две части, например – на красно-оранжево-жёлтую и зелёно-сине-фиолетовую, и соберем каждую из этих групп специальной линзой, то в результате получим два смешанных цвета, смесь которых в свою очередь также даст нам белый цвет. Если мы удалим из спектра один цвет, например, зеленый, и посредством линзы соберем оставшиеся цвета – красный, оранжевый, желтый, синий и фиолетовый, – то полученный нами смешанный цвет окажется красным, то есть цветом, дополнительным по отношению к удаленному нами зеленому. Если мы удалим желтый цвет, – то оставшиеся цвета – красный, оранжевый, зеленый, синий и фиолетовый – дадут нам фиолетовый цвет, то есть цвет, дополнительный к желтому. Два цвета, объединение которых дает белый цвет, называются дополнительными цветами. Фактически, идеально чистые дополнительные друг к другу цвета “убивают” друг друга. Каждый цвет является дополнительным по отношению к смеси всех остальных цветов спектра. В смешанном цвете мы не можем увидеть отдельные его составляющие. В этом отношении глаз отличается от уха с хорошим музыкальным слухом, которое может выделить любой из звуков аккорда. Пример дополнительных цветов:
Если мы удалим желтый цвет, – то оставшиеся цвета – красный, оранжевый, зеленый, синий и фиолетовый – дадут нам фиолетовый цвет, то есть цвет, дополнительный к желтому. Два цвета, объединение которых дает белый цвет, называются дополнительными цветами. Фактически, идеально чистые дополнительные друг к другу цвета “убивают” друг друга. Каждый цвет является дополнительным по отношению к смеси всех остальных цветов спектра. В смешанном цвете мы не можем увидеть отдельные его составляющие. В этом отношении глаз отличается от уха с хорошим музыкальным слухом, которое может выделить любой из звуков аккорда. Пример дополнительных цветов:
Это сочетание, используемое в интерьере, так же очень броское, хоть и не такое навязчивое, как контрастные цвета. Оно воспринимается немного мягче, и если использовать один или оба цвета разбеленными, то можно получить неплохие в итоге сочетания. Но – необходимо быть очень осторожными с дополнительными цветами. Особенно это касается освещения. Об этом – в другой статье.
Об этом – в другой статье.
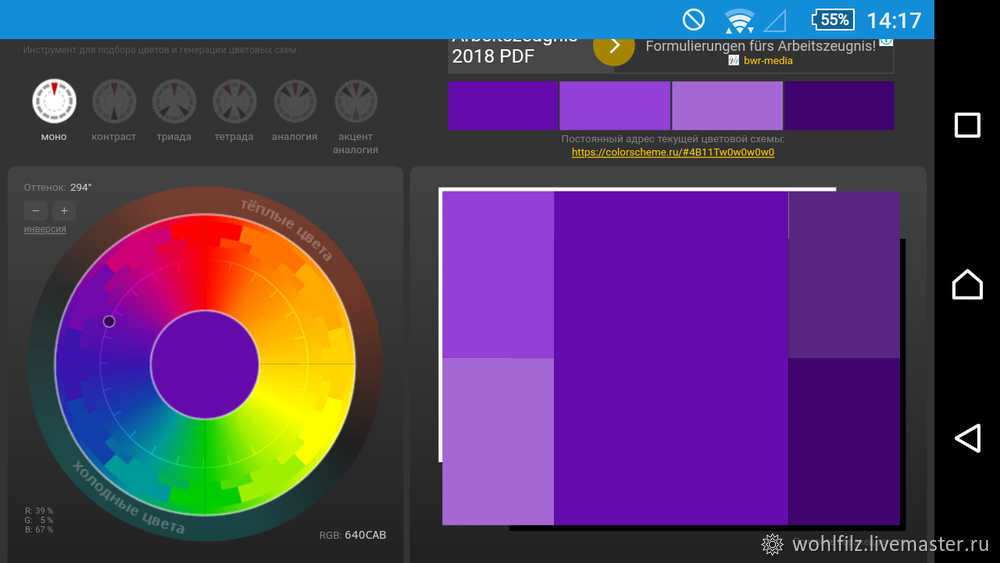
Монохроматические цвета – это комбинации яркости и насыщенности в пределах одного и того же цвета. Такое сочетание называют еще нюансным. В оформлении комнаты используются оттенки одного цвета (составляющие одного и того же сегмента круга). Такая композиция способствует поддержанию атмосферы спокойствия и отдыха, если для нее выбираются цвета из холодной части круга, и атмосферы мягкой открытости, способствующей общению и активности, если используются цвета из теплой части круга.
Любые три следующих друг за другом цвета или их оттенки на цветовом круге называются родственными. Выбирайте любой цвет на круге и добавляйте к нему оба соседних цвета на боковых сегментах. Такая выборка цвета еще называется в некоторых изданиях гармоничной. Всего может быть 12 троек главных родственных (гармоничных) сочетаний. Какие бы тройки гармоничных цветов вы не выбрали, интерьер, выполненный с помощью этих цветов, будет смотреться очень хорошо, при этом иметь различный по восприятию характер для каждого из 12 возможных вариантов, в зависимости от того, выбрана палитра из теплых или из холодных цветов. Пример выборки цветов по родственному типу:
Пример выборки цветов по родственному типу:
Эти 12 вариантов главных троек могут быть расширены за счет использования разной светлоты (разбеленные и затемненные эти же цвета) выбранного цвета (расширяем за счет монохроматических цветов, см. далее) на расширенном цветовом круге. При этом по светлоте каждый из трех цветов может быть аналогичным другому или значительно отличаться друг от друга, один может быть очень осветлен и использован на больших поверхностях: стенах, потолке, другие – затемнены и использованы в качестве отдельных небольших элементов: подушек, декоративных ваз, рамок для картин. Можно использовать иной, противоположный вариант, когда одна или часть стен выполняется в темном цвете, а мебель, пол и мелкие предметы – в осветленных вариантах гармоничных ему цветов.
НейтральныеЕсли взять два рядом расположенных цвета в пределах двух полос цветов на цветовом круге, сгладить один из них добавлением родственных оттенков или “разбавить” ахроматическим (белым или черным), то в итоге мы получим нейтральные цвета. Пример нейтральных цветов:
Пример нейтральных цветов:
Цвета с оттенками , расположенными на круге непосредственно слева и справа от цвета, дополнительного ему на цветовом круге. Пример таких цветов:
Каждый цвет вызывает определенные ассоциации, какие подходят вам?
Оттенки от желтого к зеленому – спокойная и оптимистичная гамма, снимает усталость.
Пастельные оттенки от желтого к бежевому – «примиряющие» и комфортные цвета.
Бирюза – дает ощущение свежести (подходит для ванной).
Светло-голубой – успокаивает, вызывает сонливость — идеален для спальни и комнат отдыха, а вот в кабинетах и рабочих зонах противопоказан.
Темно-голубой – «охлаждает» пространство и пыл (например, за столом переговоров), считается серьезным и деловым цветом.
Желтый и оранжевый – стимулирует и тонизирует (не годится для спальни), подходит для комнаты окнами на север.
Белый – может вызывать ощущение холода и дискомфорта, с другой стороны – «чистый лист» — идеальный фон для любых дизайнерских решений.
Красный или терракотовый в виде акцентов – бодрит, поднимает настроение.
Черный в виде акцентов – придает интерьеру графичность и особый стиль.
Светло-серый в «миксе» с другими цветами – деловая обстановка.
Всегда помните что, создавая художественное произведение, будь то картина или интерьер, следует руководствоваться интуицией и вашими собственными ощущениями, а не законами и правилами о сочетаниях цветов.
Подбор цвета онлайн
Этот сервис помогает подобрать гармоничные цвета исходя из цветов любой картинки. Огромное количество готовых палитр, навигация по которым организована тегами. Загрузите свою картинку или фото и сервис подберёт вам гармоничные цвета.
С которыми можно обратиться к Студии Лебедева, если вы занимаетесь оформлением своего стартапа и относитесь к вопросам дизайна всерьез, вам наверняка понадобятся инструменты для подбора цветовых схем. Хорошо, что в сети достаточно инструментов , которые помогут вам бесплатно в вашем нелегком труде.
Хорошо, что в сети достаточно инструментов , которые помогут вам бесплатно в вашем нелегком труде.
1. Color Explorer
Color Explorer – один из самых полезных инструментов для подбора цветовых схем и сочетаний. Позволяет на основе одного базового цвета подобрать релевантную цветовую гамму и разные оттенки, а также проанализировать потенциальную конверсию для разных типов цветовой схемы. Еще позволяет составлять цветовые схемы на основе выбранных изображений, импортировать css/html код из файлов и работать с RGB и hex-кодировкой цветов.
2. Adobe Kuler
Adobe Kuler – тоже классная штука. Позволяет при помощи палитры-колеса составлять цветовые гаммы и создавать готовые цветовые схемы, которые потом можно использовать на сайте или в приложении.
3. Slayeroffice Color Palette Generator
Следующий в нашем списке — slayeroffice . Очень простой и удобный генератор палитр. Предлагает вам также оттенки, когда вы подбираете основной цвет.
4.
 ColorBlender
ColorBlenderColorBlender – инструмент, который хорош для последующего использования полученных палитр в Photoshop или Illustrator. Есть готовая библиотека наборов, которые можно брать и использовать в вашем приложении.
5. 0 to 255
0 to 255 – еще один «подборщик» фильтров, при помощи которого можно взять и получить темные / светлые оттенки цветов. Для тех, кто увлекается градиентами и тенями – самое то.
6. Colorspire
Если все предыдущие инструменты вам почему-то не подошли – попробуйте Сolorspire . В нем еще есть настройка сатурации и всякие быстрые настройки выбранного цвета.
7. Color Schemer
Этот инструмент предлагает палитру из 16 цветов (в большинстве предыдущих вариантов базовых цветов 5). Еще его можно использовать без подключения к интернету на Mac или PC.
8. Color hunter
При помощи Сolor hunter можно выбирать готовые комбинации, основываясь на тегах, коде hex-цветов или по адресу URL изображений. Палитру цветов можно получить на основе загруженного изображения.
Палитру цветов можно получить на основе загруженного изображения.
9. ColorCombos
ColorCombos – снова схемы цветов, полная библиотека готовых образцов, можно сделать и собственную. Есть инструментарий для получения цветов с готового сайта.
10. WebAIM
И завершает подборку , который палитры не генерирует, но позволяет выбирать контрастные цвета. Для тех, кто знает толк не только в оттенках, но и в контрастах. Особенно если у вас контент-проект , и текст с заголовками должен хорошо читаться.
Следующий уникальный калькулятор служит для перевода экзотических единиц длины в…
Следующий онлайн калькулятор о фунтах. Ранее он был очень популярен,…
Следующий онлайн калькулятор может вычислить уровень жидкости в цилиндрической таре…
Следующий онлайн калькулятор переводит температуры между разными шкалами. Помните калькулятор…
Следующий калькулятор интересен тем, что он переводит древние российские денежные…
Следующий калькулятор будет очень полезен тем, кто решил купить или…
Следующий калькулятор работает очень просто, вам нужно ввести всего одно…
Следующий онлайн калькулятор считает рост человека благодаря русской системе мер…
Следующий онлайн калькулятор может вычислить габариты экрана телевизоров, компьютеров, проекторов,…
Перед вами 2 калькулятора: один поможет вам подобрать формат снимков…
Следующие 2 калькуляторы переводят заданное число плиток в квадратные метры…
Перед вами 2 онлайн-калькулятора.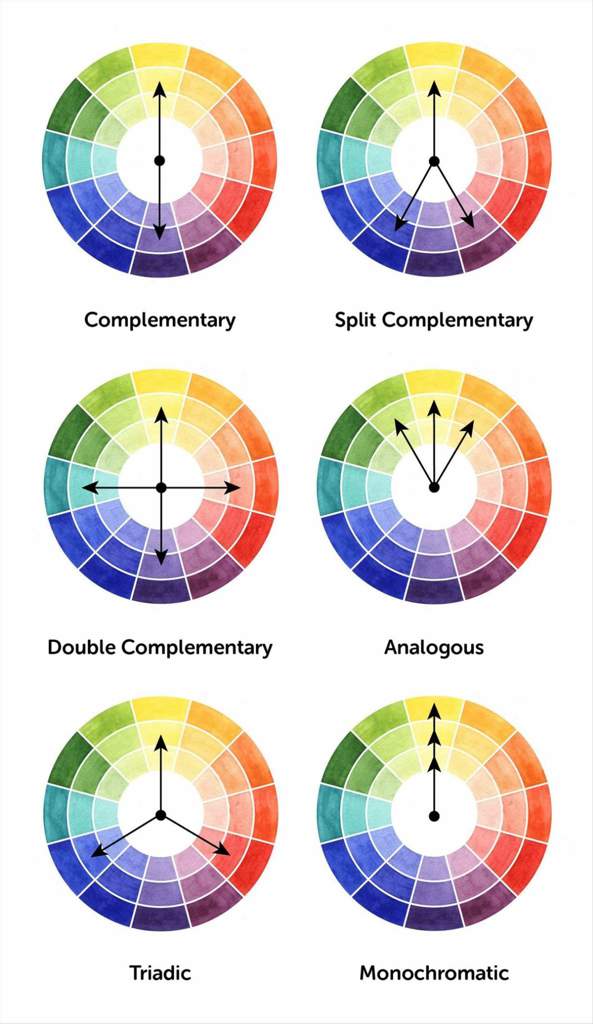 Они переводят меры площади из метрической…
Они переводят меры площади из метрической…
Следующий необычный калькулятор переводит меры длины из русской системы в…
Перед вами 2 калькулятора, которые предназначены для перевода мер длины…
Следующий простенький калькулятор переводит введенную вами toC из кельвинов в…
Следующий калькулятор предназначен для перевода кг в фунты. Также есть…
Подборка цвета – один из важнейших этапов в процессе создания хорошего дизайна.
Чтобы облегчить вам задачу, мы решили составить подборку, состоящую из лучших сервисов для создания цветовых схем. Они помогут сэкономить время, и при этом получить достойный результат.
01. Adobe Colour CC
Компания Adobe переименовала свой проект Kuler в Colour
Вы можете быть знакомы с этим инструментом по его прежнему названию — Adobe Kuler
. Однако совсем недавно компания Adobe переименовала одно из своих популярных веб-приложений в Adobe Colour CC
.
Он позволяет подбирать, создавать и сохранять различные цветовые схемы, в каждой из которых может присутствовать до пяти цветов. Инструмент доступен как в браузерной, так и в настольной версии. Если вы используете настольную версию, то вы сможете экспортировать цветовую схему прямо в Photoshop , Illustrator и InDesign .
02. Mudcube Colour Sphere
Если вы не уверены по поводу вашей цветовой схемы, то у Mudcude есть собственная галерея готовых ресурсов
Mudcube Colour Sphere – очень удобный миниатюрный ресурс для дизайнеров, который не только предлагает hex-коды выбранных цветов, но и позволяет создавать цветовые схемы для собственных проектов. Также стоит отметить, что в Mudcube имеется собственная галерея готовых ресурсов, которые также можно использовать.
03. Check my Colours
Check my Colours
разработан специально для оценки и подборки комбинации фона и основного цвета для всех DOM-элементов
. А также для того, чтобы выяснить, достаточно ли элементы гармоничны между собой. Все тесты основаны на алгоритмах, рекомендованных World Wide Web Consortium
(W3C ).
Все тесты основаны на алгоритмах, рекомендованных World Wide Web Consortium
(W3C ).
04. The Color App
Приложение поможет узнать RGB, HEX, а также HSLA-значения выбранных цветов
iOS-инструмент The Color App позволит легко и просто определять цвета при помощи большой цветовой палитры. Он позволяет узнать RGB , HEX и HSLA-значения цветов, а также создавать собственные цветовые схемы для сайта.
05. Color Hunter
Color Hunter формирует цветовую схему на основе выбранного изображения
Это очень удобный инструмент, особенно если необходимо найти какой-то конкретный цвет. Выберите изображение и загрузите его в Color Hunter . Инструмент создаст цветовую палитру на основе выбранного изображения. Это отличный метод создания собственных цветовых схем.
06.
Если вам нужно получить конкретный цвет, просто введите HEX-значение в URL
На этом сайте используется база данных, состоящая из 10 миллионов изображений, доступных бесплатно по лицензионному соглашению Creative Commons
, которые создатели тщательно отобрали с Flickr
. Их можно использовать для генерации соответствующих цветовых схем.
Их можно использовать для генерации соответствующих цветовых схем.
07. Color
Удобное миниатюрное веб-приложение. Наведите курсор мыши на экран, и определите нужный цвет, затем прокрутите немного, чтобы подобрать оттенок. После чего инструмент выдаст все необходимые HEX-коды , которые можно использовать в собственных проектах. Один из самых простых в использовании инструментов.
08.
Бесплатный генератор цветовых схем, который предоставляет информацию о цвете, а также позволяет конвертировать его в любые схемы (RGB , CMYK и другие ). Здесь доступны различные форматы цветовых схем, включая триадные, монохромные и другие.
09.
На можно выбрать до пяти оттенков при помощи удобной палитры на всю страницу, которая поможет без труда найти именно те цветовые схемы HTML
, которые вы ищете. После этого сайт сгенерирует страницу со всеми изображениями из базы данных, в которых используется похожая цветовая комбинация. Также будут предоставлены HEX-значения
, которые можно использовать в собственных проектах. А изображения можно сохранять в коллекциях на сайте.
Также будут предоставлены HEX-значения
, которые можно использовать в собственных проектах. А изображения можно сохранять в коллекциях на сайте.
10. ColorExplorer
Один из самых продуманных веб-инструментов, который предлагает множество функций, связанных с дизайном, настройкой и аналитикой цветовых схем. Здесь представлены инструменты, которые помогут определить WCAG-валидность цветовых схем , а также сгенерировать собственные цветовые палитры.
11. Hex Color Scheme Generator
Небольшой удобный инструмент для генерирования комбинации цветов на основе одного выбранного оттенка. Вставьте Hex-значение цвета, а инструмент предоставит набор подходящих цветов, которые можно будет использовать вместе с основным.
12. COLOURlovers
COLOURlovers представляет собой сообщество для обмена цветовыми схемами. Здесь можно черпать вдохновение из цветовых наборов других пользователей, а также создавать собственные и делиться ими.
13.
 Color Scheme Designer
Color Scheme DesignerЭтот онлайн-инструмент предлагает интересные способы генерирования цветовых схем, позволяя настраивать их яркость и регулировать контраст. Здесь можно создать несколько популярных математических моделей цветовых схем, включая монохромную.
14. COPASO
Один из инструментов с сайта COLOURlovers . Но COPASO достоин отдельного внимания, так как представляет собой невероятное решение «все в одном », и позволяет легко генерировать готовые цветовые схемы для сайта. Здесь представлено множество инструментов для подбора цвета, и все они размещаются в удобном и простом интерфейсе. Кроме этого к палитрам можно добавлять заметки, загружать изображения и т.п.
15. Colourmod
Colourmod
представляет собой программное обеспечение, которое позволяет выбирать отдельные цвета из области виджетов, независимо от того, используете ли вы Mac
или Konfabulator
на Windows
. Это не совсем простой инструмент для работы с цветовыми палитрами, однако он поможет быстро и просто определять цвета без необходимости загружать тяжеловесные программы.
16. ColorZilla
ColorZilla доступен как для Chrome, так и для Firefox
Этот проект начинался как плагин для Firefox , однако сегодня он также доступен и для Google Chrome . ColorZilla представляет собой расширение, которое включает в себя несколько инструментов, предназначенных для работы с цветом, среди которых палитра, генератор css-градиентов и пипетка.
17. Colormunki
Удобный онлайн-инструмент для подбора цветовых схем от создателей Colormunki . С его помощью можно без труда создавать привлекательные цветовые палитры из образцов на основе Pantone с использованием нескольких методик.
18. colr.org
Colr.org позволяет установить диапазон цветов любого изображения
Этот инструмент позволяет провести подробный анализ цветов изображения, который обычно автоматизирован в других инструментах. Это позволит выбрать наиболее подходящий цвет. Мы рекомендуем познакомиться с этим инструментом, хотя его интерфейс не настолько продуман, как в других приложениях.
19. ColourGrab
Этот удобный инструмент создает цветовые палитры из любого изображения. Вставьте адрес изображения, которое хотите проанализировать, и сервис автоматически сгенерирует трехмерный график с информацией по использованным цветам. Хотя это приложение не совсем подходит для подбора цветовой схемы для сайта, но с его помощью можно изучить изображения и их цветовые характеристики.
20. ColorBlender
ColorBlender генерирует палитру из пяти сочетающихся цветов
Один из простейших инструментов, который позволяет настраивать цветность и в режиме реального времени получать пять сочетающихся между собой цветов. Сгенерированную палитру можно скачать в Photoshop или Illustrator в виде EPS-файла .
21. GrayBit
GrayBit позволяет анализировать сайты, чтобы понять, как бы они выглядели в градации серого
Этот инструмент поможет увидеть, как ваш сайт смотрится в серых тонах. Отличный сервис, который позволит выявить проблемные по контрасту места.
22. COLRD
Инструмент, который можно использовать в качестве источника вдохновения или для обмена цветовыми схемами. Конечно, этот ресурс не поможет с генерированием схем, но его обязательно следует взять на заметку.
23. Shutterstock Spectrum
Изображения можно фильтровать по цветовому балансу и яркости
Иногда проверить будет ли цветовая схема сочетаться легче всего путем просмотра стоковых картинок. Практически все основные стоковые ресурсы предлагают подобные инструменты, однако Shutterstock Spectrum имеет очень удобный интерфейс. После использования слайдера для определения цвета вы сможете указать ключевые слова, которые позволят определить тему снимков. Кроме этого можно отфильтровать изображения по цветовому балансу и яркости.
24. Stripe Generator 2.0
Может показаться, что этот инструмент уже давно устарел. Однако вы все равно сможете эффективно использовать его для создания готовых цветовых схем для сайта и привлекательных паттернов.
25. Colors on the Web
Colors on the Web принимает отдельные цвета в HEX или RGB , и выдает цветовые схемы, основанные на различных математических вычислениях. Подобный механизм используется и в Kuler . Этот веб-инструмент не будет работать на iPad или iPhone из-за использования технологии Flash .
26. Pictaculous
Этот инструмент позволяет загружать изображения и генерировать цветовые схемы из используемых в них цветов. Проект совмещает в себе и другие инструменты, предлагая одновременно функционал Kuler и Colourlovers .
27. Contrast-A
Необычный инструмент для создания цветовых схем, отвечающих требованиям WCAG . Сервис позволяет симулировать дальтонизм, плохое зрение, а также клиническую слепоту. Кроме этого здесь представлено множество ссылок на очень полезные ресурсы и инструкции.
28. ColoRotate
Инструмент предлагает схожий с Kuler функционал, но при этом красиво визуализирует цветовые палитры, а также позволяет генерировать более пяти цветов в одной схеме. Его можно напрямую интегрировать в некоторые приложения Creative Suite. Этот инструмент также доступен в виде приложения для iPad, предлагая отличную интеграцию с Photoshop, где он может выступать в роли панели цветов.
Его можно напрямую интегрировать в некоторые приложения Creative Suite. Этот инструмент также доступен в виде приложения для iPad, предлагая отличную интеграцию с Photoshop, где он может выступать в роли панели цветов.
Перевод статьи “The 28 best tools for choosing a colour scheme ” был подготовлен дружной командой проекта .
Использование предлога in в английском языке
Употребление и произношение in
Сочетание с повторением онлайн калькулятор. Сочетания без повторений: Комбинаторика в MS EXCEL
Рассмотрим задачу подсчета числа выборок из данного множества в общем виде. Пусть имеется некоторое множество N , состоящее из n элементов. Любое подмножество, состоящее из m элементов можно рассматривать без учета их порядка, так и с его учетом, т.е. при изменении порядка переходим к другой m – выборке.
Сформулируем следующие определения:
Размещения без повторения
Размещением без
повторения из n элементов по m N ,
содержащее m различных элементов .
Из определения следует, что два размещения отличаются друг от друга, как элементами, так и их порядком, даже если элементы одинаковы.
Теорема 3 . Число размещений без повторения равно произведению m сомножителей, наибольшим из которых является число n . Записывают:
Перестановки без повторений
Перестановками из n элементов называются различные упорядочения множества N .
Из этого определения следует, что две перестановки отличаются только порядком элементов и их можно рассматривать как частный случай размещений.
Теорема 4 . Число различных перестановок без повторений вычисляется по формуле
Сочетания без повторений
Сочетанием без повторения из n элементов по m называется любое неупорядоченное подмножество множества N , содержащее m различных элементов.
Из определения
следует, что два сочетания различаются
только элементами, порядок не важен.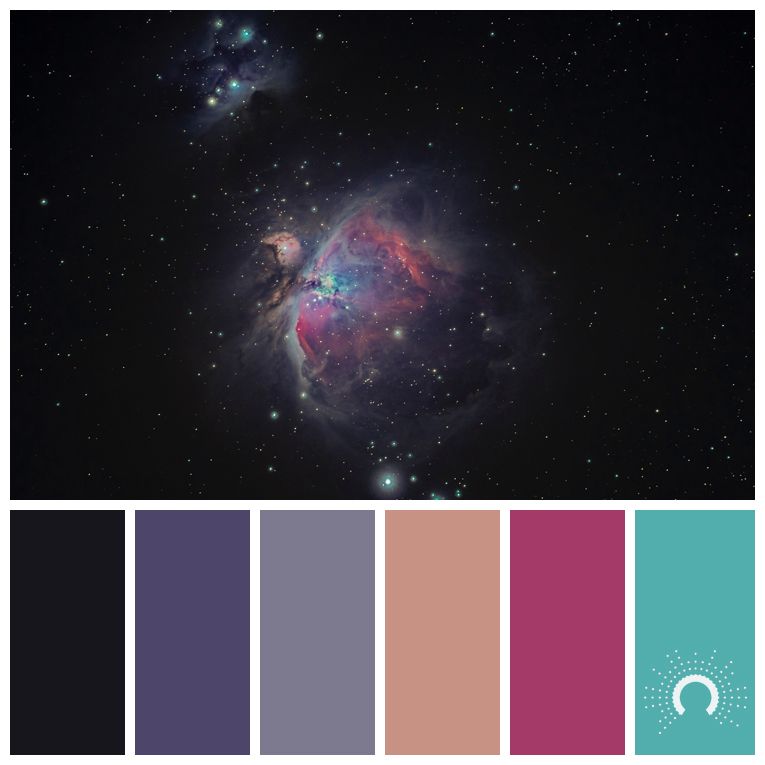
Теорема 5 . Число сочетаний без повторений вычисляют по одной из следующих формул:
Пример 1 . В комнате 5 стульев. Сколькими способами можно разместить на них
а) 7 человек; б) 5 человек; в) 3 человека?
Решение: а) Прежде всего надо выбрать 5 человек
из 7 для посадки на стулья. Это можно
сделать
способом. С каждым выбором конкретной
пятерки можно произвести
перестановок местами. Согласно теореме
умножения искомое число способов посадки
равно.
Замечание: Задачу можно решать, используя только теорему произведения, рассуждая следующим образом: для посадки на 1-й стул имеется 7 вариантов, на 2-й стул-6 вариантов, на 3-й -5, на 4-й -4 и на 5-й -3. Тогда число способов посадки 7 человек на 5 стульев равно . Решения обоими способами согласуются, так как
б) Решение очевидно
—
в) — число выборов занимаемых стульев.
— число размещений трех человек на трех выбранных стульях.
Общее число выборов
равно
.
Не трудно проверить
формулы
;
;
Число всех подмножеств множества, состоящего из n элементов.
Размещения с повторением
Размещением с повторением из n элементов по m называется всякое упорядоченное подмножество множества N , состоящее из m элементов так, что любой элемент ожжет входить в это подмножество от 1 до m раз, либо вообще в нем отсутствовать .
Число размещений с повторением обозначают и вычисляют по формуле, представляющей собой следствие из теоремы умножения:
Пример 2 .
Пусть дано множество из трех букв N
= {a,
b,
c}.
Назовем словом любой набор из букв,
входящих в это множество. Найдем
количество слов длиной 2, которые можно
составить из этих букв:
.
Замечание: Очевидно, размещения с повторением
можно рассматривать и при
.
Пример 3 .
Требуется из букв {a,
b},
составить всевозможные слова длиной
3. Сколькими способами это можно сделать?
Сколькими способами это можно сделать?
Ответ :
На первом месте в ряду может стоять любой из N элементов, следовательно, получается N вариантов. На втором месте — любой, кроме того, который уже был использован для первого места. Следовательно, для каждого из N уже найденных вариантов есть (N — 1) вариантов второго места, и общее количество комбинаций становится N*(N — 1).
Это же можно повторить для остальных элементов ряда. Для самого последнего места остается только один вариант — последний оставшийся элемент. Для предпоследнего — два варианта, и так далее.
Следовательно, для ряда из N неповторяющихся элементов возможных перестановок равно произведению всех целых от 1 до N. Это произведение называется N и N! (читается «эн факториал»).
В предыдущем случае количество возможных элементов и количество мест ряда совпадали, и их число было равно N. Но возможна ситуация, когда в ряду меньше мест, чем имеется возможных элементов. Иными словами, количество элементов в выборке равно некоторому числу M, причем M Во-первых, может потребоваться сосчитать общее количество возможных способов, которыми можно выстроить в ряд M элементов из N. Такие способы размещениями.
Такие способы размещениями.
Во-вторых, исследователя может интересовать число способов, которыми можно выбрать M элементов из N. При этом порядок расположения элементов уже не важен, но любые два варианта должны различаться между собой хотя бы одним элементом. Такие способы называются сочетаниями.
Чтобы найти количество размещений по M элементов из N, можно прибегнуть к такому же способу рассуждений, как и в случае с перестановками. На первом месте здесь по-прежнему может стоять N элементов, на втором (N — 1), и так далее. Но для последнего места количество возможных вариантов равняется не единице, а (N — M + 1), поскольку, когда размещение будет закончено, останется еще (N — M) неиспользованных элементов.
Таким образом, число размещений по M элементов из N равняется произведению всех целых чисел от (N — M + 1) до N, или, что то же самое, частному N!/(N — M)!.
Очевидно, что количество сочетаний по M элементов из N будет меньше количества размещений. Для каждого возможного сочетания есть M! возможных размещений, зависящих от порядка элементов этого сочетания.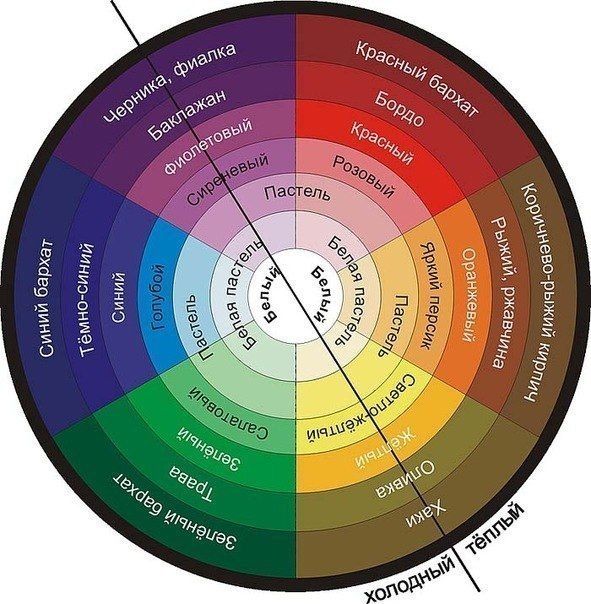 Следовательно, чтобы найти это количество, нужно разделить число размещений по M элементов из N на N!. Иными словами, количество сочетаний по M элементов из N равно N!/(M!*(N — M)!).
Следовательно, чтобы найти это количество, нужно разделить число размещений по M элементов из N на N!. Иными словами, количество сочетаний по M элементов из N равно N!/(M!*(N — M)!).
Источники:
- количество сочетаний
Факториал натурального числа – это произведение всех предыдущих натуральных чисел, включая само число. Факториал нуля равен единице. Кажется, что посчитать факториал числа очень просто – достаточно перемножить все натуральные числа, не превышающие заданное. Однако, значение факториала настолько быстро возрастает, что некоторые калькуляторы не справляются с этой задачей.
Вам понадобится
- калькулятор, компьютер
Инструкция
Чтобы посчитать факториал натурального числа перемножьте все , не превосходящие данное. Каждое число учитывается только один раз. В виде формулы это можно записать следующим образом:n! = 1*2*3*4*5*…*(n-2)*(n-1)*n, гдеn – натуральное число, факториал которого требуется посчитать.
0! принимается равным единице (0!=1).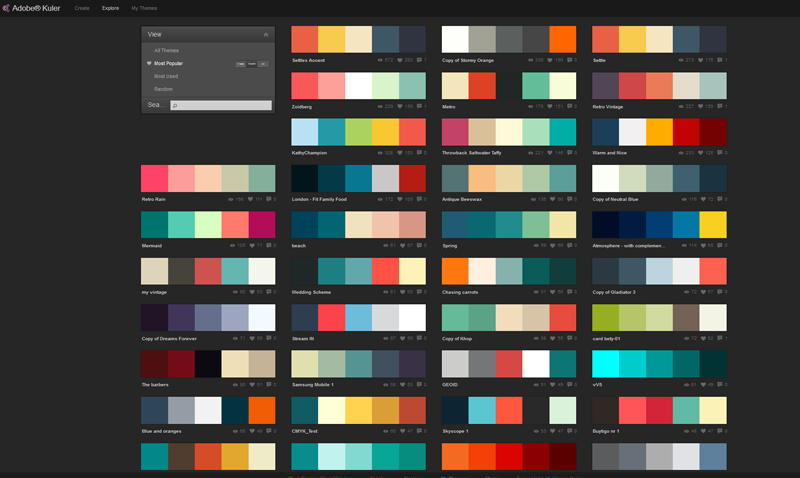 При возрастании аргумента значение факториала очень быстро увеличивается, поэтому обычный (бухгалтерский) уже для факториала 15-ти вместо результата может выдать об ошибке.
При возрастании аргумента значение факториала очень быстро увеличивается, поэтому обычный (бухгалтерский) уже для факториала 15-ти вместо результата может выдать об ошибке.
Чтобы посчитать факториал большого натурального числа, возьмите инженерный калькулятор. То есть, такой калькулятор на клавиатуре которого имеются обозначения математических функций (cos, sin, √). Наберите на калькуляторе исходное число, а затем нажмите кнопку вычисления факториала. Обычно такая кнопка как «n!» или аналогично (вместо «n» может стоять «N» или «х», но восклицательный знак «!» в обозначении факториала должен присутствовать в любом случае).
При больших значениях аргумента результаты вычислений начинают отображаться в «экспоненциальном» (показательном) виде. Так, например, факториал 50 будет представлен в форме: 3,0414093201713378043612608166065e+64 (или похожем). Чтобы получить результат вычислений в обычном виде, припишите к числу, показанному до символа «е», столько нулей, сколько указано после «е+» (если, конечно, хватит места).
Число сочетаний
Сочетанием из n по k называется набор k элементов, выбранных из данных n элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений .
Явные формулы
Число сочетаний из n по k равно биномиальному коэффициенту
При фиксированном значении n производящей функцией чисел сочетаний с повторениями из n по k является:
Двумерной производящей функцией чисел сочетаний с повторениями является:
Ссылки
- Р. Стенли Перечислительная комбинаторика. — М.: Мир, 1990.
- Вычисление числа сочетаний онлайн
Wikimedia Foundation . 2010 .
Смотреть что такое «Число сочетаний» в других словарях:
70 семьдесят 67 · 68 · 69 · 70 · 71 · 72 · 73 40 · 50 · 60 · 70 · 80 · 90 · 100 Факторизация: 2×5×7 Римская запись: LXX Двоичное: 100 0110 … Википедия
Световое число, условное число, однозначно выражающее внеш. условия при фотосъёмке (обычно яркость объекта съёмки и светочувствительность применяемого фотоматериала). Любому значению Э. ч. можно подобрать неск. сочетаний диафрагменное число… … Большой энциклопедический политехнический словарь
условия при фотосъёмке (обычно яркость объекта съёмки и светочувствительность применяемого фотоматериала). Любому значению Э. ч. можно подобрать неск. сочетаний диафрагменное число… … Большой энциклопедический политехнический словарь
Форма числа, выделяющая два предмета как по отношению к единичному предмету, так и по отношению к множеству предметов. В современном русском языке эта форма не существует, но остатки ее влияния сохранились. Так, сочетания два стола (ср. мн. ч.… … Словарь лингвистических терминов
Комбинаторная математика, комбинаторика, раздел математики, посвященный решению задач выбора и расположения элементов нек рого, обычно конечного, множества в соответствии с заданными правилами. Каждое такое правило определяет способ построения… … Математическая энциклопедия
В комбинаторике сочетанием из по называется набор элементов, выбранных из данного множества, содержащего различных элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания… … Википедия
Занимается изучением событий, наступление которых достоверно неизвестно. Она позволяет судить о разумности ожидания наступления одних событий по сравнению с другими, хотя приписывание численных значений вероятностям событий часто бывает излишним… … Энциклопедия Кольера
Она позволяет судить о разумности ожидания наступления одних событий по сравнению с другими, хотя приписывание численных значений вероятностям событий часто бывает излишним… … Энциклопедия Кольера
1) то же, что математический Комбинаторный анализ. 2) Раздел элементарной математики, связанный с изучением количества комбинаций, подчинённых тем или иным условиям, которые можно составить из заданного конечного множества объектов… … Большая советская энциклопедия
— (греч. paradoxos неожиданный, странный) в широком смысле: утверждение, резко расходящееся с общепринятым, устоявшимся мнением, отрицание того, что представляется «безусловно правильным»; в более узком смысле два противоположных утверждения, для… … Философская энциклопедия
— (или принцип включений исключений) комбинаторная формула, позволяющая определить мощность объединения конечного числа конечных множеств, которые в общем случае могут пересекаться друг с другом … Википедия
Математическая теория, занимающаяся определением числа различных способов распределения данных предметов в известном порядке; имеет особенно важное значение в теории уравнений и в теории вероятностей. Простейшие задачи этого рода заключаются в… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Простейшие задачи этого рода заключаются в… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Книги
- Число судьбы. Гороскоп совместимости. Желания. Страсти. Фантазии (количество томов: 3) , Майер Максим. Число судьбы. Как составить индивидуальный нумерологический прогноз. Нумерология — одна из самых древних эзотерических систем. Невозможно точно установить времяее возникновения. Однако в…
Комбинаторика — это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов. Основы комбинаторики очень важны для оценки вероятностей случайных событий, т.к. именно они позволяют подсчитать принципиальновозможное количество различных вариантов развития событий.
Основная формула комбинаторики
Пусть имеется k групп элементов, причем i-я группа состоит из n i элементов.
Выберем по одному элементу из каждой группы. Тогда общее число N способов,
которыми можно произвести такой выбор, определяется соотношением N=n 1 *n 2 *n 3 *. ..*n k .
..*n k .
Пример 1. Поясним это правило на простом примере. Пусть имеется две группы элементов, причем первая группа состоит из n 1 элементов, а вторая — из n 2 элементов. Сколько различных пар элементов можно составить из этих двух групп, таким образом, чтобы в паре было по одному элементу от каждой группы? Допустим, мы взяли первый элемент из первой группы и, не меняя его, перебрали все возможные пары, меняя только элементы из второй группы. Таких пар для этого элемента можно составить n 2 . Затем мы берем второй элемент из первой группы и также составляем для него все возможные пары. Таких пар тоже будет n 2 . Так как в первой группе всего n 1 элемент, всего возможных вариантов будет n 1 *n 2 .
Пример 2. Сколько
трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если
цифры могут повторяться?
Решение: n 1 =6
(т.к. в качестве первой цифры можно взять любую цифру из 1, 2, 3, 4, 5, 6), n 2 =7
(т.к. в качестве второй цифры можно взять любую цифру из 0, 1, 2, 3, 4, 5,
6), n 3 =4 (т.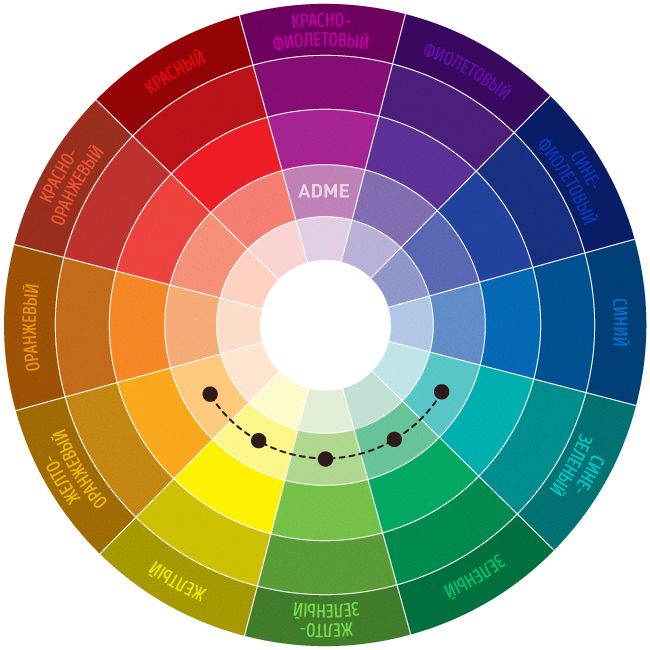 к. в качестве третьей цифры можно взять любую цифру из 0, 2, 4,
6).
к. в качестве третьей цифры можно взять любую цифру из 0, 2, 4,
6).
Итак, N=n 1 *n 2 *n 3 =6*7*4=168.
В том случае, когда все группы состоят из одинакового числа элементов, т.е. n 1 =n 2 =…n k =n можно считать, что каждый выбор производится из одной и той же группы, причем элемент после выбора снова возвращается в группу. Тогда число всех способов выбора равно n k . Такой способ выбора в комбинаторики носит название выборки с возвращением.
Пример 3. Сколько всех четырехзначных чисел
можно составить из цифр 1, 5, 6, 7, 8?
Решение. Для каждого разряда
четырехзначного числа имеется пять возможностей, значит N=5*5*5*5=5 4 =625.
Рассмотрим множество, состоящие из n элементов. Это множество в комбинаторике называется генеральной совокупностью .
Число размещений из n элементов по m
Определение 1. Размещением из n элементов по m в комбинаторике называется
любой упорядоченный набор из m различных
элементов, выбранных из генеральной совокупности в n элементов.
Пример 4. Различными размещениями из трех элементов {1, 2, 3} по два будут наборы (1, 2), (2, 1), (1, 3), (3, 1), (2, 3),(3, 2). Размещения могут отличаться друг от друга как элементами, так и их порядком.
Число размещений в комбинаторике обозначается A n m и вычисляется по формуле:
Замечание: n!=1*2*3*…*n (читается: «эн факториал»), кроме того полагают, что 0!=1.
Пример 5 . Сколько существует двузначных
чисел, в которых цифра десятков и цифра единиц различные
и нечетные?
Решение: т.к. нечетных цифр
пять, а именно 1, 3, 5, 7, 9, то эта задача сводится к выбору и размещению на
две разные позиции двух из пяти различных цифр, т.е. указанных чисел будет:
Определение 2. Сочетанием из n элементов по m в комбинаторике называется любой неупорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов.
Пример 6 . Для множества {1, 2,
3}сочетаниями являются {1, 2}, {1, 3}, {2, 3}.
Число сочетаний из n элементов по m
Число сочетаний обозначается C n m и вычисляется по формуле:
Пример 7. Сколькими способами читатель может выбрать две книжки из шести имеющихся?
Решение: Число способов равно числу сочетаний из шести книжек по две, т.е. равно:
Перестановки из n элементов
Определение 3. Перестановкой из n элементов называется любой упорядоченный набор этих элементов.
Пример 7a. Всевозможными перестановками множества, состоящего из трех элементов {1, 2, 3} являются: (1, 2, 3), (1, 3, 2), (2, 3, 1), (2, 1, 3), (3, 2, 1), (3, 1, 2).
Число различных перестановок из n элементов обозначается P n и вычисляется по формуле P n =n!.
Пример 8. Сколькими способами семь книг разных авторов можно расставить на полке в один ряд?
Решение: эта задача о числе
перестановок семи разных книг. Имеется P 7 =7!=1*2*3*4*5*6*7=5040
способов осуществить расстановку книг.
Обсуждение. Мы видим, что число возможных комбинаций можно посчитать по разным правилам (перестановки, сочетания, размещения) причем результат получится различный, т.к. принцип подсчета и сами формулы отличаются. Внимательно посмотрев на определения, можно заметить, что результат зависит от нескольких факторов одновременно.
Во-первых, от того, из какого количества элементов мы можем комбинировать их наборы (насколько велика генеральная совокупность элементов).
Во-вторых, результат зависит от того, какой величины наборы элементов нам нужны.
И последнее, важно знать, является ли для нас существенным порядок элементов в наборе. Поясним последний фактор на следующем примере.
Пример 9. На родительском собрании
присутствует 20 человек. Сколько существует различных вариантов состава
родительского комитета, если в него должны войти 5 человек?
Решение: В этом примере нас
не интересует порядок фамилий в списке комитета. Если в результате в его
составе окажутся одни и те же люди, то по смыслу для нас это один и тот же
вариант. Поэтому мы можем воспользоваться формулой для подсчета числа сочетаний из 20 элементов по 5.
Поэтому мы можем воспользоваться формулой для подсчета числа сочетаний из 20 элементов по 5.
Иначе будут обстоять дела, если каждый член комитета изначально отвечает за определенное направление работы. Тогда при одном и том же списочном составе комитета, внутри него возможно 5! вариантов перестановок , которые имеют значение. Количество разных (и по составу, и по сфере ответственности) вариантов определяется в этом случае числом размещений из 20 элементов по 5.
Задачи для самопроверки
1. Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5,
6, если цифры могут повторяться?
2. Сколько существует пятизначных чисел, которые одинаково читаются слева направо и справа налево?
3. В классе десять предметов и пять уроков в день. Сколькими способами можно составить расписание на один день?
4. Сколькими способами можно выбрать 4 делегата на конференцию, если в группе 20 человек?
5. Сколькими способами можно разложить восемь различных писем по восьми различным конвертам, если в каждый конверт кладется только одно письмо?
6. Из трех математиков и десяти экономистов надо составить комиссию,
состоящую из двух математиков и шести экономистов. Сколькими способами это
можно сделать?
Из трех математиков и десяти экономистов надо составить комиссию,
состоящую из двух математиков и шести экономистов. Сколькими способами это
можно сделать?
В комбинаторике изучают вопросы о том, сколько комбинаций определенного типа можно составить из данных предметов (элементов).
Рождение комбинаторики как раздела связано с трудами Б. Паскаля и П. Ферма по теории азартных игр. Большой вклад в развитие комбинаторных методов внесли Г.В. Лейбниц, Я. Бернулли и Л. Эйлер.
Французский философ, писатель, математик и физик Блез Паскаль (1623–1662) рано проявил свои выдающиеся математические способности. Круг математических интересов Паскаля был весьма разнообразен. Паскаль доказал одну
из основных теорем проективной геометрии (теорема Паскаля), сконструировал суммирующую машину (арифмометр Паскаля), дал способ вычисления биномиальных коэффициентов (треугольник Паскаля), впервые точно определил и применил для доказательства метод математической индукции, сделал существенный шаг в развитии анализа бесконечно малых, сыграл важную роль в зарождении теории вероятности. В гидростатике Паскаль установил ее основной закон (закон Паскаля). “Письма к провинциалу” Паскаля явились шедевром французской классической прозы.
В гидростатике Паскаль установил ее основной закон (закон Паскаля). “Письма к провинциалу” Паскаля явились шедевром французской классической прозы.
Готфрид Вильгельм Лейбниц (1646–1716) — немецкий философ, математик, физик и изобретатель, юрист, историк, языковед. В математике наряду с И. Ньютоном разработал дифференциальное и интегральное исчисление. Важный вклад внес в комбинаторику. С его именем, в частности, связаны теоретико-числовые задачи.
Готфрид Вильгельм Лейбниц имел мало внушительную внешность и поэтому производил впечатление довольно невзрачного человека. Однажды в Париже он зашел в книжную лавку в надежде приобрести книгу своего знакомого философа. На вопрос посетителя об этой книге книготорговец, осмотрев его с головы до ног, насмешливо бросил: “Зачем она вам? Неужели вы способны читать такие книги?” Не успел ученый ответить, как в лавку вошел сам автор книги со словами: “Великому Лейбницу привет и уважение!” Продавец никак не мог взять втолк, что перед ним действительно знаменитый Лейбниц, книги которого пользовались большим спросом среди ученых.
В дальнейшем важную роль будет играть следующая
Лемма. Пусть в множестве элементов, а в множестве — элементов. Тогда число всех различных пар , где будет равно .
Доказательство. Действительно, с одним элементом из множества мы можем составить таких различных пар, а всего в множестве элементов.
Размещения, перестановки, сочетания
Пусть у нас есть множество из трех элементов . Какими способами мы можем выбрать из этих элементов два? .
Определение. Размещениями множества из различных элементов по элементов называются комбинации, которые составлены из данных элементов по > элементов и отличаются либо самими элементами, либо порядком элементов.
Число всех размещений множества из элементов по элементов обозначается через (от начальной буквы французского слова “arrangement”, что означает размещение), где и .
Теорема. Число размещений множества из элементов по элементов равно
Доказательство. Пусть у нас есть элементы . Пусть — возможные размещения. Будем строить эти размещения последовательно. Сначала определим — первый элемент размещения. Из данной совокупности элементов его можно выбрать различными способами. После выбора первого элемента для второго элемента остается способов выбора и т.д. Так как каждый такой выбор дает новое размещение, то все эти выборы можно свободно комбинировать между собой. Поэтому имеем:
Пусть — возможные размещения. Будем строить эти размещения последовательно. Сначала определим — первый элемент размещения. Из данной совокупности элементов его можно выбрать различными способами. После выбора первого элемента для второго элемента остается способов выбора и т.д. Так как каждый такой выбор дает новое размещение, то все эти выборы можно свободно комбинировать между собой. Поэтому имеем:
Пример. Сколькими способами можно составить флаг, состоящий из трех горизонтальных полос различных цветов, если имеется материал пяти цветов?
Решение. Искомое число трехполосных флагов:
Определение. Перестановкой множества из элементов называется расположение элементов в определенном порядке.
Так, все различные перестановки множества из трех элементов — это
Число всех перестановок из элементов обозначается (от начальной буквы французского слова “permutation”, что значит “перестановка”, “перемещение”). Следовательно, число всех различных перестановок вычисляется по формуле
Пример. k
k
Действительно, каждому -элементному подмножеству данного -элементного множества соответствует одно и только одно -элементное подмножество того же множества.
Действительно, мы можем выбирать подмножества из элементов следующим образом: фиксируем один элемент; число -элементных подмножеств, содержащих этот элемент, равно ; число -элементных подмножеств, не содержащих этот элемент, равно .
Треугольник Паскаля
В этом треугольнике крайние числа в каждой строке равны 1, а каждое не крайнее число равно сумме двух чисел предыдущей строки, стоящих над ним. Таким образом, этот треугольник позволяет вычислять числа .
Теорема.
Доказательство. Рассмотрим множество из элементов и решим двумя способами следующую задачу: сколько можно составить последовательностей из элементов данного
множества, в каждой из которых никакой элемент не встречается дважды?
1 способ. Выбираем первый член последовательности, затем второй, третий и т. д. член
д. член
2 способ. Выберем сначала элементов из данного множества, а затем расположим их в некотором порядке
Домножим числитель и знаменатель этой дроби на :
Пример. Сколькими способами можно в игре “Спортлото” выбрать 5 номеров из 36?
Искомое число способов
Задачи.
1. Номера машин состоят из 3 букв русского алфавита (33 буквы) и 4 цифр. Сколько существует различных номеров автомашин?
2. На рояле 88 клавиш. Сколькими способами можно извлечь последовательно 6 звуков?
3. Сколько есть шестизначных чисел, делящихся на 5?
4. Сколькими способами можно разложить 7 разных монет в три кармана?
5. Сколько можно составить пятизначных чисел, в десятичной записи которых хотя бы один раз встречается цифра 5?
6. Сколькими способами можно усадить 20 человек за круглым столом, считая способы одинаковыми, если их можно получить один из другого движением по кругу?
7. Сколько есть пятизначных чисел, делящихся на 5, в записи которых нет одинаковых цифр?
8.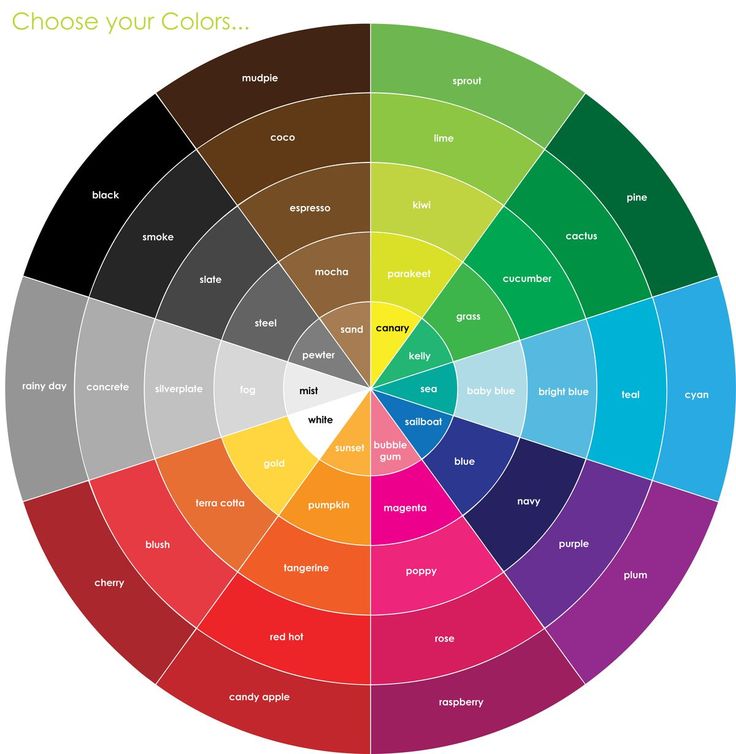 На клетчатой бумаге со стороной клетки 1 см нарисована окружность радиуса 100 см, не проходящая через вершины клеток и не касающаяся сторон клеток. Сколько клеток может пересекать эта окружность?
На клетчатой бумаге со стороной клетки 1 см нарисована окружность радиуса 100 см, не проходящая через вершины клеток и не касающаяся сторон клеток. Сколько клеток может пересекать эта окружность?
9. Сколькими способами можно расставить в ряд числа так, чтобы числа стояли рядом и притом шли в порядке возрастания?
10. Сколько пятизначных чисел можно составить из цифр , если каждую цифру можно использовать только один раз?
11. Из слова РОТ перестановкой букв можно получить еще такие слова: ТОР, ОРТ, ОТР, ТРО, РТО. Их называют анаграммами. Сколько анаграмм можно составить из слова ЛОГАРИФМ?
12. Назовем разбиением натурального числа представление его в виде суммы натуральных чисел. Вот, например, все разбиения числа :
Разбиения считаются разными, если они отличаются либо числами, либо порядком слагаемых.
Сколько существует различных разбиений числа на слагаемых?
13. Сколько существует трехзначных чисел с невозрастающим порядком цифр?
14. Сколько существует четырехзначных чисел с невозрастающим порядком цифр?
Сколько существует четырехзначных чисел с невозрастающим порядком цифр?
15. Сколькими способами можно рассадить в ряд 17 человек, чтобы и оказались рядом?
16. девочек и мальчиков рассаживаются произвольным образом в ряду из мест. Сколькими способами можно их рассадить так, чтобы никакие две девочки не сидели рядом?
17. девочек и мальчиков рассаживаются произвольным образом в ряду из мест. Сколькими способами можно их рассадить так, чтобы все девочки сидели рядом?
Комбинации Калькулятор перестановок
Найдите количество комбинаций и перестановки, когда вы выбираете подмножество r элементов из набора n элементов. За помощью в использовании калькулятор, ознакомьтесь с часто задаваемыми вопросами или просмотрите образец задачи.
Объявления
Часто задаваемые вопросы
Калькулятор | Пример задачи
Инструкции: Чтобы найти ответ на часто задаваемый
вопрос, просто нажмите на вопрос.
Что такое перестановка?
Перестановка представляет собой расположение всех или части набора объектов, с отношением к порядку расположения.
Например, предположим, что у нас есть набор из трех букв: A, B и C. Мы могли бы спросить, сколькими способами мы можем расположить 2 буквы из этого набора. Каждый возможная договоренность была бы примером перестановки. Полный список Возможные перестановки: AB, AC, BA, BC, CA и CB.
Когда статистики говорят о перестановках, они используют терминология. Они описывают перестановки как n взято отдельных объектов r вовремя. Перевод: n означает количество объектов, из которых образуется перестановка; и r относится к числу объектов, используемых для образуют перестановку. Рассмотрим пример из предыдущего пункта. перестановки были образованы из 3 букв (А, В и С), поэтому n = 3; а также каждая перестановка состояла из 2 букв, поэтому r = 2.
Обратите внимание, что AB и BA считаются двумя перестановками, потому что
порядок, в котором выбираются объекты, имеет значение. Это ключ
различие между
комбинация
и перестановка.
Комбинация фокусируется на выборе объектов без относительно порядка их выбора. Перестановка, напротив,
фокусируется на расположении объектов с в отношении порядка, в котором
они устроены. Итог: AB и BA представляют две перестановки, но только одну комбинацию.
Это ключ
различие между
комбинация
и перестановка.
Комбинация фокусируется на выборе объектов без относительно порядка их выбора. Перестановка, напротив,
фокусируется на расположении объектов с в отношении порядка, в котором
они устроены. Итог: AB и BA представляют две перестановки, но только одну комбинацию.
Пример с подсчетом перестановок см. в примере задачи 1.
Что такое комбинация?
Комбинация представляет собой выбор всех или части набора объектов, без учета порядка, в котором объекты расположены выбрано.
Например, предположим, что у нас есть набор из трех букв: A, B и C. Мы могли бы спросить, сколькими способами мы можем выбрать 2 буквы из этого набора. Каждый возможный выбор был бы примером комбинации. Полный список возможных выбор будет: AB, AC и BC.
Когда статистики говорят о комбинациях, они используют
терминология. Они описывают комбинации как n различных объектов, взятых r вовремя. Перевод: n означает количество объектов, из которых
образуется комбинация; и r относится к числу объектов, используемых для
образуют комбинацию. Рассмотрим пример из предыдущего пункта.
комбинации образовались из 3 букв (А, В и С), поэтому n = 3; а также
каждая комбинация состояла из 2 букв, поэтому r = 2.
Рассмотрим пример из предыдущего пункта.
комбинации образовались из 3 букв (А, В и С), поэтому n = 3; а также
каждая комбинация состояла из 2 букв, поэтому r = 2.
Обратите внимание, что AB и BA считаются одной комбинацией, потому что порядок, в котором выбираются объекты, не имеет значения. Это ключ различие между комбинацией и перестановка. Комбинация фокусируется на выборе объектов без относительно порядка их выбора. Перестановка, напротив, фокусируется на расположении объектов с в отношении порядка, в котором они устроены. Итог: AB и BA представляют две перестановки, но только одну комбинацию.
Пример подсчета количества комбинаций см. в примере задачи 2.
Как подсчитать количество комбинаций?
Комбинация представляет собой набор всех или части набора объектов, без относительно порядка, в котором они были выбраны. Это означает, что XYZ считается той же комбинацией, что и ZYX.
Количество комбинаций r объектов, которые можно выбрать из набора n объектов, равно
обозначается n C r . И формула для вычисления этого числа:
И формула для вычисления этого числа:
n C r = n(n — 1)(n — 2) … (n — r + 1)/r! = п! / г!(п — г)!
Примечание: В приведенной выше формуле n! относится к n факториалу, где n! равно n ( n -1)( n -2) … (3)(2)(1).
Как подсчитать количество перестановок?
Перестановка — выбор всех или части набора объектов, с относительно порядка, в котором они были выбраны. Это означает, что XYZ считается другой перестановкой, чем ZYX.
Количество перестановок r объектов, которые можно выбрать из набора n объектов, равно обозначается n Р р . И формула для вычисления этого числа:
n P r = n(n — 1)(n — 2) … (n — r + 1) = n! / (н — р)!
Примечание: В приведенной выше формуле n! относится к n факториалу, где n! равно n ( n -1)( n -2) … (3)(2)(1).
В чем разница между комбинацией и перестановкой?
Различие между комбинацией и перестановкой
имеет отношение к последовательности или порядку появления объектов.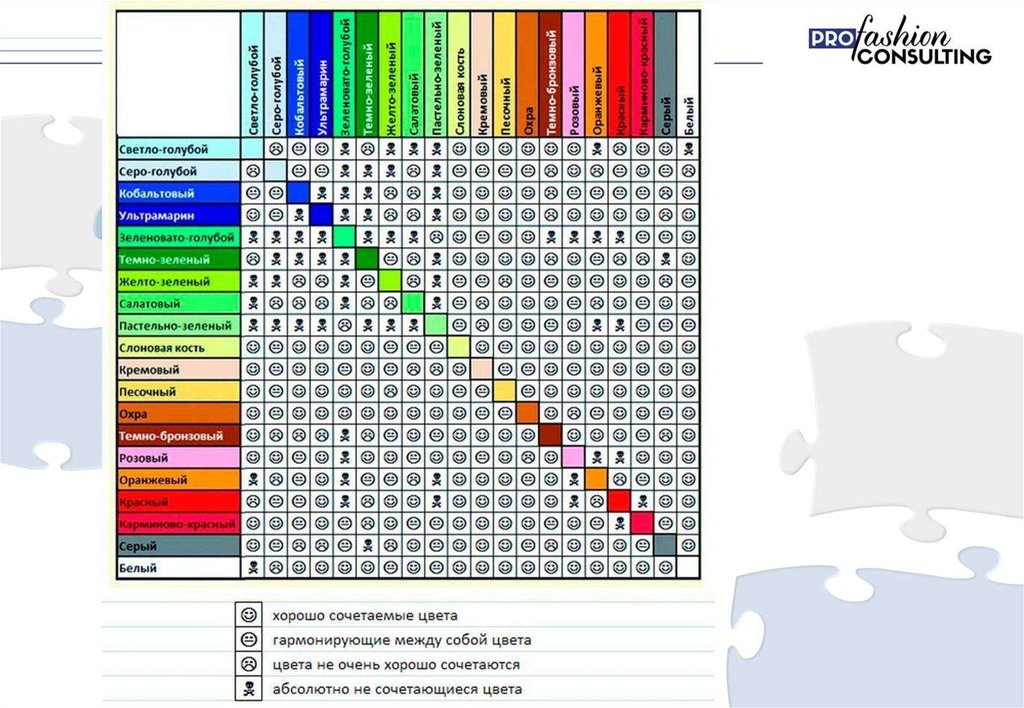 Комбинация
фокусируется на выборе объектов без учета порядка они выбраны. Перестановка, напротив, фокусируется на расположении
объекты с относительно порядка их расположения.
Комбинация
фокусируется на выборе объектов без учета порядка они выбраны. Перестановка, напротив, фокусируется на расположении
объекты с относительно порядка их расположения.
Например, рассмотрим буквы A и B. Используя эти буквы, мы можем создать две двухбуквенные перестановки — AB и BA. Потому что важен порядок к перестановке, AB и BA считаются разными перестановками. Тем не менее, АБ и BA представляют только одну комбинацию, потому что порядок не важен для комбинация.
Что такое нотация E?
Калькулятор комбинаций и перестановок использует нотацию E для выражения очень большие числа. Нотация E — это способ записи слишком больших или слишком мал, чтобы быть кратко записанным в десятичном формате.
В обозначении Е буква Е представляет «умноженное на десять, возведенное в степень числа». Вот пример числа, записанного с использованием Е-обозначения:
3,02E+12 = 3,02 * 10 12 = 3 020 000 000 000
Насколько точен этот калькулятор?
Когда количество комбинаций или перестановок отображается как обычное целое число, результат является точным. Когда количество комбинаций или перестановок отображается с помощью
E, результат не точен; но это
очень хорошее приближение, с точностью до 16 знаков после запятой.
Когда количество комбинаций или перестановок отображается с помощью
E, результат не точен; но это
очень хорошее приближение, с точностью до 16 знаков после запятой.
Пример задачи
Калькулятор | Часто задаваемые вопросы
Сколько трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6 и 7, если каждую цифру можно использовать только один раз?
Решение:
Решение этой задачи включает подсчет количества перестановок 7 отдельные объекты, взятые по 3 за раз. Количество перестановок n различных объектов, взятых r за раз это:
n P r = n! / (н — р)!
7 P 3 = 7! / (7 — 3)! = 7! / 4! = (7)(6)(5) = 210Таким образом, из цифр 1, 2, 3, 4, 5, 6 и 7. Чтобы решить эту задачу с помощью Калькулятор комбинаций и перестановок, сделайте следующее:
- Введите «3» для «Размер подмножества».
- Введите «7» для «Установить размер».

- Нажмите кнопку «Рассчитать».
Ответ 210 отображается в текстовом поле «Перестановки», как показано ниже.
Команда Atlanta Braves устраивает пробный лагерь для бейсболисты. Тридцать игроков появляются в лагере, но тренеры могут выбирать только четыре. Сколькими способами можно выбрать четырех игроков из 30 показанных? вверх?
Решение:
Решение этой задачи включает в себя подсчет количества комбинаций 30 игроков, взятых по 4 за раз. Количество комбинаций n различных объектов, взятых r за раз это:
n C r = n! / р! (н-р)!
30 С 4 = 30! / 4!(30 — 4)! = 30! / 4! 26! = 27 405Таким образом, возможно 27 405 различных группировок из 4 игроков. Решать эту проблему с помощью Калькулятор комбинаций и перестановок, сделайте следующее:
- Введите «4» для «Размер подмножества».
- Введите «30» для «Установить размер».

- Нажмите кнопку «Рассчитать».
Ответ 27 405 отображается в текстовом поле «Комбинации», как показано ниже.
Генератор комбинаций — Генерация всех случайных комбинаций и пар
Генератор случайных пар
Генератор случайных пар — это онлайн-инструмент для генерации всех возможных комбинаций и случайных пар в случайном или отсортированном порядке путем ввода из одного или двух списков элементов .
В Генераторе случайных комбинаций вы можете выбрать генерацию всех (уникальных) комбинаций случайным образом, отсортировать по входным данным, сгруппировать по первому или второму списку или просто выбрать фиксированное количество случайных пар. Вам больше никогда не придется использовать Excel для создания комбинаций.
Новое: теперь вы также можете генерировать комбинации из 3 предметов на комбинацию с одним списком предметов.
Настройки
Добавить списки элементовСписок элементов 1
Количество: 0
Список элементов 2
Количество: 0
Разделить элементы списка запятой
Варианты сопряженияТипы комбинаций
AllUniqueВсе сгруппировано по списку 1Все сгруппировано по списку 2Все комбинации только из списка 1Все комбинации только из списка 2Выберите количество комбинаций
Количество комбинаций 9000 Сортировка комбинаций
RandomSorted
Элементов в комбинации
23 (Много комбинаций, может быть медленным)
Уникальные комбинации (каждый элемент макс. 1 раз)
1 раз)
Разрешить повторяющиеся комбинации
Вывод отдельных комбинаций с помощью:
Новая строкаСтрока между запятыми (, )Первая черта ( | )Пробел ( )
Комбинации
Все комбинации
Что такое Генератор
Совместное использование, печать или копирование 900 комбинаций1?
Генератор комбинаций или Генератор пар — это онлайн-инструмент для сопряжения и создания всех возможных (уникальных) комбинаций из одного или двух списков элементов или имен, которые можно сортировать по группам, случайным образом или по вводу.
В генераторе случайных пар вы можете выбрать, хотите ли вы сгенерировать несколько случайных комбинаций или все возможные комбинации без повторения. Все комбинации могут быть уникальными, случайными, отсортированными по входным данным и/или сгруппированными в один список.
Вы также можете создавать комбинации из одного списка элементов, которые будут создавать пары или комбинации. Также возможно генерировать комбинации из 3 предметов в каждой комбинации.
Введя один или два списка предметов, вы увидите возможное количество комбинаций. При выборе определенного количества комбинаций это всегда будет случайная комбинация. Вы также можете выбрать, как вы хотите разделить комбинации: с помощью новой строки, запятой, вертикальной чертой, пробелом или линией между ними.
Хотите новые функции для комбинатора? Пожалуйста, отправьте нам сообщение через Facebook или Instagram, чтобы мы могли создать эту функцию для вас.
Для чего я могу использовать генератор комбинаций?
Существует множество вариантов использования генератора комбинаций:
- Разделите свои упражнения на 2 категории, например. одна клавиша в последовательности нот.
- Разделите две команды людей на группы по 2 человека, по одному человеку от каждой команды.

- Создавайте случайные комбинации напитков и еды.
- Создавайте пары коллег на основе их навыков, например. список 1: коллеги с младшими навыками, список 2: коллеги со старшими навыками.
- Создавайте пары для спортивных игр из 2 команд.
- Чтобы не использовать Excel для создания комбинаций.
- Подберите игроков с уникальной позицией.
- Генератор комбинации цифр или генератор комбинации букв.
У вас есть другие примеры использования комбинированного генератора? Мы хотели бы услышать это.
Примеры генератора комбинаций
Простой пример вывода генератора комбинаций со списком букв и списком чисел.
Ввод первого списка элементов:
- A.
- B.
Ввод второго списка элементов::
- 1.
- 2. 13 Вывод выбранных комбинаций тип:
- Все (случайные): «B — 2 | A — 1 | A — 2 | B — 1».
- Все (отсортировано): «А — 1 | А — 2 | Б — 1 | Б — 2».

- Уникальные (случайные): «A — 2 | B — 1».
- Уникальный (отсортированный): «A — 1 | B — 2».
- Все сгруппированные по списку 1 (случайно): «A — 2 | A — 1» и «B — 2 | B — 1».
- Все сгруппировано по списку 1 (отсортировано): «A — 1 | A — 2» и «B — 1 | B — 2».
- Все сгруппировано по списку 2 (случайно): «A — 1 | B — 1» и «A — 2 | B — 2».
- Все сгруппировано по списку 2 (отсортировано): «B — 1 | A — 1» и «B — 2 | A — 2».
- Все комбинации только из списка 1: «A — B».
- Все комбинации только из списка 2: «1 — 2».
- ПИН-коды
Сколько пятизначных ПИН-кодов мы можем составить, используя четные числа? - Усвоение
Учащийся усваивает предмет для экзамена по чешскому языку на 98%, по математике на 86% и по экономике на 71%. Какова вероятность того, что он потерпит неудачу по математике, а другие преуспеют? - Блюда
Из 5 разных блюд HOD должен протестировать как минимум три разных блюда, прежде чем выставлять оценки учащимся. Сколькими способами он может выбрать блюда? - Пересечение) 1566
В скольких точках пересекаются девять прямых на плоскости, из которых четыре параллельны друг другу, а из остальных пяти никакие две не параллельны (а если предположить, что через каждое пересечение проходят только две прямые) ? - Произвольно 69194
На плоскости есть десять произвольных точек. Сколько кругов мы можем сделать из них?
Сколько кругов мы можем сделать из них? - MATES
В MATES (малая телевизионная хитрость) из 35 случайных чисел выпадает 5 выигрышных номеров. Сколько возможных комбинаций существует? - Тест из шести вопросов
В тесте шесть вопросов. На каждый есть три ответа, правильный только один. Для сдачи экзамена студенты должны правильно ответить не менее чем на четыре вопроса. Алан не выучил, поэтому обвел ответы, только угадывая. Какова вероятность того, что - 7 героев
9 героев скачут на 9 лошадях позади. Сколькими способами мы можем отсортировать их сзади? - Вероятность 3219
В последние годы в марте 12 дней шли дожди. Какова вероятность того, что 18 марта шел дождь? - Три кости
Игрок, бросающий три кости, задал Г. Галилею вопрос: «На сумму 11 или на сумму 12?» Что ответил ему Галилей? Подсказка: запишите все три тройки чисел, которые можно выбросить, и: всего 11 всего 12 - Семисегментный дисплей
Электронные устройства иногда используют тип цифр, приведенный ниже, где каждая цифра использует число из коротких полос. Например, семерка использует три маленькие полоски. Какое самое большое трехзначное число можно составить, если использовать двадцать полосок?
Например, семерка использует три маленькие полоски. Какое самое большое трехзначное число можно составить, если использовать двадцать полосок? - Равносторонний 75284
Даны 6 отрезков длиной 3 см, 4 см, 5 см, 7 см, 8 см и 9 см. Сколько равносторонних треугольников можно составить из них? Перечислите все варианты. - Следующие
Следующие данные представляют количество ящиков кофе или фильтров, проданных четырьмя торговыми представителями в ходе недавнего конкурса продаж. продавец; Гурман; Единая чашка; фильтры; Тотал Коннор; 142; 325; 30; 497 Пейдж ; 42; 125; 40; 207 Брайс ; 9; 100; 10; 119 Молл - Четырехзначный код
Даны цифры 0-7. Если повторение запрещено, сколько возможны четырехзначные коды, которые больше 2000 и делятся на 4? - Аккорды
Сколько четырехтональных аккордов (аккорд = одновременно звучащие разные тона) можно сыграть в пределах 7 тонов? - Блоки
Существует девять интерактивных основных строительных блоков организации. Сколько существует комбинаций из двух блоков?
Сколько существует комбинаций из двух блоков? - десятичные дроби
- fractions
- triangle ΔABC
- percentage %
- permille ‰
- prime factors
- complex numbers
- LCM
- GCD
- LCD
- combinatorics
- equations
- statistics
- … all maths calculators
- Посетите этот сайт по указанной ссылке.

- После этого введите общее количество объектов и размер выборки значений.
- Теперь пусть этот калькулятор выполнит вычисления.
- Наконец, просмотрите рассчитанное значение комбинации.
- На этом веб-сайте пользователи могут найти множество математических вычислений, таких как Калькулятор процентов, Калькулятор процентной ошибки, Калькулятор кубического уравнения, Калькулятор функции ошибки, и многое другое.
- Откройте этот веб-сайт, используя предоставленную ссылку .
- После этого введите количество объектов, которые вы хотите получить из выборки или большего набора.
- Далее укажите общее количество выборок большего заданного значения.
- В конце нажмите на кнопку Рассчитать , чтобы узнать точное значение комбинации.
- На этом веб-сайте пользователи могут найти множество математических онлайн-калькуляторов, таких как 9Калькулятор факториала 0017, Калькулятор четных перестановок, Калькулятор круговых перестановок, и многое другое.
- Запустите этот веб-сайт и откройте калькулятор перестановок и комбинаций.

- После этого введите значения Set (n) и Subset (r) .
- Затем нажмите кнопку Calculate , чтобы просмотреть значение выходной комбинации.
- Математические калькуляторы : Он предлагает множество математических калькуляторов, таких как Научный калькулятор, Калькулятор дробей, Калькулятор процентов, Калькулятор экспоненты, и многое другое.
- Финансовые калькуляторы : Он предоставляет пользователям финансовые калькуляторы, такие как ипотечные калькуляторы , калькуляторы рефинансирования, калькуляторы годовых, калькуляторы первоначального взноса, и другие.
- Посетите этот сайт по указанной ссылке.
- После этого введите общих опций и опций, которые будут выбраны.
- Наконец, нажмите кнопку Рассчитать возможные комбинации , чтобы просмотреть рассчитанное значение возможных комбинаций.
- На этом веб-сайте пользователи получают множество Математика, Физика, и Химия калькуляторы, такие как Алгебра Калькулятор, Калькулятор площади, Калькулятор работы, Калькулятор длины волны, Калькулятор молярного значения, Калькулятор химического уравнения, и многое другое.

- Откройте этот веб-сайт и получите доступ к калькулятору комбинаций.
- Теперь введите значения n и r .
- Теперь укажите порядок имеет значение? и могут ли элементы повторяться? значений.

- Наконец, нажмите кнопку Calculate , чтобы просмотреть итоговое значение комбинации.
- Генератор комбинаций : Он может генерировать и перечислять все возможные комбинации нескольких элементов.
- Запустите этот веб-сайт и введите значение количество вещей (n) .
- После этого введите номер , который нужно взять (r) значение.
- Наконец, нажмите кнопку Execute , чтобы начать процесс расчета и просмотреть итоговое значение комбинации nCr .
- Этот веб-сайт предлагает множество дополнительных образовательных тем, таких как Функция вероятности, Специальная функция, Численное интегрирование, и другие.
- Запустите этот веб-сайт и откройте калькулятор комбинаций.
- После этого введите значения n и r .
- Далее укажите, важны ли порядок и повторение.
- Наконец, просмотрите вычисленные значения перестановки и комбинации.
- Этот веб-сайт предлагает множество математических расчетов и тем, связанных с Алгеброй, данными, геометрией, мерами, числами, физикой, и другими.
- Откройте этот веб-сайт и введите значения n и r .
- После этого выберите количество комбинаций из меню Что нужно рассчитать.
- Далее укажите, хотите ли вы повторения или нет.
- Наконец, нажмите кнопку Calculate , чтобы начать расчет.

- На этом веб-сайте представлено большое количество полезных калькуляторов, таких как калькулятор процентилей, калькулятор линейной регрессии, калькулятор квадратичной регрессии, калькулятор Z-показателя и другие.
- Запустите этот веб-сайт и получите доступ к калькулятору подсчета комбинаций.
- После этого введите значения n и r .
- Затем нажмите кнопку Count , чтобы начать процесс расчета. После завершения расчета вы можете просмотреть значения всех возможных комбинаций.
- Математика : В этом разделе представлены теоретические материалы и калькуляторы, связанные с символьными вычислениями, арифметикой, комбинаторикой, рядами, статистикой и т. д.
- Посетите этот сайт по указанной ссылке.
- После этого введите значения n и k .
- Далее укажите порядок и статус повторения.
- Наконец, нажмите Кнопка «Рассчитать «.
- На этом веб-сайте пользователи также могут найти расчеты, связанные с десятичными знаками, дробями, процентами, НОК, уравнениями, и т. д., калькуляторами.
- Расчетная комбинация набора
- Номер расстановки комплекта калькулятор : расстановка.
 Вычислить онлайн количество расположения p элементов множества из n элементов.
Вычислить онлайн количество расположения p элементов множества из n элементов. - Расчет биномиальных коэффициентов: binomial_coefficient. Калькулятор биномиального коэффициента, который позволяет вычислить биномиальный коэффициент из двух целых чисел.
- Для подсчета комбинаций: комбинация. Вычислить количество k элементов части множества из n элементов.
- Преобразователь Base-n : base_converter. Калькулятор позволяет выполнять десятичные, двоичные, шестнадцатеричные преобразования и, в более общем случае, преобразование в любое основание n от 2 до 36.
- Калькулятор простой факторизации: prime_factorization. Функция prime_factorization используется для онлайн-расчета разложения целого числа на простые множители.
- Калькулятор частного и остатка: euclidean_division. Калькулятор позволяет найти в режиме онлайн частное и остаток при евклидовом делении двух многочленов или двух целых чисел.
- Четность числа: is_odd. Функция Is_odd возвращает true, если переданное число нечетное, иначе false.

- Четность числа: is_even. Функция Is_even возвращает 1, если число четное, иначе 0.
- Калькулятор факториала: факториал. Факториал натурального числа n — это произведение натуральных чисел, меньших или равных n. Калькулятор факториала позволяет найти это число.
- Калькулятор перестановок: перестановки. Подсчитать онлайн количество перестановок набора из n элементов.
- Расчет НОД онлайн: НОД. Калькулятор НОД, который использует алгоритм Евклида для определения шагов вычисления НОД.
- Наименьшее общее кратное: lcm. Калькулятор LCM для расчета наименьшего общего кратного (НОК).
- Калькулятор теоремы Пифагора: пифагорейский. Калькулятор использует теорему Пифагора, чтобы проверить прямоугольность треугольника или найти длину одной стороны прямоугольного треугольника.
- Решатель обратного отсчета: arithmetic_solver. Этот решатель обратного отсчета позволяет найти целевое число из набора целых чисел с помощью арифметических операций.

Все комбинации
Уникальные комбинации
Все пары, сгруппированные по списку
Комбинации в одном списке
Видео: Генератор случайных пар
Узнайте, как использовать наш генератор случайных пар, посмотрев наш обучающий видеоролик.
Часто задаваемые вопросы
В приведенном ниже списке вы можете найти ответы на часто задаваемые вопросы о нашем инструменте. Вашего конкретного вопроса нет в списке? Пожалуйста, отправьте нам сообщение через Facebook или Instagram.
Вашего конкретного вопроса нет в списке? Пожалуйста, отправьте нам сообщение через Facebook или Instagram.
Вы можете сгенерировать все возможные комбинации из одного списка предметов. По умолчанию он будет генерировать комбинации с парами из 2 предметов.
Вы также можете выбрать вариант для создания комбинаций с 3 предметами в комбинации. Это может создать огромный список комбинаций, который может занять некоторое время.
Вы можете выбрать способ сортировки всех возможных комбинаций: случайный или отсортированный по вводу. Также возможно сгруппировать комбинацию по одному из двух списков.
Генератор комбинаций сначала сгенерирует все возможные комбинации на основе ввода одного или двух списков элементов. После этого перемешиваем все комбинации или группу комбинаций. Затем мы выбираем и фильтруем случайные комбинации в зависимости от типа комбинаций.
Инструменты генератора случайных чисел
Комбинаторный калькулятор, калькулятор комбинаций, вариаций, перестановок
Узнайте, сколькими способами можно выбрать k предметов из n предметов набора. С/без повторения, с/без порядка.
С/без повторения, с/без порядка.
Расчет:
Ck(n)=(kn)=k!(n−k)!n! n=10 k=4 C4(10)=(410)=4!(10 −4)!10!=4⋅3⋅2⋅110⋅9⋅8⋅7=210
Количество комбинаций: 210
Вариантов
Разновидностью k-го класса из n элементов является упорядоченная группа k-элементов, образованная из множества n элементов. Элементы не повторяются и зависят от порядка элементов группы (поэтому расположены).
Количество вариаций можно легко подсчитать, используя комбинаторное правило произведения. Например, если у нас есть набор n = 5 чисел 1,2,3,4,5 и мы должны сделать вариации третьего класса, их V 3 (5) = 5 * 4 * 3 = 60.
Vk(n)=n(n−1)(n−2)…(n−k+1)=(n−k)!n!
н! мы называем факториалом числа n, которое является произведением первых n натуральных чисел. Обозначение с факториалом только более понятное, эквивалентное. Для вычислений вполне достаточно использовать процедуру, вытекающую из комбинаторного правила произведения.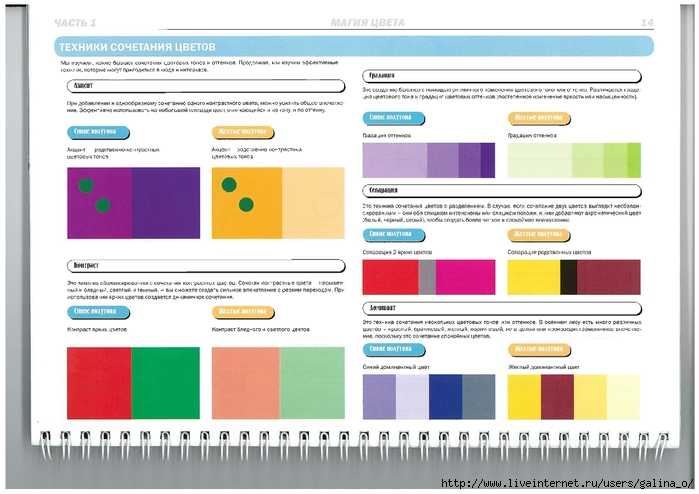
Перестановки
Перестановка является синонимом вариации n-го класса n-элементов. Таким образом, это любая упорядоченная группа из n элементов, состоящая из n элементов. Элементы не повторяются и зависят от порядка элементов в группе. P(n)=n(n−1)(n−2)…1=n! Типичный пример: у нас есть 4 книги, и сколькими способами мы можем расположить их рядом на полке?
Вариации с повторением
Разновидностью k-го класса из n элементов является упорядоченная группа k-элементов, состоящая из множества n элементов, причем элементы могут повторяться и зависят от их порядка. Типичным примером является образование чисел из чисел 2,3,4,5 и нахождение их числа. Рассчитываем их количество по комбинаторному правилу произведения: Vk′(n)=n⋅n⋅n⋅n…n=nk
Перестановки с повторением
Повторяющаяся перестановка представляет собой упорядоченную группу k-элементов из n-элементов, при этом некоторые элементы повторяются в группе.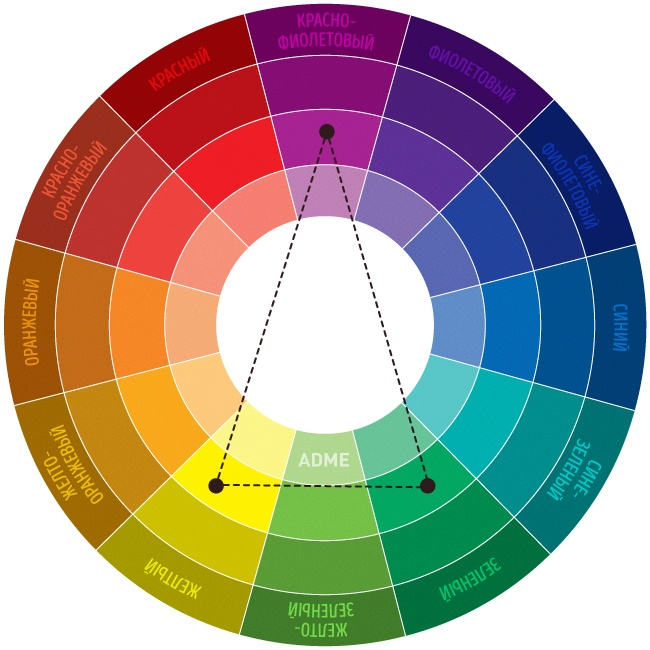 Повторение некоторых (или всех в группе) уменьшает количество таких повторяющихся перестановок.
Pk1k2k3…km′(n)=k1!k2!k3!…km!n!
Типичный пример — узнать, сколько семизначных чисел образовано из чисел 2,2,2, 6,6,6,6.
Повторение некоторых (или всех в группе) уменьшает количество таких повторяющихся перестановок.
Pk1k2k3…km′(n)=k1!k2!k3!…km!n!
Типичный пример — узнать, сколько семизначных чисел образовано из чисел 2,2,2, 6,6,6,6.
Комбинации
Комбинация k-го класса из n элементов представляет собой неупорядоченную группу k-элементов, образованную из множества n элементов. Элементы не повторяются, и порядок элементов группы не имеет значения. В математике неупорядоченные группы называются множествами и подмножествами. Их количество является комбинационным числом и рассчитывается следующим образом: Ck(n)=(kn)=k!(n−k)!n! Типичный пример комбинаций: у нас 15 учеников, и мы должны выбрать троих. Сколько их будет?
Комбинации с повтором
Здесь мы выбираем k групп элементов из n элементов, независимо от порядка, и элементы могут повторяться. k логически больше n (иначе мы получили бы обычные комбинации).
Их счет:
Ck′(n)=(kn+k−1)=k!(n−1)!(n+k−1)!
Пояснение к формуле — количество комбинаций с повторением равно количеству расположений n − 1 разделителей на n-1 + k местах.
Типичный пример: мы идем в магазин, чтобы купить 6 шоколадок. Предлагают всего 3 вида. Сколько вариантов у нас есть?
к = 6, п = 3.
k логически больше n (иначе мы получили бы обычные комбинации).
Их счет:
Ck′(n)=(kn+k−1)=k!(n−1)!(n+k−1)!
Пояснение к формуле — количество комбинаций с повторением равно количеству расположений n − 1 разделителей на n-1 + k местах.
Типичный пример: мы идем в магазин, чтобы купить 6 шоколадок. Предлагают всего 3 вида. Сколько вариантов у нас есть?
к = 6, п = 3.
Основы комбинаторики в текстовых задачах
другие математические задачи »
Candyflipping и другие комбинации: идентификация комбинаций наркотиков и наркотиков на онлайн-форуме
1. Введение
Новые психоактивные вещества (НПВ) относятся к новым синтетическим соединениям или производным более широко известных веществ, вызывающих зависимость, которые появились в течение последних двух лет. десятилетия (1). Примеры включают производные каннабиса, замещенные фенилэтиламины или катиноны (соли для ванн). Термин НПВ может включать вещества, используемые в других культурах, но новые для западных пользователей, такие как кат (прародитель солей для ванн), кратом или Шалфей . Более широкое использование NPS связано с распространением социальных сетей как средства обсуждения использования NPS и распространения фактического продукта (2).
Более широкое использование NPS связано с распространением социальных сетей как средства обсуждения использования NPS и распространения фактического продукта (2).
Использование НПВ является проблемой общественного здравоохранения. Использование замещенных амфетаминов связано с внезапной сердечной смертью и почечной недостаточностью (3). Использование солей для ванн связано с острыми и стойкими психозами (3). Использование производных триптамина связано с психозом и долгосрочными психическими расстройствами, включая тревогу и паранойю (4). Авторы не смогли найти в литературе исследований, в которых количественно оценивалось бы воздействие новых психоактивных веществ с точки зрения количества лет жизни с поправкой на болезнь или денежного воздействия.
Химические анализы новых психоактивных веществ, добровольно представленные пользователями, показывают, что новые психоактивные вещества часто употребляются вместе с другими веществами, а не изолированно (5). Комбинация веществ может иметь меньше побочных эффектов, чем любое отдельное вещество. Термин «переворачивание конфет» относится к комбинации ЛСД и МДМА (экстази) (6). Эта комбинация была впервые описана в начале 1980-х годов, через несколько лет после того, как МДМА стал более широко доступным (7). Candyflipping, по-видимому, увеличивает силу и продолжительность эффектов, подобных МДМА, одновременно снижая вероятность передозировки МДМА. Также известно, что МДМА сочетается с другими амфетаминами, алкоголем и синтетическими каннабиноидами (8). Сообщения об употреблении поливеществ могут также отражать заражение во время подпольного производства и распространения.
Термин «переворачивание конфет» относится к комбинации ЛСД и МДМА (экстази) (6). Эта комбинация была впервые описана в начале 1980-х годов, через несколько лет после того, как МДМА стал более широко доступным (7). Candyflipping, по-видимому, увеличивает силу и продолжительность эффектов, подобных МДМА, одновременно снижая вероятность передозировки МДМА. Также известно, что МДМА сочетается с другими амфетаминами, алкоголем и синтетическими каннабиноидами (8). Сообщения об употреблении поливеществ могут также отражать заражение во время подпольного производства и распространения.
Социальные сети стали информативным источником данных для отслеживания поведения населения в целом. Подростки и молодые люди, наиболее широко описанные потребители НПВ (3, 9), часто откровенно общаются в Интернете. Все еще устанавливается, позволяет ли качество данных из социальных сетей быть аналогичным качеству данных из более традиционных средств синдромного наблюдения. О достоверных дозах декстрометорфана можно судить по комментариям на YouTube (10). Оценки географического распространения злоупотребления опиоидами в Соединенных Штатах, полученные в Твиттере, полностью совпадают с оценками, полученными в Национальном исследовании по употреблению наркотиков и здоровью (11). Язык в Твиттере коррелирует с географическим распространением сердечных заболеваний (12).
Оценки географического распространения злоупотребления опиоидами в Соединенных Штатах, полученные в Твиттере, полностью совпадают с оценками, полученными в Национальном исследовании по употреблению наркотиков и здоровью (11). Язык в Твиттере коррелирует с географическим распространением сердечных заболеваний (12).
Традиционные средства синдромного надзора трудно применить к эпидемиологии новых психоактивных веществ. Национальные обследования, такие как Национальное обследование употребления наркотиков и состояния здоровья, проводятся раз в год и включают личные интервью. Анализ звонков в токсикологические центры или встреч с поставщиками медицинских услуг дает предвзятую картину моделей употребления НПВ.
Наш подход преследовал две основные цели:
1. Продемонстрировать, что данные об употреблении различных психоактивных веществ можно извлечь из онлайн-сообщений пользователей
2. Продемонстрировать, что из этих данных мы можем сделать вывод о новых, а также известных комбинациях веществ.
Предположение об известных комбинациях веществ повысит доверие к онлайн-сообщениям как к источнику данных такого типа. Наш подход заключался в использовании методов обработки естественного языка и больших данных для анализа Lycaeum. Lycaeum — это веб-сайт и интернет-форум, посвященный распространению информации о психоактивных веществах (13).
2. Материалы и методы
2.1. Обзор
Мы написали программное обеспечение на языке программирования Python (14) для извлечения сообщений пользователей из Lycaeum, выявления новых психоактивных веществ и анализа содержания сообщений. Сообщения состоят из неструктурированного текста, также называемого свободным текстом, аналогично разделу «Комментарии» после онлайн-статей на веб-сайтах New York Times или Financial Times. Мы включили только публичные посты для анализа. Мы опускали сообщения, которые были отмечены как удаленные или отмечены модератором.
2.2. Приобретение пользовательских постов
Мы разработали веб-скрапер с пакетом Python scrapy (15) для извлечения всех доступных сообщений ( n = 9,289) с момента запуска Lycaeum в 1996 году до декабря 2016 года. Мы лемматизировали сообщения и удалили стоп-слова, используя nltk , Набор инструментов естественного языка Python (16). Лемматизация относится к приведению всех лексических и семантических вариантов слова к одной базовой форме. Один лемматизирует, например, чтение, чтение и чтение чтение. Лемматизация — это один из способов перейти от фактического неструктурированного текста к понятному представлению лежащей в его основе семантики. Удаление стоп-слов означает отфильтровывание таких слов, как «the» или «a», которые встречаются часто, но добавляют мало информации в текст. Удаление стоп-слов — это распространенный подход к тому, чтобы частота слов более точно соответствовала относительной распространенности понятий в фрагменте текста.
Мы лемматизировали сообщения и удалили стоп-слова, используя nltk , Набор инструментов естественного языка Python (16). Лемматизация относится к приведению всех лексических и семантических вариантов слова к одной базовой форме. Один лемматизирует, например, чтение, чтение и чтение чтение. Лемматизация — это один из способов перейти от фактического неструктурированного текста к понятному представлению лежащей в его основе семантики. Удаление стоп-слов означает отфильтровывание таких слов, как «the» или «a», которые встречаются часто, но добавляют мало информации в текст. Удаление стоп-слов — это распространенный подход к тому, чтобы частота слов более точно соответствовала относительной распространенности понятий в фрагменте текста.
2.3. Идентификация веществ
Мы использовали трехэтапный процесс для идентификации веществ. Мы использовали nltk для идентификации всех существительных до лемматизации. Авторы MC и AM вручную составили этот список, чтобы определить те существительные, которые, вероятно, относятся только к наркотикам. Для последующего анализа использовались только те существительные, которые были идентифицированы как AM, так и MC как относящиеся только к наркотикам. Автор DY сопоставляет этот список с Википедией, PubChem и DrugBank, чтобы предоставить стандартное написание и список синонимов для каждого потенциального вещества. Эта перекрестная ссылка, например, сопоставила xanny , вариант ксанакса и алпразолама. Авторы DY и MC аннотировали каждое лекарство в соответствии с его классом. Мы рассмотрели следующие классы: седативно-снотворные, галлюциногенные, стимулирующие, ноотропные, психиатрические, антихолинергические, анальгетические, жаропонижающие, противорвотные, антигипертензивные, каннабиноидные или загрязняющие.
Для последующего анализа использовались только те существительные, которые были идентифицированы как AM, так и MC как относящиеся только к наркотикам. Автор DY сопоставляет этот список с Википедией, PubChem и DrugBank, чтобы предоставить стандартное написание и список синонимов для каждого потенциального вещества. Эта перекрестная ссылка, например, сопоставила xanny , вариант ксанакса и алпразолама. Авторы DY и MC аннотировали каждое лекарство в соответствии с его классом. Мы рассмотрели следующие классы: седативно-снотворные, галлюциногенные, стимулирующие, ноотропные, психиатрические, антихолинергические, анальгетические, жаропонижающие, противорвотные, антигипертензивные, каннабиноидные или загрязняющие.
2.4. Вычисление корреляции
Для выявления закономерностей совместного упоминания веществ мы создали матрицу «лекарство-пост» , так что ij -й элемент этой матрицы равен 1, если лекарство i упоминается в посте j иначе −1. Затем мы рассчитали корреляцию между моделями упоминания всех пар наркотиков в корпусе Lycaeum. Мы рассчитали корреляцию между любыми двумя препаратами, a и b , как внутреннее произведение соответствующих строк в матрице «лекарство-пост», нормированное на количество постов n , ra,b=a→⋅b →/н. Другими словами, мы рассматривали каждое лекарство как многомерный вектор. Каждое измерение соответствует посту. Корреляция между любыми двумя наркотиками по столбам представляет собой косинус угла, образованного между двумя соответствующими векторами. Уравнение, представленное ранее, вычисляет косинус этого угла. Это уравнение адаптировано из работы. (17). Мы получили порог статистической значимости для корреляции между наркотиками a и лекарство b, r a , b путем случайного перетасовки матрицы «лекарство-пост» 10 000 раз и пересчета всех корреляций пар лекарств для получения эмпирической функции распределения вероятностей для r a
Мы рассчитали корреляцию между любыми двумя препаратами, a и b , как внутреннее произведение соответствующих строк в матрице «лекарство-пост», нормированное на количество постов n , ra,b=a→⋅b →/н. Другими словами, мы рассматривали каждое лекарство как многомерный вектор. Каждое измерение соответствует посту. Корреляция между любыми двумя наркотиками по столбам представляет собой косинус угла, образованного между двумя соответствующими векторами. Уравнение, представленное ранее, вычисляет косинус этого угла. Это уравнение адаптировано из работы. (17). Мы получили порог статистической значимости для корреляции между наркотиками a и лекарство b, r a , b путем случайного перетасовки матрицы «лекарство-пост» 10 000 раз и пересчета всех корреляций пар лекарств для получения эмпирической функции распределения вероятностей для r a
3. Результаты
В число 20 наиболее часто упоминаемых веществ вошли обычные галлюциногены, стимуляторы, седативно-снотворные средства, а также, что интересно, звуковые (рис. 1). Ось x на рисунке 1 показывает количество постов, в которых вещество упоминается хотя бы один раз. В следующих параграфах мы подробно обсудим некоторые из этих веществ, поскольку они могут быть незнакомы читателю.
1). Ось x на рисунке 1 показывает количество постов, в которых вещество упоминается хотя бы один раз. В следующих параграфах мы подробно обсудим некоторые из этих веществ, поскольку они могут быть незнакомы читателю.
Рисунок 1 . Топ-20 наиболее часто упоминаемых веществ. x — Ось обозначает количество сообщений, в которых вещество было упомянуто хотя бы один раз. МДМА, 3,4-метилендиоксиметамфетамин, также известный как экстази; ДМТ, N,N -диметилтриптамин; ДХМ, декстрометорфан; LSA, амид лизергиновой кислоты, также известный как эргин.
Мы объединили фразы бинауральные ритмы, бинауральный звук и бинауральная музыка в токен звук 9.0004 . Все они относятся к подаче на каждое ухо чистых синусоидальных волн, различающихся только частотой. В сообщениях Lycaeum часто описывалось прослушивание бинауральных ритмов с использованием веществ для усиления ощущений. Бинауральный звук может улучшить концентрацию на задаче по сравнению с тишиной (18). Не было продемонстрировано изменения эмоционального возбуждения (19). Авторам не удалось найти исследования, посвященного сочетанию бинаурального звука с каким-либо психоактивным веществом, несмотря на его распространенность в нашем наборе данных. Мы исключили упоминания о бинауральных ритмах из последующего анализа, поскольку основное внимание в этом исследовании уделялось комбинациям препаратов. Непонятно, почему в постах так часто упоминаются эти звуки. Детальный анализ контекста, в котором 9Было упомянуто 0003 бинауральных ударов , что выходит за рамки данного исследования.
Не было продемонстрировано изменения эмоционального возбуждения (19). Авторам не удалось найти исследования, посвященного сочетанию бинаурального звука с каким-либо психоактивным веществом, несмотря на его распространенность в нашем наборе данных. Мы исключили упоминания о бинауральных ритмах из последующего анализа, поскольку основное внимание в этом исследовании уделялось комбинациям препаратов. Непонятно, почему в постах так часто упоминаются эти звуки. Детальный анализ контекста, в котором 9Было упомянуто 0003 бинауральных ударов , что выходит за рамки данного исследования.
ЛСД (лизергиновый диэтиламид) является каноническим галлюциногеном (18). Шалфей, то есть Salvia divinorum , относится к психоактивному растению из Оахаки, Мексика, богатому саливинорином А, к агонистом опиоидных рецепторов (20).
Диазепам — это бензодиазепиновый седативно-снотворный препарат, продаваемый в США под торговой маркой Валиум. Прием диазепама вместе с галлюциногеном может уменьшить беспокойство, дисфорию или учащенное сердцебиение, связанные с некоторыми галлюциногенами. Одновременное употребление седативно-гипнотического средства и галлюциногена может усиливать предполагаемый эффект галлюциногена (21). Назначение бензодиазепинов является частью начального лечения симптоматической передозировки галлюциногенов (22). Этанол и кофеин являются широко потребляемыми психоактивными веществами. МДМА (3,4-метилендиоксиметамфетамин; также называемый экстази) является каноническим энтактогеном-эмпатогеном, веществом, которое усиливает чувство близости, привязанности, сопереживания и сексуального влечения (23). ДМТ ( N,N -диметилтриптамин) — галлюциногенное производное триптамина. Он считается основным психоактивным соединением в галлюциногенных растениях, таких как Mimosa tenuiflora (24) и меланж аяхуаска (25). Амфетамин (также называемый скорость ) является давно признанным стимулятором. Псилоцибин — еще один канонический галлюциноген; это активный ингредиент «волшебных грибов» (26).
Одновременное употребление седативно-гипнотического средства и галлюциногена может усиливать предполагаемый эффект галлюциногена (21). Назначение бензодиазепинов является частью начального лечения симптоматической передозировки галлюциногенов (22). Этанол и кофеин являются широко потребляемыми психоактивными веществами. МДМА (3,4-метилендиоксиметамфетамин; также называемый экстази) является каноническим энтактогеном-эмпатогеном, веществом, которое усиливает чувство близости, привязанности, сопереживания и сексуального влечения (23). ДМТ ( N,N -диметилтриптамин) — галлюциногенное производное триптамина. Он считается основным психоактивным соединением в галлюциногенных растениях, таких как Mimosa tenuiflora (24) и меланж аяхуаска (25). Амфетамин (также называемый скорость ) является давно признанным стимулятором. Псилоцибин — еще один канонический галлюциноген; это активный ингредиент «волшебных грибов» (26).
Атропин, гиосцин (также называемый скополамин) и гиосциамин являются компонентами дурмана, снотворного и галлюциногена. LSA (амид лизергиновой кислоты; также называемый эргином) является спорыньей, родственной ЛСД, и наиболее изученным галлюциногеном в ипомеи (27). Он появился как альтернатива ЛСД; популярные статьи предполагают, что LSA также является точкой сравнения при описании эффектов метилона (28).
LSA (амид лизергиновой кислоты; также называемый эргином) является спорыньей, родственной ЛСД, и наиболее изученным галлюциногеном в ипомеи (27). Он появился как альтернатива ЛСД; популярные статьи предполагают, что LSA также является точкой сравнения при описании эффектов метилона (28).
Каннабис является широко употребляемым седативным средством, хотя некоторые штаммы могут оказывать галлюциногенное или стимулирующее действие (29). Термин каннабиноид , вероятно, относится к синтетическим каннабиноидам. Синтетические каннабиноиды являются агонистами каннабиноидных рецепторов, а также дофаминергических, сертонинергических и адренергических рецепторов; синтетические каннабиноиды могут с большей вероятностью вызывать психоз, чем каннабис (30).
Чтобы лучше понять, как посты описывают сочетание веществ, мы рассчитали корреляцию по всем документам для всех пар веществ. На рис. 2 показаны все комбинации, корреляции которых статистически значимы. Мы использовали бутстрэппинг (см. Материалы и методы) для определения порога статистически значимых корреляций.
Материалы и методы) для определения порога статистически значимых корреляций.
Рисунок 2 . Тепловая карта коэффициента корреляции пар ко-упоминание вещество-вещество, корреляция которых была статистически значимой. Каждая крошечная коробка представляет одну пару веществ. Названия лекарств по осям x и y определяют пару, связанную с каждым полем. Цвет крошечного прямоугольника указывает на корреляцию в соответствии с увеличением в правом нижнем углу.
На рис. 2 представлена кластерная тепловая карта, графическое изображение матрицы «лекарство-пост» . Цвет ij -й квадрат указывает на корреляцию между наркотиками i и наркотиками j . Более теплые цвета указывают на корреляции ближе к 1. Более холодные цвета указывают на корреляции ближе к -1. Эта тепловая карта симметрична по диагонали, потому что корреляция между лекарством и и лекарством и такая же, как корреляция между лекарством и и лекарством и . Диагональ не рисуется, чтобы избежать эффекта потолка, искажающего фигуру. Заказы веществ на x и y оси одинаковы. Порядок веществ по оси х такой же, как и по оси у . Такой порядок был выбран, чтобы сгруппировать вместе пары лекарств с похожими корреляциями.
Диагональ не рисуется, чтобы избежать эффекта потолка, искажающего фигуру. Заказы веществ на x и y оси одинаковы. Порядок веществ по оси х такой же, как и по оси у . Такой порядок был выбран, чтобы сгруппировать вместе пары лекарств с похожими корреляциями.
Видны три больших кластера. Если двигаться слева направо по горизонтальной оси, то один кластер начинается с прамипексола и заканчивается буталбиталом. Этот кластер содержит вещества, обычно обозначаемые как ноотропы (прамипексол, гинко, левометамфетамин) или катиноны (соли для ванн; пентилон, бутирон, нафирон). Следующий кластер начинается с модафинила и заканчивается халипонгой. Он содержит галлюциногенные растения (закатечичи, халипонга) и психиатрические препараты (венлафаксин, оланзипин). Третий кластер содержит стимуляторы (кофеин, кокаин, никотин, метилфенидат) и галлюциногенные растения. Синий квадрат в левом нижнем углу указывает на то, что соединения из первого кластера (ноотропы и катиноны) редко обсуждаются с соединениями из третьего кластера (стимуляторы и некоторые галлюциногенные растения). Отрицательная корреляция (синий цвет) между двумя веществами означает, что при упоминании первого вещества второе вещество упоминается с меньшей вероятностью. Это не означает, что при упоминании одного вещества в сообщениях явно обсуждается отказ от второго вещества.
Отрицательная корреляция (синий цвет) между двумя веществами означает, что при упоминании первого вещества второе вещество упоминается с меньшей вероятностью. Это не означает, что при упоминании одного вещества в сообщениях явно обсуждается отказ от второго вещества.
Термин Piper, вероятно, относится к Piper methysticum источнику кавы, травяного анксиолитика (31). Пайпер может также относиться к фенилпиперазинам, новому классу стимуляторов, продаваемых как альтернатива солям для ванн (32). Гуперзин — это ингибитор ацетилхолинэстеразы, продаваемый как ноотроп (усилитель когнитивных функций), хотя исследования на людях показывают минимальные эффекты (33).
Рисунок 2 демонстрирует внешнюю обоснованность этого подхода к токсиконадзору и дает новые идеи. Кофеин является обычной примесью в образцах кокаина (34, 35). Те, кто употребляет кокаин, чаще потребляют никотин и кофеин (36).
Корреляция между моделями упоминания пентилона, бутилона и нафирона (верхняя левая группа), вероятно, отражает споры об относительном воздействии каждого вещества, хотя они могут отражать незарегистрированные модели использования. Новым открытием является то, что в обсуждениях упоминается bk-MDMA (также называемый метилоном), другой катинон, довольно часто упоминается метамфетамин и галлюциногены (буфотенин, мимоза), но не другие соли для ванн. Амфетамины часто загрязняют соли для ванн (37).
Новым открытием является то, что в обсуждениях упоминается bk-MDMA (также называемый метилоном), другой катинон, довольно часто упоминается метамфетамин и галлюциногены (буфотенин, мимоза), но не другие соли для ванн. Амфетамины часто загрязняют соли для ванн (37).
Некоторые зарегистрированные модели использования здесь не наблюдаются. На рисунке 2 не показано значительных совместных упоминаний ингибиторов моноаминоксидазы (ИМАО) с производными триптамина, такими как диметилтриптамин. Ингибиторы моноаминоксидазы (ИМАО) усиливают действие диметилтриптамина, предотвращая метаболизм ДМТ в желудочно-кишечном тракте (25). Mimosa (38) и chaliponga (39) являются растительными источниками ДМТ. Аяуаска является источником ДМТ, который используется в южноамериканских религиозных церемониях и все чаще используется в Соединенных Штатах (40). Гармалин это β -карболин RIMA (обратимый ингибитор моноаминоксидазы А (41)). Возможно, из-за того, что комбинация ИМАО и галлюциногенов была описана (42), на онлайн-форумах предполагается, что эта тема известна. Или эта тема может обсуждаться на других форумах.
Или эта тема может обсуждаться на других форумах.
Чтобы выявить закономерности совместного употребления в разных классах, на рисунке 3 упоминания веществ сгруппированы по классам. Наиболее часто упоминаемыми классами являются седативно-гипнотические средства, галлюциногены и стимуляторы, за которыми следуют ноотропы, психиатрические препараты и антихолинергические средства. Для целей рисунка 3 каждое лекарство было отнесено только к одному классу. В действительности лекарство может иметь несколько эффектов, причем только разные эффекты проявляются в разных дозах. Мы выбрали класс, отражающий действие препаратов в обычно принимаемых внутрь дозах. Мы, например, классифицируем дифенгидрамин (Бенадрил) как антигистаминный препарат, хотя в более высоких дозах он является антихолинергическим средством. Нам не удалось извлечь информацию о дозировке для дальнейшей классификации.
Рисунок 3 . Тепловая карта взаимоупоминаний вещества-вещества по классам. Каждая крошечная коробка представляет одну пару классов веществ. Метки на осях x — и y указывают классы веществ, связанные с каждой коробкой. Цвет крошечного прямоугольника указывает на абсолютную частоту упоминаний в соответствии с цветовой шкалой в правом нижнем углу.
Метки на осях x — и y указывают классы веществ, связанные с каждой коробкой. Цвет крошечного прямоугольника указывает на абсолютную частоту упоминаний в соответствии с цветовой шкалой в правом нижнем углу.
Для выявления моделей употребления психоактивных веществ, включающих более двух веществ, мы построили социальную сеть наркотиков (рис. 4) следующим образом. Мы создавали связь между двумя наркотиками, если эти два препарата имели значительную корреляцию. Мы изобразили эту связь графически в виде линии. Ширина линии отражает силу корреляции. Объединение этих парных соединений создает большую сеть следующим образом. Наркотик А устанавливает непрямую связь с наркотиком С через наркотик Б, если модели упоминания наркотиков А и наркотиков Б коррелируют так же, как и модели упоминаний наркотиков В и С.
Рисунок 4 . Социальная сеть дискуссий о наркотиках. Каждый узел (текст) представляет собой вещество. Каждое ребро (соединительная линия) представляет соотношение между упоминаниями двух связанных веществ. Чем толще линия, тем сильнее корреляция.
Чем толще линия, тем сильнее корреляция.
Мы определили шесть групп, состоящих более чем из трех членов. Мы называем эти более крупные группы семантическими островами. Сообщения, в которых упоминается одно лекарство на семантическом острове, обычно упоминают вещества из того же острова, только если они упоминают более одного вещества. В центре вверху находится опиоидный островок. Далее по часовой стрелке расположены остров стимуляторов (центром является кофеин), центром СИОЗС (центром является пароксетин), островом растительных галлюциногенов (центрами являются ДМТ и мимоза), островом синтетических галлюциногенов (центрами являются ЛСД и звук), и бензодиазепиновый остров.
Островок СИОЗС образован циталопрамом, сертралином, пароксетином, флуоксетином и венлафаксином. В островке СИОЗС пароксетин образует узел, он напрямую связан со всеми остальными членами острова. Одна интерпретация этой схемы заключается в том, что пароксетин (торговое название Paxil) формирует систему отсчета для оценки других СИОЗС.
В синтетическом галлюциногене ЛСД является узлом, соединяющим два субострова. Левый субостров острова галлюциногенов содержит вещества, канонически считающиеся антихолинергическими. Гиосцин и гиосциамин являются тропановыми алкалоидами, обнаруженными в дурмане. Правый субостров содержит производные амфетамина, такие как МДМА и производные МДМА (соли для ванн), бк-МДМА ( β -кето МДМА; метилон) и бк-МДЭА (этилон).
Триада, образованная этанолом, аиром и туйоном, отражает дискуссию об абсенте, который, как считалось, обладает галлюциногенными свойствами. Считалось, что выдержка спирта в полыни придает раствору α -туйон. Аир, относящийся к Acorus calamus , также считался галлюциногенным компонентом абсента.
Триада, образованная армодафанилом, модафинилом и адрафинилом, отражает дискуссии о том, как получить модафинил без рецепта. Модафинил (торговое название Provigil) и Armodafinil (торговое название Nuvigil) в настоящее время доступны только по рецепту в Соединенных Штатах. Адрафинил метаболизируется в модафинил и не считается контролируемым веществом в США.
Адрафинил метаболизируется в модафинил и не считается контролируемым веществом в США.
Связь между ниацином и ГАМК связана с отдельными сообщениями о том, что комбинированное пероральное введение ниацина и ГАМК увеличивает количество ГАМК, проникающего через гематоэнцефалический барьер. Насколько известно авторам, рецензируемых отчетов по этому поводу нет. Также не было сообщений о сочетании прамипексола (агониста дофамина) с нефазодоном (СИОЗС).
4. Обсуждение
В этом исследовании представлен первый формальный анализ моделей обсуждения на онлайн-форумах, описывающих модели совместного приема вещества. Наша цель состояла в том, чтобы одновременно продемонстрировать обоснованность использования интернет-форумов для синдромального наблюдения и обнаружить новые совместные упоминания веществ. Наш анализ Lycaeum выявил 183 комбинации. Из этих комбинаций 44 никогда не изучались напрямую, но подобны комбинациям, которые изучались непосредственно. Три комбинации, нефазодон и прамипексол, закатечичи (полынь) и шлемник, а также ниацин и ГАМК, не имеют предшественников в литературе.
Мы обнаружили, что разговоры с упоминанием синтетических галлюциногенов, как правило, делятся на упоминания галлюциногенов, полученных из амфетамина, и галлюциногенов, полученных из спорыньи. В разговорах, в которых упоминались синтетические галлюциногены, обычно не упоминались растительные галлюциногены.
Мы также обнаружили, что соли для ванн обычно обсуждаются с седативными и снотворными средствами и ноотропами, в то время как более канонические стимуляторы обсуждаются с растительными галлюциногенами и психиатрическими препаратами. В дискуссиях, в которых упоминаются седативно-снотворные средства, чаще всего также упоминаются галлюциногены и стимуляторы. Вещества всех классов часто сравнивают с МДМА, ДМТ, кокаином и атропином при попытке описать их эффекты.
Это исследование имеет множество ограничений. В нем анализируются модели обсуждения тех, кто решил поделиться информацией о моделях употребления наркотиков. Нет никаких аналитических данных, подтверждающих, что какие-либо вещества, упомянутые вместе, принимались вместе. В этом исследовании не проводился детальный лингвистический анализ всего текста. «Совместное упоминание» между лекарственным средством i и лекарственным средством j может означать прием внутрь лекарственного средства i и лекарственного средства j , избегание одновременного приема обоих веществ или потребление одного, но не другого. Мы искали явные упоминания каждого вещества.
В этом исследовании не проводился детальный лингвистический анализ всего текста. «Совместное упоминание» между лекарственным средством i и лекарственным средством j может означать прием внутрь лекарственного средства i и лекарственного средства j , избегание одновременного приема обоих веществ или потребление одного, но не другого. Мы искали явные упоминания каждого вещества.
Возможно, сообщения маскируют упоминания об использовании сленгом даже на онлайн-форумах, посвященных обсуждению новых психоактивных веществ. Насколько известно авторам, не существует исчерпывающего или независимо проверенного словаря сленга, относящегося к новым психоактивным веществам. Мы попытались стандартизировать словарный запас, используя ручное курирование. Система классификации, используемая на рисунке 2, отличается от общепринятой передовой практики в биомедицинской онтологии. Например, антихолинергический и примеси не исключают друг друга и описывают свойства на разных уровнях абстракции. Первый термин описывает связывающее свойство химического вещества. Последний термин описывает свойство, которым вещество обладает благодаря своему местонахождению. Термин циталопрам – это не свойство, а вещество. Система классификации также упрощает тот факт, что многие НПВ связываются со многими рецепторами и имеют активные метаболиты. Мы выбрали эту простую систему классификации, чтобы отразить классификацию, используемую клиницистами. Последующие исследования, направленные на объединение данных из социальных сетей с существующими хранилищами знаний, возможно, должны будут разработать более формальное и логически последовательное представление знаний в этой области.
Первый термин описывает связывающее свойство химического вещества. Последний термин описывает свойство, которым вещество обладает благодаря своему местонахождению. Термин циталопрам – это не свойство, а вещество. Система классификации также упрощает тот факт, что многие НПВ связываются со многими рецепторами и имеют активные метаболиты. Мы выбрали эту простую систему классификации, чтобы отразить классификацию, используемую клиницистами. Последующие исследования, направленные на объединение данных из социальных сетей с существующими хранилищами знаний, возможно, должны будут разработать более формальное и логически последовательное представление знаний в этой области.
Текстовый анализ также ограничен тем, что не было предпринято никаких попыток сделать вывод, почему посты предпочли одну пару веществ другой. Возможно, более сложные методы обработки естественного языка или искусственного интеллекта могли бы выявить такие скрытые переменные.
Вклад автора
MC написал программу для анализа данных Lycaeum, вручную отобрал некоторые категории лекарств, написал и отредактировал рукопись. DY написал программное обеспечение для получения данных от Lycaeum и вручную курировал некоторые категории лекарств. AM руководил анализом данных и помогал пересматривать рукопись.
DY написал программное обеспечение для получения данных от Lycaeum и вручную курировал некоторые категории лекарств. AM руководил анализом данных и помогал пересматривать рукопись.
Заявление о конфликте интересов
Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов.
Благодарности
Авторы хотели бы выразить признательность административному персоналу Пресвитерианско-Нью-Йоркской средней школы Квинса и Бронкса.
Ссылки
1. Orsolini L, Papanti D, Vecchiotti R, Valchera A, Corkery J, Schifano F. Новые психоактивные вещества. Европейская психиатрия (2016) 33: S59–60. doi:10.1016/j.eurpsy.2016.01.945
Полный текст CrossRef | Google Scholar
2. Бойер Э.В., Лапен П.Т., Макалино Г., Хибберд П.Л. Распространение информации о психоактивных веществах инновационными потребителями наркотиков. Cyberpsychol Behav (2007) 10 (1): 1–6. doi:10.1089/cpb.2006.9999
Cyberpsychol Behav (2007) 10 (1): 1–6. doi:10.1089/cpb.2006.9999
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
3. Нельсон М.Е., Брайант С.М., Акс С.Е. Новые наркотики злоупотребления. Dis Mon (2014) 60 (3): 110–32. doi:10.1016/j.disamonth.2014.01.001
Полнотекстовая перекрестная ссылка | Google Scholar
4. Титтарелли Р., Маннокки Г., Пантано Ф., Саверио Ромоло Ф. Рекреационное использование, анализ и токсичность триптаминов. Curr Neuropharmacol (2015) 13(1):26–46. doi:10.2174/1570159X13666141210222409
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
5. Хеландер А., Бек О., Хагерквист Р., Хультен П. Выявление употребления новых психоактивных веществ в Швеции на основе лабораторного анализа — первый опыт проекта STRIDA. Scand J Clin Lab Invest (2013) 73(5):400–6. doi:10.3109/00365513.2013.793817
Полный текст CrossRef | Google Scholar
6. Шехтер, доктор медицины. «Конфетное переворачивание»: синергетический дискриминационный эффект ЛСД и МДМА. Eur J Pharmacol (1998) 341(2):131–4. doi:10.1016/S0014-2999(97)01473-8
«Конфетное переворачивание»: синергетический дискриминационный эффект ЛСД и МДМА. Eur J Pharmacol (1998) 341(2):131–4. doi:10.1016/S0014-2999(97)01473-8
Полный текст CrossRef | Google Scholar
7. Миллер Н.С., Голд М.С. ЛСД и экстази: фармакология, феноменология и лечение. Psychiatr Ann (1994) 24 (3): 131–3. Дои: 10.3928/0048-5713-19940301-07
Полный текст CrossRef | Google Scholar
8. Schifano F, Di Furia L, Forza G, Minicuci N, Bricolo R. Потребление МДМА («экстази») в контексте полинаркомании: отчет о 150 пациентах. Наркотики Алкоголь Зависимость (1998) 52(1):85–90. doi:10.1016/S0376-8716(98)00051-9
Полный текст CrossRef | Google Scholar
9. Conway KP, Vullo GC, Nichter B, Wang J, Compton WM, Iannotti RJ, et al. Распространенность и модели употребления полисахарида в репрезентативной на национальном уровне выборке учащихся 10-х классов в США. J Adolesc Health (2013) 52(6):716–23. doi:10.1016/j.jadohealth. 2012.12.006
2012.12.006
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
10. Чари М., Парк Э.Х., Маккензи А., Сан Дж., Манини А.Ф., Джинс Н. Признаки и симптомы воздействия декстрометорфана с YouTube. PLoS One (2014) 9(2):e82452. doi:10.1371/journal.pone.0082452
Полный текст CrossRef | Google Scholar
11. Чари М., Джин Н., Жиро-Кэрриер С., Хэнсон С., Нельсон Л.С., Манини А.Ф. Эпидемиология из твитов: оценка злоупотребления отпускаемыми по рецепту опиоидами в США из социальных сетей. J Med Toxicol (2017) 13(4):278–86. doi:10.1007/s13181-017-0625-5
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
12. Eichstaedt JC, Schwartz HA, Kern ML, Park G, Labarthe DR, Merchant RM, et al. Психологический язык в Твиттере предсказывает смертность от сердечных заболеваний на уровне округа. Psychol Sci (2015) 26 (2): 159–69. doi:10.1177/0956797614557867
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
13. Halpern JH, Pope HG Jr. Галлюциногены в Интернете: обширный новый источник подпольной информации о наркотиках. Am J Psychiatry (2001) 158(3):481–3. doi:10.1176/appi.ajp.158.3.481
Halpern JH, Pope HG Jr. Галлюциногены в Интернете: обширный новый источник подпольной информации о наркотиках. Am J Psychiatry (2001) 158(3):481–3. doi:10.1176/appi.ajp.158.3.481
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
14. Ван Россум Г., Дрейк, Флорида. Справочное руководство по языку Python . Бристоль: Теория сети (2003).
Google Scholar
15. Майерс Д., Макгаффи Дж.В. Выбор скрапа. J Comput Sci Coll (2015) 31(1):83–9.
Google Scholar
16. Bird S, Klein E, Loper E. Обработка естественного языка с помощью Python: анализ текста с помощью набора инструментов для работы с естественным языком . Севастополь, Калифорния: O’Reilly Media, Inc. (2009).
Google Scholar
17. Даян П., Эбботт Л.Ф. Теоретическая неврология . (Том 806). Кембридж, Массачусетс: MIT Press (2001).
Google Scholar
18. Hommel B, Sellaro R, Fischer R, Borg S, Colzato LS. Высокочастотные бинауральные ритмы повышают когнитивную гибкость: свидетельство перекрестных помех при выполнении двух задач. Front Psychol (2016) 7:1287. doi:10.3389/fpsyg.2016.01287
Front Psychol (2016) 7:1287. doi:10.3389/fpsyg.2016.01287
PubMed Abstract | Полный текст перекрестной ссылки | Академия Google
19. López-Caballero F, Escera C. Бинауральные ритмы: неспособность усилить мощность ЭЭГ и эмоциональное возбуждение. Front Hum Neurosci (2017) 11:557. doi:10.3389/fnhum.2017.00557
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
20. Roth BL, Baner K, Westkaemper R, Siebert D, Rice KC, Steinberg S, et al. Сальвинорин А: сильнодействующий природный безазотистый селективный агонист опиоидов κ . Proc Natl Acad Sci USA (2002) 99(18):11934–9. doi:10.1073/pnas.182234399
CrossRef Full Text | Google Scholar
21. Schepis TS, West BT, Teter CJ, McCabe SE. Распространенность и корреляты одновременного приема рецептурных транквилизаторов и других психоактивных веществ у нас, старшеклассников: результаты национального опроса. Поведение наркомана (2016) 52:8–12. doi:10.1016/j.addbeh.2015.08.002
doi:10.1016/j.addbeh.2015.08.002
Полный текст CrossRef | Google Scholar
22. Солурш Л.П., Клемент В.Р. Использование диазепама при галлюциногенных наркотических кризах. JAMA (1968) 205(9):644–5. doi:10.1001/jama.205.9.644
Полный текст CrossRef | Google Scholar
23. Даунинг Дж. Психологическое и физиологическое воздействие МДМА на нормальных добровольцев. J Psychoactive Drugs (1986) 18(4):335–40. doi:10.1080/027
.1986.10472366
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
24. Pachter IJ, Zacharias DE, Ribeiro O. Индольные алкалоиды Acer saccharinum (клен серебристый), Dictyoloma incanescens, Piptadenia colubrina и Mimosa hostilis . J Org Chem (1959) 24(9):1285–7. doi:10.1021/jo01091a032
Полный текст CrossRef | Google Scholar
25. McKenna DJ, Towers GN, Abbott F. Ингибиторы моноаминоксидазы в южноамериканских галлюциногенных растениях: триптамин и β -карболиновые составляющие аяуаски. J Ethnopharmacol (1984) 10(2):195–223. doi:10.1016/0378-8741(84)-5
J Ethnopharmacol (1984) 10(2):195–223. doi:10.1016/0378-8741(84)-5
Полный текст CrossRef | Академия Google
26. Шварц Р.Х., Смит Д.Е. Галлюциногенные грибы. Clin Pediatr (1988) 27(2):70–3. doi:10.1177/000992288802700202
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
27. Хофманн А. Теонанакатль и ололиуки, два древних волшебных снадобья Мексики. Bull Narc (1971) 23(1):3–14.
Google Scholar
28. Power M. Наркотики 2.0: Интернет-революция, которая меняет то, как мир становится кайфом . Нью-Йорк, Нью-Йорк: Книги Портобелло (2014).
Google Scholar
29. Томас Х. Психиатрические симптомы у потребителей каннабиса. Br J Psychiatry (1993) 163(2):141–9. doi:10.1192/bjp.163.2.141
CrossRef Полный текст | Google Scholar
30. Сили К.А., Лапойнт Дж., Моран Дж.Х., Фатторе Л. Спайсовые препараты — это больше, чем безвредные травяные смеси: обзор фармакологии и токсикологии синтетических каннабиноидов. Prog Neuropsychopharmacol Biol Psychiatry (2012) 39(2):234–43. doi:10.1016/j.pnpbp.2012.04.017
Prog Neuropsychopharmacol Biol Psychiatry (2012) 39(2):234–43. doi:10.1016/j.pnpbp.2012.04.017
Реферат PubMed | Полный текст перекрестной ссылки | Google Scholar
31. Эрнст Э. Переоценка кавы ( Piper methysticum ). Br J Clin Pharmacol (2007) 64(4):415–7. doi:10.1111/j.1365-2125.2007.02932.x
Полный текст CrossRef | Google Scholar
32. Bossong M, Van Dijk J, Niesink R. Метилон и mCPP, два новых наркотика? Addict Biol (2005) 10 (4): 321–3. doi:10.1080/13556210500350794
PubMed Abstract | Полный текст перекрестной ссылки | Академия Google
33. Ян Г., Ван Ю, Тянь Дж., Лю Дж.-П. Huperzine A для болезни Альцгеймера: систематический обзор и метаанализ рандомизированных клинических испытаний. PLoS One (2013) 8(9):e74916. doi:10.1371/journal.pone.0074916
Полный текст CrossRef | Google Scholar
34. Бернардо Н.П., Сикейра MEPB, де Пайва MJN, Майя Р.П. Кофеин и другие примеси при изъятии уличного кокаина в Бразилии. Int J Drug Policy (2003) 14(4):331–4. doi:10.1016/S0955-3959(03)00083-5
Int J Drug Policy (2003) 14(4):331–4. doi:10.1016/S0955-3959(03)00083-5
Полнотекстовая перекрестная ссылка | Google Scholar
35. Шнайдер С., Мейс Ф. Анализ образцов незаконного кокаина и героина, изъятых в Люксембурге в 2005–2010 гг. Forensic Sci Int (2011) 212(1):242–6. doi:10.1016/j.forsciint.2011.06.027
Полный текст CrossRef | Google Scholar
36. Budney AJ, Higgins ST, Hughes JR, Bickel WK. Использование никотина и кофеина у кокаинозависимых лиц. J Subst Abuse (1993) 5(2):117–30. дои: 10.1016/0899-3289(93)
-H
Реферат PubMed | Полный текст перекрестной ссылки | Google Scholar
37. Проссер Дж.М., Нельсон Л.С. Токсикология солей для ванн: обзор синтетических катинонов. J Med Toxicol (2012) 8(1):33–42. doi:10.1007/s13181-011-0193-z
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
38. Гарднер Д.Р., Риет-Корреа Ф., Пантер К.Е., Пфистер Дж., Шильд А.Л., Виренга Т. Алкалоидные профили Mimosa tenuiflora и связанные методы анализа. 8-й Международный симпозиум по ядовитым растениям (ISOPP8) . Жоао Пессоа, Параиба, Бразилия: CABI (2011). п. 600–5.
8-й Международный симпозиум по ядовитым растениям (ISOPP8) . Жоао Пессоа, Параиба, Бразилия: CABI (2011). п. 600–5.
Google Scholar
39. O’Mahony Carey S, et al. Психоактивные вещества: справочник по этноботаническим растениям и травам, синтетическим химическим веществам, соединениям и продуктам . Южный Типперэри: Служба по борьбе со злоупотреблением психоактивными веществами, НИУ ВШЭ (2014 г.).
Google Scholar
40. Heise CW, Brooks DE. Воздействие аяуаски: описательный анализ звонков в токсикологические центры США с 2005 по 2015 год. J Med Toxicol (2017) 13(3):245–8. doi:10.1007/s13181-016-0593-1
Полный текст CrossRef | Google Scholar
41. Отт Дж. Фармауаска: человеческая фармакология перорального ДМТ плюс гармин. J Psychoactive Drugs (1999) 31(2):171–7. doi:10.1080/027
.1999.10471741
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
42. Шифано Ф., Папанти Г.Д., Орсолини Л. , Коркери Дж.М. Новые психоактивные вещества: фармакология стимуляторов и галлюциногенов. Expert Rev Clin Pharmacol (2016) 9(7):943–54. doi:10.1586/17512433.2016.1167597
, Коркери Дж.М. Новые психоактивные вещества: фармакология стимуляторов и галлюциногенов. Expert Rev Clin Pharmacol (2016) 9(7):943–54. doi:10.1586/17512433.2016.1167597
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
10 лучших бесплатных онлайн-сайтов с калькуляторами комбинаций
Вот список из лучших бесплатных онлайн-сайтов с калькуляторами комбинаций . Комбинация — это способ выбора продуктов из коллекции, где порядок выбранных продуктов не имеет значения. Если вы также хотите узнать все возможные способы выбора продукта из большего набора, посетите эти веб-сайты онлайн-калькуляторов комбинаций.
Эти онлайн-калькуляторы используют общее количество объектов (n) и количество элементов, взятых (r) значений, чтобы найти комбинацию (nCr) . Для выполнения расчета эти веб-сайты используют nCk = n!/k!(n-k)! Формула . Некоторые веб-сайты также показывают шагов расчета вместе с примерами , чтобы помочь пользователям. Процесс расчета немного отличается от сайта к сайту. Таким образом, я включил этапы расчета комбинации в описание каждого веб-сайта.
Некоторые веб-сайты также показывают шагов расчета вместе с примерами , чтобы помочь пользователям. Процесс расчета немного отличается от сайта к сайту. Таким образом, я включил этапы расчета комбинации в описание каждого веб-сайта.
Помимо поиска всех возможных комбинаций, некоторые из этих веб-сайтов также могут вычислять значения перестановок, используя тот же набор входных значений. Помимо этого, они также предлагают дополнительные калькуляторы, такие как Научный калькулятор , Калькулятор дробей, Калькулятор процентов, Калькулятор экспоненты, и другие. Просмотрите список, чтобы узнать больше об этих веб-сайтах.
Мой любимый онлайн-калькулятор комбинаций Веб-сайт:
omnicalculator.net — мой любимый веб-сайт, поскольку он может рассчитывать как комбинации, так и комбинации с повторениями. Кроме того, он также позволяет выполнять вычисления перестановок, используя тот же набор входных значений.
Вы также можете ознакомиться со списками лучших бесплатных онлайн-калькуляторов биномиального распределения, онлайн-калькулятора подсети IPv6 и онлайн-калькулятора прибыли от майнинга.
omnicalculator.net
omnicalculator.net — это бесплатный универсальный онлайн-калькулятор, который также можно использовать в качестве онлайн-калькулятора комбинаций . Используя этот калькулятор, пользователи могут легко узнать все возможные значения комбинации. Помимо комбинации, его также можно использовать для расчета комбинаций с повторениями, перестановками, и перестановками со значениями повторений . Для выполнения всех этих расчетов пользователям достаточно указать общее количество объектов (n) и размер выборки (r) значений. Теперь выполните следующие шаги.
Как рассчитать возможные комбинации онлайн с помощью omnicalculator.net:
Дополнительные функции:
Заключительные мысли:
Это еще один хороший онлайн-калькулятор комбинаций, с помощью которого пользователи могут одновременно выполнять вычисления комбинаций и перестановок.
Домашняя страница
calculatesoup.com
calculatesoup.com – это бесплатный онлайн-калькулятор комбинаций. Используя этот веб-сайт, пользователи могут узнать количество возможных комбинаций , которые могут возникнуть, извлекая образец элементов из большего набора. Проще говоря, он определяет количество возможных подмножеств, которые можно создать из большего набора. Теперь проверьте следующие шаги, чтобы выполнить расчет комбинации онлайн.
Проще говоря, он определяет количество возможных подмножеств, которые можно создать из большего набора. Теперь проверьте следующие шаги, чтобы выполнить расчет комбинации онлайн.
Как рассчитать возможные комбинации онлайн с помощью calculatesoup.com:
Дополнительные функции:
Заключительные мысли:
Это простой онлайн-калькулятор комбинаций, с помощью которого пользователи могут быстро узнать точное значение комбинации.
Домашняя страница
calculate.net
calculate.net — еще один бесплатный веб-сайт онлайн-калькулятора комбинаций. В основном это веб-сайт онлайн-калькулятора, на котором размещено множество математических калькуляторов, одним из которых является 9.0017 Калькулятор перестановок и комбинаций . Используя этот калькулятор, пользователи могут выполнять как перестановочные, так и комбинированные вычисления. Чтобы выполнить расчет комбинации, пользователям просто нужно ввести общую сумму в наборе (n) и сумму в каждом значении подмножества (r) . После выполнения расчета он показывает результаты как перестановки, так и комбинации. Этот веб-сайт также предлагает пользователям примеры и формулы, которые помогут им понять процесс расчета. Теперь выполните следующие шаги.
Как рассчитать возможные комбинации онлайн с помощью calculate.net:
Дополнительные функции:
Заключительные мысли:
Это еще один хороший онлайн-калькулятор комбинаций, который любой может использовать для быстрого выполнения вычислений комбинаций и перестановок.
Домашняя страница
byjus.
 com
combyjus.com – это бесплатный онлайн-калькулятор комбинаций. На этом веб-сайте пользователи также могут найти учебные материалы для студентов в различных областях. Чтобы узнать все возможные комбинации, он предлагает калькулятор комбинаций. В этом калькуляторе пользователям необходимо ввести параметры Tota (n) и параметры , которые будут выбраны (r) , чтобы начать расчет. После завершения расчета пользователи могут просмотреть окончательное значение всех возможных комбинаций. Теперь выполните следующие шаги.
Как рассчитать возможные комбинации онлайн с помощью byjus.com:
Дополнительные функции:
Заключительные мысли:
Это еще один хороший онлайн-калькулятор комбинаций, который любой может использовать для легкого расчета всех возможных значений комбинаций.
Домашняя страница
statshowto.com
statshowto.com – еще один бесплатный сайт онлайн-калькулятора комбинаций. Этот сайт предлагает Перестановка/Комбинация калькулятор. Этот калькулятор использует всего вариантов (n) и вариантов для выбора (r) значений, чтобы узнать все возможные значения комбинации. Этот калькулятор также может учитывать входные данные заказа и повторения товара при расчете. Теперь выполните следующие шаги, чтобы выполнить расчет комбинации.
Как рассчитать возможные комбинации на сайте statshowto.com:
Дополнительная функция:
Заключительные мысли:
Это один из самых простых онлайн-калькуляторов комбинаций, который каждый может использовать, чтобы узнать все возможные значения комбинаций.
Домашняя страница
keisan.casio.com
keisan.casio.com — еще один бесплатный онлайн-калькулятор комбинаций. Этот веб-сайт предлагает простой калькулятор комбинаций, который позволяет пользователям находить все возможные комбинации, когда подмножество берет вещи из набора. Он также предлагает формулу решения комбинации в своем интерфейсе, чтобы помочь пользователям. Теперь выполните следующие шаги.
Как рассчитать возможные комбинации онлайн с помощью keisan.
 casio.com:
casio.com:Дополнительные функции:
Заключительные мысли:
Это еще один хороший онлайн-калькулятор комбинаций, который предлагает все необходимые инструменты для расчета комбинаций.
Домашняя страница
mathisfun.com
mathisfun.com — еще один бесплатный сайт онлайн-калькулятора комбинаций. Как следует из названия, это веб-сайт, посвященный математике, который предлагает множество тем для изучения математики, а также математические калькуляторы. Одним из его калькуляторов является калькулятор комбинаций и перестановок 9.0018 . Этот калькулятор может найти все возможные комбинации и значения перестановок, используя всего вариантов (n) и чисел для выбора (r) значений. Теперь выполните следующие шаги, чтобы выполнить расчет.
Одним из его калькуляторов является калькулятор комбинаций и перестановок 9.0018 . Этот калькулятор может найти все возможные комбинации и значения перестановок, используя всего вариантов (n) и чисел для выбора (r) значений. Теперь выполните следующие шаги, чтобы выполнить расчет.
Как рассчитать возможные комбинации онлайн с помощью mathisfun.com:
Дополнительные функции:
Заключительные мысли:
Этот онлайн-калькулятор комбинаций предлагает простой и удобный в использовании калькулятор комбинаций.
Домашняя страница
goodcalculators.com
goodcalculators.com — еще один бесплатный онлайн-калькулятор комбинаций. На этом веб-сайте пользователи могут рассчитать комбинацию (nCr) и перестановку (nPr). Чтобы рассчитать как комбинацию, так и перестановку, пользователям необходимо ввести общее количество объектов (n) и количество взятых элементов (r). Хотя за один раз он может вычислить либо перестановку, либо комбинацию. Перед началом процесса расчета пользователи могут указать, хотят ли они повторения в выводе или нет. Теперь выполните следующие шаги.
Как рассчитать возможные комбинации онлайн с помощью goodcalculators.com:
Дополнительные характеристики:
Заключительные мысли:
Это еще один хороший онлайн-калькулятор комбинаций, который также может легко рассчитать перестановку.
Домашняя страница
dcode.fr
dcode.fr – еще один бесплатный онлайн-калькулятор комбинаций. Этот веб-сайт предлагает несколько инструментов для решения комбинаций, таких как 9Генератор комбинаций 1236, комбинации с порядком, комбинации с повторяющимися элементами, калькулятор подсчета комбинаций, комбинации и лотереи, и многое другое. Хотя для выполнения расчета первичной комбинации вам нужен только калькулятор подсчета комбинаций, который использует значения n и r . Теперь проверьте следующие шаги.
Как рассчитать возможные комбинации онлайн с помощью dcode.fe:
Дополнительные возможности:
Заключительные мысли:
Это еще один хороший онлайн-калькулятор комбинаций, который также можно использовать для создания комбинаций.
Домашняя страница
hackmath.net
hackmath.net — последний бесплатный сайт онлайн-калькулятора комбинаций. Это предлагает множество математических калькуляторов, одним из которых является комбинаторный калькулятор. Этот калькулятор может определить различные способы выбора продуктов k из набора продуктов n . Для этого вам нужно ввести Элемент для выбора (n) и выбранных элементов (k) значений. Помимо этого, вы также можете указать, разрешены ли порядок и повторение или нет. Теперь выполните следующие шаги.
Этот калькулятор может определить различные способы выбора продуктов k из набора продуктов n . Для этого вам нужно ввести Элемент для выбора (n) и выбранных элементов (k) значений. Помимо этого, вы также можете указать, разрешены ли порядок и повторение или нет. Теперь выполните следующие шаги.
Как рассчитать возможные комбинации онлайн с помощью hackmath.net:
Дополнительные функции:
Заключительные мысли:
Это еще один функциональный веб-сайт онлайн-калькулятора комбинаций, который любой может использовать без особых хлопот.
Домашняя страница
Похожие сообщения
Написать комментарий
Онлайн калькулятор комбинаций — Комбинаторика
Комбинация, расчет онлайн
Резюме:
Чтобы вычислить количество k элементов части набора из n элементов.
Комбинация онлайн
Описание:
Калькулятор используется для расчета онлайн числа комбинации набора k элементов из n элементов . Комбинация набора из k элементов среди n элементов рассчитывается следующим образом: `»n!»/»p!(n-p)!»`. Знак ! представляет факториал функция. Т.е. количество комбинаций набора из k среди n элементов равно количеству перестановка разделить на р!. Это число комбинации является биномиальный коэффициент .
Калькулятор способен вычислить количество комбинаций набора из k элементов из n элементов
с результатами в точной форме: например, чтобы вычислить количество комбинаций набора из 3 элементов из 5 элементов, введите
комбинация(`5;3`),
после расчета возвращается результат.
Синтаксис:
комбинация(n;k), где n и k — целые числа
Примеры:
комбинация(`5;3`), возвращает 10
Расчет онлайн с комбинацией (для подсчета количества комбинаций)
См. также
Список связанных калькуляторов:

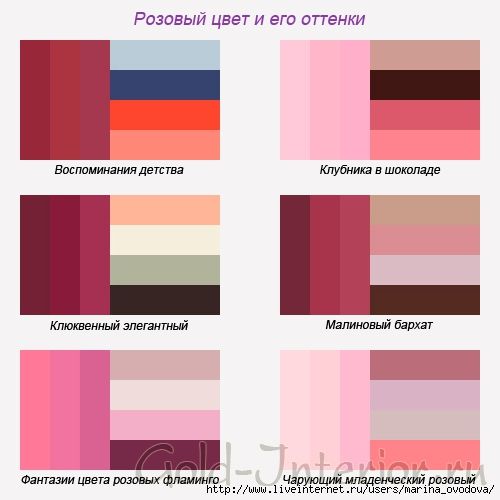
 Откроется диалоговое окно Переименовать. Фокус будет в поле «Имя документа».
Откроется диалоговое окно Переименовать. Фокус будет в поле «Имя документа».




 Сколько кругов мы можем сделать из них?
Сколько кругов мы можем сделать из них?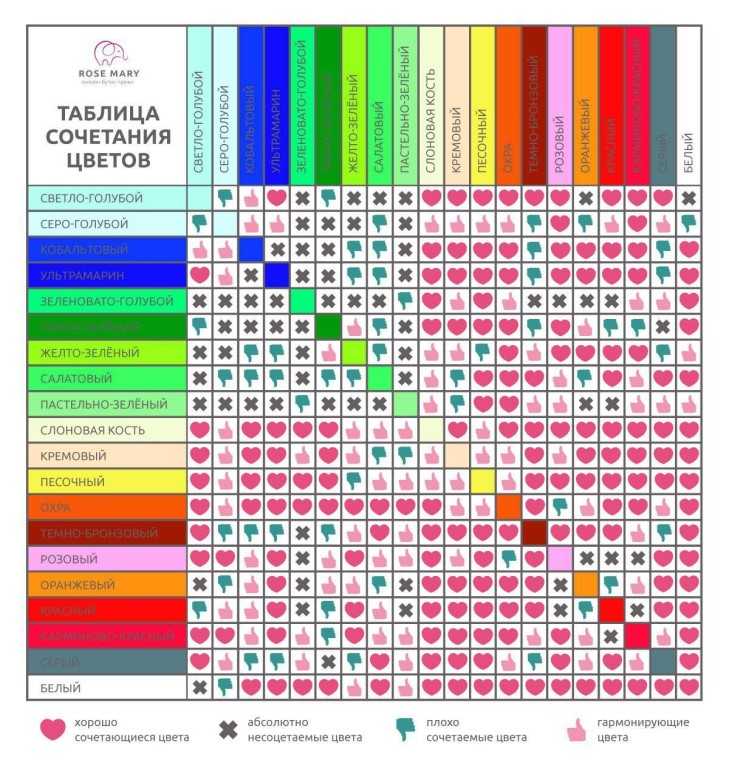 Например, семерка использует три маленькие полоски. Какое самое большое трехзначное число можно составить, если использовать двадцать полосок?
Например, семерка использует три маленькие полоски. Какое самое большое трехзначное число можно составить, если использовать двадцать полосок? Сколько существует комбинаций из двух блоков?
Сколько существует комбинаций из двух блоков?