Сокращение числитель 12 разделили. Сокращение дробей
Разберемся в том, что такое сокращение дробей, зачем и как сокращать дроби, приведем правило сокращения дробей и примеры его использования.
Yandex.RTB R-A-339285-1
Что такое «сокращение дробей»
Сократить дробь
Сократить дробь — значит разделить ее числитель и знаменатель на общий делитель, положительный и отличный от единицы.
В результате такого действия получится дробь с новым числителем и знаменателем, равная исходной дроби.
К примеру, возьмем обыкновенную дробь 6 24 и сократим ее. Разделим числитель и знаменатель на 2 , в результате чего получим 6 24 = 6 ÷ 2 24 ÷ 2 = 3 12 . В этом примере мы сократили исходную дробь на 2 .
Приведение дробей к несократимому виду
В предыдущем примере мы сократили дробь 6 24 на 2 , в результате чего получили дробь 3 12 . Нетрудно заметить, что эту дробь можно сократить еще. Как правило, целью сокращения дробей является получение в итоге несократимой дроби. Как привести дробь к несократимому виду?
Как правило, целью сокращения дробей является получение в итоге несократимой дроби. Как привести дробь к несократимому виду?
Это можно сделать, если сократить числитель и знаменатель на их наибольший общий делитель (НОД). Тогда, по свойству наибольшего общего делителя, в числителе и в знаменателе будут взаимно простые числа, и дробь окажется несократимой.
a b = a ÷ Н О Д (a , b) b ÷ Н О Д (a , b)
Приведение дроби к несократимому виду
Чтобы привести дробь к несократимому виду нужно ее числитель и знаменатель разделить на их НОД.
Вернемся к дроби 6 24 из первого примера и приведем ее к несократимому виду. Наибольший общий делитель чисел 6 и 24 равен 6 . Сократим дробь:
6 24 = 6 ÷ 6 24 ÷ 6 = 1 4
Сокращение дробей удобно применять, чтобы не работать с большими цифрами. Вообще, в математике существует негласное правило: если можно упростить какое-либо выражение, то нужно это делать. Под сокращением дроби чаще всего подразумевают ее приведение к несократимому виду, а не просто сокращение на общий делитель числителя и знаменателя.
Правило сокращения дробей
Чтобы сокращать дроби достаточно запомнить правило, которое состоит из двух шагов.
Правило сокращения дробей
Чтобы сократить дробь нужно:
- Найти НОД числителя и знаменателя.
- Разделить числитель и знаменатель на их НОД.
Рассмотрим практические примеры.
Пример 1. Сократим дробь.
Дана дробь 182 195 . Сократим ее.
Найдем НОД числителя и знаменателя. Для этого в данном случае удобнее всего воспользоваться алгоритмом Евклида.
195 = 182 · 1 + 13 182 = 13 · 14 Н О Д (182 , 195) = 13
Разделим числитель и знаменатель на 13 . Получим:
182 195 = 182 ÷ 13 195 ÷ 13 = 14 15
Готово. Мы получили несократимую дробь, которая равна исходной дроби.
Как еще можно сокращать дроби? В некоторых случаях удобно разложить числитель и знаменатель на простые множители, а потом из верхней и нижней частей дроби убрать все общие множители.
Пример 2. Сократим дробь
Дана дробь 360 2940 . Сократим ее.
Сократим ее.
Для этого представим исходную дробь в виде:
360 2940 = 2 · 2 · 2 · 3 · 3 · 5 2 · 2 · 3 · 5 · 7 · 7
Избавимся от общих множителей в числителе и знаменателе, в результате чего получим:
360 2940 = 2 · 2 · 2 · 3 · 3 · 5 2 · 2 · 3 · 5 · 7 · 7 = 2 · 3 7 · 7 = 6 49
Наконец, рассмотрим еще один способ сокращения дробей. Это так называемое последовательное сокращение. С использованием этого способа сокращение производится в несколько этапов, на каждом из которых дробь сокращается на какой-то очевидный общий делитель.
Пример 3. Сократим дробь
Сократим дробь 2000 4400 .
Сразу видно, что числитель и знаменатель имеют общий множитель 100 . Сокращаем дробь на 100 и получаем:
2000 4400 = 2000 ÷ 100 4400 ÷ 100 = 20 44
20 44 = 20 ÷ 2 44 ÷ 2 = 10 22
Получившийся результат снова сокращаем на 2 и получаем уже несократимую дробь:
10 22 = 10 ÷ 2 22 ÷ 2 = 5 11
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Деление и числителя и знаменателя дроби на их общий делитель , отличный от единицы, называют сокращением дроби .
Чтобы сократить обыкновенную дробь, нужно разделить ее числитель и знаменатель на одно и то же натуральное число.
Это число является наибольшим общим делителем числителя и знаменателя данной дроби.
Возможны следующие формы записи решения примеров на сокращение обыкновенных дробей.
Учащийся вправе выбрать любую форму записи.
Примеры. Упростить дроби.
Сократим дробь на 3 (делим числитель на 3;
делим знаменатель на 3).
Сокращаем дробь на 7.
Выполняем указанные действия в числителе и знаменателе дроби.
Полученную дробь сокращаем на 5.
Сократим данную дробь 4) на 5·7³ — наибольший общий делитель (НОД) числителя и знаменателя, который состоит из общих множителей числителя и знаменателя, взятых в степени с наименьшим показателем.
Разложим числитель и знаменатель этой дроби на простые множители.
Получаем: 756=2²·3³·7 и 1176=2³·3·7² .
Определяем НОД (наибольший общий делитель) числителя и знаменателя дроби 5) .
Это произведение общих множителей, взятых с наименьшими показателями.
НОД(756; 1176)=2²·3·7 .
Делим числитель и знаменатель данной дроби на их НОД, т. е. на 2²·3·7 получаем несократимую дробь 9/14 .
А можно было записать разложения числителя и знаменателя в виде произведения простых множителей, не применяя понятие степени, а затем произвести сокращение дроби, зачеркивая одинаковые множители в числителе и знаменателе. Когда одинаковых множителей не останется — перемножаем оставшиеся множители отдельно в числителе и отдельно в знаменателе и выписываем получившуюся дробь 9/14 .
И, наконец, можно было сокращать данную дробь 5) постепенно, применяя признаки деления чисел и к числителю и к знаменателю дроби. Рассуждаем так: числа 756 и 1176 оканчиваются четной цифрой, значит, оба делятся на 2 . Сокращаем дробь на 2 . Числитель и знаменатель новой дроби — числа 378 и 588 также делятся на 2 . Сокращаем дробь на 2 . Замечаем, что число 294 — четное, а 189 — нечетное, и сокращение на 2 уже невозможно. Проверим признак делимости чисел 189 и 294
Сокращаем дробь на 2 . Замечаем, что число 294 — четное, а 189 — нечетное, и сокращение на 2 уже невозможно. Проверим признак делимости чисел 189 и 294
(1+8+9)=18 делится на 3 и (2+9+4)=15 делится на 3, следовательно, и сами числа 189 и 294 делятся на 3 . Сокращаем дробь на 3 . Далее, 63 делится на 3, а 98 — нет. Перебираем другие простые множители. Оба числа делятся на 7 . Сокращаем дробь на 7 и получаем несократимую дробь 9/14 .
В этой статье мы рассмотрим основные действия с алгебраическими дробями :
- сокращение дробей
- умножение дробей
- деление дробей
Начнем с сокращения алгебраических дробей .
Казалось бы, алгоритм очевиден.
Чтобы сократить алгебраические дроби , нужно
1. Разложить числитель и знаменатель дроби на множители.
2. Сократить одинаковые множители.
Однако, школьники часто делают ошибку, «сокращая» не множители, а слагаемые. Например, есть любители, которые в дроби «сокращают» на и получают в результате , что, разумеется, неверно.
Рассмотрим примеры:
1. Сократить дробь:
1. Разложим на множители числитель по формуле квадрата суммы, а знаменатель по формуле разности квадратов
2. Разделим числитель и знаменатель на
2. Сократить дробь:
1. Разложим на множители числитель. Так как числитель содержит четыре слагаемых, применим группировку.
2. Разложим на множители знаменатель. Так же применим группировку.
3. Запишем дробь, которая у нас получилась и сократим одинаковые множители:
Умножение алгебраических дробей.
При умножении алгебраических дробей мы числитель умножаем на числитель, а знаменатель умножаем на знаменатель.
Важно! Не нужно торопиться выполнять умножение в числителе и знаменателе дроби. После того, как мы записали в числителе произведение числителей дробей, а в знаменателе — произведение знаменателей, нужно разложить на множители каждый множитель и сократить дробь.
Рассмотрим примеры:
3. Упростите выражение:
1. Запишем произведение дробей: в числителе произведение числителей, а в знаменателе произведение знаменателей:
2. Разложим каждую скобку на множители:
Теперь нам нужно сократить одинаковые множители. Заметим, что выражения и отличаются только знаком: и в результате деления первого выражения на второе получим -1.
Итак,
Деление алгебраических дробей мы выполняем по такому правилу:
То есть чтобы разделить на дробь, нужно умножить на «перевернутую».
Мы видим, что деление дробей сводится к умножению, а умножение, в конечном итоге, сводится к сокращению дробей.
Рассмотрим пример:
4. Упростите выражение:
Вот и добрались до сокращения. Применяется здесь основное свойство дроби. НО! Не всё так просто. Со многими дробями (в том числе из школьного курса) вполне можно им обойтись. А если взять дроби «покруче»? Разберём подробнее!
Рекомендую посмотреть материалов с дробями.
А если взять дроби «покруче»? Разберём подробнее!
Рекомендую посмотреть материалов с дробями.
Итак, мы уже знаем, что числитель и знаменатель дроби можно умножать и делить на одно и тоже число, дробь от этого не изменится. Рассмотрим три подхода:
Подход первый.
Для сокращения делят числитель и знаменатель на общий делитель. Рассмотрим примеры:
Сократим:
В приведенных примерах мы сразу видим какие взять делители для сокращения. Процесс несложен – мы перебираем 2,3.4,5 и так далее. В большинстве примеров школьного курса этого вполне достаточно. А вот если будет дробь:
Тут процесс с подбором делителей может затянуться надолго;). Конечно, такие примеры лежат вне школьного курса, но справляться с ними нужно уметь. Чуть ниже рассмотрим как это делается. А пока вернёмся к процессу сокращения.
Как рассмотрено выше, для того чтобы сократить дробь, мы осуществляли деление на определённый нами общий делитель(ли). Всё правильно! Стоит лишь добавить признаки делимости чисел:
— если число чётное то оно делится на 2.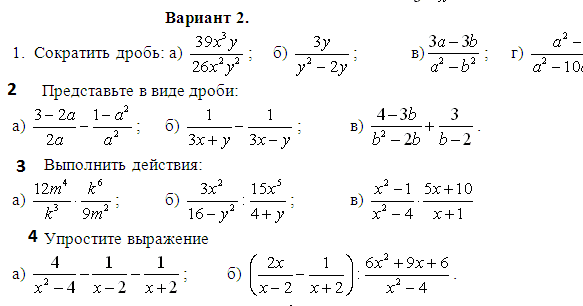
— если число из последних двух цифр делится на 4, то и само число делится на 4.
— если сумма цифр из которых состоит число делится на 3, то и само число делится на 3. Например 125031, 1+2+5+0+3+1=12. Двенадцать делится на 3, значит и 123031 делится на 3.
— если в конце числа стоит 5 или 0, то число делится на 5.
— если сумма цифр из которых состоит число делится на 9, то и само число делится на 9. Например 625032 =.> 6+2+5+0+3+2=18. Восемнадцать делится на 9, значит и 623032 делится на 9.
Второй подход.
Если кратко суть, то на самом деле всё действо сводится к разложению числителя и знаменателя на множители и далее к сокращению равных множителей в числителе и знаменателе (данный подход – это следствие из первого подхода):
Визуально, чтобы не запутаться и не ошибиться равные множители просто перечёркивают. Вопрос – а как разложить число на множители? Нужно определить перебором все делители. Это тема отдельная, она несложная, посмотрите информацию в учебнике или интернете. Никаких великих проблем с разложением на множители чисел, которые присутствуют в дробях школьного курса, вы не встретите.
Никаких великих проблем с разложением на множители чисел, которые присутствуют в дробях школьного курса, вы не встретите.
Формально принцип сокращения можно записать так:
Подход третий.
Тут самое интересное для продвинутых и тех, кто хочет им стать. Сократим дробь 143/273. Попробуйте сами! Ну и как, быстро получилось? А теперь смотрите!
Переворачиваем её (числитель и знаменатель меняем местами). Делим уголком полученную дробь переводим в смешанное число, то есть выделяем целую часть:
Уже проще. Мы видим, что числитель и знаменатель можно сократить на 13:
А теперь не забываем снова перевернуть дробь обратно, давайте запишем всю цепочку:
Проверено – времени уходит меньше, чем на перебор и проверку делителей. Вернёмся к нашим двум примерам:
Первый. Делим уголком (не на калькуляторе), получим:
Эта дробь попроще конечно, но с сокращением опять проблема. Теперь отдельно разбираем дробь 1273/1463, переворачиваем её:
Тут уже проще. Можем рассмотреть такой делитель как 19. Остальные не подходят, это видно: 190:19= 10, 1273:19 = 67. Ура! Запишем:
Можем рассмотреть такой делитель как 19. Остальные не подходят, это видно: 190:19= 10, 1273:19 = 67. Ура! Запишем:
Следующий пример. Сократим 88179/2717.
Делим, получим:
Отдельно разбираем дробь 1235/2717, переворачиваем её:
Можем рассмотреть такой делитель как 13 (до 13 не подходят):
Числитель 247:13=19 Знаменатель 1235:13=95
*В процессе увидели ещё один делитель равный 19. Получается, что:
Теперь записываем исходное число:
И не важно, что будет больше в дроби – числитель или знаменатель, если знаменатель, то переворачиваем и действуем как описано. Таким образом мы можем сократить любую дробь, третий подход можно назвать универсальным.
Конечно, два примера рассмотренные выше это непростые примеры. Давайте попробуем эту технологию на уже рассмотренных нами «несложных» дробях:
Две четвёртых.
Семьдесят две шестидесятых. Числитель больше знаменателя, переворачивать не нужно:
Разумеется, третий подход применили к таким простым примерам просто как альтернативу. Способ, как уже сказано, универсальный, но не для всех дробей удобный и корректный, особенно это относится к простым.
Способ, как уже сказано, универсальный, но не для всех дробей удобный и корректный, особенно это относится к простым.
Многообразие дробей велико. Важно, чтобы вы усвоили именно принципы. Строгого правила по работе с дробями просто нет. Посмотрели, прикинули каким образом удобнее действовать и вперёд. С практикой придёт навык и будете щёлкать их как семечки.
Вывод:
Если видите общий(ие) делитель(и) для числителя и знаменателя, то используйте их для сокращения.
Если умеете быстро раскладывать на множители число, то разложите числитель и знаменатель, далее сокращайте.
Если никак не можете определить общий делитель, то воспользуйтесь третьим подходом.
*Для сокращения дробей важно усвоить принципы сокращения, понимать основное свойство дроби, знать подходы к решению, быть крайне внимательным при вычислениях.
И запомните! Дробь принято сокращать до упора, то есть сокращать её пока есть общий делитель.
C уважением, Александр Крутицких.
На первый взгляд алгебраические дроби кажутся очень сложными, и неподготовленный учащийся может подумать, что с ними невозможно ничего сделать. Нагромождение переменных, чисел и даже степеней навевает страх. Тем не менее, для сокращения обычных (например, 15/25) и алгебраических дробей используются одни и те же правила.
Шаги
Сокращение дробей
Ознакомьтесь с действиями с простыми дробями. Операции с обычными и алгебраическими дробями аналогичны. К примеру, возьмем дробь 15/35. Чтобы упростить эту дробь, следует найти общий делитель . Оба числа делятся на пять, поэтому мы можем выделить 5 в числителе и знаменателе:
15→
5 * 335 → 5 * 7
Теперь можно сократить общие множители , то есть вычеркнуть 5 в числителе и знаменателе. В результате получаем упрощенную дробь 3/7 . В алгебраических выражениях общие множители выделяются точно так же, как и в обычных. В предыдущем примере мы смогли легко выделить 5 из 15 — тот же принцип применим и к более сложным выражениям, таким как 15x – 5. Найдем общий множитель. В данном случае это будет 5, так как оба члена (15x и -5) делятся на 5. Как и ранее, выделим общий множитель и перенесем его влево .
В предыдущем примере мы смогли легко выделить 5 из 15 — тот же принцип применим и к более сложным выражениям, таким как 15x – 5. Найдем общий множитель. В данном случае это будет 5, так как оба члена (15x и -5) делятся на 5. Как и ранее, выделим общий множитель и перенесем его влево .
15x – 5 = 5 * (3x – 1)
Чтобы проверить, все ли правильно, достаточно умножить на 5 стоящее в скобках выражение — в результате получатся те же числа, что были сначала. Сложные члены можно выделять точно так же, как и простые. Для алгебраических дробей применимы те же принципы, что и для обычных. Это наиболее простой способ сократить дробь. Рассмотрим следующую дробь:
(x+2)(x-3)(x+2)(x+10)
Отметим, что и в числителе (сверху), и в знаменателе (снизу) присутствует член (x+2), поэтому его можно сократить так же, как общий множитель 5 в дроби 15/35:
(x+2) (x-3)→
(x-3)(x+2) (x+10) → (x+10)
В результате получаем упрощенное выражение: (x-3)/(x+10)
Сокращение алгебраических дробей
Найдите общий множитель в числителе, то есть в верхней части дроби. При сокращении алгебраической дроби первым делом следует упростить обе ее части. Начните с числителя и постарайтесь разложить его на как можно большее число множителей. Рассмотрим в данном разделе следующую дробь:
При сокращении алгебраической дроби первым делом следует упростить обе ее части. Начните с числителя и постарайтесь разложить его на как можно большее число множителей. Рассмотрим в данном разделе следующую дробь:
15x+6
Начнем с числителя: 9x – 3. Для 9x и -3 общим множителем является число 3. Вынесем 3 за скобки, как это делается с обычными числами: 3 * (3x-1). В результате данного преобразования получится следующая дробь:
3(3x-1)15x+6
Найдите общий множитель в числителе. Продолжим выполнение приведенного выше примера и выпишем знаменатель: 15x+6. Как и раньше, найдем, на какое число делятся обе части. И в этом случае общим множителем является 3, так что можно записать: 3 * (5x +2). Перепишем дробь в следующем виде:
3(3x-1)3(5x+2)
Сократите одинаковые члены. На этом шаге можно упростить дробь. Сократите одинаковые члены в числителе и знаменателе. В нашем примере это число 3.
В нашем примере это число 3.
→
(3x-1)3 (5x+2) → (5x+2)
Определите, что дробь имеет простейший вид. Дробь полностью упрощена в том случае, когда в числителе и знаменателе не осталось общих множителей. Учтите, что нельзя сокращать те члены, которые стоят внутри скобок — в приведенном примере нет возможности выделить x из 3x и 5x, поскольку полными членами являются (3x -1) и (5x + 2). Таким образом, дробь не поддается дальнейшему упрощению, и окончательный ответ выглядит следующим образом:
(3x-1) (5x+2)
Потренируйтесь сокращать дроби самостоятельно. Лучший способ усвоить метод заключается в самостоятельном решении задач. Под примерами приведены правильные ответы.
4(x+2)(x-13)(4x+8)
Ответ: (x=13)
2x 2 -x5x
Ответ: (2x-1)/5
Специальные приемы
Вынесите отрицательный знак за пределы дроби. Предположим, дана следующая дробь:
Предположим, дана следующая дробь:
5(4-x)
Заметьте, что (x-4) и (4-x) “почти” идентичны, но их нельзя сократить сразу, поскольку они “перевернуты”. Тем не менее, (x — 4) можно записать как -1 * (4 — x), подобно тому как (4 + 2x) можно переписать в виде 2 * (2 + x). Это называется “переменой знака”.
-1 * 3(4-x)5(4-x)
Теперь можно сократить одинаковые члены (4-x):
-1 * 3 (4-x)5 (4-x)
Итак, получаем окончательный ответ: -3/5 . Научитесь распознавать разницу квадратов. Разница квадратов — это когда квадрат одного числа вычитается из квадрата другого числа, как в выражении (a 2 — b 2). Разницу полных квадратов всегда можно разложить на две части — сумму и разницу соответствующих квадратных корней. Тогда выражение примет следующий вид:
A 2 — b 2 = (a+b)(a-b)
Этот прием очень полезен при поиске общих членов в алгебраических дробях.
- Проверьте, правильно ли вы разложили то или иное выражение на множители. Для этого перемножьте множители — в результате должно получиться то же самое выражение.
- Чтобы полностью упростить дробь, всегда выделяйте наибольшие множители.
15/24 упрощенный
Сократите / упростите любую дробь до наименьшего значения с помощью нашего калькулятора дроби до простейшей формы.
Пожалуйста, заполните два левых поля ниже:| Ввод дробь: | Целое число часть: | Фракция часть: | Как Десятичный: | |||
| знак равно | знак равно | |||||
| Детали: Детали.  .. .. | ||||||
Как уменьшить дробь
Среди различных способов упрощения дроби мы покажем две процедуры ниже:
Метод 1 — Деление на меньшее число, если возможно
Начните с деления числителя и знаменателя дробь на одно и то же число, и повторять это до тех пор, пока невозможно разделить. Начните делить на маленькие числа, такие как 2, 3, 5, 7. Например,
Упростите дробь 42/98
- Сначала разделите оба (числитель/знаменатель) на 2, чтобы получить 21/49.
- Делить на 3 и 5 не получится, значит,
- Разделите числитель и знаменатель на 7, чтобы получить 3/7. Примечание: 21 ÷ 7 = 3 и 49 ÷ 7 = 7
В дроби 3/7 3 делится только на себя, а 7 не делится ни на какие другие числа, кроме себя и 1, поэтому дробь максимально упрощена. Дальнейшее сокращение невозможно, поэтому 42/98 равно 3/7 при уменьшении до наименьших значений. Это ПРАВИЛЬНАЯ Дробь, если абсолютное значение верхнего числа или числителя (3) меньше абсолютного значения нижнего числа или знаменателя (7).
Метод 2. Наибольший общий делитель
Чтобы привести дробь к наименьшему члену (также называемому ее простейшей формой), просто разделите числитель и знаменатель на НОД (наибольший общий делитель).
Например, 3/4 находится в низшей форме, а 6/8 не в низшей форме (НОД 6 и 8 равен 2), а 6/8 можно записать как 3/4. Вы можете сделать это, потому что значение дроби останется прежним, если числитель и знаменатель разделить на одно и то же число.
Примечание. Наибольший общий делитель (GCF) для чисел 6 и 8, обозначение gcf(6,8), равен 2. Объяснение:
- Факторы 6 равны 1,2,3,6;
- Факторы 8 равны 1,2,4,8.
Итак, несложно заметить, что «Наибольший общий делитель» или «Делитель» равен 2, потому что это наибольшее число, которое делится на все из них без остатка.
См. также:
- +, -, × и ÷ Калькулятор дробей
- Калькулятор эквивалентных дробей
- Калькулятор десятичной дроби
А также:
- Калькулятор процентов к дробям
- Калькулятор дроби в десятичную дробь
- Калькулятор доли в процентах
Упрощение дробей.
 Some Examples:
Some Examples:- Simplify 79/36
- Simplify 88/19
- Simplify 4/69
- Simplify 33/34
- Simplify 97/24
- Simplify 9/79
- Simplify 8/72
- Упростить 22/18
- Упростить 55/14
- Упростить 1/17
- Упростить 95/9
- Упростить 80/89
Упрощение 15/24
CREATIOR/REATIOR/SUMPIFIT FRACTION/Simply FRACTION TOMPRACTIOR TOSTIOR FRACTION. с помощью нашего калькулятора от дроби до простейшей формы. Найдите ответ на такие вопросы, как: Упростить 15/24 или что такое 15/24, приведенное к простейшей форме?
Пожалуйста, заполните два левых поля ниже:| Ввод дробь: | Целое число часть: | Фракция часть: | Как Десятичный: | |||
| знак равно | знак равно | |||||
| Детали: Детали.  .. .. | ||||||
Как уменьшить дробь
Среди различных способов упрощения дроби мы покажем две процедуры ниже:
Метод 1 — Деление на меньшее число, если возможно
Начните с деления числителя и знаменателя дробь на одно и то же число, и повторять это до тех пор, пока невозможно разделить. Начните делить на маленькие числа, такие как 2, 3, 5, 7. Например,
Упростите дробь 42/98
- Сначала разделите оба (числитель/знаменатель) на 2, чтобы получить 21/49..
- Делить на 3 и 5 не получится, значит,
- Разделите числитель и знаменатель на 7, чтобы получить 3/7. Примечание: 21 ÷ 7 = 3 и 49 ÷ 7 = 7
В дроби 3/7 3 делится только на себя, а 7 не делится ни на какие другие числа, кроме себя и 1, поэтому дробь максимально упрощена. Дальнейшее сокращение невозможно, поэтому 42/98 равно 3/7 при уменьшении до самого низкого уровня. Это ПРАВИЛЬНАЯ Дробь, если абсолютное значение верхнего числа или числителя (3) меньше абсолютного значения нижнего числа или знаменателя (7).
Метод 2. Наибольший общий делитель
Чтобы привести дробь к наименьшим членам (также называемым ее простейшей формой), просто разделите числитель и знаменатель на НОД (наибольший общий делитель).
Например, 3/4 находится в низшей форме, а 6/8 не в низшей форме (НОД 6 и 8 равен 2), а 6/8 можно записать как 3/4. Вы можете сделать это, потому что значение дроби останется прежним, если числитель и знаменатель разделить на одно и то же число.
Примечание. Наибольший общий делитель (GCF) для чисел 6 и 8, обозначение gcf(6,8), равен 2. Объяснение:
- Факторы 6 равны 1,2,3,6;
- Факторы 8 равны 1,2,4,8.
Итак, несложно заметить, что «Наибольший общий делитель» или «Делитель» равен 2, потому что это наибольшее число, которое делится на все из них без остатка.
См. также:
- +, -, × и ÷ Калькулятор дробей
- Калькулятор эквивалентных дробей
- Калькулятор десятичной дроби
А также:
- Калькулятор процентов к дробям
- Калькулятор дроби в десятичную дробь
- Калькулятор доли в процентах
Упрощение дробей.

