Теорема о соотношениях между сторонами и углами треугольника
Теорема:
| В треугольнике: 1) против большей стороны лежит больший угол; 2) обратно, против большего угла лежит большая сторона. |
Доказательство:
1) Дано: АВС, АВАС.
Доказать: СВ.
Доказательство:
Отложим на стороне АВ отрезок АD, равный стороне АС.
АDАВ, т.к. по построению АD = АС, а по условию АСАВ, значит, точка D лежит между точками А
Итак, С1, 1 =2, значит, С2, при этом 2В, следовательно, СВ.
2) Дано: АВС, СВ.
Доказать: АВАС.
Доказательство:
Предположим, что это не так. Тогда возможны два варианта:
- либо АВ = АС, тогда АВС — равнобедренный с основанием ВС, значит, С =В (как углы при основании), что противоречит условию: СВ.
- либо АВАС, тогда СВ, т.к. против большей стороны лежит больший угол (смотри 1 часть доказательства), что противоречит условию: СВ
Значит, наше предположение неверно, следовательно, АВАС. Что и требовалось доказать.
Следствие 1
Доказательство:
Дано: АВС, ВС — гипотенуза, А — прямой.
Доказать: ВСАС, ВС АВ.
Доказательство:
АВС — прямоугольный, А — прямой, следовательно, углы В и С острые, тогда АВ и АС, значит, ВСАС, ВСАВ (в треугольнике против большего угла лежит большая сторона). Что и требовалось доказать.
Следствие 2
| Если два угла треугольника равны, то треугольник равнобедренный (признак равнобедренного треугольника). |
Доказательство:
Дано: АВС, В =С.
Доказать: АС = АВ.
Доказательство:
Предположим, что одна из сторон будет больше, т.е. АСАВ, тогда и угол лежащий против этой стороны будет больше, т.е. ВС (в треугольнике против большей стороны лежит больший угол), а это противоречит условию: В =С,
Итак, в АВС равны две стороны (АС = АВ), следовательно, данный треугольник — равнобедренный. Что и требовалось доказать.
budu5.com
Теорема о соотношении между сторонами и углами треугольника
Данный видеоурок поможет пользователям получить представление о теме «Теорема о соотношении между сторонами и углами треугольника». В ходе урока все желающие смогут сформулировать и доказать важную теорему, касающуюся соотношения между сторонами и углами треугольника.
Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Основы геометрии»
Теорема: В треугольнике
1. Против большей стороны лежит больший угол
2. Обратно, против большего угла лежит большая сторона.
1. Дано: АВ>АС
Доказать: ∠С>∠В.
Доказательство: Отложим отрезок AD равный отрезку АС и тогда точка D будет лежать между точек А и В. Луч CD рассечёт угол АСВ на два угла, при этом ∠1=∠2. ΔАСВ состоит из углов ∠1 и ∠3. ∠2 – внешний для треугольника CDB, значит он больше угла В.
Рис. 1. Теорема о соотношении между сторонами и углами треугольника
AD=AC<AB
∠1=∠2<∠ACB
∠2=∠B+∠3>∠B
∠1>∠B
∠ACB>∠B, что и требовалось доказать.
2. Дано: ∠С>∠В
Доказать: ∠АВ>∠AC
Доказательство: Докажем методом от противного.
Рис. 2. Обратная теорема о соотношении между сторонами и углами треугольника , но ∠С>∠В по условию, следовательно, остается только случай, если АВ>АС, что и требовалось доказать.
Ещё раз сформулируем теорему и распространим её на все углы треугольника.
Теорема: В треугольнике
1. Против большей стороны лежит больший угол
2. Обратно, против большего угла лежит большая сторона.
Рис. 3. Чертёж к теореме
Если АВ>AC>BC, то ∠C>∠B>∠A.
Если ∠C>∠B>∠A, то АВ>AC>BC.
Следствие 1: В прямоугольном треугольнике гипотенуза больше катета.
Доказательство:
Рис. 4. Чертёж к следствию 1
∠А+∠В+90=180, ∠А+∠В=90=∠С. Отсюда следует, что ∠А<90, ∠В<90. Значит, СВ<АВ, СА<АВ. Гипотенуза АВ больше одного катета и больше другого катета. Следствие доказано.
Следствие 2: Если два угла треугольника равны, то треугольник равнобедренный (признак равнобедренного треугольника).
Дано: ∠В=∠С
Доказать: АС=АВ
Доказательство: Докажем методом от противного.
Рис. 5. Чертёж к следствию 2
АВ>АС ∠С>∠В, то есть АВ=АС. Следствие доказано.
Обсудим следствие 2. Треугольник называется равнобедренным, если его две стороны равны. Из этого вытекает его свойство: углы при основании равны. А теперь у нас есть признак, что если углы при какой-либо стороне равны, то треугольник равнобедренный. Мы имеем признак равнобедренного треугольника.
Пример 1: Сравните углы треугольника и выясните, может ли быть угол А тупым, если АВ=АС<ВС.
Рис. 6. Чертёж к примеру 1
АВ=АС ∠С=∠В. АС<ВС ÐВ<ÐА. Мы получили соотношение между углами: ∠С=∠В ∠А=180-(∠В+∠С).
Пример: ∠В=∠С=10, тогда ∠А=180-(10+10)=160.
Ответ: 1) ∠В=∠С<∠А 2) ∠А может быть тупым.
На сегодняшнем уроке мы рассмотрели теорему об отношении между сторонами и углами треугольника. На следующем уроке мы рассмотрим тему о неравенстве треугольников.
Список рекомендованной литературы
- Александров А.Д., Вернер А. Л., Рыжик В. И. и др. Геометрия 7. Издание М.: Просвещение.
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия 7. 5 издание. М.: Просвещение.
- Бутузов В. Ф., Кадомцев С. Б., Прасолов В.В., под редакцией Садовничего В. А. Геометрия 7. М.: Просвещение. 2010 г.
Рекомендованные ссылки на интернет-ресурсы
- Фестиваль педагогических идей «Открытый урок» (Источник).
- Kaknauchit.ru (Источник).
Рекомендованное домашнее задание
- №50. Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В., под редакцией Садовничего В. А. Геометрия 7. М.: Просвещение. 2010 г.
- Отрезок АК – медиана треугольника АВС с прямым углом С. Докажите, что ∠ВАК<∠АВС<∠АКС<∠АСВ.
- Докажите, что гипотенуза прямоугольного треугольника больше катета.
- Прямые, содержащие биссектрисы внешних углов при вершинах В и С треугольника АВС, пересекаются в точке О. Найдите угол ВОС, если угол А равен a.
interneturok.ru
Соотношения между сторонами и углами треугольника
Теорема 1. Против большей стороны в треугольнике лежит и больший угол.
Пусть в ΔАВС сторона АВ больше стороны ВС. Докажем, что угол С, лежащий против большей стороны АВ, больше угла А, лежащего против меньшей стороны ВС (рис.).
Отложим на стороне АВ от точки В отрезок ВD, равный стороне ВС, и соединим отрезком , точки D и С.
Треугольник DВС равнобедренный. Угол ВDС равен углу ВСD, так как они лежат против равных сторон в треугольнике.
Угол ВDС — внешний угол треугольника АDС, поэтому он больше угла А.
Так как ∠ВСD = ∠ВDС, то и угол ВСD больше угла А: ∠ВСD > ∠A. Но угол ВСD составляет только часть всего угла С, поэтому угол С будет и подавно больше угла A.
Докажем теперь обратные теоремы.Теорема 2. Против равных углов в треугольнике лежат и равные стороны.
Пусть в Δ AВС ∠A = ∠С (рис.). Докажем, что AВ = ВС, т. е. треугольник АBС равнобедренный.
Между сторонами АВ и ВС может быть только одно из трёх следующих соотношений:
1) АВ > ВС;
2) АВ
3) АВ = ВС.
Если бы сторона AВ была больше ВС, то угол С был бы больше угла A, но это противоречит условию теоремы, следовательно, АВ не может быть больше ВС.
Точно так же АВ не может быть меньше ВС, так как в этом случае угол С был бы меньше угла A.
Следовательно, возможен только третий случай, т. е.
АВ = ВС
Итaк, мы доказали: против равных углов в треугольнике лежат и равные стороны.
Теорема 3. Против большего угла в треугольнике лежит большая сторона.
Пусть в треугольнике АВС (рис.) ∠ C >∠ B
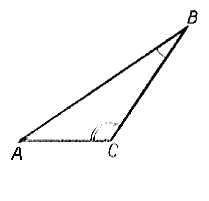
Докажем, что АВ > АС.
Здесь также может быть одно из трёх следующих соотношений:
1) АВ = АС;
2) АВ
3) АВ > АС.
Если бы сторона АВ была равна стороне АС, то ∠ С был бы равен ∠ В. Но это противоречит условию теоремы. Значит, АВ не может равняться АС
Точно так же АВ не может быть меньше АС, так как в этом случае угол С был бы меньше угла B, что также противоречит данному условию.
Следовательно, возможен только один случай, а именно:
АВ > АС.
Мы доказали: против большего угла в треугольнике лежит и большая сторона.
Следствие. В прямоугольном треугольнике гипотенуза больше любого из его катетов.
Соотношения между сторонами и углами в прямоугольном треугольнике
Пусть дан прямоугольный треугольник ABC. Обозначим его стороны через а, b и с.
По определению тригонометрических функций:
a/c = sin ∠А; a/c = cos ∠В; b/c= sin ∠ В; b/c = cos ∠А.
Отсюда а = с sin ∠ А = с cos ∠В; b = c sin ∠B = с соs ∠A,
т. е. катет прямоугольного треугольника равен гипотенузе, умноженной на синус угла, противолежащего этому катету, или на косинус угла, прилежащего к нему.
Из того же прямоугольного треугольника имеем, что
a/b = tg ∠А , отсюда a = b tg ∠А;
b/a = ctg ∠А, откуда b = a ctg ∠А,
т.е. катет прямоугольного треугольника равен другому катету, умноженному на тангенс угла, противолежащего первому катету, или на котангенс угла, прилежащего к первому катету.
razdupli.ru
Соотношение между углами и сторонами треугольника.
Тема «Соотношение между сторонами и углами треугольника. Решение треугольника.»
Цели урока:
1 . Закрепление и углубление знаний учащихся о теоремах синусов и косинусов и их применение к решению треугольников, а также их соотношение между углами треугольника и противоположными сторонами.
2. Развитие активности учащихся, формирование учебно-познавательных действий, коммуникативных навыков, умение анализировать и устанавливать связь между элементами темы. показать связь теории с практикой, способствовать выработке навыков решения задач, применяя раннее изученный материал.
3. Воспитывать ответственное отношение к учебному труду.
Воспитывать способность к самоанализу, рефлексии.
Оборудование: презентация, проектор, таблица Брадиса, лист самоконтроля.
ХОД УРОКА
Организационный момент. ( сообщение темы и целей урока)
Класс делится на три команды. Выбор капитанов. Название команды.
Мотивация урока.
Один мудрец сказал: «Высшее проявление духа – это разум. Высшее проявление разума – это геометрия. Клетка геометрии – это треугольник. Он так же неисчерпаем, как и Вселенная. Окружность – душа геометрии. Познайте окружность, и вы не только познаете душу геометрии, но возвысите свою душу».
Давайте делиться своими идеями, которые придут вам в голову, и не бойтесь ошибиться, любая мысль может дать нам новое направление поиска. Пусть наши достижения и не покажутся кому-то крупными, но ведь это будут наши собственные достижения!
Актуализация опорных знаний.
«Истина – ложь» (в листе конроля записать номера неверных утверждений )
Треугольник это геометрическая фигура имеющая 3 стороны и 3 угла (И)
Каждая сторона треугольника равна сумме двух других сторон (Л)
В треугольнике против меньшего угла лежит большая сторона (Л)
Площадь треугольника равна половине произведения его стороны на высоту проведенную к этой стороне (И)
Квадрат стороны треугольника равен сумме квадратов двух других сторон (Л)
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе (И)
(И)
(И)
Решить треугольник — значит найти угол и сторону этого треугольника. (Л)
Подведение итогов. Номера правильных ответов в презентации.
Решение задач.
Задачи на клетчатой бумаге.
Найти тангенсы острых углов.
Конкурс Знатоков. Диктант.
Математика, геометрия, планиметрия, котангенс, треугольник, гипотенуза, параллелограмм.
III. Решение задач с практическим содержанием.
ИСТОРИЧЕСКАЯ СПРАВКА
Тригонометрия— «измерение треугольников» — развивалась, прежде всего в связи с потребностями астрономии, географии, навигации. Поэтому её зачатки были в Древнем Вавилоне, где астрономия получила значительное развитие. Синус и косинус появляются в астрономических сочинениях индийских ученных 9-10вв.
Тангенс появился в связи с задачей определения высоты Солнца по длине тени, решение которой необходимо для изготовления солнечных часов. Выделение тригонометрии в специальный раздел математики связано с именем выдающегося персидского ученого Н а с и р э д д и н а Т у с и (1201-1274). В Европе первое изложение тригонометрии было дано в 15в. немецким ученым Р е г и о м о н т а н о м ( 1436-1476). Современный вид тригонометрия получила в трудах крупнейшего математика 18в. Леонарда Э й л е р а (1707-1783).
Теорему косинусов знали еще древние греки, ее доказательство содержится во 2 книге «Начал» Евклида как обобщенная теорема Пифагора. Нить практической геометрии тянулась от вавилонян и древних египтян через Герона вплоть до новых времён. В этот период появляется много руководств по геометрии, в которых излагаются правила, формулы и рецепты для решения тех или иных практических задач.
Решение задач в группах. ( 3 варианта)
1 группа:
Футбольный мяч находится в точке А футбольного поля на расстояниях 23 м и 24 м от оснований В и стоек ворот. Футболист направляет мяч в ворота. Найдите угол α попадания мяча в ворота, если ширина ворот равна 7 м.
Решение:
Решим треугольник АВС(задача 1) и найдем угол А, равный α
По теореме косинусов определим cos А
Ответ: 16057/
2 группа:
Наблюдатель находится на расстоянии 50 м от башни, высоту которой хочет определить.
Основание башни он видит под углом 2° к горизонту, а вершину — под углом 45° к горизонту.
Какова высота башни?
Дано: АВ=50 м, BDH=20, CDH=450, DH||AB.
Найти: СВ
Решение
DH || AB →BDH=DBA=20, как накрест лежащие.
cos DBA= ДВ=
Применим терему синусов:
ΔСDB:
3 группа.
Здание шириной 10 м имеет двускатную крышу с наклоном 35o с одной стороны и 41o — с другой. Найти длину скатов крыши с точностью до сантиметра.
Решение
1)Угол крыши
2)По теореме синусов
3)По теореме синусов:
Ответ: 5,912 см; 6,762 м.
ДОПОЛНИТЕЛЬНО.
Задача 1.
Две стороны треугольника имеют длины 6см и 12 см, а угол между ними равен 1200. Найдите длину большей стороны.
Решение
Пусть дан треугольник АВС:АВ=6 см, ВС=12 см, Сторона АС-наибольшая, так как она лежит против тупого угла. По теореме косинусов имеем:
cos 1200=
36 + 144 — 2612(-0,5) = 252; AC = (см)
4. Подведение итогов.
Выставление оценок в лист самоконтроля.
Рефлексия
Ребята, что узнали на уроке нового, как работал каждый из вас. Где на уроке почувствовали неуверенность, что показалось сложным. Ребята предлагаю сейчас каждому из вас высказаться одним предложением, выбирая начало фразы из рефлексивного экрана на доске:
Сегодня я узнал…
Мне было интересно…
Мне было трудно…
Я попробую…
Меня удивило…
Мне не понравилось…
Сегодня мы решили несколько задач на нахождения неизвестных сторон треугольника, попробовали свои силы для определения расстояния до недоступного предмета, применив изученные способы решения треугольников. И мы попробовали свои силы, оценили свои знания, свои возможности. Ведь «самое трудное – познать самого себя»(Фалес).
5. Домашнее задание № 1037.
infourok.ru
Сумма углов треугольника — урок. Геометрия, 7 класс.
Сумма углов треугольника равна \(180°\).

Доказательство
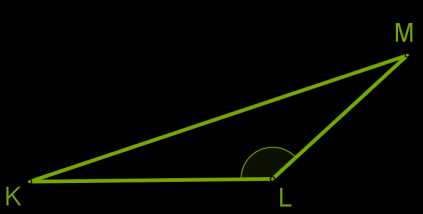
Рассмотрим произвольный треугольник \(KLM\) и докажем, что ∡ \(K\) \(+\) ∡ \(L\) \(+\) ∡ \(M =\) 180°.
Проведём через вершину \(L\) прямую \(a\), параллельную стороне \(KM\).
Углы, обозначенные \(1\), являются накрест лежащими углами при пересечении параллельных прямых \(a\) и \(KM\) секущей \(KL\), а углы, обозначенные \(2\) — накрест лежащими углами при пересечении тех же параллельных прямых секущей \(ML\).
Очевидно, сумма углов \(1\), \(2\) и \(3\) равна развёрнутому углу с вершиной \(L\), т. е.
∡ \(1\) \(+\) ∡ \(2\) \(+\) ∡ \(3 =\) 180°, или ∡ \(K\) \(+\) ∡ \(L\) \(+\) ∡ \(M =\) 180°.
Теорема доказана.
Следствия из теоремы о сумме углов треугольника
Следствие 1. Сумма острых углов прямоугольного треугольника равна 90°.
Следствие 2. В равнобедренном прямоугольном треугольнике каждый острый угол равен 45°.
Следствие 3. В равностороннем треугольнике каждый угол равен 60°.
Следствие 4. В любом треугольнике либо все углы острые, либо два угла острые, а третий — тупой или прямой.
Следствие 5. Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
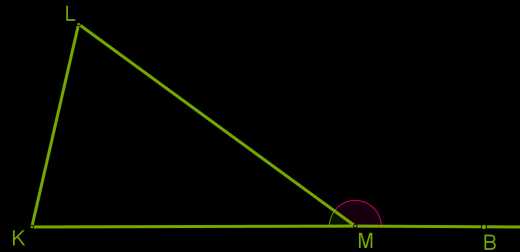
Доказательство
Из равенств ∡ \(KML\) \(+\) ∡ \(BML=\) 180° и ∡ \(K\) \(+\) ∡ \(L\) \(+\) ∡ \(KML =\) 180° получаем, что ∡ \(BML =\) ∡ \(K\) \(+\) ∡ \(L\).
Остроугольный, прямоугольный и тупоугольный треугольники
Как гласит четвёртое следствие из теоремы о сумме углов треугольника, можно выделить три вида треугольников в зависимости от углов.
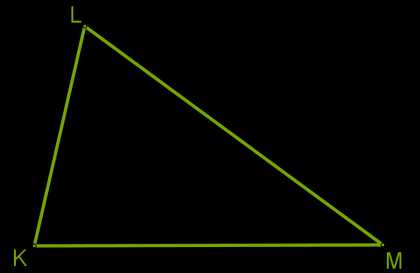
У треугольника \(KLM\) все углы острые.
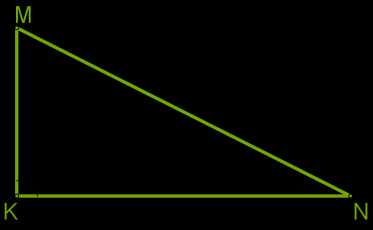
У треугольника \(KMN\) угол \(K = 90\)°.
У прямоугольного треугольника сторона, лежащая против прямого угла, называется гипотенузой, а две остальные стороны — катетами.
На рисунке \(MN\) — гипотенуза, \(MK\) и \(KN\) — катеты.
У треугольника \(KLM\) один угол тупой.
www.yaklass.ru
Соотношение между сторонами и углами треугольника
☰
В треугольнике между его сторонами и углами существуют определенные соотношения. Если какой-либо угол треугольника больше другого, то напротив его лежит сторона с большей длиной, чем напротив другого. Другими словами, напротив самого большого угла треугольника лежит самая большая сторона, напротив среднего угла — средняя сторона, а напротив самого маленького угла — самая маленькая сторона.
Понятно, что если углы треугольника равны, то и стороны, напротив которых они лежат, равны.
Сформулировать теорему о соотношениях сторон и углов треугольника можно так: в треугольнике напротив большего угла лежит большая сторона. Однако можно сформулировать обратную ей: в треугольнике напротив большей стороны лежит больший угол.
В прямой теореме нам известны размеры углов, и из этого делается утверждение о размере сторон. А в обратной теореме известны размеры сторон, и делается вывод о размерах углов. Это значит, что при доказательстве прямой теоремы нам дано соотношение углов и требуется доказать соотношение сторон. При доказательстве обратной — дано соотношение сторон, требуется доказать соотношение углов.
Докажем прямую теорему. Пусть дано, что в ∆ABC угол A меньше угла B (∠A
Напротив ∠A лежит сторона BC, а напротив ∠B лежит сторона AC. Требуется доказать, что BC
Внутри ∠B от стороны AB отложим угол, равный ∠A. Понятно, что этот угол будет меньше, чем ∠B треугольника ABC, так как по условию ∠A
Поскольку ∠A = ∠ABD, то ∆ABD равнобедренный. У него сторона AD равна стороне BD.
Сторона AC складывается из двух отрезков — AD и CD: AC = AD + CD. Но так как AD = BD мы можем записать, что AC = BD + CD.
Теперь рассмотрим ∆BCD. В нем BD и CD — это две стороны. Третья сторона — это BC. Как известно из теоремы о неравенстве треугольника, любая его сторона меньше суммы двух других. То есть BC
Значит BC
scienceland.info
| 1. |
Отношение сторон в прямоугольном треугольнике
Сложность: лёгкое |
|
| 2. |
Отношение сторон в прямоугольном треугольнике, теорема Пифагора
Сложность: лёгкое |
|
| 3. |
Синус или косинус
Сложность: лёгкое |
|
| 4. |
Тангенс, синус или косинус
Сложность: лёгкое |
|
| 5. |
Тангенс острого угла прямоугольного треугольника
Сложность: лёгкое |
|
| 6. |
Катет прямоугольного треугольника, свойство прямоугольного треугольника
Сложность: лёгкое |
|
| 7. |
Диагональ и сторона прямоугольника
Сложность: лёгкое |
|
| 8. |
Высота трапеции
Сложность: лёгкое |
|
| 9. |
Синус, косинус и тангенс острого угла, гипотенуза прямоугольного треугольника
Сложность: среднее |
|
| 10. |
Гипотенуза и катет прямоугольного треугольника
Сложность: среднее |
|
| 11. |
Площадь параллелограмма и треугольника, дан острый угол
Сложность: среднее |
|
| 12. |
Свойства прямоугольных треугольников, имеющих угол в 30 или 45 градусов.
Сложность: среднее |
|
| 13. |
Синус, косинус или тангенс, площадь прямоугольного треугольника
Сложность: среднее |
|
| 14. |
Катет прямоугольного треугольника, дан тангенс острого угла
Сложность: лёгкое |
|
| 15. |
Синус и косинус острого угла, гипотенуза прямоугольного треугольника
Сложность: лёгкое |
|
| 16. |
Катет прямоугольного треугольника, использование синуса или косинуса
Сложность: лёгкое |
|
| 17. |
Прямоугольный треугольник, тригонометрия
Сложность: лёгкое |
|
| 18. |
Сторона и площадь квадрата, дана его диагональ
Сложность: среднее |
|
| 19. |
Сторона равностороннего треугольника
Сложность: среднее |
|
| 20. |
Стороны и площадь прямоугольника
Сложность: среднее |
|
| 21. |
Площадь равнобедренной трапеции
Сложность: среднее |
|
| 22. |
Диагональ и сторона прямоугольника
Сложность: среднее |
|
| 23. |
Сторона и площадь квадрата, дана его диагональ
Сложность: среднее |
|
| 24. |
Стороны и площадь прямоугольника
Сложность: среднее |
|
| 25. |
Диагональ прямоугольной трапеции
Сложность: сложное |
www.yaklass.ru
