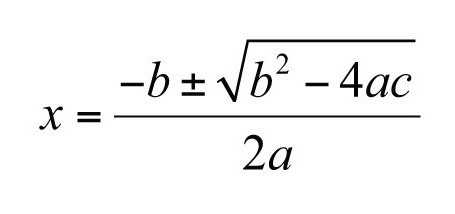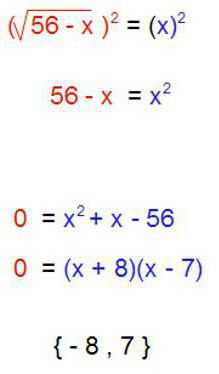Как найти корень квадратного уравнения – «Как вычислить корни квадратного уравнения?» – Яндекс.Знатоки

формула квадратного уравнения. как найти корни через дискриминант?

квадратное уравнение имеет вид: ax^2+bx+c=0, где a, b, c — произвольные числа и a не = 0. Тогда (если b — нечетное число) дискриминант вычисляется по формуле D = (-b)^2 — 4ac и корни при неотрицательном дискриминанте вычисляются по формуле x1,2 = (-b + или — корень из D)/(2a). Если же b — четное число, то вычисляют D1 = (-b/2)^2 — ac, и при неотрицательном D1 корни квадратного уравнения вычисляются по формуле x1,2 = ((-b/2) + или — корень из D1)/a. D1 еще называют (обозначают) D/4. Особой роли не играет. Обозначения равнознычны и определяются предпочтениями учителя.

Дискриминант = b^2 — 4ac x1,2 = (-b -+ sqrt Дискриминант ) / 2

Найти действительные корни уравнения `ax^2+bx+c=0` с помощью дискриминанта. Разложить многочлен вида `ax^2+bx+c` на множители

есди а=0 тогда x1*x2=-b x1*x2=c

Andrei Chetrean:это не дискриминант, это теорема Виета

touch.otvet.mail.ru

линейного, квадратного, кубического? :: SYL.ru

Уравнения в математике так же важны, как глаголы в русском языке. Без умения находить корень уравнения сложно утверждать, что ученик усвоил курс алгебры. К тому же для каждого их вида существуют свои особенные пути решения.

Что это такое?

Уравнение – это два произвольных выражения, содержащих переменные величины, между которыми поставлен знак равенства. Причем количество неизвестных величин может быть произвольным. Минимальное количество – одна.

Решить его – это значит узнать, есть ли корень уравнения. То есть число, которое превращает его в верное равенство. Если его нет, то ответом является утверждение, что «корней нет». Но может быть и противоположное, когда ответом является множество чисел.

Какие виды уравнений существуют?

Линейное. Оно содержит переменную, степень которой равна единице.

• Квадратное. Переменная стоит со степенью 2, или преобразования приводят к появлению такой степени.
• Уравнение высшей степени.
• Дробно-рациональное. Когда переменная величина оказывается в знаменателе дроби.
• С модулем.
• Иррациональное. То есть такое, которое содержит алгебраический корень.

Как решается линейное уравнение?

Оно является основным. К такому виду стремятся привести все остальные. Так как у него найти корень уравнения достаточно просто.

• Сначала нужно выполнить возможные преобразования, то есть раскрыть скобки и привести подобные слагаемые.
• Перенести все одночлены с переменной величиной в левую часть равенства, оставив свободные члены в правой.
• Привести подобные члены в каждой части решаемого уравнения.
• В получившемся равенстве в левой его половине будет стоять произведение коэффициента и переменной, а в правой – число.
• Осталось найти корень уравнения, разделив число справа, на коэффициент перед неизвестной.

Как найти корни квадратного уравнения?

Сначала его нужно привести к стандартному виду, то есть раскрыть все скобки, привести подобные слагаемые и перенести все одночлены в левую часть. В правой части равенства должен остаться только ноль.

• Воспользуйтесь формулой для дискриминанта. Возведите в квадрат коэффициент перед неизвестной со степенью «1». Перемножьте свободный одночлен и число перед переменной в квадрате с числом 4. Из полученного квадрата вычтите произведение.
• Оцените значение дискриминанта. Он отрицательный – решение закончено, так как у него корней нет. Равен нулю – ответом будет одно число. Положительный – два значения у переменной.

• 

  Найдите два корня уравнения по формуле, в которой квадратный корень из дискриминанта нужно вычесть или сложить с отрицательным коэффициентом при переменной в первой степени. Потом разделить на удвоенный коэффициент, стоящий перед квадратом неизвестной. (В случае равенства дискриминанта нулю прибавлять или вычитать нужно будет ноль, поэтому два корня совпадут.)

Как решить кубическое уравнение?

Сначала найдите корень уравнения x. Он определяется методом подбора из чисел, которые являются делителями свободного члена. Этот способ удобно рассмотреть на конкретном примере. Пусть уравнение имеет вид: х³ — 3х² — 4х + 12 = 0.

Его свободный член равен 12. Тогда делителями, которые требуется проверить, будут положительные и отрицательные числа: 1, 2, 3, 4, 6 и 12. Перебор можно закончить уже на числе 2. Оно дает верное равенство в уравнении. То есть его левая часть оказывается равной нулю. Значит число 2 – это первый корень кубического уравнения.

Теперь необходимо разделить исходное уравнение на разность переменной и первого корня. В конкретном примере это (х — 2). Несложное преобразование приводит числитель к такому разложению на множители: (х — 2)(х + 2)(х — 3). Одинаковые множители числителя и знаменателя сокращаются, а оставшиеся две скобки при раскрытии дают простое квадратное уравнение: х² — х — 6 = 0.

Здесь найдите два корня уравнения по принципу, описанному в предыдущем разделе. Ими оказываются числа: 3 и -2.

Итого, у конкретного кубического уравнения получилось три корня: 2, -2 и 3.

Здесь предложен метод исключения неизвестных. Он заключается в том, чтобы выразить одну неизвестную через другую в одном уравнении и подставить это выражение в другое. Причем решением системы из двух уравнений с двумя неизвестными всегда является пара переменных величин.

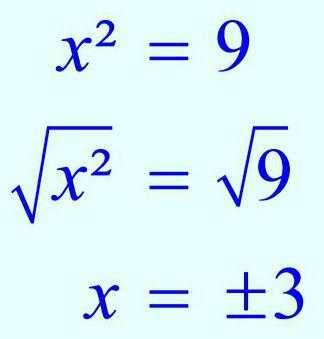
Если в них переменные обозначены буквами х₁ и х₂, то можно из первого равенства вывести, к примеру, х₂. Потом оно подставляется во второе. Проводится необходимое преобразование: раскрытие скобок и приведение подобных членов. Получается простое линейное уравнение, корень которого вычислить легко.

Теперь возвратитесь к первому уравнению и найдите корень уравнения x₂, используя получившееся равенство. Эти два числа являются ответом.

Простой совет

Для того чтобы быть уверенным в полученном ответе, рекомендуется всегда делать проверку. Ее не обязательно записывать.

Если решается одно уравнение, то каждый из его корней нужно подставить в исходное равенство и получить одинаковые числа в обеих его частях. Все сошлось – решение верное.

При работе с системой корни необходимо подставлять в каждое решение и выполнять все возможные действия. Получается верное равенство? Значит решение правильное.

www.syl.ru

корни приведенного квадратного уравнения по теореме Виета

Записи с меткой «корни приведенного квадратного уравнения по теореме Виета»

Часто требуется найти сумму квадратов  (x₁²+x₂²)  или сумму кубов (x₁³+x₂³) корней квадратного уравнения, реже — сумму обратных значений квадратов корней или сумму арифметических квадратных корней из корней квадратного уравнения:

Помочь в этом может теорема Виета:

Сумма корней приведенного квадратного уравнения x²+px+q=0 равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:

x₁+x₂=-p;  x₁∙x₂=q.

Выразим через p и q:

1) сумму квадратов корней уравнения x²+px+q=0;

2) сумму кубов корней уравнения x²+px+q=0.

Решение.

1) Выражение x₁²+x₂²  получится, если взвести в квадрат обе части равенства x₁+x₂=-p;

(x₁+x₂)²=(-p)²;  раскрываем скобки: x₁²+2x₁x₂+ x₂²=p²;  выражаем искомую сумму: x₁²+x₂²=p²-2x₁x₂=p²-2q. Мы получили полезное равенство: 

x₁²+x₂²=p²-2q.

2) Выражение x₁³+x₂³ представим по формуле суммы кубов в виде:

(x₁³+x₂³)=(x₁+x₂)(x₁²-x₁x₂+x₂²)=-p·(p²-2q-q)=-p·(p²-3q).

Еще одно полезное равенство: x₁³+x₂³=-p·(p²-3q).

Примеры.

3) x²-3x-4=0. Не решая уравнение, вычислите значение выражения  x₁²+x₂² .

Решение.

По теореме Виета сумма корней этого приведенного квадратного уравнения

x₁+x₂=-p=3, а произведение 

x₁∙x₂=q=-4. Применим полученное нами (в примере 1) равенство:

x₁²+x₂²=p²-2q. У нас -p=x₁+x₂=3 → p²=3²=9; q=x₁x₂=-4. Тогда x₁²+x₂²=9-2·(-4)=9+8=17.

Ответ: x₁²+x₂²=17.

4) x²-2x-4=0. Вычислить: x₁³+x₂³.

Решение.

По теореме Виета сумма корней этого приведенного квадратного уравнения x₁+x₂=-p=2, а произведение x₁∙x₂=q=-4. Применим полученное нами (

в примере 2) равенство: x₁³+x₂³=-p·(p²-3q)=2·(2²-3·(-4))=2·(4+12)=2·16=32.

Ответ:  x₁³+x₂³=32.

Вопрос: а если нам дано не приведенное квадратное уравнение? Ответ: его всегда можно «привести», разделив почленно на первый коэффициент.

5) 2x²-5x-7=0. Не решая, вычислить: x₁²+x₂².

Решение. Нам дано полное квадратное уравнение. Разделим обе части равенства на 2 (первый коэффициент) и получим приведенное квадратное уравнение: x²-2,5x-3,5=0.

По теореме Виета сумма корней равна 2,5; произведение корней равно -3,5.

Решаем так же, как пример 3), используя равенство: 

x₁²+x₂²=p²-2q.

x₁²+x₂²=p²-2q=2,5²-2∙(-3,5)=6,25+7=13,25.

Ответ: x₁²+x₂²=13,25.

6) x²-5x-2=0. Найти:

Преобразуем это равенство и, заменив по теореме Виета сумму корней через -p, а произведение корней через q, получим еще одну полезную формулу. При выводе формулы использовали равенство 1): x₁²+x₂²=p²-2q.

В нашем примере  x₁+x₂=-p=5; x₁∙x₂=q=-2. Подставляем эти значения  в полученную формулу:

7) x²-13x+36=0. Найти:

Преобразуем эту сумму и получим формулу, по которой можно будет находить сумму арифметических квадратных корней из корней квадратного уравнения.

У нас  x₁+x₂=-p=13; x₁∙x₂=q=36. Подставляем эти значения в выведенную формулу:

Совет: всегда проверяйте возможность нахождения корней квадратного уравнения по подходящему способу, ведь 4 рассмотренные полезные формулы позволяют быстро выполнить задание, прежде всего, в тех случаях, когда дискриминант — «неудобное» число. Во всех простых случаях находите корни и оперируйте ими. Например, в последнем примере подберем корни по теореме Виета: сумма корней должна быть равна 13, а произведение корней 36. Что это за числа? Конечно, 4 и 9. А теперь считайте сумму квадратных корней из этих чисел: 2+3=5. Вот так то!

 

I. Теорема Виета для приведенного квадратного уравнения.

Сумма корней приведенного квадратного уравнения x²+px+q=0 равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:

x₁+x₂=-p;  x₁∙x₂=q.

 Найти корни приведенного квадратного уравнения, используя теорему Виета.

Пример 1) x²-x-30=0. Это приведенное квадратное уравнение ( x²+px+q=0), второй коэффициент  p=-1, а свободный член q=-30. Сначала убедимся, что данное уравнение имеет корни, и что корни (если они есть) будут выражаться целыми числами. Для этого достаточно, чтобы дискриминант был полным квадратом целого числа.

Находим дискриминант D=b²

— 4ac=(-1)²-4∙1∙(-30)=1+120=121=11².

Теперь по теореме Виета сумма корней должна быть равна второму коэффициенту, взятому с противоположным знаком, т.е. (-p), а произведение равно свободному члену, т.е. (q). Тогда:

x₁+x₂=1; x₁∙x₂=-30. Нам надо подобрать такие два числа, чтобы их произведение было равно -30, а сумма – единице. Это числа -5 и 6. Ответ: -5; 6.

Пример 2) x²+6x+8=0. Имеем приведенное квадратное уравнение со вторым коэффициентом р=6 и свободным членом q=8. Убедимся, что есть целочисленные корни. Найдем дискриминант D₁, так как второй коэффициент – четное число. D₁=3²-1∙8=9-8=1=1². Дискриминант D

1 является полным квадратом числа 1, значит, корни данного уравнения являются целыми числами. Подберем корни по теореме Виета: сумма корней равна –р=-6, а произведение корней равно q=8. Это числа -4 и -2.

На самом деле: -4-2=-6=-р; -4∙(-2)=8=q. Ответ: -4; -2.

Пример 3) x²+2x-4=0. В этом приведенном квадратном уравнении второй коэффициент р=2, а свободный член q=-4. Найдем дискриминант D₁, так как второй коэффициент – четное число. D₁=1²-1∙(-4)=1+4=5. Дискриминант не является полным квадратом числа, поэтому, делаем вывод: корни данного уравнения не являются целыми числами и найти их по теореме Виета нельзя. Значит, решим данное уравнение, как обычно, по формулам (в данном случае по формулам для частного случая с четным вторым коэффициентом). Получаем:

Пример 4). Составьте квадратное уравнение по его корням, если x₁=-7, x₂=4.

Решение. Искомое уравнение запишется в виде: x²+px+q=0, причем, на основании теоремы Виета –p=x₁+x₂=-7+4=-3 → p=3; q=x₁∙x₂=-7∙4=-28. Тогда уравнение примет вид: x²+3x-28=0.

Пример 5). Составьте квадратное уравнение по его корням, если:

II. Теорема Виета для полного квадратного уравнения ax²+bx+c=0.

Сумма корней равна минус b, деленному на а, произведение корней равно с, деленному на а:

x₁+x₂=-b/a;  x₁∙x₂=c/a.

Пример 6). Найти сумму корней квадратного уравнения 2x²-7x-11=0.

Решение.

Убеждаемся, что данное уравнение будет иметь корни. Для этого достаточно составить выражение для дискриминанта, и, не вычисляя его, просто убедиться, что дискриминант больше нуля. D=7²-4∙2∙(-11)>0. А теперь воспользуемся теоремой Виета для полных квадратных уравнений.

x₁+x₂=-b:a=- (-7):2=3,5.

Пример 7). Найдите произведение корней квадратного уравнения 3x²+8x-21=0.

Решение.

Найдем дискриминант D₁, так как второй коэффициент (8) является четным числом. D₁=4²-3∙(-21)=16+63=79>0. Квадратное уравнение имеет 2 корня, по теореме Виета произведение корней x₁∙x₂=c:a=-21:3=-7.     

www.mathematics-repetition.com

Как найти корень уравнения?

Одним из основных разделов математики является раздел, посвященный решению уравнений и нахождению корня уравнений.

Перед тем как найти корень уравнения, нужно сначала разобраться, что это такое.

Корень уравнения — это значение неизвестной величины в уравнении, обозначаемой латинскими буквами (чаще — x, y, но могут быть и другие буквы). Об этом говорилось в нашей статье — Что такое корень уравнения.

Рассмотрим, как найти все корни, на разных видах уравнений и конкретных примерах.

Уравнение вида ax+b=0

Это линейное уравнение с одной переменной, где a и b — числа, x-корень уравнения.

Количество корней уравнения зависит от значений a и b:

1. Если а=b=0, то уравнение имеет бесконечное количество корней.
2. Если а=0, b не равно 0, то уравнение не имеет корней.
3. Если а не равно 0, то корень находим по формуле: х= — (b/а)

Пример:

• 5х + 2 = 0
• а=5, b = 2
• х= — (2/5)
• х= -0,4

Ответ: корень уравнения равен 0,4

Уравнение вида ax²+bx+c=0.

Это квадратное уравнение. Есть несколько способов нахождения корней в квадратном уравнении. Мы рассмотрим общий, который подходит для решения при любых значениях а, b и с.

Для начала нужно найти значение дискриминанта (D) этого уравнения.

Для этого существует формула:

В зависимости от того, какой поучился дискриминант, есть 3 варианта дальнейшего решения:

1. Если D >0, то корней 2. И они вычисляются по формулам:
   • x₁= (-b + √ D) / 2а.
   • х₂= (-b — √ D) / 2a
2. Если D =0, то корень один — его можно найти по формуле: х= — (b/2а)
3. Если D<0, то уравнение не имеет корней.

Пример:

Здесь а=1, b=3, с= -4

• D= 3² — (4*1*(-4))
• D= 9- (-16)
• D=9+16
• D=25

D>0, значит в уравнении будет 2 корня.

Подставляем все значения в нашу формулу:

• х₁ = (-3 +5)/2*1
• х₁=2/2
• х₁=1
• х₂= (-3-5)/ 2*1
• х₂= (-8)/2
• х₂= -4

Ответ: Корни уравнения равны 1 и -4.

Уравнение вида ax³+bx²+cx+d=0

Это кубическое уравнение.

Есть специальные формулы математика Кардано, по которым можно решить такое уравнение, но они очень сложные. Мы пойдем другим, более понятным путем.

Кубические уравнения всегда имеют хотя бы один корень, и его значение обычно целое число от -3 до 3. То есть мы в имеющееся уравнение будем по очереди подставлять вместо х числа: -3, -2, -1, 0, 1, 2 и 3. Это будет Х_1.

Это гораздо проще и быстрее, чем кажется, и уж точно проще, чем по формулам Кардано.

После того как мы найдем х₁ , переходим к поиску Х₂ и Х_3.

Для этого поделим наше уравнение на (х-х₁) — это можно сделать путем вынесения за скобки. У нас должно остаться квадратное уравнение, которое мы решали в этой статье чуть выше.

Пример:

• х³ — 3х² — 13х + 15 = 0

Методом подбора мы выясняем, что Х₁=1, 

elhow.ru

Внеклассный урок — Формулы корней квадратного уравнения. Дискриминант

 Формулы корней квадратного уравнения. Дискриминант.

  

Формула №1:

         —b ± √D
x =  ————,  где D = b² – 4ac.
             2a

Латинской буквой D обозначают дискриминант.

Дискриминант — это выражение, от которого зависит число корней данного уравнения.

Если D < 0, то уравнение не имеет корней.

Если D = 0, то уравнение имеет один корень.

Если D > 0, то уравнение имеет два корня.

Пример. Решим уравнение 12x² + 7x + 1 = 0.

Сначала вычислим дискриминант.

Мы видим, что а = 12, b = 7, c = 1.

Итак:

D = b² – 4ac = 7² – 4 · 12 · 1 = 49 – 48 = 1.

D > 0. Значит, уравнение имеет корни (причем два корня), а значит, можно вычислять дальше.

Чтобы найти корни, применим формулу корней квадратного уравнения:

         —b ± √D      -7 ± √1         -7 ± 1
x =  ———— = ———— = ————
             2a                24                 24

Находим оба значения x:

        -7 + 1        -6      -1          1
x₁ = ——— = —— = — = – —
           24           24       4          4

 

         -7 – 1       -8       -1         1
x₂ = ——— = —— = — = – — .
           24           24       3          3

 

                        1                   1
Ответ: x₁ = – —,    x₂ = – —
                        4                   3

 

Формула №2.

Из формулы №1 можно получить другую формулу, которой удобно пользоваться в случаях, когда второй коэффициент – четное число. В этом случае раскладываем его на множители, один из которых – множитель 2. То есть второй коэффициент представляем в виде 2k, где k – это половина изначально заданного числа. Тогда удобно пользоваться формулой:

      —k ± √D₁
x = ————,   где D₁ = k² – ac
             a

Пример. Решим уравнение 5x² – 16x + 3 = 0.

Записываем -16x в виде 2 · (-8x). Тогда k = -8,  a = 5,  c = 3. Мы уже можем найти дискриминант D₁:

D₁ = k² – ac = (-8)² – 5 · 3 = 64 – 15 = 49.

Теперь находим оба значения x:

      —k ± √D₁       — (-8) ± √49      8 ± 7
x = ———— =  ————— = ———
             a                     5                  5

Отсюда:

          8 + 7       15
x₁ = ——— =  — = 3
            5            5

 

         8 – 7         1
x₂ = ——— =  — = 0,2
             5           5 

 

Ответ: x₁ = 3; x₂ = 0,2.

 

При решении квадратного уравнения по данным формулам целесообразно поступать следующим образом:

1) вычислить дискриминант и сравнить его с нулем;

2) если дискриминант положителен или равен нулю, то воспользоваться формулой корней; если дискриминант отрицателен, то записать, что корней нет.

 

raal100.narod.ru

Презентация по математике «Как найти корни квадратного уравнения?»

Презентация на тему: Как найти корни квадратного уравнения?

Скачать эту презентацию

Скачать эту презентацию

№ слайда 1 Описание слайда:

Как найти корни квадратного уравнения? Авторы: учащиеся 8 классаРуководитель: Родина Алевтина КарловнаМОУ «Блюментальская основная общеобразовательная школа»

№ слайда 2 Описание слайда:

Привет, восьмиклассник! Твоему вниманию предоставляется проект, который поможет тебе научиться находить корни, квадратных уравнений.Здесь ты найдёшь и общий алгоритм решения квадратных уравнений, и теоретические сведения и различные интересные задачи и многое другое.Так что – дерзай! Сядь поудобнее, засучи рукава и …ВПЕРЁД!

№ слайда 3 Описание слайда:

Цель проекта Цель данного проекта – привлечь внимание учащихся к исследовательской деятельности, вызвать интерес к изучению математики, а именно к решению квадратных уравнений. Данный проект предназначен для развития творческих способностей учащихся: предполагает развитие математического и логического мышления при решении поставленных проблем, нацеливает на самостоятельную исследовательскую деятельность, формирует навыки решения квадратных уравнений, активизирует учащихся к работе в предполагаемых проектах и созданию собственных творческих работ. Основной вопрос, на который должны ответить участники проекта: Как найти корни квадратного уравнения?

№ слайда 4 Описание слайда:

Дидактические цели проекта Совершенствование прикладных навыков работы с персональным компьютером в аспекте алгебраических исследований.Теоретическое и практическое владение основами решения квадратных уравнений.Дальнейшее формирование навыков самостоятельной работы в познавательной деятельности.

№ слайда 5 Описание слайда:

Методические цели проекта Научить школьников проводить исследования в области математики.Научить учащихся понимать структуру формулы и алгоритм вычисления корней.Научить школьников оформлять информацию, собранную им самим.

№ слайда 6 Описание слайда:

Этапы и ход работы 1 этап. Класс разбивается на группы 5-6 человек.2 этап. Перед группой ставиться проблемный вопрос.3 этап. Распределение работ внутри группы.4 этап. Каждая группа должна выполнить:               поиск материала;               анализ материала;    оформить презентацию и буклет.

№ слайда 7 Описание слайда:

Этапы и ход работы Над проектом мы будем работать в течении 3-х недель. За это время мы… Должны решить, что будем делать и зачем.Как разделиться—кто и с кем.Теорию отлично изучить.Задачи подобрать.И алгоритмы получше осветить.И вам, друзьям об этом рассказать!

№ слайда 8 Описание слайда:

Подробнее о проекте Проект «Как найти корни квадратного уравнения?» посвящен изучению темы «Квадратные уравнения» В рамках проекта школьники знакомятся с учебным материалом по данной теме. После чего разбиваются на группы. Перед каждой группой ставится проблемный вопрос. Группа проводит поиск и анализ информации с целью проверки собственных гипотез по сформировавшимся вопросам. По итогам проекта каждая группа подготавливает отчет в виде мультимедийных презентаций, буклетов. В рамках проекта предусматривается выступление перед классом по разрабатываемой теме.

№ слайда 9 Описание слайда:

Темы исследования учащихся 1. «Квадратное уравнение и его корни»2. «Неполные квадратные уравнения»3. «Метод выделения полного квадрата»4. «Решение квадратных уравнений»5. «Приведённое квадратное уравнение. Теорема Виета.»

№ слайда 10 Описание слайда:

Немного истории Уравнение 2 – й степени умели решать ещё в Древнем Вавилоне во втором тысячелетии до н.э. Математики Древней Греции решали квадратные уравнения геометрически; например, Евклид – при помощи деления отрезка в среднем и крайнем отношениях. Задачи, приводящие к квадратным уравнениям, рассматриваются во многих древних математических рукописях и трактатах. Формула корней квадратного уравнения «переоткрывалась» неоднократно. Один из первых дошедших до наших дней выводов этой формулы принадлежит индийскому математику Брахмагупте (около 598 г.). Средне –азиатский учёный аль — Хорезми ( 19 век) в трактате «Китаб аль — джебр валь — мукабала» получил эту формулу методом выделения полного квадрата

№ слайда 11 Описание слайда:

Немного истории Франсуа Виет (1540 – 1603)- французский математик, ввёл систему алгебраических символов, разработал основы элементарной алгебры. Он был одним из первых , кто числа стал обозначать буквами, что существенно развило теорию уравнений.

№ слайда 12 Описание слайда:

Неполные квадратные уравнения Квадратное уравнение а х2 + в х + с = 0 называют неполным, если хотя бы один из коэффициентов в или с равен 0 . Таким образом, неполное квадратное уравнение есть уравнение одного из следующих видов: а х2 = 0, а х 2 + с = 0, c ≠ 0 a x ² + b x = 0, b ≠ 0.

№ слайда 13 Описание слайда:

Решение неполных квадратных уравнений Решим уравнение 5х2 = 0. Разделив обе части этого уравнения на 5, получим: х2 = 0, откуда х = 0. Ответ : 0Решим уравнение – 3 х2 + 5 х = 0.Разложим левую часть уравнения на множители, получим: х( — 3 х + 5 ) = 0, откуда х1 = 0, х2 = 5/3.Ответ : 0, 5/3.

№ слайда 14 Описание слайда:

Решение неполных квадратных уравнений Решить уравнение 2х2 + 7 = 0.Уравнение можно записать так: х2 = — 7/2.Это уравнение действительных корней не имеет, так как х2 ≥ 0 для любого действительного числа х.Решить уравнение 3х2 – 27 = 0.Разделим обе части уравнения на 3: х2 – 9 = 0.Это уравнение можно записать так: х2 = 9, откуда х 1,2 = ± 3. Проверь себя! Решите уравнения.х2 = 0;9 х2 = 81;4х2 – 64 = 0;9х2 + 1 = 0;3 х2 = 1/3;(х2 – 1)/3 = 5

№ слайда 15 Описание слайда:

Квадратное уравнение и его корни Квадратным называюталгебраическое уравнение 2-й степени, т.е. уравнение вида а х2 + в х + с = 0, где а ≠ 0 .Выражение D = b2 – 4ac называют дискриминантом трёхчлена а х2 + в х + с Уравнение а х2 + в х + с = 0, где а ≠ 0 . имеет два корня:при этом если D > 0, то корнидействительные и различные, при D = 0 корни совпадают (говорят, что уравнение имеет корень кратности два), при D < 0 уравнение не имеет корней.

№ слайда 16 Описание слайда:

Метод выделения полного квадрата Для решения квадратных уравнений применяется метод выделения полного квадрата. Поясним этот метод на примерах.Задача1.Решить квадратное уравнение х2 + 2х — 3 = 0Преобразуем это уравнение так:х2 + 2х = 3,х2 +2х + 1 = 3 + 1,(х + 1 )2 = 4.Следовательнох + 1 = 2 или х + 1 = — 2,откудах1 = 1, х2 = — 3.Ответ : 1, — 3.

№ слайда 17 Описание слайда:

Метод выделения полного квадрата Задача 2. Решить уравнение 4 х 2 – 8х + 3 = 04 х 2 – 8х = -3,(2х)2 – 2*2*2х = -3,(2х)2 – 2*2*2х + 4 = -3 + 4,( 2х – 2 )2 = 1,2х – 2 = 1 или 2х – 2 = -1,2х = 3 2х = 1Х1 = 3/2, х2 = ½Ответ: 3/2, ½.Задача 3. Решить уравнение х2 + 5х – 14 =0. х2 + 5х = 14 . Х2 + 2*5/2х + 25/4 = 14 + 25/4, (х + 5/2) 2 = 81/4, х + 5/2 =± 9/2. х1 = 9/2 – 5/2 = 2, х2 = — 9/2 – 5/2 = -7.Ответ: 2, — 7.

№ слайда 18 Описание слайда:

Решение квадратных уравнений Задача 1. Решить уравнение 6х2 +х – 2 = 0. Здесь а = 6, в = 1, с = -2 . По формуле находим: х 1, 2 = ( -1 ±7)/12, откуда х1 =( -1 + 7)/12 = ½, х2 = (-1 – 7)/12 = -2/3. Ответ: ½, -2/3

№ слайда 19 Описание слайда:

Решение квадратных уравнений Задача 2. Решить уравнение 4х2 – 4х +1 = 0.Здесь а = 4, в = -4, с = 1 . По формуле находим: х 1, 2 = ( 4 ±0)/8 = ½. Ответ: ½.

№ слайда 20 Описание слайда:

Решение квадратных уравнений Если b ² — 4 a c < 0, уравнение a x ² + b x + c = 0 не имеет действительных корней.Задача 3. Доказать, что уравнение x² — 4 x + 5 = 0 не имеет действительных корней. Здесь а = 1, b = — 4, с = 5, b² — 4ac = (-4)2 – 4*1*5 = — 4 < 0. Следовательно данное уравнение не имеет действительных корней

№ слайда 21 Описание слайда:

Приведённое квадратное уравнение Квадратное уравнение x ² + p x + q = 0 называется приведенным. В этом уравнении старший коэффициент равен единице.Например, уравнение x ² + 3 x — 4 = 0 является приведённым. Всякое квадратное уравнение а х ² + b x + c = 0 может быть приведено к виду x ² + p x + q = 0 делением обеих частей уравнения на a ≠ 0.Для приведённого квадратного уравнения формула корней приведенного квадратного уравнения Этой формулой удобно пользоваться когда p – чётное число. Например, решим уравнение x ² — 14 x — 15 = 0. По формуле находим: х 1,2 = 7 ± √ (49 + 15) = 7 ± 8 Х1 = 7 + 8 , х2 = 7 — 8 Х1 = 15, х2 = — 1 Ответ: 15, -1.Для приведённого квадратного уравнения справедлива следующая теорема

№ слайда 22 Описание слайда:

Теорема Виета Если х1, х2 – корни уравнения х2 + рх + g = 0то справедливы формулы х1+х2 = — р, х1х2 = g. т.е. сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

№ слайда 23 Описание слайда:

Теорема Виета Например уравнение х2 – 13 х + 30 = 0 имеет корни х1 = 10, х2 = 3; сумма его корней х1 + х2 = 13, а их произведение х1х2 = 30.Отметим, что теорема Виета справедлива и в случае, когда квадратное уравнение имеет два равных корня: х1 = х2 = — р/2.Например, уравнение х2 – 6х + 9 = 0 имеет равные корни: х1=х2 = 3; их сумма х1 + х2 = 6, произведение х1х2 = 9Задача1. Один из корней уравнения x ² + p x — 12 = 0 равен Х1 = 4. Найти коэффициент p и второй корень х2 , этого уравнения. По теореме Виета х1+х2 = — p , х1х2 = — 12, Так как Х1 = 4, то 4 х2 = — 12, откуда х2 = — 3, p = — ( х1 + х2) = -(4 – 3) = -1Ответ: 3, — 1.

№ слайда 24 Описание слайда:

Теорема Виета Задача 2. Составить приведённое квадратное уравнение корни которого х1= 3, х2 = 4. Так как х1=3, х2=4 – корни уравнения х2 + рх + g = 0, то по теореме Виета р = — (х 1 + х 2) = — 7, g = х1х2 = 12.Ответ: х2 – 7х +12 =0.Задача 3. Один из корней уравнения 3х2 + 8х – 4 = 0 положителен. Не решая уравнения, определить знак второго корня. Разделив обе части уравнения на 3, получим: х2 + (8/3)х – 4/3 = 0.По теореме Виета х1х2 = — 4/3<0. По условию х1>0, следовательно, х2 <0

№ слайда 25 Описание слайда:

Обратная теорема Виета При решении некоторых задач применяется следующая теорема. Обратная теореме Виета:Если число р, g, х1, х2 таковы, что х1+х2 = — р, х1х2 = g, то х1 и х2 – корни уравнения х2 + рх + g = 0Используя теорему, обратную теореме Виета, иногда можно подбором найти корни квадратного уравненияЗадача. Подбором найти корни уравнения х2 + 5х + 6 = 0. Здесь р = — 5, g = 6. Подберём два числа х1 и х2 так, чтобы х1+х2 = 5, х1х2 = 6, Заметим, что 6 = 2*3, а 2 + 3 = 5, по теореме, обратной теореме Виета, получаем, что х1 = 2, х2 = 3 – корни уравнения х2 + 5х + 6 = 0.

№ слайда 26 Описание слайда:

Участники проекта Группа теоретиков:учит основы теории решения квадратных уравненийвыступает на семинаре первыми! Группа практиков:Учит алгоритм решения квадратных уравнений выступает на семинаре вторыми!

№ слайда 27 Описание слайда:

Используемые ресурсы Учебник «Алгебра 8» Ш.А. Алимов. И др.«История математики в школе.» Г.И.Глейзер. 60-1-10.

ppt4web.ru