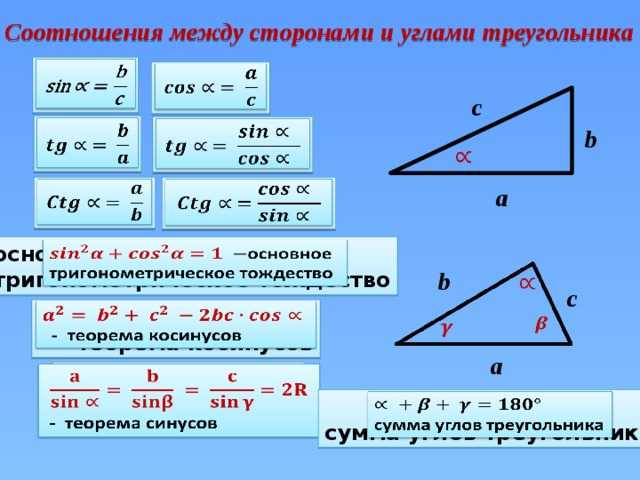
Соотношения Между Сторонами и Углами Треугольника
Главная » геометрия
Обновлено
Теорема о соотношениях между углами и сторонами
треугольника звучит так:
В треугольнике напротив большего угла лежит
большая сторона, и обратно, напротив большей
стороны лежит больший угол.
Доказательство теоремы
Эту теорему мы докажем, используя рисунок 1, где изображен
треугольник DFE.
1. Предположим, что в треугольнике DFE сторона FE < DF.
Докажем, что ∠E >∠D.
Отложим на стороне DF отрезок FP = FE.
В результате ∠1 = ∠2,
а сторона PF = FE, следовательно треугольник PFE — равнобедренный.
∠1 является частью ∠E, значит ∠1 < ∠С. ∠2 — внешний угол
треугольника PDE, поэтому∠2 > ∠D. Так, как ∠1 и ∠2 равны, а ∠1
является частью ∠E, ∠2 > ∠D, значит ∠E > ∠D.
2. Допустим, что в треугольнике DFE ∠E > ∠D. Докажем,
что сторона FD > FE.
Предположим, что это не так. Тогда сторона FD = FE, или сторона FD < FE.
В первом случае треугольник FDE — равнобедренный, значит∠E = ∠D.
Во втором же случае ∠D > ∠E — напротив большей стороны лежит больший угол.
Утверждение в первом и втором случае противоречит условию: ∠E > ∠D. Из этого
следует то, что наше предположение неверно, и, следовательно DF > FE, ∠E >∠D, ч.т.д.
Теорема доказана.
Следствия из доказанной теоремы
Из теоремы, которую мы сейчас доказали следует вот что:
- Гипотенуза в прямоугольном треугольнике больше катета,
так как катеты лежат напротив острых углов, а гипотенуза
лежит напротив прямого угла. - Если две стороны или два угла треугольника равны, то
треугольник равнобедренный, действительно, если в
треугольнике два угла равны, значит и стороны
напротив этих углов равны.
- В равнобедренном треугольнике при равных сторонах два
угла равны, а третий больший угол лежит
напротив большей стороны.
Соотношения между сторонами и углами треугольника
Теорема 1. Против большей стороны в треугольнике лежит и больший угол.
Пусть в ΔАВС сторона АВ больше стороны ВС. Докажем, что угол С, лежащий против большей стороны АВ, больше угла А, лежащего против меньшей стороны ВС (рис.).
Отложим на стороне АВ от точки В отрезок ВD, равный стороне ВС, и соединим отрезком , точки D и С.
Треугольник DВС равнобедренный. Угол ВDС равен углу ВСD, так как они лежат против равных сторон в треугольнике.
Угол ВDС — внешний угол треугольника АDС, поэтому он больше угла А.
Так как ∠ВСD = ∠ВDС, то и угол ВСD больше угла А: ∠ВСD > ∠A. Но угол ВСD составляет только часть всего угла С, поэтому угол С будет и подавно больше угла A.
Докажем теперь обратные теоремы.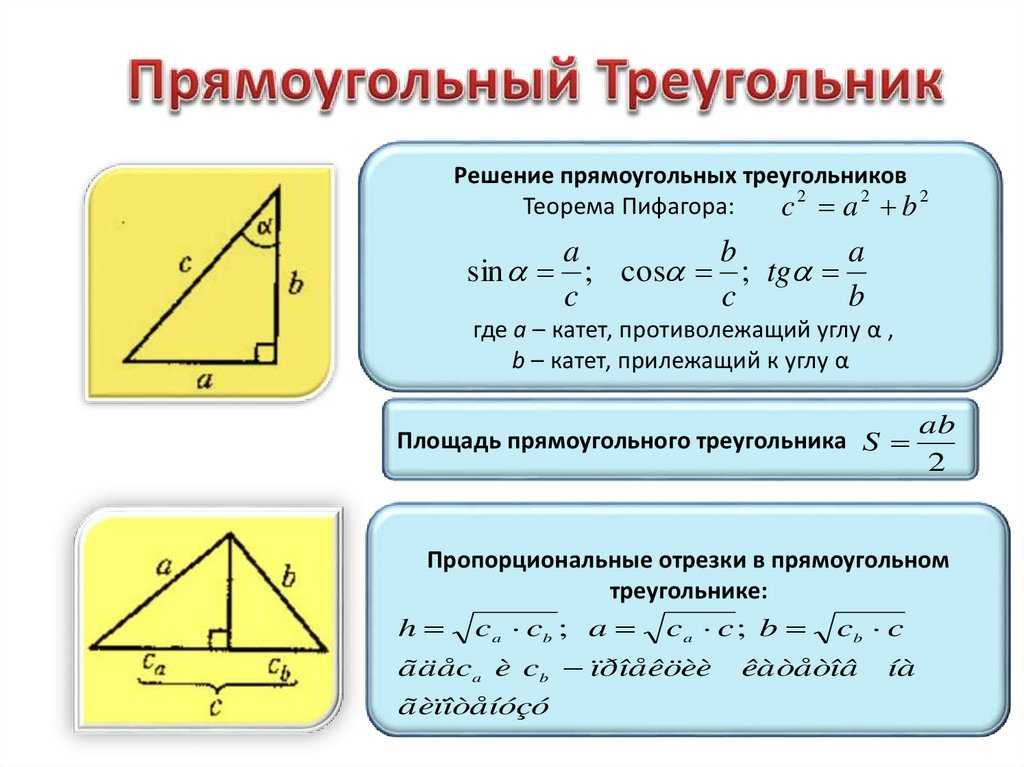
Теорема 2. Против равных углов в треугольнике лежат и равные стороны.
Пусть в Δ AВС ∠A = ∠С (рис.). Докажем, что AВ = ВС, т. е. треугольник АBС равнобедренный.
Между сторонами АВ и ВС может быть только одно из трёх следующих соотношений:
1) АВ > ВС;
2) АВ
3) АВ = ВС.
Если бы сторона AВ была больше ВС, то угол С был бы больше угла A, но это противоречит условию теоремы, следовательно, АВ не может быть больше ВС.
Точно так же АВ не может быть меньше ВС, так как в этом случае угол С был бы меньше угла A.
Следовательно, возможен только третий случай, т. е.
АВ = ВС
Итaк, мы доказали: против равных углов в треугольнике лежат и равные стороны.
Теорема 3. Против большего угла в треугольнике лежит большая сторона.
Пусть в треугольнике АВС (рис.) ∠ C >∠ B
Докажем, что АВ > АС.
Здесь также может быть одно из трёх следующих соотношений:
1) АВ = АС;
2) АВ
3) АВ > АС.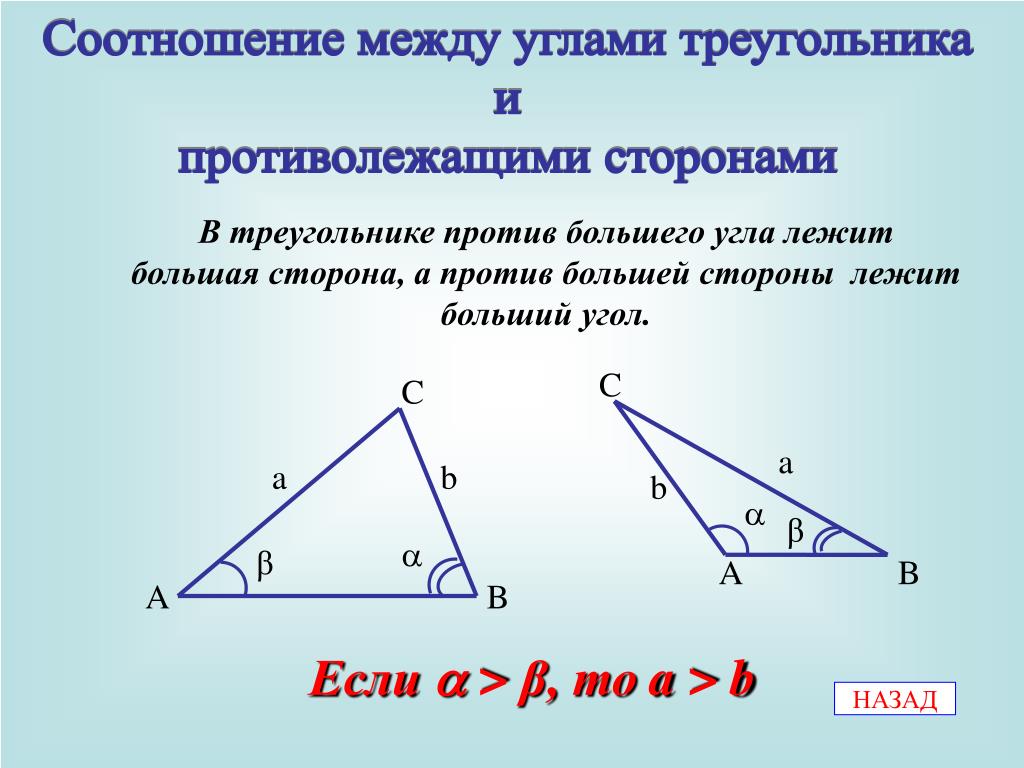
Если бы сторона АВ была равна стороне АС, то ∠ С был бы равен ∠ В. Но это противоречит условию теоремы. Значит, АВ не может равняться АС
Точно так же АВ не может быть меньше АС, так как в этом случае угол С был бы меньше угла B, что также противоречит данному условию.
Следовательно, возможен только один случай, а именно:
АВ > АС.
Мы доказали: против большего угла в треугольнике лежит и большая сторона.
Следствие. В прямоугольном треугольнике гипотенуза больше любого из его катетов.
Пусть дан прямоугольный треугольник ABC. Обозначим его стороны через а, b и с.
По определению тригонометрических функций:
a/c = sin ∠А; a/c = cos ∠В; b/c= sin ∠ В; b/c = cos ∠А.
Отсюда а = с sin ∠ А = с cos ∠В; b = c sin ∠B = с соs ∠A,
т.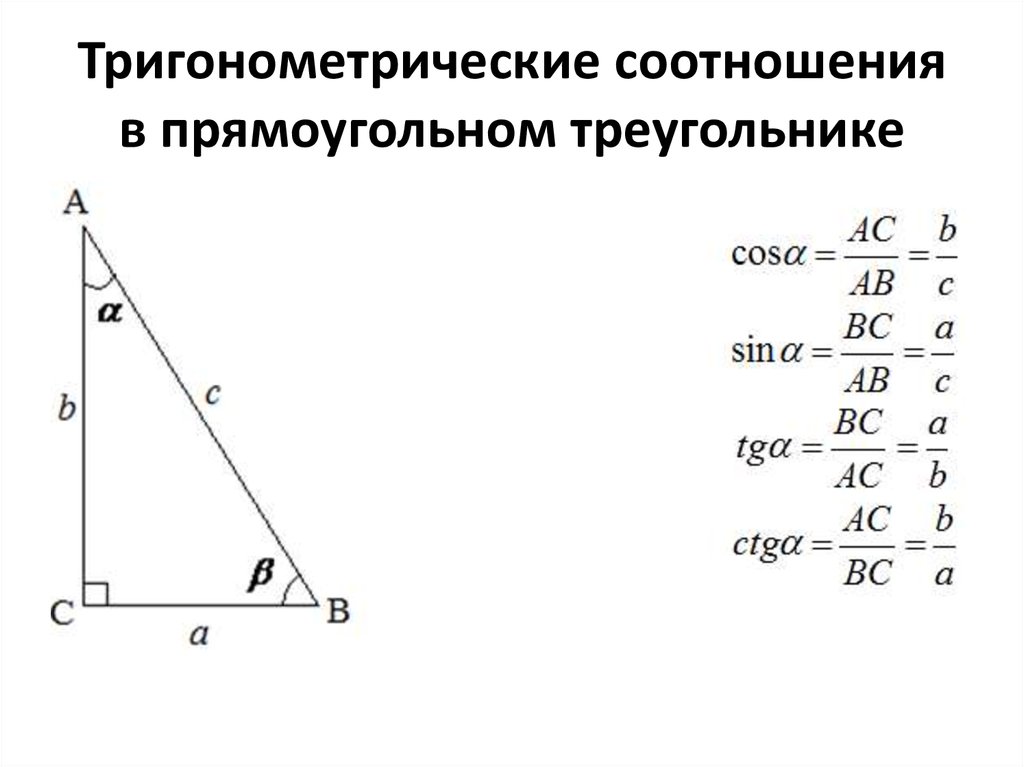
е. катет прямоугольного треугольника равен гипотенузе, умноженной на синус угла, противолежащего этому катету, или на косинус угла, прилежащего к нему.
Из того же прямоугольного треугольника имеем, что
a/b = tg ∠А , отсюда a = b tg ∠А;
b/a = ctg ∠А, откуда b = a ctg ∠А,
т.е. катет прямоугольного треугольника равен другому катету, умноженному на тангенс угла, противолежащего первому катету, или на котангенс угла, прилежащего к первому катету.
Отношения между сторонами и углами треугольника: типы
- Автор Гнанамбигай GS
- Последнее изменение 06-10-2022
Отношения между сторонами и углами треугольника: Это факт, что, как следует из названия, треугольник имеет три угла и три стороны. Математически треугольник определяется как любая замкнутая фигура, образованная тремя пересекающимися линиями.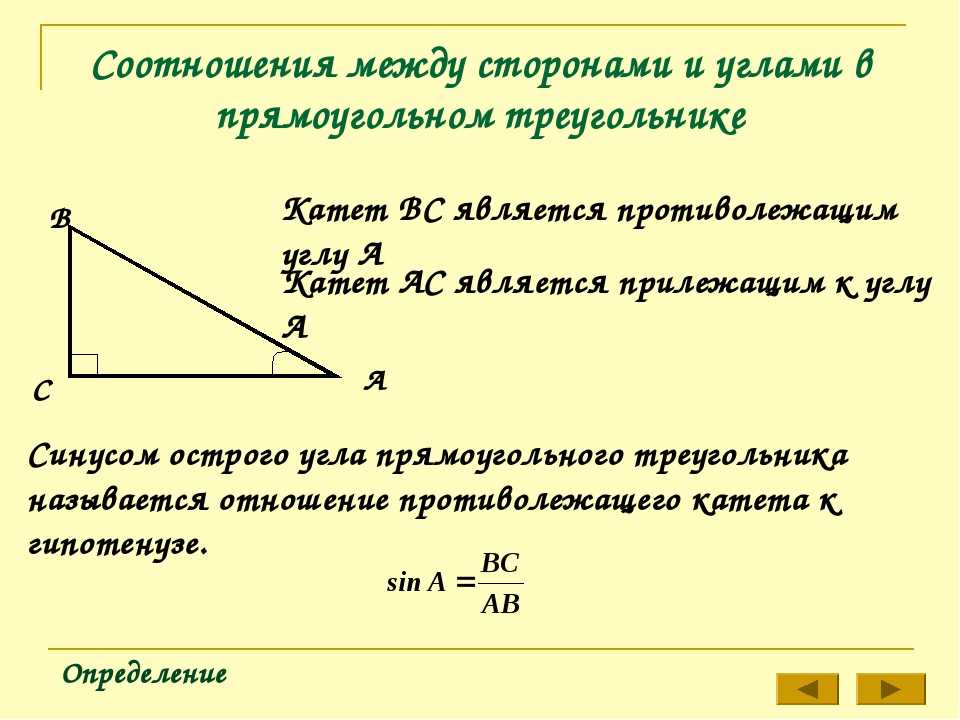
Хотя такие свойства треугольника, как стороны, углы, биссектрисы, конгруэнтность и подобие, используются чаще, как, по вашему мнению, стороны и углы в треугольнике связаны друг с другом? Как вы думаете, любые отрезки из трех прямых могут образовывать треугольник? В треугольнике меру сторон часто можно использовать для вычисления углов и наоборот.
В этой статье давайте узнаем, как связаны стороны и углы треугольников, и изучим теоремы, касающиеся этих отношений.
Отношения между сторонами треугольника
Теорема о неравенстве треугольника определяет отношение между сторонами треугольника. Теорема утверждает, что сумма длин двух сторон треугольника больше длины третьей стороны.
На показанном рисунке выполняются следующие неравенства.
\(а+b>с\)
\(b+c>a\)
\(c+a>b\)
Эта теорема также служит условием для проверки того, можно ли построить треугольники, используя заданные длины сторон. Другими словами, если и только если все эти три неравенства верны, заданные длины сторон образуют треугольник.
Типы углов в треугольнике
В любом треугольнике есть три стороны и два типа углов, а именно. внутренние углы и внешние углы, и они обозначены, как показано на рисунке ниже.
9{\rm{o}}}.\)Классификация треугольников
Существуют различные инструменты для определения сторон и углов в треугольниках. Их можно разделить на два типа:
1. Геометрическая связь между сторонами и углами
2. Тригонометрическая связь между сторонами и углами
Геометрическая связь между сторонами и внутренними углами
внутренние углы.
Теорема об отношении углов к сторонам утверждает, что в любом треугольнике: 92}\)
Тригонометрические соотношения прямоугольных треугольников
Для \(\theta ,\) острого угла в прямоугольном треугольнике тригонометрические функции определяются следующим образом.
\( \sin \theta = \frac{{{\rm{ напротив}}}}{{{\rm{гипотенуза}}}}\)
\(\cos \,\theta = \frac{{ {\rm{соседняя}}}}{{{\rm{гипотенуза}}}}\)
\(\tan \,\theta = \frac{{{\rm{напротив}}}}{{{\ rm{соседние}}}}\)
\( \cot \theta = \frac{{{\rm{соседние }}}}{{{\rm{противоположные }}}}\)
\( \sec \theta = \frac{{{\rm{ гипотенуза }}}}{{{\rm{ смежный }}}}\)
\({\rm{cosec}}\,\theta = \frac{{{\rm{гипотенуза}}}}{{{\rm{противоположный}}}}\)
Тригонометрические соотношения косоугольных треугольников Косоугольный треугольник — это любой треугольник, не являющийся прямоугольным.
.
Две формулы помогают нам решать такие косые треугольники.
1. Закон синусов
Этот закон, также называемый правилом синусов, гласит, что отношение длины стороны и угла, противоположного этой стороне, является постоянным для всех сторон и углов треугольника.
Задается следующим образом:
\(\frac{a}{{ \sin A}} = \frac{b}{{ \sin B}} = \frac{c}{{\sin C}}\ )
Доказательство: На рисунке h — высота. Для каждого треугольника мы знаем, что
\(\sin A = \frac{h}{b}\)
\(\sin B = \frac{h}{a}\)
Переставляя, мы получаем , \(h = a \sin B.\)
\( \Rightarrow \sin A = \frac{{a\sin B}}{b}\)
\(\frac{a}{{\sin A}} = \frac{b}{{ \sin B}}\)
Точно так же мы можем написать
\(\frac{b}{{ \sin B}} = \frac{c}{{ \sin C}}\)
Приравнивая, получаем,
\(\frac{a}{{ \ sin A}} = \frac{b}{{ \sin B}} = \frac{c}{{ \sin C}}\)
Обратите внимание, что для того, чтобы использовать закон синусов, вы должны знать либо два угла и длина стороны или две длины сторон и угол, противолежащий одному из них.
2. Закон косинусов
Закон косинусов используется, когда известны длины двух сторон и угла между ними или длины трех сторон. В нем говорится, что 9{\rm{o}}} = 0.\) Следовательно, третьего члена не будет.
Теорему Пифагора можно считать частным случаем закона косинусов.
3. Закон тангенсов
Закон тангенсов устанавливает соотношение между двумя сторонами треугольника и тангенсами суммы и разности противоположных углов. Он определяется как
\(\tan \frac{{B – C}}{2} = \frac{{b – c}}{{b + c}}\cot \frac{A}{2} \)
\(\tan \frac{{C – A}}{2} = \frac{{c – a}}{{c + a}}\cot \frac{B}{2}\)
\(\tan \frac{{A – B}}{2} = \frac{{a – b}}{{a + b}}\cot \frac{C}{2}\)
Доказательство: Используя закон синусов,
\(\frac{a}{{ \sin A}} = \frac{b}{{ \sin B}} = \frac{c}{{ \sin C} } = k(скажем)\)
\(\следовательно \frac{{b – c}}{{b + c}} = \frac{{k( \sin B – \sin C)}}{{k ( \sin B + \sin C)}}\)
\( = \frac{{2 \cos \frac{{B + C}}{2} \sin \frac{{B – C}}{2 }}}{{2 \sin \frac{{B + C}}{2} \cos \frac{{B – C}}{2}}}\)
\(\cot \frac{{B + C}}{2} \tan \frac{{B – C}}{2}\)
\( = \cot \left( {\frac{\pi }{2} – \frac{A}{2}} \right) \tan \frac{{B – C}}{2}\)
\( = \frac{{ \tan \frac{{B – C}}{2}}}{{ \cot \frac{A}{2}}}\)
\(\следовательно \tan \frac {{B – C}}{2} = \frac{{b – c}}{{b + c}} \cot \frac{A}{2}\)
Используя аналогичные рассуждения, мы можем получить другое тоже две формулы.
4. Правило проекции
Треугольники имеют \(6\) параметров. Формула проекции выражает сумму двух сторон через третью сторону.
Закон проектирования гласит, что в любом треугольнике cos B + b\cos A = c\)
Доказательство: Используя закон синусов,
\(\frac{a}{{ \sin A}} = \frac{b}{{ \sin B }} = \frac{c}{{ \sin C}} = k\,(скажем)\)
Переставляя, получаем,
\(a = k\sin A\)
\(b = k \sin B\)
\(c = k\sin C\)
Доказать \(b\cos C + c\cos B = a,\)
Подставляя значения \(b\) и \(c,\), получаем
L.H.S. \( = k\sin B\cos C + k\sin C \cos B\)
\( = k( \sin B \cos C + \sin C \cos B)\)
\( = k \ sin (B + C)\)
В любом треугольнике \(A + B + C = \pi ,\)
\( = k \sin (\pi – A)\)
\( = k \ sin A\)
\(=a?\) R.H.S.
Используя аналогичные рассуждения, мы можем вывести две другие формулы.
5. Теорема m-n
Для точки \(D\) на \(BC\), которая делит его в отношении \(m:n,\), теорема утверждает, что 9{\rm{o}}} – (\theta + \beta )\)
In \(\Delta ABD,\frac{{BD}}{{ \sin \alpha }} = \frac{{AD}} {{ \sin (\theta – \alpha )}}\)
In \(\Delta ADC,\frac{{DC}}{{ \sin \beta }} = \frac{{AD}}{{ \ sin (\theta + \beta )}}\)
\(\frac{{BD}}{{DC}}\frac{{ \sin \beta }}{{ \sin \alpha }} = \frac{ { \sin (\theta + \beta )}}{{ \sin (\theta – \alpha )}}\)
\( \Rightarrow \frac{{m \sin \beta}}{{n \sin \ альфа }} = \frac{{ \sin (\theta + \beta )}}{{ \sin (\theta – \alpha )}}\)
\(\frac{{m \sin \beta }}{{n \sin \alpha }} = \frac{{ \sin \theta \cos \beta + \cos \theta \sin \beta}}{{ \sin \theta \cos \alpha – \cos \theta \sin \alpha }}\)
\(m \sin \beta ( \sin \theta \cos \alpha – \cos \theta \sin \alpha ) = n \sin \alpha ( \sin \theta \cos \beta + \cos \theta \sin \beta )\)
\(m \cot \alpha – m \cot \theta = n \cot \beta + n \ cot \theta \)
\((m + n) \cot \theta = m \cot \alpha – n \cot \beta \)
Точно так же мы можем получить и другой аргумент.
92}c \cos C\)
\( = ab(b \cos A + a \cos B) + bc(c \cos B + b \cos C) + ac(c \cos A + a \cos C) \)
Используя проекционную формулу, имеем
\( = ab(c) + bc(a) + ac(b)\)
\( = 3abc\)
Следовательно, доказано.
Эта статья поможет нам понять различные способы связи углов и сторон треугольника. В нем перечислены боковые отношения через теорему о неравенстве треугольника, угловые отношения через сумму углов в треугольнике. Затем он объясняет геометрические и тригонометрические отношения сторон и углов в треугольнике. Мы также учимся доказывать закон синусов, закон косинусов, закон тангенсов, правило проектирования и теорему \(m-n\). Решенные примеры помогают нам понять, как использовать изученные таким образом геометрические и тригонометрические отношения между сторонами и углами треугольника.
Часто задаваемые вопросы (FAQ)
Q.1. Как связаны между собой длины сторон и углы треугольников?
Ответ: Теорема об отношении углов к сторонам утверждает, что в любом треугольнике:
1.
Наименьший угол лежит против наименьшей стороны
Наибольший угол лежит против наибольшей стороны на вторую по величине сторону
Q.2. Как связаны между собой 3 стороны любого треугольника?
Ответ: Сумма длин двух сторон треугольника больше длины третьей стороны. Это называется теоремой о неравенстве треугольника.
Q.3. Кто установил соотношение между сторонами и углами в прямоугольном треугольнике?
Ответ: Теорема Пифагора названа в честь греческого философа и математика Пифагора. Хотя эта теорема могла быть известна \(1000\) лет назад, он был первым, кто доказал ее. 9{\rm{o}}}\) каждый. Следовательно, треугольник может иметь не более одного прямого угла.
Q.5. Как найти угол прямоугольного треугольника по двум сторонам?
Ответ: Меру угла можно вычислить, используя тригонометрические отношения между сторонами и углами прямоугольного треугольника.
Например, мы можем вычислить отношение противоположности к гипотенузе как \(\sin\,\theta .\) Затем мы находим значение, чтобы получить меру угла.
Мы надеемся, что эта подробная статья о соотношениях между сторонами и углами треугольника помогла вам в ваших исследованиях. Если у вас есть какие-либо сомнения, вопросы или предложения относительно этой статьи, не стесняйтесь спрашивать нас в разделе комментариев, и мы будем более чем рады помочь вам. Приятного обучения!
Соотношение длин сторон и углов треугольника
Соотношение длин сторон и углов треугольника — Открытый справочник по математикеОткрытый справочник по математике
Дом Контакт О Предметный указатель
В любом треугольнике:
- Самая короткая сторона всегда находится напротив наименьшей внутренний угол
- Самая длинная сторона всегда находится напротив наибольшего внутреннего угла
Попробуйте это
Перетащите оранжевые точки на треугольник ниже.
Напомним, что в неравносторонний треугольник, все стороны имеют разную длину и все внутренние углы имеют разные меры. В таком треугольнике меньшая сторона всегда лежит против наименьшего угла. (Они выделены жирным шрифтом выше) Точно так же самая длинная сторона находится напротив наибольшего угла.
На рисунке выше перетащите любой вершина треугольника и смотри, какая сторона короче, противолежащий угол также наименьший. Затем нажмите «Показать самый большой» и увидите, что, как бы вы ни изменяли форму треугольника, самая длинная сторона всегда находится напротив наибольшего внутреннего угла.
Детали среднего размера
Если против наименьшего угла лежит наименьшая сторона, а против наибольшего угла — наибольшая сторона, то отсюда следует, что поскольку треугольник имеет только три стороны, сторона среднего размера находится напротив угла среднего размера.Равнобедренные треугольники
Равносторонний треугольник у него все стороны равны по длине и все внутренние углы равны.