Угол виды углов – острый, прямой, развёрнутый, смежные и вертикальные

Урок математики на тему » Угол. Виды углов»

Урок математики во 2 классе

Тема: «Угол. Виды углов»

Цель: формирование общего понятия об угле, видах углов.

Задачи: — учить различать прямой, острый и тупой угол;

— учить строить прямой угол;

— развивать познавательный интерес, умение сравнивать, обобщать;

— развивать внимание, воображение учащихся.

Ход урока:

I. Организационный момент.

II. Устный счёт.

1) Игра «Гусеница-растеряша».

— Гусеница растеряла числа, посмотрите на оставшиеся, разгадайте по какому правилу можно продолжить ряд чисел. (Дети называют правило: это чётные числа; каждое последующее число на 2 больше предыдущего).

— Какие же числа растеряла гусеница?

2) Игра «Математический баскетбол».

— Любой из вас забьёт гол, если правильно решит пример. (Дети по цепочке решают примеры).

30 + 7 25 + 5 32 – 12 66 + 4 80 – 7

28 – 10 45 – 45 53 + 7 59 – 9 90 + 9

3) Игра «Четвёртый лишний».

— Посмотрите на фигуры в каждой рамке. Какая из них лишняя? Почему? (Учащиеся называют лишние фигуры, обосновывают свой выбор).

— Разделите все оставшиеся фигуры на две группы. Как это можно сделать?

(Оставшиеся фигуры можно разделить на две группы: линии и многоугольники.)

— Назовите виды линий и многоугольников, известные вам. (Линии: прямая, ломаная, кривая. Многоугольники: квадрат, трапеция, прямоугольник, четырёхугольник, пятиугольник, шестиугольник, многоугольник).

III. Актуализация знаний. Повторение изученного.

4) Игра «Самый внимательный».

— Посмотрите внимательно на рисунок, части всех предметов похожи на какие-то фигуры.

— Самый внимательный из вас найдёт на рисунке нужные фигуры. Подсказку ищите в верхнем правом углу рисунка. (Дети указкой показывают треугольники и квадраты).

IV. Работа над новым материалом.

1) — Тему урока вам подскажет кроссворд.

Кроссворд «Геометрический».

1. Часть прямой, у которой есть начало, но нет конца. (Луч).

2. Геометрическая фигура, не имеющая углов. (Круг).

3. Самая маленькая геометрическая фигура. (Точка).

4. Геометрическая фигура, имеющая форму вытянутого круга. (Овал).

— Тема нашего урока спряталась по вертикали. Найдите её. (Угол).

— На уроке мы познакомимся с разными видами углов, их свойствами, научимся их обозначать буквами.

2) Игра «Им угол имя подарил».

— Угол важная фигура. Многим фигурам он помог дать имя. Назовите фигуры.

— Что общего в названиях фигур? Почему первая часть слов везде разная?

— Углы окружают нас и в повседневной жизни. Посмотрите на рисунки: уголок соединительный для труб и уголок канцелярский для бумаг; угольник плотника и угольник чертёжный; угловой стол и угловой диван.

— Обернитесь, рассмотрите наш класс. Приведите свои примеры, где можно найти углы вокруг нас.

3) Определение угла.

— На листе тетради отметьте точку и обозначьте её буквой А.

Проведите из точки А два луча. На сколько частей лучи разделили плоскость? Меньшую часть заштрихуйте цветным карандашом. Какую фигуру вы заштриховали? (Угол).

Угол – это геометрическая фигура, образованная двумя разными лучами

с общим началом.

4) Обозначение углов.

(Учитель комментирует флэш-ролик «Обозначение углов»).

— Точка О – вершина угла. Угол можно назвать одной буквой, записанной около его вершины. Угол О. Но может быть несколько углов, имеющих одну вершину. Как быть тогда?

— В таких случаях если называть разные углы одной буквой, то будет непонятно, о каком угле идёт речь. Чтобы этого не произошло, на каждой стороне угла можно отметить по одной точке, поставить около неё букву и обозначить угол тремя буквами, при этом всегда в середине записывают букву, обозначающую вершину угла. Угол АОВ. Лучи АО и ОВ – стороны угла.

5) Практическая работа. Построение модели прямого угла.

— Углы бывают разные, но сначала мы познакомимся с самым главным углом.

Возьмите лист бумаги. Сложите лист пополам, а потом ещё раз пополам. Обведите линии сгиба карандашом. На сколько частей прямые линии разделили плоскость? (На четыре).

— Сколько углов получилось? (Четыре).

— Это особенные углы. Может быть, кто-то знает название этих углов? (Эти углы прямые).

— На пересечении линий сгиба поставьте точку. Обозначьте один прямой угол буквами. Заштрихуйте цветным карандашом его внутреннюю часть.

6) Определение и построение прямого угла.

— Посмотрите на рисунок, я выделила на нём некоторые углы. Вы найдите и покажите только прямые углы.

(На слайде отмечены для проверки некоторые из них).

— Не всегда удобно определять прямой угол на глаз. Для этого используют линейку-угольник. Чтобы определить прямой угол или нет угла, нужно совместить вершину и одну сторону угла с вершиной и стороной прямого угла на линейке-угольнике.

— Какой же угол из трёх предложенных прямой? (Нижний; сиреневый).

— Почему вы так решили? (Вершина и стороны угла совпали с прямым углом на линейке-угольнике).

Работа по учебнику.

— Используя модель прямого угла, найди прямые углы и выпиши их номера. (Дети выполняют задание самостоятельно, затем один ученик называет свой вариант ответа, все проверяют работу).

— С помощью угольника удобно не только определять прямые углы, но главное – строить их. Построим прямой угол, каждый сам назовёт его одной или тремя буквами. (Учитель на доске, а дети в тетрадях строят прямой угол. Выполняется взаимопроверка в парах).

7) Виды углов.

— На рисунке видно, что бывают и другие углы не прямые. Каким цветом выделен угол больше прямого? (Голубым).

— Меньше прямого? (Зелёным).

— Каждый из углов имеет своё название.

Острый угол – это угол, который меньше прямого.

Тупой угол – это угол, который больше прямого.

— Рассмотрите рисунки. Какое правило работы важно помнить, при определении вида угла с помощью линейки-угольника? (Нужно совмещать вершину и одну сторону угла с вершиной и стороной прямого угла на линейке-угольнике).

Работа в тетради.

— Начертите в тетради острый и тупой угол, подпишите их. Острый угол заштрихуйте зелёным карандашом, а тупой угол синим.

— Чем похожи и чем различаются эти углы? (Похожи: есть вершина, две стороны. Различаются: один больше, другой меньше прямого угла; разные названия).

— С помощью линейки-угольника проверьте работу друг друга в парах.

Определить угол сначала «на глаз», потом проверить с помощью угольника.

— Чтобы определить вид угла, надо совместить его вершину и сторону соответственно с вершиной и стороной прямого угла на угольнике. Если вторая сторона окажется внутри прямого угла, то угол острый, а если вторая сторона окажется снаружи – то тупой.

8) «Проверь себя!»

Угол – это … (Угол – это геометрическая фигура, образованная двумя разными лучами с общим началом).

Стороны угла – это … а) отрезки; б) лучи; в) прямые. (Стороны угла – это лучи).

На рисунке изображён угол … а) КОМ; б) ОМК; в) КМО. (Угол КОМ).

Острый угол … прямого, а тупой угол … прямого. (Острый угол меньше прямого, а тупой угол больше прямого).

Какого вида эти углы? (Тупой, острый, прямой).

V. Итог урока.

— Что вы узнали нового, интересного?

— Какое задание понравилось больше всего?

Домашнее задание. Игра «Весёлый конструктор»

— Придумайте и нарисуйте различные предметы, используя круги, овалы, точки, лучи и углы.

infourok.ru

Угол. Виды углов. Построение углов.

Этапы урока

Время

(мин)

Деятельность учителя.

Деятельность учеников

1. Организация начала занятия.

1

Учитель приветствует учащихся, проверяет их готовность к уроку(наличия рабочей тетради, дневника, учебника, ручки, карандаша, инструментов)

дети проверяют готовность рабочего места

2. Устный счет

2

На доске: 51 7 150 400 3,1

— замените проценты десятичной дробью.

— сколько процентов одно число составляет от другого? 7 от 14; 9 от 72; 1 от 25; 18 от 9.

— сколько процентов фигуры закрашено?

— сколько процентов фигуры не закрашено?

—   На вершину холма ведут пять  тропинок. Сколько существует способов подняться на холм и спуститься с него, если спускаться и подниматься по разным тропинкам.

Дети работают устно совместно с учителем.

Ответы учеников:

— 0,51; 0,07; 1,5; 4; 0,031.

— 50; 12,5%; 4%; 200%.

-50%; 50% 50%.

-50%; 50%; 50%.

-20 способов

3. Постановка цели и задач урока. Мотивация учебной деятельности учащихся.

3

Учитель работает с классом. «Запишите число, классную работу и тему сегодняшнего урока. Угол. Виды углов. Построение углов.»

Давайте договоримся о том, что мы сегодня хотим узнать к концу урока, чему научиться.

— что такое угол?

— как обозначают угол?

-из каких элементов состоит угол?

— какие бывают виды углов?

-построение углов

Дети работают с учителем.

Обозначают тему урока «Углы».

Ставят учебные цели.

4. Изучение нового материала

8

Так же, как самое большое здание складывается из маленьких кирпичей, так и сложные геометрические фигуры составляются из простейших геометрических фигур. Вспомните, какие простейшие геометрические фигуры вы знаете? (слайд 4)

— Сегодня мы познакомимся еще с одной такой фигурой. Это угол. (слайд 5). Посмотрите внимательно и скажите, из каких простейших геометрических фигур состоит угол? Значит, как можно сформулировать его определение?

Угол ВАС – это часть плоскости, ограниченная двумя лучами, выходящими из одной точки. Точка А- общее начало лучей ВА и СА, точка А- вершина угла.

Для обозначения угла имеется общепринятый символ: предложенный в 1634 году французским математиком Пьером Эригоном .

В обозначении угла вершина всегда ставится в серидине: ˂ВАС. Лучи АВ и АС – стороны угла.

Ответы учеников:

«Точка, прямая, отрезок, луч»

Записывают в тетрадь определение угла.

5. Первичное закрепление знаний.

4

Задание 1. (слайд 6)

Дети выполняют задание в тетради, осуществляют взаимоконтроль.

6. Физкультминутка.

1

А теперь, ребята, встали. Быстро руки вверх подняли, в стороны, вперед, назад. Повернулись в право, влево, тихо сели, вновь за дело.

Дети показывают ответы в движении.( наклоны, повороты, хлопки)

7. Изучение второго блока нового материала.

5

5

— В начальных классах вы научились измерять отрезки. А как измерить угол? Оказывается, есть такой инструмент, называется он транспортир. С его помощью и измеряют величину угла. Величина угла измеряется в градусах. (слайд 7). Начертите любой угол и приложите к нему транспортир так, чтобы (слайд 8):

а) вершина угла совпала с черточкой – серединой основания транспортира;

б) одна сторона угла совпадала с основанием транспортира, соответствующим 0⁰.

Вторая сторона угла укажет на шкале угол в градусах.

— Виды углов (слайд 9).

Среди всех углов выделяют прямой угол. Прямой угол содержит 90⁰ . по отношению к нему остальные углы делятся на две группы: острые углы – меньше 90⁰, и тупые углы – больше 90⁰. Угол, равный 180⁰, называется развернутым.

Работают в тетрадях, учатся измерять углы с помощью транспортира.

8. Закрепление материала.

10

— Задание 2 (слайд 10)

— выполнить задание № 1613, 1614, 1615(устно)

Обдумывают задания, выполняют их, осуществляют взаимоконтроль.

9. Рефлексия, подведение итогов.

5

Справились ли мы с поставленной в начале урока задачей? Что мы узнали на уроке? Что было трудным? Что осталось непонятным? (слайд 11,12)

А теперь попрошу вас выполнить тест.

Осуществляют рефлексию.

10. Домашнее задание.

1

Что учить? Записи в тетради + стр. . 248; № 1638, 1639, 1640

infourok.ru

Разработка урока внеурочной деятельности «Точки. Углы, виды углов»

Логика 3 класс

Тема: «Точки. Углы, виды углов»

Цель:

• познакомить ребят с историей возникновения геометрии;

• ;

• способствовать развитию умений анализировать, сравнивать, обобщать, выделять главное; развивать осознанную математическую речь; развитие познавательного интереса учащихся;

• содействовать воспитанию таких качеств как: самостоятельность, целеустремленность, настойчивость, целенаправленность, трудолюбие, аккуратность, ответственность

Задачи:

— Продолжить формирование навыков контроля результатов деятельности.

— Способствовать развитию коммуникативных навыков. Развивать умение анализировать, обобщать материал, выступать перед аудиторией, развивать интеллектуальные, творческие и исследовательские способности, активизировать интерес к учебным предметам.

— Формирование логического, абстрактного, эвристического, системного мышления.

Оборудование: проектор, экран, компьютер, презентации

План.

1. Организационные моменты

2. История возникновения геометрии.

Заглянем в прошлое, когда зародилась наука геометрия….

Для первобытных людей важную роль играла форма окружавших их предметов. По форме и цвету они отличали съедобные грибы от несъедобных, пригодные для построек породы деревьев от тех, которые годятся лишь на дрова, вкусные орехи от горьких и т.д. Особенно вкусными казались им орехи кокосовой пальмы, которые имеют форму шара. А добывая каменную соль, люди наталкивались на кристаллы, имевшие форму куба. Так, овладевая окружающим их миром, люди знакомились с простейшими геометрическими формами.

Уже 200 тысяч лет тому назад были изготовлены орудия сравнительно правильной геометрической формы, а потом люди научились шлифовать их. Специальных названий для геометрических фигур, конечно, не было. Говорили: «такой же, как кокосовый орех» или «такой же, как соль» и т.д.

А когда люди стали строить дома из дерева, пришлось глубже разобраться в том, какую форму следует придавать стенам и крыше, какой формы должны быть бревна. Сами того не зная, люди все время занимались геометрией: женщины, изготавливая одежду, охотники, изготавливая наконечники для копий или бумеранги сложной формы, рыболовы, делая такие крючки из кости, чтобы рыба с них не срывалась.

Когда стали строить здания из камня, пришлось перетаскивать тяжелые каменные глыбы. Для этого применялись катки. И заметили, что перекатка проще, если взять кусок дерева с почти одинаковой толщиной в начале и в конце. Так люди познакомились с одним из важнейших тел – цилиндром. Скалками цилиндрической формы пользовались и женщины, раскатывая белье после стирки.

Перевозить грузы на катках было довольно тяжело, потому что сами древесные стволы весили много. Чтобы облегчить работу, стали вырезать из стволов тонкие круглые пластинки и с их помощью перетаскивать грузы. Так появилось первое колесо.

Но не только в процессе работы знакомились люди с геометрическим фигурами.

Издавна они любили украшать себя, свою одежду, свое жилище (бусинки, браслеты, кольца, украшения из драгоценных камней и металлов, роспись дворцов).

Для того, чтобы взимать налоги с земли, необходимо было знать их площадь. Гончару необходимо было знать, какую форму следует придать сосуду, чтобы в него входило то или иное количество жидкости. Астрономы, наблюдавшие за небом и дававшие на основе этих наблюдений указания, когда начинать полевые работы, должны были научиться определять положение звезд на небе. Для этого понадобилось измерять углы.

Так практическая деятельность людей привела к дальнейшему углублению знаний о формах фигур, развитию геометрии. Люди стали учиться измерять и площади, и объемы, и длины и т.д.

Древние египтяне были замечательными инженерами. До сих пор не могут до конца разгадать загадки огромных гробниц Египетских царей – Фараонов.

Пирамиды – а они построены более 5 тыс. лет назад – состоят из каменных блоков весом 15 тонн, и эти «кирпичики» так подогнаны друг к другу, что не возможно между ними протиснуть и почтовую открытку. А при строительстве использовали лишь простейшие механизмы – рычаги и катки.

«Все боится времени, но само время боится пирамид».

В Вавилоне при раскопках ученые обнаружили остатки каменных стен, высотой в несколько десятков метров, а высота Вавилонской башни достигает 82 метра.

Без математических знаний все эти сооружения невозможно было бы построить. И все же математические знания египтян и вавилонян были разрозненные и представляли собой свод правил, проверенных практикой, поэтому правила надо было зазубривать, не понимая, почему надо применять то, а не другое.

Почти все великие ученые древности и средних веков были выдающимися геометрами. Девиз древней школы был: «Не знающие геометрии не допускаются!»

Настает время привести все разрозненные знания в систему.

Геометрия… откуда взялось это слово? Что оно означает? Попробуем разгадать его смысл. Ведь вам постоянно встречаются похожие слова: география, геология, геодезия… а есть еще геоботаника и т.п. это все названия различных наук или разделов наук. Со смыслом слова география вы уже знакомы. «Гео» означает «Земля», «метр» — это единица измерения длины (от греческого слова «метрео» — «измеряю». Таким образом, получается, что геометрия в переводе с греческого означает «измерение земли» или «землемерие».

«Геометрия была открыта египтянами и возникла при измерении земли. Нет ничего удивительного в том, что эта наука как и другие, возникла из потребностей человека. Всякое возникающее знание из несовершенного состояния переходит в совершенное. Зарождаясь путем чувственного восприятия, оно постепенно становится предметом рассмотрения и наконец, делается достоянием разума». Эти замечательные слова приписывают греческому ученому Евдему Родосскому, жившему в IV в.до н.э.

В «Энциклопедическом словаре юного математика» написано: «Геометрия – одна из наиболее древних математических наук. Первые геометрические факты мы находим в вавилонских клинописных таблицах и египетских папирусах (III тысячелетие до н.э.), а также в других источниках».

И наиболее удачно была изложена геометрия, как наука о свойствах геометрических фигур, греческим ученым Евклидом (III в. до н. э.) в своих книгах «Начала». Евклид жил в Александрии, был современником царя Птоломея I и учеником Платона. Славу Евклиду создал его собирательный труд «Начала». Произведение состояло из 13 томов, описанная в этих книгах геометрия получила название Евклидова. Величайшая заслуга его состояла в том, что он подвел итог построению геометрии придал ее изложению столь совершенную форму, что на 2 тысячи лет «Начала» стали основным руководством по геометрии. В течение многих веков «Начала» были единственной учебной книгой, по которым молодежь изучала геометрию. Были и другие. Но лучшими признавались «Начала» Евклида. И даже сейчас, в наше время, учебники написаны под большим влиянием «Начал» Евклида.

Конечно, геометрия не может быть создана одним ученым. В работе Евклид опирался на труды десятков предшественников и дополнил работу своими открытиями и изысканиями. Сотни раз книги были переписаны от руки, а когда изобрели книгопечатание, то она много раз переиздавалась на языках всех народов и стала одной из самых распространенных книг в мире.

В одной легенде говорится, что однажды египетский царь Птолемей I спросил древнегреческого математика, нет ли более короткого пути для понимания геометрии, чем тот, который описан в его знаменитом труде, содержащемся в 13 книгах.

3. Что изучает геометрия.

Геометрия – это раздел математики, которая изучает пространство, а также всяческие отношения, который в этом пространстве возникают. Всю геометрию можно разделить на несколько типов. Например, классическая геометрия решает все вопросы связанные с точками, прямыми, плоскостями и т.д. Она сама включает в себя планиметрию, стереометрию и другие дисциплины. Существует также аналитическая геометрия, которая построена на координатном способе познания. Например, именно таким способом изучаются вектора, прямые и отрезки, которые заданы формулами и условиями. Также существует дифференциальная геометрия, которая задается дифференциальными уравнениями, а также занимается отображением этих уравнения в различных пространствах. И завершает это ряд такая дисциплина как топология, которая изучает непрерывность в наиболее общем виде.
Считается, что родоначальниками геометрии были греки, которые впервые опубликовали свои первые труды, например, знаменитые «Начала» Евклида. Греки занимались сравнением различных фигур, а также их принадлежность друг другу. Такая геометрия занималась простейшими фигурами, на плоскости и в пространстве.
Средние века не много дали геометрии, а вот уже в XVII веке Декарт придумал свой координатный метод, что заставило геометрию сделать новый виток в своей истории. Также кооринатный метод используется и в другом виде геометрии — дифференциальном, ГД координаты занимают одну из ведущих ролей. В дифференциальной геометрии все задается уже относительно гладкими графиками, что является более сложным и более развитие уровнем геометрии.
Сегодня геометрия используется довольно широко в прикладных моментах. Она касается не только обмера земли (как и тысячелетия назад) а также и другими, более развитыми и более сложными научными вычислениями.

4. Знакомство с элементами геометрических фигур.

Сказка о Точке

В далеком математическом государстве жила маленькая-маленькая Точка, которую никто не любил. Да и чего ее любить: сама крохотная, еле-еле видно, ни длины, ни ширины не имеет, а попробуй не поставить на нужном месте или пропустить!.. Сколько нагоняев из-за нее получено, сколько двоек…

Точка, конечно же, чувствовала такое отношение к себе и очень кручинилась: как трудно быть хорошей, когда тебя не любят и все время раздражаются! Задумала она сбежать из математического государства, да все решимости не хватало. «Все-таки страшно, ведь правда, маленькая я, — думала Точка, — одно слово — ни длины, ни ширины… Далеко не убежишь…»

Но однажды приключилась в старших классах контрольная, и один ученик пропустил точку, переписывая пример на умножение. Представляете, какой результат он получил? А какую оценку? Вот… Ох, и кипятился же он и ворчал: «Из-за такой малости — все наперекосяк! Ну, что такое ТОЧKА! Ведь она даже определения не имеет!!!» «Kак?! — ахнула про себя Точка. — Я столько работаю, выслушиваю всякие гадости и при этом даже не имею определения?! Это же возмутительно! Нет, надо бежать отсюда куда глаза глядят…»

«Kак я тебя понимаю!» — услышала Точка тяжелый вздох рядом с собой. Это была Стройная Прямая: «Я ведь тоже не имею определения! Все говорят: прямая, прямая… Проведите прямую, отметьте на прямой… А что такое Я? Что такое прямая — никто еще толком не сказал… Грустно! Давай-ка, точка, я тебе помогу! Прыгай на меня и беги, не останавливаясь. Я ведь ухожу в бесконечность! Хочешь увидеть бесконечность вместе со мной?»

«Конечно, хочу!» — пискнула Точка, прыгнула и покатилась, как сказочный Колобок, по прямой…

А что началось уже через десять минут после исчезновения Точки! Числа гомонят и волнуются — некому их обозначить на числовом луче! Да и сами лучи на глазах растворяются: где точка, чтобы ограничить прямую с одного конца? А уж из чисел, желавших умножиться, целая очередь образовалась: ведь вместо Точки в примерах на умножение пришлось ставить Kосой Kрестик. А что взять с Kрестика, к тому же Kосого?

         Словом, без маленькой и довольно противной Точки рухнуло математическое государство на пятнадцатой минуте…

А что же Точка? Бежала она долго-долго… Лишь когда потускневшее солнце опустилось за горизонт и на землю лег сумрак, остановилась точка отдохнуть. А утром от того места, где она остановилась на ночлег, побежал в бесконечность Луч. По этому Лучу и поднялась она на небо, по этому Лучу и ушла она куда-то в глубь Млечного Пути.

Посмотри, не видишь ли ты ее посреди миллиарда звезд, рассыпавшихся на небе?..

Углы, виды углов.

Угол — это геометрическая фигура, которая состоит из двух лучей и вершины.

Вершина угла — это точка, в которой два луча берут начало.

Стороны угла — это лучи, которые образуют угол.

Например:

Вершина угла — точка O. 
Стороны угла — OA и OB.

Для обозначения угла в тексте используется символ: AOB

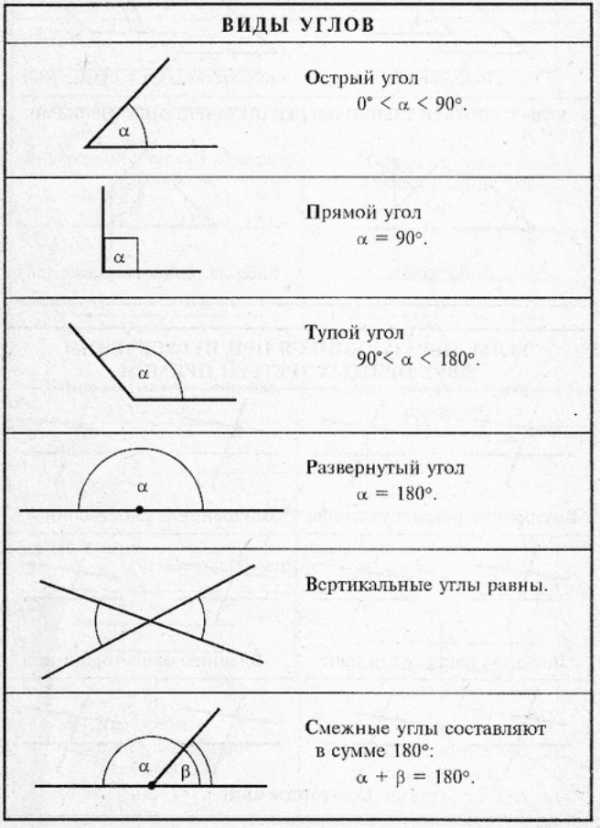
Способы обозначения углов

Одной заглавной латинской буквой, указывающей его вершину.

Угол: O

Тремя заглавными латинскими буквами, которыми обозначены вершина и две точки, расположенные на сторонах угла.

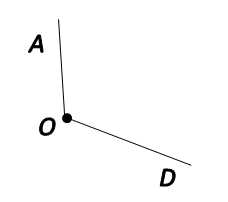Угол: AOD

Называть угол можно с любого края, но НЕ с вершины.

Угол с рисунка выше имеет два названия: AOD иDOA.

При таком обозначении вершина угла должна всегда находиться в середине названия.

Двумя строчными латинскими буквами.Угол: fn

Единица измерения углов — градусы. Углы измеряют с помощью специального прибора — транспортира.

Для обозначения градусов в тексте используется символ: °

50 градусов обозначаются так: 50°

Виды углов

Вид угла

Размер в градусах

Пример

Прямой

Равен 90°

Острый

Меньше 90°

Тупой

Больше 90°

Развернутый

Равен 180°

Два угла могут иметь одну общую сторону.

Обратите внимание на рисунок ниже. Попробуйте сосчитать и назвать все углы на изображении.

Если насчитали три угла, то вы правы. Давайте их назавём:

AOB

BOC

AOC

Углы AOB и BOC имеют общую сторону OB.

Сказка об углах

«ГОРОД УГЛОВ»

Я с детства не любил овал!

Я с детства угол рисовал!

Друзья, я хочу рассказать вам о стране, которая не обозначена ни на одной карте. Это страна Геометрия – чудесный уголок Мира. В ней – прекрасные небольшие города, где все отлично знают друг друга. Там Прямая и Точка – основные фигуры, все их уважают за прямоту и точность.

Один из городов – город Углов – раскинулся у подножия горы. В этой долине с незапамятных времен жили Углы: Развёрнутые, Прямые, Острые, Тупые. Они произошли от Лучей, когда — то спустившихся с гор. Самыми большими (их градусная мера всегда была 180⁰) и добрыми были Развёрнутые Углы. В их доме часто собирались друзья, и было весело. Каждый путник встречал у них радушный приём.

Напротив жили Прямые Углы. Дом их был в два раза меньше, чем у Развёрнутых Углов, ведь их градусная мера равна 90⁰. Это были честные и прямые Углы. В городе все обращались к ним, если надо было узнать правду.

Рядом с развёрнутыми Углами стоял дом Острых Углов. В нём обитали самые остроумные и приятные жители города. Несмотря на то, что их градусная мера всегда была меньше 90⁰ и домик был небольшой, они не унывали: много играли, читали, соревновались в сочинении острых сатирических куплетов, которые распевали на улицах города.

На окраине города стоял дом Тупых Углов. Он был поменьше дома Развёрнутых Углов, но больше дома Прямых Углов (ведь градусная мера всякого Тупого Угла больше 90⁰, но меньше 180⁰). Очень тупыми и заносчивыми были хозяева дома. Никак они не могли понять, что надо всем жить в мире и согласии. Сами в гости не ходили и к себе не звали. Очень они гордились своей тупостью.

Жизнь в городе текла спокойно. Но однажды раннее обычного распахнулись, сверкая разноцветными стеклами, окна домов. Жители города узнали, что в нём появилась юная путешественница. Прекрасная Биссектриса – Луч. Эта была маленькая, тоненькая, задорная и очень весёлая девочка. Много нового она внесла в жизнь старого города. Все горожане, даже Тупые Углы, наперебой приглашали её в гости. Очень нравились игры Биссектрисы, она прячется, а все её ищут. Те, кто хорошо учились в школе, знали, что Биссектриса делит угол пополам. Они быстро находили гостью и игра продолжалась.

Исчезло одиночество. Стали появляться семьи Углов. Первую свадьбу сыграли Смежные Углы. У них была одна сторона общая, а две другие – дополнительные полупрямые. Несмотря на то, что в паре могут быть два Прямых Угла, а может быть один Острый, а другой Тупой, их отличает то что они – семья и их сумма всегда равна 180⁰. Пробовали два Острых Угла, два Тупых Угла стать смежными, но это им не удалось. Не знаете почему?

Вторую свадьбу сыграли Вертикальные Углы. У них стороны одного угла – дополнительные полупрямые сторон другого угла. Скоро все узнали, что Вертикальные Углы равны между собой.

Шло время. И вот разнеслась новая весть: высоко в горах, куда не всякий орёл долетает, оказывается, у Углов живёт ещё много родственников: Полные Углы, Центральные Углы, Вписанные и другие Углы. И живут они по совсем иным законам.

Просмотреть презентации к уроку

5. Практическая работа.

Выполните задания:

1.Приведите примеры прямых углов в классе, дома, на улице.

2.Начертите любой острый, тупой и прямой угол. Обозначьте эти углы. Запишите вершины и стороны этих углов.

6. Итоги урока

Что вы сегодня узнали на уроке? Что больше всего запомнилось?

7. Домашнее задание.

Придумать математический сказку.

infourok.ru

Конспект урока математики «Угол.Виды углов» (2 класс)

Урок математики во 2 классе.

Тема урока: Угол. Виды углов.

Тип урока: Урок получения новых знаний.

Цели урока:

1.Научить детей видеть углы, строить их при помощи угольника и различать по видам.

2.Развивать математическую речь, внимание, память, пространственное воображение.

3.Формировать графические умения. 

Оборудование: проектор (презентация «Виды углов»), лист бумаги для практической работы, набор плоских геометрических фигур, прямоугольник, буквы для названия темы урока «УГОЛ», тестовое задание на листочках по теме «Угол. Виды углов».

Ход урока. 

1.Мотивация.

«Вот звонок нам дал сигнал:

Поработать час настал.

Так что время не теряем

И работать начинаем»

-У нас сегодня необычный урок. На уроке у нас гость.

— Повернитесь, ребята к нашему гостю, поприветствуйте его улыбкой.

— Повернитесь лицом к соседу, возьмитесь за руки, улыбнитесь и скажите ему:

— Я желаю тебе добра;

2. Актуализация знаний.

Устный счет. Слайд 2.

Математический диктант.

— В каком числе 7 дес. 2 ед.? (72.)

— Сумма чисел 8 и 7. (15)

— Уменьшаемое 12, вычитаемое 9. Найдите разность. (3)

— Назовите число, которое стоит перед 37. (36)

— Назовите число, которое стоит после 48. (49)

— Разность чисел 27 и 6. (21)

— Если к 5 дес. прибавить 2 дес. Какое число получится? (70)

— Какое число больше 42 на 5? (47)

— Какое число меньше 59 на 6? (53) Слайд с числами.)

Найдите среди данных чисел лишнее. (Лишним является число 70, так как все числа не круглые, а это число круглое. Число 3, так как все числа двузначные, а оно однозначное.)

-Какой цифрой на письме обозначают число 3? (Цифрой 3).

-Давайте вспомним как пишется цифра 3.

-Из скольких элементов состоит цифра 3? (Из 2 элементов. Правых полуовалов.)

Показ написания цифры учителем. Письмо в воздухе.

Откройте тетрадочки и запишите в них по образцу цифру 3. Подчеркните 3 самых красивых цифры.

3.Самоопределение к учебной деятельности.

-На слайде нарисованы фигуры (Слайд 3.). На какие две группы можно разделить эти фигуры? (Фигуры, имеющие и не имеющие углы.)

— На кие три группы можно разделить оставшиеся фигуры? (Треугольники, четырехугольники и пятиугольники.)

— Что общего у фигур в каждой группе? (Количество углов и сторон.)

-Сколько углов у этих фигур? (У пятиугольников 5, у четырехугольников 4, у треугольников 3.) (Слайд 4.)

-Как вы думаете, о чем пойдет речь сегодня на уроке? (Об углах.)

-Правильно тема нашего сегодняшнего урока «Угол. Виды углов».

— А какова цель нашего урока? (Узнаем, что такое угол. Научимся различать виды углов.)

4. Работа над темой урока.

— Как вы думаете, что такое угол? Посмотрите внимательно на доску и попробуйте объяснить, из чего он состоит. Из каких геометрических фигур?

— Как называется фигура, у которой есть начало, но нет конца?

(Точка и 2 луча.)

— Откуда проведены лучи? (Из одной точки)

(Слайд 5.) Вывод: т.е. угол – это фигура, образованная двумя лучами, выходящими из одной точки. Лучи— это стороны угла. Точка, из которой лучи проведены, — вершина угла.

-Как построить угол? Для того, чтобы построить угол необходимо провести из одной точки два луча. (Слайд 6.)

-Посмотрите на доску и скажите одинаковые углы, вы видите на доске. (Нет, все углы различны.)

-Сейчас мы с вами познакомимся с видами углов.

— Каждый из вас сделает из листа бумаги, который лежит на парте, модель одного из видов углов. Как это сделать, подскажет учебник. Открываем учебник на странице 8.

—Покажите стороны прямого угла и вершину.

— Посмотрите вокруг себя, назовите предметы, где есть прямые углы.

Работа в парах.

Задание: у вас на столах лежат карточки, на которых изображены углы. Найдите среди данных углов прямой, используя угольник или модель прямого угла. Для этого прикладываем прямой угол треугольника к этому углу так, чтобы вершина и одна из сторон совпали. Если обе стороны совпали, то это прямой угол.

4

1

2

3

-Назовите номера прямых углов. (1 и 3.)

-Посмотрите на угол под номером 2. Что можно о нем сказать по отношению к прямому углу. Он меньше или больше прямого угла? (Меньше.)

— Такой угол называют острым. Давайте дадим определение острого угла.

-Острым углом называют угол, который меньше прямого.

-Посмотрите на угол под номером 4. Что можно о нем сказать по отношению к прямому углу. Он меньше или больше прямого угла? (Больше.)

— Такой угол называют тупым. Давайте дадим определение тупому углу.

-Тупым углом называют угол, который больше прямого.

Работа с интерактивной доской (Слайд 7).

-Со сколькими видами углов вы познакомились? (С 3 видами.)

— Назовите эти виды. (Прямой, острый и тупой углы.)

-Чем отличается острый угол от прямого? (Острый угол меньше прямого.)

-Чем отличается тупой угол от прямого? (Тупой угол больше прямого.)

Алгоритм определения видов угла:

1.Прикладываем угольник к вершине и к одной из сторон.

2.Смотрим, где прошла вторая сторона: за пределами прямого угла или внутри прямого угла (смотрим, угол меньше или больше прямого угла.)

3.Определяем вид угла.

Работа в группах.

— А сейчас ребята поработаем в группах по рядам. Первая группа — это первый ряд, вторая группа -это второй ряд и третья группа- это третий ряд.

Для этого работаем на стр. 9 номер1. Первая группа записывает номера всех прямых углов. Вторая группа записывает все номера острых углов и третья группа записывает все номера тупых углов.

1 группа прямые углы: 2, 4, 7, 8, 10, 12.

2 группа острые углы: 1, 3, 5.

3 группа тупые углы: 6, 9, 11.

Самостоятельная работа.

— А сейчас, ребята, вам нужны будут новые знания для выполнения следующего задания.

1 вариант: построить острый угол.

2 вариант: построить тупой угол.

— У кого правильно?

— Что получилось, что было трудно? Почему? (Самооценка)

— Что помогло вам справиться с заданием?

— Проверим ваши знания, решив небольшой тест.

1. Как называется геометрическая фигура, которая состоит из двух лучей и общей вершины?

а) угол б) отрезок в)ломаная

2. Что является сторонами угла, подчеркни правильный ответ:

а) отрезки; б) лучи; в) прямые.

3. Чем отличается острый и тупой углы от прямого, подчеркни правильный ответ.

острый угол (больше, меньше) прямого угла

тупой угол (больше, меньше) прямого угла

4. Напиши, что такое вершина угла. (Вершина.)

Проверка по эталону. Если все ответы совпали, то ставят +

Рефлексия.

— Какую цель ставили на урок?

— Достигли ли вы этой цели?

— Что узнали сегодня на уроке? Чему научились?

— С какими видами углов вы познакомились сегодня на уроке?

— Как узнать, острый угол или тупой?

Оцените свою работу на уроке.

Если урок прошел удачно: вы активно участвовали в работе класса, с заданиями справились успешно. Очень довольны собой, то начертите прямой угол желтого цвета.

Если сегодня на уроке не все задания оказались такими уж легкими. Было не легко, но вы справились. Вполне довольны собой, то начертите прямой угол зеленого цвета!

Если задания на уроке оказались слишком трудными. Мне нужна помощь, то начертите прямой угол красного цвета.

infourok.ru

«Виды углов. Измерение углов»

Муниципальное бюджетное общеобразовательное учреждение

«Средняя общеобразовательная школа №6 Муниципальное образование «Ахтубинский район»

Конспект урока по математике
в 5 классе

«Виды углов. Измерение углов»

подготовила

учитель математики и информатики и ИКТ

Попова Светлана Петровна

г. Ахтубинск

2013

Тема: Виды углов. Измерение углов.

Планируемые результаты:

Личностные: сотрудничать в группах, уважать мнение одноклассников, видеть

значимость материала в жизни человека.

Метопредметные: высказывать свою точку зрения, аргументировать, выстраивать

логические цепочки, обсуждать решение, использовать алгоритм при

построении углов.

Предметные: строить и измерять углы, определять виды углов,

расширит представление о построении углов, используя

различные инструменты.

Урок применения полученных знаний.

Оборудование:

Видеопроектор, кроссворд, раздаточный материал(карточки), модели углов , презентация.

Ход урока

1. орг.момент.

-Здравствуйте. Посмотрите, все ли готово к уроку? Сегодня мы будем работать как индивидуально, так и в группах по 2 и по 4 человека.

2. Мотивационный.

-Все вы, наверняка, любите решать кроссворды?… Поэтому я хочу предложить вам решить небольшой кроссворд (на экране кроссворд http://learningapps.org/display?v=pyg27wept )

-Ребята, разгадаем его.

-Теперь прочтем слово, которое получилось в первом вертикальном столбце? (транспортир) Что означает это слово? (это инструмент) Для чего используют этот предмет? (для измерения и построения углов)

Постройте углы, указанные в задаче (слайд 1)

Один ученик строит на доске первый угол, за ним другой ученик — второй и следующий – третий ученик. Остальные ученики у себя в тетрадях. После чего сверяют правильность решения.

— Посмотрите на слайд и назовите углы (слайд 2)

— все углы имеют одинаковый вид? (нет) Какие углы вы можете назвать? (прямые, тупые, острые, развернутые) Все ли эти углы мы с вами знаем и умеем измерять и строить?

— Предлагаю решить следующую задачу в группах по 2 человека: (слайд 3)

На решение задачи в тетрадях даю 2-3 минуты. Какие результаты вы получили? ( возможно 140˚ или 20˚) Прошу объяснить полученные результаты. У доски по одному ученику с разными результатами показывают решение. Проведем анализ полученных результатов.

3.Постановка целей.

Итак, сформулируйте цели урока (применение полученных знаний для построения, измерения и определения вида углов)

Запишем тему урока: Виды углов. Измерение углов.

4. Аналитический.

Теперь развернитесь друг к другу по две парты и поработайте в группе по 4 человека. На столе у каждой группы три макета углов трех цветов: красный-90˚, зеленый-45˚, синий- 30˚ .Я попрошу вас составить из них следующие углы: 135˚, 150˚, 75˚, 15˚

От каждой группы один ученик демонстрирует по одному решению на доске. Я предлагаю свой вариант на слайде (слайд №4-7)

Физкультминутка:

— Вы хорошо потрудились, а теперь дадим немного отдохнуть нашему телу. Встаньте и покажите руками углы, которые я буду называть.

-тупой угол

-развернутый угол

-прямой угол

-острый угол

-Хорошо, прошу садиться.

5.Оценочный.

Индивидуальная самостоятельная работа по карточкам:

Обозначьте углы, измерьте их, и назовите их виды.

Обменяйтесь с соседом по парте и проверьте, выставив оценку.

Учащиеся проверяют ответы, сверяя с кодом на слайде № 8.

В оставшееся время предлагаю решить задачи из рабочей тетради № 133, 137

6.Рефлексия.

-Чтоб фундамент заложить, какой угол надо отложить? (развернутый)

-Чтобы дом построить прочный – стены, под каким углом? (прямым)

-Чтобы крыша не текла, мы построим угол?.. (тупой)

-Что было наиболее трудным на уроке?

-Как можно еще использовать полученные знания на уроке?

Домашнее задание: 1) построить углы с помощью транспортира 68˚,134˚, 55˚, 90˚ обозначит и

определить их вид.

2) Можно ли построить треугольник АВС, в котором угол А равен 40˚, угол

В равен 80˚, угол С равен 50˚? Объясни.

При выходе из класса, я попрошу вас оставить на моем столе угол того цвета, который соответствует вашему настроению на данном уроке:

-красный — все понравилось, было все понятно, трудностей не вызывало;

-зеленый — урок понравился, но были некоторые трудности при решении заданий;

— синий – на уроке чувствовал себя не комфортно, задания слишком трудные.

Список использованной литературы

1. А.Г.Мерзляк, В.Б.Полонский, М.С.Якир, Е.В.Буцко, Математика 5 класс,Москва «Вентана-Граф»,2012

2. А.Г.Мерзляк, В.Б.Полонский, М.С.Якир, Рабочая тетрадь №1 Математика 5 класс, Москва «Вентана-Граф»,2012

Интернет-источники

1. Интернет ресурс LearningApps.org кроссворд http://learningapps.org/display?v=pyg27wept

Источники иллюстраций

1. Рисунок №1 , Рисунок №2 А.Г.Мерзляк, В.Б.Полонский, М.С.Якир, Рабочая тетрадь №1 Математика 5 класс, Москва «Вентана-Граф»,2012

2. Иллюстрации автора.

infourok.ru

Виды и типы углов. Острый, тупой, развернутый угол. Вертикальные углы. Смежные углы. Примерно 5-9 класс (10-14 лет)

Техническая информация тут Перевод единиц измерения величин Таблицы числовых значений Алфавиты, номиналы, единицы Математический справочник тут Физический справочник Химический справочник Материалы Рабочие среды Оборудование Инженерное ремесло Инженерные системы Технологии и чертежи Личная жизнь инженеров Калькуляторы Поиск на сайте DPVAПоставщики оборудованияПолезные ссылкиО проектеОбратная связьОтветы на вопросы.Оглавление

Адрес этой страницы (вложенность) в справочнике dpva.ru:  главная страница  / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа.  / / Виды и типы углов. Острый, тупой, развернутый угол. Вертикальные углы. Смежные углы. Примерно 5-9 класс (10-14 лет) Виды и типы углов. Острый, тупой, развернутый угол. Вертикальные углы. Смежные углы. Примерно 5-9 класс (10-14 лет) Поиск в инженерном справочнике DPVA. Введите свой запрос: Дополнительная информация от Инженерного cправочника DPVA, а именно — другие подразделы данного раздела: Шпаргалки по математике, алгебре и геометрии Правила сложения и вычитания. Таблица сложения от 1 до 10. Таблица сложения до 20. Таблица сложения в пределах 10. Таблица вычитания от 1 до 10. Таблица вычитания до 20. Таблица вычитания через десяток. Таблица умножения для 2 класса — традиционная 10×10, 12х12 и 20х20 Таблицы деления — традиционная 10×10 и 12х12 Единицы (измерения) длины см-дм-м, единицы измерения площади см2-дм2. Примерно 3 класс (8-9 лет). Доли и дроби. Арифметические действия с дробями. Сокращение дроби. Умножение и деление дроби на натуральное число. Умножение и деление дробей. Сложение и вычитание дробей с различными знаменателями. Перевод взаимный метрических единиц измерения площади: см2, дм2, м2, ар (сотка), гектра (га), км2 — таблица. Примерно 4 класс (9-10 лет).

dpva.ru

Виды углов. Измерение углов

Давайте представим себе такую историю.

– Ну и как же мне здесь разобраться? – бормотал Саша.

– Саша, что случилось? – спросил Паша.

– Мама, прежде чем уйти на работу, сказала, что купила один очень важный предмет, который мне пригодится на уроках математики.

– Здорово! – обрадовался за друга Паша. – И что это за предмет такой важный?

– Вот в этом и проблемка – загрустил Саша. – Мама спрятала этот предмет, но, чтобы я его нашёл, она подготовила инструкцию, где написано, что мне нужно сделать.

– Так давай я тебе помогу! – предложил Паша. – Показывай свою инструкцию!

– Смотри! – обрадовался Саша.

– В первом пункте написано, что я должен сделать 10 шагов прямо.

– Ну и что тут сложного? – удивился Паша.

– Ничего! – ответил Саша. – Шаги то я сделал, а вот в следующих пунктах сказано, что я должен повернуть вправо на величину, равную прямому углу, а затем сделать ещё 5 шагов. Что значит повернуть вправо на величину, равную прямому углу? Что это за величина-то такая и что за прямой угол?

– Да… проблемка! – задумался Паша. – Давай спросим у Электроши. Он точно сможет нам помочь!

– Ребята, прежде чем я вам расскажу об измерении углов, давайте немного разомнёмся и выполним устные задания, – предложил Электроша.

– Давайте сверимся! Посмотрите, что у вас должно было получиться!

– Ну а теперь поговорим об измерении углов, – предложил Электроша. – Но для начала давайте вспомним, что вообще называют углом.

– Углом называется геометрическая фигура, образованная двумя лучами, выходящими из одной точки – сказал Саша.

– Молодец! – похвалил Сашу Электроша. – Вы уже знаете, как измеряют отрезки. Скажите, что значит измерить отрезок?

– Измерить отрезок – означает подсчитать, сколько единичных отрезков в нём помещается – сказал Паша. – Для измерения отрезков мы использовали единичный отрезок (1 мм, 1 см и другие).

– Правильно! – подтвердил Электроша. – Тогда, как вы думаете, что значит измерить угол?

– Ну, наверное, – начал Паша, – измерить угол – означает подсчитать, сколько единичных углов в нём помещается.

– Верно! – сказал Электроша. – Однако для измерения углов у нас пока ещё нет такого единичного угла. Но мы можем сами его создать. И сейчас я вам покажу, как это сделать.

– Давайте нарисуем круг и разделим его на 360 равных частей. Угол, образованный двумя соседними лучами, выбирают за единицу измерения. И такой уголок принято называть градусом. Кстати, градус происходит от латинского слова и переводится как «шаг», «ступенька».

– То есть 1 градус – это и есть наш единичный угол, с помощью которого мы сможем определить величину нужного нам угла? – решили уточнить мальчишки.

– Правильно! – сказал Электроша. Запомните! Градус – это общепринятая единица, которой пользуются для измерения углов. Для обозначения градусов в тексте используют вот такой знак: ^о.

Так как мы с вами делили круг на 360 равных частей, то угол, равный плоскости круга, составляет 360 градусов, и называется такой угол полным углом.

– Электроша, а если полный угол разделить пополам, мы получим половинный угол? – поинтересовался Паша.

– Если плоскость круга разделить на 2 равные части, то плоскость одного полукруга составит угол в 180 градусов.

Запомните! Угол, равный полуплоскости круга, составляет 180 градусов и называется развёрнутым углом. Обратите внимание, стороны развёрнутого угла образуют прямую.

– А если бы мы разделили круг на 4 части? – спросил Саша.

– Если плоскость круга разделить на 4 равные части, то плоскость одной части составит угол в 90 градусов.

Запомните! Угол, равный четвёртой части круга, составляет девяноста градусов и называется прямым углом. Прямой угол обозначают вот таким значком: .

Существуют и другие виды углов.

Так, например, угол, градусная мера которого меньше 90 градусов, называют острым.

Угол, градусная мера которого больше 90 градусов, но меньше 180 градусов, называют тупым.

– Электроша, спасибо! Теперь я понял, что значит повернуть вправо на величину, равную прямому углу. Сейчас я быстренько найду предмет, который спрятала мама.

– Смотрите, какую необычную линейку купила мне мама! – воскликнул Саша. – Разве такая линейка пригодится на уроках математики?

– Саша, конечно, пригодится! – успокоил мальчика Электроша. – Такую линейку используют для измерения углов, а также для построения угла нужной величины. А называется эта линейка «транспортир».

– Вообще, этот инструмент может иметь разный внешний вид, но у любого транспортира есть шкала, которая расположена на полуокружности.

Давайте поближе рассмотрим Сашин транспортир.

Посмотрите, внешне он напоминает полукруглую линейку со шкалой и делениями. Внизу, на ровной поверхности, расположена привычная нам прямая линейка для измерения отрезков. В верхней части – полукруг с двойной шкалой для измерений. В каждом из направлений шкала рассредоточена по транспортиру от 0 до 180 градусов. Каждое деление шкалы транспортира равно 1 градусу. Центр шкалы отмечен штрихом или отверстием.

– Электроша, а как измерять углы транспортиром? – уточнили ребята.

– Это совсем несложно, – сказал Электроша. – Давайте рассмотрим алгоритм измерения углов на примере.

Итак, найдём величину угла АОВ. Для начала совместим вершину угла с центром транспортира. Затем расположим транспортир так, чтобы одна из сторон угла прошла по линейке. У нас это сторона ОВ. А теперь найдём штрих на шкале, через который проходит вторая сторона угла. Этот штрих и укажет градусную меру (величину) нашего угла. Посмотрите, в нашем случае градусная мера угла АОВ равна 60 градусам. Записывают это так: .

– Электроша, ты говорил, что с помощью транспортира можно строить углы, – решил уточнить Саша. – Научишь нас?

– Конечно! – обрадовался Электроша. – Давайте рассмотрим алгоритм построения углов на конкретном примере.

– Итак, давайте построим угол АВС, равный 120 градусам. Для начала отметим произвольную точку и обозначим её буквой В. Затем начертим луч с началом в точке В и на нём отметим точку А. Получим луч ВА. Теперь приложим к этому лучу транспортир так, чтобы его центр совпал с точкой В, а сам луч ВА прошёл через начало отсчёта на шкале. Затем на этой же шкале найдём штрих, который соответствует 120 градусам. За штрихом отметим точку и обозначим её буквой С. Осталось провести луч ВС. Вот так мы с вами построили угол АВС, равный 120 градусам.

– Как видите, всё очень легко! Нужно просто один раз попробовать и всё обязательно получится!

– А теперь скажите, какие углы мы называем равными? – спросил у ребят Электроша.

– Два угла называют равными, если они совпадают при наложении, – ответили мальчишки.

– Молодцы! – похвалил ребят Электроша. – Так как равные углы полностью совмещаются при наложении, то можем сделать вывод, что равные углы имеют равные градусные меры. А значит, из двух неравных углов большим будем считать тот, градусная мера которого больше, и, соответственно, меньшим тот, градусная мера которого меньше.

– Посмотрите, я нарисовал 3 разных угла, – продолжил Электроша. – Что вы можете сказать об их величинах?

– Даже не измеряя транспортиром, видно, что угол MNP больше угла QST, – начал Паша. – Ещё можно сказать, что угол EFG меньше угла MNP.

– А если измерить эти углы, – продолжил Саша, то увидим, что угол QST равен углу EFG.

– Ещё вам следует знать свойство величины угла.

Запомните! Если между сторонами угла ABC провести луч BD, то градусная мера угла ABC равна сумме градусных мер углов ABD и DBC. Записывают это свойство так: .

– Вот, например, градусная мера угла ABD равна 30 градусам, а градусная мера угла DBC равна 20 градусам. Тогда чему будет равна градусная мера угла ABC?

– По свойству величины угла, – начал Паша, – мы должны сложить величины углов ABD и DBC. Тогда величина угла ABC равна 50 градусам.

– А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним задание.

Итак, угол ABC разделён лучом BD на два угла ABD и DBC так, что градусная мера угла ABD равна 29 градусам, а градусная мера угла DBC равна 61 градусу. Постройте угол ABC и определите его вид.

Решение: для начала нам нужно выяснить градусную меру угла ABC. Применяя свойство величины угла, получаем, что угол ABC равен 90 градусов. Теперь построим этот угол. И осталось определить его вид. Мы знаем, что угол, который составляет 90 градусов, называется прямым углом. Значит, наш угол ABC – прямой.

videouroki.net