Составить уравнение касательной к графику функции параллельной прямой: Напишите уравнение касательной к графику функции f(x)=x3-6×2+10x-1 параллельной прямой y=-2x+1

Прямая параллельна касательной к графику функции

Рассмотрим задания из №7 ЕГЭ, в которых данная прямая параллельна касательной к графику функции.

№1

Прямая y=9x+5 параллельна касательной к графику функции y=x²-5x+54. Найти абсциссу точки касания.

Решение:

Прямые y=k₁x+b₁ y=k₂x+b₂ параллельны,если их угловые коэффициенты равны: k₁=k₂.

y=9x+5, отсюда k₁=9.

Угловой коэффициент касательной равен значению производной в точке касания: k₂=f'(x_o).

f'(x)=(x²-5x+54)’=2x-5;

f'(x_o)=2x_o-5.

Таким образом, 2x_o-5=9; 2x_o=14; x_o=7.

Ответ: 7.

№2

Прямая y=14-2x является касательной к графику функции y=x³+1,5x²-8x+4. Найти абсциссу точки касания.

Решение:

Угловой коэффициент касательной равен значению производной в точке касания: k=f'(x_o).

f'(x)=(x³+1,5x²-8x+4)’=3x²+3x-8;

f'(x_o)=3x_o²+3x_o-8.

По условию, y=14-2x. Отсюда k=-2.

3x_o²+3x_o-8=-2

3x_o²+3x_o-6=0

x_o²+x_o-2=0

x_o=1 либо x_o=-2.

Точка касания принадлежит и касательной, и графику функции.

x_o³+1,5x_o²-8x_o+4=14-2x_o.

Проверяем, выполняется ли равенство при x_o=1:

1³+1,5·1²-8·1+4=14-2·1?

-1,5≠12.

При x_o=-2:

(-2)³+1,5·(-2)²-8·(-2)+4=14-2·(-2)

18=18.

Абсцисса точки касания равна x_o=-2.

Ответ: -2.

№3

Прямая y=11x+8 является касательной к графику функции y=ax²+7x-2. Найти a.

Решение:

Угловой коэффициент касательной равен значению производной в точке касания: k=f'(x_o).

f'(x)=(ax²+7x-2)’=2ax+7;

f'(x_o)=2ax_o

+7.

По условию, уравнение касательной y=5x+1, поэтому k=5.

Имеем: 2ax_o+7=11, откуда ax_o=2.

Точка касания принадлежит и касательной, и графику функции, поэтому

ax_o²+7x_o-2=11x_o+8. Подставив в это равенство ax_o=2, получим

2x_o+7x_o-2=11x_o+8, откуда x_o=-5.

ax_o=2

-5_a=2

a=-0,4.

Ответ: 0,4.

№4

Прямая y=-6x+7 является касательной к графику функции y=6x²+bx+13. Найти b, учитывая, что абсцисса точки касания меньше 0.

Решение:

Угловой коэффициент касательной равен значению производной в точке касания: k=f'(x_o).

f'(x)=(6x²+bx+13)’=12x+b;

f'(x_o)=12x_o+b.

По условию, уравнение касательной y=-6x+7, поэтому k=-6.

Имеем: 12x_o+b=-6, откуда b=-12x

o-6.

Точка касания принадлежит и касательной, и графику функции.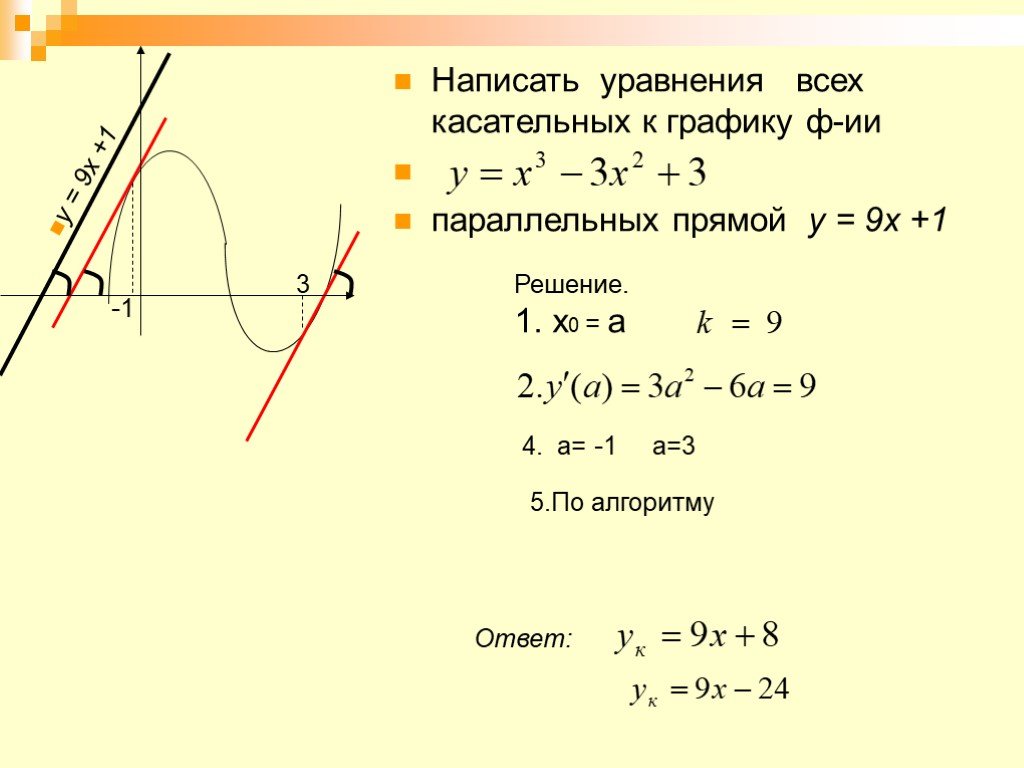

6x_o²+bx_o+13=-6x_o+7

6x_o²+(-12x_o-6)x_o+13=-6x_o+7

6x_o²-12x_o²-6x_o+13+6x_o-7=0

-6x_o²+6=0

x_o=1 либо x_o=-1.

По условию, x_o<0, следовательно, x_o=-1.

b=-12·(-1)-6=6.

Ответ: 6.

№5

Прямая y=2x+4 является касательной к графику функции y=x²-4x+c. Найти c.

Решение:

Угловой коэффициент касательной равен значению производной в точке касания: k=f'(x_o).

f'(x)=(x²-6x+c)’=2x-6;

f'(x_o)=2x_o-6.

По условию, уравнение касательной y=2x+4, поэтому k=2.

Имеем: 2x_o-6=2, откуда x_o

=4.

Точка касания принадлежит и касательной, и графику функции, поэтому

x_o²-4x_o+с=2x_o+4. Подставив в это равенство x_o=4, получим

16-16+с=8+4

с=12.

Ответ: 12.

Уравнение касательной к графику функции

Похожие презентации:

Уравнение касательной к графику функции

Уравнение касательной к графику функции

Уравнение касательной к графику функции. 10 класс

Касательная к графику функции

Уравнение касательной к графику функции

Касательная к графику функции

Уравнение касательной. Условие касания

Касательная. Уравнение касательной

Функции и их свойства. Предел последовательности и функции. Производная функции и дифференциал

Производная сложной функции

1. Уравнение касательной к графику функции

2. Верно ли определение?

Касательная – это прямая,
имеющая с данной кривой
одну общую точку.

3. Пусть дана и две прямые и , имеющая с данной параболой одну общую точку М (1;1).

Пуст ь дана y x 2 и две прямые x 1 и y 2 x 1 ,
имеющая с данной параболой одну общую т очку М
(1;1).
x 1

4.

На данном уроке:1. выясним, что же такое касательная к
графику функции в точке, как составить
уравнение касательной;
2. рассмотрим основные задачи на
составление уравнения касательной.
Для этого:
вспомним общий вид уравнения прямой
условия параллельности прямых
определение производной
правила дифференцирования
Формулы дифференцирования

5. Определение производной

Пусть функция y f (x) определена в
некотором интервале, содержащем внутри
себя точку x0 . Дадим аргументу x
приращение такое, чтобы не выйти из этого
интервала. Найдем соответствующее
приращение y функции и составим
y
отношение x .Если существует предел
отношения при x 0 , то указанный предел
называют производной функции
y f (x)
‘
в точке x0 и обозначают f ( x0 ) .
y
lim
f ‘ ( x0 )
x 0 x

6. Правила дифференцирования

1. Производная суммы равна сумме производных.
f x g x ‘ f ‘ x g ‘ x
2. Постоянный множитель можно вынести за знак
производной.
‘
‘
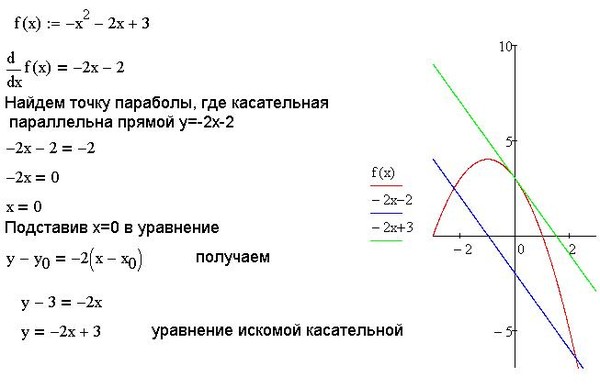
kf x kf x
3. Производная произведения двух функций равна сумме
двух слагаемых; первое слагаемое есть произведение
производной первой функции на вторую функцию, а второе
слагаемое есть произведение первой функции на
производную второй функции.
f x g x f ‘ x g x f x g ‘ x
‘
4. Производная частного
f x
f ‘ x g x f x g ‘ x
2
x
g
x
g
‘

7. Основные формулы дифференцирования

f (x)
С
1
x
x
x
‘
f ( x)
‘
f (x)
f ( x)
0
sin x
cos x
1
2
x
cos x
sin x
1
2 x
x
1
tgx
ctgx
1
cos 2 x
1
2
sin x

8. Две прямые параллельны тогда и только тогда, когда их угловые коэффициенты равны

Параллельны ли прямые:
a ) y 2 x 1;
б) y 2 x 2;
в) y 3 x 1.

9. Пусть дан график функции y=f(x). На нем выбрана точка M(a;f(a)), в этой точке к графику функции проведена касательная (мы

предполагаем, что она существует). Найти угловой
коэффициент касательной.
y f x , M a; f a
k сек
y
x
k кас lim kcек
x 0
k кас
y
lim
x 0 x

10. Геометрический смысл производной

Если к графику функции y = f (x) в точке
x a можно провести касательную,
непараллельную оси у, то f ‘ (a)
выражает угловой коэффициент
касательной
kкас
y
f (a x) f (a)
‘
lim
lim
f a
x 0 x
x a
(a x) a

11. Геометрический смысл производной

Производная в точке
x x0 равна
угловому коэффициенту
касательной к
графику функции
y = f(x) в этой точке.
.
Т.е.
f ( x0 ) tg
‘
Причем, если :
1. f ‘ ( x0 ) tg 0, то острый
2. f ‘ ( x0 ) tg 0, то развернутый
3. f ‘ ( x0 ) tg 0, то тупой

12. Вывод уравнения касательной

y kx m, M a; f a
Пусть прямая задана уравнением:
k f ‘ (a)
f a ka m
m f a ka
y kx f a ka
y f a f
‘
a x a
уравнение касательной к
графику функции
y f (x)

13.

Составить уравнение касательной:к графику функции
M 1;1
f (1) 12 1
f ‘ ( x) 2 x
f ‘ (1) 2 1 2
y f (a ) f ‘ (a )( x a )
y 1 2 ( x 1)
y 1 2x 2
y 2x 1
f ( x) x
2
в точке

14. Составить уравнение касательной:

к графику функции
f (0) tg 0 0
1
f ( x)
cos 2 x
1
‘
f ( 0)
1
2
cos 0
y f (a ) f ‘ (a )( x a )
‘
y 0 1 ( x 0)
y x
y tgx
в точке M 0;0

15. Алгоритм нахождения уравнения касательной к графику функции y=f(x).

1. Обозначим абсциссу точки касания буквой
x=a.
2. Вычислим f (a ) .
3. Найдем f ‘ ( x) и f ‘ (a) .
4. Подставим найденные числа a , в формулу
y f a f a x a .
‘

16. Составить уравнение касательной к графику функции в точке .

Составить уравнение касательной к
1
графику функции y в точке x 1 .
x
1
f ( x)
x
1) a 1
2) f (a) f (1) 1
1
‘
3) f ( x) 2
x
1
f (a ) f (1) 2 1
1
‘
‘
4) y 1 ( x 1)
y 2 x
Ответ
y 2 x
:

17.

К графику функции провести касательную так, чтобы она была параллельна прямой .x3
К графику функции y 3
провести касательную так,
чтобы она была параллельна прямой y 4 x 5 .
kкас 4, k кас f ‘ ( x) f ‘ ( x) 4
x
f ( x)
3
‘
1
3 x 2 x 2
3
f ‘ (a) a 2 a 2 4,
3
‘
.
1) a1 2, a2 2
3
(
2
)
8
2
8 , f (a )
2) f (a1 )
2
3
3
3 3
3
3) f ‘ (a1 ) f ‘ (a2 ) 4
16
16
4) y 4 x
, y 4x
3
3
,
y
lim
f ‘ ( x0 )
x 0 x
f ‘ ( x0 ) tg
острый tg 0
f ‘ ( x0 )
Ответ : f (2) 0,5
2 1
0,5
4 2
Самостоятельная работа
Напишите уравнение касательной к графику функции
у=f(x) в точке с абсциссой а.
1) f(x) = х²+ х+1, а=1
2) f(x)= х-3х², а=2

20. Ответьте на вопросы:

1. Что называется касательной к графику
функции в точке?
2. В чем заключается геометрический
смысл производной?
3. Сформулируйте алгоритм нахождения
уравнения касательной?

English     Русский Правила

2+3, что параллельно 8x-y+3=0.

Подписаться І 1

Подробнее

Отчет

2 ответа от опытных наставников

Лучший Новейшие Самый старый

Автор: Лучшие новыеСамые старые

Брэдфорд Т. ответил 15.01.21

Репетитор

4.9(29)

Инженер на пенсии / преподаватель математики высшей категории

См. таких репетиторов

Смотрите таких репетиторов

8x-y +3=0 —>

y = 8x +3 = mx + b

Линия, параллельная y = 8x+3, будет иметь такой же наклон, m=8. Наклон также является производной от y=2x ² +3

y’ = 4x = 8 —> x = 2

y = 2(2) ² +3 = 11. Таким образом, точка пересечения (2,11)

Чтобы получить уравнение для прямой, проходящей через эту точку

y-11 = 8(x-2) —> y = 8x-16+11 = 8x-5

y = 8x-5

Голосовать за 0 голос против

Подробнее

Отчет

Джош Ф.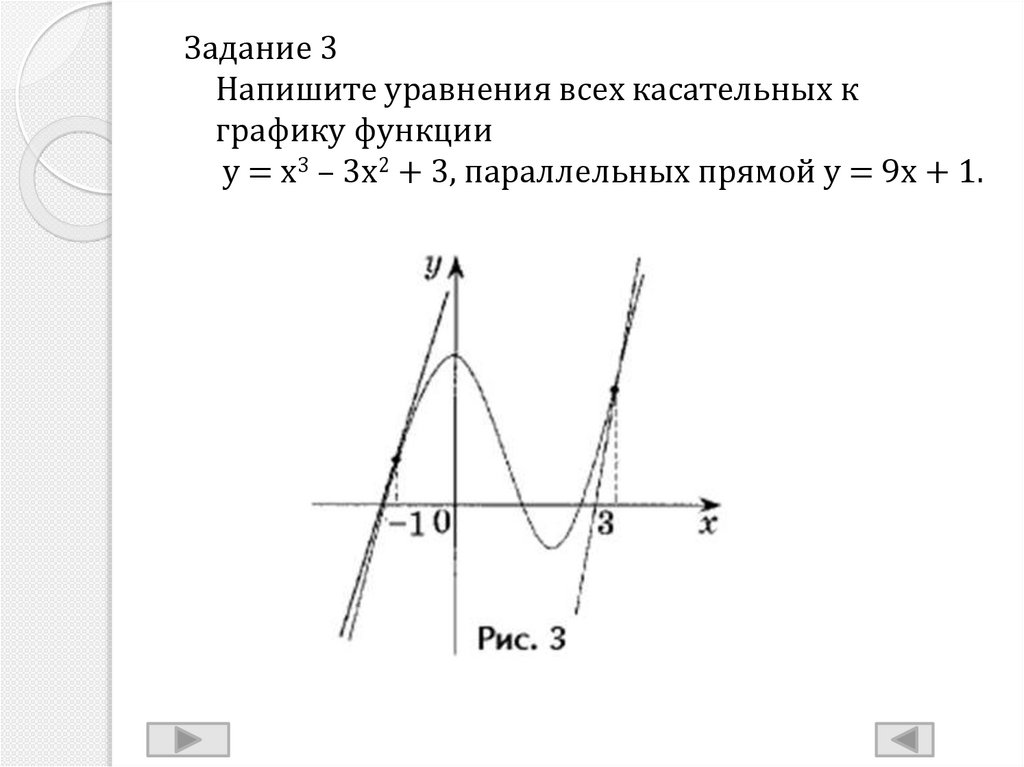 ответил 15.01.21

Репетитор

5,0 (170)

Джош Ф.: Опытный репетитор по математике, английскому языку и подготовке к экзаменам

Об этом репетиторе ›

Об этом репетиторе ›

Данная линия имеет наклон = 8.

Вы хотите взять производную от квадрата и установить ее = 8.

y ‘ = 4x = 8 , x = 2

Наконец, найдите точку на параболе ( квадратичный) при x = 2, и напишите уравнение касательной с наклоном = 8, содержащей эту точку (проще всего использовать форму pt-наклона линии): 92 +3 = 11, поэтому (2, 11) — точка касания, а y — 11 = 8 (x — 2) — уравнение касательной.

Голосовать за 0 голос против

Подробнее

Отчет

Все еще ищете помощи? Получите правильный ответ, быстро.

Задайте вопрос бесплатно

Получите бесплатный ответ на быстрый вопрос.
Ответы на большинство вопросов в течение 4 часов.

ИЛИ

Найдите онлайн-репетитора сейчас

Выберите эксперта и встретьтесь онлайн. Никаких пакетов или подписок, платите только за то время, которое вам нужно.

3-3-skills-practice-slopes-of-lines-worksheet-answers — Googlesuche

AlleBilderVideosShoppingMapsNewsBücher

suchoptionen

[PDF] 3-3 — Практические навыки

tmpsantafe.org › загрузки › 2018/08 › CW_G_SP_3-3_ans

Глава 3. 19. Геометрия Glencoe. Практика навыков. Наклоны линий. Определить наклон линии, содержащей данные точки. 1. S(-1, 2), W(0, 4) 2.

[PDF] Геометрия Glencoe — ASB Bangna — Математические курсы средней школы

asb-bangna-highschoolmath.weebly.com › geo_3.3_prac_answers .pdf

3-3 Практические навыки. Наклоны линий. Определить наклон линии, содержащей данные точки. 1. S(-1, 2), W(0, 4) 2. 2. G(-2, 5), H(1, -7)-4.

[PDF] Наклон линий AK.pdf

www.lmtsd.org › cms › lib › Centricity › Домен › Наклон линий AK

KEY. Упражняться. Наклоны линий. Определите наклон линии, содержащей… Найдите наклон каждой прямой. 3. ЛМ. М = 2/3. М. 5. линия, параллельная GR.

[PDF] Практика — McConnMath

mcconnmath.pbworks.com › file › fetch › 3-3 Практические ответы

ПЕРИОД. Глава 3. 20. Геометрия Гленко. Упражняться. Наклоны линий. Определить наклон линии, содержащей данные точки. 1. В(-4, 4), R(0, 2)-.

[PDF] geom-3-1-3-4-rev-key.pdf — ahodginscc

ahodginscc.files.wordpress.com › 2014/10 › geom-3-1-3-4-rev- ключ

31 Практика навыков. Параллельные прямые и… 3. все отрезки, пересекающие GH… Определить наклон прямой, содержащей заданные точки.

[PDF] Ch 3 Sec 3 Skills Practice Solutions.pdf

www.waynesville.k12.mo.us › cms › lib › Centricity › Domain › Ch 3…

3-3 Skills Practice. Скорость изменения и наклон. Найдите наклон прямой, проходящей через каждую пару точек. 1. (0,1). 0. (2,5). 2. Да. (3, 1).

3 3 навыка отработки уклонов линий ответы на лист

dainvestmax.de › 3-3-навыки-практика-наклоны-линий-…

D. Параллельные линии и 3. Рабочий лист HW Solutions 4 3 Основные разделы 4 1 3 Математика 110 112 Практический тест 7 Практика 6 2 Наклон 3-4 Навыки Практика Наклон Пересечение …

3 3 Навыки Практика наклона линий стр. 20 PDF, Doc, изображения

www.pdfprof.com › PDF_Image

2. ИЗМЕРЕНИЕ На каждый ярд приходится 3 фута. 3. Используйте график, показывающий количество пройденных кругов с течением времени. домашнее задание, практика, уклон, ответы .