Составить уравнение высоты треугольника проведенной из вершины онлайн: Уравнение высоты треугольника

Уравнение высоты треугольника

Длина сторон треугольника:
|AB| = 15
|AC| = 11.18
|BC| = 14.14
Расстояние d от точки M: d = 10
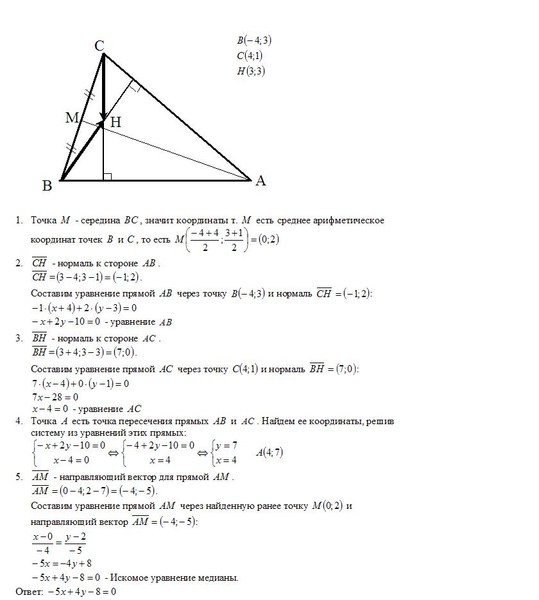
Даны координаты вершин треугольника: A(-5,2), B(7,-7), C(5,7).
2) Длина сторон треугольника
Расстояние d между точками M₁(x₁; y₁) и M₂(x₂; y₂) определяется по формуле:




8) Уравнение прямой
Прямая, проходящая через точки A₁(x₁; y₁) и A₂(x₂; y₂), представляется уравнениями:

Уравнение прямой AB
Каноническое уравнение прямой: или
или y = ^-3/₄x ^-7/₄ или 4y + 3x +7 = 0
Уравнение прямой AC
Каноническое уравнение прямой: или
или y = ¹/₂x + ⁹/₂ или 2y -x — 9 = 0
Уравнение прямой BC
Каноническое уравнение прямой: или

5) уравнение окружности, для которой высота CD есть диаметр;
Уравнение окружности радиуса R с центром в точке E(a;b) имеет вид:
(x-a)² + (y-b)² = R²

Система линейных неравенств:
y ≥ ^-3/₄x ^-7/₄ или y + ³/₄x ≥ ^-7/₄ или 3x + 4y ≥ -7
y ≤ ¹/₂x + ⁹

зачет — презентация онлайн

1) Два угла называются вертикальными, если стороны
одного угла являются продолжениями сторон другого. 2
3) а) Длина отрезка АВ равна:
АВ = √(0 + 2)² + (3 — 1)² = √4 + 4 = √8 = 2√2.
CD = √(2 — 4)² + (-1 — 1)² = √4 + 4 = √8 = 2√2.
Длины отрезков равны, значит, AB = CD.
Найдём координаты вектора AB:
AB{0 + 2; 3 — 1}
AB{2; 2}.
Теперь координаты вектора DC:
DC{4 — 2; 1 + 1}
DC{2; 2}.
Координаты векторов равны, тогда они коллинеарны, а, значит, и
параллельны.
б) Найдём длины отрезков BC и AD:
BC = √(4 — 0)² + (1 — 3)² = √16 + 4 = √20 = 2√5.
AD = √(2 + 2)² + (-1 — 1)² = √16 + 4 = √20 = 2√5.
Тогда AB = CD, BC = AD => ABCD — параллелограмм.
PABCD = 2√5•2 + 2√2•2 = 4√5 + 4√2 = 4(√5 + √2).
1)Треугольники ABC и A1B1C1 считаются равными в том
случае, если их можно совместить наложением. При этом, все
стороны и вершины фигур полностью наложатся друг на
друга, а все соответствующие углы совместятся.
Признаки: 1. Если две стороны и угол между ними одного
треугольника равны соответствующим двум сторонам и углу
между ними другого треугольника, то такие фигуры равны. 2=16 |
5
3
1) Две прямые плоскости называются параллельными, если они
не пересекаются. Если каждая из двух прямых параллельна
одной и той же третьей прямой, то они параллельны и между
собой.
2) Пусть дан треугольник АВС, достроим его до параллелограмма
АВСД, тругю АВС и ДСВ равны по трем сторонам (ВС-общая, АС=ВД
как противоположные стороны параллелограмма,) их площади
раывны. Следовательно площадь треуг АВС равна половине
площади Параллелограммв АВСД, т.е. S1/2AB*CH
1) 1.Если две параллельные прямые пересечены третьей прямой,
1) Сумма углов треугольника на евклидовой плоскости равна 180°.
7 2)
6 то внутренние накрест лежащие углы равны. 2. Если две
3) Нарисуем трапецию АВСД, отвечающую условию задачи.
Отложим большее основание АД и из А перпендикуляр АН.
Он будет высотой равнобедренного пр/тр ВАС, проведенной из
вершины прямого угла ВАС к меньшему основанию ВС
( гипотенузе тре-ка ВАС), т.к. тре-ик р/б, и будет также высотой
трапеции. Высота АН является и медианой – тре-ик р/б,а медиана пр/тр равна половине гипотенузы: h=10:2=5 см.
S=h(a+b):2
S=5*(10+20):2=75 см²
1) Внешний угол равен разности между 180° и
внутренним углом, он может принимать значения
от 0 до 180° не включительно. Свойста: Внешний
угол треугольника равен сумме двух оставшихся углов
треугольника, не смежных с этим внешним углом.
2) Длина окр-ти: L = π*D; длина дуги:
3) Сумма наибольшей и наименьшей сторон в первом
4угольнике равна 2+5=7, во втором = 28, т.е. коэф.
подобия = 4. Отношения площадей 4угольников
равняется коэф. в квадрате, т.е. S₂ к S₁ = 4² = 16, а
стороны второго 4угольника = 2*4, 3*4, 4*4, 5*4, т.е.
8, 12, 16, 20.
9
параллельные прямые пересечены секущей, то сумма внутренних
односторонних углов равна 180°. 3. Если две параллельные
прямые пересечены секущей, то соответственные углы равны.
2) Суммой векторов, следующих друг за другом, называется вектор, начало
которого совпадает с началом первого вектора, а конец с концом
последнего вектора. Разностью двух векторов а и b называется такой вектор
,сумма которого с вектором b равна вектору а.
а
b
В
С
А
Пусть а и b – два вектора
1)
Отметим точку А
2)
Отложим АВ=а
3)
Отложим ВС=b
4)
АС-сумма векторов a и b
Данный способ – правило тре-ка
3) S параллелограмма abcd = ad*bm=cd*bk, следовательно
bm=cd*bk/ad=15*12/18=10 см.
Sin a = bm/ab=12/18=2/3=0,66, следовательно угол а = 42 градуса.
Угол a=c=42 градуса. Угол в=d=138 градусов
1)Около любого треугольника можно описать окружность, и только
одну. Центром окружности, описанной около треугольника, является
точка пересечения серединных ерпендикуляров к
сторонам треугольника.
2)Поскольку пр/тр DFC равен пр/тр AEB то чет-ик AEFB –
прямоугольник. Поэтому SABCD = SAEFD = a ha , чтд
. Докажем, что в каждый ромб можно вписать окружность.
заметим что тре-ик ABD и BCD равны в силу признака равенства
треугольников «По трём сторонам => диагональ BD – бис-са углов
B и D, а бисс-сы углов A и C пересекаются в некоторой точке O,
лежащей на диагонали BD. Точка O и является центром
вписанной в ромб окружности. Если r – радиус вписанной в
дельтоид окружности, то
10
8
3) Пусть имеем трапецию АВСД с прямыми углами А
и В.
Из вершины С опустим перпендикуляр СЕ на АД.
ЕД = √(17² — 15²) = √(289 — 225) = √64 = 8 см.
Тогда ВС = АЕ = 18 — 8 = 10 см.
Получаем периметр Р = 10+18+15+17 = 30 см.
Для нахождения точки О пересечения диагоналей найдём их уравнения в
прямоугольной системе координат. Ноль в точке А.
АС: у = (15/10)х = (3/2)х.
ВД: у = (-15/18)х + 15 = (-5/6)х + 15.
Приравняем: (3/2)х = (-5/6)х + 15.
(3х/2) + (5х/6) = 15.
Приведём к общему знаменателю:
9х + 5х = 80.
14х = 80
х = 80/14 = 40/7.
Находим расстояние от точки пересечения диагоналей трапеции до ее
основания — это отрезок ОН = у = (3/2)*(40/7) = 60/7 = 8(4/7) см.
1)В любой треугольник можно вписать окружность, причем только
одну. Центром вписанной в треугольник окружности является точка,
в которой пересекаются все биссектрисы треугольника.
11
2)
3)
1)Параллелограмм — это четырехугольник, у которого противоположные
1)
стороны попарно параллельны и равны.
•Четырёхугольник является параллелограммом, если его противоположные
стороны попарно равны.
•Четырёхугольник является параллелограммом, если его диагонали
пересекаются и точкой пересечения делятся пополам.
•Четырёхугольник является параллелограммом, если две его стороны
параллельны и равны. 2)
– пара-ам у которого все углы прямые
13 1)Прямоугольник
Свойства: диагонали пр-ка равны BD=CA; все отрезки, которые 14
12
получаются при пересечении диагоналей пря-ка равны –
OA=OB=OC=OD
2)
описанная окрВписанная окр-ость в правильном тре-ке
ость в правильном
тре-ке через
сторону и высоту
3) Расстояние между двумя точками вычисляются по формуле
АВ=√(х2-х1)²+(у2-у1)².
НF=√(6-1)²+(3-3)²=√25=5.
FQ=√(6-1)²+(3-8)²=√50=5√2.
НQ=√(1-1)²+(8-3)²=√25=5.
ΔHFQ — равнобедренный HQ=HF=5.
Можно сразу определить вид данного треугольника: прямоугольный
равнобедренный, значит острые углы по 45°.
Ответ:45 °.
Но можно по формуле косинусов определить острый угол С.
FQ²=HF²+HQ²-2·HF·HQ·cosH=25+25-2·5·5·cosH=50.
50-50·cosH=50.
50(1-cosH)=50.
1-cosH=50/50.
1-cosH=1.
cosH=0.
∠H=90°, значит два острых угла равны по 45°.
Ответ: ∠F=45°.
2)
3)Обозначим внутренний угол за Х, тогда внешний равен 5Х.
Составим уравнение
2)
Х+5Х= 180
6Х=180
Х=30
5*30=150
180-30-30=120
Ответ: внутренние два угла при основании равны по 30 градусов, внутренний
при вершине равен 120 градусов, внешний равен 150 градусов,
=>
=>
1)Ромб – пара-ам у которого все стороны равны
Свойства: диагонали ромба пересекаются под прямым углом;
Диагонали ромба являются биссе-ами его улов
2)
Средняя линия треугольника — отрезок, который
15 1)соединяет
середины двух сторон. В любом треугольнике
1) Средняя линия трапеции — отрезок, соединяющий
16 середины боковых сторон этой трапеции.
можно провести три средних линии.
2) Просто высота h к стороне а равна b*sinC, где С — угол
между a и b.
S = a*h/2 = a*b*sinC/2;
И будьте внимательны к обозначениям — малыми буквами
обычно обозначаются стороны, противолежащие
одноименным углам — сторона a (= ВС) напротив угла А,
сторона b (=АС) напротив угла В, сторона с (=АВ) напротив
угла С.
То есть между сторонами a и b лежит угол С.
Или S=Hc*c/2, где Hc — высота, проведенная из вершины С
к стороне с.
Hc=b*sin(A)
По теореме синусов a/sin(A)=c/sin(C) с=a*sin(C)/sin(A)
S=b*sin(A)*a*sin(C)/2*sin(A)=b*a*sin(C)/2
2)
3)
17
1)
2)
3)
18
1)
19
Если две стороны одного треугольника пропорциональны двум
сторонам другого треугольника, а углы, заключённые между этими
сторонами равны, то такие треугольники подобны.
Если два угла одного треугольника равны двум углам другого
треугольника, то такие треугольники подобны.
Если стороны одного треугольника пропорциональны сторонам
другого треугольника, то такие треугольники подобны
Чтобы доказать подобие данных треугольников, требуется доказать, что DF = kAC,
так как подобие треугольников определяется по трем пропорциональным
сторонам.
Найдем стороны AC и DF по теореме косинусов (квадрат стороны треугольника
равен сумме квадратов двух других сторон за вычетом удвоенного
произведения этих сторон, умноженному на косинус угла между ними):
AC2 = AB2 + BC2 – 2 · AB · BC · cos B
DF2 = DE2 + EF2 – 2 · DE · EF · cos E
Так как ∠B = ∠E и AB = kDE, BC = kEF, то мы можем выразить квадрат стороны DF
через угол и стороны треугольника ABC:
DF2 = (kAB)2 + (kBC)2 – 2 · kAB · kBC · cos B
Вынесем k2 за скобку:
DF2 = k2(AB2 + BC2 – 2 · AB · BC · cos B)
Выражение в скобках равно ранее выраженному через теорему косинусов
квадрату стороны AC. Поэтому можно записать так:
DF2 = k2AC2 Отсюда получаем, что DF = kAC, что и требовалось доказать.
2)
3)
1) Вписанный угол — это угол, вершина которого лежит на окружности.
Вписанный угол равен половине центрального угла, опирающегося на ту
же дугу, и дополняет до 180° половину центрального угла, опирающегося
на дополнительную дугу.
есть треугольник, вписанный в окружность.
21 1)Пусть
22
Обозначим его как ABC. Что бы доказать всю
20 1)
2)
=>
2) Дана прямая а и точка М, не лежащая на ней.
Проводим дугу с центром в точке М (черная), произвольного радиуса, большего
расстояния от точки М до прямой.
Получили две точки пересечения дуги и прямой а. Обозначим их А и В.
Теперь построим две окружности (красных), с центрами в данных точках, произвольного
одинакового радиуса (большего половины отрезка АВ).
Точки пересечения этих окружностей назовем К и Н.
Проводим прямую КН.
КН — искомый перпендикуляр к прямой а.
Доказательство:
Если точка равноудалена от концов отрезка, значит она лежит на серединном
перпендикуляре к отрезку.
АК = КВ как равные радиусы, значит К лежит на серединном перпендикуляре к отрезку
АВ.
АН = НВ как равные радиусы, значит Н лежит на серединном перпендикуляре к отрезку
АВ.
КН — серединный перпендикуляр к отрезку АВ.
МА = МВ как равные радиусы черной окружности, значит и точка М лежит на прямой КН,
т.е. перпендикуляр к прямой а проходит через точку М
теорему, так как треугольник имеет произвольные
размеры, можно доказать только то, что соотношение
1-ной произвольной стороны к противолежащему
углу соответствует 2R. Допустим, это будет 2R =
a/sin а , т.е. если смотреть по чертежу 2R = BC / sin
A. Проведем диаметр |BG| для описанной
окружности. Из свойства углов, которые вписаны в
окружность, угол GCB будет прямым, а
угол CGB равен либо а когда точки A и G находятся
по одну сторону от прямой BC, или пи-а в
противоположном варианте. Так как sin (пи-а) =sin а,
в обоих случаях получаем: Повторяем это же
рассуждение для оставшихся сторон треугольника..чт
2)
3) Пусть большая сторона ВС=Х , а меньшая сторона АВ = У.
Составим систему Х — У=12 и Х/У=7/3
Х=12+У подставим первое уравнение во второе , получим :
(12+у)/У=7/3
3·(12+У)=7У
36+3У=7У
4У=36
У=9 ( меньшая сторона
9+12=21 ( большая сторона )
Р=2·(21+9)=60
Ответ : 60
1) Выпуклым многоугольником называется многоугольник, все
точки которого лежат по одну сторону от любой прямой,
проходящей через две его соседние вершины. Сумма углов
выпуклого n-угольника равна 180˚ *(n-2)
2)
С помощью линейки проводим прямую а и на
ней с помощью циркуля отложим отрезок АВ,
равный отрезку МК. Для этого произвольно на прямой а ставим
точку А, с помощью циркуля измеряем отрезок МК и строим окружность с
центром в точке А радиуса МК (всю окружность строить необязательно,
смотри, выделенное красным цветом). Точку пересечения окружности с
прямой а обозначаем В.
1) 1. Если при пересечении двух прямых секущей, накрест лежащие углы
23 равны, то прямые параллельны.
2. Если при пересечении двух прямых секущей, соответственные углы
равны, то прямые параллельны.
3. Если при пересечении двух прямых секущей, сумма односторонних
углов равна 180°, то прямые параллельны.
1)Если катеты одного треугольника соответственно равны катетам другого
24 треугольника, то такие прямоугольные треугольники равны. Если катет и
2)
25
прилежащий острый угол одного треугольника соответственно равны катету и
прилежащему острому углу другого треугольника, то такие прямоугольные
треугольники равны. Если гипотенуза и острый угол одного треугольника
соответственно равны гипотенузе и острому углу другого треугольника, то такие
прямоугольные треугольники равны.
Если гипотенуза и катет одного
треугольника соответственно равны гипотенузе и катету другого треугольника, то
такие прямоугольные треугольники равны. ДОК-ВО_3:
Дано: тре-ик АВС и тре-ик А1В1С1, <C=<C1=90,AB=A1B1, <A=<A1
Док-ать: : тре-ик АВС = тре-ик А1В1С1
Док-во: Доказываем наложением тре-ик АВС на тре-ик А1В1С1. Гипотенузы при
этом совместятся. АС пойдет по А1С1, так как <A=<A1. Но ВС АС и B1C1 A1C1. BC
совпадает с В1С1. ЧТД
2) прямая, имеющая с окр-тью только одну общую точку, называтся
касательной к окр-ти, а их лбщая точка называется точкой касания прямой
и окр-тию. Если прямая проходит через конец радиуса, лежащий на
окружности, и перпендикулярна этому радиусу, то она
является касательной.
Далее, с помощью циркуля измеряем отрезок ОЕ и строим окружность с
центром в точке А радиуса ОЕ (всю окружность строить необязательно,
смотри, выделенное синим цветом). Далее, с помощью циркуля измеряем
отрезок FG и строим окружность с центром в точке B радиуса FG (всю
окружность строить необязательно, смотри, выделенное зеленым цветом).
Точку пересечения окружностей с центрами в
точках А и В радиусами ОЕ и FG соответственно обозначаем С. Соединяем
с помощью линейки точки А и В с точкой С. Получаем треугольник АВС, в
котором по построению АВ = МК, ВС = FG, АС = ОЕ, следовательно, тре-ик
абс искомый.
Дано: ABCD – квадрат, окр (О; R) – опис. Около ква-та окр-ость
Найти: Sabcd/Sкруга — ?
3) Центром окружности, описанной около треугольника, является точка
пересечения его срединных
перпендикуляров. В правильном треугольнике центры описанной и
вписанной окружностей совпадают. а срединные перпендикуляры – его
высоты ( биссектрисы, медианы). Медианы точкой пересечения делятся
в отношении 2:1, считая от вершины. Следовательно,
радиус R окружности, описанной около правильного треугольника,
равен 2/3 его медианы ( высоты), а радиус r вписанной окружности равен
1/3 медианы (высоты).
r=R/2=6:2=3 см.
————————
Задачи на правильные треугольники и окружности, вписанные и описанные
около них, встречаются часто. поэтому полезно запомнить это свойство,
когда требуется решение без лишних вычислений: r=R/2=6:2=3 см.
1) В треугольнике: 1) против большей стороны лежит больший угол; 2) обратно,
против большего угла лежит большая сторона. Неравенство тре-ка:
2)
3)
26

Калькулятор высоты треугольника

Автор: Ханна Памула, доктор философии

Рецензию сделали Богна Шик и Адена Бенн

Последнее обновление: 01 марта 2023 г.

• Какова высота треугольника?
• Как найти высоту треугольника – формулы
• Как найти высоту равностороннего треугольника
• Как найти высоту равнобедренного треугольника
• Как найти высоту прямоугольного треугольника
• Как найти высоту треугольника с помощью этого калькулятора высоты треугольника?
• Часто задаваемые вопросы

Если вы ищете простой инструмент для расчета высоты в любом треугольнике , вы находитесь в правильном месте — этот калькулятор высоты треугольника является инструментом для вас. Если вы ищете формулы высоты треугольника для специальных треугольников, таких как прямоугольный, равносторонний или равнобедренный треугольник или любой разносторонний треугольник, этот калькулятор является безопасной ставкой — он может вычислить высоты треугольника, а также стороны треугольника, углы, периметр, площадь. Пожалуйста, не ждите больше; Попробуй!

Если вас все еще интересует формула высоты равностороннего треугольника или как найти высоту без площади, продолжайте прокручивать, и вы найдете ответ.

Какова высота треугольника?

Каждая сторона треугольника может быть основанием, и из каждой вершины можно провести линию, перпендикулярную линии, содержащей основание – это высота треугольника. Каждый треугольник имеет три высоты, которые также называются высотами . Рисование высоты известно как падение высоты в этой вершине.

Как найти высоту треугольника – формулы

Существует много способов найти высоту треугольника. Наиболее популярная формула использует площадь треугольника, но существует множество других формул:

1. Заданная площадь треугольника

   Известное уравнение площади треугольника можно преобразовать в формулу высоты прямоугольного треугольника:

   • площадь=b×h/2\mathrm{площадь} = b \times h / 2площадь=b×h/2, где bbb — основание, hhh — высота; и

   • Итак, h=2×площадь/bh = 2 \times \mathrm{площадь} / bh=2×площадь/b.

   Но как найти высоту треугольника без площади? Самые популярные формулы:

2. Данные стороны треугольника

   Использование уравнения, называемого формулой Герона, позволяет вычислить площадь по сторонам треугольника. Затем, когда вы знаете площадь, вы можете использовать основное уравнение, чтобы узнать, какова высота треугольника:

   Формула Герона :

площадь = 0,25 × (a+b+c)×(−a+b+c)×(a−b+c)×(a+b−c)\qquad \маленький \начать{разделить} \mathrm{площадь}=\ &0,25 \times \sqrt{(a + b + c)}\\[0,5em] & \times\sqrt{(-a + b + c)} \\[.5em] &\times\sqrt{ (a — b + c)}\\[.5em] &\times\sqrt{ (а + б — в)} \конец{разделить} площадь = ​0,25×(a+b+c)

​×(−a+b+c)

​×(a−b+c)

​×(a+b−c)

​

Следовательно, :

h=0,5b×(a+b+c)×(−a+b+c)×(a−b+c)×(a+b−c)\qquad \маленький \начать{разделить} h = \frac{0.

​×(−a+b+c)

​×(a−b+c)

​×(a+b−c)

Более подробно об этом уравнении вы можете узнать в нашем специальном Калькулятор формулы Герона.

3. Даны две стороны и угол между ними

   Используйте тригонометрию или другую формулу площади треугольника:

площадь=0,5×a×b×sin⁡(γ)\qquad \маленький \mathrm{площадь} = 0,5 \times a \times b \times \sin(\gamma)площадь=0,5×a×b×sin(γ)

(или площадь=0,5×a×c×sin⁡(β) \mathrm{площадь} = 0,5 \times a \times c \times \sin(\beta)площадь=0,5×a×c×sin(β) или площадь=0,5×b×c×sin⁡(α)\mathrm{ площадь} = 0,5 \times b \times c \times \sin(\alpha)area=0,5×b×c×sin(α), если даны разные стороны):

ч=2×0,5×а×b×sin⁡(γ)b=a×sin⁡(γ)\qquad \маленький \начать{разделить} h &= \frac{2 \times 0,5 \times a \times b \times \sin(\gamma)}{b} \\ &= а\раз\грех(\гамма) \end{split}h​=b2×0. 5×a×b×sin(γ)​=a×sin(γ)​

Если ваша фигура относится к особому типу треугольника, прокрутите вниз, чтобы найти формулы высоты треугольника. Упрощенные версии общих уравнений легче запомнить и вычислить.

Как найти высоту равностороннего треугольника

Равносторонний треугольник — это треугольник, у которого все три стороны равны и все три угла равны 60°60\градус60°. Все три высоты имеют одинаковую длину, которая может быть рассчитана из:

• hΔ=a×3/2hΔ = a \times \sqrt{3} / 2hΔ=a×3​/2, где aaa — сторона треугольника.

В равностороннем треугольнике высоты, биссектрисы, биссектрисы и медианы совпадают.

Если вас интересуют формулы площади и периметра, посетите наш специальный калькулятор равностороннего треугольника.

Как найти высоту равнобедренного треугольника

Равнобедренный треугольник — это треугольник, две стороны которого имеют одинаковую длину. Есть две разные высоты равнобедренного треугольника; формула для вершины: 92}\раз б/у \end{split}ha​=2×площадь/a=a2−(0,5×b)2

​×b/a​

Тригонометрия :

ha=b×sin⁡(β)\qquad \маленький h_{\rm a} = b \times \sin(\beta)ha​=b×sin(β)

Формулы площади и периметра треугольника этого типа можно найти на нашем специальном калькуляторе равнобедренного треугольника.

Как найти высоту прямоугольного треугольника

Прямоугольным треугольником называется треугольник, один угол которого равен 90°90\градус90°. Две высоты найти несложно, так как катеты перпендикулярны: если более короткий катет — основание, то более длинный катет — высота (и наоборот). Третью высоту треугольника можно вычислить по формуле:

hc=площадь×2/c=a×b/ch_c=\mathrm{площадь}\times 2/c = a\times b/chc​=площадь×2/c=a×b/c

Если вы Вас интересуют уравнения площади и периметра этого треугольника, посмотрите на наш калькулятор прямоугольного треугольника.

Как найти высоту треугольника с помощью этого калькулятора высоты треугольника?

Прочитав наше объяснение, мы почти уверены, что теперь вы понимаете, как найти высоту треугольника без заданной площади или какова высота треугольника. Но давайте рассмотрим простой пример, чтобы показать вам гибкость нашего инструмента:

1. Выберите тип треугольника . Предположим, мы хотим вычислить высоты разностороннего треугольника, поэтому мы не меняем параметр по умолчанию.
2. Введите указанные значения . Это может быть три стороны или две стороны и угол. Остановимся на первом варианте: a=6 ina = 6\ \mathrm{in}a=6 in, b=14 inb = 14\ \mathrm{in}b=14 in, c=17 inc = 17\ \mathrm {дюйм}c=17 дюймов 90 010
3. Калькулятор высоты треугольника отобразил все три высоты — они равны 13,17 дюйма, 13,17\ \mathrm{дюйма}13,17 дюйма, 5,644 дюйма, 5,644\ \mathrm{дюйма}, 5,644 дюйма и 4,648 дюйма, 4,648\ \mathrm {in}4,648 дюйма. Более того, калькулятор показал нам все углы треугольника, площадь и периметр.

Разве это не прекрасно?

Часто задаваемые вопросы

Как найти высоту треугольника, если все стороны равны?

Чтобы определить высоту равностороннего треугольника:

1. Запишите длину стороны вашего треугольника.
2. Умножьте на √3 ≈ 1,73 .
3. Разделить результат на 2 .
4. Вот оно! В результате получится высота вашего треугольника!

Все ли высоты треугольника равны?

Обычно нет , каждая высота треугольника может иметь разную длину. Однако если все три высоты имеют равные длины , то этот треугольник равносторонний , то есть все его стороны тоже равны (но не равны высотам!).

Как найти высоту треугольника по углам?

Вы не можете определить высоту треугольника, зная только углы треугольника. Это потому, что треугольников с такими углами бесконечно много, и длины высот в каждом из этих треугольников разные!

Как найти высоту прямоугольного треугольника?

Каждая из перпендикулярных сторон (катетов) прямоугольного треугольника является его высотой. Чтобы вычислить третью высоту h ₃ , воспользуемся формулой площади:

½ × катет ₁ × катет ₂ = площадь = ½ × гипотенуза × h ₃ 9 0026

В результате:

h ₃ = катет ₁ × катет ₂ / гипотенуза

Какова наименьшая высота треугольника 3 4 5?

Ответ: 2. 4 . Чтобы получить этот результат, обратите внимание, что площадь равна Площадь = ½ × 3 × 4 = 6 .

С другой стороны, Площадь = ½ × Гипотенуза × Наименьшая высота .

Так как Гипотенуза = 5 и Площадь = 6 , мы получаем Кратчайшая высота = 2 × Площадь / Гипотенуза = 2 × 6 / 5 = 2,4 .

Ханна Памула, доктор философии

Особый треугольник?

Высоты (высоты)

Углы

Прочие

Периметр

Посмотреть 18 подобных калькуляторов треугольников 🔺

30 60 90 треугольник45 45 90 треугольникПлощадь прямоугольного треугольника… Еще 15 03

Треугольник:

калькулятор решает треугольник, заданный тремя его свойствами. Каждый треугольник имеет шесть основных характеристик: три стороны a, b, c и три угла (α, β, γ). Классическая задача тригонометрии состоит в том, чтобы указать три из этих шести характеристик и найти остальные три. Конечно, наш калькулятор решает треугольники из комбинаций основных и производных свойств, таких как площадь, периметр, высота, медиана и т. д. Обычно по длине трех сторон (SSS), сторона-угол-сторона или угол-сторона-угол.

Как этот калькулятор решает треугольник?

Расчет общего треугольника состоит из двух фаз:

1. Экспертная фаза различна для разных задач. Калькулятор пытается по введенным данным вычислить размеры трех сторон треугольника. Он постепенно применяет базу знаний к введенным данным, которая представлена, в частности, отношениями между отдельными параметрами треугольника. Они последовательно применяются и комбинируются, и вычисляются параметры треугольника. Калькулятор повторяется до тех пор, пока треугольник не вычислит все три стороны.
   Например, соответствующая высота вычисляется из заданной площади треугольника и соответствующей стороны. По известным высоте и углу можно рассчитать прилегающую сторону и т. д. Калькулятор использует знания, например, формулы и отношения, такие как теорема Пифагора, теорема синусов, теорема косинуса и формула Герона.
2. Второй этап — вычисление свойств треугольника по имеющимся длинам трех его сторон.

Примеры ввода треугольника:

  Что означают символы?  
 a, b, c... стороны BC, AC, AB 
 A, B, C или α, β, γ... внутренние углы 
 ha, hb, hc... высоты 
 ma, mb, mc. .. медианы 
 T ... площадь 
 p ... периметр 
 s ... полупериметр