Сравнение чисел с одинаковыми основаниями но разными степенями: Сравнить числа 8^80 и 6^90

Своя игра. Степень с натуральным показателем

1. СВОЯ ИГРА

2. Нестандартный урок Алгебра 7 класс

Тема: «Степень с натуральным показателем»
Учитель: Смирнова Екатерина Алексеевна
Творческая группа: Воеводина Алина
Терняева Анна
Гаспарян Грета
Кондратова Ангелина
Елисеева Полина
Предмет математики
настолько серьезен,
что полезно не упустить
Блез Паскаль
(1623 – 1662 гг.)
Французский математик,
физик, религиозный философ
и писатель
случая сделать его
немного занимательным.

4. Правила игры:

• Игра состоит из 3х раундов: 1 раунд и 2 раунд
состоят из 5 тем каждый. В теме – 5 вопросов.
Вопросы располагаются слева направо по
возрастанию степени сложности.
• В 1 раунде стоимость вопросов от 2х до 8
баллов, во 2 раунде- от 3х до 10 баллов. На
обсуждение дается от 30 секунд до 2х минут.
Для проведения игры класс разбит на две
команды. Игра начинается с жеребьёвки.
Победившая команда первой выбирает
задание.
• Выбор темы и вопроса осуществляет
капитан. В первом раунде ответ на вопрос
дает выбранный капитаном член команды
или сам капитан. Во 2 раунде капитан после
выполнения задания поднимает сигнальную
карту и сдает решение жюри. Выполняют
задания обе команды. Если команда,
выбиравшая вопрос, выполнила задание
неверно, то 2 команда дает ответ на вопрос.
Если её ответ верен, то она получает баллы.
• После каждого раунда жюри подводит
итоги. Во 2 раунде игру начинает команда,
набравшая в 1 раунде больше баллов.
• В финальном раунде команды делают ставку
в пределах 20 баллов, записывают её на
бумаге и сдают жюри.
• Капитаном с помощниками дается задание
«Дидактическая игра».
• Выполнив задание, капитаны с
помощниками сдают решение жюри и
присоединяются к командам, которые в это
время решают кроссворд по теме «Степень
с натуральным показателем».
• Правильный ответ в финальном раунде
увеличивает общую сумму команды на
сделанную ставку, а неверный – уменьшает.
• Жюри подсчитывает баллы и оглашает
результаты.
• Выигрывает команда, набравшая больше
число баллов!

9. Формула успеха

«Мы помножим ум и ловкость,
К ним прибавим оптимизм,
С нашей формулой успеха –
Вся и всех мы победим!»

10. Коэффициент удачи

КОЭФФИЦИЕНТ УДАЧИ
Будем мыслить, рассуждать
И конечно побеждать!
А удача улыбнётся,
Только тем, кто не сдаётся!
Повторение и систематизация материала темы;
Формирование умения применять приемы
сравнения, переноса знаний в измененную
нестандартную ситуацию;
Развитие мышления, эрудиции, интуиции,
любознательности;
Формирование интереса к предмету;
Воспитание активности, трудолюбия,
целеустремленности, коллективизма.

12. Рефлексия – умение человека осознавать, что он

делает, и аргументировать, обосновывать свою
деятельность.
• Выбери из предложенных рисунков тот, который
соответствует твоему настроению на начало урока
и отметь его галочкой(✓).
Мне хорошо,
я готов к уроку.
Мне безразлично.
Я тревожусь,
всё ли у меня получится.

13. Жеребьевка.

Горело 5 свечей, 2 погасли. Сколько свечей
осталось?
В семье 5 сыновей и у каждого есть сестра.
Сколько детей в семье?
• Врач прописал больному 3 укола: по уколу
через каждые полчаса. Сколько потребуется
времени, чтобы сделать все уколы?
• В темноте девочка увидела 6 пар кошачьих
глаз. Сколько пар ног у этих кошек?
• Как изменится дробь, если её числитель
увеличить на знаменатель?

14. Ответы:

•2
•6
• 1 час
• 12
• на 1
Знаю теорию
2
3
4
5
6
2
3
4
5
6
Умею логически
мыслить (верно
ли
утверждение?)
2
3
5
6
8
Знаю историю
математики
2
3
4
5
6
Считаю устно
2
3
4
5
6
Знаю свойства
Сформулировать определение степени
числа а с натуральным показателем n,
большим 1.
Ответ: степенью числа а с
натуральным показателем n,
большим 1, называется
выражение аn, равное
произведению n множителей,
каждый из которых равен а.
Сформулировать определения степени числа
а с показателем 1 и показателем 0.
Ответ: степенью числа а с
показателем 1 называется само
число а. Степень числа а, не
равного нулю, с нулевым
показателем равна единице. 00
не имеет смысла.
Сформулировать определение одночлена.
Ответ: выражения, которые
являются произведениями
чисел, переменных и их
степеней называют
одночленами.
Сформулировать определения степени числа
а с показателем 1 и показателем 0.
Ответ: степенью числа а с
показателем 1 называется само
число а. Степень числа а, не
равного нулю, с нулевым
показателем равна единице. 00
не имеет смысла.
Сформулировать определение
одночлена стандартного вида.
Ответ: одночлен, записанный
в виде произведения
числового множителя,
стоящего на первом месте и
степеней различных
переменных, называют
одночленом стандартного
вида.
Сформулировать определение степени
одночлена.
Ответ: степенью одночлена
называют сумму показателей
степеней всех входящих в него
переменных. Если одночлен не
содержит переменных и является
числом, отличным от нуля, то
степень этого одночлена считают
равной 0.
Заполните пропуски. Сформулируйте
соответствующее правило.
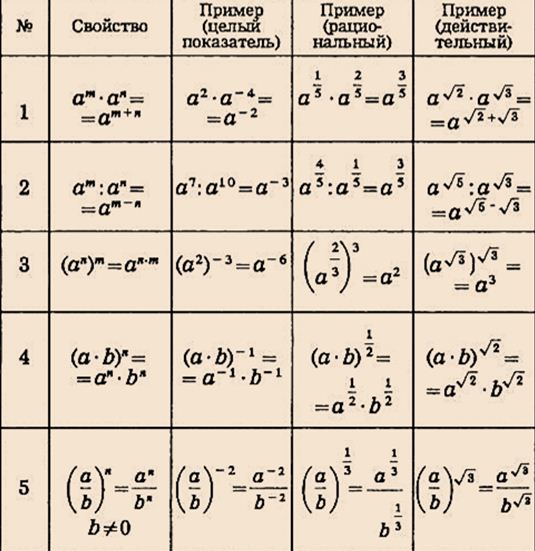
am . an = …
Ответ: am . an = am+n, а – любое число
m и n – произвольные натуральные
числа.
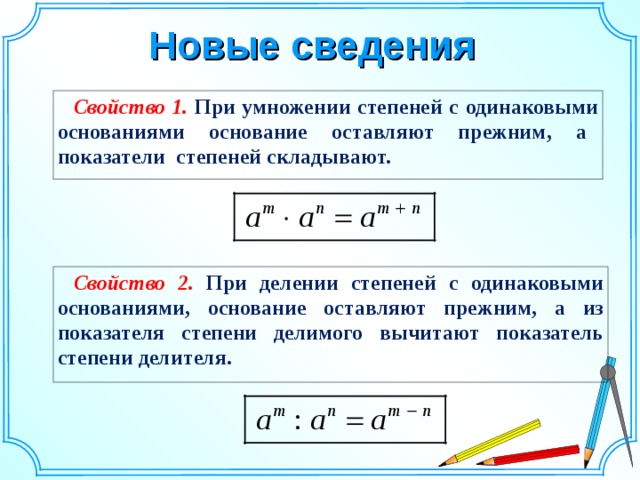
При умножении степеней с
одинаковыми основаниями
основание оставляют прежним, а
показатели степеней складывают.
Заполните пропуски. Сформулируйте
соответствующее правило.
am : an = …
Ответ: am : an = am-n, а ≠ 0; m и n –
натуральные числа, m > n.
При делении степеней с
одинаковыми основаниями
основание оставляют прежним, а
из показателя степени делимого
вычитают показатель степени
делителя.
Заполните пропуски. Сформулируйте
соответствующее правило.
(am)n = …
Ответ: при возведении степени в
степень основание оставляют
тем же, а показатели
перемножают.
(аm)n = amn, a – любое число,
m и n – произвольные
натуральные числа.
Заполните пропуски. Сформулируйте
соответствующее правило.
(abc)n = …
Ответ: Чтобы возвести в степень
произведение достаточно
возвести в эту степень каждый
множитель и результаты
перемножить.
(abc)n = anbncn
a,b,c- любые числа,
n – натуральное число
Заполните пропуски. Сформулируйте
соответствующее правило.
an . bn = …
Ответ: При умножении степеней с
разными основаниями и
одинаковыми показателями
основания перемножают, а
показатель оставляют тем же.
an . bn = (ab)n, a и b – любые числа, а
n – произвольное натуральное число.
Верно ли утверждение?
Если квадраты двух чисел равны, то
равны и сами числа.
Ответ: нет,
например: (-5)2 = 52; -5 ≠ 5.
Верно ли утверждение?
Если кубы двух чисел равны, то равны и
сами числа.
Ответ: да.
Верно ли утверждение?
Квадрат натурального числа может
оканчиваться любой цифрой.
Ответ: нет, может оканчиваться
только 0; 1; 4; 9; 6; 5.
Верно ли утверждение?
Четвертая степень натурального числа
может оканчиваться только одной из
цифр 0; 1; 5; 6.
Ответ: да.
Верно ли утверждение?
Если к отрицательному числу прибавить
его квадрат, то получится положительное
число.
Ответ: нет,
например: -0,1+(-0,1)2=
= -0,1+0,01 = -0,09.
Какой математик впервые ввел
современную запись степени х3; х10 ?
Ответ: Рене Декарт,
французский математик.
Происхождение слова «алгебра».
Ответ: слово «алгебра»
арабского происхождения;
термин «аль-джебр» взят из
названия книги
среднеазиатского ученого
Мухаммеда из Хорезма
(9 век).
Кому принадлежат слова:
«Математика – царица наук,
арифметика – царица математики»?
Ответ: Карлу Гауссу,
немецкому математику 19
века, «королю» математиков.
Каким математиком впервые введены
термины «абсцисса», «ордината»,
«координата»?
Ответ: впервые введены
немецким математиком
Готфридом Лейбницем
в XIX веке.
Самая древняя «счётная машина».
Ответ: пальцы рук и ног,
камешки и другие мелкие
предметы.
Вычислите:
102 — 32
Ответ: 100 – 9= 91.
Вычислите:
(-½)5 . 8
Ответ: —
.
8 = -¼.
Вычислите:
0,2515 . 415
Ответ: (0,25 . 4)15 = 1.
Вычислить:
9 . 75
7
—————-496
14
7
——-Ответ: 712 = 72 = 49.
Вычислите:
-62 – (-1)4
Ответ: -36 – 1 = -37
Упражнения
3
5
6
8
10
Задачи
3
5
7
8
10
Вычислить
3
4
5
6
8
Уравнения
3
5
7
9
10
Преобразование
выражений
3
5
7
8
10
Сравнить числа:
а) (-2,4)4 и (-5,2)3
б) -6,82 и -5,72
Ответ: (-2,4)4 > (-5,2)3 , так как
(-2,4)4 > 0, а (-5,2)3 < 0.
-6,82 < -5,72 , так как 6,82 > 5,72
Заменить М одночленом так, чтобы
получилось тождество
М2 . 12х6 = 108х8
Ответ: М = ±3х
М2 = 108х8 :
(12х6)
М2 = 9х2
М = ±3х
Поставить вместо пропущенных выражений
такие, чтобы получилось тождество.
(….) 2 . (….) 3 = -27b 11
Ответ: b4 и -3b
Докажите, что число 196374 + 391 164 – 2
делится на 5
Ответ: 196 374 оканчивается
цифрой 6
391 164 оканчивается цифрой 1.
Данное число оканчивается
цифрой 5, следовательно
делится на 5.
Какой цифрой оканчивается число 1989 1989
Ответ: 1989 1 оканчивается
цифрой 9
1989 2 оканчивается цифрой 1
1989 3 оканчивается цифрой 9
1989 4 оканчивается цифрой 1
Показатель степени – нечетное
число. Значит, число
оканчивается цифрой 9.
Как изменится площадь круга, если его
радиус уменьшить в 2 раза?
Ответ:S = ∏R 2
Уменьшится в 4 раза.
На покраску квадрата израсходовали 40 г
краски. Хватит ли 350 г краски, чтобы
покрасить квадрат, сторона которого в 3
раза больше?
Ответ:S = а 2 , площадь
увеличится в 9 раз. На покраску
израсходуют 40 . 9 = 360(г).
Краски не хватит.
Объем шара вычисляется по формуле V =
где r – радиус шара. Найти объем шара
радиуса 3 см.
округлить до целых.
Ответ:
=108(см 3)
= 4 . 3 3 ; V = 4 . 27=
,
Найти площадь кольца, если r1 = 2см, r2 =
= 4см.
округлите до целых.
Ответ:
S = 3 . 42 — 3 . 22 = 3(16-4) =
= 36 (cм2)
Бассейн, имеющий форму куба, наполняется
трубой за 40 мин. Успеют ли за 5 часов
наполнить через такую же трубу бассейн,
имеющий форму куба, ребро которого в 2 раза
больше?
Ответ: V = а 3. Объем
увеличивается в 8 раз. Времени
потребуется 40 . 8 = 320 (мин).
5 ч = 5 . 60 = 300 (мин).
Наполнить бассейн не успеют.
Ответ:
=
Ответ:
=
=1
0
Ответ: 1 + = 2,25
+5
Ответ:
=
Ответ:
Ответ:
x = 19.
Ответ:
Ответ:
Ответ:
Решите уравнение при всех значениях
параметра а.
ax = 2 — a
Ответ: при а ≠ 0
при а = 0 корней нет.
Выполните действия.
(3xy)3 × (-2x2y3)2
Ответ: 27x3y3 × 4x4y6 = 108x7y9
Запишите одночлен в стандартном виде и
найдите его значение .
3
Ответ: __ а5 =
2
16
х __ = — __
81
__ х
(-
2
__
3
) х (- __ )4 = -1 х
Представьте выражение в виде квадрата или
куба одночлена.
Ответ:
Упростить выражение
Ответ:
Вычислите:
Найти значение выражения
(5x – 3y) х 4×2 – 5×2(4x + y)
при х = ; y = -27
Ответ: 20×3 — 12x2y – 20×3 — 5x2y =
= -17x2y.
При х = ; y = -27
-17 х х (-27) = 51

73. Дидактическая игра.

• Дается 2 минуты на то, чтобы запомнить выражения,
записанные в клетках квадрата. Затем по памяти
заполнить клетки квадрата. Для того, чтобы
запомнить и правильно воспроизвести, необходимо
установить закономерность в записи выражений.
(a6b12)2
(a3b8)4
(a4b8)3
(a2b4)6
a12b24
(a2b4)6
(a6b12)2
(a3b8)4
(a4b8)3

74. Кроссворд

6
7
9
1
8
2
3
4
5
10

По горизонтали:
1. Действие, с помощью которого вычисляются значения степени.
2. Произведение, состоящее из одинаковых множителей.
3. Действие показателей степеней при возведении степени в степень.
4. Действие степеней, при которых показатели степеней вычитаются.
5. Немецкий математик, который ввел термин «показатель степени».
По вертикали:
6. Число всех одинаковых множителей.
7. Степень с нулевым показателем.
8. Повторяющийся множитель.
5
10
9. Значение выражения :
23 ∗ 55
• 10. Показатель степени, который обычно не пишут

76. Дидактическая игра.

• Дается 2 минуты на то, чтобы запомнить выражения,
записанные в клетках квадрата. Затем по памяти
заполнить клетки квадрата. Для того, чтобы
запомнить и правильно воспроизвести, необходимо
установить закономерность в записи выражений.
(a6b12)2
(a3b8)4
(a4b8)3
(a2b4)6
a12b24
(a2b4)6
(a6b12)2
(a3b8)4
(a4b8)3

77. Заполненный кроссворд

П
О
К
Е
А
В О З В Е Д Е Н И
А
И
Т
Н
О
Е
И
С Т
Л
Ц
Ь
А
Н
О
П Р О И З В Е
А
Д Е Л Е Н И
И
Ш Т И Ф Е Л
Ч
Е
Т
Ы
Р
Е П Е Н Ь
Д
И
Д Е Н И Е
И
Е
Ц
А
ь

78.

Рефлексия – умение человека осознавать, что он делает, и аргументировать, обосновывать свою
деятельность.
• Выберите из предложенных рисунков тот, который
соответствует твоему настроению после
пройденного урока и отметь его галочкой(✓).
Мне понравилось,
я доволен собой.
Мне все равно.
Мне грустно,
я не всё усвоил.
Подведение итогов
игры!!!
Спасибо за игру!!!
«Учение, лишенное всякого интереса,
?
и взятое только силою принуждения,
убивает в ученике охоту к учению,
без которой он далеко не уйдет,
а учение, основанное только на
интересе, не дает возможности
окрепнуть самообладанию и воле
ученика, так как не все в учении
К.Д. Ушинский
интересно и придет многое,
что надобно будет взять силою воли»

{53}$ больше.

$\endgroup$

Показатели и степени | Блог

У Ришаба день рождения. У него 5 лучших друзей. Он хочет подарить своим друзьям шоколадки таким образом, чтобы:

• 1-й друг получил 2 шоколадки
• 2-й друг получает вдвое больше конфет, чем 1-й друг, т. е.
  2 × 2 = 4
• 3-й друг получает в два раза больше конфет, чем 2-й друг, т. е.
  4 × 2 = 8
• 4-й друг получает вдвое больше конфет, чем 3-й друг, т. е.
  8 × 2 = 16
• 5-й друг получает вдвое больше конфет, чем 4-й друг, т. е.
  16 × 2 = 32

Обратите внимание на таблицу:

Примечание: double = два раза

Точно так же, как многократное сложение выражается как умножение, повторное умножение выражается как ПОЛНОМОЧИЯ.

Давайте посмотрим видео, чтобы узнать немного больше об экспонентах и ​​степенях.

В этом видео мы увидели

• как можно использовать экспоненциальную форму чисел, чтобы
  легко представлять, понимать, сравнивать и вычислять числа.
• как экспоненциальные числа используются в реальных приложениях.

Вы помните, как изучали измерения на предыдущих уроках? Как вы запомнили формулу и единицы площади? Площадь рассчитывается путем возведения в квадрат двух сторон, а единица записывается как квадрат. Квадрат здесь не что иное, как сила. Все единицы площади записываются в виде квадратов.

Понятия

Глава «Экспоненты и степени» охватывает следующие концепции:

Экспоненты Законы показателей Десятичная система счисления Выражение больших чисел в стандартной форме

Экспоненты

Числа могут быть выражены в различных формах:

Экспоненциальная форма — это более простой способ записать число как произведение многих факторов. Экспоненциальную форму можно использовать для простого представления, понимания, сравнения и вычисления больших чисел.

Мы узнали, что экспоненциальная форма — это более простой способ записать большое число как произведение многих факторов.

Рассмотрим квадраты и кубы числа.

В обоих контекстах большее число выражается через меньшее число, возведенное в определенную степень.

Следовательно, для любого ненулевого целого числа «a» и целого числа «m» обобщенная экспоненциальная форма имеет вид am,

, где «a» — основание, а «m» — показатель степени.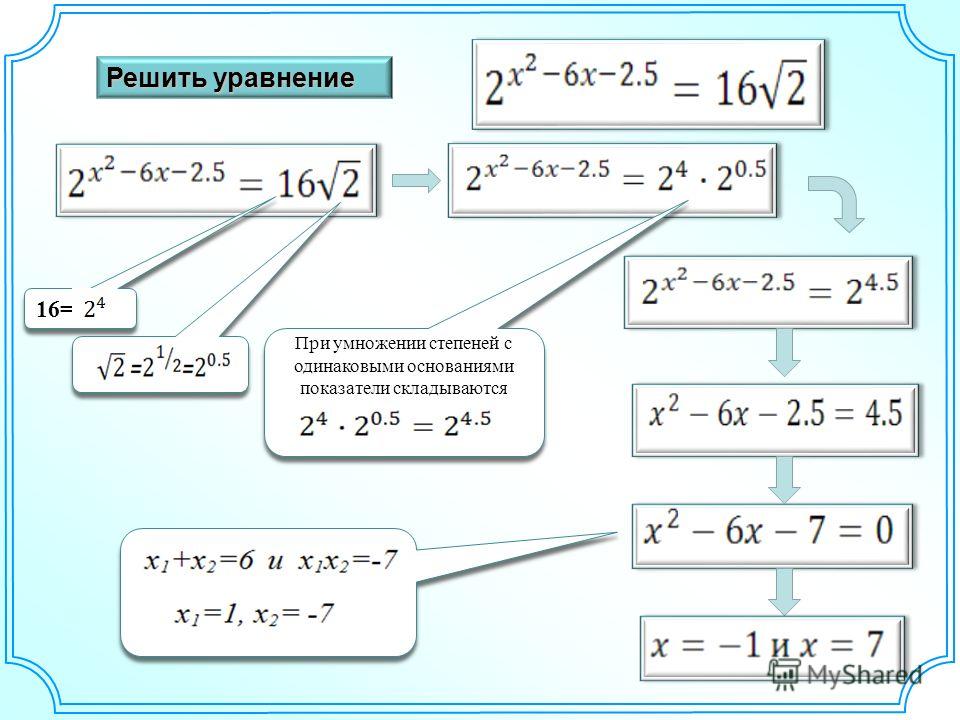

• База — База — это число, которое многократно умножается.
• Показатель степени – Показатель степени соответствует количеству раз, когда основание используется в качестве множителя.

​ Примеры:

• 5 × 5 × 5 × 5 × 5 = 5 ⁵ , т. е. многократное умножение 5 может быть выражено в экспоненциальной форме.
• Экспоненциальная форма 12 ⁴ может быть записана в форме многократного умножения, т. е. 12 ⁴ = 12 × 12 × 12 × 12.

Мы знаем, что 1, возведенная в степень любого числа, дает нам 1. Но будет ли -1, возведенная в степень любого числа, по-прежнему давать 1? Нет!

Таким образом, любое отрицательное число , возведенное в степень четного числа , дает положительное число, , а если его возвести в степень нечетного числа, , то получается отрицательное число.

Примеры:

• (-3) ³ = -3 × -3 × -3 = -27, отрицательное число
• Наоборот, (-3) ⁴ = -3 × -3 × -3 × -3 = 81, положительное число

Мы знаем, что квадрат числа p записывается как p ² = p × p, а куб числа r записывается как r ³ = r × r × r.

Таким образом, значение числа, возведенного в любую степень, которое находится в экспоненциальной форме , можно определить, разбив его на множители.

Если ‘a’ и ‘b’ два целых числа, то значение

Например, 4 ² × 5 ³ = 4 × 4 × 5 × 5 × 5 = 16 × 125 = 2000.

Сравнивать числа по одному основанию легко. Например, 4 ⁴ 5. Теперь давайте посмотрим, как сравнивать числа с разными основаниями и разными показателями. Сравним 4 ⁵ и 5 ⁴ .

4 ⁵ = 4 × 4 × 4 × 4 × 4 = 1024

5 ⁴ = 5 × 5 × 5 × 5 = 625

1024 > 625

Отсюда следует, что 4 ⁵ > 5 ⁴

2 9

Знаете ли вы, как упорядочить экспоненциальную форму чисел? Найдя значение чисел в экспоненциальной форме, мы можем расположить экспоненциальную форму чисел в порядке возрастания или убывания.

Например, расположите 2 ³ , 3 ³ , 4 ² в порядке возрастания.

2 ³ = 2 × 2 × 2 = 8

3 ³ = 3 × 3 × 3 = 27

4 ² = 4 × 4 = 16

5 8

Следовательно, , 2 ³ 2 3

Чтобы выразить числа как произведение степеней их простых множителей, , нам нужно знать, как выполнить разложение на простые множители.

Рассмотрим число 30.

Выполним разложение на простые множители:

Получаем 30 = 2 × 3 × 5.

Любое натуральное число можно представить как произведение степеней его простых множителей.

Можно ли каждое число выразить в экспоненциальной форме? Да. Нужно ли все числа представлять в экспоненциальной форме? №

Итак, мы узнали об экспоненциальной форме чисел и о том, как выражать различные числа в виде степеней или произведения степеней их простых множителей.

Однако рассмотрим число 33.

33 можно выразить как 33 × 10 ⁰ или 3 ¹ × 11 ¹

Оба являются экспоненциальными формами числа 33. Но нет необходимости выражать 33 в экспоненциальной форме. Точно так же такие числа, как 10, 15, 55, 119, 133 и т. д., не обязательно должны быть выражены в экспоненциальной форме.

Экспоненциальная форма используется для обработки очень больших или очень маленьких чисел.

Расширяем степени до многократного умножения, упрощаем и решаем выражения со степенями. Мы используем правило BODMAS для упрощения выражений, включающих степени со многими операциями.

Законы экспонент

Решим еще несколько примеров:

• 46 ⁵ × 46 ²⁰ = 46 ²⁵
• b ²⁰ × b ¹² × b ⁸ = b ^20+12+8 = b ⁴⁰

Когда произведение двух или более степеней имеет одно и то же основание с разными/одинаковыми показателями, мы можем сложить показатели основания.

Используя следующую стратегию, мы можем решать задачи, связанные с полномочиями.

• Выразите все числа как степень их простых множителей
• Сгруппировать числа по одному основанию
• Определите соответствующие законы показателей степени
• Упростить.

Чтобы найти значение неизвестных показателей , мы следуем стратегии, приведенной ниже.

• Оценить выражение на LHS.
• Приравняйте показатели степени слева к и справа.
• Решите уравнение и найдите результат.

Взяв степень экспоненциального числа, т.е. степень степени, мы просто умножаем степени.

Теперь рассмотрим:

Теперь решим 7 ⁴ ÷ 5 ⁴

Запишем это как 7 ⁴ / 5 ⁴ = 7 × 7 × 5 × 5 / 5 5 = (7/5) ⁴

Теперь рассмотрим:

Любое ненулевое число, возведенное в степень ‘0’, равно 1.

Быстро вспомним весь закон показателей:

Для любых ненулевых целых чисел ‘a’ и ‘b’ и, целые числа ‘m’ и ‘n’

Десятичная система счисления

Рассмотрим целое число 78 392. Мы можем выразить это в расширенной форме как

78392 = 7 × 10000 + 8 × 1000 + 3 × 100 + 9 × 10 + 2 × 1

Но мы знаем, что 10000 = 10 ⁴ , 1000 = 10 ³ , 100 = 10 ² , 10 = 10 ¹ , 1 = 10 ⁰

Следовательно, мы можем написать 78392 как 7 × 10 ⁴ + 8 × 10 ³ + 3 × 10. 100181 + 3 × 10. 100181 + 3 × 100181. ² + 9 × 10 ¹ + 2 × 10 ⁰

Рассмотрим другой пример.

Обратите внимание, как показатели степени 10 начинаются с максимального значения 8 и затем уменьшаются на 1 с шагом слева направо до «0».

И наоборот, мы можем идентифицировать число, когда дана расширенная форма числа.

Давайте посмотрим на пример.

Выражение больших чисел в стандартной форме

Любое число может быть выражено как десятичное число от 1,0 до 10,0, включая 1,0, умноженное на степень 10. Такая форма числа называется стандартной формой.

Теперь давайте посмотрим, как большие числа могут быть представлены в стандартной форме.

Масса Земли = 5 976 000 000 000 000 000 000 000 кг.

Стандартные формы массы Земли следующие:

Стандартная форма — это научное обозначение, которое используется для выражения очень больших или очень маленьких чисел.

Мы только что научились преобразовывать любое число в его стандартную форму. Теперь давайте посмотрим, как преобразовать стандартную форму числа в его обычную форму.

Преобразовать 4,397 × 10 ³ в обычный вид.

В обычном виде у нас нет показателей степени, поэтому мы можем написать,

4,397 × 10 ³ = 4,397 × 1000 = 4397, что является его обычной формой.

Теперь давайте посмотрим, как записать числа в стандартной форме, когда дано утверждение

В галактике в среднем 100 000 000 000 звезд.

100 000 000 000=1 × 100000000000

= 1 × 10 ¹¹ звезд в стандартной форме.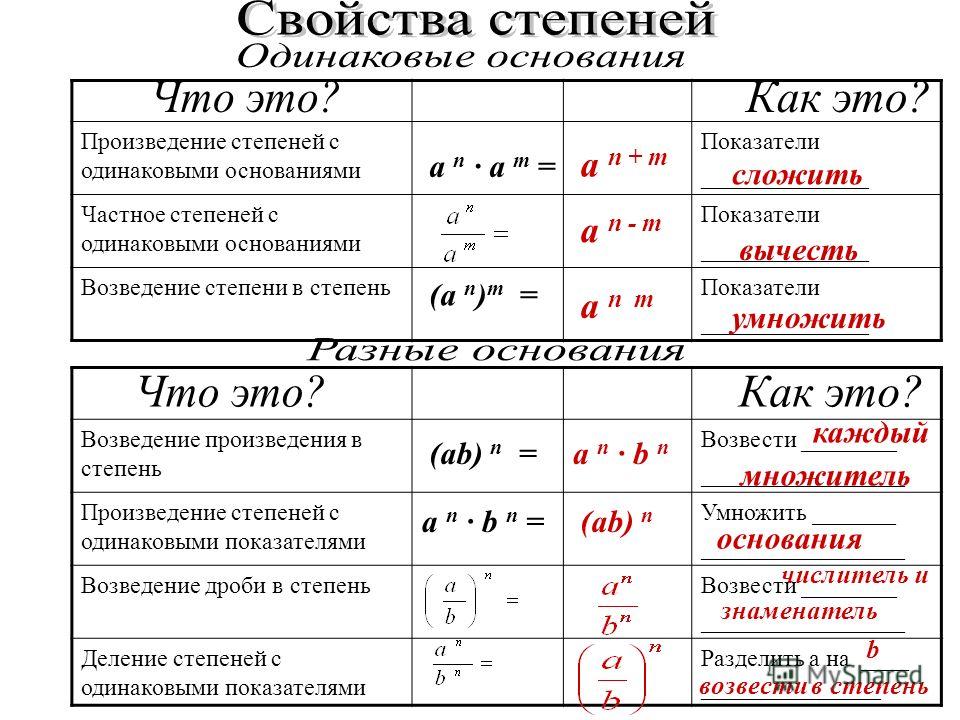

Теперь давайте научимся сравнивать два числа, записанные в стандартной форме.

Сравните 7,5 × 10 ⁷ и 3,2 × 10 ¹¹

Для сравнения двух чисел, представленных в стандартной форме, достаточно сравнить их степени 10, т. е.

Рассмотрим 10 ⁷ и 10 ¹¹

11> 7

Это подразумевает 10 ¹¹ > 10 ⁷

Следовательно, 3,2 × ¹¹ > 7,5,591801801801801801801801801801801801801801801801801801801801801801801801801818

. Ошибки

Ниже приведены темы, в которых учащиеся допускают распространенные ошибки при работе с показателями и степенями:

• 1. 11 ² не то же самое, что (2 × 11)
• 2. -3 ² не то же самое, что (-3) ²
• 3. 4 ^-2 не то же самое, что -4 ²
• 4. 3 ² не то же самое, что 2 ³
• 5. Расширенная форма чисел
• 6. 6 ⁵ × 6 ²⁰ не равно 6 ¹⁰⁰
• 7. 7. 2 ⁰ не является 0

11

² Не то же самое, что (2 × 11)

Выражение 11 ² означает умножение 11 само на себя дважды, а не 11, умноженное на 2.

11 ^{21 ×} = 11

-3

² Не то же самое, что (-3) ²

Выражение -3 ² означает сначала умножить две тройки вместе (в порядке операций), а затем взять отрицательное значение этого ответа .

Выражение (-3) ² означает умножение двух (-3) вместе.

4

^-2 Не то же самое, что -4 ²

4 ² означает умножение на 4 два раза.

4 ² = 4 × 4 = 16

Таким же образом 4 ^-2 означает деление на 4 два раза.

​4 ^-2 = (1/4) ²

3

² Не то же самое, что 2 ³

3 ^{2 умножить на 2}

.

3 ² = 3 × 3 = 9

Таким же образом 2 ³ означает умножение на 2 три раза.

​2 ³ = 2 × 2 × 2 = 8

Расширенная форма чисел

Как вы представите 256 в расширенной форме? Данное число равно 256.

Поскольку 2 стоит в разряде сотен и является третьим числом справа, его разрядное значение равно 2 × 100 , а не 2 × 1000 . Точно так же 5 стоит на разряде десятков и является вторым числом справа, поэтому его позиционное значение равно 9.0113 5 × 10 и не 5 × 100.

Кроме того, разрядное значение 6 равно 6 × 1 и не 6 × 10.

Следовательно, расширенная форма 2 × 100 + 5 × 5 10 + 6 × 1

не 2 × 1000 + 5 × 100 + 6 × 10

6

⁵ × 6 ²⁰ Не равно 6 ¹⁰⁰ 90,8 k9 k ^q × k ^r = k ^{p + q + r}

2

⁰ Is Not 0

Любое ненулевое число, возведенное в степень ‘0’, равно 1, т.

No related posts.