Сравнить два числа: Онлайн калькулятор сравнения чисел

Сравнение чисел – методика, примеры (6 класс, математика)

4.4

Средняя оценка: 4.4

Всего получено оценок: 858.

4.4

Средняя оценка: 4.4

Всего получено оценок: 858.

В реальной жизни часто нужно производить сравнение чисел. Сравнивать положительные числа все умеют с детства. В данной статье подробно рассказывается, как сравнить любые два числа, в том числе имеющие разные знаки.

Какое число больше

Проведем координатную ось: отметим на прямой точку начала координат (число 0), выберем масштабную единицу и направление.

Рассмотрим два числа a и b. Изобразим на координатной оси точки, соответствующие в выбранном масштабе данным числам.

Из двух чисел большим будет то, которое расположено правее на координатной оси.

Рис. 1. Сравнение двух чисел.

Пример

Рассмотрим числа -1 и 2 и соответствующие им точки на координатной оси.

Рис. 2. Сравнение чисел -1 и 2.

Поскольку число 2 на координатной оси лежит правее числа -1, оно является большим из этих двух чисел.

Обозначение: 2 > -1.

Положительные и отрицательные числа

Все числа, которые на координатной оси лежат правее нуля, называются положительными.

Все числа, которые на координатной оси лежат левее нуля, называются отрицательными.

Число нуль не является ни положительным, ни отрицательным, а его название в переводе с латинского означает «никакой». Впервые нуль как число начали использовать в Индии. А древние римляне, китайцы и греки обходились без него. А в древнем Египте, хотя и не использовали нуль, но обозначали его иероглифом, который означал «прекрасный».

Понятие отрицательного числа ввели китайские математики. Положительные числа они обозначали палочками красного цвета, а отрицательные – палочками черного цвета. Необходимость ввести отрицательные числа возникла при проведении финансовых расчетов. Они использовались при подсчете долгов.

Методика сравнения двух чисел

Рассмотрим возможные случаи сравнения двух чисел. Обозначим их, как a и b.

1) Пусть одно из чисел (a) является положительным, а другое (b) – отрицательным. Тогда бОльшим будет положительное число: a > b.

Таким образом, любое положительное число больше любого отрицательного.

Пример

Сравним числа 5 и -7. Имеем: 5 > -7.

2) Из двух отрицательных чисел меньшим будет то число, модуль которого больше.

Пример

Сравним числа -5 и -7.

Модуль числа -5 равен 5, а модуль числа -7 равен 7. Поскольку 7 > 5, -7 < -5.

Имеем: -5 > -7.

3) Любое положительное число больше 0, а любое отрицательное число меньше 0.

Пример

Рассмотрим числа 3 и -2. Имеем: 3 > 0, -2 < 0.

Неотрицательные и неположительные числа

Все положительные числа и нуль называются неотрицательными.

Все отрицательные числа и нуль называются неположительными.

Пример

Изобразим на координатной оси отрезок, начало которого лежит в точке -2, а конец – в точке 3.

Рис. 3. Отрезок на числовой прямой.

Будем рассматривать целые числа внутри данного отрезка. Из них:

• положительные числа 1, 2, 3;
• неотрицательные числа 0, 1, 2, 3;
• отрицательные числа -2, -1;
• неположительные числа -2, -1, 0.

Сравнение дробей

Чтобы сравнить две дроби одного знака, нужно привести их к общему знаменателю.

Пример

Сравним числа ${2 \over 3} и {5 \over 9}$.

Приведем эти числа к общему знаменателю (9): ${2 \over 3} = {6 \over 9}$.

Поскольку ${6 \over 9} > {5 \over 9},$ имеем: ${2 \over 3} > {5 \over 9}$.

Двойные неравенства

Пусть для числа a одновременно выполняется два неравенства: a > 6 и a < 10. Тогда можно написать двойное неравенство

6 < a < 10 .

Что мы узнали?

Мы ввели правило сравнения двух чисел с помощью точек на координатной оси. Также мы рассмотрели определения отрицательного, положительного, неотрицательного и неположительного числа.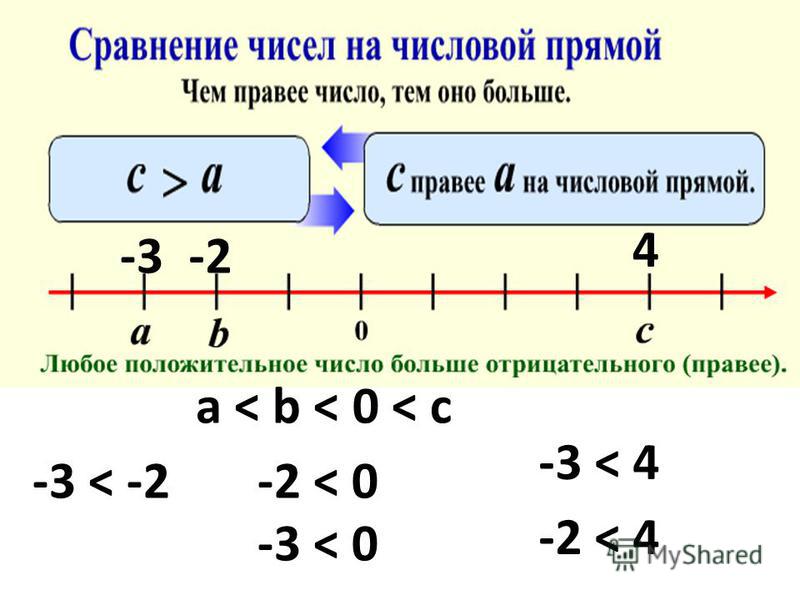

Затем мы рассмотрели все возможные случаи сравнения чисел с учетом их знака.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Александр Митченко

  5/5

• Николай Андреев

  5/5

• Виктор Оськин

  5/5

• Мария Котова

  5/5

• Никита Поцелуев

  5/5

• Паша Бойцов

  4/5

• Ольга Румянцева

  4/5

• Максим Быков

  5/5

• Галина Садыкова

  5/5

• Валентина Белоусова

  5/5

Оценка статьи

4.4

Средняя оценка: 4.4

Всего получено оценок: 858.

---

А какая ваша оценка?

php — Как можно сравнить два числа с плавающей точкой?

Вопрос задан 12 месяцев назад

Изменён 10 месяцев назад

Просмотрен 326 раз

Мне необходимо произвести сравнения по типу

if ($a + $b < $c) { /*true*/ } else { /*false*/ }

но так как все три переменных представляют собой числа с плавающей точкой с двумя знаками после запятой, сравнение делаю так:

if ($a + $b - $c < -0. 001) { /*true*/ } else { /*false*/ }

Правильно делаю? Видел пример проверки на равенство тут: https://www.php.net/manual/ru/language.types.float.php, но примеров для проверки меньше/больше не нашёл.

• php
• float
• compare

9

Если Ваши переменные действительно по условиям задачи имеют точность не более двух знаков после запятой, то все прекрасно работает как говорится из коробки, по крайней мере на php v7.4.10. Так что думаю, что делать сравнение как в Вашем варианте — излишне.

<?php
$a = 0.11;
$b = 0.12;
$c = 0.24;
echo '$a = '.$a."\n";
echo '$b = '.$b."\n";
echo '$c = '.$c."\n";
echo '1) $a + $b < $c = ';
if ( $a + $b < $c ) { 
 echo "true\n";
} else { echo "false\n"; }
echo '2) $a + $b < $c = ';
if ( floatval($a) + floatval($b) < floatval($c) ) { 
 echo "true\n";
} else { echo "false\n"; }

Результат

$a = 0. 11
$b = 0.12
$c = 0.24
1) $a + $b < $c = true
2) $a + $b < $c = true

1

Зарегистрируйтесь или войдите

Регистрация через Google

Регистрация через Facebook

Регистрация через почту

Отправить без регистрации

Почта

Необходима, но никому не показывается

Отправить без регистрации

Почта

Необходима, но никому не показывается

Нажимая на кнопку «Отправить ответ», вы соглашаетесь с нашими пользовательским соглашением, политикой конфиденциальности и политикой о куки

Разница в процентах



Разница в процентах

Сравнение процентной разницы вычисляет процентную разницу между двумя числовыми значениями в порядке чтобы определить, насколько они близки относительно большего значения.

Процентная разница (PD) между двумя числами рассчитывается за один двумя способами следующим образом:

Если использовать большее число в качестве знаменателя (см. Варианты ниже) = Да:

, если использовать большее число в качестве знаменателя = Нет:

где:

PD = разница в процентах

n1 = меньшее из двух сравниваемых чисел

n2 = большее из двух сравниваемых чисел

Итак, для пары значений «50» и «75»:

n1 = 50 и

n2 = 75,

, что дает процентную разницу 75-50 = 25/75 = 0,33 * 100 = 33%, если использовать большее число в качестве знаменателя = Да или

75-50 = 25/50 = 0,50*100 = 50%, если Использовать большее число в качестве знаменателя = Нет

Использовать

Используйте сравнение процентной разницы, чтобы сопоставить числовые значения, которые относительно близко друг к другу. Это полезно при сравнении числа такие значения, как сумма заказа, которая может варьироваться от очень низкой до очень высокой, что означает сравнение абсолютной разницы приведет к вводящим в заблуждение результатам с точки зрения того, насколько похожи два числа. друг другу. Например, значения «0,5» и «1,20» может рассматриваться как гораздо более слабое совпадение, чем значения «8200» и «8300».

Это сравнение поддерживает использование диапазонов результатов.

Опции

Опция	Тип	Назначение	Значение по умолчанию
Сопоставление пар без данных?	Да/Нет	Этот параметр определяет результат сравнения при сравнении двух Нет значений данных для идентификатора. Если установлено значение «Нет», при сравнении будет получен результат «нет данных». значение «Нет данных» против другого значения «Нет данных». Если установлено Да, сравнение даст полное совпадение (разница в процентах 0%) при сравнении значения «Нет данных» с другое значение «Нет данных». Результат «нет данных» будет возвращен только в том случае, если нет Значение данных сравнивается с заполненным значением.	№
Использовать большее число в качестве знаменателя?	Да/Нет	Этот параметр позволяет изменить способ отображения процентной разницы между два числа вычисляются, как показано выше. Если установлено значение «Да», будет использоваться первое уравнение выше, а абсолютный Разница между двумя числами будет связана с большим числом. Например, «25» и «75» будут иметь процентную разницу. 67%. Если установлено значение «Нет», будет использоваться второе уравнение выше, а абсолютный Разница между двумя числами будет связана с меньшим числом. Например, «25» и «75» будут иметь процентную разницу. 200%.	Да

Пример

В этом примере сравнение процентной разницы используется для определения числа, относительно близкие друг к другу. Следующие параметры указаны:

Пример конфигурации

Сопоставление пар без данных? = Нет

Использовать большее число в качестве знаменателя? = Да

Пример результатов

В приведенной выше конфигурации в следующей таблице показан пример результаты сравнения:

Значение А	Значение В	Результат сравнения (Разница в процентах)
50	75	33%
200	250	20%
0,005	0,0053	6%
4089	8044	49%
Нуль	Нуль	нет данных

Справка по Oracle ® Enterprise Data Quality, версия 9. 0
Copyright © 2006, 2011 Oracle и/или ее дочерние компании. Все права защищены.

Рабочие листы для сравнения двух чисел

Как сравнивать два числа? Нам все время приходится сопоставлять огромные числа, чтобы понять, какое из них лучше или меньше всего. Если кто-то позволит вам выбрать одну из двух разных сумм денег, вам, скорее всего, понадобится лучшая сумма. Чем более примечательно количество цифр, тем более заметным является число. Если два числа имеют одинаковое количество цифр, более примечательно число с большей цифрой в левой части. Если крайние левые цифры одинаковы, мы сопоставляем следующую цифру с привилегией и продолжаем делать это до тех пор, пока цифры не станут уникальными. Эти рекомендации на самом деле не применяются, когда включены десятичные или отрицательные числа.

Хороший способ научить сравнивать значения — сначала использовать числовую строку. Двигаясь влево по числовой строке, тем больше отрицательное значение. Движение вправо по числовой прямой увеличивает положительное значение целого числа. Когда мы помещаем эти значения в числовую строку, значение, найденное дальше справа, является наибольшим значением. Значение, найденное слева от числовой строки, является наименьшим значением. Помните, что если значения не равны, просто укажите стрелкой на меньшее значение. Эти рабочие листы объясняют, как сравнивать два числа или два набора и определять, какое из них больше. Студенты также будут считать простые рисунки.

Получите бесплатные рабочие листы в свой почтовый ящик!

---

Нажмите кнопки, чтобы распечатать каждый рабочий лист и ключ ответа.

Этот рабочий лист объясняет, как использовать числовые ряды, чтобы определить, какое из двух чисел больше. Примерная задача решена.

>Учащиеся будут использовать числовые ряды, чтобы определить, какое из двух чисел больше. Решается примерная задача и предлагаются две практические задачи.

Посмотрите на строку выше и сопоставьте первое число в задаче с этой строкой. Если это стоит перед вторым числом в строке, значит оно меньше второго; Это имеет более низкое значение. Если он выше на линии, чем второй, то он больше, чем секунда; она имеет более высокое значение.

Обведите слова с правильным ответом. Дано десять задач.

Учащиеся потренируются сравнивать два значения, чтобы определить, какое из них больше. Предлагается восемь задач.

Учащиеся будут использовать сравнение двух целых чисел, чтобы определить большее и меньшее значение. Предлагаются три задачи.

Посмотрите на строку выше и сопоставьте первое число в задаче с этой строкой. Если это стоит перед вторым числом в строке, значит оно меньше; оно имеет меньшее значение, второе.

Если он выше на линии, чем второй, то он лучше чем; она имеет более высокое значение, чем вторая.

Учащиеся будут использовать числовые линии в качестве эталона, чтобы определить, какое число больше. Дано десять задач.

В этом листе рассматривается, как сравнивать два значения. Решается примерная задача и предлагаются шесть практических задач.

Студенты демонстрируют свое мастерство в этом навыке. Дано десять задач.

Студенты узнают, где стоит одно число в свете другого. Предлагаются три задачи, а также место, где учащиеся могут скопировать правильный ответ, когда он будет дан.

Этот рабочий лист объясняет, как сравнить два набора изображений, чтобы увидеть, какая группа больше. Примерная задача решена.

Учащиеся просматривают и тренируются сравнивать два набора картинок, чтобы определить, какой из них больше. Решается примерная задача и предлагаются две практические задачи.

Даны две группы. Сосчитай количество предметов и поставь войдите в поле, чтобы показать, в какой группе больше объектов.

Как мы видим, первая группа состоит из 10 оленей, а вторая из шести обезьян. Поэтому в первой группе больше животных, поэтому мы будем использовать символ >. знак ‘>’ используется, когда количество объектов, т. е. объект слева, больше, чем объект справа. Сходным образом, ‘

Учащиеся будут практиковаться в определении того, какой набор изображений больше, и использовать ряд символов, чтобы сообщить об этом. Предлагается восемь задач.

Отличный способ повторить или познакомить с этим навыком весь класс одновременно.

Этот рабочий лист объясняет, как сравнить два набора изображений и определить, сколько объектов больше в большем наборе. Примерная задача решена.

На сколько больше груш у Джона, чем у Марка? В каждой группе по 4 груши, но 2 груши не совпадают. Следовательно, у Джона 2 больше груш, чем Марк.

Учащиеся будут сравнивать и считать, используя картинки в качестве наглядных пособий. Дано десять задач.

Имея картинки в качестве наглядных пособий, учащиеся будут сравнивать и считать, чтобы узнать, сколько еще картинок в большем наборе. Дано десять задач.

Нарисуйте коробку вокруг дерева, на котором больше фруктов. Напишите сколько еще.

Подчеркните группу справа, в которой больше объектов, чем в группе дано с левой стороны. Напишите разницу объектов между двумя группами

В этом листе объясняется, как определить, больше или меньше заданное число. Примерная задача решена.

Просматривая таблицу, мы обнаружим, что в первой строке 12 больше, чем 10. Во второй строке 13 больше 10. Обведите числа, которые больше 10, т.е. 12 и 13.

Подчеркивание чисел больше 30 и черный прямоугольник вокруг числа менее 30.

Учащиеся сравнивают числа и определяют, больше они или меньше заданного числа. Дано десять задач.

Учащиеся будут практиковаться в сравнении ряда значений, и их задача состоит в том, чтобы определить, больше они или меньше друг друга. Предлагается восемь задач.

Учащиеся обведут прямоугольником каждое число, соответствующее параметрам. Дано двадцать пять задач.

Подчеркните числа больше 60, но меньше 70.

Учащиеся повторят и попрактикуются в том, как определить взаимосвязь между двумя заданными числами. Решается примерная задача и предлагаются две практические задачи.

Когда число имеет меньшее значение, чем другое, оно считается меньшим количество. Если оно имеет более высокое значение, чем оно больше. Мы сравниваем числа по пометив их знаком , или =. Номер в открытой части знака

Учащиеся определят соотношение между двумя заданными числами. Дано десять задач.

Отметьте, больше ли первое число >, меньше ли

Учащиеся демонстрируют свое умение определять отношения между двумя заданными числами. Дано десять задач.

Посмотрите, насколько хорошо вы можете разобрать этот навык в теории.

Мы сравниваем числа, помечая их знаком , или =. Номер в открытой части знака

Учащиеся будут сравнивать два значения, используя следующие символы (). Решается примерная задача и предлагаются две практические задачи.

Больше того же здесь для студентов. Дано десять задач.

Поместите символ (), чтобы указать связь между этими двумя значениями. Дано десять задач.

Укажите, насколько на самом деле похожи эти значения.

Учащиеся демонстрируют навыки, используя все, что вы уже узнали.