2. Решение систем линейных алгебраических уравнений.
2.1. Системы линейных алгебраических уравнений (слау): понятие, определения.
Системы линейных алгебраических уравнений (далее – СЛАУ) используются во многих областях прикладной математики.
В общем виде система m линейных уравнений с n неизвестными записывается так:
| (1) |
Уравнения системы считаются пронумерованными: первое, второе, …, m-ое. Числа называютсянеизвестными системы; —коэффициентами при неизвестных системы.
Коэффициент при
неизвестном 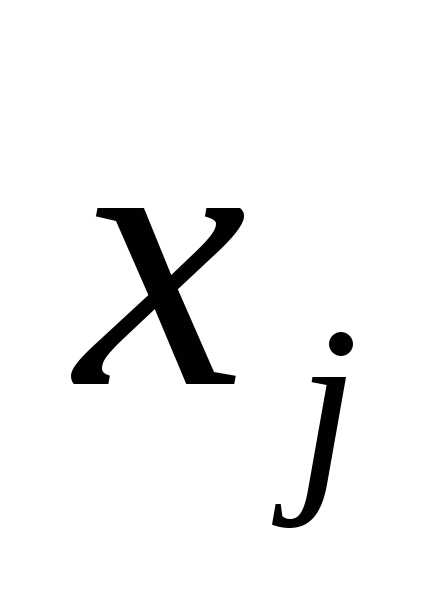 вi-ом
уравнении обозначается через
вi-ом
уравнении обозначается через 
Например, коэффициентa23 находится во втором уравнении системы при неизвестном x3.
Числа называютсясвободными членами системы.
Решением СЛАУ (1) называется любая совокупность чисел , которая, при подстановке на место неизвестныхв уравнения данной системы, обращает все эти уравнения в тождества.
СЛАУ (1) называется совместной, если она имеет решение. Если СЛАУ не имеет решения, то она называется несовместной (или противоречивой). Совместная СЛАУ может иметь одно или несколько решений и называется определенной, если имеет одно единственное решение, и неопределенной, если имеет больше одного решения.
Всюду далее будем рассматривать СЛАУ, имеющие единственное решение.
Две СЛАУ с одним и тем же числом неизвестных называются эквивалентными, если они или обе несовместны, или обе совместны и имеют одни и те же решения.
Элементарными преобразованиями СЛАУ, переводящими ее в эквивалентную СЛАУ, являются:
перестановка двух уравнений системы;
умножение обеих частей уравнения системы на любое отличное от нуля число;
прибавление (вычитание) к обеим частям одного уравнения соответствующих частей другого уравнения, умноженных на любое число.
2.2. Характеристика методов решения слау.
Все методы решения СЛАУ делятся на две группы – прямые и итерационные (повторяющиеся).
Прямые методы | Итерационные методы | |||
Дают решение после выполнения конечного числа операций. | Используют последовательные приближения (итерации) к искомому результату. | |||
«+» | Достаточно универсальны, всегда дают результат, причем за конечное, заранее известное, число шагов. | «+» | Позволяют получить решение с любой заданной точностью. | |
«-» | Нет сведений о точности полученного решения. | «-» | При их использовании заранее неизвестно количество предстоящих итераций. В некоторых случаях вообще не дают решения. | |
2.3. Прямые методы решения слау: метод Гаусса.
Рассмотрим СЛАУ (2), состоящую из n уравнений с n неизвестными:
| (2) |
Метод Гаусса или метод последовательного исключения неизвестных наиболее распространенный из точных (прямых) методов решения СЛАУ.
Прямой ход приводит систему (2) к эквивалентной ей системе вида (2’).
| ( |
Для этого сначала первое неизвестное исключают из второго и последующих уравнений системы, затем второе неизвестное исключают из третьего и последующих уравнений и так далее. Таким образом, в последнем уравнении остается только одно неизвестное. Для реализации прямого хода используют следующие известные правила:
— любое уравнение системы можно умножить на постоянный коэффициент;
— можно сложить два любых уравнения системы и результат записать вместо одного из этих уравнений.
Переход от системы (2)
к системе ( )
возможен при выполнении следующих
преобразований. Пусть
)
возможен при выполнении следующих
преобразований. Пусть 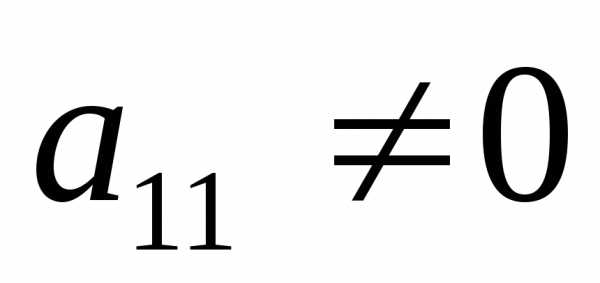 (если это не так, то можно поменять
местами два уравнения системы). Разделим
все члены первого уравнения системы
(2) на
(если это не так, то можно поменять
местами два уравнения системы). Разделим
все члены первого уравнения системы
(2) на ,
все члены второго уравнения на
,
все члены второго уравнения на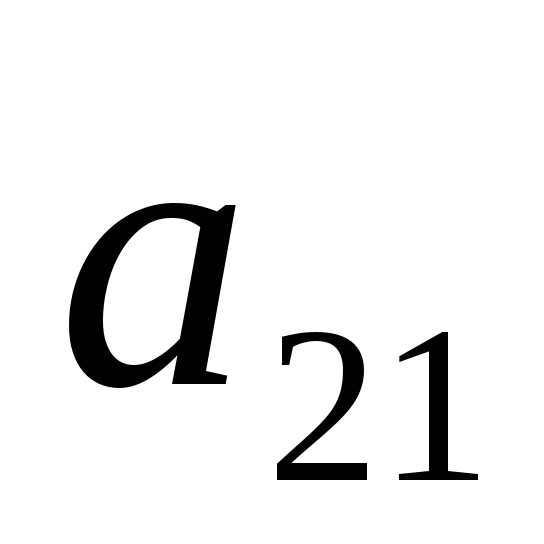 ,
третьего – на
,
третьего – на
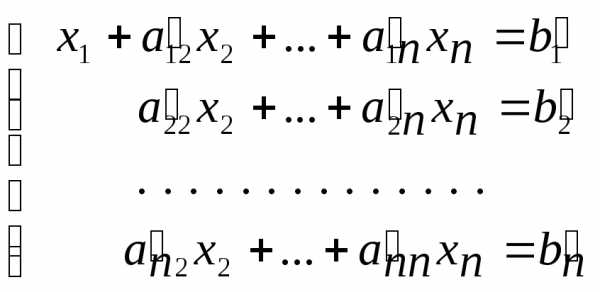
Первое уравнение
оставим без изменений, а оставшиеся
преобразуем аналогично. Так последовательно
систему (2) приводим к виду ( ).
).
Обратный ход: последовательно вычисляют значения всех неизвестных, начиная с последнего.
Пример. Решить
СЛАУ 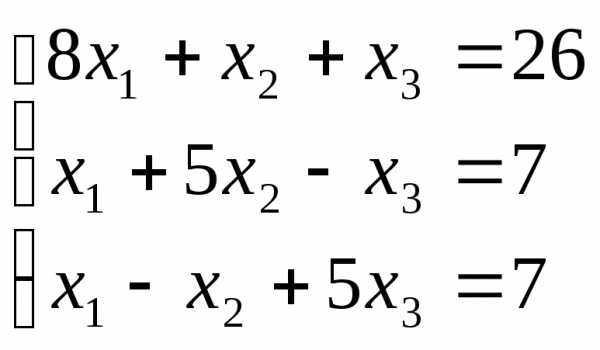 методом Гаусса.
методом Гаусса.
Решение. Прямой ход.
Разделим все члены
первого уравнения на 8, получим: 
Вычтем из второго и
третьего уравнений первое: 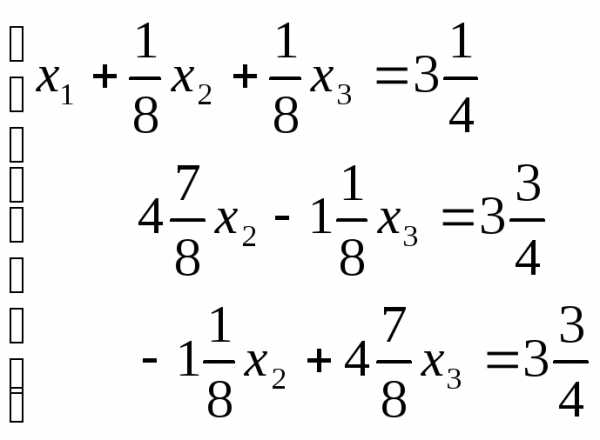 .
.
Разделим все члены
второго уравнения на 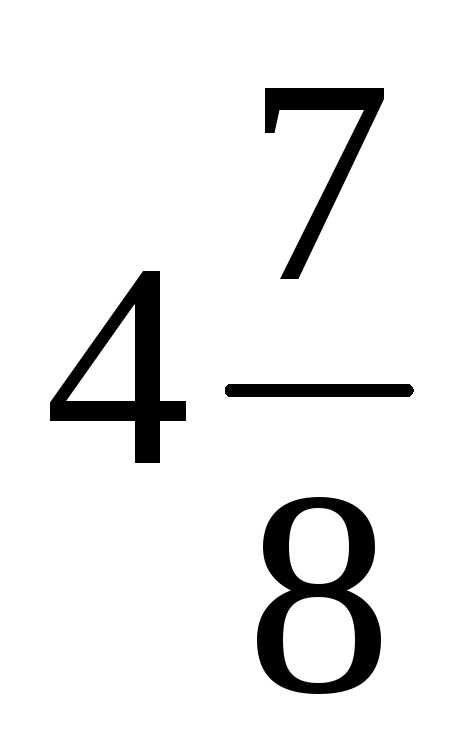 ,
а третьего – на
,
а третьего – на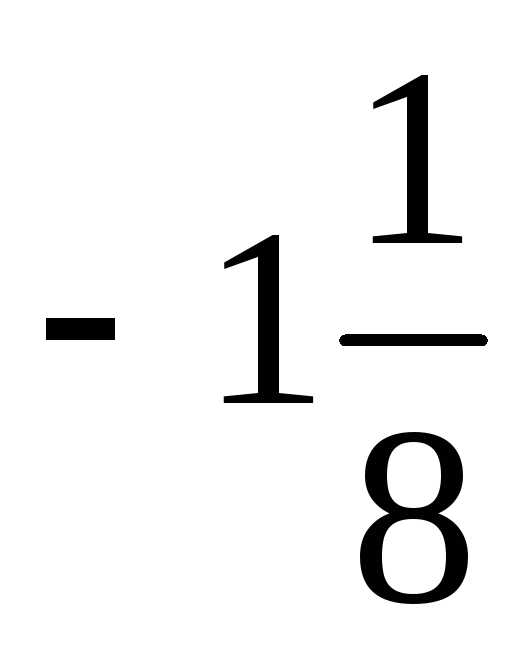 ,
получим
,
получим
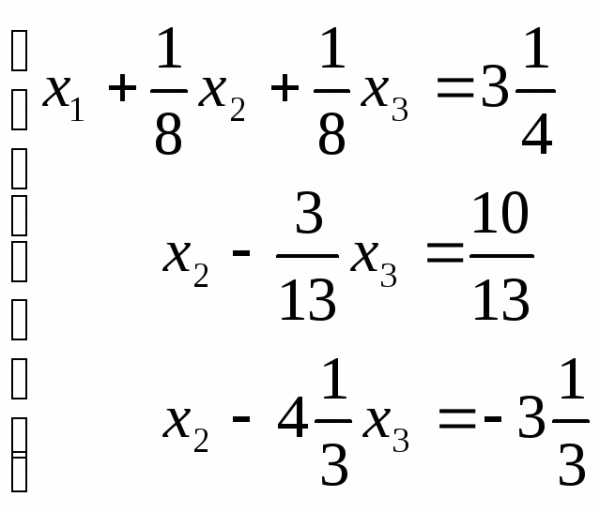 .
.
Вычтем из третьего
уравнения второе: 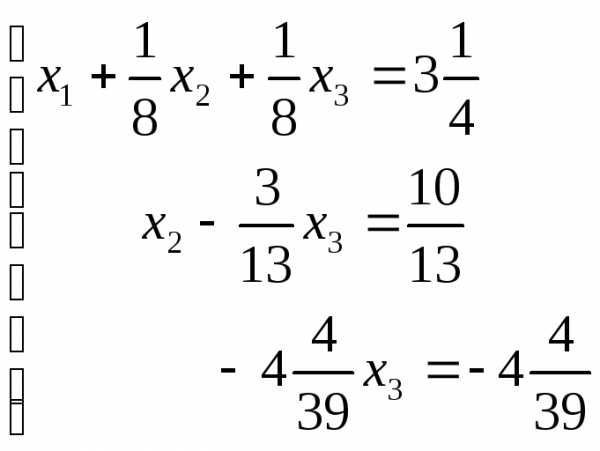
Прямой ход завершен.
Обратный ход: выразим
из последнего уравнения системы 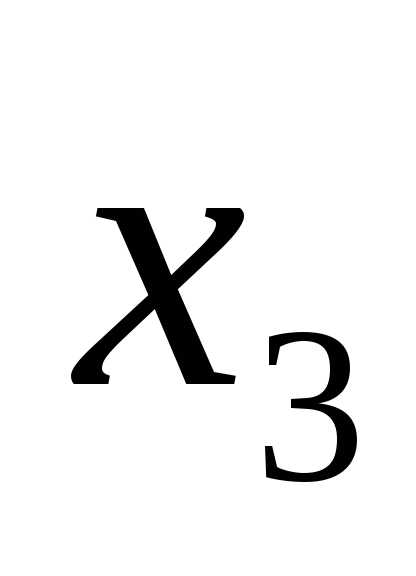 .
.
.
Из второго уравнения выразим .
Из первого уравнения выразим .
Получаем следующее
решение системы: 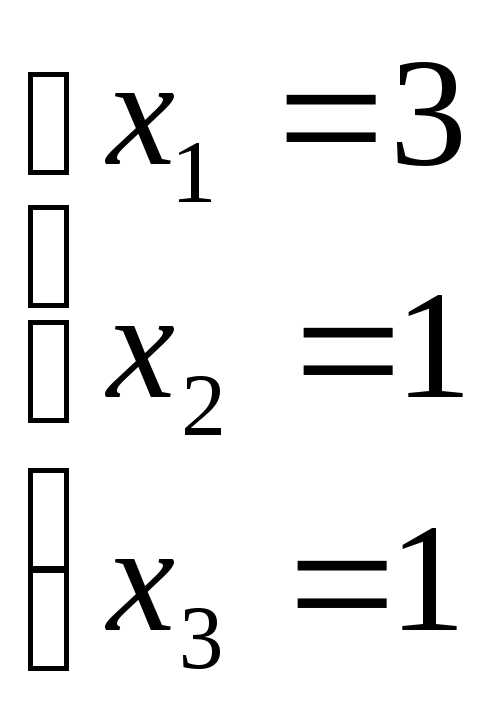 .
.
Убедимся, что найдено верное решение системы, подставив его в исходную систему уравнений:
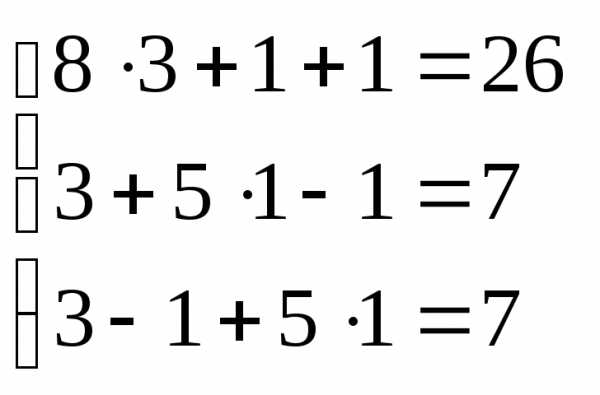
 .
.
studfiles.net
Решение произвольных систем линейных уравнений
Дисциплина: Высшая математика
Тема: Решение произвольных систем линейных уравнений
1. Решение произвольных систем линейных алгебраических уравнений
Выше рассмотрены решения квадратных невырожденных систем линейных алгебраических уравнений матричным методом и методом Крамера. Однако они не пригодны в тех случаях, когда квадратная система уравнений вырождена или когда система вообще не является квадратной.
В связи с этим перейдем к рассмотрению систем линейных алгебраических уравнений общего вида, когда
:В данном случае матрица системы является прямоугольной, у нее нет определителя, и метод Крамера для решения системы не применим. Поэтому, прежде чем решать данную систему, рассмотрим две теоремы.
Теорема 1.1. Если ранг матрицы совместной системы линейных алгебраических уравнений равен числу неизвестных, то система имеет единственное решение .
Доказательство. Если ранг матрицы системы равен
, то есть числу неизвестных, то строк у матрицы должно быть тоже . Следовательно, . Итак, по условию . Но тогда любая, не входящая в базисный минор, строка расширенной матрицы является линейной комбинацией базисных строк и может быть обращена в ноль. То же самое происходит и с уравнением, соответствующим этой строке. Значит, исходная система эквивалентна уравнениям с коэффициентами из базисного минора. Остальные уравнений из системы можно убрать, так как они является линейной комбинацией оставшихся. Получаем квадратную невырожденную систему линейных алгебраических уравнений с неизвестными, которая согласно правилу Крамера имеет единственное решение, что и требовалось доказать. Теорема 1.2. Если ранг матрицы совместной системы линейных алгебраических уравнений меньше числа неизвестных, то система имеет бесконечное множество решений .Доказательство. По условию система совместна и
. Будем считать, что базисный минор расположен в левом верхнем углу расширенной матрицы системы . Если это не так, то, переставляя строки и столбцы матрицы, можно получить нужный результат.Минор будет иметь вид:
.Так как любая строка матрицы
, не вошедшая в базисный минор, является линейной комбинацией базисных, то ее можно обратить в ноль. Тогда, по аналогии с теоремой 1.1, из исходной системы можно убрать те уравнения, коэффициенты которых не попали в базисный минор. Следовательно, в ней останется линейных алгебраических уравнений и исходную систему можно записать в виде:или
Придавая неизвестным
произвольные значения , получаем систему из уравнений с неизвестными:Так как числа
могут быть заданы произвольно, то число решений системы бесконечно. Какое-то одно решение будет иметь вид: .Неизвестные, коэффициенты при которых входят в базисный минор, называются базисными. Остальные неизвестные называются свободными.
2. Система однородных линейных алгебраических уравнений
Важное место среди всех систем линейных алгебраических уравнений занимают однородные системы с произвольными
и :Данные системы всегда совместны, так как обязательно имеют решение вида
, которое называется нулевым или тривиальным.Если
, то, согласно теореме 1.1, это решение будет единственным. В частности, в случае однородной невырожденной квадратной системы ее единственное решение будет тривиальным.В случае, когда ранг матрицы системы меньше числа неизвестных, то решений, согласно теореме 1.2, будет бесконечное множество. Пусть в этом случае матрицы — столбцы
, ,…, являются некоторыми решениями системы: , ,…, .Тогда выражение
будет называться их линейной комбинацией. Очевидно, что можно ввести понятие линейно зависимой и линейно независимой системы этих решений. Необходимо иметь в виду, что линейная комбинация решений системы линейных алгебраических уравнений также будет ее решением. Действительно, .Теорема. Если ранг матрицы однородной системы линейных алгебраических уравнений меньше числа неизвестных, то есть , то существует линейно независимых решений системы , ,…, , а любые другие решения можно представить как их линейную комбинацию .
Доказательство. Пусть ранг основной матрицы системы
. Тогда базисными неизвестными будут , а остальные неизвестных будут свободными. В этом случае произвольное решение системы можно записать в виде: .Здесь
– произвольные числа, а однозначно определяются из системы для выбранных .Рассмотрим
следующих решений системы:, ,…, .
По аналогии с результатом п. 6.3 все они линейно независимы, и произвольное решение системы можно представить в виде:
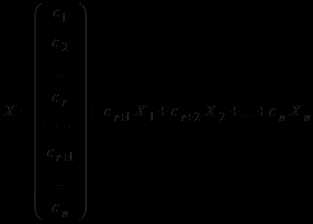 ,
,что и требовалось доказать.
Определение. Фундаментальной системой решений однородной системы линейных алгебраических уравнений называется совокупность всех ее линейно независимых решений .
Если в фундаментальной системе решений свободные неизвестные по очереди выражаются через единицу, в то время как остальные равны нулю, то такая фундаментальная система решений называется нормированной.
mirznanii.com
Система линейных уравнений, формулы и примеры
Определение и формулы системы линейных уравнений
Например.
Решение системы линейных уравнений
Решением СЛАУ называется совокупность значений неизвестных , при подстановке которых в каждое уравнения системы они обращаются в тождества.
Например. Пара чисел является решением системы поскольку при подстановке указанных значений в уравнения системы, последние превращаются в тождества:
Матрицей СЛАУ называется матрица, составленная из коэффициентов при неизвестных.
Например. Матрицей системы будет матрица
Матрицей правых частей или матрицей свободных коэффициентов называется матрица-столбец, составленная из правых частей СЛАУ.
Например. Матрицей свободных коэффициентов системы есть матрица
Расширенной матрицей СЛАУ называется матрица системы, после вертикальной черты справа от которой записана матрица правых частей.
Например. Расширенная матрица системы — это матрица
СЛАУ (1) можно записать в матричном виде , где
— матрица системы;
— матрица-столбец неизвестных;
— матрица правых частей.
СЛАУ, которая имеет хотя бы одно решение, называется совместной; если решений нет, то СЛАУ называется несовместной.
СЛАУ (1) называется однородной, если все ее правые части равны нулю одновременно: :
Например.
Однородная СЛАУ (2), имеющая единственное нулевое решение, называется тривиально совместной; в противном случае — нетривиально совместной.
ru.solverbook.com

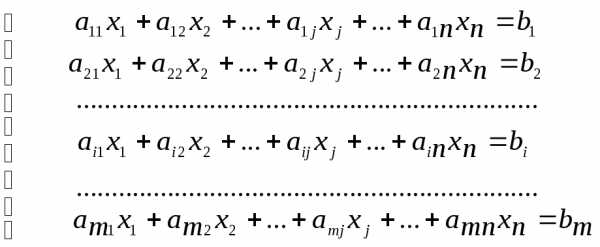
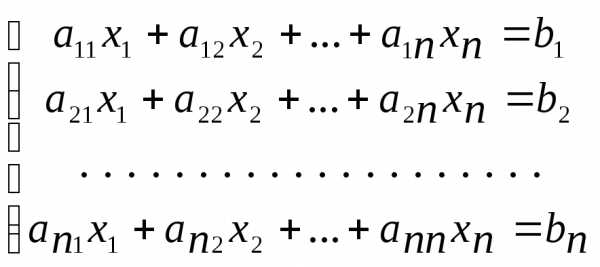
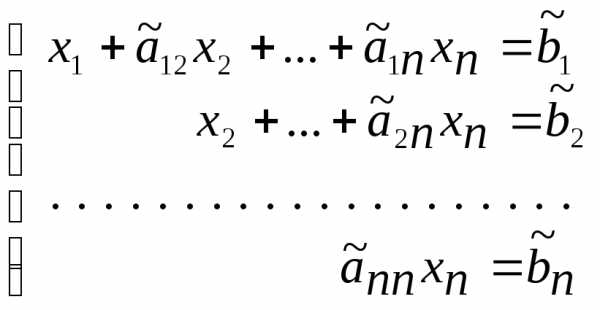
 )
)