Средние величины
Средняя величина – это своеобразная числовая характеристика множества функций и чисел. Также есть и другое значение, средняя величина – это некоторое число, которое заключено между наибольшим и наименьшим значением.
Изучение средних величин началось еще в Древней Греции, когда Пифагор и ученики его школы изучали и исследовали пропорции. Строгого различия между понятиями «средняя величина» и «пропорция» тогда не проводилось. С арифметической точки зрения, значительный толчок в теории пропорций был дан греческими математиками Паппом Александрийским и Никомахом Герасским. Однако нас интересует все-таки средняя величина. Первым этапом развития «средней величины», как отдельного понятия является этап, когда эта средняя величина стала считаться центральным членом пропорции. Следующим же этапом был переход от непрерывных пропорций к прогрессии – геометрической, арифметической и гармонической.
Если мы заглянем в истории статистики, то увидим, что широкое употребление такого понятия, как «средние величины» впервые ввел английский математик и ученный У.
- собственно средние;
- средние арифметические.
Собственно средние величины представляют число, вещь, которые действительно существуют. Средние арифметические величины являются числами, которые дают возможность близкого представления в математике о многих, различных числах, хоть и однородных.
Среднее арифметическое двух величин
| a + b 2 |
Среднее арифметическое «n» величин
| a1 + a2 + … + an |
| n |
Среднее геометрическое (среднее пропорциональное) двух величин
Среднее геометрическое (среднее пропорциональное) «n» величин
| n |
√ | a1 * a2 * . .. * an |
||
Среднее квадратичное двух величин
| √ |
|
Среднее квадратичное «n» величин
| √ | 1 n |
|
|
Среднее гармоническое двух величин
| 2 | ||
| 1 a1 |
+ | 1 a2 |
Среднее гармоническое «n» величин
| n | ||||
| 1 a1 |
+ | 1 a2 |
+ . .. + |
1 an |
Среднее геометрическое чисел – формула и примеры
Средние величины в статистике дают обобщающую характеристику анализируемого явления. Самая распространенная из них – среднее арифметическое. Она применяется, когда агрегатный показатель образуется с помощью суммы элементов. Например, масса нескольких яблок, суммарная выручка за каждый день продаж и т.д. Но так бывает не всегда. Иногда агрегатный показатель образуется не в результате суммирования, а в результате умножения.
Такой пример. Месячная инфляция – это изменение уровня цен одного месяца по сравнению с предыдущим. Если известны показатели инфляции за каждый месяц, то как получить годовое значение? С точки зрения статистики – это цепной индекс, поэтому правильный ответ: с помощью перемножения месячных показателей инфляции. То есть общий показатель инфляции – это не сумма, а произведение. А как теперь узнать среднюю инфляцию за месяц, если имеется годовое значение? Нет, не разделить на 12, а извлечь корень 12-й степени (степень зависит от количества множителей).
В общем случае среднее геометрическое рассчитывается по формуле:
То есть корень из произведения исходных данных, где степень определяется количеством множителей. Например, среднее геометрическое двух чисел – это квадратный корень из их произведения
Среднее геометрическое трех чисел – кубический корень из произведения
и т.д.
Если каждое исходное число заменить на их среднее геометрическое, то произведение даст тот же результат.
Чтобы лучше разобраться, чем отличаются среднее арифметическое и среднее геометрическое, рассмотрим следующий рисунок. Имеется прямоугольный треугольник, вписанный в круг.
Из прямого угла опущена медиана a (на середину гипотенузы). Также из прямого угла опущена высота b, которая в точке P делит гипотенузу на две части m и n. Т.к. гипотенуза – это диаметр описанного круга, а медиана – радиус, то очевидно, что длина медианы a – это среднее арифметическое из m и n.
Рассчитаем, чему равна высота b. В силу подобия треугольников АВP и BCP справедливо равенство
Откуда
Значит, высота прямоугольного треугольника – это среднее геометрическое из отрезков, на которые она разбивает гипотенузу. Такое наглядное отличие.
В MS Excel среднюю геометрическую можно найти с помощью функции СРГЕОМ.
Все очень просто: вызвали функцию, указали диапазон и готово.
На практике этот показатель используют не так часто, как среднее арифметическое, но все же встречается. Например, есть такой индекс развития человеческого потенциала, с помощью которого сравнивают уровень жизни в разных странах. Он рассчитывается, как среднее геометрическое из нескольких индексов.
Ниже видео, как найти среднее геометрическое чисел в Excel.
Поделиться в социальных сетях:
Среднее двух чисел со знаком
Учитель сообщает среднюю оценку за тест.
Вы прочитали о среднем количестве калорий, сожженных в час для вашего любимого упражнения.
Что означают эти цифры?
На средние два числа означает сложить числа вместе, и затем разделить на $\,2\,$.
Таким образом:
$$ \text{среднее значение } \,a\, \text{ и } \,b\, \text{ равно } \,\фракция{а+б}{2} $$
Усреднение двух разных чисел всегда дает число ровно наполовину между, как показано ниже:
В этом веб-упражнении вы вычислите средние значения двух
числа, где числа могут быть
$\,-10,-9,\ldots,9,10\,$.
Следует помнить две ключевые идеи:
- Если два усредняемых числа близки друг другу, просто визуализируйте числовую линию и изобразите число, которое находится ровно посередине между ними.
- Если усредняемые числа достаточно далеко друг от друга
что вы не можете легко решить, какое число
на полпути между ними, затем выполните арифметику:
сложите два числа и разделите на $\,2\,$.
Ясно, что формула $\,\frac{a+b}2\,$ дает какой-то номер ; но откуда мы это знаем число, заданное этой формулой, равно , на самом деле , всегда , на полпути между $\,а\,$ и $\,б\,$?
Хотя неоднократные испытания (с большим количеством разных чисел) довольно убедительно, это из конечно невозможно проверить каждые пара действительных чисел.
Чтобы увидеть доказательство, прочитай текст!
Примеры
Вопрос: Каково среднее значение $\,-3\,$ и $\,-5\,$?
Решение:
визуализировать
$\,-3\,$ и $\,-5\,$ на числовой прямой.
Ответ: $-4$
Вопрос: Каково среднее значение $\,7\,$ и $\,10\,$?
Решение:
визуализировать
$\,7\,$ и $\,10\,$ на числовой прямой.
Какое число находится на полпути между ними?
Ответ:
$8.5$
Вопрос: Каково среднее значение $\,-7\,$ и $\,9\,$?
Решение: Эти числа слишком далеки друг от друга, чтобы их можно было легко визуализировать посередине. Сделай арифметику: $$\frac{-7+9}2 = \frac{2}2 = 1$$ Ответ: $1$
Более продвинутые читатели могут захотеть изучить (необязательно):
Применение концепций усреднения: разложение квадратичного числа на множители.
Практика
В этом упражнении вы должны написать свои ответы в десятичной форме (при необходимости). То есть писать (скажем) $\,2.5\,$, а не $\,5/2\,$.
Концептуальная практика
Вероятность. Почему среднее значение определяется как сумма данных, деленная на общее количество данных?
$\begingroup$
Где бы я ни искал в Интернете, определение среднего больше похоже на просто формулу для него-
суммируйте значения, а затем разделите результат на количество значений, вы получить число, это число является средним.
Хорошо, но что он собой представляет? Центральное значение? Хорошо, но откуда математики узнали, что это центральное значение представляет собой сумму значений, деленную на количество значений?
Короче говоря, мне любопытно узнать, что привело к формуле среднего как сумма данных / количество данных.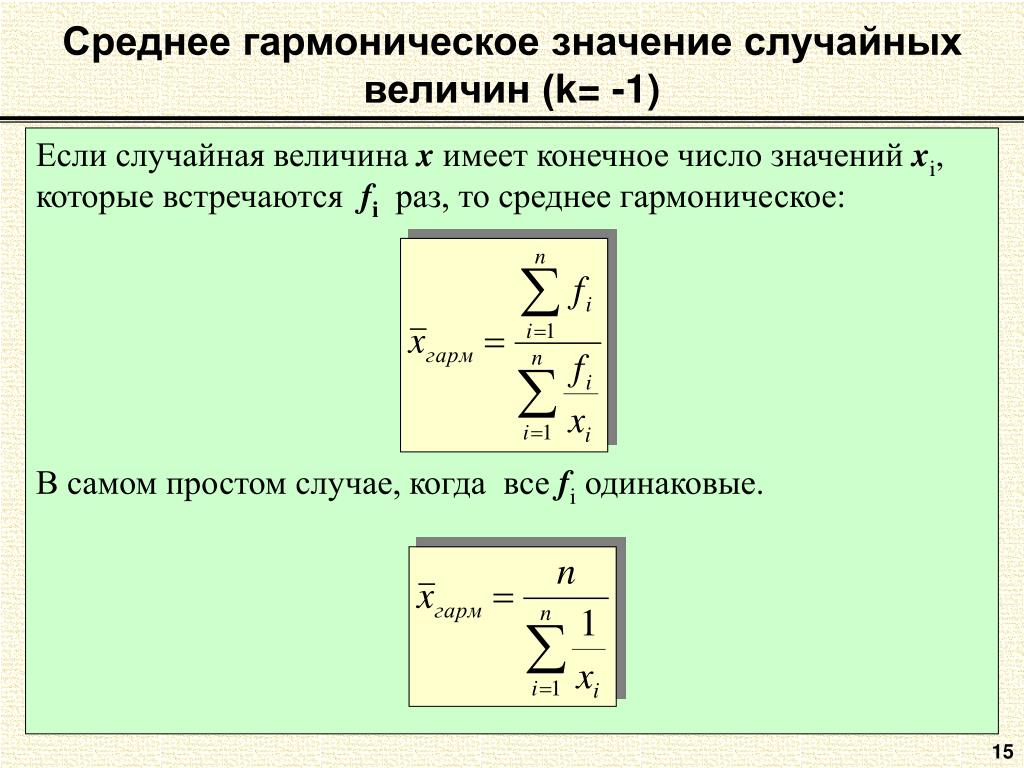
Я считаю, что ответ заключается в знании значения понятия среднего.
- вероятность
- статистика
- среднее
$\endgroup$
3
$\begingroup$
Существуют различные способы вычисления «среднего значения», каждый из которых представляет разные концепции. Среднее значение, которое вы описываете, называется средним арифметическим (или часто просто означает ), и оно представляет собой «равное распределение» общей стоимости по всем элементам.
Предположим, у вас есть 10 кувшинов с водой, каждый из которых наполнен разным объемом воды. Средний объем — это количество воды, которое было бы в каждом кувшине, если бы вы распределили воду поровну между 10 кувшинами, то есть просто общее количество воды, деленное на 10.
Вы можете или не можете найти среднее значение полезной или значимой мерой «среднего» в зависимости от того, что вы хотите описать, и лежащего в основе распределения данных.
Среднее значение весьма полезно в качестве сводной статистики для данных с центральной тенденцией, например, если количество воды в кувшинах примерно нормально распределено — в этом случае среднее значение обычно представляет значение, «близкое» к тому, что вы ожидаете. найти, выбрав кувшин наугад. Это может быть менее полезно в качестве сводной статистики, если данные распределены без центральной тенденции, например, если половина кувшинов пуста, а половина заполнена 10 л воды — здесь среднее значение составляет 5 л и по-прежнему представляет собой «равное распределение» вода во всех кувшинах, но на самом деле ни в одном из кувшинов нет и близко 5 литров.
Другой пример, когда среднее значение может быть не очень полезным, — это крайние выбросы, например, если 9 кувшинов пусты, а в одном 1000 л воды — среднее значение в этом случае равно 100 л, но большинство кувшинов не вообще ничего не держи. Здесь медиана может быть более полезной мерой «среднего», но это действительно зависит от того, что вы собираетесь передать с помощью статистики.