Вычисление среднего значения ряда чисел
Excel
Формулы и функции
Формулы
Формулы
Вычисление среднего значения ряда чисел
Excel для Microsoft 365 Excel для Интернета Excel 2021 Excel 2019 Excel 2016 Excel 2013 Excel 2010 Excel 2007 Еще…Меньше
Предположим, вам нужно найти среднее количество дней для выполнения задач разными сотрудниками. Или вы хотите вычислить среднюю температуру для определенного дня на основе 10-летнего промежутка времени. Существует несколько способов расчета среднего для группы чисел.
Функция СРЗНАЧ вычисляет среднее значение, то есть центр набора чисел в статистическом распределении. Существует три наиболее распространенных способа определения среднего значения:
-
 Например, средним значением для чисел 2, 3, 3, 5, 7 и 10 будет 5, которое является результатом деления их суммы, равной 30, на их количество, равное 6.
Например, средним значением для чисел 2, 3, 3, 5, 7 и 10 будет 5, которое является результатом деления их суммы, равной 30, на их количество, равное 6.
-
Медиана Среднее число числа. Половина чисел имеют значения больше медианой, а половина чисел имеют значения меньше медианой. Например, медианой для чисел 2, 3, 3, 5, 7 и 10 будет 4.
-
Мода Наиболее часто встречается число в группе чисел. Например, модой для чисел 2, 3, 3, 5, 7 и 10 будет 3.
При симметричном распределении множества чисел все три значения центральной тенденции будут совпадать. В акосимном распределении группы чисел они могут быть другими.
Выполните действия, описанные ниже.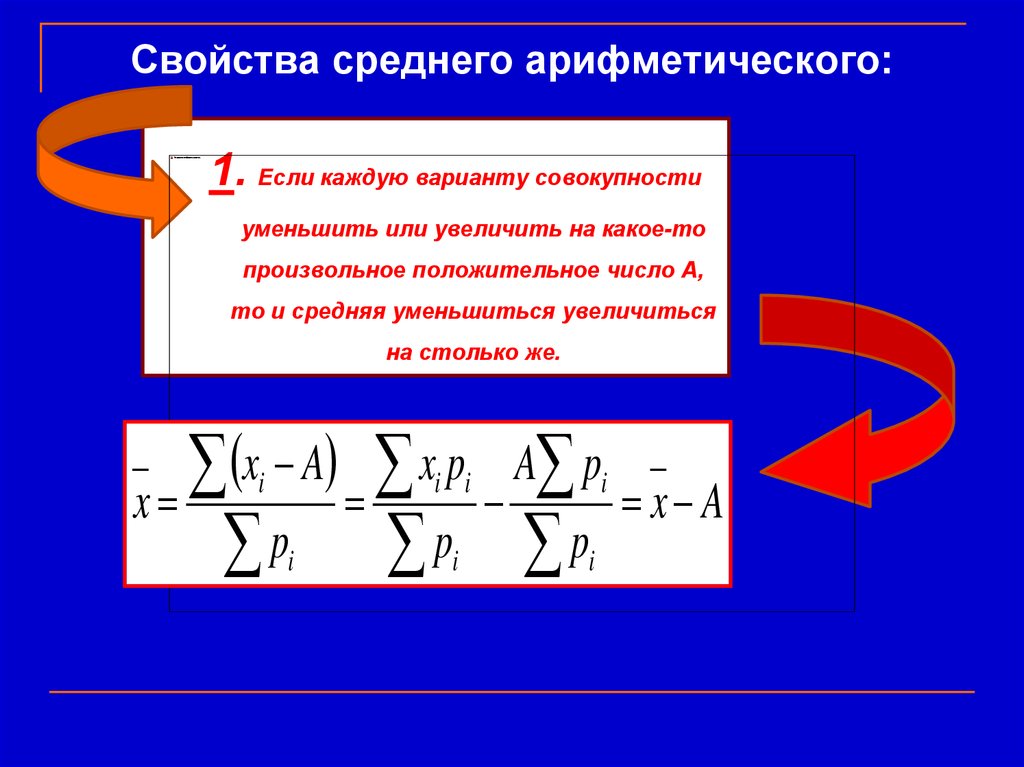
-
Щелкните ячейку снизу или справа от чисел, для которых необходимо найти среднее.
-
На вкладке «Главная» в группе «Редактирование» щелкните стрелку рядом с кнопкой » «, выберите «Среднее» и нажмите клавишу ВВОД.
Для этого используйте функцию С AVERAGE.
|
Формула |
Описание (результат) |
|
=СПБ(A2:A7) |
Среднее значение всех чисел в списке выше (9,5). |
|
=СПБ(A2:A4;A7) |
Среднее значение 3-го и последнего числа в списке (7,5). |
|
=С AVERAGEIF(A2:A7;»<>0″) |
Среднее значение чисел в списке за исключением тех, которые содержат нулевые значения, например ячейка A6 (11,4). |
Для этой задачи используются функции СУММПРОИВ ИСУММ. В этом примере вычисляется средняя цена за единицу для трех покупок, при которой каждая покупка приобретает различное количество единиц по разной цене.
Скопируйте приведенную ниже таблицу на пустой лист.
|
|
Для этой задачи используются функции С AVERAGE и ЕСЛИ. Скопируйте приведенную ниже таблицу и имейте в виду, что при копировании на пустой лист может быть проще понять этот пример.
|
Формула |
Описание (результат) |
|
=С AVERAGEIF(A2:A7;»<>0″) |
Среднее значение чисел в списке за исключением тех, которые содержат нулевые значения, например ячейка A6 (11,4). |
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
См. также
СРЗНАЧ
С AVERAGEIF
СУММ
СУММПРОИЗВ
Средняя арифметическая разность температур. (Arithmetic Mean Temperature Difference — AMTD), Средняя логарифмическая разность температур (Logarithmic Mean Temperature Difference — LMTD или DTLM). Средняя арифметическая разность температур и средняя логарифмическая разность температур используется для оценки теплообмена, при процессе конвекционной теплопередачи. В связи с законом Ньютона-Римана, процесс теплопередачи зависит от мгновенной разницы температур холодного и теплого вещества.
Средняя разность температур. Средняя разность температур в процессе передачи тепла зависит от направления потока жидкости, включенного в процесс. Главная и второстепенная жидкости в процессе теплопередачи могут
Если в первичном контуре рабочее тело — насыщенный пар, то первичная температура может считаться постоянной, т.к процесс теплопередачи идет как результат изменения агрегатного состояния. Температурная кривая первичного потока не зависит от направления потока. Средняя логарифмическая разность температур (Logarithmic Mean Temperature Difference — LMTD или DTLM). Изменение температуры рабочей среды во вторичном контуре — нелинейно. Именно поэтому её лучше представить в логарифмическом виде:
Средняя логарифмическая разность температур всегда меньше средней арифметической разности температур. Средняя арифметическая разность температур. (Arithmetic Mean Temperature Difference — AMTD) Более простой, но менее точный способ вычислить разницу температур. AMTD выражается как:
Средняя арифметическая разность температур даст удовлетворительное приближения для средней разности температур, когда наименьшая из разниц входящей и выходищей температур будет больше чем половина наибольшей разницы входящей и выходящей температур. Когда тепло передается как результат изменения фазового состояния (конденсация или испарение), температура первичного и вторичного контура остается постоянной.
Калькулятор средних арифметических и логарифмических разниц температурКалькулятор ниже используется для вычисления средних арифметических и логарифмических разниц температур в противоположных и параллельных потоках.
Пример — Средняя арифметическая и логарифмическая разница температур, Горячая вода нагревает воздухГорячая вода температурой 80 oC нагревает воздух с 0 oC до 20 oC в параллельном потоке теплообмена. Средняя арифметическая разница температур вычисляется:
Средняя логарифмическая разница температур вычисляется:
График логарифмической разницы температур | |
Дополнительная информация от TehTab.ru: | |
Как рассчитать среднюю стоимость товаров: формулы средних цен
Соглашение о конфиденциальности
и обработке персональных данных
1. Общие положения
Общие положения
1.1.Настоящее соглашение о конфиденциальности и обработке персональных данных (далее – Соглашение) принято свободно и своей волей, действует в отношении всей информации, которую ООО «Инсейлс Рус» и/или его аффилированные лица, включая все лица, входящие в одну группу с ООО «Инсейлс Рус» (в том числе ООО «ЕКАМ сервис»), могут получить о Пользователе во время использования им любого из сайтов, сервисов, служб, программ для ЭВМ, продуктов или услуг ООО «Инсейлс Рус» (далее – Сервисы) и в ходе исполнения ООО «Инсейлс Рус» любых соглашений и договоров с Пользователем. Согласие Пользователя с Соглашением, выраженное им в рамках отношений с одним из перечисленных лиц, распространяется на все остальные перечисленные лица.
1.2.Использование Сервисов означает согласие Пользователя с настоящим Соглашением и указанными в нем условиями; в случае несогласия с этими условиями Пользователь должен воздержаться от использования Сервисов.
1.3.Сторонами (далее – «Стороны) настоящего Соглашения являются:
«Инсейлс» – Общество с ограниченной ответственностью «Инсейлс Рус», ОГРН 1117746506514, ИНН 7714843760, КПП 771401001, зарегистрированное по адресу: 125319, г. Москва, ул.Академика Ильюшина, д.4, корп.1, офис 11 (далее — «Инсейлс»), с одной стороны, и
Москва, ул.Академика Ильюшина, д.4, корп.1, офис 11 (далее — «Инсейлс»), с одной стороны, и
«Пользователь» –
либо физическое лицо, обладающее дееспособностью и признаваемое участником гражданских правоотношений в соответствии с законодательством Российской Федерации;
либо юридическое лицо, зарегистрированное в соответствии с законодательством государства, резидентом которого является такое лицо;
либо индивидуальный предприниматель, зарегистрированный в соответствии с законодательством государства, резидентом которого является такое лицо;
которое приняло условия настоящего Соглашения.
1.4.Для целей настоящего Соглашения Стороны определили, что конфиденциальная информация – это сведения любого характера (производственные, технические, экономические, организационные и другие), в том числе о результатах интеллектуальной деятельности, а также сведения о способах осуществления профессиональной деятельности (включая, но не ограничиваясь: информацию о продукции, работах и услугах; сведения о технологиях и научно-исследовательских работах; данные о технических системах и оборудовании, включая элементы программного обеспечения; деловые прогнозы и сведения о предполагаемых покупках; требования и спецификации конкретных партнеров и потенциальных партнеров; информацию, относящуюся к интеллектуальной собственности, а также планы и технологии, относящиеся ко всему перечисленному выше), сообщаемые одной стороной другой стороне в письменной и/или электронной форме, явно обозначенные Стороной как ее конфиденциальная информация.
1.5.Целью настоящего Соглашения является защита конфиденциальной информации, которой Стороны будут обмениваться в ходе переговоров, заключения договоров и исполнения обязательств, а равно любого иного взаимодействия (включая, но не ограничиваясь, консультирование, запрос и предоставление информации, и выполнение иных поручений).
2.Обязанности Сторон
2.1.Стороны соглашаются сохранять в тайне всю конфиденциальную информацию, полученную одной Стороной от другой Стороны при взаимодействии Сторон, не раскрывать, не разглашать, не обнародовать или иным способом не предоставлять такую информацию какой-либо третьей стороне без предварительного письменного разрешения другой Стороны, за исключением случаев, указанных в действующем законодательстве, когда предоставление такой информации является обязанностью Сторон.
2.2.Каждая из Сторон предпримет все необходимые меры для защиты конфиденциальной информации как минимум с применением тех же мер, которые Сторона применяет для защиты собственной конфиденциальной информации. Доступ к конфиденциальной информации предоставляется только тем сотрудникам каждой из Сторон, которым он обоснованно необходим для выполнения служебных обязанностей по исполнению настоящего Соглашения.
Доступ к конфиденциальной информации предоставляется только тем сотрудникам каждой из Сторон, которым он обоснованно необходим для выполнения служебных обязанностей по исполнению настоящего Соглашения.
2.3.Обязательство по сохранению в тайне конфиденциальной информации действительно в пределах срока действия настоящего Соглашения, лицензионного договора на программы для ЭВМ от 01.12.2016г., договора присоединения к лицензионному договору на программы для ЭВМ, агентских и иных договоров и в течение пяти лет после прекращения их действия, если Сторонами отдельно не будет оговорено иное.
2.4.Не будут считаться нарушением настоящего Соглашения следующие случаи:
(а)если предоставленная информация стала общедоступной без нарушения обязательств одной из Сторон;
(б)если предоставленная информация стала известна Стороне в результате ее собственных исследований, систематических наблюдений или иной деятельности, осуществленной без использования конфиденциальной информации, полученной от другой Стороны;
(в)если предоставленная информация правомерно получена от третьей стороны без обязательства о сохранении ее в тайне до ее предоставления одной из Сторон;
(г)если информация предоставлена по письменному запросу органа государственной власти, иного государственного органа, или органа местного самоуправления в целях выполнения их функций и ее раскрытие этим органам обязательно для Стороны. При этом Сторона должна незамедлительно известить другую Сторону о поступившем запросе;
При этом Сторона должна незамедлительно известить другую Сторону о поступившем запросе;
(д)если информация предоставлена третьему лицу с согласия той Стороны, информация о которой передается.
2.5.Инсейлс не проверяет достоверность информации, предоставляемой Пользователем, и не имеет возможности оценивать его дееспособность.
2.6.Информация, которую Пользователь предоставляет Инсейлс при регистрации в Сервисах, не является персональными данными, как они определены в Федеральном законе РФ №152-ФЗ от 27.07.2006г. «О персональных данных».
2.7.Инсейлс имеет право вносить изменения в настоящее Соглашение. При внесении изменений в актуальной редакции указывается дата последнего обновления. Новая редакция Соглашения вступает в силу с момента ее размещения, если иное не предусмотрено новой редакцией Соглашения.
2.8.Принимая данное Соглашение Пользователь осознает и соглашается с тем, что Инсейлс может отправлять Пользователю персонализированные сообщения и информацию (включая, но не ограничиваясь) для повышения качества Сервисов, для разработки новых продуктов, для создания и отправки Пользователю персональных предложений, для информирования Пользователя об изменениях в Тарифных планах и обновлениях, для направления Пользователю маркетинговых материалов по тематике Сервисов, для защиты Сервисов и Пользователей и в других целях.
Пользователь имеет право отказаться от получения вышеуказанной информации, сообщив об этом письменно на адрес электронной почты Инсейлс — [email protected].
2.9.Принимая данное Соглашение, Пользователь осознает и соглашается с тем, что Сервисами Инсейлс для обеспечения работоспособности Сервисов в целом или их отдельных функций в частности могут использоваться файлы cookie, счетчики, иные технологии и Пользователь не имеет претензий к Инсейлс в связи с этим.
2.10.Пользователь осознает, что оборудование и программное обеспечение, используемые им для посещения сайтов в сети интернет могут обладать функцией запрещения операций с файлами cookie (для любых сайтов или для определенных сайтов), а также удаления ранее полученных файлов cookie.
Инсейлс вправе установить, что предоставление определенного Сервиса возможно лишь при условии, что прием и получение файлов cookie разрешены Пользователем.
2.11.Пользователь самостоятельно несет ответственность за безопасность выбранных им средств для доступа к учетной записи, а также самостоятельно обеспечивает их конфиденциальность. Пользователь самостоятельно несет ответственность за все действия (а также их последствия) в рамках или с использованием Сервисов под учетной записью Пользователя, включая случаи добровольной передачи Пользователем данных для доступа к учетной записи Пользователя третьим лицам на любых условиях (в том числе по договорам или соглашениям). При этом все действия в рамках или с использованием Сервисов под учетной записью Пользователя считаются произведенными самим Пользователем, за исключением случаев, когда Пользователь уведомил Инсейлс о несанкционированном доступе к Сервисам с использованием учетной записи Пользователя и/или о любом нарушении (подозрениях о нарушении) конфиденциальности своих средств доступа к учетной записи.
Пользователь самостоятельно несет ответственность за все действия (а также их последствия) в рамках или с использованием Сервисов под учетной записью Пользователя, включая случаи добровольной передачи Пользователем данных для доступа к учетной записи Пользователя третьим лицам на любых условиях (в том числе по договорам или соглашениям). При этом все действия в рамках или с использованием Сервисов под учетной записью Пользователя считаются произведенными самим Пользователем, за исключением случаев, когда Пользователь уведомил Инсейлс о несанкционированном доступе к Сервисам с использованием учетной записи Пользователя и/или о любом нарушении (подозрениях о нарушении) конфиденциальности своих средств доступа к учетной записи.
2.12.Пользователь обязан немедленно уведомить Инсейлс о любом случае несанкционированного (не разрешенного Пользователем) доступа к Сервисам с использованием учетной записи Пользователя и/или о любом нарушении (подозрениях о нарушении) конфиденциальности своих средств доступа к учетной записи. В целях безопасности, Пользователь обязан самостоятельно осуществлять безопасное завершение работы под своей учетной записью по окончании каждой сессии работы с Сервисами. Инсейлс не отвечает за возможную потерю или порчу данных, а также другие последствия любого характера, которые могут произойти из-за нарушения Пользователем положений этой части Соглашения.
В целях безопасности, Пользователь обязан самостоятельно осуществлять безопасное завершение работы под своей учетной записью по окончании каждой сессии работы с Сервисами. Инсейлс не отвечает за возможную потерю или порчу данных, а также другие последствия любого характера, которые могут произойти из-за нарушения Пользователем положений этой части Соглашения.
3.Ответственность Сторон
3.1.Сторона, нарушившая предусмотренные Соглашением обязательства в отношении охраны конфиденциальной информации, переданной по Соглашению, обязана возместить по требованию пострадавшей Стороны реальный ущерб, причиненный таким нарушением условий Соглашения в соответствии с действующим законодательством Российской Федерации.
3.2.Возмещение ущерба не прекращают обязанности нарушившей Стороны по надлежащему исполнению обязательств по Соглашению.
4.Иные положения
4.1.Все уведомления, запросы, требования и иная корреспонденция в рамках настоящего Соглашения, в том числе включающие конфиденциальную информацию, должны оформляться в письменной форме и вручаться лично или через курьера, или направляться по электронной почте адресам, указанным в лицензионном договоре на программы для ЭВМ от 01. 12.2016г., договоре присоединения к лицензионному договору на программы для ЭВМ и в настоящем Соглашении или другим адресам, которые могут быть в дальнейшем письменно указаны Стороной.
12.2016г., договоре присоединения к лицензионному договору на программы для ЭВМ и в настоящем Соглашении или другим адресам, которые могут быть в дальнейшем письменно указаны Стороной.
4.2.Если одно или несколько положений (условий) настоящего Соглашения являются либо становятся недействительными, то это не может служить причиной для прекращения действия других положений (условий).
4.3.К настоящему Соглашению и отношениям между Пользователем и Инсейлс, возникающим в связи с применением Соглашения, подлежит применению право Российской Федерации.
4.3.Все предложения или вопросы по поводу настоящего Соглашения Пользователь вправе направлять в Службу поддержки пользователей Инсейлс www.ekam.ru либо по почтовому адресу: 107078, г. Москва, ул. Новорязанская, 18, стр.11-12 БЦ «Stendhal» ООО «Инсейлс Рус».
Дата публикации: 01.12.2016г.
Полное наименование на русском языке:
Общество с ограниченной ответственностью «Инсейлс Рус»
Сокращенное наименование на русском языке:
ООО «Инсейлс Рус»
Наименование на английском языке:
InSales Rus Limited Liability Company (InSales Rus LLC)
Юридический адрес:
125319, г. Москва, ул. Академика Ильюшина, д. 4, корп.1, офис 11
Москва, ул. Академика Ильюшина, д. 4, корп.1, офис 11
Почтовый адрес:
107078, г. Москва, ул. Новорязанская, 18, стр.11-12, БЦ «Stendhal»
ИНН: 7714843760 КПП: 771401001
Банковские реквизиты:
Р/с 40702810600001004854
В ИНГ БАНК (ЕВРАЗИЯ) АО, г.Москва,
к/с 30101810500000000222, БИК 044525222
Электронная почта: [email protected]
Контактный телефон: +7(495)133-20-43
Как рассчитать средний балл аттестата и диплома при поступлении в зарубежный вуз?
Рассчитать средний балл ОНЛАЙН >>
Очень часто, выпускникам вузов и школ нужно рассчитать средний балл полученного аттестата. Его могут потребовать при поступлении в зарубежный вуз, при устройстве на работу. Мы расскажем, что такое GPA, как правильно рассчитать свой средний балл и нужно ли при этом учитывать зачеты.
Что такое GPA
GPA — это средний балл диплома или аттестата, общий показатель успеваемости школьника или студента. Эта аббревиатура расшифровывается как grade point average. При заполнении заявки на подготовительные программы, первое высшее и поступлении в магистратуру за рубежом, многие университеты требуют сообщить им GPA абитуриента. Так, большинство вузов США потребуют от абитуриентов обязательного указания GPA. Подробнее о поступлении на бакалавра в США читайте здесь, о том, как поступить в магистратуру США — здесь.
Эта аббревиатура расшифровывается как grade point average. При заполнении заявки на подготовительные программы, первое высшее и поступлении в магистратуру за рубежом, многие университеты требуют сообщить им GPA абитуриента. Так, большинство вузов США потребуют от абитуриентов обязательного указания GPA. Подробнее о поступлении на бакалавра в США читайте здесь, о том, как поступить в магистратуру США — здесь.
Как рассчитать GPA
При подсчете GPA учитываются все оценки, указанные в аттестате или дипломе. Это могут быть итоговые оценки: по предметам, за курсовые и дипломную работы, за госэкзамены. Если документ об образовании уже у вас на руках, учитывать какие-либо промежуточные оценки, которые проставлены у вас в школьном электронном журнале или зачетной книжке, не нужно.
Следующий момент касается только студентов: нужно ли учитывать зачеты и если да, то как именно их учитывать.
Если ваш вуз использует 5-тибалльную систему оценки знаний плюс «зачёт/ незачёт», рассчитать средний балл диплома, студенты, поступающие в зарубежные вузы, могут одним из двух способов:
- «Зачёты» учитываются.
 «Зачёт» = 5 баллов, «незачёт» = 0 баллов. Средний балл диплома = среднее арифметическое баллов за все предметы во вкладыше, включая «зачёт» и «незачёт».
«Зачёт» = 5 баллов, «незачёт» = 0 баллов. Средний балл диплома = среднее арифметическое баллов за все предметы во вкладыше, включая «зачёт» и «незачёт». - «Зачёты» не учитываются. Средний балл диплома = среднее арифметическое всех полученных баллов.
Среднее арифметическое как школьной успеваемости, так и дипломных оценок считают по формуле:
GPA = «cумма всех полученных оценок» разделить «число предметов».
Пример расчета GPA
В приведенной примере мы показываем расчет среднего балла для студентов, но школьники считают по той же схеме. Поскольку в большинстве школ не сдаются зачеты, то и в расчете этот вид оценки успеваемости не участвует.
Студент бакалавриата по программе «Менеджмент организации» получил такие оценки:
| № | Название предмета | Оценка |
|---|---|---|
| 1 | Философия | 4 (Хорошо) |
| 2 | Социология | 4 (Хорошо) |
| 3 | Отечественная история | Зачёт |
| 4 | Правоведение | Зачёт |
| 5 | Английский язык | 5 (Отлично) |
| 6 | Математика | 5 (Отлично) |
| 7 | Теория вероятностей | Зачёт |
| 8 | Математическая статистика | 4 (Хорошо) |
| 9 | Социальная информатика | 5 (Отлично) |
| 10 | Основы менеджмента | 5 (Отлично) |
| 11 | История менеджмента | Зачёт |
| 12 | Экономическая теория | 5 (Отлично) |
| 13 | История социологии | 3 (Удовл) |
| 14 | Теория организации | 4 (Отлично) |
| Всего | 14 предметов | 4 зачёта и 10 экзаменов |
По формуле, указанной выше, средний балл диплома будет равен:
64/14 = 4. 64 с учетом зачетов или
64 с учетом зачетов или
44/10 = 4.4 — если зачеты не учитывать.
В случае если у студента нет «незачетов», первая система расчета поднимает средний балл диплома студента. Многие университеты не определяют порядок расчёта среднего балла диплома, и выбор способа расчета остается за абитуриентом.
Как узнать GPA, если учеба еще не завершена
Как правило, поступление в зарубежный вуз начинается за год или полтора. Если в это время школьник или студент еще продолжает учебу, он может самостоятельно подсчитать средний балл на основе промежуточных оценок, чтобы оценить свои шансы на поступление. В этом случае за основу при подсчете GPA можно взять оценки за:
1. Только завершенные предметы, по которым уже выставлены итоговые оценки.
2. Все завершенные и самые последние оценки за незавершенные предметы.
При отправке же официальной заявки в вуз, если аттестат или диплом еще не получен, абитуриенту необходимо предоставить транскрипт — письмо с оценками, в котором средний балл укажет вуз. Кроме того, абитуриенту необходимо сообщить вузу сроки предоставления итоговых оценок.
Кроме того, абитуриенту необходимо сообщить вузу сроки предоставления итоговых оценок.
Как указать GPA в заявке на поступление
Правило указания GPA в заявке на поступление простое: указывайте не только средний балл, но и сообщайте приёмной комиссии максимально возможный балл на вашей программе, так как в разных странах максимальный балл может составлять 4, 5 или 10 баллов.
Например: если у вас в вузе/школе принята 5-балльная система оценок и ваш средний балл, скажем, 4.1, то в заявке на поступление вам нужно сообщить «GPA 4.1 out of 5».
Укажите максимальный балл GPA
Сообщая средний балл диплома, не забудьте указать максимально возможный балл. В приведённом выше примере, это будет «4.64 out of 5» или «4.4 out of 5». Диплом о первом высшем образовании или транскрипт абитуриента будет прилагаться к заявке на поступление, поэтому вуз в любом случае будет видеть все оценки ваши оценки.
Читайте о том, как поступить в вузы США.
GPA в образовательных системах мира
В мировой университетской практике наиболее распространены несколько способов подсчета среднего балла. Так, в Британии, зачастую, не учитывают оценки с первых курсов, а в США и Европе считают средний балл с учетом кредитных часов, которые набрал студент (причем вес кредитов в Америке и Европе разный).
Для того чтобы оценить свои шансы на поступление в тот или иной университет, американские и европейские студенты должны узнать свой средний балл и, возможно, перевести его в другую образовательную систему. Для этого они пользуются специальными онлайн калькуляторами, но важно отметить, что результат, который они получают при переводе в иностранную образовательную систему, не является официальным. Официальным переводом GPA в другие образовательные системы (например, между Британией и США) занимаются специальные организации.
Больше узнать о GPA и аналогичных ему показателях успеваемости в зарубежных образовательных системах в сравнении с Россией можно здесь:
Великобритания: О соотнесении оценок российских и британских дипломов | Степени отличия британского бакалавриата (Honours)
США: Что такое кредитные часы в вузах США | Сколько кредитных часов нужно набрать студенту американского вуза
Германия: Как рассчитать средний балл диплома для вузов Германии
Россия: Как оформить транскрипт (письмо с оценками) для зарубежного вуза | Как перевестись в британский вуз из университета России и стран СНГ | О соотнесении оценок российских и британских дипломов
В отличие от Британии и США, рассчитать средний балл российского диплома или аттестата несложно — достаточно, следуя инструкциям в данной статье, составить очень простую таблицу в Excel или воспользоваться онлайн калькулятором.
Средняя численность работников (СЧ): среднесписочная численности (ССЧ)
Значения среднесписочной численности необходимы в расчетах налогов. От нее зависит, каким способом компания представит отчетность в налоговую. Например, если вы индивидуальный предприниматель или организация, в которой средняя численность сотрудников больше 130 человек, вы не можете применять «упрощенку». Если у вас среднесписочная численность больше 25 человек, то вы не можете сдавать на бумаге 4-ФСС. А если получателей дохода больше 10 человек — то РСВ надо сдавать в электронной форме.
Как мы видим из этих примеров, бухгалтеры сталкиваются с терминами «среднесписочная численность», «средняя численность», «количество застрахованных лиц» в отчетах по сотрудникам. Давайте разберемся с основными понятиями, затем рассмотрим особенности указания численности в различных отчетах.
Среднесписочная и средняя численность — в чем разница
Итак, среднесписочную численность (ССЧ) и среднюю численность (СЧ) можно рассчитать по правилам, отраженным в Указаниях, утвержденных Приказом Росстата от 27 ноября 2019 г. № 711.
№ 711.
Средняя численность — более широкое понятие. Она включает в себя:
- среднесписочную численность работников по трудовым договорам;
- среднюю численность тех, кто работает по внешнему совместительству;
- среднюю численность людей, работавших по договорам ГПХ.
Чтобы посчитать среднюю численность за год или квартал, нужно знать этот показатель за каждый месяц периода. Так, средняя численность за первый квартал 2021 года будет равна сумме средней численности в январе, феврале и марте, деленной на три.
Средняя численность за месяц равна сумме среднесписочной численности работников за месяц, средней численности внешних совместителей и работников по ГПД.
СЧ работников по договорам ГПХ за месяц (включая граждан иных государств) исчисляется по методу определения ССЧ работников на трудовых договорах. Работники с договорами ГПХ учитываются как целые единицы за каждый календарный день, пока действует договор, вне зависимости от сроков выплаты им зарплаты (вознаграждения). Для выходного или праздничного (нерабочего) дня принимается численность работников за последний предшествующий ему рабочий день.
Для выходного или праздничного (нерабочего) дня принимается численность работников за последний предшествующий ему рабочий день.
Для внешних совместителей формула другая: СЧ внешних совместителей = кол-во отработанных за месяц часов / кол-во рабочих часов в месяце.
Пример расчета СЧ за месяц
В апреле 2021 года:
- среднесписочная численность работников по ТД — 22 человека;
- средняя численность внешних совместителей — 1,3 человека;
- средняя численность работников по ГПД — 4 человека.
СЧ в апреле — 27,8 человек (22 чел. + 1,8 чел. + 4 чел.). По правилам округляем — 28 человек.
Среднесписочная численность включает только сотрудников, которые работают по трудовым договорам, внешние совместители и работники на ГПД сюда не входят. Именно показатель ССЧ используется чаще. Большое количество вопросов вызывает его расчет за конкретный период времени.
Чтобы рассчитать среднесписочную численность за несколько месяцев, сначала считается среднее арифметическое от суммы ежемесячных ССЧ. Чтобы рассчитать среднесписочную численность за конкретный месяц, нужно:
Чтобы рассчитать среднесписочную численность за конкретный месяц, нужно:
Шаг 1. Посчитать за все календарные дни месяца в отдельности количество работников на «полном рабочем дне».
В это количество не входят лица, не подлежащие включению в среднесписочную численность (п. 78 Указаний), и внешние совместители. Также для расчета ССЧ не считаются работники, находящиеся в отпуске по беременности и родам, а также по уходу за ребенком, и работники, находящиеся в отпуске без сохранения заработной платы в связи с обучением в образовательных учреждениях или поступлением в них, в тех случаях, когда такой отпуск предоставлен в соответствии с законом (п. 79.1 Указаний).
Зато здесь учитываются как фактически находящиеся на работе сотрудники, так и отсутствующие на работе по различным причинам (отпускники, командированные, находящиеся на больничном).
В выходные и праздничные дни численность работников такая же, как и в последний рабочий день до этого. Но если работник уволился в пятницу, включать его в списочную численность на субботу и воскресенье не нужно. Если предприятие не проработало полный месяц, за который рассчитывается ССЧ, то суммируется количество работников только за рабочие дни, и эта сумма делится на общее количество дней в этом месяце.Шаг 2. Сложить результат за каждый отдельный день месяца и поделить на количество дней в месяце.
Если предприятие не проработало полный месяц, за который рассчитывается ССЧ, то суммируется количество работников только за рабочие дни, и эта сумма делится на общее количество дней в этом месяце.Шаг 2. Сложить результат за каждый отдельный день месяца и поделить на количество дней в месяце.
Шаг 3. Добавить среднюю численность работников, работающих согласно договору по неполному графику. Расчет выполняется так:
Сначала определите сумму отработанных дней по каждому работнику отдельно: Сумма = Кол-во отработанных человеко-часов в месяце / Длительность рабочего дня. При этом за дни отпуска, болезни, неявок,приходящихся на рабочие дни, в число отработанных человеко-часов условно включены часы по предыдущему рабочему дню.
Затем определите среднюю численность неполностью занятых работников за отчетный месяц: ССЧнеполн = Кол-во отработанных человеко-дней / Кол-во рабочих дней по календарю в отчетном месяце.
Полученный результат участвует в расчете ССЧ за месяц: суммируется со средней численностью работающих полный рабочий день, затем округляется до целого числа.
Шаг 4. Полученный результат округлить до целых.
Пример расчета ССЧ за месяц
На 1 апреля 2021 года в организации числится 12 работников. Из них 10 с полным рабочим днем, один внешний совместитель, и один сотрудник с неполным рабочим временем (отработано 110 часов). С 19 апреля одна сотрудница ушла в декрет, а 24 апреля на ее место приняли другого человека.
Всего в апреле 2021 года — 175 рабочих часов.
Считаем списочную численность работников с полным рабочим днем:
- с 1 по 18 апреля и с 24 по 30 апреля (25 дней) — 10 человек;
- с 19 по 23 апреля (5 дней) — 9 человек.
ССЧ полностью занятых работников в апреле — 9,83 человек = (10 чел. × 25 дн. + 5 дн. × 9 чел.) / 30 дн.
Внешние совместители в расчете не участвуют.
СЧ работников с неполным рабочим днем — 0,57 чел. = (100 ч. / 175 ч.)
ССЧ всех работников в апреле с учетом округления — 10 чел. = (9,83 чел. + 0,57 чел.
)
Где и какой показатель использовать
Мы перечислили случаи, когда бухгалтеры встречаются со средней и среднесписочной численностью. Расскажем, где и какой показатель использовать.
Ограничение по численности сотрудников на спецрежимах — СЧ
Для перехода на спецрежим или его применения нужно выполнить ограничения по численности сотрудников. Так, перейти на УСН можно, если средняя численность за год не превысила 100 человек, а применять этот режим — если средняя численность не превышает 130 человек. Для предпринимателей на патенте тоже есть ограничение — средняя численность не должна быть больше 15 человек.
Получается, что для сохранения права на применение спецрежима надо следить не только за числом сотрудников на трудовых договорах, но и за внешними совместителями, и за работниками на гражданско-правовых договорах.
Применение льгот — СЧ или ССЧ
Тут нужный показатель зависит от конкретной льготы. Например, среднюю численность должны контролировать организации, которые ведут деятельность в сфере IT и хотят применять пониженные тарифы по страховым взносам — она ограничена 7 человек за 9 месяцев прошлого года. А вот вновь созданные организации, чтобы получить ту же льготу, должны проследить, чтобы среднесписочная численность не превышала 7 человек.
А вот вновь созданные организации, чтобы получить ту же льготу, должны проследить, чтобы среднесписочная численность не превышала 7 человек.
Организации инвалидов, чтобы получить льготы по налогу на имущество или освобождение от НДС, смотрят среднесписочную численность инвалидов среди работников — она должна быть не менее 50 %.
Способ сдачи деклараций и расчётов — ССЧ
Среднесписочную численность надо знать, чтобы понять, в какой форме сдавать отчетность. Налоговые декларации плательщики обязаны сдавать в электронном виде, если ССЧ за предыдущий год у них превысила 100 человек. Помните, что декларации по НДС сдаются электронно всегда.
РСВ и 6-НДФЛ сдают электронно те, у кого число получателей дохода больше 10 человек. Обратите внимание, тут речь идет не о среднесписочной или средней численности, а просто о тех, кто получал доходы и является застрахованным лицом.
Форму 4-ФСС в электронной форме подают работодатели, у которых среднесписочная численность получателей выплат 25 человек или больше. Персонифицированную отчетность в ПФР (СЗВ-М, СЗВ-ТД, СЗВ-СТАЖ) в электронном виде сдают те, у кого среднесписочная численность 25 или больше.
Персонифицированную отчетность в ПФР (СЗВ-М, СЗВ-ТД, СЗВ-СТАЖ) в электронном виде сдают те, у кого среднесписочная численность 25 или больше.
Расчет по страховым взносам — количество застрахованных и ССЧ
В отчете РСВ на титульном листе есть два поля, касающиеся численности сотрудников:
- Количество застрахованных лиц, на которых представлены сведения о сумме выплат и иных вознаграждений и/или страховом стаже. Тут нужно указать общее количество застрахованных лиц в соответствии с количеством работников, указанных в разделе №6 (он заполняется на каждого).
- Среднесписочная численность. Здесь указывается ССЧ работников компании или ИП за отчетный и расчетные периоды. Расчет производится по общим правилам, в соответствии с Указаниями. Отдельный отчет по ССЧ с 2021 года отменен.
4-ФСС — ССЧ и СЧ
В форме 4-ФСС на титульном листе в поле «Среднесписочная численность работников» указывается ССЧ, которую нужно рассчитывать согласно вышеупомянутым Указаниям. Этот показатель отражается за период с начала года. При этом поля «Численность работающих инвалидов» и «Численность работников, занятых на работах с вредными/опасными производственными факторами» заполняются исходя из списочной численности на отчетную дату.
Этот показатель отражается за период с начала года. При этом поля «Численность работающих инвалидов» и «Численность работников, занятых на работах с вредными/опасными производственными факторами» заполняются исходя из списочной численности на отчетную дату.
Отчетность в Росстат — ССЧ
В отчетах по формам П-4, П-5 и некоторых других статистических отчетах показатели численности заполняются одинаково, в соответствии с данными Указаниями. Собственно, эти указания и предназначались изначально для заполнения этих форм.
Расчет СЧ или ССЧ — не единственное, что нужно для правильной отчетности. С онлайн-сервисом Контур.Бухгалтерия отчитаться будет намного проще. Ведите учет в Бухгалтерии, рассчитывайте зарплату, отправляйте отчетность и избавьтесь от рутины. Сервис подходит для совместной работы бухгалтера и директора.
Попробовать бесплатно на 5 дней
Как рассчитать среднюю цифру? — Ваша онлайн-энциклопедия
Содержание
- — Как посчитать среднее значение на калькуляторе?
- — Как обозначить среднее значение?
- — Как рассчитывается среднее арифметическое значение?
- — Как найти среднее значение скорости?
- — Как посчитать среднее значение формула?
- — Как рассчитать среднее значение между двумя числами?
- — Как пишется среднее арифметическое?
- — Какие средние значения бывают?
- — Как найти моду в ряду чисел?
- — Как вычислить среднее значение в процентах?
- — Как найти среднее арифметическое статистика?
- — Как найти V среднее?
- — Как найти среднее арифметическое чисел с дробями?
- — Как можно найти медиану?
Среднее значение Это арифметическое и вычисляется путем с добавления группы чисел и деления на их количество. Например, средним значением для чисел 2, 3, 3, 5, 7 и 10 будет 5, которое является результатом деления их суммы, равной 30, на их количество, равное 6.
Например, средним значением для чисел 2, 3, 3, 5, 7 и 10 будет 5, которое является результатом деления их суммы, равной 30, на их количество, равное 6.
Как посчитать среднее значение на калькуляторе?
Подсчет среднего арифметического
Формула для вычислений предельно проста: P = (a1 + a2 + … an) / n, где an – значение величины, n – общее количество значений.
Как обозначить среднее значение?
Для обозначения среднего арифметического всей совокупности чисел обычно используется греческая буква μ. … Если X — случайная переменная, тогда математическое ожидание X можно рассматривать как среднее арифметическое значений в повторяющихся измерениях величины X. Это является проявлением закона больших чисел.
Как рассчитывается среднее арифметическое значение?
Чтобы найти среднее арифметическое двух чисел, надо сложить эти числа и результат разделить на 2: (33,3 + 55,5) : 2 = 88,8 : 2 = 44,4.
Как найти среднее значение скорости?
Чтобы найти среднюю скорость, нужно разделить весь путь, пройденный объектом, на все время его движения.
Как посчитать среднее значение формула?
Среднее значение — это среднее арифметическое, которое вычисляется путем сложения набора чисел с последующим делением полученной суммы на их количество. Например, средним значением для чисел 2, 3, 3, 5, 7 и 10 будет 5, которое является результатом деления их суммы, равной 30, на их количество, равное 6.
Как рассчитать среднее значение между двумя числами?
Чтобы найти среднее арифметическое двух чисел, надо сложить эти числа и результат поделить на 2: (2 + 5):2=3,5.
Как пишется среднее арифметическое?
Чтобы найти среднее арифметическое, нужно сложить все числа и поделить их сумму на их количество. Пример: Найти среднее арифметическое 2, 3 и 4. Обозначим среднее арифметическое буквой «m».
Какие средние значения бывают?
Существует 2 класса средних величин: степенные и структурные. К структурным средним относятся мода и медиана, но наиболее часто применяются степенные средние различных видов.
К структурным средним относятся мода и медиана, но наиболее часто применяются степенные средние различных видов.
Как найти моду в ряду чисел?
Среднее арифметическое, размах, мода и медиана
- Средним арифметическим ряда чисел называется частное от деления суммы этих чисел на число слагаемых. …
- Размахом ряда чисел называется разность между наибольшим и наименьшим из этих чисел. …
- Модой ряда чисел называется число, которое встречается в данном ряду чаще других.
Как вычислить среднее значение в процентах?
Общая формула вычисления выглядит следующим образом: «=(число)/(общая_сумма)*100%. Итак, для того, чтобы показать вычисления на практике, узнаем, сколько процентов составляет число 9 от 17.
Как найти среднее арифметическое статистика?
Для того чтобы вычислить среднюю арифметическую, необходимо сумму всех значений признаков разделить на их число. Она применяется в тех случаях, когда объем варьирующего признака для всей совокупности является суммой значений признаков отдельных ее единиц.
Она применяется в тех случаях, когда объем варьирующего признака для всей совокупности является суммой значений признаков отдельных ее единиц.
Как найти V среднее?
Чтобы найти среднюю скорость, весь пройденный путь делим на все время движения: 29:5=5,8 км/ч.
Как найти среднее арифметическое чисел с дробями?
1) посчитать сумму всех чисел; 2) посчитать количество чисел; 3) разделить сумму всех чисел на их количество; 4) полученное число – это и есть среднее арифметическое.
Как можно найти медиану?
Если у вас четное количество чисел, вычеркните по одному числу с каждой стороны, пока у вас не останется два числа посередине. Сложите их и разделите на два. Это и есть значение медианы. Если вам дан ряд чисел 1, 2, 5, 3, 7, 10, то два средних числа — это 5 и 3.
Интересные материалы:
Где найти настройки браузера Гугл Хром?
Где найти настройки клавиатуры на андроиде?
Где найти Орбека?
Где найти осколки фляги с Эстусом в Dark Souls 2?
Где найти отличные доспехи школы волка?
Где найти отвертку в гренни?
Где найти параметры на компьютере?
Где найти параметры Nvidia на Windows 10?
Где найти пароль конференции в зуме?
Где найти паслен в Скайриме?
Mean Calculator — Вычислите среднее арифметическое набора чисел
Используйте этот калькулятор, чтобы легко вычислить среднее арифметическое, часто называемое средним арифметическим, набора чисел. Принимает числа в экспоненциальном представлении (например, 2,95E-5).
Быстрый переход:
- Что такое среднее арифметическое?
- Формула среднего арифметического
- Полезные свойства среднего арифметического
- Как не ввести в заблуждение средние
- Когда среднее значение набора мало что нам говорит
- «Среднее» не означает «типичное»
- Изучить полные данные
Среднее арифметическое является одним из наиболее часто используемых статистических данных . Среднее значение, часто называемое просто «средним» или «средним» , представляет собой описательную статистику, используемую в качестве сводной меры атрибута выборки (набора данных). Он рассчитывается путем суммирования всех чисел в наборе данных с последующим делением на количество элементов данных и является наиболее понятным показателем центральной тенденции. Термин «среднее» иногда используется для описания других статистических данных, таких как медиана или мода, в то время как термин «среднее» может относиться к другим средствам, таким как среднее геометрическое или среднее гармоническое, вот почему термин «среднее арифметическое» предпочтительнее для ясности . В статистике среднее значение обычно обозначается чертой, скажем, x (читается «x bar»), что означает среднее значений x 1 , x 2 … x n .
Среднее значение, часто называемое просто «средним» или «средним» , представляет собой описательную статистику, используемую в качестве сводной меры атрибута выборки (набора данных). Он рассчитывается путем суммирования всех чисел в наборе данных с последующим делением на количество элементов данных и является наиболее понятным показателем центральной тенденции. Термин «среднее» иногда используется для описания других статистических данных, таких как медиана или мода, в то время как термин «среднее» может относиться к другим средствам, таким как среднее геометрическое или среднее гармоническое, вот почему термин «среднее арифметическое» предпочтительнее для ясности . В статистике среднее значение обычно обозначается чертой, скажем, x (читается «x bar»), что означает среднее значений x 1 , x 2 … x n .
Например, среднее арифметическое набора 1, 2, 3, 4, 7, 10 равно 1 + 2 + 3 + 4 + 7 + 10 / 6 = 4,5 (проверено с помощью этого калькулятора среднего арифметического). Как вы могли заметить, число 4,5 не является частью исходного набора чисел, и это довольно распространено. Среднее значение не является надежной статистикой, а это означает, что на него сильно влияют выбросы / экстремальные значения. Например, добавление числа 99 к предыдущему набору чисел увеличит среднее значение с 4,5 до 18, что значительно больше, чем все значения в наборе, кроме одного. В одних случаях это желаемое свойство, а в других оно делает простое среднее непригодным для цели.
Как вы могли заметить, число 4,5 не является частью исходного набора чисел, и это довольно распространено. Среднее значение не является надежной статистикой, а это означает, что на него сильно влияют выбросы / экстремальные значения. Например, добавление числа 99 к предыдущему набору чисел увеличит среднее значение с 4,5 до 18, что значительно больше, чем все значения в наборе, кроме одного. В одних случаях это желаемое свойство, а в других оно делает простое среднее непригодным для цели.
В некоторых случаях «среднее» или «среднее» может относиться к взвешенному среднему , в котором разным точкам набора данных присваиваются разные веса на основе некоторых их характеристик. Этот калькулятор среднего не поддерживает средневзвешенные значения, поскольку для них требуется более сложный набор входных данных.
Формула среднего арифметическогоСимволическое представление формулы:
n — это, конечно, количество элементов в наборе данных. Чтобы найти среднее значение, просто замените имеющиеся значения в формуле и решите простое уравнение. Например, если это числа 2, 4 и 6, их среднее арифметическое можно найти, суммировав 2, 4 и 6, а затем разделив их на их количество (3), в результате чего (2 + 4 + 6) / 3 = 12 / 3 = 4,
Чтобы найти среднее значение, просто замените имеющиеся значения в формуле и решите простое уравнение. Например, если это числа 2, 4 и 6, их среднее арифметическое можно найти, суммировав 2, 4 и 6, а затем разделив их на их количество (3), в результате чего (2 + 4 + 6) / 3 = 12 / 3 = 4,
Свойства, которые делают полезным среднее арифметическое, заключаются в том, что числа слева от среднего уравновешиваются числами справа от среднего, другими словами — остатки, или производные от оценки суммируются до нуля. Еще одним замечательным свойством является то, что он минимизирует сумму квадратов отклонений (имеет наименьшую среднеквадратичную ошибку — сумму (x i — x) 2 ), поэтому он служит лучшим единственным предиктором для набора. Для выборок, взятых из совокупности (например, опрос), среднее значение выборки является статистически несмещенной оценкой среднего значения совокупности. Это все причины, чтобы воспользоваться нашим калькулятором среднего арифметического.
Как и любое отдельное число, используемое для представления набора данных, среднее значение обязательно будет неполным и в некотором смысле неточным представлением. Средние значения широко использовались до изобретения компьютеров, когда построение графиков или иная визуализация даже умеренно больших наборов данных представляли собой огромную задачу, и мало кто мог понять графики. Однако в настоящее время у нас есть очень мощные и очень простые способы показать весь набор данных, все распределение, так что представление только среднего арифметического может быть плохой практикой .
Когда среднее значение набора мало что нам говорит
Возьмем, к примеру, эти 3 набора данных, каждый для 17 сотрудников из трех разных компаний: A, B и C:
Все вышеперечисленное имеет одно и то же среднее арифметическое, несмотря на разный диапазон и распределение. Также обратите внимание, что ось Y не имеет одинакового масштаба для всех трех графиков. Вот те же данные в той же системе координат:
Вот те же данные в той же системе координат:
Разница в индивидуальных зарплатах совершенно очевидна, однако среднее значение одинаково для всех трех компаний : 57 705,88 долларов в год. Даже в компании С, где распределение заработной платы самое плоское, 14 из 17 сотрудников (82%) получают меньше, чем в среднем. Несмотря на это, многие интуитивно ожидают, что около 50% сотрудников получают более 57 705 долларов в год. , распределение Гаусса).
Когда интуиция или предположения о симметрии или асимметрии данных подводят нас, среднее значение может вводить в заблуждение, поэтому всегда, когда это возможно, исследуйте полное распределение.
«Среднее» не означает «типичное». На самом деле первый может быть более точно аппроксимирован модой (наиболее часто встречающееся значение) или медианой (значение, которое делит набор на два набора с равным количеством членов), если только не обсуждается рост или процентный прирост или балансировка индекса, где подходят геометрические или гармонические средства.
 При поиске «типичного» значения вы можете изучить процентиль, скажем, средние 50%, 60% или 80%, и измерить их среднее арифметическое, чтобы лучше понять, что такое «типичное».
При поиске «типичного» значения вы можете изучить процентиль, скажем, средние 50%, 60% или 80%, и измерить их среднее арифметическое, чтобы лучше понять, что такое «типичное». Вот почему нужно быть очень, очень осторожным при использовании средних значений для принятия любого решения. Например, если вы хотите заняться конкретным бизнесом, можно посмотреть на среднюю зарплату, не понимая, что распределение, вероятно, следует степенному закону (распределение Паретиана). При таком распределении заработок многих людей падает ниже среднего, а у некоторых намного превышает его. Пример из учебника: агент по недвижимости пытается предложить вам дом по соседству, говоря, что средний собственный капитал людей, живущих там, составляет десятки миллионов, «забывая» упомянуть, что одним из них является Билл Гейтс. В то время как остальные его соседи тоже могли быть миллионерами, они могли зарабатывать 60 000 долларов в год, а в среднем все еще могли быть десятки миллионов, в зависимости от размера района.
Изучите полные данные
Где возможно, всегда запрашивайте полные данные или, по крайней мере, визуальное представление распределения данных! Имея данные, вы всегда можете рассчитать их среднее значение, воспользовавшись либо нашим калькулятором среднего арифметического, либо Excel, либо более продвинутым настольным или онлайновым программным обеспечением. Этот совет приходит после многих лет изучения средних значений для всех видов данных: лучше всего не доверять среднему значению, а стремиться понять весь набор данных. Среднее арифметическое лучше всего работает для приблизительно нормально распределенных данных, где большинство точек данных сгруппированы вокруг середины, например рост человека. Если практические соображения не позволяют этого, попросите дополнительные статистические данные, такие как медиана и мода, диапазон и т. д.
Усреднение углов и времени суток
Особое внимание следует уделить усреднению углов — при этом следует быть очень осторожным, так как в геометрическом смысле среднее арифметическое значения в градусах может быть плохим дескриптором набор. Например. среднее значение между 5 ° и 355 ° составляет 180 °, но более подходящим средним значением может быть 0 °, поскольку оно находится между двумя на окружности. Предпочтительным подходом в этом случае может быть преобразование углов в соответствующие единицы на точечной окружности, например. α к (cosα, sinα). После преобразования из полярных в декартовы координаты вычислите среднее арифметическое для точек, а затем преобразуйте обратно в полярные координаты.
Например. среднее значение между 5 ° и 355 ° составляет 180 °, но более подходящим средним значением может быть 0 °, поскольку оно находится между двумя на окружности. Предпочтительным подходом в этом случае может быть преобразование углов в соответствующие единицы на точечной окружности, например. α к (cosα, sinα). После преобразования из полярных в декартовы координаты вычислите среднее арифметическое для точек, а затем преобразуйте обратно в полярные координаты.
Аналогичные соображения и шаги можно предпринять для усреднения дневного времени.
Среднее арифметическое калькулятор двух чисел
✖ Термин 1 может быть любое число в математике может использоваться в статистике или серии. -10% | |||
✖Слагаемое 2 может быть любым математическим числом, которое можно использовать в статистике или рядах.ⓘ Слагаемое 2 [t 2 ] | +10% -10% |
✖Среднее арифметическое заданного набора целых чисел можно рассчитать путем деления суммы всех заданных целых чисел на общее количество целых чисел. | ⎘ Копировать |
👎
Формула
Перезагрузить
👍
Среднее арифметическое двух чисел Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1: Преобразование входных данных в базовые единицы
Термин 1: 3 —> преобразование не требуется
Термин 2: 2 —> преобразование не требуется
ШАГ 2 : Вычислить формулу
ШАГ 3: Преобразование результата в единицу измерения
2.5 —> Преобразование не требуется
< 10+ калькуляторов арифметической прогрессииN-й член арифметической прогрессии по p-му и q-му члену
N-й член = ((P-й член*(Позиция в ряду q-1)-Q-й член*(Позиция в ряду p-1))/(Позиция в ряду q-Позиция в ряду p))+(Всего членов-1)* ((Qth Term-Pth Term)/(Позиция в ряду q-Позиция в ряду p)) Идти
Сумма первых n членов арифметической прогрессии с учетом общей разницы
Сумма первых n членов = (Всего членов/2)*(2*Первый член+(Всего членов-1)*Общая разница) Идти
Общая разница с учетом p-го и q-го членов
Общая разность = ((Qth Term-Pth Term)/(Позиция в ряду q-Позиция в ряду p)) Идти
Позиция p-го термина с учетом p-го термина, первого термина и общей разницы
Позиция в ряду p = ((P-й член-первый член)/Общая разница)+1 Идти
Общая разница с учетом первого члена и p-го члена
Общая разница = (Pth Term-First term)/(Позиция в ряду p-1) Идти
Количество терминов, заданное суммой первых n терминов, первого термина и последнего термина
Всего терминов = ((2*Сумма первых n терминов)/(Первый термин+Последний термин)) Идти
Общая разница с учетом первого термина, последнего термина и количества терминов
Общая разница = ((Последний срок-Первый срок)/(Всего сроков-1)) Идти
Последний термин с учетом количества терминов, первого термина и общей разницы
Последний срок = ((Всего сроков-1)*Общая разница)+Первый срок Идти 92)/среднее гармоническое Идти
Среднее арифметическое двух чисел
Среднее арифметическое = (термин 1 + термин 2)/2 Идти
Формула среднего арифметического двух чисел
Среднее арифметическое = (термин 1 + термин 2)/2
АМ = (t 1 + t 2 )/2
Что такое среднее арифметическое?
Среднее арифметическое заданного набора целых чисел можно рассчитать, разделив сумму всех заданных целых чисел на общее количество целых чисел. Например, среднее арифметическое (1,2,3,4,5) равно (1+2+3+4+5)/5 = 3.
Например, среднее арифметическое (1,2,3,4,5) равно (1+2+3+4+5)/5 = 3.
Как вычислить среднее арифметическое двух чисел?
Калькулятор среднего арифметического двух чисел использует Среднее арифметическое = (Срок 1+Срок 2)/2 для расчета среднего арифметического. Формула среднего арифметического двух чисел определяется как среднее число чисел. Его можно рассчитать по формуле |(термин 1+термин 2)/2. Среднее арифметическое обозначается символом AM .
Как посчитать среднее арифметическое двух чисел с помощью этого онлайн-калькулятора? Чтобы использовать этот онлайн-калькулятор для вычисления среднего арифметического двух чисел, введите Term 1 (t 1 ) & Срок 2 (t 2 ) и нажмите кнопку расчета. Вот как можно объяснить вычисление среднего арифметического двух чисел с заданными входными значениями -> 2,5 = (3+2)/2 .
Часто задаваемые вопросы
Что такое среднее арифметическое двух чисел?
Формула среднего арифметического двух чисел определяется как среднее число чисел.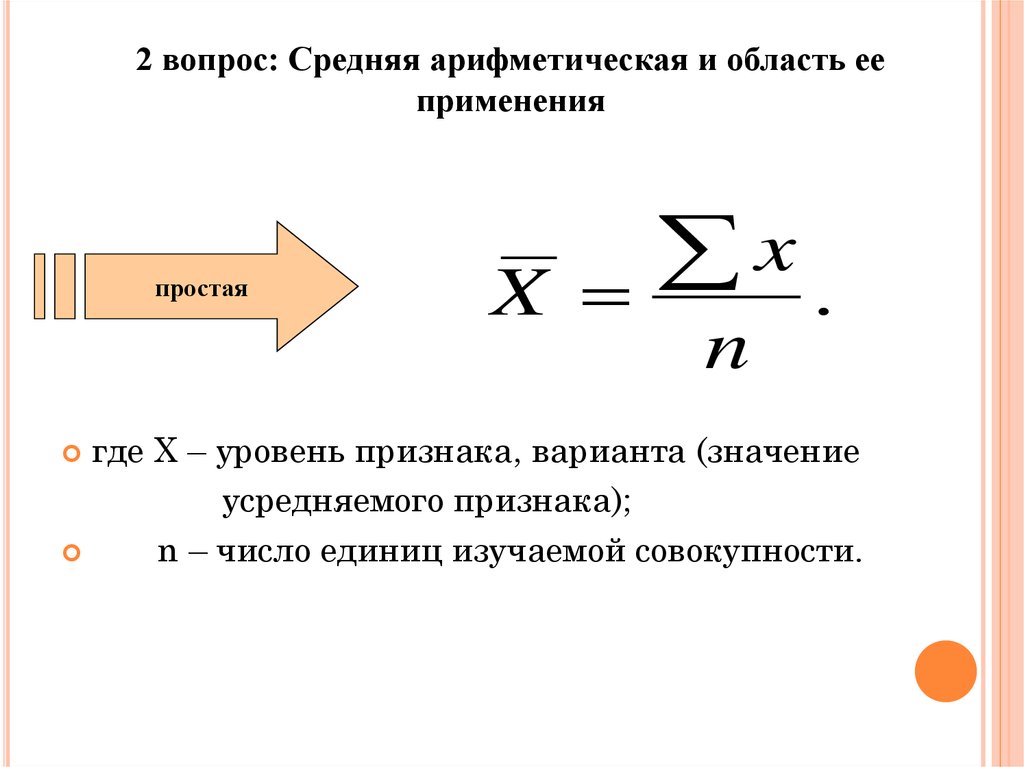 Его можно рассчитать по формуле |(термин 1+термин 2)/2 и представить как AM = (t 1 +t 2 )/2 или Среднее арифметическое = (Элемент 1+Элемент 2)/2 . Термин 1 может быть любым числом в математике, может использоваться в статистике или рядах, а Термин 2 может быть любым числом в математике, которое может использоваться в статистике или рядах.
Его можно рассчитать по формуле |(термин 1+термин 2)/2 и представить как AM = (t 1 +t 2 )/2 или Среднее арифметическое = (Элемент 1+Элемент 2)/2 . Термин 1 может быть любым числом в математике, может использоваться в статистике или рядах, а Термин 2 может быть любым числом в математике, которое может использоваться в статистике или рядах.
Как вычислить среднее арифметическое двух чисел?
Формула среднего арифметического двух чисел определяется как среднее число чисел. Его можно рассчитать по формуле |(термин 1+термин 2)/2 рассчитывается с использованием Среднее арифметическое = (Элемент 1+Элемент 2)/2 . Чтобы вычислить среднее арифметическое двух чисел, вам нужно Термин 1 (t 1 ) и Термин 2 (t 2 ) . С помощью нашего инструмента вам нужно ввести соответствующее значение для условия 1 и условия 2 и нажать кнопку расчета. Вы также можете выбрать единицы измерения (если есть) для ввода (ов) и вывода.
Сколько существует способов вычисления среднего арифметического?
В этой формуле среднее арифметическое использует термин 1 и термин 2. Мы можем использовать 2 других способа (ов) для вычисления того же самого, которые следующие: — 92)/Среднее гармоническое
Доля
Скопировано!
Калькулятор среднего арифметико-геометрического | Good Calculators
Этот калькулятор среднего арифметико-геометрического можно использовать для определения повторяющихся средних значений, таких как среднее арифметико-геометрическое (AGM), среднее геометрическое-гармоническое (GHM), среднее арифметико-квадратичное (AQM) и среднее арифметическое -среднее гармоническое (AHM).
Просто вставьте значения для x и y, выберите два типа средних, которые следует применить, по одному из каждого раскрывающегося меню, и нажмите кнопку «Рассчитать среднее». Порядок, в котором вы выбираете типы средств, которые вы хотите применить, не имеет значения; таким образом, если вы хотите определить AGM, вы можете выбрать «Геометрический» в первом меню и «Арифметический» во втором; выход будет тот же.
Порядок, в котором вы выбираете типы средств, которые вы хотите применить, не имеет значения; таким образом, если вы хотите определить AGM, вы можете выбрать «Геометрический» в первом меню и «Арифметический» во втором; выход будет тот же.
Среднее арифметико-геометрическое (AGM)
AGM — это итеративное среднее, которое работает путем определения пары вычислений.
Чтобы вычислить AGM двух заданных чисел, x и y , вам нужно начать с вычисления их средних арифметических и геометрических значений следующим образом:
(x + y)/2 и sqrt(xy)
Затем вы можете использовать выходные данные для определения среднего арифметического и геометрического двух новых чисел. Впоследствии вы повторяете этот процесс несколько раз с каждой новой вычисляемой парой чисел. Со временем алгоритм стабилизируется на фиксированном числе. Этот номер представляет собой общее собрание двух номеров, с которых вы начали.
Альтернативным способом выражения AGM x и y является выполнение двух зависимых рекурсивных уравнений: n+1 = sqrt(A n B n ),
, где A 0 = x, B 0 = y и sqrt = квадратный корень.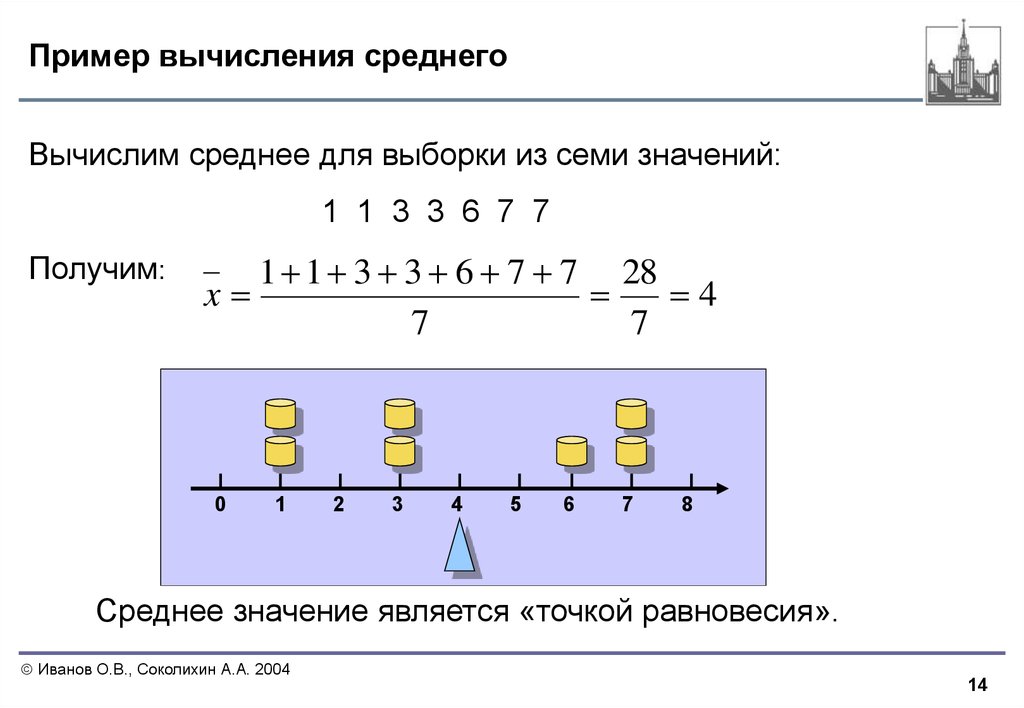
Поскольку n бесконечно, значения A n и B n будут сходиться к одному числу. Это число представляет годовое общее собрание х и х . При условии, что x и y не равны, AGM всегда ниже среднего арифметического и выше среднего геометрического.
Среднее геометрическое гармоническое (GHM)
Среднее геометрическое гармоническое (GHM) представляет собой еще один пример итеративного среднего.
, если C 0 = X и D 0 = Y и
C N + 1 = 2C N D N /(C N + D N ) 9 N + D N ) 9003 9 9.0002 D n+1 = sqrt(C n D n ),
согласованным значением последовательности является GHM x и y . Есть некоторые интересные корреляции между AGM(x,y) и GHM(x,y):
AGM(x,y)GHM(x,y) = xy
GHM(x,y) = xy/AGM(x ,y) = 1/AGM(x -1 , y -1 )
Среднее арифметическое-гармоническое (AHM)
Повторение среднего арифметического и гармонического приводит к среднему геометрическому.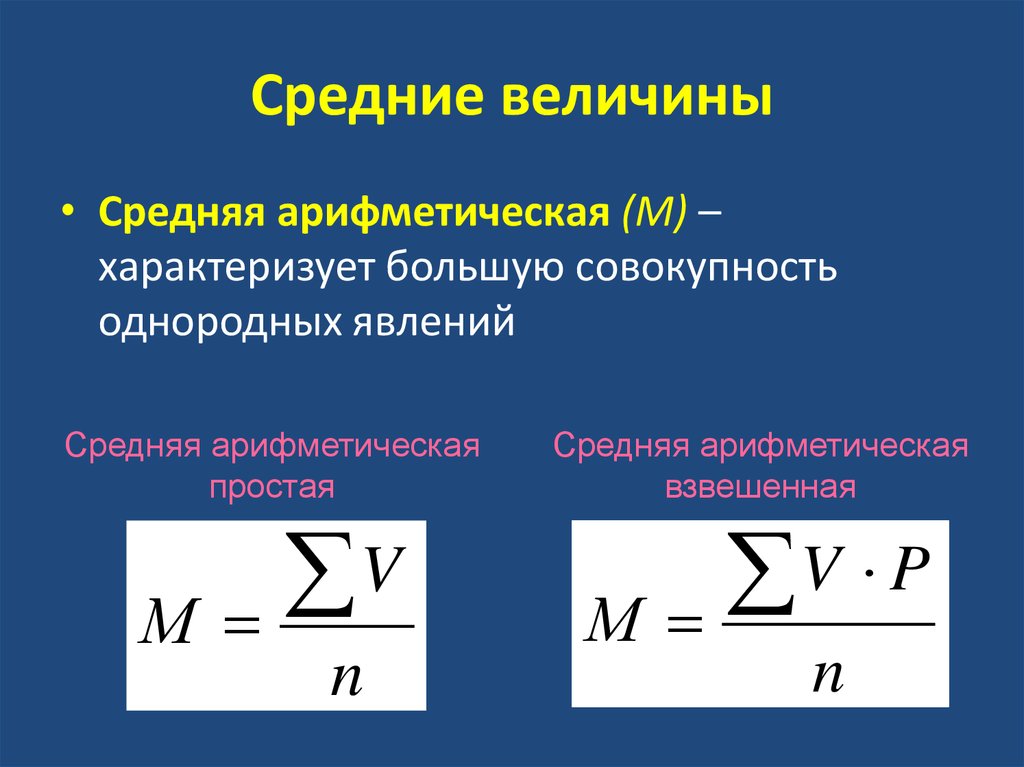
Контрагармоническое среднее гармоническое
Повторение среднего значения контрагармоники и гармоники дает среднее арифметическое.
Среднее контрагармонное среднее
Среднее контрагармоническое значение x и Y составляет следующее:
(x 2 + y 2 )/(x + y)
для N вычислить противогармоническое среднее следующим образом:
(x 1 2 + x 2 2 + … + x n 2 )/(x 9093 + x 2 + … + x n )
сообщите об этом объявлении
Среднее арифметическое
Среднее двух или более чисел называется средним. Среднее арифметическое представляет собой наиболее часто используемое среднее значение. Вычисление среднего арифметического включает сложение всех значений и их деление на количество значений.
Для n значений среднее арифметическое равно (x 1 + x 2 + . .. + x n )/n
.. + x n )/n
Например, среднее арифметическое 3, 4 и 5 равно (3 + 4 + 5)/3 = 4,
Среднее геометрическое
Среднее геометрическое двух чисел x и y представлено следующим образом: — это кубический корень из xyz, или (xyz) 1/3 .
Среднее геометрическое n чисел выглядит следующим образом:
(x 1 · x 2 · … · x n ) 1/n
9 Гармоническое среднее0031
Среднее гармоническое обычно используется для усреднения отношений в науке и бизнес-приложениях. Учитывая два числа, x и y , среднее гармоническое равно 2xy/(x + y).
Для трех чисел, x , y и z , среднее гармоническое равно 3xyz/(xy + xz + yz).
Среднее гармоническое n чисел выглядит следующим образом: Квадратное среднее)
Среднеквадратичное значение, которое также обычно называют средним квадратичным, часто используется в статистических и инженерных приложениях, особенно когда рассматриваются отрицательные точки данных. Одним из примеров среднеквадратичного значения является стандартное отклонение набора чисел (т. е. среднеквадратичное значение отклонений между средним арифметическим и каждой точкой данных).
Одним из примеров среднеквадратичного значения является стандартное отклонение набора чисел (т. е. среднеквадратичное значение отклонений между средним арифметическим и каждой точкой данных).
Когда даны два числа, x и y , среднее квадратичное равно sqrt[(x 2 + у 2 )/2].
для N переменные, это следующее:
SQRT [(x 1 2 + x 2 2 + … + x N 2 )/n]
Калькулятор среднего числа — Расчет среднего значения чисел онлайн
Что такое среднее значение? Что это значит?
Среднее значение — это центральное вычисленное значение из списка или массива чисел. Сумма всех значений, деленная на общее количество значений, дает вам среднее значение. Это также известно как среднее арифметическое.
Если у вас возник вопрос, как найти среднее значение? Тогда мы вас прикроем. Обычный метод нахождения среднего выглядит следующим образом:
Например, у вас есть четыре числа, 6,7,9,4, теперь сначала сложите их, 6+7+9+4 = 26. Теперь разделите этот ответ на общее количество значений, равное 4. Ответом на это деление будет 26/4 = 6,5. Итак, среднее из приведенных чисел равно 6,5.
Теперь разделите этот ответ на общее количество значений, равное 4. Ответом на это деление будет 26/4 = 6,5. Итак, среднее из приведенных чисел равно 6,5.
Существуют различные типы средних значений, но наиболее часто используются три типа: среднее значение, мода и медиана. Среднее среди них наиболее идентично основному среднему.
«Среднее» — это тип среднего значения, при котором вы складываете все значения, а затем делите их на количество этих значений. Это почти похоже на фактическое и обсуждавшееся выше определение среднего.
Среднее и среднее одно и то же?
Среднее значение — это широкий термин в математике, который используется в различных формах. Вы можете найти множество типов средних значений, которые используются. Однако одним из наиболее распространенных типов среднего является среднее. Формула для нахождения среднего почти такая же, как и для среднего.
Как рассчитать среднее значение с помощью калькулятора среднего?
- Подсчитайте количество значений в вашем массиве или списке
- Сложите все значения, чтобы найти сумму
- Разделить сумму на общее количество значений
Формула среднего значения
Среднее x̄ массива представляет собой сумму общих значений, деленную на общее количество значений.
Однако вы можете избавиться от этой проблемы и выбрать простой способ найти среднее значение набора данных с помощью онлайн-калькулятора среднего значения. Онлайн-инструмент позволит вам сэкономить ваше время и усилия и предоставит вам точные результаты в мгновение ока.
Типы средних значений — среднее, медиана, мода
Как обсуждалось ранее, средние значения подразделяются на различные типы, и люди используют их все в соответствии со своими потребностями. Но есть три типа, которые используются в образовательном секторе, программировании или даже в исследовательских целях: среднее, срединное и модальное. Методы нахождения этих типов средних значений также отличаются друг от друга.
Как рассчитать медиану?
Давайте разберемся с процессом нахождения медианы на примере.
Значения, из которых вы хотите найти медиану: 3,7,8,1,5,9,10,6,2
Медиана — это среднее значение массива, поэтому сначала нам нужно упорядочить значения в числовом порядке.
То есть 1,2,3,5,6,7,8,9,10.
Общее количество значений равно 9. 9+1=10, 10/2=5. (5-е число)
Медиана = 6
Как рассчитать диапазон?
Чтобы вычислить диапазон набора данных 3,7,8,1,5,9,10,6,2, найдите наибольшее число в списке,
, что равно 10. Теперь найдите наименьшее число, равное 1.
Чтобы найти диапазон: Наибольшее значение – Наименьшее значение = 10 – 1 = 9.
Диапазон = 9.
Как рассчитать режим ?
Если вы хотите найти режим в том же примере набора данных, 3,7,8,1,5,9,10,6,2, то сначала вы должны понять определение режима.
Режим — это значение, которое повторяется большую часть времени в заданном наборе данных.
Теперь в заданных значениях 3,7,8,1,5,9,10,6,2. Вы можете видеть, что ни одно значение не повторяется. Таким образом, для этого примера режима не будет.
Но если у вас есть другой пример, например 8,7,6,8,3,4. Затем вы можете видеть, что 8 повторяется большую часть времени, поэтому 8 будет режимом в этом примере.
Как работает наш калькулятор среднего значения?
Процесс использования нашего онлайн-калькулятора среднего/среднего значения прост и понятен. Следующие простые шаги позволят вам использовать этот онлайн-калькулятор суммы без каких-либо хлопот.
- Введите свои значения в этот Калькулятор Среднего, просто написав или скопировав/вставив его.
- Когда вы закончите с этим, выберите процесс, который вы хотите применить, из заданных вариантов. С помощью этого инструмента вы можете легко найти среднее значение, моду, медиану и многое другое.
- Нажмите кнопку «Проверить среднее», чтобы начать процесс.
- Бум! Вы получите точные результаты в мгновение ока.
Результаты, которые вы получите после использования нашего Калькулятора средних значений
Наш онлайн-калькулятор средних значений предоставляет вам обширный список математических операций, которые можно легко использовать. Среди них:
Арифметика:
Сумма всех значений, деленная на общее количество значений, дает среднее арифметическое.
Геометрический:
Среднее геометрическое — это особый тип среднего, в котором мы умножаем значения, а затем извлекаем квадратный корень (для двух значений) и кубический корень (для трех значений) и т. д.
Гармоническое:
среднее гармоническое для набора данных вычисляется путем деления количества наблюдений на обратную величину каждого числа.
Сумма:
Если вы хотите получить сумму большого набора данных, то наш калькулятор сумм — лучший вариант, который вы можете найти в Интернете.
Count:
Этот инструмент также дает вам возможность подсчитать общее количество значений одним щелчком мыши на вашем устройстве.
Медиана:
Вы можете быстро получить медианное значение набора данных, просто сложив все значения, а затем разделив их на два.
Наибольшее число:
Инструмент позволяет найти наибольшее число в вашем наборе данных в результатах, отображаемых на экране после обработки.
Наименьшее число:
После запуска процесса также будет отображаться наименьшее число в вашем наборе данных.
Диапазон:
Получите диапазон вашего набора данных в результатах путем вычитания наименьшего значения из наибольшего значения.
Калькулятор среднего геометрического с формулой и решением
Онлайн-калькулятор среднего геометрического помогает вычислить среднее геометрическое для заданного набора данных, состоящего из чисел или процентов. Другими словами, этот калькулятор среднего геометрического позволяет найти среднее геометрическое статистического набора чисел/процентов.
Теперь внимательно прочитайте этот важный и полезный контент, чтобы узнать о формуле среднего геометрического, о том, как ее вычислить шаг за шагом и с помощью калькулятора, а также о различных связанных терминах. Во-первых, мы собираемся начать с самых основ!
Что такое среднее геометрическое? Число, представляющее центральную тенденцию, взятое из n-го корня из произведения n чисел, называется средним геометрическим. Кроме того, известно, что среднее геометрическое определяется как «произведение n чисел, возведенных в степень 1/n». В среднем арифметическом мы складываем общие числа, а затем делим их на общие числа. В среднем геометрическом мы умножаем числа, затем извлекаем корень n-й степени.
В среднем арифметическом мы складываем общие числа, а затем делим их на общие числа. В среднем геометрическом мы умножаем числа, затем извлекаем корень n-й степени.
В соответствии с формулой среднего геометрического все числа в наборе данных должны иметь одинаковый знак, все они должны быть положительными или отрицательными.
Кроме того, попробуйте этот онлайн-диапазон режима медианы и онлайн-калькулятор среднего значения, чтобы найти режим и диапазон среднего значения для заданного набора данных.
Что такое формула среднего геометрического?Этот онлайн-калькулятор среднего геометрического использует следующую формулу для нахождения GM,
Где,
n — общее количество значений
xi — значения (x1, x2, x3, xn).
Это уравнение среднего геометрического равно
Бесплатный калькулятор среднего значения с помощью онлайн-калькулятора позволяет узнать среднее или среднее значение для заданных значений набора данных. Вы также можете попробовать этот лучший калькулятор коэффициента вариации для расчета среднего значения набора данных, поскольку коэффициент дисперсии называется отношением стандартного отклонения к среднему (среднему).
Вы также можете попробовать этот лучший калькулятор коэффициента вариации для расчета среднего значения набора данных, поскольку коэффициент дисперсии называется отношением стандартного отклонения к среднему (среднему).
Коэффициент дисперсии (CV) представляет собой отношение стандартного отклонения к среднему (среднему).
Среднее геометрическое для отрицательных чисел:Как видно из приведенной выше формулы и определения, мы можем вычислить среднее геометрическое только для всех положительных чисел, иначе числа должны быть одного знака. Взяв среднее геометрическое положительных отрицательных чисел, мы получим мнимое число. Но это не значит, что мы не можем найти среднее геометрическое отрицательных чисел.
Допустим, у нас есть изменения производства в течение трех лет подряд в виде роста на 7%,9% снижение, 10% рост. Общий рост за три года составляет 6,89%. Но как рассчитать годовой темп роста?
Мы можем записать все значения в пропорциях, как,
7% рост = 1+7% = 1+7/100 = 1,07
9% снижение = 1-9% = 1-9/100 = 0,91
Рост на 10% = 1+10% = 1+10/100 = 1,1
Тогда GM = 1,0231
Этот калькулятор среднего геометрического работает по этому сценарию, поэтому нет необходимости выполнять ручное преобразование. В этом онлайн-инструменте вы можете вводить значения в процентах, например 2%, -8%, 34%.
В этом онлайн-инструменте вы можете вводить значения в процентах, например 2%, -8%, 34%.
Когда мы имеем дело с двумя разными диапазонами значений, предполагая, что они равны, один из них имеет малый диапазон, например, от 0 до 5, а другой имеет большой диапазон от 900 до 1000, тогда это идеальный случай для использования среднего геометрического вместо арифметического. Среднее арифметическое пренебрегает малым числом.
Когда данные смещены вниз и имеют большие положительные выбросы, тогда удобно использовать среднее геометрическое, а не среднее арифметическое.
Математическая связь между средним арифметическим и средним геометрическим:
Среднее арифметическое ≥ среднего геометрического
среднее/среднее встречаются чаще, чем данные, далекие от среднего/среднего.
Нахождение среднего геометрического с точки зрения логарифма: Вы также можете вычислить среднее геометрическое путем логарифмирования чисел набора данных.
Общая формула логарифмирования приведена ниже:
log(a*b*c)1/3 = 1/3 * log (a*b*c) = (1/3) * ((log a ) + (log b) + (log c))
Проще говоря, среднее геометрическое можно найти по формуле:
• Возьмем логарифм чисел.
• Вычислить среднее арифметическое данных.
• Затем, взяв антилогарифм результата, узнать среднее геометрическое.
О калькуляторе среднего геометрического:Онлайн-калькулятор среднего геометрического может легко вычислить среднее геометрическое для заданных статистических данных, таких как числа или проценты. Этот калькулятор среднего геометрического покажет вам пошаговые расчеты для заданного набора чисел/процентов и найдет различные математические связанные термины.
Как найти среднее геометрическое с помощью калькулятора: С помощью этого бесплатного онлайн-калькулятора очень легко найти среднее геометрическое между числами и процентами. Итак, просто выполните указанные шаги, чтобы найти среднее геометрическое двух чисел и процентов.
Читайте дальше!
Ввод:
- Прежде всего, выберите из выпадающего меню способ разделения чисел. Он отделяется запятой, пробелом или определяется пользователем. (Если вы выбрали «Определить пользователем», то введите метод разделения в следующем поле)
- Затем введите числа или проценты, для которых вы хотите выполнить вычисления
- В конце выберите тип чисел.
- Наконец, нажмите кнопку расчета.
Выходы:
Как только вы заполните все поля калькулятора среднего геометрического, он сгенерирует:
- Среднее геометрическое набора данных.
- Завершить пошаговый расчет.
- Расположите числа в порядке возрастания.
- Расположите числа в порядке убывания.
- Четные числа в данных.
- Нечетные числа в данных.
- Общая сумма чисел.
- Максимальное значение.
- Минимальное значение.
- Всего номеров.

Среднее геометрическое используется в различных областях, таких как финансы, геометрия социальных наук и математика. В финансах, когда вы хотите оценить предложение по депозиту со сложными процентами или иметь дело с погашением, вам придется иметь дело со средним геометрическим, а не со средним арифметическим. В социальных науках, когда вам нужно сказать скорость роста населения, и она выражается в процентах, тогда полезно ответить на вопрос о среднем геометрическом. Можно сказать, что «средний темп прироста населения города X за Y лет равен Z».
Но часто используется в геометрии. В прямоугольном треугольнике перпендикуляром называется прямая, проведенная перпендикулярно от гипотенузы к его вершине. Если эта линия делит гипотенузу на две части, то среднее геометрическое этих длин равно длине перпендикуляра. Среднее геометрическое играет важную роль в определении формата 16:9 на экранах современных телевизоров и мониторов.
Кроме того, вы можете попробовать онлайн-калькулятор среднего гармонического, который поможет вам вычислить среднее гармоническое из набора данных путем деления суммы обратных величин набора данных.
Как найти среднее геометрическое вручную (шаг за шагом)?
Для вычисления среднего геометрического между числами используется следующая формула:
Эта формула эквивалентна:
Пример среднего геометрического:
Найдите среднее геометрическое между 12,23,34?
Решение:
Шаг 1:
G.M = 3√ (12 × 23 × 34)
Шаг 2:
G.M = 3√ (9384)
Шаг 3:
0002 G.M = 21.0926
Пример вручную для типа процентных чисел:Вычислить геометрическое между 11%, 22%, 33%?
Решение:
Шаг 1:
G.M = 3√ ((1+11/100) × (1+22/100) × (1+33/100))
Шаг 2:
G.M = 3 √ (1,11 × 1,22 × 1,33)
Шаг 3:
G.M = 3√ (1,8010)
Шаг 4:
G.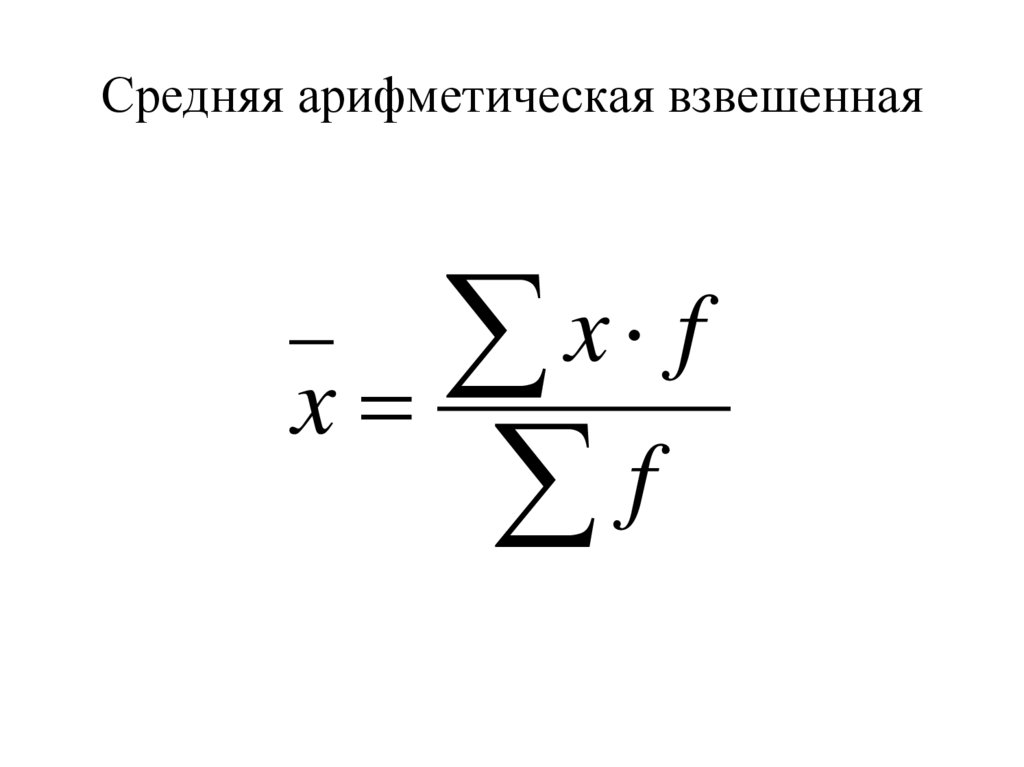 M = 1,216
M = 1,216
Шаг 5:
G.M = (1.216-1) × 100
Шаг 6:
G.M = 21,66%
Вы можете попробовать наш калькулятор среднего геометрического, чтобы проверить этот пример задачи.
Часто задаваемые вопросы (FAQ): Как рассчитывается среднее геометрическое?Среднее геометрическое вычисляется путем умножения нескольких чисел в степени 1/n.
Чему равно среднее геометрическое чисел 4 и 9?Среднее геометрическое 4 и 9 равно 6.
Умножение 9 и 4 дает 36, затем извлечение квадратного корня из 36 дает 6 как среднее геометрическое между 4 и 9.
Чему равно среднее геометрическое 6 и 13?8,83 — среднее геометрическое 6 и 13.
Почему среднее геометрическое лучше арифметического? Среднее геометрическое лучше, чем арифметическое, поскольку оно также имеет дело с начислением сложных процентов от периода к периоду. Вот почему инвесторы используют среднее геометрическое, а не среднее арифметическое, поскольку оно дает точную оценку доходности.
Вот почему инвесторы используют среднее геометрическое, а не среднее арифметическое, поскольку оно дает точную оценку доходности.
Арифметическая последовательность — это последовательность, имеющая одинаковую разность между двумя последовательными членами, в то время как геометрическая последовательность имеет постоянное отношение между членами.
Какая связь между средним арифметическим и средним геометрическим?Пусть A.M и G.M являются арифметическими и геометрическими между двумя положительными числами, тогда
A. M>G.M. Среднее арифметическое никогда не может быть меньше среднего геометрического.
Среднее геометрическое совпадает с медианой?Да, среднее геометрическое совпадает с медианой, потому что среднее геометрическое включает произведение членов.
Как найти обыкновенное отношение среднего геометрического?В геометрической последовательности
- Разделите каждый член на его предыдущий член.

- Затем сравните результаты, если они совпадают, то последовательность геометрическая.
Чтобы найти среднее геометрическое в Excel, используется следующая функция:
=GEOMEAN (число1, [число2], ….)
Где,
число1 = первое значение или ссылка на ячейку.
число2 = второе значение или ссылка на ячейку второго значения.
End-Note:Среднее геометрическое очень полезно во многих ситуациях, таких как расчет темпов роста процента, определение сложных процентов, средних значений площади и объема, фондового рынка и многих других. Таким образом, вы можете использовать этот бесплатный онлайн-калькулятор среднего геометрического, который позволит вам рассчитать среднее геометрическое между числами или в процентах с полным пошаговым расчетом.
Ссылки:Из источника Википедии: Среднее геометрическое и вычисление, Связь с логарифмами и многое другое!
Из источника investopedia: Анализ среднего геометрического в инвестировании
Из источника themodelmill: Среднее геометрическое и стандартное отклонение (используется для инвестиций с горизонтом погашения)
Формула среднего арифметического | Калькулятор (примеры с шаблоном Excel)
Формула среднего арифметического (Содержание)
- Формула
- Примеры
- Калькулятор
Термин «среднее арифметическое» в основном относится к математическому среднему значению двух или более чисел. Однако метод расчета среднего арифметического может варьироваться в зависимости от частоты каждой переменной в наборе данных — простое среднее (равновзвешенное) или средневзвешенное. Формула среднего арифметического для одинаково взвешенных переменных может быть получена путем суммирования всех переменных в наборе данных и последующего деления результата на количество переменных. Математически это представляется как
Однако метод расчета среднего арифметического может варьироваться в зависимости от частоты каждой переменной в наборе данных — простое среднее (равновзвешенное) или средневзвешенное. Формула среднего арифметического для одинаково взвешенных переменных может быть получена путем суммирования всех переменных в наборе данных и последующего деления результата на количество переменных. Математически это представляется как
Среднее арифметическое значение = (x 1 + x 2 +…. + X N ) / N
или
. Где, В случае неодинаково взвешенных переменных формула для среднего арифметического может быть получена путем суммирования произведений каждой переменной и ее частоты, а затем результат делится на сумму частот. Математически это представляется как Среднее арифметическое значение = (F 1 *x 1 + F 2 *x 2 +…. or Arithmetic Mean = ∑ (f i * x i ) / f i Where Давайте рассмотрим пример, чтобы лучше понять расчет среднего арифметического. Вы можете скачать этот шаблон формулы Excel для расчета среднего арифметического здесь. Шаблон Excel для расчета среднего арифметического. + F N *x N ) / (F 1 + F 2 29 2. + ….. + f n )
+ F N *x N ) / (F 1 + F 2 29 2. + ….. + f n )
Примеры формулы расчета среднего арифметического (с шаблоном Excel) Формула для расчета среднего арифметического. Пример № 1. один год: 45, 65, 7, 10, 43, 35, 25, 17, 78, 91. Рассчитайте средний показатель игрока с битой за последние 10 иннингов.

Solution:
Arithmetic Mean is calculated using the formula given below
Arithmetic Mean = ∑ x i / n
- Arithmetic Mean = (45 + 65 + 7 + 10 + 43 + 35 + 25 + 17 + 78 + 91) / 10
- Среднее арифметическое = 41,60
Таким образом, средний показатель игрока с битой оставался равным 41,60 ран за иннинг в его последних 10 иннингах.
Формула среднего арифметического – Пример №2
Возьмем в качестве примера класс с 45 учениками. Недавно был проведен еженедельный тест по естественным наукам, в котором учащиеся оценивались по шкале от 1 до 10. На основании следующей информации рассчитайте средние баллы в тесте.
Решение:
Среднее арифметическое вычисляется по приведенной ниже формуле
Среднее арифметическое = ∑ (f i * x i ) / f i
- Среднее арифметическое = ((3 * 3) + (4 * 9) + (6 * 18) + (7 * 12) + (9 * 3)) / 45
- Среднее арифметическое = 264/45
- Среднее арифметическое = 5,87
Таким образом, средний балл класса в тесте по естественным наукам составил 5,87.
Формула среднего арифметического – Пример №3
Рассмотрим пример двух наборов данных с двумя разными средними арифметическими значениями. Первый набор данных имеет 10 переменных со средним значением 45, а второй набор данных имеет 7 переменных и среднее значение 42. Определите среднее арифметическое двух объединенных наборов данных.
Решение:
Арифметические средние значения комбинированного набора данных рассчитывают с использованием формулы, приведенной ниже
Среднее значение = (M 2 *N 1 ) + (M 2 *N 1 ) + (M 2 *N 1 ) + (M 2 *N 1 ) + (M 2 *N 1 ) + (M 2 *N 1 ) + (M 2 *N n 2 )) / (n 1 +n 2 )
- Среднее арифметическое = (45 * 10 + 42 * 7) / (10 + 7)
- Среднее арифметическое = 43,76
Следовательно, среднее арифметическое объединенного набора данных равно 43,76.
Объяснение
Формулу для расчета среднего арифметического можно рассчитать, выполнив следующие шаги:
Шаг 1: Сначала соберите и отсортируйте переменные, для которых необходимо вычислить среднее арифметическое. Переменные обозначаются x i .
Шаг 2: Далее определяется количество переменных в наборе данных, которое обозначается n в случае переменных с одинаковым весом. В противном случае вычислите частоту каждой переменной, и они обозначаются f i , а количество переменных представляет собой сумму частот.
Шаг 3: Наконец, формула для среднего арифметического для одинаково взвешенных переменных может быть получена путем сложения всех переменных, а затем результат делится на количество переменных в наборе данных, как показано ниже.
Среднее арифметическое = ∑ x i / n
Однако в случае средневзвешенного значения формула для среднего арифметического может быть получена путем суммирования произведений каждой переменной и ее частоты, а затем результата делится на сумму частот, как показано ниже.
Среднее арифметическое значение = ∑ F I *x I /F I
Соответствие и использование арифметической средней формулы
Концепция среднего арифмета является очень простым и элементарным. Но он по-прежнему очень важен, поскольку часто используется в качестве статистического показателя для оценки среднего результата в наборе данных. Фактически он позволяет оценить, какие из переменных лучше или ниже среднего по группе. Он также используется в качестве меры для представления среднего значения по всему ряду данных. Кроме того, среднее арифметическое используется в тех случаях, когда среднее геометрическое или гармоническое среднее менее полезны, например, средний сорт, вес и т. д.
Калькулятор формулы среднего арифметического
Вы можете использовать следующий калькулятор среднего арифметического
| x 1 | |
| x 2 | |
| x 3 | |
| x 4 | |
| n | |
| Arithmetic Mean | |
| Среднее арифметическое | = |
|
|
Рекомендуемые статьи
Это справочник по формуле среднего арифметического.

 Например, средним значением для чисел 2, 3, 3, 5, 7 и 10 будет 5, которое является результатом деления их суммы, равной 30, на их количество, равное 6.
Например, средним значением для чисел 2, 3, 3, 5, 7 и 10 будет 5, которое является результатом деления их суммы, равной 30, на их количество, равное 6.




 (inlet primary и secondary) (oF, oC)
(inlet primary и secondary) (oF, oC)
 Вода покидает теплообменник при температуре 60 oC.
Вода покидает теплообменник при температуре 60 oC. «Зачёт» = 5 баллов, «незачёт» = 0 баллов. Средний балл диплома = среднее арифметическое баллов за все предметы во вкладыше, включая «зачёт» и «незачёт».
«Зачёт» = 5 баллов, «незачёт» = 0 баллов. Средний балл диплома = среднее арифметическое баллов за все предметы во вкладыше, включая «зачёт» и «незачёт».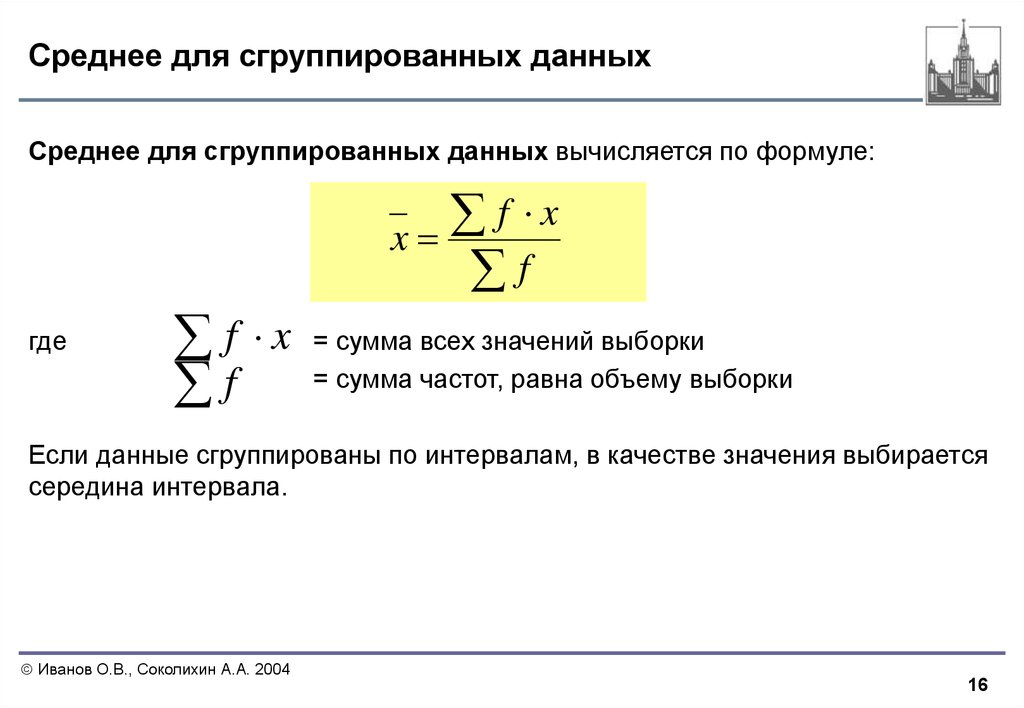 )
) ⓘ Среднее арифметическое двух чисел [AM]
ⓘ Среднее арифметическое двух чисел [AM]
