Средняя линия трапеции ABCD: определение, свойства, признак, длина
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Геометрия Что такое средняя линия трапеции
В данной публикации мы рассмотрим определение, свойства и признак средней линии трапеции, а также разберем пример решения задачи для лучшего понимания изложенного материала.
- Определение средней линии трапеции
- Свойства средней линии трапеции
- Свойство 1
- Свойство 2
- Свойство 3
- Признак средней линии трапеции
- Вторая средняя линия
- Пример задачи
Определение средней линии трапеции
Отрезок, соединяющий середины боковых сторон трапеции, называется ее 
- LM – средняя линия трапеции ABCD
- L – середина стороны AB, т.е. AL = LB
- M – середина стороны CD, т.е. CM = MD
Свойства средней линии трапеции
Свойство 1
Средняя линия трапеции параллельна ее основаниям и равняется их полусумме.
Для рисунка выше:
Свойство 2
Средняя линия трапеции делит пополам любой отрезок, концы которого лежат на основаниях данной трапеции.
Свойство 3
Средняя линия трапеции делит ее на две другие трапеции, площади которых соотносятся следующим образом (см. первый чертеж публикации):
Признак средней линии трапеции
Если отрезок, выходящий из середины боковой стороны трапеции, пересекает ее вторую боковую сторону и, при этом, параллелен основаниям фигуры, то он является средней линией этой трапеции.
Вторая средняя линия
Иногда дополнительно выделяют вторую среднюю линию трапеции – отрезок, соединяющий середины ее оснований. При этом следует помнить, что к ней не применимы Свойства 1-3 и Признак, рассмотренные выше.
При этом следует помнить, что к ней не применимы Свойства 1-3 и Признак, рассмотренные выше.
Вторая средняя линия равнобедренной трапеции одновременно является ее высотой.
Пример задачи
Средняя линия трапеции равняется 25 см, а ее высота – 7 см. Найдите площадь фигуры.
Решение
Как мы знаем, площадь трапеции равняется полусумме оснований, умноженной на высоту h: S = (a+b)/2 ⋅ h
В данном случае полусумма оснований – это и есть средняя линия. Обозначим ее буквой m. То есть m = (a+b)/2.
Таким образом, S = m ⋅ h = 25 см ⋅ 7 см = 175 см2.
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Средняя линия трапеции
Четырёхугольник, у которого две противоположные стороны параллельны, а другие две — не параллельны, называется трапецией.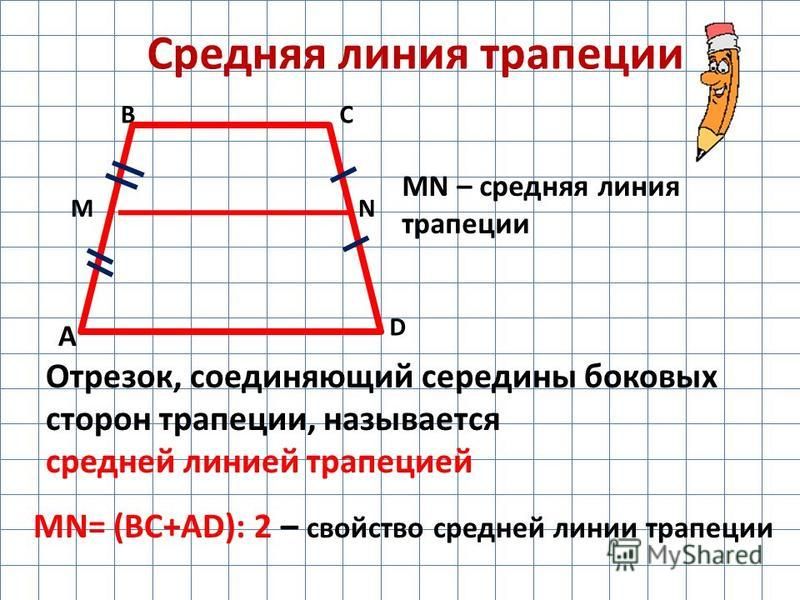
На чертеже 252 у четырёхугольника АВDС АВ || СD, AC ||BD. АВDС — трапеция.
Параллельные стороны трапеции называются её основаниями; АВ и СD — основания трапеции. Остальные две стороны называются боковыми сторонами трапеции; АС и ВD — боковые стороны трапеции.
Если боковые стороны равны, то трапеция называется равнобедренной.
Трапеция АВОМ равнобедренная, так как АМ=ВО (рис. 253).
Трапеция, у которой одна из боковых сторон перпендикулярна к основанию, называется прямоугольной (рис. 254).
Средней линией трапеции называется отрезок, соединяющий середины боковых сторон трапеции.
Теорема. Средняя линия трапеции параллельна каждому из ее оснований и равна их полусумме.
Дано: ОС — средняя линия трапеции АВDК, т. е. ОК = ОА и ВС = СD (рис. 255).
Надо доказать:
1) ОС || КD и ОС || АВ;
2) OC = \(\frac{KD + AB}{2}\)
Доказательство. Через точки А и С проведём прямую, пересекающую продолжение основания КD в некоторой точке Е.
Через точки А и С проведём прямую, пересекающую продолжение основания КD в некоторой точке Е.
В треугольниках АBС и DСЕ:
ВС = СD — по условию;
∠1 = ∠2, как вертикальные,
∠4 = ∠3, как внутренние накрест лежащие при параллельных АВ и KЕ и секущей ВD. Следовательно, \(\Delta\)АBС = \(\Delta\)DСЕ.
Отсюда АС = СЕ, т.е. ОС является средней линией треугольника КАЕ. Следовательно:
1) ОС || КЕ и, значит, ОС || КD и ОС || AВ;
2) OC = \(\frac{KE}{2} = \frac{KD + DE}{2}\), но DЕ = АВ (из равенства треугольников АBС и DСЕ), поэтому отрезок DЕ можно заменить равным ему отрезком АВ. Тогда получим:
OC = \(\frac{KD + AB}{2}\)
Теорема доказана.
Свойства трапеции, которые часто используются при решении задач:
- Диагонали трапеции разбивают её начетыре треугольника с общей вершиной. Площади треугольников, прилежащие к боковым сторонам, равны.
- В любой трапеции середины оснований, точка пересечения диагоналей и точка пересечения прямых, на которой лежат боковые стороны, лежат на одной прямой (точки М, N, О и К).

- В равнобокой трапеции углы при основании равны.
- В равнобокой трапеции прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии этой трапеции
- В равнобокой трапеции диагонали равны.
- В равнобокой трапеции высота, опущенная на большее основание из конца меньшего основания, делит его на два отрезка, один из которых равен полуразности оснований, а другой — их полусумме.
- Во всякой трапеции серединам боковых сторон и середины диагоналей лежат на одной прямой.
- Во всякой трапеции отрезок, соединяющий середины диагоналей, параллелен основаниям и равен полуразности оснований.
- Во всякой трапеции сумма квадратов диагоналей равна сумме квадратов боковых сторон и удвоенного произведения оснований.
- Трапецию можно вписать в окружность тогда и только тогда, когда она равнобокая.

- Трапецию можно описать около окружности тогда и только тогда, когда сумма оснований равна сумме боковых сторон.
Математическая задача: Длина 26 — вопрос № 68714, статистика, среднее
Длина медианы трапеции 10 дюймов. Медиана делит трапецию на две части, соотношение которых равно 3:5. Длина более короткого основания:
Правильный ответ:
c = 5 вПошаговое объяснение:
м=10 дюймов S1:S2 = 3:5 (a+c)/2 = m a+c = 2⋅ m = 20 in h2=h3 h2+h3=h S1 = h2⋅ (a+m)/2 S2 = h3⋅ (c+m)/2 = h2⋅ (c+m)/2 h2⋅ (c+m)/2 : h2⋅ (a+m)/2 = 3:5 (c+m) : (a+m) = 3: 5 (c+m)=53⋅ (a+m) (a+c)/2=m (c+10)=53⋅ (a+10) (a+c)/2=10 (c+ 10)=3/5⋅ (a+10) (a+c)/2=10 3a−5c=20 a+c=20 2-й ряд – 31 ⋅ 1-й ряд → 2-й ряд 3a-5c=20 2,67c=13,33 c= 2,6666666713,33333333=5 a=320+5c=320+5⋅ 5=15 a=15 c=5=5 в
Нашли ошибку или неточность? Не стесняйтесь
пишите нам . Спасибо!
Спасибо!
Советы по использованию связанных онлайн-калькуляторов
Нужна помощь в вычислении среднего арифметического?
Ищете статистический калькулятор?
Воспользуйтесь нашим калькулятором коэффициентов.
У вас есть линейное уравнение или система уравнений и вы ищете ее решение? Или у вас есть квадратное уравнение?
См. также наш калькулятор тригонометрического треугольника.
Для решения этой математической задачи вам необходимо знать следующие знания:
- статистика
- среднее
- геометрия
- подобие треугольников 900 30 алгебра
- уравнение
- система уравнений
- выражение переменной из формулы
- контуры
- площадь фигуры
- треугольник
- трапеция
- основные функции
- соотношение
Единицы физических величин:
- площадь
Уровень словесной задачи:
- практика для 14-летних 900 68
- Трапеция — центральная медиана
Центральная медиана делит трапецию на две меньшие трапеции. Найдите отношение его площадей. - МО Z9–I–2 — 2017
VO является более длинным основанием в трапеции VODY, а диагональное пересечение K делит линию VD в отношении 3:2. Площадь треугольника КОВ равна 13,5 см². Найдите площадь всей трапеции. - Вычислите 47763
Вычислите площадь равнобедренной трапеции ABCD, длинное основание которой равно 48 см, меньшее основание составляет 3/4 наибольшего основания, а катет трапеции составляет 2/3 большего основания. Результат округляется до сотых. - Трапеция KLMN
Трапеция KLMN имеет основания KL 40см и MN 16см. В основании KL находится точка P. Отрезок NP делит трапецию на звенья одинаковой площади. На каком расстоянии точка P от точки K? - Герб
Класс создал свой герб, который имел форму, состоящую из равнобедренной трапеции ABCD (более короткое основание а = 4,5 см в длину, более длинное 2а = 9 см, высота трапеции 6 см) и полукруга с центром S и диаметр АВ. Три одинаковых равнобедренных треугольника fo
Три одинаковых равнобедренных треугольника fo - MO Z8–I–6 2018
Трапеция KLMN, KL имеет основание 40 см и MN 16 см. Точка P лежит на прямой KL так, что отрезок NP делит трапецию на две части одинаковой площади. Найдите длину линии КП. - Внутренние углы
Величина внутреннего угла при центральной вершине C равнобедренного треугольника ABC равна 72°. Прямая p, параллельная основанию этого треугольника, делит треугольник на трапецию и меньший треугольник. Насколько велики внутренние углы трапеций - Разрез куба
Ребро СС’ направляет куб ABCDA’B’C’D’, плоскость, которая делит куб на две перпендикулярные четырехгранные и треугольные призмы, объемы которых составляют 3:2. Определите, в каком отношении ребро AB делит эту плоскость. - Терции трапеции
Трапеция ABCD имеет параллельные стороны AB и CD. Точка Е лежит на стороне АВ. Отрезок DE делит трапецию на две части одинаковой площади. Найдите длину отрезка AE. - Равнобедренная трапеция
Какова высота равнобедренной трапеции, длина основания которой 11 см и 8 см, а длина катета 2,5 см? - Тимоти
Рост Тимоти 56 4/5 дюймов. Тереза на 1 1/6 дюйма ниже Тимоти, а Джейн на 1 1/3 дюйма ниже Терезы. Какой рост у Джейн?
Тереза на 1 1/6 дюйма ниже Тимоти, а Джейн на 1 1/3 дюйма ниже Терезы. Какой рост у Джейн? - Рассчитать 3993
Медиана трапеции p равна 18,6 см, а основание a = 29,8 см. Вычислите размер второго основания c. - Томас 2
Рост Томаса 56 3/4 дюйма. Джиллиан на 1 3/8 дюйма ниже Томаса, а Джейн на 1 1/5 дюйма ниже Джиллиан. Какой рост у Джейн? Подпишите имена на диаграмме ленты, чтобы представить эту проблему. Джейн Джиллиан Томас Отлично! - Трапеция
Длина основания и высота основания трапеции находятся в соотношении 5:3:2. Площадь трапеции 128 см². Вычислите длину основания и высоту трапеции. - Разделить равнобедренный треугольник
Как разделить равнобедренный треугольник на две части с равными площадями, перпендикулярными оси симметрии (на трапецию и треугольник)? - Золотое сечение
Разделите линию длиной 14 см на две части так, чтобы отношение меньшей части к большей было таким же, как отношение большей части ко всей длине линии.
- Периметры 81399
Даны два квадрата. У первого длина стороны 5 см, у второго 10 см. Запишите отношение: для а- их сторон для б- их периметров для с- их площадей
Рекомендуем посмотреть это обучающее видео по этой математической задаче. : video1 video2
: video1 video2
Площадь трапеции с медианой
Главная » Площадь геометрических фигур » Площадь трапеции с медианой
Последнее обновление: Идо Сариг · Этот веб-сайт получает доход от рекламы и использует файлы cookie · Условия использования · Политика конфиденциальности
В дополнение к стандартной формуле площади трапеции с использованием ее оснований, мы можем также вычислить площадь трапеции с ее медианой и высотой. Медиана — это линия, соединяющая две середины катетов трапеции — непараллельные стороны трапеции. Медиана также называется срединным сегментом или срединной линией.
Задача
BCD трапеция, AB || CD . EF — линия, соединяющая середины ветвей AD и BC , AE = ED и BF = FC . h — высота трапеции. Найдите формулу для его площади, используя h и |EF|
h — высота трапеции. Найдите формулу для его площади, используя h и |EF|
Стратегия
Давайте посмотрим, как мы можем связать то, что мы знаем о медиане трапеции, с уже имеющейся формулой площади трапеции. Площадь трапеции равна (короткое основание+длинное основание)·высота/2, или А =½( АВ + DC )·ч.
В этой задаче у нас есть высота и медиана или середина. Из теоремы о среднем отрезке трапеции мы имеем отношение между средним отрезком и основаниями: | ЭФ| = ½ ( АВ + DC ). Глядя на две формулы, мы видим, что мы можем просто заменить EF на ½ ( AB + DC ) в формуле площади и получить A =| ЭФ| ·ч
Раствор
(1) A =½( AB + DC )·h // Площадь трапеции
(2) AE = ED , BF = FC //дано
(3 ) EF – срединный отрезок //(2), Определение срединного отрезка
(4) |EF| = ½( AB + DC ) //(3), теорема о середине трапеции
(5) A = |EF| ·h //(1), (4), подстановка
Другой способ решения этой задачи
В предыдущем разделе мы полагались на признание того, что формула площади трапеции — A =½( AB + DC )·h выглядит очень похоже на формулу для длины среднего отрезка — |EF| = ½( AB + DC ) и сделал замену, которая привела к очень компактному и элегантному решению.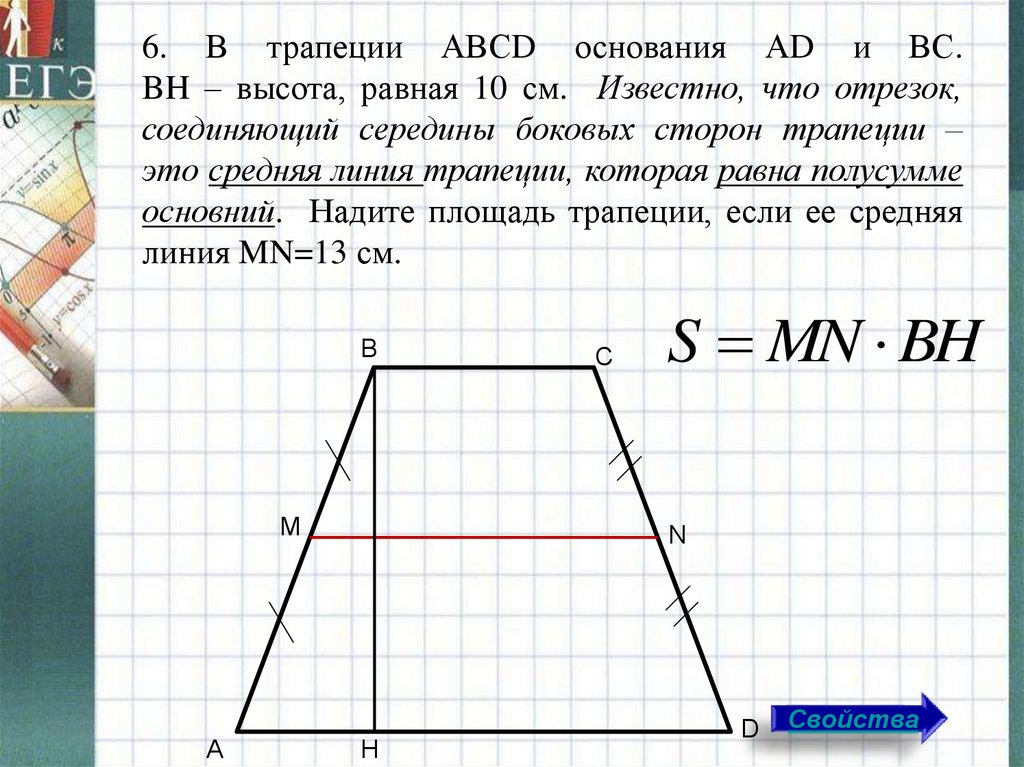
Но что, если мы сразу не заметим, что формулы подобны, или не вспомним, что середина равна половине суммы оснований? Давайте посмотрим на другой способ решить эту проблему, не полагаясь на это.
Поскольку EF — это линия, соединяющая середины сторон, мы могли бы использовать теорему о середине треугольника, но для этого нам нужен треугольник. Итак, давайте нарисуем один, используя диагональ AC:
Решение с использованием теоремы о середине треугольника
В треугольнике ∆ACD, |EG| это прямая, параллельная основанию CD, которая начинается из середины стороны AD, поэтому по теореме о середине обратного треугольника это средний отрезок, равный половине основания. Установим |EG|=x. Если x равен половине основания, то основание CD должно быть равно 2x.
Теперь давайте посмотрим на другой треугольник, ΔACB. Используя те же рассуждения, что и выше, |GF| начинается от середины стороны BC и параллельна AB, поэтому по теореме о середине обратного треугольника это середина, равная половине основания.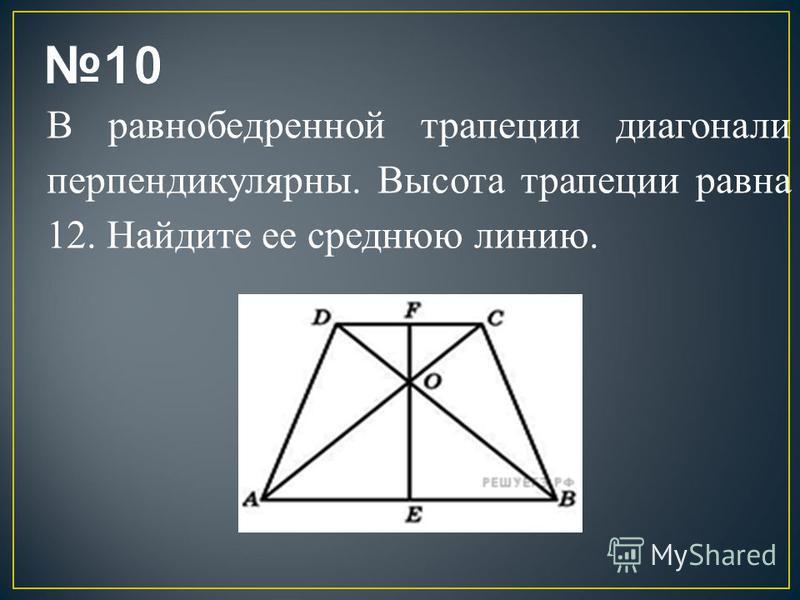


 Три одинаковых равнобедренных треугольника fo
Три одинаковых равнобедренных треугольника fo Тереза на 1 1/6 дюйма ниже Тимоти, а Джейн на 1 1/3 дюйма ниже Терезы. Какой рост у Джейн?
Тереза на 1 1/6 дюйма ниже Тимоти, а Джейн на 1 1/3 дюйма ниже Терезы. Какой рост у Джейн?