Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
Решено
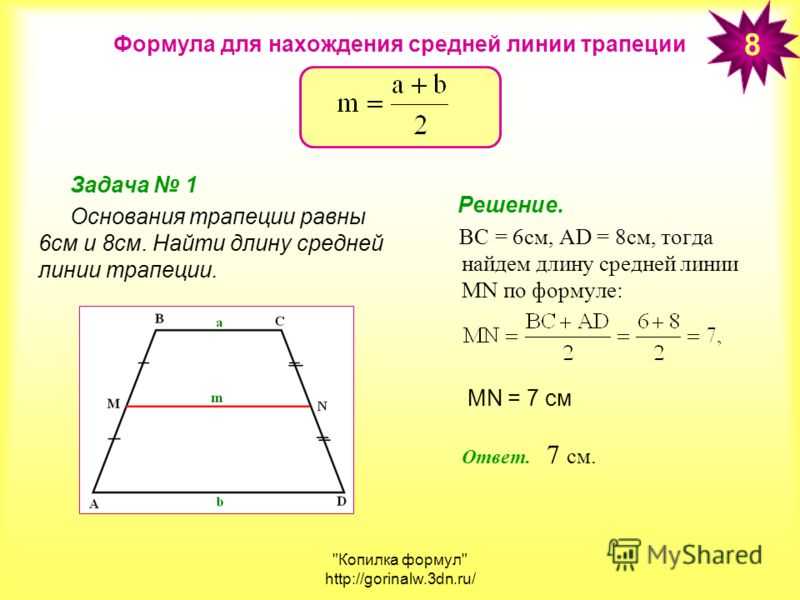
Помогите пожалуйста решить задачу 4-го класса.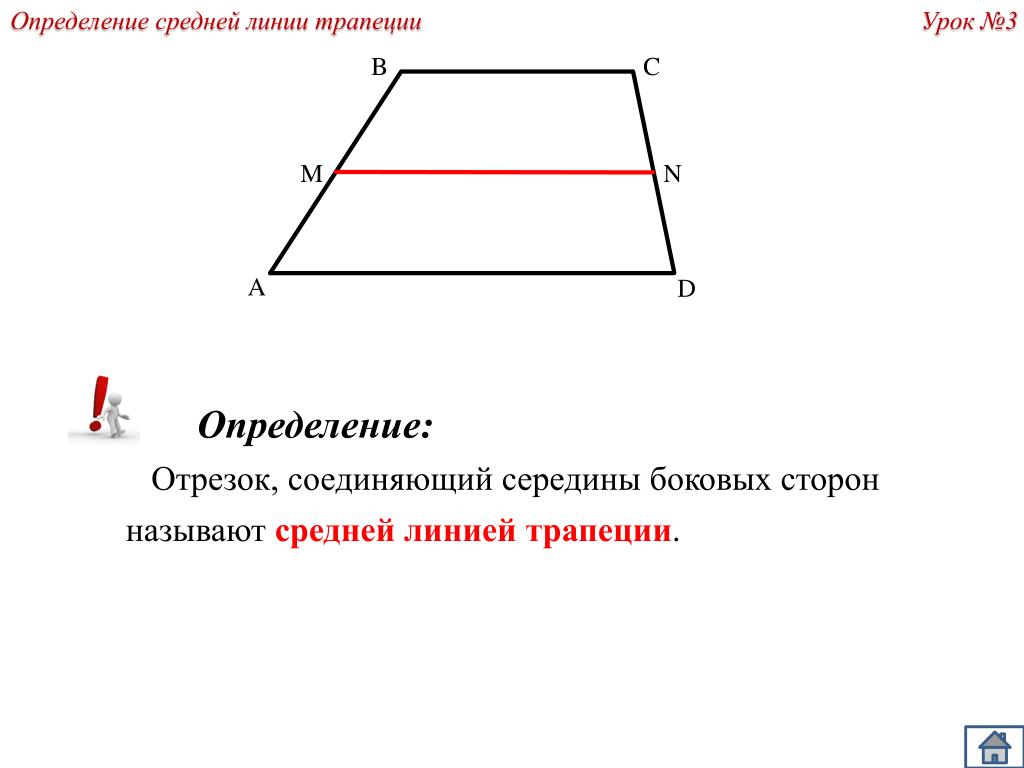 Если около каждого дома посадить по 9 саженцев, то не зватит 100 саженцев, а если по 5 саженцев, то 20 саженцев останется. Сколько домов? Сколько
Если около каждого дома посадить по 9 саженцев, то не зватит 100 саженцев, а если по 5 саженцев, то 20 саженцев останется. Сколько домов? Сколько
Решено
На сторонах угла D отмечены точки М и К так, что DМ = DК. Точка Р лежит внутри угла D, и РК = РМ. Докажите, что луч DР – биссектриса угла МDК.
Сколькими нулями оканчивается произведение всех натуральных чисел от 41 до 64 включительно
В треугольнике ABC угол A равен 45 градусов, угол B равен 60 градусов, BC= 6√6. Найдите AC.
Вычислить площадь и высоту параллелограмма, построенного на векторах а=2j+k и b=j+2k
Пользуйтесь нашим приложением
| Тема урока: Трапеция.  Средняя линия трапеции.(слайд 1) Средняя линия трапеции.(слайд 1)
Цель урока: образовательные: формировать навыки решения задач с применением теоремы Фалеса, свойств трапеции в зависимости от её вида, теоремы о средней линии трапеции; решать задачи по готовым чертежам; развивающие: развитие навыков логического мышления учащихся, память, вычислительные навыки, умение применять полученные знания на практике воспитательные: формировать самостоятельность, воспитывать познавательную активность, внимательность, аккуратность, дисциплинированность, интерес к изучению математике. I. Организационный момент. II. Проверка домашнего задания. В равнобедренную трапецию, боковая сторона которой равна 23 дм, вписана окружность. Найти среднюю линию трапеции. III. Повторение основных понятий, теорем. 1)Нужно назвать каждый из четырехугольников и дать понятие четырехугольнику: (слайд 2-5) Какой четырех угольник называется трапецией? Как называются стороны трапеции? Какая трапеция называется прямоугольной? Равнобедренной? Сформулируйте свойства равнобедренной трапеции. 
Сформулируйте признаки равнобедренной трапеции. Что такое средняя линия трапеции? Сформулируйте свойство средней линии трапеции. Виды трапеций. Если предложение верное, то «+» в столбце «А»; если неверное «+» в столбце «В», а если ученик не может ответить верно или нет, то ответ записывает в столбец «С». Средняя линия трапеции – это отрезок, соединяющий середины боковых сторон. (А). Трапецией называется четырехугольник, у которого противоположные стороны параллельны. (В). В любом треугольнике можно провести только одну среднюю линию. (В). Средняя линия трапеции параллельна основаниям и равна их полу сумме. (А). У равнобокой трапеции углы при основании равны. (А) В прямоугольном треугольнике с углом в 30° катет, противолежащий этому углу, равен половине гипотенузы. (А). У равностороннего треугольника все углы разные.  (В). (В).
Треугольник называется прямоугольным, если у него есть гипотенуза. (В). IV Решение упражнений (слайд 6)Решение задач устно по готовому чертежу. MN – средняя линия трапеции АВСD, PR – средняя линия трапеции АMND. ВС = 6 см., АD= 10 см. Найдите: MN и PR. (слайд 7)Чем являются отрезки МК и КN, если MN – средняя линия трапеции АВСD? Работа по формированию навыков решения задач (на каждый стол посередине положен листок с напечатанными задачами) .(слайд 8) 3.Большее основание трапеции равно 8см, а меньшее на 3см меньше средней линии. Найти основания трапеции. 4.В равнобокой трапеции диагональ делит острый угол пополам. Периметр её равен 54дм, большее её основание — 1,8м. Вычислите меньшее основание трапеции. Задача 3. Большее основание трапеции равно 8см, а меньшее на 3см.  меньше средней линии. меньше средней линии.
Дано:
Дано:
3х =54-18 3х = 36 х =12 Ответ: ВС =12дм. 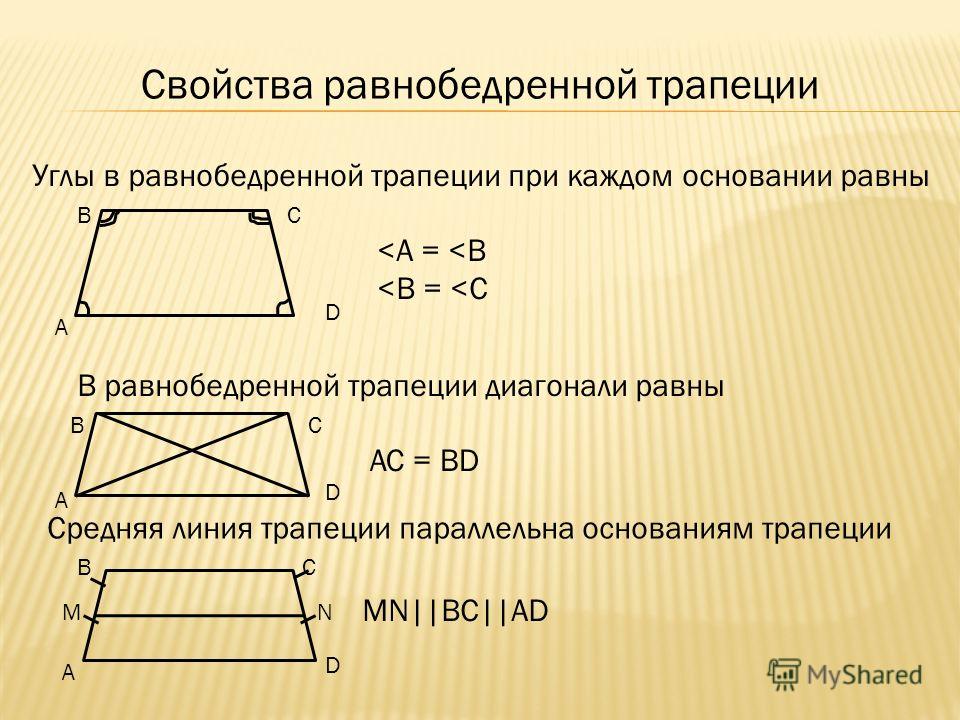
Отгадайте, какое слово зашифровано(столик). Трапеция (от греческого слова trapezion- буквальный перевод – столик) 4. Решение задач по готовому чертежу. 5) (слайд 10) ВС — ? АД — ? если МК = 4см, KN = 9см. 6) (слайд 11) Дано: АВСД –трапеция, МN – средняя линия, ВС : АД = 2 : 3, MN = 5 см. Найти: ВС — ? АД — ? Решение: Пусть x см – 1 часть, тогда ВС = 2x см, АД = 3х см. MN = (ВС + АД) / 2, 5 = (2x + 3x) / 2, 5х = 10 х = 2 2*2 = 4 см. 2*3 = 6 см. 
Ответ: ВС = 4 см, АД = 6 см. 7. Подведение итогов урока Домашнее задание: (слайд 12) Меньшее основание трапеции равно 14см, а большее на 5см больше средней линии. Найти основания трапеции. жүктеу/скачать 61.5 Kb. Достарыңызбен бөлісу: |
Срединная линия трапеции равна половине большего основания. Трапеция, средняя линия трапеции, треугольник
Ваша конфиденциальность важна для нас. По этой причине мы разработали Политику конфиденциальности, в которой описывается, как мы используем и храним вашу информацию. Пожалуйста, ознакомьтесь с нашей политикой конфиденциальности и сообщите нам, если у вас есть какие-либо вопросы.
Сбор и использование личной информации
Личная информация относится к данным, которые могут быть использованы для идентификации конкретного лица или связи с ним.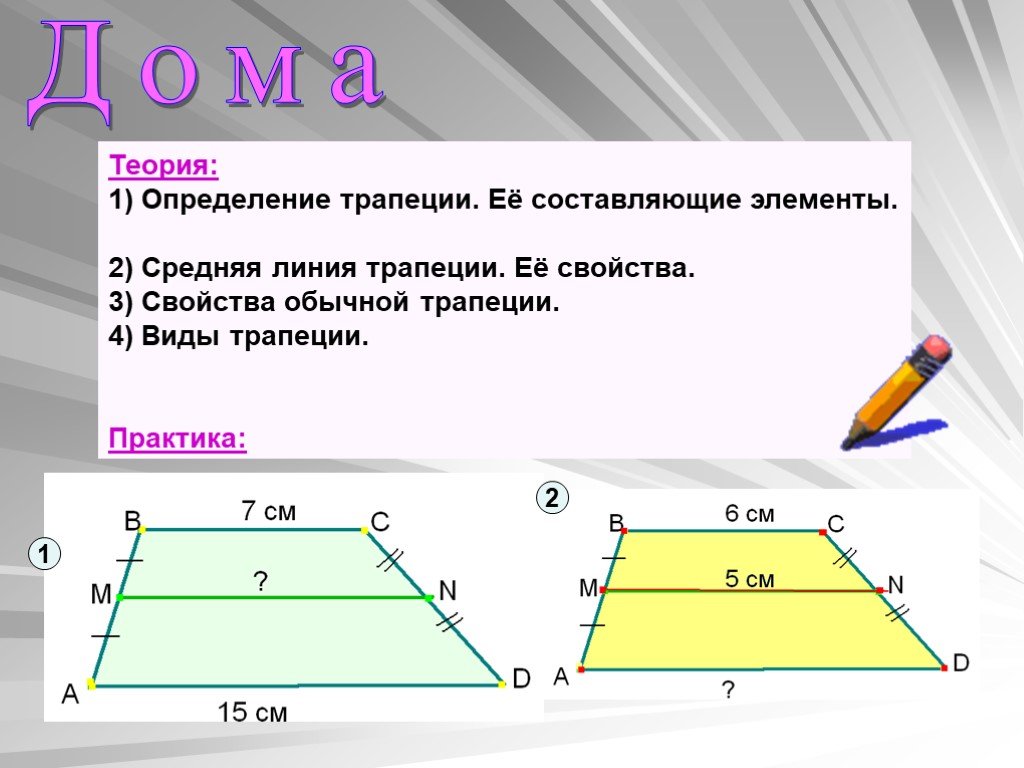
Вас могут попросить предоставить личную информацию в любое время, когда вы свяжетесь с нами.
Ниже приведены некоторые примеры типов личной информации, которую мы можем собирать, и того, как мы можем использовать такую информацию.
Какую личную информацию мы собираем:
- Когда вы подаете заявку на сайте, мы можем собирать различную информацию, включая ваше имя, номер телефона, адрес электронной почты и т. д.
Как мы используем вашу личную информацию:
- Личная информация, которую мы собираем, позволяет нам связываться с вами и информировать вас об уникальных предложениях, рекламных акциях и других событиях и предстоящих мероприятиях.
- Время от времени мы можем использовать вашу личную информацию для отправки вам важных уведомлений и сообщений.
- Мы также можем использовать личную информацию для внутренних целей, таких как проведение аудитов, анализ данных и различные исследования, чтобы улучшить предоставляемые нами услуги и предоставить вам рекомендации относительно наших услуг.

- Если вы участвуете в розыгрыше призов, конкурсе или аналогичном поощрении, мы можем использовать предоставленную вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от вас информацию третьим лицам.
Исключения:
- В случае необходимости — в соответствии с законом, судебным приказом, в порядке судопроизводства и/или на основании публичных запросов или запросов государственных органов на территории Российской Федерации — раскрывать свои персональные данные. Мы также можем раскрывать информацию о вас, если решим, что такое раскрытие необходимо или уместно в целях безопасности, правоохранительных органов или по другим причинам, представляющим общественный интерес.
- В случае реорганизации, слияния или продажи мы можем передать личную информацию, которую мы собираем, соответствующему правопреемнику третьей стороны.
Защита личной информации
Мы принимаем меры предосторожности, в том числе административные, технические и физические, для защиты вашей личной информации от потери, кражи и неправомерного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.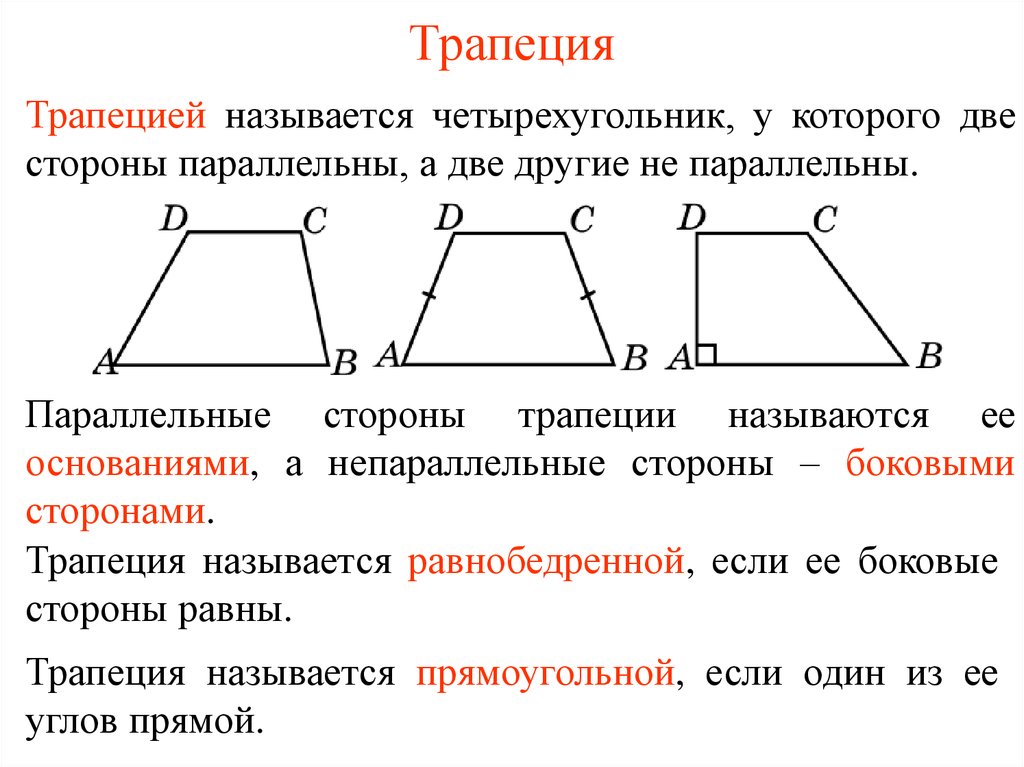
Обеспечение конфиденциальности на уровне компании
Чтобы обеспечить безопасность вашей личной информации, мы сообщаем нашим сотрудникам о правилах конфиденциальности и безопасности и строго следим за соблюдением правил конфиденциальности.
Ваша конфиденциальность важна для нас. По этой причине мы разработали Политику конфиденциальности, в которой описывается, как мы используем и храним вашу информацию. Пожалуйста, ознакомьтесь с нашей политикой конфиденциальности и сообщите нам, если у вас есть какие-либо вопросы.
Сбор и использование личной информации
Личная информация относится к данным, которые могут быть использованы для идентификации конкретного лица или связи с ним.
Вас могут попросить предоставить личную информацию в любое время, когда вы свяжетесь с нами.
Ниже приведены некоторые примеры типов личной информации, которую мы можем собирать, и того, как мы можем использовать такую информацию.
Какую личную информацию мы собираем:
- Когда вы подаете заявку на сайте, мы можем собирать различную информацию, включая ваше имя, номер телефона, адрес электронной почты и т.
 д.
д.
Как мы используем вашу личную информацию:
- Личная информация, которую мы собираем, позволяет нам связываться с вами и информировать вас об уникальных предложениях, рекламных акциях и других событиях и предстоящих событиях.
- Время от времени мы можем использовать вашу личную информацию для отправки вам важных уведомлений и сообщений.
- Мы также можем использовать личную информацию для внутренних целей, таких как проведение аудитов, анализ данных и различные исследования, чтобы улучшить предоставляемые нами услуги и предоставить вам рекомендации относительно наших услуг.
- Если вы участвуете в розыгрыше призов, конкурсе или аналогичном поощрении, мы можем использовать предоставленную вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от вас информацию третьим лицам.
Исключения:
- В случае необходимости — в соответствии с законом, судебным приказом, в порядке судопроизводства и/или на основании публичных запросов или запросов государственных органов на территории Российской Федерации — раскрыть свои персональная информация.
 Мы также можем раскрывать информацию о вас, если решим, что такое раскрытие необходимо или уместно в целях безопасности, правоохранительных органов или по другим причинам, представляющим общественный интерес.
Мы также можем раскрывать информацию о вас, если решим, что такое раскрытие необходимо или уместно в целях безопасности, правоохранительных органов или по другим причинам, представляющим общественный интерес. - В случае реорганизации, слияния или продажи мы можем передать личную информацию, которую мы собираем, соответствующему правопреемнику третьей стороны.
Защита личной информации
Мы принимаем меры предосторожности, в том числе административные, технические и физические, для защиты вашей личной информации от потери, кражи и неправомерного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Обеспечение конфиденциальности на уровне компании
Чтобы обеспечить безопасность вашей личной информации, мы сообщаем нашим сотрудникам о правилах конфиденциальности и безопасности и строго следим за соблюдением правил конфиденциальности.
Понятие средней линии трапеции
Для начала вспомним, какая фигура называется трапецией.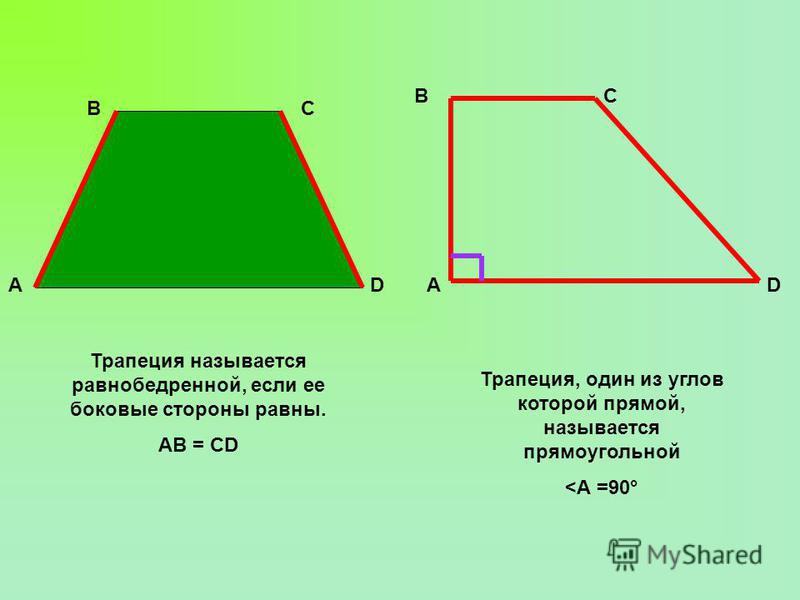
Определение 1
Трапеция – это четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
При этом параллельные стороны называются основаниями трапеции, а не параллельные — сторонами трапеции.
Определение 2
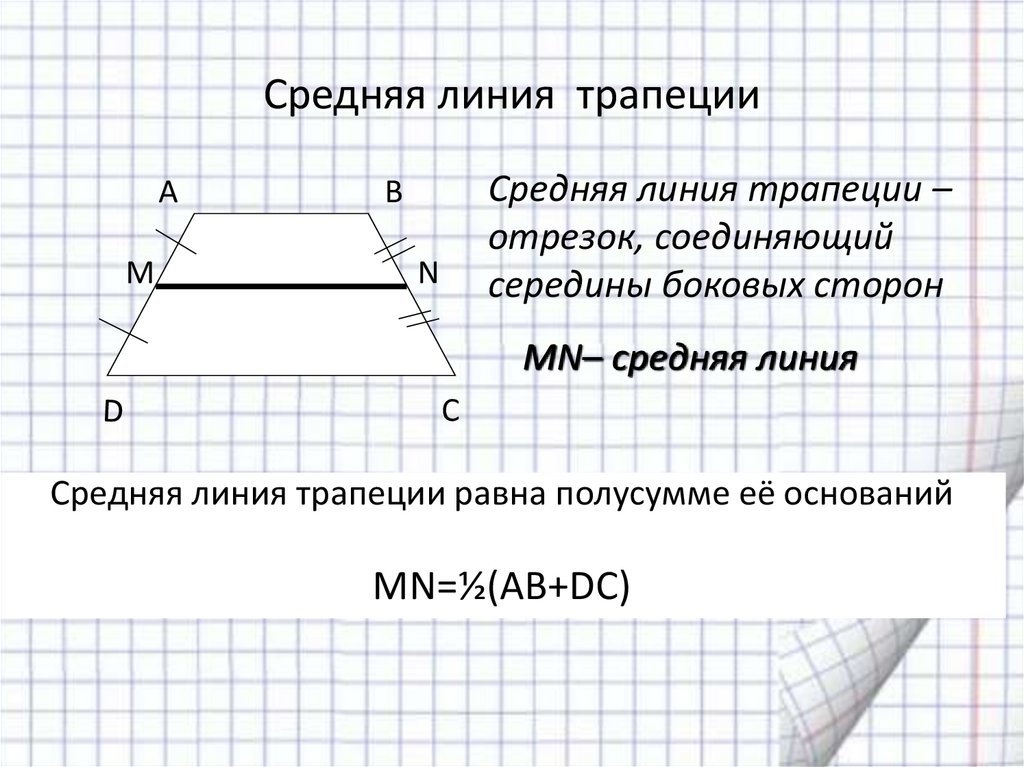
Средняя линия трапеции — это отрезок, соединяющий середины сторон трапеции.
Теорема о средней линии трапеции
Теперь введем теорему о средней линии трапеции и докажем ее векторным методом.
Теорема 1
Средняя линия трапеции параллельна основаниям и равна половине их суммы.
Доказательство.
Дана трапеция $ABCD$ с основаниями $AD\ и\ BC$. И пусть $MN$ — средняя линия этой трапеции (рис. 1).
Рис. 1. Средняя линия трапеции
Докажем, что $MN||AD\ и \ MN=\frac(AD+BC)(2)$.
Рассмотрим вектор $\overrightarrow(MN)$. Далее мы используем правило многоугольника для сложения векторов. С одной стороны получаем, что
С другой стороны
Складывая два последних равенства, получаем
Так как $M$ и $N$ — середины сторон трапеции, то
Получаем:
Следовательно
Из того же равенства (поскольку $\overrightarrow(BC)$ и $\overrightarrow(AD )$ сонаправлены и, следовательно, коллинеарны), получаем, что $MN||AD$.
Теорема доказана.
Примеры заданий на понятие средней линии трапеции
Пример 1
Стороны трапеции равны $15\см$ и $17\см$ соответственно. Периметр трапеции равен $52\см$. Найдите длину средней линии трапеции.
Раствор.
Обозначим среднюю линию трапеции через $n$.
Сумма сторон равна
Следовательно, поскольку периметр равен $52\см$, сумма оснований равна
Отсюда по теореме 1 получаем
Ответ: $10\cm$.
Пример 2
Концы окружности диаметром $9$ см и $5$ см соответственно от касательной. Найдите диаметр этого круга.
Раствор.
Дана окружность с центром $O$ и диаметром $AB$. Проведите касательную $l$ и постройте расстояния $AD=9\ см$ и $BC=5\ см$. Проведем радиус $OH$ (рис. 2).
Рисунок 2.
Поскольку $AD$ и $BC$ — расстояния до касательной, то $AD\bot l$ и $BC\bot l$, а поскольку $OH$ — радиус, то $OH\bot l$, следовательно, $OH |\влево|AD\вправо||BC$. Из всего этого получаем, что $ABCD$ — трапеция, а $OH$ — ее средняя линия. По теореме 1 получаем
Из всего этого получаем, что $ABCD$ — трапеция, а $OH$ — ее средняя линия. По теореме 1 получаем
\[(\Большой(\текст(Произвольная трапеция)))\]
Определения
Трапеция – это выпуклый четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
9\круг\). 2) Так как \(AD\параллель BC\) и \(BD\) секанс, то \(\угол DBC=\угол BDA\) лежит поперек.
Также \(\угол BOC=\угол AOD\) как вертикальный.
Следовательно, в двух углах \(\треугольник BOC\sim\треугольник AOD\).
Докажем, что \(S_(\треугольник AOB)=S_(\треугольник COD)\). Пусть \(h\) — высота трапеции. Тогда \(S_(\треугольник ABD)=\frac12\cdot h\cdot AD=S_(\треугольник ACD)\). Затем: \
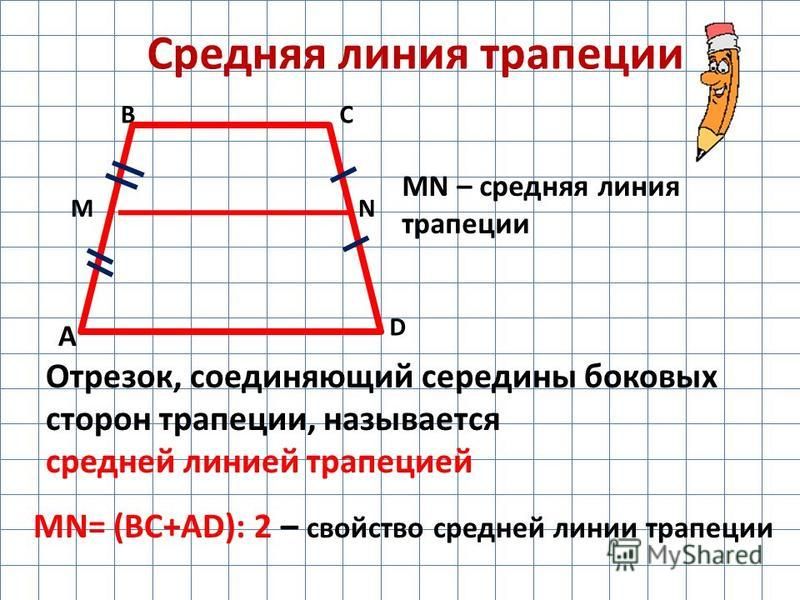
Определение
Средняя линия трапеции — это отрезок, соединяющий середины сторон.
Теорема
Средняя линия трапеции параллельна основаниям и равна половине их суммы.
Доказательство*
1) Докажем параллелизм.
Проведите линию \(MN»\параллельно AD\) (\(N»\в CD\) ) через точку \(M\) ). Тогда по теореме Фалеса (поскольку \(MN»\параллельно AD\параллельно BC, AM=MB\)) точка \(N»\) является серединой отрезка \(CD\)… Следовательно, точки \(N\) и \(N»\) совпадут.
2) Докажем формулу.
Нарисуем \(BB»\perp AD, CC»\perp AD\) . Пусть будет \(BB»\cap MN=M», CC»\cap MN=N»\).
Тогда по теореме Фалеса \(M»\) и \(N»\) являются серединами отрезков \(BB»\) и \(CC»\) соответственно. Итак, \(MM»\) — это средняя линия \(\треугольник ABB»\) , \(NN»\) — это средняя линия \(\треугольник DCC»\) . Вот почему: \
Поскольку \(MN\parallel AD\parallel BC\) и \(BB», CC»\perp AD\) , то \(B»M»N»C»\) и \(BM»N»C\) являются прямоугольниками. По теореме Фалеса из \(MN\parallel AD\) и \(AM=MB\) следует, что \(B»M»=M»B\) . Следовательно, \(B»M»N»C»\) и \(BM»N»C\) равные прямоугольники, следовательно, \(M»N»=B»C»=BC\) .
Таким образом:
\ \[=\dfrac12 \left(AB»+B»C»+BC+C»D\right)=\dfrac12\left(AD+BC\right)\]
Теорема: свойство произвольной трапеции
Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений боковых сторон лежат на одной прямой.
Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы «Похожие треугольники».
1) Докажем, что точки \(P\), \(N\) и \(M\) лежат на одной прямой.
Проведите линию \(PN\) (\(P\) — точка пересечения продолжений сторон, \(N\) — середина \(BC\) ). Пусть она пересекает сторону \(AD\) в точке \(M\) . Докажем, что \(M\) является серединой \(AD\) .
Рассмотрим \(\треугольник BPN\) и \(\треугольник APM\) . Они подобны по двум углам (\(\угол APM\) — общий, \(\угол PAM=\угол PBN\) как соответствующие при \(AD\параллели BC\) и секущей \(AB\)). Означает: \[\dfrac(BN)(AM)=\dfrac(PN)(PM)\]
Рассмотрим \(\triangle CPN\) и \(\triangle DPM\) . Они подобны по двум углам (\(\угол DPM\) — общий, \(\угол PDM=\угол PCN\) как соответствующие при \(AD\параллели BC\) и секущей \(CD\)). Означает: \[\dfrac(CN)(DM)=\dfrac(PN)(PM)\]
Отсюда \(\dfrac(BN)(AM)=\dfrac(CN)(DM)\). Но \(BN=NC\) , следовательно, \(AM=DM\) .
2) Докажем, что точки \(N, О, М\) лежат на одной прямой.
Пусть \(N\) — середина \(BC\) , \(O\) — точка пересечения диагоналей. Нарисуйте линию \(NO\) , она пересечет сторону \(AD\) в точке \(M\) . Докажем, что \(M\) является серединой \(AD\) .
\(\треугольник BNO\sim \треугольник DMO\) на два угла (\(\угол OBN=\угол ODM\) лежащие при \(BC\параллели AD\) и \(BD\) секущей; \(\ угол BON=\угол DOM\) как вертикальный). Означает: \[\dfrac(BN)(MD)=\dfrac(ON)(OM)\]
Аналогично \(\треугольник CON\sim \треугольник AOM\). Означает: \[\dfrac(CN)(MA)=\dfrac(ON)(OM)\]
Отсюда \(\dfrac(BN)(MD)=\dfrac(CN)(MA)\). Но \(BN=CN\) , следовательно, \(AM=MD\) .
\[(\Большой(\текст(Равнобедренная трапеция)))\]
Определения
Трапеция называется прямоугольной, если один из ее углов прямой.
Трапеция называется равнобедренной, если ее стороны равны.
Теоремы: свойства равнобедренной трапеции
1) У равнобедренной трапеции углы при основании равны.
2) Диагонали равнобедренной трапеции равны.
3) Два треугольника, образованные диагоналями и основанием, равнобедренные.
Доказательство
1) Рассмотрим равнобедренную трапецию \(ABCD\) .
Из вершин \(B\) и \(C\) опустим на сторону \(AD\) перпендикуляры \(BM\) и \(CN\) соответственно. Так как \(BM\perp AD\) и \(CN\perp AD\) , то \(BM\parallel CN\) ; \(AD\parallel BC\) , тогда \(MBCN\) является параллелограммом, следовательно, \(BM = CN\) .
Рассмотрим прямоугольные треугольники\(ABM\) и \(CDN\) . Поскольку у них равные гипотенузы и катет \(BM\) равен катету \(CN\) , эти треугольники конгруэнтны, следовательно, \(\угол DAB = \угол CDA\) .
2)
Так как \(AB=CD, \угол A=\угол D, AD\) — общее, то по первому признаку. Следовательно, \(AC=BD\) .
3) Поскольку \(\треугольник ABD=\треугольник ACD\), то \(\угол BDA=\угол CAD\) . Следовательно, треугольник \(\треугольник AOD\) равнобедренный. Аналогично доказывается, что \(\треугольник BOC\) равнобедренный.
Теоремы: признаки равнобедренной трапеции
1) Если углы при основании трапеции равны, то она равнобедренная.
2) Если диагонали трапеции равны, то она равнобедренная.
Доказательство
Рассмотрим трапецию \(ABCD\) такую, что \(\угол A = \угол D\) .
Достроим трапецию до треугольника \(AED\), как показано на рисунке. Так как \(\угол 1 = \угол 2\) , то треугольник \(AED\) равнобедренный и \(AE = ED\) . Углы \(1\) и \(3\) равны, так как соответствуют параллельным прямым \(AD\) и \(BC\) и секущей \(AB\) . Точно так же углы \(2\) и \(4\) равны, но \(\угол 1 = \угол 2\) , тогда \(\угол 3 = \угол 1 = \угол 2 = \угол 4\ ), поэтому треугольник \(BEC\) также равнобедренный и \(BE = EC\) .
В конце концов \(AB = AE — BE = DE — CE = CD\), т.е. \(AB = CD\) , что и требовалось доказать.
2) Пусть \(AC=BD\) . Так как \(\треугольник AOD\sim \треугольник BOC\), то мы обозначаем их коэффициент подобия через \(k\) . Тогда если \(BO=x\) , то \(OD=kx\) . Подобно \(CO=y \Rightarrow AO=ky\) .
Тогда если \(BO=x\) , то \(OD=kx\) . Подобно \(CO=y \Rightarrow AO=ky\) .
Поскольку \(AC=BD\) , тогда \(x+kx=y+ky \Rightarrow x=y\) . Итак, \(\треугольник AOD\) равнобедренный и \(\угол OAD=\угол ODA\) .
Таким образом, по первому признаку \(\треугольник ABD=\треугольник ACD\) (\(AC=BD, \угол OAD=\угол ODA, AD\)- общий). Итак, \(AB=CD\) , поэтому.
В этой статье мы постараемся максимально полно отразить свойства трапеции. В частности, речь пойдет об общих признаках и свойствах трапеции, а также о свойствах вписанной трапеции и о окружности, вписанной в трапецию. Затронем также свойства равнобедренной и прямоугольной трапеции.
Пример решения задачи с использованием рассмотренных свойств поможет вам разобраться в голове и лучше запомнить материал.
Трапеция и все-все-все
Для начала кратко вспомним, что такое трапеция и какие еще понятия с ней связаны.
Итак, трапеция – это четырехугольник, две стороны которого параллельны друг другу (это основания). А две не параллельны — это стороны.
А две не параллельны — это стороны.
В трапеции высоту можно не указывать — перпендикулярно основаниям. Проводятся средняя линия и диагонали. А также из любого угла трапеции можно провести биссектрису.
Про различные свойства, связанные со всеми этими элементами и их комбинациями, мы сейчас и поговорим.
Свойства диагоналей трапеции
Чтобы было понятнее, при чтении нарисуйте трапецию ACME на листе бумаги и проведите в ней диагонали.
- Если найти середины каждой из диагоналей (назовем эти точки X и T) и соединить их, получится отрезок. Одно из свойств диагоналей трапеции состоит в том, что отрезок XT лежит на средней линии. А его длину можно получить, разделив разность оснований на два: ХТ = (а — б) / 2 .
- Перед нами та самая трапеция ACME. Диагонали пересекаются в точке O. Рассмотрим треугольники AOE и IOC, образованные отрезками диагоналей вместе с основаниями трапеции. Эти треугольники подобны. Коэффициент подобия k треугольников выражается через отношение оснований трапеции: k = AE/KM.

Отношение площадей треугольников AOE и IOC описывается коэффициентом k 2 . - Все та же трапеция, те же диагонали, пересекающиеся в точке О. Только на этот раз мы будем рассматривать треугольники, которые диагональные отрезки образовали вместе со сторонами трапеции. Площади треугольников АКО и ЭМО равны — их площади одинаковы.
- Еще одним свойством трапеции является построение диагоналей. Итак, если мы продолжим стороны АК и МЕ в сторону меньшего основания, то рано или поздно они пересекутся в какой-то точке. Далее проведите прямую линию через середины оснований трапеции. Он пересекает основания в точках X и T.
Если теперь продолжить линию XT, то она соединит точку пересечения диагоналей трапеции O, точку, в которой пересекаются продолжения сторон и середины оснований X и T. - Через точку пересечения диагоналей проводим отрезок, который соединит основания трапеции (Т лежит на меньшем основании КМ, Х — на большем АЕ). Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОН = КМ/АЭ .

- А теперь через точку пересечения диагоналей проводим отрезок, параллельный основаниям трапеции (а и б). Точка пересечения разделит его на две равные части. Длину отрезка можно найти по формуле 2ab/(a + b) .
Свойства средней линии трапеции
Проведите среднюю линию трапеции параллельно ее основаниям.
- Длину средней линии трапеции можно вычислить, сложив длины оснований и разделив их пополам: м = (а + b)/2 .
- Если провести любой отрезок (высоту, например) через оба основания трапеции, то средняя линия разделит ее на две равные части.
Свойство биссектрисы трапеции
Выберите любой угол трапеции и проведите биссектрису. Возьмем, к примеру, угол КАЕ нашей трапеции АСМЕ. Выполнив построение самостоятельно, вы легко увидите, что биссектриса отсекает от основания (или его продолжения на прямой вне самой фигуры) отрезок такой же длины, как и сторона.
Свойства угла трапеции
- Какой бы из двух пар углов, примыкающих к стороне, вы ни выбрали, сумма углов в паре всегда равна 180 0 : α + β = 180 0 и γ + δ = 180 0 .

- Соедините середины оснований трапеции отрезком ТХ. Теперь посмотрим на углы при основаниях трапеции. Если сумма углов для любого из них равна 90 0 , длину отрезка ТХ легко вычислить по разнице длин оснований, деленной пополам: ТХ = (АЭ — КМ) / 2 .
- Если провести параллельные линии через стороны угла трапеции, то они разделят стороны угла на пропорциональные отрезки.
Свойства равнобедренной (равнобедренной) трапеции
- У равнобедренной трапеции углы при любом основании равны.
- Теперь снова постройте трапецию, чтобы легче было представить, о чем она. Посмотрите внимательно на основание АЕ — вершина противоположного основания М проецируется в некоторую точку на прямой, содержащей АЕ. Расстояние от вершины А до точки проекции вершины М и средней линии равнобедренной трапеции равно.
- Несколько слов о свойстве диагоналей равнобедренной трапеции — их длины равны. А также углы наклона этих диагоналей к основанию трапеции одинаковы.

- Только вблизи равнобедренной трапеции можно описать окружность, так как обязательным условием для этого является сумма противоположных углов четырехугольника 180 0 .
- Свойство равнобедренной трапеции следует из предыдущего абзаца — если вокруг трапеции можно описать окружность, то она равнобедренная.
- Из особенностей равнобедренной трапеции следует свойство высоты трапеции: если ее диагонали пересекаются под прямым углом, то длина высоты равна половине суммы оснований: h = (a + б)/2 .
- Снова проведите линию ТХ через середины оснований трапеции — в равнобедренной трапеции она перпендикулярна основаниям. И в то же время ТХ является осью симметрии равнобедренной трапеции.
- На этот раз опустите к большему основанию (назовем его а) высоту от противоположной вершины трапеции. Вы получите два разреза. Длину одного можно найти, если сложить длины оснований и разделить пополам: (а+б)/2 . Второе мы получим, если из большего основания вычтем меньшее и разделим полученную разницу на два: (a – b)/2 .

Свойства трапеции, вписанной в окружность
Поскольку речь уже идет о трапеции, вписанной в окружность, остановимся на этом вопросе подробнее. В частности, где находится центр окружности по отношению к трапеции. Здесь тоже рекомендуется не полениться взять в руки карандаш и нарисовать то, о чем пойдет речь ниже. Так вы быстрее поймете и лучше запомните.
- Расположение центра окружности определяется углом наклона диагонали трапеции к ее стороне. Например, диагональ может выходить из вершины трапеции под прямым углом к стороне. В этом случае большее основание пересекает центр описанной окружности ровно посередине (R = ½AE).
- Диагональ и сторона могут сходиться под острым углом, тогда центр окружности находится внутри трапеции.
- Центр описанной окружности может находиться вне трапеции, за ее большим основанием, если между диагональю трапеции и боковой стороной имеется тупой угол.
- Угол, образованный диагональю и большим основанием трапеции ACME (вписанный угол), равен половине соответствующего ей центрального угла: MAE = ½MY .

- Кратко о двух способах нахождения радиуса описанной окружности. Способ первый: внимательно посмотрите на свой рисунок — что вы видите? Вы легко заметите, что диагональ разбивает трапецию на два треугольника. Радиус можно найти через отношение стороны треугольника к синусу противоположного угла, умноженное на два. Например, R = АЕ/2 * sinAME . Аналогично формулу можно записать для любой из сторон обоих треугольников.
- Способ второй: находим радиус описанной окружности через площадь треугольника, образованного диагональю, стороной и основанием трапеции: R = AM * ME * AE / 4 * S AME .
Свойства трапеции, описанной около окружности
В трапецию можно вписать окружность, если выполняется одно условие. Подробнее об этом ниже. А вместе это сочетание фигур имеет ряд интересных свойств.
- Если в трапецию вписана окружность, то длину ее средней линии легко найти, сложив длины сторон и разделив полученную сумму пополам: м = (с + d)/2 .

- Для трапеции ACME, описанной около окружности, сумма длин оснований равна сумме длин сторон: AK + ME = KM + AE .
- Из этого свойства оснований трапеции следует обратное утверждение: в ту трапецию, сумма оснований которой равна сумме сторон, можно вписать окружность.
- Точка касания окружности радиуса r, вписанной в трапецию, делит боковую сторону на два отрезка, назовем их a и b. Радиус окружности можно рассчитать по формуле: r = √ab .
- И еще одно свойство. Чтобы не запутаться, нарисуйте этот пример сами. У нас есть старая добрая трапеция ACME, описанная вокруг окружности. В нем проведены диагонали, пересекающиеся в точке О. Треугольники АОК и ЕОМ, образованные отрезками диагоналей и сторон, прямоугольные.
Высоты этих треугольников, опущенные на гипотенузы (т. е. стороны трапеции), совпадают с радиусами вписанной окружности. А высота трапеции равна диаметру вписанной окружности.
Свойства прямоугольной трапеции
Прямоугольной называется трапеция, один из углов которой прямой.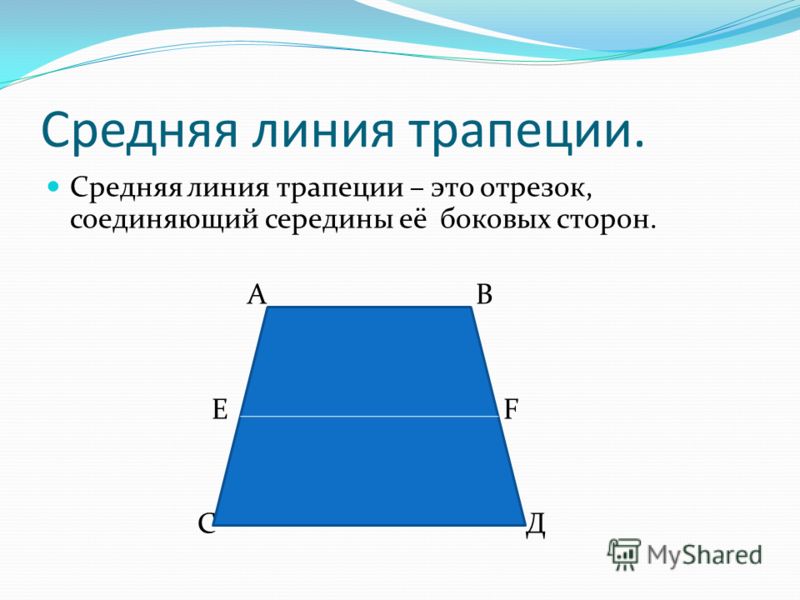 И его свойства вытекают из этого обстоятельства.
И его свойства вытекают из этого обстоятельства.
- У прямоугольной трапеции одна сторона перпендикулярна основаниям.
- Высота и сторона трапеции, примыкающие к прямому углу, равны. Это позволяет вычислить площадь прямоугольной трапеции (общая формула S = (a + b) * h/2 ) не только через высоту, но и через сторону, примыкающую к прямому углу.
- Для прямоугольной трапеции актуальны уже описанные выше общие свойства диагоналей трапеции.
Доказательства некоторых свойств трапеции
Равенство углов при основании равнобедренной трапеции:
- Вы наверное уже догадались, что здесь нам снова понадобится трапеция ACME — нарисуйте равнобедренную трапецию. Из вершины M проведите прямую MT, параллельную стороне AK (MT || AK).
Получившийся четырехугольник АКМТ является параллелограммом (АК || МТ, КМ || АТ). Поскольку ME = KA = MT, ∆ MTE равнобедренный и MET = MTE.
АК || МТ, следовательно, МТЭ = КАЭ, МЭТ = МТЭ = КАЭ.
Где АКМ = 180 0 — МЕТ = 180 0 — КАЭ = КМЭ.
К.Э.Д.
Теперь, основываясь на свойстве равнобедренной трапеции (равенстве диагоналей), докажем, что трапеция ACME равнобедренная :
- Для начала проведем прямую МХ – МХ || КЭ. Получаем параллелограмм КМНЕ (основание — МХ || КЕ и КМ || ЕХ).
∆AMH равнобедренный, так как AM = KE = MX и MAX = MEA.
МХ || KE, KEA = MXE, следовательно, MAE = MXE.
Оказалось, что треугольники АКЕ и ЕМА равны между собой, так как АМ = КЕ и АЕ — общая сторона двух треугольников. А также MAE=MXE. Можно заключить, что AK = ME, а значит, трапеция AKME равнобедренная.
Задача для повторения
Основания трапеции АСМЕ равны 9 см и 21 см, сторона КА, равная 8 см, образует с меньшим основанием угол 150 0 . Вам нужно найти площадь трапеции.
Решение: Из вершины К опускаем высоту к большему основанию трапеции. И начнем смотреть на углы трапеции.
Углы АЕМ и КАН односторонние.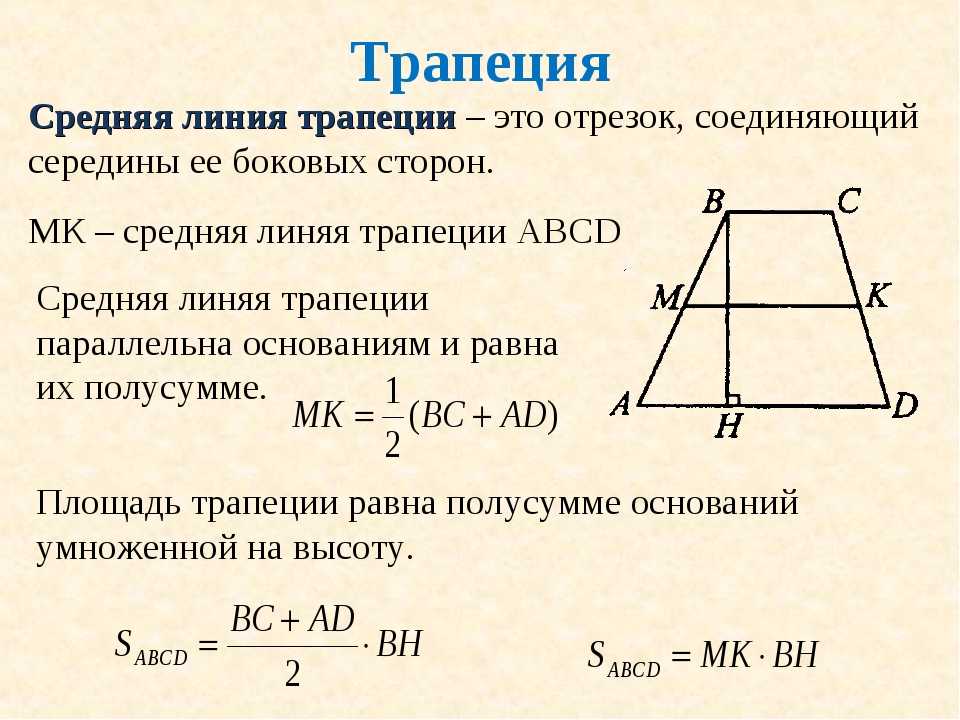 Значит, в сумме они составляют 1800. Следовательно, КАН = 30 0 (исходя из свойства углов трапеции).
Значит, в сумме они составляют 1800. Следовательно, КАН = 30 0 (исходя из свойства углов трапеции).
Рассмотрим теперь прямоугольный ∆ANK (я думаю, что это очевидно для читателей без дополнительных доказательств). Из него находим высоту трапеции КН — в треугольнике это катет, который лежит напротив угла 30 0 . Следовательно, КН = ½АВ = 4 см.
Площадь трапеции находится по формуле: S АКМЭ = (КМ + АЭ) * КН / 2 = (9 + 21) * 4/2 = 60 см 2 .
Послесловие
Если вы внимательно и вдумчиво изучили эту статью, не поленились нарисовать карандашом в руках трапеции всех вышеперечисленных свойств и разобрать их на практике, вы должны были хорошо усвоить материал.
Конечно, информации здесь много, разнообразной и местами даже запутанной: не так уж сложно спутать свойства описываемой трапеции со свойствами вписанной. Но вы сами видели, что разница огромна.
Теперь у вас есть подробная сводка всех общих свойств трапеции. А также специфические свойства и особенности равнобедренных и прямоугольных трапеций. Очень удобно использовать для подготовки к зачетам и экзаменам. Попробуйте сами и поделитесь ссылкой с друзьями!
Очень удобно использовать для подготовки к зачетам и экзаменам. Попробуйте сами и поделитесь ссылкой с друзьями!
блог.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Введение, формула, свойства, решенные примеры и часто задаваемые вопросы
Математические формы трапеций
Изучая двухмерные фигуры, мы столкнемся с формой трапеции или трапеции. Итак, давайте узнаем, что такое трапеция.
Четырехсторонняя двумерная фигура, одна из противоположных сторон которой параллельна, а две другие стороны не параллельны, называется трапецией. Противоположные стороны называются основаниями, непараллельные стороны называются катетами трапеции, а перпендикулярное расстояние между двумя параллельными сторонами называется высотой или высотой трапеции.
Трапеции Определение
Четырехугольник, одна сторона которого параллельна, а две другие стороны не параллельны, называется трапецией. Трапецию также называют трапецией.
Трапецию также называют трапецией.
Трапециевидные формы
После того, как мы поняли, что такое трапеция, теперь давайте посмотрим на трапециевидные формы. Математика форм трапеций поможет вам идентифицировать различные формы трапеций. Согласно определению трапеции, трапеция — это четырехсторонняя фигура с двумя параллельными сторонами и двумя непараллельными сторонами. Существуют разные формы трапеций или, по их форме, можно сказать, что трапеции бывают разных типов.
Различные формы трапеций Математика
Давайте сначала посмотрим на различные свойства трапеций и различных типов трапеций. Свойства трапеции помогут вам построить трапецию.
Свойства трапеции
Вот некоторые из основных свойств трапеции:
Основания параллельны друг другу.
Нижний базовый угол и верхний базовый угол образуют линейную пару, т.
 е. 1800.
е. 1800.Медиана параллельна обоим основаниям. А длина медианы — это среднее длин двух оснований, т. е. m = a+b/2
В трапеции, если обе пары ее противоположных сторон параллельны, это будет параллелограмм.
В трапеции, если обе пары ее противоположных сторон параллельны и все ее стороны имеют одинаковую длину и расположены под прямым углом друг к другу, то это квадрат
В трапеции, если обе пары ее противоположные стороны параллельны; его противоположные стороны имеют одинаковую длину и расположены под прямым углом друг к другу, то это прямоугольник.
Типы трапеций:
Различные типы трапеций:
Прямоугольные трапеции
Трапеция, имеющая пару прямых углов, называется прямой трапецией.
Равнобедренные трапеции
В данной трапеции, если непараллельные стороны или катеты трапеции равны по длине, она называется равнобедренной трапецией.
Разносторонние трапеции
В данной трапеции, если ни стороны, ни углы трапеции не равны, мы называем ее разносторонней трапецией.
Площадь трапеции
Площадь трапеции вычисляется путем умножения среднего значения оснований на высоту трапеции.
Площадь трапеции = (a + b/2) x h, где a и b — два основания, а h — высота трапеции.
Площадь трапеции = ½ (a+ b) h Если a, b, c и d — все четыре стороны трапеции, то формула периметра имеет вид:0003 Perimeter of trapezoid = a + b + c + d
Median of a Trapezoid The median is a отрезок, проведенный из середины непараллельной стороны так, чтобы он был параллелен обоим основаниям. Длина медианы рассчитывается как среднее длин двух оснований: м = a+b/2, где a и b площади основания 92} \] Решенные примеры Пример 1. Дана трапеция с основаниями 6 м, 10 м и высотой 5 м. Найдите площадь трапеции. Решение: имеем a = 6см, b = 10м и h = 5м 5 = 8 x 5 = 40 м2 Пример 2. Если основания трапеции равны 5 см, 8 см, 4 см и 6 см. Найдите периметр трапеции. Решение: имеем a = 5 см, b = 8 см, c = 4 см и d = 6 см, тогда По формуле периметра имеем Периметр трапеции = a + b + c+ d = 5 + 8 + 4 + 6 = 23 см Викторина Время
|

 12.18
12.18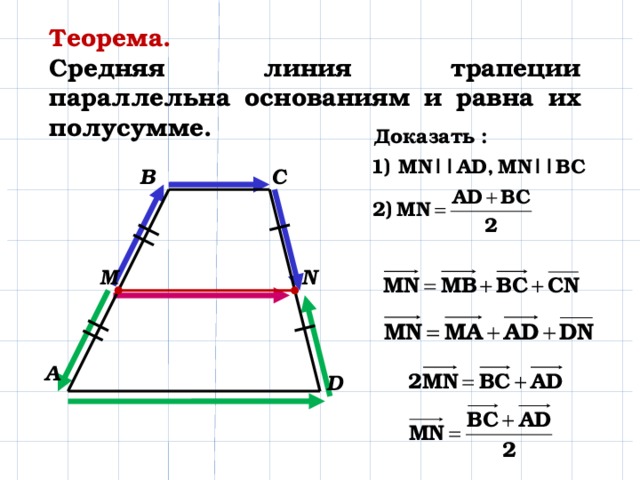
 д.
д.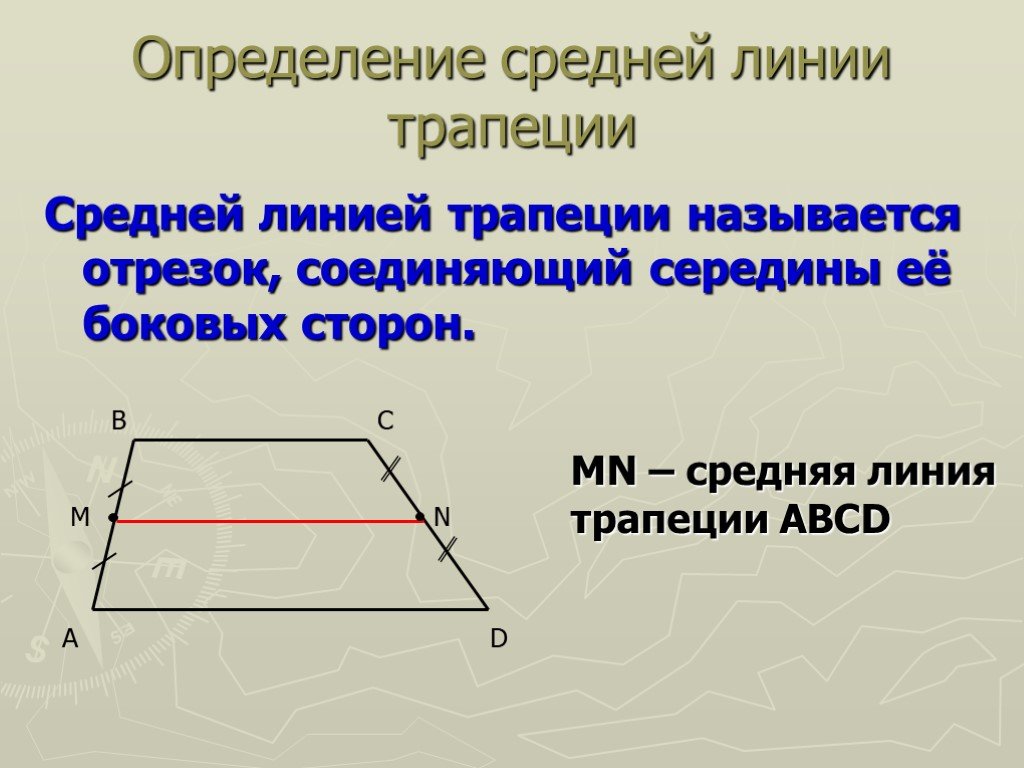 Мы также можем раскрывать информацию о вас, если решим, что такое раскрытие необходимо или уместно в целях безопасности, правоохранительных органов или по другим причинам, представляющим общественный интерес.
Мы также можем раскрывать информацию о вас, если решим, что такое раскрытие необходимо или уместно в целях безопасности, правоохранительных органов или по другим причинам, представляющим общественный интерес.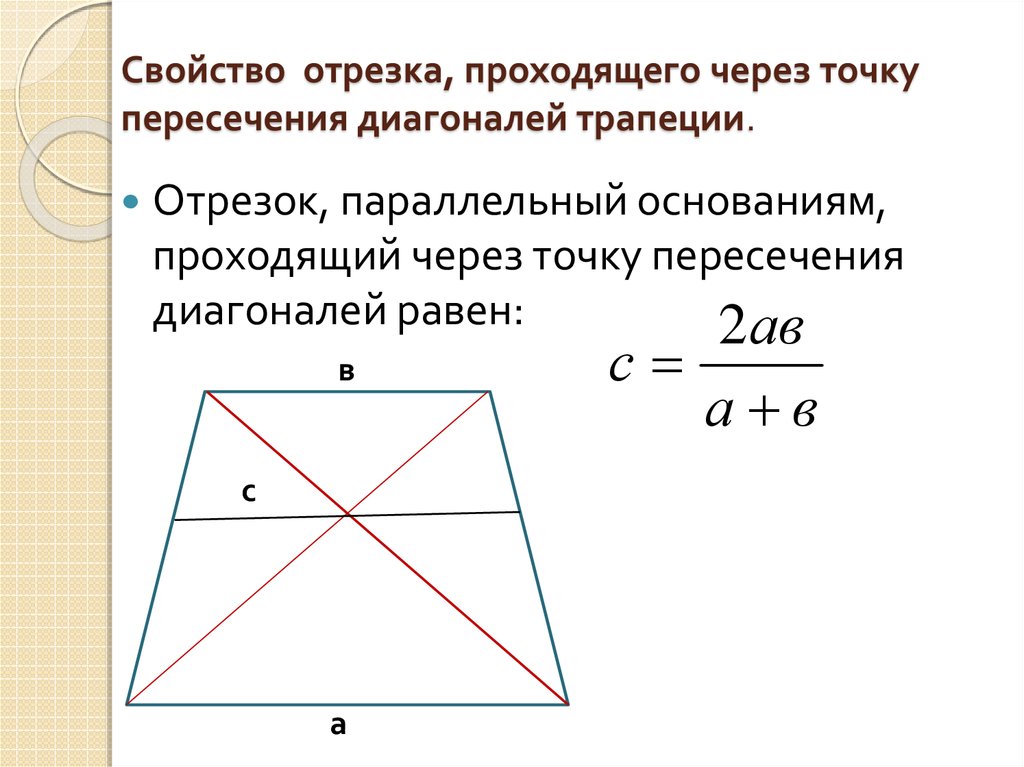



 е. 1800.
е. 1800.
