2+n-72)=1/(n+9)НОУ ИНТУИТ | Лекция | Комплексные корни n-й степени из единицы и решение уравнений
< Лекция 5 || Лекция 6: 123 || Лекция 7 >
Аннотация: В данной лекции рассматриваются комплексные корни n-й степени из единицы. Приведены формулы для решения уравнений третьей и четвертой степеней, доказан ряд теорем. Рассмотрен ряд характерных задач, а также приведены задачи для самостоятельного рассмотрения
Ключевые слова: Окружность, доказательство, группа, первообразная, пункт, ПО, дискриминант кубического многочлена, действительный, радиус, значение функции, функция, композиция, минимум, многочлен, многочлен неприводимый, поле, определение, умножение, кратность
Комплексные корни n-й степени из единицы
Так как , r=1, , то формула для корней n -й степени из 1 принимает вид
Точки wk являются вершинами правильного n -угольника, вписанного в окружность единичного радиуса с центром в начале координат, при этом одной из вершин этого многоугольника является 1.
Например, при n=8
Теорема 2.9.1. Совокупность всех n корней n -й степени из 1 с операцией умножения является коммутативной группой (подгруппой в ).
Доказательство.
- Если , т. е. wn=1, zn=1, то , поэтому . Таким образом, на Tn определена операция умножения (очевидно, коммутативная и ассоциативная).
- Ясно, что 1n=1, т. е. , и 1 — нейтральный элемент в Tn.
- Если , то wn=1, и поэтому .
Замечание 2.9.2. Группа Tn является циклической, т. е. все ее элементы являются степенями одного элемента, называемого циклическим образующим (в качестве одного из циклических образующих можно взять , так как wk=(w1)k для , т.
е. все элементы wk группы Tn являются степенями корня w1, такие корни называются первообразными). Покажите, что является первообразным корнем тогда и только тогда, когда наибольший общий делитель чисел k и n равен 1.
Упражнение 2.9.3. Доказать, что сумма всех k -х степеней корней уравнения xn=1 равна
n, если k делится на n ;
0, если k не делится на n.
Задача 2.9.4. Если , то |z|=1, но z не является корнем из единицы (т. е. для любого ).
Задача 2.9.5. Доказать, что
а) ;
б) .
Указание. Пусть
(все корни степени 2n из 1 ).
(так как xn=-1, x2n=1 ). Но , поэтому
Следовательно,
Полагая x=1, имеем
Пункт б) доказывается аналогично.
Дальше >>
< Лекция 5 || Лекция 6: 123 || Лекция 7 >
3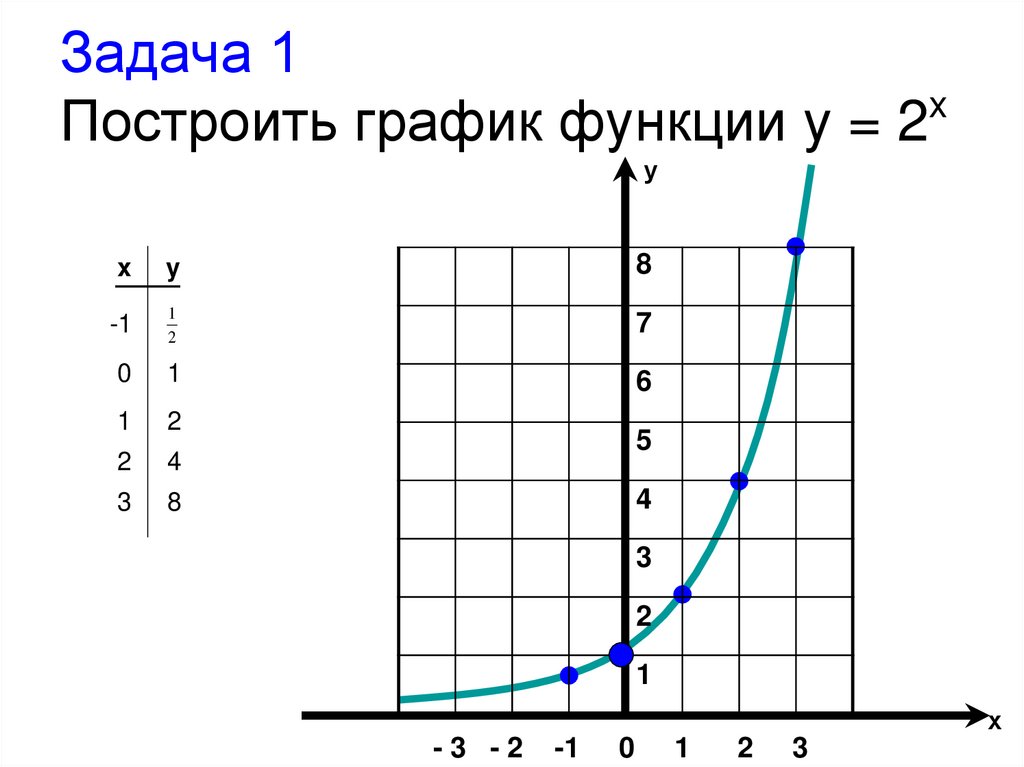
Микро 100 RSC-187-1X | Угол 60 градусов 3/16″ Хвостовик x 2″ OAL Наконечник Твердосплавный односторонний гравировальный инструмент с покрытием AlTiN
Микро 100
28,95 долларов США
Текущий запас:
Количество:
- Марка:
- Микро 100
- Форма точки:
- Предупрежден
- Угол точки:
- 60 градусов
- Диаметр хвостовика (дюйм):
- 3/16 дюйма
- Диаметр хвостовика (десятичные дюймы):
- 0,1875″
- Общая длина (дюймы):
- 2 дюйма
- Общая длина (десятичный дюйм):
- 2,00″
- Отделка/покрытие:
- Алтин
- Материал:
- Карбид
- Односторонний или двусторонний:
- Одноместный
- Корабли:
- Из партнерского объекта
- Снято с производства:
- Артикул:
- 25131074
- СКП:
- Вес:
- 0,01 фунта
- Доставка:
- Расчет на кассе
- Функции
- Отзывы
Спецификации продукта
| Накрытие | ALTIN |
| Диаметр хвостовика (дюйм) | 3/16 « |
