Степень рассчитать: Как посчитать степень — онлайн калькулятор

Содержание

Расчет коэффициента задолженности — формула по балансу

Коэффициент задолженности — формула по балансу этого аналитического показателя содержит особый набор компонентов. О разновидностях данного коэффициента и структуре используемых при их расчете балансовых показателей пойдет речь в нашем материале.

Формула для расчета коэффициента задолженности

Коэффициент задолженности (К_З) — один из расчетных показателей, используемых при анализе финансового состояния компании. Он отражает долю активов, сформированных в результате привлечения долгового финансирования, и рассчитывается по формуле:

К_З= (КЗ + ДЗ) / А,

где:

(КЗ + ДЗ) — общая сумма задолженности фирмы;

А — суммарные активы.

Формула расчета К_З, представленная через строки баланса, имеет следующий вид:

К_З= (стр. 1400 + стр. 1500) / стр. 1600.

С детализацией балансовых строк знакомьтесь с помощью статьи «Расшифровка строк бухгалтерского баланса (1230 и др. )».

Нормальным считается следующий диапазон значений К_З:

0 ≤ К_З≤ 0,5.

Если К_З близок к нулю, это свидетельствует о наличии у компании крайне незначительных долговых обязательств в сравнении с ее собственным капиталом. Это один из показателей финансовой устойчивости.

Приближение коэффициента к 1 указывает на то, что практически весь собственный капитал сформирован за счет заемных средств. В большинстве случае такое значение К_З показывает высокую степень зависимости от контрагентов и кредиторов, что может негативно повлиять на финансовую устойчивость компании при неблагоприятном развитии событий.

Регулярный расчет К_З позволяет своевременно отследить негативные тенденции в финансовой ситуации предприятия и принять меры по их устранению.

Как анализируется финансовая устойчивость компании? узнайте из материала «Проведение анализа коэффициентов финансовой устойчивости».

Базовые понятия и порядок расчета коэффициентов для проведения финансового анализа хозяйственной деятельности предприятия можно найти в КонсультантПлюс. Чтобы все сделать правильно, получите пробный доступ к системе и переходите в Типовую ситуацию.

Разновидности коэффициентов задолженности (текущей, краткосрочной и др.)

Коэффициент задолженности, рассмотренный в предыдущем разделе, имеет значение при оценке общего финансового состояния компании, поскольку при его расчете используется общий (суммарный) показатель долгов. Для более детализированного анализа требуется расчет дополнительных коэффициентов задолженности, например:

Коэффициент текущей задолженности (К_ТЗ)

К_ТЗпоказывает долю краткосрочной задолженности в общей сумме капитала и рассчитывается по формуле:

К_ТЗ= ТЗ / ВБ,

где:

ТЗ — суммарная величина текущей задолженности;

ВБ — валюта баланса.

Коэффициент краткосрочной задолженности (К_КЗ)

К_КЗотражает долю долгов компании со сроком погашения менее 12 месяцев в общей структуре задолженности:

КЗ = КЗ / (КЗ + ДЗ),

где:

КЗ — объем краткосрочной задолженности;

(КЗ + ДЗ) — сумма краткосрочных и долгосрочных долгов компании.

Коэффициент финансового левериджа (К_ФЛ)

К_ФЛ демонстрирует степень зависимости компании от внешних источников заимствования и рассчитывается (как и вышеуказанные коэффициенты) по показателям, отражаемым в балансе:

К_ФЛ= ЗК / СК,

где:

ЗК — заемный капитал;

СК — собственный капитал.

Методику расчета показателя СК см. в материале «Собственный капитал в балансе — это…»

При проведении финансового анализа коэффициенты финансовой задолженности применяются вместе с другими коэффициентами, что значительно расширяет возможности анализа и позволяет оценивать финансовое состояние компании с различных позиций.

Знакомьтесь с алгоритмами расчета разнообразных коэффициентов с помощью размещенных на нашем сайте материалов:

«Основные финансовые коэффициенты и формулы их расчета»;
«Нормативный коэффициент эффективности капитальных вложений».

Итоги

Коэффициент задолженности показывает долю активов, сформированных в результате привлечения долгового финансирования. Данный коэффициент отражает степень финансовой устойчивости компании, а нормативное его значение находится в диапазоне от 0 до 0,5.

Степень огнестойкости зданий и сооружений – таблица

Уровень огнестойкости относится к самым главным параметрам, влияющим на пожаробезопасность зданий и сооружений. Проектирование новых строительных объектов обязательно должно учитывать весь комплекс мероприятий по эвакуации людей при возникновении пожара. Высокая степень огнестойкости объектов продлевает наступление критического момента после возгорания, когда еще сохраняется физическая возможность для людей покинуть здание с минимальными последствиями для здоровья.

Уровень стойкости к огню определяется назначением объекта и четко регламентируется нормативами. Если строение не соответствует нормативам по степени огнестойкости, то ввод объекта в эксплуатацию невозможен, так как безопасность людей не может быть обеспечена.

Мы готовы помочь обеспечить четкое соответствие нормам пожарной безопасности любых объектов.

Определение степени огнестойкости

Степень огнестойкости строительных объектов и их класс пожарной опасности оценивается при проектировании системы противопожарных мероприятий, как этого требуют статьи 13 и 14 ФЗ-123, которые необходимо жестко выполнить архитектору и конструктору при проектировании и реконструкции сооружений.

Огнестойкость характеризуется временем сопротивления здания или сооружения к воздействию огня. Ее рассчитывают, применяя ст. 30 ФЗ 123. Пожароопасность для каждого объекта определяют с учетом пожароопасности строительных материалов, применяемых при его строительстве.

Степень огнестойкости и класс пожароопасности дает возможность оценить скорость распространения огня по объекту во время пожара.

Предел стойкости зданий определяется временем, в пределах которого пожар воздействует на объект до его полного разрушения.

Огнестойкость строительных объектов

Каждый строящийся объект должен соответствовать требованиям пожаробезопасности с учетом его назначения и применяемых материалов. Степень огнестойкости сооружений определяется в соответствии с Федеральным Законом ФЗ-123 — ст 30:

здания определяется огнестойкостью его строительных конструкций (І, ІІ, ІІІ, ІV, V).

Показателем огнестойкости является предел огнестойкости конструкции, который в соответствии с ГОСТ 30247 устанавливается в минутах до наступления одного из предельных состояний:

R — потеря несущей способности;
E — потеря целостности;
I — потеря теплоизолирующей способности.

Класс конструктивной пожарной опасности здания определяется степенью участия строительных конструкций в развитии пожара и образовании его опасных факторов (С0, С1, С2, С3).

Класс конструктивной опасности С устанавливается в зависимости от этажности , площади отсеков, функциональной опасности.

Класс функциональной пожарной опасности здания и его частей определяется их назначением (Ф1, Ф2, Ф3, Ф4, Ф5).

Класс пожарной опасности строительных конструкций К0, К1 К2 К3 должен соответствовать принятому классу конструктивной опасности зданий:

КО — непожароопасные;
К1— малопожароопасные;
К2 — умеренно пожароопасные;
К3— пожароопасные.

Если показатель огнестойкости и класса пожароопасности вновь проектируемого объекта строительства ниже требуемого, необходимо выполнить комплекс мер по улучшению огнестойкости, чтобы была возможность оперативно эвакуировать людей из сооружения и сделать несущие балки максимально устойчивыми к огню. т.е выполнить их защиту от огня. Эти меры должны выполняться с применением сертифицированных материалов, одними из которых являются производимые нами материалы для огнезащиты ФЕРУМ.

Как влияют технологии на огнестойкость сооружений

Анализ строительной документации дает возможность изучить наличие (отсутствие) технологий, повышающих огнестойкость строительных конструкций. Сначала нужно осмотреть визуально все конструкции здания. Потом изучить все внутренние помещения, лестницы, подсобки и т.д.

Часто для снижения расходов недальновидные заказчики для лестниц и подсобок применяют самые дешевые материалы с низким уровнем огнестойкости. Поэтому при пожаре огонь распространяется по этим самым слабым участкам конструкции. Все это надо обязательно изучать и учитывать при разработке методов огнезащиты и расчетах огнестойкости.

5 степеней огнестойкости

Всего имеется пять степеней огнестойкости. У каждой из них есть свои особенности и свой критический предел.

Первая степень

К ней относятся самые стойкие к огню конструкции — здания и сооружения с применением железобетона, камня, огнеупорных плит и листовых материалов. У них самая высокая стойкость к воздействию огня и высокой температуры.

Вторая степень

Фактически первая степень огнестойкости, но с небольшими отличиями, слегка менее жесткие требования. Сооружения для этой категории могут строиться с применением стальных конструкций.

Третья степень

Существует три подвида огнестойкости в 3-й категории:

Третья. Сооружения с бетонными, железобетонными, каменными несущими конструкциями, в которых применяются ограждения с деревянными перекрытиями. Для огнестойкого покрытия применяют трудногорючие плиты и листовые материалы, штукатурку.

Третья «а». Каркасные здания, при строительстве которых используется незащищенная сталь. Ограждения делают из профилированного стального листа. Другие материалы тоже не боятся огня.

Третья «б». Одноэтажные деревянные каркасные конструкции, обработанные огнезащитным составом. Панельные ограждения также изготовлены из дерева, предварительно пропитанного составами.

Четвертая степень

Включает два разных норматива по огнестойкости:

Четвертая. Сооружения с несущими конструкциями и ограждениями из легко воспламеняемых материалов, например, древесины. Защита от высоких температур обеспечивается покрытием из плитки или штукатурки. К перекрытиям нет высоких требований по огнестойкости. Чердак из дерева обязательно обрабатывают огнезащитными спецсоставами.

Четвертая «а». Одноуровневые здания с каркасной схемой. Каркас — стальной, а ограждения делают из профильных листов с утеплителем из горючего материала.

Пятая степень

Самый низкий порог к огнестойкости и скорости распространения огня. Такие сооружения не предполагают постоянного наличия людей, они не предназначены для хранения горючих и взрывоопасных материалов и для использования в них электроприборов.

Надежные огнезащитные материалы от производителя. Приглашаем к сотрудничеству. Партнерские программы для коллег

Предел огнестойкости строительных конструкций
Степень огнестойкости зданий, сооружений, строений и пожарных отсеков	Несущие стены, колонны и другие несущие элементы	Наружные ненесущие стены	Перекрытия междуэтажные (в том числе чердачные и над подвалами)	Строительные конструкции бесчердачных покрытий		Строительные конструкции лестничных клеток
	Несущие стены, колонны и другие несущие элементы	Наружные ненесущие стены		настилы (в том числе с утеплителем)	фермы, балки, прогоны	внутренние стены	марши и площадки лестниц
I	R 120	E 30	REI 60	RE 30	R 30	REI 120	R 60
II	R 90	E 15	REI 45	RE 15	R 15	REI 90	R 60
III	R 45	E 15	REI 45	RE 15	R 15	REI 60	R 45
IV	R 15	E 15	REI 15	RE 15	R 15	REI 45	R 15
V	не нормируется	не нормируется	не нормируется	не нормируется	не нормируется	не нормируется	не нормируется

Индекс оксигенации.

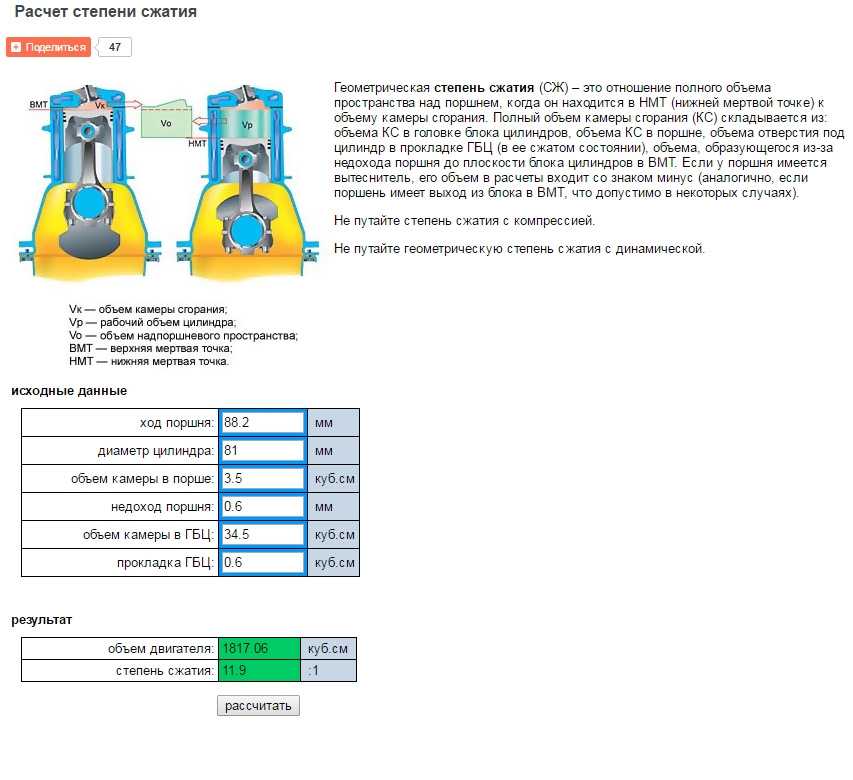Калькулятор. PaO2/FiO2 в интенсивной терапии.

Индекс оксигенации (oxygenation index, OI; PF ratio – PF соотношение; респираторный индекс, PaO₂ / FiO₂) — это параметр, используемый в анестезиологии-реаниматологии и интенсивной терапии для оценки функции обмена кислорода в легких. Расчет индекса оксигенации производят по формуле, как соотношение PaO₂ / FiO₂ (отношение парциального напряжения кислорода в артериальной крови к фракции кислорода на вдохе). Данный критерий относится к международным шкалам, которые ежедневно используются в рутинной практике анестезиолога. Индекс оксигенации является одним из важных прогностических критериев при ИВЛ у больных новой коронавирусной инфекцией (COVID-19).
Рекомендуем: Интубация трахеи; Трудные дыхательные пути; Алгоритм VORTEX; Рекомендации ASA; Протокол DAS; Рекомендации SOBA; Шкала Маллампати; Шкала Кормака-Лехана, Шкала MACOCHA
FiO₂(fraction of inspired oxygen) — фракция кислорода во вдыхаемой газовой смеси.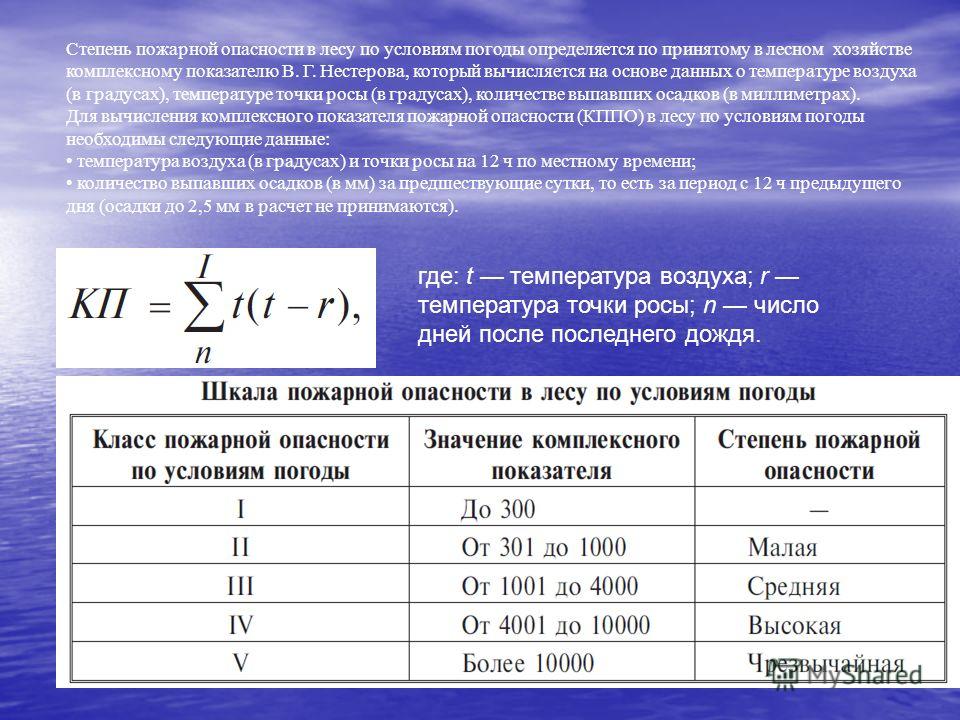 FiO₂ влияет на корреляцию между SpO₂ и PaO₂, подробнее здесь

Калькулятор индекса оксигенации № 1

PaO2, мм рт.ст.

FiO2, %

Результат

Интерпретация индекса оксигенации в анестезиологии

Индекс оксигенации (респираторный индекс) является качественным признаком для определения степени острой дыхательной недостаточности. В норме индекс оксигенации равен примерно 500 ( PaO₂ : FiO₂ = 100 mmHg/0,21 = 476). Известно, что снижение индекса оксигенации (PaO₂/ FiO₂) считается одним из главных критериев острого респираторного дистресс-синдрома (ОРДС). При этом степень нарушения оксигенирующей функции легких является и дифференциально-диагностическим критерием для острого повреждения легких (ОПЛ) и его наиболее тяжелой стадии — ОРДС:
индекс оксигенации (РаО₂/ FiО₂) < 300 — ОПЛ;
индекс оксигенации (РаО₂/ FiО₂) < 200 — ОРДС.

Степень тяжести ОРДС	Индекс оксигенации	Летальность
легкая	200–300	27%
средняя	100–200	32%
тяжелая	< 100	45%

Однако, индекс оксигенации является достаточно уязвимым признаком ОРДС, динамика изменений которого зависит от многих легочных и внелегочных причин. Для определения степени тяжести ОДН (в том числе и при COVID-19) диагностики ОРДС необходимо учитывать как причины развития и формы острого повреждения легких, так и характер проводимой интенсивной терапии.

Существует и другая формула индекса оксигенации, где для расчета используется не только соотношение PaO₂/FiO₂, но и среднее давление в дыхательных путях.

Калькулятор индекса оксигенации № 2

FiO2, %

Pmean, мм вод. ст.

PaO2, мм рт.ст.

Результат

ФОРМУЛА

Источники

1. Marshall JC, Cook DJ, Christou NV, et. al. Multiple organ dysfunction score: a reliable descriptor of a complex clinical outcome. Crit Care Med. 1995 Oct;23(10):1638-52. Review. PMID: 7587228
2. Ortiz RM, Cilley RE, Bartlett RH. Extracorporeal membrane oxygenation in pediatric respiratory failure. Pediatr Clin North Am. 1987 Feb;34(1):39-46.
3. Власенко А.В., Мороз В.В., Яковлев В.Н., Алексеев В.Г. Информативность индекса оксигенации при диагностике острого респираторного дистресс-синдрома. Общая Реаниматология, 2009; 5 (5), 54–62.
4. Karbing DS, Kjaergaard S, Smith BW, Espersen K, Allerød C, Andreassen S, Rees SE. Variation in the PaO2/FiO2 ratio with FiO2: mathematical and experimental description, and clinical relevance. Crit Care. 2007;11(6):R118.
5. Whiteley JP, Gavaghan DJ, Hahn CE. Variation of venous admixture, SF6 shunt, PaO2, and the PaO2/FIO2 ratio with FIO2. Br J Anaesth. 2002 Jun;88(6):771-8.
6. Bilan N., Dastranji A., Ghalehgolab Behbahani A. Comparison of the spo2/fio2 ratio and the pao2/fio2 ratio in patients with acute lung injury or acute respiratory distress syndrome. J Cardiovasc Thorac Res. 2015; 7(1):28-31.
7. Hsu-Ching Kao, Ting-Yu Lai, Heui-Ling Hung. Sequential Oxygenation Index and Organ Dysfunction Assessment within the First 3 Days of Mechanical Ventilation Predict the Outcome of Adult Patients with Severe Acute Respiratory Failure. ScientificWorldJournal, 2013

Возведение в степень в Microsoft Excel

Возведение в степень – одна из самых популярных математических задач, применяемая во время работы с электронными таблицами в Excel. При помощи встроенной функциональности программы вы можете реализовать данный вид операции всего в несколько кликов, выбрав наиболее подходящий метод. Кроме того, можно записать число как текст, если нужно только обозначить степень, но не считать ее.

Обо всем этом и пойдет речь в следующих разделах статьи. и вторую цифру, обозначающую степень. После нажатия клавиши Enter произойдет расчет, и в ячейке отобразится итоговое число возведения.

То же самое можно сделать, если необходимо посчитать степень числа, стоящего в конкретной ячейке. Число может измениться во время редактирования таблицы, но сама математическая операция останется. В таком случае оптимально записать в формуле номер ячейки, а затем указать, в какую степень следует возвести число, стоящее в ней. Используйте ту же методику записи, что показана в предыдущем абзаце.

Комьюнити теперь в Телеграм

Подпишитесь и будьте в курсе последних IT-новостей

Способ 2: Добавление функции степени

Одна из стандартных функций Excel позволяет вычислить степень числа, предварительно используя все входные данные. Использование данной формулы актуально в тех случаях, когда приведенный выше метод записи не подходит или само действие уже является частью обширной формулы. Вы можете использовать ручную запись или графическое окно добавления функции, которое мы и рассмотрим в качестве примера.

Активируйте ячейку для расположения функции, кликнув по ней левой кнопкой мыши. Затем нажмите по значку fx для открытия соответствующего окна.
В нем выберите категорию, отображающую полный перечень функций. Отыщите «‎СТЕПЕНЬ» и дважды кликните по этой строке.
В отдельном поле задайте число, а ниже укажите степень, в которую необходимо возвести число. В качестве числа можете использовать ячейку, имеющую определенное значение.
Примените изменения и вернитесь к таблице, чтобы ознакомиться с результатом. На следующем скриншоте вы видите, какую запись имеет эта функция, поэтому можете использовать ее для ручного ввода, если так будет проще.

Способ 3: Обозначение возведения в степень

Два рассмотренных выше способа подразумевают обязательное возведение числа в степень с отображением результата. Узнать, какая степень ему присвоена, не получится без нажатия по строке для отображения функции. Не всем пользователям подходит такая методика, поскольку некоторые заинтересованы в обычном отображении числа с обозначением, показывающим степень. Для реализации подобной задачи формат ячейки необходимо перевести в текстовый, а затем произвести запись с изменением символа.

Активируйте курсор на строке для ввода числа и на главной вкладке разверните список «‎Число», из которого выберите пункт «‎Текстовый».
Напишите два числа рядом: первое будет выступать основой, а второе – степенью.
Выделите то, которое является степенью, и щелкните по нему правой кнопкой мыши. Из контекстного меню выберите пункт «‎Формат ячеек».
Отметьте галочкой «‎Надстрочный» и примените изменения.
Вернитесь в таблицу и убедитесь в том, что результат отображается корректно, то есть так, как это показано на изображении ниже.

Вкратце разберем другой способ добавления желаемого символа без ручного изменения формата ячеек и перехода в меню редактирования. Для этого используйте специальную вставку.

Перейдите на вкладку с соответствующим названием и вызовите окно «‎Символы».
В нем укажите набор «‎Верхние и нижние индексы», после чего отыщите подходящий символ, который и будет выступать степенью.

Остается вставить его в ячейку рядом с уже написанным основанием. К слову, саму степень можно копировать и добавлять к другим ячейкам, если это потребуется.

Учитывайте, что подобные методы обозначения степени без ее возведения сразу конвертируют ячейку в текстовую и делают невозможными любые математические операции. Используйте подобное редактирование исключительно для визуального обозначения, а для подсчетов – Способ 1 и Способ 2.

Помощь студентам в учёбе от Людмилы Фирмаль

Здравствуйте!

Я, Людмила Анатольевна Фирмаль, бывший преподаватель математического факультета Дальневосточного государственного физико-технического института со стажем работы более 17 лет. На данный момент занимаюсь онлайн обучением и помощью по любыми предметам. У меня своя команда грамотных, сильных бывших преподавателей ВУЗов. Мы справимся с любой поставленной перед нами работой технического и гуманитарного плана. И не важно: она по объёму на две формулы или огромная сложно структурированная на 125 страниц! Нам по силам всё, поэтому не стесняйтесь, присылайте.

Срок выполнения разный: возможно онлайн (сразу пишите и сразу помогаю), а если у Вас что-то сложное – то от двух до пяти дней.

Для качественного оформления работы обязательно нужны методические указания и, желательно, лекции. Также я провожу онлайн-занятия и занятия в аудитории для студентов, чтобы дать им более качественные знания.

Моё видео:


Вам нужно написать сообщение в Telegram . После этого я оценю Ваш заказ и укажу срок выполнения. Если условия Вас устроят, Вы оплатите, и преподаватель, который ответственен за заказ, начнёт выполнение и в согласованный срок или, возможно, раньше срока Вы получите файл заказа в личные сообщения.
Сколько может стоить заказ?Стоимость заказа зависит от задания и требований Вашего учебного заведения. На цену влияют: сложность, количество заданий и срок выполнения. Поэтому для оценки стоимости заказа максимально качественно сфотографируйте или пришлите файл задания, при необходимости загружайте поясняющие фотографии лекций, файлы методичек, указывайте свой вариант.
Какой срок выполнения заказа?Минимальный срок выполнения заказа составляет 2-4 дня, но помните, срочные задания оцениваются дороже.
Как оплатить заказ?Сначала пришлите задание, я оценю, после вышлю Вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.
Какие гарантии и вы исправляете ошибки?В течение 1 года с момента получения Вами заказа действует гарантия. В течении 1 года я и моя команда исправим любые ошибки в заказе.
Качественно сфотографируйте задание, или если у вас файлы, то прикрепите методички, лекции, примеры решения, и в сообщении напишите дополнительные пояснения, для того, чтобы я сразу поняла, что требуется и не уточняла у вас. Присланное качественное задание моментально изучается и оценивается.
Теперь напишите мне в Telegram или почту и прикрепите задания, методички и лекции с примерами решения, и укажите сроки выполнения. Я и моя команда изучим внимательно задание и сообщим цену.
Если цена Вас устроит, то я вышлю Вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.
Мы приступим к выполнению, соблюдая указанные сроки и требования. 80% заказов сдаются раньше срока.
После выполнения отправлю Вам заказ в чат, если у Вас будут вопросы по заказу – подробно объясню. Гарантия 1 год. В течении 1 года я и моя команда исправим любые ошибки в заказе.





<noscript><img loading='lazy' src='/800/600/http/images.myshared.ru/9/948929/slide_4.jpg' /></noscript> youtube.com/embed/vOuj6t2Zyeg&#187; frameborder=&#187;0&#8243; allow=&#187;accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture&#187; allowfullscreen=&#187;&#187;/>





<noscript><img loading='lazy' src='' /></noscript> youtube.com/embed/ElMEic2MJ-U&#187; frameborder=&#187;0&#8243; allow=&#187;accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture&#187; allowfullscreen=&#187;&#187;/>



Можете смело обращаться к нам, мы вас не подведем. Ошибки бывают у всех, мы готовы дорабатывать бесплатно и в сжатые сроки, а если у вас появятся вопросы, готовы на них ответить. {-5}=\)\(\frac{1}{32}\)
Аргумент и основание логарифма

Любой логарифм имеет следующую «анатомию»:
 

Аргумент логарифма обычно пишется на его уровне, а основание — подстрочным шрифтом ближе к знаку логарифма. А читается эта запись так: «логарифм двадцати пяти по основанию пять».

Как вычислить логарифм?

Чтобы вычислить логарифм — нужно ответить на вопрос: в какую степень следует возвести основание, чтобы получить аргумент?
 
 Например, вычислите логарифм:  а) \(\log_{4}{16}\)     б) \(\log_{3}\)\(\frac{1}{3}\)     в) \(\log_{\sqrt{5}}{1}\)     г) \(\log_{\sqrt{7}}{\sqrt{7}}\)      д) \(\log_{3}{\sqrt{3}}\)

а) В какую степень надо возвести \(4\), чтобы получить \(16\)? Очевидно во вторую. Поэтому: 

\(\log_{4}{16}=2\)

б) В какую степень надо возвести \(3\), чтобы получить \(\frac{1}{3}\)? В минус первую, так как именно отрицательная степень «переворачивает дробь» (здесь и далее пользуемся свойствами степени). 

\(\log_{3}\)\(\frac{1}{3}\)\(=-1\)

в) В какую степень надо возвести \(\sqrt{5}\), чтобы получить \(1\)? А какая степень делает любое число единицей? Ноль, конечно!

\(\log_{\sqrt{5}}{1}=0\)

г) В какую степень надо возвести \(\sqrt{7}\), чтобы получить \(\sqrt{7}\)? В первую – любое число в первой степени равно самому себе.

\(\log_{\sqrt{7}}{\sqrt{7}}=1\)

д) В какую степень надо возвести \(3\), чтобы получить \(\sqrt{3}\)? Из свойств степени мы знаем, что корень – это дробная степень, и значит квадратный корень — это степень \(\frac{1}{2}\).

\(\log_{3}{\sqrt{3}}=\)\(\frac{1}{2}\)
 Пример: Вычислить логарифм \(\log_{4\sqrt{2}}{8}\)
 Решение:

\(\log_{4\sqrt{2}}{8}=x\)
 
                               
Нам надо найти значение логарифма, обозначим его за икс. {b}=c\)       \(\Leftrightarrow\)       \(\log_{a}{c}=b\)
 

\(\log_{4}{10}=5x-4\)
 
  
Зеркально перевернем уравнение, чтобы икс был слева
 

\(5x-4=\log_{4}{10}\)
 
  
Перед нами линейное уравнение. Перенесем \(4\) вправо.

И не пугайтесь логарифма, относитесь к нему как к обычному числу. 
 

\(5x=\log_{4}{10}+4\)
 
  
Поделим уравнение на 5
 

\(x=\)\(\frac{\log_{4}{10}+4}{5}\)
  

Вот наш корень. Да, выглядит непривычно, но ответ не выбирают.
 
 Ответ: \(\frac{\log_{4}{10}+4}{5}\)
Десятичный и натуральный логарифмы

Как указано в определении логарифма, его основанием может быть любое положительное число, кроме единицы \((a>0, a\neq1)\). И среди всех возможных оснований есть два встречающихся настолько часто, что для логарифмов с ними придумали особую короткую запись:

Натуральный логарифм: логарифм, у которого основание — число Эйлера \(e\) (равное примерно \(2,7182818…\)), и записывается такой логарифм как \(\ln{a}\). 
 

То есть, \(\ln{a}\) это то же самое, что и \(\log_{e}{a}\), где \(a\) — некоторое число.

Десятичный логарифм: логарифм, у которого основание равно 10, записывается \(\lg{a}\).
 

То есть, \(\lg{a}\) это то же самое, что и \(\log_{10}{a}\), где \(a\) — некоторое число. {2}=25\)
     
Ответ готов.
 Ответ: \(25\)
Как число записать в виде логарифма?

Как уже было сказано выше – любой логарифм это просто число. Верно и обратное: любое число может быть записано как логарифм. Например, мы знаем, что \(\log_{2}{4}\) равен двум. Тогда можно вместо двойки писать \(\log_{2}{4}\). 

Но \(\log_{3}{9}\) тоже равен \(2\), значит, также можно записать \(2=\log_{3}{9}\)  . Аналогично и с \(\log_{5}{25}\), и с \(\log_{9}{81}\), и т.д. То есть, получается  

\(2=\log_{2}{4}=\log_{3}{9}=\log_{4}{16}=\log_{5}{25}=\log_{6}{36}=\log_{7}{49}…\)

Таким образом, если нам нужно, мы можем где угодно (хоть в уравнении, хоть в выражении, хоть в неравенстве) записывать двойку как логарифм с любым основанием – просто в качестве аргумента пишем основание в квадрате. 

Точно также и с тройкой – ее можно записать как \(\log_{2}{8}\), или как \(\log_{3}{27}\), или как \(\log_{4}{64}\)… Здесь мы как аргумент пишем основание в кубе:

\(3=\log_{2}{8}=\log_{3}{27}=\log_{4}{64}=\log_{5}{125}=\log_{6}{216}=\log_{7}{343}…\)

И с четверкой:

\(4=\log_{2}{16}=\log_{3}{81}=\log_{4}{256}=\log_{5}{625}=\log_{6}{1296}=\log_{7}{2401}…\)

И с минус единицей:

\(-1=\) \(\log_{2}\)\(\frac{1}{2}\)\(=\) \(\log_{3}\)\(\frac{1}{3}\)\(=\) \(\log_{4}\)\(\frac{1}{4}\)\(=\) \(\log_{5}\)\(\frac{1}{5}\)\(=\) \(\log_{6}\)\(\frac{1}{6}\)\(=\) \(\log_{7}\)\(\frac{1}{7}\)\(…\)

И с одной третьей:

\(\frac{1}{3}\)\(=\log_{2}{\sqrt[3]{2}}=\log_{3}{\sqrt[3]{3}}=\log_{4}{\sqrt[3]{4}}=\log_{5}{\sqrt[3]{5}}=\log_{6}{\sqrt[3]{6}}=\log_{7}{\sqrt[3]{7}}…\)

И так далее.

Любое число \(a\) может быть представлено как логарифм с основанием \(b\):       \(a=\log_{b}{b^{a}}\)
 
 Пример: Найдите значение выражения \(\frac{\log_{2}{14}}{1+\log_{2}{7}}\)
 Решение:

\(\frac{\log_{2}{14}}{1+\log_{2}{7}}\)\(=\)
 
           
Превращаем единицу в логарифм с основанием \(2\): \(1=\log_{2}{2}\)
 

\(=\)\(\frac{\log_{2}{14}}{\log_{2}{2}+\log_{2}{7}}\)\(=\)
 
  
Теперь пользуемся свойством логарифмов: 

\(\log_{a}{b}+\log_{a}{c}=\log_{a}{(bc)}\)
 

\(=\)\(\frac{\log_{2}{14}}{\log_{2}{(2\cdot7)}}\)\(=\)\(\frac{\log_{2}{14}}{\log_{2}{14}}\)\(=\)
 
  
В числителе и знаменателе одинаковые числа – их можно сократить. 
 

\(=1\)
 
  
Ответ готов.
 
 Ответ: \(1\)
 Смотрите также:
Логарифмические уравнения
Логарифмические неравенства
 Калькулятор градусов, градиента и уклона 
 Наклон или уклон линии описывает направление и крутизну линии. Уклон может быть выражен в углах, градиентах или градусах.
 наклон, выраженный под углом 
  S _Угол = TAN ^-1 (Y / X) (1) 
  Где 
  S _Угол = угол (RAD, градусы (°))) 
  x = горизонтальная длина (м, фут..) 
  y = вертикальная высота (м, футы …) 
 Пример — уклон как угол 
 Уклон как угол для высоты  1 м  на расстоянии  2 м  можно рассчитать как
  S _Угол = TAN ^-1 ((1 м)/(2 м)) 
  = 26,6 ° 
 Наклон выражена как класс 
  S _(%) = (100 %) г/х                       (2) 
  где 
  S _{уклон (%)} = уклон (%) 
 Пример — Откос как уклон 
 Уклон как уклон для отметки  1 м  на расстоянии
9 1 2 м 9 может быть рассчитан AS 
  S _{GRADE (%)} = (1 м)/(2 м) 
  = 50 (%) 
 
 и наклона на крыше 
 Крыша крыши — это наклон, созданный стропила. Вы можете найти шаг крыши в виде x:12, например, 4/12 или 9./12. (3)
  S _{Степень ( %)} = (100 %) 4 /12 
  = 33,3 %
 Шаг крыши на форме X: 12 можно выразить в углах
  S _Угол =  загар ^-1 (x / 12)                      (3b) 
 Example — Roof Picth 4/12 as Angle 
  S _angle =   tan ^-1 (4 / 12)  
 
          = 18.4 °  
 Inclination or Slope Calculator 
 Расчет угловых градусов, уклона и длины склона.
    x — горизонтальная длина (м, футы, дюймы….) 
  y — вертикальная высота (м, футы, дюймы….) 
 (включить всплывающее окно)
 Марка ярлык для этого калькулятора на главном экране?
 Таблица наклона или уклона 
 Используйте эту таблицу для оценки наклона или уклона. Измерьте горизонтальный ход и вертикальный подъем и начертите линии на графике, чтобы оценить наклон.
 Загрузка и наклонная наклонная график/склона
 Уклоны против градиентов против % классов 
 Наклон
  Угла 
 (градуса)   угла 
 (градуса)   угла 
 (градуса) 9018  .
  Y   X 
 0.1  1  573.0  0.17
 0.2  1  286.5  0.35
 0.3  1  191.0  0.52
 0.4  1  143.2  0.70
 0.5  1  114.6  0.87
 0.57  1  100   1 
 0. 6  1  95.49  1.05
 0.7  1  81.85  1.22
 0.8  1  71.62  1.40
 0.9  1  63.66  1.57
  1  1  57.29  1.75
 2  1  28.64  3.49
 3  1  19.08  5.24
 4  1  14.30  6.99
 5  1  11.43  8.75
 5.71  1  10   10 
 6  1  9.514  10.5
 7  1  8.144  12.3
 8  1  7. 115  14.1
 9  1  6.314  15.8
  10  1  5.671  17.6
 11  1  5.145  19.4
 12  1  4.705  21.3
 13  1  4.331  23.1
 14  1  4.011  24.9
 15  1  3.732  26.8
 16  1  3.487  28.7
 17  1  3.271  30.6
 18  1  3.078  32.5
 19  1  2.904  34.4
 20  1  2.747  36. 4
 21  1  2.605  38.4
 22  1  2.475  40.4
 23  1  2.356  42.4
 24  1  2.246  44.5
 25  1  2.145  46.6
 26  1  2.050  48.8
 27  1  1.963  51.0
 28  1  1.881  53.2
 29 1  1.804  55.4
 30  1  1.732  57.7
 31  1  1.664  60.1
 32  1  1.600  62.5
 33  1  1. 540  64.9
 34  1  1.483  67.5
 35  1  1.428  70.0
 36  1  1.376  72.7
 37  1  1.327  75.4
 38  1  1.280  78.1
 39  1  1.235  81.0
 40  1  1.192  83.9
 41  1  1.150  86.9
 42  1  1.111  90.0
 43  1  1.072  93.3
 44  1  1.036  96.6
 45  1  1.000  100.0
 46  1  0. 9657  103.6
 47  1  0.9325  107.2
 48  1  0.9004  111.1
 49  1  0.8693  115.0
 50  1  0.8391  119.2
 51  1  0.8098  123.5
 52  1  0.7813  128.0
 53  1  0.7536  132.7
 54  1  0.7265  137.6
 55  1  0.7002  142.8
 56  1  0.6745  148.3
 57  1  0.6494  154.0
 58  1  0.6249  160. 0
 59  1  0.6009  166.4
 60  1  0.5774  173.2
 61  1  0.5543  180.4
 62  1  0.5317  188.1
 63  1  0.5095  196.3
 64  1  0.4877  205.0
 65  1  0.4663  214.5
 66  1  0.4452  224.6
 67  1  0.4245  235.6
 68  1  0.4040  247.5
 69  1  0.3839  260.5
 70  1  0.3640  274.7
 71  1  0. 3443  290.4
 72  1  0.3249  307.8
 73  1  0.3057  327.1
 74  1  0.2867  348.7
 75  1  0.2679  373.2
 76  1  0.2493  401.1
 77  1  0.2309  433.1
 78  1  0.2126  470.5
 79  1  0.1944  514.5
 80  1  0.1763  567.1
 81  1  0.1584  631.4
 82  1  0.1405  711.5
 83  1  0.1228  814. 4
 84  1  0.1051  951.4
 85  1  0.08749  1143
 86  1  0.06993  1430
 87  1  0.05241  1908
 88  1  0.03492  2864
 89  1  0.01746  5729
 90  1  0.00000  ∞
  1% уклона = 0,57 градуса = 1 см на 100 см = 1 дюйм на 100 дюймов = 0,125 дюйма на фут0007
 Горизонтальные площади в наклонные — дюймы/футы
 Горизонтальные площади в наклонные — см/м
 Калькулятор преобразования углов 
 Базовый калькулятор
 Угловой преобразователь
 Откуда: радианыградусыминутысекундызнакоктантыэкстантыквадрантоборотыгонмиль
 Кому:
радианградусминутысекундызнакоктантыэкстантквадрантреволюциягонмил
 Значение для преобразования 
 Ответ:
 = 0,01745329252 рад
 Для быстрого преобразования 
 разделите градус на 57,3
 
 
 Чем может быть лучше этот калькулятор?
 Поделитесь этой ссылкой для ответа: help 
 Вставьте эту ссылку в электронное письмо, текст или социальные сети.
 
 Получить виджет для этого калькулятора
 © Calculator Soup
 Поделитесь этим калькулятором и страницей
 Калькулятор Использование 
 Преобразуйте единицы измерения углов, введя значение для преобразования, а также единицы измерения из и в.
 Как преобразовать единицы измерения углов 
 Преобразование выполняется с использованием коэффициента преобразования. Зная коэффициент преобразования, преобразование между единицами может стать простой задачей на умножение:
  S * C = E 
 Где  S  — наше начальное значение,  C  — наш коэффициент преобразования, а  E  — наш конечный результат преобразования.
 Чтобы просто перевести из любых единиц в градусы, например, из 5 радиан, просто   умножить на   значение в правом столбце в таблице ниже.
 5 радиан * 57,29578 [градус/радиан] = 286,4789 градуса
 Для обратного преобразования градусов в единицы в левом столбце   разделить на   значение в правом столбце или умножить на обратную величину 1/x.
 286,4789 градусов / 57,29578 [градусов / радиан] = 5 радиан
 Чтобы преобразовать какие-либо единицы в левом столбце, скажем, из A в B, вы можете умножить на коэффициент для A, чтобы преобразовать A в градусы, а затем разделить на коэффициент для B, чтобы преобразовать из градусов. Или вы можете найти нужный вам фактор, разделив коэффициент A на коэффициент B.
 Например, чтобы преобразовать радианы в обороты, нужно умножить на 57,29578, а затем разделить на 360. Или умножить на 57,29578/360 = 0,15. Таким образом, чтобы преобразовать непосредственно из радианов в обороты, вы умножаете на 0,159. 1549.
 Чтобы понять, как конвертировать единицы, следуйте этому примеру. Скажем, вы хотите преобразовать из радианов в градусы. Поскольку вы можете умножить что угодно на 1 и при этом сохранить исходное значение, но в других единицах, настройте его так, чтобы радианы сокращались, оставляя вас с градусами.
 С: 
 1 градус = 0,01745329 радиан, 1 градус / 0,01745329 радиан = 1
 Мы можем записать преобразование как: 
 1 радиан = 1 радиан * (1 градус / 0,01745329 радиан) = 57,29578 градуса
 Теперь у нас есть коэффициент для преобразования радианов в градусы, поскольку 1 * 57,29578 = 57,29578. Обратите внимание, что в этих значениях есть ошибки округления.
 Зная, что 1 радиан = 57,29578 градусов, теперь мы можем найти коэффициент преобразования для обратного преобразования. Разделив обе части уравнения на 57,29578, мы получим примерно 0,01745329 радиан = 1 градус. Таким образом, коэффициент преобразования, на который нужно умножить градусы в радианы, составляет около 0,01745329.. 
 Таблица угловых преобразований 
 Единицы, символы и значения преобразования 
 used in angular conversion to degrees
 radian
 rad
 degree
 180/π
 57.29578
 minutes
 ‘
 degree
 1/60
 0.016667
 seconds
 »
 degree
 1/ 3600
 2,777778 e-4
 октант
 octant
 degree
 360/8
 45
 sextant
 sextant
 degree
 360/6
 60
 quadrant
 quadrant
 degree
 360/ 4
 90
 Революция
 R
 градус
 360/1
 360
 GON
 GON
 градус
 360/400
 0,9
 MIL
 MIL
 0,
 MIL
 MIL
 MIL
 MIL
0002 градус
 360/ 6400
 0,05625
 Единицы, символы и переводные значения 
 Используется при угловом преобразовании в Радианы
 градус
 °
 Radian
 π/180
 0,01745329
 ‘
 Radian
 (π/180)/60
 2.
 (π/180)/60 0003
 2.
 2.
 (π/180)/600003
 2.
 2,
 (π/180). секунды
 »
 радиан
 (π/180)/ 3600
 4,848137 e-06
 октант
 octant
 radian
 2π/8
 0.7853982
 sextant
 sextant
 radian
 2π/6
 1.047196
 quadrant
 quadrant
 radian
 2π/4
 1.570796
 Революция
 R
 Radian
 2π
 6.283185
 GON
 GON
 RADIAN
 2π/ 400
 0,01570796
 MIL
 0,01570796
 MIL
 0,01570796-  Руководство NIST по использованию Международной системы единиц  — Приложение B, подразделы
B.8 Коэффициенты для единиц, перечисленных в алфавитном порядке и
B.9 Факторы для единиц, перечисленных по видам величин или областям науки.
 Лиде, Дэвид Р. , Даниэль (главный редактор).  CRC Handbook of Chemistry and Physics, 89th Edition  New York, NY: CRC Press, p. 1-28, 2008.
 участников Википедии. «Конвертация единиц» Википедия, Бесплатная энциклопедия. Википедия, свободная энциклопедия, последнее посещение 26 июня 2011 г.
  
 Подписаться на CalculatorSoup: 
 Как мы рассчитали окупаемость инвестиций в высшее образование | Престон Купер 
 Мы сравнили заработок выпускников колледжей с их доходами, если бы они не поступили в колледж. 
 Фото Брюса Марса на Unsplash Наша газета  Стоит ли учиться в колледже? Комплексный анализ рентабельности инвестиций  рассчитывает чистую финансовую прибыль (увеличение доходов за вычетом затрат на образование), которую студенты могут ожидать от тысяч программ бакалавриата по всей Америке. Проект включает данные из оценочной карты колледжей Министерства образования США, опроса американского сообщества, Национального лонгитюдного исследования молодежи и Интегрированной системы данных о послесреднем образовании для создания интерактивной базы данных, призванной помочь учащимся сделать лучший выбор в отношении того, поступать ли в колледж. куда идти и чему учиться.
 На этой странице описывается методология построения базы данных ROI. ROI степени бакалавра сочетает в себе три элемента:
  Предполагаемый доход:  Сумма, которую студент, окончивший школу с определенной степенью бакалавра, может рассчитывать заработать в течение своей жизни.
  Предполагаемый заработок  : Сумма, которую та же ученица заработала бы в течение своей жизни, если бы она не поступила в колледж. Это число включает в себя доход, который ученица заработала бы, пока она училась в школе.
  Расходы на обучение в колледже : Сумма, которую учащийся тратит на обучение, необходимые сборы и другие расходы, связанные с образованием, такие как книги и оборудование. Сюда не входят расходы на проживание, так как студентка должна тратить деньги на проживание и питание независимо от того, поступает ли она в колледж.
 ROI эквивалентен расчетному заработку за вычетом суммы предполагаемого заработка и затрат на обучение в колледже. Я предполагаю, что учащаяся поступает в колледж сразу же после окончания средней школы в возрасте 18 лет. В основном описании она учится в колледже в течение четырех лет, получает степень бакалавра и начинает работать в возрасте 23 лет. Ее трудовая карьера длится 42 года, между в возрасте 23 и 64 лет. (Альтернативные спецификации изменяют некоторые из этих предположений.) Все денежные потоки дисконтируются по реальной ставке 3% к году, в котором студенту исполняется 18 лет. Если не указано иное, я привожу все цифры к долларам 2020 года.
 Расчетный заработок  Набор данных «Оценочная карта колледжей по областям обучения» Министерства образования США предоставляет информацию о среднем заработке выпускников колледжей по более чем 30 000 уникальных программ бакалавриата. Данные предоставляются на уровне учебных заведений и программ: набор данных не только показывает разницу в доходах между выпускниками Пенсильванского государственного университета и Суортморского колледжа, но также и разницу в доходах между специалистами по экономике и политологии, которые учились в Суортморе.
 Заработок по оценочной карточке определяется как сумма дохода в виде заработной платы и оклада (форма W-2) и положительного дохода от самозанятости для лиц, получавших федеральную финансовую помощь по Разделу IV. Те, кто не работал, исключаются из когорт доходов. Наблюдения за программами учебных заведений с небольшими размерами когорт скрыты по соображениям конфиденциальности, поэтому данные о доходах доступны не для всех 84 000 степеней бакалавра, перечисленных в базе данных Scorecard. Но подавляющее большинство студентов завершили программу с отчетными данными: согласно документации Scorecard, только 14% получателей степени бакалавра, получающих федеральную помощь, участвовали в программе с закрытыми данными.
 Основным ограничением Scorecard является то, что он измеряет доходы учащихся только в течение первых двух лет после выпуска. Но поскольку профили заработной платы, как правило, крутые в начале карьеры, заработок в системе показателей может значительно недооценивать пожизненную отдачу от получения высшего образования. По этой причине я дополнил данные Scorecard данными опроса американского сообщества (ACS), предоставленного базой данных IPUMS USA в Университете Миннесоты.
 Проводимая Бюро переписи населения США, ACS ежегодно обследует случайную 1%-ю выборку населения США, собирая основные демографические данные вместе с информацией о доходах отдельных лиц. С 2009 года, ACS также спросила обладателей степени бакалавра об их специальности бакалавриата. Однако ACS не спрашивает респондентов, где они учились в колледже.
 Для оценки прибыли за жизненный цикл программ Scorecard я использую подвыборку наборов данных ACS за период с 2009 по 2019 год. (Я исключаю выборку за 2020 год, поскольку сбои в сборе данных во время пандемии Covid-19 могут привести к ненадежным оценкам. ) В объединенную подвыборку входят лица со степенью бакалавра и выше. Я исключаю всех моложе 24 лет или старше 65 лет. (Доходы указаны за предыдущий год, так что это фактически дает мне выборку доходов для людей в возрасте от 23 до 64 лет.) Чтобы соответствовать определению когорты в оценочной таблице, я также исключить тех, кто в настоящее время учится в школе или колледже, безработных или не работающих, а также всех, кто имеет реальный заработок ниже 10 000 долларов в год (поскольку это может свидетельствовать об отсутствии работы в предыдущем году, когда измерялся заработок). Это дает выборку из 4,5 миллионов наблюдений.
 Я делю выборку на четырнадцать возрастных групп по три года в каждой, начиная с возраста от 24 до 26 лет (что соответствует заработкам в возрасте от 23 до 25 лет). В каждой из возрастных групп я рассчитываю среднее значение и стандартное отклонение натурального журнала личного дохода для каждой из 373 уникальных специальностей колледжа, указанных в оценочной таблице. Это дает оценку среднего заработка за карьеру для каждой специальности. Крутые профили заработной платы для многих выпускников колледжей очевидны. Для специалистов по экономике средний заработок в возрасте от 23 до 25 лет составляет 52 635 долларов; в возрасте от 44 до 46 лет средний заработок возрастает до 9 долларов.7 253.
 Одна из проблем касается лиц с высшим образованием, поскольку я должен разделить часть их заработка, приходящуюся на степень магистра, по сравнению со степенью бакалавра. Простое исключение их из анализа исказило бы мои оценки, поскольку люди, решившие поступить в аспирантуру, могут иметь более высокий потенциал заработка, чем сверстники с той же специальностью, но имеющие только степень бакалавра.
 Я предполагаю, что 80% разницы между средними заработками людей со степенью бакалавра и людьми с учеными степенями (в пределах каждой возрастной/основной категории бакалавриата) приходится на ученую степень, в соответствии с результатами Altonji & Zhong ( 2021). Другими словами, я вычитаю 80% разницы между средним заработком по степени бакалавра и средним заработком по степени бакалавра для каждой возрастной/основной группы из доходов всех лиц с высшим образованием. Я делаю это индивидуально для каждого уровня ученой степени (магистр, профессионал и докторантура).
 После расчета среднего заработка по каждой специальности я сравниваю отдельные наблюдения из оценочных карт со средними заработками ACS для соответствующей основной категории в возрастной группе от 23 до 25 лет, что примерно соответствует возрасту, для которого оцениваются заработки по оценочным картам. В частности, я рассчитываю Z-оценку для каждого наблюдения в оценочной таблице. Z-оценка эквивалентна логарифмической разнице между доходами по отдельным оценочным таблицам и средними доходами ACS для этой специальности, деленной на стандартное отклонение ACS для этой специальности. Z-оценка является мерой того, насколько аномально высоким или низким является наблюдение в оценочной таблице по сравнению со средним значением для этой специальности.
 Рассмотрим следующий пример, используя мою alma mater (Swarthmore College) и мою специальность бакалавриата (экономика).
 Для экономической программы в Swarthmore College оценочная карта колледжа сообщает, что заработок через год после выпуска составляет 70 390 долларов, а заработок через два года после выпуска составляет 82 707 долларов. Таким образом, средний доход по оценочной таблице для этого наблюдения составляет 76 549 долларов (11 246 в натуральном логарифмическом выражении). Средний заработок по ACS для специалистов по экономике в возрасте от 23 до 25 лет составляет 52 635 долларов (10,871 в логарифмическом выражении), а стандартное отклонение ACS для этой группы в логарифмическом выражении составляет 0,612. Z-показатель экономической программы Суортмора равен (11,246–10,871)/0,612 = 0,612. Другими словами, заработок для экономических специальностей Swarthmore на 0,612 стандартных отклонений выше среднего для всех экономических специальностей.
 Я повторяю этот процесс для всех программ с данными в Scorecard. Единственным исключением являются программы, в которых имеется менее 50 соответствующих наблюдений в возрастной группе от 23 до 25 лет с ОКС, поскольку я считаю, что размер выборки слишком мал для получения надежных оценок. Я не рассчитываю ROI для этих наблюдений.
 Взвешенный по зачислению средний Z-балл программы Scorecard составляет 0,057. Это говорит о том, что доходы Scorecard немного превышают средние показатели ACS для соответствующих основных направлений деятельности. Вероятным объяснением является тот факт, что выборка ACS включает все годы между 2009 ии 2019 года, в то время как прибыль с помощью Scorecard измерялась только в 2017 и 2018 годах. Последние были годами экономического бума, поэтому мы ожидаем, что прибыль Scorecard будет немного выше, чем в среднем по ACS. Тем не менее, тот факт, что средневзвешенный Z-показатель довольно близок к нулю, предполагает, что ACS является надежным косвенным показателем доходов учащихся, отраженных в оценочной таблице.
 Рассчитав Z-показатели для всех наблюдений по оценочным картам, я использую среднее значение ACS и стандартное отклонение для других возрастных групп, чтобы рассчитать заработок для каждой программы с оценочными картами на всех этапах карьеры учащихся. Я предполагаю, что средний заработок по каждой программе сохраняет один и тот же Z-показатель (по отношению к среднему заработку ACS по этой специальности) для всех возрастных групп на протяжении всего жизненного цикла.
 Продолжая экономический пример с Суортмором, вспомним, что Z-показатель для этого наблюдения составил 0,612. Ключевое предположение состоит в том, что типичный заработок студентов, изучающих экономику Суортмора, останется на 0,612 стандартного отклонения выше среднего значения для всех экономических специальностей на протяжении всей карьеры студентов. Для возрастной группы от 26 до 28 лет средний заработок ACS для специалистов по экономике составляет 64 588 долларов (11,076 в логарифмическом выражении), а стандартное отклонение ACS (в логарифмическом выражении) составляет 0,645. Расчетный заработок для специалистов по экономике Swarthmore в возрасте от 26 до 28 лет равен 11,076 + (0,612 * 0,645) = 11,471 в логарифмическом выражении и 9 долларов.5877 в долларовом выражении. Я повторяю этот процесс для каждой возрастной группы до выхода на пенсию.
 Расчеты дают оценку среднего заработка (в трехлетнем возрастном диапазоне) в возрасте от 23 до 64 лет для каждого наблюдения программы учебного заведения в оценочной карточке колледжа с отчетными данными о доходах. Я дисконтирую все оценки по ставке 3% к году, в котором учащемуся исполнилось 18 лет. Я также предполагаю, что заработок равен нулю в возрасте от 19 до 22 лет, пока учащийся учится в школе.
 Предполагаемый доход  Разумная оценка окупаемости инвестиций в колледж не будет заключаться в простом сравнении доходов выпускников колледжей с доходами тех, кто имеет только среднее образование; такая оценка будет смещена вверх по многим причинам. Те, кто решил поступить в колледж, и особенно те, кто закончил его, во многом отличаются от тех, кто так и не получил высшего образования. В научной литературе строгие причинно-следственные оценки финансовой отдачи от колледжа, как правило, отстают от разницы в необработанных доходах между выпускниками колледжей и выпускниками средней школы (хотя причинно-следственная отдача от колледжа все еще значительна). Другими словами, если бы выпускники колледжей не поступили в колледж, они все равно зарабатывали бы значительно больше, чем средний выпускник средней школы.
 Поэтому я корректирую гипотетический заработок с учетом различных демографических и географических различий между выпускниками средней школы и выпускниками колледжей. Я также делаю поправку на другие факторы, которые могут коррелировать как с заработком, так и с посещаемостью колледжа, такие как когнитивные способности, мотивация, здоровье и семейное положение. Вполне вероятно, что я не полностью учел все ненаблюдаемые различия, но мои оценки гипотетических заработков наверняка будут ближе к истинным цифрам, чем нескорректированные средние заработки выпускников средних школ. Я рассчитываю различные гипотетические доходы для каждого наблюдения из оценочной карты, чтобы учесть демографические и другие различия между школами и программами.
 Чтобы рассчитать гипотетический доход, я возвращаюсь к выборке ACS за 2009–2019 годы. Я ограничиваю выборку лицами, имеющими как минимум среднее образование, но не более одного года обучения в колледже, без высшего образования. Я отбрасываю людей моложе 20 или старше 65 лет (фактически давая мне образец заработка для людей в возрасте от 19 до 64 лет). Чтобы соответствовать выборке выпускников колледжей ACS, я также исключаю людей, которые не работают или не работают, людей, обучающихся в школе или колледже, и людей, чей доход за предыдущий год был менее 10 000 долларов. Эти исключения дают выборку из 5,5 миллионов человек.
 Я использую выборку ACS для построения регрессионной модели OLS, которая прогнозирует логарифм личного дохода человека на основе возраста, пола, расы, этнической принадлежности, штата и города. Я использую эту модель, чтобы предсказать гипотетический доход для каждого наблюдения Scorecard на основе расовой и гендерной разбивки программы и местоположения колледжа.
 Интегрированная система данных о высшем образовании (IPEDS) Национального центра статистики образования собирает данные о расовой и гендерной разбивке получателей степени бакалавра в американских колледжах и университетах. В оценочной карточке колледжа также представлена разбивка по полу для 13 000 программ бакалавриата с достаточно большими размерами когорты, чтобы избежать подавления конфиденциальности. Моя модель корректирует предполагаемый заработок на основе гендерной разбивки каждой программы или гендерной разбивки школы, если гендерные данные на уровне программы недоступны. Модель также корректирует предполагаемый заработок каждого наблюдения в зависимости от расового и этнического состава школы; это основано на предположении, что расовое и этническое разнообразие одинаково во всех программах одной и той же школы.
 Модель также корректирует предполагаемые доходы в зависимости от местоположения школы (штат и город). Выпускники средней школы в Нью-Йорке, как правило, зарабатывают больше, чем выпускники средней школы в сельской Алабаме; поэтому предполагаемые доходы колледжей в Нью-Йорке выше, чем у колледжей в сельской Алабаме. Эта корректировка предполагает, что колледжи, как правило, привлекают студентов из близлежащих географических районов; данные опроса показывают, что большинство студентов посещают колледжи в пределах 100 миль от дома и около трех четвертей остаются в своем родном штате.
 Возвращаясь к экономическому примеру Суортмора, для этого наблюдения модель предсказывает гипотетические доходы выпускника средней школы, проживающего в штате Пенсильвания и столичном районе Филадельфия-Камден-Уилмингтон, где расположен Суортмор. Доходы этого вымышленного человека взвешиваются в зависимости от пола (программа экономики составляет 37% женщин) и расы / этнической принадлежности (выпускники Swarthmore — 50% белых, 18% азиатов, 16% латиноамериканцев, 7% чернокожих и 9% других). Модель дает отдельные оценки для каждого этапа карьеры, в том числе во время обучения студентов в колледже. Например, предполагаемый заработок в возрасте 20 лет составляет 22,39 доллара США.5; предполагаемый заработок в возрасте 45 лет составляет 44 728 долларов.
 Регрессионная модель дает оценку гипотетического дохода после поправки на основные демографические и географические факторы. Но есть много других факторов, влияющих на предполагаемый заработок, в том числе способности и семейное положение. Однако ACS не собирает данные по большинству этих факторов.
 Вместо этого я обращаюсь к Национальному лонгитюдному исследованию молодежи, когорта 1997 года (NLSY97). NLSY97 представляет собой национально репрезентативную выборку из 8,9 баллов.84 человека, родившихся между 1980 и 1984 годами. Впервые эти люди были опрошены в 1997 году, когда большинство из них учились в средней школе, и впоследствии с ними периодически связывались повторно. Последний просмотр доступных данных был в 2017 году, когда респондентам NLSY97 было от 33 до 37 лет. Помимо основных данных о демографии, образовании и доходе, NLSY97 собирает исчерпывающую информацию о многих других аспектах происхождения и личности каждого человека.
 Чтобы использовать богатый набор переменных NLSY97, я следую стратегии, использованной Дугом Уэббером (2014). Во-первых, я регрессирую журнал доходов респондентов по базовой демографической информации и набору бинарных переменных для нескольких категорий уровня образования. Коэффициенты для этих бинарных переменных представляют «нескорректированную» надбавку к заработку, связанную с каждой категорией образования.
 К сожалению, небольшой размер выборки NLSY97 означает, что я могу исследовать уровень образования только в рамках широких категорий. К этим категориям относятся: степени бакалавра государственных университетов в области инженерии и информатики, других физических наук, бизнеса и управления, социальных наук, здравоохранения, образования, гуманитарных наук и других специальностей; степени бакалавра частных некоммерческих университетов в области физических наук, бизнеса, социальных наук и образования, гуманитарных наук и других специальностей; и степени бакалавра частных коммерческих университетов по любой специальности. Я также включаю фиктивную переменную для лиц, имеющих степень младшего специалиста. Чтобы привести мою выборку в соответствие с ACS и оценочной карточкой колледжа, я исключил лиц, зарабатывающих менее 10 000 долларов США, тех, кто учится в школе, и тех, кто имеет образование ниже среднего. Я также корректирую заработок людей с высшим образованием, как я сделал для выборки ACS.
 Затем я проведу вторую регрессию дохода по демографическим и образовательным переменным, но я также включу богатый набор элементов управления для способностей, самовосприятия и семейного положения. Коэффициенты переменных уровня образования представляют собой «скорректированную» надбавку к заработку, связанную с каждой категорией образования, — другими словами, часть дохода от образования, которую нельзя объяснить измеряемыми способностями, семейным положением или другими наблюдаемыми факторами. Аналогичным образом, разница между коэффициентами образовательной подготовки между первой и второй регрессиями представляет собой часть надбавки за образование, которая  — это , связанный с этими факторами.
 Дополнительные элементы управления во второй регрессии включают:
   Характеристики семейного фона.   Доход семьи, когда учащийся учился в старшей школе, наивысший уровень образования родителей и показатели отсутствия одного или обоих родителей.
   Характеристики старшей школы по словам учащегося.   Доля учащихся, планирующих поступать в колледж, доля учащихся, пропустивших занятия, качество учителей и частота нарушений в школе.
   Личные характеристики, о которых сообщила учащаяся или ее родители.   Состояние здоровья, употребление психоактивных веществ и общий показатель «тяжелых времен» в детстве.
   Черты характера.   Степень, в которой студент считает себя организованным, добросовестным, надежным, тщательным, приятным, готовым к сотрудничеству, гибким и доверчивым.
   Показатели способностей.   Баллы учащегося по Батарее профессиональных способностей вооруженных сил (стандартизированный тест с более широким предметом, чем SAT или ACT, часто используемый в качестве показателя способностей в академической литературе).
 Маловероятно, что эти элементы управления полностью отражают ненаблюдаемые различия между выпускниками средних школ и колледжей, но их включение должно улучшить мои оценки гипотетических доходов. Я беру разницу между коэффициентами первой и второй регрессий для каждой категории образования и добавляю эти «поправочные коэффициенты» к моим оценкам гипотетических заработков. Поскольку NLSY97 опрашивает своих респондентов несколько раз, я могу провести регрессии для разных возрастных категорий, чтобы получить разные поправочные коэффициенты для возрастов от 23 до 34 лет. Поскольку NLSY97 респондентов в последний раз были опрошены в возрасте около тридцати пяти лет, я должен предположить, что поправочный коэффициент остается постоянным до конца карьеры.
 В таблице ниже представлены результаты регрессии для каждой возрастной группы и категории уровня образования. Референтная категория – выпускники средней школы.
 Например, коэффициент к показателю для студентов со степенью бакалавра социальных наук или образования частного некоммерческого университета составляет 0,139 по первой регрессии (без контроля) и 0,046 по второй регрессии (с контролем) для 23- возрастная категория до 25 лет. Разница между этими двумя значениями составляет 0,09.2, что означает, что предполагаемый заработок в возрасте от 23 до 25 лет для всех степеней бакалавра социальных наук в частных некоммерческих университетах должен быть скорректирован в сторону увеличения на 0,092 логарифмических пункта с учетом способностей и семейного положения.
 Таким образом, предполагаемый заработок для специалистов по экономике Swarthmore в возрасте от 23 до 25 лет увеличивается с 29 246 долларов (10,284 в логарифмическом выражении) до 32 074 долларов (10,379 в логарифмическом выражении) после применения поправочного коэффициента. Это дает мои окончательные оценки гипотетических заработков (в трехлетних возрастных группах) в возрасте от 23 до 64 лет для всех наблюдений Scorecard с доступными данными, а также оценки гипотетических заработков для 19-летнего возраста.до 20 лет и в возрасте от 21 до 22 лет.
 Я вычитаю гипотетический заработок из оценочного заработка, чтобы получить оценку прироста заработка в течение жизни в результате получения определенного диплома в конкретном колледже, как показано на диаграмме ниже для Swarthmore College economics майоры. Чтобы вычислить увеличение доходов, я дисконтирую все предполагаемые и предполагаемые доходы по ставке 3% к году, в котором студенту исполнилось 18 лет. Для экономических специальностей Swarthmore увеличение доходов — или предполагаемая стоимость диплома колледжа — составляет примерно 1,8 миллиона долларов. на протяжении студенческой карьеры.
 Расходы на обучение в колледже  Последним элементом расчета ROI являются расходы на обучение в колледже: сколько учащийся и его семья должны заплатить, чтобы получить предполагаемую прибавку к доходам. Я оцениваю стоимость обучения после учета всех источников безвозмездной помощи — федеральных, государственных, местных и институциональных — но до помощи в виде студенческих ссуд. Я включаю стоимость учебников и оборудования в расходы колледжа, но не расходы на проживание, поскольку студенты должны оплачивать основные расходы на проживание независимо от того, посещают ли они колледж.
 Данные об оплате обучения и финансовой помощи доступны в IPEDS, хотя переменная «чистая цена» IPEDS включает расходы на проживание и поэтому не подходит для моих целей. Вместо этого я строю свою собственную оценку чистой цены на основе опубликованных цен на обучение и средней финансовой помощи. Я беру сумму опубликованной платы за обучение, требуемую плату и ориентировочную стоимость книг и оборудования. Я использую обучение в штате для государственных университетов, которые взимают дифференцированную плату за обучение в зависимости от места жительства.
 Я вычитаю среднюю финансовую помощь из этой меры «стикерных» затрат. IPEDS сообщает о средней сумме федеральной, государственной, местной и институциональной помощи, предоставляемой студентам дневного отделения в первый год их зачисления, которые получают федеральную финансовую помощь Раздела IV. (Переменная включает только студентов, оплачивающих обучение в государственных университетах по государственной ставке.)
 Поскольку многие университеты урезают гранты на финансовую помощь после первого года обучения, я уменьшаю размер помощи на первый год на небольшую сумму, чтобы рассчитать помощь на каждый последующий год. Согласно Национальному исследованию помощи студентам после окончания средней школы за 2015–2016 годы, студенты государственных университетов получают на 2% меньше помощи на втором курсе, на 12% меньше помощи на младшем курсе, на 9% меньше помощи на старшем курсе и на 42%. меньше помощи в любые последующие годы. Сокращение помощи в частных университетах сопоставимо.
 Для сравнения с когортой студентов в оценочной таблице колледжа я использую средние показатели платы за обучение и помощи за 2015–16 и 2016–17 учебные годы. Данные об оплате отсутствуют в IPEDS для 291 наблюдения в оценочной таблице. Я дисконтирую все платежи за обучение по ставке 3% до года, в котором студенту исполняется 18 лет.
 Swarthmore College взимал фиксированную цену в размере 53 340 долларов США в течение соответствующего периода времени, включая стоимость учебников и оборудования. Тем не менее, он также предоставил пакет финансовой помощи студентам Title IV на сумму 47,89 долларов.5 в год, а это означает, что чистая стоимость обучения для этой группы студентов составляла в среднем всего 5445 долларов. Таким образом, четырехлетняя стоимость обучения по специальности экономика Swarthmore составляет 21 780 долларов (без учета скидки).
 Несколько слов о чистой стоимости обучения. И данные о доходах из Scorecard, и данные о финансовой помощи IPEDS отражают только студентов, которые использовали федеральные программы финансовой помощи Раздела IV. Поскольку студенты с большими финансовыми потребностями с большей вероятностью подадут заявку на помощь по Разделу IV, а также получат более крупные пакеты помощи от университетов, чистая плата за обучение для студентов по Разделу IV ниже, чем чистая плата за обучение для всех студентов.
 В то время как большинство студентов колледжей используют Раздел IV в целом, доля в некоторых очень избирательных колледжах намного меньше. Например, в Swarthmore College только 11% студентов пользуются федеральными кредитами. Таким образом, данные о плате за обучение в Swarthmore основаны на меньшинстве студентов, которые платят за обучение гораздо меньше, чем обычный студент. Другими словами, средний студент Swarthmore, вероятно, платит за обучение гораздо больше, чем 5445 долларов в год. Из-за ограничений данных, к сожалению, это невозможно исправить; это просто предостережение, которое читатель должен иметь в виду.
 Я вычитаю текущую стоимость этих платежей за обучение из предполагаемого прироста заработка в течение всей жизни; для степени экономики Swarthmore это дает ROI в размере 1,7 миллиона долларов.
 Корректировка результатов завершения  Инвестиции в высшее образование обычно окупаются только в том случае, если студент действительно получает степень. Но менее половины студентов заканчивают обучение вовремя, а многие вообще не заканчивают. Таким образом, для студентов, не уверенных в своих шансах на получение диплома, колледж — рискованное предложение. Моя основная мера ROI предполагает, что вероятность того, что студент закончит обучение вовремя, составляет 100%, но на самом деле это не так. Поэтому я рассчитываю альтернативный показатель рентабельности инвестиций, который включает в себя разную вероятность завершения обучения в различных учебных заведениях.
 IPEDS сообщает данные о результатах завершения обучения для студентов дневной формы обучения, впервые поступающих в колледж по программе бакалавриата, на уровне учебного заведения. Количество студентов сообщается для шести различных результатов завершения: окончание за четыре года со степенью бакалавра, окончание за пять лет со степенью бакалавра, окончание за шесть лет со степенью бакалавра, перевод, продолжение обучения через шесть лет и полный отсев. пока не прошло шесть лет. (Я исключаю студентов седьмой категории, тех, кто начинает обучение по программе бакалавриата, но покидает колледж в течение шести лет с более низким уровнем квалификации, например, со степенью младшего специалиста, которых, как правило, очень мало.)
 Поскольку IPEDS сообщает данные только на уровне учебного заведения, я должен предположить, что показатели завершения одинаковы для всех программ в учреждении.
 Затем я рассчитываю рентабельность инвестиций для четырех отдельных результатов завершения учебы: получить степень бакалавра за четыре года, закончить за пять лет, закончить через шесть лет и бросить учебу. Студенты, которым требуется пять или шесть лет, чтобы получить степень, должны платить за обучение в течение пяти или шести лет, оставаться вне рабочей силы в течение пяти или шести лет и сокращать свою трудовую карьеру на один или два года по сравнению с теми, кто заканчивает обучение вовремя.
 Согласно продольному исследованию студентов, поступающих в высшие учебные заведения для начинающих (BPS:12/17), среднее количество студентов, получивших степень бакалавра, которые не закончили обучение в течение шести лет, бросают учебу через три года. Поэтому я предполагаю, что в среднем бросившие школу оплачивают обучение за три года, остаются вне рынка труда в течение трех лет и не получают никакой финансовой выгоды от учебы в колледже.
 Данные IPEDS не отслеживают, что происходит с учащимися после их перевода из учебного заведения. Опираясь на данные BPS:12/17 еще раз, я предполагаю, что 31% переведенных выпускников заканчивают обучение в течение четырех лет, 21% заканчивают обучение в течение пяти лет, 16% заканчивают обучение в течение шести лет и 32% никогда не получают степени. Точно так же я предполагаю, что одна треть студентов, которые все еще зачислены после шести лет (как правило, очень небольшое число), в конечном итоге получают степень.
 Я комбинирую эти вероятности и вычисляю средневзвешенную рентабельность инвестиций по четырем результатам завершения. В IPEDS Swarthmore College сообщает, что 88% студентов заканчивают обучение через четыре года, 4% — через пять лет и 2% — через шесть лет. Пять процентов студентов бросают учебу, и незначительное число переводится или остается зачисленным через шесть лет. Я подсчитал, что окупаемость инвестиций в течение всей жизни для студента, окончившего экономическую программу Swarthmore за четыре года, составляет 1,7 миллиона долларов, но окупаемость инвестиций падает до 1,6 миллиона долларов для пятилетнего выпуска и до 1,5 миллиона долларов для шестилетнего выпуска. Для выбывших ROI составляет минус 126 000 долларов США. Окупаемость инвестиций экономической программы Swarthmore с поправкой на результаты составляет 1,6 миллиона долларов.
 Корректировка полной стоимости обучения  Большинство студентов не оплачивают полную стоимость обучения. Государственные программы финансовой помощи, такие как гранты Пелла, перекладывают часть расходов на налогоплательщиков. Государственные колледжи и университеты получают ассигнования от правительств штатов, что позволяет им взимать субсидируемую плату за обучение. Даже в частных колледжах может существовать разрыв между чистой платой за обучение и базовой стоимостью образования, который компенсируется льготными по налогообложению пожертвованиями и программами для выпускников. В то время как будущие студенты должны быть больше всего заинтересованы в том, оправдывает ли увеличение доходов от их степени плату за обучение, которую они заплатили, другие заинтересованные стороны могут быть заинтересованы в том, оправдывает ли это увеличение доходов основные расходы.
 Показатели ROI, учитывающие базовые расходы, по существу заменяют чистую плату за обучение расходами колледжа, связанными с образованием, на одного студента очной формы обучения в расчете ROI. Расходы, связанные с образованием, представляют собой сумму расходов на обучение, академическую поддержку, услуги для студентов и институциональную поддержку (администрацию). Он не включает расходы на исследования и общественные услуги, а также расходы на вспомогательные предприятия, такие как общежития, и независимые операции, такие как больницы.
 Чистая плата за обучение в Swarthmore College составляет 5 445 долларов США, но расходы, связанные с образованием, на одного учащегося составляют 72 534 доллара США. Выполнение расчета ROI на основе расходов, а не платы за обучение снижает расчетную рентабельность экономической программы с 1,7 млн долларов до 1,5 млн долларов. Если я также включу поправку на результаты завершения, рентабельность инвестиций упадет до 1,4 миллиона долларов.
 Предостережения  В этом отчете я постарался максимально приблизиться к показателю истинной отдачи от обучения в колледже. Тем не менее, упражнение по-прежнему требовало принятия нескольких допущений, которые в действительности могут не соответствовать действительности. В интересах полной прозрачности я перечислил наиболее важные предостережения ниже, упорядоченные по их последствиям для моих оценок рентабельности инвестиций.
 Предостережения, которые обычно должны приводить к завышенным оценкам ROI:
 Переменные в NLSY97, вероятно, не полностью контролируют все источники систематической ошибки выбора между выпускниками колледжей и выпускниками средних школ. Это приводит к тому, что я недооцениваю контрфактические доходы.
 Женщины, не посещающие колледж, чаще всего добровольно работают неполный рабочий день. Женщины, окончившие колледж, гораздо реже делают это. Поскольку предполагаемые заработки женщин с высшим образованием основаны на заработках женщин, не имеющих высшего образования, феномен неполной занятости может привести к недооценке предполагаемых заработков женщин с высшим образованием, которые с большей вероятностью выберут полный рабочий день. работать, даже если они не учились в колледже.
 Я предполагаю, что расходы на проживание одинаковы независимо от того, решит ли студент поступить в колледж. Но студенты могут платить больше за проживание, если они посещают колледж, особенно если они живут в общежитиях на территории кампуса.
 В оценочной карточке колледжа сообщается о доходах только студентов, получающих право на получение Титула IV, и мои оценки чистой платы за обучение включают среднюю помощь для студентов, получающих Титул IV, а не всех студентов. Поскольку учащиеся по Разделу IV получают больше помощи, это приводит к занижению чистой платы за обучение для «среднего» учащегося.
 Я предполагаю, что каждый студент поступает в колледж в самом начале своей взрослой жизни и работает до выхода на пенсию. Но многие студенты поступают в колледж в более позднем возрасте, и у них остается меньше лет, чтобы применить свою степень на рынке труда. ROI для этих старших студентов будет значительно ниже в действительности.
 Предостережения, которые обычно должны приводить к занижению ROI:
 Я предполагаю, что расчетный ACS заработок для сегодняшних 35-летних является точным показателем того, сколько сегодняшние 25-летние заработают через десять лет. Но если заработок выпускников колледжей будет расти быстрее, чем заработок выпускников средних школ, как предсказывают некоторые аналитики, то мои оценки рентабельности инвестиций будут занижать возвращение в колледж сегодняшних выпускников.
 Я приписываю большую часть надбавки, которую люди с учеными степенями зарабатывают по сравнению со сверстниками со степенью бакалавра, ученой степени, а не степени бакалавра. Но подготовка к получению прибыльной степени магистра может быть частью экономической ценности колледжа для некоторых студентов. Это может привести к недооценке ROI, особенно для областей с высокой посещаемостью аспирантуры (таких как биология и науки о жизни).
 Данные системы показателей охватывают только работающих лиц. Для согласованности я исключаю безработных из своих оценок доходов, полученных с помощью ACS, и предполагаемых доходов. Уровень безработицы ниже среди выпускников колледжей, но мои оценки ROI не включают вероятность безработицы — только заработок для людей, у которых есть работа.
 Предостережения, которые могут привести к завышению или занижению ROI:
 Я предполагаю, что Z-показатель для каждой программы по отношению к среднему заработку в этой области остается постоянным на протяжении всей карьеры выпускников. На самом деле, многие выпускники будут перемещаться по распределению заработка в течение своей жизни.
 Я должен предположить, что некоторые данные, доступные только на уровне учебного заведения, а именно процент выпускников и расовый/этнический состав, одинаковы для всех специальностей. Если количество выпускников по конкретной программе выше, чем количество выпускников в соответствующем университете, мои цифры будут занижать рентабельность инвестиций для этой программы, и наоборот.
 Ограниченный размер выборки NLSY97 означает, что я могу только оценить долю надбавки за образование, относящуюся к способностям и семейному положению, в пределах широких категорий образования. Например, я могу оценить эти цифры для всех частных некоммерческих университетов, но не для узкоспециализированных некоммерческих университетов. Поскольку отборные школы набирают учащихся с высокими способностями, это может привести к тому, что я занижу предполагаемый заработок для высокоизбирательных школ (и переоценю рентабельность инвестиций). Точно так же я могу переоценить предполагаемые доходы менее избирательных школ и недооценить их рентабельность инвестиций.
 Я не учитываю социальные пособия или социальные расходы колледжа. Хорошо образованные работники могут повысить производительность в масштабах всей экономики, а это означает, что некоторые люди могут не реализовать всю ценность своего образования в виде более высоких заработков. Но у колледжа есть и социальные издержки, поскольку большее количество работников с высшим образованием подпитывает инфляцию дипломов, которая снижает заработную плату для людей, не имеющих высшего образования. Учет этих внешних эффектов может повысить или понизить предполагаемую рентабельность инвестиций.
 Как и в притче о слепых и слоне, расчет окупаемости инвестиций в высшее образование требует изучения данных из различных источников, которые раскрывают лишь части всей картины. Мой анализ объединяет эти различные фрагменты данных для оценки рентабельности инвестиций, но для этого требуются предположения. В то время как более полный набор данных был бы идеальным, исследователи должны работать с имеющейся у нас информацией. Приведенные выше предостережения следует рассматривать как части головоломки, которые нам еще предстоит собрать воедино, и мы надеемся, что будущие выпуски данных позволят нам собрать их.
 Как рассчитать угол в градусах? 
 Угол измеряется в градусах (°) и радианах. Он образуется между двумя соседними сторонами многоугольника. Каждый многоугольник имеет разные стороны и разное количество углов. Формула для нахождения углов в градусах полезна в геометрии и тригонометрии. Важно понимать другие понятия математики, такие как дуга, центральный угол окружности и т. д.  
 Полный круг = 360°
 Прямая линия = 180°
 Полуокружность = 180°
 Четверть окружности = 90°
 Расчет углов в градусах 
 Существует три различных метода нахождения углов в градусах:
 Использование протектора D
4
4 теорема Пифагора и тригонометрическая функция в прямоугольном треугольнике в сантиметрах или миллиметрах. Протектор, используемый для измерения углов, имеет форму буквы «D» со значением угла, отмеченным от 0 до 180 ° в любом направлении (вправо или влево). Нам нужно выровнять ось с линией на D, чтобы измерить угол. Средняя окружность протектора совмещена с вершиной измеряемого угла. Лучи, проходящие через вершину угла, помогут найти угол в градусах.
 Использование теоремы Пифагора и функции тригонометрии в прямоугольном треугольнике   
 В тригонометрии есть шесть функций:  синус, кос, косек, тангенс, кот,  и  сек.  Прямоугольный треугольник имеет три стороны, основание, перпендикуляр и гипотенузу.
  Основание:  Сторона, примыкающая к углу 90°.
  Перпендикуляр:  Также является примыкающей стороной к углу 90°.
  Гипотенуза:  Сторона, противоположная углу 90°.
 Прямоугольный треугольник представлен углом 90° как одним из углов. Сумма всех углов треугольника равна 180°.
  Cosecθ:  Представляется гипотенузой, деленной перпендикуляром.
 Cosecθ =
  Cotθ:  Представляется как основание, разделенное перпендикуляром.
 Cotθ =
 Остальные тригонометрические функции представлены как:
 sinθ =
 cosθ =
 tanθ =
 secθ =
 cosecθ также может быть представлен как 1/ sinθ
 Secθ также может быть представлен как 1/ cosθ
 Cotθ также может быть представлен как 1/ tanθ
 Где,
 Θ угол  
  Теорема Пифагора 
 Если известны две стороны прямого угла, мы можем легко вычислить третью сторону прямоугольного треугольника. В прямоугольном треугольнике теорема Пифагора дается формулой:
  (гипотенуза) ² = (основание) ² + (перпендикуляр) ² 
 Формула суммы углов, образующих сумму внутренних углов многоугольника 
 между двумя сторонами. Если у многоугольника шесть сторон, то и углов примерно шесть. Это помогает найти угол, если известны другие углы и сумма углов многоугольника.
 Формула для нахождения суммы углов многоугольника:
  Total sum of angles = 180 (n – 2) 
 Where,
 n is the number of sides of a polygon
  Example: 
 If n = 4,
 Сумма углов = 180 (4 – 2)
 = 180 (2)
 = 360°
 Если n = 5,
 Сумма углов = 180 (5 – 2)
 = 3)
 = 540°
 Если n = 6
 Сумма углов = 180 (6 – 2)
 = 180 (4)
 = 720°
 Центральный угол окружности точка. Расстояние между центральной точкой и границей называется радиусом окружности. Угол, образованный двумя радиусами окружности, называется центральным углом. Значение центрального угла окружности лежит в пределах от 0 до 360 градусов.
 Формула для расчета центрального угла окружности:
 Длина дуги = 2πr × (θ/360)
 Θ = 360L/2πr
 Где
 r — радиус окружности
 AB — дуга
 Тета — угол в градусах.
 L = длина дуги  
 Примеры задач 
  Вопрос 1: Найдите центральный угол окружности радиусом 2 м с длиной дуги 4 м? 
  Решение  : 
 Формула для расчета центрального угла окружности:
 Θ = 360L/2πr
 Где
 r — радиус окружности
 Тета — угол в градусах.
 L = длина дуги
 Θ = угол в градусах
 r = 2 м
 L = 4 м
 Θ = 360 × 4 /2× π × 2
 Θ = 190,6 центрального угла 0° окружность 114,6°.
  Вопрос 2: Найдите центральный угол окружности радиусом 10 см с длиной дуги 18 см? 
  Решение  : 
 Формула для расчета центрального угла окружности: в градусах.
 L = Длина дуги
 R = 10 см
 L = 18 см
 θ = угол в градусах
 θ = 360 × 18 /2 × π × 10
 θ = 103.13 °
 Таким образом окружность 103,13°.
  Вопрос 3: Найдите угол параллелограмма, если три других угла равны 80°, 95° и 105°? 
  Решение  : 
 В параллелограмме четыре стороны с суммой углов 360°.
 Формула для нахождения суммы углов = 180 (n – 2)
 Где
 n количество сторон многоугольника
 Здесь n = 4,
 Сумма углов = 180 (4 – 2)
 = 180 (2)
 = 360°
 Общая сумма = Угол 1 + Угол 2 + Угол 3 + Угол 4
 360 = 80+ 95+ 105+ Угол 4
 360 = 280 + Угол 4
 Угол 4 = 360 – 280
 Угол 9 °
  Вопрос 4: Найдите угол А на данном рисунке. 
  Решение  :
 Дано: Гипотенуза = 12
 Перпендикуляр = 6
 Тригонометрическая функция для вычисления угла определяется как:
2 sinA
03 
 A = 30°
  Вопрос 5: Найдите угол A на данном рисунке. 
  Решение :
 Дано: гипотенуза = 10
 Основание = 5
 Функция тригонометрии для расчета угла задается:
 COSA = 5/10
 A = 60 °
.
  Вопрос 6. Найдите угол пятиугольника, если остальные четыре угла равны 115°, 100°, 105° и 100°? 
  Решение  : 
 В пятиугольнике пять сторон с суммой углов 540°.
 Формула для нахождения суммы углов = 180 (n – 2)
 Где
 n – количество сторон многоугольника
 Здесь n = 5,
 Сумма углов = 180 (5 – 2)
 = 180 (3)
 = 540°
 Общая сумма = Угол 1 + Угол 2 + Угол 3 + Угол 4 + Угол 5
 540 = 115° + 100° + 105°+100° + Угол 5
 540 = 420 + Угол 5
 Угол 5 = 540 – 420
 Угол 5 = 120°
  Вопрос 7: Найдите угол А на данном рисунке. 
  Решение :
 Дано: Базу = √3
 Перпендикуляр = 1
 Функция тригонометрии для расчета угло A = 30°
  Вопрос 8: Найдите угол параллелограмма, если три других угла равны 100°, 70° и 80°? 
  Решение  :
 У параллелограмма четыре стороны с суммой углов 360°.
 Формула для нахождения суммы углов = 180 (n – 2)
 Где
 n – количество сторон многоугольника
 Здесь n = 4,
 Сумма углов = 180 (4 – 2)
 = 180 (2)
 = 360°
 Общая сумма = Угол 1 + Угол 2 + Угол 3 + Угол 4
 360 = 100 + 70 + 80 + Угол 4
 Угол 4 = 360 – 250
 Угол 4 = 110°
 Таким образом, второй угол равен 110°.
  Вопрос 9: Найдите угол шестиугольника, если остальные пять углов равны 120°, 115°, 110°, 125° и 105°? 
  Решение  : 
 В шестиугольнике шесть сторон с суммой углов 720°.
 Формула для нахождения суммы углов = 180 (6 – 2)
 Где,
 n – количество сторон многоугольника
 Здесь, n = 6,
 Общая сумма углов = 180 (6 – 2)
 = 180 (4)
 = 720°
 Общая сумма = Угол 1 + Угол 2 + Угол 3 + Угол 4 + Угол 5 + Угол 6
 720 = 120 + 115 + 110 + 125 + 105 + Угол 6
 720 = 575 + Угол 6
 Угол 6 = 720 – 575
 Угол 6 = 0002°, шестиугольника составляет 145°.
 
 Расчет уклона и общих уклонов в архитектуре 
 Архитекторы постоянно предоставляют информацию об уклоне на своих чертежах, используя градиенты, градусы или проценты в зависимости от приложения. Например, крыши отмечаются с помощью уклонов, а поперечные уклоны тротуаров обычно обозначаются в градусах. Полезно понять, как рассчитать каждый метод.
 Расчет градиента уклона
 Расчет уклона в процентах
 Расчет уклона в градусах
 Таблица общих уклонов в архитектуре
 Уклоны крыши
 Крыши с малым уклоном
 Крыши с крутым уклоном
 Уклоны сантехнических труб
 Существует три различных способа указания наклона поверхности относительно горизонтальной плоскости: градусы, градиент и проценты.
 Расчет градиента уклона 
 Расчет градиента уклона Градиенты уклона записываются в виде Y:X, где Y — единица подъема, а X — протяженность. Оба числа должны использовать одни и те же единицы измерения. Например, если вы путешествуете на 3 дюйма по вертикали и на 3 фута (36 дюймов) по горизонтали, уклон составит 3:36 или 1:12. Это читается как «один из двенадцати наклонов».
 Расчет уклона в процентах 
 Расчет уклона в процентах Процент уклона рассчитывается почти так же, как градиент. Переведите рост и пробег в одни и те же единицы, а затем разделите рост на пробег. Умножьте это число на 100, и вы получите процент наклона. Например, подъем 3 дюйма, разделенный на длину 36 дюймов = 0,083 x 100 = уклон 8,3%.
 Вычисление уклона в градусах 
 Вычисление уклона в градусах Самый сложный способ вычисления уклона — в градусах, и он требует немного математики средней школы. Тангенс данного угла (в градусах) равен подъему, деленному на пробег. Следовательно, арктангенс подъема, деленный на разбег, даст угол.
 Таблица общих уклонов в архитектуре 
 В таблице ниже показаны некоторые распространенные уклоны. Полы с уклоном 1:20 не требуют поручней, но все, что круче 1:20, считается пандусом и требует наличия поручней. Пандусы с наклоном 1:12 — это максимальный уклон, разрешенный кодами ADA, и для них требуются поручни. Федеральные коды ADA указывают, что максимальный поперечный уклон доступного маршрута составляет 1:48, что составляет чуть более 2%. Однако мы видели некоторые юрисдикции, которые допускают максимальный поперечный уклон 1:50.
9 90180
9 901810
 DEGREES  GRADIENT  PERCENT
 0.6°  1 : 95.49  1.0%
 1°  1 : 57.29  1.7%
 1.15°  1 : 50  2%
 1. 19°  1 : 48  2.08%
 2.86°  1 : 20  5%
 4.76°  1 : 12  8.3%
 7.13°  1 : 8  12.5% 
 10°  1 : 5.67  17.6%
 14.04°  1 : 4  25%
 15°  1 : 3.73  26.8%
 26.57°  1 : 2  50%
 30°  1 : 1. 73  57.7%
 45°  1 : 1  100%
 56.31°  1: 0.67  150%
 60°  1 : 0.6  173.2%
  63.43°  1 : 0.5  200%
 78,69 °  1: 0,2  500%
 89,43 °  1: 0,1  1000%
 1000%
 1000% 110 9210  1000% .
 Уклоны крыш 
 Уклоны крыш определяются с использованием метода градиента, описанного выше, где подъем варьируется, но уклон обычно равен 12. На некоторых очень крутых крышах вы можете увидеть инвертированный уклон, так что уклон меняется, но подъем держится как 12.
 Крыши с малым уклоном 
 Крыши с малым уклоном имеют уклон 3:12 или меньше. Они должны иметь мембранную систему крыши для обеспечения водонепроницаемости.
 ROOF GRADIENT  DEGREES  PERCENT
 1/4 : 12  1.19°  2.08%
 1/2 : 12  2.39°  4.17%
 1 : 12  4,76°  8,3%
 2 : 12  9. 46°  16.67%
 3 : 12  14.04°  25%
 Steep Slope Roofs 
 Anything above 3:12 is considered a steep roof and can be covered with metal panels , черепица или черепица — эти крыши не пропускают воду и не считаются водонепроницаемыми.
 2° 9.24316 9.02316 33.33% НАКЛОН КРЫШИ  ГРАДУСЫ  ПРОЦЕНТ
 4 : 12
 5 : 12  22.62°  41.67%
 6 : 12  26.57°  50%
 7 : 12  30.26°  58. 33%
 8 : 12  33.69°  66.67%
 9 : 12  36.87°  75%
 10 : 12  39.81°  83.33%
 11 : 12  42,51°  91,67%
 12 : 12  45°  100%
 Крыши могут быть круче, чем показано в таблице выше. На самом деле крыша может быть почти вертикальной.
 Уклоны водопроводных труб 
 Как обсуждалось в нашей статье об уклонах труб, уклоны дренажных и канализационных труб, как правило, минимальны. Идея состоит в том, чтобы поддерживать поток воды и твердых частиц. Используются три общих уклона, на которые ссылаются в Международном сантехническом кодексе.
 2,08 %
 2,08 %16 1/4 «на ногу
 2,08 %6 1/4″ на фут.
 0,52% Минимальный наклон  Минимальный наклон %  Градиент наклона  Диаметр трубы
 1/4 «на ногу  1/4″ на ногу
 1/8 «на ногу  1,04%  1/8: 12  3″ до 6 «
 1/16″ на ногу  0,52%  1/16 «на ногу  0,52%  1/16″ на ногу  1/16 «.  8 дюймов или больше
 Статья обновлена: 23 июля 2022 г.
 Помогите сделать Archtoolbox лучше для всех. Если вы обнаружили ошибку или устаревшую информацию в этой статье (даже если это всего лишь незначительная опечатка), сообщите нам об этом.
 Полезные инструменты для архитекторов и проектировщиков зданий 
 Калькулятор градусов, минут, секунд в десятичных градусах и наоборот 
 Замените значения по умолчанию в синих полях ниже широтой
или долгота вашего местоположения. Вводите только положительные числа (например, от 0 до 360 градусов).
 Целые градусы  минут  секунд
 Декабрь  Мин.  Секунда
 Расчет
Сбросить
 Десятичные градусы 
 4 десятичных знака  Десятичные градусы 
 5 знаков после запятой  Десятичные градусы 
 6 знаков после запятой
 4 места уб.  5 мест  6 мест уб
 Уравнение расчета простое:  Десятичные градусы = целое число градусов плюс
минуты, разделенные на 60, плюс секунды, разделенные на 3600 
  Обратный процесс: введите десятичные градусы, и результат будет представлен в формате град/мин/сек. 
 Десятичные градусы
 Десятичный градус
 Расчет
Сбросить
    Всего 
 градусов  минут  секунд
 Хеми  Дек  Мин.  Секунда
 Хеми  Дек  Мин.   
 Если у вас есть GPS-приемник, на дисплее может отображаться долгота 117 градусов и 29 градусов.0,842 минуты. В этом случае используйте первые два синих поля.
выше и поставьте цифру 0 (т.е. ноль) в поле секунд. Если у вас есть дисплей GPS-приемника, например, 117 градусов, 29 минут и 50,5 секунд, установите
номера во всех трех синих полях выше так же, как показано с номерами по умолчанию.
 На многих GPS-приемниках можно переключать формат настроек отображения широты-долготы. Изучите свои параметры GPS и, если вы можете получить
отображение в десятичных градусах, таких как 117,4974 градуса, то пользоваться этим калькулятором не нужно.
 Протестируйте, щелкнув, чтобы вычислить результат с числами по умолчанию. Ответ должен быть 117,4974 десятичных градуса. то есть чуть меньше 117 с половиной
градусов. Даются три альтернативных ответа, первый до 4 знаков после запятой (точность 11 м по экватору), третий до 6 знаков после запятой (точность
11 см по экватору). Если калькулятор не работает, вам необходимо включить javascript в вашем браузере.
 Точность: если вы заметили значительные расхождения между вашим местоположением в широте и долготе, показанным с помощью карт Google, по сравнению с показаниями GPS или физической бумаги. карты, то вы должны убедиться, что используемые системы координат основаны на одной и той же системе координат. Датам, называемый WGS84, является обычным, но на многих старых бумажных картах
используются разные локальные данные. Конфигурация вашего приемника GPS может позволять выбирать одну из множества альтернативных датумов.
 Данные карты содержат физическое местоположение с соответствующей парой цифр широта/долгота, а также математическую модель формы Земли. Физическое местоположение может быть триггерной точкой
удобная горная вершина. Предполагаемая форма Земли, экваториальный диаметр, полярный диаметр и т. д. могут незначительно отличаться в зависимости от сделанных предположений. На отдаленных островах, как правило, есть свои собственные
датумы относятся к местной горной вершине.
 Любые проблемы или комментарии, или сообщения о нарушении авторских прав, пожалуйста, напишите мне по электронной почте Эрик Джонстон
Этот калькулятор защищен авторским правом (c) 2005 — 2021 Satellite Signals Ltd
. Оригинал: 16 марта 2005 г.
 Изменено 5 октября 2006 г.: Если вы введете отрицательное число для целых градусов, предполагается, что вы находитесь на западной долготе, и будут учитываться минуты.
и доли секунд (введите без минуса) как уводящие вас дальше на запад. Выходное десятичное число отображается отрицательным, что указывает на градусы запада.
Добавлен более точный вывод 5 знаков после запятой. Точность предполагает, что окружность земли вокруг экватора составляет 40075,16 км. Значит 1 град = 1000
х 40075,16 / 360 = 1113190,88889 м    Таким образом, 0,0001 градус = 11 м и 0,00001 градус = 1 м. Точность определения долготы улучшается ближе к полюсам
так как линии долготы ближе друг к другу. Ошибка широты более или менее одинакова везде, но если вы привередливы, вы можете решить
ошибка основана на полярной окружности земли 40008 км.
 Поправка от 1 ноября 2010 г.:   Если у вас долгота больше 180 градусов, то это относится к местоположениям в диапазоне от 0 до 180 градусов западной долготы.
No related posts.
Навигация по записям
Предыдущая статьяПеревод из ворда в пдф онлайн бесплатно: Word в PDF | Конвертировать документы в PDF онлайн бесплатно
Следующая статьяКосинус 1: Таблица синусов и косинусов
Добавить комментарий Отменить ответ
Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий *
Имя * 
Email * 
Сайт 
  
  Найти:   
Рубрики
Геометрия
Математика
Физика
Химия
Школьная жизнь
Разное
© 2015 - 2019 Муниципальное казённое общеобразовательное учреждение «Таловская средняя школа»
Карта сайта