| ГОСТы, СНиПы Карта сайта TehTab.ru Поиск по сайту TehTab.ru | Навигация по справочнику TehTab.ru: главная страница / / Техническая информация/ / Математический справочник/ / Комплексные числа. Мнимая единица. / / Мнимая единица. Степени мнимой единицы.
| |||||||||||||||||||||||||||||||||||||||||||||
Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу. | ||||||||||||||||||||||||||||||||||||||||||||||
TehTab.ru Реклама, сотрудничество: [email protected] | Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями. | |||||||||||||||||||||||||||||||||||||||||||||
.. (и т. д.)I в степени n комплексные числа. Возведение комплексных чисел в степень. Извлечение корней из комплексных чисел. Квадратное уравнение с комплексными корнями
Начнем с любимого квадрата.
Пример 9
Возвести в квадрат комплексное число
Здесь можно пойти двумя путями, первый способ это переписать степень как произведение множителей и перемножить числа по правилу умножения многочленов.
Второй способ состоит в применение известной школьной формулы сокращенного умножения :
Для комплексного числа легко вывести свою формулу сокращенного умножения:
Аналогичную формулу можно вывести для квадрата разности, а также для куба сумма и куба разности. Но эти формулы более актуальны длязадач комплексного анализа. Что делать, если комплексное число нужно возвести, скажем, в 5-ую, 10-ую или 100-ую степень? Ясно, что в алгебраической форме проделать такой трюк практически невозможно, действительно, подумайте, как вы будете решать пример вроде?
И здесь на помощь приходит тригонометрическая форма комплексного числа и, так называемая, формула Муавра : Если комплексное число представлено в тригонометрической форме , то при его возведении в натуральную степеньсправедлива формула:
Просто
до безобразия.
Пример 10
Дано комплексное число , найти.
Что нужно сделать? Сначала нужно представить данное число в тригонометрической форме. Внимательные читатели заметили, что в Примере 8 мы это уже сделали:
Тогда, по формуле Муавра:
Упаси боже, не нужно считать на калькуляторе , а вот угол в большинстве случае следует упростить. Как упростить? Образно говоря, нужно избавиться от лишних оборотов. Один оборот составляетрадиан или 360 градусов. Выясним сколько у нас оборотов в аргументе. Для удобства делаем дробь правильной:, после чего становится хорошо видно, что можно убавить один оборот:. Надеюсь всем понятно, чтои– это один и тот же угол.
Таким образом, окончательный ответ запишется так:
Отдельная разновидность задачи возведения в степень – это возведение в степень чисто мнимых чисел.
Пример 12
Возвести в степень комплексные числа ,,
Здесь тоже всё просто, главное, помнить знаменитое равенство.
Если мнимая единица возводится в четную степень, то техника решения такова:
Если мнимая единица возводится в нечетную степень, то «отщипываем» одно «и», получая четную степень:
Если есть минус (или любой действительный коэффициент), то его необходимо предварительно отделить:
Извлечение корней из комплексных чисел.
Квадратное уравнение с комплексными корнямиРассмотрим пример:
Нельзя извлечь корень? Если речь идет о действительных числах, то действительно нельзя. В комплексных числах извлечь корень – можно! А точнее, два корня:
Действительно ли найденные корни являются решением уравнения ? Выполним проверку:
Что и требовалось проверить.
Часто используется сокращенная запись, оба корня записывают в одну строчку под «одной гребёнкой»: .
Такие корни также называют сопряженными комплексными корнями .
Как извлекать квадратные корни из отрицательных чисел, думаю, всем понятно: ,,,,и т.д. Во всех случаях получаетсядва сопряженных комплексных корня.
Начнем с любимого квадрата.
Пример 9
Возвести в квадрат комплексное число
Здесь можно пойти двумя путями, первый способ это переписать степень как произведение множителей и перемножить числа по правилу умножения многочленов.
Второй способ состоит в применение известной школьной формулы сокращенного умножения :
Для комплексного числа легко вывести свою формулу сокращенного умножения:
Аналогичную формулу можно вывести для
квадрата разности, а также для куба
сумма и куба разности.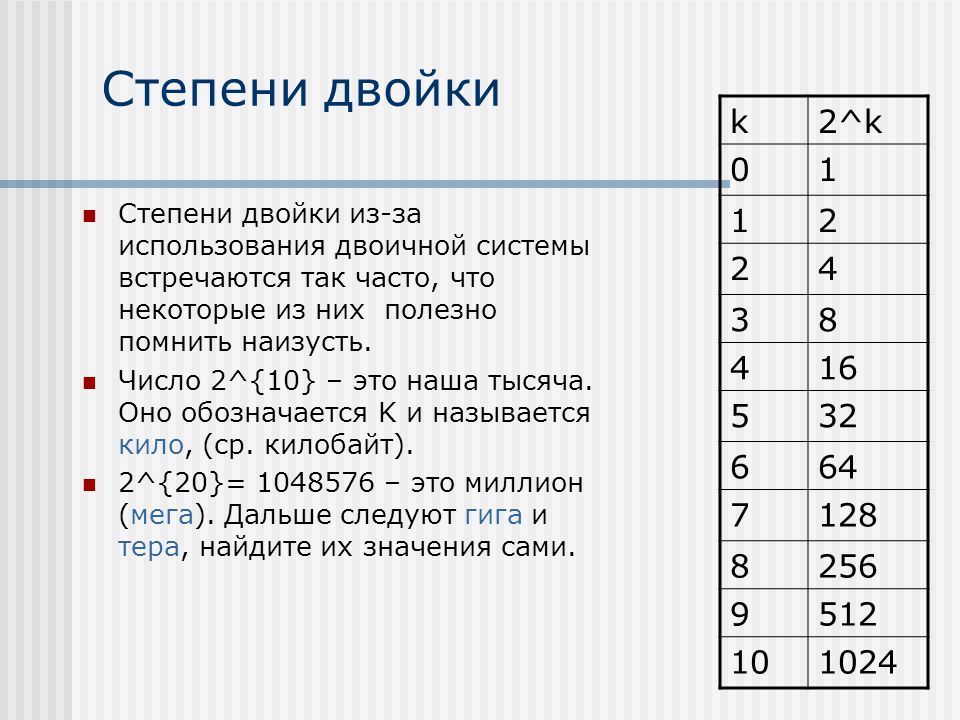
Но эти формулы
более актуальны длязадач
комплексного анализа. Что делать,
если комплексное число нужно возвести,
скажем, в 5-ую, 10-ую или 100-ую степень?
Ясно, что в алгебраической форме проделать
такой трюк практически невозможно,
действительно, подумайте, как вы будете
решать пример вроде?
И здесь на помощь приходит тригонометрическая форма комплексного числа и, так называемая, формула Муавра : Если комплексное число представлено в тригонометрической форме , то при его возведении в натуральную степеньсправедлива формула:
Просто до безобразия.
Пример 10
Дано комплексное число , найти.
Что нужно сделать? Сначала нужно представить данное число в тригонометрической форме. Внимательные читатели заметили, что в Примере 8 мы это уже сделали:
Тогда, по формуле Муавра:
Упаси
боже, не нужно считать на калькуляторе
,
а вот угол в большинстве случае следует
упростить. Как упростить? Образно
говоря, нужно избавиться от лишних
оборотов.
Один оборот составляетрадиан
или 360 градусов. Выясним сколько у нас
оборотов в аргументе.
Для удобства делаем дробь правильной:,
после чего становится хорошо видно, что
можно убавить один оборот:.
Надеюсь всем понятно, чтои–
это один и тот же угол.
Таким образом, окончательный ответ запишется так:
Отдельная разновидность задачи возведения в степень – это возведение в степень чисто мнимых чисел.
Пример 12
Возвести в степень комплексные числа ,,
Здесь тоже всё просто, главное, помнить знаменитое равенство.
Если мнимая единица возводится в четную степень, то техника решения такова:
Если мнимая единица возводится в нечетную степень, то «отщипываем» одно «и», получая четную степень:
Если есть минус (или любой действительный коэффициент), то его необходимо предварительно отделить:
Извлечение корней из комплексных чисел. Квадратное уравнение с комплексными корнями
Рассмотрим пример:
Нельзя
извлечь корень? Если речь идет о
действительных числах, то действительно
нельзя.
В комплексных числах извлечь
корень – можно! А точнее, два корня:
Действительно ли найденные корни являются решением уравнения ? Выполним проверку:
Что и требовалось проверить.
Часто используется сокращенная запись, оба корня записывают в одну строчку под «одной гребёнкой»: .
Такие корни также называют сопряженными комплексными корнями .
Как извлекать квадратные корни из отрицательных чисел, думаю, всем понятно: ,,,,и т.д. Во всех случаях получаетсядва сопряженных комплексных корня.
Пример 13
Решить квадратное уравнение
Вычислим дискриминант:
Дискриминант отрицателен, и в действительных числах уравнение решения не имеет. Но корень можно извлечь в комплексных числах!
По известным школьным формулам получаем два корня: – сопряженные комплексные корни
Таким образом, уравнение имеет два сопряженных комплексных корня:,
Теперь вы сможете решить любое квадратное уравнение!
И
вообще, любое уравнение с многочленом
«энной» степени
имеет
ровнокорней,
часть из которых может быть комплексными.
Простой пример для самостоятельного решения:
Пример 14
Найти корни уравнения и разложить квадратный двучлен на множители.
Разложение на множители осуществляется опять же по стандартной школьной формуле.
Пример построения логики: Полномочия
Пример логического построения: ПолномочияПонимание математики по Питер Альфельд, кафедра математики, Университет Юты
Пример логической конструкции
Полномочия
Математические концепции строятся на более простых математических
концепции. Удивительно, как быстро можно перейти от
простые факты к очень сложным. я постараюсь
проиллюстрировать это явление на этой странице, рассматривая
силы.
В идеале вы показываете, например, что два поднятых
в степени три означает два раза два раза два, , но не
намного больше. Двойка называется основанием числа
степени, а три — показатель степени (просто чтобы мы не
должны сказать «число сверху» или «на
нижний «).
Итак, мы определяем для всех
натуральные числа
н:
(1)
Число a, возведенное в степень n, получается записью основание в n раз и запись знаков умножения в между а. Если бы вместо этого мы написали плюсики, то получили бы произведение n раз а. Это чрезвычайно просто. Но большой вопросы вытекают из малых.
В определении (1) основание a может быть любым действительным
количество. Но показатель степени ограничен естественным
количество.
Я предполагаю, что вы понимаете определение (1) и
ничего больше о полномочиях. (Эта страница была бы очень
эффективным, если бы это было правдой.) Вы поверите, что
время, когда вы просматриваете эту страницу, возможно, через полчаса после
теперь ты поймешь, что
(2)
а на самом деле намного больше?
Восемь в отрицательной степени четыре трети равно 1 шестнадцатой!? Вы имеете в виду, если вы запишете восемь отрицательных раз по четыре трети и соедини эти восьмерки с полученными знаками умножения одна шестнадцатая? Это не имеет смысла! Тем не менее, (2) есть истинный! Только представьте, как вы можете увлечь вашу дату в вашем следующую возможность, небрежно упомянув интересные факты, такие как что!
Но как мы придем к этому факту? Что ж, надо продлить
определение (1) соответствующим образом.
Отрицательные четыре трети – это
Рациональное число,
но пока мы в этом, мы могли бы также пройти весь путь до
настоящий
экспоненты. Так как же нам «расширить определение (1)»?
Почему бы просто не сделать (2) определение и покончить с этим?
Руководящий принцип при обобщении математической концепции заключается в том, чтобы позаботиться о том, чтобы все, что было правдой до обобщение остается верным. Другими словами, мы хотим чтобы все было последовательно.
Пойдем по шагам и начнем с показателя степени 0. Подходящий
Исходное наблюдение состоит в том, что если мы умножим на на
степень три и в степени четыре, то мы
получить a в степени семь, так как мы написали a в общей сложности семь раз и умножить все эти вместе.
Другими словами, для всех натуральных чисел м и п
(3)
Любое определение a в нулевой степени должно сохранять свойство (3) (и на самом деле ряд других, но я просто дать вам вкус вещей). Так что, в частности, мы должны имеют
(4)
Другими словами, умножая на в степени сущ. с а в степени 0 нет замените на в степени n . Как это может быть, если
(5)
Таким образом, мы делаем (5) определение для как для
мощность ноль. Мы тщательно выбрали это определение, чтобы быть
в соответствии с тем, что мы делали раньше. Если бы мы разрабатывали
власти серьезно, мы должны были бы подумать еще более тщательно
о том, может ли (5) противоречить чему-либо еще, что мы
думал, что мы поняли раньше.
(Это действительно так, если база
равен нулю. Подумай об этом!)
А как насчет того, чтобы показатель степени был отрицательным целым числом? Давайте снова вызовем это правило (3). Мы должны иметь, для всех целые числа n, что
(6)
Как может быть , если только
? (7)
Но мы должны быть осторожны! Что если а=0 (и n=1 , скажем). Тогда мы будем делить на ноль, что мы должны не делать. (Причина этого в том, что деление на ноль нельзя определить, не впадая в противоречия. Там может быть ссылка здесь когда-нибудь на подходящий аргумент.) Итак, чтобы избежать этого осложнения
мы требуем, чтобы основание было ненулевым.
Теперь вперед к рациональным показателям! давайте сделаем еще один наблюдение. Если мы возьмем два в степени три, и все что в степени четыре, то запишем два в степени три четыре раза (сделай это!). Таким образом, мы записываем число два в общей сложности двенадцать раз. Обобщая это наблюдение ясно, что для всех натуральных чисел м и п
(8)
Сначала рассмотрим случай, когда показатель степени равен единице. половина. В этом случае должно применяться правило № 8, т. е. мы должен иметь
(9)
Итак, ясно, что равно в степени 1/2.
квадратный корень из из a , т. е. этот номер
квадрат которого равен .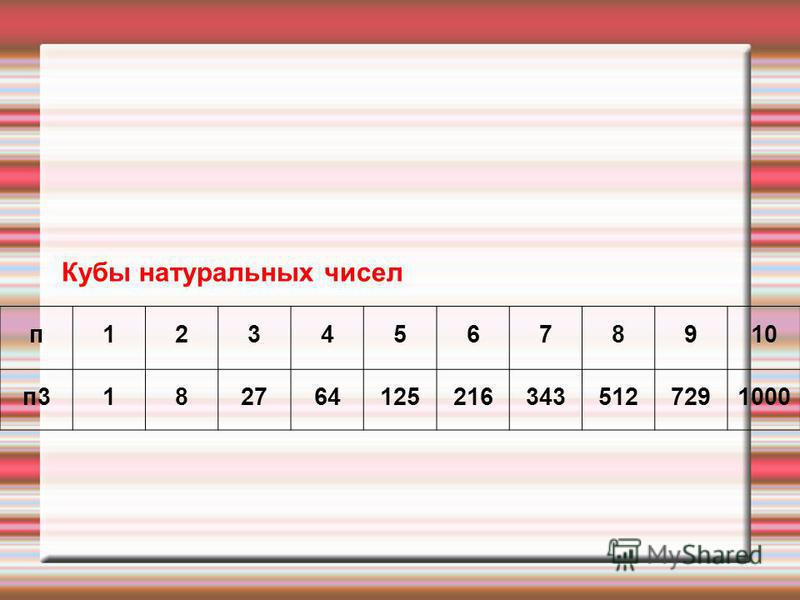
Но опять же, мы должны быть осторожны.
Не существует действительного числа, квадрат которого равен единице, ибо
пример. Мы могли бы преодолеть эту трудность, позволив
полномочия, значения которых
комплексные числа.
Но это было бы слишком технически, поэтому давайте
просто требуй этого
(10)
Теперь давайте обобщим идею квадратного корня. Для любого рационального число q мы должны иметь (чтобы сохранить справедливость правила (8)), что
(11)
что явно требует, чтобы мы определили
(12)
Чтобы получить определение рациональных показателей п/к где p и q — целые числа, а q не равно нулю, мы снова используем правило 8 (или более именно, мы делаем определение, которое согласуется с правилом (8)):
(13)
Теперь мы можем решить головоломку, с которой начали, используя правило (13) и требование, чтобы правило (7) применялось к рациональным показатели:
(14)
Итак, мы достигли нашей цели.
Конечно развитие дано
здесь не полный. В частности, можно расслабить
требование, чтобы база была положительной, допуская сложные
чисел и путем ограничения показателей. Однако вы видели
основные идеи в действии: сделать определения, которые
соответствует тому, что было раньше.
Один заключительный комментарий. Определить полномочия (с положительными основаниями) а также настоящий показатели используются методы, разработанные в исчислении. К дать вам вкус, если показатель степени квадратный корень из двух рассматривается последовательность рациональных чисел, которая получает все ближе и ближе к квадратному корню из двух, и соответствующую последовательность полномочий. Эта последовательность приближается и ближе к действительному числу, которое мы затем определяем как требуемая мощность:
(15)
[26 ноября 1996 г.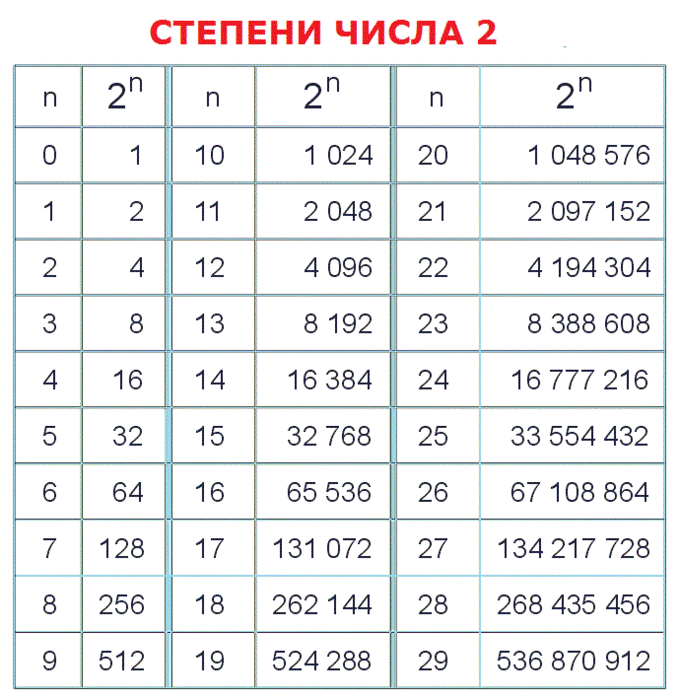
]
Перейдите на домашнюю страницу Питера Альфельда.
Мелкий шрифт, ваши комментарии, больше ссылок, Питер Альфельд, PA1UM
[08 апреля 1996 г.]
Степени 10 — Значение, Факты, Примеры
Степени числа 10 относятся к числам, в которых основание равно 10, а показатель степени — целое число. Например, 10 2 , 10 3 , 10 6 показывают разные степени числа 10. Это можно понять с помощью понятия, что когда 10 умножается определенное количество раз, то это может быть выражено в форме показателей, и они называются степенями числа 10. Давайте узнаем больше о степенях числа 10 на этой странице.
| 1. | Что означает степень 10? |
2. | 10 в степени 2 |
| 3. | 10 в степени 3 |
| 4. | 10 в степени 1 |
| 5. | Степени 10 Диаграмма |
| 6. | Часто задаваемые вопросы о степени числа 10 |
Что означает степень 10?
Степени 10 означают, что при умножении 10 определенное количество раз произведение можно выразить с помощью показателей степени. Эти числа, которые записываются как степени 10. Если мы умножим 10 пару раз, будет трудно написать число, как в этом случае, 10 × 10 × 10 × 10 × 10 × 10 × 10 × 10 × 10 = 1000000000. Теперь, если нам нужно умножить 10 тридцать раз, будет еще сложнее написать произведение с таким количеством нулей. Следовательно, показатели степени помогают легко выразить это, и это значение (10 × 10 × 10 × 10 × 10 × 10 × 10 × 10 × 10 = 1000000000) может быть выражено как 10 9 . Здесь 10 — основание, 9 — степень, и это читается как 10 в девятой степени.
А теперь попробуем понять это с другой стороны. Например, 10 в 7-й степени означает 10 7 . Это значит, что нам нужно умножить 10 семь раз, то есть 10 7 = 10 × 10 × 10 × 10 × 10 × 10 × 10
Это можно объяснить и по-другому.
Степени числа 10 имеют вид 10 x , где x — целое число. 10 х читается как «10 в степени x». Если x положителен, мы упрощаем 10 x , умножая 10 само на себя x раз. Например, 10 3 = 10 × 10 × 10 (3 раза) = 1000. Если x отрицательно, то мы применяем свойство показателей, a -m = 1/a m , а затем применяем та же логика, что описана ранее. Например, 10 -3 = 1/10 3 = (1/10) 3 = 1/10 × 1/10 × 1/10 = 1/1000 = 0,001. Используя эти два примера, мы можем сделать вывод о двух вещах, которые очень полезны для вычисления степеней числа 10.
- Когда степень положительна, 10 x = «1, за которой следует x нулей».
Например, 10 6 = 1 000 000. Здесь после 1 стоит 6 нулей, потому что степень числа 10 равна 6. - Когда степень отрицательна, 10 -x = ‘0 баллов, за которыми следует (x -1) количество нулей, за которыми следует 1″.
Например, 10 -6 = 0,000001. Здесь мы поместили 5 нулей после запятой (за которыми следует 1), так как степень была отрицательной 6, а 6 — 1 = 5,9.0263
10 в степени 2
10 в степени 2 также называется второй степенью числа десять. Это записывается как 10 2 , и это означает, что 10 умножается на два. Другими словами, 10 × 10 = 10 2 . Здесь 10 — основание, а 2 — показатель степени. Далее это можно оценить как 10 2 = 100.
10 в степени 3
10 в степени 3 называется третьей степенью десяти и записывается как 10 3 . Это означает, что 10 × 10 × 10 = 10 3 . В этом выражении 10 в третьей степени, 10 — основание, а 3 — его степень или показатель степени.
Это также можно оценить как 10 3 = 1000.
10 в степени 1
10 в степени 1 означает первую степень десяти, которая равна 10 1 . Мы знаем, что любое число в степени 1 означает, что это само число. Итак, здесь 10 1 = 10
.
Степени 10 Таблица
Таблица степеней 10 показывает, что разные степени 10 имеют разные значения. Например, если мы запишем 10 5 в расширенной форме, это будет 10 5 = 10 × 10 × 10 × 10 × 10. Теперь значение 10 5 в десятичной форме будет 100000. А если записать в виде дроби, то будет 100000/1. Точно так же, если мы запишем 10 -5 в развернутом виде, это будет 10 -5 = 1/(10 × 10 × 10 × 10 × 10). Теперь значение 10 -5 в десятичном виде будет 0,00001. А если записать в виде дроби, то будет 1/100000. В следующей таблице показаны степени 10, которые включают положительные и отрицательные степени.
Положительные силы числа 10
Силы числа 10 имеют определенные названия (хотя и не все силы) для некоторых особых способностей.
Например, 10 6 (10 в степени 6) известен как «миллион», а префикс SI 10 в степени 6 — это «гига», который представлен символом SI G. Точно так же у нас есть некоторые конкретные имена для некоторых положительных степеней числа 10, которые приведены в следующей таблице.
| Положительные степени числа 10 | Имя | Префикс (символ) |
|---|---|---|
| 10 1 = 10 | Десять | Дека (D) |
| 10 2 = 100 | Сотня | Гекто (H) |
| 10 3 = 1000 | тысяча | Кило (К) |
| 10 6 = 1 000 000 | Миллион | Мега (М) |
| 10 9 = 1 000 000 000 | миллиард | Гига (Г) |
| 10 12 = 1 000 000 000 000 | Триллион | Тера (Т) |
| 10 15 = 1 000 000 000 000 000 | Квадриллион | Пета (П) |
| 10 18 = 1 000 000 000 000 000 000 | Квинтиллион | Экса (Е) |
| 10 21 = 1 000 000 000 000 000 000 000 | Секстиллион | Зетта (Z) |
| 10 24 = 1 000 000 000 000 000 000 000 000 | Септиллион | Йотта (Я) |
Отрицательные степени числа 10
Отрицательные степени числа 10 выражаются по-другому.
Мы знаем, что отрицательная степень (отрицательная экспонента) определяется как мультипликативная инверсия основания. Это означает, что мы пишем обратное число, а затем решаем его как положительные показатели степени. Например, (4/5) -2 можно записать как (5/4) 2 . Точно так же отрицательная степень числа 10, например 10 -3 , может быть записана как 1/10 3 или 1/(10 × 10 × 10) = 1/1000 = 0,001
Точно так же, как у нас есть некоторые необычные названия для положительных степеней числа 10, у нас есть некоторые названия для некоторых отрицательных степеней числа 10. Некоторые из них приведены в следующей таблице.
| Отрицательные степени числа 10 | Имя | Префикс (символ) |
|---|---|---|
| 10 -1 = 0,1 | Десятый | Деци (д) |
| 10 -2 = 0,01 | Сотый | Сенти (с) |
| 10 -3 = 0,001 | Тысячная | Милли (м) |
| 10 -6 = 0,000001 | Миллионный | Микро (мк) |
| 10 -9 = 0,000000001 | Миллиардный | Нано (н) |
| 10 -12 = 0,000000000001 | Триллионный | Пико (р) |
| 10 -15 = 0,000000000000001 | Квадриллионный | Фемто (ф) |
| 10 -18 = 0,0000000000000000001 | Квинтиллионный | Атто (а) |
| 10 -21 = 0,0000000000000000000001 | Шестимиллиардный | Зепто (г) |
| 10 -24 = 0,000000000000000000000001 | Септиллион | Йокто (у) |
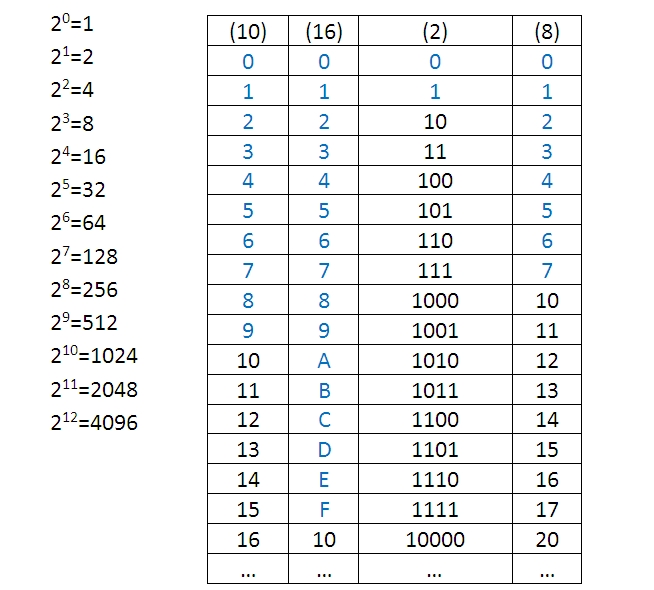
2 в степени 10
Следует отметить, что 2 в степени 10 — это , а не то же самое, что 10 в степени 2.
2 в степени 10 означает число, в котором 2 основание и 10 показатель степени. Это записывается как 2 10 , и это означает, что 2 умножается на десять, то есть 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 1024,
Вычисление степеней числа 10
Чтобы вычислить сумму, разность, произведение и частное степеней числа 10, мы можем сначала найти значения степеней числа 10, а затем выполнить соответствующую операцию. Например, 10 3 /10 2 = 1000/100 = 10. Но иногда эта процедура затруднительна, если показатель степени очень велик. В таких случаях помогут следующие процедуры.
Сложение и вычитание степеней 10
Чтобы сложить и вычесть степени 10, мы берем минимальную степень 10 в качестве общего множителя, а затем упрощаем остальные. Например,
- 10 5 + 10 8 = 10 5 (1 + 10 3 ) = 10 5 (1 + 1000) = 10 5 (1001) = 100,172 = 100,1366666666666666666 (1 + 1000) = 10 5 (1001) = 10017666 (1 + 1000).
Умножение степеней 10
Чтобы умножить степени 10, мы применяем правило экспоненты, которое гласит: m × a n = a m + n Это правило говорит о том, что нам нужно складывать показатели степени, когда основания одинаковы. Следовательно, это правило можно применять для умножения двух или более степеней 10. Вот несколько примеров.
- 10 5 × 10 8 = 10 5 + 8 = 10 13
- 10 -3 × 10 6 = 10 -3 + 6 = 10 3
Делительные степени числа 10
Существует правило показателей, a m / a n = a m — n . Мы используем это правило, чтобы разделить степени числа 10. Это правило говорит, что нам нужно вычесть степени, когда основания одинаковы. Вот несколько примеров.
- 10 17 / 10 15 = 10 17 — 15 = 10 2 = 100
- 10 -6 / 10 -12 = 10 -6 + 12 = 10 6
Важные советы по степеням числа 10
- Степени числа 10 относятся к таким числам, как 10 5 или 10 6 , где 10 — основание, а 5 и 6 — его степени.
- 2 в степени 10 означает число, в котором 2 — основание, а 10 — показатель степени, то есть 2 10 .
- Точно так же, как 2 в степени 10 означает 2 10 , другие фразы, такие как 3 в степени 10, означают 3 10 , 4 в степени 10 означает 4 10 . Их не следует путать со степенями числа 10, которые мы изучали на этой странице.
☛ Связанные темы
- Экспоненциальные правила
- Умножение показателей степени
- Как выразить 10 в степени 10?
Часто задаваемые вопросы о степени 10
Каковы степени числа 10 в математике?
Степени числа 10 относятся к числам, в которых 10 является основанием, а любое целое число является показателем степени. Например, 10 3 , 10 6 , 10 -7 — это несколько примеров степеней числа 10.
Сколько будет 10 в степени 10?
10 в степени 10 означает выражение, в котором 10 — основание, а 10 — показатель степени.
Это можно выразить как 10 10 и это означает, что 10 умножается на 10, то есть 10 × 10 × 10 × 10 × 10 × 10 × 10 × 10 × 10 × 10, что равно 10000000000.
Как преобразовать 0,00001 в степень 10?
Чтобы преобразовать 0,00001 в степень 10, сначала нам нужно преобразовать это десятичное число в форму дроби. Это составит 1/100000. Теперь эту дробь можно записать в экспоненциальной форме, которая будет равна 1/10 5 . Далее это можно выразить как отрицательную экспоненту,10 -5
Как преобразовать число в степень 10?
Чтобы преобразовать число в степень 10, мы записываем его в экспоненциальной записи. Например, число 5040000000000000 немного сложно написать, и было бы проще, если бы мы записали его в стандартной форме, где мы используем степени 10. Таким образом, это выражается как 5,04 × 10 15 . Давайте посмотрим, как записать это число в стандартной экспоненциальной форме, используя следующие шаги:
- Шаг 1: Подсчитайте количество нулей в конце заданного числа. В данном числе 5040000000000000 количество нулей в конце равно 13.
- Шаг 2: Используйте начальную часть заданного числа и напишите цифры слева до последней отличной от нуля цифры, за которой следует 10, возведенная в степень, равную числу конечных нулей. Это означает 504 и 10 13
- Шаг 3: Поставьте десятичную точку после первой цифры с левой стороны и прибавьте количество десятичных разрядов, которые были созданы, в степени 10, которая записана. Здесь мы поставим десятичную точку после 5, и она станет 5,04. Поскольку в версии 5.04 было создано 2 десятичных знака, мы добавим 2 к существующей степени 10. Существующая степень 10 была равна 13, потому что было 13 нулей в конце, но теперь она станет 15. Это сделает ее 5,04 × 10 15 . Следовательно, 5040000000000000 можно записать как 5,04 × 10 15
В данном числе 5040000000000000 количество нулей в конце равно 13.Как записать 100 в степени 10?
Чтобы записать 100 как степень числа 10, мы сначала посчитаем количество нулей в 100, то есть два.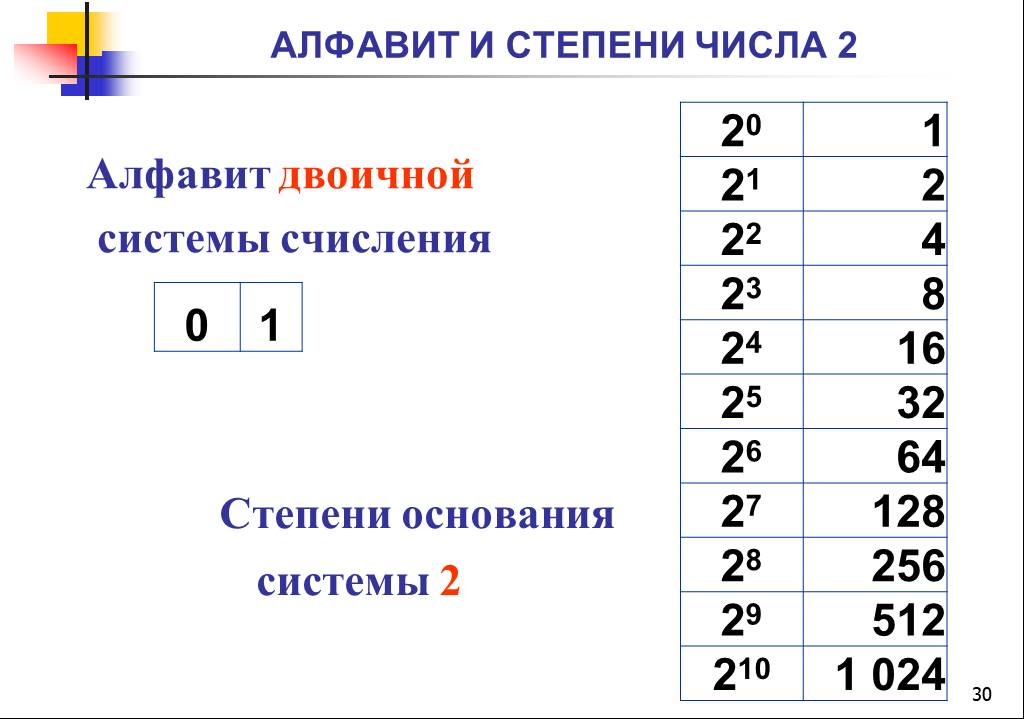
Это означает, что 100 = 10 × 10. Следовательно, 100 как степень числа 10 можно записать как 10 2
Что такое вторая степень числа 10?
Вторая степень числа 10 может быть записана как 10 2 . Это также известно как 10 в степени 2 и равно 100, потому что 10 2 = 10 × 10 = 100.
Чему равна первая степень числа 10?
Первая степень числа 10 записывается как 10 1 . Это также читается как 10 в степени 1, и мы знаем, что любое число в степени 1 является самим числом, поэтому 10 1 = 10.
Как умножить десятичные дроби на степени 10?
Чтобы умножать десятичные числа на степени 10, нам нужно запомнить простое правило. Мы выражаем произведение таким образом, что мы записываем данное десятичное число и перемещаем десятичную точку вправо в соответствии с числом, заданным как показатель степени 10. Если показатель степени 10 равен 3, мы запишем данное число и переместим десятичные 3 знака справа, чтобы получить ответ легко.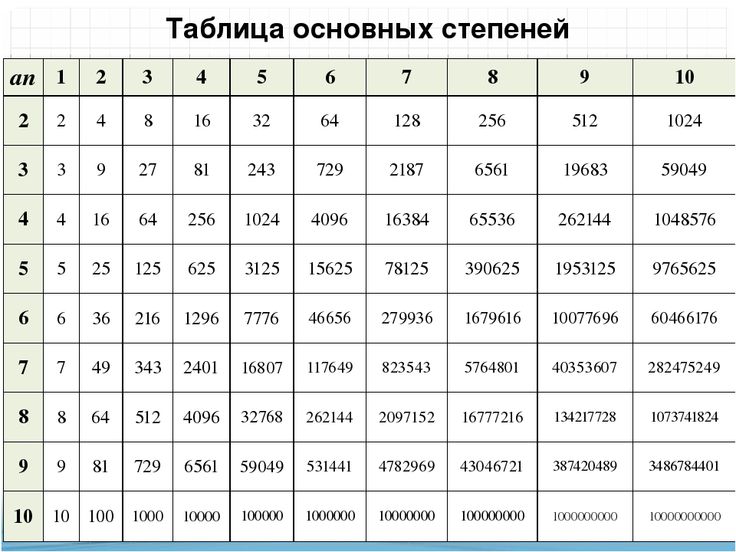
Например, если нам нужно умножить 46,3 × 10 4 , мы видим, что показатель степени 10 равен 4, поэтому мы переместим десятичную точку на 4 знака вправо. Это означает, что 46,3 × 10 4 = 463000.
Сколько будет 2 в степени 10?
2 в степени 10 означает выражение, где 2 — основание, а 10 — показатель степени. Это может быть выражено как 2 10 , и это означает, что 2 умножается в десять раз, то есть 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 1024.
Как записать Данное число как степень 10?
- Чтобы выразить заданное число (>1) как степень 10, просто запишите его как 10 n (n положительное число), где n — количество нулей после 1 в заданном числе. Например, 10000 = 10 4 .
- Чтобы выразить заданное число (<1) в степени 10, просто подсчитайте количество нулей после «0» и перед «1», добавьте 1 к результату, а затем поставьте это число вместе со знаком «минус» в виде показатель степени числа 10.
