Степени двоичной системы счисления – . ., ,

Двоичная система счисления

☰

В двоичной системе счисления используются всего две цифры 0 и 1. Другими словами, двойка является основанием двоичной системы счисления. (Аналогично у десятичной системы основание 10.)

Чтобы научиться понимать числа в двоичной системе счисления, сначала рассмотрим, как формируются числа в привычной для нас десятичной системе счисления.

В десятичной системе счисления мы располагаем десятью знаками-цифрами (от 0 до 9). Когда счет достигает 9, то вводится новый разряд (десятки), а единицы обнуляются и счет начинается снова. После 19 разряд десятков увеличивается на 1, а единицы снова обнуляются. И так далее. Когда десятки доходят до 9, то потом появляется третий разряд – сотни.

Двоичная система счисления аналогична десятичной за исключением того, что в формировании числа участвуют всего лишь две знака-цифры: 0 и 1. Как только разряд достигает своего предела (т.е. единицы), появляется новый разряд, а старый обнуляется.

Попробуем считать в двоичной системе:
0 – это ноль
1 – это один (и это предел разряда)
10 – это два
11 – это три (и это снова предел)
100 – это четыре
101 – пять
110 – шесть
111 – семь и т.д.

Перевод чисел из двоичной системы счисления в десятичную

Не трудно заметить, что в двоичной системе счисления длины чисел с увеличением значения растут быстрыми темпами. Как определить, что значит вот это: 10001001? Непривычный к такой форме записи чисел человеческий мозг обычно не может понять сколько это. Неплохо бы уметь переводить двоичные числа в десятичные.

В десятичной системе счисления любое число можно представить в форме суммы единиц, десяток, сотен и т.д. Например:

1476 = 1000 + 400 + 70 + 6

Можно пойти еще дальше и разложить так:

1476 = 1 * 10³ + 4 * 10² + 7 * 10¹ + 6 * 10⁰

Посмотрите на эту запись внимательно. Здесь цифры 1, 4, 7 и 6 — это набор цифр из которых состоит число 1476. Все эти цифры поочередно умножаются на десять возведенную в ту или иную степень. Десять – это основание десятичной системы счисления. Степень, в которую возводится десятка – это разряд цифры за минусом единицы.

Аналогично можно разложить и любое двоичное число. Только основание здесь будет 2:

10001001 = 1*2⁷ + 0*2⁶ + 0*2⁵ + 0*2⁴ + 1*2³ + 0*2² + 0*2¹ + 1*2⁰

Если посчитать сумму составляющих, то в итоге мы получим десятичное число, соответствующее 10001001:

1*2⁷ + 0*2⁶ + 0*2⁵ + 0*2⁴ + 1*2³ + 0*2² + 0*2¹ + 1*2⁰ = 128 + 0 + 0 + 0 + 8 + 0 + 0 + 1 = 137

Т.е. число 10001001 по основанию 2 равно числу 137 по основанию 10. Записать это можно так:

10001001₂ = 137₁₀

Почему двоичная система счисления так распространена?

Дело в том, что двоичная система счисления – это язык вычислительной техники. Каждая цифра должна быть как-то представлена на физическом носителе. Если это десятичная система, то придется создать такое устройство, которое может быть в десяти состояниях. Это сложно. Проще изготовить физический элемент, который может быть лишь в двух состояниях (например, есть ток или нет тока). Это одна из основных причин, почему двоичной системе счисления уделяется столько внимания.

Перевод десятичного числа в двоичное

Может потребоваться перевести десятичное число в двоичное. Один из способов – это деление на два и формирование двоичного числа из остатков. Например, нужно получить из числа 77 его двоичную запись:

77 / 2 = 38 (1 остаток)
38 / 2 = 19 (0 остаток)
19 / 2 = 9 (1 остаток)
9 / 2 = 4 (1 остаток)
4 / 2 = 2 (0 остаток)
2 / 2 = 1 (0 остаток)
1 / 2 = 0 (1 остаток)

Собираем остатки вместе, начиная с конца: 1001101. Это и есть число 77 в двоичном представлении. Проверим:

1001101 = 1*2⁶ + 0*2⁵ + 0*2⁴ + 1*2³ + 1*2² + 0*2¹ + 1*2⁰ = 64 + 0 + 0 + 8 + 4 + 0 + 1 = 77

inf1.info

Двоичная система счисления

Главная / Ассемблер / Для чайников / Системы счисления /

Чисто технически было бы очень сложно сделать компьютер, который бы «понимал» десятичные числа. А вот сделать компьютер, который понимает двоичные числа достаточно легко. Двоичное число оперирует только двумя цифрами – 0 и 1. Несложно сопоставить с этими цифрами два состояния – вЫключено и включено (или нет напряжения – есть напряжение). Процессор – это микросхема с множеством выводов. Если принять, что отсутствие напряжения на выводе – это 0 (ноль), а наличие напряжения на выводе – это 1 (единица), то каждый вывод может работать с одной двоичной цифрой. Сейчас мы говорим о процессоре очень упрощённо, потому что мы изучаем не процессоры, а системы исчисления. Об устройстве процессора вы можете почитать здесь: Структура процессора.

Конечно, это касается не только процессоров, но и других составляющих компьютера, например, шины данных или шины адреса. И когда мы говорим, например, о разрядности шины данных, мы имеем ввиду количество выводов на шине данных, по которым передаются данные, то есть о количестве двоичных цифр в числе, которое может быть передано по шине данных за один раз. Но о разрядности чуть позже.

Итак, процессор (и компьютер в целом) использует двоичную систему, которая оперирует всего двумя цифрами: 0 и 1. И поэтому основание двоичной системы равно 2. Аналогично, основание десятичной системы равно 10, так как там используются 10 цифр.

Каждая цифра в двоичном числе называется бит

(или разряд). Четыре бита – это полубайт (или тетрада), 8 бит – байт, 16 бит – слово, 32 бита – двойное слово. Запомните эти термины, потому что в программировании они используются очень часто. Возможно, вам уже приходилось слышать фразы типа слово данных или байт данных. Теперь, я надеюсь, вы понимаете, что это такое.

Отсчёт битов в числе начинается с нуля и справа. То есть в двоичном числе самый младший бит (нулевой бит) является крайним справа. Слева находится старший бит. Например, в слове старший бит – это 15-й бит, а в байте – 7-й. В конец двоичного числа принято добавлять букву b. Таким образом вы (и ассемблер) будете знать, что это двоичное число. Например,

101 – это десятичное число
101b – это двоичное число, которое эквивалентно десятичному числу 5.

А теперь попробуем понять, как формируется двоичное число.

Ноль, он и в Африке ноль. Здесь вопросов нет. Но что дальше. А дальше разряды двоичного числа заполняются по мере увеличения этого числа. Для примера рассмотрим тетраду. Тетрада (или полубайт) имеет 4 бита.

Двоичное	Десятичное	Пояснения
0000	0	—
0001	1	В младший бит устанавливается 1.
0010	2	В следующий бит (бит 1) устанавливается 1, предыдущий бит (бит 0) очищается.
0011	3	В младший бит устанавливается 1.
0100	4	В следующий бит (бит 2) устанавливается 1, младшие биты (бит 0 и 1) очищаются.
0101	5	В младший бит устанавливается 1.
0110	6	Продолжаем в том же духе…
0111	7	…
1000	8	…
1001	9	…
1010	10	…
1011	11	…
1100	12	…
1101	13	…
1110	14	…
1111	15	…

Итак, мы видим, что при формировании двоичных чисел разряды числа заполняются нулями и единицами в определённой последовательности:

Если младший равен нулю, то мы записываем туда единицу. Если в младшем бите единица, то мы переносим её в старший бит, а младший бит очищаем. Тот же принцип действует и в десятичной системе:

0…9
10 – очищаем младший разряд, а в старший добавляем 1

Всего для тетрады у нас получилось 16 комбинаций. То есть в тетраду можно записать 16 чисел от 0 до 15. Байт – это уже 256 комбинаций и числа от 0 до 255. Ну и так далее. На рис. 2.2 показано наглядно представление двоичного числа (двойное слово).

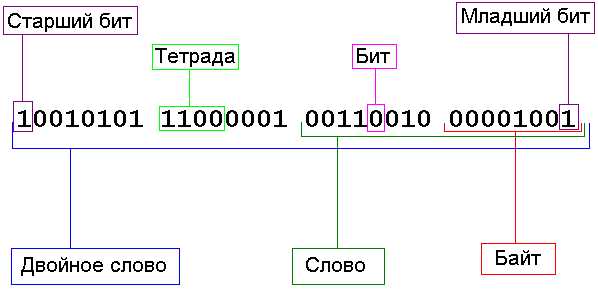
Рис. 2.2. Двоичное число.

www.av-assembler.ru

Двоичная система счисления

Для каждой счетной системы можно составить таблицы сложения и других арифметических действий. В двенадцатеричной системе 5+8=11, а Зх4=10. В семеричной системе 3+6=12, а 5х3=21. Нам это может показаться странным, поскольку мы не используем подобные системы. Но если мы проводим все расчеты в рамках одной из таких систем, мы видим, что система также отвечает поставленным целям. Человечество остановилось на

десятеричной системе по той простой причине, что на руках у человека десять пальцев, а вовсе не потому, что эта система более логична, чем любая другая.

Однако в отдельных случаях и для конкретных целей может оказаться, что какая-то система счета является гораздо более функциональной, нежели другие. Это справедливо в случае системы, основанной на 2, то есть двоичной системы.

Выражение 10 в двоичной системе равно 2 в десятеричной системе. Следовательно, в такой системе только две цифры, 0 и 1.

Перевод числа из двоичной системы в десятеричную не составляет труда. Рассмотрим, например, выражение 11001 в двоичной системе. Оно эквивалентно $(1\times2^4)+(1\times2^3)+(0\times2^2)+(0\times2^1)+(1\times2^0)$, или 16+8+0+0+1, или 25, что соответствует эквиваленту, приведенному в таблице.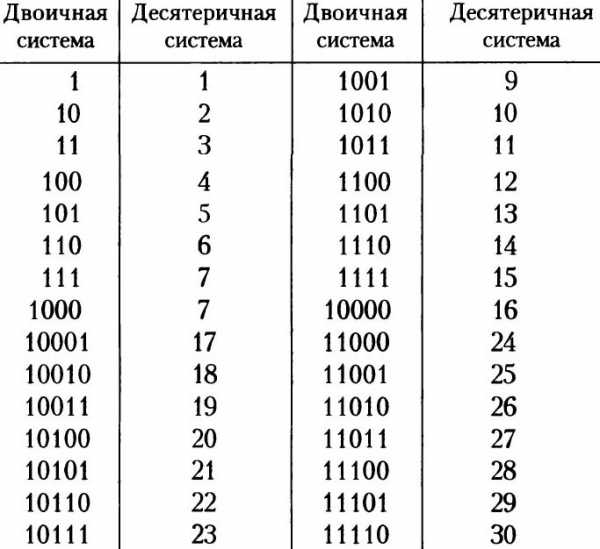

Этот процесс можно упростить, если принять во внимание, что число 2, возведенное в степень, умножается либо на 0, и тогда результат тоже будет равен нулю и его можно не учитывать, либо на 1, и тогда это просто 2, возведенное в какую-то степень.

Таким образом, мы можем проставить порядковый номер справа налево, как это показано ниже:

Каждое маленькое число — это степень числа 2, определяемая положением цифры в числе, представленном в двоичной системе. Следует учитывать только те показатели степени, которые стоят против единиц. Показатели, стоящие против нулей, можно опускать. Используя такой подход, можно записать число 11001 как $2^4+2^3+2^0$, или 16+8+1, или 25.

Большие числа, такие как 1 110 010 100 001 001, можно переводить в десятеричную систему таким же образом.

Поскольку единицам соответствуют позиции 0, 3, 8, 10, 13, 14 и 15, то число будет равняться $2^{15}+2^{14}+2^{13}+2^{10}+2^8+2^3+2^0$, или $32 768+16 384+8 192+1 024+256+8+1$, или $58 633$.

Обратный перевод из двоичной системы в десятеричную не очень сложен, но более длителен. Предположим, число 1562 выражено в десятеричной системе. В двоичную систему его можно перевести следующим образом:

Наибольшее число, соответствующее двойке, возведенной в степень, и меньшее 1562, — это $2^{10}$ (или 1024). Если мы вычтем 1024 из 1562, у нас останется 538. Теперь наибольшее число, соответствующее двойке, возведенной в степень, и меньшее 538, — это $2^9$ (или 512). После вычитания этой величины из 538 у нас остается 26. Ближайшее и меньшее число теперь — $2^4$ (или 16). После вычитания остается 10. Теперь ближайшее число — это $2^3$ (или 8). После вычитания остается 2 или $2^0$. Таким образом, $1562=2^{10}+2^9+2^4+2^3+2^1$.

Теперь надо только правильно расставить по местам показатели степени справа налево. Единицы будут стоять на 1, 3, 4, 9 и 10-й позициях. На остальных позициях мы поставим нули. Таким образом, мы получаем число 11 000 011 010, двоичный эквивалент числа 1562 в десятеричной системе.

В двоичной системе очень простые таблицы сложения и умножения:

И это весь список.

Таким образом, в двоичной системе:

Правильность этих вычислений можно, при желании, проверить, учитывая, что числа 11, 110 и 1001 в двоичной системе равны соответственно 3, 6 и 9 в десятеричной системе.

Теперь представьте себе, что у вас есть счетная электронная машина с набором переключателей (например, полупроводниковых). Каждый переключатель может находиться в одной из двух позиций — «включено» (когда ток проходит через переключатель) или «выключено» (когда ток не проходит через переключатель).

Теперь предположим, что положение «включено» соответствует 1, а положение «выключено» соответствует 0. В этом случае счетную машину можно спроектировать таким образом, чтобы переключение электрического сигнала различными переключателями подчинялось правилам сложения, умножения и другим действиям с единицами и нулями в двоичной системе.

Такая машина будет так быстро производить переключение и производить вычисления с такой скоростью, что сможет выполнить за считанные секунды такой объем вычислений, на который человеку потребовалось бы не меньше месяца.

Материалы по теме:

Поделиться с друзьями:

Загрузка…

matemonline.com

Двоичная система — это… Что такое Двоичная система?

Двоичная система счисления — это позиционная система счисления с основанием 2. В этой системе счисления натуральные числа записываются с помощью всего лишь двух символов (в роли которых обычно выступают цифры 0 и 1).

Двоичная система используется в цифровых устройствах, поскольку является наиболее простой и соответствует требованиям:

• Чем меньше значений существует в системе, тем проще изготовить отдельные элементы, оперирующие этими значениями. В частности, две цифры двоичной системы счисления могут быть легко представлены многими физическими явлениями: есть ток — нет тока, индукция магнитного поля больше пороговой величины или нет и т. д.
• Чем меньше количество состояний у элемента, тем выше помехоустойчивость и тем быстрее он может работать. Например, чтобы закодировать три состояния через величину индукции магнитного поля, потребуется ввести два пороговых значения, что не будет способствовать помехоустойчивости и надёжности хранения информации.
• Двоичная арифметика является довольно простой. Простыми являются таблицы сложения и умножения — основных действий над числами.
• Возможно применение аппарата алгебры логики для выполнения побитовых операций над числами.

В цифровой электронике одному двоичному разряду в двоичной системе счисления соответствует один двоичный логический элемент (инвертор с логикой на входе) с двумя состояниями (открыт, закрыт).

1 + 0 = 1
1 + 1 = 10
10 + 10 = 100

Таблица умножения двоичных чисел

0 • 0 = 0
0 • 1 = 0
1 • 0 = 0
1 • 1 = 1

Использование двоичной системы при измерении дюймами

При указании линейных размеров в дюймах по традиции используют двоичные дроби, а не десятичные, например: 5¾″, 7¹⁵/₁₆″, 3¹¹/₃₂″ и т. д.

Преобразование чисел

Для преобразования из двоичной системы в десятичную используют следующую таблицу степеней основания 2:

512

256

128

64

32

16

8

4

2

1

Начиная с цифры 1 все цифры умножаются на два. Точка, которая стоит после 1 называется двоичной точкой.

Преобразование двоичных чисел в десятичные

Допустим, вам дано двоичное число 110011. Какому числу оно эквивалентно? Чтобы ответить на этот вопрос, прежде всего запишите данное число следующим образом:

512	256	128	64	32	16	8	4	2	1
				1	1	0	0	1	1
				32	+16			+2	+1

Затем, начиная с двоичной точки, двигайтесь влево. Под каждой двоичной единицей напишите её эквивалент в строчке ниже. Сложите получившиеся десятичные числа. Таким образом, двоичное число 110011 равнозначно 51.
Либо .

Преобразование методом Горнера

Для того, что бы преобразовывать числа из двоичной в десятичную систему данным методом, надо суммировать цифры слева-направо, умножая ранее полученный результат на основу системы (в данном случае 2). Например, двоичное число 1011011 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+0=22 >> 22*2+1=45 >> 45*2+1=91 То есть в десятичной системе это число будет записано как 91. Или число 101111 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+1=23 >> 23*2+1=47 То есть в десятичной системе это число будет записано как 47.

Преобразование десятичных чисел к ближайшей степени двойки, неменьшей этого числа

Ниже приведена функция, возвращающая число, неменьшее аргумента, и являющееся степенью двух.

unsigned int to_deg_2(unsigned int num){
  int i;
  if ( num == 1 ) return 2;
  for( num-=1,i=1; i < sizeof(unsigned int)*8; i*=2 ) num = num|(num>>i);
  return num+1;
}

Преобразование десятичных чисел в двоичные

Допустим, нам нужно перевести число 19 в двоичное. Вы можете воспользоваться следующей процедурой :

19 /2 = 9  с остатком 1
9  /2 = 4  c остатком 1
4  /2 = 2  с остатком 0
2  /2 = 1  с остатком 0
1  /2 = 0  с остатком 1

Итак, мы делим каждое частное на 2 и записываем в остаток 1 или 0. Продолжать деление надо пока в делимом не будет 1. Ставим числа из остатка друг за другом, начиная с конца. В результате получаем число 19 в двоичной записи (начиная с конца): 10011.

Другие системы счисления

В статье «Системы счисления (продолжение)»^[1] описываются преимущества и недостатки 4-ричной системы счисления по сравнению с двоичной в компьютерах, созданных Хитогуровым.

См. также

Ссылки

1. ↑ http://potan.livejournal.com/91399.html Системы счисления (продолжение)

Wikimedia Foundation. 2010.

dic.academic.ru

Двоичная система счисления

<<Назад  |  Содержание  |  Далее>>

 

 

Двоичная (бинарная) система счисления имеет основание 2. Ее алфавит – цифры 0 и 1. Для перевода числа из двоичной системы счисления в десятичную также справедливо правило (6). Представим в десятичном виде число 1101₍₂₎, или, что то же самое, &1101 (& — амперсант, — этим символом принято указывать то, что следующая за ним запись двоичная).

1101₍₂₎=1*2³+1*2²+0*2¹+1*2⁰=1*8+1*4+0*2+1*1=13₍₁₀₎

 

 

Рис. 14. Перевод числа из двоичной СС в десятичную.

Но двоичная система имеет некоторые приятные особенности, т.к. коэффициентами при степенях двойки в ней могут быть только либо нули (и тогда можно просто игнорировать разряд числа, имеющий значение “0”), либо единицы (умножение на “1” также можно опустить).

Т.е. достаточно просуммировать “два в соответствующей степени” только в тех позициях двоичного числа, в которых находятся единицы. Степень же, в которую нужно возводить число 2, равна номеру позиции.

Арифметические операции в любой позиционной системе счисления также имеют общую логику.

Таблица 4.

 

1		“Круглые” числа в двоичной СС
&101	= 5(10)	&1	= 20	= 1
+        1		&10	= 21	= 2
&110	= 6(10)	&100	= 22	= 4
+        1		&1000	= 23	= 8
&111	= 7(10)	&10000	= 24	= 16

 

 

Каждый разряд двоичного числа имеет информационную емкость 1 бит. На основании одного двоичного разряда можно закодировать только два десятичных числа — &0=0₍₁₀₎, &1=1₍₁₀₎, на основании двух двоичных разрядов можно закодировать уже четыре десятичных числа – &00=0₍₁₀₎, &01=1₍₁₀₎ , &10=2₍₁₀₎, &11=3₍₁₀₎ , тремя двоичными разрядами можно представить восемь десятичных чисел  и т.д. в соответствии с формулой Хартли (2).

Таблица 5.

 

	20	десятичное		22	21	20	десятичное
	1	1		1	1	1	7
	0	0		1	1	0	6
				1	0	1	5
21	20	десятичное		1	0	0	4
1	1	3		0	1	1	3
1	0	2		0	1	0	2
0	1	1		0	0	1	1
0	0	0		0	0	0	0

 

Мы видим, что добавление каждого следующего разряда вдвое увеличивает количество двоичных комбинаций. Графически это может быть представлено так:

Рис. 15. Каждый следующий разряд двоичного числа удваивает количество возможных комбинаций из нулей и единиц.

 

 

Таблицу степеней числа 2 от 2⁰ до 2¹⁰ следует знать наизусть.

Таблица 6.

N	0	1	2	3	4	5	6	7	8	9	10
2N	1	2	4	8	16	32	64	128	256	512	1024

 

Открытие двоичного способа представления чисел приписывают китайскому императору Фо Ги, жизнь которого относится к 4-му тысячелетию до новой эры. Известный немецкий математик Лейбниц (1646-1716) в 1697 г. разработал правила двоичной арифметики. Он подчеркивал, что «вычисление с помощью двоек, то есть 0 и 1, в вознаграждение его длиннот, является для науки основным и порождает новые открытия, которые оказываются полезными впоследствии, даже в практике чисел, а особенно в геометрии: причиной чего служит то обстоятельство, что при сведении чисел к простейшим началам, каковы 0 и 1, всюду выявляется чудесный порядок».

Блестящие предсказания Лейбница сбылись только через 2,5 столетия, когда именно двоичная система счисления нашла применение в качестве универсального способа кодирования информации в компьютерах.

<<Назад  |  Содержание  |  Далее>>

inf5.ru

Что такое двоичная система счисления? Как перевести десятичное число в двоичное? :: SYL.ru

С двоичной системой счисления мы сталкиваемся при изучении компьютерных дисциплин. Ведь именно на базе этой системы построена работа процессора и некоторые виды шифрования. Существуют специальные алгоритмы для записи десятичного числа в двоичной системе и наоборот. Если знать принцип построения системы, оперировать в ней будет несложно.

Принцип построения системы из нулей и единиц

Двоичная система счисления построена с использованием двух цифр: ноль и один. Почему именно эти цифры? Это связано с принципом построения сигналов, которые используются в работе процессора. На самом низком уровне сигнал принимает только два значения: «ложь» и «истина». Поэтому было принято отсутствие сигнала, «ложь», обозначать нулем, а наличие его, «истину», единицей. Такое сочетание легко реализовать технически. Числа в двоичной системе формируются так же, как и в десятичной. Когда разряд достигает своей верхней границы, он обнуляется, и добавляется новый разряд. По такому принципу осуществляется переход через десяток в десятичной системе. Таким образом, числа состоят из сочетаний нулей и единиц, и это сочетание называется «двоичная система счисления».

Запись числа в системе
В десятичной	В двоичной	В десятичной	В двоичной
0	0	5	101
1	1	6	110
2	10	7	111
3	11	8	1000
4	100	9	1001

Как двоичное число записать в виде десятичного?

Существуют онлайн-сервисы, которые осуществляют перевод числа в двоичную систему и наоборот, но лучше уметь делать это самостоятельно. Двоичная система при переводе обозначается нижним индексом 2, например, 101₂. Каждое число в любой системе можно представить в виде суммы чисел, например: 1428 = 1000 + 400 + 20 + 8 – в десятичной системе. Так же представляется число в двоичной. Возьмем произвольное число 101 и рассмотрим его. В нем 3 разряда, поэтому раскладываем число по порядку таким способом: 101₂=1×2²+0×2¹+1×2⁰=4+1=5_10, где индекс 10 обозначает десятичную систему.

Как записать простое число в двоичной системе?

Очень легко осуществить перевод в двоичную систему счисления с помощью деления числа на два. Делить необходимо до тех пор, пока это будет возможно выполнить нацело. Например, возьмем число 871. Начинаем делить, обязательно записывая остаток:

871:2=435 (остаток 1)

435:2=217 (остаток 1)

217:2=108 (остаток 1)

108:2=54 (остаток 0) и так далее до конца.

Ответ записывается по полученным остаткам по направлению от конца к началу: 871₁₀=101100111₂. Проверить правильность вычислений можно с помощью обратного перевода, описанного ранее.

Для чего нужно знать правила перевода?

Двоичная система счисления применяется в большинстве дисциплин, связанных с микропроцессорной электроникой, кодированием, передачей и шифрованием данных, в различных направлениях программирования. Знания основ перевода из любой системы в двоичную помогут программисту разрабатывать различные микросхемы и осуществлять управление работой процессора и других подобных систем программным способом. Двоичная система счисления также необходима для реализации способов передачи пакетов данных по зашифрованным каналам и создания на их основе программных проектов типа «Клиент-сервер». В школьном курсе информатики основы перевода в двоичную систему и наоборот являются базовым материалом для изучения программирования в будущем и создания простейших программ.

www.syl.ru

Двоичная система счисления — это… Что такое Двоичная система счисления?

Системы счисления в культуре
Индо-арабская система счисления
Арабская Индийские Тамильская Бирманская	Кхмерская Лаоская Монгольская Тайская
Восточноазиатские системы счисления
Китайская Японская Сучжоу Корейская	Вьетнамская Счётные палочки
Алфавитные системы счисления
Абджадия Армянская Ариабхата Кириллическая	Греческая Эфиопская Еврейская Катапаяди
Другие системы
Вавилонская Египетская Этрусская Римская	Аттическая Кипу Майская
Позиционные системы счисления
Десятичная система счисления (10)
2, 3, 4, 5, 6, 7, 8, 9, 12, 16, 20, 60
Нега-позиционная система счисления
Симметричная система счисления
Смешанные системы счисления
Фибоначчиева система счисления
Непозиционные системы счисления
Единичная (унарная) система счисления
Список систем счисления

Двоичная система счисления — позиционная система счисления с основанием 2.

Двоичные цифры

В этой системе счисления числа записываются с помощью двух символов (0 и 1).

История

• В 1605 году Френсис Бэкон описал систему, буквы алфавита которой могут быть сведены к последовательностям двоичных цифр, которые в свою очередь могут быть закодированы как едва заметные изменения шрифта в любых случайных текстах. Важным шагом в становлении общей теории двоичного кодирования является замечание о том, что указанный метод может быть использован применительно к любым объектам.^[7] (См. Шифр Бэкона)

• Современная двоичная система была полностью описана Лейбницем в XVII веке в работе Explication de l’Arithmétique Binaire^[8]. В системе счисления Лейбница были использованы цифры 0 и 1, как и в современной двоичной системе. Как человек, увлекающийся китайской культурой, Лейбниц знал о книге Перемен и заметил, что гексаграммы соответствуют двоичным числам от 0 до 111111. Он восхищался тем, что это отображение является свидетельством крупных китайских достижений в философской математике того времени.^[9]

• В 1937 году Клод Шеннон представил к защите кандидатскую диссертацию Символический анализ релейных и переключательных схем в MIT, в которой булева алгебра и двоичная арифметика были использованы применительно к электронным реле и переключателям. На диссертации Шеннона по существу основана вся современная цифровая техника.

• В ноябре 1937 года Джордж Штибиц, впоследствии работавший в Bell Labs, создал на базе реле компьютер «Model K» (от англ. «Kitchen», кухня, где производилась сборка), который выполнял двоичное сложение. В конце 1938 года Bell Labs развернула исследовательскую программу во главе со Штибицом. Созданный под его руководством компьютер, завершённый 8 января 1940 года, умел выполнять операции с комплексными числами. Во время демонстрации на конференции American Mathematical Society в Дартмутском колледже 11 сентября 1940 года Штибиц продемонстрировал возможность посылки команд удалённому калькулятору комплексных чисел по телефонной линии с использованием телетайпа. Это была первая попытка использования удалённой вычислительной машины посредством телефонной линии. Среди участников конференции, бывших свидетелями демонстрации, были Джон фон Нейман, Джон Мокли и Норберт Винер, впоследствии писавшие об этом в своих мемуарах.

Запись двоичных чисел

Двоичная система счисления является комбинацией двоичной системы кодирования и показательной весовой функции с основанием равным 2. Положительные целые числа (без знака) записываются в виде:

где:

•  — представляемое число, первый индекс — основание системы кодирования (размерность множества цифр a={0,1}), второй индекс — основание весовой показательной функции b (в двоично-десятичном кодировании b=10),
•  — запись числа, строка цифровых знаков,
•  — обозначение основания системы кодирования и основания системы счисления,
•  — количество цифр (знаков) в числе x_2,2,
•  — порядковый номер цифры,
•  — цифры числа x_2,2 из множества a={0,1}, в двоичной системе счисления основание системы кодирования равно 2,
•  — основание показательной весовой функции, основание системы счисления,
•  — весовая показательная функция, создающая весовые коэффициенты.

Количество записываемых кодов (чисел) зависит от основания системы кодирования — c, определяется в комбинаторике и равно числу размещений с повторениями:

где:

Количество записываемых кодов (чисел) от основания показательной функции — b не зависит.
Основание показательной функции — b определяет диапазон представляемых числами x_2,b величин и разреженность представляемых чисел на числовой оси.

Целые числа являются частными суммами степенного ряда:

в котором коэффициенты a_n берутся из множества R=a{0,1}, X=2, n=k, а верхний предел в частных суммах ограничен с до — n-1.

Целые числа со знаком записываются в виде:

где:

•  — знак числа из множества z={+,-}, у положительных целых чисел знак зачастую опускается.

Дробные числа записываются в виде:

где:

•  — число цифр дробной части числа,
•  — весовые коэффициенты из множества ,
• основание системы кодирования равно 2,
•  — основание показательной весовой функции, основание системы счисления.

Следует отметить, что число может быть записано в двоичном коде, а система счисления при этом может быть не двоичной, а с другим основанием. Пример: двоично-десятичное кодирование, в котором десятичные цифры записываются в двоичном виде, а система счисления — десятичная.

Сложение, вычитание и умножение двоичных чисел

Таблица сложения

Пример сложения «столбиком» (14 + 5 = 19):

		1	↖
+		1	1	1	0
			1	0	1
	1	0	0	1	1

Таблица вычитания

—	0	1
0	0	1
1	(заём из старшего разряда) 1	0

Таблица умножения

Пример умножения «столбиком» (14 × 5 = 70):

×				1	1	1	0
					1	0	1
+				1	1	1	0
		1	1	1	0
	1	0	0	0	1	1	0

Преобразование чисел

Для преобразования из двоичной системы в десятичную используют следующую таблицу степеней основания 2:

512

256

128

64

32

16

8

4

2

1

Начиная с цифры 1 все цифры умножаются на два. Точка, которая стоит после 1, называется двоичной точкой.

Преобразование двоичных чисел в десятичные

Допустим, вам дано двоичное число 110001. Для перевода в десятичное просто запишите его справа налево как сумму по разрядам следующим образом:

.

Можно записать это в виде таблицы следующим образом:

512	256	128	64	32	16	8	4	2	1
				1	1	0	0	0	1
				+32	+16				+1

Точно так же, начиная с двоичной точки, двигайтесь справа налево. Под каждой двоичной единицей напишите её эквивалент в строчке ниже. Сложите получившиеся десятичные числа.
Таким образом, двоичное число 110001 равнозначно десятичному 49.

Преобразование методом Горнера

Для того, чтобы преобразовывать числа из двоичной в десятичную систему данным методом, надо суммировать цифры слева направо, умножая ранее полученный результат на основу системы (в данном случае 2). Например, двоичное число 1011011 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+0=22 >> 22*2+1=45 >> 45*2+1=91 То есть в десятичной системе это число будет записано как 91. Или число 101111 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+1=23 >> 23*2+1=47 То есть в десятичной системе это число будет записано как 47. Перевод дробных чисел методом Горнера 1) 0,1101₂=0,X₁₀ (рассматриваем цифры в обратном порядке)
1:2=0,5
0,5+0=0,5
0,5:2=0,25
0,25+1=1,25
1,25:2=0,625
0,625+1=1,625
1,625:2=0,8125
Ответ: 0,1101₂= 0,8125₁₀
2) 0,356₈=0,X₁₀ (рассматриваем цифры в обратном порядке)
6:8=0,75
0,75+5=5,75
5,75:8=0,71875
0,71875+3=3,71875
3,71875:8=0,46484375
Ответ: 0,356₈=0,46484375₁₀
3) 0,A6E₁₆=0,X₁₀ (рассматриваем цифры в обратном порядке)
14:16=0,875
0,875+6=6,875
6,875:16=0,4296875
0,4296875+10=10,4296875
10,4296875:16=0,65185546875
Ответ: 0,A6E₁₆=0,65185546875₁₀

Преобразование десятичных чисел в двоичные

Допустим, нам нужно перевести число 19 в двоичное. Вы можете воспользоваться следующей процедурой :

19 /2 = 9  с остатком 1
9  /2 = 4  c остатком 1
4  /2 = 2  без остатка 0
2  /2 = 1  без остатка 0
1  /2 = 0  с остатком 1

Итак, мы делим каждое частное на 2 и записываем остаток в конец двоичной записи. Продолжаем деление до тех пор, пока в частном не будет 0. Результат записываем справа налево. То есть нижнее число будет самым левым и.т.д. В результате получаем число 19 в двоичной записи: 10011.

Преобразование дробных двоичных чисел в десятичные

Нужно перевести число 1011010,101 в десятичную систему. Запишем это число следующим образом:

Или по таблице:

64	32	16	8	4	2	1	0.5	0.25	0.125
1	0	1	1	0	1	0.	.1	0	1
+64		+16	+8		+2		+0.5		+0.125

Преобразование дробных десятичных чисел в двоичные

Перевод дробного числа из десятичной системы счисления в двоичную осуществляется по следующему алгоритму:

• Вначале переводится целая часть десятичной дроби в двоичную систему счисления;
• Затем дробная часть десятичной дроби умножается на основание двоичной системы счисления;
• В полученном произведении выделяется целая часть, которая принимается в качестве значения первого после запятой разряда числа в двоичной системе счисления;
• Алгоритм завершается, если дробная часть полученного произведения равна нулю или если достигнута требуемая точность вычислений. В противном случае вычисления продолжаются с предыдущего шага.

Пример: Требуется перевести дробное десятичное число 206,116 в дробное двоичное число.

Перевод целой части дает 206₁₀=11001110₂ по ранее описанным алгоритмам; дробную часть умножаем на основание 2, занося целые части произведения в разряды после запятой искомого дробного двоичного числа:
0,116 • 2 = 0,232
0,232 • 2 = 0,464
0,464 • 2 = 0,928
0,928 • 2 = 1,856
0,856 • 2 = 1,712
0,712 • 2 = 1,424
0,424 • 2 = 0,848
0,848 • 2 = 1,696
0,696 • 2 = 1,392
0,392 • 2 = 0,784
и т. д.
Получим: 206,116₁₀=11001110,0001110110₂

Применения

В цифровых устройствах

Двоичная система используется в цифровых устройствах, поскольку является наиболее простой и соответствует требованиям:

• Чем меньше значений существует в системе, тем проще изготовить отдельные элементы, оперирующие этими значениями. В частности, две цифры двоичной системы счисления могут быть легко представлены многими физическими явлениями: есть ток (ток больше пороговой величины) — нет тока (ток меньше пороговой величины), индукция магнитного поля больше пороговой величины или нет (индукция магнитного поля меньше пороговой величины) и т. д.
• Чем меньше количество состояний у элемента, тем выше помехоустойчивость и тем быстрее он может работать. Например, чтобы закодировать три состояния через величину напряжения, тока или индукции магнитного поля, потребуется ввести два пороговых значения и два компаратора, что не будет способствовать помехоустойчивости и надёжности хранения информации.^{[источник не указан 770 дней]}
• Двоичная арифметика является довольно простой. Простыми являются таблицы сложения и умножения — основных действий над числами.

В цифровой электронике одному двоичному разряду в двоичной системе счисления соответствует (очевидно) один двоичный разряд двоичного регистра, то есть двоичный триггер с двумя состояниями (0,1).

В английской системе мер

При указании линейных размеров в дюймах по традиции используют двоичные дроби, а не десятичные, например: 5¾″, 7¹⁵/₁₆″, 3¹¹/₃₂″ и т. д.

Интересные факты

См. также

Примеры чисел-степеней двойки

Степень	Значение
0	1
1	2
2	4
3	8
4	16
5	32
6	64
7	128
8	256
9	512
10	1024
11	2048
12	4096
13	8192
14	16384
15	32768
16	65536
17	131072
18	262144
19	524288
20	1048576
21	2097152
22	4194304
23	8388608
24	16777216
25	33554432
26	67108864
27	134217728
28	268435456
29	536870912
30	1073741824
31	2147483648
32	4294967296
33	8589934592
34	17179869184
35	34359738368
36	68719476736
37	137438953472
38	274877906944
39	549755813888
40	1099511627776
41	2199023255552
42	4398046511104
43	8796093022208
44	17592186044416
45	35184372088832
46	70368744177664
47	140737488355328
48	281474976710656
49	562949953421312
50	1125899906842624
51	2251799813685248

Примечания

1. ↑ Sanchez, Julio & Canton, Maria P. (2007), «Microcontroller programming: the microchip PIC», Boca Raton, Florida: CRC Press, с. 37, ISBN 0-8493-7189-9 
2. ↑ W. S. Anglin and J. Lambek, The Heritage of Thales, Springer, 1995, ISBN 0-387-94544-X
3. ↑ Ordish George, Hyams, Edward. The last of the Incas: the rise and fall of an American empire. — New York: Barnes & Noble, 1996. — С. 80. — ISBN 0-88029-595-3
4. ↑ Experts ‘decipher’ Inca strings. Архивировано из первоисточника 18 августа 2011.
5. ↑ Carlos Radicati di Primeglio, Gary Urton Estudios sobre los quipus. — P. 49.
6. ↑ Dale Buckmaster (1974). «The Incan Quipu and the Jacobsen Hypothesis». Journal of Accounting Research 12 (1): 178-181. Проверено 2009-12-24.
7. ↑ Bacon, Francis, «The Advancement of Learning», vol. 6, London, сс. Chapter 1, <http://home.hiwaay.net/~paul/bacon/advancement/book6ch2.html> 
8. ↑ http://www.leibniz-translations.com/binary.htm Leibniz Translation.com EXPLANATION OF BINARY ARITHMETIC
9. ↑ Aiton, Eric J. (1985), «Leibniz: A Biography», Taylor & Francis, сс. 245–8, ISBN 0-85274-470-6 

Ссылки

dic.academic.ru