Например:
2²=2*2=4
Обратите внимание. Существуют также специальные степени, имеющие стандартное название.
Например:
а² — квадрат числа а (запись выглядит так же как площадь квадрата)
а³- куб числа а
а²=а*а
а³=а*а*а
Обратите внимание. Важно помнить, что и в числовых и в буквенных выражения при наличии степенного значения оно выполняется в первую очередь.
- (7-2)²*5²+6³:(245-236) = 5²*5²+216:9 = 25*25+24=625+24=649
Решим уравнение:
- 11²-2х=135:5
121-2х=27
2x=121-27
2x=94
x=94:2=47
Проверка
121-94=27
27=27
- 4²x-3³=5
16х-27=5
16х=5+27
16х=32
х=32:16
х=2
Проверка:
16*2-27=5
32-27=5
5=5
Важно знать. Ещё в Древнем Египте как и в Древнем Вавилоне математики вычисляли степень, однако они это делали как отношение одинаковых показателей. Однако понятие степени тогда ещё не вводилось.
Эти названия затормозили дальнейшее развитие степени. Однако ими пользовались вплоть до 16 века.
Немецкие математики издавали свои труды и хотели сократить запись. В этом преуспел Михель Штифель в «Полной арифметике».
В 16 веке итальянский математик Рафаэль Бомбелли в книге «Алгебра» использовал идеи француза Николя Шюке и начал вводить современное понятие степени.
Он надписывал показатель степени почти как современные математики и школьники. То есть показатель был вверху над числом и гораздо меньшим по размеру в сравнении с основанием степени.
Однако это были лишь попытки, а не появление осознанного термина.
Николя Шюке в работе «Наука о числах в трёх книгах» рассматривал степени с отрицательными и нулевыми показателями.
Попытки немецких математиков повлияли на нидерландского математика Симона Стевина.
Несмотря на то, что Стевин взял идею Бомбелли, его реализация была направлена по отношению к неизвестной величине.
Важно знать. 4 звучало как а в четвёртой степени.
4 звучало как а в четвёртой степени.
Его идеи продолжил Рене Декарт в «Геометрии». Он обозначил а квадрат, а в четвёртой степени. Однако он не соглашался заменять а*а на а².
Запомните. Только знаменитый немецкий математик Лейбниц воспринял всю символику Декарта и обозначал ее в привычных нам современных символах.
Благодаря Декарту и Лейбницу современные степени приобрели краткий, понятный для всех вид.
Вывод. Появление степени числа намного упростило запись умножения одинаковых множителей и сократило время на их перемножение.
Поделиться статьей в соцсетях
Урок «Степень числа», УМК Мерзляк А.Г., Полонский В.Б., Якир М.С., ФГОС
Класс 5 Тема: «Степень числа».Тип и особенности: урок изучения нового материала.Учебник: Математика 5. (А.Г. Мерзляк, В.Б. Полонский, Ч.С. Якир.)Оборудование: проектор, компьютер, презентация к уроку, каточки для индивидуальной и парной работы.Цели урокаОбразовательные (предметные результаты):познакомить обучающихся с понятиями степень числа, основание степени, показатель степени, научить правильно записывать и читать степень числа (квадрат и куб числа). Воспитательные (личностные результаты):формировать положительную мотивацию, независимость суждений, воспитывать культуру поведения при фронтальной, индивидуальной, парной работе.Развивающие (метапредметные результаты):определять и формулировать цель на уроке с помощью учителя; оценивать правильность выполнения действий; планировать свои действия в соответствии с поставленной задачей.
Воспитательные (личностные результаты):формировать положительную мотивацию, независимость суждений, воспитывать культуру поведения при фронтальной, индивидуальной, парной работе.Развивающие (метапредметные результаты):определять и формулировать цель на уроке с помощью учителя; оценивать правильность выполнения действий; планировать свои действия в соответствии с поставленной задачей.
Этапы урока | Задачи урока | Визуальный ряд | Деятельность учителя | Деятельность учащихся | Формируемые УУД |
Организация учащихся к уроку | Создать благоприятный психологический настрой на работу Определить тему и цель урока | На доске дата (тема урока пока не записывается) Слайд №1. | Приветствие, проверка подготовленности к учебному занятию, организация внимания детей. | Дежурные проходят по классу собирают тетради с домашним заданием и раздают проверенные. | Регулятивные: саморегуляция Личностные: самоопределение Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками. |
Здравствуйте ребята! Я рада вас видеть. Долгожданный дан звонок, начинается урок! Очень тихо вы садитесь и работать не ленитесь! Я хочу, чтобы вам этот урок принес новые знания, которые вы с успехом могли бы применять на практике. | |||||
Актуализация знаний | Актуализация опорных знаний и способов действий. | Слайд № 2 Слайд № 3 | — В домашней работе были задания на повторение предыдущих тем. — Проверим ваши умения. — Упростите выражение и найдите его значение 5+5+5+5 6+6+6+6+6 10+10+10+10+10+10+10+10+10+10 4+4+4+4+4+4 Каким действием заменяем сумму одинаковых слагаемых? — Найдите значение выражения 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 | — Произведением. (Ученики по поднятой руке дают ответы к примерам.) — 64 | Коммуникативные: сотрудничество с товарищем, организация взаимопроверки. Познавательные: выбор наиболее эффективных способов решения задач в зависимости от конкретных условий. Регулятивные: контроль, коррекция, выделение, осознание того, что уже усвоено и что ещё подлежит усвоению Личностные: самоопределение |
Создание проблемной ситуации. Формулировка проблемы Определение целей урока | Познать новое, совершенствовать приёмы счёта |
| — Посмотрите на эту запись, что собой представляет данное выражение? — Она удобна? Свой ответ обоснуйте. — Упростите это выражение, сделайте короче. — Вы не смогли сделать запись произведения одинаковых множителей короче. Значит, вам не все математические действия с натуральными числами известны. Так что вы должны узнать сегодня на уроке? Сформулируйте возникшую проблему. | — Произведение одинаковых множителей. — Нет, очень длинная. — Предлагают свои варианты, но не могут обосновать, что в их записи означает каждый знак. Затрудняются выполнить данное задание. — Как можно записывать произведение одинаковых множителей короче? | Познавательные: поиск и выделение необходимой информации. Регулятивные: постановка цели Коммуникативные: сотрудничать с товарищами, задавать вопросы с целью получения нужной информации. |
План решения проблемы Работа над проблемой Определение темы урока Открытие нового знания Работа с учебником (поисковая работа с элементами исследования) | Повторение ранее изученного материала | На маленькой доске слово ПЛАН (на магнит крепить ответы) Слайд №4 Слайд №5 Работа с учебником Слайд № 6 + на доске закрепить названия О, П, С | — Составим план решения проблемы. — Если мы знакомимся с новым арифметическим действием, что нам необходимо о нем знать. — Помогает наводящими вопросами сформулировать все пункты плана, записывает их на доске, после чего выводит слайд на экран. 1. Научиться записывать короче произведение одинаковых множителей 2. Изучить новое арифметическое действие 3. Как называется? — Поможет решить вам проблему изучение темы: «Степень числа». Запишите ее в тетради. — Попробуем разобраться вместе с возникшей проблемой. — Внимательно посмотрите на данные равенства.- Сравните выражения слева и справа от знака «равно». Попробуйте объяснить, что означает каждый знак в правой части: 4*4*4= 5*5*5*5*5*5= 7*7= — Такая запись произведения одинаковых множителей удобна, понятна? — Проверим, правильно ли мы рассуждали. — Откройте учебник на странице 135, прочитайте текст §20. Найдите ответы на вопросы в тексте. Обсудите свои ответы с соседом по парте. Учитель раздает карточки с вопросами к тексту. 1) Как автор предлагает записывать произведение одинаковых множителей 7 ∙ 7 ∙ 7 ∙ 7, если количество множителей 4? 2) Как называется такая запись? 3) Как прочитать её? 4) Что означает каждый знак в этой записи ? (отвечают, комментируют ответ другого, затем остальных учащихся дают свою оценку правильности или неправильности услышанных ответов). | -Научиться записывать короче произведение одинаковых множителей. Изучить новое арифметическое действие. — Как оно называется. Как записывается и читается. Каким по порядку выполняется в числовых выражениях — Записывают тему урока и число в тетрадях. — 4 – это число, которое перемножают само на себя, а 3 – количество таких множителей. — 5 – число, которое перемножают само на себя, 6 – количество таких множителей. -7 – число, которое перемножают само на себя, 2 – количество таких множителей. — Да, понятная и удобная. — учащиеся работают в парах, обсуждают вопросы, дают ответы. Демонстрируют ответ у доски | Познавательные: анализировать условие задачи. Регулятивные: умение проговаривать последовательность действий, высказывать своё предположение, оценивать правильность выполнения действия. Коммуникативные: уметь оформлять мысли в устной и письменной форме, учитывать разные мнения. |
Первичное закрепление новых знаний Работа по учебнику | Работа по учебнику и на доске. Слайд № 7 (на листочках) | Закрепим новые понятия, выполним задание №548 (устно) на определение основания и показателя степени. — Вы хорошо справились с этим заданием. А насколько понятно вам , что означают основание и показатель степени? (Ученики выполняют задание в тетрадях, «по цепочке» у доски.) — Представьте степень в виде произведения. — Молодцы! А теперь попробуйте сами выполнить. — Можно ли записать в виде степени (на закрытой доске), если да, запишите: 2*2*2*2*2*2*2 2*3*4*5*6 6+6+6+6 10*10*10*10*10*10 — Молодцы, что заметили лишнюю сумму и произведение. А теперь, зная в чем отличие этих выражений соедините линиями выражения, соответствующие друг другу. Обсудите со своим партнером по парте в течение 1 минуты. 1) 5+5+5+5 а) 54 2) 6 ∙ 6 ∙ 6 б) 5∙4 3) 5 ∙ 5 ∙ 5 ∙ 5 в) 63 4) 7+7+7+7+7 г) 7 ∙ 5 5) 6+6+6 д) 75 6) 7 ∙ 7 ∙ 7 ∙ 7 ∙ 7 е) 6 ∙ 3 — Поблагодарите своего партнера. Оцените свою работу. Нет ошибок – «5» 1,2 ошибки – «4» 3 ошибки – «3» | — Ученики читают степень и записывают её в виде произведения. — Ученики дают обоснованные ответы — учащиеся работают парами в карточках — учащиеся дают обоснованные ответы | Коммуникативные: высказывать своё мнение при обсуждении задания Личностные: формирование математической компетентности, положительное отношение к урокам математики | |
Физкультминутка | Снять утомление | Вы, наверное, устали? Потянули их слегка. Быстро поменяли руки! Нам сегодня не до скуки. Мы осанку исправляем | Записывают в тетрадь то, как читают | ||
Первичное закрепление новых знаний | Заготовка на столах | Поработаем в парах. Для того, чтобы в дальнейшем было легче вычислять квадраты чисел, нам с вами предстоит сейчас сделать закладки-шпаргалки. (На столах у ребят лежат заготовки). Вам необходимо заполнить табличку. А чтобы работу выполнить быстрее, распределите между собой, кто какие клеточки будет заполнять. (М/б консультанты) — Проверим, кто не успел- закончить дома. | Работают в парах, решают примеры, обсуждают полученные ответы, договариваются, кто будет отвечать | Коммуникативные: высказывать своё мнение при обсуждении задания Личностные: формирование математической компетентности, положительное отношение к урокам математики | |
Повторение и закрепление изученного ранее материала. | Самостоятельное выполнение заданий теста | Сдать на проверку | — Проверьте себя: насколько хорошо вы поняли материал. Самостоятельно выполните тест. Можете использовать закладку-шпаргалку. | Ученики выполняют задания самостоятельно работая на листочках | |
Итог урока | Слайд № 9 | — Какую проблему мы решали на уроке? — Как вы думаете, удалось нам достичь результата? Изучая новое арифметическое действие, на какой вопрос мы еще не ответили? Вот этим мы и займемся на следующем уроке. | Учащиеся отвечают на вопросы учителя Не знаем порядок действия в примерах | Регулятивные: планировать шаги по устранению пробелов | |
Слайд № 10 | Какие новые понятия вы узнали? | Степень, основание, показатель | |||
Рефлексия | Оцените свою работу на уроке (приём «ладони») | Учащиеся отмечают, что им удалось на уроке. | |||
Домашнее задание. | Слайд№ 11, 12 | Доделать закладку-шпаргалку. № 551 103 – (102 + 10) = 890 Проанализируйте ответ в выражении и продолжите сказку: Жили – были 4 брата: Сложение, Вычитание, Умножение и Деление. Были они очень дружны и каждый из них знал своё место. Однажды в гости к ним пришла старшая сестра Степень. Завели они спор, кто теперь из них главнее… — Ребята! Спасибо за урок. | Учащиеся записывают задание в дневник. |
Сингапурская математика для 5 класса: онлайн-практика
Наша учебная программа является спиральной
Обратите внимание, что наша виртуальная учебная программа по сингапурской математике для 5 класса является спиральной и предусматривает повторение важных понятий, которые учащиеся изучили в 4 классе. концепции построены на темах, рассмотренных ранее, с повышенным уровнем сложности. Наша онлайн-учебная программа по математике K-5 согласуется со всеми стандартными сериями учебников по математике в Сингапуре и включает в себя весь контент, охватываемый этими сериями, от детского сада до пятого класса.
концепции построены на темах, рассмотренных ранее, с повышенным уровнем сложности. Наша онлайн-учебная программа по математике K-5 согласуется со всеми стандартными сериями учебников по математике в Сингапуре и включает в себя весь контент, охватываемый этими сериями, от детского сада до пятого класса.
Наша сингапурская математика для 5--го -го класса может вводить некоторые темы на один уровень раньше. В тех немногих случаях, когда разделы 5 th не совсем совпадают между нашей учебной программой и учебниками, вы все равно сможете найти соответствующую тему в нашей программе, обратившись к оглавлению нашего 5 th или 4 -го -го уровня.
Соответствие 5A и 5B
Для справки: следующие темы в нашей учебной программе соответствуют классам 5A и 5B по сингапурской математике:
Singapore Math 5A
Понимание системы стоимостных оценок; умножение и деление целых чисел; числовые выражения и шаблоны; десятичные дроби; сложение и вычитание десятичных знаков; умножение и деление десятичных дробей.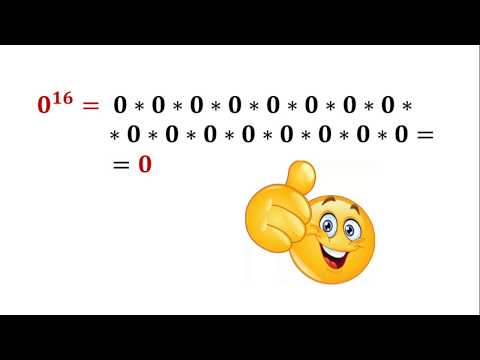
Singapore Math 5B
Сложение и вычитание дробей и смешанных чисел; умножение и деление дробей; перевод единиц измерения; объем; двухмерные фигуры; координатная плоскость и графики.
Предварительные знания учащихся
Учащиеся должны быть знакомы с понятиями разрядности чисел до 1 000 000, включая сравнение и упорядочивание целых чисел до шести разрядов. Учащиеся должны уметь мысленно прибавлять/вычитать однозначное число к/из двузначного числа. Учащиеся должны знать, как использовать стандартный алгоритм сложения и вычитания многозначных чисел; знать факты умножения и деления; уметь умножать и делить многозначное целое число на однозначное целое по стандартному алгоритму. Учащиеся должны знать понятия единичной дроби, эквивалентных дробей, смешанных чисел и неправильных дробей. Учащиеся должны уметь складывать и вычитать дроби с одинаковым знаменателем или с родственными знаменателями, где один знаменатель кратен другому. Студенты должны знать, как найти площадь прямоугольника и быть знакомы с единицами площади.
Студенты должны знать, как найти площадь прямоугольника и быть знакомы с единицами площади.
5
th Grade Singapore Math Scope and Sequence- Понимание системы стоимостных значений
Этот модуль в первую очередь представляет собой обзор концепций разрядных значений, изученных на более ранних уровнях, и охватывает многозначные числа. Учащиеся расширят свои знания о разрядной стоимости до сотен миллиардов или чисел до 12 цифр в стандартной и расширенной форме.
- Умножение и деление целых чисел
Этот модуль охватывает умножение на десятки, сотни и тысячи; умножение целых чисел, степени 10, деление целых чисел, текстовые задачи на умножение и деление. Студенты узнают, как мысленно умножать и делить целые числа до четырех цифр на десятки, сотни или тысячи.
- Числовые выражения и шаблоны
Этот модуль охватывает интерпретацию числовых выражений и использование букв в качестве чисел.

- Десятичные дроби
Этот модуль охватывает понимание десятых, сотых, тысячных, а также сравнение и округление десятичных дробей. Учащиеся смогут связать каждую цифру в десятичной дроби с ее значением, сравнивать и упорядочивать десятичные дроби, записывать десятичные дроби в виде дробей и округлять десятичные дроби до одного или двух знаков после запятой.
- Сложение и вычитание десятичных знаков
Этот модуль охватывает сложение и вычитание десятичных знаков и решение текстовых задач с использованием десятичных знаков.
- Умножение и деление десятичных дробей
Этот модуль охватывает умножение, деление и оценку десятичных дробей, а также решение текстовых задач на умножение и деление десятичных дробей.
- Сложение и вычитание дробей и смешанных чисел
Этот модуль охватывает сложение и вычитание различных дробей, понимание дроби как деления, сложение и вычитание смешанных чисел, решение текстовых задач с использованием дробей и смешанных чисел.

- Умножение и деление дробей
Этот модуль охватывает умножение правильных и неправильных дробей, умножение смешанных и целых чисел, умножение дробей для нахождения площади, деление дроби на целое число, деление целого числа на единичную дробь и решение слов. задачи на умножение и деление дробей.
- Преобразование единиц измерения
Эта единица охватывает метрические и обычные длины, массу, вес, объем, время и преобразование метрических единиц.
- Том
Этот модуль охватывает понимание и измерение объема, объема прямоугольной призмы, объема жидкости и решение текстовых задач на объем.
- Двухмерные фигуры
В этом разделе рассматривается классификация треугольников и четырехсторонних фигур. Учащиеся расширят свои знания о площади и составных фигурах, чтобы найти площадь и классифицировать треугольники и четырехсторонние фигуры.

- Координатная плоскость и графики
Этот модуль охватывает отображение данных с использованием линейного графика, системы координат, а также анализ шаблонов и взаимосвязей.
- Соотношение
Этот модуль охватывает понимание концепции отношения; коэффициент нахождения; сравнение двух или трех величин с помощью коэффициента; выражение отношения двух или трех величин в простейшей форме; использование модели сравнения для представления соотношения двух величин; решение текстовых задач на отношения двух или трех величин.
- Проценты
Этот модуль охватывает чтение и интерпретацию процентов от целого; выражение дроби в процентах; выражение десятичных дробей в процентах; выражение процента в виде дроби; решение словесных задач, связанных с процентным налогом, скидкой и процентами.
Мосты по классам Уровень: 5
Представляем третье издание Bridges in Mathematics!
Узнайте, что нового в учебной программе!
Первый блок посвящен объему и включает в себя обзор фактов умножения и стратегий умножения многозначных чисел.
В 5 классе учащиеся учатся умножать и делить дроби. Модуль 6 вводит новые геометрические концепции, включая построение координатных графиков и использование иерархий для классификации двумерных фигур по их свойствам.
В Разделе 7 учащиеся разрабатывают точные и эффективные стратегии деления целых чисел, десятичных дробей и дробей (дробные единицы на целые числа и целые числа на дробные части). Блок 8 объединяет естественные науки, инженерию и математику. В этом последнем разделе учащиеся применяют знания и навыки, которые они приобрели в течение года, изучая солнечную энергию и проектируя солнечные дома.


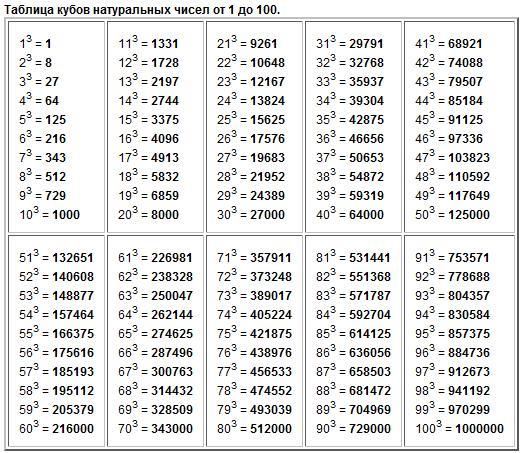
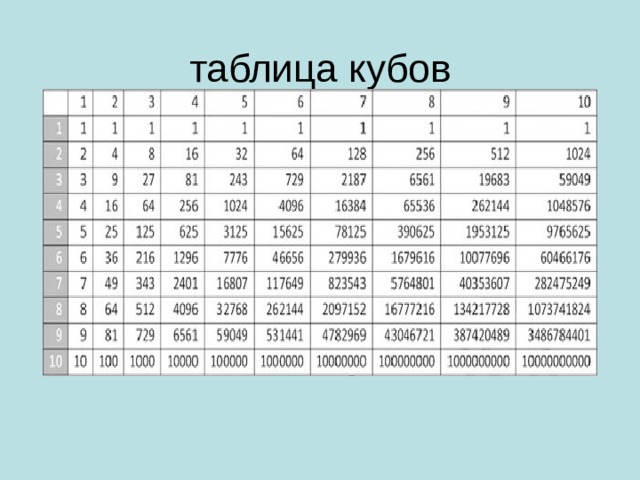

 Закрепить на доске предложения учеников.
Закрепить на доске предложения учеников.


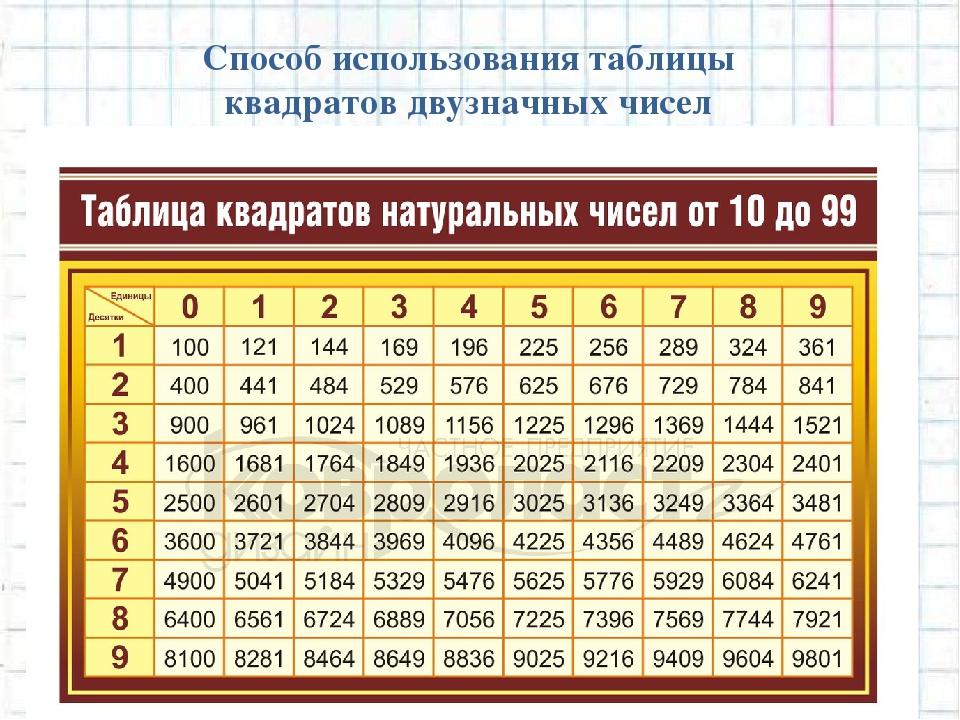 А теперь первый ответ называет ученик…
А теперь первый ответ называет ученик… 3 — «а в кубе».
3 — «а в кубе».



