Формула суммы n первых членов арифметической прогрессии 9 класс онлайн-подготовка на Ростелеком Лицей
Тема 11.
Формула суммы n первых членов арифметической прогрессии.
Сегодня мы выведем 2 формулы для нахождения суммы первых n-членов арифметической прогрессии.
Давным-давно сказал один мудрец
Что прежде надо
Связать начало и конец
У численного ряда.
Пусть требуется найти сумму первых ста натуральных чисел:
1+2+3+…+98+99+100.
Задача очень непроста:
Как сделать, чтобы быстро
От единицы и до ста
Сложить в уме все числа?
Пять первых связок изучи,
Найдёшь к решению ключи.
С этой задачей связана история, которую рассказывают об известном немецком математике Карле Гауссе.
Когда учитель предложил ученикам сложить натуральные числа от 1 до 100, то маленький Карл моментально пришел с ответом. Вероятно, он заметил, что сумма первого и последнего слагаемого равна 101, сумма второго и предпоследнего слагаемого, тоже 101 и ничего странного в этом нет. Второе слагаемое на единицу больше первого, а предпоследнее на единицу меньше последнего, так что сумма должна быть такой же. То же будет происходить и с каждой новой парой чисел. Таких сумм 50, так как всего чисел 100 и все они разделены на пары. Значит, вся сумма равна числу 101 умноженному на 50. И Гаусс подсчитал, что сумма равна 5050.
1+2+3+4+…..+97+98+99+100
1+100=101
2+99=101
3+98=101
1+2+3+4+…+97+98+99+100=101∙50=5050
С помощью аналогичных рассуждений можно найти сумму n-первых членов арифметической прогрессии:
Обозначим сумму первых n-членов арифметической прогрессии Sn и запишем эту сумму дважды, расположив в первом случае слагаемые в порядке возрастания, а во втором в порядке убывания:
Sn=a1+a2+a3+…+an-2+an-1+an (1)
Sn=an+an-1+an-2+…+a3+a2+a1 (2)
Сумма каждой пары членов прогрессии, расположенных друг под другом равна a1 + an, число таких пар равно n, поэтому сложив почленно равенства (1) и (2), получим:
2Sn=a1+an∙n
Разделим обе части этого равенства на 2 и получим формулу суммы первых n-членов арифметической прогрессии:
Sn=(a1+an)2∙n
Этой формулой удобно пользоваться, когда известны первый и последний члены арифметической прогрессии.
Sn=(a1+an)2∙n=a1+a1+dn-12∙n=2a1+dn-12∙n
Для нахождения суммы первых n-членов арифметической прогрессии, используя эту формулу, достаточно знать первый член и разность арифметической прогрессии.
Разберем несколько примеров:
Найдем сумму первых 10-ти членов арифметической прогрессии, первый член которой равен минус 23, а десятый член равен 4. Воспользуемся формулой:Sn=(a1+an)2∙n, получим
S10=(-23+4)2∙10=-192∙10=-19∙5=-95
Рассмотрим еще один пример:
Вычислим сумму первых двадцати двух членов арифметической прогрессии:
-15; -11; -7; -3; ….
Итак, a1=-15,d=4, значит, можно воспользоваться второй формулой: Sn=2a1+dn-12∙n, получим:
S22=2∙-15+4∙(22-1)2∙22=-30+842∙22=54∙11=594.
А теперь давай найдем сумму членов арифметической прогрессии с пятнадцатого по тридцатый включительно, если первый член равен 10 и разность равна 3.
Как найти сумму с 15-го по 30-й член включительно, давай подумаем: S30=a1+a2+…+a14+a15+…+a30, если мы найдем сумму тридцати членов и вычтем из нее сумму первых 14-ти членов, то мы получим необходимую сумму с 15-го по 30-й члены.
Итак, S30=2∙10+3∙292∙30=1072∙30=107∙15=1605
S14=2∙10+3∙132∙14=592∙14=59∙7=413
S15-30=S30-S14=1605-413=1192
Ответ: 1192.
Эту же сумму мы могли найти и другим, способом, если бы ввели новую арифметическую последовательность, первый член которой был бы равен пятнадцатому члену нашей прогрессии.
А теперь давай решим уравнение:
x+1+x+5+x+9+…+x+69=684
Можно, конечно, расписать все слагаемые, привести подобные и решить это линейное уравнение, но это займет очень много времени. А если внимательно посмотреть на это уравнение, то можно заметить, что каждое следующее слагаемое отличается от предыдущего на 4. То, есть последовательность:
А если внимательно посмотреть на это уравнение, то можно заметить, что каждое следующее слагаемое отличается от предыдущего на 4. То, есть последовательность:
x + 1; x + 5; x + 9; … ; x + 69 является арифметической, сумма членов которой равна 684.
Итак, имеем: a1=x+1,a2=x+5,an=x+69, Sn=684.
Найдем разность арифметической прогрессии:
d=a2-a1=x+5-x+1=4
Найдем номер последнего члена, для этого воспользуемся формулой n-го члена: an = a1 + d(n — 1)
x + 69 = x + 1 + 4(n — 1)
x + 69 = x + 1 + 4n — 4
4n = 72, n = 18
Подставим все данные в формулу суммы первых n-членов арифметической прогрессии, получим:
684=x+1+x+52∙18
684 = (2x + 70) ∙ 9, отсюда 2x + 70 = 76 2x=6, x=3
Ответ:3
Калькулятор арифметической прогрессии с формулами и примерами решений
Представим, что подряд выписаны все четные натуральные числа: 2, 4, 6, 8, 10, 12, 14, 18, 18, 20, 22. .. Это — последовательность четных натуральных чисел. Число 2 — ее первый член, 4 — второй, 6 — третий, 20 — десятый и т. д.
.. Это — последовательность четных натуральных чисел. Число 2 — ее первый член, 4 — второй, 6 — третий, 20 — десятый и т. д.
Приведем еще несколько примеров числовых прогрессий:
- 1, 2, 3, 4, 5… — последовательность натуральных чисел,
- 1, 3, 5, 7, 9… — последовательность нечетных натуральных чисел,
- 1, 1/2, 1/3, 1/4, 1/5… – последовательность чисел, обратных к натуральным.
Последовательности бывают конечные и бесконечные. Конечной, например, есть последовательность однозначных натуральных чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9.
Последовательность всех натуральных чисел — бесконечная. Записывая бесконечную последовательность, после нескольких ее первых членов ставят многоточие. Первый, второй, третий члены последовательности четных натуральных чисел равны соответственно 2, 4, 6. Пишут: a1 = 2, а2 = 4, а3 = 6
А чему равен ее n-й член An? Поскольку каждый член последовательности парных натуральных чисел вдвое больше от своего порядкового номера, то ее n-й член равен 2n, т. е.
е.
An = 2n.
Это формула n-го члена последовательности парных натуральных чисел.
An = 2n − 1
Формула n-го члена последовательности нечетных натуральных чисел.
Если известна формула n-го члена последовательности, то нетрудно вычислить любой ее член. Напишем несколько первых членов последовательности, n-й член которой:
An = n2 + 2
Предоставляя переменной п значения 1, 2, 3, 4, 5… получим первые члены последовательности: 6, 11, 18, 27, 38, 51… Тысячный член этой последовательности а1000 = 10002 + 2 = 1000002.
Гораздо труднее решать обратную задачу — для данной последовательности найти ее n-й член. Например, формула n-го члена последовательности простых чисел: 2, 3, 5, 7, 11, 13… — неизвестна до сих пор, хотя математики искали ее более 2000 лет.
Несколько первых членов последовательности не задают ее однозначно.
Например, существует множество различных последовательностей, первые члены которых 2, 4, 6, 8. В частности, такие первые члены имеют последовательности, n-е члены которых:
В частности, такие первые члены имеют последовательности, n-е члены которых:
- An = 2n
- Cn = 2 n + (n − 1) (n − 2) (n − 3) (n − 4)
Из двух соседних членов a1 и a2 последовательности член a2 называют следующим за а1, а а1 — предыдущим по отношению к а2. Последовательность называют растущей, если каждый ее член, начиная со второго, больше предыдущего. Последовательность называется убывающей, если каждый ее член, начиная со второго, меньше предыдущего.
Замечания
Иногда рассматривают также прогрессивности, членами, которых являются различные выражения, функции, фигуры то что. Можно говорить и о последовательности месяцев в году, дней в неделе, букв в слове, фамилий в списке, вагонов в поезде, станций на железной дороге и т. д. Мы дальше будем говорить только о числовых последовательностях, хотя и зовем их коротко последовательностями.
Понятие арифметической прогрессии
Арифметической прогрессией называется прогрессивность, каждый член которой, начиная со второго, равен предыдущему члену, к которому добавляют одно и то же число. Это постоянное для данной последовательности число d называется разницей арифметической прогрессии.
Это постоянное для данной последовательности число d называется разницей арифметической прогрессии.
Первый член и разность арифметической прогрессии могут быть какими угодно числами. Арифметическая прогрессия растущая, если ее разница положительная, или нисходящая, если ее разница отрицательная.
Пример нисходящей арифметической прогрессии: 11, 9, 7, 5, 3, 1, −1, −3…
Чтобы получить любой член арифметической прогрессии, начиная со второго, надо к предыдущему члена добавить разницу d. Поэтому если первый член и разность арифметической прогрессии равны соответственно а и d, то первые члены этой арифметической прогрессии:
a1, a1 + d, a1 + 2d, a1 + 3d, a1 + 4d…
Обратите внимание: коэффициент при d на 1 меньше порядкового номера члена прогрессии. Так же находим а6 = а1 + 5d, а7 = а1 + 6d и вообще:
An = a1 + (n − 1)d
Это формула n-го члена арифметической прогрессии. Сумма членов конечной арифметической прогрессии равна полусумме крайних ее членов, умноженной на число членов.
Sn = [(a1 + an) / 2] × n
Примеры задач
Пример 1
В арифметической прогрессии a1 = 4, d = 3. Найдите a20.
В калькуляторе задаем:
- Первое число: 3
- Последнее число: 20
- Разница (шаг): 3
Получаем:
- Арифметическая прогрессия: 61
- Сумма членов прогрессии: 650
- Последовательность: 4, 7, 10, 13, 16, 19, 22, 25, 28, 31, 34, 37, 40, 43, 46, 49, 52, 55, 58, 61
Проверяем самостоятельно по формулам с теории:
- a20 = а1 + 19d = 4 + 19 × 3 = 61
Пример 2
Найдите сумму первых двадцати членов арифметической прогрессии 5, 7, 9…
В калькуляторе задаем:
- Первое число: 5
- Последнее число: 20
- Разница (шаг): 2
Результаты рассчета:
- Арифметическая прогрессия: 43
- Сумма членов прогрессии: 480
- Последовательность: 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 41, 43
Проверяем:
- Здесь а1 = 5, d = 2.
 Поэтому а20 = 5 + 19 × 2 = 43
Поэтому а20 = 5 + 19 × 2 = 43 - S = [(5 + 43) / 2] × 20 = 480
Онлайн-калькулятор делает вычисления намного проще: он экономит время, избавляя от необходимости делать вычисления вручную по формулам.
Сумма формулы арифметической прогрессии для n-го и суммы n членов
Сумма формулы арифметической прогрессии \(S_n=a_1+(a_1 + d) + (a_1 + 2d) + … + [a_1 + (n–1)d] \). Арифметическая прогрессия (АП) — это последовательность, в которой каждый член получается прибавлением постоянного числа к предыдущему члену. Пример арифметической прогрессии: дни в месяце следуют определенной последовательности, количество учеников в классе следует арифметической прогрессии и так далее.
Сумма арифметической прогрессии Формула Первый член равен \(a_1\), второй член равен \(a_1 + d\), третий член равен \(a_1 + 2d\) и т. д. Это приводит к нахождению суммы арифметического ряда , \(S_n\), начиная с первого члена и последовательно добавляя общую разность.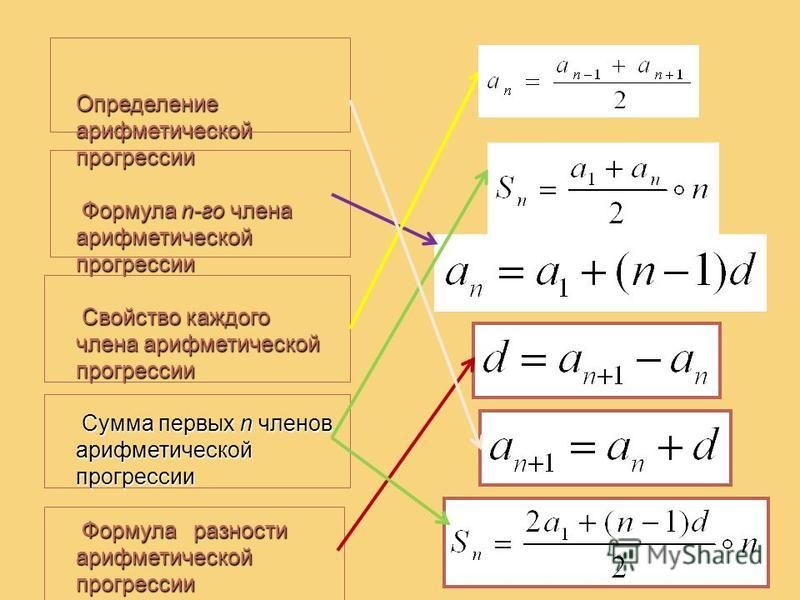
Формула суммы арифметической прогрессии: \(S_n=a_1+(a_1 + d) + (a_1 + 2d) + … + [a_1 + (n–1)d]\)
Мы могли бы также начать с n-й член и последовательно вычитаем общую разность, так что
\(S_n = a_n + (a_n – d) + (a_n– 2d) + … + [a_n – (n–1)d]\)
Если сложить оба уравнения, получим,
\(S_n=a_1+ (a_1 + d) + (a_1 + 2d) + … + [a_1 + (n–1)d]\)
\(S_n = a_n + (a_n – d) + (a_n– 2d) + … + [a_n – (n–1)d]\)
где,
- S = сумма n членов AP
- n = общее количество членов
- a = первый член
- d = общая разность
n членов формулы арифметической прогрессии
\(2S_n = (a_1 + a_n) + (a_1 + a_n) + (a_1 + a_n) + … + [a_1 + a_n]\)
\(2S_n = n (a_1 + a_n)\)
\ (S_n = {n(a_1 + a_n )\over2}\)
\(S_n = {n\over2}(a_1 + a_n )\)
Подставив \(a_n = a_1 + (n – 1)d\ ) в последнюю формулу имеем
\(S_n = {n\over2}[a_1 + a_1 + (n – 1)d]\)
Сумма n членов формулы арифметической прогрессии: \(S_n = {n\over2}[2 a_1 + (n – 1)d]\)
где,
- \(S_n\) = сумма n членов AP
- n = общее количество членов
- a = первый член
- d = общая разность
Эти две формулы позволяют нам быстро найти сумму арифметического ряда.
Узнайте о гармонической прогрессии
N-й член формулы арифметической прогрессииМы можем найти n-й член арифметической прогрессии, используя следующую формулу.
n-й член формулы арифметической прогрессии: \(a_n=a_1+(n – 1)d\)
где,
- a — первое слагаемое
- d — общая разность
- n — количество слагаемых
- \(a_n\) — n-ое слагаемое
Узнать о сумме бесконечной ГП и свойствах Арифметическая прогрессия
Примеры формулы суммы арифметической прогрессииПример 1: Найдите сумму первых 35 членов арифметической прогрессии, третий член которой равен 7, а седьмой член в два раза больше третьего члена. .
Решение: Предположим, что «а» — первый член, а «d» — общая разность данной арифметической прогрессии.
Согласно задаче,
3-й член арифметической прогрессии равен 7
т.е. 3-й член = 7
a + (3 – 1)d = 7
a + 2d = 7 ……………… . (i)
(i)
, а седьмой член в два раза больше третьего члена.
т. е. 7-й член = 3 × 3-й член + 2
a + (7 – 1)d = 3 × [a + (3 – 1)d] + 2
а + 6d = 3 × [а + 2d] + 2
Подставляем значение а + 2d = 7 получаем,
а + 6d = 3 × 7 + 2
а + 6d = 21 + 2
а + 6d = 23 ………………. (ii)
Теперь вычтите уравнение (i) из (ii), мы получим,
4d = 16
d = 4
Подставим значение d = 4 в уравнение (i), мы получим,
a + 2 × 4 = 7
a + 8 = 7
a = 7 – 8
a = -1
Следовательно, первый член арифметической прогрессии равен -1, а общая разность арифметической прогрессии равна 4.
Теперь сумма первых 35 членов арифметической прогрессии \(S_{35} = {35\over2}[2 × (-1) + (35 – 1) × 4]\),
\(\ begin{массив}
={35\over2}[-2 + 34 × 4] ={35\over2}[-2 + 136] ={35\over2}[134] \end{массив}\)
= 35 × 67
= 2345.
вы также можете прочитать о Матрицах.
Пример 2: Если 5-й и 12-й члены арифметической прогрессии равны 30 и 65 соответственно, найдите сумму 26 ее членов.
A. Предположим, что «а» — первый член, а «d» — общая разность данной арифметической прогрессии.
Согласно задаче,
5-й член арифметической прогрессии равен 30
т.е. 5-й член = 30
a + (5 – 1)d = 30
a + 4d = 30 ……………… . (i)
и 12-й член арифметической прогрессии равен 65
т. е. 12-й член = 65
a + (12 – 1)d = 65
a + 11d = 65 ……………….. ( ii)
Теперь, вычтем уравнение (i) из (ii), мы получим,
7d = 35
d = 357357
d = 5
Подставим значение d = 5 в уравнение (i) мы получить,
а + 4 × 5 = 30
а + 20 = 30
а = 30 – 20
а = 10
Следовательно, первый член арифметической прогрессии равен 10, а общая разность арифметической прогрессии равна 5.
Теперь сумма первых 26 членов арифметической прогрессии \(S_{26} = {26\over}[2 × 10 + (26 – 1) × 5]\),
= 13[20 + 25 × 5]
= 13[20 + 125]
= 13[145]
= 1885
Надеюсь, что эта статья о формуле суммы арифметической прогрессии была информативной. Попрактикуйтесь в том же в нашем бесплатном приложении Testbook. Скачать сейчас!
Попрактикуйтесь в том же в нашем бесплатном приложении Testbook. Скачать сейчас!
В.1 Что такое арифметическая прогрессия?
Ans.1 Арифметическая прогрессия (AP) представляет собой последовательность, в которой каждый член получается путем добавления постоянного числа к предыдущему члену.
Q.2 Что такое формула суммы арифметической прогрессии?
Ans.2 Формула суммы арифметической прогрессии: \(S_n=a_1+(a_1 + d) + (a_1 + 2d) + … + [a_1 + (n–1)d]\)
Q.3 Что такое сумма n членов формулы арифметической прогрессии?
Ответ 3 Сумма n членов формулы арифметической прогрессии: \(S_n = {n\over2}[2 a_1 + (n – 1)d]\)
Термин в формуле арифметической прогрессии?
Ans.4 N-й член формулы арифметической прогрессии: \(a_n=a_1+(n – 1)d\)
Q. 5 Приведите несколько примеров арифметической прогрессии.
5 Приведите несколько примеров арифметической прогрессии.
Ответ 5 Некоторые примеры арифметической прогрессии: дни в месяце следуют определенной последовательности, число учащихся в классе следует арифметической прогрессии.
Скачать публикацию в формате PDF| Центр масс: твердого тела, тонкого стержня и центра тяжести с условиями равновесия | |
| Столкновения, второй закон Ньютона для системы частиц с примерами | Состояние вещества и характеристики твердого тела, жидкости, газа, плазмы |
| Открытие электрона, протона и нейтрона | |
| Составные функции: символ, домен, диапазон, свойства и примеры |
Слово ряд подразумевает сумму . Мы можем преобразовать данную арифметическую последовательность в арифметическую серию, добавив члены последовательности.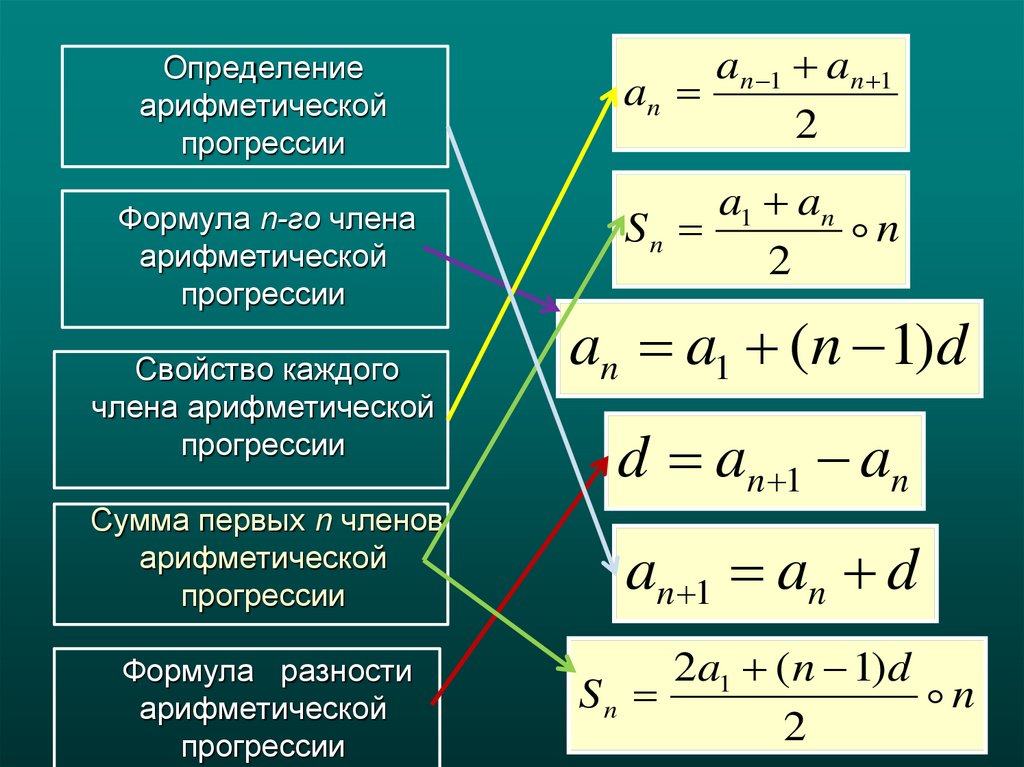 Пример ниже подчеркивает разницу между ними.
Пример ниже подчеркивает разницу между ними.
Последовательность против серии
Арифметическая последовательность (список):
\large{2,4,6,8,10,…}
Арифметическая последовательность (сумма):
\large{2 + 4 + 6 + 8 + 10…}
Обратите внимание, что в последовательности мы перечисляем термины, разделенные запятыми, а в сериях термины добавляются, как указано символами плюса.
Следовательно, арифметическая последовательность — это просто сумма членов арифметической последовательности . В частности, сумма первых \large\color{red}{n} членов арифметической последовательности называется частичная сумма . Частичная сумма обозначается символом \large{{S_n}}.
Ниже приведена общая форма формулы арифметического ряда. Лучше всего это работает, если в задаче заданы первый и последний члены.
Примечания:
▶︎ Формула арифметического ряда также известна как формула частичной суммы.
▶︎ Формула частичной суммы может быть описана словами как произведение среднего значения первого и последнего членов и общее количество членов в сумме.
▶︎ Формула арифметической последовательности включена в формулу частичной суммы. На самом деле это n-й член или последний член \large\color{blue}{a_n} в формуле.
▶︎ Ознакомьтесь с и формулой арифметического ряда и формулой арифметической последовательности (формула n-го члена), потому что они идут рука об руку при решении многих задач.
\Large{{S_n} = n\left( {{{{a_1} + \,{a_n}} \over 2}} \right)}
и
\large{{a_n} = {a_1} + \left( {n — 1} \right)d}
Прежде чем мы начнем работать с примерами, вы можете вспомнить, как я упоминал, что формула арифметической последовательности вписана в формулу арифметического ряда. Если мы заменим и расширим формулу n-го слагаемого в формулу частичной суммы, мы получим новую и полезную форму формулы арифметического ряда.
Ниже приведена альтернативная формула арифметического ряда. Рассмотрим это, если последний член равен , а не .
Формула альтернативного арифметического ряда
где:
\large{{a_1}} — первый член
\large{{d}} — обычная разность
\large{{n}} — число слагаемых в сумме
Примеры применения формулы арифметического ряда
Пример 1: Найдите сумму первых 100 натуральных чисел.
Это простая задача. Цель этой задачи — служить вводным примером. Это должно помочь вам быстро ознакомиться с формулой арифметического ряда. Как только вы поймете, как использовать формулу, вы сможете решать более сложные задачи, как вы увидите позже в этом уроке.
Напомним, что натуральные числа — это счетные числа. Мы можем записать конечную арифметическую последовательность как
1,2,3,4,…,100
и связанную с ней арифметическую последовательность как
1 + 2 + 3 + 4 + … + 100
Очевидно, что первый член 1, последний член равен 100, и количество добавляемых членов также равно 100.
Подставьте значения в формулу, затем упростите, чтобы получить сумму.
Поскольку {a_1} = 1, {a_{100}} = 100 и n = 100, мы имеем
Таким образом, сумма первых 100 натуральных или счетных чисел равна 5050.
Если вы хотите больше попрактиковаться в нахождении суммы первых 200, 300, 400 и 500 натуральных чисел, вы можете использовать список частичных сумм натуральных чисел до 1000, который я создал в качестве ключа к ответу.
Пример 2:
\large{7 + 12 + 17 + 22 + … + 187}
Если вы впервые решаете задачу такого типа, это может показаться вам немного сложным. Не то чтобы это сложно, а потому, что нужные вам значения не указаны явно. Это может сбить вас с толку, потому что вы даже не знаете, с чего начать. Однако, если у вас есть стратегия с самого начала, вы поймете, что эта проблема не так уж и плоха.
Нам нужно изучить данную серию. Определите ценности, которые важны и полезны для нас. Иногда, делая это таким образом, нам открывается следующий логический шаг.
Иногда, делая это таким образом, нам открывается следующий логический шаг.
Итак, это информация, которую мы собрали из сериала. Первый член равен 7. Так как 12-7=5, 17-12=5 и 22-17=5, то общая разность равна 5. Последний член равен 187. Это означает количество членов \large\color{ red}n, добавляемый в серию, отсутствует.
\большой{a_1} = 7
\large{d=5}
\large{a_n} = 187
\large{n = \,?}
Надеюсь, сейчас вы согласитесь со мной, что у нас нет другого выбора, кроме как использовать формула n-го члена , чтобы найти \large\color{red}n. Как только мы найдем значение для \large{n}, мы подставим его в формулу арифметического ряда вместе с первым и последним членами, чтобы найти сумму данного арифметического ряда.
Теперь давайте найдем \large{n}, используя формулу n-го слагаемого.
Наконец, у нас есть все значения, необходимые для вычисления суммы заданного ряда: \large{n=37}, \large{a_1} = 7 и \large{a_n} = 187,
Пример 3: Найдите сумму первых \больших{51} членов арифметической прогрессии.
\large{12\,\,19\,\,26\,\,33\,…}
Стратегия аналогична примеру 2. Вместо нахождения количества членов \ большой\цвет{красный}n, мы будем использовать формулу n-го члена, чтобы найти 51-й член. Затем мы используем формулу арифметического ряда для вычисления суммы первых 51 членов последовательности.
Итак, какое значение мы можем извлечь из данной задачи?
Ну, количество добавляемых терминов \large\color{red}n явно задано в задаче, которая равна n=51.
Теперь из арифметической последовательности легко определить первый член и общую разность. Первый член, очевидно, равен 12, а общая разность равна 7, поскольку 19 — 12 = 7, 26 — 19 = 7 и 33 — 26 = 7.
Итак, вот информация, которую мы собрали. Это означает, что n-й член — это то, что мы ищем.
\большие{a_1}=12
\большие{n=51}
\large{d=7}
\large{a_n}=\,?
Подставьте значения в формулу n-го члена , затем упростите, чтобы получить 51-й член.
Наконец мы можем найти сумму первых 51 слагаемых, потому что мы знаем количество слагаемых n=51, первое слагаемое {a_1}=7 и последнее слагаемое {a_n}=362.
Пример 4: 10-й член арифметической последовательности равен 17, а 30-й член равен -63. Чему равна 50-я частичная сумма \large{S_{50}} арифметической прогрессии?
Вот общая картина. Чтобы найти 50-ю частичную сумму, нам нужно знать первый член \large{a_1} и последний член \large{a_n}, который совпадает с 50-м членом. Очевидно, что в ряду будет 50 терминов, потому что мы суммируем термины с первого по 50-й член.
Чтобы найти первый член \large{a_1}, мы будем использовать формулу n-го члена вместе с данной информацией в задаче, чтобы создать систему уравнений, где неизвестными являются первый член \large{a_1} и общая разница d.
\large{{a_n} = {a_1} + \left( {n — 1} \right)d}
Следовательно, имеем
- 10-й член равен 17
- 30-й член равен -63
Вот эту систему уравнений мы и собираемся решить.
 Мы можем найти значения первого члена \large{a_1} и общей разности \large{d}.
Мы можем найти значения первого члена \large{a_1} и общей разности \large{d}.Мы решим эту систему уравнений, используя метод исключения. Мы вычтем уравнение №2 из уравнения №1, чтобы избавиться от \large{a_1}, тем самым изолировав \large{d}.
Это дает нам
Так как мы уже знаем значение общей разности \large{d}, мы можем легко найти первый член \large{a_1}. Выберите любое из двух уравнений, уравнение №1 или уравнение №2, подставьте значение \large{d}, затем решите для \large{a_1}. Мы выберем уравнение № 1, потому что с ним гораздо проще работать.
Зная первый член и общую разность последовательности, мы можем составить формулу, которая может определить любой член в последовательности.
Используя формулу, которую мы придумали, теперь мы можем найти 50-й член \large{{a_{50}}} в последовательности.
Наконец, у нас есть все, что нужно для вычисления 50-й частичной суммы с использованием формулы арифметического ряда.
Подставьте значения в формулу и упростите.

Пример 5: 10-й член арифметической прогрессии равен 23, а его 12-я частичная сумма равна 192. Найдите сумму первых 40 членов последовательности.
Чтобы найти первые 40 членов арифметической прогрессии, воспользуемся формулой основного арифметического ряда. Однако нам нужно указать недостающие значения в формуле, а именно первый член \large{{{a_1}}} и последний член \large{{{a_n}}}. Количество добавляемых членов \large{n} уже задано и равно 40.
Теперь построим систему уравнений, в которой неизвестными являются первый член \large{a{}_1} и общая разность \ большой {д}.
Первое уравнение исходит из данной информации, что \large{{a_{10}} = 23}. Подставьте значения в формулу n-го члена.
Второе уравнение исходит из данной информации, что \large{{S_{12}} = 192}. Подставьте значения в альтернативную формулу арифметического ряда.
Это система уравнений, которую мы будем решать методом исключения.


 Поэтому а20 = 5 + 19 × 2 = 43
Поэтому а20 = 5 + 19 × 2 = 43 Мы можем найти значения первого члена \large{a_1} и общей разности \large{d}.
Мы можем найти значения первого члена \large{a_1} и общей разности \large{d}.
