простые и наименьший — Поиск количества и суммы
Делитель — это число, на которое нацело делится делимое. У делимого может быть один или несколько делителей, найти их все можно с помощью простого алгоритма, который без проблем реализуется на Python 3.
Нахождение делителей числа
С практической точки зрения будет полезно, если программа на Python не только будет находить делители числа, искать их сумму, определять минимальный и максимальный, а также простые делители.
Каждая подзадача так или иначе связана с предыдущей, поэтому код последующей программы — это немного модернизированный код предыдущей. Кроме того, весь функционал при необходимости можно объединить в одной программе.
Алгоритм нахождения очень простой. В цикле перебираются значения от делимого минус единица до двух включительно. Если делимое нацело делится на текущее значение, то оно является делителем.
Пользователь вводит целое число, делителей которого будет искать программа, тогда код выглядит так:
numb = int(input("Введите целое число: "))
print("Результат:", end = " ")
for i in range(numb - 1, 1, -1):
if (numb % i == 0):
print(i, end = " ")Например, пользователь ввёл число 625.
Введите целое число: 625 Результат: 125 25 5
Простые делители числа
Простой делитель — это делитель, который делится только на единицу и самого себя. Для нахождения простых делителей с помощью Python нужно немного модернизировать программу, добавив в неё дополнительный цикл for и переменную счётчик.
Программа построена по следующему алгоритму:
- Обнулить счётчик.
- В цикле искать делители.
- Если найден, искать во вложенном цикле его делители. Это для того, чтобы определить: является ли он простым.
- Если найден, увеличить счётчик.
- Если счётчик равен нулю, то число простое и надо вывести значение делителя в консоль.
- Перейти на следующую итерацию внешнего цикла.
Цикл теперь выглядит так:
numb = int(input("Введите целое число: "))
print("Простые:", end = " ")
for i in range(numb - 1, 1, -1):
is_simple = 0 # Счётчик
if (numb % i == 0):
for j in range(i - 1, 1, -1):
if (i % j == 0):
is_simple = is_simple + 1 # Увеличиваем, если находим делитель
if (is_simple == 0): # Если делителей не было найдено, выводим
print(i, end = " ")Понятно, что если значение счётчика больше нуля — то число точно не простое.
Можно оптимизировать немного код и сразу завершать вложенный цикл после увеличения счётчика. Для этого можно воспользоваться оператором break в условном операторе, находящемся во вложенном цикле.
Результат работы программы:
Введите целое число: 63 Простые: 7 3
Делители расположены в порядке убывания. И если надо вывести только самый большой простой делитель с помощью Python, то можно после того, как выведется первое число, воспользоваться оператором break для выхода из цикла.
Сумма делителей
Для того чтобы найти сумму всех делителей числа с помощью Python, достаточно добавить в начальную программу переменную, к которой в цикле будет прибавляться каждый найденный делитель.
Код программы:
numb = int(input("Введите целое число: "))
sum_of_dividers = 0
for i in range(numb - 1, 1, -1):
if (numb % i == 0):
sum_of_dividers += i
print("Сумма:", sum_of_dividers)Результат выполнения кода:
Введите целое число: 63 Сумма: 40
Количество делителей
Этот вариант программы также лишь незначительно отличается от изначального.
numb % i == 0» будет выполняться.numb = int(input("Введите целое число: "))
count_of_dividers = 0
for i in range(numb - 1, 1, -1):
if (numb % i == 0):
count_of_dividers += 1
print("Количество равно:", count_of_dividers)Результаты выполнения программы:
Введите целое число: 63 Количество равно: 4
Максимальный и минимальный делитель
Для нахождения минимального и максимального делителя в код на Python нужно добавить две переменные: min_divider и max_divider. В цикле делитель будет сравниваться со значением этих переменных и, если необходимо, записываться в них.
Код программы:
numb = int(input("Введите целое число: "))
min_divider = numb
max_divider = 1
for i in range(numb - 1, 1, -1):
if (numb % i == 0):
if (min_divider > i):
min_divider = i
if (max_divider < i):
max_divider = i
print("Минимальный равен:", min_divider)
print("Максимальный равен:", max_divider)Результат выполнения:
Введите целое число: 63 Минимальный равен: 3 Максимальный равен: 21
Нахождение наименьшего и наибольшего делителя, подсчёт суммы делителей и их количества можно объединить в одну программу на Python.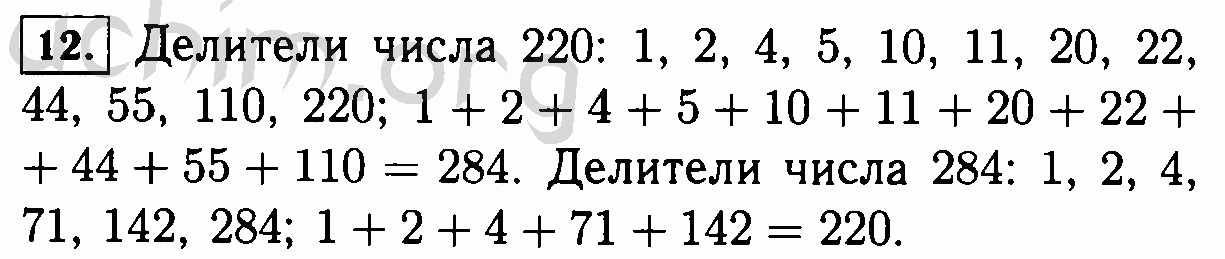
Это не должно вызвать каких-либо проблем или конфликтов, потому что программа работает с 4 независимыми переменными.
Сумма делителей числа формула — Dudom
В данной статье мы поговорим о том, как найти все делители числа. Начнем с доказательства теоремы, с помощью которой можно задать вид всех делителей определенного числа. Далее возьмем примеры нахождения всех нужных делителей и покажем, как именно определить, сколько делителей имеет конкретное число. В последнем пункте подробно рассмотрим примеры задач на нахождение общих делителей нескольких чисел.
Как найти все делители числа
Чтобы понять материал, изложенный в данном пункте, нужно хорошо знать, что вообще из себя представляют кратные числа и делители. Здесь мы поговорим только о поиске делителей натуральных чисел, т.е. целых положительных. Этим можно ограничиться, поскольку свойство делимости гласит, что делители целого отрицательного числа аналогичны делителям целого положительного, которое будет противоположным по отношению к этому числу.
Если речь идет о простом числе, то его можно разделить только на единицу и на само себя. Значит, у любого простого числа a есть всего 4 делителя, два из которых больше 0 и два меньше: 1 , — 1 , a , — a . Возьмем простое число 7 : у него есть делители 7 , — 7 , 1 и — 1 , и все. Еще один пример: 367 – тоже простое число, которое можно разделить лишь на 1 , — 1 , 367 и — 367 .
Сложнее определить все делители составного числа. Сформулируем теорему, которая лежит в основе данного действия.
Допустим, у нас есть выражение, означающее каноническое разложение числа на простые множители, вида a = p 1 s 1 · p 2 s 2 · … · p n s n . Тогда натуральными делителями числа a будут следующие числа: d = p 1 t 2 · p 2 t 2 · … · p n t n , где t 1 = 0 , 1 , … , s 1 , t 2 = 0 , 1 , … , s 2 , … , t n = 0 , 1 , … , s n .
Перейдем к доказательству этой теоремы.
Зная основное определение делимости, мы можем утверждать, что a можно разделить на d , если есть такое число q , что делает верным равенство a = d · q , т.е. q = p 1 ( s 1 − t 1 ) · p 2 ( s 2 — t 2 ) · … · p n ( s n — t n ) .
Любое число, делящее a , будет иметь именно такой вид, поскольку, согласно свойствам делимости, других простых множителей, кроме p 1 , p 2 , … , p n , оно иметь не может, а их показатели в данном случае не превысят s 1 , s 2 , … , s n .
Учитывая доказательство этой теоремы, мы можем сформировать схему нахождения всех положительных делителей данного числа.
Для этого нужно выполнить следующие действия:
- Выполнить каноническое разложение на простые множители и получить выражение вида a = p 1 s 1 · p 2 s 2 · … · p n s n .
- Найти все значения d = p 1 t 2 · p 2 t 2 · … · p n t n , где числа t 1 , t 2 , … , t n будут принимать независимо друг от друга каждое из значений t 1 = 0 , 1 , … , s 1 , t 2 = 0 , 1 , … , s 2 , … , t n = 0 , 1 , … , s n .
Самым трудным в таком расчете является именно перебор всех комбинаций указанных значений. Разберем подробно решения нескольких задач, чтобы наглядно показать применение данной схемы на практике.
Условие: найти все делители 8 .
Решение
Разложим восьмерку на простые множители и получим 8 = 2 · 2 · 2 . Переведем разложение в каноническую форму и получим 8 = 2 3 . Следовательно, a = 8 , p 1 = 2 , s 1 = 3 .
Поскольку все делители восьмерки будут значениями p 1 t 1 = 2 t 1 , то t 1 может принять значения нуля, единицы, двойки, тройки. 3 будет последним значением, ведь s 1 = 3 . Таким образом, если t 1 = 0 , то 2 t 1 = 2 0 = 1 , если 1 , то 2 t 1 = 2 1 = 2 , если 2 , то 2 t 1 = 2 2 = 4 , а если 3 , то 2 t 1 = 2 3 = 8 .
Для нахождения делителей удобно все полученные значения оформлять в виде таблицы:
| t 1 | 2 t 1 |
| 0 | 2 0 = 1 |
| 1 | 2 1 = 2 |
| 2 | 2 2 = 4 |
| 3 | 2 3 = 8 |
Значит, положительными делителями восьмерки будут числа 1 , 2 , 4 и 8 , а отрицательными − 1 , − 2 , − 4 и − 8 .
Ответ: делителями данного числа будут ± 1 , ± 2 , ± 4 , ± 8 .
Возьмем пример чуть сложнее: в нем при разложении числа получится не один, а два множителя.
Условие: найдите все делители числа 567 , являющиеся натуральными числами.
Решение
Начнем с разложения данного числа на простые множители.
567 189 63 21 7 1 3 3 3 3 7
Приведем разложение к каноническому виду и получим 567 = 3 4 · 7 . Затем перейдем к вычислению всех натуральных множителей. Для этого будем присваивать t 1 и t 2 значения 0 , 1 , 2 , 3 , 4 и 0 , 1 , вычисляя при этом значения 3 t 1 · 7 t 2 . Результаты будем вносить в таблицу:
| t 1 | t 2 | 3 t 1 · 7 t 2 |
| 0 | 0 | 3 0 · 7 0 = 1 |
| 0 | 1 | 3 0 · 7 1 = 7 |
| 1 | 0 | 3 1 · 7 0 = 3 |
| 1 | 1 | 3 1 · 7 1 = 21 |
| 2 | 0 | 3 2 · 7 0 = 9 |
| 2 | 1 | 3 2 · 7 1 = 63 |
| 3 | 0 | 3 3 · 7 0 = 27 |
| 3 | 1 | 3 3 · 7 1 = 189 |
| 4 | 0 | 3 4 · 7 0 = 81 |
| 4 | 1 | 3 4 · 7 1 = 567 |
Ответ: натуральными делителями 567 будут числа 27 , 63 , 81 , 189 , 1 , 3 , 7 , 9 , 21 и 567 .
Продолжим усложнять наши примеры – возьмем четырехзначное число.
Условие: найти все делители 3 900 , которые будут больше 0 .
Решение
Проводим разложение данного числа на простые множители. В каноническом виде оно будет выглядеть как 3 900 = 22 · 3 · 52 · 13 . Теперь приступаем к нахождению положительных делителей, подставляя в выражение 2 t 1 · 3 t 2 · 5 t 3 · 13 t 4 значения t 1 , равные 0 , 1 и 2 , t 2 = 0 , 1 , t 3 = 0 , 1 , 2 , t 4 = 0 , 1 . Результаты представляем в табличном виде:
| t 1 | t 2 | t 3 | t 4 | 2 t 1 · 3 t 2 · 5 t 3 · 13 t 4 |
| 0 | 0 | 0 | 0 | 2 0 · 3 0 · 5 0 · 13 0 = 1 |
| 0 | 0 | 0 | 1 | 2 0 · 3 0 · 5 0 · 13 1 = 13 |
| 0 | 0 | 1 | 0 | 2 0 · 3 0 · 5 1 · 13 0 = 5 |
| 0 | 0 | 1 | 1 | 2 0 · 3 0 · 5 1 · 13 1 = 65 |
| 0 | 0 | 2 | 0 | 2 0 · 3 0 · 5 2 · 13 0 = 25 |
| 0 | 0 | 2 | 1 | 2 0 · 3 0 · 5 2 · 13 1 = 325 |
| 0 | 1 | 0 | 0 | 2 0 · 3 1 · 5 0 · 13 0 = 3 |
| 0 | 1 | 0 | 1 | 2 0 · 3 1 · 5 0 · 13 1 = 39 |
| 0 | 1 | 1 | 0 | 2 0 · 3 1 · 5 1 · 13 0 = 15 |
| 0 | 1 | 1 | 1 | 2 0 · 3 1 · 5 1 · 13 1 = 195 |
| 0 | 1 | 2 | 0 | 2 0 · 3 1 · 5 2 · 13 0 = 75 |
| 0 | 1 | 2 | 1 | 2 0 · 3 1 · 5 2 · 13 1 = 975 |
| t 1 | t 2 | t 3 | t 4 | 2 t 1 · 3 t 2 · 5 t 3 · 13 t 4 |
| 1 | 0 | 0 | 0 | 2 1 · 3 0 · 5 0 · 13 0 = 2 |
| 1 | 0 | 0 | 1 | 2 1 · 3 0 · 5 0 · 13 1 = 26 |
| 1 | 0 | 1 | 0 | 2 1 · 3 0 · 5 1 · 13 0 = 10 |
| 1 | 0 | 1 | 1 | 2 1 · 3 0 · 5 1 · 13 1 = 130 |
| 1 | 0 | 2 | 0 | 2 1 · 3 0 · 5 2 · 13 0 = 50 |
| 1 | 0 | 2 | 1 | 2 1 · 3 0 · 5 2 · 13 1 = 650 |
| 1 | 1 | 0 | 0 | 2 1 · 3 1 · 5 0 · 13 0 = 6 |
| 1 | 1 | 0 | 1 | 2 1 · 3 1 · 5 0 · 13 1 = 78 |
| 1 | 1 | 1 | 0 | 2 1 · 3 1 · 5 1 · 13 0 = 30 |
| 1 | 1 | 1 | 1 | 2 1 · 3 1 · 5 1 · 13 1 = 390 |
| 1 | 1 | 2 | 0 | 2 1 · 3 1 · 5 2 · 13 0 = 150 |
| 1 | 1 | 2 | 1 | 2 1 · 3 1 · 5 2 · 13 1 = 1950 |
| t 1 | t 2 | t 3 | t 4 | 2 t 1 · 3 t 2 · 5 t 3 · 13 t 4 |
| 2 | 0 | 0 | 0 | 2 2 · 3 0 · 5 0 · 13 0 = 4 |
| 2 | 0 | 0 | 1 | 2 2 · 3 0 · 5 0 · 13 1 = 52 |
| 2 | 0 | 1 | 0 | 2 2 · 3 0 · 5 1 · 13 0 = 20 |
| 2 | 0 | 1 | 1 | 2 2 · 3 0 · 5 1 · 13 1 = 260 |
| 2 | 0 | 2 | 0 | 2 2 · 3 0 · 5 2 · 13 0 = 100 |
| 2 | 1 | 0 | 1 | 2 2 · 3 0 · 5 2 · 13 1 = 1300 |
| 2 | 1 | 0 | 0 | 2 2 · 3 1 · 5 0 · 13 0 = 12 |
| 2 | 1 | 0 | 1 | 2 2 · 3 1 · 5 0 · 13 1 = 156 |
| 2 | 1 | 1 | 0 | 2 2 · 3 1 · 5 1 · 13 0 = 60 |
| 2 | 1 | 1 | 1 | 2 2 · 3 1 · 5 1 · 13 1 = 780 |
| 2 | 1 | 2 | 0 | 2 2 · 3 1 · 5 2 · 13 0 = 300 |
| 2 | 1 | 2 | 1 | 2 2 · 3 1 · 5 2 · 13 1 = 3900 |
Ответ: делителями числа 3 900 будут: 195 , 260 , 300 , 325 , 390 , 650 , 780 , 975 , 75 , 78 , 100 , 130 , 150 , 156 , 13 , 15 , 20 , 25 , 26 , 30 , 39 , 50 , 52 , 60 , 65 , 1 , 2 , 3 , 4 , 5 , 6 , 10 , 12 , 1 300 , 1 950 , 3 900
Как определить количество делителей конкретного числа
Чтобы узнать, сколько положительных делителей у конкретного числа a, каноническое разложение которого выглядит как a = p 1 s 1 · p 2 s 2 · … · p n s n , нужно найти значение выражения ( s 1 + 1 ) · ( s 2 + 1 ) · … · ( s n + 1 ) .
О количестве наборов переменных t 1 , t 2 , … , t n мы можем судить по величине записанного выражения.
Покажем на примере, как это вычисляется. Определим, сколько будет натуральных делителей у числа 3 900 , которое мы использовали в предыдущей задаче. Каноническое разложение мы уже записывали: 3 900 = 2 2 · 3 · 5 2 · 13 . Значит, s 1 = 2 , s 2 = 1 , s 3 = 2 , s 4 = 1 . Теперь подставим значения s 1 , s 2 , s 3 и s 4 в выражение ( s 1 + 1 ) · ( s 2 + 1 ) · ( s 3 + 1 ) · ( s 4 + 1 ) и вычислим его значение. Имеем ( 2 + 1 ) · ( 1 + 1 ) · ( 2 + 1 ) · ( 1 + 1 ) = 3 · 2 · 3 · 2 = 36 . Значит, это число имеет всего 36 делителей, являющихся натуральными числами. Пересчитаем то количество, что у нас получилось в предыдущей задаче, и убедимся в правильности решения. Если учесть и отрицательные делители, которых столько же, сколько и положительных, то получится, что у данного числа всего будет 72 делителя.
Условие: определите, сколько делителей имеет 84 .
Решение
Раскладываем число на множители.
84 42 21 7 1 2 2 3 7
Записываем каноническое разложение: 84 = 2 2 · 3 · 7 . Определяем, сколько у нас получится положительных делителей: ( 2 + 1 ) · ( 1 + 1 ) · ( 1 + 1 ) = 12 . Для учета отрицательных нужно умножить это число на 2 : 2 · 12 = 24 .
Ответ: всего у 84 будет 24 делителя – 12 положительных и 12 отрицательных.
Как вычислить общие делители нескольких чисел
Зная свойства наибольшего общего делителя, можно утверждать, что количество делителей некоторого набора целых чисел будет совпадать с количеством делителей НОД тех же чисел. Это будет справедливо не только для двух чисел, но и для большего их количества. Следовательно, чтобы вычислить все общие делители нескольких чисел, надо определить их наибольший общий множитель и найти все его делители.
Разберем пару таких задач.
Условие: сколько будет натуральных общих делителей у чисел 140 и 50 ? Вычислите их все.
Решение
Начнем с вычисления НОД ( 140 , 50 ) .
Для этого нам потребуется алгоритм Евклида:
140 = 50 · 2 + 40 , 50 = 40 · 1 + 10 , 40 = 10 · 4 , значит, НОД ( 50 , 140 ) = 10 .
Далее выясним, сколько положительных делителей есть у десяти. Разложим его на простые множители и получим 2 0 · 5 0 = 1 , 2 0 · 5 1 = 5 , 2 1 · 5 0 = 2 и 2 1 · 5 1 = 1 0 . Значит, все натуральные общие делители исходного числа – это 1 , 2 , 5 и 10 , а всего их четыре.
Ответ: данные числа имеют четыре натуральных делителя, равные 10 , 5 , 2 и 1 .
Условие: выясните, сколько общих положительных делителей есть у чисел 585 , 315 , 90 и 45 .
Решение
Вычислим их наибольший общий делитель, разложив число на простые множители. Поскольку 90 = 2 · 3 · 3 · 5 , 45 = 3 · 3 · 5 , 315 = 3 · 3 · 5 · 7 и 585 = 3 · 3 · 5 · 13 , то таким делителем будет 5 : НОД ( 90 , 45 , 315 , 585 ) = 3 · 3 · 5 = 3 2 · 5 .
Чтобы узнать количество этих чисел, нужно выяснить, сколько положительных делителей имеет НОД.
НОД ( 90 , 45 , 315 , 585 ) = 3 2 · 5 : ( 2 + 1 ) · ( 1 + 1 ) = 6 .
Ответ: у данных чисел шесть общих делителей.
Пусть или —сумма всех натуральных делителей натурального числа имеющего каноническое разложение (1).
Легко понять, что
так как слагаемые произведения совпадают с делителями числа .
Суммируя каждый сомножитель по формуле для суммы членов геометрической прогрессии, получаем
Если в каноническом разложении числа прибавить сомножитель , взаимно простой с остальными, то в правой части (1) появится дополнительный сомножитель, а в правой части (2) —сомножитель —, равный сумме делителей числа .
Вообще для взаимно простых и
откуда видно, что функция мультипликативная.
Совершенные числа. Специальные простые числа
Определение совершенных и дружественных чисел
Делители числа (имеются в виду натуральные делители), за исключением самого числа, называются его собственными делителями; их сумма равна .
Если для двух чисел сумма собственных делителей каждого из них равна другому, то такие числа называются дружественными; для них
Натуральное число называется совершенным, если оно равно сумме своих собственных делителей (или если оно дружественно самому себе), т. е. удовлетворяет условию
Определение совершенных и дружественных чисел имеются уже в «Началах» Евклида, они упоминаются и Платоном. Греки видели в них некую совершенную гармонию и приписывали им мистический характер.
Древним грекам была известна пара дружественных чисел и и четыре совершенных числа: .
Функция делителей — арифметическая функция, связанная с делителями целого числа. Функция известна также под именем функция дивизоров. Применяется, в частности, при исследовании связи дзета-функции Римана и рядов Эйзенштейна для модулярных форм. Изучалась Рамануджаном, который вывел ряд важных равенств в модульной арифметике и арифметических тождеств.
,!,>
где d | n <displaystyle >
означает «d делит n». Обозначения d(n), ν(n) и τ(n) (от немецкого Teiler = делитель) используются также для обозначения σ0(n), или функции числа делителей [1] [2] . Если x равен 1, функция называется сигма-функцией или суммой делителей [3] , и индекс часто опускается, так что σ(n) эквивалентна σ1(n) [4] .
Аликвотная сумма s(n) для n — это сумма собственных делителей (то есть делители, за исключением самого n [5] , и равна σ1(n) − n. Аликвотная последовательность для n образуется последовательным вычислением аликвотной суммы, то есть каждое последующее значение в последовательности равно аликвотной сумме предыдущего значения.
Примеры [ править | править код ]
Например, σ0(12) — количество делителей числа 12:
σ 0 ( 12 ) = 1 0 + 2 0 + 3 0 + 4 0 + 6 0 + 12 0 = 1 + 1 + 1 + 1 + 1 + 1 = 6 , <displaystyle <eginsigma _<0>(12)&=1^<0>+2^<0>+3^<0>+4^<0>+6^<0>+12^<0>\&=1+1+1+1+1+1=6,end>>
в то время как σ1(12) — сумма всех делителей:
σ 1 ( 12 ) = 1 1 + 2 1 + 3 1 + 4 1 + 6 1 + 12 1 = 1 + 2 + 3 + 4 + 6 + 12 = 28 , <displaystyle <eginsigma _<1>(12)&=1^<1>+2^<1>+3^<1>+4^<1>+6^<1>+12^<1>\&=1+2+3+4+6+12=28,end>>
и аликвотная сумма s(12) собственных делителей равна:
s ( 12 ) = 1 1 + 2 1 + 3 1 + 4 1 + 6 1 = 1 + 2 + 3 + 4 + 6 = 16.
<1>\&=1+2+3+4+6=16.end>>
Таблица значений [ править | править код ]
| n | Делители | σ0(n) | σ1(n) | s(n) = σ1(n) − n | Комментарии |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 0 | квадрат: значение σ0(n) нечётно; степень 2: s(n) = n − 1 (почти совершенное) |
| 2 | 1,2 | 2 | 3 | 1 | простое: σ1(n) = 1+n, так что s(n) =1 |
| 3 | 1,3 | 2 | 4 | 1 | простое: σ1(n) = 1+n, так что s(n) =1 |
| 4 | 1,2,4 | 3 | 7 | 3 | квадрат: σ0(n) нечётно; степень 2: s(n) = n − 1 (почти совершенное) |
| 5 | 1,5 | 2 | 6 | 1 | простое: σ1(n) = 1+n, так что s(n) =1 |
| 6 | 1,2,3,6 | 4 | 12 | 6 | первое совершенное число: s(n) = n |
| 7 | 1,7 | 2 | 8 | 1 | простое: σ1(n) = 1+n, так что s(n) =1 |
| 8 | 1,2,4,8 | 4 | 15 | 7 | степень 2: s(n) = n − 1 (почти совершенное) |
| 9 | 1,3,9 | 3 | 13 | 4 | квадрат: σ0(n) нечётно |
| 10 | 1,2,5,10 | 4 | 18 | 8 | |
| 11 | 1,11 | 2 | 12 | 1 | простое: σ1(n) = 1+n, так что s(n) =1 |
| 12 | 1,2,3,4,6,12 | 6 | 28 | 16 | первое избыточное число: s(n) > n |
| 13 | 1,13 | 2 | 14 | 1 | простое: σ1(n) = 1+n, так что s(n) =1 |
| 14 | 1,2,7,14 | 4 | 24 | 10 | |
| 15 | 1,3,5,15 | 4 | 24 | 9 | |
| 16 | 1,2,4,8,16 | 5 | 31 | 15 | квадрат: σ0(n) нечётно; степень 2: s(n) = n − 1 (почти совершенное) |
Случаи x = 2 <displaystyle x=2>
, x = 3 <displaystyle x=3> и так далее входят в последовательности
Свойства [ править | править код ]
Для целых, не являющихся квадратами, каждый делитель d числа n имеет парный делитель n/d, а значит, σ 0 ( n ) <displaystyle sigma _<0>(n)>
всегда чётно для таких чисел.
<epsilon >).»/>
Северин Вигерт дал более точную оценку
lim sup n → ∞ log d ( n ) log n / log log n = log 2. <displaystyle limsup _<frac <log d(n)><log n/log log n>>=log 2.>
lim inf n → ∞ d ( n ) = 2. <displaystyle liminf _d(n)=2.>
В терминах О-большое, Дирихле показал, что средний порядок функции делителей удовлетворяет следующему неравенству (см. теорему 3.3 книги Апостола)
для всех x ≥ 1 , ∑ n ≤ x d ( n ) = x log x + ( 2 γ − 1 ) x + O ( x ) , <displaystyle xgeq 1,sum _d(n)=xlog x+(2gamma -1)x+O(<sqrt >),>
где γ <displaystyle gamma >
— постоянная Эйлера — Маскерони.
Задача улучшить границу O ( x ) <displaystyle O(<sqrt >)> в этой формуле — это проблема Дирихле о делителях
Поведение сигма функции неравномерно. Асимптотическую скорость роста сигма функции можно выразить формулой:
lim sup n → ∞ σ ( n ) n log log n = e γ , <displaystyle limsup _<frac <sigma (n)>>=e^<gamma >,>
где lim sup — верхний предел.
<gamma >,>
В 1915 году Рамануджан доказал, что при выполнении гипотезы Римана неравенство
σ ( n ) e γ n log log n <displaystyle sigma (n)
(неравенство Робина)
выполняется для всех достаточно больших n [8] . В 1984 году Гай Робин доказал, что неравенство верно для всех n ≥ 5041 в том и только в том случае, если гипотеза Римана верна [9] . Это теорема Робина и неравенство стало широко известно после доказательства теоремы. Наибольшее известное число, нарушающее неравенство — это n=5040. Если гипотеза Римана верна, то нет чисел, больших этого и нарушающих неравенство. Робин показал, что в случае ошибочности гипотезы существует бесконечно много чисел n, нарушающих неравенство, и известно, что наименьшее из таких чисел n ≥ 5041 должно быть сверхизбыточным числом [10] . Было показано, что неравенство выполняется для больших нечётных свободных от квадратов чисел, и что гипотеза Римана эквивалентна выполнению неравенства для всех чисел n, делящихся на пятую степень простого числа [11]
Джефри Лагариас (Jeffrey Lagarias) в 2002 году доказал, что гипотеза Римана эквивалентна утверждению
σ ( n ) ≤ H n + ln ( H n ) e H n <displaystyle sigma (n)leq H_+ln(H_)e^>>
для любого натурального n, где H n <displaystyle H_> — n-е гармоническое число [12] .
Робин доказал, что неравенство
σ ( n ) e γ n log log n + 0.6483 n log log n <displaystyle sigma (n)
выполняется для n ≥ 3 без каких-либо дополнительных условий.
4.2: Мультипликативные теоретико-числовые функции
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 8839
- Виссам Раджи
- Американский университет Бейрута
Теперь мы представляем несколько мультипликативных теоретико-числовых функций, которые сыграют решающую роль во многих теоретико-числовых результатах. Мы начнем с обсуждения фи-функции Эйлера, которая была определена в предыдущей главе. Затем мы определяем функцию суммы делителей и функцию числа делителей вместе с их свойствами.
\(\phi\)-функция Эйлера
Как определено ранее, \(\phi\)-функция Эйлера подсчитывает количество целых чисел, меньших и взаимно простых с заданным целым числом. Сначала вычислим значение \(фи\)-функции при простых числах и степенях простых чисел.
Если \(p\) простое число, то \(\phi(p)=p-1\). Наоборот, если \(p\) такое целое число, что \(\phi(p)=p-1\), то \(p\) простое число.
Первая часть очевидна, поскольку каждое натуральное число, меньшее \(p\), взаимно просто с \(p\). Наоборот, предположим, что \(p\) не простое число. Тогда \(p=1\) или \(p\) — составное число. Если \(p=1\), то \(\phi(p)\neq p-1\). Теперь, если \(p\) составное, то \(p\) имеет положительный делитель. Таким образом, \(\phi(p)\neq p-1\). Получили противоречие и, значит, \(p\) простое число. 99=512.\)
Теперь докажем, что \(\phi\) является мультипликативной функцией.
Пусть \(m\) и \(n\) — два взаимно простых натуральных числа. Тогда \(\phi(mn)=\phi(m)\phi(n)\).
Обозначим \(\phi(m)\) через \(s\) и пусть \(k_1,k_2,.
..,k_s\) будет редуцированной системой вычетов по модулю \(m\). Точно так же обозначим \(\phi(n)\) через \(t\) и пусть \(k_1′,k_2′,…,k_t’\) будет редуцированной системой вычетов по модулю \(n\). Заметим, что если \(x\) принадлежит редуцированной системе вычетов по модулю \(mn\), то \[(x,m)=(x,n)=1.\] Таким образом, \[x\equiv k_i(mod\ m) \mbox{и} \ \ x\equiv k_j'(mod \ n)\] для некоторого \(i,j\). Наоборот, если \[x\equiv k_i(mod\ m) \mbox{and} \ \ x\equiv k_j'(mod \ n)\] некоторый \(i,j\), то \((x,mn)= 1\) и, таким образом, \(x\) принадлежит редуцированной системе вычетов по модулю \(mn\). Таким образом, редуцированная система вычетов по модулю \(mn\) может быть получена путем определения всех \(x\), конгруэнтных \(k_i\) и \(k_j’\) по модулю \(m\) и \(n\). ) соответственно. По китайской теореме об остатках система уравнений \[x\equiv k_i(mod\ m) \mbox{and} \ \ x\equiv k_j'(mod \ n)\] имеет единственное решение. Таким образом, разные \(i\) и \(j\) дадут разные ответы. Таким образом, \(\phi(mn)=st\).
9{a_j})\) четно. Следовательно, \(\phi(n)\) четно.
Пусть \(n\) — целое положительное число. Тогда \[\sum_{d\mid n}\phi(d)=n.\]
Разобьем целые числа от 1 до \(n\) на классы. Поместите целое число \(m\) в класс \(C_d\), если наибольший общий делитель \(m\) и \(n\) равен \(d\). Таким образом, количество целых чисел в классе \(C_d\) — это количество положительных целых чисел, не превосходящих \(n/d\), которые взаимно просты с n/d. Таким образом, у нас есть \(\phi(n/d)\) целых чисел в \(C_d\). Таким образом, мы видим, что \[n=\sum_{d\mid n}\phi(n/d).\] Поскольку \(d\) пробегает все делители \(n\), то же самое происходит и с \(n/d \). Отсюда \[n=\sum_{d\mid n}\phi(n/d)=\sum_{d\mid n}\phi(d).\]
Функция суммы делителей
Функция суммы делителей, обозначаемая \(\sigma(n)\), представляет собой сумму всех положительных делителей числа \(n\).
\(\sigma(12)=1+2+3+4+6+12=28.\)
Обратите внимание, что мы можем выразить \(\sigma(n)\) как \(\sigma(n) =\sum_{d\mid n}d\).
Теперь докажем, что \(\sigma(n)\) является мультипликативной функцией.
Функция суммы делителей \(\sigma(n)\) является мультипликативной.
В теореме 35 мы доказали, что сумматорная функция мультипликативна, если \(f\) мультипликативна. Итак, пусть \(f(n)=n\) и заметим, что \(f(n)\) мультипликативно. В результате \(\sigma(n)\) является мультипликативным. 93-1}{5-1}=15,31=465.\)
Функция числа делителей
Функция числа делителей, обозначаемая \(\tau(n)\), представляет собой сумму всех положительные делители \(n\).
\(\tau(8)=4.\)
Мы также можем выразить \(\tau(n)\) как \(\tau(n)=\sum_{d\mid n}1\).
Мы также можем доказать, что \(\tau(n)\) является мультипликативной функцией.
Функция числа делителей \(\tau(n)\) является мультипликативной.
По теореме 36 при \(f(n)=1\) \(\tau(n)\) мультипликативно. 92)=(3+1)(2+1)=12\).
Упражнения
- Найдите \(\phi(256)\) и \(\phi(2.3. 5.7.11)\).
- Покажите, что \(\phi(5186)=\phi(5187)\).
- Найдите все положительные целые числа \(n\) такие, что \(\phi(n)=6\).
- Покажите, что если \(n\) — натуральное число, то \(\phi(2n)=\phi(n)\), если \(n\) нечетно.
- Покажите, что если \(n\) — натуральное число, то \(\phi(2n)=2\phi(n)\), если \(n\) четно.
- Покажите, что если \(n\) — нечетное целое число, то \(\phi(4n)=2\phi(n)\). 9313\).
- Какие натуральные числа имеют нечетное число положительных делителей.
- Какие натуральные числа имеют ровно два положительных делителя.
5.7.11)\).Авторы и ссылки
Доктор Виссам Раджи, доктор философии, Американского университета в Бейруте. Его работа была выбрана фондом Saylor Foundation Open Textbook Challenge для публичного выпуска под лицензией Creative Commons Attribution ( CC BY ) лицензия.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Виссам Раджи
- Лицензия
- СС BY
- Показать страницу TOC
- нет
- Теги
- ϕ-функция Эйлера
Есть ли формула для вычисления суммы всех правильных делителей числа?
спросил
Изменено 17 дней назад
Просмотрено 94k раз
$\begingroup$
Мне не нужно перечислять все правильные делители, я просто хочу получить их сумму.
Потому что для небольшого числа проверка всех правильных делителей и их сложение не представляет большого труда. Однако для большого числа это будет работать очень медленно. Есть идеи?
Для собственных множителей вычтите из этой суммы $n$. Это может быть быстрее, а может и нет, в зависимости от числа и того, как вы получите простую факторизацию, но это типичный метод для школьных конкурсных задач такого рода.
$\endgroup$
10
$\begingroup$
Просто потому, что это интересно:
На самом деле существует (менее известная) рекурсивная формула для вычисления $\sigma(n)$, суммы делителей $n$. 92-i}{2})n \right), $$ где мы положили $\sigma(i) = 0$ для $i\leq 0$, а $\delta(\cdot,\cdot)$ — дельта Кронекера.
Обратите внимание, что вычисление $\sigma(n)$ уже требует $\sigma(n-1)$, поэтому его сложность составляет не менее $\mathcal O(n)$, что делает его бесполезным для практических целей.
{n/2} \; i\mathbin{\cdot}((\mathop{\text{sign}}(n/i-\lfloor n/i\rfloor)+1)\mathbin{\text{mod}}2)$$
Вот и все. Прямо и легко.
$\endgroup$
5
$\begingroup$
Если вам нужны числовые значения, то калькулятор на сайте ниже покажет все делители заданного положительного целого числа, количество делителей и их сумму. В нем также есть ссылки на калькуляторы для других функций теории чисел, таких как функция Эйлера.
http://www.javascripter.net/math/calculators/divisorscalculator.htm 9х \ влево | \text{sign}(x \text{ mod } n) — 1 \right| * n $$
Краткое пояснение:
$ \text{sign}(x \text{ mod } n) $ равно $0$, если $n$ является делителем $x$ (или равно $1$, если $n$ не является делителем $x$), поэтому мы должны инвертировать его, вычитая из него единицу ($0$ -> $-1$; $1$ -> $0$) и взяв абсолютное значение результата .