Сумма и разность векторов определение: Сложение и вычитание векторов. Умножение вектора на число — урок. Геометрия, 10 класс.

Сложение и вычитание векторов.

Сложение и вычитание векторов.

Сумма двух векторов. Законы сложения векторов. Правило параллелограмма.

Представим себе такую ситуацию. Направляясь из школы домой, вам захотелось пить и вы решили зайти сначала в магазин, а затем уже домой. Цель достигнута: вы из школы добрались домой. Сейчас мы описали принцип первого правила сложения векторов.

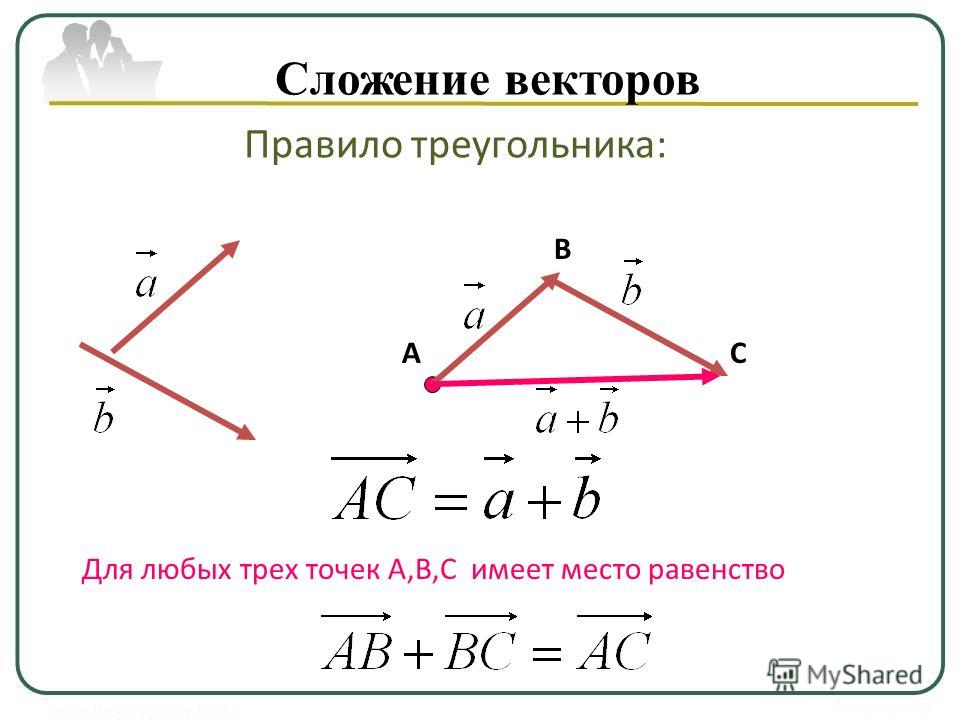
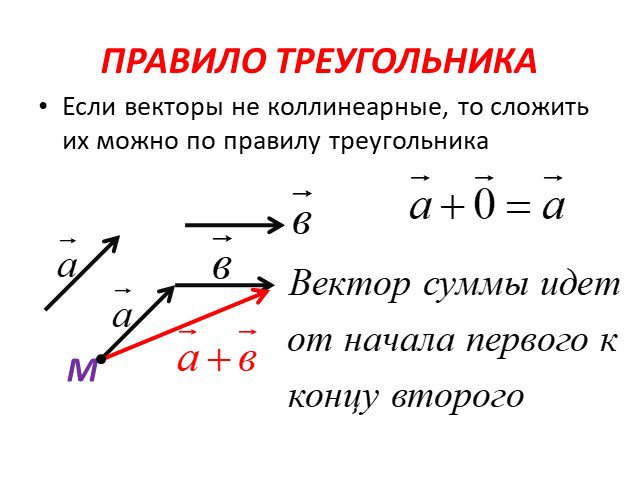
Правило треугольника.

Чтобы найти вектор суммы двух векторов и , нужно:

1. совместить параллельным переносом начало вектора с концом вектора ;

2. провести вектор из начала вектора в конец вектора ;

3. получившийся вектор и есть вектор суммы: .

Если к вектору прибавить нулевой вектор по правилу треугольника, то получим вектор , т. е. справедливо равенство: .

Утверждение. Если и – произвольные точки, то .

Например, .

Сложение векторов подчиняется алгебраическим законам.

ТЕОРЕМА. Для любых векторов и справедливы равенства:

(переместительный закон)

(сочетательный закон).

Дано:

Доказать: 1)

2)

Доказательство.

Доказательство теоремы в случае, когда векторы коллинеарны достаточно простое. Его вы можете провести самостоятельно. Мы рассмотрим случай, когда данные векторы неколлинеарны.

1). Отметим произвольную точку и отложим от этой точки вектор . Воспользуемся правилом треугольника и прибавим к нему вектор . Вектором суммы этих двух векторов является вектор . (Рисунок слева).

Теперь от точки и отложим вектор . По правилу треугольника прибавим к нему вектор . Вектором суммы этих двух векторов является вектор . (Рисунок справа).

– параллелограмм и точка совпадает с точкой . Значит, , т.е.

2
). От точки отложим вектор , от точки отложим вектор , а от точки – вектор . Найдём суммы векторов по правилу треугольника.

Теорема доказана.

При доказательстве первой формулы получился параллелограмм, причём, из точки выходят два вектора и , а вектор их суммы является диагональю параллелограмма. На основе этого возникает второе правило геометрического сложения векторов.

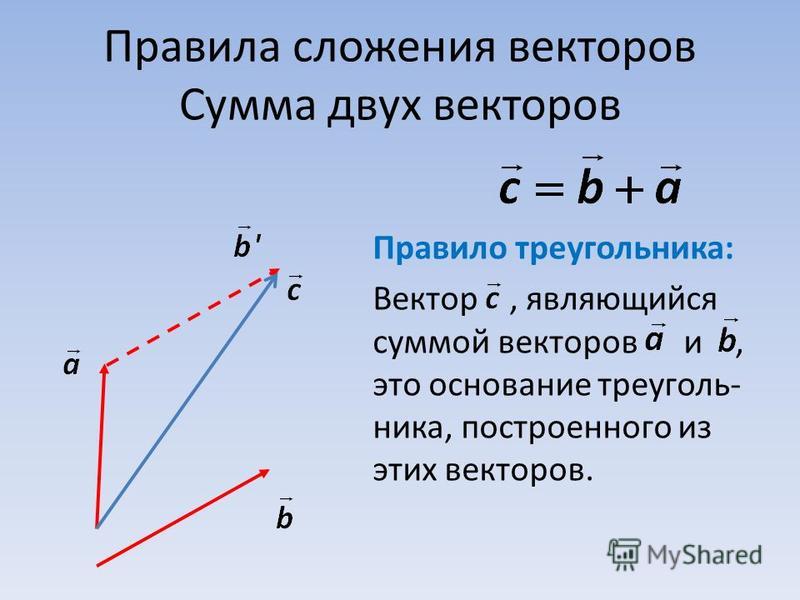
Правило параллелограмма.

Чтобы найти вектор суммы двух векторов и , нужно:

1. совместить параллельным переносом начала векторов и ;

2. на этих векторах достроить параллелограмм;

3. вектором суммы является вектор, который лежит на диагонали параллелограмма, имеющий своё начало в начале исходных векторов.

Сумма нескольких векторов.

Сложение нескольких векторов происходит по принципу правила треугольника. Складываются два вектора, к вектору суммы прибавляется следующий вектор и т.д. Приведём пример.

Сложить векторы .

О тметим точку и отложим от неё вектор . Прибавим к нему вектор по правилу треугольника. . Теперь к вектору прибавим вектор . . К вектору прибавляем вектор . . Осталось к вектору прибавить вектор . .

Итак, . Значит, суммой векторов является вектор, с началом в начале первого вектора и концом – в конце последнего. Такое сложение векторов называется правилом многоугольника.

Правило многоугольника.

Чтобы найти вектор суммы нескольких векторов, нужно:

1. последовательно совместить параллельным переносом начало последующего вектора с концом предыдущего;

2. вектором суммы всех векторов является вектор, с началом в начале первого вектора и концом – в конце последнего.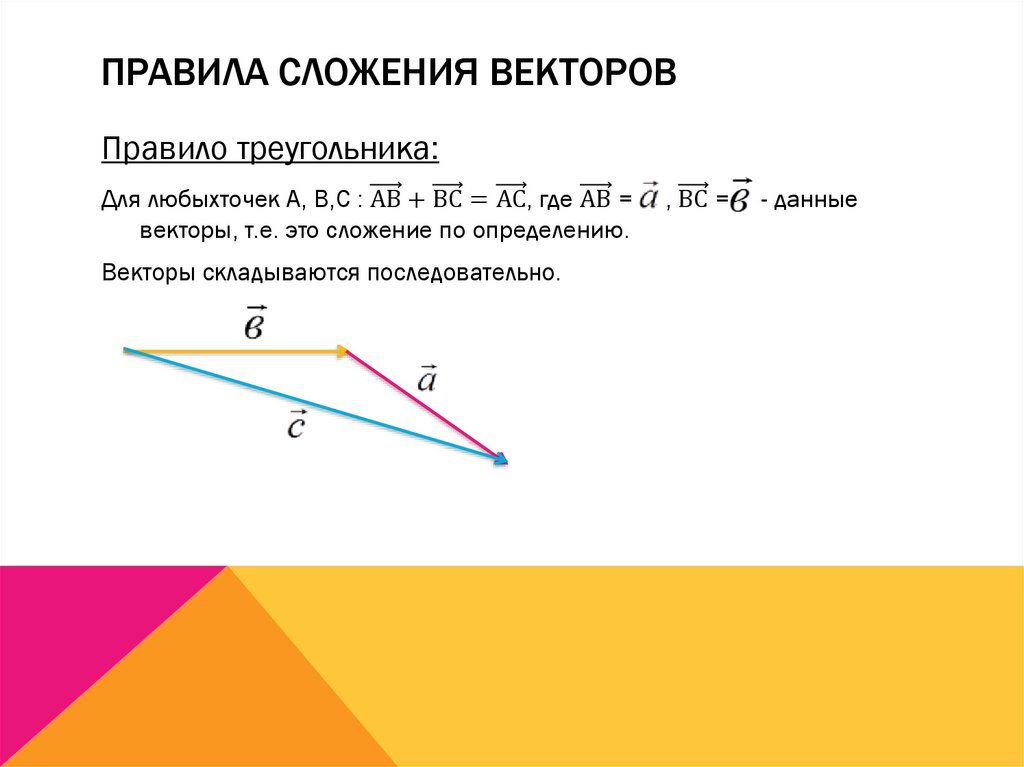

Вычитание векторов.

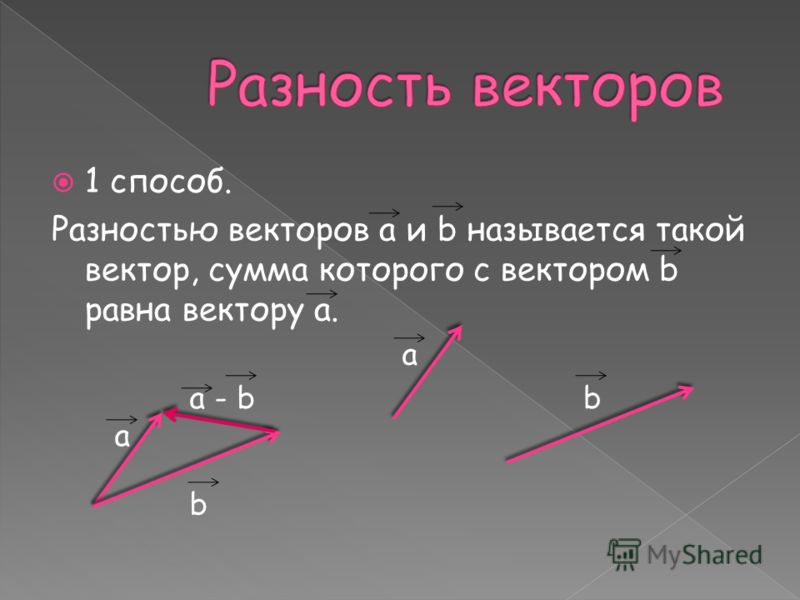
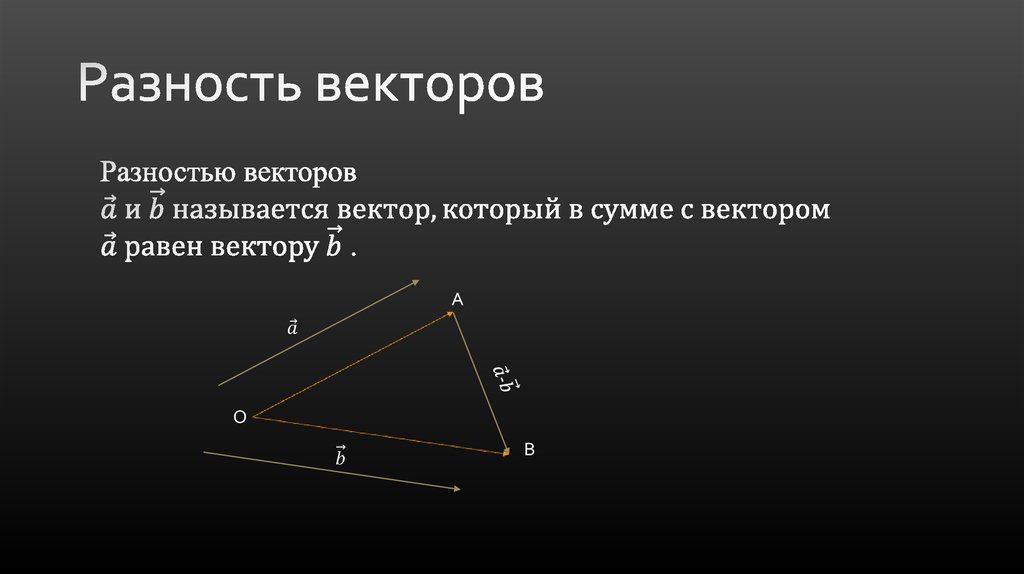
Определение. Разностью двух векторов и называется такой вектор , что при сложении его с вектором получается вектор .

В ычитание векторов можно производить, руководствуясь двумя понятиями: следствием из правила треугольника сложения векторов; определением разности двух чисел. Разберём каждое из них.

Сложим векторы и по правилу треугольника. По рисунку видно, что . Отсюда, и . Значит, разность двух векторов можно составить, совмещая их начала, либо совмещая их концы. Отсюда два правила:

I правило вычитания векторов.

Чтобы найти вектор разности двух векторов, нужно:

1. совместить параллельным переносом начала этих векторов;

2. вектором разности является вектор с началом в конце второго вектора и концом в конце первого вектора.

II правило вычитания векторов.

Чтобы найти вектор разности двух векторов, нужно:

1. совместить параллельным переносом концы этих векторов;

2. вектором разности является вектор с началом в начале первого вектора и концом в начале второго вектора.

Далее, из алгебры мы знаем, что для того, чтобы из числа вычесть число , нужно к числу прибавить число, противоположное числу , т.е. . Такое же правило справедливо и для векторов.

ТЕОРЕМА. Для любых векторов справедливо равенство:

Дано:

Доказать:

Доказательство.

1. Найдём разность векторов по I правилу. Вектором разности является вектор (рисунок слева). А теперь найдём сумму векторов по правилу треугольника, где – вектор, противоположный вектору . Вектором суммы является вектор (рисунок справа). Не трудно заметить, что . Они сонаправлены и имеют одинаковые модули.

2. А теперь докажем то же самое аналитически. По определению разности векторов,

Что и требовалось доказать.

Из этой теоремы следует третье правило вычитания векторов.

III правило вычитания векторов.

Чтобы найти вектор разности двух векторов, нужно к первому вектору прибавить вектор, противоположный второму.

Используя это правило вычитания векторов, способ сложения векторов выбирается произвольно.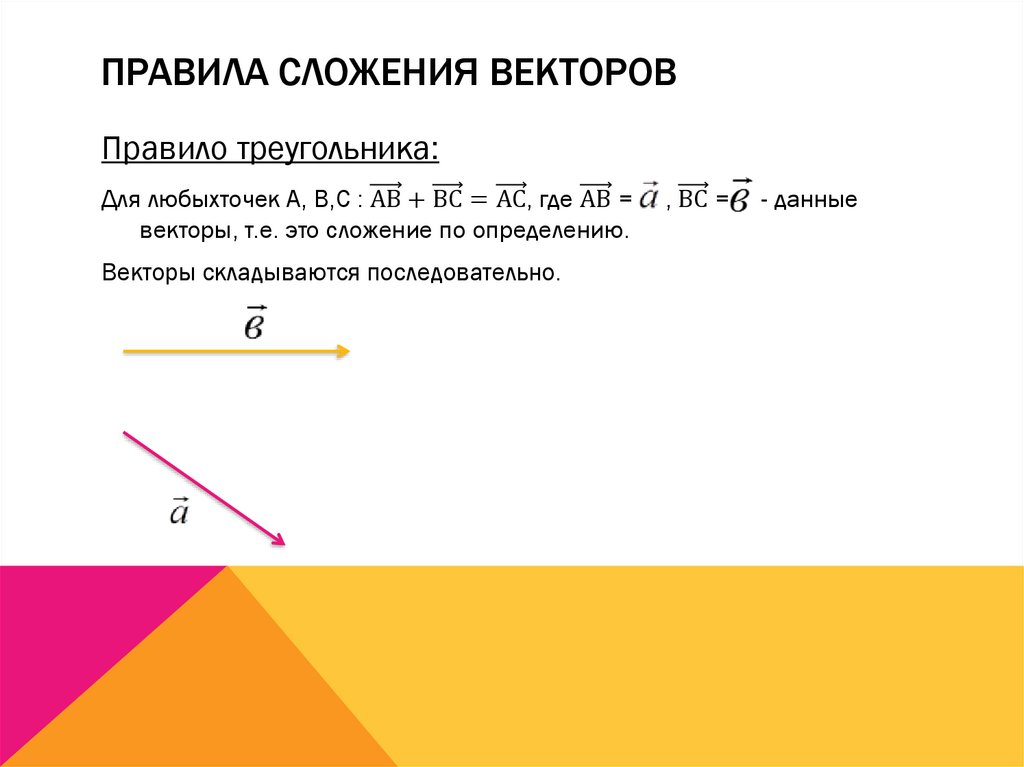

1. В ектор является суммой векторов и . Определите, какой из четырёх рисунков верный.

1. Проведите векторы . Какая геометрическая фигура у вас получилась?

2. В ектор является разностью векторов и . Определите, какой из четырёх рисунков верный.

1. В ектор является суммой векторов и . Определите, какой из четырёх рисунков верный.

1. В ыразите вектор через векторы , используя рисунок.

1. В ыразите вектор через векторы , используя рисунок.

1. Упростите выражения:

2. Длина вектора равна , а длина вектора равна . Сколько различных целых значений может принимать длина вектора ?

3. Длина вектора равна , а длина вектора равна . Сколько различных целых значений может принимать длина вектора ?

4. Длина вектора равна , а длина вектора равна . Сколько различных целых значений может принимать длина вектора ?

5. Длина вектора равна , а длина вектора равна . Сколько различных целых значений может принимать длина вектора ?

6. Длина вектора равна , а длина вектора равна . Сколько различных целых значений может принимать длина вектора ?

7. В квадрате проведены диагонали и . Укажите номера верных утверждений.

8. – параллелограмм. Найдите сумму векторов .

9. – прямоугольник. Диагонали и пересекаются в точке . Укажите номера верных утверждений.

10. – параллелограмм. Выразите векторы и через векторы и .

1. – параллелограмм. Выразите векторы и через векторы и .

1. – прямоугольник. Выразите векторы и через векторы и .

1. – параллелограмм. Выразите векторы и через векторы и .

1. Н айдите длины векторов , изображённых на клетчатой бумаге с размерами клетки 1 х 1.

1. Д ве стороны прямоугольника равны 20 и 21. Найдите длину суммы векторов и .

1. Д ве стороны прямоугольника равны 7 и 24. Найдите длину разности векторов и .

1. Н а каждом рисунке найдите длину вектора (размеры клетки 1 х 1).

1. Н а каждом рисунке найдите длину суммы векторов и (размеры клетки 1 х 1).

1. Н а каждом рисунке найдите длину разности векторов и , изображённых на клетчатой бумаге с размерами клетки 1 х 1.

5

Определение вектора, его длины. Равные и противоположные векторы. Сложение и вычитание векторов. Умножение вектора на число.

Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: Археология Биология Генетика География Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия Экология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления

⇐ ПредыдущаяСтр 2 из 15Следующая ⇒                                           Рассмотрим произвольный отрезок. На нем можно  указать два направления: от                                                                                                      одного конца к другому и наоборот.        Чтобы выбрать одно из направлений, один конец отрезка назовем началом, а другой – концом и будем считать, что отрезок направлен от начала к концу.         ®                                                В                  Конец вектора А                                                         Вектором, или направленным отрезком,   Начало вектора                  называется отрезок вместе с его направлением.          На рисунках вектор изображается отрезком со стрелкой, показывающей направление вектора. Векторы обозначают двумя заглавными латинскими буквами со стрелкой над ними, например . Первая буква обозначает начало вектора, вторая – конец. Векторы часто обозначают и одной латинской буквой со стрелкой над ней:          Любая точка плоскости также является вектором. В этом случае вектор называется нулевым. Начало нулевого вектора совпадает с его концом, а на рисунке такой вектор изображается одной точкой. Если, например, точка, изображающая нулевой вектор, обозначена буквой М, то данный нулевой вектор можно обозначить . Нулевой вектор обозначается символом . Длиной или модулем ненулевого вектора называется длина отрезка АВ. Длина вектора ( ) обозначается так: . Длина нулевого вектора считается равной нулю: . Ненулевые векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых; нулевой вектор считается коллинеарным любому вектору.          · М                                       A                                                B                  F                                                          ·                         D        E                                 C                        Векторы  (вектор нулевой) коллинеарные, а векторы , а также  не коллинеарны.        Если два ненулевых вектора  и коллинеарны, то они могут быть направлены либо одинаково, либо противоположно. В первом случае векторы  и  называются сонаправленными, а во втором – противоположно направленными.        Два ненулевых вектора, лежащие на параллельных прямых, называются сонаправленными (противоположно направленными) если их концы лежат по одну сторону (по разные стороны) от прямой, проходящей через начала.          Если векторы  и сонаправлены, то пишут: ­­ , а если они противоположно направлены, пишут: ­¯ .        Начало нулевого вектора совпадает с его концом, поэтому нулевой вектор не имеет какого-либо определенного направления. Иначе говоря, любое направление можно считать направлением нулевого вектора. Условимся считать, что нулевой вектор сонаправлен с любым вектором. Ненулевые коллинеарные векторы обладают следующими свойствами:                                                                                                                                                                                                                                                                                                                                Векторы называются равными, если они сонаправлены и их длины равны. Пусть — два вектора. Отметим произвольную             B                    точку А и отложим от этой точки вектор ,                                            равный . Затем от точки В отложим вектор , равный .     A                C             Вектор  называется суммой векторов . Сумма векторов   и  обозначается так: Суммой векторов  называется вектор , началом которого является начало вектора , конечной точкой будет конец вектора , отложенного от конца вектора . Это правило сложения векторов называется правилом треугольника. Cправедливо равенство . Правило треугольника можно сформулировать также следующим образом: если А, В и С – произвольные точки, то . Это равенство справедливо для произвольных точек А, В и С, в частности, в том случаае, когда две из них или все три совпадают. Рассмотрим свойства сложения векторов. Теорема. Для любых векторов ,   и  справедливы равенства: 1.  + = +  (переместительное свойство) 2. (  + ) +  = + (  + ) (сочетательное свойство) Доказательство. 1. Рассмотрим случай, когда векторы  не коллинеарны. B         C              От произвольной точки А отложим векторы                                                    и на этих векторах построим                                          параллелограмм ABCD. По правилу треугольника                             . Аналогично                                       . Отсюда следует, что  А             D             + = +                       B          C                      2. От произвольной точки А отложим                                                       вектор , от точки В – вектор ,                                              а от точки С – вектор .                                                       Применяя правило треугольника, получим:         A                       D          (  + ) +  =        + (  + ) =        Þ (  + ) +  = + (  + ).        При доказательстве свойства 1 мы обосновали так называемое правилопараллелограмма сложения неколлинеарных векторов: чтобы сложить неколлинеарные векторы и , нужно отложить от какой-нибудь точки А векторы и  и построить параллелограмм ABCD. Тогда вектор  равен  + . Правило параллелограмма часто используется в физике, например при сложении двух сил.        Сложение нескольких векторов производится следующим образом: первый вектор складывается со вторым, затем их сумма складывается с третьим вектором и т. д. Из закона сложения векторов следует, что сумма нескольких векторов не зависит от того, в каком порядке они складываются.                                                         Правило построения суммы нескольких                                                      векторов называется правилом много —                                                              угольника.                                                                        Правило многоугольника можно                                                                            сформулировать также следующим                                                                    образом: если А1, А2, …, Аn  —                                                             произвольные точки плоскости, то                       .                                                                           Это равенство справедливо для любых точек А1, А2, …, Аn ,   в частности, в том случае, когда некоторые из них совпадают. Например, если начало первого совпадает с концом последнего вектора, то сумма данных векторов равна нулевому вектору.                                                             + + + + =                                                  Разностью векторов  и называется такой вектор, сумма которого с вектором  равна вектору .        Разность векторов и  обозначается так: — .        Рассмотрим задачу о построении разности двух векторов.        Задача. Даны векторы и . Построить вектор — .        Решение.              А                         Отметим на плоскости произвольную точку О и                                               отложим от этой точки векторы и .                —                     По правилу треугольника , или                                            . Таким образом, сумма векторов и  равна вектору   О              В                       По определению разности векторов это означает, что , т.е. вектор  искомый.        Введем понятие вектора, противоположного данному.            В                                   Пусть — произвольный ненулевой вектор.                             Вектор называется противоположным вектору , если векторы  и                         имеют равные длины и противоположно направлены                                                             .         Вектор  является противоположным вектору . Вектором, противоположным нулевому вектору, считается нулевой вектор.        Вектор, противоположный вектору , обозначается так: — . Очевидно,  + (- ) = .        Теорема. Для любых векторов и справедливо равенство — = + (- ).        Доказательство. По определению разности векторов ( — ) +  = . Прибавив к обеим частям этого равенства вектор (- ), получим:        ( — ) + + (- ) = + (- ), или ( — ) +  = + (- ), откуда — = + (- ). Отметим на плоскости произвольную точку О и отложим от этой точки вектор                                      . Затем от точки А отложим вектор  По теореме о                 —                         разности векторов — = + (- ), поэтому — =  т.е. вектор искомый.                                                    Произведением ненулевого вектора  на число k называется такой вектор , длина которого равна , причем векторы  и сонаправлены при k ³ 0 и противоположно направлены при k < 0. Произведением нулевого вектора на любое число считается нулевой вектор.        Произведение вектора  на число k обозначается так: k .     k × = , если:                                                                                                 3                                                                                                                                                                                                                                                                 —2                                                                                              Из определения произведения вектора на число следует, что: 1) произведение любого вектора на число нуль есть нулевой вектор; 2) для любого числа k и любого вектора  векторы   и k  коллинеарны.   Следствия из определения: 1. × 0 = 0; 2. Для любого числа k и любого вектора  векторы   и k  коллинеарные.                             Основные свойства умножения вектора на число: 1. ( kl )  = k × ( l ) (сочетательный закон) 2. ( k + l)  = k  + l  (первый распределительный закон ) 3. k (  + ) = k  + k  (второй распределительный закон)        Умножение вектора на число обладает следующими основными свойствами: для любых чисел k , l и любых векторов ,  справедливы равенства:              Доказательство. Если k ¹ 0, l ¹ 0,  ¹ , то оба вектора (kl )  и k (l ) имеют одну и ту же длину, равную , и одно и то же направление. Это направление такое же, как и у , если k и l одного знака, и противоположно , если k и l разного знака.        2)                                                                         О k           А l В                 Если сумма k + l > 0, то векторы (k + l)  и k  + l  будут сонаправлены с вектором  и иметь одинаковые длины:  (k + l)  = k  + l .        Если (k + l) < 0, то (-k – l) > 0 и, по доказанному, (-k — l)  = — (k  + l ). Откуда умножением на (-1) получаем (k + l)  = k  + l .                             А                           3)   А1                                                                                                                                  О + В1       В                   D ОАВ ~ D ОА1В1 с коэффициентом подобия k, поэтому . С другой стороны,  Таким образом, k(  + ) = k  + k . ⇐ Предыдущая12345678910Следующая ⇒ Читайте также:  Коммуникативные барьеры и пути их преодоления Рынок недвижимости. Сущность недвижимости Решение задач с использованием генеалогического метода История происхождения и развития детской игры 

Последнее изменение этой страницы: 2020-10-24; просмотров: 109; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0. 005 с.)

Предварительное исчисление

алгебры. Как найти перекрестное произведение внутренней суммы и разницы между двумя векторами?

спросил 2 года 10 месяцев назад

Изменено 1 год, 9 месяцев назад

Просмотрено 757 раз

$\begingroup$

Проблема в следующем: 9{\circ}) \right \rangle$

Но попытки использовать эти отношения, кажется, слишком расширяют алгебру. Существует ли другой способ? некоторое упрощение?. А может быть, я что-то упускаю из виду?

Может ли кто-нибудь помочь мне с этим?.

• алгебра-предварительное исчисление
• векторы
• евклидова геометрия
• перекрестное произведение

$\endgroup$

$\begingroup$

Подсказка.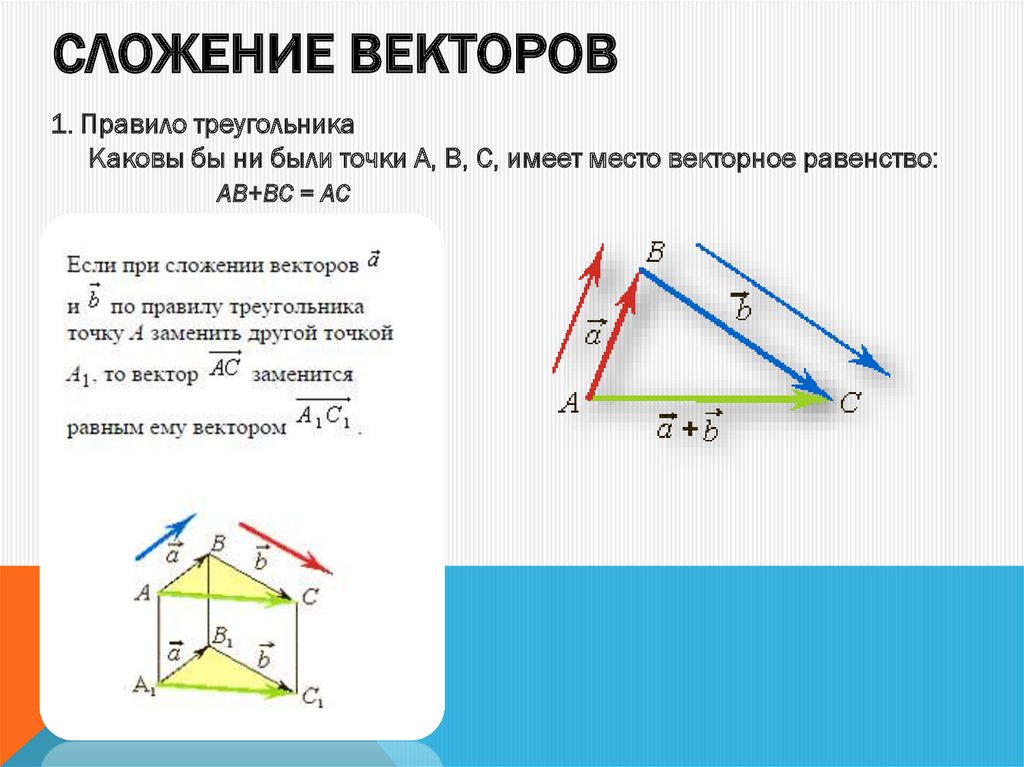 Разлагая векторное произведение, мы находим $$(\vec{A}+\vec{B})\times(\vec{A}-\vec{B})=\vec{A}\times\vec{A}+\vec{B}\ раз\vec{A}-\vec{A}\times\vec{B}-\vec{B}\times\vec{B}.$$ Сможете ли вы найти каждое из 4 перекрестных произведений в правой части? 9\circ)=\frac92$, поэтому ответ равен $-9\vec k$; чтобы понять, почему именно это, а не $9\vec k$, воспользуемся правилом правой руки.

$\endgroup$

4

$\begingroup$

Перекрестное произведение ассоциативно и антикоммутативно. (А+ В)Х(А-В)= AXA- AXB+ BXA- BXB= -AXB- AXB= -2AXB. Да, поскольку и A, и B лежат в плоскости xy, AXB находится в отрицательном направлении по оси z. А поскольку $|AXB|= |A||B| sin(\theta)$, здесь |AXB|= 2(3)(3) sin(150)= 9. (А+В)Х(А-В)= -9к

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Формулы суммы и разности – объяснение и примеры

В тригонометрии формулы суммы и разности – это уравнения, содержащие синус и косинус, которые определяют синус или косинус суммы или разности двух углов.

Формулы суммы и разности требуют знания синуса и косинуса обоих углов. Они позволяют легко находить малые углы после запоминания значений больших углов.

Как и другие тригонометрические тождества, формулы суммы и разности полезны в технических и физических науках.

Обязательно ознакомьтесь с тригонометрическими тождествами, прежде чем читать больше о формулах суммы и разности.

Этот раздел Covers Covers:

• Сумма Формула
• Происхождение суммы и разности. Формула

• Разница Формула

• Difference Formula for Sine

• Difference Formula for Cosine

• Tangent Difference Formula

• Other Sum and Difference Formulas

Sum Formula

The sum формула — это тождество, показывающее взаимосвязь между значениями синуса и косинуса для двух углов и суммой тригонометрической функции для этих двух углов.

То есть для заданной тригонометрической функции $fun$ формула суммы дает значение $funx+funy$ для любых двух углов $x$ и $y$ в радианах.

Существуют формулы суммы как для синуса, так и для косинуса. Поскольку остальные четыре тригонометрические функции могут быть получены из этих двух функций, также существуют уравнения для их суммы и разности.

Обратите внимание, однако, что формулы суммы синуса и косинуса требуют, чтобы синус и косинус обоих углов были известны. То есть формула суммы для $sinx+siny$ требует, чтобы были известны $sinx, siny, cosx,$ и $cosy$. Точно так же формула суммы для $cosx+cosy$ требует, чтобы были известны $sinx, siny, cosx,$ и 4cosy$.

Происхождение формул суммы и разности

Великий индийский математик XII века Бхаскара II внес важный вклад в математику тригонометрии. Как и многие ранние математики, Бхаскара II заинтересовался изучением тригонометрии из-за своих занятий астрономией, но он был одним из первых, кто заинтересовался самим предметом, помимо его полезности.

Из-за этого сделал таблицу значений синусов. Он также открыл формулы для синуса суммы двух углов и синуса разности двух углов.

У математика Клавдия Птолемея из Александрии второго века тоже была формула, предшествующая формулам суммы углов синуса и косинуса. В его время тригонометрия сосредоточилась на хордах, а не на отношениях между сторонами прямоугольных треугольников.

Птолемей составил таблицу значений аккордов (аналогичную таблице значений синусов), чтобы помочь ему в его астрономических работах. Хотя он не использовал синус и косинус, его функция аккорда может быть преобразована в современный синус триггерной функции. В частности, $chord(x) = 120sin(\frac{x}{2}).

После учета преобразования функции сумма угла хорды Птолемея и тождества разности совпадают с современными тождествами суммы и разности углов синуса и косинуса.

Формула суммы для синуса

Формула суммы для синуса:

$sin(x+y) = sinxcosy+cosxsiny$.

То есть синус суммы любых двух углов $x$ и $y$ равен сумме синуса $x$, умноженного на косинус угла $y$, и косинуса $y$, умноженного на синус угла $x. $.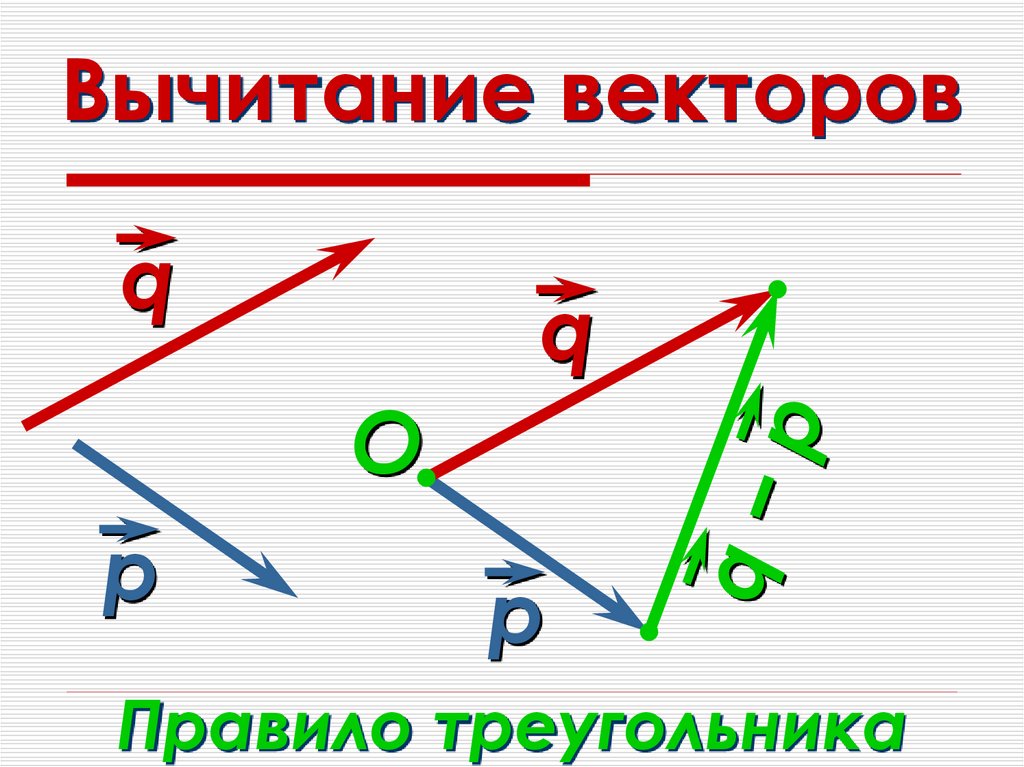

Отсюда и уравнение $sin(2x)=2sinxcosx$. Поскольку $sin(2x) = sin(x+x)$, $sin(2x) = sinxcosx+cosxsinx = 2sinxcosx$.

Доказательство формулы суммы для синуса

Хотя существует множество доказательств формулы суммы синуса и угла, большинство из них относительно сложны. Здесь нужна сопровождающая фигура.

Предположим, что эта фигура построена на единичной окружности с $FG$ в качестве оси x. Пусть красный угол (HFG) будет углом $x$, а зеленый угол (HFI) будет углом $y$. Тогда угол $x+y$ является углом $GFI$.

Требуется показать, что синус этого угла равен $sinxcosy+cosxcosy$.

Теперь углы $FJM$ и $JIM$ равны углу $x$ из-за подобных треугольников.

Поскольку $FI=1$, $siny=IJ$ и $cosy=FJ$.

Тогда по определению синуса $sinx = \frac{JL}{FJ}$. Следовательно, $FJsinx=JL$. Но $FJ=cosy$, поэтому $JL = cosysinx$.

Аналогично, $cosx = \frac{IM}{IJ}$. Следовательно, $IJcosx=IM$. Но $IJ=siny$, поэтому $sinycosx = IM$.

Теперь по построению $JLKM$ является квадратом.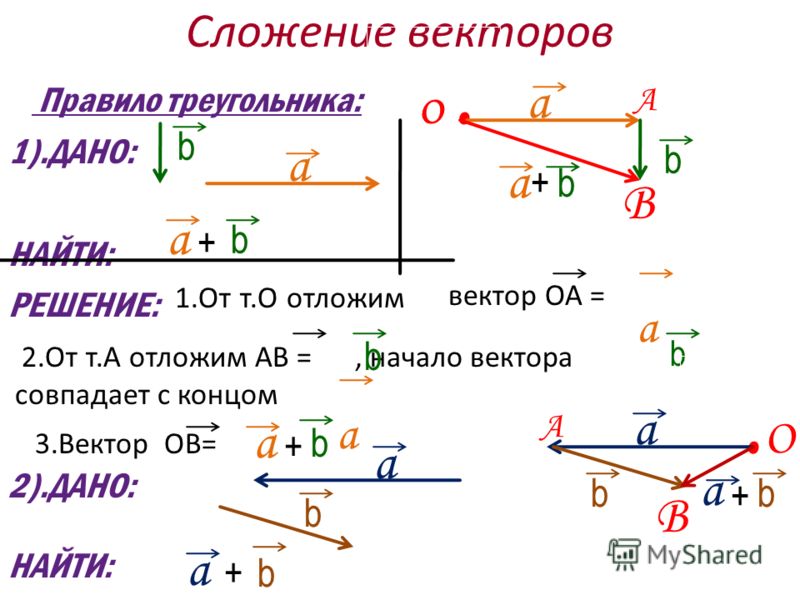 Следовательно, $JL=MK$.

Тогда по построению единичной окружности синус угла $x+y$ есть отрезок $IK$. Его можно разбить на два меньших сегмента: $IM$ и $MK$.

Уже было показано, что $IM = sinycosx$. Но, поскольку $MK = JL$ и $JL = cosysinx$, $MK = cosysinx$.

Следовательно, $sin(x+y) = IK = IM+MK = sinycosx+cosysinx$.

Аналогично следуют другие формулы суммы и разности для синуса и косинуса.

Формула суммы для косинуса

Формула суммы для косинуса:

$cos(x+y) = cosxcosy-sinxsiny$.

То есть косинус суммы любых двух углов $x$ и $y$ равен сумме косинуса $x$, умноженного на косинус угла $y$, и синуса $x$, умноженного на синус угла $ у $. 92x$.

Формула суммы тангенса

Поскольку и для синуса, и для косинуса есть формула суммы двух углов, существует также формула тангенса суммы двух углов.

Используя формулы синуса и косинуса, тангенс $x+y$ для любых двух углов $x$ и $y$ равен:

$tan(x+y) = \frac{sin(x+y) }{cos(x+y)} = \frac{sinxcosy+cosxsiny}{cosxcosy-sinxsiny}$.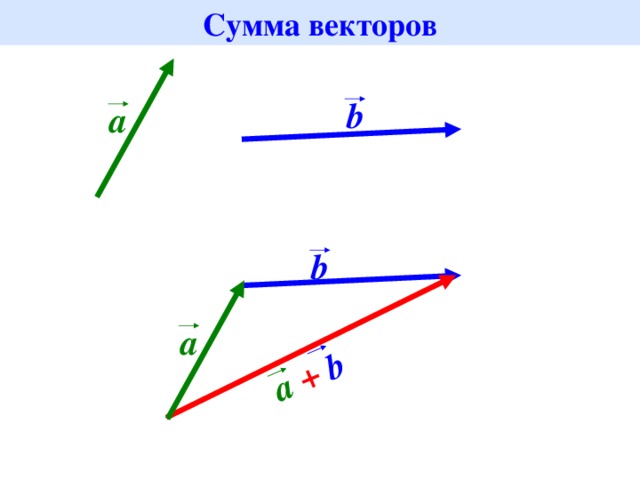

Альтернативно, тангенс суммы двух углов равен:

$tan(x+y) = \frac{tanx+tany}{1-tanxtany}$.

Чтобы увидеть это, начните с расширения $tan(x+y) = \frac{sinxcosy+cosxsiny}{cosxcosy-sinxsiny}$. Затем разделите числитель и знаменатель на $cosxcosy$. Это дает:

$tan(x+y) = \frac{sinxcosy+cosxsiny}{cosxcosy-sinxsiny} = \frac{\frac{sinxcosy}{cosxcoxy}+\frac{cosxsiny}{cosxcosy}}{\frac {cosxcosy}{cosxcosy}+\frac{sinxsiny}{cosxcosy}}$.

Тогда это упрощается до $\frac{tanx+tany}{1-tanxtany}$.

Формула разности

Формула разности дает тригонометрическое отношение разности между двумя углами, если известны синус и косинус исходных двух углов. Как и формула суммы, она дает возможность найти тригонометрические соотношения для малых углов, если известны большие углы.

Существуют разные формулы для синуса и косинуса. Обе формулы используют отношения синуса и косинуса для обоих начальных углов.

Опять же, напомним, что остальные четыре тригонометрических соотношения следуют из синуса и косинуса. Таким образом, тангенс, котангенс, косеканс и секанс разности двух углов можно найти с помощью формул разности синуса и косинуса.

Формула разности для синуса

Формула разности для синуса — это формула для синуса угла, равного разности двух углов, $x$ и $y$. Эта формула зависит от синуса и косинуса как $x$, так и $y$.

$sin(x-y)=sinxcosy-cosxsiny$.

Напомним, что функция синуса нечетная. Это означает, что для любого угла $x$ $sin(-x) = -sinx$.

Это означает, что порядок угла важен для формулы разности. То есть $sin(x-y) \neq sin(y-x)$. Фактически, поскольку $y-x = -(x-y)$, $sin(y-x) = sin(-(x-y) = -(sinxcosy-cosxsiny) = cosxsiny-sinxcosy$.

Формула разности для косинуса

Формула разности для косинус — это формула косинуса угла, равная разности двух углов $x$ и $y$.Как и формула разности синуса, эта формула зависит как от синуса, так и от косинуса как $x$, так и $у$.

$cos(x-y) = cosxcosy+sinxsiny$.

Обратите внимание, что порядок $x$ и $y$ в этой формуле не имеет значения. То есть, поскольку $cos(y-x) = cosycosx+sinysinx = cosxcosy+sinxsiny = cos(x-y)$.

Это имеет смысл, поскольку косинус — четная функция. Напомним, что даже функции имеют одинаковое значение y для положительных и отрицательных значений x. То есть $cos(-x) = cosx$. Тогда, поскольку $y-x = -(x-y)$, $cos(y-x) = cos(x-y)$.

Формула разности тангенсов

Формула разности тангенсов может быть получена из формул разности для синуса и косинуса. Для двух углов $x$ и $y$ тангенс разности $x$ и $y$ равен:

$tan(x-y) = \frac{tanx-tany}{1+tanxtany}$.

Поскольку тангенс равен синусу, деленному на косинус, тангенс разности двух углов $x$ и $y$ равен:

$tan(x-y) = \frac{sin(x-y)}{cos( х-у)}$.

Используя разностные формулы для синуса и косинуса, получаем:

$tan(x-y) = \frac{sinxcosy-cosxsiny}{cosxcosy+sinxsiny}$.

Аналогично формуле суммы для тангенса, выведите формулу разности тангенсов, разделив числитель и знаменатель на $cosxcosy$.

$tan(xy) = \frac{\frac{sinxcosy-cosxsiny}{cosxcosy}}{\frac{cosxcosy+sinxsiny}{cosxcosy}}$.

Это упрощается до:

$tan(x-y) = \frac{tanx-tany}{1+tanxtany}$.

Как и функция синуса, функция тангенса является нечетной. Следовательно, $tan(y-x) = tan(-(x-y)) = -tan(x-y) = -(\frac{tanx-tany}{1+tanxtany}) = \frac{tany-tanx}{-1-tanxtany }$.

Другие формулы суммы и разности

Доказательства формул суммы и разности для других тригонометрических функций, а именно котангенса, косеканса и секанса, можно получить из формул суммы и разности углов для синуса и косинуса.

Хотя для формул синуса и косинуса предпочтительнее использовать синус и косинус, это неверно для других тригонометрических функций. В общем, формулы косеканса и секанса должны быть в терминах косеканса и секанса. Для формул котангенса они должны быть выражены в терминах котангенса (точно так же, как формулы тангенса должны быть выражены в терминах тангенса).

Обычно при выводе этих формул сначала используются определения обратных функций. Затем разделите числитель и знаменатель полученного выражения на один и тот же член, чтобы преобразовать его в термины секанса и косеканса или котангенса.

Пример общей формулы для суммы углов и разности углов для косеканса приведен в примере 4. Затем практическая задача 3 включает в себя вывод формул для суммы углов и разности углов для секанса.

Для котангенса формула суммы углов:

$cot(x+y) = \frac{cotxcoty-1}{cotx+coty}$.

Тогда формула для разности углов будет следующей:

$cot(x-y) = \frac{cotxcoty+1}{cotx-coty}$.

Неопределенные значения

Для секанса, косеканса, тангенса и котангенса некоторые значения не определены. Это связано с тем, что эти функции могут быть записаны так, чтобы в знаменателе были другие триггерные функции.

В частности, $secx = \frac{1}{cosx}$, $cscx = \frac{1}{sinx}$, $tanx = \frac{sinx}{cosx}$ и $cotx = \frac{ sinx}{cosx}$.

Поскольку и синус угла, и косинус угла могут быть равны $0$, все эти функции имеют углы, для которых они не определены.

Следовательно, нельзя использовать формулы суммы и разности для углов, имеющих сумму или разность в неопределенной точке.

Например, котангенс не определен при $0$, потому что синус равен $0$ при $0$ радианах. Но котангенс любых двух углов, сумма которых равна $0$, будет неопределенным на основе его формулы. Конкретно:

$cot(0) = cot(x-x) = \frac{cotxcot(x)+1}{cotx-cotx}$.

Но в знаменателе здесь $cotx-cotx = 0$. Следовательно, $cot(0)$ не определено даже с использованием формулы разности.

Примеры

В этом разделе рассматриваются распространенные примеры задач на формулы суммы и разности и их пошаговые решения.

Пример 1

Напишите общую формулу для синуса суммы трех углов $x, y,$ и $z$ в радианах. Подсказка: используйте формулу суммы дважды.

Решение

Для этой формулы потребуется формула синуса суммы двух углов. Фактически, он будет использован дважды.

Для начала пусть $w=x+y$. Теперь синус суммы $x, y,$ и $z$ равен сумме $w$ и $z$.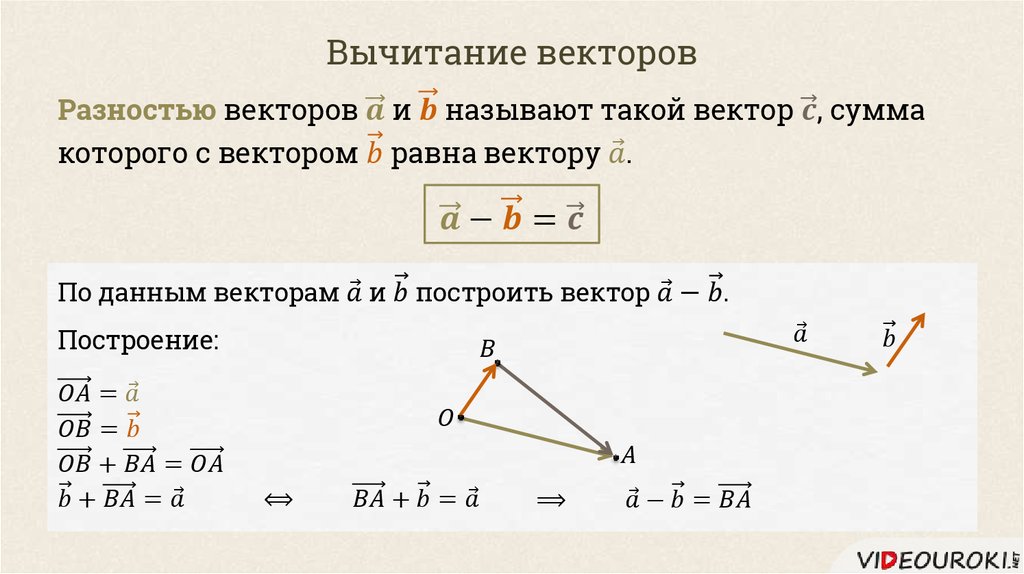 То есть:

$sin(x+y+z) = sin(w+z)$.

По формуле суммы углов для синуса синус $w+z$ равен:

$sin(w+z) = sinwcosz + sinzcosw$.

Теперь, поскольку $w=x+y$, синус $w$ равен синусу $x+y$. То есть $sin(w) = sin(x+y)$. По формуле синуса суммы это:

$sin(w) = sin(x+y) = sinxcosy + sinycosx$.

Обратите внимание, что $sin(w+z)$ также зависит от косинуса $w$. Используя формулу косинуса суммы, это:

$cos(w) = cos(x+y) = cosxcosy + sinxsiny$.

Теперь подставьте уравнения для $sin(w)$ и $cos(w)$ обратно в исходное уравнение для $sin(w+z)$.

$sin(w+z) = sinwcosz+sinzcosw = (sinxcosy+sinycosx)cosz + sinz(cosxcosy+sinxsiny)$.

Затем распределите, чтобы получить:

$sinxcosycosz + sinycosxcosz+sinzcosxcosy + sinxsinysinz$.

Ни один из этих терминов не похож на другой, так что это формула суммы трех углов. Поскольку это довольно длинная формула, ее обычно не включают в общие формулы для тригонажных тождеств.

$sin(x+y+z) = sinxcosycosz+sinycosxcosz+sinzcosxcosy+sinxsinysinz$.

Пример 2

Найдите синус угла $\frac{7\pi}{12}$ радиан. Используйте формулу суммы и тот факт, что $\frac{7\pi}{12} = \frac{3\pi+4\pi}{12} = \frac{\pi}{4}+\frac{\pi {3}$ радиан в помощь.

Решение

По формуле суммы углов для синуса синус суммы двух углов равен:

$sinxcosy+sinycosx$.

В этом случае $\frac{7\pi}{12} = \frac{\pi}{4}+\frac{\pi}{3}$. Поэтому пусть $\frac{\pi}{4}$ равно $x$, а $\frac{\pi}{3}$ равно $y$. Следовательно:

$sin(\frac{\pi}{12}) = sin(\frac{\pi}{4})cos(\frac{\pi}{3}) + sin(\frac{\pi {3})cos(\frac{\pi}{4})$.

Так как $\frac{\pi}{4}$ и $\frac{\pi}{3}$ являются большими углами, их значения синусов и косинусов либо запоминаются, либо легко доступны в таблице. Конкретно:

• $sin(\frac{\pi}{4}) = \frac{\sqrt{2}}{2}$
• $cos(\frac{\pi}{3}) = \frac{1 {2}$
• $sin(\frac{\pi}{3}) = \frac{\sqrt{3}}{2}$
• $cos(\frac{\pi}{4}) = \ гидроразрыва {\ sqrt {2} {2} $.

Подстановка этих значений в формулу синуса $\frac{7\pi}{12}$ дает:

$sin(\frac{7\pi}{12} =  (\frac{\sqrt{ 2}}{2})(\frac{1}{2}) + (\frac{\sqrt{3}}{2})(\frac{\sqrt{2}}{2})$.

Это упрощается до:

$\frac{\sqrt{2}}{4} + \frac{\sqrt{2}sqrt{3}}{4} = \frac{\sqrt{2}(1+\sqrt {3}}{4} = \frac{1+\sqrt{3}}}{2\sqrt{2}}$.

Следовательно, косинус $\frac{\pi}{12}$ радиан равен $\frac{1+\sqrt{3}}}{2\sqrt{2}}$.

Пример 3

Найдите косинус $-\frac{\pi}{12}$ радиан, используя формулы суммы углов и разности для косинуса.

Решение

Угол $-\frac{\pi}{12}$ радиан не является большим углом. Большинство людей запоминают только тригонометрические соотношения больших углов $\frac{\pi}{6}$, $\frac{\pi}{4}$ и $\frac{\pi}{3}$ и соответствующие им углы в других квадрантах. В качестве альтернативы, эти углы, скорее всего, будут в таблице или на графике.

Это означает, что точное значение косинуса $-\frac{\pi}{12}$ радиан должно быть найдено с использованием этих значений главного угла.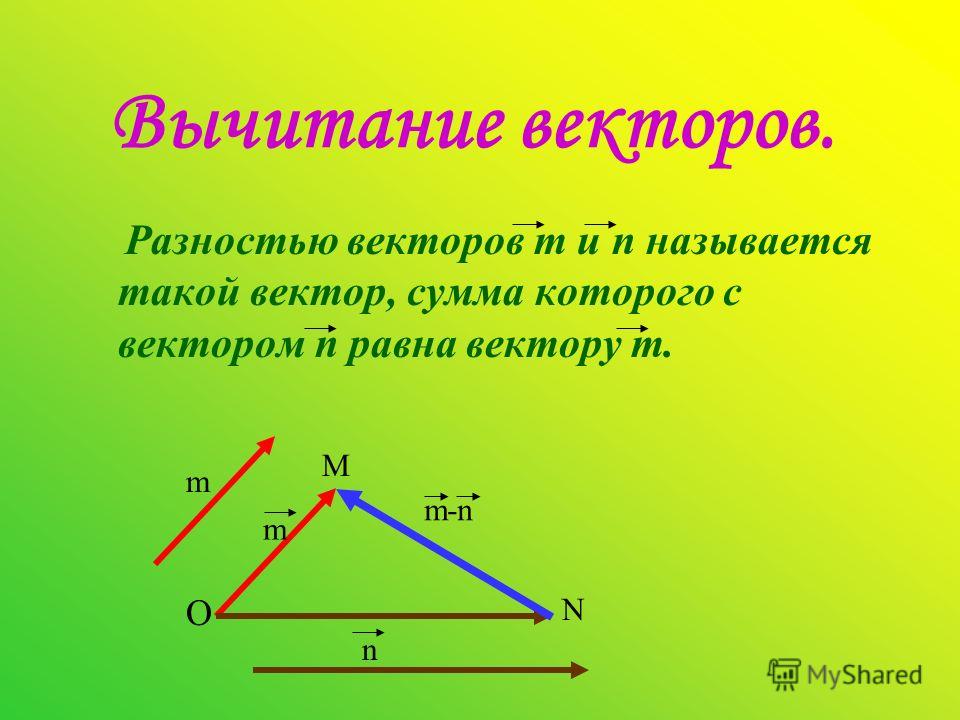 В этом случае $-\frac{\pi}{12} = \frac{\pi}{6}-\frac{\pi}{4}$, поэтому формула разности даст точное соотношение.

Напомним, что формула разности для косинуса:

$cos(x-y) = cosxcosy + sinxsiny$.

В этом случае пусть $x$ равно $\frac{\pi}{6}$, а $y$ равно $\frac{\pi}{4}$. Таким образом, косинус $-\frac{\pi}{12}$ равен:

$cos(\frac{\pi}{6})cos(\frac{\pi}{4}) + sin(\frac {\pi}{6})sin(\frac{\pi}{4})$.

Синус и косинус угла $\frac{\pi}{4}$ равны $\frac{\sqrt{2}}{2}$. Тогда синус $\frac{\pi}{6}$ равен $\frac{1}{2}$, а косинус равен $\frac{\sqrt{3}}{2}$.

Таким образом, подставив эти значения в уравнение:

$cos(-\frac{\pi}{12}) = (\frac{\sqrt{2}}{2})(\frac{\sqrt{3 }}{2}) + (\frac{1}{2})(\frac{\sqrt{2}}{2})$.

Тогда это упрощается до:

$\frac{\sqrt{2}\sqrt{3}}{4} + \frac{\sqrt{2}}{2} = \frac{\sqrt{2} (\sqrt{3}+1)}{4} = \frac{\sqrt{3}+1}{2\sqrt{2}}$.

Пример 4

Используйте формулы суммы и разности для синуса и косинуса, чтобы найти формулу суммы для косеканса. Затем используйте аналогичный процесс, чтобы найти формулу разности для косеканса.

Решение

Формула суммы косеканса

Так как косеканс является обратной величиной синуса, то косеканс суммы двух углов $x$ и $y$ равен:

$csc(x+y) = \frac{ 1}{sin(x+y)}$.

Тогда, используя формулу синуса суммы двух углов, это равно:

$csc(x+y) = \frac{1}{sinxcosy+sinycosx}$.

Хотя это работает как формула, формулы для косеканса и секанса обычно зависят только от секанса и косеканса. Таким образом, необходимо манипулировать правой частью уравнения так, чтобы в ней были не синус и косинус, а косеканс и секанс.

Для этого сначала разделите числитель и знаменатель на $cosxcosysinxsiny$.

Это дает:

$\frac{\frac{1}{cosxcosysinxsiny}}{\frac{sinxcosy+sinycosx}{cosxcosysinxsiny}}$.

Затем это упрощается до:

$\frac{secxsecycscxcscy}{secxcscy+cscxsecy}$.

Так как это только с точки зрения секанса и косеканса, это общая формула для косеканса суммы двух углов.

Формула разности косеканса

Опять же, поскольку косеканс является обратной величиной синуса, формула разности для косеканса:

$csc(x-y) = \frac{1}{sinxcosy – sinycosx}$.

Как и прежде, это уравнение верно. Но предпочтительно, чтобы в формулах для косеканса использовались только косеканс и секанс. Следовательно, необходимо алгебраически манипулировать этим уравнением, чтобы оно использовало только те функции.

Еще раз начните с деления числителя и знаменателя правой части на произведение $sinx, cosy, siny,$ и $cosx$. Это дает:

$csc(xy) = \frac{\frac{1}{sinxcosysinycosx}}{\frac{sinxcosy – sinycosx}{sinxcosysinycosx}}$.

Теперь это можно еще упростить:

$csc(x-y) = \frac{cscxsecycscysecx}{cscysecx – cscxsecy}$.

Эта формула похожа на формулу суммы косекансов, $\frac{secxsecycscxcscy}{secxcscy + cscxsecy}$. Единственное отличие состоит в том, что знаменатель представляет собой сумму, а не разность.

Пример 5

Найдите тангенс угла $\frac{13\pi}{12}$ в радианах, найдя сначала тангенс $\frac{\pi}{12} = \frac{\pi}{3 }-\frac{\pi}{4}$ радиан, а затем найти тангенс суммы $\pi$ и $\frac{\pi}{12}$ радиан.

Решение

Эта проблема требует нескольких шагов. В частности, он устанавливает угол $\frac{11\pi}[12}$ радиан как:

$\frac{13\pi}{12} = \pi+(\frac{\pi}{3}-\ frac{\pi}{4})$.

Начните с нахождения тангенса разности между $\frac{\pi}{3}$ и $\frac{\pi}{4}$. Формула тангенса разности:

$\frac{tanx-tany}{1+tanxtany}$.

Тангенс $\frac{\pi}{4}$ радиан равен 1, потому что синус и косинус равны под этим углом. При $\frac{\pi}{3}$ синус равен $\frac{\sqrt{3}}{2}$, а косинус равен $\frac{1}{2}$. Следовательно, касательная равна $\sqrt{3}$. Подстановка этих значений в приведенное выше выражение дает:

$\frac{\sqrt{3}-1}{1+\sqrt{3}}$.

Это выражение легко упрощается за счет добавления разницы квадратов в знаменатель. Для этого умножьте выражение на $1 = \frac{\sqrt{3}-1}{\sqrt{3}-1}$. Это дает: 92}{3-1} = \frac{3-2\sqrt{3}+1}{2} = \frac{4-2\sqrt{3}}{2} = 2-sqrt{3}$.

Сумма тангенсов

Затем найдите тангенс суммы $\pi+\frac{\pi}{12}$ радиан.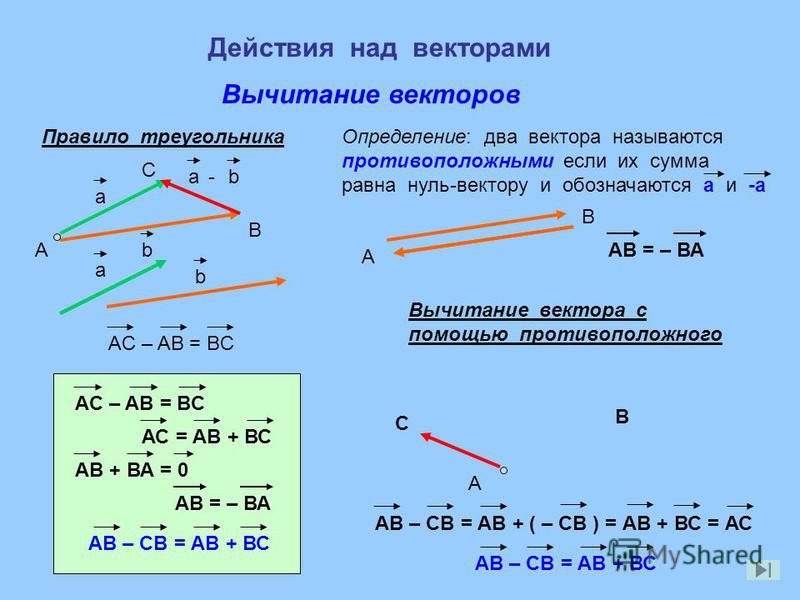 {\circ})$ равно: 9{\circ})$.

Подставляя известные значения, это:

$(0,342)(0,951) – (0,309)(940) = 0,325242 – 0,29046 = 0,034782$.

Округлив до тысячных, получится $0,035$.

Значения косинуса

Начните с формулы суммы углов. Для косинуса это:

$cos(x+y) = cosxcosy-sinxsiny$.

В этом случае, поскольку $20+18=38$, это:

$cos(38) = cos(20)cos(18)-sin(20)sin(18)$.

Замена известных значений дает: 9{\ circ}) = (0,940) (0,951) + (0,342) (0,309) = 0,89394 + 0,105678 = 0,99618 $.

Если округлить до тысячных, получится $1.000$.

Пример 7

Попробуйте найти значение $tan(\frac{\pi}{4}+\frac{\pi}{4})$, используя формулу суммы тангенсных углов. Почему это невозможно?

Решение

Напомним, что формула суммы тангенсов углов выглядит так:

$tan(x+y) = \frac{tanx+tany}{1-tanxtany}$.

Пусть в этом случае $x$ и $y$ равны $\frac{\pi}{4}$. Поскольку $tan(x) = 1$ в $\frac{\pi}{4}$, это:

$tan(\frac{\pi}{2}) = \frac{1+1}{1-(1)(1)} = \frac{2}{1-1} = \frac{2} {0}$.