Задание 1. Брошены 2 игральные кости. Найти вероятность того, что сумма очков на выпавших гранях равна 7.
Ответ:
Задание 2. Брошены 2 игральные кости. Найти вероятности следующих событий: a) сумма выпавших очков равна 8, а разность –4; b) сумма выпавших очков равна 8, если известно, что их разность равна 4.
Ответ: a) b) .
Задание 3. Брошены две игральные кости. Найти вероятности следующих событий: а) сумма выпавших очков равна семи; б) сумма выпавших очков равна пяти, а произведение – четырем.
Ответ: a) b) .
Задание 4. Монета брошена два раза. Найти вероятность того, что хотя бы один раз появится «герб».
Ответ: .
Задание
5. В коробке
шесть одинаковых, занумерованных
кубиков. Наудачу по одному извлекают
все кубики. Найти вероятность того, что
номера извлеченных кубиков появится
в возрастающем порядке.
Ответ:
Задание 6. В урне 15 шаров: 5 белых, 10 черных. Какова вероятность вынуть из урны синий шар?
Ответ:0.
Задание 7. В урне 12 шаров: 3 белых, 4 черных, 5 красных. Какова вероятность вынуть из урны черный шар.
Ответ:
Пример 4. В ящике 10 одинаковых деталей, помеченных номерами
1, 2, …, 10. Наудачу извлечены шесть деталей. Найти вероятность того, что среди извлеченных деталей окажутся: а) деталь № 1; б) детали № 1 и № 2.
Решение. А) общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь шесть деталей из десяти, т.е.
Найдем
число исходов, благоприятствующих
интересующему нас событию: среди
отобранных шести деталей есть деталь
№ 1 и, следовательно, остальные пять
деталей имеют другие номера.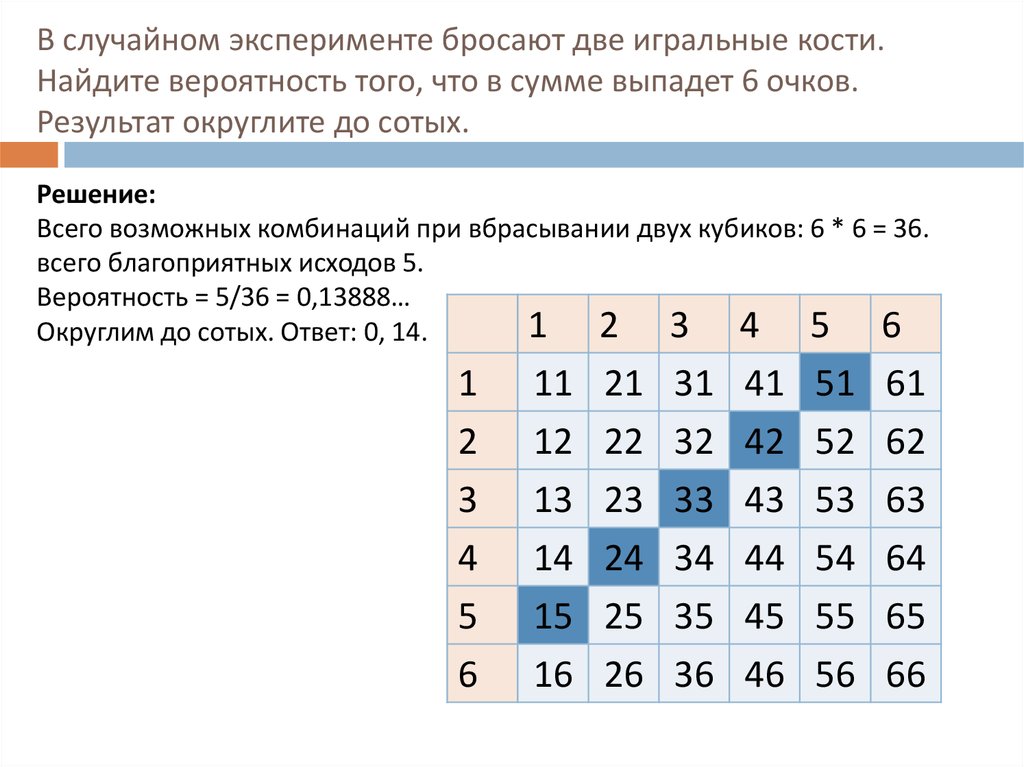
Искомая вероятность равна отношению числа исходов, благоприятствующих рассматриваемому событию, к общему числу возможных элементарных исходов: .
Б) Число исходов, благоприятствующих интересующему нас событию (среди отобранных деталей есть детали № 1 и « 2, следовательно, четыре детали имеют другие номера), равно числу способов, которыми можно извлечь четыре детали из оставшихся восьми, т.е . Искомая вероятность Р= .
Пример 5. В урне 10 шаров: 6 белых и 4 черных. Вынули 2 шара. Какова вероятность, что оба шара белые..
Решение. Общее число случаев: .
Число благоприятных случаев: , .
Ответ: .
Задание 1.В
ящике имеется 15 деталей, среди которых
10 окрашенных. Сборщик наудачу извлекает
три детали.
Найти вероятность того, что
извлеченные детали окажутся окрашенными.
Ответ: .
Задание 2. В конверте среди 100 фотокарточек находится одна разыскиваемая. Из конверта наудачу извлечены 10 карточек. Найти вероятность того, что среди них окажется нужная.
Ответ: .
Задание 3. В ящике 100 деталей, из них 10 бракованных. Наудачу извлечены четыре детали. Найти вероятность того, что среди извлеченных деталей: а) нет бракованных; б) нет годных.
Ответ:а) 0.65; б)0.00005.
Задание 4.Набирая номер телефона, абонент забыл последние три цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры.
Ответ: .
Определение вероятности Задачи с решениями
- Комбинаторика в задачах на нахождение вероятностей событий.
- Классическое, статистическое и геометрическое определение вероятностей.
Все задачи Бесплатные решения
Брошены две игральные кости. Найти вероятность того, что сумма очков на выпавших гранях – чётная, причём на грани хотя бы одной из костей появится шестерка.
При перевозке ящика, в котором содержались 21 стандартная и 10 нестандартных деталей, утеряна одна деталь, причём неизвестно какая. Наудачу извлеченная (после перевозки) из ящика деталь оказалась стандартной. Найти вероятность того, что была утеряна: а) стандартная деталь; б) нестандартная деталь.
Задумано двузначное число. Найти вероятность того, что задуманным числом окажется: а) случайно названное двузначное число; б) случайно названное двузначное число, цифры которого различны.
Указать ошибку «решения» задачи: брошены две игральные кости; найти вероятность того, что сумма выпавших очков равна 3 (событие А).
Брошены две игральные кости.
Найти вероятности следующих событий: а) сумма выпавших очков равна семи; б) сумма выпавших очков равна восьми, а разность четырем; в) сумма выпавших очков равна восьми, если известно, что их разность равна четырем; г) сумма выпавших очков равна пяти, а произведение – четырем.
Куб, все грани которого окрашены, распилен на тысячу кубиков одинакового размера, которые затем тщательно перемешаны. Найти вероятность того, что наудачу извлеченный кубик имеет окрашенных граней: а) одну; б) две; в) три.
Монета брошена два раза. Найти вероятность того, что хотя бы один раз появится «герб».
В коробке 6 одинаковых занумерованных кубиков. Наудачу по одному извлекают все кубики. Найти вероятность того, что номера извлеченных кубиков появятся в возрастающем порядке.
Найти вероятность того, что при бросании трёх игральных костей шестерка выпадет на одной (безразлично какой) кости, если на гранях двух других костей выпадут числа очков, не совпадающих между собой (и не равные шести).
В пачке 20 перфокарт, помеченных номерами 101, 102,…, 120 и произвольно расположенных. Перфокарторщица наудачу извлекает две карты. Найти вероятность того, что извлечены карты с номерами 101 и 120.
В ящике 10 одинаковых деталей, помеченных номерами 1, 2,…, 10. Наудачу извлечены шесть деталей. Найти вероятность того, что среди извлеченных деталей окажутся: а) деталь
В ящике имеется 15 деталей, среди которых 10 окрашенных. Сборщик наудачу извлекает три детали. Найти вероятность того, что извлеченные детали окажутся окрашенными.
В конверте среди 100 фотокарточек находится одна разыскиваемая. Из конверта наудачу извлечены 10 карточек. Найти вероятность того, что среди них окажется нужная.
В ящике 100 деталей, из них 10 бракованных. Наудачу извлечены четыре детали.
Найти вероятность того, что среди извлеченных деталей: а) нет бракованных; б) нет годных.
Устройство состоит из пяти элементов, из которых два изношены. При включении устройства включаются случайным образом два элемента. Найти вероятность того, что включенными окажутся не изношенные элементы.
Набирая номер телефона, абонент забыл последние три цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры.
В партии из N деталей имеется n стандартных. Наудачу отобраны m деталей. Найти вероятность того, что среди отобранных деталей ровно k стандартных.
В цехе работают шесть мужчин и четыре женщины. По табельным номерам наудачу отобраны семь человек. Найти вероятность того, что среди отобранных лиц окажутся три женщины.
На складе имеется 15 кинескопов, причем 10 из них изготовлены Львовским заводом. Найти вероятность того, что среди пяти взятых наудачу кинескопов окажутся три кинескопа Львовского завода.
В группе 12 студентов, среди которых 8 отличников. По списку наудачу отобраны 9 студентов. Найти вероятность того, что среди отобранных студентов пять отличников.
В коробке пять одинаковых изделий, причем три из них окрашены. Наудачу извлечены два изделия. Найти вероятность того, что среди двух извлеченных изделий окажутся: а) одно окрашенное изделие; б) два окрашенных изделия; в) хотя бы одно окрашенное изделие.
В «секретном» замке на общей оси четыре диска, каждый из которых разделен на пять секторов, на которых написаны различные цифры. Замок открывается только в том случае, если диски установлены так, что цифры на них составляют определенное четырехзначное число. Найти вероятность того, что при произвольной установке дисков замок будет открыт.
Отдел технического контроля обнаружил пять бракованных книг в партии из случайно отобранных 100 книг. Найти относительную частоту появления бракованных книг.
По цели произведено 20 выстрелов, причем зарегистрировано 18 попаданий.
При испытании партии приборов относительная частота годных приборов оказалась равной 0,9. Найти число годных приборов, если всего было проверено 200 приборов.
На отрезке L длины 20см помещен меньший отрезок l длины 10см. Найти вероятность того, что точка, наудачу поставленная на больший отрезок, попадет также и на меньший отрезок. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения.
На отрезок ОА длины L числовой оси Ох наудачу поставлена точка В(х). Найти вероятность того, что меньший из отрезков ОВ и ВА имеет длину, большую, чем . Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения на числовой оси.
В круг радиуса R помещен меньший круг радиуса 
Предполагается, что вероятность попадания точки в круг пропорциональна площади круга и не зависит от его расположения.
Плоскость разграфлена параллельными прямыми, находящимися друг от друга на расстоянии 2а. На плоскость наудачу брошена монета радиуса r<а. Найти вероятность того, что монета не пересечет ни одной из прямых.
На плоскость с нанесенной сеткой квадратов со стороной a наудачу брошена монета радиуса r<a/2. Найти вероятность того, что монета не пересечет ни одной из сторон квадрата. Предполагается, что вероятность попадания точки в плоскую фигуру пропорциональна площади фигуры и не зависит от её раположения.
На плоскость, разграфленную параллельными прямыми, отстоящими друг от друга на расстоянии 6см, наудачу брошен круг радиуса 1см. Найти вероятность того, что круг не пересечет ни одной из прямых. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения.
На плоскости начерчены две концентрические окружности, радиусы которых 5 и 10см соответственно. Найти вероятность того, что точка, брошенная наудачу в большой круг, попадет также и в кольцо, образованное построенными окружностями. Предполагается, что вероятность попадания точки в плоскую фигуру пропорциональна площади этой фигуры и не зависит от ее расположения.
Внутрь круга радиуса R наудачу брошена точка. Найти вероятность того, что точка окажется внутри вписанного в круг: а) квадрата; б) правильного треугольника. Предполагается, что вероятность попадания точки в часть круга пропорциональна площади этой части и не зависит от ее расположения относительно круга.
Быстро вращающийся диск разделен на четное число равных секторов, попеременно окрашенных в белый и черный цвет. По диску произведен выстрел. Найти вероятность того, что пуля попадет в один из белых секторов. Предполагается, что вероятность попадания пули в плоскую фигуру пропорциональна площади этой фигуры.
На отрезке ОА длины L числовой оси Ох наудачу поставлены две точки В(х) и С(у). Найти вероятность того, что длина отрезка ВС меньше расстояния от точки О до ближайшей к ней точке. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения на числовой оси.
SchecterAdvancedMath
SchecterAdvancedMath Фитинг линейный
Функции
Давай, сделай это! В частности, вы можете протестировать простую версию
это уравнение самостоятельно.
Поднимитесь на высокое место с секундомером и
посмотрите вниз, чтобы убедиться, что внизу нет людей. Бросьте небольшой
предмет вроде камня или монеты (что-то, на что не слишком влияет
ветер), и одновременно запустить секундомер. Через t секунд объект будет иметь
упал 16 т 2 футов.
Разумеется, точность этого измерения зависит от того, насколько тщательно
читаешь и нажимаешь на секундомер, а ветер будет мешать
идеальный расчет. Тем не менее, это довольно круто, что вы можете
измеряйте высоту секундомером! Допустим, вы находитесь в Гранд
Каньон, а твой брат говорит: «Чувак, держу пари, что падает больше 1000
футов!» Вы можете проверить это, бросив камень (убедитесь, что вы
не по другой тропе — иначе ваш эксперимент превратится в урок
при массивных травмах головы, если камень попадает в другого туриста), и время
сколько секунд нужно, чтобы услышать, как он приземлится. Если это займет 5 секунд,
это означает, что камень упал на 16 х 5 х 5 = 400 футов. Как долго бы
что нужно сделать, чтобы упасть на 1000, о котором мечтал твой брат?
Вы должны были бы спросить, когда 16т 2 =
1000? Ответ: когда t равно квадратному корню
1000/16.
Это равно примерно 7,9 секунды. Предсказание
уравнение называется квадратным
уравнение и человечество знало все о решении квадратных уравнений
со времен вавилонян (1800 г. до н. э. — время Авраама Авину).
Физика — великая наука, потому что она способна предсказывать многие отличное явление очень точно. Другие области науки труднее вывести точные уравнения. Некоторые предсказания просто слишком сложно сделать идеально, а затем мы делаем следующую лучшую вещь — найти уравнение, которое предсказывает довольно точно. Простейший тип уравнения является линейным уравнением, и очень часто линейные уравнения привыкли примерно прогнозировать сложное поведение.
Ученый берет свои данные и пытается реконструировать линейное уравнение
из данных. Вы усвоили последний урок, как это сделать, когда
иметь две точки данных. Например: допустим, вы
измеряя рост растения, и на 2-й день оно достигает 4 дюймов в высоту, а
на 5 день это 12 дюймов в высоту.
Чтобы получить линейную функцию для этого
данных, напомним, что мы сначала вычисляем наклон. Наклон — это сколько
рост растения делится на то, сколько времени прошло. В этом
В этом случае наклон равен 8/3. Затем составим уравнение, которое выглядит
примерно так: Рост = (8/3) х Дней. Это означает, что каждый
раз мы добавляем день, растение вырастет на 8/3 дюйма, так что через 3 дня
он вырастет на 8 имчей. Теперь растение может не расти в
постоянная скорость, и в этом случае наш прогноз 8/3 дюйма в день будет
быть выключено, но это разумное простое приближение. Но мы
еще не совсем готово, потому что, когда мы подставляем 2 для дней, мы получаем (8/3) x 2
= 16/3, и помните, что растение на самом деле имеет высоту 4 дюйма, а не 16/3.
дюймы. Это несоответствие можно исправить, просто вычитая 4/3
дюйм. Следовательно, наше окончательное уравнение будет таким:
Рост = (8/3) х Дней — 4/3.
Попробуйте сейчас на 5, чтобы убедиться, что мы не сделали ошибок.
У нас должно получиться 12 дюймов, и действительно (8/3) х 5 — 4/3 = 12, что проверяет
выходит правильно.
Предупреждение:
Я считают, что понимание того, почему в математике все работает, ключевой. Конечно, вы можете продвинуться довольно далеко, просто подражая и методы запоминания, но вы никогда не сможете применить материал к любую новую идею, и вы навсегда останетесь учеником, чьи способности в математики ограничены подражанием примерам того, что у них уже есть. видимый. Такая математика для компьютеров и умных лошадей, а не для людей. Не будь таким учеником, который говорит или думает «Я никогда не видел этого раньше, поэтому я не могу этого сделать». Вместо этого подумайте: «Как то, что я знаю и понимаю, помогает мне решить эту новую проблему».0008
Сейчас
если вы думаете, что это трудно до сих пор, я должен напомнить вам, что до
теперь идеи
и причины того, почему и как все работает для линейных функций,
в пределах досягаемости любого ученика средней школы.
Если вы все еще не получили
это
тем не менее, тогда это просто вопрос практики, изучения, руководства и
время. Никогда не сдавайся. Никогда не удовлетворяйтесь только
запоминание или подражание.
С учетом сказанного
однако мы собираемся войти в мир, о котором я предупреждаю вас заранее
ты не сможешь
понять, почему
все работает. Вы все равно сможете понять, как это
работает
и на самом деле использовать, оценивать и делать соответствующие расчеты, но
причины, по которым эти методы просто выходят за рамки средней школы
мир. Я не люблю учить математику таким образом, но в этом
случае, когда практическое использование метода, который вы изучите, перевешивает
педагогический недостаток в том, что он не может понять, почему это
работает.
Итак,
перейти к следующему разделу предупрежден, что иногда полный
картина по математике будет выше вашей головы, и лучшее, на что вы можете надеяться
является механическим подходом.
Однажды в 5-10 лет, когда вы находитесь в
колледж, вы можете вернуться и внимательно изучить область под названием линейная алгебра, где вы можете изучать
концепция решения по методу наименьших квадратов
к системе нормальных уравнений.
Линейная аппроксимация методом наименьших квадратов
Давайте
скажем, что вместо двух точек данных у нас есть 4 точки данных, но это не
все три точки лежат на одной прямой. В этом случае мы могли бы
взять любую пару точек (всего шесть разных пар — напомним, как
подсчитайте, выбрав 2 из 4), и для каждой пары мы получим разные
линейное уравнение. Каждое уравнение работает только для двух точек и
для остальных. Например, рассмотрим точки: (2, 4), (5, 12), (3, 4) и
(1, 3), где первое число каждой пары — количество дней
прошло, а второе число — это высота растения в дюймах.
Уравнение Рост = (8/3) x Дней
—
4/3 , который работает для (2, 4) и (5, 12), не будет работать для
(1, 3) или (3, 4).
Попробуйте и посмотрите. Когда Days равно 1, мы
получить (8/3) х 1 — 4/3 = 4/3 и это не 3! Когда количество дней равно 3,
мы получаем (8/3) x 3 — 4/3 = 20/3, а это не 4!
Есть
не существует единого линейного уравнения, которое соответствовало бы всем точкам с такой же точностью, как
нет прямой линии, которая проходит через них всех. Если это
верно, то какое линейное уравнение мы должны использовать? Вот некоторые
выбор:
Выберите любые две точки (6 вариантов) и используйте уравнение, которое соответствует
именно эти две точки.
Найдите уравнение, которое не соответствует ни одной из точек, но каким-то образом минимизирует
кумулятивная ошибка.
Лучший способ оценить эти возможности — взглянуть на
картина. Четыре точки нарисованы ниже. Линия между
показаны (2, 4) и (5, 12), а также еще одна линия, охватывающая все
точки, но не попадает ни в одну из них, и красная линия, которая попадает в одну точку
близко и пропускает остальных.
Как вы думаете, какой из них
лучше подходит из
Это
трудно решить, что на самом деле означает лучшая подгонка, поэтому математики
придумал определение, которое интуитивно определяет линию как
лучше всего подходит, если он минимизирует сумму квадратов расстояний до
точки данных. Есть и другие определения, в которых используется сумма
расстояния до точек, и тот, который использует сумму вертикальных
расстояния до точек, но они не стандартные. Смотреть
здесь
исследовать различия между этими тремя определениями и играть
с некоторыми примерами самостоятельно. Вы должны посмотреть здесь
для более простого и удобного инструмента исследования и нажмите o гизмо для » линий наилучшего соответствия с использованием наименьшего
Квадраты «.
Оставшаяся часть этого обзора предназначена для того, чтобы показать, как механически найти
уравнение прямой, минимизирующее сумму квадратов
расстояния, или метод наименьших квадратов
решение.
Это черный ящик
часть этого обзора, а это значит, что вы увидите, как это сделать, но
внутренняя работа и причины, по которым она работает, пока останутся
тайна.
Учимся на примере пошагово.
Пусть четыре точки будут:
(2, 4), (5, 12), (3, 4) и (1, 3). Шаг 1:
От
этих точек, составим два уравнения: 4x + 11y = 23 и 11x +
39г = 83, 4, потому что есть 4 точки. 11 это сумма
первые координаты точек. 23 это сумма секунд
координаты точек. 39 это сумма квадратов
первые координаты точек, то есть: 2×2 + 5×5 + 3×3 +
1×1. 83 — это сумма произведений координат
очков, то есть: 2х4+5х12+3х4+1х3. Я сказал тебе, что не будет
смысл! Но убедитесь, что вы все еще можете сделать это для любого другого набора
точек. Попробуйте для (0, 1), (2, 7), (4, 9)), (5, 10), (8,
20).
Шаг 2:
Найти
точка (x, y), удовлетворяющая обоим уравнениям.
Есть много
способов сделать это, и, возможно, у вас уже есть свой любимый.
Самый простой способ — решить x через y в одном уравнении, а затем
подставить выражение в другое выражение. Этот
эффективно превращает два уравнения и два неизвестных в одно уравнение и
один неизвестный. В нашем примере первое уравнение дает x =
(23-11 лет)/4. Подставив это во второе уравнение 11x + 39у
= 83, дает 11 ((23-11y)/4) + 39y = 83. Упрощение дает (35/4)
y = 79/4, и решение для y дает y = 79/35. Вы можете вернуться к
любое уравнение, чтобы найти, что x = -16/35. Дважды проверьте это
расчет, убедившись, что значения x = -16/35 и y = 79/35
удовлетворяют обоим уравнениям 4x
+ 11y = 23 и 11x + 39y = 83.
Шаг
3:
Нарисуйте линию Высота = (79/35)
Дни — 16/35. Эта линия лучше всего соответствует исходным точкам
используя метод наименьших квадратов. Он показан красным цветом выше в
предыдущая схема.
Проблемы: Приближаются
Под Строительство Круглый год
назад
Напишите мне: [email protected]
Мой профессиональная домашняя страница
Методы распределения — история
Распределение
Также в этом разделе:
- Методы распределения
- Законодательство о распределении 1890 – присутствует 90 180
- Законодательство о распределении 1840 — 1880
- Законодательство о распределении 1790 — 1830
Этот Javascript выделяет страницу, на которой вы находитесь, и отменяет ее URL-адрес.
После каждой десятилетней переписи места в Палате представителей перераспределяются между штатами в соответствии с их населением. Существует несколько различных методов распределения, перечисленных ниже, каждый из которых распределяет места немного по-разному.
Метод Гамильтона/Винтона
Метод Гамильтона/Винтона устанавливает делитель как долю от общей численности населения на одно место в доме. После деления населения каждого штата на делитель целое число частного сохраняется, а дробь отбрасывается. Это приведет к избытку мест в доме. Первое избыточное место отводится штату с наибольшей долей после первоначального деления. Следующее присваивается штату со второй по величине дробью и так далее. Например:
Если в стране 4 штата и 20-местная Палата представителей…
2560 + 3315 + 995 + 5012 = 11882
11882 ⁄ 20 = 594,1
| Население | человекЧастное | Первое распределение мест | Остаток десятичной дроби | Распределение мест | |
|---|---|---|---|---|---|
| А | 2560 | 2560 ⁄ 594,1 = 4,31 | 4 | . 31 | 4 |
| Б | 3315 | 3315 ⁄ 594,1 = 5,58 | 5 | .58 | 6 |
| С | 995 | 995 ⁄ 594,1 = 1,67 | 1 | .67 | 2 |
| Д | 5012 | 5012 ⁄ 594,1 = 8,44 | 8 | .44 | 8 |
| Всего = 20 мест | |||||
Метод Джефферсона
Метод Джефферсона позволяет избежать проблемы распределения, приводящего к избытку или дефициту мест в Палате представителей, за счет использования делителя, который приведет к распределению правильного количества мест. Например:
Если в стране 4 штата и 20-местная Палата представителей…
2560 + 3315 + 995 + 5012 = 11882
11882 ⁄ 20 = 594,1
| Штат | Население | человекКоэффициент | Распределение мест | ||
|---|---|---|---|---|---|
| А | 2560 | 2560 ⁄ 594,1 = 4,31 | 4 | ||
| Б | 3315 | 3315 ⁄ 594,1 = 5,58 | 5 | ||
| С | 995 | 995 ⁄ 594,1 = 1,67 | 1 | ||
| Д | 5012 | 5012 ⁄ 594,1 = 8,44 | 8 | ||
| Итого = 18 мест (2 избытка) | |||||
Но если бы делитель был 550 вместо 594.
a…
| Состояние | Население | человекЧастное | Распределение мест | ||
|---|---|---|---|---|---|
| А | 2560 | 2560 ⁄ 550 = 4,65 | 4 | ||
| Б | 3315 | 3315 ⁄ 550 = 6,03 | 6 | ||
| С | 995 | 995 ⁄ 550 = 1,81 | 1 | ||
| Д | 5012 | 5012 ⁄ 550 = 9,11 | 9 | ||
| Всего = 20 мест | |||||
Метод Вебстера
Метод Вебстера представляет собой модифицированную версию метода Гамильтона/Винтона. После того, как население штата разделено на делитель, те, у кого коэффициенты составляют дроби 0,5 или выше, получают дополнительное место.
Состояния с частным с дробью ниже 0,5 имеют пониженную дробь. Размер палаты представителей устанавливается для расчета делителя, но может быть увеличен при окончательном распределении, если большое количество штатов имеют дроби выше 0,5.
Если в стране 4 штата и планируется 20-местная Палата представителей…
2560 + 3315 + 995 + 5012 = 11882
11882 ⁄ 20 = 594,1
| Население | человекЧастное | Первое распределение мест | Остаток десятичной дроби | Распределение мест | |
|---|---|---|---|---|---|
| А | 2560 | 2560 ⁄ 594,1 = 4,31 | 4 | .31 | 4 |
| Б | 3315 | 3315 ⁄ 594,1 = 5,58 | 5 | . 58 | 6 |
| С | 995 | 995 ⁄ 594,1 = 1,67 | 1 | .67 | 2 |
| Д | 5012 | 5012 ⁄ 594,1 = 8,44 | 8 | .44 | 8 |
| Всего = 20 мест | |||||
Метод Хантингтона-Хилла
Метод Хантингтона-Хилла представляет собой модифицированную версию метода Вебстера, но в нем используется немного другой метод округления. В то время как метод Вебстера округляет до 0,5, метод Хантингтона-Хилла округляет до среднего геометрического, что описано ниже. Если частное штата выше его среднего геометрического, ему будет выделено дополнительное место. Этот метод почти всегда приводит к желаемому количеству мест.
Среднее геометрическое двух чисел равно квадратному корню из их произведения.
Например, среднее арифметическое чисел 4 и 5 равно 4,5:
(4 + 5) ⁄ 2 = 4,5
Среднее геометрическое равно 4,47:
(4 x 5) = 20
√(20) = 4,47
Если в стране 4 штата и планируется 20-местная Палата представителей.