Свойства арифметической прогрессии: Формулы и свойства арифметической прогрессии.

определение, формулы, свойства. Как найти разность арифметической прогрессии

Содержание

1. Математическое определение
2. Понятие о прогрессии алгебраической
3. Примеры арифметических прогрессий.
4. Решение без использования формул
5. Геометрическая прогрессия.
6. Общий вид арифметической прогрессии
7. Что вы узнаете
8. Формулы для определения элементов прогрессии
9. Формулы разности прогрессии арифметической
10. Свойства арифметической прогрессии.
11. Онлайн калькуляторсумма арифметической прогрессии

Математическое определение

Итак, если речь идет о прогрессии арифметической или алгебраической (эти понятия определяют одно и то же), то это означает, что имеется некоторый числовой ряд, удовлетворяющий следующему закону: каждые два соседних числа в ряду отличаются на одно и то же значение. Математически это записывается так:

a_{n + 1}-a_n = d

Здесь n означает номер элемента a_n в последовательности, а число d – это разность прогрессии (ее название следует из представленной формулы).

О чем говорит знание разности d? О том, как “далеко” друг от друга отстоят соседние числа. Однако знание d является необходимым, но не достаточным условием для определения (восстановления) всей прогрессии. Необходимо знать еще одно число, которым может быть совершенно любой элемент рассматриваемого ряда, например, a₄, a10, но, как правило, используют первое число, то есть a₁.

Понятие о прогрессии алгебраической

Числовая прогрессия представляет собой последовательность чисел, в которой каждый последующий элемент можно получить из предыдущего, если применить некоторый математический закон. Известно два простых вида прогрессии: геометрическая и арифметическая, которую называют также алгебраической. Остановимся на ней подробнее.

Представим себе некоторое рациональное число, обозначим его символом a1, где индекс указывает его порядковый номер в рассматриваемом ряду. Добавим к a1 некоторое другое число, обозначим его d. Тогда второй элемент ряда можно отразить следующим образом: a2 = a1+d. Теперь добавим d еще раз, получим: a3 = a2+d. Продолжая эту математическую операцию, можно получить целый ряд чисел, который будет называться прогрессией арифметической.

Как можно понять из изложенного выше, чтобы найти n-ый элемент этой последовательности, необходимо воспользоваться формулой: an = a1 + (n-1)*d. Действительно, подставляя n=1 в выражение, мы получим a1 = a1, если n = 2, тогда из формулы следует: a2 = a1 + 1*d, и так далее.

Например, если разность прогрессии арифметической равна 5, а a1 = 1, то это значит, что числовой ряд рассматриваемого типа имеет вид: 1, 6, 11, 16, 21, … Как видно, каждый его член больше предыдущего на 5.

Примеры арифметических прогрессий.

1. Натуральный ряд 1, 2, 3, 4, 5,… является арифметической прогрессией, в которой 1-й член , а разность .

1, -1, -3, -5, -7 — первые пять членов арифметической прогрессии, в которой и .

2. Если каждый элемент некоторой последовательности имеет такую же величину, как и остальные элементы этой системы и равен некоторому числу , тогда это является арифметической прогрессией, в которой и . В частности, является арифметической прогрессией с разностью .

3. Сумма 1-х натуральных чисел выражают формулой:

.

Решение без использования формул

Решим первую задачу, при этом не будем использовать никакие из приведенных формул. Пусть даны элементы ряда: а6 = 3, а9 = 18. Найти разность прогрессии арифметической.

Известные элементы стоят близко друг к другу в ряду. Сколько раз нужно добавить разность d к наименьшему, чтобы получить наибольшее из них? Три раза (первый раз добавив d, мы получим 7-й элемент, второй раз – восьмой, наконец, третий раз – девятый). Какое число нужно добавить к трем три раза, чтобы получить 18? Это число пять. Действительно:

3 + 5 + 5 + 5 = 18

Таким образом, неизвестная разность d = 5.

Конечно же, решение можно было выполнить с применением соответствующей формулы, но этого не было сделано намеренно. Подробное объяснение решения задачи должно стать понятным и ярким примером, что такое арифметическая прогрессия.

Геометрическая прогрессия.

Геометрическая прогрессия — это последовательность чисел (членов прогрессии), в которой каждое число, начиная со 2-го, получают из предыдущего путем умножения его на определённое число (знаменатель прогрессии), где , : .

Или другими словами: геометрическая прогрессия – это численная последовательность, каждое из чисел равняется предыдущему, умноженному на определенное постоянное число q для данной прогрессии, которое называется знаменателем геометрической прогрессии.

Каждый член геометрической прогрессии можно вычислить при помощи формулы:

Когда и , значит, прогрессия возрастает , когда , значит, прогрессия убывает, а при — знакочередуется.

Название геометрическая прогрессия взяла из своего характеристического свойства:

т.е. все члены равны среднему геометрическому их соседей.

Общий вид арифметической прогрессии

a₁, a₁ + d, a₁ + 2d, … a₁ + (n – 1) d, …

d – шаг или разность прогрессии; это и есть постоянное слагаемое.

Члены прогрессии:

• a₁
• a₂ = a₁ + d
• a₃ = a₂ + d = a₁ + 2d
• и т.д.

Цифры 1,2,3… – это их порядковые номера, т.е. место, которое они занимают в последовательности.

Что вы узнаете

В жизни мы часто сталкиваемся с числовыми последовательностями. Например, средняя температура воздуха для каждого дня в сентябре или расходы на транспорт в каждом месяце года.

Пусть каждому натуральному числу

nn

n поставлено в соответствие некоторое единственное действительное число

ana_n

an​ (при этом разным натуральным числам

nn

n могут соответствовать и одинаковые действительные числа). Тогда можно сказать, что задана числовая последовательность

a1,a2,a3,. {infty }}_{=1}

{an​}n∞​=1​.

Последовательности, о которых пойдет речь в данной главе, обладают интересными свойствами: очередной член последовательности можно вычислить, зная предыдущий член, по определенной формуле. Если использовать свойства этих последовательностей, то многие задачи математики, физики и экономики значительно упрощаются.

Начнем с арифметической прогрессии.

Формулы для определения элементов прогрессии

В общем, информации выше уже достаточно, чтобы переходить к решению конкретных задач. Тем не менее до того, как будет дана прогрессия арифметическая, и найти разность ее будет необходимо, приведем пару полезных формул, облегчив тем самым последующий процесс решения задач.

Несложно показать, что любой элемент последовательности с номером n может быть найден следующим образом:

a_n = a₁ + (n – 1) * d

Действительно, проверить эту формулу может каждый простым перебором: если подставить n = 1, то получится первый элемент, если подставить n = 2, тогда выражение выдает сумму первого числа и разности, и так далее.

Условия многих задач составляются таким образом, что по известной паре чисел, номера которых в последовательности также даны, необходимо восстановить весь числовой ряд (найти разность и первый элемент). Сейчас мы решим эту задачу в общем виде.

Итак, пусть даны два элемента с номерами n и m. Пользуясь полученной выше формулой, можно составить систему из двух уравнений:

a_n = a₁ + (n – 1) * d;

a_m = a₁ + (m – 1) * d

Для нахождения неизвестных величин воспользуемся известным простым приемом решения такой системы: вычтем попарно левую и правую части, равенство при этом останется справедливым. Имеем:

a_n = a₁ + (n – 1) * d;

a_n – a_m = (n – 1) * d – (m – 1) * d = d * (n – m)

Таким образом, мы исключили одну неизвестную (a₁). Теперь можно записать окончательное выражение для определения d:

d = (a_n – a_m) / (n – m), где n > m

Мы получили очень простую формулу: чтобы вычислить разность d в соответствии с условиями задачи, необходимо лишь взять отношение разностей самих элементов и их порядковых номеров. Следует обратить на один важный момент внимание: разности берутся между “старшим” и “младшим” членами, то есть n > m (“старший” – имеется в виду стоящий дальше от начала последовательности, его абсолютное значение может быть как больше, так и меньше более “младшего” элемента).

Выражение для разности d прогрессии следует подставить в любое из уравнений в начале решения задачи, чтобы получить значение первого члена.

Далее в статье приведем примеры решения задач на вычисления d и на восстановление числового ряда алгебраической прогрессии. Здесь же хотелось бы отметить один важный момент.

В наш век развития компьютерных технологий многие школьники стараются найти решения для своих заданий в Интернете, поэтому часто возникают вопросы такого типа: найти разность арифметической прогрессии онлайн. По подобному запросу поисковик выдаст ряд web-страниц, перейдя на которые, нужно будет ввести известные из условия данные (это могут быть как два члена прогрессии, так и сумма некоторого их числа) и моментально получить ответ.

Тем не менее такой подход к решению задачи является непродуктивным в плане развития школьника и понимания сути поставленной перед ним задачи.

Формулы разности прогрессии арифметической

Из приведенного выше определения рассматриваемого ряда чисел следует, что для его определения необходимо знать два числа: a1 и d. Последнее называется разностью этой прогрессии. Оно однозначно определяет поведение всего ряда. Действительно, если d будет положительным, то числовой ряд будет постоянно возрастать, наоборот, в случае d отрицательного, будет происходить возрастание чисел в ряду лишь по модулю, абсолютное же их значение будет уменьшаться с ростом номера n.

Чему равна разность прогрессии арифметической? Рассмотрим две основные формулы, которые используются для вычисления этой величины:

d = an+1-an, эта формула следует непосредственно из определения рассматриваемого ряда чисел.

d = (-a1+an)/(n-1), это выражение получается, если выразить d из формулы, приведенной в предыдущем пункте статьи. Заметим, что это выражение обращается в неопределенность (0/0), если n=1. Связано это с тем, что необходимо знание как минимум 2-х элементов ряда, чтобы определить его разность.

Эти две основные формулы используются для решения любых задач на нахождение разности прогрессии. Однако существует еще одна формула, о которой также необходимо знать.

Свойства арифметической прогрессии.

1. Общий член арифметической прогрессии.

Член арифметической прогрессии с номером можно найти с помощью формулы:

,

где — 1-й член прогрессии, — разность прогрессии.

2. Характеристическое свойство арифметической прогрессии.

Последовательность – это арифметическая прогрессия для элементов этой прогрессии выполняется условие:

.

3. Сумма 1-х членов арифметической прогрессии.

Сумму 1-х членов арифметической прогрессии можно найти с помощью формул:

,

где — 1-й член прогрессии,

— член с номером ,

— число суммируемых членов.

,

где — 1-й член прогрессии,

— разность прогрессии,

— число суммируемых членов.

4. Сходимость арифметической прогрессии.

Арифметическая прогрессия является расходящейся при и сходящейся при . При этом:

5. Связь между арифметической и геометрической прогрессиями.

Есть — арифметическая прогрессия с разностью , где число . Тогда последовательность, которая имеет вид является геометрической прогрессией, имеющей знаменатель .

Онлайн калькуляторсумма арифметической прогрессии

Известный член прогрессии A

Бытует мнение, что формула суммы арифметической прогрессии была открыта еще Гауссом, как быстрый и точный способ расчета суммы чисел в определенной последовательности. Он заметил, что такая прогрессия является симметричной, то есть сумма симметрично расположенных с начала и конца членов прогрессии является постоянной для данного ряда.

a₁+a_n=a₂+a_(n-1)=a₃+a_(n-2)=⋯

Соответственно, он нашел данную сумму и умножил ее на половину от общего количества чисел в последовательности, участвующих в расчете суммы. Таким образом, была выведена формула суммы арифметической прогрессии

Пример. Предположим, задано условие: “Найдите сумму первых десяти (10) членов арифметической прогрессии”. Для этого понадобится следующие данные: разность прогрессии и первый ее член. Если в задаче дан какой-либо n член арифметической прогрессии вместо первого, тогда сначала нужно воспользоваться разделом, где представлена формула нахождения первого члена прогрессии, и найти его. Затем исходные данные вбиваются в калькулятор и он производит расчеты, складывая первый и десятый члены, и умножая полученную сумму на половину от общего количества складываемых членов – на 5. Аналогично происходит, если нужно

найти сумму первых шести членов или любого другого количества.

В случае, когда необходимо найти сумму членов арифметической прогрессии, начинающихся не с первого, а с пятого члена, к примеру, тогда среднее арифметическое остается тем же, а общее количество членов берется как увеличенная на единицу разность между порядковыми номерами взятых членов.

 

Источники

• https://FB.ru/article/432010/kak-nayti-raznost-arifmeticheskoy-progressii-formulyi-i-primeryi-resheniy
• https://1Ku.ru/obrazovanie/10028-kak-najti-raznost-arifmeticheskoj-progressii/
• https://www.calc.ru/Progressii-Arifmeticheskaya-Geometricheskaya-Formuly.html
• https://MicroExcel.ru/arifmeticheskaya-progressiya/
• https://lampa.io/p/%D0%B0%D1%80%D0%B8%D1%84%D0%BC%D0%B5%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B0%D1%8F-%D0%BF%D1%80%D0%BE%D0%B3%D1%80%D0%B5%D1%81%D1%81%D0%B8%D1%8F-00000000753cfa14d82214511e944e87
• https://allcalc. ru/node/1002

Шаг (разность) прогрессии d
Произвести вычисления для n равного

Характеристическое свойство показательной прогрессии или новое числовое среднее

Автор: Гульманов Нуртай Кудайбергенович

Рубрика: Математика

Опубликовано в Молодой учёный №6 (192) февраль 2018 г.

Дата публикации: 12.02.2018 2018-02-12

Статья просмотрена: 221 раз

Скачать электронную версию

Скачать Часть 1 (pdf)

Библиографическое описание:

Гульманов, Н. К. Характеристическое свойство показательной прогрессии или новое числовое среднее / Н. К. Гульманов. — Текст : непосредственный // Молодой ученый. — 2018. — № 6 (192). — С. 1-4. — URL: https://moluch.ru/archive/192/48026/ (дата обращения: 16.09.2022).



Как известно, числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с некоторым числом, называется арифметической прогрессией [1]. А числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, умноженному на некоторое отличное от нуля постоянное число, называется геометрической прогрессией

[1]. Из определения арифметической и геометрической прогрессий мы видим, что они основаны на арифметических действиях суммы (разности) и умножения (деления). Возникает вопрос: существует ли прогрессия, которая основана на действии возведение в степень число. В работе [2] был определен новый вид прогрессии — показательная прогрессия.

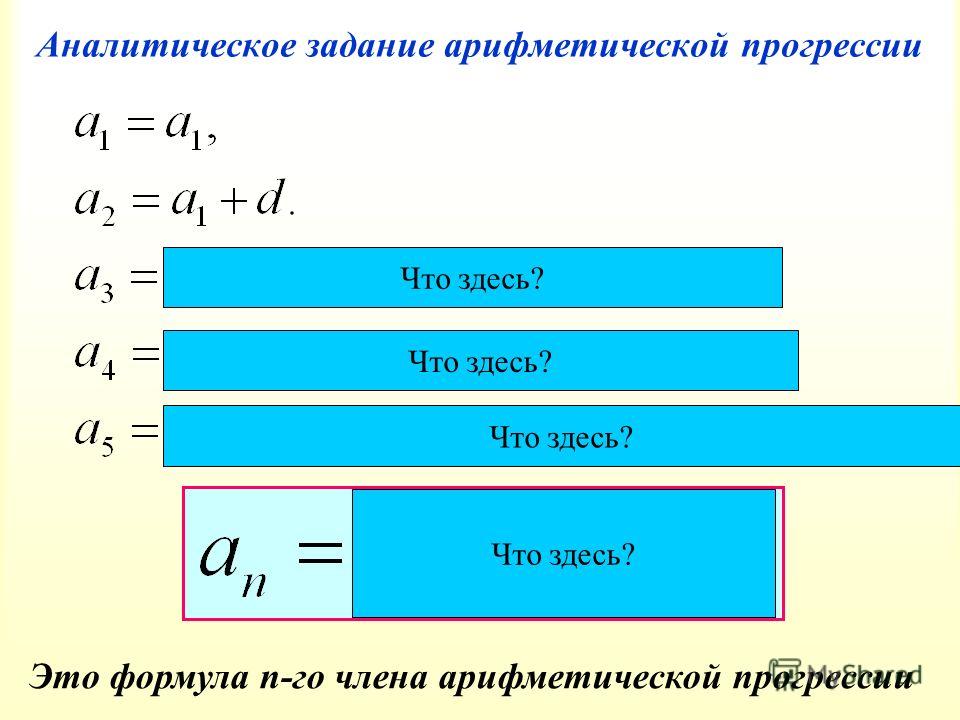
Также в работе [2] в качестве характеристического свойства показательной прогрессии рассматривается следующее утверждение. Если — показательная прогрессия, то для любого натурального выполняется равенство

В данном проекте будет доказана другая формула, описывающая характеристическое свойство показательной прогрессии. Также будет рассмотрено неравенство — аналог неравенству Коши [3].

Ключевые слова: числовые последовательности, прогрессия, показательная прогрессия, неравенство Коши.

Докажем следующую теорему, описывающую характеристическое свойство показательной прогрессии.

Теорема 1. Для каждого члена показательной прогрессии, начиная со второго, выполняется равенство:

Доказательство. По определению [2] показательной прогрессии

Отсюда следует, что

т. е.

Преобразуем полученное выражение

(1)

что и требовалось доказать.

Выразим из равенства (1).

Так как характеристическое свойство арифметической прогрессии построено на основе арифметической средней, а геометрическая прогрессия — на основе геометрической средней, то характеристическое свойство показательной прогрессии должно построено на основе какой-то другой числовой средней. В качестве этой средней будем считать последнее из равенств.

Определение 1. Пусть даны два положительных числа . Причем эти числа либо больше единицы, либо меньше единицы одновременно. Средним показательным чисел называется величина, определяемая следующим образом:

(2)

Замечание 1. Если заменить местами , значение средней показательной не изменится.

Доказательство. Преобразуем выражение (2) следующим образом:

что и требовалось доказать.

Замечание 2. Среднюю показательную можно определить и следующим образом:

где — это такое произвольное положительное число, как , одновременно с ними либо больше единицы, либо — меньше.

Доказательство. Преобразуем выражение (2) следующим образом:

что и требовалось доказать.

Введем обобщенное определение средней показательной для чисел.

Определение 2. Пусть даны положительные числа и . Причем эти числа либо больше единицы, либо меньше единицы одновременно. Средним показательным чисел называется величина, определяемая следующим образом:

Среднее арифметическое двух неотрицательных чисел не меньше их среднего геометрического — это неравенство называется неравенством Коши [3]: если , , то

В более общем виде: для неотрицательных чисел справедливо неравенство между их средним арифметическим и средним геометрическим

причем равенство возможно лишь при условии .

Рассмотрим следующую теорему, описывающую связь между неравенством Коши и средним показательным.

Теорема 2. Пусть даны числа , каждое из которых больше единицы. Тогда выполняется следующее неравенство:

причем равенство возможно лишь при условии

Доказательство. Запишем неравенство Коши для чисел .

Используя свойства логарифма числа, преобразуем это выражение следующим образом:

что и требовалось доказать.

Теорема 3. Пусть даны числа , каждое из которых меньше единицы. Тогда выполняется следующее неравенство:

Причем равенство возможно лишь при условии

Доказательство. Запишем неравенство Коши для чисел .

Используя свойства логарифма числа, преобразуем это выражение следующим образом:

или

что и требовалось доказать.

Замечание 3. Пусть даны положительные числа и . Тогда выполняются неравенства

причем равенство возможно лишь при условии .

Литература:

1. Н. Я. Виленкин / Алгебра для 9 класса: Учеб. пособие для учащихся шк. и кл. с углубл. изуч. математикик / Н. Я. Виленкин, Г. С. Сурвилло, А. С. Симонов, А. И. Кудрявцев / — 3-е изд. — М.: Просвещение, 1999. — С.384: ил. — ISBN 5–09–009020–3
2. Н. К. Гульманов / Определение нового вида прогрессии, основанной на операции возведения в степень, и изучение ее основных свойств / Н. К. Гульманов, Н. А. Марчук // «Высокое качество и лидерство в образовании»: сборник докладов Международной научно-практической конференции (13–15 ноября 2013 года)/ АОО «Назарбаев Интеллектуальные школы». Часть 1. — Астана, 2013. — С. 120–124
3. П. П. Коровкин / Неравенства / Популярные лекции по математике, выпуск № 5/ — М.: Издательство «Наука», 1974. — С. 54
4. И. С. Соминский / Метод математической индукции / Популярные лекции по математике, выпуск № 3/ — М.: Издательство «Наука», 1972. — С. 63

Основные термины (генерируются автоматически): показательная прогрессия, число, характеристическое свойство, неравенство, геометрическая прогрессия, равенство, арифметическая прогрессия, Кош, свойство логарифма числа, числовая последовательность.

Ключевые слова

числовые последовательности, прогрессия, показательная прогрессия, неравенство Коши

числовые последовательности, прогрессия, показательная прогрессия, неравенство Коши

Похожие статьи

Показательно—геометрическая прогрессия и некоторые ее. ..

показательная прогрессия, показательно—геометрическая прогрессия, характеристическое свойство, член прогрессии, геометрическая прогрессия, знаменатель показателя прогрессии, член, формула…

Некоторые

свойства арифметико-геометрической прогрессии

К таким последовательностям относятся арифметическая и геометрическая прогрессии, последовательность Фибоначчи и др. [1]. В данной статье представлены итоги исследования рекуррентной последовательности , заданной по правилу , где числа и называем…

Развитие исследовательских навыков учащихся при изучении.

..

геометрическая прогрессия, арифметическая прогрессия, учащийся, характеристическое свойство, показательная прогрессия, предполагаемый ответ учащихся, противный случай, Таблица…

Типология текстовых задач в Едином государственном экзамене…

Арифметическая прогрессия — это последовательность чисел, в которой каждое следующее число, начиная со второго, получается прибавлением к предыдущему постоянного числа

Построение формальной

арифметики в рамках изучения…

Если Q есть свойство, которым обладает натуральное число 0, и для всякого натурального числа x

Этих аксиом достаточно для построения не только арифметики натуральных чисел, но и для

Эта теория первого порядка с равенством имеет единственную предикатную букву. ..

Анализ псевдослучайных

последовательностей на…

арифметическая прогрессия, примитивный многочлен, последовательность, образующий элемент, работа, поле, неприводимый многочлен, кривой, генератор, характеристический многочлен.

Характеристическое свойство показательной прогрессии или…

Показательно—геометрическая прогрессия и некоторые ее свойства.

Развитие исследовательских навыков учащихся при изучении темы «Числовые последовательности».

О некоторых бинарных задачах для

прогрессий | Статья…

В работе рассматривается задача о распределении натуральных чисел, принадлежащих заданному классу вычетов по некоторому модулю и представимых в виде суммы u+v, где u,v- члены двух заданных последовательностей натуральных чисел.

Похожие статьи

Показательно—геометрическая прогрессия и некоторые ее…

показательная прогрессия, показательно—геометрическая прогрессия, характеристическое свойство, член прогрессии, геометрическая прогрессия, знаменатель показателя прогрессии, член, формула…

Некоторые

свойства арифметико-геометрической прогрессии

К таким последовательностям относятся арифметическая и геометрическая прогрессии, последовательность Фибоначчи и др. [1]. В данной статье представлены итоги исследования рекуррентной последовательности , заданной по правилу , где числа и называем. ..

Развитие исследовательских навыков учащихся при изучении…

геометрическая прогрессия, арифметическая прогрессия, учащийся, характеристическое свойство, показательная прогрессия, предполагаемый ответ учащихся, противный случай, Таблица…

Типология текстовых задач в Едином государственном экзамене…

Арифметическая прогрессия — это последовательность чисел, в которой каждое следующее число, начиная со второго, получается прибавлением к предыдущему постоянного числа

Построение формальной

арифметики в рамках изучения…

Если Q есть свойство, которым обладает натуральное число 0, и для всякого натурального числа x

Этих аксиом достаточно для построения не только арифметики натуральных чисел, но и для

Эта теория первого порядка с равенством имеет единственную предикатную букву. ..

Анализ псевдослучайных

последовательностей на…

арифметическая прогрессия, примитивный многочлен, последовательность, образующий элемент, работа, поле, неприводимый многочлен, кривой, генератор, характеристический многочлен.

Характеристическое свойство показательной прогрессии или…

Показательно—геометрическая прогрессия и некоторые ее свойства.

Развитие исследовательских навыков учащихся при изучении темы «Числовые последовательности».

О некоторых бинарных задачах для

прогрессий | Статья…

В работе рассматривается задача о распределении натуральных чисел, принадлежащих заданному классу вычетов по некоторому модулю и представимых в виде суммы u+v, где u,v- члены двух заданных последовательностей натуральных чисел.

Арифметическая прогрессия

Весьма распространенными задачами на вступительных испытаниях по математике являются задачи, связанные с понятием арифметической прогрессии. Для успешного решения таких задач необходимо хорошо знать свойства арифметической прогрессии и иметь определенные навыки их применения. 

Предварительно напомним основные свойства арифметической прогрессии и приведем наиболее важные формулы, связанные с этим понятием.

Определение. Числовая последовательность  , в которой каждый последующий член отличается от предыдущего на одно и то же число , называется арифметической прогрессией. При этом число    называется  разностью прогрессии. 

 

Для арифметической прогрессии справедливы формулы

                                           ,                                          (1)

                                            ,                                            (2)

где  . Формула (1) называется формулой общего члена арифметической прогрессии, а формула (2) представляет собой основное свойство арифметической прогрессии: каждый член прогрессии совпадает со средним арифметическим своих соседних членов   и  .

Отметим, что именно из-за этого свойства рассматриваемая прогрессия называется «арифметической».  

Приведенные выше формулы (1) и (2) обобщаются следующим образом:

                                                                                      (3)

                                                                                          (4)

где         и      .

Для вычисления суммы     первых     членов арифметической прогрессии     обычно применяется формула

                                                                   (5)               где      и   .

Если принять во внимание формулу (1), то из формулы (5) вытекает

                                              .                                 (6)

Если  обозначить  ,  то   

                                              ,                           (7)

                                     ,               (8)

где  . Так как , то формулы (7) и (8) являются обобщением соответствующих формул (5) и (6).

В частности, из формулы (5) следует, что

.

К числу малоизвестных большинству учащихся относится свойство арифметической прогрессии, сформулированное посредством следующей теоремы.

   

Теорема.   Если    ,  то

                                ,                (9)                где  .

Доказательство.  Если  , то

,

или  .

Теорема доказана.

Например, используя теорему, можно показать, что     

,

 или  .

Перейдем к рассмотрению типовых примеров решения задач на тему «Арифметическая прогрессия».

Пример 1. Пусть    и . Найти .

Решение.  Применяя формулу (6), получаем . Так как    и , то    или .

Ответ:  .

Пример 2.  Пусть в три раза больше , а при делении на   в частном получается  2  и  в остатке 8. Определить и .  

Решение.  Из условия примера вытекает система уравнений

                                                                                                (10)                            

Так как  ,  ,    и  , то из системы уравнений (10) получаем

  или     

Решением данной системы уравнений являются    и  .

Ответ:  , .

 

Пример 3.  Найти  ,  если    и  .

Решение.  Согласно формуле (5) имеем    или   .  Однако, используя свойство (9), получаем .

Так как    и  , то из равенства   вытекает уравнение    или  .

Ответ:   .

 

Пример 4.  Найти  ,  если  .

Решение.  По формуле (5) имеем

                                   .                      (11)

Однако, используя теорему, можно записать

  или   .

Отсюда и из формулы (11) получаем .

Ответ:   .

 

Пример 5.  Дано:  . Найти .

Решение.  Так как  , то  . Однако  , поэтому  .

Ответ:  .

Пример 6.  Пусть  ,     и  .  Найти  .   

Решение. Используя формулу (9), получаем . Поэтому, если   , то     или  .

Так как    и ,  то здесь  имеем систему уравнений

    решая которую,  получаем     и   .

Далее, принимая во внимание формулу (6), можно записать

.

Натуральным корнем уравнения  является  .

Ответ:  .

 Пример 7.  Найти  ,  если    и  .

Решение.  Так как по формуле (3) имеем, что  , то из условия задачи вытекает система уравнений   

Если подставить выражение    во второе уравнение системы, то получим    или   .

Корнями квадратного уравнения являются    и  .

Рассмотрим два случая.

1. Пусть  , тогда  . Поскольку    и  , то  .

В таком случае, согласно формуле (6), имеем

.

 2. Если  , то  ,    и  

.

Ответ:     и  .

Пример 8.  Известно, что    и . Найти  .

Решение.    Принимая во внимание формулу (5) и условие примера, запишем    и  .

Отсюда следует система уравнений  

Если первое уравнение системы умножим на 2, а затем сложим его со вторым уравнением, то получим  

                                              .                           (12)

Согласно формуле (9) имеем . В этой связи из (12) вытекает     или   .

Поскольку    и  , то  .

Ответ:  .

 

Пример 9.  Найти  , если и  .

Решение.    Поскольку  ,    и  по условию , то     или  .  

Из формулы (5) известно, что .  Так как  , то  .

Следовательно, здесь имеем систему линейных уравнений

Отсюда получаем и . Принимая во внимание формулу (8), запишем  .

Ответ:   .

Пример 10. Решить уравнение   .

Решение. Из заданного уравнения следует, что  . Положим, что  , ,  и  .  В таком случае .

Согласно формуле (1), можно записать  или  .

Далее, из формулы (5) получаем . Однако по условию  и  , поэтому имеем уравнения    или  

                                                 .                          (13)

Так как  , то уравнение (13) имеет единственный подходящий корень  .

Ответ:  .

Пример 11.   Найти максимальное значение при условии, что  и  .

Решение. Так как  , то рассматриваемая арифметическая прогрессия является убывающей. В этой связи выражение принимает максимальное значение в том случае, когда    является номером минимального положительного члена прогрессии.

Воспользуемся формулой (1) и тем фактом, что и  . Тогда получим, что    или .

Поскольку  , то или . Однако в этом неравенстве  наибольшее натуральное число, поэтому  .

Если значения  ,  и   подставить в формулу (6), то получим  .

Ответ:  .

Пример 12. Определить сумму всех двузначных натуральных чисел, которые при делении на число 6 дают в остатке 5.

Решение. Обозначим через    множество всех двузначных натуральных чисел, т.е. . Далее, построим подмножество , состоящее из тех элементов (чисел)  множества  , которые при делении на число 6 дают в остатке 5.

Нетрудно установить, что . Очевидно, что элементы множества образуют арифметическую прогрессию , в которой    и  .

Для установления мощности (числа элементов) множества   положим, что  . Так как и , то из формулы (1) следует  или  . Принимая во внимание формулу (5), получим  .

Ответ:  .

    Приведенные выше примеры решения задач ни в коем случае не могут претендовать на исчерпывающую полноту. Настоящая статья написана на основе анализа современных методов решения типовых задач на заданную тему. Для более глубокого изучения методов решения задач, связанных с арифметической прогрессией, целесообразно обратиться к списку рекомендуемой литературы.

Рекомендуемая литература

1. Сборник задач по математике для поступающих во втузы / Под ред. М.И. Сканави. – М.: Мир и Образование, 2013. – 608 с.

2. Супрун В.П. Математика для старшеклассников: дополнительные разделы школьной программы. – М.: Ленанд / URSS, 2014. – 216 с.

3. Медынский М.М. Полный курс элементарной математики в задачах и упражнениях. Книга 2: Числовые последовательности и прогрессии. – М.: Эдитус, 2015. – 208 с.

   

Остались вопросы? 

Чтобы получить помощь репетитора – зарегистрируйтесь.

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Внеклассный урок — Арифметическая прогрессия

Арифметическая прогрессия

Прогрессия – это определенная последовательность чисел.
Последовательность обозначается так: (a_n)

Числа, образующие последовательность, называют членами последовательности.

Члены последовательности обычно обозначают буквами с индексами, указывающими порядковый номер члена (a₁, a₂, a₃ и т.д.- читается так: «а первое», «а второе», «а третье» и т. д.).

Последовательность может быть бесконечной или конечной.

 

Понятие арифметической прогрессии.

Арифметическая прогрессия – это такая последовательность чисел, которая получается в результате сложения каждого последующего члена с одним и тем же числом.

Пример:

Возьмем последовательность чисел 3; 10; 17; 24; 31.
Здесь каждое последующее число на 7 больше предыдущего. То есть последовательность получилась в результате прибавления одного и того же числа 7 к каждому последующему члену. Это и есть арифметическая прогрессия:

3+7=10

10+7=17

17+7=24

24+7=31

 

Формула арифметической прогрессии.

Любая арифметическая прогрессия может быть задана формулой: an = kn + b, где k и b – некоторые числа. И наоборот: если последовательность задана подобной формулой, то эта последовательность точно является арифметической прогрессией.

Пример: формула a_n = 8n – 2 является формулой арифметической прогрессии, так как она задана формулой типа a_n = kn + b. В ней k = 8, b = –2.

 

Разность арифметической прогрессии.

Разность арифметической прогрессии – это разность между последующим и предыдущим членами прогрессии. Ее обычно обозначают буквой d.

Пример:
Вернемся к нашей прогрессии 3; 10; 17; 24; 31. В ней разность между второй и первой, третьей и второй и т.д. членами равна 7. Число 7 и является разностью данной арифметической прогрессии.

 

Свойства арифметической прогрессии.

1) Каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому предыдущего и последующего членов. 2) Верно и обратное утверждение: если в последовательности чисел каждый член, начиная со второго, равен среднему арифметическому предыдущего и последующего членов, то эта последовательность является арифметической прогрессией.

В нашем примере второй член равен средней арифметической первого и третьего членов:

3 + 17
——— = 10.
    2

Точно так же третий член равен средней арифметической второго и четвертого членов и т.д.

 

Как найти определенный член арифметической прогрессии.

Чтобы найти n-й член арифметической прогрессии, следует применить формулу: an = a1 + d(n – 1)

Пример:

Возьмем некую арифметическую прогрессию, в которой первый член равен 3, а разность арифметической прогрессии составляет 4. Надо найти 45-й член этой прогрессии.

Дано:
b₁ = 3
d = 4
n = 45
———
b₄₅ — ?

Решение.

Применим формулу b_n = b₁ + d(n – 1):

b₄₅ = 3 + 4(45 – 1) = 3 + 4 · 44 = 3 + 176 = 179.

Ответ: 45-й член заданной арифметической прогрессии – число 179.

 

Как найти сумму первых n членов арифметической прогрессии.

Сумму любого количества первых членов арифметической прогрессии можно найти с помощью формулы:                                                                                 (a1 + an) n                                                                        Sn = —————                                                                                        2 Если заданы первый член и разность арифметической прогрессии, то удобно пользоваться другой формулой:                                                                                 2a1 + d(n – 1)                                                                     Sn = —————— n                                                                                        2

Пример 1: Найдем сумму первых ста членов арифметической прогрессии 1+2+3+4+5 и т. д.+100.

Дано:
a₁ = 1
n = 100
a_n = 100
————
S₁₀₀ — ?

Решение:

           (1 + 100) · 100          101 · 100
S₁₀₀ = ——————— = ————— = 5050
                       2                           2

Ответ: Сумма первых ста членов заданной арифметической прогрессии равна 5050.

 

Пример 2: Найдем сумму первых двадцати членов арифметической прогрессии, в которой первый член равен 5, разность арифметической прогрессии составляет 3.

Дано:
a₁ = 5
d = 3
————
S₂₀ — ?

Решение:

1) Найдем сначала двадцатый член по уже известной нам формуле a_n = a₁ + d(n – 1):
a₂₀ = 5 + 3 (20 – 1) = 5 + 3 · 19 = 62.

2) Теперь уже легко решить нашу задачу.

По формуле 1:

              (5 + 62) · 20
S₂₀ = ———————  = 670
                      2

 

По формуле 2:

             2 · 5 + 3 · (20 – 1)
S₂₀ = ————————— · 20  = 670
                           2

Ответ: Сумма первых двадцати членов заданной арифметической прогрессии равна 670.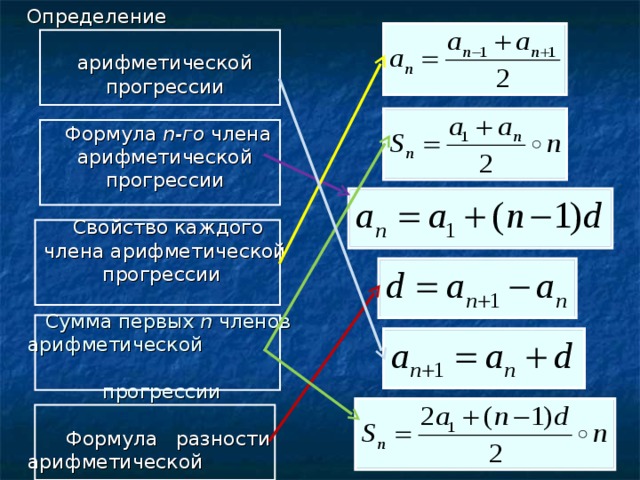

 

Презентация к уроку математики в 9 классе Понятие арифметической прогрессии. Свойства арифметической прогрессии доклад, проект

Слайд 1Текст слайда:

АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ

Урок математики в 9 классе.

---

Слайд 2Текст слайда:

Устный счет

1) Последовательность уn задана формулой
уn= 9 – 5n.
Найдите у2, у3, у5.
2) Последовательность задана формулой
an = – 3n + 15
Найдите номер члена последовательности, равного 6; 0; -3; -9.

Михайлова Г.И. учитель математики МОУ-СОШ с.Карпенка

---

Слайд 3Текст слайда:

4; 6; 8; 10; …

2) 2; 3; 5; 6; 8; …

1; 3; 5; 7; …

1; 2; 3; 4; …

5) 1; 4; 9; 16; …

Михайлова Г.И. учитель математики МОУ-СОШ с.Карпенка

12; 14

9; 11

9; 11

5; 6

25; 36

✓

✓

✓

---

Слайд 4Текст слайда:

Что такое прогрессия?

Это частный случай числовой последовательности.
Слово прогрессия латинского происхождения и означает «движение вперед».
Прогрессии были известны в Древнем Египте и Вавилоне около 2000 лет до н.э.

Михайлова Г.И. учитель математики МОУ-СОШ с.Карпенка

---

Слайд 5Текст слайда:

Определение арифметической прогрессии

Числовую последовательность,
каждый последующий член которой равен предшествующему, сложенному с постоянным для данной последовательности числом, называют арифметической прогрессией.

Михайлова Г.И. учитель математики МОУ-СОШ с.Карпенка

---

Слайд 6Текст слайда:

Разность арифметической прогрессии

Михайлова Г.И. учитель математики МОУ-СОШ с.Карпенка

---

Слайд 7Текст слайда:

Дано: (аn) – арифметическая прогрессия, a1- первый член прогрессии, d – разность.
a2 = a1 + d
a3 = a2 + d =(a1 + d) + d = a1+2d
a4 = a3 + d =(a1+2d) +d = a1+3d
a5 = a4 + d =(a1+3d) +d = a1+4d
. . .

Задание арифметической прогрессии формулой n – ого члена

an = a1+ (n-1)·d

Михайлова Г.И. учитель математики МОУ-СОШ с.Карпенка

---

Слайд 8Текст слайда:

Характеристическое свойство:

Любой член арифметической прогрессии, кроме первого, есть среднее арифметическое предшествующего и последующего членов.

Михайлова Г.И. учитель математики МОУ-СОШ с.Карпенка

---

Слайд 9Текст слайда:

Способы задания арифметической прогрессии

а) рекуррентной формулой:

б) формулой n-го члена:

в) формулой вида:
Примеры последовательностей
1) 2; 5; 8; 11;…
2) 20; 17; 14; 11;… 3) 8; 8; 8; 8;…

Михайлова Г.И. учитель математики МОУ-СОШ с.Карпенка

---

Слайд 10Текст слайда:

№ 621

Дано: ( an ): 2; 7; 12; 22; 27; …
Найти: а) разность между последующим членом
и предыдущим;
б) ( an ) – арифметическая прогрессия?
Решение:
a2 – a1 = a3 – a2 = a5 – a4 =7 – 2 = 12 – 7= 27 – 22 =5,
но a4 – a3 =22 – 12 =10,
10≠5,
значит, …

Михайлова Г. И. учитель математики МОУ-СОШ с.Карпенка

аn не арифметическая прогрессия

---

Слайд 11Текст слайда:

№ 627 (а,г) Дано: ( an ) – арифметическая прогрессия

а)а3=5; a4=9.
Найти: a2 и d.
Решение:

г) а6= – 15; a8= –11 .
Найти: a7 и d.
Решение:

Михайлова Г.И. учитель математики МОУ-СОШ с.Карпенка

d =a4 – a3= 9 – 5 =4,
a2=a3 – d= 5 – 4 = 1.
Или a3 =(a2+a4):2, тогда
a2= 2a3–a4 =2·5 – 9 = 1
Ответ: a2=1, d=4.

a7 = (a6+a8): 2,
a7 =(–15 – 11):2= – 13,
d =a8 – a7= –11 –(–13)= 2.
Ответ: a7= –13, d=2.

---

Слайд 12Текст слайда:

№ 622

Дано: а1=3; d = 2; an= a1 +(n — 1)·d . Найти пять первых членов арифметической прогрессии.
Решение:
а2 = a1 + d= 3+2=…
a3= a1 +2d=….
a4 =…
a5 =…

Ответ:

Михайлова Г.И. учитель математики МОУ-СОШ с.Карпенка

---

Слайд 13Текст слайда:

№ 630(а)

В арифметической прогрессии (an ) найти a2 + a9,
если a1 + a10 = 120.
Решение:
a1+ a10 = a1 +(a1+9d)= 120,
2a1+9d= (a1+d) + (a1 +8d)=

Ответ:

Михайлова Г.И. учитель математики МОУ-СОШ с.Карпенка

---

Слайд 14Текст слайда:

№ 632 (а)

Является ли число 12 членом арифметической прогрессии — 10; — 8; -6; …?
Решение:
d= a2 – a1 =– 8 – (–10)=2,
a1 + (n– 1)·d = an ,
– 10 +(n– 1)·2 = 12,

Михайлова Г.И. учитель математики МОУ-СОШ с.Карпенка

Т.к. 12 – целое число, значит a12 =12.
Ответ: число 12 является 12-м членом
арифметической прогрессии.

---

Слайд 15Текст слайда:

Дополнительное задание

В арифметической прогрессии найти a10, если
a25 − a20 = 10 и a16 = 13.
Решение:
a25= a1 +24d, a20= a1+19d, a16= a1+15d.
(a1 +24d) – (a1+19d)=10,
a1+15d =13.
Решая эту систему, найдем , , .
Тогда a10= a1+ 9d=
Ответ:

Михайлова Г. И. учитель математики МОУ-СОШ с.Карпенка

---

Слайд 16Текст слайда:

Итог урока

Какую последовательность называют арифметической прогрессией?
Что называют разностью арифметической прогрессии? Как ее найти?
Какова формула n-го члена арифметической прогрессии?
Какими свойствами обладает арифметическая прогрессия?

Михайлова Г.И. учитель математики МОУ-СОШ с.Карпенка

---

Слайд 17Текст слайда:

Домашнее задание

§6, п.6.1.,
№ 629, 633.

Михайлова Г.И. учитель математики МОУ-СОШ с.Карпенка

СПАСИБО ЗА УРОК

---

План урока — ксп — Арифметическая прогрессия

Навигация по странице: Школа: Дата: ФИО учителя Тема урока Арифметическая прогрессия Вид урока Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу) Навыки использования ИКТ Ход урока Запланированные этапы урока Тип работы Группа №1. Задачи про альпинистов. Группа №2 Задачи про копателей колодцевГруппа №3 Дескрипторы для каждой группы (при необходимости в зависимости от уровня группы можно раздать дескипторы ученикам) Дифференциация – каким образом Вы планируете оказать больше поддержки Какие задачи Вы планируете поставить перед более способными учащимися Оценивание – как Вы планируете проверить уровень усвоения материала учащимися Здоровье и соблюдение техники безопасности Используйте данный раздел для размышлений об уроке. Ответьте на самые важные вопросы о Вашем уроке из левой колонки. Общая оценка Какие два аспекта урока прошли хорошо (подумайте как о преподавании, так и об обучении) 1: 2 Что я выявил(а) за время урока о классе или достижениях/трудностях отдельных учеников, на что необходимо обратить внимание на последующих уроках

Единственный в мире Музей Смайликов Самая яркая достопримечательность Крыма Скачать 25. 19 Kb. Название Арифметическая прогрессия Дата 08.12.2021 Размер 25.19 Kb. Формат файла Имя файла План урока.docx Тип Урок #296132 Подборка по базе: Бизнес план по открытию Барбер Шопа.docx, Конспект открытого урока по ОБЖ и истории _ ВВС РФ_.docx, Бизнес план.docx, уч план рязань.docx, Поурочное планирование 7 класс.odt, Технологическая карта открытого урока _Графики_ (6 класс) и само, разбор урока.docx, План-конспект урока английского языка в 3 классе по теме _Body p, ОБЖ. 5 КЛАСС. УРОК №1. ОПАСНЫЕ И ЧРЕЗВЫЧАЙНЫЕ СИТУАЦИИ. ПЛАН-КОН, производство план.docx Проверил Рук.МО Последовательности Школа: Дата: ФИО учителя: Класс: 9 Количество присутствующих: отсутствующих: Тема урока Арифметическая прогрессия Вид урока Урок обобщение Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу) 9. 2.3.5 знать и применять формулы n-го члена, суммы n первых членов и характеристическое свойство арифметической прогрессии; Цели урока Учащиеся будут: распознавать арифметическую прогрессию среди данных последовательностей; находить общий член последовательности; находить сумму n первых членов арифметической прогрессии; Критерии оценивания Знает формулу n-го члена арифметической прогрессии Применяет формулу n-го члена арифметической прогрессии при решении задач прямо и обратно Знает и применяет формулу суммы n первых члена арифметической прогрессии Знает и применяет характеристическое свойство арифметической прогрессии Обобщает характеристическое свойство арифметической прогрессии Языковые цели Учащиеся будут: использовать предметную лексику и терминологию раздела при решении задач; аргументировать использование арифметической и геометрической прогрессий при решении задач; комментировать решение задач на банковский процент; Лексика и терминология, специфичная для предмета: числовая последовательность; способы задания последовательностей; предыдущий член последовательности, последующий член последовательности; первый член последовательности и т. д.,n-й член последовательности; формула n-го члена последовательности; рекуррентная формула; возрастающая, убывающая последовательность; разность арифметической прогрессии; знаменатель геометрической прогрессии; среднее арифметическое; среднее геометрическое; сумма n первых членов арифметической/геометрической прогрессии; бесконечно убывающая геометрическая прогрессия; Полезные выражения для диалогов и письма: n –й член последовательности можно представить в виде формулы…; следующим элементом последовательности будет…; чтобы найти …член …прогрессии…; последовательность является убывающей/возрастающей, так как…; чтобы найти сумму …первых членов …прогрессии…; числа…являются членами арифметической прогрессии, так как…; числа…являются членами геометрической прогрессии, так как…; так как а1=…,аn=…, то сначала нужно найти …; чтобы перевести периодическую дробь…в обыкновенную…; Межпредметные связи История математики, экономика, физика Навыки использования ИКТ Использование ИД для демонстрации презентации, использование графического редактора ГеоГебра Предварительные знания Понятие числовой последовательности; последовательности, содержащей степени. Умение определять закономерности и находить недостающие члены последовательности, содержащей степень с целым показателем. Понятие процента, нахождение процента от числа, числа по его проценту, процентного отношения. Задачи на проценты. Делимость чисел, признаки делимости. Ход урока Запланированные этапы урока Запланированная деятельность на уроке Ресурсы Начало урока 5 минут — концентрация внимания учащихся -проверка домашней работы — определение «зону ближайшего и дальнего развития» учащихся, ожидания к концу урока Середина урока 15 минут 15 минут Активити Вы уже знаете, свойства арифметической прогрессии. Сегодня мы будем обобщать ваши знания. Для начала давайте вспомним их с помощью следующего активити. Найдя правильно сумму членов арифметической прогрессии и сопоставив с подходящим ответом, вы узнаете кто впервые доказал формулу суммы первых n членов арифметической прогрессии. Тип работы: Индивидуальный. Первый решивший на доске показывает решение Оценивание: учителем и одноклассниками устно Групповая работа на применение арифметической прогрессии. Группы создаются таким образом, чтобы в каждой были ученики разных уровней, для того, чтобы каждый член команды работал, так как задания подбираются от легкого до сложного. Если учеников в классе очень много, можно дублировать задания для групп. (Например, задачи про альпинистов решают 1,3,5 группа) Группа №1. Задачи про альпинистов. Группа №2 Задачи про копателей колодцев Группа №3 Задачи про свободное падение Тип работы: Групповой. Ребята делятся между собой задачи. Решение показывают друг другу и принимают решение о правильности решении задачи Оценивание: учителем и одноклассниками Дескрипторы для каждой группы (при необходимости в зависимости от уровня группы можно раздать дескипторы ученикам): Задача №1. Находит или показывает первый член арифметической прогрессии Находит или показывает разность арифметической прогрессии Находит или показывает номер искомого члена арифметической прогрессии Применяет формулу n-го члена арифметической прогрессии при решении задач Находит n-ый член арифметической прогрессии Задача №2 Использует данные из первого пункта (первый и последний член, разность, номер последнего члена) Подставляет под формулу суммы n первых члена арифметической прогрессии Находит сумму n первых членов арифметической прогрессии или из суммы находит номер последнего члена Задача №3 Использует данные из первого пункта (первый член, разность, номер искомого члена) Применяет свойство об арифметической средней Находит искомый член прогрессии Если останется время, предложите ученикам задачи из сайта https://www. math20.com/ru/zadachi/zadachi-na-arifmeticheskie-progressii/easy/ Преимущества: показывает решение при необходимости, делает проверку, выдает количество правильных ответов, внизу страницы можно выбрать уровень заданий (легкий, средний, сложный). Если есть проблемы с доступом в интернет для каждого ученика, можно использовать ИД, а задачи распределить между учениками в зависимости от их способностей и их проблем Приложение 1,2,3 Конец урока 5 минут В конце урока учащиеся проводят рефлексию: — что узнал, чему научился — что осталось непонятным — над чем необходимо работать Где возможно учащиеся могут оценить свою работу и работу своих одноклассников по определенным критериям Домашняя работа: Выяснить, как и где применяется арифметическая прогрессия, привести пример Дифференциация – каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися? Оценивание – как Вы планируете проверить уровень усвоения материала учащимися? Здоровье и соблюдение техники безопасности Работа в группах предполагает дифференциацию по типу — сильный поддерживает слабого. Индивидуальная работа на уровневые задачи. Дифференцированные группы Оценивание при помощи ИКТ, Взаимооценивание во время групповой работы. оценивание по дескрипторам — во время индивидуальной и групповой работы. Здоровьесберегающие технологии. Рефлексия по уроку Были ли цели урока/цели обучения реалистичными? Все ли учащиеся достигли ЦО? Если нет, то почему? Правильно ли проведена дифференциация на уроке? Выдержаны ли были временные этапы урока? Какие отступления были от плана урока и почему? Используйте данный раздел для размышлений об уроке. Ответьте на самые важные вопросы о Вашем уроке из левой колонки. Общая оценка Какие два аспекта урока прошли хорошо (подумайте как о преподавании, так и об обучении)? 1: 2: Что могло бы способствовать улучшению урока (подумайте как о преподавании, так и об обучении)? 1: 2: Что я выявил(а) за время урока о классе или достижениях/трудностях отдельных учеников, на что необходимо обратить внимание на последующих уроках?

Свойства арифметической прогрессии с важной формулой, часто задаваемые вопросы

Тема, которую мы собираемся начать сегодня, относится к категории алгебры. Алгебра — одна из очень широких областей математики, которая занимается изучением переменных. Точно так же, как арифметические формулы и выражения используются с постоянными числами, где два или более постоянных числа могут быть сложены, вычтены, умножены и т. д., мы можем выполнять аналогичные операции и с переменными. Алгебра — это в основном изучение математических символов и способов манипулирования ими с помощью определенных арифметических операций.

Что такое арифметическая прогрессия?

Рассмотрим последовательно все четные натуральные числа. Итак, если мы внимательно посмотрим на те числа, которые расположены последовательно, мы поймем, что между ними есть общее различие. Натуральные числа — это те числа, которые используются для подсчета и упорядочивания. В общепринятой математической терминологии слова, используемые в разговорной речи для подсчета, называются «количественными числами», а слова, используемые для упорядочивания, — «порядковые числа». Любое число в последовательности, вычтенное из следующего числа в последовательности, дает общую разность 2. Тот же случай происходит, когда мы рассматриваем нечетные натуральные числа, расположенные одно за другим последовательно.

Это то, что мы называем арифметической прогрессией. Арифметическая прогрессия — это последовательность чисел, в которой различия между двумя последовательными членами последовательности остаются одинаковыми.

Эта разность известна как общая разность этой конкретной арифметической прогрессии.

Арифметические прогрессии могут быть как возрастающими, так и убывающими. Возрастающая последовательность чисел, имеющая одинаковую общую разность, называется возрастающей арифметической прогрессией, а убывающая последовательность чисел, имеющая одну и ту же общую разность, называется убывающей арифметической прогрессией.

У нас также есть третий тип арифметической прогрессии, в котором все числа в последовательности имеют одинаковое значение. Это называется постоянной арифметической прогрессией, имеющей общую разность 0.

Следует отметить следующие важные моменты в отношении общей разности арифметической прогрессии.

• Возрастающая арифметическая прогрессия всегда будет иметь положительную общую разность.
• Убывающая арифметическая прогрессия всегда будет иметь отрицательную общую разность.
• Постоянная арифметическая прогрессия всегда будет иметь нулевую общую разность.
• Арифметическая прогрессия, имеющая мнимую общую разность, называется мнимой арифметической прогрессией.

Общая разность арифметической прогрессии обозначается d.

Давайте теперь поговорим о различных свойствах арифметической прогрессии.

Свойства арифметической прогрессии

Перед изучением некоторых очень важных свойств арифметической прогрессии, давайте узнаем о нескольких важных терминах, связанных с арифметической прогрессией

• Член арифметической прогрессии

Любой член арифметической прогрессии обозначается \(T_n\) или \(t_n\).

• Общая разность арифметической прогрессии

Мы уже читали о термине общая разность арифметической прогрессии. \(d=t_n-t_{n-1}\)

• Сумма арифметической прогрессии до n членов.

Это в основном сумма AP до n количества терминов. У нас есть формула и для этого. Мы придем к формуле на более позднем этапе.

Примечание: Арифметическая прогрессия может быть конечной последовательностью чисел или бесконечной последовательностью чисел.

Конечная последовательность: \({\{t_1,t_2,t_3…..,t_n\}}\)

Бесконечная последовательность: \({\{t_1,t_2,t_3….\}}\)

Алгоритм определения того, является ли последовательность арифметической прогрессией или нет.

Мы покажем алгоритм в несколько шагов. Итак, посмотрите на шаги ниже, чтобы понять это.

1. Сначала найдите n-й член последовательности, то есть \({t_n}\), через n.
2. Замените член n везде в формуле \({t_n}\), чтобы получить формулу или выражение \({t_{n-1}}\).
3. Вычтите выражение \({t_{n-1}}\) из выражения \({t_n}\).
4. После вычитания посмотрите на полученное выражение. Если это выражение является постоянным числом или чем-либо, не зависящим от члена n, последовательность является арифметической прогрессией.

Несколько примеров

Que: Найдите общую разность последовательности 1, 3, 5, 7…..

Ответ: Чтобы найти общее различие, нам нужно вычесть любой член из следующего за ним или справа от него.

Выберем 5 и 7

\({7-5=2}\)

Таким образом, общая разность равна \({d=2}\).

Que: Найдите общую разность последовательности a, a-b, a-2b…..

Ответ: Нам нужен тот же подход, что и в предыдущем вопросе, чтобы решить этот. Возьмем любой из двух последовательных терминов. Произнесите а-б и а-2б.

\({(a-b)-(a-2b)=-b}\)

Таким образом, общая разность отрицательна, если b — положительное число, и положительна, если b — отрицательное число. Таким образом, если b — положительное число, то арифметическая прогрессия — убывающая, а если b — отрицательное число, то возрастающая.

Que: Покажите, что последовательность, определяемая выражением \({t_n=5n+4}\)= 5n+4, является арифметической прогрессией. Кроме того, узнайте общую разницу.

Ответ: Дано: \({t_n=5n+4}\)

Таким образом, теперь мы будем следовать алгоритму, который мы упоминали выше, чтобы решить эту сумму.

Для этого нам нужно заменить \({n}\) в \({t_n}\) на \({n-1}\).

Таким образом, проделав то же самое, мы находим, что \({t_{n-1}=5n-1}\).

Таким образом, \({(5n+4)-(5n-1)=5}\).

Это означает, что общая разность этой арифметической прогрессии равна 5, и, следовательно, это возрастающая арифметическая прогрессия.

Теперь, когда мы знаем основы арифметической прогрессии и ее точное значение, давайте теперь узнаем о ней немного больше. Это свойства арифметической прогрессии.

Надеюсь, вам понравилась эта часть. Если вы хотите узнать больше об основах арифметической прогрессии или чувствуете, что у вас могут быть некоторые сомнения относительно этого,

Нажмите на эту ссылку, чтобы получить больше информации об этом.

Свойства арифметической прогрессии

В этом разделе мы углубимся в некоторые из более сложных тем, связанных с арифметической прогрессией, а также решим несколько примеров.

Общий член арифметической прогрессии

Пусть a — первый член арифметической прогрессии, d — его общая разность, а l — последний член арифметической прогрессии, имеющей в общей сложности n членов.

Таким образом, мы можем записать эту арифметическую прогрессию следующим образом:

\({a, a+d, a+2d,……., l-2d, l-d, l}\).

Определение n-го члена АП с начала

1-го члена с начала: \(t_1=a=a+(1-1)d\)

2-го члена с начала: \( {t_2=a+d=a+(2-1)d}\)

3-й член с начала: \({t_3=a+2d=a+(3-1)d}\)

.

.

.

n-й член с начала: \({t_n=a+(n-1)d}\)

Таким образом, n-й член от начала AP равен \({t_n=a+(n-1)d}\ ).

Определение конечного срока АП с конца.

Первый член с конца: \({l=l-(1-1)d}\).

Второй член с конца: \({l-d=l-(2-1)d}\).

.

.

.

n-й член с конца: \({l-(n-1)d}\).

Итак, n-й член с конца равен \({l-(n-1)d}\).

Теперь очень важное замечание:

Если первый член ряда равен a, а последний член ряда равен l, то сумма любых двух членов, равноудаленных от начала и конца, равна \ ({а+1}\).

В значительной степени ясно, что приведенное выше предложение справедливо только для конечной арифметической прогрессии, так как для бесконечной арифметической прогрессии нет четкого последнего члена.

Некоторые важные моменты, на которые следует обратить внимание

• Если вы видите, что в последовательности есть члены, которые попеременно являются положительными и отрицательными, то из данной последовательности должно быть ясно, что она никогда не может быть арифметической прогрессией.
• Чтобы данную последовательность можно было назвать арифметической прогрессией, выражение для n-го члена последовательности должно быть линейным полиномом. Если выражение n-го члена данной последовательности не является линейным полиномом и имеет степень больше 1, то его никогда нельзя назвать арифметической прогрессией.
• Член n также можно назвать общим членом арифметической прогрессии.
• Если у нас есть три последовательных члена арифметической прогрессии, скажем, \({t_{n-2},t_{n-1},t_n}\), то сумма первого члена и последнего члена среди членов данный всегда будет равен удвоенному среднему термину, указанному здесь.

В математическом выражении это можно записать следующим образом:

\({t_{n-2}+t_n=2t_{n-1}}\)

Также обратите внимание на следующее: Среднее значение любых двух членов которые равноудалены от двух концов данной арифметической прогрессии, всегда будут равны среднему члену данной арифметической прогрессии, если арифметическая прогрессия имеет нечетное число членов, и будут равны среднему значению двух средних членов арифметической прогрессии прогрессию, если данная арифметическая прогрессия имеет четное число членов.

• Если первый член арифметической прогрессии равен a, а последний член арифметической прогрессии равен l, то формула общей разности данной арифметической прогрессии будет \({d={{l-a}\over{n +1}}}\), где n — количество членов арифметической прогрессии.

Некоторые члены арифметической прогрессии

Пусть имеется арифметическая прогрессия, имеющая «а» в качестве первого члена, «l» в качестве последнего члена, «d» в качестве общей разности и сумму всех члены арифметической прогрессии до n-го члена обозначаются \({S_n}\).

Таким образом, значение \({S_n}\) будет следующим:

\({S_n={n\over2}(a+l)}\)

Теперь подставим значение l в данное уравнение

Мы знаем, что \({l={a+(n-1)d}}\)

Подставляя это в приведенное выше уравнение, мы получаем:

\({S_n={n\over2}(a+( n-1)d)}\)

Это общая формула суммы всех членов арифметической прогрессии от первого до n-го члена.

Примечание. Вы можете получить n-й член арифметической прогрессии, если вычесть сумму n членов арифметической прогрессии из суммы n-1 членов той же арифметической прогрессии. 92+bn}\) Где a и b — константы, не зависящие от n.

Если сумма n членов арифметической прогрессии обозначается \({S_n}\) и общая разность равна d, то \({d=S_n-2S_{n-1}+S_{n-2} }\)

Несколько важных советов по решению сумм, связанных со свойствами арифметической прогрессии

• Когда вас просят найти три последовательных члена арифметической прогрессии, сумма которой указана, и вам нужно выполнить некоторые другие операции, всегда возьмите термины как \({a-d,a,a+d}\).
• Когда вас попросят взять четыре последовательных члена арифметической прогрессии, сумма которой задана, и вам нужно выполнить некоторые другие операции, возьмите члены как \({a-3d,a-d,a+d,a+3d }\), где общая разница будет равна 2d.

Теперь, когда мы знаем обо всех важных свойствах арифметической прогрессии, мы сможем решить все суммы, связанные с AP.

Чтобы решить некоторые суммы, относящиеся к арифметической прогрессии, нажмите здесь.

Не хотите прекращать учиться? Хотите узнать все о геометрической прогрессии? Что ж, у нас есть кое-что для вас. Нажмите здесь, чтобы узнать о геометрических прогрессиях.

Улучшите свою подготовку к математике, зарегистрировавшись сегодня в тестовой тетради. Торопиться!!

У нас также есть приложение, в котором вы можете получить много замечательных преимуществ. Загрузите приложение testbook сегодня и начните учиться даже на своем телефоне.

Свойства арифметической прогрессии – часто задаваемые вопросы

В.1 Что такое арифметическая прогрессия?

Ответ 1 Арифметическая прогрессия — это последовательность чисел (в основном целых чисел), в которой различия между двумя последовательными элементами последовательности остаются одинаковыми.

Q.2 Как выражается n-й член арифметической прогрессии?

Ответ 2 N-й член от начала AP равен \({t_n=a+(n-1)d}\).

Q.3 Как выражается сумма n членов арифметической прогрессии?

Ответ 3 \({S_n={n\over2}(a+(n-1)d)}\). Это общая формула суммы всех членов арифметической прогрессии от первого до n-го члена.

Q.4 Какова формула обыкновенной разности арифметической прогрессии?

Ответ 4 Если первый член арифметической прогрессии равен a, а последний член арифметической прогрессии равен l, то формула общей разности данной арифметической прогрессии будет \({d={ {l-a}\over{n+1}}}\), где n — количество членов арифметической прогрессии.

Q.5 Что такое постоянная арифметическая прогрессия?

Ответ 5 У нас также есть третий тип арифметической прогрессии, в котором все числа в последовательности имеют одинаковое значение. Это называется постоянной арифметической прогрессией, имеющей общую разность 0.

Скачать публикацию в формате PDF

Подробнее с testbook.com

33333333333333330 гг. (AP, GP, HP) — GeeksforGeeks

Прогрессии (или последовательности и серии) — это числа, расположенные в определенном порядке, так что они образуют предсказуемый порядок. Под предсказуемым порядком мы подразумеваем, что по некоторым числам мы можем найти следующие числа в ряду.

Арифметическая прогрессия (AP)

Последовательность чисел называется арифметической прогрессией, если разница между любыми двумя последовательными членами всегда одинакова. Проще говоря, это означает, что следующее число в ряду вычисляется путем прибавления фиксированного числа к предыдущему числу в ряду. Это фиксированное число называется общей разностью.
Например, 2,4,6,8,10 является AP, потому что разница между любыми двумя последовательными членами ряда (общая разница) одинакова (4 – 2 = 6 – 4 = 8 – 6 = 10 – 8 = 2 ).

Если «a» — первый член, а «d» — общая разность,
• n-й член AP = a + (n-1) d
• Среднее арифметическое = сумма всех членов в AP / количество терминов в AP
• Сумма n членов AP = 0,5 n (первый член + последний член) = 0,5 n [ 2a + (n-1) d ]

Геометрическая прогрессия (ГП)

Последовательность число называется геометрической прогрессией, если отношение любых двух последовательных членов всегда одинаково. Проще говоря, это означает, что следующее число в ряду вычисляется путем умножения фиксированного числа на предыдущее число в ряду. Это фиксированное число называется обыкновенным отношением.
Например, 2,4,8,16 является GP, потому что отношение любых двух последовательных членов ряда (общая разность) одинаково (4/2 = 8/4 = 16/8 = 2).

Если «a» — первый член, а «r» — знаменатель,
• n-й член GP = a r ^n-1
• Среднее геометрическое = n-й корень произведения n членов GP
• Сумма из n членов ЗП (r < 1) = [a (1 – r ⁿ )] / [1 – r]
• Сумма n членов ЗП (r > 1) = [a (р ^н – 1)] / [р – 1]
• Сумма бесконечных членов ГП (r < 1) = (a) / (1 – r)

Гармоническая прогрессия (ГП)

Последовательность чисел называется гармонической прогрессией, если обратные члены равны в АП. Проще говоря, a,b,c,d,e,f находятся в HP, если 1/a, 1/b, 1/c, 1/d, 1/e, 1/f находятся в AP.

Для двух членов ‘a’ и ‘b’,
• Среднее гармоническое = (2 a b) / (a ​​+ b)

Для двух чисел, если A, G и H являются соответственно средними арифметическими, геометрическими и гармоническими, затем

• A ≥ G ≥ H
• A H = G ² , т. е. A, G, H входят в GP

Примеры задач

Вопрос 1 : AP n-й член для , 23, 29, …
Решение : Здесь a = 11, d = 17 – 11 = 23 – 17 = 29 – 23 = 6
Мы знаем, что n-й член АП равен a + (n – 1) d
=> n-й член для данной AP = 11 + (n – 1) 6
=> n-й член для данной AP = 5 + 6 n
Мы можем проверить ответ, подставив значения ‘n’.
=> n = 1 -> Первый член = 5 + 6 = 11
=> n = 2 -> Второй член = 5 + 12 = 17
=> n = 3 -> Третий член = 5 + 18 = 23
и и так далее …
 
Вопрос 2 : Найдите сумму AP в приведенном выше вопросе до первых 10 членов.
Решение: Из приведенного выше вопроса
=> n-й член для данного AP = 5 + 6 n
=> Первый член = 5 + 6 = 11
=> Десятый член = 5 + 60 = 65
=> Сумма из 10 членов АП = 0,5 n (первый член + последний член) = 0,5 х 10 (11 + 65)
=> Сумма 10 членов AP = 5 x 76 = 380
 
Вопрос 3 : Для элементов 4 и 6 проверьте, что A ≥ G ≥ H.
Решение: A = среднее арифметическое = (4 + 6) / 2 = 5
G = Среднее геометрическое = = 4,8989
H = Среднее гармоническое = (2 x 4 x 6) / (4 + 6) = 48 / 10 = 4,8
Следовательно, A ≥ G ≥ H
 
Вопрос 4 : Найдите сумму ряда 32, 16, 8, 4, … до бесконечности.
Решение: Первое слагаемое, a = 32
Обычное отношение, r = 16 / 32 = 8 / 16 = 4 / 8 = 1 / 2 = 0,5
Мы знаем, что для бесконечной ВП Сумма членов = a / (1 – r)
=> Сумма членов ВП = 32 / (1 – 0,5) = 32 / 0,5 = 64
 
Вопрос 5 : Сумма трех чисел в GP равна 26, а их произведение равно 216. Найдите числа.
Решение: Пусть числа будут a/r, a, ar.
=> (a / r) + a + a r = 26
=> a (1 + r + r ² ) / r = 26
Также дано, что произведение = 216
=> (a / r) х (а) х (ар) = 216
=> а ³ = 216
=> a = 6
=> 6 (1 + r + r ² ) / r = 26
=> (1 + r + r ² ) / r = 26 / 6 = 13 / 3
=> 3 + 3 r + 3 r ² = 13 r
=> 3 r ² – 10 r + 3 = 0
=> (r – 3) (r – (1 / 3) ) = 0
=> r = 3 или r = 1 / 3
Таким образом, нужные числа 2, 6 и 18.

Задачи на прогрессии (AP,GP, HP) | Set-2

Эта статья была подготовлена ​​пользователем Nishant Arora

Пожалуйста, напишите комментарии, если у вас есть какие-либо сомнения, связанные с темой, обсуждаемой выше, или если вы столкнулись с трудностями в каком-либо вопросе, или если вы хотели бы обсудить вопрос, отличный от упомянутых выше.
 
Пожалуйста, напишите комментарии, если вы обнаружите что-то неправильное, или вы хотите поделиться дополнительной информацией по теме, обсуждаемой выше

Арифметические свойства — коммутативные, ассоциативные, дистрибутивные

Умножение и сложение имеют особые  арифметические свойства  , которые характеризуют эти операции. В произвольном порядке это коммутативные, ассоциативные, дистрибутивные, тождественные и обратные свойства.

Коммутативное свойство

Операция является коммутативной, если изменение порядка операндов не меняет результат.

Коммутативное свойство сложения означает, что порядок добавления чисел не имеет значения. Это означает, что если вы сложите 2 + 1, чтобы получить 3, вы также можете добавить 1 + 2, чтобы получить 3.

Другими словами, расположение слагаемых можно изменить, и результаты будут одинаковыми. Точно так же коммутативное свойство умножения означает, что места множителей можно менять, не влияя на результат.

Ассоциативное свойство

В выражении, содержащем два или более вхождений только сложения или только умножения, порядок выполнения операций не имеет значения, пока последовательность операндов не изменяется. Это называется ассоциативным свойством .

То есть перестановка скобок в таком выражении не изменит его значения.

Например, сгруппируйте и добавьте:

$\ 1 + 5 + 9 + 5 = ?$

Чтобы упростить это, используйте свойство коммутативности, чтобы изменить порядок, а затем используйте свойство ассоциативности, чтобы сгруппировать $1$ и $9$, $5$ и $5$, поскольку эти обе пары дают в сумме 10$, поэтому окончательный результат равен 20$.

Распределительное свойство

Распределительное свойство объединяет сложение и умножение. Если число умножает сумму в скобках, скобки можно убрать, если мы умножим каждый член в скобках на одно и то же число.

Количество членов в скобках не имеет значения, оно всегда будет действительным.
Это свойство обычно применяется, когда неизвестное входит в состав сложения, и позволяет выделить неизвестные.

Элемент идентификации

Элемент идентификации или нейтральный элемент представляет собой элемент, который оставляет другие элементы неизменными при объединении с ними. Идентификационный элемент для сложения равен 0, а для умножения равен 1.

Обратный элемент

Мультипликативное обратное или обратное число $x$, обозначаемое $\frac{1}{x}$, — это число, которое при умножении на $x$ дает мультипликативное тождество, 1. Мультипликативное обратная дробь $\frac{x}{y}$ равна  $\frac{y}{x}$

Аддитивная обратная числа $x$ – это число, которое при прибавлении к $x$ дает нуль. Это число также известно как , противоположное (число), изменение знака и отрицание. Для действительного числа оно меняет знак: противоположное положительному числу отрицательное, а противоположное отрицательному числу положительное. Ноль является аддитивной инверсией самого себя.

Например, обратное число 5 равно $\frac{1}{5}$, а число, противоположное числу 5, равно -5.

В чем разница между коммутативным и ассоциативным свойством?

Когда вы думаете о сложении или умножении, важно знать некоторые свойства или законы. В математике это вещи, которые остаются неизменными.

Переместительное свойство против ассоциативного свойства

Переместительное свойство или закон перестановочности означает, что вы можете изменить порядок сложения или умножения чисел и получить тот же результат.

Например, в переместительном свойстве сложения, если у вас есть 2 + 4, вы можете изменить его на 4 + 2, и вы получите тот же ответ (6).

То же самое с коммутативным свойством умножения. Если у вас есть 2 х 4, вы можете изменить его на 4 х 2 и получить тот же результат (8).

Отличие от ассоциативного свойства или ассоциативного закона заключается в том, что оно включает более двух чисел. Неважно, как вы группируете числа или что вы складываете или умножаете в первую очередь. Важно то, что это только сложение или только умножение.

Вы можете изменить порядок сложения или умножения чисел и получить тот же результат.

Ассоциативность сложения означает, что вы можете складывать числа в любом порядке. Пример: 2 + 3 + 1 + 5 + 6 = 17. Это верно, если вы прибавляете 2 к 3 к 1 к 5 к 6 или если вы складываете 2 и 3 вместе, чтобы получить 5, а затем складываете 1, 5 и 6 вместе. чтобы получить 12, и 5 и 12 вместе, чтобы получить 17.

Ассоциативное свойство для умножения то же самое. Если у вас есть три или более чисел, вы можете умножать их в любом порядке, чтобы получить тот же результат.

Например, в задаче: 2 x 3 x 5 x 6 вы можете умножить 2 x 3, чтобы получить 6, затем 5 x 6, чтобы получить 30, а затем умножить 6 x 30, чтобы получить 180. Вы можете умножать числа В любом порядке и получит 180.

Арифметические свойства.

(199,4 КиБ, 1225 обращений)

   Распределяемое свойство (311,9 КиБ, 1398 совпадений)

Арифметическая прогрессия — вывод, применение и вопросы

В математике арифметическая прогрессия (AP) или арифметическая последовательность — это последовательность чисел, в которой разница между последовательными элементами является постоянной и известна как общая разность . Например, последовательность 2, 4, 6, 8, … является арифметической последовательностью с общей разностью 2.

Мы можем найти общую разность AP, найдя разницу между любыми двумя соседними терминами.

История

Факты показывают, что вавилоняне , некоторые 4000 лет назад знали арифметические и геометрические последовательности. Согласно Боэцию , арифметические и геометрические последовательности были известны ранним греческим писателям.

Среди индийских математиков Арьябхатта первым дал формулу суммы квадратов и кубов натуральных чисел в своей знаменитой работе ‘9{й}\) срок.

Отмечено: Индийские математики Брахмгупта , Махавира и Бхаскара также считаются дающими сумму квадратов и кубов.

Члены арифметической прогрессии

Последовательность \(a, a_1, a_2, a_3, …, a_n\) называется арифметической последовательностью или арифметической прогрессией.

Где
\(a\) — первый член.
\(a_1\) является вторым членом и может быть задан как \(a_1 = a + d\),
{th}\) член
n число членов
a первый член
d общая разность

(или) разделить (на ненулевую константу ) на каждый член А.П., результирующая последовательность также является А.П. здесь a, b и c равны 1-й, 2-й и 3-й срок соответственно.

Если это верно, то мы можем сказать, что эти три термина находятся в A.P. члены 1, 4, 7 находятся в A.P.

Сумма арифметической прогрессии

Сумма членов конечной арифметической прогрессии называется арифметическим рядом .

Производная

\(
S_n = a + (a + d) + (a + 2d) + … + (a + (n-2)d) + (a + (n-1)d) …(i)\\
S_n = (a + (n-1)d) + (a + (n-2)d) + … + (a + 2d) + (a + d) + a …(ii)\\
\mbox{добавление ( i) & (ii)}\\
\mbox{Все термины, включающие ‘d’, исключают уход}\\
2S_n = n(a + a_n)\\
S_n = \frac{n}{2}(a + a_n)\\
\mbox{потому что } a_n = a + (n-1)d\\
S_n = \frac{n}{2}(2a + (n-1)d)\\
\)

Приложения арифметической прогрессии

Последовательности полезны в нескольких математических дисциплинах для изучения функций , пространств и других математических структур с использованием свойств сходимости последовательностей . В частности, последовательности являются основой для рядов, которые важны в дифференциальных уравнениях и анализе .

Вопросы

Давайте рассмотрим некоторые вопросов арифметической прогрессии :

Вопрос 1. 9{й}\) член равен –112.

Раствор.

Первый член, a = 2

Сумма первых 5 членов, S_5 = -112

Следовательно, \(10 + 10d = \frac{1}{4}(10 + 35d)\)

=> 40 + 40d = 10 + 35d

=> d = -6

Следовательно, \(a_{20} = 2 + (20 – 1)(-6) = (-112)\)

Следовательно, 20-е число срок -112.

Подробнее о прогрессии: гармонические прогрессии

Часто задаваемые вопросы

По какой формуле вычисляется «D»? 92 = \ гидроразрыва {n (n + 1) (2n + 1)} {6} \)

Введение в арифметическую прогрессию

В соответствии с последней версией 10 класса CBSE Учебный план по математике , Глава 5 Арифметическая прогрессия является частью Блока 2 Алгебры. Модуль 2 имеет вес 20 баллов на экзаменах CBSE Class 10 Maths Board Exams.

Прямая кишка Latus: определение, уравнение, важные свойства, с подробными изображениями
Иррациональные числа: изучите определения, списки символов, свойства на примерах!
Типы, реакции, структура, формула и свойства ароматических соединений
Постулаты, важность, ограничения валентной теории связей
Группа 1 Элементы: периодические, физические свойства и химические гости

Содержание Что такое арифметическая прогрессия? Свойства арифметической прогрессии Notation in Arithmetic Progression (A.P) Sum of n Terms of an Arithmetic Progression Arithmetic Mean Sample Questions

Read Also: Difference Between Sequence и серия

---

Что такое арифметическая прогрессия?

[Нажмите здесь, чтобы просмотреть примеры вопросов]

Арифметическая прогрессия (AP) — это арифметическая прогрессия, последовательность рядов или чисел с общей разницей между двумя последовательными числами в последовательности. Последовательность устроена в чрезвычайно особом порядке, так что отношение между двумя последовательными членами ряда или последовательности обычно постоянно.

Прогресс встречается в нашей обычной жизни точно так же, как количество учеников в классе, количество дней в неделе или месяцев в году. Прогрессия может быть формой последовательности, из которой можно получить формулу для n-го члена. Прогрессия или AP может быть последовательностью, в которой каждый новый термин после основного получается путем добавления продолжающегося различия, называемого общим различием.

На простом языке прогрессия может быть набором целых чисел внутри каждого термина, который является результатом добавления константы к предыдущему термину помимо основного термина.

Например, 2,4,6,8,10,12

5,10,15,20,25,30,35,40

Арифметическая прогрессия: Объяснение

Ниже перечислены три стиля прогрессии. :

• Арифметическая прогрессия (АП)
• Геометрическая прогрессия (ГП)
• Гармоническая прогрессия (ГП)

Арифметическая прогрессия

Арифметическая прогрессия может быть образцом последовательности двух членов ряда, который имеет типичную связь между двумя членами ряда . Это последовательность чисел, в которой каждый член последовательности отличается от последующего члена на постоянную величину.

Читайте также:

---

Свойства арифметической прогрессии

[Щелкните здесь, чтобы просмотреть примеры вопросов]

1. Если неумолимо, то добавляется к каждому числу АР, результирующая последовательность дополнительно является АР
9096 AP является продолжением результирующей последовательности, дополнительно являющейся AP.
2. Если каждый член АП разделить на ненулевую константу, то полученная последовательность дополнительно является АП.
3. Если из каждого члена AP вычесть константу, результирующая последовательность будет дополнительно AP.

Подробнее.

n= общее количество членов

an= n-й член (где n=1,2,3,…,n)

Sn=сумма первых n членов

Общий член арифметической прогрессии

Любая последовательность a1 a2 a3…. и называется прогрессией, если an + 1=an+d, n€N

Предположим, что основным термином AP может быть общая разница d

т. е. a, a+d, a+2d, a+3d……

1-й член = a = a+(1-1) d

2-й член = а+d = а+(2-1) d

3-й член = а+2d = а+(3-1) d.

.

.

.

N-й член = an a+(n-1) d

Читайте также:

---

Сумма n членов арифметической прогрессии

[Нажмите здесь, чтобы просмотреть примеры вопросов]

Сумма n элементов AP представляет собой сложение первых n элементов автоматизированной последовательности. Простыми словами, сумма до n делится на двойную сумму удвоенного основного члена «а», а также произведение разности между 2-м и, следовательно, первым общим различием

Сумма n членов в AP	n/2[2a+(n-1)d]
Сумма квадратов n натуральных чисел	[n(n+1)(2n+1)]/6
Sum of Cube of a natural numbers	[n(n+1)/2]2
Sum of natural numbers	n(n+1)/2

Пример:- Найдите сложение первых 22 членов АР: 8, 4, -2, . …..

Ответ: a=8, d=4-8=-4, n =22

Мы знаем, что S= n/2[2a+(n-1)d]

Следовательно, S= 22/2[16+21(-4)]

= 11(16-84)

= 11(-68)

= -748.

Также проверьте:

---

Среднее арифметическое

[Нажмите здесь, чтобы просмотреть примеры вопросов]

Если a,b,c находятся в A.P, тогда b=(a+c)/2, а b называется средним арифметическим.

Важные моменты

1. Общая форма AP: a, a+d, a+2d,…..
2. Если a, b, c находятся в AP, то b-a=c-b или 2b=a+ c и b называется средним арифметическим значений a и c
3. Если в AP 3 члена, то предполагают a-d, a, a+d
4. Если в AP 4 термина, то считать a-3d, a-d, a+d, a+3d.

Также проверьте больше:

---

Примеры вопросов

Вопросы: При каком значении K будут K+9, 2k-1 и 2k+7 последовательными членами AP?

Ответ = (2k-1) — (k+9) = (2k+7) — (2k-1)

= k-10=8

= k= 8

Итак, значение K будет равно 8.

Вопросы: Найдите «d» АП, в котором a21-a7=84? (2017)

Ans = a+(21-1)d — [a+(7-1)d] =84 [формула: tn=a+(n-1)d]

= (a+20d) — (a +6d) =84

= 14d=84

= d= 84/14 = 6

Итак, общая разность АП равна 6.

Вопросы: Найдите общую разность АП, первая член равен 4, последний член равен 49, а сумма всех его членов равна 265. 

Ответ:

 a=4, l=49, S=265

Мы знаем, что Sn=n/2 (а+л)

Следовательно, 265=n/2(4+49)

265=n/2(53)

n/2=265/53

n/2=5

n=10 общее количество членов равно 10. 

Мы знаем, что l=a+(n-1)d

Следовательно, 49=4+(10-1)d

45=9d

d=45/9

d= 5

Таким образом, общая разность равна 5.

Вопросы: Сложение четырех последовательных чисел в AP равно 32, а доля кратного первого и последнего членов кратна двум средним сроки 7:15. Найдите числа.

Ответ: Предположим, четыре последовательных числа равны a-3d, a-d, a+d, a+3d. 8

Кроме того,

(a-3d)(a+2d)/(a-d)(a+d)= a2-9d2/a2-d2=7/15

15a2-135d2=7a2-7d2

8a2 =128d2

d2=8/2

d2=4

d= ±2

Теперь найдем четыре последовательных числа ,

a-3d=8-3(2)= 2

a-d=8-2= 6

a+d=8+2= 10

a+3d=8+3(2)= 14

Итак, четыре последовательных числа равны 2, 6, 10 и 14.

Вопрос: Найдите сумму всех множителей 7, лежащих между 500 и 900.

Ответ = Наш первый член будет 504, а последний член будет 896.

Мы знаем, что l=a+( n-1)d

Следовательно, 896=504+(n-1)7

392=(n-1)7

n-1=392/7=56

n=57

Мы знаем, что Sn=n/2(a+l)

Следовательно, Sn=57/2(504+896)

= 57/2×1400

= 39900

Ques If: отношение сложения первых n членов двух АП равно (7n+1):(4n+27), затем найдите долю их 9-го члена.

Ответ: Предположим, что первый член (7n+1)= a1 и общая разность = d1

Предположим, что первый член (4n+27)= a2 и общая разность = d2

Итак, наше отношение равно 24:19.

Вопрос: Сумма первых n членов АП равна Sn=3n2+2n. Определите АР и его 15-й член.

Ответ: мы знаем, что Sn= 3n2+2n

Сначала найдем S1, S2 и a2,

S1=a1=3(1)2+2(1)

=5

S2=3(2)2+2(2)

=12+4

=16

a2=S2-S1=16-5=11

Итак, d=a2-a1=11-5= 6

Теперь узнаем AP,

AP= a, a+d, a+2d,…….= 5, 11, 17,…..

А теперь мы увидим 15-й член,

a15=a+14d

=5+14(6)

=5+84= 89

Итак, общая разность равна 6, а ее 15-й член равен 89.

Вопрос: Оператор телевизоров произвел 600 телевизоров в 3-й год и 700 телевизоров в 7-й год. Предполагая, что производство постоянно увеличивается на фиксированную величину каждый год, найдите производство в 1-й год, 10-й год и общее производство в первые 7 лет.

Ответ: Так как производство постоянно увеличивается на фиксированное число каждый год, нет. телевизоров, эксплуатируемых в 1-м, 2-м, 3-м,….. годах, составят АП.

Обозначим через an число эксплуатируемых телевизоров в n-м году.

Тогда a3= 600 и a7= 700

или, a+2d=600

И a+6d=700

Решая эти уравнения, мы получаем d=25 и a=550.

Следовательно, производство телевизоров в 1-м году равно 550.

Теперь a10=a+9d

=550+9×25

= 775

Итак, производство телевизоров в год равно 775.

Кроме того, s7=7/2[2×550+(7-1)×25]

=7/2 (1100+150)

= 4375

Таким образом, общий объем производства телевизоров за первые 7 лет составляет 4375.

Вопрос. арифметический ряд. Когда 30 платежей выплачены, он умирает, оставляя одну треть невыплаченной ссуды. Найдите стоимость первого взноса.

Ответ: Человеку удается погасить кредит в размере 3600 рупий 40 ежегодными платежами, которые образуют A. P., т. е. сумма всех 40 платежей = 3600

S40 = 3600

Мы знаем, что Sn = n /2 [2a+(n-1)d]

40/x[2a+(40-1)d]=3600

2a+39d=3600/20=180….. (i)

Умер, уйдя не погашена треть кредита. Это означает, что он заплатил оставшиеся деньги 30 частями.

Следовательно, деньги, которые он заплатил 30 частями = 3600-3600/3=3600-1200

Итак, s30=2400

S40=2400=30/2[2a+(30-1)d]=2400

Следовательно, Sn=n/2[2a+(n-1)d]

2a+2ad =2400/15=160…. (ii)

1. -(ii) = 2a+39d=180

2a+29d=160/0+10d=20

d=20/10=2

Положим d= 2 в (ii) 2a +29(2)=160

2a=102

A=102/2= 51

Следовательно, стоимость его первого взноса = 51.

Вопрос: Мужчина получил 32 рупии в течение 1-го года. , 36 рупий во втором году, и таким образом он ежегодно увеличивал свои сбережения на 4 рупии. Найдите, через какое время его обеспеченные деньги будут составлять 200 рупий.

Ответ: Экономия за 1-й год (a1) = 32 рупий

Экономия за 2-й год (a2) = 36 рупий

Увеличение заработной платы каждый год (d) = 4 рупии будет 200

= Sn=200

= n/2[2a+(n-1)d=200

= n/2(64+4n-4)=200

N/2(4n+60 )=200

=2n2+30n=200

=n2+15-100=0 [при делении на 2]

=n2+20n-5n-100=0

=n(n+20)-5 (n+20)=0

(n+20)(n-5)=0

Если n+20=0 или n-5=0

N=-20 или n=5 [Отклонено, так как n не может быть отрицательным]

Следовательно, через 5 лет его сбережения составят 200 рупий.

Вопрос: Человек заработал 16500 за 10 лет. Каждый год после первого он получал на 100 рупий больше, чем в предыдущем году. Сколько он заработал за 1-й год?

Ответ: Пусть «а» будет деньгами, которые он заработал в первый год

= Первый год, когда он заработал деньги =

рупий. Он сэкономил на 100 рупий больше, чем в предыдущем году.

= На второй год он заработал деньги = Rs (a+100)

= На третий год он накопил деньги = Rs [a+2(100)]

Итак, последовательность такова, a+100, a+ 2(100), ……, Это АП с общей разностью (d)=100

= Сумма денег, которую он заработал за десять лет S10=16 500 рупий

Мы знаем, что Sn=n/2[2a+(n -1)d]

S10=10/2[2a+(10-1)100]

16500=5(2a+9×100)

2a +900=16500/5=3300

2a=2400

A=2400/2=1200

Следовательно, он сэкономил деньги в первый год (a) = 9 рупий.0011 1200 .

Математика Ссылки по теме:

Обзор, вопросы, простые приемы, правила, подготовка

Содержание

1. Что такое арифметическая прогрессия?
2. Арифметическая прогрессия Веса в классе 10
3. scrollTo(duration=200)»> Арифметическая прогрессия Вес в классе 11
4. Иллюстрированные примеры арифметической прогрессии
5. Часто задаваемые вопросы об арифметической прогрессии

Что такое арифметическая прогрессия?

Прогрессия — это особый тип последовательности, для которого можно получить формулу n-го члена. Благодаря легким и простым формулам арифметическая прогрессия была самой известной последовательностью в математике. Любая последовательность или серия в том порядке, в котором разница между любыми последовательными числами постоянна, называется арифметической прогрессией. Более того, в случае любого набора последовательных нечетных и четных, разница будет равна двум.

Общее уравнение

Для последовательности _n , где общая разность равна d, а первый член равен ₁ . Уравнение будет таким:

a _n =a ₁ +(n-1)d

Ключевые свойства арифметической прогрессии

Ниже приведены некоторые ключевые свойства арифметической прогрессии:

1 90,00 Если a,b,c в любом случайном ряду принадлежат A.P, то 2b = a + c.

2. Общим отличием будет «a» для последовательности в A.P, где n ^th в последовательности имеет форму an + b.

3. Последовательность также может быть в A.P, если ненулевое постоянное число делится, умножается, прибавляется или вычитается из каждого члена ряда в A.P.

4. Арифметическая прогрессия является убывающей последовательностью, если общая разность отрицательна, т.е. dn-1>a _n

5. Арифметическая прогрессия является возрастающей последовательностью, если общая разность положительна, т.е. d>0, и удовлетворяет условию a _n-1 n.

Суммы арифметических прогрессий

В AP с общей разностью d и первым членом a сумма первых n членов определяется как:

S = n/2[2a + (n − 1) × d]

Арифметическая прогрессия Вес в 10-м классе

Программа 10-го класса по математике представляет арифметическую прогрессию в главе 5 раздела II Алгебра. Глава получает 5 баллов на контрольных экзаменах и охватывает такие темы, как вывод n-го члена и сумма первых n членов AP.

Арифметическая прогрессия Вес в классе 11

Программа 11 класса по математике представляет арифметическую прогрессию в последовательности главы 7 и серии из раздела Алгебра. Этот блок содержит 30 важных баллов и охватывает общую практику, средние арифметические и другие основные темы.

Иллюстрированные примеры по арифметической прогрессии

1. Субба Рао начал работать в 1995 году с годовой зарплатой 5000 рупий и каждый год получал надбавку на 200 рупий. В каком году его доход составил 7000 руб.?

Решение:

Учитывая, что заработная плата увеличивается на 200 каждый год

Следовательно, ряд будет,

5000,5200,5400……..,an

a=5000, d=200, an= 7000

Таким образом,

a _n = a+(n−1) d

7000 = 5000 + (n-1) 200

n = 11

На 11-м курсе зарплата составит 7000.

2. Найдите сумму первых 22 членов АП, в которых d = 7, а 22 ^-й -й член равен 149.

Решение:

Дано, d = 7, a ₂₂ = 149

Из формулы, a = 2

Теперь, 22/2 (2 + 149)

S ₂₂ = 1661

3. Запишите первые четыре члена А.П., когда первый член а и общая разность где а = 10, d = 10.

Решение:

Дано, a = 10, d = 10

Следовательно, ряд будет 10,20,30,40,50,…

Первые четыре члена: 10,20,30,40,

Часто задаваемые вопросы об арифметической прогрессии

В: Зачем нужна арифметическая прогрессия?

О: В нашей повседневной жизни арифметическая прогрессия в основном используется для обобщения набора терминов.

В: Приведите несколько случаев АП в нашей повседневной жизни?

A: Наша повседневная жизнь представляет собой множество примеров арифметической прогрессии, начиная от календарных дат, таблиц данных и т.