§ Площадь сферы. Объем шара
Длина окружности. Число Пи Площадь круга Площадь сферы. Объём шара
Многие из нас любят играть в футбол или, по крайней мере, почти каждый из нас слышал про эту знаменитую спортивную игру. Всем известно, что в футбол играют мячом.
Если спросить прохожего, форму какой геометрической фигуры имеет мяч, то часть людей скажут, что форму шара, а часть, что формы сферы. Так кто же из них прав? И в чем разница между сферой и шаром?
Важно!
Шар — это пространственное тело. Внутри шар чем-либо заполнен. Поэтому у шара можно найти объем.
Примеры шара в жизни: арбуз и стальной шарик.
Шар и сфера, подобно кругу и окружности, имеют центр, радиус и диаметр.
Важно!
Сфера — поверхность шара. У сферы можно найти площадь поверхности.
Примеры сферы в жизни: волейбольный мяч и шарик для игры в настольный
теннис.
Как найти площадь сферы
Запомните!
Формула площади сферы: S = 4πR2
Для того, чтобы найти площадь сферы, необходимо вспомнить,
что такое степень числа.
Зная определение степени,
можно записать формулу площади сферы следующим образом.
S = 4π R2 =
4πR · R;
Закрепим полученные знания и решим задачу на площадь сферы.
Зубарева 6 класс. Номер 692(а)
Условие задачи:
- Вычислите площадь сферы, если её радиус равен 1 м. (возьмите π как 3)
Вспомнив, как выделить целую часть и перемножить дроби, воспользуемся формулой площади сферы:
S = 4 · πR2 = 4 · 3
· (1
) 2 = 4 ·
· (
) 2 = 4 ··
| 441 |
| 121 |
=
| 4 · 22 · 441 |
| 7 · 121 |
=
=
| 4 · 22 · 63 |
| 121 |
=
| 4 · 2 · 63 |
| 11 |
=
| 504 |
| 11 |
= 45
м2
Как найти объем шара
Запомните!
- Формула объема шара: V = πR3
Зная определение степени,
можно записать формулу объема шара следующим образом.
- V = π R3 = π R · R · R;
Для отработки полученных знаний решим задачу на объем шара.
Зубарева 6 класс. Номер 691(а)
Условие задачи:
- Вычислите радиус шара, если его объем равен 4 м3 (возьмите π как 3)
Выразим из формулы объема шара радиус.
- V = π R3
- π R3 = V
- π R3 =
- R3 =
3V 4 π
Подставим в формулу известные нам значения. Число π возьмем как задано в задании «3
».
R3 = (3 ·
4
)
Чтобы не запутаться, отдельно рассчитаем
числитель дроби.
3 · 4
= 3 ·
| 21 · 4 + 4 |
| 21 |
=
| 3 · 88 |
| 21 |
=
Теперь снова подставим полученное значение в нашу формулу:
- R3 =
/ (4 · 3)
=
/ (4 · )
=
/ (
) = = · (4 · 22 7
) =7 4 · 22
=88 · 7 7 · 4 · 22
= = 188 4 · 22 - R3 = 1
- R = 1 м
Важно!
Уважаемые родители!
При окончательном расчете радиуса
не надо заставлять ребенка считать кубический корень. Учащиеся
6-го класса еще не проходили и не знают определение корней в математике.
Учащиеся
6-го класса еще не проходили и не знают определение корней в математике.
В 6 классе при решении такой задачи используйте метод перебора.
Спросите ученика, какое число, если его умножить 3 раза на самого себя даст единицу.
Длина окружности. Число Пи Площадь круга Площадь сферы. Объём шара
Сфера объем и площадь. Сфера, шар, сегмент и сектор
Сфера и шар – это аналог круга и окружности в трехмерном пространстве. Стоит поговорить о каждой из этих фигур, выделить сходства и различия, а так же формулы, свойственные этим фигурам.
Большая часть геометрических построений производится в плоскости, но в старших классах начинают изучать трехмерные фигуры. Двухмерное пространство имеет только две характеристики: длину и ширину. В трехмерных областях добавляется высота. В математике 6 класса изучаются отдельные 3д фигуры.
На плоскости фигуру характеризовала площадь и периметр. В трехмерных объектах к ним прибавляется объем. 3\over3}$
3\over3}$
Объем показывает, какое пространство занимает фигура. Чтобы понять, что такое объем нужно представить себе фигуру полой. Тогда объем это количество воды, которое можно налить в эту фигуру
Шар, как и любую другую трехмерную фигуру, можно рассечь плоскостью. Секущей плоскостью шара является круг, центр которого можно найти, опустив из центра шара перпендикуляр на окружность.
Рис. 2. Сечение шара.
Сфера это фигура, представляющая собой множество точек в пространстве, равноудаленных от центра сферы. Сфера:
- Имеет те же формулы объема и площади поверхности, что и шар.
- Секущая плоскость сферы это окружность
- Центр секущей окружности, находится так же, как и в случае с шаром
Рис. 3. Сфера.
В чем различие
Тогда возникает вопрос, а чем отличается шар от сферы кроме определения? Дело в том, что различия шара и сферы куда более размыты, нежели различия круга и окружности. Сфера так же имеет объем и площадь поверхности.
Пожалуй, кроме определения, разница заключается в том, что в задачах никогда не находят объем сферы. Как правило, ищут объем шара. Это не значит, что у сферы нет объема. Это трехмерная фигура, поэтому объем у нее есть.
Просто проводится аналогия с окружностью, у которой нет площади. Это не правило, но скорее традиция, которую нужно запомнить: в геометрии не приветствуется формулировка объем сферы.
Еще одно отличие, которое можно считать более или менее значимым: секущая плоскость сферы: окружность, которая не имеет внутреннего пространства, но имеет длину. Секущая плоскость шара: круг, который имеет площадь и не имеет длины окружности. Поэтому стоит быть аккуратным в формулировках задачи, чтобы не было ошибок из-за подобных мелочей.
Что мы узнали?
Мы узнали, что такое сфера и шар. Поговорили об их сходствах и различии. Узнали, что различий у этих фигур почти нет. Решили, что не стоит приводить такую формулировку, как объем сферы.
Тест по теме
Оценка статьи
Средняя оценка: 4. 7
. Всего получено оценок: 105.
7
. Всего получено оценок: 105.
Многие из нас любят играть в футбол или, по крайней мере, почти каждый из нас слышал про эту знаменитую спортивную игру. Всем известно, что в футбол играют мячом.
Если спросить прохожего, форму какой геометрической фигуры имеет мяч, то часть людей скажут, что форму шара, а часть, что формы сферы. Так кто же из них прав? И в чем разница между сферой и шаром?
Важно!
Шар — это пространственное тело. Внутри шар чем-либо заполнен. Поэтому у шара можно найти объем.
Примеры шара в жизни: арбуз и стальной шарик.
Шар и сфера, подобно кругу и окружности, имеют центр, радиус и диаметр.
Важно!
Сфера — поверхность шара. У сферы можно найти площадь поверхности.
Примеры сферы в жизни: волейбольный мяч и шарик для игры в настольный теннис.
Как найти площадь сферы
Запомните!
Формула площади сферы: S = 4π R 2
Для того, чтобы найти площадь сферы, необходимо вспомнить,
что такое степень числа . Зная определение степени,
можно записать формулу площади сферы следующим образом.
Зная определение степени,
можно записать формулу площади сферы следующим образом.
S = 4π
R 2 =
4π
R · R;
Закрепим полученные знания и решим задачу на площадь сферы.
Зубарева 6 класс. Номер 692(а)
Условие задачи:
- Вычислите площадь сферы, если её радиус равен 1 =
3 ·
=
=
/ (4 · 3)
= ) =
= ) =
- R 3 = 1
- R = 1 м
Важно!
Уважаемые родители!
При окончательном расчете радиуса не надо заставлять ребенка считать кубический корень. Учащиеся 6-го класса еще не проходили и не знают определение корней в математике.
В 6 классе при решении такой задачи используйте метод перебора.
Спросите ученика, какое число, если его умножить 3 раза на самого себя даст единицу.
Определение.
Сфера (поверхность шара ) — это совокупность всех точек в трехмерном пространстве, которые находятся на одинаковом расстоянии от одной точки, называемой центром сферы (О).
Сферу можно описать, как объёмную фигуру, которая образуется вращением окружности вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.
Определение.
Шар — это совокупность всех точек в трехмерном пространстве, расстояние от которых не превышает определенного расстояния до точки, называемой центром шара (О) (совокупность всех точек трехмерного пространства ограниченных сферой).Шар можно описать как объёмную фигуру, которая образуется вращением круга вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.
Определение. Радиус сферы (шара) (R) — это расстояние от центра сферы (шара) O к любой точке сферы (поверхности шара).
Определение. Диаметр сферы (шара) (D) — это отрезок, соединяющий две точки сферы (поверхности шара) и проходящий через ее центр.
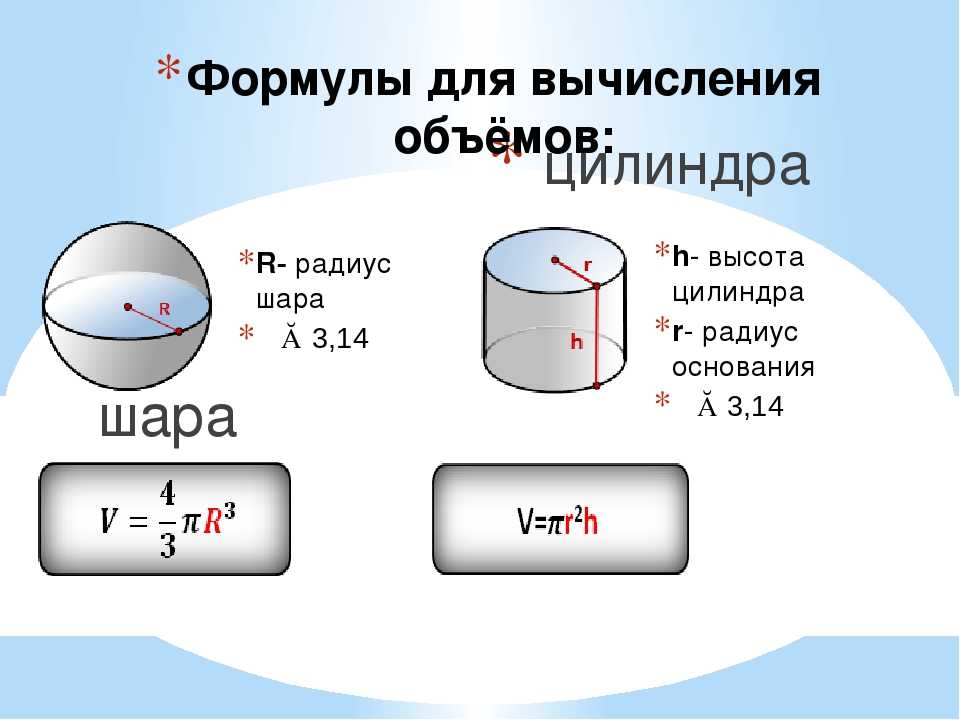
Формула. Объём шара :
| V = | 4 | π R 3 = | 1 | π D 3 |
| 3 | 6 |
Формула.
S = 4π R 2 = π D 2
Уравнение сферы
1. Уравнение сферы с радиусом R и центром в начале декартовой системе координат :
x 2 + y 2 + z 2 = R 2
2. Уравнение сферы с радиусом R и центром в точке с координатами (x 0 , y 0 , z 0) в декартовой системе координат :
(x — x 0) 2 + (y — y 0) 2 + (z — z 0) 2 = R 2
Определение. Диаметрально противоположными точками называются любые две точки на поверхности шара (сфере), которые соединены диаметром.
Основные свойства сферы и шара
1. Все точки сферы одинаково удалены от центра.
2. Любое сечение сферы плоскостью является окружностью.
3. Любое сечение шара плоскостью есть кругом.
4. Сфера имеет наибольший объём среди всех пространственных фигур с одинаковой площадью поверхности.
5. Через любые две диаметрально противоположные точки можно провести множество больших окружностей для сферы или кругов для шара.
6. Через любые две точки, кроме диаметрально противоположных точек, можно провести только одну большую окружность для сферы или большой круг для шара.
7. Любые два больших круга одного шара пересекаются по прямой, проходящей через центр шара, а окружности пересекаются в двух диаметрально противоположных точках.
8. Если расстояние между центрами любых двух шаров меньше суммы их радиусов и больше модуля разности их радиусов, то такие шары пересекаются , а в плоскости пересечения образуется круг.
Секущая, хорда, секущая плоскость сферы и их свойства
Определение. Секущая сферы — это прямая, которая пересекает сферу в двух точках. Точки пересечения называются точками протыкания поверхности или точками входа и выхода на поверхности.
Определение. Хорда сферы (шара) — это отрезок, соединяющий две точки сферы (поверхности шара).
Определение. Секущая плоскость — это плоскость, которая пересекает сферу.
Определение.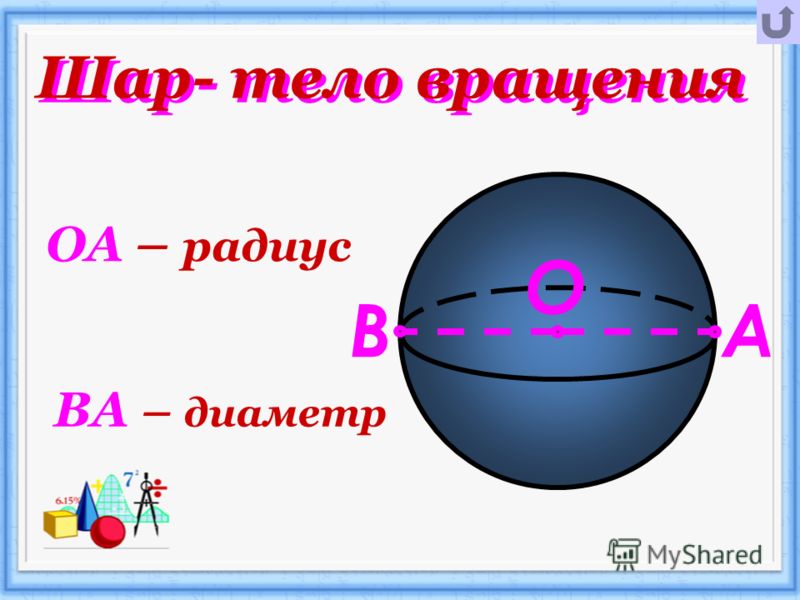 Диаметральная плоскость — это секущая плоскость, проходящая через центр сферы или шара, сеченме образует соответственно большую окружность и большой круг . Большая окружность и большой круг имеют центр, который совпадают с центром сферы (шара).
Диаметральная плоскость — это секущая плоскость, проходящая через центр сферы или шара, сеченме образует соответственно большую окружность и большой круг . Большая окружность и большой круг имеют центр, который совпадают с центром сферы (шара).
Любая хорда, проходящая через центр сферы (шара) является диаметром.
Хорда является отрезком секущей прямой.
Расстояние d от центра сферы до секущей всегда меньше чем радиус сферы:
d
Расстояние m между секущей плоскостью и центром сферы всегда меньше радиуса R:
m
Местом сечения секущей плоскости на сфере всегда будет малая окружность , а на шаре местом сечения будет малый круг . Малая окружность и малый круг имеют свои центры, не совпадающих с центром сферы (шара). Радиус r такого круга можно найти по формуле:
r = √R 2 — m 2 ,
Где R — радиус сферы (шара), m — расстояние от центра шара до секущей плоскости.
Определение. Полусфера (полушар) — это половина сферы (шара), которая образуется при ее сечении диаметральной плоскостью.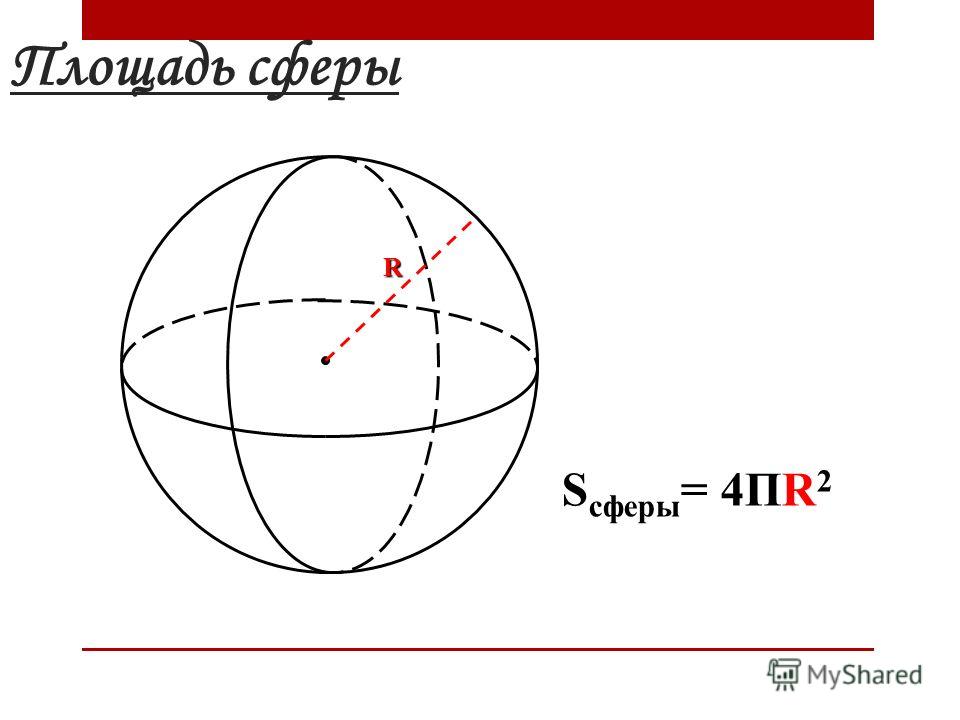
Касательная, касательная плоскость к сфере и их свойства
Определение. Касательная к сфере — это прямая, которая касается сферы только в одной точке.
Определение. Касательная плоскость к сфере — это плоскость, которая соприкасается со сферой только в одной точке.
Касательная пряма (плоскость) всегда перпендикулярна радиусу сферы проведенному к точке соприкосновения
Расстояние от центра сферы до касательной прямой (плоскости) равно радиусу сферы.
Определение. Сегмент шара — это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Высотой сегмента h называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента.
Формула. Площадь внешней поверхности сегмента сферы с высотой h через радиус сферы R:
S = 2π Rh
Площадь сферы — формулы и примеры вычислений » Kupuk.net
Идеально круглый геометрический объект, который определяется как множество всех точек, равноудалённых от одной заданной, называется сфера. Площадь ее поверхности, в сравнении с другими трёхмерными телами, имеет наибольший объём. По сути, это шар, имеющий однородную форму, то есть как ни повернуть, он всегда будет выглядеть одинаково.
Площадь ее поверхности, в сравнении с другими трёхмерными телами, имеет наибольший объём. По сути, это шар, имеющий однородную форму, то есть как ни повернуть, он всегда будет выглядеть одинаково.
Важные измерения
Радиус (обозначается r) — единственное необходимое измерение. Это расстояние от любой точки на поверхности сферы до её центра. Самый длинный отрезок, равный двум r, называется диаметром (d). Земля называется сфероидом, потому что она очень близка к шару, но не идеально круглая. Она немного вытянута на северном и южном полюсах.
Впервые вычислить площадь (S) поверхности шара удалось Архимеду. Именно он установил, что для того, чтобы найти S любого трёхмерного объекта, необходимо измерить его радиус. Для сферы получилась следующая формула: S = 4 * π * r ². Для того чтобы понять, как это работает, следует рассмотреть пример. Известно, что радиус детского мяча 10 см. Остаётся ещё одна неизвестная — число π. Это математическая константа, которая выражает отношение длины окружности к её диаметру и равна примерно 3,14. Далее, следует подставить цифры в уравнение:
Далее, следует подставить цифры в уравнение:
Таким образом, можно найти площадь сферы через её радиус по формуле, полученной ещё в античности. Ещё одна важная характеристика — это объём (V) фигуры. Он вычисляется следующим образом: V = (4/3) * π * r³. Если придерживаться условий задачи, то V мяча = (4/3) * 3,14 * 10³ равен ≈ 4187 см ³. Сейчас можно избежать длительных расчётов, если нужно узнать площадь сферы, онлайн-калькуляторы — сервисы, которые очень в этом помогают.
Сектор сферы — это слой между двумя правильными круговыми конусами, имеющими общую вершину в центре шара и общую ось.
Надо сказать, что внутренний конус может иметь основание с нулевым радиусом. Формула, по которой определяют площадь сектора, следующая: S = 2 * π * r * h, где h — высота. К слову, эта же формула применима, если необходимо найти S части шара, отрезанной плоскостью, то есть полусферы. Такая же формула применяется при нахождении S сегмента (часть между двумя параллельными плоскостями) и зоны сферы (изогнутая поверхность сферического сегмента).
Такая же формула применяется при нахождении S сегмента (часть между двумя параллельными плоскостями) и зоны сферы (изогнутая поверхность сферического сегмента).
Терминология и сферическая геометрия
Окружность на шаре, которая имеет тот же центр и радиус, что и сама фигура, а следовательно, делит её на две части, называется большим кругом. Если конкретную (произвольную) точку этого геометрического тела обозначить как его северный полюс, то соответствующая антиподальная точка будет южным полюсом. А большой круг станет экватором и будет равноудалённым от них. Если он будет проходить через два полюса, тогда это уже линии долготы (меридианы).
Круги на сфере, проходящие параллельно экватору, называются линиями широты. Все эти термины используются для приблизительно сфероидальных астрономических тел. Любая плоскость, которая включает в себя центр шара, делит его на два равных полушария (полусферы).
Многие теоремы из классической геометрии верны и для сферической, но отнюдь не все, потому что сфера не удовлетворяет некоторым аксиомам, например, постулату параллельности. Такая же ситуация складывается и в тригонометрии — отличия есть во многих отношениях. Например, сумма внутренних углов сферического треугольника всегда превышает 180 градусов. Помимо этого, две таких одинаковых фигуры будут конгруэнтными.
Одиннадцать свойств
В своей книге «Геометрия и воображение» Дэвид Гилберт и Стефан Кон-Фоссен описывают свойства сферы и обсуждают, однозначны ли такие характеристики. Несколько пунктов справедливы и для плоскости, которую можно представить как шар с бесконечным радиусом:
 И здесь прослеживается аналогия с окружностями Аполлония, то есть с фигурами в плоскости.
И здесь прослеживается аналогия с окружностями Аполлония, то есть с фигурами в плоскости.
Сфера превращается в себя трёхпараметрическим семейством жёстких движений. Любое вращение вокруг линии, проходящей через начало координат, может быть выражено как комбинация вращений вокруг трёхкоординатной оси.
О шаре и цилиндре
Так называлась работа, опубликованная античным математиком Архимедом. Она вышла в двух томах в 225 году до н. э. Он был первым, кто сделал полный и подробный трактат по основам вычисления площади поверхности сферы, объёма шара и аналогичных значений для таких элементов, как цилиндр. Результатами его деятельности пользуются до сих пор.
Архимед особенно гордился формулой объёма шара, где он доказал, что эта величина составляет две трети объёма описанного цилиндра.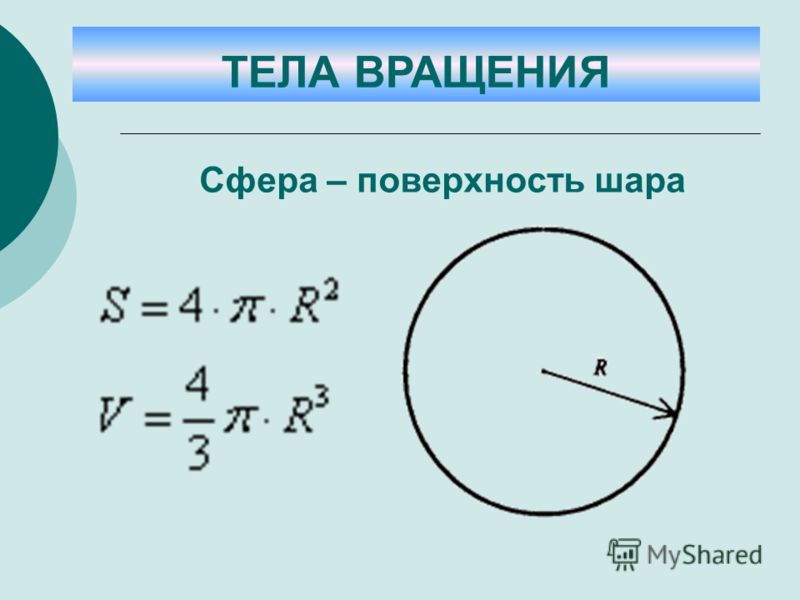 Он даже попросил сделать чертёж этих предметов на своей надгробной плите. Позже римский философ Цицерон обнаружил такую гробницу, к сожалению, сильно заросшую окружающей растительностью.
Он даже попросил сделать чертёж этих предметов на своей надгробной плите. Позже римский философ Цицерон обнаружил такую гробницу, к сожалению, сильно заросшую окружающей растительностью.
Аргумент, который Архимед использовал для доказательства формулы V шара, был довольно сложным и сильно вовлечён в его геометрию. Поэтому во многих современных учебниках используется упрощённая версия, основанная на концепции предела, которого, конечно, не было в античные времена. Великий математик создавал в сфере усечённый конус путём построения и вращения геометрических фигур, и только после этого он определил объём.
Сейчас кажется, что он специально выбирал такие оригинальные методы. Однако это был всего лишь лучший из тех, которые были ему доступны в греческой математике. Его основные работы были вновь открыты в XX веке. Например, Метод механических теорем, как он назывался в трактате автора.
Площадь сферы — формулы и примеры вычислений
Идеально круглый геометрический объект, который определяется как множество всех точек, равноудалённых от одной заданной, называется сфера. Площадь ее поверхности, в сравнении с другими трёхмерными телами, имеет наибольший объём. По сути, это шар, имеющий однородную форму, то есть как ни повернуть, он всегда будет выглядеть одинаково.
Площадь ее поверхности, в сравнении с другими трёхмерными телами, имеет наибольший объём. По сути, это шар, имеющий однородную форму, то есть как ни повернуть, он всегда будет выглядеть одинаково.
Содержание
- Важные измерения
- Терминология и сферическая геометрия
- Одиннадцать свойств
- О шаре и цилиндре
Важные измерения
Радиус (обозначается r) — единственное необходимое измерение. Это расстояние от любой точки на поверхности сферы до её центра. Самый длинный отрезок, равный двум r, называется диаметром (d). Земля называется сфероидом, потому что она очень близка к шару, но не идеально круглая. Она немного вытянута на северном и южном полюсах.
Впервые вычислить площадь (S) поверхности шара удалось Архимеду. Именно он установил, что для того, чтобы найти S любого трёхмерного объекта, необходимо измерить его радиус. Для сферы получилась следующая формула: S = 4 * π * r ². Для того чтобы понять, как это работает, следует рассмотреть пример. Известно, что радиус детского мяча 10 см. Остаётся ещё одна неизвестная — число π. Это математическая константа, которая выражает отношение длины окружности к её диаметру и равна примерно 3,14. Далее, следует подставить цифры в уравнение:
Известно, что радиус детского мяча 10 см. Остаётся ещё одна неизвестная — число π. Это математическая константа, которая выражает отношение длины окружности к её диаметру и равна примерно 3,14. Далее, следует подставить цифры в уравнение:
Таким образом, можно найти площадь сферы через её радиус по формуле, полученной ещё в античности. Ещё одна важная характеристика — это объём (V) фигуры. Он вычисляется следующим образом: V = (4/3) * π * r³. Если придерживаться условий задачи, то V мяча = (4/3) * 3,14 * 10³ равен ≈ 4187 см ³. Сейчас можно избежать длительных расчётов, если нужно узнать площадь сферы, онлайн-калькуляторы — сервисы, которые очень в этом помогают.
Сектор сферы — это слой между двумя правильными круговыми конусами, имеющими общую вершину в центре шара и общую ось.
Надо сказать, что внутренний конус может иметь основание с нулевым радиусом. Формула, по которой определяют площадь сектора, следующая: S = 2 * π * r * h, где h — высота. К слову, эта же формула применима, если необходимо найти S части шара, отрезанной плоскостью, то есть полусферы. Такая же формула применяется при нахождении S сегмента (часть между двумя параллельными плоскостями) и зоны сферы (изогнутая поверхность сферического сегмента).
Формула, по которой определяют площадь сектора, следующая: S = 2 * π * r * h, где h — высота. К слову, эта же формула применима, если необходимо найти S части шара, отрезанной плоскостью, то есть полусферы. Такая же формула применяется при нахождении S сегмента (часть между двумя параллельными плоскостями) и зоны сферы (изогнутая поверхность сферического сегмента).
Терминология и сферическая геометрия
Окружность на шаре, которая имеет тот же центр и радиус, что и сама фигура, а следовательно, делит её на две части, называется большим кругом. Если конкретную (произвольную) точку этого геометрического тела обозначить как его северный полюс, то соответствующая антиподальная точка будет южным полюсом. А большой круг станет экватором и будет равноудалённым от них. Если он будет проходить через два полюса, тогда это уже линии долготы (меридианы).
Круги на сфере, проходящие параллельно экватору, называются линиями широты.
Все эти термины используются для приблизительно сфероидальных астрономических тел. Любая плоскость, которая включает в себя центр шара, делит его на два равных полушария (полусферы).
Многие теоремы из классической геометрии верны и для сферической, но отнюдь не все, потому что сфера не удовлетворяет некоторым аксиомам, например, постулату параллельности. Такая же ситуация складывается и в тригонометрии — отличия есть во многих отношениях. Например, сумма внутренних углов сферического треугольника всегда превышает 180 градусов. Помимо этого, две таких одинаковых фигуры будут конгруэнтными.
Одиннадцать свойств
В своей книге «Геометрия и воображение» Дэвид Гилберт и Стефан Кон-Фоссен описывают свойства сферы и обсуждают, однозначны ли такие характеристики. Несколько пунктов справедливы и для плоскости, которую можно представить как шар с бесконечным радиусом:
 Можно сделать единственный вывод: это обычное определение и оно однозначно. А также отношение расстояний между двумя фиксированными точками является постоянным. И здесь прослеживается аналогия с окружностями Аполлония, то есть с фигурами в плоскости.
Можно сделать единственный вывод: это обычное определение и оно однозначно. А также отношение расстояний между двумя фиксированными точками является постоянным. И здесь прослеживается аналогия с окружностями Аполлония, то есть с фигурами в плоскости.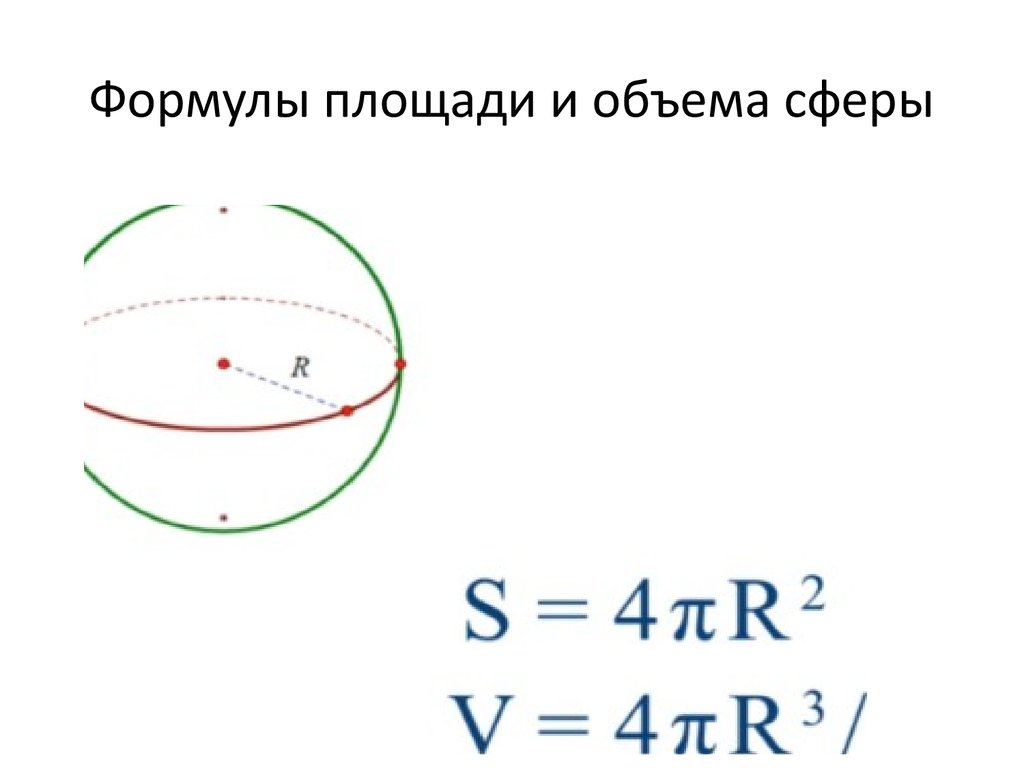 Для сферы кривизны всех нормальных сечений одинаковы, поэтому омбилической будет каждая точка.
Для сферы кривизны всех нормальных сечений одинаковы, поэтому омбилической будет каждая точка.
Сфера превращается в себя трёхпараметрическим семейством жёстких движений. Любое вращение вокруг линии, проходящей через начало координат, может быть выражено как комбинация вращений вокруг трёхкоординатной оси.
О шаре и цилиндре
Так называлась работа, опубликованная античным математиком Архимедом. Она вышла в двух томах в 225 году до н. э. Он был первым, кто сделал полный и подробный трактат по основам вычисления площади поверхности сферы, объёма шара и аналогичных значений для таких элементов, как цилиндр. Результатами его деятельности пользуются до сих пор.
Архимед особенно гордился формулой объёма шара, где он доказал, что эта величина составляет две трети объёма описанного цилиндра. Он даже попросил сделать чертёж этих предметов на своей надгробной плите. Позже римский философ Цицерон обнаружил такую гробницу, к сожалению, сильно заросшую окружающей растительностью.
Он даже попросил сделать чертёж этих предметов на своей надгробной плите. Позже римский философ Цицерон обнаружил такую гробницу, к сожалению, сильно заросшую окружающей растительностью.
Аргумент, который Архимед использовал для доказательства формулы V шара, был довольно сложным и сильно вовлечён в его геометрию. Поэтому во многих современных учебниках используется упрощённая версия, основанная на концепции предела, которого, конечно, не было в античные времена. Великий математик создавал в сфере усечённый конус путём построения и вращения геометрических фигур, и только после этого он определил объём.
Сейчас кажется, что он специально выбирал такие оригинальные методы. Однако это был всего лишь лучший из тех, которые были ему доступны в греческой математике. Его основные работы были вновь открыты в XX веке. Например, Метод механических теорем, как он назывался в трактате автора.
Предыдущая
ГеометрияСкрещивающиеся прямые — определение, теорема и примеры
Следующая
ГеометрияПлощадь равнобедренного треугольника — формулы вычисления
Площадь сферы.
 Объем шара
Объем шараИмея при себе всего одну формулу и зная изначально, чему равен диаметр или радиус, можно с лёгкостью вычислить площадь поверхности шара. Формула будет иметь вид S =4πR2 , где число «пи» умножается на 4, затем на радиус шара в квадратной степени. Но перед непосредственными вычислениями следует сразу разобраться в терминах.
Трактовка значений
Это следует знать:
- Шар – геометрический объект, получившийся в результате вращательных полукруговых движений вокруг центра. Любая точка поверхности шара находится на одинаковом расстоянии от центра.
- Сфера – не то же самое, что шар. Если тот является объёмным объектом и включает в себя внутреннее пространство, то сфера – это лишь поверхность данного объекта и имеет только свою площадь. Иными словами – нельзя сказать, что сфера имеет такой-то объём, в отличие от шара.
- Число «пи» — это постоянное число, равное отношению длины окружности к её диаметру. В сокращённом виде его принято обозначать числом, равным 3,14.
 Но на самом деле, после тройки идёт больше тысячи цифр!
Но на самом деле, после тройки идёт больше тысячи цифр! - Радиус шара равен ½ его диаметру . Точный диаметр можно вычислить с использованием нескольких плоских и ровных предметов. Нужно лишь зажать шар между этими предметами, которые зажимают шар и расположены перпендикулярно друг к другу, а затем измерить получившийся диаметр.
- Квадратная степень обозначается в виде двойки и означает то, что это число надо умножить на само себя один раз. Если бы степень числа была в виде тройки, то умножать на само себя нужно было бы два раза. Записав выражение на бумаге, можно понять, почему используются именно двойка и тройка, а не единица и двойка.
- Объём – величина, обозначающая размер в пространстве, занимающее объектом. От диаметра зависит объём шара. Формула будет равна четырём трети, умноженным на число «пи» и вновь умноженным на его радиус в кубе.
- Площадь – величина, обозначающая размер поверхности объекта, но не внутреннего пространства.

Занимательные факты
Это интересно:
- У числа «пи» есть собственные фан-клубы по всему миру. Члены общества пытаются запомнить как можно больше знаков из этого числа, а также пытаются разгадать вселенские тайны, сокрытые в числе.
- Площадь суши Земли составляет всего 29,2 % от её общей поверхности. Точное число площади сложно назвать из-за неравномерного рельефа Земли, такие как впадины и горы.
- Знания о формуле площади шара можно применять и в быту. Также этими знаниями можно подавлять соперника в споре.
Продемонстрировав объём своих знаний в области геометрии, можно изначально заставить вас уважать, а ремонтникам и продавцам можно дать понять, что вас просто так не обмануть.
Применение формулы
Рассмотрим на примере, как вычислить площадь круглого шара , диаметр которого равен 50 см. Следуя формуле, нужно 50 разделить на два (чтобы получить радиус), возвести полученное число в квадрат и умножить всё это дело сначала на 4, затем на 3,14. В итоге получим число в 7 850 квадратных сантиметров.
В итоге получим число в 7 850 квадратных сантиметров.
Формула вычисления площади применяется не только среди учителей в школе и научных сотрудников в лаборатории. Данная формула может пригодиться обычному маляру. Ведь если шар большой, а краски мало, то возникает вопрос – хватит ли ему этой смеси, чтобы покрасить весь объект. И это далеко не единственный бытовой случай, где может пригодиться формула.
Формула вычисления объёма может пригодиться и строительной бригаде, что делает ремонт. И неважно, какой это объект – промышленное здание, небольшой дом или обычная квартира. Этим и отличаются профессионалы – они умеют применять свои знания на практике.
Но как быть, если не представляется возможным измерить объект? Такой вопрос может возникнуть в случае огромных размеров объекта или его недосягаемости. В этом случае могут помочь электронные технологии, в основе работы которых лежит сканирование пространства определёнными частотами и лазерами. С современными технологиями необязательно знать все формулы наизусть.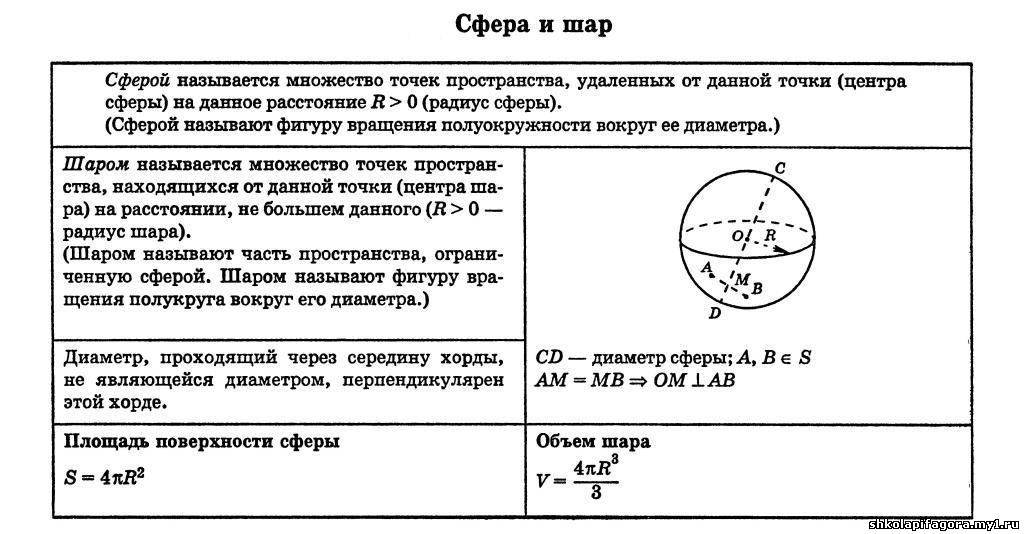 Достаточно иметь подключение к интернету и зайти на любой онлайн-калькулятор.
Достаточно иметь подключение к интернету и зайти на любой онлайн-калькулятор.
Принято считать, что первый, кто нашёл и вывел формулу объёма и площади шара, был Архимед . Это величайший древнегреческий учёный, живший за 300 лет до нашей эры. Он был не только математиком, но и физиком, и инженером. Он один из первых людей, кто попытался «оцифровать» окружающий нас мир. Его теоремы и труды используются по сей день.
Именно Архимед определил границы числа «пи» и обозначил их, не имея никаких современных гаджетов. Сам Архимед очень гордился найденной формулой, с помощью которой вычисляется объём шара. Его потомки в честь этого изобразили на его могильном камне цилиндр и шар.
Если бы каким-то чудом он переродился в наше время, то он сразу же смог бы преобразить этот мир и вывести его на новый уровень.
Видео
На примере этого видео вам будет легко понять, как найти площадь поверхности шара.
Мы даем здесь очень простой, хотя и не совсем строгий вывод формулы для площади сферической поверхности; по своей идее он очень близок к методам интегрального исчисления. Итак, пусть дан некоторый шар радиуса R. Выделим на его поверхности какую-либо малую область (рис. 412) и рассмотрим пирамиду или конус с вершиной в центре шара О, имеющие эту область своим основанием; строго говоря, мы лишь условно говорим о конусе или пирамиде, так как основание не плоское, а сферическое. Но при малых размерах основания по сравнению с радиусом шара оно будет весьма мало отличаться от плоского (так, например, при измерении не очень большого земельного участка пренебрегают тем, что он лежит не на плоскости, а на сфере).
Итак, пусть дан некоторый шар радиуса R. Выделим на его поверхности какую-либо малую область (рис. 412) и рассмотрим пирамиду или конус с вершиной в центре шара О, имеющие эту область своим основанием; строго говоря, мы лишь условно говорим о конусе или пирамиде, так как основание не плоское, а сферическое. Но при малых размерах основания по сравнению с радиусом шара оно будет весьма мало отличаться от плоского (так, например, при измерении не очень большого земельного участка пренебрегают тем, что он лежит не на плоскости, а на сфере).
Тогда, обозначая через площадь этого участка — основание «пирамиды», найдем ее объем как произведение одной трети высоты на площадь основания (высотой служит радиус шара):
Если теперь всю поверхность шара разложить на очень большое число N таких малых областей , тем самым объем шара на N объемов «пирамид», имеющих эти области своими основаниями, то весь объем представится суммой
где последняя сумма равна полной поверхности шара:
Итак, объем шара равен одной трети произведения его радиуса на площадь поверхности. Отсюда для площади поверхности имеем формулу
Отсюда для площади поверхности имеем формулу
Последний результат формулируется так:
Площадь поверхности шара равна учетверенной площади его большого круга.
Приведенный вывод пригоден и для площади поверхности сектора шара (имеем в виду только основание, т. е. сферическую поверхность, или «шапочки»; см. рис. 409). И в этом случае объем сектора равен одной трети произведения радиуса шара на площадь его сферического основания:
откуда находим для площади шапочки формулу
Шаровым поясом (см. рис. 408) называют сферическую поверхность шарового слоя. Чтобы вычислить площадь поверхности шарового пояса, находим разность поверхностей двух сферических шапочек:
где — высота слоя. Итак, площадь поверхности шарового пояса для данного шара зависит только от высоты соответствующего слоя, но не от его положения на шаре.
Задача. Боковая поверхность конуса, описанного вокруг шара, имеет площадь, равную полуторной площади поверхности шара.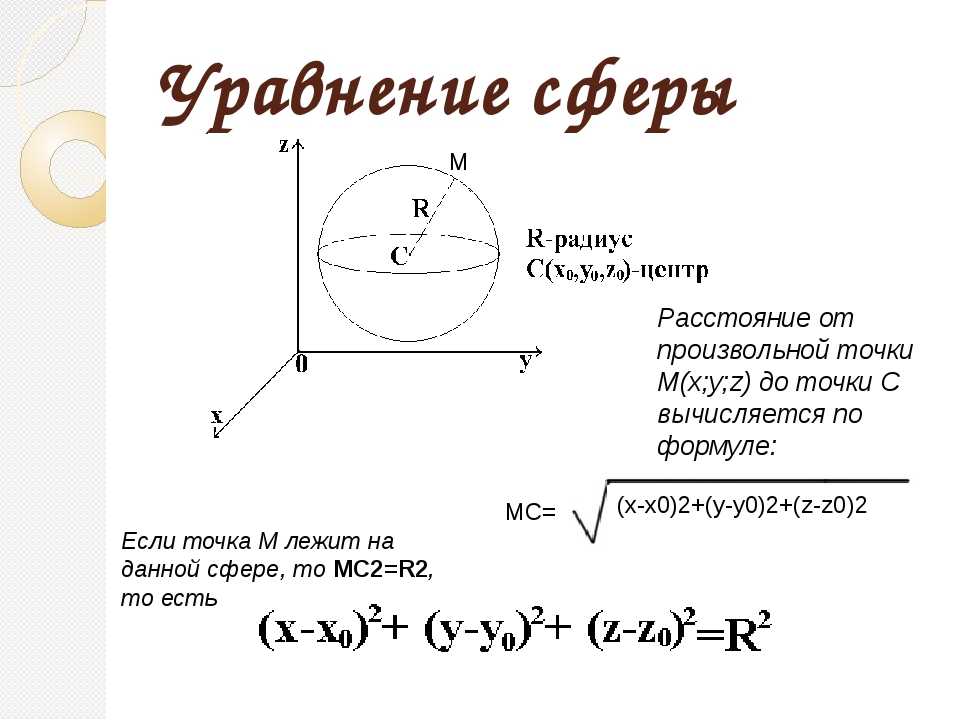 Найти высоту конуса, если радиус шара равен .
Найти высоту конуса, если радиус шара равен .
Решение. Введем для удобства угол а между высотой и образующей конуса (рис. 413). Найдем для высоты, радиуса основания и образующей конуса выражения
Шаром называют уйма всех точек в пространстве, простирающемся от точки-центра на расстоянии определенного радиуса R. Радиус в свою очередь – это отрезок, соединяющий центр шара с всякий точкой его поверхности.
Вам понадобится
- – формула поверхности площади шара;
- – формула объема шара;
- – навыки арифметического счета.
Инструкция
1. В повседневной жизни нередко появляется надобность вычислить площадь шаровой поверхности либо его части, дабы рассчитать, скажем, расход материала. Вычислив объем шара , вы можете через удельный вес рассчитать массу вещества, составляющего содержимое сферы. Для того дабы обнаружить площадь и объем шара , довольно знать его радиус либо диаметр.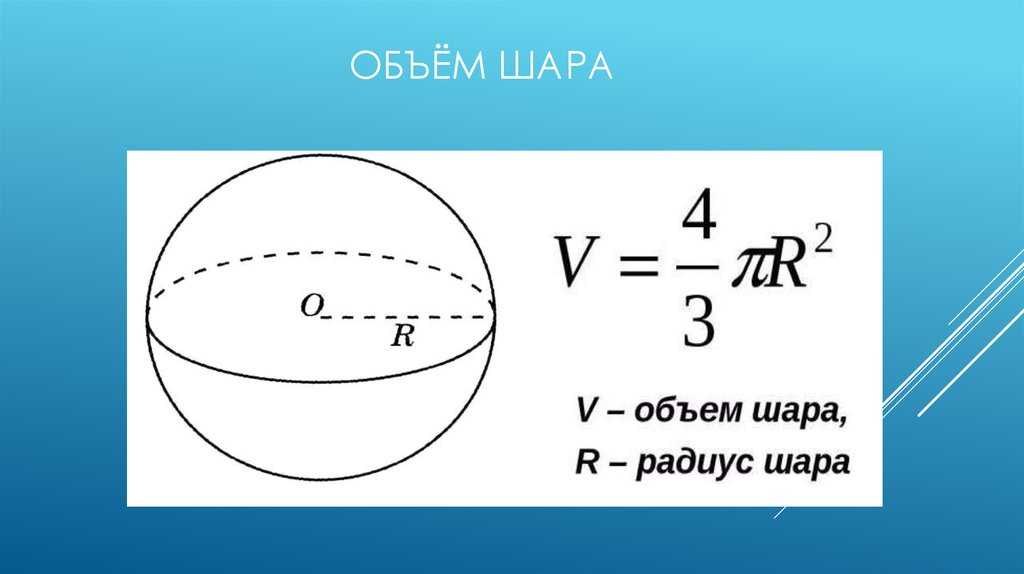 По формулам, которые сегодняшние школьники выводят в 11 классе общеобразовательной школы, вы легко можете рассчитать эти параметры.
По формулам, которые сегодняшние школьники выводят в 11 классе общеобразовательной школы, вы легко можете рассчитать эти параметры.
2. Скажем, диаметр футбольного мяча, согласно каждым требованиям ФИФА, должен быть в пределах 21,8-22,2 см. Усредните для простоты счета до 22 см. Следственно, радиус (R) будет равен (22:2) – 11 см. Чай увлекательно узнать, какова площадь поверхности футбольного мяча?
3. Возьмите формулу площади поверхности шара : Sшара = 4ттR2Подставьте в приведенную формулу значение радиуса футбольного мяча – 11 см.S = 4 x 3.14 x 11х11 .
4. Позже проведения несложных математических действий вы получаете итог: 1519.76. Таким образом, площадь поверхности футбольного мяча составляет 1 519.76 квадратных сантиметров.
5. Сейчас рассчитайте объем мяча. Берите формулу расчета объема шара : V = 4/3ттR3Подставляйте вновь же значение радиуса футбольного мяча – 11 см.V = 4/3 x 3. 14 x 11 х 11 х 11.
14 x 11 х 11 х 11.
6. Позже подсчетов, скажем, на калькуляторе вы получаете: 5576.89.Оказывается, объем воздуха в футбольном мяче составляет 5 576.89 кубических сантиметров.
Шар – это простейшая объемная геометрическая фигура, для указания размеров которой довольно каждого одного параметра. Границы этой фигуры принято называть сферой. Объем пространства, ограничиваемого сферой, дозволено вычислить как с поддержкой соответствующих тригонометрических формул, так и подручными средствами.
Инструкция
1. Используйте классическую формулу объема (V) сферы, если из условий знаменит ее радиус (r) – возведите радиус в третью степень, умножьте на число Пи, а итог увеличьте еще на треть. Записать эту формулу дозволено так: V=4*?*r?/3.
2. Если есть вероятность измерить диаметр (d) сферы, то поделите его напополам и используйте как радиус в формуле из предыдущего шага. Либо обнаружьте одну шестую часть от возведенного в куб диаметра, умноженного на число Пи: V=?*d?/6.
3. Если вестим объем (v) цилиндра, в тот, что вписана сфера, то для нахождения ее объема определите, чему равны две трети от вестимого объема цилиндра: V=?*v.
4. Если вестима средняя плотность (p) материала, из которого состоит сфера, и ее масса (m), то этого тоже довольно для определения объема – поделите второе на первое: V=m/p.
5. Воспользуйтесь какими-нибудь мерными емкостями в качестве подручных средств для измерения объема сосуда сферической формы. Скажем, наполните его водой, измеряя с подмогой мерной емкости число заливаемой жидкости. Полученное значение в литрах переведите в кубические метры – эта единица принята в интернациональной системе СИ для измерения объема. В качестве показателя перевода из литров в кубометры используйте число 1000, потому что один литр приравнен к одному кубическому дециметру, а их в всякий кубический метр вмещается ровно тысяча штук.
6. Используйте правило измерения, противоположный описанному в предыдущем шаге, если тело в форме сферы невозможно наполнить жидкостью, но дозволено погрузить в нее. Заполните мерный сосуд водой, подметьте ярус, погрузите измеряемое сферическое тело в жидкость и по разнице ярусов определите число вытесненной воды. После этого переведите полученный итог из литров в кубометры так же, как это описано в предыдущем шаге.
Заполните мерный сосуд водой, подметьте ярус, погрузите измеряемое сферическое тело в жидкость и по разнице ярусов определите число вытесненной воды. После этого переведите полученный итог из литров в кубометры так же, как это описано в предыдущем шаге.
Видео по теме
Ремонт, переезд, покраска объекта – все это затребует вычисления площади. Не проступок припомнить школьную программу.
Инструкция
1. Припомним, что такое площадь. Площадь — это мера плоской фигуры по отношению к стандартной фигуре. Либо правильная величина, численное значение которой владеет следующими свойствами: Если фигуру дозволено разбить на части, которые будут являться примитивными фигурами, то площадь такой фигуры будет равна сумме площадей ее частей Площадь квадрата со стороной, которая равна единице измерения, равна единице Равные фигуры владеют равными площадямиИз этих правил следует, что площадь это не определенная величина, то есть площадь дает только условную колляцию какой-нибудь фигуре.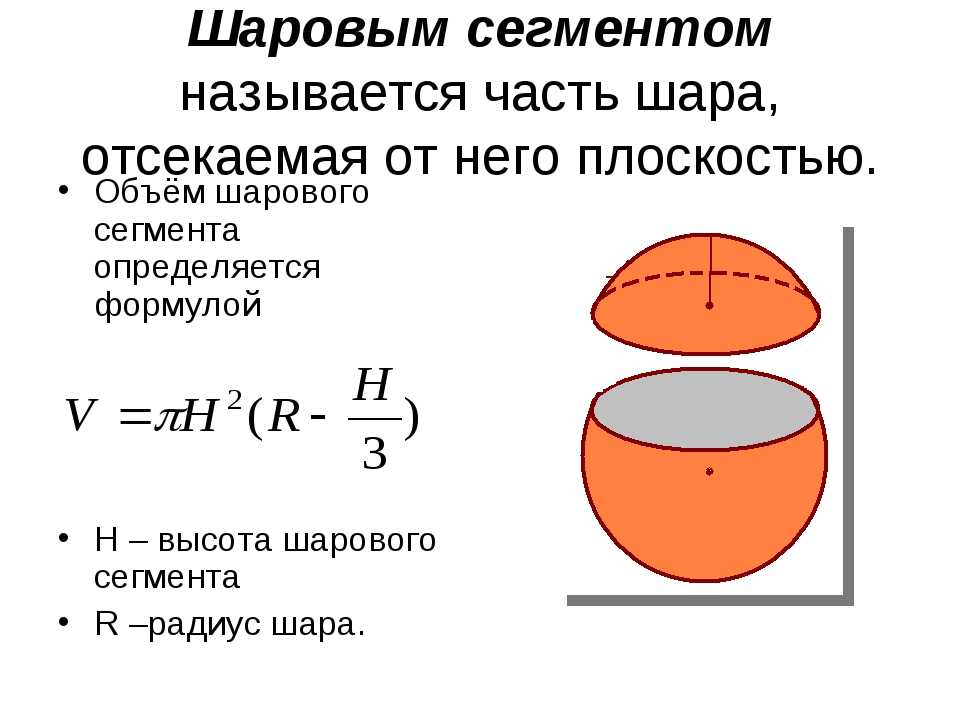 Когда нужно обнаружить площадь произвольной фигуры, то надобно вычислить, сколько квадратов со стороной (которая равняется единице), эта фигура в себя может вместить.
Когда нужно обнаружить площадь произвольной фигуры, то надобно вычислить, сколько квадратов со стороной (которая равняется единице), эта фигура в себя может вместить.
2. Пример: Возьмем фигуру – прямоугольник, такой, в котором квадратный сантиметр укладывается в шесть раз. Тогда площадь такого прямоугольника будет равняться – 6 см2. Если взять больше трудную фигуру, скажем, трапецию, то получится что: Если трапеция такой величины, что квадратный сантиметр укладывается в нее только два раза, а третья часть не влезает целиком и остается маленький треугольник. Дабы измерить площадь этого оставшегося треугольника необходимо применить к нему доли квадратного сантиметра, дозволено взять миллиметр. Правда, данный метод для трудных фигур не дюже комфортный. Следственно для вычисления площади различных фигур существуют разные формулы. Если надобно вычислить площадь определенной фигуры, то дозволено взять учебник по геометрии и припомнить материал, тот, что когда-то проходили в школе. Так, формула площади куба: площадь куба равна числу граней умноженное на площадь грани, т.е. 6 * a2
Так, формула площади куба: площадь куба равна числу граней умноженное на площадь грани, т.е. 6 * a2
Видео по теме
Все планеты ясной системы имеют форму шара . Помимо того, шарообразную либо близкую к таковой форму имеют и многие объекты, сделанные человеком, включая детали технических устройств. Шар, как и всякое тело вращения, имеет ось, которая совпадает с диаметром. Впрочем это не исключительное главное качество шара . Ниже рассмотрены основные свойства этой геометрической фигуры и метод нахождения ее площади.
Инструкция
1. Если взять полукруг либо круг и провернуть его вокруг своей оси, получится тело, называемое шаром. Иными словами, шаром именуется тело, ограниченное сферой. Сфера представляет собой оболочку шара , и ее сечением является окружность. От шара она отличается тем, что является полой. Ось как у шара , так и у сферы совпадает с диаметром и проходит через центр. Радиусом шара именуется отрезок, проложенный от его центра до всякий внешней точки.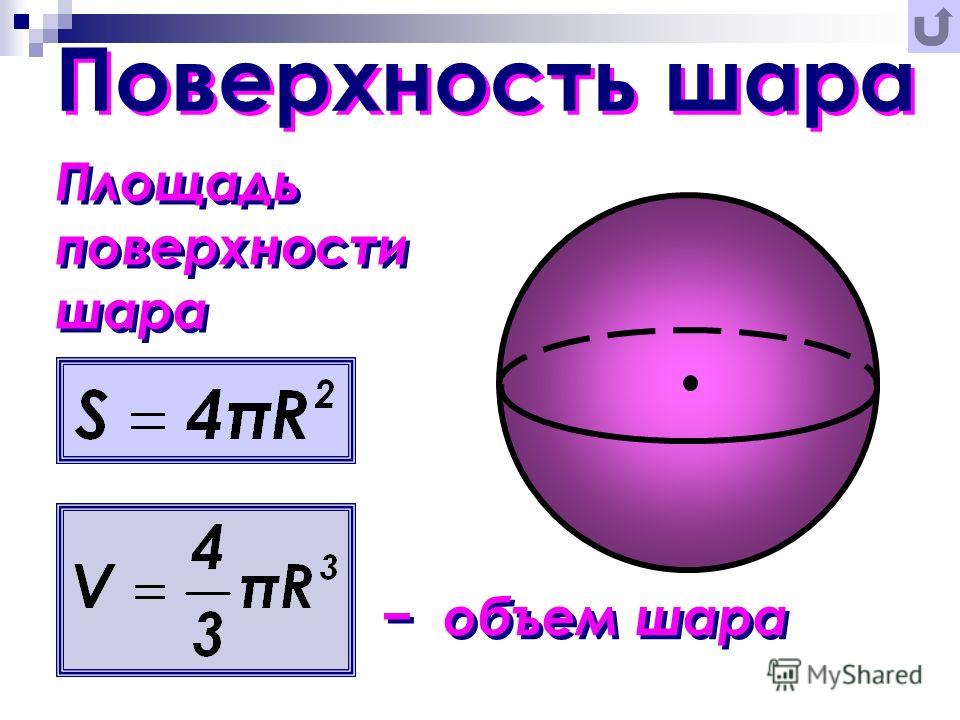 В противоположность сфере, сечения шара представляют собой круги. Форму, близкую к шарообразной, имеет множество планет и небесных тел. В различных точках шара имеются идентичные по форме, но неодинаковые по величине, так называемые сечения – круги различной площади.
В противоположность сфере, сечения шара представляют собой круги. Форму, близкую к шарообразной, имеет множество планет и небесных тел. В различных точках шара имеются идентичные по форме, но неодинаковые по величине, так называемые сечения – круги различной площади.
2. Шар и сфера – взаимозаменяемые тела, в различие от конуса, невзирая на то, что конус также является телом вращения. Сферические поверхности неизменно в своем сечении образуют окружность, самостоятельно от того, как именно она вращается – по горизонтали либо по вертикали. Коническая же поверхность получается лишь при вращении треугольника по его оси, перпендикулярной основанию. Следственно конус, в различие от шара , и не считается взаимозаменяемым телом вращения.
3. Самый огромный из допустимых кругов получается при сечении шара плоскостью, проходящей через центр О. Все круги, которые проходят через центр О, пересекаются между собой в одном диаметре. Радиус неизменно равен половине диаметра. 2
2
5. Данная формула может быть пригодна в том случае, если вестим либо диаметр, либо радиус шара либо сферы. Впрочем, эти параметры приведены в качестве условий не во всех геометрических задачах. Существуют и такие задачи, в которых шар вписан в цилиндр. В этом случае, следует воспользоваться теоремой Архимеда, суть которой заключается в том, что площадь поверхности шара в полтора раза поменьше полной поверхности цилиндра:S = 2/3 S цил., где S цил. –площадь полной поверхности цилиндра.
Видео по теме
Шаром называют простейшую объемную фигуру геометрически положительной формы, все точки пространства внутри границ которой удалены от ее центра на расстояние, не превышающее радиуса. Поверхность, образуемая большинством максимально удаленных от центра точек, именуется сферой. Для количественного выражения меры пространства, заключенного внутри сферы, предуготовлен параметр, тот, что именуется объемом шара.
Инструкция
1.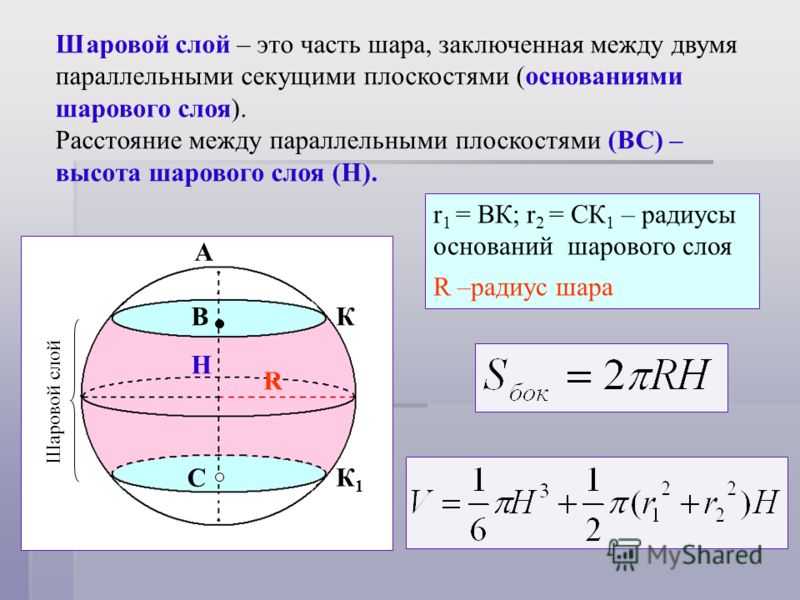 Если требуется измерить объем шара не теоретически, а только подручными средствами, то сделать это дозволено, скажем, определив объем вытесненной им воды. Данный метод применим в том случае, когда есть вероятность разместить шар в какую-нибудь соизмеримую ему емкость – мензурку, стакан, банку, ведро, бочку, бассейн и т.д. В этом случае перед помещением шара подметьте ярус воды, сделайте это вторично позже полного его погружения, а после этого обнаружьте разность между отметками. Традиционно мерная емкость заводского производства имеет деления, показывающие объем в литрах и производных от него единицах – миллилитрах, декалитрах и т.д. Если полученное значение нужно перевести в кубические метры и кратные ему единицы объема, то исходите из того, что один литр соответствует одному кубическому дециметру либо одной тысячной доле кубометра.
Если требуется измерить объем шара не теоретически, а только подручными средствами, то сделать это дозволено, скажем, определив объем вытесненной им воды. Данный метод применим в том случае, когда есть вероятность разместить шар в какую-нибудь соизмеримую ему емкость – мензурку, стакан, банку, ведро, бочку, бассейн и т.д. В этом случае перед помещением шара подметьте ярус воды, сделайте это вторично позже полного его погружения, а после этого обнаружьте разность между отметками. Традиционно мерная емкость заводского производства имеет деления, показывающие объем в литрах и производных от него единицах – миллилитрах, декалитрах и т.д. Если полученное значение нужно перевести в кубические метры и кратные ему единицы объема, то исходите из того, что один литр соответствует одному кубическому дециметру либо одной тысячной доле кубометра.
2. Если знаменит материал, из которого изготовлен шар, и плотность этого материала дозволено узнать, скажем, из справочника, то определить объем дозволено взвесив данный предмет. Примитивно поделите итог взвешивания на справочную плотность вещества изготовления: V=m/p.
Примитивно поделите итог взвешивания на справочную плотность вещества изготовления: V=m/p.
3. Если радиус шара вестим из условий задачи либо его дозволено измерить, то для вычисления объема дозволено применять соответствующую математическую формулу. Умножьте учетверенное число Пи на третью степень радиуса, а полученный итог поделите на тройку: V=4*?*r?/3. Скажем, при радиусе в 40см объем шара составит 4*3,14*40?/3 = 267946,67см? ? 0,268м?.
4. Измерить диаметр почаще бывает проще, чем радиус. В этом случае нет необходимости разделять его напополам для применения с формулой из предыдущего шага – класснее упростить саму формулу. В соответствии с преобразованной формулой умножьте число Пи на диаметр в третьей степени, а итог поделите на шестерку: V=?*d?/6. Скажем, шар диаметром в 50см должен иметь объем в 3,14*50?/6 = 65416,67см? ? 0,654м?.
Задачи на вычисление площади круга зачастую встречаются в школьном курсе геометрии. Дабы обнаружить площадь круга, нужно знать длину диаметра либо радиуса окружности, в которую он заключен.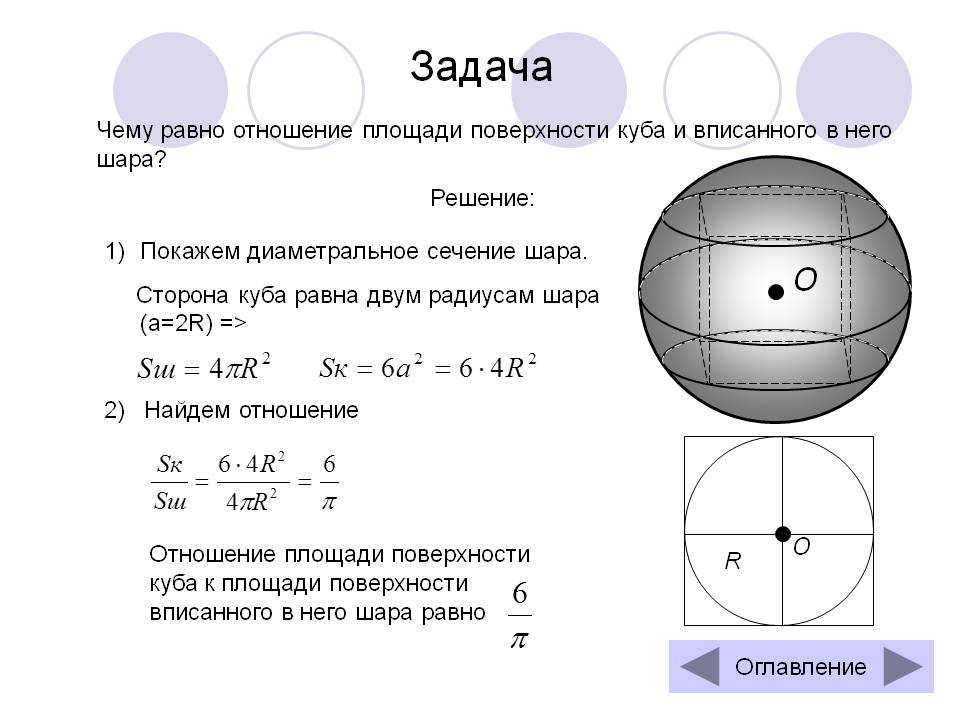 2, где R, r – радиусы внешней и внутренней окружностей кольца соответственно.
2, где R, r – радиусы внешней и внутренней окружностей кольца соответственно.
Полезный совет
Существует Интернациональный день числа «пи», тот, что отмечается 14 марта. Точное время наступления триумфальной даты — 1 час 59 минут 26 секунд, согласно цифрам числа — 3,1415926…
Видео по теме
Обратите внимание!
Увлекательно: объем шара с диаметром, превышающим в три раза диаметр иного шара, огромнее суммарного объема 3 таких шаров в 9 раз.
Полезный совет
Дабы развить у детей увлечение к математическим вычислениям, предлагайте в качестве примеров для расчета окружающие предметы: мяч, арбуз, клубок бабушкиной пряжи. Это наглядно и потому увлекательно.
Определение.
Сфера (поверхность шара ) — это совокупность всех точек в трехмерном пространстве, которые находятся на одинаковом расстоянии от одной точки, называемой центром сферы (О).
Сферу можно описать, как объёмную фигуру, которая образуется вращением окружности вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.
Определение.
Шар — это совокупность всех точек в трехмерном пространстве, расстояние от которых не превышает определенного расстояния до точки, называемой центром шара (О) (совокупность всех точек трехмерного пространства ограниченных сферой).
Шар можно описать как объёмную фигуру, которая образуется вращением круга вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.
Определение. Радиус сферы (шара) (R) — это расстояние от центра сферы (шара) O к любой точке сферы (поверхности шара).
Определение. Диаметр сферы (шара) (D) — это отрезок, соединяющий две точки сферы (поверхности шара) и проходящий через ее центр.
Формула. Объём шара :
| V = | 4 | π R 3 = | 1 | π D 3 |
| 3 | 6 |
Формула. Площадь поверхности сферы через радиус или диаметр:
S = 4π R 2 = π D 2
Уравнение сферы
1. Уравнение сферы с радиусом R и центром в начале декартовой системе координат :
Уравнение сферы с радиусом R и центром в начале декартовой системе координат :
x 2 + y 2 + z 2 = R 2
2. Уравнение сферы с радиусом R и центром в точке с координатами (x 0 , y 0 , z 0) в декартовой системе координат :
(x — x 0) 2 + (y — y 0) 2 + (z — z 0) 2 = R 2
Определение. Диаметрально противоположными точками называются любые две точки на поверхности шара (сфере), которые соединены диаметром.
Основные свойства сферы и шара
1. Все точки сферы одинаково удалены от центра.
2. Любое сечение сферы плоскостью является окружностью.
3. Любое сечение шара плоскостью есть кругом.
4. Сфера имеет наибольший объём среди всех пространственных фигур с одинаковой площадью поверхности.
5. Через любые две диаметрально противоположные точки можно провести множество больших окружностей для сферы или кругов для шара.
6. Через любые две точки, кроме диаметрально противоположных точек, можно провести только одну большую окружность для сферы или большой круг для шара.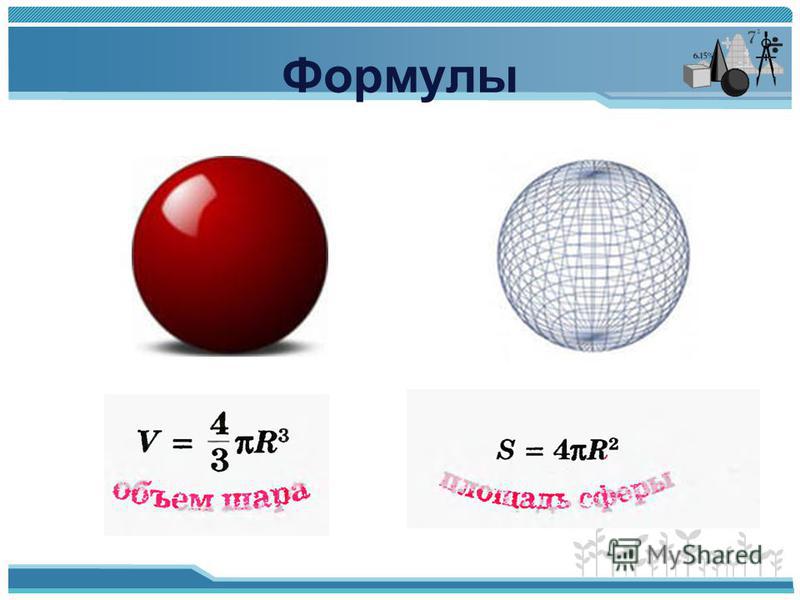
7. Любые два больших круга одного шара пересекаются по прямой, проходящей через центр шара, а окружности пересекаются в двух диаметрально противоположных точках.
8. Если расстояние между центрами любых двух шаров меньше суммы их радиусов и больше модуля разности их радиусов, то такие шары пересекаются , а в плоскости пересечения образуется круг.
Секущая, хорда, секущая плоскость сферы и их свойства
Определение. Секущая сферы — это прямая, которая пересекает сферу в двух точках. Точки пересечения называются точками протыкания поверхности или точками входа и выхода на поверхности.
Определение. Хорда сферы (шара) — это отрезок, соединяющий две точки сферы (поверхности шара).
Определение. Секущая плоскость — это плоскость, которая пересекает сферу.
Определение. Диаметральная плоскость — это секущая плоскость, проходящая через центр сферы или шара, сеченме образует соответственно большую окружность и большой круг . Большая окружность и большой круг имеют центр, который совпадают с центром сферы (шара).
Большая окружность и большой круг имеют центр, который совпадают с центром сферы (шара).
Любая хорда, проходящая через центр сферы (шара) является диаметром.
Хорда является отрезком секущей прямой.
Расстояние d от центра сферы до секущей всегда меньше чем радиус сферы:
d
Расстояние m между секущей плоскостью и центром сферы всегда меньше радиуса R:
m
Местом сечения секущей плоскости на сфере всегда будет малая окружность , а на шаре местом сечения будет малый круг . Малая окружность и малый круг имеют свои центры, не совпадающих с центром сферы (шара). Радиус r такого круга можно найти по формуле:
r = √R 2 — m 2 ,
Где R — радиус сферы (шара), m — расстояние от центра шара до секущей плоскости.
Определение. Полусфера (полушар) — это половина сферы (шара), которая образуется при ее сечении диаметральной плоскостью.
Касательная, касательная плоскость к сфере и их свойства
Определение. Касательная к сфере — это прямая, которая касается сферы только в одной точке.
Касательная к сфере — это прямая, которая касается сферы только в одной точке.
Определение. Касательная плоскость к сфере — это плоскость, которая соприкасается со сферой только в одной точке.
Касательная пряма (плоскость) всегда перпендикулярна радиусу сферы проведенному к точке соприкосновения
Расстояние от центра сферы до касательной прямой (плоскости) равно радиусу сферы.
Определение. Сегмент шара — это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Высотой сегмента h называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента.
Формула. Площадь внешней поверхности сегмента сферы с высотой h через радиус сферы R:
S = 2π Rh
| шара цилиндра | |
| Площадь поверхности цилиндра: | ед.2 |
Площадь поверхности шара формула: Площадь поверхности цилиндра формула: | |
Площадь поверхности сферы с диаметром
LearnPracticeDownload
Площадь поверхности сферы в пересчете на диаметр – это пространство, занимаемое изогнутой поверхностью сферы в пересчете на ее диаметр. Сфера – это трехмерная круглая форма, не имеющая ни краев, ни вершин. В этом разделе мы обсудим площадь поверхности сферы с точки зрения диаметра вместе с решенными примерами. Давайте начнем с предварительных знаний, необходимых для понимания темы, площади поверхности сферы с точки зрения диаметра.
| 1. | Что такое площадь поверхности сферы с точки зрения диаметра? |
2. | Формула площади поверхности сферы через диаметр |
| 3. | Как найти площадь поверхности сферы по диаметру? |
| 4. | Часто задаваемые вопросы о площади поверхности сферы с точки зрения диаметра |
Что такое площадь поверхности сферы с точки зрения диаметра?
Площадь поверхности сферы в пересчете на диаметр – это площадь, покрытая криволинейной поверхностью сферы в пересчете на ее диаметр. Сфера – это трехмерная фигура, полностью круглая по форме. Математически сфера определяется как набор точек, находящихся на одинаковом расстоянии (r) от общей точки (центра сферы) в трехмерном пространстве. Эта общая точка называется центром сферы, а расстояние между любой точкой и центром называется радиусом сферы. Площадь поверхности сферы выражается в квадратных единицах, таких как м 2 , см 2 , дюймы 2 или футы 2 и т. д.
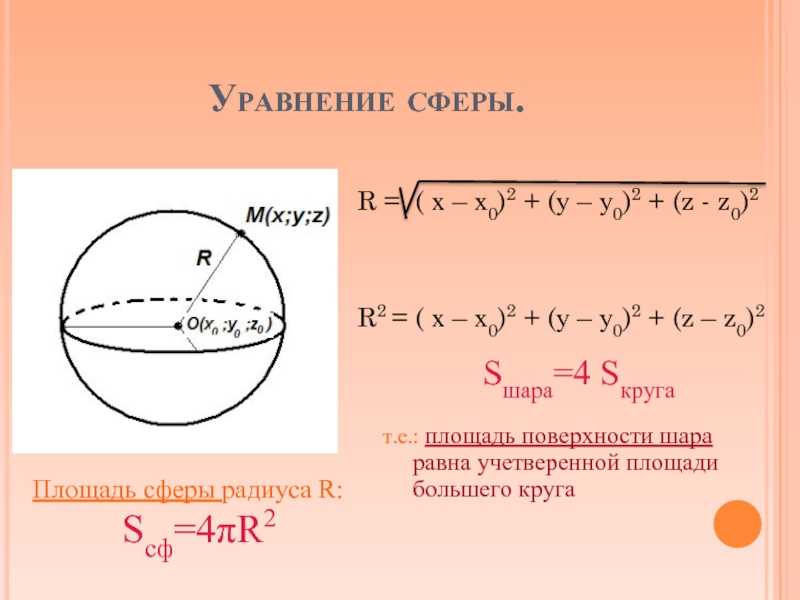
Формула площади поверхности сферы через диаметр
Для сферы, если указан ее диаметр, то площадь ее поверхности может быть определена как πD 2 .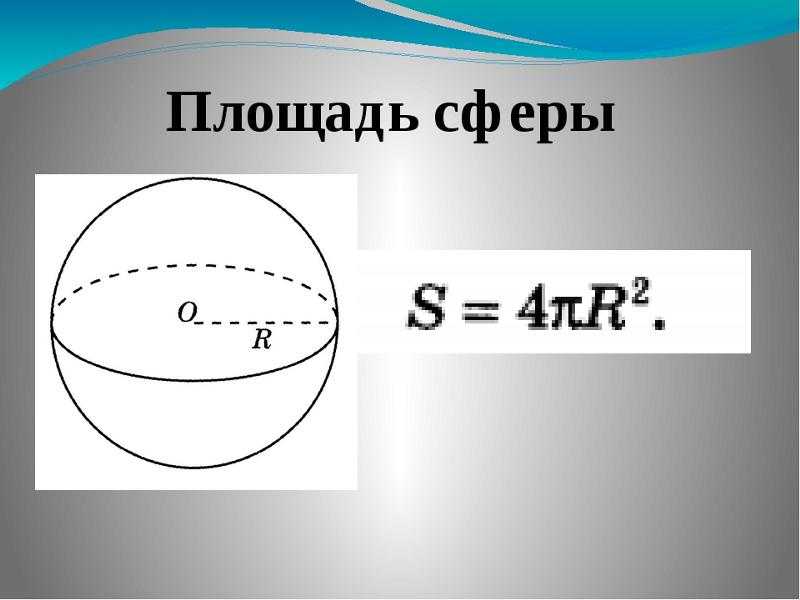
Таким образом, площадь поверхности сферы (в пересчете на диаметр) = площадь криволинейной поверхности сферы = πD 2
Площадь поверхности сферы (в пересчете на радиус) = 4πr 2 где r — радиус сферы
Как найти площадь поверхности сферы через диаметр?
Как мы узнали из предыдущего раздела, площадь поверхности сферы равна πD 2 . Таким образом, мы следуем шагам, показанным ниже, чтобы найти площадь поверхности сферы с точки зрения диаметра.
- Шаг 1: Определите диаметр сферы и назовите его D.
- Шаг 2: Найдите площадь поверхности сферы через диаметр по формуле πD 2 .
- Шаг 3: Представьте окончательный ответ в квадратных единицах.
Пример: Найдите площадь поверхности сферы диаметром 7 единиц. (Используйте π = 22/7)
Решение: Учитывая D = 7 единиц
Площадь поверхности полушария = πD 2 = (22/7)(7) 2 = 22 × 7 = 154 единицы 2
Ответ:
Пример 1: Найти площадь поверхности сферы диаметром = 21 единица.
 (Используйте π = 22/7)
(Используйте π = 22/7)Решение: Дан диаметр сферы (D) = 21 единица
Площадь поверхности сферы = πD 2 = (22/7) 21 2 = 22 × 3 × 21 = 1386 единиц 2Пример 2: Найдите диаметр полушария, если площадь его поверхности составляет 308 единиц 2 . (Используйте π = 22/7)
Решение: Учитывая A = 308 единиц 2
⇒ π D 2 = 308
⇒ D 2 = 308/(2π) = 49
⇒ D = 7 единицОтвет: Диаметр сферы 7 единиц
перейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о площади поверхности сферы с точки зрения диаметра
Что такое площадь поверхности сферы с точки зрения диаметра?
Площадь поверхности сферы в пересчете на диаметр — это площадь, покрываемая сферой в пересчете на ее диаметр.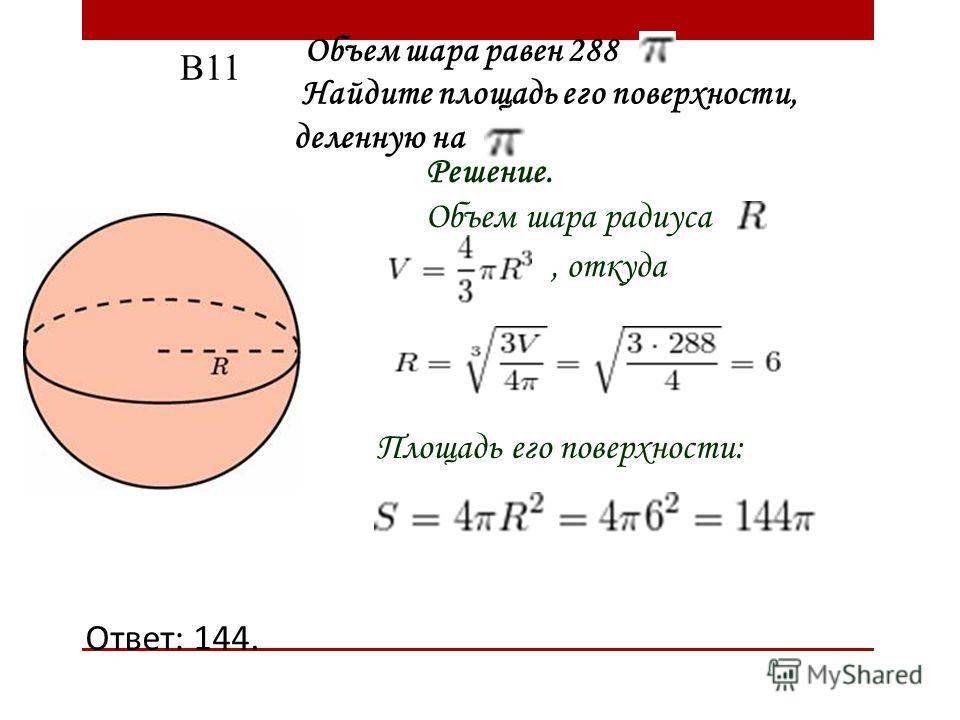 Сфера — это полученное трехмерное тело круглой формы, не имеющее ребер или вершин. Общая площадь поверхности сферы такая же, как площадь ее изогнутой поверхности из-за отсутствия ребер или вершин.
Сфера — это полученное трехмерное тело круглой формы, не имеющее ребер или вершин. Общая площадь поверхности сферы такая же, как площадь ее изогнутой поверхности из-за отсутствия ребер или вершин.
Какова формула площади поверхности сферы через диаметр?
Формула площади поверхности сферы в пересчете на диаметр дается как πD 2 где «D» — диаметр сферы. Эта формула показывает зависимость площади поверхности сферы от диаметра сферы.
Какова единица площади поверхности сферы в терминах диаметра?
Единица площади поверхности сферы в пересчете на диаметр указывается в квадратных единицах, например, м 2 , см 2 , дюймы 2 или футы 2 и т. д.
Как найти площадь поверхности сферы в терминах диаметра?
Мы используем шаги, показанные ниже, чтобы найти площадь поверхности сферы с точки зрения диаметра.
- Шаг 1: Определите диаметр сферы.
- Шаг 2: Определите площадь поверхности сферы в пересчете на диаметр по формуле πD 2 .

- Шаг 3: Теперь представьте окончательный ответ в квадратных единицах.
Как найти диаметр сферы, если известна площадь поверхности сферы в пересчете на диаметр?
Мы используем шаги, показанные ниже, чтобы найти диаметр сферы, если площадь поверхности сферы выражается в диаметре.
- Шаг 1: Определите данные размеры сферы и пусть это будет «D».
- Шаг 2: Подставьте значения в формулу πD 2 .
- Шаг 3: Решите для «D»
- Шаг 3: Теперь представьте окончательный ответ в квадратных единицах.
Что произойдет с площадью поверхности сферы с точки зрения диаметра, если ее диаметр удвоится?
Площадь поверхности сферы в пересчете на диаметр увеличивается в четыре раза, если ее диаметр удваивается, поскольку буква «D» в формуле заменяется на «2D», что дает формулу πD 2 = π(2D) 2 = 4 (πD 2 ), что в четыре раза больше исходной площади поверхности сферы.
Что произойдет с площадью поверхности сферы с точки зрения диаметра, если ее диаметр уменьшить вдвое?
Площадь поверхности сферы в пересчете на диаметр становится одной четвертой от ее первоначального значения , если ее диаметр уменьшается вдвое, поскольку буква «D» в формуле заменяется на «D/2», что дает формулу πD 2 = π(D /2) 2 = (1/4) × (πD 2 ), что составляет одну четвертую исходной площади поверхности сферы.
Скачать БЕСПЛАТНЫЕ учебные материалы
Рабочий лист площади поверхности
Рабочие листы по математике и
наглядный учебный план
Объяснение урока: Площади поверхности сфер
В этом объяснении мы научимся использовать формулу площади поверхности сферы в через радиус или диаметр, чтобы найти площадь, радиус или диаметр сферы.
Определение: площадь поверхности сферы
Сфера является трехмерным аналогом окружности. Его можно определить как идеально закругленный объект, не имеющий ни краев, ни вершин.
Все точки, расположенные на поверхности сферы, находятся на равном расстоянии от центра. Это расстояние называется радиусом, который обычно обозначается 𝑟.
Интересным свойством сферы является то, что среди всех трехмерных фигур одинакового объема она имеет наименьшую площадь поверхности. По этой причине сферы возникают в различных физических системах, где площадь поверхности минимальна, например, в каплях воды и мыльных пузырях!
Площадь поверхности сферы можно рассчитать по следующей формуле.
Формула: Площадь поверхности сферы
Площадь поверхности 𝐴 сферы радиуса 𝑟 определяется по формуле 𝐴=4𝜋𝑟.
Поскольку 𝜋=3,14159… — это просто число, это означает, что, пока мы знаем радиус сферы, мы всегда можем применить эту формулу, чтобы найти площадь ее поверхности.
Начнем с простого примера.
Пример 1. Нахождение площади поверхности сферы по ее радиусу
Найдите площадь поверхности данной сферы с точностью до десятых.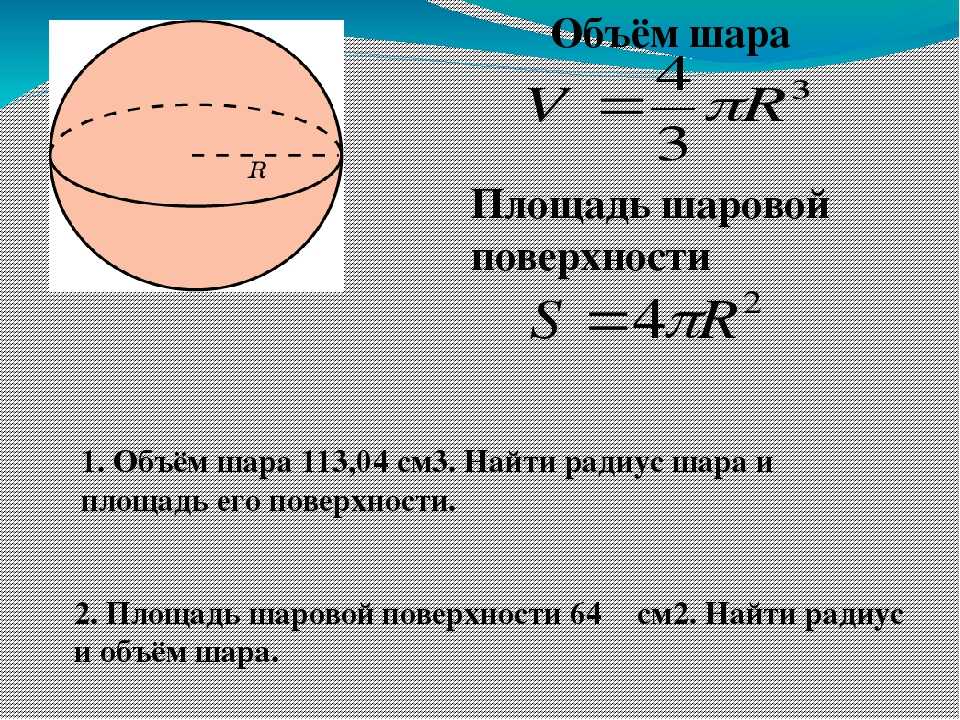
Ответ
Напомним, что площадь поверхности 𝐴 сферы радиуса 𝑟 определяется по формуле 𝐴=4𝜋𝑟.
Судя по диаграмме, эта сфера имеет радиус 𝑟=6, поэтому мы можем подставить это значение в формулу и переставить, чтобы получить 𝐴=4×𝜋×𝑟=4×𝜋×6=4×𝜋×36=4×36×𝜋=144×𝜋=452,389….
Нас попросили округлить ответ до десятых. Помните, что цифра десятых — это первая цифра после запятой, в данном случае это 3. Следующая за ней цифра (цифра сотых) — это 8, поэтому ответ округляется до 452,4 до ближайшей десятой.
Так как радиус сферы указан в сантиметрах, площадь поверхности должна быть в квадратных сантиметрах. Площадь поверхности сферы, округленная до десятых, равна 452,4 см 2 .
Далее мы рассмотрим пример, в котором нам дан диаметр сферы, а не радиус. Наш подход очень похож, но с одним дополнительным шагом. Всегда проверяйте, указан ли вам в вопросе радиус или диаметр.
Пример 2. Определение площади поверхности сферы по ее диаметру с использованием аппроксимации Pi
Найдите площадь поверхности шара диаметром 12,6 см. Используйте 𝜋=227.
Используйте 𝜋=227.
Ответ
Напомним, что площадь поверхности 𝐴 сферы радиуса 𝑟 определяется по формуле 𝐴=4𝜋𝑟.
Здесь нам дан диаметр сферы 12,6 см, что вдвое больше ее радиуса. Чтобы применить формулу для расчета площади поверхности, нам сначала нужно вычислить радиус, поэтому мы разделим диаметр вдвое, чтобы получить 𝑟=12,6÷2=6,3. Тогда, подставляя 𝑟 в формулу, имеем 𝐴=4×𝜋×𝑟=4×𝜋×(6,3)=4×𝜋×39.69=4×39,69×𝜋=158,76×𝜋.
Обратите внимание, что в вопросе нам дано приближение 227 для 𝜋, поэтому подстановка этого значения дает 𝐴=158,76×𝜋=158,76×227=158,76×227=3492,727=498,96.
Поскольку диаметр указан в сантиметрах, площадь поверхности должна быть в квадратных сантиметрах; площадь поверхности сферы 498,96 см 2 .
Формула площади поверхности сферы содержит только две переменные, 𝐴 и 𝑟. Это означает, что если нам дана площадь поверхности сферы, то мы всегда можем работать в обратном направлении, чтобы найти ее радиус. Как только мы определили радиус, при необходимости мы можем удвоить это значение, чтобы получить диаметр. В следующем примере показано, как изменить формулу для решения такого типа задач.
Как только мы определили радиус, при необходимости мы можем удвоить это значение, чтобы получить диаметр. В следующем примере показано, как изменить формулу для решения такого типа задач.
Пример 3. Нахождение диаметра сферы по площади ее поверхности
Каков диаметр сферы, площадь поверхности которой равна 36𝜋 см 2 ?
Ответ
Сначала вспомним формулу для расчета площади поверхности 𝐴 сферы радиусом 𝑟: 𝐴=4𝜋𝑟.
Нам дана площадь поверхности, 𝐴=36𝜋, поэтому подставляя в формулу, мы имеем 36×𝜋=4×𝜋×𝑟.
Для удобства нам была дана площадь поверхности в терминах 𝜋, что позволяет нам аккуратно разделить обе части нашего уравнения на 𝜋, чтобы получить 36=4×𝑟.
Затем мы делим обе части на 4, что дает 9=𝑟.
Теперь мы можем найти радиус нашей сферы, взяв квадратные корни из обеих частей этого уравнения:
√9=√𝑟,
поэтому 3=𝑟, что совпадает с 𝑟=3. Стоит отметить, что на самом деле у этого уравнения есть два решения. Хотя мы могли бы сказать, что 𝑟=±3, в этом случае 𝑟 представляет собой длину, и поэтому мы можем игнорировать отрицательное решение.
Хотя мы могли бы сказать, что 𝑟=±3, в этом случае 𝑟 представляет собой длину, и поэтому мы можем игнорировать отрицательное решение.
Площадь поверхности измеряется в квадратных сантиметрах, поэтому радиус измеряется в сантиметрах. Удвоив значение радиуса, получим, что диаметр сферы равен 2×3=6см.
Обратите внимание, что в приведенном выше примере мы подставили значение 𝐴, площади поверхности сферы, в формулу 𝐴=4𝜋𝑟, а затем изменили порядок, чтобы найти значение радиуса 𝑟. Альтернативный подход к этой стратегии состоит в том, чтобы изменить формулу, чтобы сделать 𝑟 субъектом, а затем напрямую заменить 𝐴 следующим образом.
Начиная с исходной формулы 𝐴=4𝜋𝑟 и переписывая правую часть, чтобы включить знаки умножения, мы имеем 𝐴=4×𝜋×𝑟.
Разделив обе части на 4, а затем на 𝜋, получим 𝐴4𝜋=𝑟.
Наконец, мы извлекаем квадратные корни из обеих частей: 𝐴4𝜋=√𝑟, так 𝑟=𝐴4𝜋.
Опять же, мы можем смело игнорировать отрицательное решение при определении этого отношения, поэтому мы получили нашу формулу для радиуса.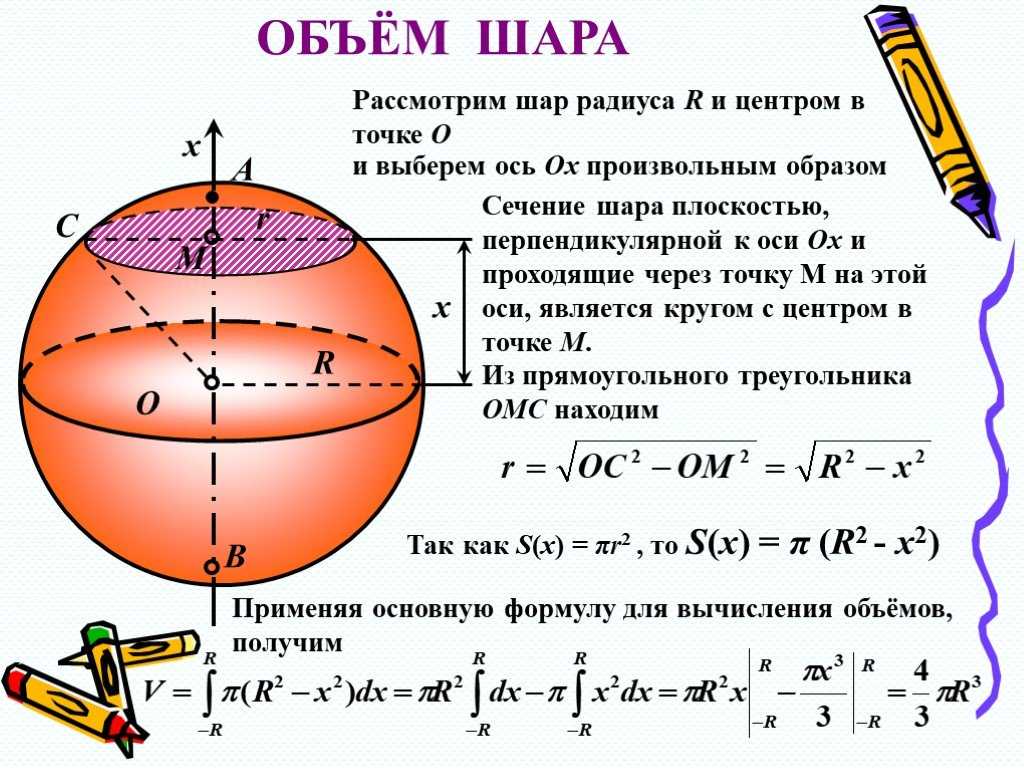 Если бы мы подставили 𝐴=36𝜋 прямо в эту формулу, мы бы получили 𝑟=3. Как и ожидалось, это то же самое значение радиуса, которое мы вычислили в предыдущем примере.
Если бы мы подставили 𝐴=36𝜋 прямо в эту формулу, мы бы получили 𝑟=3. Как и ожидалось, это то же самое значение радиуса, которое мы вычислили в предыдущем примере.
Формула: радиус сферы с учетом площади ее поверхности
Радиус 𝑟 сферы с площадью поверхности 𝐴 определяется по формуле 𝑟=𝐴4𝜋.
Теперь мы рассмотрим очень важную концепцию при изучении сфер: большой круг.
Определение: Большой круг
Большой круг — это самый большой круг, который можно нарисовать на любой заданной сфере. Он может быть образован на поверхности сферы пересечением плоскости, проходящей через центр сферы. Поскольку центр большого круга совпадает с центром родительской сферы, он также будет иметь общий радиус 𝑟.
Большой круг всегда делит сферу на две равные полусферы, как показано на рис. 1.
На поверхности сферы можно рисовать другие окружности, которые не проходят через центр сферы. Эти круги не будут большими кругами и будут иметь меньший радиус, чем большой круг (и родительская сфера).
На рис. 2 показан большой круг радиуса 𝑟 и другой круг, лежащий на поверхности сферы и имеющий радиус 𝑟. Меньший круг делит сферу на две неравные части.
Центры обеих окружностей имеют общую ось, которая, по определению большого круга, также проходит через центр сферы.
На рис. 3 показан вид сверху вниз на сферу, показанную на рис. 2.
Принимая этот вид, мы ясно видим, что радиус большого круга 𝑟 является радиусом сферы. Мы также можем видеть для сравнения, что радиус любого другого круга на поверхности сферы (обозначенной 𝑟 в этом примере) будет меньше, чем радиус сферы, поэтому 𝑟𝑟.
Наконец, мы знаем, что все круги на данной сфере, классифицируемые как большой круг, будут иметь одинаковый радиус 𝑟. Таким образом, мы можем заключить, что все большие окружности на сфере будут идентичны друг другу, даже если они занимают разное множество точек на поверхности сферы.
Обратите внимание, что мы обнаруживаем еще один интересный факт, вспоминая формулу площади круга 𝐴 через его радиус:
𝐴=𝜋𝑟.
Сравнивая это с формулой площади поверхности сферы, мы видим, что площадь сферы будет ровно в четыре раза больше площади круга с таким же радиусом, который, как мы теперь знаем, является большим кругом. ; то есть, 𝐴=4𝜋𝑟=4×𝜋𝑟=4𝐴.
Формула: площадь поверхности сферы, учитывая ее большую окружность
𝐴: 𝐴=4𝐴.
Так как большой круг разделяет некоторые свойства с родительской сферой, вам может быть предложено решить вопросы, используя взаимосвязь между этими двумя формами. Давайте посмотрим на пример.
Пример 4. Нахождение площади поверхности сферы по информации о ее большом круге
Найдите площадь поверхности сферы с точностью до десятых, если площадь большого круга равна 441 𝜋 в 2 .
Ответ
Напомним, что площадь поверхности 𝐴 сферы радиуса 𝑟 определяется по формуле 𝐴=4𝜋𝑟.
Наша стратегия будет заключаться в том, чтобы вычислить значение 𝐴 из площади большого круга, заданного в вопросе.
Любой большой круг имеет тот же радиус, что и его родительская сфера. Следовательно, площадь этого большого круга 𝐴 будет определяться формулой 𝐴=𝜋𝑟.
Используя эту последнюю формулу, мы можем заменить 𝜋𝑟 в формуле площади поверхности следующим образом: 𝐴=4𝜋𝑟=4×𝜋𝑟=4𝐴.
Теперь, когда мы выразили площадь поверхности сферы через площадь ее большого круга, мы можем использовать тот факт, что 𝐴=441𝜋, чтобы получить 𝐴=4𝐴=4×441𝜋=4×441×𝜋=1764×𝜋=5541,769….
Исходя из вопроса, ответ нужно округлить до десятых. Цифра десятых — это первая цифра после запятой, которая здесь равна 7. Следующая за ней цифра (цифра сотых) — 6, поэтому наш ответ нужно округлить до 5 541,8 до ближайшей десятой.
Площадь большого круга указана в квадратных дюймах, поэтому площадь поверхности сферы также будет выражена в квадратных дюймах. Мы заключаем, что площадь поверхности сферы составляет 5 541,8 в 2 с округлением до ближайшей десятой доли квадратного дюйма.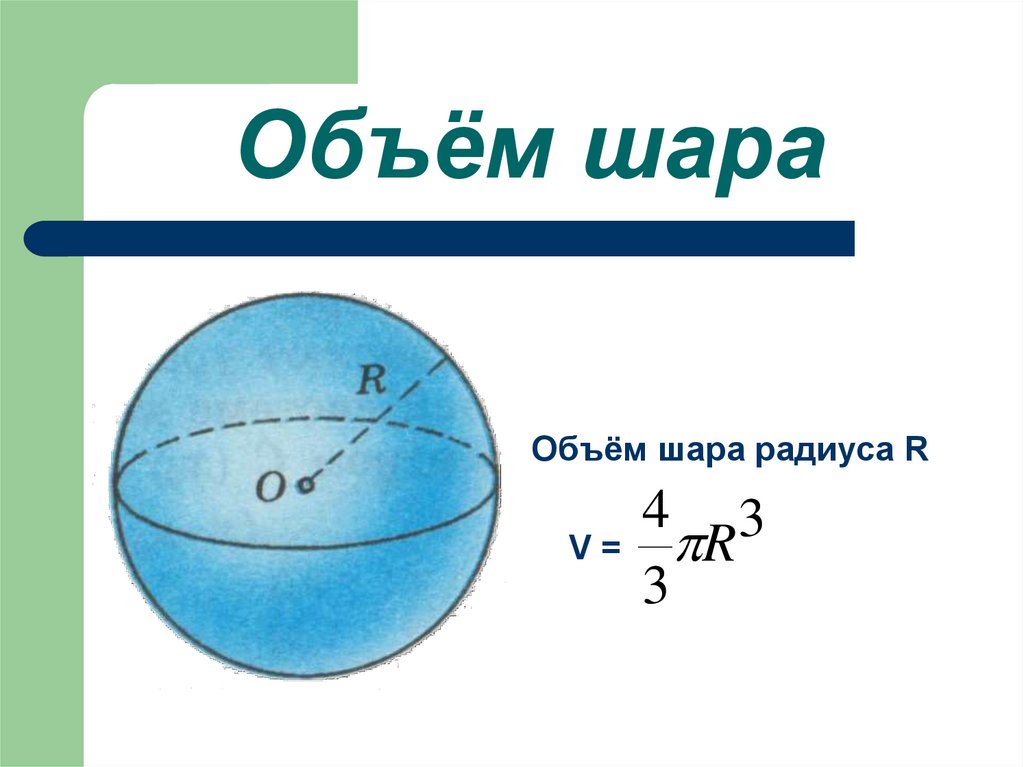
Далее у нас есть еще один пример, в котором мы должны использовать свойства большого круга для построения поверхности. площадь его родительской сферы; на этот раз нам дана окружность.
Пример 5. Нахождение площади поверхности сферы по окружности большого круга
Найдите с точностью до десятых площадь поверхности сферы, длина окружности которой равна 140𝜋 футов.
Ответ
Вспомните формулу для площади поверхности 𝐴 сферы радиуса 𝑟: 𝐴=4𝜋𝑟.
Здесь нам дана длина окружности большого круга. Поскольку мы знаем, что радиусы большого круга и его родительской сферы одинаковы, то нашим первым шагом будет использование этой информации для вычисления значения 𝑟. Мы знаем, что отношение между длиной окружности и радиусом равно окружность=2𝜋𝑟.
Теперь подставим значение 140𝜋 для длины окружности, чтобы получить 140𝜋=2𝜋𝑟.
Чтобы решить это уравнение относительно 𝑟, мы разделим обе части на 2𝜋, поэтому
140𝜋2𝜋=𝑟,
что означает 𝑟=70.
Теперь у нас есть знакомая ситуация, когда площадь поверхности сферы 𝐴 можно найти с помощью нашей формулы. Подставляя 𝑟, мы имеем 𝐴=4×𝜋×𝑟=4×𝜋×(70)=4×𝜋×4900=4×4900×𝜋=19600×𝜋=61575,216….
Вопрос гласит, что мы должны дать ответ на точность до ближайшей десятой. Цифра десятых — это первая цифра после запятой, которая здесь равна 2. Цифра, следующая за ней (цифра сотых), равна 1, поэтому наш ответ нужно округлить до 61 575,2 до ближайшей десятой.
Длина окружности большого круга указана в футах, поэтому площадь поверхности сферы будет выражена в квадратных футах. Мы заключаем, что площадь поверхности сферы составляет 61 61 2 футов, округленных до десятых долей квадратного фута.
Помните, что большой круг всегда делит сферу на два равных полушария. Следовательно, мы можем использовать информацию о больших кругах, чтобы вычислить площадь поверхности соответствующих полушарий или других частей сферы. Вот пример.
Пример 6.
 Нахождение общей площади поверхности полушария по его радиусу
Нахождение общей площади поверхности полушария по его радиусуНайдите общую площадь поверхности полусферы. Округлите ответ до десятых.
Ответ
Диаграмма включает в себя большой круг с радиусом 18 см. Поскольку мы знаем, что радиус большого круга также равен радиусу 𝑟 его родительской сферы (или полушария), то 𝑟=18.
Теперь вспомним формулу площади поверхности 𝐴 сферы радиуса 𝑟: 𝐴=4𝜋𝑟.
Обратите внимание, что общая поверхность полушария состоит из изогнутой поверхности и плоской круглой поверхности. Площадь изогнутой части, которую мы будем называть 𝐴, составляет половину площади поверхности соответствующей сферы; то есть, 𝐴=12×𝐴=12×4𝜋𝑟=2𝜋𝑟.
Кроме того, поверхность at представляет собой просто круг радиуса 𝑟, поэтому, записав 𝐴 для его площади, мы имеем 𝐴=𝜋𝑟.
Следовательно, общая площадь поверхности полушария, которую мы можем записать как 𝐴, должна удовлетворять 𝐴=𝐴+𝐴.
Подставляя 𝐴 и 𝐴 сверху, получаем
𝐴=2𝜋𝑟+𝜋𝑟=3𝜋𝑟.
Наконец, мы имеем 𝑟=18, так что эта замена дает 𝐴=3×𝜋×𝑟=3×𝜋×(18)=3×𝜋×324=3×324×𝜋=972×𝜋=3053,628….
Нас попросили дать ответ ближайшему десятый. Цифра десятых — это первая цифра после запятой, которая здесь равна 6. Следующая за ней цифра (цифра сотых) — это 2, поэтому наш ответ нужно округлить до 3 053,6 до ближайшей десятой.
Радиус большого круга указан в сантиметрах, поэтому общая площадь поверхности полушария будет выражена в квадратных сантиметрах.
Общая площадь поверхности полушария составляет 3 053,6 см 2 , округленная до ближайшей десятой доли квадратного сантиметра.
В нашем последнем примере у нас есть вопрос с реальным контекстом, который задан в виде словесной задачи и без диаграммы. В подобных случаях всегда важно внимательно прочитать вопрос и точно определить, что нас просят найти.
Пример 7. Решение текстовой задачи с участием полушария
Водный объект можно смоделировать как полусферу, основание которой расположено на квадратном патио. Если диаметр полушария равен 4 футам, а длина стороны внутреннего дворика равна 6 футам, какова будет видимая площадь внутреннего дворика? Дайте ответ с точностью до двух знаков после запятой.
Если диаметр полушария равен 4 футам, а длина стороны внутреннего дворика равна 6 футам, какова будет видимая площадь внутреннего дворика? Дайте ответ с точностью до двух знаков после запятой.
Ответ
Вспомним, что большой круг всегда делит сферу на два равных полушария. Следовательно, основанием полушария в водном объекте будет большой круг. Более того, большой круг и его родительское полушарие должны иметь одинаковый радиус 𝑟. Наша стратегия будет заключаться в том, чтобы использовать информацию о полушарии для вычисления площади этого большого круга. Затем мы можем вычесть его из площади всего внутреннего дворика, чтобы найти видимую площадь внутреннего дворика.
Нам сказали, что патио квадратное со стороной 6 футов, поэтому площадь всего патио 6×6=36.
Мы также знаем, что диаметр полушария равен 4 футам, поэтому, чтобы найти его радиус 𝑟, мы делим его на 2, чтобы получить 𝑟=4÷2=2. Таким образом, его основанием будет большой круг радиусом 2.
При этом площадь этого большого круга будет
𝐴=𝜋×𝑟=𝜋×2=𝜋×4=4𝜋.
Пока мы сохраняем этот ответ в его точной форме, потому что нам нужно использовать его в дальнейших вычислениях.
Наш последний шаг — получить видимую площадь патио, вычитая площадь круга из площади квадрата, что дает 36−4𝜋=36−12,566…=23,433…, что равно 23,43 с точностью до двух знаков после запятой.
Длина в вопросе была указана в футах, поэтому эта площадь должна быть в квадратных футах. Видимая площадь внутреннего дворика с точностью до двух знаков после запятой составляет 23,43 фута 2 .
Давайте закончим повторением некоторых ключевых понятий из этого объяснения.
Ключевые точки
- Площадь поверхности 𝐴 сферы радиуса 𝑟 определяется по формуле 𝐴=4𝜋𝑟.
- Формулу можно изменить, чтобы легче было найти радиус (или диаметр) сферы, зная площадь ее поверхности: 𝑟=𝐴4𝜋.
- Всегда проверяйте, дан ли вам радиус или диаметр сферы в вопросе.
- Большой круг — это пересечение сферы с плоскостью, проходящей через центр сферы.
 Он разрезает сферу ровно пополам, образуя две полусферы.
Он разрезает сферу ровно пополам, образуя две полусферы. - Большой круг — это самый большой круг, который может быть сформирован на поверхности его родительской сферы, и обе формы имеют одинаковый радиус.
- Площадь сферы 𝐴 ровно в четыре раза больше площади ее большого круга 𝐴.
- Мы можем использовать эту формулу, чтобы найти площадь поверхности полушария или других частей сферы, в частности, в реальных вопросах, представленных в виде текстовых задач.
Площадь и объем шара – формулы и примеры
Как найти площадь поверхности шара?
Мы можем вычислить площадь поверхности сферы, умножив произведение пи на квадрат радиуса сферы на 4. Таким образом, формула площади поверхности сферы будет следующей: 92}$
где $latex A_{s}$ представляет площадь поверхности сферы, а r представляет длину радиуса.
Вычислить площадь поверхности сферы, используя диаметр
Если мы знаем длину диаметра, мы можем вычислить площадь его поверхности двумя основными способами. Первый способ заключается в делении длины диаметра на 2 и использовании стандартной формулы площади поверхности сферы.
Первый способ заключается в делении длины диаметра на 2 и использовании стандартной формулы площади поверхности сферы.
Второй метод заключается в нахождении формулы площади поверхности сферы через диаметр. Следовательно, подставляя выражение 93}$
где r длина радиуса сферы.
Формулу объема сферы можно доказать с помощью интегрального исчисления.
Вычислить объем сферы, используя диаметр
Чтобы вычислить объем сферы, используя ее диаметр, мы можем использовать два разных метода. Первый способ заключается в делении диаметра на 2 для получения радиуса и использовании стандартной формулы объема сферы.
93}$где d длина диаметра.
Вычисление объема полой сферы
Мы можем вычислить объем полой сферы, вычитая объем полой части из общего объема сферы. Следовательно, если мы используем $latex r_{1}$ для представления радиуса всей сферы и $latex r_{2}$ для представления внутреннего радиуса, то есть радиуса полой части, мы имеем:
$ латекс V=\frac{4}{3}\pi {{r_{1}}^3}-\frac{4}{3}\pi {{r_{2}}^3}$ 93})$
Площадь поверхности и объем сферы – Примеры с ответами
Формулы площади поверхности и объема сферы используются для решения следующих примеров. Попробуйте решить проблемы самостоятельно, прежде чем искать решение.
Попробуйте решить проблемы самостоятельно, прежде чем искать решение.
Найдите площадь поверхности сферы радиусом 4 дюйма.
Решение
Используя формулу площади поверхности с длиной $latex r=4$, имеем: 93})$
$латекс V=\frac{4}{3}\pi (125-64)$
$латекс V=\frac{4}{3}\pi (152)$
$латекс V=255,5$
Объем равен 255,5 дюймов³.
Площадь поверхности и объем сферы – практические задачи
Используйте формулы площади поверхности и объема сферы для решения следующих задач. Нажмите «Проверить», чтобы убедиться, что ваш ответ правильный.
Найдите площадь поверхности сферы радиусом 3 м.
Выберите ответ 93}$
См. также
Хотите узнать больше о площади и объеме геометрических фигур? Взгляните на эти страницы:
- Площадь и объем цилиндра – формулы и примеры
- Площадь и объем куба – формулы и примеры
- Площадь и объем прямоугольной призмы – формулы и примеры
- Площадь и объем треугольной призмы – формулы и примеры
- Площадь и объем пирамиды – формулы и примеры
Объем и площадь поверхности сферы (видео)
mp4″ src=»https://player.vimeo.com/video/563257081?app_id=122963&h=664026e12d» frameborder=»0″ allow=»autoplay; fullscreen; picture-in-picture» allowfullscreen=»»>TranscriptPractice
Сферы удивительны. Они идеально симметричны. Они очень сильные, потому что у них нет слабых мест. В природе они встречаются в виде крошечных вещей, таких как атомы, маленькие вещи, такие как капли воды и пузыри, и огромные вещи, такие как наше солнце. И мы можем вычислить объем и площадь поверхности всех этих объектов, используя относительно простые формулы. Все, что нам нужно знать, это радиус сферы, который является расстоянием от центра сферы до любой точки на поверхности сферы.
Давайте сначала займемся громкостью. Объем сферы — это мера того, сколько места она занимает. Мы измеряем это в кубических единицах, таких как кубические дюймы или кубические сантиметры. Мы можем представить эти единицы в виде кубов, которые мы могли бы поместить внутрь сферы, чтобы увидеть, сколько мы можем поместить. Но поскольку сфера изогнута, даже кубики миллиметрового размера не дадут точного объема. Это похоже на попытку сделать сферу из игрушечных строительных блоков — она никогда не будет похожа на настоящую сферу, какими бы маленькими ни были блоки. 9{3}\)
Но поскольку сфера изогнута, даже кубики миллиметрового размера не дадут точного объема. Это похоже на попытку сделать сферу из игрушечных строительных блоков — она никогда не будет похожа на настоящую сферу, какими бы маленькими ни были блоки. 9{3}\)
Где \(r\) — радиус сферы. Формула не совсем новая. Древнегреческий философ Архимед открыл его более 2000 лет назад. Но сейчас он работает так же хорошо, как и тогда. Возможно, даже лучше, поскольку в наши дни у нас есть электронные калькуляторы.
Итак, давайте найдем объем обычного предмета — бильярдного шара, используемого для игры в пул.
Восьмерка имеет диаметр 5,7 сантиметра. Помните, что радиус круга равен половине диаметра, поэтому все, что нам нужно сделать, это разделить 5,7 на 2, чтобы найти наш радиус, 2,85 сантиметра. Теперь мы можем подставить это в нашу формулу: 9{3}\)
Итак, наш ответ чуть меньше 100 кубических сантиметров. Представьте себе, что вы пытаетесь построить сферу размером с восемь шаров из 100-сантиметровых кубов.
Не очень! Но он 6 сантиметров в высоту и примерно такого же объема. Кажется, мы должны быть рады, что нам не нужно строить из маленьких кубиков, чтобы найти объем сфер!
Мы также можем найти площадь поверхности нашей восьмерки. В отличие от призм и твердых тел, у нашей сферы нет граней. Или, может быть, у него бесконечное количество граней. В любом случае, мы не можем найти площадь поверхности, сложив площадь лица. Вместо этого мы находим площадь всей его поверхности сразу, используя формулу площади поверхности для сферы: 9{2}\)
Наш ответ: чуть больше 100 квадратных сантиметров. Помните, что площадь поверхности — это мера площади в двух измерениях, поэтому наши единицы измерения должны быть квадратными, как квадраты на нашей миллиметровке.
Итак, как мы можем использовать эти формулы, чтобы найти объем и площадь поверхности повседневных предметов? Ключевым моментом является нахождение радиуса, но найти его напрямую немного сложно, потому что нам нужно иметь возможность измерять от центра сферы. 2\) 92\)
2\) 92\)
Площадь поверхности сферы составляет приблизительно \(615,75\) квадратных дюймов.
Скрыть ответ
Вернуться к видео по геометрии
786928
Площадь поверхности сферы – объяснение и примеры
Сфера – одна из важных трехмерных фигур в геометрии. Напомним, что сфера — это трехмерный объект, каждая точка которого находится на равном расстоянии (на одном и том же расстоянии) от фиксированной точки, известной как центр сферы. Диаметр шара делит его на две равные половины, называемые полушариями.
Площадь поверхности сферы — это мера области, покрытой поверхностью сферы.
В этой статье вы узнаете как найти площадь поверхности сферы, используя формулу площади поверхности сферы .
Как и у окружности, расстояние от центра сферы до поверхности называется радиусом. Площадь поверхности сферы в четыре раза больше площади круга того же радиуса.
Площадь поверхности сферы формула
Площадь поверхности сферы определяется формулой:
Площадь поверхности сферы = 4πr 2 квадратных единиц ……………. (Формула площади поверхности сферы)
Для полушария (половина сферы) площадь поверхности определяется выражением;
Площадь поверхности полусферы = ½ × площадь поверхности сферы + площадь основания (окружности) …………………. (Формула площади поверхности полушария)
Где r = радиус данной сферы.
Давайте решим несколько примеров задач на площадь поверхности сферы.
Пример 1
Вычислите площадь поверхности сферы радиусом 14 см.
Решение
Дано:
Радиус, r =14 см
По формуле,
Площадь поверхности шара = 4πr 2
При подстановке получаем,
СА = 4 х 3,14 х 14 х 14
= 2461,76 см 2 .
Пример 2
Диаметр бейсбольного мяча 18 см. Найдите площадь поверхности шара.
Найдите площадь поверхности шара.
Решение
Дано,
Диаметр = 18 см ⇒ радиус = 18/2 = 9 см 3,14 х 9 х 9
SA = 1017,36 см 2
Пример 3
Площадь поверхности сферического объекта равна 379,94 м 2 . Каков радиус объекта?
Solution
Given,
SA = 379.94 m 2
But, surface area of a sphere = 4πr 2
⇒ 379.94 = 4 x 3.14 x r 2
⇒ 379.94 =12.56 r 2
Разделите обе части на 12,56 и найдите квадрат результата
⇒ 379,94/12,56 = R 2
⇒ 30,25 = R 2
⇒ R = √30,25
= 5,5
Следовательно, радиопереда
Пример 4
Стоимость кожи 10$ за квадратный метр. Найдите стоимость изготовления 1000 футбольных мячей радиусом 0,12 м.
Решение
Сначала найдите площадь поверхности шара
SA = 4πr 2
= 4 x 3,14 x 0,12 x 0,12
= 0,181 м 2
Стоимость изготовления мяча = 0,181 м 2 x $ 10 за квадратный метр
= 1,81
С. шары = 1,81 доллара x 1000
шары = 1,81 доллара x 1000
= 1810 долларов
Пример 5
Говорят, что радиус Земли равен 6371 км. Какова площадь поверхности Земли?
Решение
Земля представляет собой шар.
SA = 4πr 2
= 4 x 3,14 x 6,371 x 6,371
= 5,098 x 10 8 км 2
333. Пример 6
33333. Слитная область 6
333333. Слитная область. радиус 10 см.
Решение
Дано:
Радиус, r = 10 см
Для полушария площадь поверхности определяется как:
SA = 3πr 2
3 90.
SA = 3 х 3,14 х 10 х 10
= 942 см 2
Итак, площадь поверхности сферы 942 см 2 .
Пример 7
Площадь поверхности твердого полусферического объекта составляет 150,86 футов 2 . Каков диаметр полушария?
Каков диаметр полушария?
Решение
Дано:
SA = 150,86 футов 2 .
Площадь поверхности сферы = 3πr 2
⇒ 150,86 = 3 x 3,14 x r 2
⇒ 150,86 = 9,42 R 2
Разделите обе стороны на 9,42,
⇒ 16,014 = R 2
R = √16,014
= 4
hared, RADIUS, но и RADIIS, Butrius, Butrius, Butrius, Butrius, Butrius, Butrius, Butrius. диаметр в два раза больше радиуса.
Итак, диаметр полусферы равен 8 футов.
Пример 8
Вычислите площадь поверхности сферы, объем которой равен 1436,03 мм 3 .
Раствор
Since, we already know that:
Volume of a sphere = 4/3 πr 3
1,436.03 = 4/3 x 3.14 x r 3
1,436.03 = 4.19 r 3
Divide both sides на 4,19
r 3 = 343
r = 3 √343
r = 7
Итак, радиус сферы равен 7 мм.
Теперь вычислите площадь поверхности сферы.
Площадь поверхности сферы = 4πr 2
= 4 х 3,14 х 7 х 7
= 615,44 мм 2 .
Example 9
Calculate the surface area of a globe of radius 3.2 m
Solution
Surface area of a sphere
= 4π r 2
= 4π (3.2) 2
.
Объем сферы – формула, примеры
Объем сферы- Вы заметили, почему мяч для крикета кажется тяжелее теннисного мяча? Или почему крошечный шарик трудно разбить? Ответ кроется в их объемах. Хотя они сделаны из разных материалов, их объемы играют важную роль в определении их веса. Объем — это пространство внутри трехмерного объекта или формы. Двумерные объекты не будут иметь объема. Объем сферы означает емкость, которую она может вместить. Что это значит или какова его формула? Давай выясним!
Двумерные объекты не будут иметь объема. Объем сферы означает емкость, которую она может вместить. Что это значит или какова его формула? Давай выясним!
Как упоминалось выше, объем сферы — это вместимость, которую она может вместить. Если шар разрезать на две части, то внутреннее пространство или наполнитель внутри него будет его объемом. Если внутри есть пространство, то сфера полая. В то время как если материал наполнителя находится внутри, сфера будет твердой.
Объем сферы определяется тремя координатами x, y и z. Почему? Потому что трехмерный объект будет лежать по всем трем осям. Объем измеряется в кубических метрах, кубических футах, кубических дюймах и подобных единицах. Обозначается символами см 3 ,m 3 ,in 3 и т.д.
Тогда как найти объем шара? Ну, это зависит от диаметра сферы. Если площадь поверхности умножить на диаметр, то получится объем, в котором каждая точка его поверхности равноудалена от его центра. Математически для расчета объема сферы используется следующая формула:
Объем сферы = 4/3 𝜋 r³, где r — радиус сферы.
Объем является фиксированной величиной и может быть найден по закону Архимеда. Согласно Архимеду, если бросить твердый шар в сосуд, наполненный водой, то объем вытесненной воды будет равен объему шара. Объем изменится, когда изменятся значения диаметра или радиуса сферы. В противном случае формула объема сферы останется прежней.
Всегда ли этот метод подходит для измерения объема? Должны ли мы каждый раз держать ванну с водой, чтобы измерить объем? Теперь, подойдя к тому, как это происходит? Откуда взялась эта формула объема? Для этого пришло время пойти элементарным методом и изучить некоторые другие 3D-формы.
Откуда берется объем сферы?
Уравнение для объема сферы может быть получено из метода интегрирования и объемов конуса и цилиндра.
Метод 1: метод интегрирования
Рассмотрим сферу с множеством тонких сферических дисков, расположенных над другим, как показано на рисунке. Поскольку сфера состоит из тонких круглых дисков, расположенных коллинеарно, их диаметры будут различаться по всей длине сферы. В результате объем будет меняться и по всему диаметру сферы.
В результате объем будет меняться и по всему диаметру сферы.
Теперь рассмотрим тонкий диск радиусом r и толщиной dy, расположенный на расстоянии y от оси x. Также объем сферы будет произведением площади круга на его толщину. Мы можем представить радиус кругового диска r через y, используя теорему Пифагора.
Таким образом, объем элемента диска, dV, может быть определен как:
dV = r² dy
dV = 𝜋 (R² – y²) dy
Путем интегрирования приведенного выше уравнения общий объем сферы будет равен :
Таким образом, окончательная формула объема сферы дается как V = 4/3 𝜋 r³.
Метод 2: Из объемов конуса и цилиндра
Знаете ли вы, что сфера, цилиндр и конус имеют связь? Именно, их объемы имеют связь! Объем цилиндра равен сумме объема конуса и объема шара. Математически
V Цилиндр = V Конинг + V Сфера
Следовательно, мы можем найти объем сферы Cone = V Cylinder — V CONE = V CYALIND 2 h, где h — наклонная высота конуса.
V цилиндр = ⅓ 𝜋r 2 h, где h высота цилиндра.
Следовательно, V сфера = ⅓ 𝜋 r 2 h – 𝜋r 2 h = 2/3 𝜋r 2 h
Если мы посмотрим на сферу, мы увидим, что высота равна диаметру сферы. Следовательно, h = 2r.
Подставляя значение h в итоговое уравнение, получаем
V сфера = ⅔ 𝜋r 2 (2r) = 4/3 𝜋 r 3 , что является объемом сферы.
Изучение объема полой сферы
Более того, объем полой сферы связан с объемом сферы. В полой сфере внешний радиус обозначается буквой R, а внутренний радиус — буквой r. Тогда объем полого шара определяется выражением
V полый = 4/3 𝜋 R 3 – 4/3 𝜋 r 3
Также можно записать как V полый = 4/3 𝜋 (R 3 902 904 – 4 r 3) . Единицей объема полого шара являются кубические метры.
Как найти объем шара?
После того, как мы узнали объем сферы, все, что нам нужно сделать, это найти объем! Любой может найти объем сферы, не используя калькулятор объема сферы. Выполните следующие действия и найдите объем:
Выполните следующие действия и найдите объем:
Шаг 1: Внимательно просмотрите данные, указанные в вопросе.
Шаг 2: Проверить, какое значение задано; радиус, диаметр, площадь поверхности или окружность.
Шаг 3: Найдите радиус сферы. Если диаметр дан, разделите его на 2, чтобы найти радиус. Если площадь поверхности дана, найдите значение радиуса из площади поверхности сферы по формуле 4𝜋r. Если дана длина окружности, найдите радиус по формуле 2𝜋r.
Шаг 4: Тщательно осмотрите отряды. Преобразуйте все единицы, эквивалентные друг другу, в одну единую форму.
Шаг 5: Получите куб радиуса, т. е. r³.
Шаг 6: Умножьте значение r³ на 𝜋.
Шаг 7: Умножьте значение, найденное в шаге 6, на 4/3.
Шаг 8: Окончательное значение будет требуемым объемом сферы.
Применение объема сферы в реальном мире
В реальном мире объем сферы используется несколькими способами. Если мы знаем его формулу, нам не нужен калькулятор объема сферы, чтобы вычислять его каждый раз. Вот несколько приложений, в которых часто используется формула объема:
Если мы знаем его формулу, нам не нужен калькулятор объема сферы, чтобы вычислять его каждый раз. Вот несколько приложений, в которых часто используется формула объема:
- Формула объема используется во многих отраслях промышленности при производстве таких предметов, как шары, шарики, подшипники, пузырьки и т. д.
- Полезно рассчитать количество воздуха, необходимое для предотвращения утечек в воздушном шаре.
- Расчет объема необходим при перевозке любого вредного химического вещества в сферическом контейнере.
- Объем полой сферы используется для определения количества любого материала, содержащегося в чаше или полусферической оболочке.
Время выучить объем сферы на примерах
Пример 1. Найдите объем сферы, длина окружности которой составляет 144 единицы.
Решение: Учитывая, что длина окружности сферы составляет 144 единицы.
Мы знаем, что длина окружности равна 2𝜋r, где r — радиус.
Следовательно, C = 2𝜋r = 144
Решив это, мы получим r = 22,9 единиц.
Формула дает объем шара, V = 4/3 𝜋 r 3
Подставляя значение r, получаем V = 4/3 𝜋 (22,92) 3
V = 50453,197 единиц³.
Пример 2: Полая сфера спроектирована компанией таким образом, что ее толщина составляет 10 см, а внутренний диаметр — 6 м. Каков будет объем сферы, спроектированной компанией?
Решение: Учитывая, что внутренний диаметр 6 м и толщина 10 см, равна 0,1 м.
Следовательно, внешний диаметр будет 6 + 0,1 м = 6,1 м.
Объем полой сферы обозначается как: Объем = 4/3 𝜋R 3 – 4/3 𝜋r 3 , где R — радиус внешней сферы, а r — радиус внутренней сферы.
Подставляя значения в приведенное выше уравнение, мы получаем,
V = 4/3 𝜋 (3,05 3 – 3 3 ) = 4/3 𝜋 (1,37)
Следовательно, V = 5,735 м 3 .
Пример 3. Найдите объем шара, если площадь его поверхности 100 квадратных метров.


 Все эти термины используются для приблизительно сфероидальных астрономических тел. Любая плоскость, которая включает в себя центр шара, делит его на два равных полушария (полусферы).
Все эти термины используются для приблизительно сфероидальных астрономических тел. Любая плоскость, которая включает в себя центр шара, делит его на два равных полушария (полусферы). Но на самом деле, после тройки идёт больше тысячи цифр!
Но на самом деле, после тройки идёт больше тысячи цифр!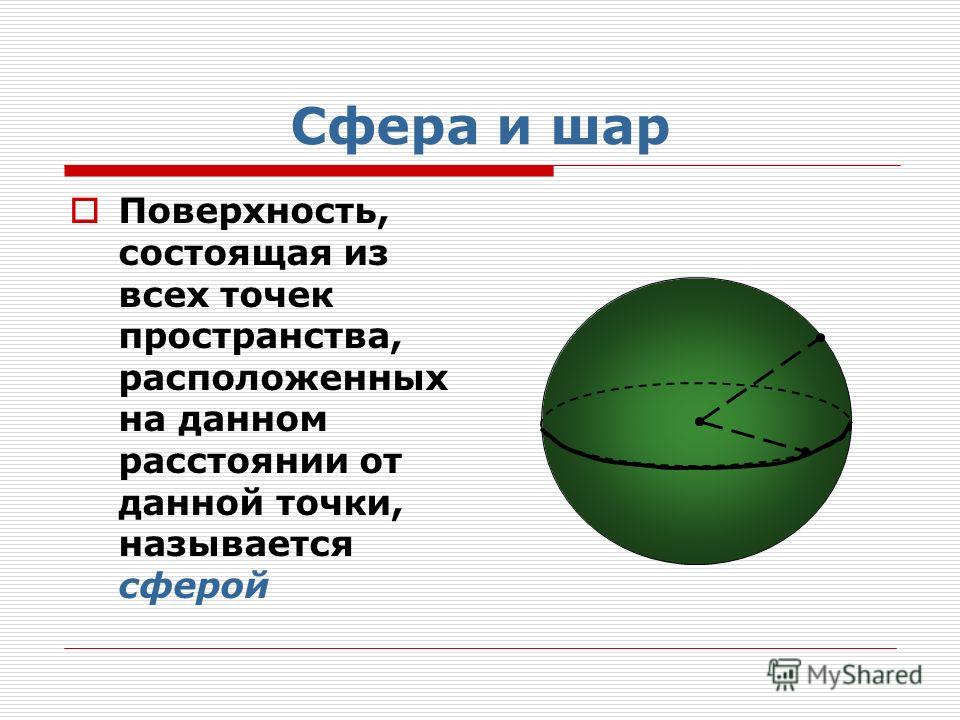
 Касательная плоскость к сфере
Касательная плоскость к сфере 3
3 Следовательно, рассчитать площадь фигуры поверхности можно, используя такой вид формулы:
Следовательно, рассчитать площадь фигуры поверхности можно, используя такой вид формулы: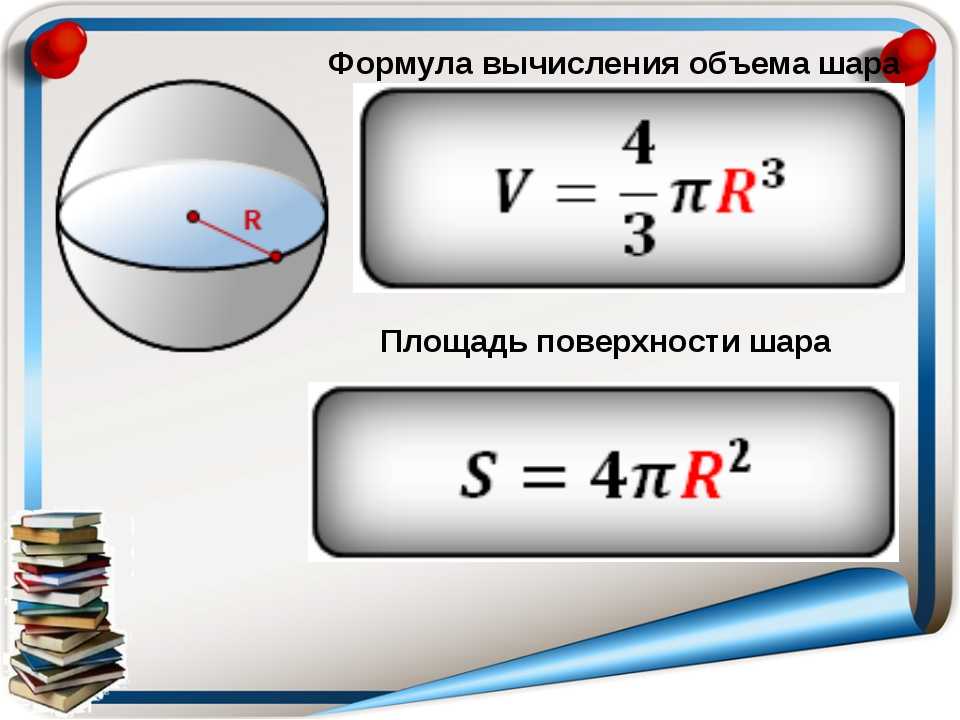 При этом уровень жидкости поднялся с отметки 24 см до отметки 26 см.
При этом уровень жидкости поднялся с отметки 24 см до отметки 26 см.
 2, то искомая площадь равна 4cdot 4 = 16.
2, то искомая площадь равна 4cdot 4 = 16. Центр окружности лежит на пересечении диагоналей прямоугольника.
Центр окружности лежит на пересечении диагоналей прямоугольника. ru/ploshad-shara/
ru/ploshad-shara/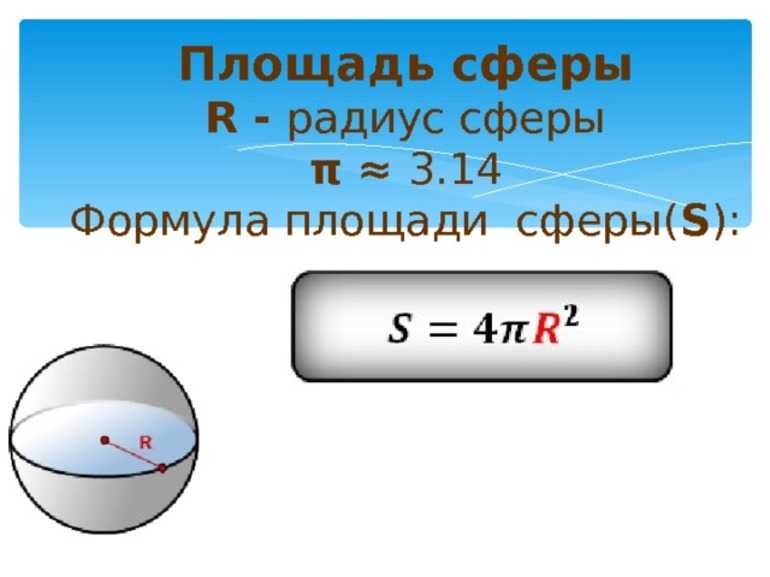 (Используйте π = 22/7)
(Используйте π = 22/7)