Десятичные логарифмы | это… Что такое Десятичные логарифмы?
Рис. 1. Графики логарифмических функций
Логарифм числа b по основанию a определяется как показатель степени, в которую надо возвести число a, чтобы получить число b. Обозначение: . Из определения следует, что записи и ax = b равносильны.
Пример: , потому что 23 = 8.
Содержание
|
Вещественный логарифм
Логарифм вещественного числа loga

Наиболее широкое применение нашли следующие виды логарифмов.
- Десятичные: , основание: число 10.
- Натуральные: , основание: e (число Эйлера).
- Двоичные: или , основание: число 2. Они применяются в теории информации и информатике.
Если рассматривать логарифмируемое число как переменную, мы получим логарифмическую функцию, например: . Эта функция определена в правой части числовой прямой: x > 0, непрерывна и дифференцируема там (см. рис. 1).
Свойства
- Основное логарифмическое тождество:
- (замена основания логарифма)
Натуральные логарифмы
Для производной натурального логарифма справедлива простая формула:
По этой причине в математических исследованиях преимущественно используют именно натуральные логарифмы. Они нередко появляются при решении дифференциальных уравнений, исследовании статистических зависимостей (например, распределения простых чисел) и т.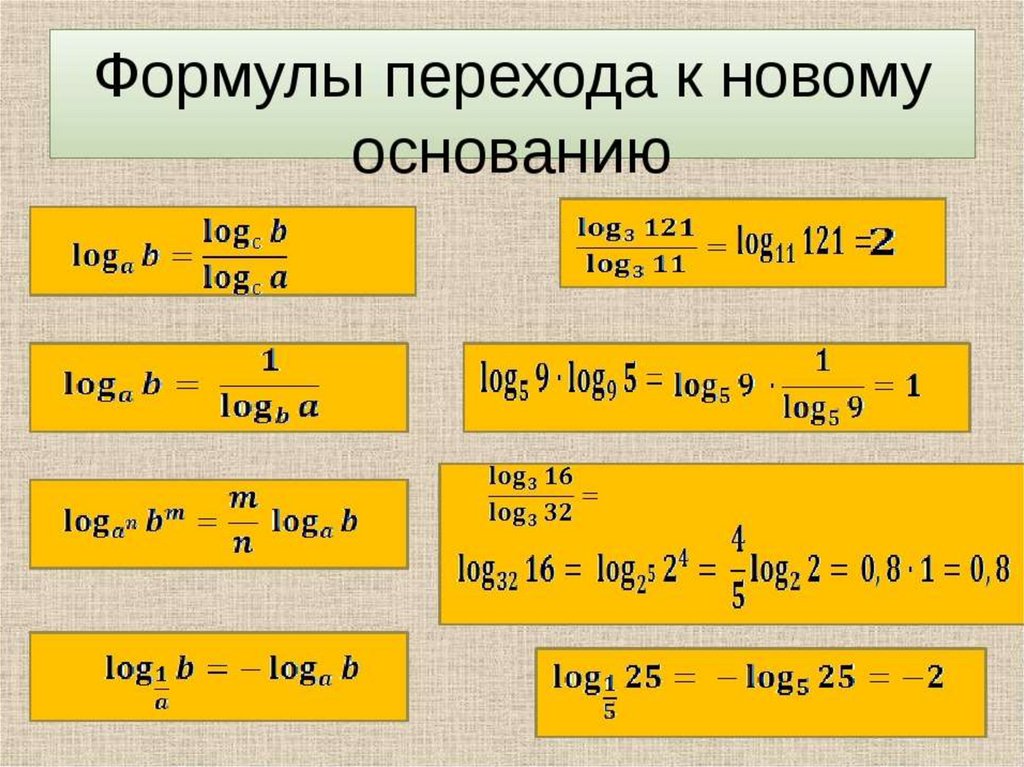
При справедливо равенство
| (1) |
В частности,
Формула (1) не имеет большой практической ценности из-за того, что ряд очень медленно сходится и значение x ограничено весьма узким диапазоном. Однако нетрудно получить из неё более удобную формулу:
| (2) |
Этот ряд сходится быстрее, а кроме того, левая часть формулы теперь может выразить логарифм любого положительного числа.
Связь с десятичным логарифмом: .
Десятичные логарифмы
Рис. 2. Логарифмическая шкала
Логарифмы по основанию 10 (обозначение: lg a) до изобретения калькуляторов широко применялись для вычислений. Неравномерная шкала десятичных логарифмов обычно наносится и на логарифмические линейки. Подобная шкала широко используется в различных областях науки, например:
- Физика — интенсивность звука (децибелы).
- Астрономия — шкала яркости звёзд.

- Химия — активность водородных ионов (pH).
- Сейсмология — шкала Рихтера.
- Теория музыки — нотная шкала, по отношению к частотам нотных звуков.
Логарифмическая шкала также широко применяется для выявления показателя степени в степенных зависимостях и коэффициента в показателе экспоненты. При этом график, построенный в логарифмическом масштабе по одной или двум осям, принимает вид прямой, более простой для исследования.
Комплексный логарифм
Многозначная функция
Для комплексных чисел логарифм определяется так же, как вещественный. Начнём с натурального логарифма, который обозначим и определим как множество всех комплексных чисел z таких, что ez = w. Комплексный логарифм существует для любого , и его вещественная часть определяется однозначно, в то время как мнимая имеет бесконечное множество значений. По этой причине его называют многозначной функцией. Если представить w в показательной форме:
- ,
то логарифм находится по формуле:
Здесь — вещественный логарифм, r = | w | , k — произвольное целое число. Значение, получаемое при k = 0, называется главным значением комплексного натурального логарифма; принято брать в нём значение аргумента в интервале ( − π,π]. Соответствующая (уже однозначная) функция называется главной ветвью логарифма и обозначается . Иногда через также обозначают значение логарифма, лежащее не на главной ветви.
Значение, получаемое при k = 0, называется главным значением комплексного натурального логарифма; принято брать в нём значение аргумента в интервале ( − π,π]. Соответствующая (уже однозначная) функция называется главной ветвью логарифма и обозначается . Иногда через также обозначают значение логарифма, лежащее не на главной ветви.
Из формулы следует:
- Вещественная часть логарифма определяется по формуле:
- Логарифм отрицательного числа находится по формуле:
Примеры (приведено главное значение логарифма):
- ln( − 1) = iπ
Аналогично рассматриваются комплексные логарифмы с другим основанием. Следует, однако, быть осторожным при преобразованиях комплексных логарифмов, принимая во внимание, что они многозначны, и поэтому из равенства логарифмов каких-либо выражений не следует равенство этих выражений. Пример ошибочного рассуждения:
- iπ = ln( − 1) = ln(( − i)2) = 2ln( − i) = 2( − iπ / 2) = − iπ — явная нелепость.

Отметим, что слева стоит главное значение логарифма, а справа — значение из нижележащей ветви ( k = − 1). Причина ошибки — неосторожное использования свойства , которое, вообще говоря, подразумевает в комплексном случае весь бесконечный набор значений логарифма, а не только главное значение.
Аналитическое продолжение
Рис. 3. Комплексный логарифм (мнимая часть)
Логарифм комплексного числа также может быть определён как аналитическое продолжение вещественного логарифма на всю комплексную плоскость. В явном виде продолжение логарифма вдоль кривой Γ, не проходящей через 0, можно осуществить по формуле (соответствующую функцию также обозначаем ln)
При этом, если Γ — простая кривая (без самопересечений), то для чисел, лежащих на ней, логарифмические тождества можно применять без опасений, например
Из формулы аналитического продолжения следует, что на любой ветви логарифма
Для любой окружности S, охватывающей точку 0:
Интеграл берётся в положительном направлении (против часовой стрелки).
Риманова поверхность
Комплексная логарифмическая функция — пример римановой поверхности; её мнимая часть (рис. 3) состоит из бесконечного числа ветвей, закрученных наподобие спирали. Эта поверхность односвязна; её единственный нуль (первого порядка) получается при z = 1, особые точки: z = 0 и (точки разветвления бесконечного порядка).
Риманова поверхность логарифма является универсальной накрывающей для комплексной плоскости без точки 0.
Исторический очерк
Вещественный логарифм
Потребность в сложных расчётах в XVI веке быстро росла, и значительная часть трудностей была связана с умножением и делением многозначных чисел. В конце века нескольким математикам, почти одновременно, пришла в голову идея: заменить трудоёмкое умножение на простое сложение, сопоставив с помощью специальных таблиц геометрическую и арифметическую прогрессии, при этом геометрическая будет исходной. Тогда и деление автоматически заменяется на неизмеримо более простое и надёжное вычитание.
В 1614 году шотландский математик-любитель Джон Непер опубликовал на латинском языке сочинение под названием «Описание удивительной таблицы логарифмов». В нём было краткое описание логарифмов и их свойств, а также 8-значные таблицы логарифмов синусов, косинусов и тангенсов, с шагом 1′. Термин логарифм, предложенный Непером, утвердился в науке.
Понятия функции тогда ещё не было, и Непер определил логарифм кинематически, сопоставив равномерное и логарифмически-замедленное движение. В современной записи модель Непера можно изобразить дифференциальным уравнением:
Строго говоря, Непер табулировал не ту функцию, которая сейчас называется логарифмом.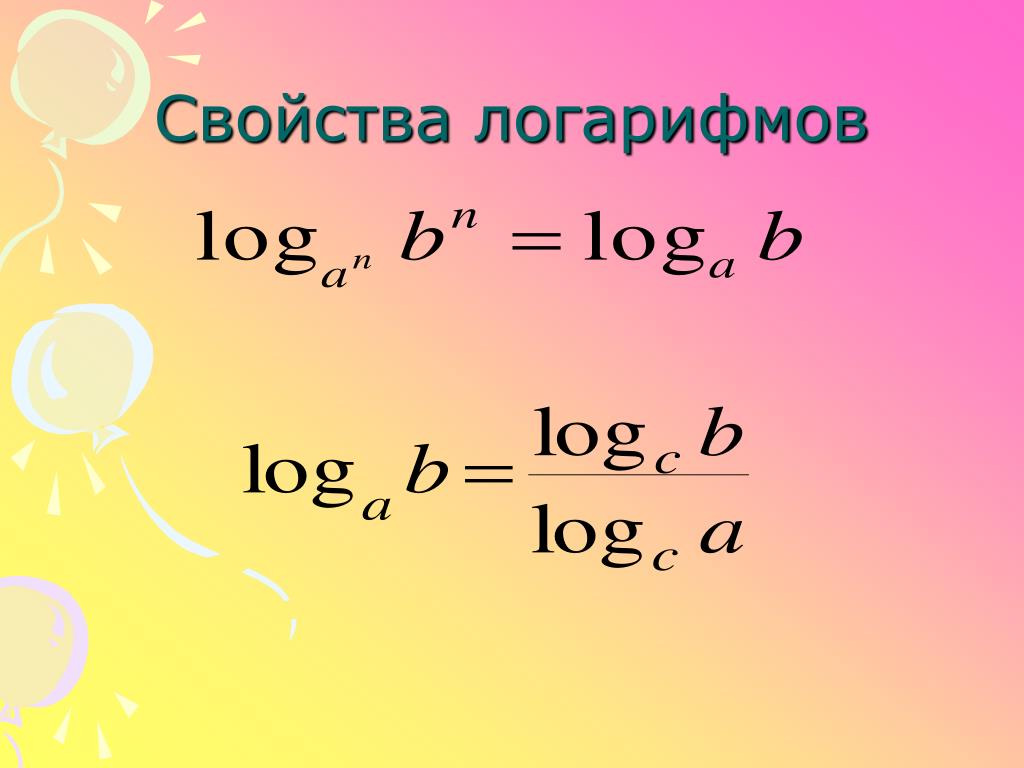 Если обозначить его функцию LogNap(x), то она связана с натуральным логарифмом следующим образом:
Если обозначить его функцию LogNap(x), то она связана с натуральным логарифмом следующим образом:
Очевидно, LogNap(M) = 0, то есть логарифм «полного синуса» есть нуль — этого и добивался Непер своим определением. LogNap(0) = ∞.
Основное свойство логарифма Непера: если величины образуют геометрическую прогрессию, то их логарифмы образуют прогрессию арифметическую. Однако правила логарифмирования для неперовой функции отличались от правил для современного логарифма.
Например, LogNap(ab) = LogNap(a) + LogNap(b) — LogNap(1).
К сожалению, все значения таблицы Непера содержали вычислительную ошибку после шестого знака. Однако это не помешало новой методике вычислений получить широчайшую популярность, и составлением логарифмических таблиц занялись многие европейские математики, включая Кеплера.
В 1620-е годы Эдмунд Уингейт и Уильям Отред изобрели первую логарифмическую линейку, до появления карманных калькуляторов — незаменимый инструмент инженера.
Близкое к современному понимание логарифмирования — как операции, обратной возведению в степень — впервые появилось у Валлиса и Иоганна Бернулли, а окончательно было узаконено Эйлером в XVIII веке. В книге «Введение в анализ бесконечных» (1748) Эйлер дал современные определения как показательной, так и логарифмической функций, привёл разложение их в степенные ряды, особо отметил роль натурального логарифма.
Эйлеру принадлежит и заслуга распространения логарифмической функции на комплексную область.
Комплексный логарифм
Первые попытки распространить логарифмы на комплексные числа предпринимали на рубеже XVII—XVIII веков Лейбниц и Иоганн Бернулли, однако создать целостную теорию им не удалось — в первую очередь по той причине, что тогда ещё не было ясно определено само понятие логарифма. Дискуссия по этому поводу велась сначала между Лейбницем и Бернулли, а в середине XVIII века — между Даламбером и Эйлером. Бернулли и Даламбер считали, что следует определить log(-x) = log(x). Полная теория логарифмов отрицательных и комплексных чисел была опубликована Эйлером в 1747—1751 годах и по существу ничем не отличается от современной.
Полная теория логарифмов отрицательных и комплексных чисел была опубликована Эйлером в 1747—1751 годах и по существу ничем не отличается от современной.
Хотя спор продолжался (Даламбер отстаивал свою точку зрения и подробно аргументировал её в статье своей «Энциклопедии» и в других трудах), однако точка зрения Эйлера быстро получила всеобщее признание.
Логарифмические таблицы
Логарифмические таблицы
Из свойств логарифма следует, что вместо трудоёмкого умножения многозначных чисел достаточно найти (по таблицам) и сложить их логарифмы, а потом по тем же таблицам выполнить потенцирование, то есть найти значение результата по его логарифму. Выполнение деления отличается только тем, что логарифмы вычитаются. Лаплас говорил, что изобретение логарифмов «продлило жизнь астрономов», многократно ускорив процесс вычислений.
При переносе десятичной запятой в числе на n разрядов значение десятичного логарифма этого числа изменяется на n. Например, lg8314,63 = lg8,31463 + 3. Отсюда следует, что достаточно составить таблицу десятичных логарифмов для чисел в диапазоне от 1 до 10.
Отсюда следует, что достаточно составить таблицу десятичных логарифмов для чисел в диапазоне от 1 до 10.
Первые таблицы логарифмов опубликовал Джон Непер (1614), и они содержали только логарифмы тригонометрических функций, причём с ошибками. Независимо от него свои таблицы опубликовал Иост Бюрги, друг Кеплера (1620). В 1617 году оксфордский профессор математики Генри Бригс опубликовал таблицы, которые уже включали десятичные логарифмы самих чисел, от 1 до 1000, с 8 (позже — с 14) знаками. Но и в таблицах Бригса обнаружились ошибки. Первое безошибочное издание на основе таблиц Вега (1783) появилось только в 1857 году в Берлине (таблицы Бремивера).
В России первые таблицы логарифмов были изданы в 1703 году при участии Л. Ф. Магницкого. В СССР выпускались несколько сборников таблиц логарифмов.
- Брадис В. М. Четырехзначные математические таблицы. 44-е издание, М., 1973.
Таблицы Брадиса (1921) использовались в учебных заведениях и в инженерных расчётах, не требующих большой точности. Они содержали мантиссы десятичных логарифмов чисел и тригонометрических функций, натуральные логарифмы и некоторые другие полезные расчётные инструменты.
Они содержали мантиссы десятичных логарифмов чисел и тригонометрических функций, натуральные логарифмы и некоторые другие полезные расчётные инструменты.
- Вега Г. Таблицы семизначных логарифмов, 4-е издание, М., 1971.
Профессиональный сборник для точных вычислений.
- Пятизначные таблицы натуральных значений тригонометрических величин, их логарифмов и логарифмов чисел, 6 изд., М.: Наука, 1972.
- Таблицы натуральных логарифмов, 2-е издание, в 2 томах, М.: Наука, 1971.
См. также
- Комплексное число
- Показательная функция
- Простаферетическая функция
- Системы счисления
- Еричная система счисления
Литература
- Выгодский М. Я. Справочник по элементарной математике. — М.: АСТ, 2003. — ISBN 5-17-009554-6
- История математики под редакцией А. П. Юшкевича в трёх томах, М.: Наука.
- Том 1 С древнейших времен до начала Нового времени.
 (1970)
(1970) - Том 2 Математика XVII столетия. (1970)
- Том 1 С древнейших времен до начала Нового времени.
- Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — М.: Наука, 1973.
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, тома I, II. — М.: Наука, 1960.
Свойства логарифмов, формулы, таблицы. Урок и презентация по алгебре за 11 класс
Дата публикации: .
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Скачать:Свойства логарифмов (PPTX)
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 11 класса
Интерактивное пособие для 9–11 классов «Тригонометрия»
Интерактивное пособие для 10–11 классов «Логарифмы»
Основные свойства логарифмов
Ребята, мы продолжаем изучать логарифмы, и все что с ними связано.
 {2-0,25log_6{12}}$.
{2-0,25log_6{12}}$.10.4 Использование свойств логарифмов — Алгебра среднего уровня 2e
Цели обучения
К концу этого раздела вы сможете:
- Использовать свойства логарифмов
- Использовать формулу смены базы
Приготовься 10.10
Прежде чем начать, пройдите этот тест на готовность.
Оценка: ⓐ a0a0 ⓑ a1.a1.
Если вы пропустили эту проблему, просмотрите пример 5.14.
Приготовься 10.11
Запишите с рациональным показателем: x2y3.x2y3.
Если вы пропустили эту проблему, просмотрите пример 8.27.
Приготовься 10.12
Округлить до трех знаков после запятой: 2,5646415.
Если вы пропустили эту проблему, просмотрите пример 1.34.
Использование свойств логарифмов
Теперь, когда мы узнали об экспоненциальных и логарифмических функциях, мы можем ввести некоторые свойства логарифмов. Это будет очень полезно, поскольку мы продолжаем решать как экспоненциальные, так и логарифмические уравнения.
Первые два свойства вытекают из определения логарифмов. Поскольку a0=1,a0=1, мы можем преобразовать это в логарифмическую форму и получить loga1=0.loga1=0. Кроме того, поскольку a1=a,a1=a, мы получаем logaa=1.logaa=1.
Свойства логарифмов
лога1=0логаа=1лога1=0логаа=1
В следующем примере мы могли бы вычислить логарифм путем преобразования в экспоненциальную форму, как мы делали ранее, но распознавание и последующее применение свойств экономит время.
Пример 10.28
Вычислить, используя свойства логарифмов: ⓐ log81log81 и ⓑ log66.log66.
Решение
ⓐ
| лог81лог81 | |
| Используйте свойство loga1=0loga1=0. | 0log81=00log81=0 |
ⓑ
log66Используйте свойство,logaa=1.1log66=1log66Используйте свойство,logaa=1. 1log66=1
1log66=1
Попробуй 10.55
Вычислить, используя свойства логарифмов: ⓐ log131log131 ⓑ log99.лог99.
Попробуй 10.56
Оценить, используя свойства логарифмов: ⓐ log51log51 ⓑ log77.log77.
Следующие два свойства также можно проверить, преобразовав их из экспоненциальной формы в логарифмическую или наоборот.
Экспоненциальное уравнение alogax=xalogax=x преобразуется в логарифмическое уравнение logax=logax,logax=logax, которое верно только для положительных значений для x .
Логарифмическое уравнение logaax=xlogaax=x преобразуется в показательное уравнение ax=ax,ax=ax, что также является верным утверждением.
Эти два свойства называются обратными свойствами, потому что, когда мы имеем одно и то же основание, возведение в степень «отменяет» бревно, а взятие бревна «отменяет» возведение в степень. Эти два свойства показывают композицию функций. Оба получили функцию тождества, которая снова показывает, что экспоненциальная и логарифмическая функции являются обратными функциями.
Обратные свойства логарифмов
Для a>0,a>0,x>0x>0 и a≠1,a≠1,
alogax=xlogaax=xalogax=xlogaax=x
В следующем примере применяются обратные свойства логарифмов.
Пример 10.29
Вычислить, используя свойства логарифмов: ⓐ 4log494log49 и ⓑ log335.log335.
Решение
ⓐ
| 4log494log49 | |
| Используйте свойство alogax=xalogax=x. | 94log49=994log49=9 |
ⓑ
| лог335лог335 | |
| Используйте свойство alogax=xalogax=x. | 5log335=55log335=5 |
Попробуй 10.57
Оцените, используя свойства логарифмов: ⓐ 5log5155log515 ⓑ log774.log774.
Попробуй 10.
 58
58Оцените, используя свойства логарифмов: ⓐ 2log282log28 ⓑ log2215.log2215.
Есть еще три свойства логарифмов, которые будут полезны в нашей работе. Мы знаем, что экспоненциальные функции и логарифмическая функция очень взаимосвязаны. Наше определение логарифма показывает нам, что логарифм является показателем эквивалентной экспоненты. Свойства показателей имеют родственные свойства показателей.
В свойстве произведения показателей, am·an=am+n,am·an=am+n, мы видим, что для умножения одного и того же основания мы складываем показатели степени. Свойство продукта логарифмов, logaM·N=logaM+logaNlogaM·N=logaM+logaN говорит нам взять журнал произведения, мы добавляем журнал факторов.
Свойство произведения логарифмов
Если M>0,N>0,a>0M>0,N>0,a>0 и a≠1,a≠1, то
loga(M·N)=logaM+logaNloga(M· N)=logaM+logaN
Логарифм произведения есть сумма логарифмов.
Мы используем это свойство, чтобы записать журнал продукта в виде суммы журналов каждого фактора.
Пример 10.30
Используйте свойство «Произведение логарифмов», чтобы записать каждый логарифм в виде суммы логарифмов. Если возможно, упростите: ⓐ log37xlog37x и ⓑ log464xy.log464xy.
Решение
ⓐ
| log464xylog464xy | |
| Используйте свойство продукта, loga(M·N)=logaM+logaNloga(M·N)=logaM+logaN. | log464+log4x+log4ylog464+log4x+log4y |
| Упростите, оценив log464log464. | 3+log4x+log4y3+log4x+log4y |
| log464xy=3+log4x+log4ylog464xy=3+log4x+log4y |
Попробуй 10.
 59
59Используйте свойство «Произведение логарифмов», чтобы записать каждый логарифм в виде суммы логарифмов. Упростите, если можно.
ⓐ log33xlog33x ⓑ log28xylog28xy
Попробуй 10.60
Используйте свойство «Произведение логарифмов», чтобы записать каждый логарифм в виде суммы логарифмов. Упростите, если можно.
ⓐ log99xlog99x ⓑ log327xylog327xy
Точно так же в Частном Свойстве Экспонент, aman=am-n,aman=am-n, мы видим, что для деления одного и того же основания мы вычитаем экспоненты. Факторное свойство логарифмов, logaMN=logaM-logaNlogaMN=logaM-logaN говорит нам взять логарифм частного, мы вычитаем логарифм числителя и знаменателя.
Факторное свойство логарифмов
Если M>0,N>0,a>0M>0,N>0,a>0 и a≠1,a≠1, то
logaMN=logaM-logaNlogaMN=logaM-logaN
Логарифм частного – это разность логарифмов.
Обратите внимание, что logaM-logaN≠loga(M-N).logaM-logaN≠loga(M-N).
Мы используем это свойство, чтобы записать логарифм частного как разницу логарифмов каждого фактора.
Пример 10.31
Используйте частное свойство логарифмов, чтобы записать каждый логарифм как разность логарифмов. Упростите, если можно.
ⓐ log557log557 и ⓑ logx100logx100
Решение
ⓐ
| лог557лог557 | |
| Используйте свойство частное, logaMN=logaM-logaNlogaMN=logaM-logaN. | log55-log57log55-log57 |
| Упрощение. | 1-log571-log57 |
| log557=1-log57log557=1-log57 |
ⓑ
| logx100logx100 | |
| Используйте свойство частное, logaMN=logaM-logaNlogaMN=logaM-logaN. | logx-log100logx-log100 |
| Упрощение. | logx-2logx-2 |
| logx100=logx-2logx100=logx-2 |
Попробуй 10,61
Используйте частное свойство логарифмов, чтобы записать каждый логарифм как разность логарифмов. Упростите, если можно.
Упростите, если можно.
ⓐ log434log434 ⓑ logx1000logx1000
Попробуй 10,62
Используйте частное свойство логарифмов, чтобы записать каждый логарифм как разность логарифмов. Упростите, если можно.
ⓐ log254log254 ⓑ log10ylog10y
Третье свойство логарифмов связано со степенным свойством показателей степени, (am)n=am·n, (am)n=am·n, мы видим, что для возведения степени в степень мы умножаем показатели степени. Свойство мощности логарифмов, logaMp=plogaMlogaMp=plogaM, говорит нам взять логарифм числа, возведенного в степень, мы умножаем степень на логарифм числа.
Степенное свойство логарифмов
Если M>0,a>0,a≠1M>0,a>0,a≠1 и pp — любое действительное число, то
logaMp=plogaMlogaMp=plogaM
Логарифм числа, возведенный в степень как произведение степени, умноженной на логарифм числа.
Мы используем это свойство для записи логарифма числа, возведенного в степень, как произведение степени, умноженной на логарифм числа. По сути, мы берем показатель степени и бросаем его перед логарифмом.
По сути, мы берем показатель степени и бросаем его перед логарифмом.
Пример 10.32
Используйте свойство мощности логарифмов, чтобы записать каждый логарифм как произведение логарифмов. Упростите, если можно.
ⓐ log543log543 и ⓑ logx10logx10
Решение
ⓐ
| лог543лог543 | |
| Используйте свойство Power, logaMp=plogaMlogaMp=plogaM. | 3log543log54 |
| log543=3log54log543=3log54 |
ⓑ
| логx10logx10 | |
| Используйте свойство Power, logaMp=plogaMlogaMp=plogaM. | 10logx10logx |
| logx10=10logxlogx10=10logx |
Попробуй 10,63
Используйте свойство мощности логарифмов, чтобы записать каждый логарифм как произведение логарифмов. Упростите, если можно.
Упростите, если можно.
ⓐ log754log754 ⓑ logx100logx100
Попробуй 10,64
Используйте свойство мощности логарифмов, чтобы записать каждый логарифм как произведение логарифмов. Упростите, если можно.
ⓐ log237log237 ⓑ logx20logx20
Мы суммируем здесь свойства логарифмов для удобства. Хотя натуральные логарифмы являются частным случаем этих свойств, часто бывает полезно также показать версию каждого свойства в виде натурального логарифма.
Свойства логарифмов
Если M>0,N>0,a>0,a≠1M>0,N>0,a>0,a≠1 и pp — любое действительное число, то
| Свойство | Основание аа | База ее |
|---|---|---|
| лога1=0лога1=0 | In1=0In1=0 | |
| логаа=1логаа=1 | lne=1lne=1 | |
| Обратные свойства | alogax=xlogaax=xalogax=xlogaax=x | elnx=xlnex=xelnx=xlnex=х |
| Свойство произведения логарифмов | loga(M·N)=logaM+logaNloga(M·N)=logaM+logaN | ln(M·N)=lnM+lnNln(M·N)=lnM+lnN |
| Частное свойство логарифмов | logaMN=logaM-logaNlogaMN=logaM-logaN | lnMN=lnM−lnNlnMN=lnM−lnN |
| Степенное свойство логарифмов | логаМп=плогаМлогаМп=плогам | lnMp=plnMlnMp=plnM |
Теперь, когда у нас есть свойства, мы можем использовать их для «расширения» логарифмического выражения. Это означает писать логарифм как сумму или разность и без каких-либо степеней.
Это означает писать логарифм как сумму или разность и без каких-либо степеней.
Обычно мы применяем свойства произведения и частного перед применением свойства мощности.
Пример 10.33
Используйте свойства логарифмов, чтобы расширить логарифм log4(2x3y2)log4(2x3y2). Упростите, если можно.
Решение
| журнал4(2x3y2)лог4(2x3y2) | |
| Используйте свойство продукта, logaM·N=logaM+logaNlogaM·N=logaM+logaN. | log42+log4x3+log4y2log42+log4x3+log4y2 |
| Используйте свойство Power, logaMp=plogaMlogaMp=plogaM, в двух последних терминах. | log42+3log4x+2log4ylog42+3log4x+2log4y |
| Упрощение. | 12+3log4x+2log4y12+3log4x+2log4y |
| log4(2x3y2)=12+3log4x+2log4ylog4(2x3y2)=12+3log4x+2log4y |
Попробуй 10,65
Используйте свойства логарифмов, чтобы расширить логарифм log2(5x4y2)log2(5x4y2).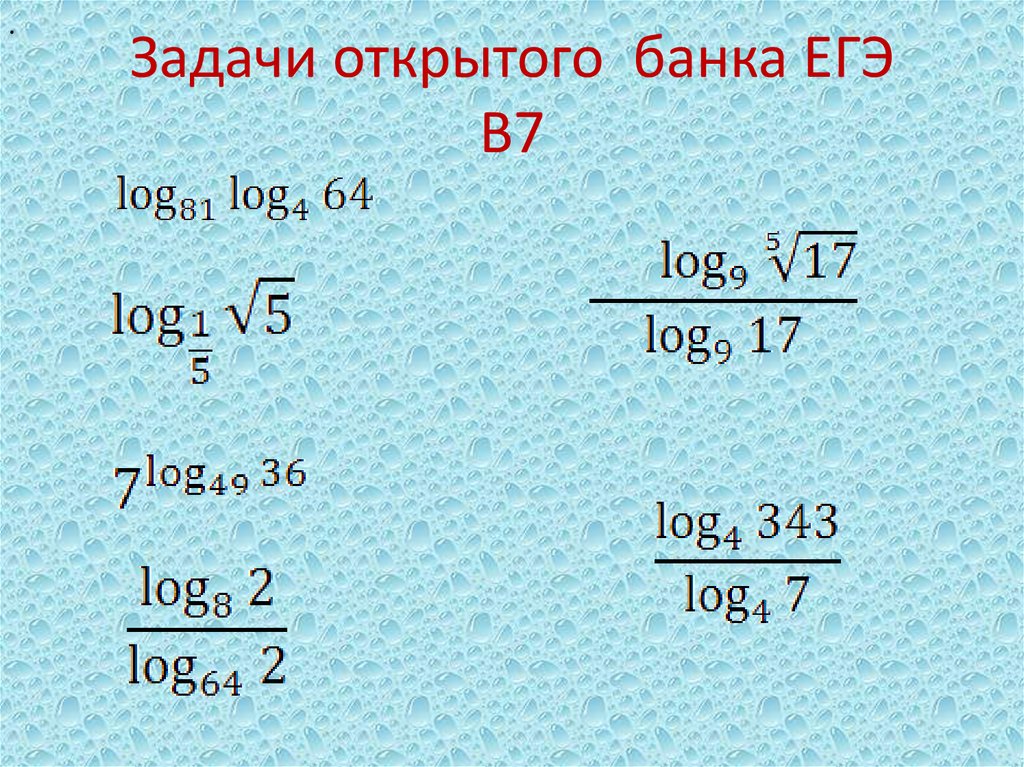 Упростите, если можно.
Упростите, если можно.
Попробуй 10,66
Используйте свойства логарифмов, чтобы расширить логарифм log3(7x5y3)log3(7x5y3). Упростите, если можно.
Когда у нас есть радикал в логарифмическом выражении, полезно сначала записать его радикал как рациональный показатель степени.
Пример 10.34
Используйте свойства логарифмов, чтобы расширить логарифм log2x33y2z4log2x33y2z4. Упростите, если можно.
Решение
| log2x33y2z4log2x33y2z4 | |
| Перепишите радикал с рациональным показателем. | журнал2(x33y2z)14log2(x33y2z)14 |
| Используйте свойство Power, logaMp=plogaMlogaMp=plogaM. | 14log2(x33y2z)14log2(x33y2z) |
| Используйте свойство «частное», logaM·N=logaM-logaNlogaM·N=logaM-logaN. | 14(log2(x3)−log2(3y2z))14(log2(x3)−log2(3y2z)) |
Использовать свойство продукта, logaM·N=logaM+logaNlogaM·N=logaM+logaN, во втором члене. | 14(log2(x3)-(log23+log2y2+log2z))14(log2(x3)-(log23+log2y2+log2z)) |
| Используйте свойство Power, logaMp=plogaMlogaMp=plogaM, в скобках. | 14(3log2x-(log23+2log2y+log2z))14(3log2x-(log23+2log2y+log2z)) |
| Упростите путем распространения. | 14(3log2x-log23-2log2y-log2z)14(3log2x-log23-2log2y-log2z) |
| log2x33y2z4=14(3log2x-log23-2log2y-log2z)log2x33y2z4=14(3log2x-log23-2log2y-log2z) |
Попробуй 10,67
Используйте свойства логарифмов, чтобы расширить логарифм log4x42y3z25log4x42y3z25. Упростите, если можно.
Попробуй 10,68
Используйте свойства логарифмов, чтобы расширить логарифм log3x25yz3log3x25yz3. Упростите, если можно.
Противоположностью расширению логарифма является сжатие суммы или разности логарифмов, имеющих одинаковое основание, в единый логарифм. Мы снова используем свойства логарифмов, чтобы помочь нам, но в обратном порядке.
Чтобы сжать логарифмические выражения с одним и тем же основанием в один логарифм, мы начинаем с использования свойства Power, чтобы получить коэффициенты логарифмических терминов равными единице, а затем, при необходимости, свойств продукта и частного.
Пример 10.35
Используйте свойства логарифмов, чтобы сократить логарифм log43+log4x-log4ylog43+log4x-log4y. Упростите, если можно.
Решение
| Все выражения журнала имеют одинаковую базу, 4. | log43+log4x-log4ylog43+log4x-log4y |
| Первые два термина добавлены, поэтому мы используем свойство продукта, logaM+logaN=logaM·NlogaM+logaN=logaM·N. | log43x-log4ylog43x-log4y |
| Поскольку журналы вычитаются, мы используем свойство Quotient, logaM-logaN=logaMNlogaM-logaN=logaMN. | log43xylog43xy |
| log43+log4x-log4y=log43xylog43+log4x-log4y=log43xy |
Попробуй 10,69
Используйте свойства логарифмов, чтобы сократить логарифм log25+log2x-log2ylog25+log2x-log2y. Упростите, если можно.
Упростите, если можно.
Попробуй 10.70
Используйте свойства логарифмов, чтобы сократить логарифм log36-log3x-log3ylog36-log3x-log3y. Упростите, если можно.
Пример 10.36
Используйте свойства логарифмов, чтобы сократить логарифм 2log3x+4log3(x+1)2log3x+4log3(x+1). Упростите, если можно.
Решение
| Выражения журнала имеют одно и то же основание, 3. | 2log3x+4log3(x+1)2log3x+4log3(x+1) |
| Используйте свойство Power, logaM+logaN=logaM·NlogaM+logaN=logaM·N. | log3x2+log3(x+1)4log3x2+log3(x+1)4 |
| Термины добавлены, поэтому мы используем свойство продукта, logaM+logaN=logaM·NlogaM+logaN=logaM·N. | log3x2(x+1)4log3x2(x+1)4 |
| 2log3x+4log3(x+1)=log3x2(x+1)42log3x+4log3(x+1)=log3x2(x+1)4 |
Попробуй 10,71
Используйте свойства логарифмов, чтобы сократить логарифм 3log2x+2log2(x−1)3log2x+2log2(x−1). Упростите, если можно.
Упростите, если можно.
Попробуй 10,72
Используйте свойства логарифмов, чтобы сократить логарифм 2logx+2log(x+1)2logx+2log(x+1). Упростите, если можно.
Используйте формулу смены базы
Чтобы вычислить логарифм с любым другим основанием, мы можем использовать Формулу смены основания. Мы покажем, как это получается.
| Предположим, мы хотим оценить logaMlogaM. | логаМлогаМ |
| Пусть y=logaMy=logaM. | y=logaMy=logaM |
| Перепишите выражение в экспоненциальной форме. | ау=май=М |
| Возьмите logblogb с каждой стороны. | logbay=logbMlogbay=logbM |
| Используйте свойство Power. | ylogba=logbMylogba=logbM |
Решите для гг. | y=logbMlogbay=logbMlogba |
| Замените y=logaMy=logaM. | logaM=logbMlogbalogaM=logbMlogba |
Формула смены базы вводит новую базу b.b. Это может быть любое основание b , которое мы захотим, где b>0,b≠1.b>0,b≠1. Поскольку в наших калькуляторах есть ключи для логарифмов по основанию 10 и основанию e , мы перепишем формулу смены основания с новым основанием как 10 или e .
Формула смены базы
Для любых логарифмических оснований a,ba,b и M>0,M>0,
Когда мы используем калькулятор для вычисления значения логарифма, мы обычно округляем до трех знаков после запятой. Это дает нам приблизительное значение, поэтому мы используем символ приблизительного равенства (≈)(≈).
Пример 10.37
Округление до трех знаков после запятой, приблизительное значение log435.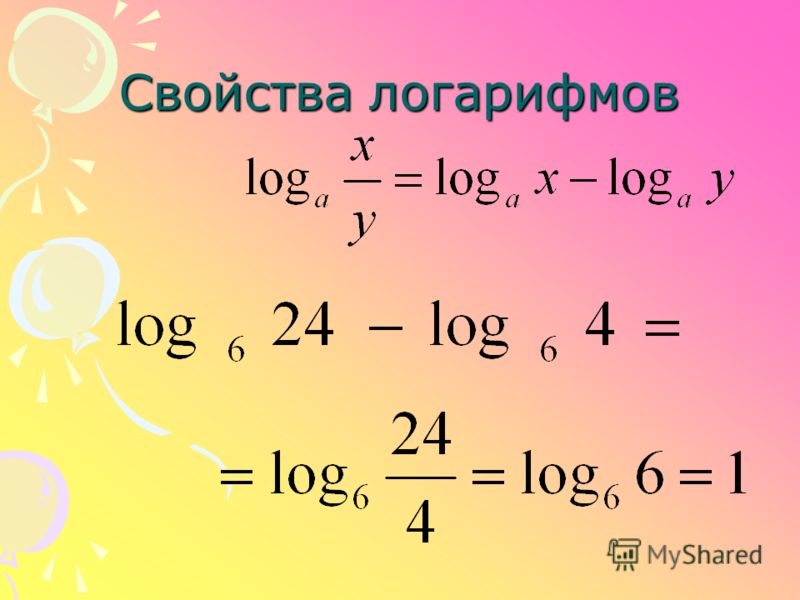 log435.
log435.
Решение
| Используйте формулу смены базы. | |
| Определите a и M . Выберите 10 для b . | |
| Введите выражение log35log4log35log4 в калькулятор , используя кнопку log для основания 10. Округлите до трех знаков после запятой. |
Попробуй 10,73
Округление до трех знаков после запятой, приблизительное значение log342.log342.
Попробуй 10,74
Округление до трех знаков после запятой, приблизительное значение log546. log546.
log546.
Раздел 10.4 Упражнения
Практика ведет к совершенству
Использование свойств логарифмов
В следующих упражнениях используйте свойства логарифмов для оценки.
218.
ⓐ log41log41 ⓑ log88log88
219.
ⓐ log121log121 ⓑ lnelne
220.
ⓐ 3log363log36 ⓑ log227log227
221.
ⓐ 5log5105log510 ⓑ log4410log4410
222.
ⓐ 8log878log87 ⓑ log66-2log66-2
223.
ⓐ 6log6156log615 ⓑ log88−4log88−4
224.
ⓐ 10log510log5 ⓑ log10-2log10-2
225.
ⓐ 10log310log3 ⓑ log10-1log10-1
226.
ⓐ eln4eln4 ⓑ lne2lne2
227.
ⓐ eln3eln3 ⓑ lne7lne7
В следующих упражнениях используйте свойство произведения логарифмов, чтобы записать каждый логарифм как сумму логарифмов. Упростите, если возможно.
228.
log46xlog46x
229.
log58ylog58y
230.
log232xylog232xy
231.
log381xylog381xy
232.
журнал100xlog100x
233.
log1000ylog1000y
В следующих упражнениях используйте частное свойство логарифмов, чтобы представить каждый логарифм как сумму логарифмов. Упростите, если возможно.
234.
log338log338
235.
log656log656
236.
log416ylog416y
237.
журнал5125xlog5125x
238.
logx10logx10
239.
log10,000ylog10,000y
240.
lne33lne33
241.
lne416lne416
В следующих упражнениях используйте свойство мощности логарифмов, чтобы раскрыть каждое из них. Упростите, если возможно.
242.
log3x2log3x2
243.
log2x5log2x5
244.
logx-2logx-2
245.
logx-3logx-3
246.
log4xlog4x
247.
log5x3log5x3
908:50 248.lnx3lnx3
249.
lnx43lnx43
В следующих упражнениях используйте свойства логарифмов, чтобы расширить логарифм. Упростите, если возможно.
250.
журнал5(4x6y4)лог5(4x6y4)
251.
журнал2(3x5y3)лог2(3x5y3)
252.
лог3(2х2)лог3(2х2)
253.
лог5(214у3)лог5(214у3)
254.
log3xy2z2log3xy2z2
255.
log54ab3c4d2log54ab3c4d2
256.
log4x16y4log4x16y4
257.
log3x2327y4log3x2327y4
258.
log22x+y2z2log22x+y2z2
259.
log33x+2y25z2log33x+2y25z2
260.
log25x32y2z44log25x32y2z44
261.
log53x24y3z3log53x24y3z3
В следующих упражнениях используйте свойства логарифмов, чтобы сжать логарифм. Упростите, если возможно.
262.
log64+log69log64+log69
263.
log4+log25log4+log25
264.
log280-log25log280-log25
265.
log336-log34log336-log34
266.
log34+log3(x+1)log34+log3(x+1)
267.
log25-log2(x-1)log25-log2(x-1)
268.
log73+log7x-log7ylog73+log7x-log7y
269.
log52-log5x-log5ylog52-log5x-log5y
270.
4log2x+6log2y4log2x+6log2y
271.
6log3x+9log3y6log3x+9log3y
272.
log3(x2-1)-2log3(x-1)log3(x2-1)-2log3(x-1)
273.
log(x2+2x+1)−2log(x+1)log(x2+2x+1)−2log(x+1)
274.
4logx-2logy-3logz4logx-2logy-3logz
275.
3lnx+4lny-2lnz3lnx+4lny-2lnz
276.
13logx−3log(x+1)13logx−3log(x+1)
277.
2log(2x+3)+12log(x+1)2log(2x+3)+12log(x+1)
Использовать формулу смены базы
В следующих упражнениях используйте формулу изменения основания, округляя до трех знаков после запятой, чтобы аппроксимировать каждый логарифм.
278.
log342log342
279.
log546log546
280.
log1287log1287
281.
журнал1593log1593
282.
log217log217
283.
log321log321
Письменные упражнения
284.
Напишите свойство продукта своими словами. Применимо ли это к каждому из следующих? loga5x,loga5x,loga(5+x).loga(5+x). Почему или почему нет?
285.
Напишите свойство мощности своими словами. Применимо ли это к каждому из следующих? logaxp,logaxp,(logax)r.(logax)r. Почему или почему нет?
286.
Используйте пример, чтобы показать, что
log(a+b)≠loga+logb.log(a+b)≠loga+logb.
287.
Объясните, как найти значение log715log715 с помощью калькулятора.
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство выполнения целей этого раздела.
ⓑ По шкале от 1 до 10, от 1 до 10, как бы вы оценили свое знание этого раздела в свете ваших ответов на контрольный список? Как вы можете улучшить это?
Логарифм числа — Математическая энциклопедия 9k$ имеют одинаковую мантисса и отличаются только характеристиками. Это свойство лежит в основе построения таблиц логарифмов, которые содержат только мантиссы логарифмов целых чисел.
Натуральные логарифмы также имеют большое значение; их основанием является трансцендентное число $e=2,71828\dots$; они обозначаются $\ln N$. Переход от одной базы к другой осуществляется по формуле $\log_bN=\log_aN/\log_ab$; множитель $1/\log_ab$ называется модулем перехода от базы $a$ к базе $b$. Формулы перехода от натуральных логарифмов к десятичным логарифмам и наоборот: 9\infty1/n!$ (ср. $e$ (число)).
С другой стороны, авторы книг по математическому и предварительному исчислению, а также производители калькуляторов обычно используют $\log N$ для десятичного (десятичного) логарифма и $\ln N$ для натурального логарифма.

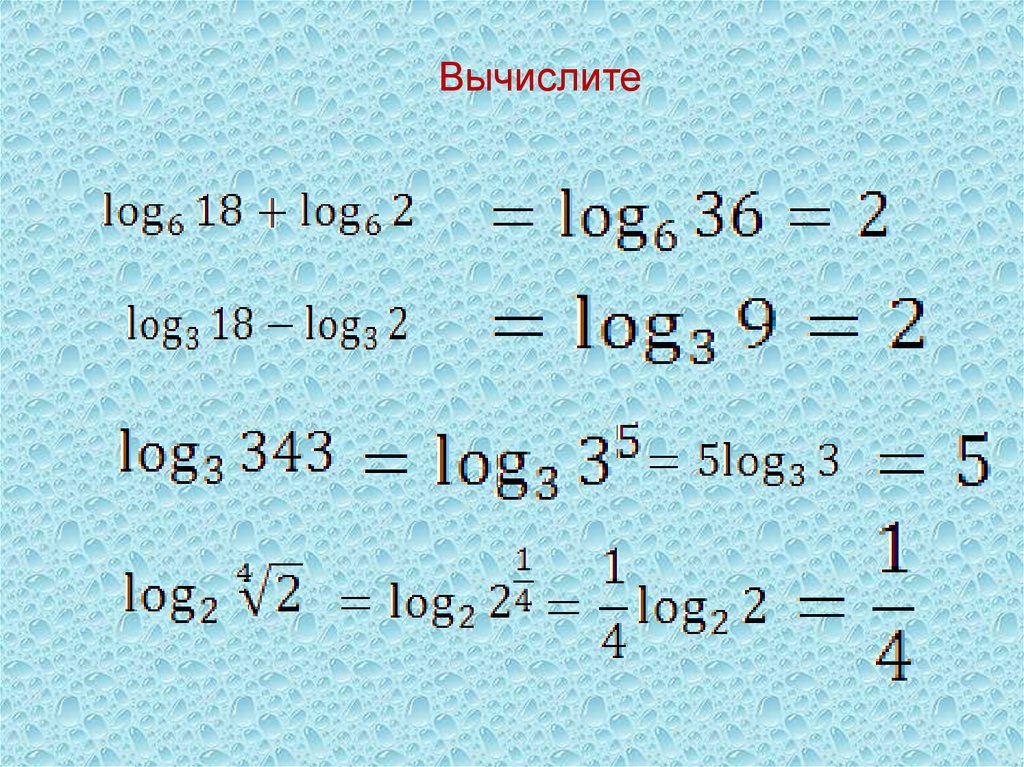

 (1970)
(1970)