Свойства модулей в неравенствах: Решение неравенств с модулем. Модуль раскрытие. Неравенства содержащие модуль. Неравенства с модулем примеры решения.

alexxlab / / Разное

Уравнения и неравенства с модулем — Мегаобучалка

Свойства модуля:

1)

Противоположные числа – числа , имеющие одинаковый модуль (говорят, что числа равны по модулю).

Геометрический смысл: – расстояние от точки с координатой до точки с координатой 0.

2) (модули противоположных чисел равны). Аналогично и для выражений, например .

3) .

Помните, модуль числа – число положительное или 0! Так, например,

, .

 

Подходы к решению уравнений и неравенств:

1) 1 или 2 модуля: раскрытие по определению.

Пример 1. .

Решение:

или .

.

Ответ: .

Пример 2. .

Решение:

или .

.

.

или .

Ответ: .

Пример 3. .

Решение:

или .

.

или . или .

. .

Ответ: .

Пример 4. .

Решение:

или .

.

Ответ: .

Пример 5. .

Решение:

Т.к. слева стоит модуль, то (*).

или .

.

.

Второй корень является посторонним, т.к. не удовлетворяет (*).

Ответ: .

Пример 6. .

Решение:

или .

.

Ответ: .

Пример 7. .

Решение:

.

.

Поскольку каждая часть неравенства положительна, можем извлечь корень:

.

,

.

Объединяя полученные решения, получим ответ.

Ответ: .

Пример 8. .

Решение:

.

.

.

.

Ответ: .

Пример 9. .

Решение:

ОДЗ: (стоит под корнем в знаменателе).

Используя свойство квадратного корня, исходное неравенство примет вид:

.

.

.

.

Ответ: .

Пример 10. .

Решение:

.

.

Последние неравенства решаем по методу интервалов:

 

 

Ответ: .

 

 

2) Несколько модулей: интервальное раскрытие.

На ЦТ такого задания быть не должно,пример рассматривается в ознакомительных целях.

Пример 11. 3|x – 1| – 2|x – 2| + |x + 3| = 2.

Решение:

Находим нули подмодульных выражений:

.

Т.о., имеется 4 интервала, на каждом из которых подмодульные выражения или >0 (‘+’) или <0 (‘–‘):

(знаки расставлены в порядке следования модулей)

Деление на интервалы (включение/невключение в интервал нулей) условное:

1) : . Данное решение не принадлежит рассматриваемому интервалу, но не волнуйтесь: оно будет решением следующего интервала.

2) : .

3) : (не принадлежит рассматриваемому интервалу).

4) : (не принадлежит рассматриваемому интервалу).

О т в е т: .

3) Уравнения и неравенства с одинаковыми компонентами.

A. Метод замены переменных.

Пример 12. .

Решение:

Пусть , тогда .

или .

Ответ: .

Пример 13. .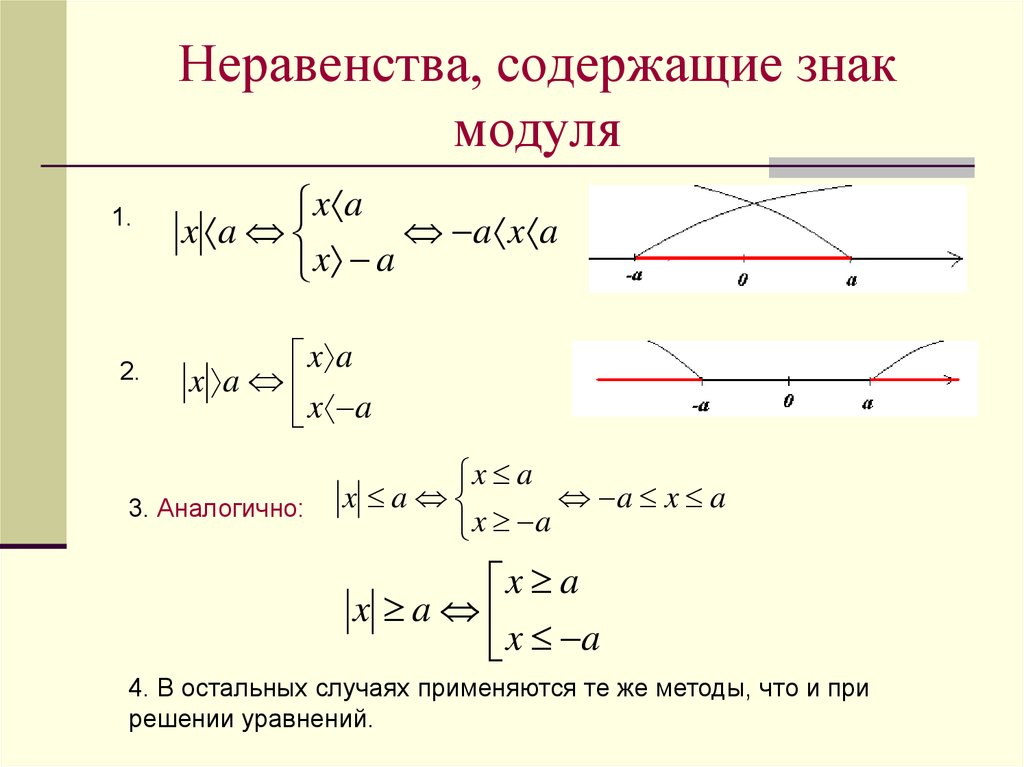

Решение:

Пусть , тогда .

или .

или .

.

Ответ: .

 

Б. Используются свойства модуля.

Пример 14. Решите уравнение .

Решение:

Перепишем уравнение в виде: .

Получается, что модуль выражения равен этому выражению, взятому с противоположным знаком. Такое возможно только в том случае, если данное выражение отрицательно или равно нулю:

.

Ответ: .

Пример 15. Решите неравенство .

Решение:

Модуль A не может быть меньше A, возможно только равенство, из которого делаем вывод:

.

Ответ: .

Пример 16. Решите неравенство .

Решение:

Перепишем уравнение в виде .

или .

.

Ответ: .

В. Используются свойства других функций.

Пример 17. Решите уравнение .

Решение:

Возможны следующие случаи:

1) х2 – х = 2 (степени равны), откуда х1 = 2, х2 = –1.

2) 0а = 0в, а > 0; в > 0, т.е. |х – 3| = 0, х3 = 3.

3) |х – 3| = 1, откуда х4 = 4; х5 = 2.

Ответ:–1; 2; 3; 4.

Модуль числа. Неравенства, содержащие модуль

Похожие презентации:

Маркировка обувных товаров. ГК Эталон

Реклама и ее виды

The coca-cola company

Анализ компании Apple

История бренда «Мерседес»

Основы мерчандайзинга в аптеке

Презентация на тему: Mersedes

SMM – маркетинг в социальных сетях

10 Этапов успешных продаж

Тренинг. Основы продаж Henkel

Домашнее задание
П. 42,
№ 1044 (б, в),
№ 1047 (б, в).
Модуль числа.
Неравенства,
содержащие модуль.
(все записать в тетрадь)
Геометрический смысл модуля
Модуль – это расстояние от начала отсчета до точки с заданной
координатой. Модуль число положительное, так как расстояние не может
быть отрицательным.
|x| = 5
Это значит, что от точки 0, мы можем отложить расстояние в 5 единичных

отрезков вправо и влево. Тое есть мы попадем в точки с координатами
х = 5 и х = -5.
расстояние 5 ед. отрезков
расстояние 5 ед. отрезков
-5
-1
0
1
5
Таким образом вы решали уравнения с модулем в 6 классе
|х| = 6
|х| = -4
|х — 7| = 12
х = -6 или х = 6
решений нет
х – 7 = -12 или х – 7 = 12
Ответ: -6; 6.
Ответ:
х = -5
х = 19
Ответ: -5; 19.
х

4. Свойства модуля числа

СВОЙСТВА МОДУЛЯ ЧИСЛА
|3| = 3
-5
-4
|3| = 3
-3
-2
-1
0
1
А(3)
2
3
4
Модуль положительного
числа равен самому числу
|0| = 0
Модуль нуля равен нулю
5

5. Свойства модуля числа

СВОЙСТВА МОДУЛЯ ЧИСЛА
А(-3) |-3| = 3
-5
-4
|-3| = 3
-3
-2
-1
0
1
2
3
4
5
Модуль отрицательного числа
равен противоположному числу
|а| ≥ 0
|-а| = |а|

6.

Модуль числаМОДУЛЬ ЧИСЛА
х 5
а, если а 0,
а
а, если а 0
х 0, то х 5
х 0, то х 5

7. Модуль числа

МОДУЛЬ ЧИСЛА
а, если а 0,
а
а, если а 0
х 2 5 х 2 0, то х 2 5
х 7
х 2 0, то х 2 5
х 3
Модуль числа
а, если a 0,
а
a, если а 0.
х
3
,
х 3
х 3.
Используя геометрический смысл,
это значит что расстояние меньше
3, что соответствует отрезку
[-3; 3].
Система
IIIIIIIIIIIIIIIIIIIIII
I I I I I I I I I I I -3
I I I I I I I I I I I3
х
х [ 3; 3]
3 х 3
Используя геометрический смысл, это значит что расстояние меньше а, что
соответствует отрезку [-а; а].
x a , где а 0
x a
x a
Система
IIIIIIIIIII
а
-а
х [ a; a]
а х а
х
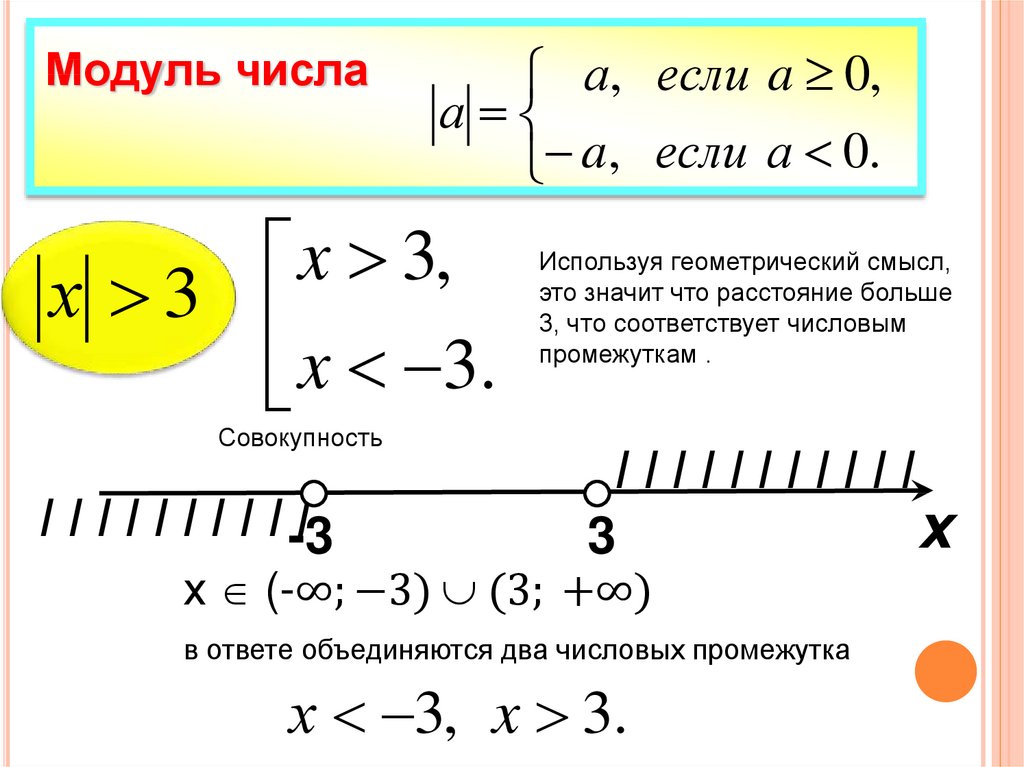
Модуль числа
а, если a 0,
а
a, если а 0.
x 3,
х 3
x 3.
Совокупность
I I I I I I I I I -3
I
Используя геометрический смысл,
это значит что расстояние больше
3, что соответствует числовым
промежуткам .
IIIIIIIIIII
х
3
х (-∞; −3) (3; +∞)
в ответе объединяются два числовых промежутка
х 3, x 3.
х а, где а 0
Совокупность
I I I I I I I I I -а
I
x a,
x a.
IIIIIIIIIII
а
х
х ( ∞; -а) (а; +∞)
х a, x a.
№1044 (а, д, е – образцы)
а) |х — 7| < 4
Помним о знаках неравенств, данное
неравенство строгое.
+4
-4
3
7
11
Ответ: (3; 11)
д) |х + 17| < -2
Решений нет, так как положительное число (модуль) не может быть
меньше отрицательного числа.
Ответ:
е) |17 — х| > -1
х – любое число, так как положительное число (модуль) больше
отрицательного числа.
Ответ: х R
№ 1047 (а, г – образец) Используем либо свойство модуля,
либо геометрический смысл модуля.
В данном случае видно, что
расстояние (модуль) больше либо
равно 3,4, то есть получаем два
числовых промежутка.
Следовательно получим
совокупность двух неравенств.
|3x — 2| ≥ 3,4
3

English     Русский Правила

неравенств типа Бесселя и Грюсса в модулях внутреннего произведения над банаховыми -алгебрами | Журнал неравенств и приложений

  • Исследовательская статья
  • Открытый доступ
  • Опубликовано:
  • А. Г. Газанфари 1 и
  • С. С. Драгомир 2,3  

Журнал неравенств и приложений том 2011 , Номер статьи: 562923 (2011) Процитировать эту статью

  • 1601 доступ

  • 2 Цитаты

  • Сведения о показателях

Abstract

Мы даем аналог неравенства Бесселя и формулируем простую формулировку неравенства типа Грюсса в модулях скалярных произведений, которая является его уточнением. Мы получаем дальнейшее обобщение неравенств типа Грюсса в модулях скалярных произведений над собственными -алгебрами и унитальными банаховыми -алгебрами для -полунорм и положительных линейных функционалов.

1. Введение

Правильная -алгебра – это комплексная банахова -алгебра, где базовое банахово пространство является гильбертовым относительно скалярного произведения, удовлетворяющим свойствам и для всех . -алгеброй называется комплексная банахова -алгебра такая, что для любого . Если собственная -алгебра или -алгебра и такова, что или , то .

Для правильной -алгебры связанный с ней класс трассировки равен . Для каждого положительного существует квадратный корень из , то есть единственный положительный такой, что квадратный корень из обозначается . Существуют положительный линейный функционал на и норма на , связанные с нормой A равенством для каждого .

Позвольте быть собственной -алгеброй или -алгеброй. Модуль полускалярного произведения над является правым модулем над вместе с обобщенным полускалярным произведением, то есть с отображением на , которое является -значным, если является собственной -алгеброй, или -значным, если является -алгеброй, имеющей следующие свойства:

(i) для всех ,

(ii) для , ,

(iii) для всех ,

(iv) для .

Мы будем говорить, что это полу-модуль скалярного произведения, если является собственной -алгеброй, и что это -модуль полускалярного произведения, если является -алгеброй.

Если, кроме того,

(v) подразумевает ,

тогда называется модулем внутреннего продукта над . Абсолютное значение определяется как квадратный корень из и обозначается .

Позвольте быть -алгеброй. Полунормой на называется вещественнозначная функция на такая, что для и : , , . Полунорма на называется -полунормой, если она удовлетворяет -условию: . По теореме Себастьена [1, теорема  38.1] каждая -полунорма на -алгебре субмультипликативна, т. е. , а по [2, раздел  39, Лемма  2(i)] . Для каждого спектральный радиус определяется как .

Функция Птака на -алгебре определяется как , где . Эта функция играет важную роль в банаховых -алгебрах, например, на -алгебрах равна норме, а на эрмитовых банаховых -алгебрах является наибольшей -полунормой. Используя свойства спектрального радиуса и функции Птака, Птак [3] показал в 1970 г.

, что элегантная теория банаховых -алгебр возникает из неравенства .

Это неравенство характеризует эрмитовы (и симметричные) банаховы -алгебры, и дальнейшие характеристики -алгебр следуют из теории Птака.

Позвольте быть -алгеброй. Определим через

(1.1)

и назовем элементы положительными.

Множество положительных элементов, очевидно, является выпуклым конусом (т. е. замкнуто относительно выпуклых комбинаций и умножения на положительные константы). Поэтому мы называем положительный конус. По определению ноль принадлежит . Ясно также, что каждый положительный элемент эрмитов.

Напомним, что банахова -алгебра называется -алгеброй, если существует вторая норма , не обязательно полная, которая является -нормой. Вторую норму будем называть вспомогательной нормой.

Определение 1.1.

Позвольте быть -алгеброй. Модуль полускалярного произведения (или модуль полускалярного произведения) представляет собой комплексное векторное пространство, которое также является правым -модулем с полуторалинейным полускалярным произведением , выполняющим

(1. 2)

для , . Кроме того, если удовлетворяет строгому условию положительности

(1.3)

, то называется модулем внутреннего продукта (или модулем внутреннего продукта).

Позвольте быть полунормой или положительным линейным функционалом на и . Если — полунорма на полу-модуле скалярного произведения, то говорят, что это — полугильбертов -модуль.

Если является нормой модуля скалярного произведения , то называется предгильбертовым -модулем.

Предгильбертовый -модуль, полный относительно своей нормы, называется гильбертовым -модулем.

Так как и самосопряжены, то получаем Следствие.

Следствие 1.2.

Если – модуль полускалярного произведения, то выполняется следующее условие симметрии:

(1.4)

Пример 1.3.

  1. (а)

    Позвольте быть -алгеброй и положительным линейным функционалом или -полунормой на . Известно, что является полугильбертовым -модулем над собой со скалярным произведением, определяемым , в данном случае .

  2. (б)

    Позвольте быть эрмитовой банаховой -алгеброй и быть функцией Птака на . Если — полу-модуль скалярного произведения и , то — полугильбертов -модуль.

  3. (с)

    Позвольте быть -алгеброй и быть вспомогательной нормой на . Если — модуль внутреннего продукта и , то — предгильбертов -модуль.

  4. (г)

    Пусть -алгебра и (полу-скалярный продукт) -модуль внутреннего продукта. Так как tr является положительным линейным функционалом на и для каждого мы имеем ; поэтому является (полугильбертовым) предгильбертовым -модулем.

В настоящей статье мы даем аналог неравенства Бесселя (2. 7) и получаем некоторое дальнейшее обобщение и простую форму для неравенств типа Грюсса в модулях скалярных произведений над -алгебрами, собственными -алгебрами и унитальными банаховыми -алгебрами .

2. Неравенство Шварца и Бесселя

Если есть полувнутренний продукт -модуль, то имеет место следующее неравенство Шварца:

(2.1)

(например, [4, Лемма  15.1.3]).

Если – модуль полускалярного произведения, то неравенство Шварца имеет две формы: для каждого

(2.2)

(2.3)

Сначала Саворотнов в [5] доказал сильное неравенство Шварца, но прямое доказательство этого для полу-модуля скалярного произведения можно найти в [6].

Теперь пусть будет -алгебра, положительный линейный функционал на и пусть будет полувнутренний -модуль. Мы можем определить полуторалинейную форму на ; неравенство Шварца для означает, что

(2.4)

В [7, Proposition  1, Remark  1] авторы представляют две другие формы неравенства Шварца в полу-внутреннем -модуле , одну для положительного линейного функционала на :

(2. 5)

и другую один для -полунормы на :

(2.6)

Классическое неравенство Бесселя утверждает, что если семейство ортонормированных векторов в гильбертовом пространстве , то

(2.7)

Кроме того, некоторые результаты, касающиеся верхних границ для выражения

(2.8)

и для выражения, относящегося к неравенству типа Грюсса

(2.9)

, были доказаны в [8]. Вариант неравенства Бесселя для -модулей скалярного произведения и -модулей скалярного произведения можно найти в [9], также его вариант для -модулей Гильберта можно найти в [10, теорема  3.1]. Мы приводим здесь аналог неравенства Бесселя для -модулей внутреннего произведения.

Лемма 2.1.

Пусть -алгебра, пусть — модуль скалярного произведения, и пусть — конечное множество ортогональных элементов в таких, которые являются идемпотентными. Затем

(2.10)

Доказательство.

Из [11, Лемма  1] или прямого вычисления следует, что

(2.11)

3.

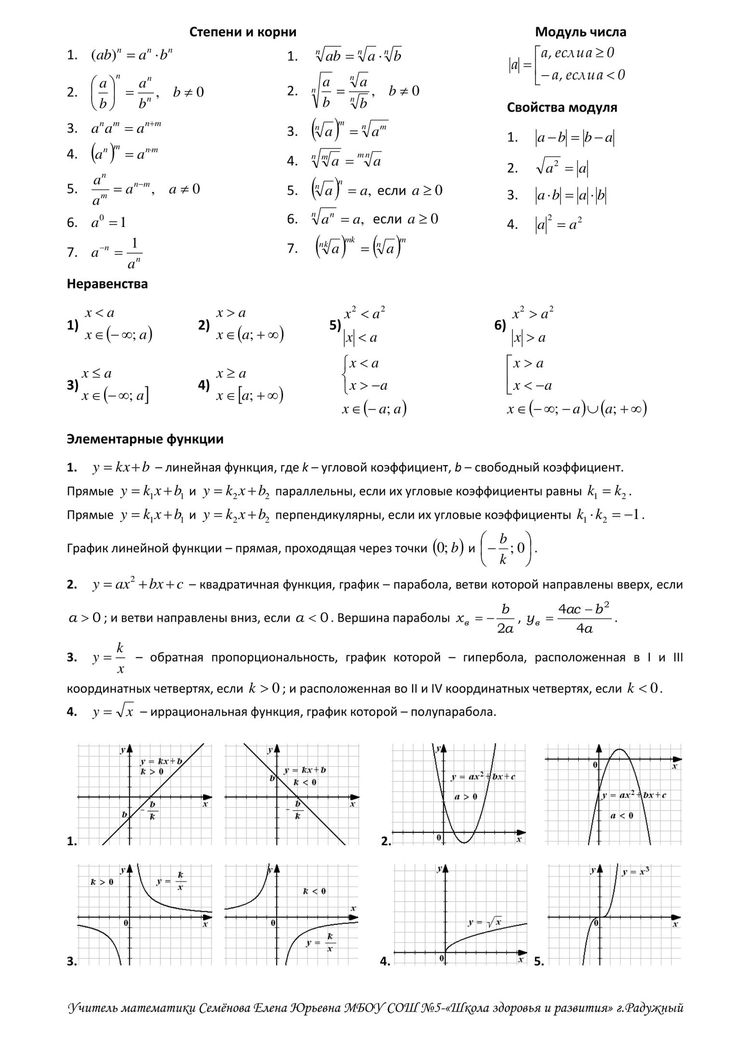Неравенства типа Грюсса

Прежде чем сформулировать основные результаты, зафиксируем остальные обозначения. Мы предполагаем, если не оговорено противное, на протяжении всего этого раздела, что это унитальная банахова -алгебра. Также, если является полу-модулем скалярного произведения и является -полунормой на , положим , а если — положительным линейным функционалом на , положим . Позвольте быть конечным набором ортогональных элементов в таких, которые идемпотентны, мы устанавливаем и .

Драгомир в [8, Лемма  4] показывает, что в гильбертовом пространстве условие

(3.1)

эквивалентно условию

(3.2)

где и , . Но для полу-модулей скалярного произведения справедлива следующая лемма, являющаяся обобщением [7, лемма  1].

Лемма 3.1.

Позвольте быть модулем полу-скалярного продукта и ,   . Тогда

(3.3)

тогда и только тогда, когда

(3.4)

Доказательство.

Из равенств следует:

(3.5)

Примечание 3. 2.

Используя предыдущую лемму 3.1, мы можем заключить следующие утверждения.

(i) Пусть модуль скалярного произведения и пусть конечное множество ортогональных элементов в таком, что они идемпотентны, тогда из неравенства (3.3) следует, что модуля и быть конечным набором ортогональных элементов в таких, которые являются идемпотентными. Если является -полунормой на, то из неравенства (3.3) следует, что

(3.7)

и если – положительный линейный функционал on из неравенства (3.3) и [2, §  37 Лемма  6(iii)], получаем

(3.8)

(iii) алгебры, пусть будет модулем скалярного произведения и пусть будет конечным набором ортогональных элементов в таких, которые являются идемпотентными. Так как для каждого неравенство (3.3) справедливо, только если

(3.9)

Теперь мы можем сформулировать наш первый основной результат.

Теорема 3.3.

Позвольте быть модулем скалярного произведения и пусть быть конечным набором ортогональных элементов в таких, которые являются идемпотентными.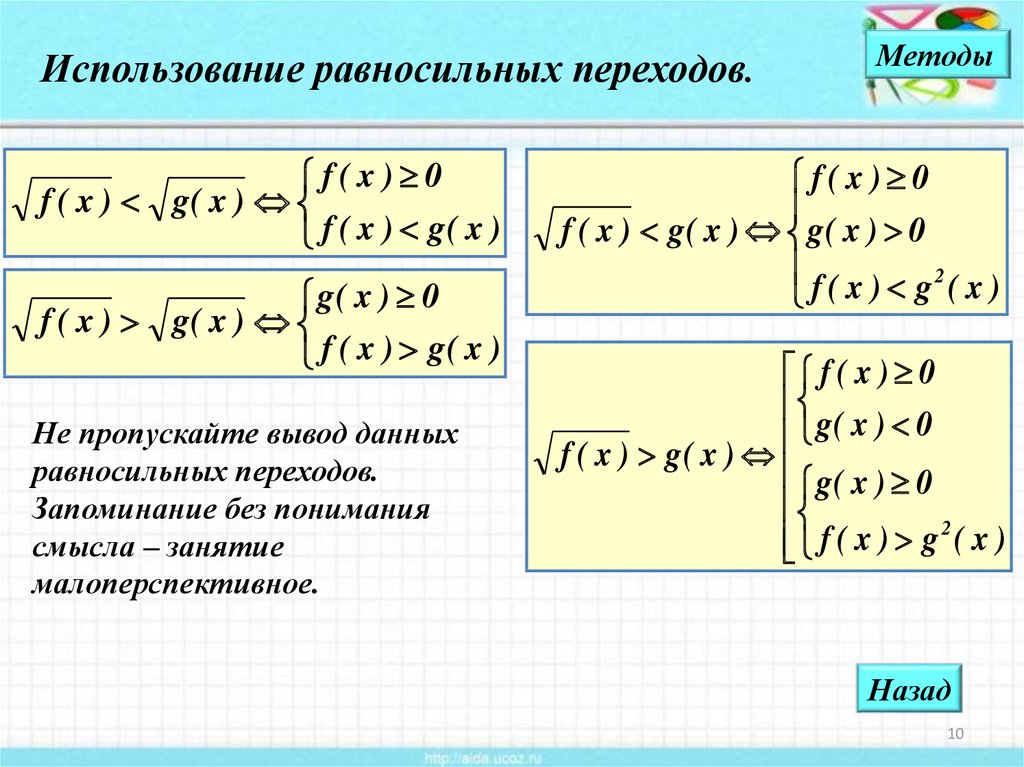 Если , , , действительные числа и такие, что

(3.10)

, то имеет место неравенство

(3.11)

Доказательство.

По [11, лемма  2] или, прямое вычисление показывает, что для любых

(3.12)

Следовательно,

(3.13)

Аналогично, для каждого имеем

  • 0 (3.14) 90 равенств Из (3.10), (3.13) и (3.14) следует, что

    (3.15)

    (3.16)

    Поскольку

    (3.17)

    , то выполняется неравенство Шварца (2.1), т. е.

    (3.18)

    Наконец, используя элементарное неравенство для действительных чисел

    (3.19)

    на

    (3.20)

    , получаем

    (3.21)

    27. Замечание.

    1. (я)

      Позвольте быть модулем скалярного произведения и пусть быть конечным набором ортогональных элементов в таких, которые являются идемпотентными. Если и таковы, что

      (3.22)

    а если положить , и , то в силу (3. 15) и (3.16) имеем

    (3.23)

    Отсюда и (3.11) следует, что

    (3.24)

    уточнение и простая формулировка [9, теорема  4.1.].

    1. (ii)

      Если для , устанавливаем

      (3.25)

    , то аналогично (3.11) является уточнением и простой формой [9, Следствие  4.3].

    Следствие 3.5.

    Позвольте быть банаховой -алгеброй, пусть быть модулем внутреннего произведения и пусть быть конечным набором ортогональных элементов в таких, которые являются идемпотентными. Если , , действительные числа и такие, что

    (3.26)

    , то имеет место неравенство

    (3.27)

    Доказательство.

    Используя неравенство Шварца (2.6), имеем

    (3.28)

    Предположения (3.26) и элементарное неравенство для действительных чисел (3.19) обеспечит желаемый результат (3.27).

    Пример 3.6.

    Пусть будет эрмитовой банаховой -алгеброй и пусть будет функцией Птака на . Если это полувнутренний продукт-модуль со свойствами

    (3.29)

    , то мы имеем

    (3.30)

    Это интересно само по себе.

    Следствие 3.7.

    Пусть будет собственная -алгебра, пусть будет -модуль внутреннего произведения и пусть будет конечное множество ортогональных элементов в таких, которые являются идемпотентными. Если , действительные числа и такие, что

    (3.31)

    , то имеет место неравенство

    (3.32)

    Доказательство.

    Используя сильное неравенство Шварца (2.3), имеем

    (3.33)

    Предположения (3.31) и элементарное неравенство для действительных чисел (3.19) дадут (3.32).

    Имеет место следующий компаньон неравенства Грюсса для положительных линейных функционалов.

    Теорема 3.8.

    Позвольте быть модулем скалярного произведения, пусть быть положительным линейным функционалом на , и пусть быть конечным набором ортогональных элементов в таких, которые являются идемпотентными. Если , , , действительные числа и такие, что

    (3.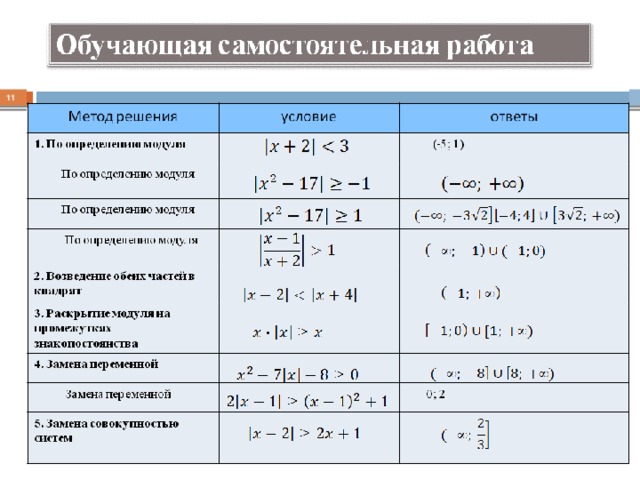 34)

    , то имеет место неравенство

    (3.35)

    Доказательство.

    Взяв обе части (3.12), получим

    (3.36)

    Аналогично

    (3.37)

    Теперь, используя неравенство Ацля для действительных чисел, т. е. напомним, что

    (3.027)

    и неравенство Шварца для положительных линейных функционалов, т. е.

    (3.39)

    , выводим (3.35).

    4. Некоторые связанные результаты

    Теорема 4.1.

    Позвольте быть модулем скалярного произведения и пусть быть конечным набором ортогональных элементов в таких, которые являются идемпотентными. Пусть и если мы определим

    (4.1)

    , то мы получим

    (4.2)

    Доказательство.

    Для каждого , , по (3.13) и (3.14) имеем

    (4.3)

    Следовательно,

    (4.4)

    Теперь, используя элементарное неравенство для действительных чисел

    (4.5)

      7 на

      (4,6)

      получаем

      (4. 7)

      Следствие 4.2.

      Позвольте быть банаховой -алгеброй, пусть быть модулем внутреннего произведения и пусть быть конечным набором ортогональных элементов в таких, которые являются идемпотентными. Пусть и положить

      (4.8)

      тогда

      (4.9)

      Следствие 4.3.

      Пусть будет собственная -алгебра, пусть будет -модуль внутреннего произведения и пусть будет конечное множество ортогональных элементов в таких, которые являются идемпотентными. Пусть и если рассматривать

      (4.10)

      , затем

      (4.11)

      С другой точки зрения, мы можем также сформулировать следующий результат.

      Теорема 4.4.

      Позвольте быть модулем скалярного произведения и пусть быть конечным набором ортогональных элементов в таких, которые являются идемпотентными. Если , , и такие, что

      (4.12)

      , то имеем неравенство

      (4.13)

      Доказательство.

      Мы знаем, что для любого и один имеет

      (4.14)

      Положим , , а так как

      (4. 15)

      используя (4.14), имеем

      (4.16)

      Теперь неравенство (4.13) следует из неравенств (3.15) и (4.16).

      Имеет место следующий компаньон неравенства Грюсса для положительных линейных функционалов.

      Теорема 4.5.

      Позвольте быть модулем скалярного произведения, пусть быть положительным линейным функционалом на , и пусть быть конечным набором ортогональных элементов в таких, которые являются идемпотентными. Если , и такие, что

      (4.17)

      , то выполняется неравенство

      (4.18)

      Доказательство.

      Из неравенства (4.14) для , следует, что

      (4.19)

      Используя неравенство (3.12) для вместо и взяв обе части, имеем

      (4.20)

      Из (4.19) и ( 4.20), мы легко выводим (4.18).

      Замечание 4.6.

      1. (я)

        Постоянный коэффициент 1 при (3.11) точен в том смысле, что его нельзя заменить меньшей величиной. Если подмодуль порожденного не равен , то существует такой, что . Ставим , тогда и для любого имеем

        (4.21)

      Для каждого , если мы положим

      (4.22)

      , то

      (4.23)

      , следовательно,

      (4.24)

      Теперь, если константа такая, что , то существует такое, что ; поэтому

      (4.25)

      1. (ii)

        Аналогично, константа 1 коэффициента в (3.32) является наилучшей, достаточно вместо (4.22) положить

        (4.26)

      1. (iii)

        Если есть ненулевой элемент в таком, что и (соответственно ), то постоянный 1 коэффициент в (3.27) (соответственно (3.35)) является наилучшим возможным. Точно так же неравенства в теореме 4.1, следствиях 4.2 и 4.3 и теоремах 4.4 и 4.5 точны. Однако подробности опущены.

      Литература

      1. «>

        Доран Р.С., Белфи В.А.: Характеристики C∗-алгебр, монографии и учебники по чистой и прикладной математике . Том 101 . Марсель Деккер, Нью-Йорк, США; 1986:xi+426.

        Google ученый

      2. Бонсолл Ф.Ф., Дункан Дж.: Полные нормированные алгебры, математические вычисления и их значение . Том 8 . Спрингер, Нью-Йорк, штат Нью-Йорк, США; 1973:х+301.

        Google ученый

      3. Птак В.: О спектральном радиусе в банаховых алгебрах с инволюцией. Бюллетень Лондонского математического общества 1970, 2: 327–334. 10.1112/blms/2.3.327

        Артикул MathSciNet МАТЕМАТИКА Google ученый

      4. Wegge-Olsen NE: K-теория и C∗-алгебры: дружественный подход, Oxford Science Publications . The Clarendon Press, Oxford University Press, Нью-Йорк, штат Нью-Йорк, США; 1993:xii+370.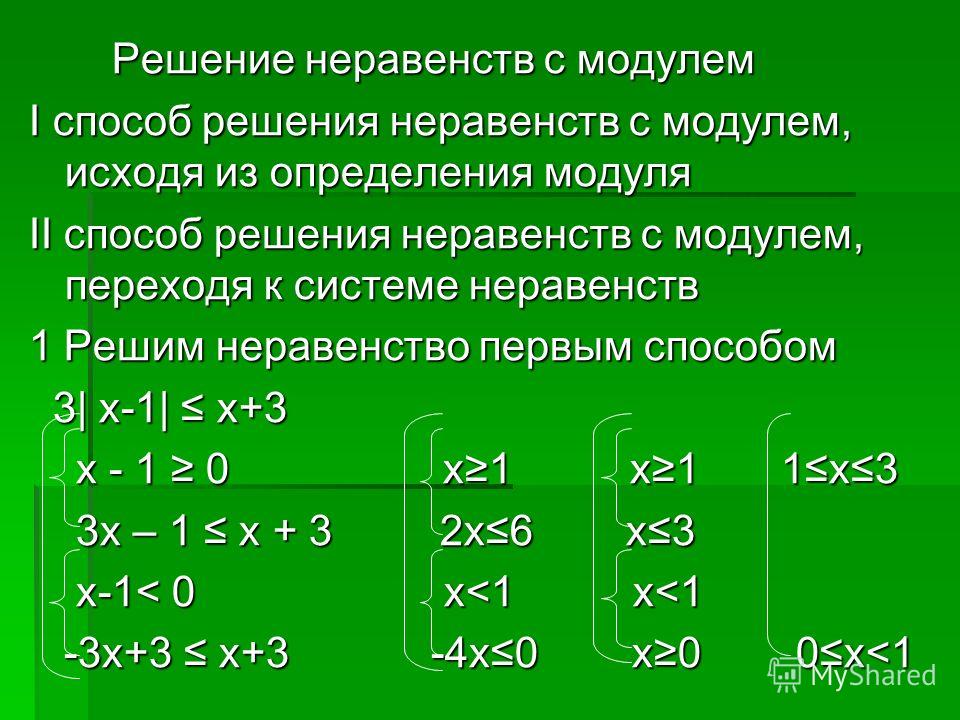

        Google ученый

      5. Saworotnow PP: Обобщенное гильбертово пространство. Математический журнал Duke 1968, 35: 191–197. 10.1215/S0012-7094-68-03520-5

        Артикул MathSciNet МАТЕМАТИКА Google ученый

      6. Molnár L: Примечание о сильном неравенстве Шварца в Гильберте -модули. Publicationes Mathematicae Debrecen 1992, 40 (3–4): 323–325.

        MathSciNet МАТЕМАТИКА Google ученый

      7. Газанфари А.Г., Драгомир С.С.: Неравенства типа Шварца и Грюсса для -полунорм и положительных линейных функционалов на банаховых -модулях. Линейная алгебра и ее приложения 2011, 434 (4): 944–956. 10.1016/j.laa.2010.10.010

        Артикул MathSciNet МАТЕМАТИКА Google ученый

      8. «>

        Dragomir SS: Успехи в неравенствах типа Шварца, Грюсса и Бесселя во внутренних пространствах произведений . Nova Science, Хауппож, Нью-Йорк, США; 2005: VIII+249.

        МАТЕМАТИКА Google ученый

      9. Банич С., Илишевич Д., Варошанец С.: Неравенства типа Бесселя и Грюсса в модулях внутреннего произведения. Труды Эдинбургского математического общества 2007, 50: 23–36. 10.1017/S0013091505001021

        Артикул MathSciNet МАТЕМАТИКА Google ученый

      10. Драгомир С.С., Хосрави М., Мослехян М.С.: Неравенства типа Бесселя в гильбертовых -модулях. Линейная и полилинейная алгебра 2010, 58 (8): 967–975. 10.1080/03081080

      11. 3361

        Артикул MathSciNet МАТЕМАТИКА Google ученый

      12. Бакич Д. , Гуляш Б.: Гильберт -модулей над -алгебр компактных операторов. Acta Scientiarum Mathematicarum 2002, 68 (1–2): 249–269.

        МАТЕМАТИКА Google ученый

      Ссылки для скачивания

      Информация об авторе

      Авторы и организации

      1. Математический факультет, Лорестанский университет, П.О. Box 465, Хорамабад, Иран

        А. Г. Газанфари

      2. Школа инженерии и науки, Университет Виктории, PO. Box 14428, Melbourne City, MC, 8001, Australia

        S Dragomir

      3. Школа вычислительной и прикладной математики, Университет Виттерсранда, Частный Bag 3 Wits 2050, Johannesburg, Южная Африка

        S Dragomir

      818

      .

      1. А. Г. Газанфари

        Просмотр публикаций автора

        Вы также можете искать этого автора в PubMed Google Академия

      2. С С Драгомир

        Посмотреть публикации автора

        Вы также можете искать этого автора в PubMed Google Scholar

      Автор, ответственный за корреспонденцию

      А Г Газанфари.

      Права и разрешения

      Открытый доступ Эта статья распространяется в соответствии с условиями международной лицензии Creative Commons Attribution 2.0 (https://creativecommons.org/licenses/by/2.0), которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии надлежащего цитирования оригинальной работы.

      Перепечатка и разрешения

      Об этой статье

      Портал обучения DepEd

      1. Математика — закономерности и алгебра

      Учебный материал, учебный модуль | PDF



      Описание
      Этот материал состоит из упражнений, направленных на развитие у учащихся навыков определения, решения и применения свойств неравенств и абсолютного значения.

      No related posts.

    • Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *