Остроугольный треугольник, элементы, свойства, признаки и формулы
Остроугольный треугольник, элементы, свойства, признаки и формулы.
Остроугольный треугольник – это треугольник, у которого все углы острые.
Остроугольный треугольник (понятие и определение)
Элементы остроугольного треугольника
Свойства остроугольного треугольника
Формулы остроугольного треугольника
Остроугольный треугольник, прямоугольный треугольник, равнобедренный треугольник, равносторонний треугольник, тупоугольный треугольник
Остроугольный треугольник (понятие и определение):
Остроугольный треугольник – это треугольник, у которого все углы острые, т.е. меньше 90°.
Остроугольный треугольник – это треугольник, у которого все три угла острые. В свою очередь, острый угол – это угол, градусная мера которого составляет менее 90 градусов.
Рис. 1. Остроугольный треугольник
1. Остроугольный треугольник
∠ АВС, ∠ BАC, ∠ BСA – острые углы треугольника
По определению, каждый правильный (равносторонний) треугольник также является остроугольным, но не каждый остроугольный треугольник – правильным (равносторонним). Иными словами, правильный (равносторонний) треугольник является частным случаем остроугольного треугольника. У равностороннего треугольника каждый угол составляет 60 °.
Рис. 2. Равносторонний треугольник
АВ = ВС = АС – стороны треугольника,
∠ АВС = ∠ BАC = ∠ BСA = 60° – углы треугольника
Остроугольный треугольник также может быть одновременно равнобедренным треугольником.
Рис. 3. Равнобедренный треугольник
АВ = ВС – боковые стороны, АС – основание,
∠ АВС – вершинный угол, ∠ BАC и ∠ BСA – углы при основании
Хотя в остроугольном треугольнике каждый угол меньше 90 градусов, сумма углов в треугольнике всегда равна 180 градусам.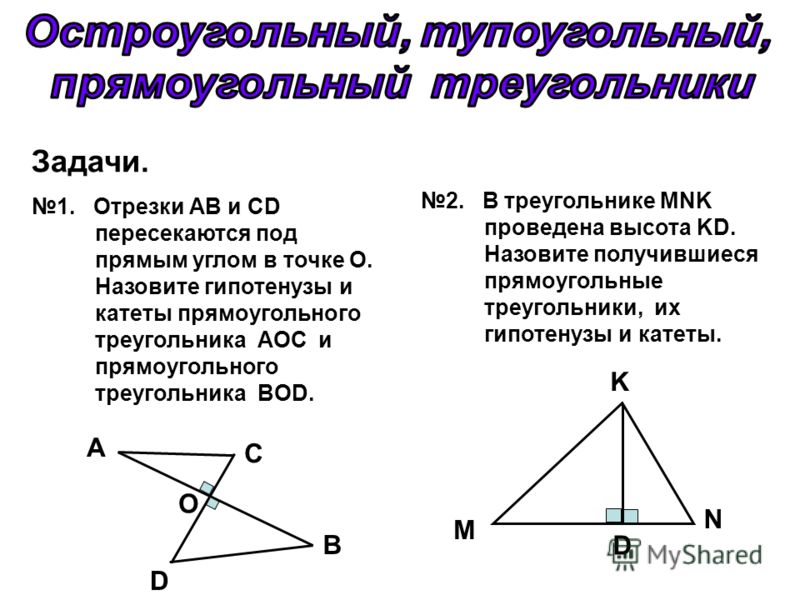
Элементы остроугольного треугольника:
Кроме сторон и углов у одностороннего треугольника также имеются внешние углы. Внешний угол это угол, смежный с внутренним углом треугольника. У любого треугольника, в т.ч. остроугольного, 6 внешних углов, по 2 на каждый внутренний. Любой внешний угол остроугольного треугольника всегда будет тупым углом.
Рис. 4. Остроугольный треугольник и внешний угол
∠ ВСD – внешний угол
Медиана остроугольного треугольника (как и любого другого треугольника), соединяющая вершину треугольника с противоположной стороной, делит ее пополам, т.е. на два одинаковых отрезка.
Рис. 5. Остроугольный треугольник и медиана остроугольного треугольника
MС – медиана остроугольного треугольника
Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.
Рис. 6. Остроугольный треугольник и высота остроугольного треугольника
MС – высота остроугольного треугольника
Высота остроугольного треугольника находится внутри треугольника. Все 3 высоты остроугольного треугольника (как и любого треугольника) пересекаются в одной точке, называемой ортоцентром.
Биссектриса в остроугольном треугольнике (как и в любом другом треугольнике) делит угол пополам. Биссектрисы пересекаются в точке, которая является центром вписанной окружности.
Рис. 7. Остроугольный треугольник и биссектриса угла остроугольного треугольника
MС – биссектриса угла остроугольного треугольника
Кроме того, биссектриса остроугольного треугольника (как и любого другого треугольника) делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
Свойства остроугольного треугольника:
Свойства остроугольного треугольника аналогичны свойствам обычного треугольника:
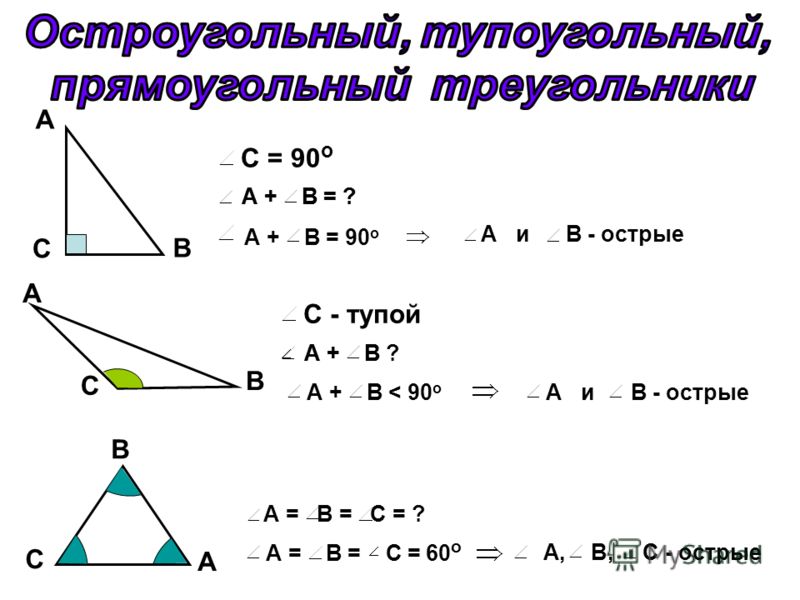
1. Против большей стороны лежит больший угол, и наоборот.
Против большей стороны лежит больший угол, и наоборот.
Рис. 8. Остроугольный треугольник
2. Против равных сторон лежат равные углы, и наоборот.
Рис. 9. Остроугольный треугольник с равными боковыми сторонами
АВ = ВС
3. Сумма углов остроугольного треугольника равна 180°.
4. Любая сторона остроугольного треугольника меньше суммы двух других сторон и больше их разности:
- a < b + c;
- a > b – c;
- b < a + c,
- b > a – c;
- c < a + b;
- c > a – b.
Квадрат
Овал
Остроугольный треугольник
Полукруг
Прямой угол
Прямоугольник
Прямоугольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Ромб
Трапеция
Тупой угол
Шестиугольник
Примечание: © Фото https://www.pexels. com, https://pixabay.com
com, https://pixabay.com
Коэффициент востребованности 10 859
Остроугольный треугольник – определение и свойства
4.5
Средняя оценка: 4.5
Всего получено оценок: 295.
Обновлено 11 Января, 2021
4.5
Средняя оценка: 4.5
Всего получено оценок: 295.
Обновлено 11 Января, 2021
В школьном курсе геометрии изучают разные виды треугольников. В задачах очень часто рассматривают остроугольный треугольник, поэтому стоит особенно пристально изучить свойства этой фигуры.
Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.
Опыт работы учителем математики — более 33 лет.
Определение понятия
Треугольником называют фигуру, состоящую из трех точек, и трех отрезков их соединяющих. В зависимости от углов треугольник может быть:
- Прямоугольным, если один из углов равен 90 градусов;
- Тупоугольный, если один из углов тупой, т.
 е. больше 90 градусов;
е. больше 90 градусов; - Остроугольным, если все углы треугольника острые.
Для решения задач с остроугольными треугольниками часто приходится использовать теорему синусов или косинусов.
Еще в Древней Греции математики изучали треугольники. Именно греки разработали основы современной геометрии, куда входит и множество теорем о треугольниках. Например, автор теоремы Пифагора родом из Древней Греции.
Характеристики
В остроугольном треугольнике каждый угол меньше 90 градусов. Но сумма углов в треугольнике всегда равна 180. В любой фигуре вершины обозначают заглавными латинскими буквами.
Одним из элементов треугольника, вместе со сторонами и углами, является внешний угол. Внешний угол это угол, смежный с внутренним углом треугольника.
У любого треугольника 6 внешних углов, по 2 на каждый внутренний. Любой внешний угол остроугольного треугольника всегда будет тупым.
Линии остроугольного треугольника
Остроугольный треугольник обладает рядом свойств.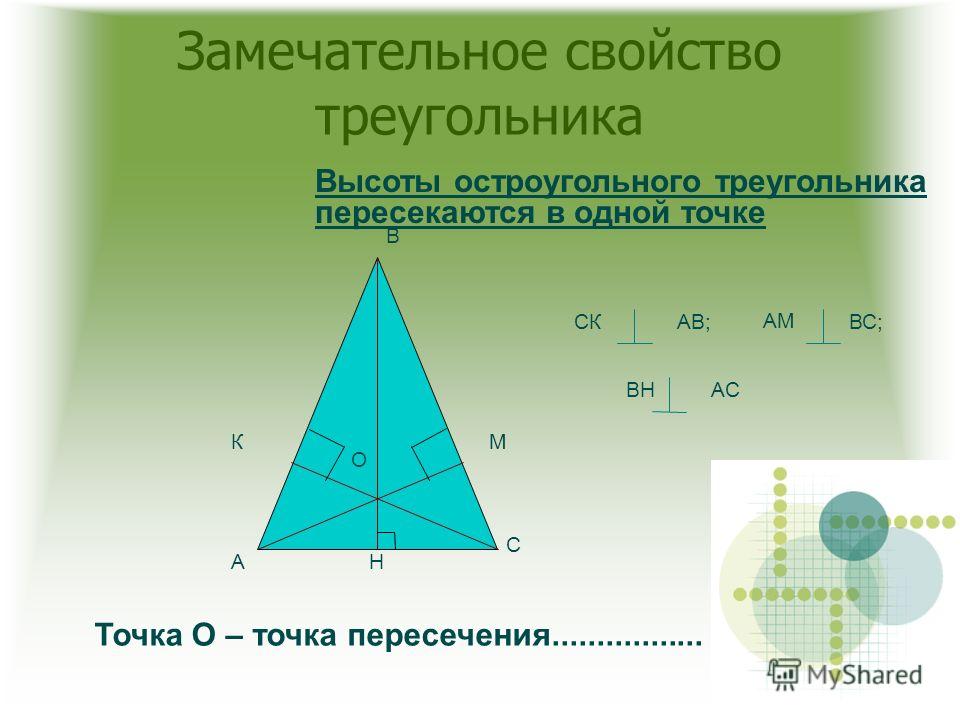
Медиана геометрической фигуры будет делить сторону, на которую она опущена, пополам. Причем можно провести этот отрезок с любой вершины. Медианы пересекаются в одной точке, и эта точка делит каждую из них в отношении 2:1.
Рис. 1. Медианы в остроугольном треугольникеИзвестно, что если провести три высоты в остроугольном треугольнике, то они будут пересекаться в одной точке, которую называют ортоцентром. Эти отрезки опускают под прямым углом к противоположным сторонам. Высоты в остроугольном треугольнике разделяют эту фигуру на прямоугольные треугольники.
Рис. 2. Высоты в остроугольном треугольникеБиссектрисы в остроугольном треугольнике не только делят углы пополам. Эти отрезки пересекаются в точке, которая является центром вписанной окружности.
Также биссектриса разделяет сторону остроугольного треугольника на две части, которые пропорциональны соответствующим боковым сторонам. Данное утверждение нужно запомнить, чтобы решать некоторые задачи.
Рис. 3. Биссектрисы в остроугольном треугольникеСвойства
Если суммировать числовые значения любых двух сторон остроугольного треугольника, то обязательно получим цифру, которая будет больше третьего отрезка данной геометрической фигуры.
Средняя линия в остроугольном треугольнике параллельна одной из сторон данной фигуры и равна ее половине.
Что мы узнали?
В остроугольном треугольнике каждый угол меньше 90 градусов. Общая сумма углов здесь также равняется 180 градусов. Нельзя забывать о характерных линиях треугольника. Поскольку с их помощью легко вычислить стороны данной треугольной фигуры или центр определенной окружности. А если в условиях задач по геометрии указаны углы, то можно воспользоваться тригонометрическими функциями.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Людмила Рогатина
10/10
Алексей Рудых
10/10
Константин Никитич
9/10
Ярик Бондарев
10/10
Глеб Быков
10/10
Оценка статьи
4.5
Средняя оценка: 4.5
Всего получено оценок: 295.
А какая ваша оценка?
Остроугольный треугольник
Треугольник — это трехсторонний многоугольник с тремя ребрами, тремя вершинами и тремя внутренними углами. Другими словами, треугольник — это замкнутая двумерная фигура с тремя сторонами и тремя углами.
Треугольники подразделяются на различные типы на основе их сторон и углов. Каждый из них имеет свои индивидуальные свойства.
Классификация треугольников на основе их сторон выглядит следующим образом:
Равносторонний треугольник: Треугольник, все три стороны которого имеют одинаковую длину.
Равнобедренный треугольник: треугольник, две стороны которого имеют одинаковую длину.
Разносторонний треугольник: треугольник, все три стороны которого не равны.

Классификация треугольников на основе их углов выглядит следующим образом
Остроугольный треугольник: Треугольник, все внутренние углы которого меньше 90°.
Прямоугольный треугольник: Треугольник, один из внутренних углов которого равен 90°.
Тупоугольный треугольник: треугольник, один из внутренних углов которого больше 90°.
В этой статье вы узнаете больше об остроугольных треугольниках, таких как их определение, свойства, формула периметра и площади, а также некоторые решенные примеры.
Определение остроугольного треугольника
Остроугольный треугольник — это треугольник с тремя острыми углами Остроугольный и тупоугольный треугольники — это два разных типа косоугольных треугольников — треугольники, которые не являются прямоугольными, потому что у них нет 9угол 0°.
Формулы остроугольного треугольника
Существуют две основные формулы остроугольного треугольника, которые приведены ниже;
Идентификация остроугольного треугольника
Согласно теореме Пифагора треугольник является остроугольным, если квадрат наибольшей стороны меньше суммы квадратов двух меньших сторон. Пусть «a», «b» и «c» — длины сторон данного треугольника, у которого сторона «a» наибольшая, тогда данный треугольник остроугольный, если a2 < b2 + c2.
Площадь остроугольного треугольника
Площадь остроугольного треугольника — это площадь, которую он занимает на двумерной поверхности. Итак, площадь остроугольного треугольника можно вычислить, если известны длина его основания и соответствующая ему высота (высота), или известны длины трех его сторон, или известны длины двух сторон и угол между ними.
Следовательно, площадь остроугольного треугольника = \[ \frac{1}{2} \] × (основание) × (высота) кв. ед.
ед.
= \[ \frac{1}{2} \] × (b) × (h) кв. s-b)(s-c)} \] кв. единиц
Где ‘a’, ‘b’ и ‘c’ — длины сторон остроугольного треугольника
И, s = полупериметр треугольника =\[ \ frac{a+b+c}{2} \]
или,
Площадь остроугольного треугольника, если заданы длины двух его сторон и угол между ними.
Площадь остроугольного треугольника = \[\frac{1}{2}\] × a × b × sinC
, где «a» и «b» – длины двух сторон, а C – угол между ними.
Периметр остроугольного треугольника
Периметр остроугольного треугольника равен сумме длин его сторон. Итак, если длины сторон остроугольного треугольника равны a, b и c единицам, то его периметр равен:
Периметр остроугольного треугольника = (a + b + c) единиц.
Метод проверки, является ли заданный треугольник остроугольным или нет
Способ 1: Если дана мера углов треугольника, то проверить величину его углов. Если все три угла треугольника меньше 90° градусов, то данный треугольник является остроугольным.
Если все три угла треугольника меньше 90° градусов, то данный треугольник является остроугольным.
Метод 2: Если даны длины трех сторон треугольника, то, используя тождество Пифагора, мы можем легко определить, является ли данный треугольник остроугольным или нет.
Согласно тождеству Пифагора, треугольник остроугольный, если квадрат наибольшей стороны меньше суммы квадратов двух меньших сторон.
Пусть «a», «b» и «c» — длины сторон данного треугольника, у которого сторона «a» наибольшая, тогда данный треугольник остроугольный, если a2 < b2 + c2.
Свойства остроугольного треугольника
Есть несколько важных свойств, которые отличают остроугольный треугольник от других типов треугольников. Свойства остроугольного треугольника перечислены ниже:
У остроугольного треугольника все внутренние углы меньше 90° градусов.

Сторона, лежащая напротив наименьшего угла, является наименьшей стороной треугольника.
Квадрат наибольшей стороны меньше суммы квадратов двух меньших сторон.
Точки параллелизма, центроид, входящий центр, центр окружности и ортоцентр лежат внутри треугольника.
Решенные примеры
Q.1. Два угла остроугольного треугольника равны 750 и 350. Найдите величину третьего угла.
Решение. Пусть третий угол равен ∠A, а ∠B = 750 и ∠C = 350. Тогда
По свойству суммы внутренних углов треугольников ∠A + 750 + 350 = 1800
⇒ ∠A + 1100 = 1800
⇒ ∠A = 180 -1100
⇒ ∠A = 700
мера третьего угла треугольника равна 70.
Q.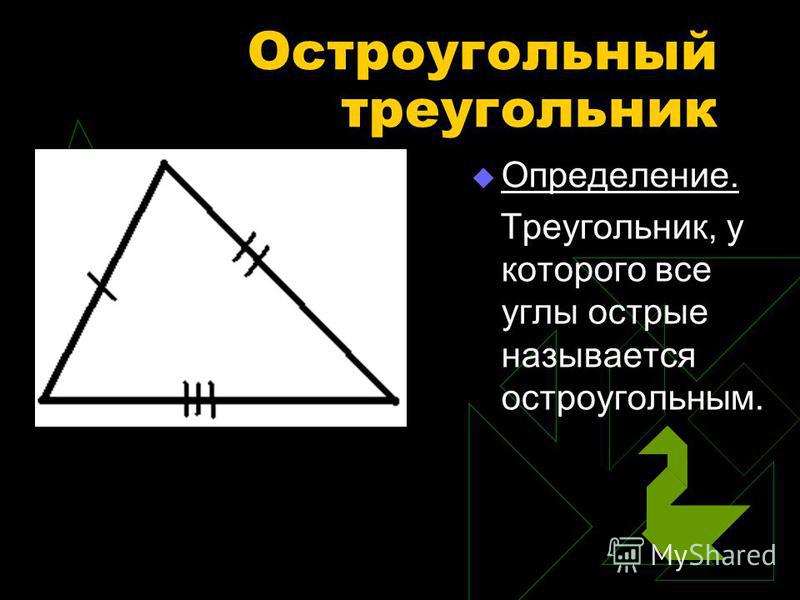 2. Найдите площадь остроугольного треугольника, основание которого равно 10 см, а высота равна 8 см.
2. Найдите площадь остроугольного треугольника, основание которого равно 10 см, а высота равна 8 см.
Решение: Дано, основание остроугольного треугольника = 10 см, а высота = 8 см.
= \[\frac{1}{2}\] 10 × 8 кв.см
= 40 кв. Узнайте, как эти формулы получены, чтобы понять основную концепцию. Попрактикуйтесь в решении вопросов, связанных с этими формулами, и разработайте свою концептуальную основу в этой теме.
Что такое остроугольный треугольник? — Факты и примеры определения
Треугольник представляет собой базовый многоугольник с тремя сторонами и тремя вершинами. Поскольку у него три стороны, у него три внутренних угла. Угол, который измеряется между 0° и 90°, называется острым углом. Остроугольный треугольник — это тип треугольника, в котором все три внутренних угла треугольника острые. Остроугольные треугольники также называют остроугольными треугольниками.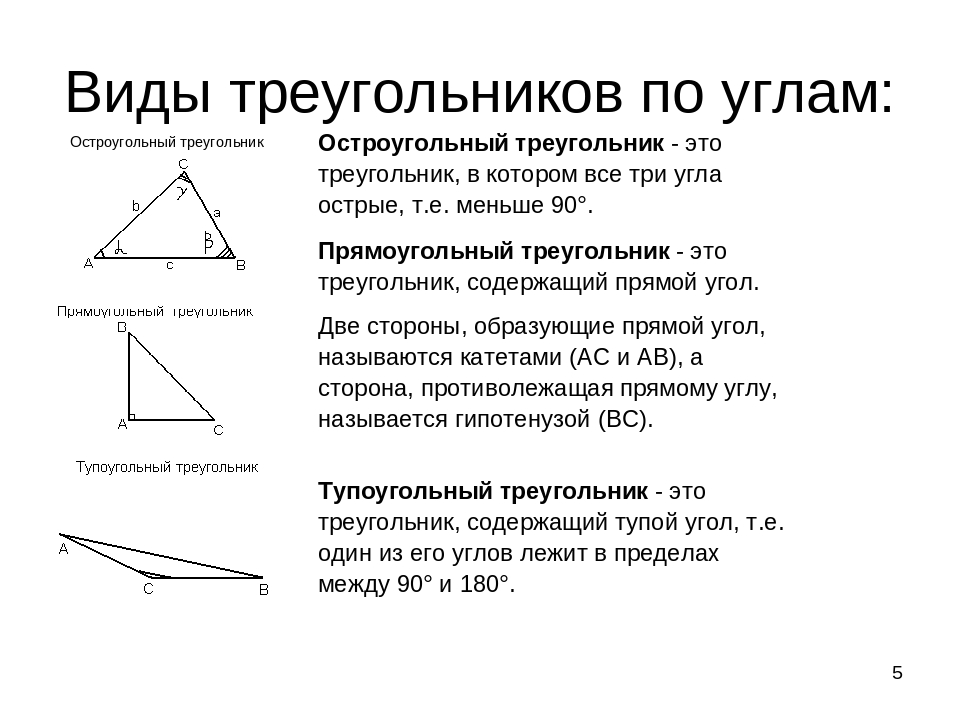 Хотя длины сторон остроугольных треугольников различны, внутренние углы никогда не превышают 90°.
Хотя длины сторон остроугольных треугольников различны, внутренние углы никогда не превышают 90°.
Остроугольные треугольники можно разделить на три различных типа в зависимости от длины стороны и углов треугольника следующим образом.
Равносторонний треугольник
Все стороны равностороннего треугольника имеют одинаковую длину — каждый внутренний угол этого треугольника равен 60°. Итак, равносторонний треугольник всегда остроугольный.
На данном рисунке равностороннего треугольника
∠A = ∠B = ∠C = 60°
Сторона AB = сторона BC = сторона AC
Остроугольный равнобедренный треугольник
Две стороны остроугольного равнобедренного треугольника имеют одинаковую длину, и углы, противоположные этим сторонам, имеют одинаковую величину.
На данном рисунке остроугольного равнобедренного треугольника
∠B = ∠C ≠ ∠A
Сторона AB = сторона AC ≠ сторона BC
Остроугольный треугольник
неравный. Все углы меньше 90 градусов.
На данном рисунке остроугольного треугольника,
∠A ≠ ∠B ≠ ∠C
Сторона AB ≠ Сторона BC ≠ Сторона AC
Основные формулы остроугольного треугольника заключаются в вычислении его периметра и площади.
Периметр измеряет внешнюю границу заданной формы. Периметр треугольника — это сумма длин всех сторон.
Площадь треугольника означает внутреннее пространство, занимаемое тремя сторонами треугольника.
Площадь остроугольного треугольника можно рассчитать по формуле площади треугольника.
Здесь b — длина основания остроугольного треугольника, а h — высота остроугольного треугольника.
Так как все три угла данного треугольника являются различными острыми углами, то это остроугольный треугольник.
В данном остроугольном равнобедренном треугольнике ABC ∠B = ∠C. Стороны, лежащие напротив этих углов, равны. Следовательно, длины сторон АВ и АС должны быть равны.
Подставив значение длины основания (b) в 5 см и высоты (h) в 6 см, мы получим
Практические задачи
1
Какая из следующих мер угла может образовать остроугольный треугольник?
60°, 70°, 50°
105°, 20°, 55°
90°, 45°, 45°
90°, 40°, 50°
Правильный ответ: 60°, 70 °, 50°
В остроугольном треугольнике все три угла меньше 90°. Только вариант а) удовлетворяет этому условию.
Только вариант а) удовлетворяет этому условию.
2
Определите тип треугольника.
Равносторонний треугольник
Остроугольный равнобедренный треугольник
Остроугольный разносторонний треугольник
Тупоугольный разносторонний треугольник
Правильный ответ: Остроугольный равнобедренный треугольник
Все три внутренних угла ∆ABC острые и AB = AC. Следовательно, ∆ABC — остроугольный равнобедренный треугольник.
3
Если три внутренних угла треугольника равны х, х + 20 и х + 40, то определите тип треугольника?
Равносторонний треугольник
Остро-равнобедренный треугольник
Остро-разносторонний треугольник
Тупо-разносторонний треугольник
Правильный ответ: остроугольный треугольник
Используя свойство суммы углов треугольника, мы получаем $x + x + 20 + x + 40 = 180$.
Итак, x должно быть равно 40, а три внутренних угла треугольника равны 40°, 60° и 80°.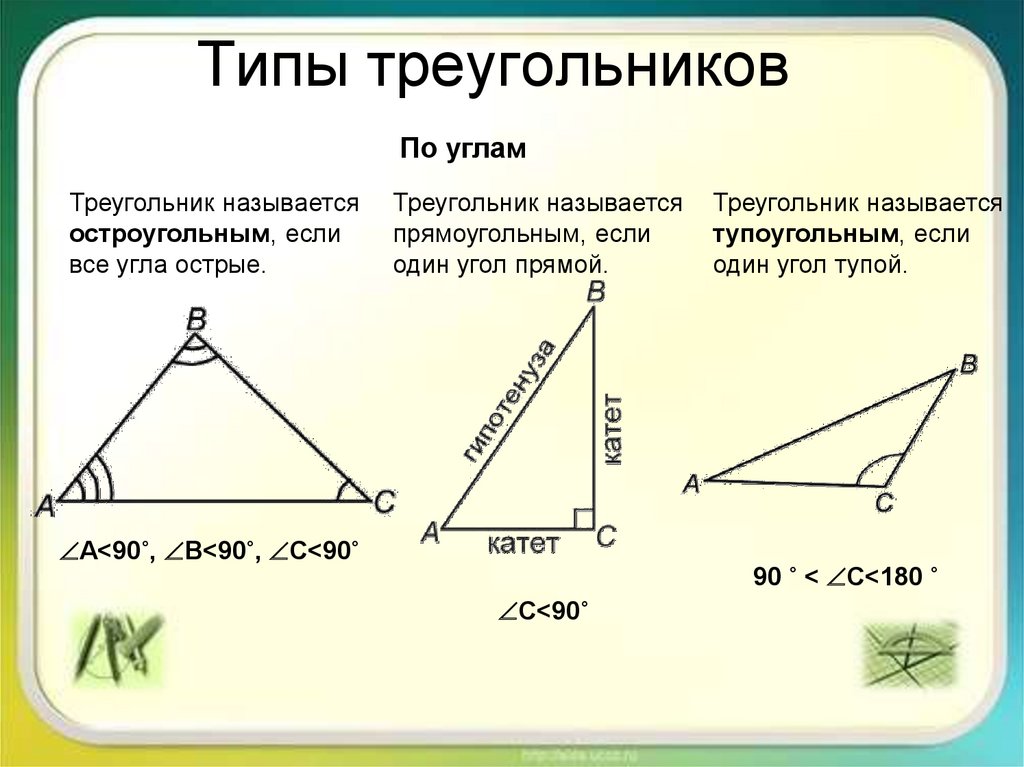

 е. больше 90 градусов;
е. больше 90 градусов;
