Свойства средней линии трапеции доказательство: Свойство средней линии трапеции — доказательство

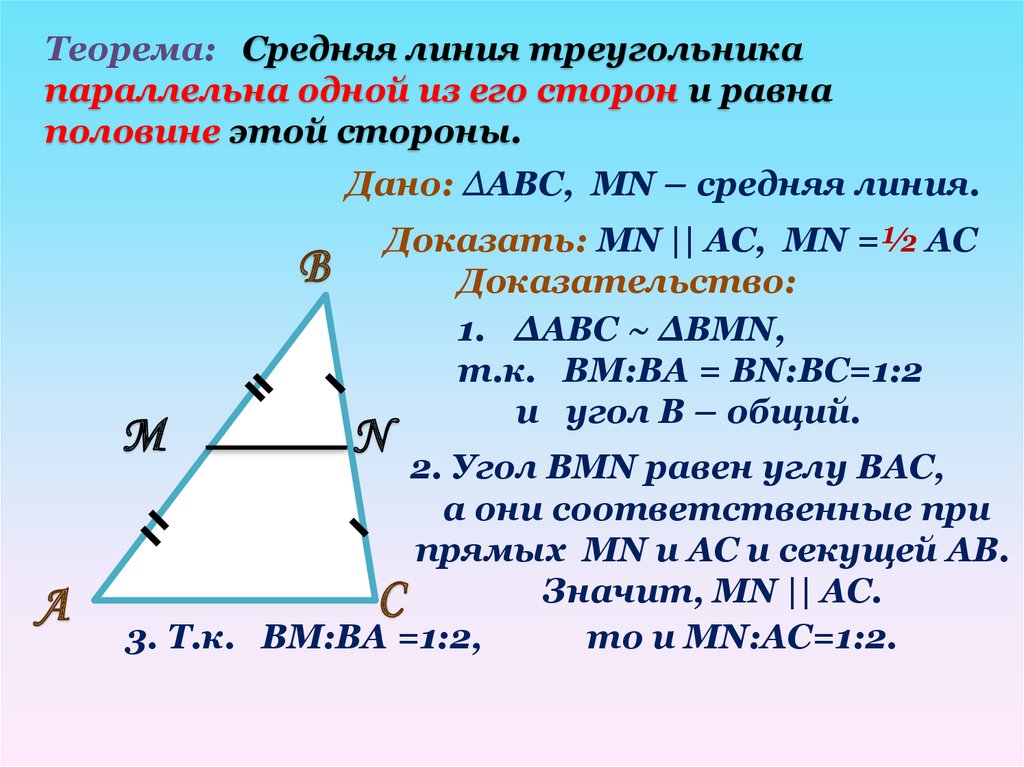
2.3. Пример работы над теоремой о средней линии трапеции.

Логико-математический анализ теоремы: «средняя линия трапеции параллельна основаниям и равна их полусумме».

Теорема сформулирована в категорической форме.

Сформулируем ее в условной форме, выделив явно разъяснительную часть: в любой трапеции, если есть ее средняя линия, то она параллельна основаниям и равна их полусумме.

Итак, структура теоремы такова:

Разъяснительная часть – в любой трапеции;

Условие – отрезок есть средняя линия трапеции;

Заключение – 1) отрезок параллелен основаниям; 2) отрезок равен полусумме оснований.

Теорема содержит два заключения, значит она сложная по структуре (но не обязательно сложным является ее доказательство).

Этапы обучения доказательству теоремы (в основе проблемное обучение, метод эксперимента).

1-й этап. Мотивация необходимости изучения данной теоремы: решение небольшой практической задачи, проблемная ситуация.

2-й этап. Актуализация опорных знаний (расчленить теорему на ряд элементарных шагов и выявить опорные знания, необходимые для понимания доказательства). Формы организации: кратковременная самостоятельная работа, решение обобщающей задачи.

Проанализировав доказательство теоремы, следует выделить опорные знания и повторить их на этапе актуализации. В данном случае уместно повторить свойство средней линии треугольника и решить следующую задачу.

Дано: ABO и DCO, АВ||CD, BO=CO.

Доказать: ABO=DCO.

3-й этап. Введение теоремы

Возможно дедуктивное введение теоремы и синтетический способ ее доказательства.

Однако активизации познавательной деятельности учащихся будет способствовать метод эксперимента.

Свойства средней линии трапеции можно «открыть» параллельно с процессом построения средней линии в произвольных трапециях. Учащимся предлагается:

Сравнить визуально взаимное расположение средней линии и оснований трапеции;

Построить отрезок, длина которого равна сумме длин оснований трапеции. Сколько раз средняя линия укладывается на этом отрезке?

На основе выполнения задания выдвигается гипотеза о том, что средняя линия параллельна основаниям трапеции и равна ее половине.

Далее формулируется теорема, делается чертеж, записывается, что дано и требуется доказать.

Дано:ABCD – трапеция, AD и ВС – основания, QP – средняя линия.

Доказать:

1. QP||AD, QP||BC,

2. QP=1/2(AD+BC).

4-й этап. Анализ. Поиск путей доказательства:

Дайте определение трапеции.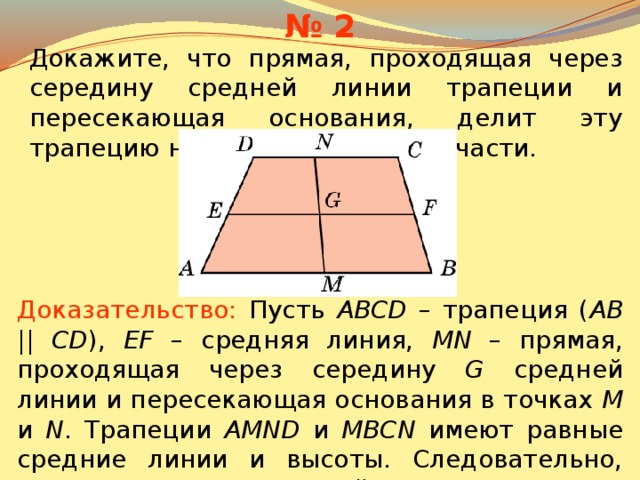 Какие прямые в нашем случае параллельны, как они называются? Требуется доказать, что средняя линия параллельна двум основаниям, то есть двум параллельным прямым. Как упростить путь доказательства этого факта? Достаточно доказать параллельность одному из оснований.

Чем можно воспользоваться? Для какой фигуры, кроме трапеции определено понятие средней линии? Нельзя ли использовать теорему о средней линии треугольника для доказательства? Можно ли отыскать или провести дополнительные построения, чтобы получить треугольник, средняя линия которого совпадает со средней линией трапеции?

5-й этап. Синтез. Составление плана доказательства.

6-й этап. Осуществление доказательства. Запись.

Доказательство:

1. Дополнительное построение: проведем луч ВР до пересечения с лучом AD. Е – точка пересечения.

2. Рассмотрим BCP и EDP:

СР=DP (P – середина CD),

BPC=EPD (как вертикальные углы),

BCP=EDP (как накрест лежащие углы при параллельных BC и AD и секущей CD),

BCP=EDP (по второму признаку).

Значит BC=DE, BP=PE (из равенства треугольников).

3. ABE:

Q – середина AB, P – середина CD,

QP – средняя линия ABE:

QP||AE, QP=1/2AE=1/2(AD+DE)=1/2(AD+BC) (по свойству средней линии и по построению).

4. BC||AD, QP||AD, значит QP||BC (по теореме о параллельности двух прямых третьей).

7-й этап. Усвоение содержания теоремы и ее доказательства:

Повторить формулировку теоремы и основные этапы ее доказательства или предложить учащимся прочитать соответствующий материал в учебнике.

Можно также применить и другой порядок работы:

Наметить план доказательства;

Провести доказательство устно;

Провести повторное доказательство с краткой записью.

8-й этап. Первичное закрепление теоремы.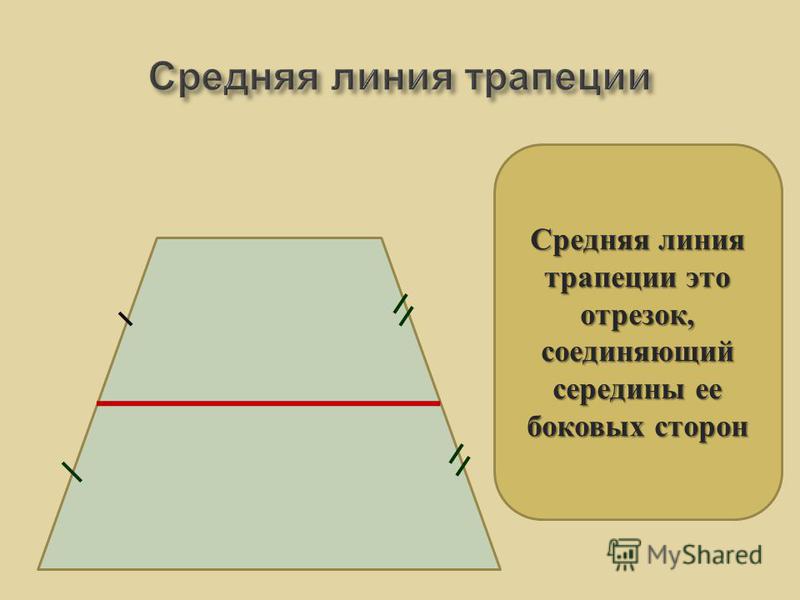 Уместны устные задачи по готовым чертежам. Например, такие:

8 класс. Геометрия. Четырехугольники. Трапеция. — Трапеция.

Комментарии преподавателя

Тра­пе­ция

Опре­де­ле­ние

Тра­пе­ция – это че­ты­рёх­уголь­ник, у ко­то­ро­го две сто­ро­ны па­рал­лель­ны, а две дру­гие – нет.

На Рис. 1. изоб­ра­же­на про­из­воль­ная тра­пе­ция.  – это бо­ко­вые сто­ро­ны (те, ко­то­рые не па­рал­лель­ны).  – ос­но­ва­ния (па­рал­лель­ные сто­ро­ны).

Рис. 1. Тра­пе­ция

Если срав­ни­вать тра­пе­цию с па­рал­ле­ло­грам­мом, то у па­рал­ле­ло­грам­ма две пары па­рал­лель­ных сто­рон. То есть па­рал­ле­ло­грамм не яв­ля­ет­ся част­ным слу­ча­ем тра­пе­ции, так как в опре­де­ле­нии тра­пе­ции чётко ска­за­но, что две сто­ро­ны тра­пе­ции не па­рал­лель­ны.

Вы­де­лим неко­то­рые виды тра­пе­ции (част­ные слу­чаи):

• рав­но­бед­рен­ная (рав­но­бо­кая) тра­пе­ция: бо­ко­вые сто­ро­ны равны;
• пря­мо­уголь­ная тра­пе­ция: один из углов равен  (из опре­де­ле­ния тра­пе­ции и свой­ства па­рал­лель­ных пря­мых сле­ду­ет, что два угла будут по ).

Опре­де­ле­ние

Сред­няя линия тра­пе­ции – от­ре­зок, со­еди­ня­ю­щий се­ре­ди­ны бо­ко­вых сто­рон.

На Рис. 2. изоб­ра­же­на тра­пе­ция со сред­ней ли­ни­ей .

Рис. 2. Сред­няя линия тра­пе­ции

Свой­ства сред­ней линии тра­пе­ции:

1.      Сред­няя линия тра­пе­ции па­рал­лель­на ос­но­ва­ни­ям тра­пе­ции.

До­ка­за­тель­ство:

Пусть се­ре­ди­на бо­ко­вой сто­ро­ны  тра­пе­ции  – точка . Про­ве­дём через эту точку пря­мую, па­рал­лель­ную ос­но­ва­ни­ям. Эта пря­мая пе­ре­се­чёт вто­рую бо­ко­вую сто­ро­ну тра­пе­ции  в точке .

По по­стро­е­нию: . По тео­ре­ме Фа­ле­са из этого сле­ду­ет: . Зна­чит,  – се­ре­ди­на сто­ро­ны . Зна­чит,  – сред­няя линия.

До­ка­за­но.

2.      Сред­няя линия тра­пе­ции равна по­лу­сум­ме ос­но­ва­ний тра­пе­ции: .

До­ка­за­тель­ство:

Про­ве­дём сред­нюю линию тра­пе­ции и одну из диа­го­на­лей: на­при­мер,  (см. Рис. 3).

Рис. 3

По тео­ре­ме Фа­ле­са па­рал­лель­ные пря­мые от­се­ка­ют на сто­ро­нах угла про­пор­ци­о­наль­ные от­рез­ки.

Так как равны от­рез­ки: . Зна­чит, от­ре­зок  яв­ля­ет­ся сред­ней ли­ни­ей тре­уголь­ни­ка , а от­ре­зок  – сред­ней ли­ни­ей тре­уголь­ни­ка .

Зна­чит, .

При­ме­ча­ние: это сле­ду­ет из свой­ства сред­ней линии тре­уголь­ни­ка: сред­няя линия тре­уголь­ни­ка па­рал­лель­на ос­но­ва­нию и равна его по­ло­вине. Пер­вая часть этого свой­ства до­ка­зы­ва­ет­ся ана­ло­гич­но с до­ка­за­тель­ством пер­во­го свой­ства сред­ней линии тра­пе­ции, а вто­рую часть можно до­ка­зать (к при­ме­ру, для сред­ней линии  тре­уголь­ни­ка ), про­ве­дя через точку  пря­мую, па­рал­лель­ную . Из тео­ре­мы Фа­ле­са будет сле­до­вать, что эта пря­мая будет яв­лять­ся сред­ней ли­ни­ей, а об­ра­зо­ван­ный че­ты­рёх­уголь­ник – па­рал­ле­ло­грам­мом (две пары по­пар­но па­рал­лель­ных сто­рон). От­сю­да уже неслож­но по­лу­чить тре­бу­е­мое свой­ство.

По­лу­ча­ем: .

До­ка­за­но.

Рас­смот­рим те­перь по­дроб­нее ос­нов­ные виды тра­пе­ции и их свой­ства.

На­пом­ним, что рав­но­бед­рен­ная тра­пе­ция – тра­пе­ция, у ко­то­рой бо­ко­вые сто­ро­ны равны. Рас­смот­рим свой­ства бо­ко­вой тра­пе­ции.

1.      Углы при ос­но­ва­нии рав­но­бед­рен­ной тра­пе­ции равны.

До­ка­за­тель­ство:

Вы­пол­ним стан­дарт­ное до­пол­ни­тель­ное по­стро­е­ние, ко­то­рое очень часто ис­поль­зу­ет­ся при ре­ше­нии раз­лич­ных задач на тра­пе­цию: про­ве­дём пря­мую  па­рал­лель­но бо­ко­вой сто­роне  (см. Рис. 4).

Рис. 4

 – па­рал­ле­ло­грамм.

От­сю­да сле­ду­ет, что: . Зна­чит, тре­уголь­ник  – рав­но­бед­рен­ный. А зна­чит, углы при его ос­но­ва­нии равны, то есть:  (по­след­ние два угла равны, как со­от­вет­ствен­ные при па­рал­лель­ных пря­мых ).

До­ка­за­но.

2.      Диа­го­на­ли рав­но­бед­рен­ной тра­пе­ции равны.

До­ка­за­тель­ство:

Для до­ка­за­тель­ства этого свой­ства вос­поль­зу­ем­ся преды­ду­щим. Дей­стви­тель­но, рас­смот­рим тре­уголь­ни­ки:  и  (см. Рис. 5.).

Рис. 5

 (по пер­во­му при­зна­ку ра­вен­ства тре­уголь­ни­ков: две сто­ро­ны и угол между ними).

Из этого ра­вен­ства сразу сле­ду­ет, что: .

До­ка­за­но.

Ока­зы­ва­ет­ся, что, как и в слу­чае с па­рал­ле­ло­грам­мом, у рав­но­бед­рен­ной тра­пе­ции свой­ства од­но­вре­мен­но яв­ля­ют­ся и при­зна­ка­ми. Сфор­му­ли­ру­ем и до­ка­жем эти при­зна­ки.

При­зна­ки рав­но­бед­рен­ной тра­пе­ции

1.      Дано:  – тра­пе­ция; .

До­ка­зать: 

До­ка­за­тель­ство:

До­ка­за­тель­ство дан­но­го при­зна­ка аб­со­лют­но ана­ло­гич­но до­ка­за­тель­ству со­от­вет­ству­ю­ще­го свой­ства. Про­ве­дём в тра­пе­ции  пря­мую  па­рал­лель­но сто­роне  (см. Рис. 6).

 – па­рал­ле­ло­грамм (две пары по­пар­но па­рал­лель­ных сто­рон).

 (со­от­вет­ствен­ные углы при па­рал­лель­ных пря­мых). От­ку­да, поль­зу­ясь усло­ви­ем, по­лу­ча­ем:  – рав­но­бед­рен­ный

Рис. 6

(равны углы при ос­но­ва­нии). Зна­чит:  (у па­рал­ле­ло­грам­ма про­ти­во­по­лож­ные сто­ро­ны равны).

До­ка­за­но.

2.      Дано:  – тра­пе­ция; .

До­ка­зать: .

До­ка­за­тель­ство:

Вы­пол­ним ещё одно стан­дарт­ное до­пол­ни­тель­ное по­стро­е­ние при ре­ше­нии задач с тра­пе­ци­ей: про­ве­дём через вер­ши­ну  пря­мую  па­рал­лель­но диа­го­на­ли  (см. Рис. 7).

Рис. 7

 – па­рал­ле­ло­грамм (две пары по­пар­но па­рал­лель­ных сто­рон).

 (со­от­вет­ствен­ные углы при па­рал­лель­ных пря­мых). Кроме того,  – рав­но­бед­рен­ный ( – по усло­вию;  – по свой­ству па­рал­ле­ло­грам­ма). А зна­чит: .

До­ка­за­но.

Рас­смот­рим несколь­ко при­ме­ров ре­ше­ния задач с тра­пе­ци­ей.

При­мер 1.

Дано:  – тра­пе­ция; .

Найти: 

Ре­ше­ние:

Сумма углов при бо­ко­вой сто­роне тра­пе­ции равна  – свой­ство внут­рен­них од­но­сто­рон­них углов при па­рал­лель­ных пря­мых. Из этого факта можно по­лу­чить два ра­вен­ства:

Ответ: .

При­мер 2.

Дано:  – тра­пе­ция; . .

Найти: 

Ре­ше­ние:

Рис. 8

Про­ве­дём вы­со­ту . По­лу­ча­ем че­ты­рёх­уголь­ник , в ко­то­ром про­ти­во­по­лож­ные сто­ро­ны по­пар­но па­рал­лель­ны, а два углы равны по . Зна­чит,  – па­рал­ле­ло­грамм, а точ­нее, пря­мо­уголь­ник.

Из этого сле­ду­ет, что . От­ку­да: .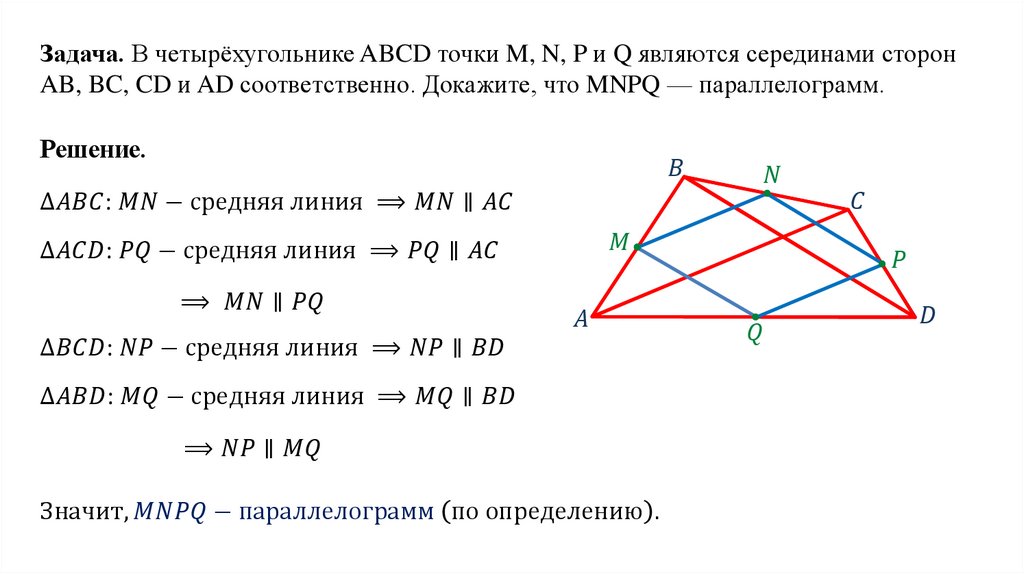

Рас­смот­рим пря­мо­уголь­ный тре­уголь­ник . В нём один из ост­рых углов, по усло­вию, равен . Зна­чит, вто­рой равен , то есть: . Вос­поль­зу­ем­ся свой­ством ка­те­та, ле­жа­ще­го про­тив угла : он в два раза мень­ше ги­по­те­ну­зы.

.

Ответ: .

На этом уроке мы рас­смот­ре­ли по­ня­тие тра­пе­ции и её свой­ства, изу­чи­ли виды тра­пе­ции, а также ре­ши­ли несколь­ко при­ме­ров ти­по­вых задач.

ИСТОЧНИК

http://interneturok.ru/ru/school/geometry/8-klass/chyotyrehugolniki/trapetsiya

http://www.youtube.com/watch?v=Yqw5oZ3iFAI

http://www.youtube.com/watch?v=1tY3omQhTuk

http://img3.proshkolu.ru/content/media/pic/std/1000000/983000/982960-b6b4e8f6a4e7b336.jpg

http://static.wixstatic.com/media/13679f_7ac2889143594b059462e77b25eda7c6.jpg

http://delaem-uroki.narod.ru/img/102/792/KZqhOMb.gif

Трапеция. Задача на среднюю линию трапеции.

http://cs323223.vk.me/v323223595/5e51/Gi2qlTPgLVo.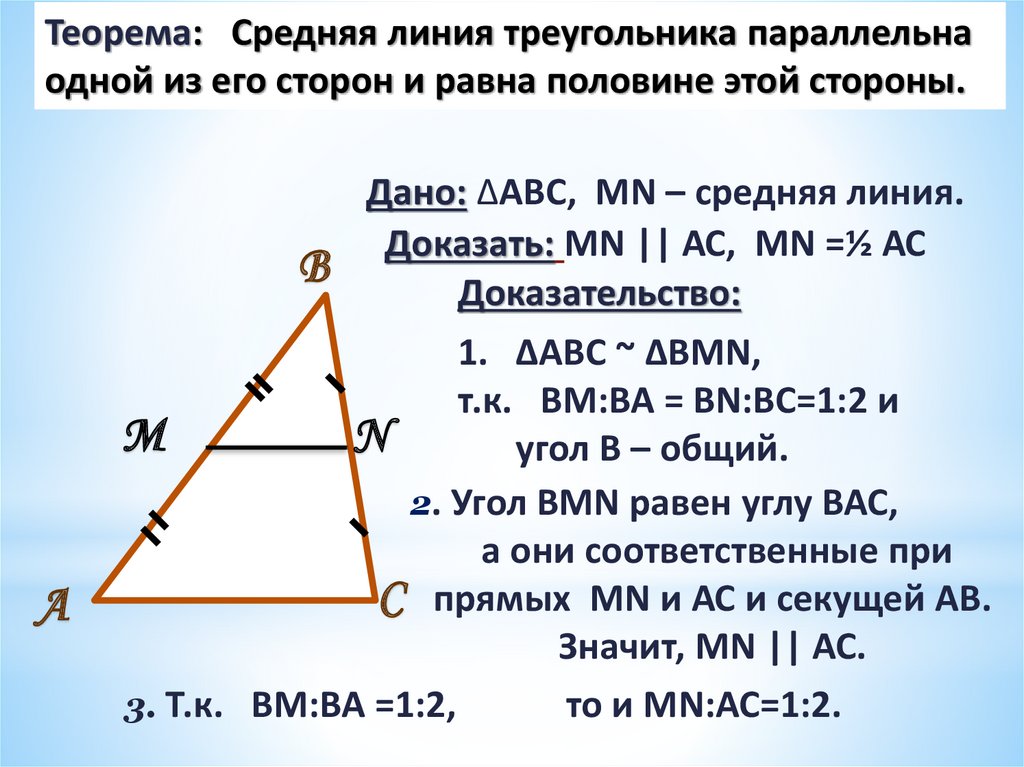 jpg

http://dok.opredelim.com/pars_docs/refs/47/46420/img2.jpg

Как найти среднюю линию трапеции?

В трапеции средней линией (или средним отрезком) называется линия, соединяющая середины сторон. В трапеции средняя линия параллельна основаниям, а ее длина равна половине их суммы . И наоборот, линия, соединяющая точки на двух сторонах рапецоида, параллельная ее основаниям и равная половине их суммы, является средней линией.

Как решить равнобедренную трапецию?

Какова формула медианы трапеции?

Медиана представляет собой прямую линию, параллельную основаниям, проходящую от середины одной ноги до середины другой. Длина медианы равна среднему значению двух оснований, поэтому ее можно найти по формуле: ((длина одного основания) + (длина другого основания)) / 2 .

Что такое теорема о средней линии?

Теорема о средней линии — это теорема о треугольнике, которая утверждает, что отрезок, соединяющий две середины треугольника, будет параллелен третьей стороне, а длина среднего отрезка будет равна половине длины третьей стороны.

Что такое истинная равнобедренная трапеция?

В любой равнобедренной трапеции две противоположные стороны (основания) параллельны, а две другие стороны (катеты) имеют одинаковую длину (свойства общие с параллелограммом). Диагонали также имеют одинаковую длину.

Как найти середину трапеции?

1. Измерьте и запишите длину двух параллельных оснований.
2. Сложите два числа.
3. Разделите результат на два. Это длина среднего сегмента.

Что такое медиана равнобедренной трапеции?

Медиана трапеции — это отрезок, соединяющий середины непараллельных сторон (катетов) . Теорема: Медиана трапеции параллельна каждому основанию, а длина медианы равна половине суммы длин двух оснований.

Какие углы при основании равнобедренной трапеции?

Унив.

Равнобедренная трапеция имеет два конгруэнтных катета и одну пару параллельных сторон. Углы при основании равны конгруэнтны друг другу , и из-за одинаковых боковых внутренних углов верхние углы являются дополнительными к соответствующим углам при основании, а это означает, что они оба равны 180 ° — (мера угла при основании).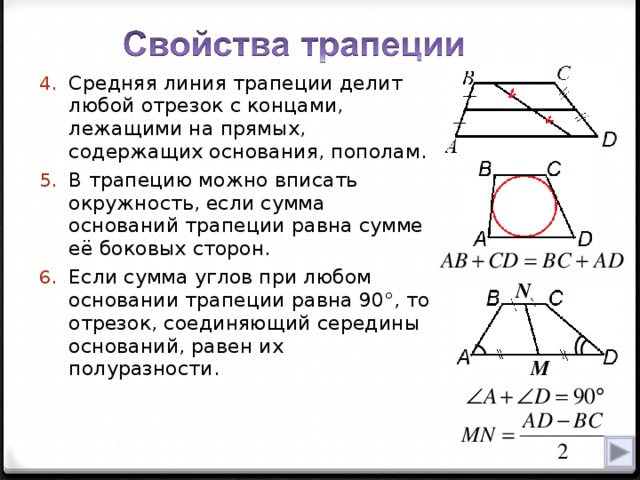

Как найти недостающее основание равнобедренной трапеции?

Как найти недостающий угол равнобедренной трапеции?

Как решить среднюю линию?

Как решить теорему о средней линии?

Как найти недостающий угол трапеции?

Что такое формула теоремы о средней линии?

Теорема о средней линии утверждает, что разрезание по средней линии треугольника создает отрезок, параллельный основанию и вдвое длиннее. Это кажется разумным? Факт 1: Вертикальные углы (противоположные углы при пересечении двух прямых) конгруэнтны (имеют одинаковую меру). м∠1 = м∠3 = 180° – м∠2 .

Какие углы основания трапеции?

Пара углов, имеющих общее основание , называется углами при основании трапеции.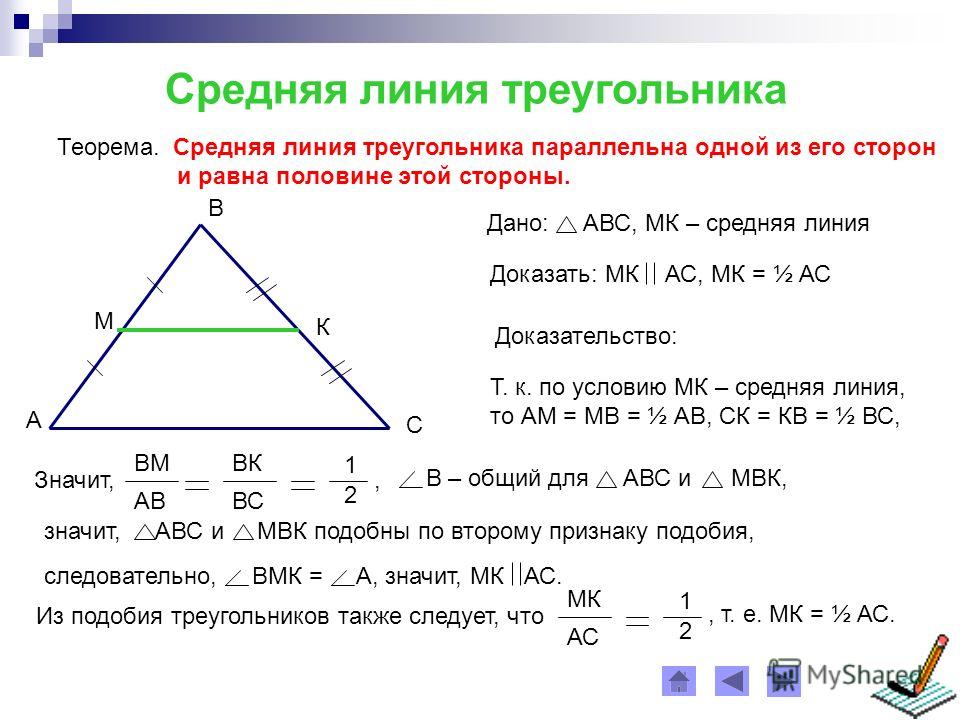 На рисунке 1 ∠ A и ∠ B или ∠ C и ∠ D являются углами при основании трапеции ABCD. Можно доказать два особых свойства равнобедренной трапеции. Теорема 53. Углы при основании равнобедренной трапеции равны.

Как называются параллельные стороны трапеции?

Трапеция – определение с примерами

Параллельные стороны трапеции известны как основания , а ее непараллельные стороны называются катетами.

Сколько пар параллельных сторон у трапеции?

Трапеция имеет одну пару параллельных сторон, а параллелограмм имеет две пары параллельных сторон.

Как найти переменные трапеции?

Как найти средний сегмент?

Соедините любые две середины сторон , и у вас есть середина треугольника. Независимо от того, какой средний отрезок вы создали, он будет составлять половину длины основания треугольника (сторона, которую вы не использовали), а средний отрезок и основание будут параллельными линиями!

EF выглядит параллельно основанию трапеций?

EF — прямая, параллельная основаниям (EF||AB||CD), образующая две подобные трапеции: ABFE ∼ EFCD.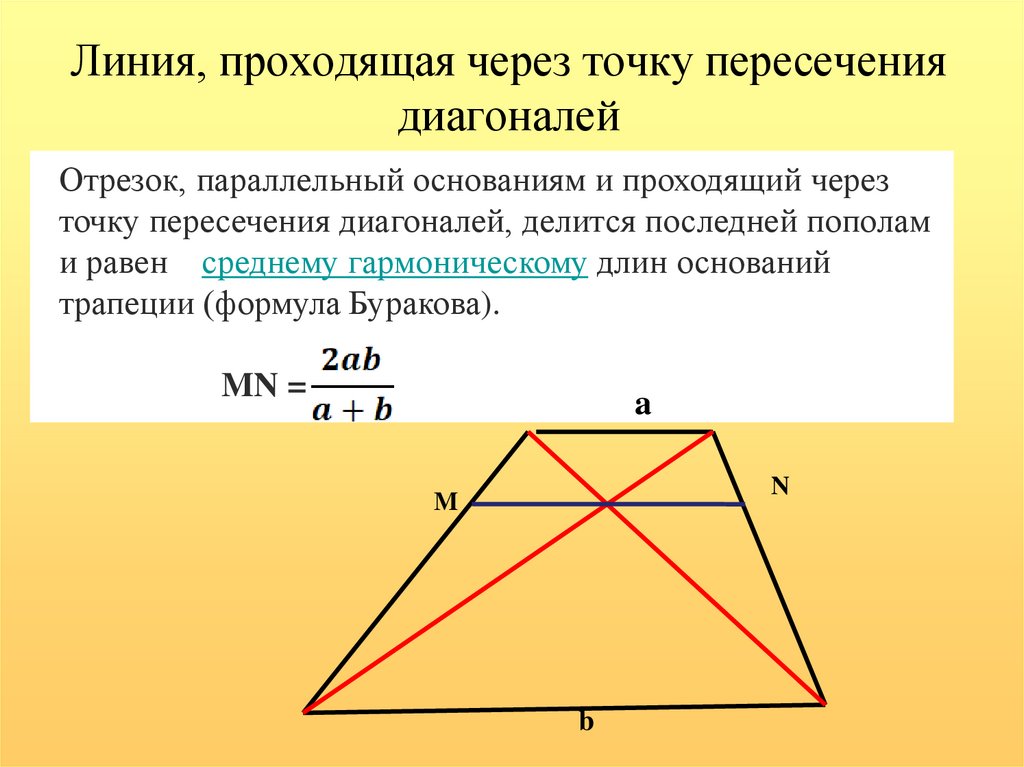 Найдите формулу длины FE через длины AB и CD.

Как найти среднюю линию треугольника?

В треугольнике средней линией (или средней линией) является любая из трех линий, соединяющих середины любой пары сторон треугольника . В треугольнике средняя линия, соединяющая середины двух сторон, параллельна третьей стороне и вдвое короче.

Как найти угол трапеции с двумя углами?

Найдите угол трапеции: пример вопроса №1

Вычитание 2(72°) из 360° дает сумму двух верхних углов, а деление полученных 216° на 2 дает значение x, равное 108 °.

Равны ли углы равнобедренной трапеции?

Углы, образованные между непараллельными сторонами и параллельными сторонами, называемые углами при основании, равны в равнобедренной трапеции . В газонной трапеции Ирины ABCD углы C и D равны.

Как называются непараллельные стороны равнобедренной трапеции?

Параллельные стороны называются основаниями, а непараллельные стороны — катетами трапеции. Равнобедренная трапеция – это трапеция, у которой две непараллельные стороны равны.

Какая фигура является трапецией только с 1 парой параллельных сторон?

Некоторые определяют трапецию как четырехугольник , имеющий только одну пару параллельных сторон (эксклюзивное определение), тем самым исключая параллелограммы. Другие определяют трапецию как четырехугольник по крайней мере с одной парой параллельных сторон (включающее определение), что делает параллелограмм особым типом трапеции.

Каковы 6 свойств равнобедренной трапеции?

• Свойство 1: Только одна пара сторон параллельна. …
• Свойство 2: Непараллельные стороны (катеты) равны по размеру. …
• Свойство 3: Диагонали равны по размеру. …
• Свойство 4: Углы при основании равны по размеру. …
• Свойство 5: Противоположные углы являются дополнительными.

Сколько пар параллельных сторон у равнобедренной трапеции?

В дополнение к одной паре параллельных сторон свойства равнобедренной трапеции включают конгруэнтность катетов, углов при основании и диагоналей.

Какими свойствами обладает равнобедренная трапеция?

Свойства

Что такое средняя линия треугольника?

Каждая сторона медиального треугольника называется средним сегментом (или средней линией). В общем случае середина треугольника — это отрезок, соединяющий середины двух сторон треугольника. Он параллелен третьей стороне и имеет длину, равную половине длины третьей стороны.

Какой сегмент является средней линией?

Средний сегмент треугольника (также называемая средней линией) — это отрезок, соединяющий середины двух сторон треугольника.

Может ли трапеция иметь 2 набора параллельных прямых?

Трапеция имеет хотя бы одну пару параллельных сторон. Может быть два ! Вы можете легко найти другие определения трапеции, которые указывают, что у нее есть только ОДНА пара параллельных сторон.

Где параллельные прямые на трапеции?

Трапеции обычно изображают с одной из параллельных сторон внизу . Параллельные ребра называются основаниями, а непараллельные — сторонами. Существует несколько видов специальных трапеций.

Что находит формула средней точки?

2.5. Чтобы найти середину любого диапазона, сложите два числа вместе и разделите на 2 . В данном случае 0 + 5 = 5, 5/2 = 2,5.

Середина треугольника (теорема, формула и видео)

Автор:

Malcolm McKinsey

11 января 2023

Факт проверен

Полом Маццола

Что такое середина треугольника?

Средняя линия треугольника — это линия, построенная путем соединения середины любых двух сторон треугольника. В любом прямоугольном, равнобедренном или равностороннем треугольнике все три стороны треугольника можно разделить пополам (разрезать пополам), при этом точка, равноудаленная от любой вершины, будет серединой этой стороны.

В  △ASH , снизу, по бокам AS и AH равны 24 см и 36 см соответственно.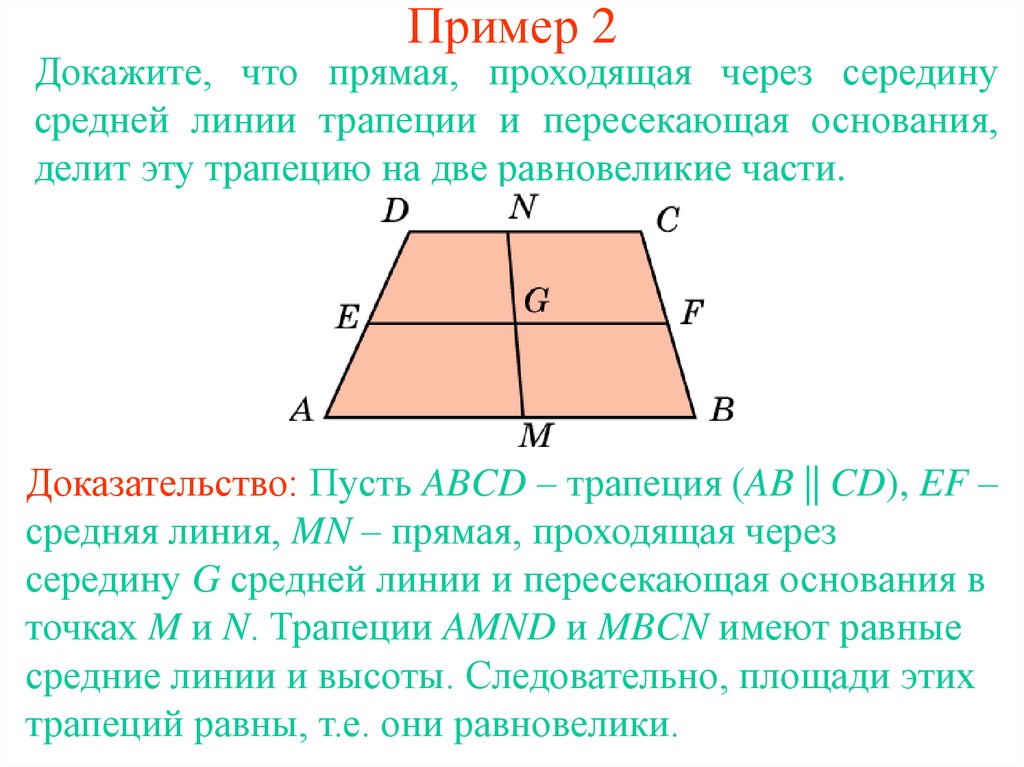 Поскольку мы знаем длины сторон, мы знаем, что точка C , середина стороны AS , точно равна 12 см от любого конца. Точка R , на AH , ровно 18 см с любого конца.

Середина треугольника

Соединение середины сторон, Точки C  и R , на △ASH делает что-то кроме всей нашей фигуры АВАРИЯ . Он создает средний сегмент, CR , который имеет пять удивительных особенностей.

Пять свойств срединного отрезка

Поскольку треугольники имеют три стороны, они могут иметь три срединных отрезка. Вы можете соединить любые две стороны в их средних точках. Один средний сегмент составляет половину длины основания (третья сторона не участвует в создании среднего сегмента). Это только одна интересная особенность. Он также:

• всегда параллелен третьей стороне треугольника; база

• Образует меньший треугольник, аналогичный исходному треугольнику

• Меньший аналогичный треугольник составляет одну четвертую площади исходного треугольника

• Меньший аналогичный треугольник имеет половину периметра исходный треугольник

Поскольку меньший треугольник, созданный средней линией, подобен исходному треугольнику, соответствующие углы двух треугольников идентичны; соответствующие внутренние углы каждого треугольника имеют одинаковые измерения.

Из пяти атрибутов срединного отрезка два самых важных заключены в теореме о срединном отрезке, утверждении, которое было доказано математически (поэтому вам не нужно доказывать его снова; вы можете воспользоваться им, чтобы сэкономить время и работай).

Теорема о средней линии треугольника

Теорема о средней линии треугольника говорит нам, что средняя линия равна половине длины третьей стороны (основания) и также параллельна основанию.

Вам не нужно доказывать теорему о середине отрезка, но вы можете доказать ее, используя вспомогательную прямую, конгруэнтные треугольники и свойства параллелограмма.

Средний сегмент Formula

Средний сегмент || Основание треугольников

Формула среднего сегмента треугольника

Это мощный материал; за одну лишь стоимость рисования одного отрезка  линии можно создать аналогичный треугольник, площадь которого в четыре раза меньше исходной, периметр в два раза меньше исходной, а основание гарантированно параллельно исходной и только вдвое короче.

Как найти середину треугольника

Нарисуйте любой треугольник, назовите его треугольником ABC. С помощью циркуля, карандаша и линейки найдите середины любых двух сторон треугольника. Вы делаете это в четыре шага:

1. Отрегулируйте циркуль для рисования так, чтобы он двигался по дуге, превышающей половину длины любой из сторон треугольника

2. Поместив стрелку компаса в каждую вершину, проведите дугу через сторону треугольника с обоих концов, создавая две противоположные стороны. , пересекающие дуги

3. Соедините точки пересечения обеих дуг с помощью линейки

4. Точка, в которой ваша линейка пересекает сторону треугольника, является серединой этой стороны)

Как найти середину треугольника

Соедините середины любых двух сторон, и вы получите середину треугольника. Независимо от того, какой средний отрезок вы создали, он будет составлять половину длины основания треугольника (сторона, которую вы не использовали), а средний отрезок и основание будут параллельными линиями!

Примеры теоремы о средней линии треугольника

Здесь правильно △DOG , со стороной DO 46 дюймов и стороной DG 38,6 дюйма .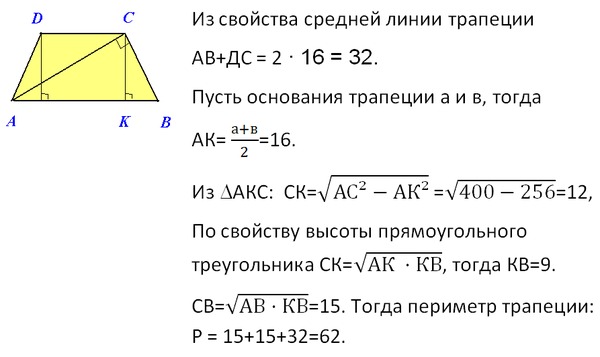 Сторона 9{2}482,5 дюйма2.

Какие точки вы соедините, чтобы создать средний сегмент?

Пример теоремы о средней линии треугольника

Только соединив точки V и Y , можно создать среднюю линию треугольника. Это сделает сторону OG основой.

Вы должны быть в состоянии ответить на все эти вопросы:

1. Каков периметр исходного △СОБАКА ?

2. Какова длина среднего сегмента ВЯ ?

3. Какова длина стороны DV ?

4. Какова длина стороны DY ?

5. Каков периметр вновь созданного аналога △DVY ?

6. Какова площадь недавно созданного △DVY ?

Вот наши ответы:

1. Добавьте длины: 46″ + 38,6″ + 25″ = 109,6″

9{2}120,625in2

Треугольник Серпинского

С помощью теоремы о среднем отрезке можно построить фигуру, используемую во фрактальной геометрии, треугольник Серпинского.