Свойства функции тангенса
Используй поиск, чтобы найти научные материалы и собрать список литературы
База статей справочника включает в себя статьи написанные экспертами Автор24, статьи из научных журналов и примеры студенческих работ из различных вузов страны
Содержание статьи
1. Геометрический смысл
2. Свойства функции $f(x)=tgx$
3. График функции $y=tgx$
4. Задача на построение тангенсоиды
Перед изучением функции тангенса и её свойств, вспомним понятие самого тангенса. Определение тангенса можно ввести двумя способами: с помощью прямоугольного треугольника и с помощью понятий синуса и косинуса.
Определение 1
Тангенсом острого угла называется отношение длины противолежащего катета к прилежащему катету прямоугольного треугольника (рис 1):
\[cos\alpha =\frac{a}{b}\]
Рисунок 1.
Определение 2
Тангенсом угла называется отношение значения синуса этого угла к значению косинуса этого угла.
Введем таблицу некоторых значений тангенса (таблица 1).
Рисунок 2. Значения тангенса.
Геометрический смысл
Рассмотрим тригонометрическую единичную окружность и прямую $x=1$. Ордината точки $B$ на прямой $x=1$ является тангенсом угла $\alpha $ (рис. 2).
Рисунок 3. Значение тангенса с помощью единичной окружности.
Поэтому, когда точка $B$ опишет вертикальную прямую $x=1$ её ордината примет все значения множества действительных чисел, откуда $tg\alpha $ — вся числовая прямая. Поэтому прямая $x=1$ называется линией тангенсов.
Свойства функции $f(x)=tgx$
Рассмотрим теперь свойства функции $f\left(x\right)=tgx$.
- По определению 2, получим, что область определения$x\in {\mathbb R}{\rm ,}{\rm \ }x\ne \frac{\pi }{2}+\pi n,\ n\in Z$.
- Из геометрического смысла следует, что область значения — все числа.
 2x}$.
2x}$.
Функция $f\left(x\right)=tgx$ возрастает, при $x\in \left(-\frac{\pi }{2}+\pi n,\frac{\pi }{2}+\pi n\right)$.
Функция имеет точку разрыва второго рода при $x=\frac{\pi }{2}+\pi n,\ n\in Z$.
${\mathop{lim}_{x\to \frac{\pi }{2}+\pi n-0} tgx\ }=-\infty $, ${\mathop{lim}_{x\to \frac{\pi }{2}+\pi n+0} tgx\ }=+\infty $,
График функции $y=tgx$
Графиком функции $y=tgx$ является тангенсоида (рис. 3).
Рисунок 4. Тангенсоида.
Задача на построение тангенсоиды
Пример 1
Построить график функции $y=tg(x-2\pi )$.
Так как $tgx$ периодическая с минимальным периодом $\pi $, то получим, что $y=tg\left(x-2\pi \right)=tg\left(x-\pi \right)=tgx$. Получаем график:
Рисунок 5.
Сообщество экспертов Автор24
Автор этой статьи Дата последнего обновления статьи: 18.02.2022
Выполнение любых типов работ по математике
Решение задач по комбинаторике на заказ Решение задачи Коши онлайн Математика для заочников Контрольная работа на тему числовые неравенства и их свойства Контрольная работа на тему умножение и деление рациональных чисел Контрольная работа на тему действия с рациональными числами Дипломная работа на тему числа Курсовая работа на тему дифференциальные уравнения Контрольная работа на тему приближенные вычисления Решение задач с инвариантами
Подбор готовых материалов по теме
Дипломные работы Курсовые работы Выпускные квалификационные работы Рефераты Сочинения Доклады Эссе Отчеты по практике Решения задач Контрольные работы
Тригонометрия: синус, косинус, тангенс, котангенс
Содержание
- 1 История тригонометрии
- 2 Основные величины тригонометрии
- 3 Тригонометрический круг
- 4 Свойства тригонометрических функций: синус и косинус
- 5 Свойства тангенсоиды и котангенсоиды
История тригонометрии
Тригонометрия, как наука, зародилась на Древнем Востоке. Первые тригонометрические соотношения были выведены астрономами для создания точного календаря и ориентированию по звездам. Данные вычисления относились к сферической тригонометрии, в то время как в школьном курсе изучают соотношения сторон и угла плоского треугольника.
Первые тригонометрические соотношения были выведены астрономами для создания точного календаря и ориентированию по звездам. Данные вычисления относились к сферической тригонометрии, в то время как в школьном курсе изучают соотношения сторон и угла плоского треугольника.
Тригонометрия – это раздел математики, занимающийся свойствами тригонометрических функций и зависимостью между сторонами и углами треугольников.
В период расцвета культуры и науки I тысячелетия нашей эры знания распространились с Древнего Востока в Грецию. Но основные открытия тригонометрии – это заслуга мужей арабского халифата. В частности, туркменский ученый аль-Маразви ввел такие функции, как тангенс и котангенс, составил первые таблицы значений для синусов, тангенсов и котангенсов. Понятие синуса и косинуса введены индийскими учеными. Тригонометрии посвящено немало внимания в трудах таких великих деятелей древности, как Евклида, Архимеда и Эратосфена.
Основные величины тригонометрии
Основные тригонометрические функции числового аргумента – это синус, косинус, тангенс и котангенс. Каждая из них имеет свой график: синусоида, косинусоида, тангенсоида и котангенсоида.
Каждая из них имеет свой график: синусоида, косинусоида, тангенсоида и котангенсоида.
В основе формул для расчета значений указанных величин лежит теорема Пифагора. Школьникам она больше известна в формулировке: «Пифагоровы штаны, во все стороны равны», так как доказательство приводится на примере равнобедренного прямоугольного треугольника.
Синус, косинус и другие зависимости устанавливают связь между острыми углами и сторонами любого прямоугольного треугольника. Приведем формулы для расчета этих величин для угла A и проследим взаимосвязи тригонометрических функций:
Как видно, tg и ctg являются обратными функциями. Если представить катет a как произведение sin A и гипотенузы с, а катет b в виде cos A * c, то получим следующие формулы для тангенса и котангенса:
Тригонометрический круг
Графически соотношение упомянутых величин можно представить следующим образом:
Окружность, в данном случае, представляет собой все возможные значения угла α — от 0° до 360°.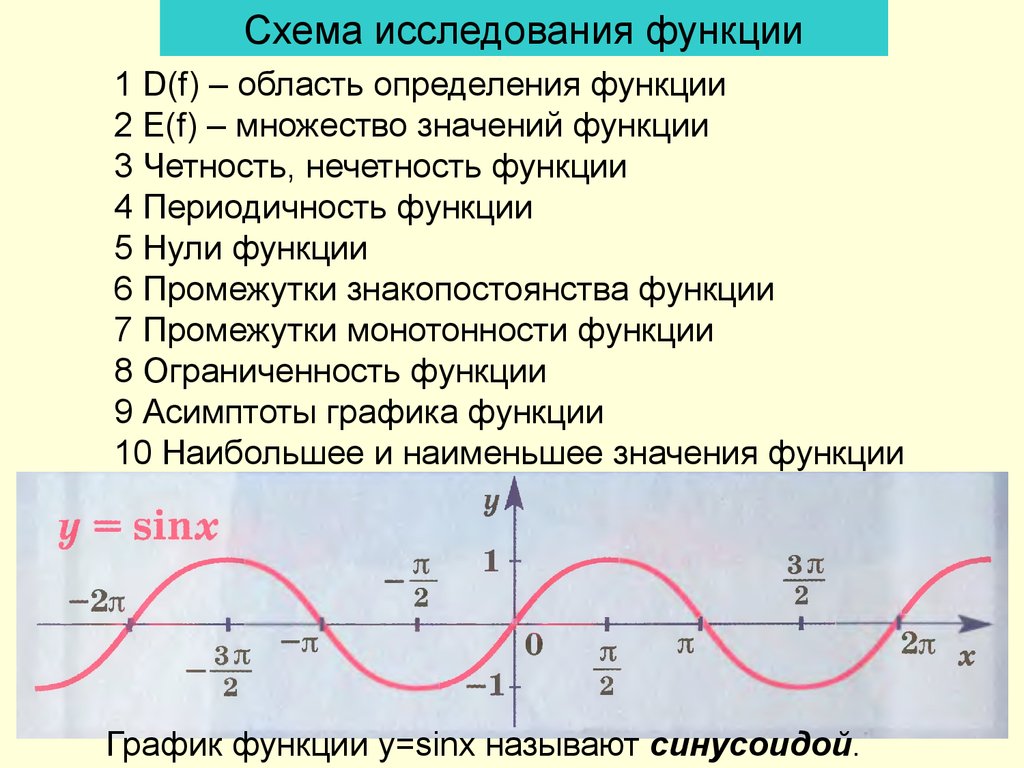 Как видно из рисунка, каждая функция принимает отрицательное или положительное значение в зависимости от величины угла. Например, sin α будет со знаком «+», если α принадлежит I и II четверти окружности, то есть, находится в промежутке от 0° до 180°. При α от 180° до 360° (III и IV четверти) sin α может быть только отрицательным значением.
Как видно из рисунка, каждая функция принимает отрицательное или положительное значение в зависимости от величины угла. Например, sin α будет со знаком «+», если α принадлежит I и II четверти окружности, то есть, находится в промежутке от 0° до 180°. При α от 180° до 360° (III и IV четверти) sin α может быть только отрицательным значением.
Попробуем построить тригонометрические таблицы для конкретных углов и узнать значение величин.
Значения α равные 30°, 45°, 60°, 90°, 180° и так далее – называют частными случаями. Значения тригонометрических функций для них просчитаны и представлены в виде специальных таблиц.
Данные углы выбраны отнюдь не случайно. Обозначение π в таблицах стоит для радиан. Рад — это угол, при котором длина дуги окружности соответствует ее радиусу. Данная величина была введена для того, чтобы установить универсальную зависимость, при расчетах в радианах не имеет значение действительная длина радиуса в см.
Углы в таблицах для тригонометрических функций соответствуют значениям радиан:
Итак, не трудно догадаться, что 2π – это полная окружность или 360°.
Свойства тригонометрических функций: синус и косинус
Для того, чтобы рассмотреть и сравнить основные свойства синуса и косинуса, тангенса и котангенса, необходимо начертить их функции. Сделать это можно в виде кривой, расположенной в двумерной системе координат.
Рассмотри сравнительную таблицу свойств для синусоиды и косинусоиды:
| Синусоида | Косинусоида |
|---|---|
| y = sin x | y = cos x |
| ОДЗ [-1; 1] | ОДЗ [-1; 1] |
| sin x = 0, при x = πk, где k ϵ Z | cos x = 0, при x = π/2 + πk, где k ϵ Z |
| sin x = 1, при x = π/2 + 2πk, где k ϵ Z | cos x = 1, при x = 2πk, где k ϵ Z |
| sin x = — 1, при x = 3π/2 + 2πk, где k ϵ Z | cos x = — 1, при x = π + 2πk, где k ϵ Z |
| sin (-x) = — sin x, т. е. функция нечетная | cos (-x) = cos x, т. е. функция четная |
| функция периодическая, наименьший период — 2π | функция периодическая, наименьший период — 2π |
| sin x › 0, при x принадлежащем I и II четвертям или от 0° до 180° (2πk, π + 2πk) | cos x › 0, при x принадлежащем I и IV четвертям или от 270° до 90° (- π/2 + 2πk, π/2 + 2πk) |
| sin x ‹ 0, при x принадлежащем III и IV четвертям или от 180° до 360° (π + 2πk, 2π + 2πk) | cos x ‹ 0, при x принадлежащем II и III четвертям или от 90° до 270° (π/2 + 2πk, 3π/2 + 2πk) |
| возрастает на промежутке [- π/2 + 2πk, π/2 + 2πk] | возрастает на промежутке [-π + 2πk, 2πk] |
| убывает на промежутках [ π/2 + 2πk, 3π/2 + 2πk] | убывает на промежутках [2πk, π + 2πk] |
| производная (sin x)’ = cos x | производная (cos x)’ = — sin x |
Определить является ли функция четной или нет очень просто.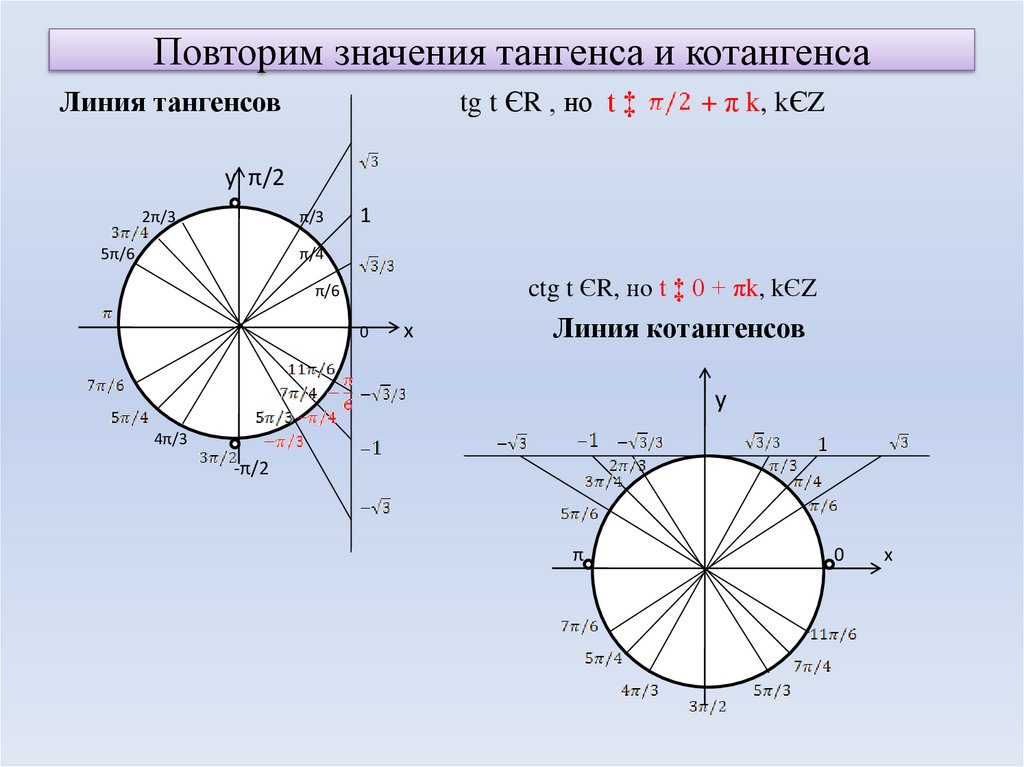 Достаточно представить тригонометрический круг со знаками тригонометрических величин и мысленно «сложить» график относительно оси OX. Если знаки совпадают, функция четная, в противном случае — нечетная.
Достаточно представить тригонометрический круг со знаками тригонометрических величин и мысленно «сложить» график относительно оси OX. Если знаки совпадают, функция четная, в противном случае — нечетная.
Введение радиан и перечисление основных свойств синусоиды и косинусоиды позволяют привести следующую закономерность:
Убедиться в верности формулы очень просто. Например, для x = π/2 синус равен 1, как и косинус x = 0. Проверку можно осуществить обративших к таблицам или проследив кривые функций для заданных значений.
Свойства тангенсоиды и котангенсоиды
Графики функций тангенса и котангенса значительно отличаются от синусоиды и косинусоиды. Величины tg и ctg являются обратными друг другу.
Основные свойства котангенсоиды:
- Y = tg x.
- В отличие от функций синуса и косинуса, в тангенсоиде Y может принимать значения множества всех действительных чисел.
- Тангенсоида стремится к значениям y при x = π/2 + πk, но никогда не достигает их.

- Наименьший положительный период тангенсоиды равен π.
- Tg (- x) = — tg x, т. е. функция нечетная.
- Tg x = 0, при x = πk.
- Функция является возрастающей.
- Tg x › 0, при x ϵ (πk, π/2 + πk).
- Tg x ‹ 0, при x ϵ ( — π/2 + πk, πk).
- Производная (tg x)’ = 1/cos2x .
Рассмотрим графическое изображение котангенсоиды ниже по тексту.
Основные свойства котангенсоиды:
- Y = ctg x.
- В отличие от функций синуса и косинуса, в тангенсоиде Y может принимать значения множества всех действительных чисел.
- Котангенсоида стремится к значениям y при x = πk, но никогда не достигает их.
- Наименьший положительный период котангенсоиды равен π.
- Ctg (- x) = — ctg x, т. е. функция нечетная.
- Ctg x = 0, при x = π/2 + πk.
- Функция является убывающей.
- Ctg x › 0, при x ϵ (πk, π/2 + πk).
- Ctg x ‹ 0, при x ϵ (π/2 + πk, πk).
- Производная (ctg x)’ = — 1/sin2x Исправить
Поделиться с друзьями:
Подборка по базе: Контрольная работа по теме _ Производная функции_, 11 класс. 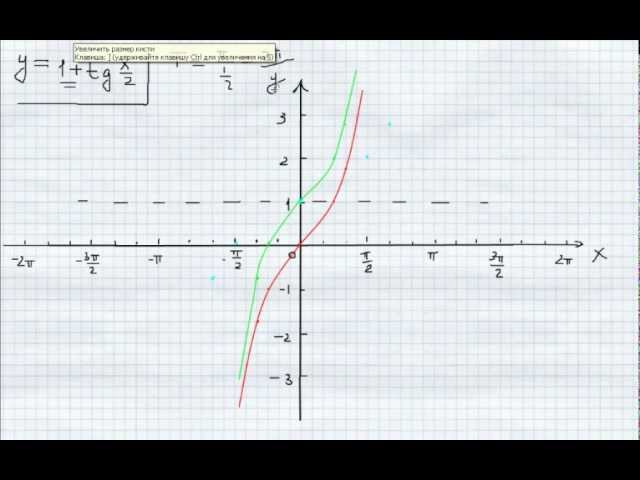 doc, Сенсомоторные функции. Гальтон.pptx, устойчивость функционорования экономики.docx, Объект, предмет, задачи и функции педагогики.pptx, +План функционирования внутренней системы оценки.docx, Средства, влияющие на функции органов дыхания..docx, Цели, задачи и функции криминалогии.docx, Особенности психического развития детей с нарушениями функций ОД, Безопасность функционирования информационных систем.doc, 10 функций семьи.pdf doc, Сенсомоторные функции. Гальтон.pptx, устойчивость функционорования экономики.docx, Объект, предмет, задачи и функции педагогики.pptx, +План функционирования внутренней системы оценки.docx, Средства, влияющие на функции органов дыхания..docx, Цели, задачи и функции криминалогии.docx, Особенности психического развития детей с нарушениями функций ОД, Безопасность функционирования информационных систем.doc, 10 функций семьи.pdfТЕМА: « ГРАФИКИ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ» ЦЕЛИ И ЗАДАЧИ УРОКА: 1. Обобщить материал по теме: «Графики тригонометрических функций», проверить умения в построении графиков функций с помощью преобразований. 2.Развивать логическое мышление, внимание, навыки самостоятельной работы, навыки самооценки. Оборудование: Трафареты, таблицы графиков тригонометрических функций, мультимедийный проектор, слайды, содержащие графики функций, карточки с заданиями, бланки для выполнения заданий. 1. Организационный момент: 2. Сообщение темы и цели урока. Во время урока постепенно мы будем использоваться тот раздаточный материал, который находится у вас на партах». II этап урока (20 минут) Повторение теоретического материала по теме «Общие свойства тригонометрических функций и их связь с графиками» Учащиеся могут дать одно из определений, приведенных ниже или их модификацию. Определение. «Зависимость переменной y от переменной x, при которой каждому значению переменной х соответствует единственное значение переменной у, называют функцией». Определение. «Соответствие f между двумя множествами X и Y, при котором каждому элементу множества X ставится в соответствие единственныйэлемент множества Y, называется функцией ». Учитель: «Назовите способы задания функции?» Учащиеся в произвольной последовательности должны перечислить способы задания функций: описательный, табличный, графический, аналитический. Учитель: «Перечислите, какими свойствами может обладать функция». Учащиеся в произвольной последовательности перечисляют свойства функций, таким образом, называют общую схему исследования функций. 1. Область определения функции . 2. Определение точек пересечения графика функции с осями координат. 3. Исследование функции на четность. 4. Исследование функции на монотонность. 5. Исследование функции на экстремум. 6. Исследование функции на периодичность. 7. 8. Исследование поведения функции на границах области определения. 9. Исследование области значений функции. 10. Построение графика функции. Учитель: Какие из тригонометрических функций вы знаете? Ответы учеников: синус, косинус, тангенс, котангенс. Учитель: Дайте определение этих функций. Определение: Числовые функции, заданные формулами у=sinx, y=cosx, y=tgx, y=ctgx, называют соответственно синусом, косинусом, тангенсом и котангенсом. Учитель: Как называются графики этих функций? Ответы учеников: синусоида, косинусоида, тангенсоида, котангенсоида. Учитель: Пред вами таблицы графиков тригонометрических функций. Используя таблицы укажите график функции, соответствующий синусоиде, косинусоиде, тангенсоиде, котангенсоиде. Ответы учеников: синусоида, косинусоида, тангенсоида, котангенсоида. Учитель: Используя общую схему исследования функции, вспомним необходимые определения и соответствующие свойства функций на графиках, которые изображены в таблицах графиков тригонометрических функций . Учащиеся формулируют: Определение. Область определения функции это множество значений независимой переменной, при которых функция имеет смысл. Учитель: «Перед вами графики тригонометрических функций, для каждого графика назовите область определения соответствующей функции». Ответы учеников: Область определения функций синус, косинус D(f)=(-), тангенс все хn, котангенc все хn Учащиеся формулируют: Т.к. осей координат две, то: а) с осью ординат. Если , то по определению функции точка пересечения с осью Oy единственная, еекоординаты . Если , то точек пересечения с осью ординат нет; б) с осью абсцисс. Абсциссы точек пересечения графика функции с осью Oxнаходятся из уравнения , число решений которого равно количеству точек пересечения графика функции с осью абсцисс. Учитель: «Сколько точек пересечения с осями координат имеет синус, косинус, тангенс, котангенс?» Ответы учеников: Синус с осью ординат имеет одну точку в начале координат, с осью абсцисс все точки с координатами (n;0) Косинус с осью ординат имеет одну точку – (0;1), с осью абсцисс все точки с координатами (n;0) Тангенс с осью ординат имеет одну точку в начале координат, с осью абсцисс все точки с координатами (n;0) Котангенс с осью ординат общих точек не имеет, с осью абсцисс все точки с координатами (n;0) Учащиеся: Определение. Если область определения функции симметрична относительно нуля и для любого 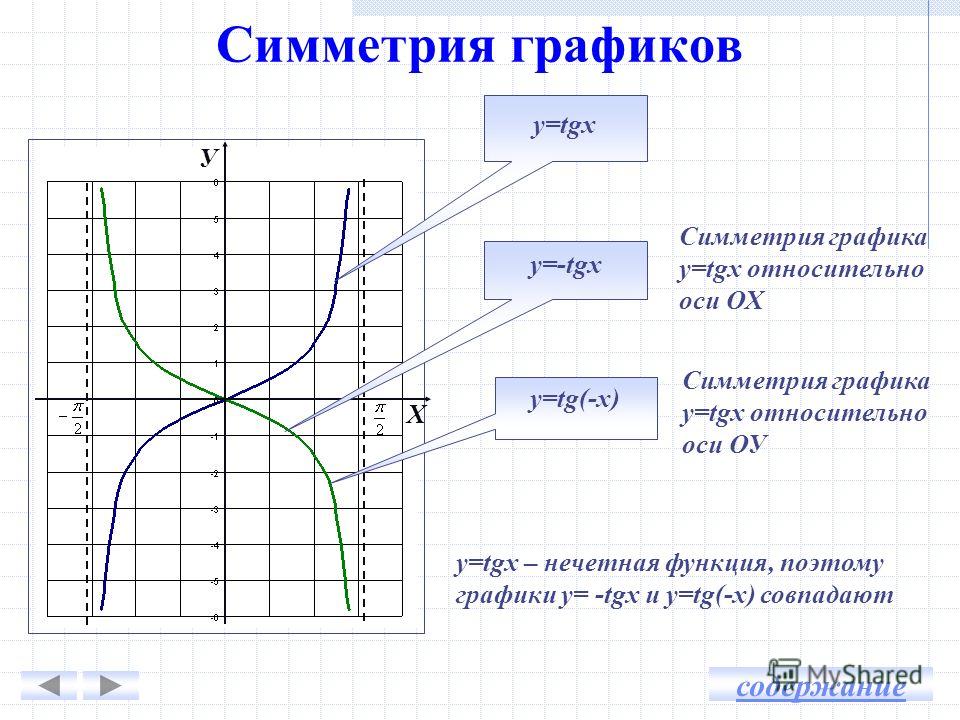 Если не выполняется ни одно из равенств, то функция ни четная, ни нечетная. Если не выполняется ни одно из равенств, то функция ни четная, ни нечетная.График четной функции симметричен относительно оси ординат (Oy). График нечетной функции симметричен относительно начала координат (точки O). Из 4 тригонометрических функций только косинус четная функция. Синус, тангенс, котангенс – нечетные. Учащиеся: Определение. Если для любых и таких, что выполнено условие , то функция называется монотонно возрастающей на X. Если , то функция называется монотонно убывающей на X. Если , то функция постоянна на X. Учитель: Какая из тригонометрических функций является монотонно возрастающей (монотонно убывающей) на всей области определения Учащиеся: Монотонно возрастающей на всей области определения является тангенс. Монотонно убывающей на всей области определения является котангенс. Учитель: Назовите промежутки монотонности синуса, косинуса. Учащиеся: Синус возрастает на промежутках , , убывает на промежутках , . Косинус возрастает на промежутках ,, и убывает на промежутках , . Учитель: Назовите экстремумы синуса, косинуса, тангенса, котангенса. Учащиеся:Точки максимума функции синус- (; 1), наибольшее значение функции равно 1, точки минимума- (-; — 1), наименьшее значение равно -1. Точки максимума функции косинус- (; 1), наибольшее значение функции равно 1, точки минимума- (; — 1), наименьшее значение равно -1. Тангенс и котангенс экстремумов не имеют. Учащиеся: Определение. Еслисуществует такое число , что для любого x из области определения функции числа и принадлежат области определения и , то функция называется периодической, а число t периодом функции. Периодом для функций синус и косинус является , тангенс и котангенс имеют период равный . Учитель: «Теперь займемся определением промежутков знакопостоянства функции. Пожалуйста, дайте определение и укажите промежутки знакопостоянства для графиков синуса, косинуса, тангенса и котангенса». Определение. Множество X, на котором функция не меняет свой знак, называется промежутком знакопостоянства функции. Синус принимает неотрицательные значения на промежутках , неположительные значения на . Косинус принимает неотрицательные значения на промежутках, неположительные значения на . Тангенс принимает положительные значения на промежутках (), отрицательные значения на (). Котангенс принимает положительные значения на промежутках (), отрицательные значения на (). Определение. Областью значений функции называется множество, в которое входят все значения, которые может принимать функция на своей области определения. Учитель: Назовите множество значений синуса, косинуса, тангенса, котангенса. Учащиеся: Множество значений функции синуса и косинуса является промежуток , тангенса и котангенса . Учитель: Ребята, какие преобразования графиков функций вы знаете? Учащиеся:1) Параллельный перенос графика функции y=f(x)+b, где b – постоянное число, на вектор (0;b) вдоль оси ординат. 2) Растяжение графика вдоль оси Оу с коэффициентом k, которое задается формулами Для построения графика функции у=kf(х) надо растянуть график функции у= f(х) в k раз вдоль оси ординат. 3) Параллельный перенос вдоль оси абсцисс на вектор (а;0) задается формулами График функции у= f(х-а) получается из графика f переносом ( вдоль оси абсцисс) на вектор (а;0). 4) Растяжение вдоль оси Ох с коэффициентом k задается формулами Для построения графика функции у=f() надо подвергнуть график функции f растяжению с коэффициентом k вдоль оси абсцисс. Учитель: Ребята, какие преобразования графиков функций вы видите на рисунках? (Приложение. Комментарий: Рисунки можно подготовить на листах и раздать их учащимся, на пленке и показать их с помощью графопроектора, с применением мультимедиа-проектора, показать на экране.) Рис. Рис.3. Параллельный перенос графика функции на вектор (0;-1) вдоль оси ординат. Рис.4. Растяжение графика вдоль оси Ох с коэффициентом равным 2. Рис.5. Параллельный перенос графика функции на вектор (0;1) вдоль оси ординат, растяжение графика вдоль оси Оу с коэффициентом равным 2. Рис.6. Растяжение графика вдоль оси Ох с коэффициентом равным 0,5. Рис.7. Растяжение вдоль оси Оу с коэффициентом равным -1, Параллельный перенос графика функции на вектор (0;1) вдоль оси ординат. Учитель: Ребята, назовите функции, которым соответствуют данные графики. Учащиеся: Рис 1. y=2sin2x, Рис2. y=-2sin2x, Рис3. y=cosx-1, Рис 4. y=cos2x, Рис 5. y=2sinx+1, Рис.6. y=sin0,5x, Рис 7. y=-sinx+1. Разноуровневая самостоятельная работа Учащимся 1-й группы учитель выдал красные карточки с задачами повышенного уровня сложности в 2-х вариантах. Для учащихся 2-й группы учитель выдал зеленые карточки в 4-х вариантах с разнообразными заданиями базового уровня сложности. Для учащихся 3-й группы учителем составлены синие карточки в 2-х вариантах с заданиями базового уровня сложности. Учащиеся 3-й группы — это, как правило, учащиеся со слабой математической подготовкой, педагогически запущенные школьники, они будут выполнять задания под контролем учителя. Все варианты содержат задания на рассмотренную на уроке тему. Вместе с заданиями учащиеся получают бланки для выполнения заданий.
у=2cos 2x, y= cos0,5x – 3, y= — cos (x+) +1
Красная карточка 2. 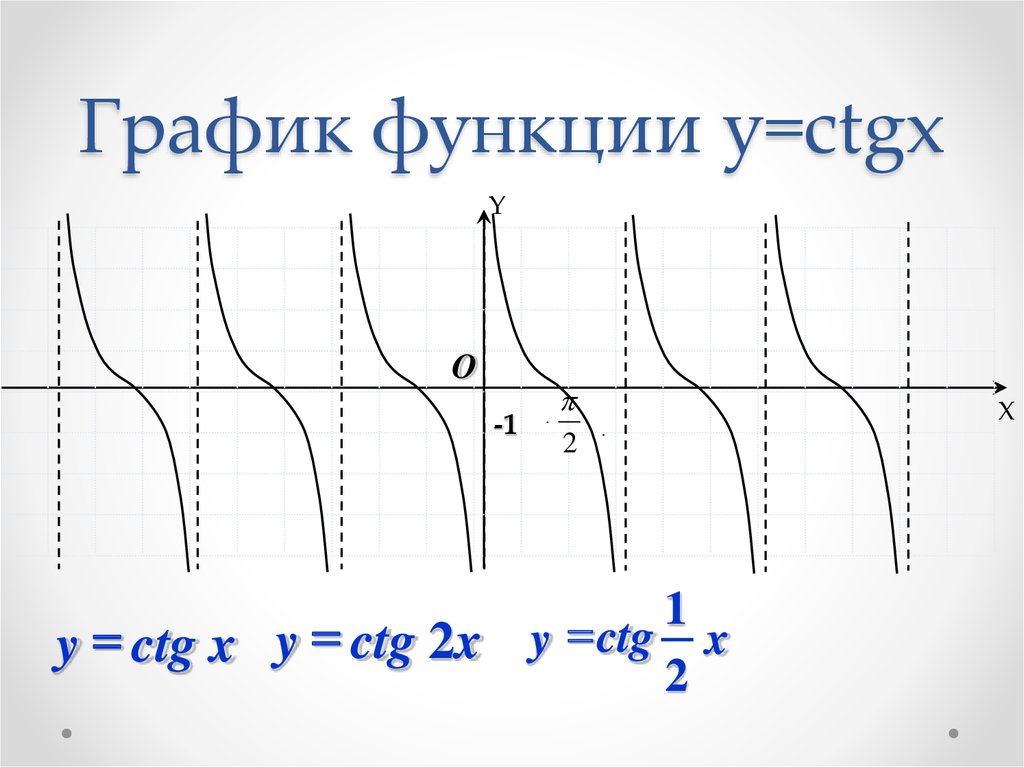
у=-tg x, y= 0,5tg2x +3, y= tg (x-) -2 2. Опишите свойства функции, изображенной на рисунке. Что это за функция? Зеленая карточка 1. 2. Опишите свойства функции, изображенной на рисунке. Что это за функция? Зеленая карточка 2. 2. Опишите свойства функции, изображенной на рисунке. Что это за функция? Зеленая карточка 3. 2. Опишите свойства функции, изображенной на рисунке. Что это за функция? Зеленая карточка 4. 2. Опишите свойства функции, изображенной на рисунке. Что это за функция? Синяя карточка 1 №1. График какой функции изображен на рисунке? 1) у=sinx 2)y=cosx 3)y=tgx 4) y=ctgx 1) [-1;1] 2)[] 3) [-2;2] 4) (-2;2) 1) 2) 3) 4) №4. Какое из чисел не входит в множество значений функции у= 2sin x -1 1) (-) 2) (- 3) (- 4) [-2; +) Синяя карточка 2. №1. График какой функции изображен на рисунке? 1) у=sinx 2)y=cosx 3)y=tgx 4) y=ctgx
1) [-1;1] 2)[] 3) [-2;2] 4) (-2;2) 1) 2) 3) 4) №4. Найдите наибольшее целое число, которое входит в множество значений функции у= 2cos3x +1 1) (-) 2) (- 3) (- 4) [-2; +) 1) 2) 3) 4) Подведение итогов урока, комментарии по домашнему заданию Учитель еще раз обращает внимание, на те теоретические факты, которые вспоминали на уроке, говорит о необходимости выучить их. Отмечает наиболее успешную работу на уроке отдельных учащихся, при необходимости выставляет отметки. В качестве домашнего задания учащиеся получают по варианту из вариантов самостоятельной работы, проведенной на уроке. Бланк ответов Лист описания функции: 2. Определение точек пересечения графика функции с осями координат. Точки пересечения с осью Ох__________________, с Оу______________ 3. Исследование функции на четность. _____________________________ 4. Исследование функции на монотонность. Функция возрастает на промежутках______________________________, Убывает на промежутках_____________________________________ 5. Исследование функции на экстремум. Точки минимума функции___________________________, Точки максимума функции___________________________, Минимумы функции________________________________, Максимумы функции________________________________. 6. Исследование функции на периодичность.Т=______________________ 7. Определение промежутков знакопостоянства. F(x)>0 на промежетке___________________________________________, F(x) 8. Область значений функции___________________________________. Бланк ответов Лист описания функции: 2. Определение точек пересечения графика функции с осями координат. Точки пересечения с осью Ох__________________, с Оу______________ 3. Исследование функции на четность. _____________________________ 4. Исследование функции на монотонность. Функция возрастает на промежутках______________________________, Убывает на промежутках_____________________________________ 5. Исследование функции на экстремум. Точки минимума функции___________________________, Точки максимума функции___________________________, Минимумы функции________________________________, Максимумы функции________________________________. 6. Исследование функции на периодичность.Т=______________________ 7. Определение промежутков знакопостоянства. F(x)>0 на промежетке___________________________________________, F(x) 8. Область значений функции___________________________________. Бланк ответов
|
1
Первый слайд презентации
11 класс ПОСТРОЕНИЕ И ПРЕОБРАЗОВАНИЕ ГРАФИКА ФУНКЦИИ у = tg х
Изображение слайда
2
Слайд 2: Содержание
Построение графика у = tgx Свойства функции у = tg х Сдвиг вдоль оси абсцисс Сдвиг вдоль оси ординат Сжатие и растяжение к оси ОХ Сжатие и растяжение к оси ОУ Симметрия графиков Графики с модулем График у = с tg x Содержание
Изображение слайда
3
Слайд 3: Построение графика у = tgx
Построим график у= tgx на промежутке (- π /2; π /2) У Х у= tgx х у у= tg х — функция нечетная, возрастающая 0 0 1 содержание
Изображение слайда
4
Слайд 4: Свойства функции
y = tgx У Х у= tgx Определена при: Асимптоты Нули функции Четная или нечетная Период нечетная График — тангенсоида содержание
Изображение слайда
5
Слайд 5: Сдвиг вдоль оси ординат
y=tgx-4 y=tgx+3 y=tgx Сдвиг вниз — Сдвиг вверх + У Х +3 -4 содержание
Изображение слайда
6
Слайд 6: Сдвиг вдоль оси абсцисс
Сдвиг вправо — Сдвиг влево + У Х y = tgx y=tg(x+ π /3) Х У y = tgx y=tg(x- π /3) содержание
Изображение слайда
7
Слайд 7: Сжатие и растяжение
Сжатие k>1 0<k<1 y = k∙tgx У У Х Х y = tgx y=2tgx y = tgx y=0,5tgx Растяжение содержание
Изображение слайда
8
Слайд 8: Сжатие и растяжение
Сжатие Растяжение k>1 0<k<1 y = tg ( kx) У У Х Х y = tgx y=tg(2x) y = tgx y=tg(0,5x) содержание
Изображение слайда
9
Слайд 9: Симметрия графиков
У Х y=tgx y=-tgx y=tg(-x) y=tgx – нечетная функция, поэтому графики у= -tgx и у= tg(-x) совпадают Симметрия графика у= tg х относительно оси ОХ Симметрия графика у= tg х относительно оси ОУ содержание
Изображение слайда
10
Слайд 10: Построение графика
y= ∣ tgx ∣
У
Х
y = tgx
y = ∣ tgx ∣ — получается симметрией относительно оси ОХ тех участков графика у = tg х, которые расположены ниже её. y= ∣ tgx ∣
содержание
y= ∣ tgx ∣
содержание
Изображение слайда
11
Слайд 11: График функции
Х У — π π y=tgx y=tg ( |x|) Часть графика функции y=tgx, лежащая левее оси y, удаляется, а часть графика, лежащая правее оси y, остается без изменений и симметрично отражается относительно оси ОУ влево у = tg | x | График функции y = tg (|x|) симметричен относительно оси ОУ содержание График функции
Изображение слайда
12
Слайд 12: Построение графика уравнения
X У -π π y=tgx |y| =tgx Участки графика функции y=tgx, лежащие ниже оси ОХ, удаляются, ∣ y ∣ = tgx а участки, лежащие выше оси ОХ, симметрично отражаются относительно оси ОХ содержание
Изображение слайда
13
Слайд 13: Построение графика функции
X У 0 y=tgx и y=arctgx являются взаимно обратными График функции y=arctgx получается из графика функции y=tgx симметрией относительно прямой y=x y=tgx y=arctgx y=x y = arctgx содержание
Изображение слайда
14
Слайд 14: Построение графика у = ctgx
Х У Построим у = ctgx на промежутке (0; π ) У Х 1 1 0 у= ctg х — нечетная, убывает y = ctgx содержание
Изображение слайда
15
Слайд 15: Свойства функции
y = ctgx У Х у= ctgx Определена при: Асимптоты Нули функции Четная или нечетная Период нечетная 0 содержание
Изображение слайда
16
Слайд 16: Построение графика функции
X У Функции y=ctgx и y=arcctgx являются взаимно обратными График функции y=arcctgx получается из графика функции y=ctgx симметрией относительно прямой y=x y=ctgx y=arcctgx y=x y = arcctgx содержание
Изображение слайда
17
Последний слайд презентации: 11 класс ПОСТРОЕНИЕ И ПРЕОБРАЗОВАНИЕ ГРАФИКА ФУНКЦИИ у = tg х: Литература
Алимов Ш. А. Алгебра и начала анализа: Учебник для 10-11 кл. общеобразовательных учреждений. – М.: Просвещение, 2005.
Генденштейн Л.Э., Ершова А.П., Ершова А.С. Наглядный справочник по алгебре и началам анализа с примерами для 7-11 классов. – М.: Илекса, Гимназия, 1997.
Литература
А. Алгебра и начала анализа: Учебник для 10-11 кл. общеобразовательных учреждений. – М.: Просвещение, 2005.
Генденштейн Л.Э., Ершова А.П., Ершова А.С. Наглядный справочник по алгебре и началам анализа с примерами для 7-11 классов. – М.: Илекса, Гимназия, 1997.
Литература
Изображение слайда
Урок алгебры в 10-м классе по теме «Первые представления о решении тригонометрических уравнений»
Цель: создать условия, при которых учащиеся:
- Повторят схему изучения функции на примере тригонометрических функций, схему изучения нового вида уравнения;
- Повторят способ решения тригонометрических уравнений при помощи числовой окружности и графика тригонометрической функции;
- «Откроют» новые классы (группы) тригонометрических уравнений и способы их решения.
Учебная задача: выделить новые типы
уравнений, которые можно решить на основе
имеющихся знаний и указать способы их решения.
Форма работы: фронтальная, групповая, индивидуальная.
Оборудование: мультимедиа-проектор, интерактивная доска.
Урок построен на основе технологии деятельностного подхода. Работа на уроке сопровождается мультимедийной презентацией (см. Приложение 1)
Ход урока
I этап. Мотивационно-ориентировочная часть.
Актуализация.
На предыдущих уроках мы изучили тригонометрические функции. На какие вопросы надо уметь отвечать при изучении функции?
Имя функции
Аналитическая и графическая модели
Реальные ситуации, которые могут быть описаны с помощью этой функции
Свойства функции
Типы задач
Ответим на эти вопросы.
Имя функции — тригонометрические.
Аналитическая модель — y=cosx, y=sinx, y=tgx, y=ctgx.
Графическая модель — косинусоида, синусоида,
тангенсоида и котангенсоида.
Реальные ситуации — гармонические колебания.
Свойства функции — область определения функции, периодичность, четность-нечетность, промежутки монотонности, ограниченность, наименьшее и наибольшее значения, непрерывность и множество значений.
Типы задач — построить график тригонометрической функции, прочитать график функции (описать свойства функции), решить уравнение, решить неравенство.
Какие типы задач мы умеем решать? Приходилось ли нам раньше решать тригонометрические уравнения? Какие?
cosx=a, sinx=a, tgx=a, ctgx=a, где а — действительное число.
Как мы их решали?
При помощи числовой окружности и при помощи графика функции.
Такие уравнения называют простейшими тригонометрическими уравнениями.
2. Мотивация.
Решить уравнения (устно, используя алгоритм решения при помощи числовой окружности или при помощи графика функции):
cosx=, sinx=, tgx= 0, ctgx=, sinx= — 2, cosx= 0,7, sinx=
— 0,3, tgx=2.
Любое ли тригонометрическое уравнение можно решить графически или с помощью числовой окружности?
Последние уравнения решить не можем. Значит, нашей базы знаний пока не хватает и существуют другие способы решения. Мы можем решать простейшие тригонометрические уравнения только для конкретных значений а.
3. Постановка учебной задачи и планирование.
Только ли такие тригонометрические уравнения существуют? Посмотрите в задачнике на с.51. Такое обилие уравнений надо как-то классифицировать, объединить по каким-то признакам, свойствам в группы.
Что мы должны знать, когда изучаем новый вид уравнений?
Что называется таким уравнением (его вид)
Что называется корнем уравнения (решением)
Что значит решить уравнение
Способы решения (аналитический и графический)
На какие вопросы должны ответить сегодня? Так какова учебная задача сегодня на урок?
Выделить те типы тригонометрических уравнений,
которые мы можем решить на основе имеющихся
знаний и указать способ их решения (попытаться
свести к ранее изученным алгебраическим
уравнениям).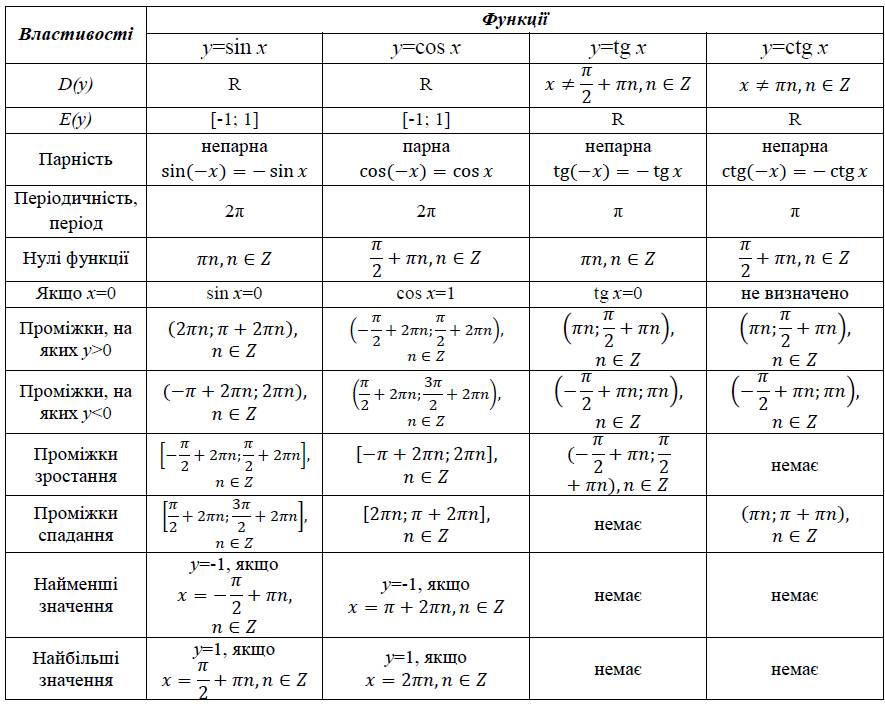
Итак, как бы сформулировали тему урока?
(запись на доске и в тетрадях)
Что мы знаем о решении тригонометрических уравнений.
или
Первые представления о решении тригонометрических уравнений.
II этап. Содержательная часть.
(работа с интерактивной доской)
Даны уравнения. Разбейте их на группы, объединив по каким-либо признакам.
Таблица 1
| ; ; х(1 — х)=0; ; ; ; ; |
; ; ; ; ; ; ; |
По каким признакам вы объединили уравнения?
Возможные варианты ответов:
Линейные уравнения — № 1 и № 5; квадратные
уравнения — № 2 и № 4; рациональные уравнения — № 3
и № 6; уравнения с модулем — № 7 и № 9;
тригонометрические — № 8-15.
1 группа (линейность) — №№ 1 и 12, 5 и 10; 2 группа (квадратичность)- №№ 2 и 8, 4 и 11, 15; 3 группа (рациональность) — №№ 3 и 14, 6 и 13; 4 группа (модуль) - №№ 7 и 9.
Если 2 варианта нет, то предложить объединить каждое уравнение из 1 столбца с каким-либо уравнением второго столбца.
Работа в группах (можно в парах или по рядам). Решение уравнений (каждая группа свой вид). Обсуждение предложенных решений. Каждая группа защищает свою работу. Все учащиеся записывают решение в тетрадь.
1 группа (используется линейность)
Таблица 2
| и линейность аргумента ; 4x=t , , Ответ: , |
и линейность относительно функции Ответ: |
2 группа (используется квадратичность)
Таблица 3
| и и Ответ: |
и () или решений нет Ответ: |
3 группа (рациональные уравнения)
Таблица 4
| х(1 — х)=0 и или НО! не
существует. Значит не является решением данного уравнения. Ответ: |
и или Ответ: , |
Уравнения с модулем — фронтальная работа
Таблица 5
| и и решений нет Ответ: |
III этап. Рефлексивно-оценочная часть.
Самостоятельное решение задач (3 уровня сложности) со взаимопроверкой. Ответы с обратной стороны доски (см. Приложение 2)
В зависимости от класса эту работу можно дать на следующем уроке.
Вспомните, какую задачу мы поставили перед собой сегодня на уроке?
Выделить те типы тригонометрических уравнений, которые мы можем решить.
Достигли мы этой цели? Какие типы тригонометрических уравнений мы можем решать?
Какими способами мы это сделали, с помощью каких приемов?
Введение новой переменной, разложение на
множители, сведение уравнения к квадратному.
Каждое ли тригонометрическое уравнение мы теперь можем решить? (вспомните проблему в начале урока). Какова задача на следующие уроки?
Найдите в задачнике на с.51 типы уравнений, которые мы не выделили сегодня. (№№ 361-364).
Какие еще задачи мы должны научиться решать?
Найти корни уравнения на заданном промежутке, найти наименьший или наибольший (положительный, отрицательный) корень уравнения.
4. Задание на дом.
1 группа — № 278, 282, 286(б, в)
2 группа — № 283, 285, 286(б, в)
3 группа — №288, 287, 353(б, в)
Оцените собственную деятельность на уроке:
Лист обратной связи.
| 1 | Какое значение для тебя имеют знания и умения, полученные ан уроке? | -
очень важны - важны — не очень важны |
| 2 | Как ты оцениваешь полученные сегодня знания? | -
глубокие - осознанные - неосознанные |
| 3 | Как оцениваешь свою деятельность? | -
отлично - хорошо - удовлетворительно |
на что он влияет в автомобиле.
 Слишком большой положительный угол. Тригонометрическая окружность. Исчерпывающее руководство (2019) Углом в тригонометрии считают
Слишком большой положительный угол. Тригонометрическая окружность. Исчерпывающее руководство (2019) Углом в тригонометрии считаютТригонометрия, как наука, зародилась на Древнем Востоке. Первые тригонометрические соотношения были выведены астрономами для создания точного календаря и ориентированию по звездам. Данные вычисления относились к сферической тригонометрии, в то время как в школьном курсе изучают соотношения сторон и угла плоского треугольника.
Тригонометрия – это раздел математики, занимающийся свойствами тригонометрических функций и зависимостью между сторонами и углами треугольников.
В период расцвета культуры и науки I тысячелетия нашей эры знания распространились с Древнего Востока в Грецию. Но основные открытия тригонометрии – это заслуга мужей арабского халифата. В частности, туркменский ученый аль-Маразви ввел такие функции, как тангенс и котангенс, составил первые таблицы значений для синусов, тангенсов и котангенсов. Понятие синуса и косинуса введены индийскими учеными. Тригонометрии посвящено немало внимания в трудах таких великих деятелей древности, как Евклида, Архимеда и Эратосфена.
Понятие синуса и косинуса введены индийскими учеными. Тригонометрии посвящено немало внимания в трудах таких великих деятелей древности, как Евклида, Архимеда и Эратосфена.
Основные величины тригонометрии
Основные тригонометрические функции числового аргумента – это синус, косинус, тангенс и котангенс. Каждая из них имеет свой график: синусоида, косинусоида, тангенсоида и котангенсоида.
В основе формул для расчета значений указанных величин лежит теорема Пифагора. Школьникам она больше известна в формулировке: «Пифагоровы штаны, во все стороны равны», так как доказательство приводится на примере равнобедренного прямоугольного треугольника.
Синус, косинус и другие зависимости устанавливают связь между острыми углами и сторонами любого прямоугольного треугольника. Приведем формулы для расчета этих величин для угла A и проследим взаимосвязи тригонометрических функций:
Как видно, tg и ctg являются обратными функциями. Если представить катет a как произведение sin A и гипотенузы с, а катет b в виде cos A * c, то получим следующие формулы для тангенса и котангенса:
Тригонометрический круг
Графически соотношение упомянутых величин можно представить следующим образом:
Окружность, в данном случае, представляет собой все возможные значения угла α — от 0° до 360°. Как видно из рисунка, каждая функция принимает отрицательное или положительное значение в зависимости от величины угла. Например, sin α будет со знаком «+», если α принадлежит I и II четверти окружности, то есть, находится в промежутке от 0° до 180°. При α от 180° до 360° (III и IV четверти) sin α может быть только отрицательным значением.
Как видно из рисунка, каждая функция принимает отрицательное или положительное значение в зависимости от величины угла. Например, sin α будет со знаком «+», если α принадлежит I и II четверти окружности, то есть, находится в промежутке от 0° до 180°. При α от 180° до 360° (III и IV четверти) sin α может быть только отрицательным значением.
Попробуем построить тригонометрические таблицы для конкретных углов и узнать значение величин.
Значения α равные 30°, 45°, 60°, 90°, 180° и так далее – называют частными случаями. Значения тригонометрических функций для них просчитаны и представлены в виде специальных таблиц.
Данные углы выбраны отнюдь не случайно. Обозначение π в таблицах стоит для радиан. Рад — это угол, при котором длина дуги окружности соответствует ее радиусу. Данная величина была введена для того, чтобы установить универсальную зависимость, при расчетах в радианах не имеет значение действительная длина радиуса в см.
Углы в таблицах для тригонометрических функций соответствуют значениям радиан:
Итак, не трудно догадаться, что 2π – это полная окружность или 360°.
Свойства тригонометрических функций: синус и косинус
Для того, чтобы рассмотреть и сравнить основные свойства синуса и косинуса, тангенса и котангенса, необходимо начертить их функции. Сделать это можно в виде кривой, расположенной в двумерной системе координат.
Рассмотри сравнительную таблицу свойств для синусоиды и косинусоиды:
| Синусоида | Косинусоида |
|---|---|
| y = sin x | y = cos x |
| ОДЗ [-1; 1] | ОДЗ [-1; 1] |
| sin x = 0, при x = πk, где k ϵ Z | cos x = 0, при x = π/2 + πk, где k ϵ Z |
| sin x = 1, при x = π/2 + 2πk, где k ϵ Z | cos x = 1, при x = 2πk, где k ϵ Z |
| sin x = — 1, при x = 3π/2 + 2πk, где k ϵ Z | cos x = — 1, при x = π + 2πk, где k ϵ Z |
| sin (-x) = — sin x, т. е. функция нечетная | cos (-x) = cos x, т. е. функция четная |
| функция периодическая, наименьший период — 2π | |
| sin x › 0, при x принадлежащем I и II четвертям или от 0° до 180° (2πk, π + 2πk) | cos x › 0, при x принадлежащем I и IV четвертям или от 270° до 90° (- π/2 + 2πk, π/2 + 2πk) |
| sin x ‹ 0, при x принадлежащем III и IV четвертям или от 180° до 360° (π + 2πk, 2π + 2πk) | cos x ‹ 0, при x принадлежащем II и III четвертям или от 90° до 270° (π/2 + 2πk, 3π/2 + 2πk) |
| возрастает на промежутке [- π/2 + 2πk, π/2 + 2πk] | возрастает на промежутке [-π + 2πk, 2πk] |
| убывает на промежутках [ π/2 + 2πk, 3π/2 + 2πk] | убывает на промежутках |
| производная (sin x)’ = cos x | производная (cos x)’ = — sin x |
Определить является ли функция четной или нет очень просто.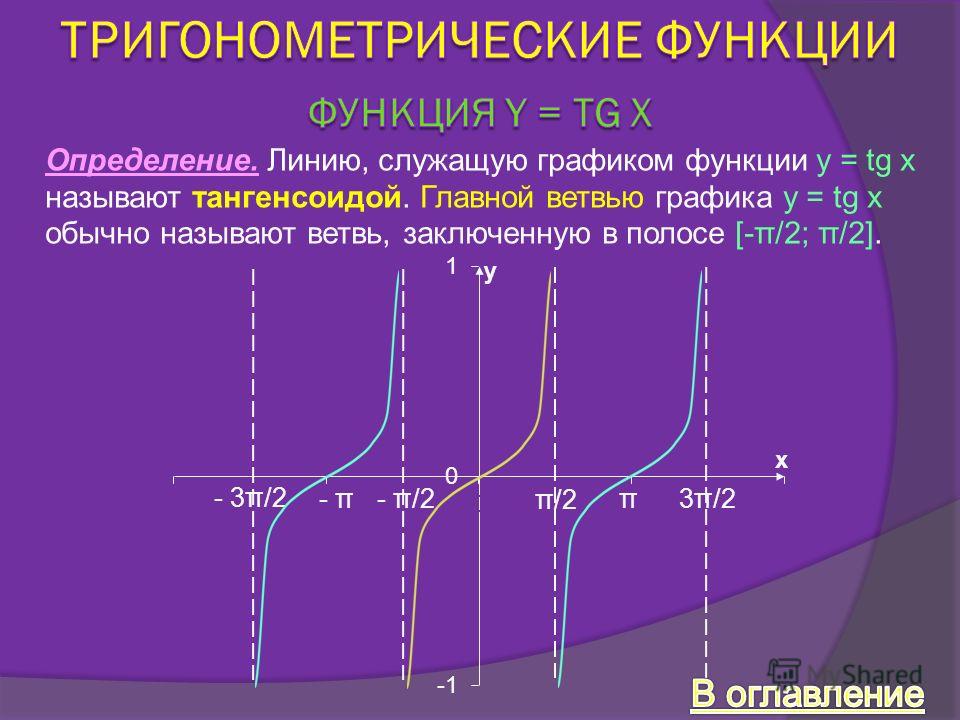 Достаточно представить тригонометрический круг со знаками тригонометрических величин и мысленно «сложить» график относительно оси OX. Если знаки совпадают, функция четная, в противном случае — нечетная.
Достаточно представить тригонометрический круг со знаками тригонометрических величин и мысленно «сложить» график относительно оси OX. Если знаки совпадают, функция четная, в противном случае — нечетная.
Введение радиан и перечисление основных свойств синусоиды и косинусоиды позволяют привести следующую закономерность:
Убедиться в верности формулы очень просто. Например, для x = π/2 синус равен 1, как и косинус x = 0. Проверку можно осуществить обративших к таблицам или проследив кривые функций для заданных значений.
Свойства тангенсоиды и котангенсоиды
Графики функций тангенса и котангенса значительно отличаются от синусоиды и косинусоиды. Величины tg и ctg являются обратными друг другу.
- Y = tg x.
- Тангенсоида стремится к значениям y при x = π/2 + πk, но никогда не достигает их.
- Наименьший положительный период тангенсоиды равен π.
- Tg (- x) = — tg x, т. е. функция нечетная.
- Tg x = 0, при x = πk.

- Функция является возрастающей.
- Tg x › 0, при x ϵ (πk, π/2 + πk).
- Tg x ‹ 0, при x ϵ (— π/2 + πk, πk).
- Производная (tg x)’ = 1/cos 2 x .
Рассмотрим графическое изображение котангенсоиды ниже по тексту.
Основные свойства котангенсоиды:
- Y = ctg x.
- В отличие от функций синуса и косинуса, в тангенсоиде Y может принимать значения множества всех действительных чисел.
- Котангенсоида стремится к значениям y при x = πk, но никогда не достигает их.
- Наименьший положительный период котангенсоиды равен π.
- Ctg (- x) = — ctg x, т. е. функция нечетная.
- Ctg x = 0, при x = π/2 + πk.
- Функция является убывающей.
- Ctg x › 0, при x ϵ (πk, π/2 + πk).
- Ctg x ‹ 0, при x ϵ (π/2 + πk, πk).
- Производная (ctg x)’ = — 1/sin 2 x Исправить
Альфа обозначает действительное число. Знак равенства в приведенных выражениях свидетельствует о том, что если к бесконечности прибавить число или бесконечность, ничего не изменится, в результате получится такая же бесконечность.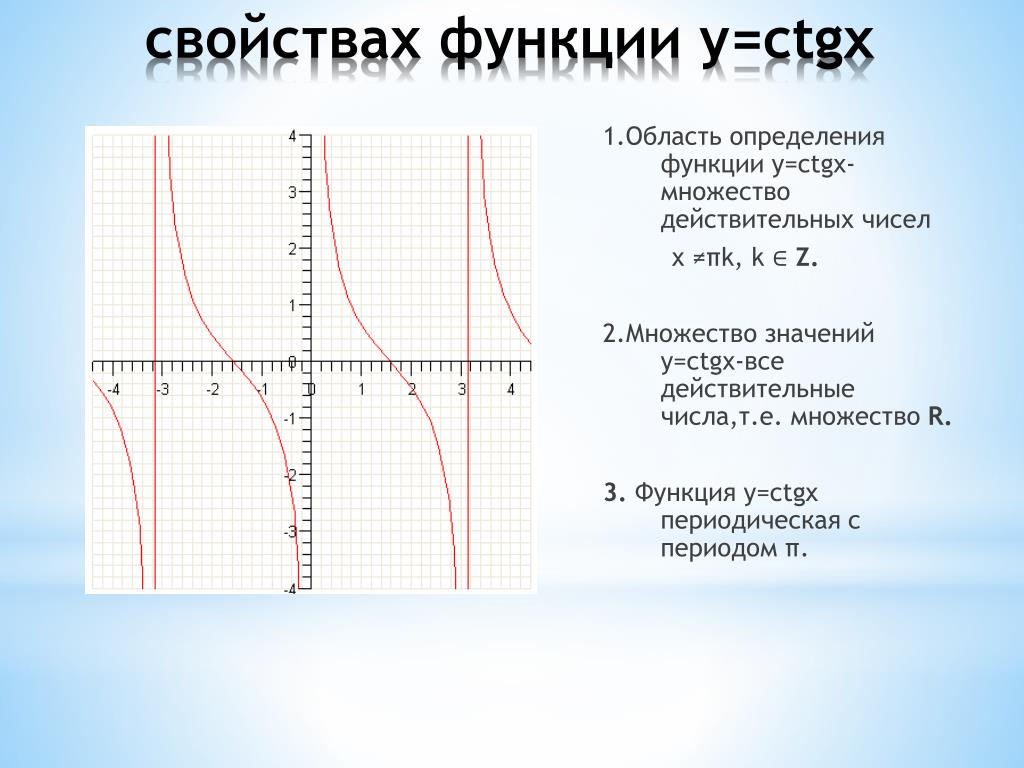 Если в качестве примера взять бесконечное множество натуральных чисел, то рассмотренные примеры можно представить в таком виде:
Если в качестве примера взять бесконечное множество натуральных чисел, то рассмотренные примеры можно представить в таком виде:
Для наглядного доказательства своей правоты математики придумали много разных методов . Лично я смотрю на все эти методы, как на пляски шаманов с бубнами. По существу, все они сводятся к тому, что либо часть номеров не занята и в них заселяются новые гости, либо к тому, что часть посетителей вышвыривают в коридор, чтобы освободить место для гостей (очень даже по-человечески). Свой взгляд на подобные решения я изложил в форме фантастического рассказа о Блондинке. На чем основываются мои рассуждения? Переселение бесконечного количества посетителей требует бесконечно много времени. После того, как мы освободили первую комнату для гостя, один из посетителей всегда будет идти по коридору из своего номера в соседний до скончания века. Конечно, фактор времени можно тупо игнорировать, но это уже будет из разряда «дуракам закон не писан». Всё зависит от того, чем мы занимаемся: подгоняем реальность под математические теории или наоборот.
Что же такое «бесконечная гостиница»? Бесконечная гостиница — это гостиница, в которой всегда есть любое количество свободных мест, независимо от того, сколько номеров занято. Если все номера в бесконечном коридоре «для посетителей» заняты, есть другой бесконечный коридор с номерами «для гостей». Таких коридоров будет бесконечное множество. При этом у «бесконечной гостиницы» бесконечное количество этажей в бесконечном количестве корпусов на бесконечном количестве планет в бесконечном количестве вселенных, созданных бесконечным количеством Богов. Математики же не способны отстраниться от банальных бытовых проблем: Бог-Аллах-Будда — всегда только один, гостиница — она одна, коридор — только один. Вот математики и пытаются подтасовывать порядковые номера гостиничных номеров, убеждая нас в том, что можно «впихнуть невпихуемое».
Логику своих рассуждений я вам продемонстрирую на примере бесконечного множества натуральных чисел. Для начала нужно ответить на очень простой вопрос: сколько множеств натуральных чисел существует — одно или много? Правильного ответа на это вопрос не существует, поскольку числа придумали мы сами, в Природе чисел не существует.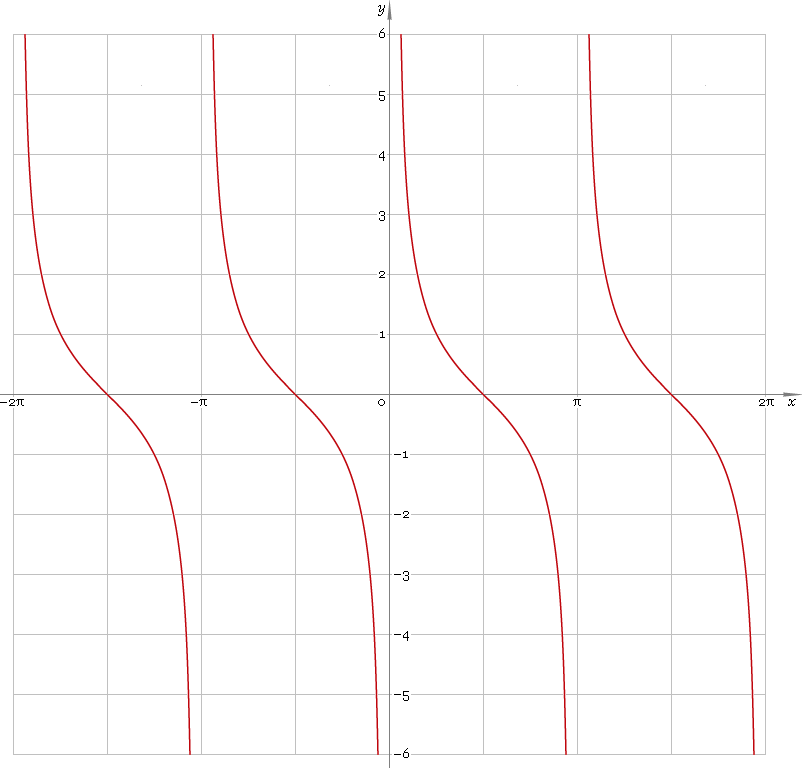 Да, Природа отлично умеет считать, но для этого она использует другие математические инструменты, не привычные для нас. Как Природа считает, я вам расскажу в другой раз. Поскольку числа придумали мы, то мы сами будем решать, сколько множеств натуральных чисел существует. Рассмотрим оба варианта, как и подобает настоящим ученым.
Да, Природа отлично умеет считать, но для этого она использует другие математические инструменты, не привычные для нас. Как Природа считает, я вам расскажу в другой раз. Поскольку числа придумали мы, то мы сами будем решать, сколько множеств натуральных чисел существует. Рассмотрим оба варианта, как и подобает настоящим ученым.
Вариант первый. «Пусть нам дано» одно-единственное множество натуральных чисел, которое безмятежно лежит на полочке. Берем с полочки это множество. Всё, других натуральных чисел на полочке не осталось и взять их негде. Мы не можем к этому множеству прибавить единицу, поскольку она у нас уже есть. А если очень хочется? Без проблем. Мы можем взять единицу из уже взятого нами множества и вернуть её на полочку. После этого мы можем взять с полочки единицу и прибавить её к тому, что у нас осталось. В результате мы снова получим бесконечное множество натуральных чисел. Записать все наши манипуляции можно так:
Я записал действия в алгебраической системе обозначений и в системе обозначений, принятой в теории множеств, с детальным перечислением элементов множества. Нижний индекс указывает на то, что множество натуральных чисел у нас одно и единственное. Получается, что множество натуральных чисел останется неизменным только в том случае, если из него вычесть единицу и прибавить эту же единицу.
Нижний индекс указывает на то, что множество натуральных чисел у нас одно и единственное. Получается, что множество натуральных чисел останется неизменным только в том случае, если из него вычесть единицу и прибавить эту же единицу.
Вариант второй. У нас на полочке лежит много разных бесконечных множеств натуральных чисел. Подчеркиваю — РАЗНЫХ, не смотря на то, что они практически не отличимы. Берем одно из этих множеств. Потом из другого множества натуральных чисел берем единицу и прибавляем к уже взятому нами множеству. Мы можем даже сложить два множества натуральных чисел. Вот что у нас получится:
Нижние индексы «один» и «два» указывают на то, что эти элементы принадлежали разным множествам. Да, если к бесконечному множеству прибавить единицу, в результате получится тоже бесконечное множество, но оно не будет таким же, как первоначальное множество. Если к одному бесконечному множеству прибавить другое бесконечное множество, в результате получится новое бесконечное множество, состоящее из элементов первых двух множеств.
Множество натуральных чисел используется для счета так же, как линейка для измерений. Теперь представьте, что к линейке вы добавили один сантиметр. Это уже будет другая линейка, не равная первоначальной.
Вы можете принимать или не принимать мои рассуждения — это ваше личное дело. Но если когда-то вы столкнетесь с математическими проблемами, задумайтесь, не идете ли вы по тропе ложных рассуждений, протоптанной поколениями математиков. Ведь занятия математикой, прежде всего, формируют у нас устойчивый стереотип мышления, а уже потом добавляют нам умственных способностей (или наоборот, лишают нас свободомыслия).
воскресенье, 4 августа 2019 г.
Дописывал постскриптум к статье о и увидел в Википедии этот замечательный текст:
Читаем: «… богатая теоретическая основа математики Вавилона не имела целостного характера и сводилась к набору разрозненных приемов, лишенных общей системы и доказательной базы.»
Вау! Какие мы умные и как хорошо можем видеть недостатки других. А слабо нам посмотреть на современную математику в таком же разрезе? Слегка перефразируя приведенный текст, лично у меня получилось следующее:
А слабо нам посмотреть на современную математику в таком же разрезе? Слегка перефразируя приведенный текст, лично у меня получилось следующее:
Богатая теоретическая основа современной математики не имеет целостного характера и сводится к набору разрозненных разделов, лишенных общей системы и доказательной базы.
За подтверждением своих слов я далеко ходить не буду — имеет язык и условные обозначения, отличные от языка и условных обозначений многих других разделов математики. Одни и те же названия в разных разделах математики могут иметь разный смысл. Наиболее очевидным ляпам современной математики я хочу посвятить целый цикл публикаций. До скорой встречи.
суббота, 3 августа 2019 г.
Как разделить множество на подмножества? Для этого необходимо ввести новую единицу измерения, присутствующую у части элементов выбранного множества. Рассмотрим пример.
Пусть у нас есть множество А , состоящее из четырех человек. Сформировано это множество по признаку «люди» Обозначим элементы этого множества через букву а , нижний индекс с цифрой будет указывать на порядковый номер каждого человека в этом множестве. Введем новую единицу измерения «половой признак» и обозначим её буквой b . Поскольку половые признаки присущи всем людям, умножаем каждый элемент множества А на половой признак b . Обратите внимание, что теперь наше множество «люди» превратилось в множество «люди с половыми признаками». После этого мы можем разделить половые признаки на мужские bm и женские bw половые признаки. Вот теперь мы можем применить математический фильтр: выбираем один из этих половых признаков, безразлично какой — мужской или женский. Если он присутствует у человека, тогда умножаем его на единицу, если такого признака нет — умножаем его на ноль. А дальше применяем обычную школьную математику. Смотрите, что получилось.
Введем новую единицу измерения «половой признак» и обозначим её буквой b . Поскольку половые признаки присущи всем людям, умножаем каждый элемент множества А на половой признак b . Обратите внимание, что теперь наше множество «люди» превратилось в множество «люди с половыми признаками». После этого мы можем разделить половые признаки на мужские bm и женские bw половые признаки. Вот теперь мы можем применить математический фильтр: выбираем один из этих половых признаков, безразлично какой — мужской или женский. Если он присутствует у человека, тогда умножаем его на единицу, если такого признака нет — умножаем его на ноль. А дальше применяем обычную школьную математику. Смотрите, что получилось.
После умножения, сокращений и перегруппировок, мы получили два подмножества: подмножество мужчин Bm и подмножество женщин Bw . Приблизительно так же рассуждают математики, когда применяют теорию множеств на практике. Но в детали они нас не посвящают, а выдают готовый результат — «множество людей состоит из подмножества мужчин и подмножества женщин». Естественно, у вас может возникнуть вопрос, насколько правильно применена математика в изложенных выше преобразованиях? Смею вас заверить, по сути преобразований сделано всё правильно, достаточно знать математическое обоснование арифметики, булевой алгебры и других разделов математики. Что это такое? Как-нибудь в другой раз я вам об этом расскажу.
Естественно, у вас может возникнуть вопрос, насколько правильно применена математика в изложенных выше преобразованиях? Смею вас заверить, по сути преобразований сделано всё правильно, достаточно знать математическое обоснование арифметики, булевой алгебры и других разделов математики. Что это такое? Как-нибудь в другой раз я вам об этом расскажу.
Что касается надмножеств, то объединить два множества в одно надмножество можно, подобрав единицу измерения, присутствующую у элементов этих двух множеств.
Как видите, единицы измерения и обычная математика превращают теорию множеств в пережиток прошлого. Признаком того, что с теорией множеств не всё в порядке, является то, что для теории множеств математики придумали собственный язык и собственные обозначения. Математики поступили так, как когда-то поступали шаманы. Только шаманы знают, как «правильно» применять их «знания». Этим «знаниям» они обучают нас.
В заключение, я хочу показать вам, как математики манипулируют с .
понедельник, 7 января 2019 г.

В пятом веке до нашей эры древнегреческий философ Зенон Элейский сформулировал свои знаменитые апории, самой известной из которых является апория «Ахиллес и черепаха». Вот как она звучит:
Допустим, Ахиллес бежит в десять раз быстрее, чем черепаха, и находится позади неё на расстоянии в тысячу шагов. За то время, за которое Ахиллес пробежит это расстояние, черепаха в ту же сторону проползёт сто шагов. Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху.
Это рассуждение стало логическим шоком для всех последующих поколений. Аристотель, Диоген, Кант, Гегель, Гильберт… Все они так или иначе рассматривали апории Зенона. Шок оказался настолько сильным, что «… дискуссии продолжаются и в настоящее время, прийти к общему мнению о сущности парадоксов научному сообществу пока не удалось… к исследованию вопроса привлекались математический анализ, теория множеств, новые физические и философские подходы; ни один из них не стал общепризнанным решением вопроса. .. » [Википедия, » Апории Зенона «]. Все понимают, что их дурят, но никто не понимает, в чем заключается обман.
.. » [Википедия, » Апории Зенона «]. Все понимают, что их дурят, но никто не понимает, в чем заключается обман.
С точки зрения математики, Зенон в своей апории наглядно продемонстрировал переход от величины к . Этот переход подразумевает применение вместо постоянных. Насколько я понимаю, математический аппарат применения переменных единиц измерения либо ещё не разработан, либо его не применяли к апории Зенона. Применение же нашей обычной логики приводит нас в ловушку. Мы, по инерции мышления, применяем постоянные единицы измерения времени к обратной величине. С физической точки зрения это выглядит, как замедление времени до его полной остановки в момент, когда Ахиллес поравняется с черепахой. Если время останавливается, Ахиллес уже не может перегнать черепаху.
Если перевернуть привычную нам логику, всё становится на свои места. Ахиллес бежит с постоянной скоростью. Каждый последующий отрезок его пути в десять раз короче предыдущего. Соответственно, и время, затрачиваемое на его преодоление, в десять раз меньше предыдущего.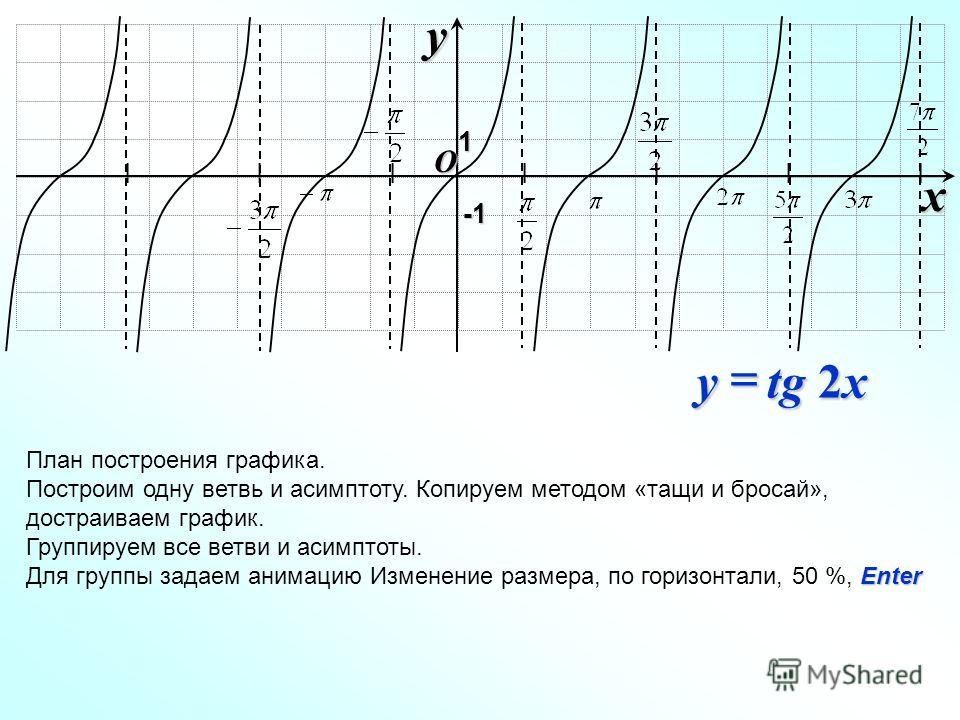 Если применять понятие «бесконечность» в этой ситуации, то правильно будет говорить «Ахиллес бесконечно быстро догонит черепаху».
Если применять понятие «бесконечность» в этой ситуации, то правильно будет говорить «Ахиллес бесконечно быстро догонит черепаху».
Как избежать этой логической ловушки? Оставаться в постоянных единицах измерения времени и не переходить к обратным величинам. На языке Зенона это выглядит так:
За то время, за которое Ахиллес пробежит тысячу шагов, черепаха в ту же сторону проползёт сто шагов. За следующий интервал времени, равный первому, Ахиллес пробежит ещё тысячу шагов, а черепаха проползет сто шагов. Теперь Ахиллес на восемьсот шагов опережает черепаху.
Этот подход адекватно описывает реальность без всяких логических парадоксов. Но это не полное решение проблемы. На Зеноновскую апорию «Ахиллес и черепаха» очень похоже утверждение Эйнштейна о непреодолимости скорости света. Эту проблему нам ещё предстоит изучить, переосмыслить и решить. И решение нужно искать не в бесконечно больших числах, а в единицах измерения.
Другая интересная апория Зенона повествует о летящей стреле:
Летящая стрела неподвижна, так как в каждый момент времени она покоится, а поскольку она покоится в каждый момент времени, то она покоится всегда.
В этой апории логический парадокс преодолевается очень просто — достаточно уточнить, что в каждый момент времени летящая стрела покоится в разных точках пространства, что, собственно, и является движением. Здесь нужно отметить другой момент. По одной фотографии автомобиля на дороге невозможно определить ни факт его движения, ни расстояние до него. Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но по ним нельзя определить расстояние. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.
среда, 4 июля 2018 г.
Я вам уже рассказывал, что , при помощи которой шаманы пытаются сортировать » » реальности. Как же они это делают? Как фактически происходит формирование множества?
Давайте внимательно разберемся с определением множества: «совокупность различных элементов, мыслимая как единое целое». А теперь почувствуйте разницу между двумя фразами: «мыслимое как единое целое» и «мыслимое как целое». Первая фраза — это конечный результат, множество. Вторая фраза — это предварительная подготовка к формированию множества. На этом этапе реальность разбивается на отдельные элементы («целое») из которых потом будет сформировано множество («единое целое»). При этом фактор, позволяющий объединить «целое» в «единое целое», внимательно отслеживается, иначе у шаманов ничего не получится. Ведь шаманы заранее знают, какое именно множество они хотят нам продемонстрировать.
Покажу процесс на примере. Отбираем «красное твердое в пупырышку» — это наше «целое». При этом мы видим, что эти штучки есть с бантиком, а есть без бантика. После этого мы отбираем часть «целого» и формируем множество «с бантиком». Вот так шаманы добывают себе корм, привязывая свою теорию множеств к реальности.
После этого мы отбираем часть «целого» и формируем множество «с бантиком». Вот так шаманы добывают себе корм, привязывая свою теорию множеств к реальности.
А теперь сделаем маленькую пакость. Возьмем «твердое в пупырышку с бантиком» и объединим эти «целые» по цветовому признаку, отобрав красные элементы. Мы получили множество «красное». Теперь вопрос на засыпку: полученные множества «с бантиком» и «красное» — это одно и то же множество или два разных множества? Ответ знают только шаманы. Точнее, сами они ничего не знают, но как скажут, так и будет.
Этот простой пример показывает, что теория множеств совершенно бесполезна, когда речь заходит о реальности. В чем секрет? Мы сформировали множество «красное твердое в пупырышку с бантиком». Формирование происходило по четырем разным единицам измерения: цвет (красное), прочность (твердое), шероховатость (в пупырышку), украшения (с бантиком). Только совокупность единиц измерения позволяет адекватно описывать реальные объекты на языке математики . Вот как это выглядит.
Вот как это выглядит.
Буква «а» с разными индексами обозначает разные единицы измерения. В скобках выделены единицы измерения, по которым выделяется «целое» на предварительном этапе. За скобки вынесена единица измерения, по которой формируется множество. Последняя строчка показывает окончательный результат — элемент множества. Как видите, если применять единицы измерения для формирования множества, тогда результат не зависит от порядка наших действий. А это уже математика, а не пляски шаманов с бубнами. Шаманы могут «интуитивно» придти к такому же результату, аргументируя его «очевидностью», ведь единицы измерения не входят в их «научный» арсенал.
При помощи единиц измерения очень легко разбить одно или объединить несколько множеств в одно надмножество. Давайте более внимательно рассмотрим алгебру этого процесса.
суббота, 30 июня 2018 г.
Если математики не могут свести понятие к другим понятиям, значит они ничего не понимают в математике. Отвечаю на : чем элементы одного множества отличаются от элементов другого множества? Ответ очень простой: числами и единицами измерения.
Это сегодня всё, что мы не возьмем, принадлежит какому-либо множеству (как нас уверяют математики). Кстати, вы в зеркале видели у себя на лбу список тех множеств, к которым принадлежите именно вы? И я такого списка не видел. Скажу больше — ни одна вещь в реальности не имеет бирочки со списком множеств, к которым эта вещь принадлежит. Множества — это всё выдумки шаманов. Как они это делают? Давайте заглянем немного в глубь истории и посмотрим, как выглядели элементы множества до того, как математики-шаманы растащили их по своим множествам.
Давним-давно, когда о математике ещё никто и не слышал, а кольца были только у деревьев и у Сатурна, огромные стада диких элементов множеств бродили по физическим полям (ведь математических полей шаманы ещё не придумали). Выглядели они приблизительно так.
Да, не удивляйтесь, с точки зрения математики все элементы множеств больше всего похожи на морских ежей — из одной точки, как иголки, во все стороны торчат единицы измерений. Для тех, кто , напоминаю, что любую единицу измерения геометрически можно представить как отрезок произвольной длины, а число — как точку. Геометрически любую величину можно представить как пучок отрезков, торчащих в разные стороны из одной точки. Эта точка — точка ноль. Рисовать это произведение геометрического искусства я не буду (нет вдохновения), но вы легко это можете представить.
Геометрически любую величину можно представить как пучок отрезков, торчащих в разные стороны из одной точки. Эта точка — точка ноль. Рисовать это произведение геометрического искусства я не буду (нет вдохновения), но вы легко это можете представить.
Какие же единицы измерения образуют элемент множества? Всякие, описывающие данный элемент с разных точек зрения. Это и древние единицы измерения, которыми пользовались наши предки и о которых все давно забыли. Это и современные единицы измерения, которыми мы пользуемся сейчас. Это и неизвестные нам единицы измерения, которые придумают наши потомки и которыми будут пользоваться они для описания реальности.
С геометрией мы разобрались — предлагаемая модель элементов множества имеет четкое геометрическое представление. А как с физикой? Единицы измерения — это и есть прямая связь математики с физикой. Если шаманы не признают единицы измерения как полноправный элемент математических теорий — это их проблемы. Настоящую науку математику без единиц измерения лично я уже не представляю.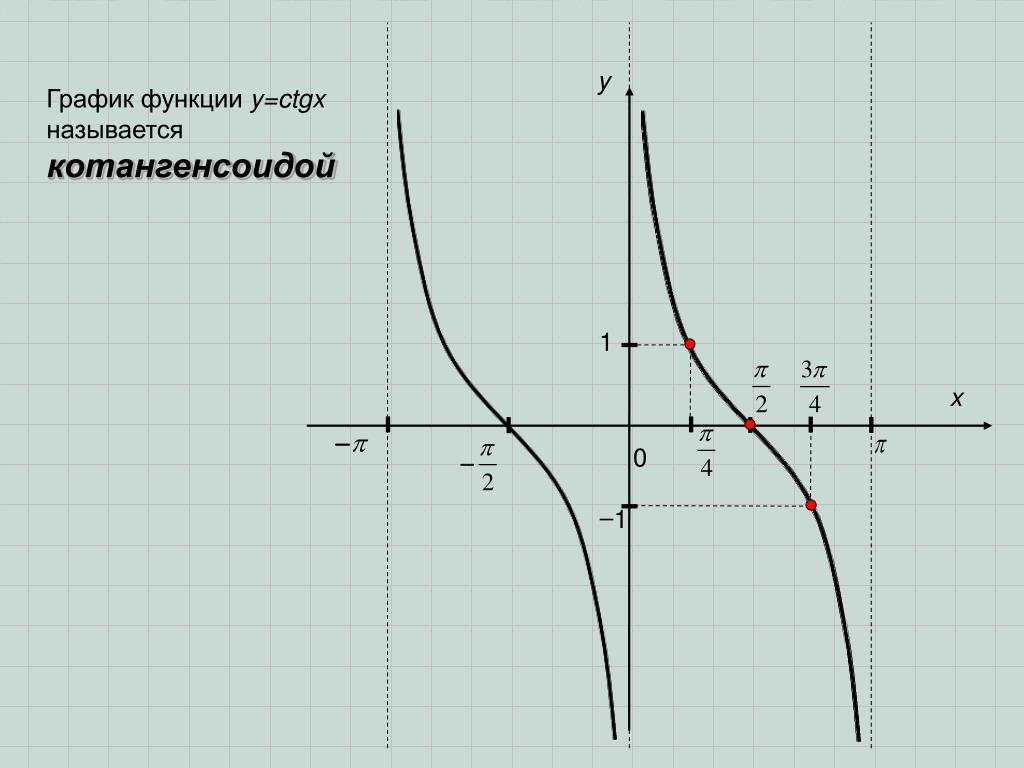 Вот почему в самом начале рассказа о теории множеств я говорил о ней как о каменном веке.
Вот почему в самом начале рассказа о теории множеств я говорил о ней как о каменном веке.
Но перейдем к самому интересному — к алгебре элементов множеств. Алгебраически любой элемент множества представляет из себя произведение (результат умножения) разных величин.Выглядит это так.
Я умышленно не применял условные обозначения, принятые в теории множеств, поскольку мы рассматриваем элемент множества в естественной среде обитания до возникновения теории множеств. Каждая пара буковок в скобках обозначает отдельную величину, состоящую из числа, обозначенного буквой «n » и единицы измерения, обозначенной буквой «a «. Индексы возле буковок указывают на то, что числа и единицы измерения — разные. Один элемент множества может состоять из бесконечного числа величин (на сколько у нас и наших потомков хватит фантазии). Каждая скобка геометрически изображается отдельным отрезком. В примере с морским ежом одна скобка — это одна иголка.
Как шаманы формируют множества из разных элементов? Фактически, по единицам измерения или по числам. Ничего не понимая в математике, они берут разных морских ежей и внимательно их рассматривают в поисках той единственной иголки, по которой они формируют множество. Если такая иголка есть, значит этот элемент принадлежит множеству, если такой иголки нет — это элемент не из этого множества. Нам же шаманы рассказывают басни о мыслительных процессах и едином целом.
Ничего не понимая в математике, они берут разных морских ежей и внимательно их рассматривают в поисках той единственной иголки, по которой они формируют множество. Если такая иголка есть, значит этот элемент принадлежит множеству, если такой иголки нет — это элемент не из этого множества. Нам же шаманы рассказывают басни о мыслительных процессах и едином целом.
Как вы уже догадались, один и тот же элемент может принадлежать к самым разным множествам. Дальше я вам покажу, как формируются множества, подмножества и прочая шаманская галиматья. Как видите, «во множестве не может быть двух идентичных элементов», но если идентичные элементы во множестве есть, такое множество называется «мультимножество». Подобную логику абсурда разумным существам не понять никогда. Это уровень говорящих попугаев и дрессированных обезьян, у которых разум отсутствует от слова «совсем». Математики выступают в роли обычных дрессировщиков, проповедуя нам свои абсурдные идеи.
Когда-то инженеры, построившие мост, во время испытаний моста находились в лодке под мостом.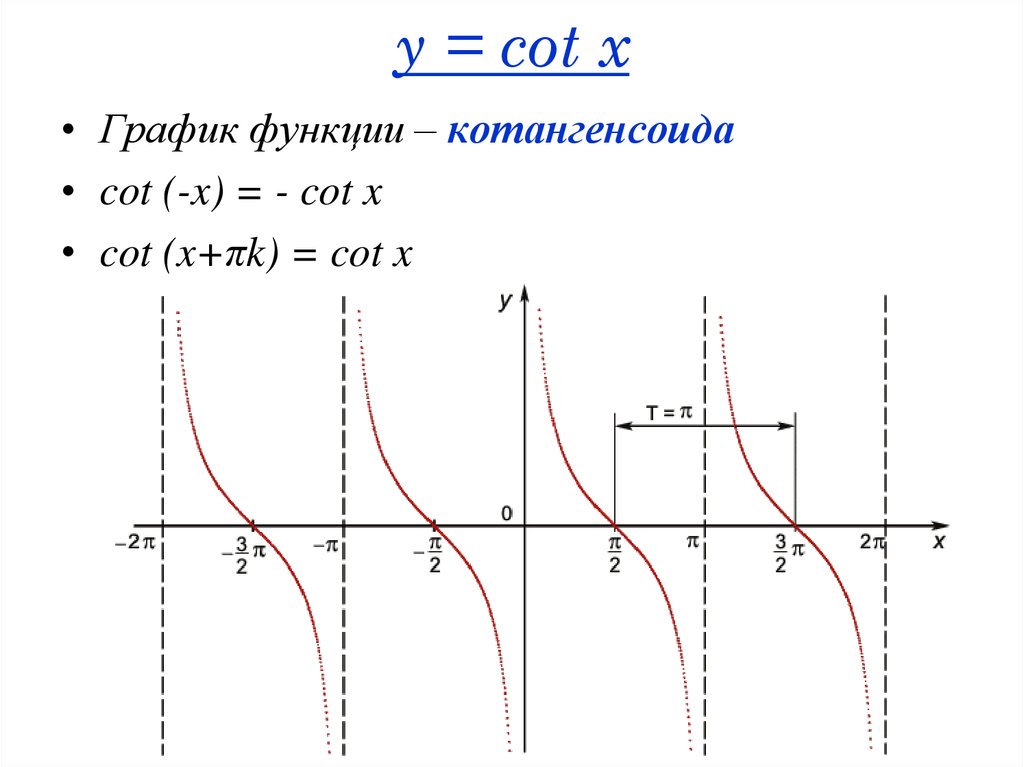 Если мост обрушивался, бездарный инженер погибал под обломками своего творения. Если мост выдерживал нагрузку, талантливый инженер строил другие мосты.
Если мост обрушивался, бездарный инженер погибал под обломками своего творения. Если мост выдерживал нагрузку, талантливый инженер строил другие мосты.
Как бы математики не прятались за фразой «чур, я в домике», точнее «математика изучает абстрактные понятия», есть одна пуповина, которая неразрывно связывает их с реальностью. Этой пуповиной являются деньги. Применим математическую теорию множеств к самим математикам.
Мы очень хорошо учили математику и сейчас сидим в кассе, выдаем зарплату. Вот приходит к нам математик за своими деньгами. Отсчитываем ему всю сумму и раскладываем у себя на столе на разные стопки, в которые складываем купюры одного достоинства. Затем берем с каждой стопки по одной купюре и вручаем математику его «математическое множество зарплаты». Поясняем математику, что остальные купюры он получит только тогда, когда докажет, что множество без одинаковых элементов не равно множеству с одинаковыми элементами. Вот здесь начнется самое интересное.
В первую очередь, сработает логика депутатов: «к другим это применять можно, ко мне — низьзя!». Дальше начнутся уверения нас в том, что на купюрах одинакового достоинства имеются разные номера купюр, а значит их нельзя считать одинаковыми элементами. Хорошо, отсчитываем зарплату монетами — на монетах нет номеров. Здесь математик начнет судорожно вспоминать физику: на разных монетах имеется разное количество грязи, кристаллическая структура и расположение атомов у каждой монеты уникально…
Дальше начнутся уверения нас в том, что на купюрах одинакового достоинства имеются разные номера купюр, а значит их нельзя считать одинаковыми элементами. Хорошо, отсчитываем зарплату монетами — на монетах нет номеров. Здесь математик начнет судорожно вспоминать физику: на разных монетах имеется разное количество грязи, кристаллическая структура и расположение атомов у каждой монеты уникально…
А теперь у меня самый интересный вопрос: где проходит та грань, за которой элементы мультимножества превращаются в элементы множества и наоборот? Такой грани не существует — всё решают шаманы, наука здесь и близко не валялась.
Вот смотрите. Мы отбираем футбольные стадионы с одинаковой площадью поля. Площадь полей одинакова — значит у нас получилось мультимножество. Но если рассматривать названия этих же стадионов — у нас получается множество, ведь названия разные. Как видите, один и тот же набор элементов одновременно является и множеством, и мультимножеством. Как правильно? А вот здесь математик-шаман-шуллер достает из рукава козырный туз и начинает нам рассказывать либо о множестве, либо о мультимножестве. В любом случае он убедит нас в своей правоте.
В любом случае он убедит нас в своей правоте.
Чтобы понять, как современные шаманы оперируют теорией множеств, привязывая её к реальности, достаточно ответить на один вопрос: чем элементы одного множества отличаются от элементов другого множества? Я вам покажу, без всяких «мыслимое как не единое целое» или «не мыслимое как единое целое».
Он характеризует максимальный угол, при котором повернется колесо автомобиля при полностью вывернутом руле. И чем меньше этот угол, тем больше точность и плавность управления. Ведь для поворота даже на небольшой угол потребуется лишь малое движение рулем.Но не стоит забывать, что чем меньше максимальный угол поворота, тем меньше радиус поворота автомобиля. Т.е. развернутся в ограниченном пространстве будет очень тяжело. Вот и приходится производителям искать некую «золотую середину», маневрируя между большим радиусом поворота и точность управления.
Изменение значений углов установки колес и их регулировка
Карта Пири Рейса была сопоставлена с современной проекцией карты. Таким образом, он пришел к выводу, что таинственная карта захватывает мир, как это видно со спутника, парящего высоко над Каиром. Другими словами — над Великой пирамидой. Удивительно, что египтологи постоянно защищают эти пространства, хотя недавно был проведен обзор одного недавно открытого коридора, который еще не принес каких-либо прорывов.
Таким образом, он пришел к выводу, что таинственная карта захватывает мир, как это видно со спутника, парящего высоко над Каиром. Другими словами — над Великой пирамидой. Удивительно, что египтологи постоянно защищают эти пространства, хотя недавно был проведен обзор одного недавно открытого коридора, который еще не принес каких-либо прорывов.
Стоит также отметить, что в пирамиде обнаружены необычные психотронные эффекты, которые, среди прочего, могут повлиять на здоровье человека. Речь идет о пространственной психотронике, создающей как энергетические, так и геомагнитные «аномальные зоны», которые далее исследуются.
Плечо обката — кратчайшее расстояние между серединой покрышки и осью поворота колеса. Если ось вращения колеса и середина колеса совпадает, то значение считается нулевым. При отрицательном значении — ось вращения будет смещаться наружу колеса, а при положительном значении — внутрь.При повороте колеса, покрышка деформируется под действием боковых сил.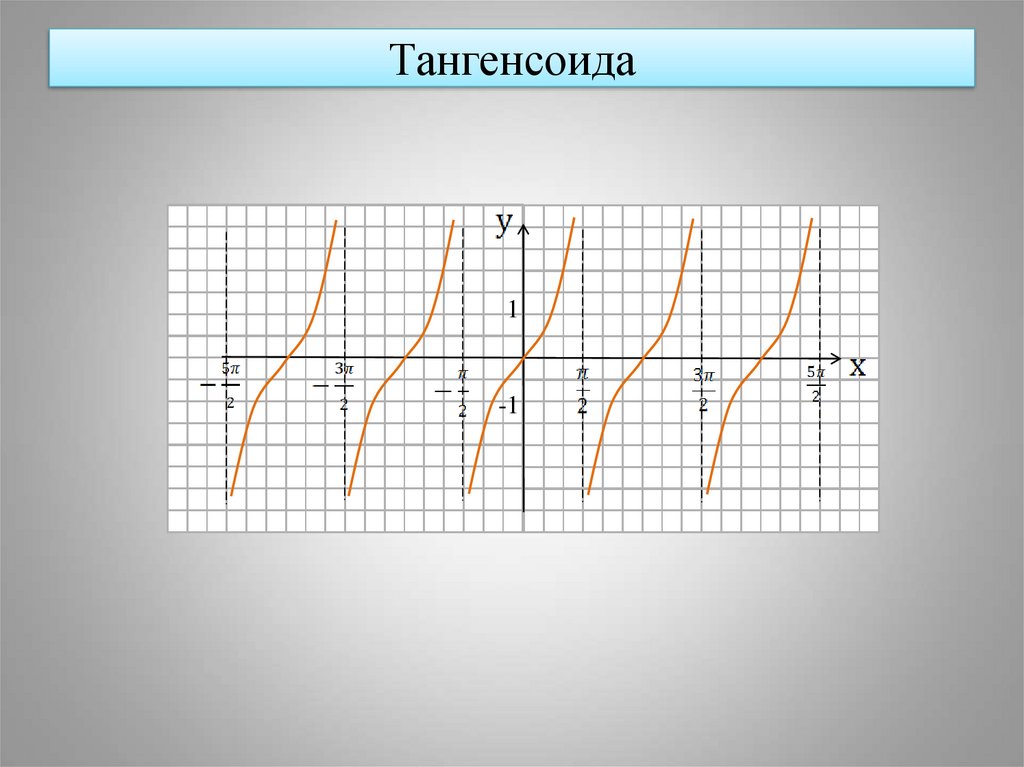 И чтобы сохранить максимальное пятно контакта с дорогой, колесо автомобиля тоже наклоняется в сторону поворота. Но везде нужно знать меру, ведь при очень большом кастере, колесо автомобиля будет сильно наклоняться, и утратит тогда сцепление с дорогой.
И чтобы сохранить максимальное пятно контакта с дорогой, колесо автомобиля тоже наклоняется в сторону поворота. Но везде нужно знать меру, ведь при очень большом кастере, колесо автомобиля будет сильно наклоняться, и утратит тогда сцепление с дорогой.
Изначально, поперечный угол наклона оси поворота был применен инженерами для устранения недостатков подвески автомобиля. Он избавлял от таких «недугов» автомобиля как положительный развал колес и положительное плечо обката.
Во время археологических раскопок также найдены странные предложения погребальных в виде птиц с распростертыми крылами.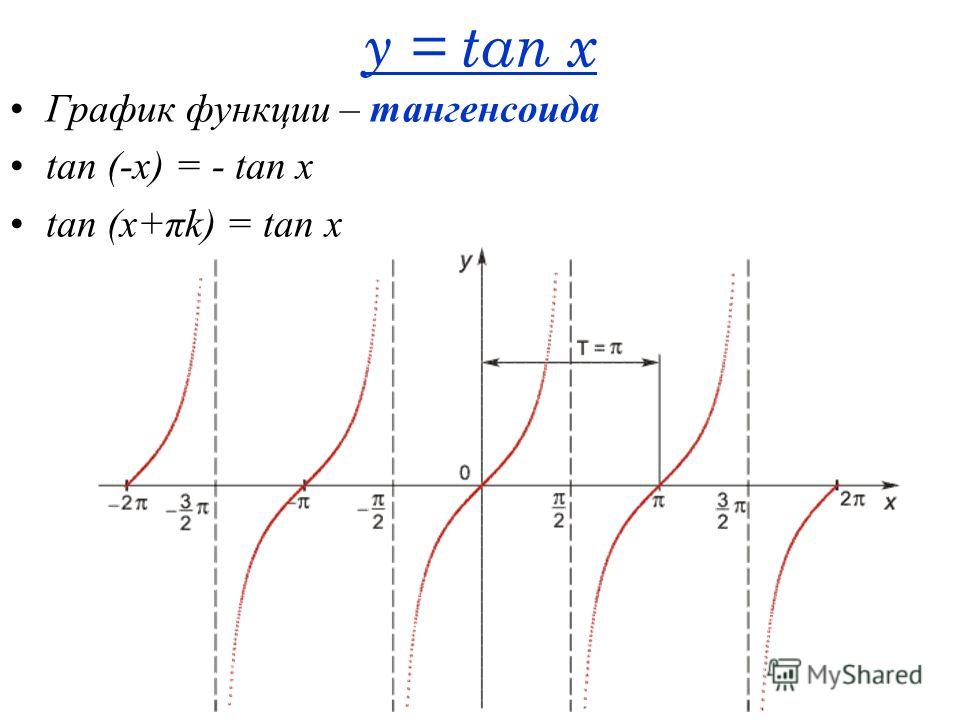 Позже аэродинамические исследования эти субъекты показали, что наиболее вероятно, являются древними моделями планеров. Одна из них была обнаружена надпись «подарок Амона.» Бог Амон в Египте поклонялись как бог ветер так ассоциируется с полетом очевидна.
Позже аэродинамические исследования эти субъекты показали, что наиболее вероятно, являются древними моделями планеров. Одна из них была обнаружена надпись «подарок Амона.» Бог Амон в Египте поклонялись как бог ветер так ассоциируется с полетом очевидна.
Но как члены этой древней цивилизации пришли к этому знанию без предварительной стадии разработки? Ответ в этом случае только. Это знание пришло от правительств тех времен, которые египтяне называли свои бог. Вполне возможно, для членов технологически развитой цивилизации, которая имеет более чем 000 лет назад, исчезли без следа.
Во многих автомобилях применяется подвеска типа «Мак-Ферсон» . Она дает возможность получить отрицательное или нулевое плечо обката. Ведь ось поворота колеса состоит из опоры одного единственного рычага, которой легко можно поместить внутрь колеса. Но и эта подвеска не совершенна, ведь из-за его конструкции сделать угол наклона оси поворота маленьким практически невозможно. В повороте он наклоняет внешнее колесо под невыгодным углом (как у положительного развала), а внутреннее колесо одновременно наклоняется в противоположную сторону.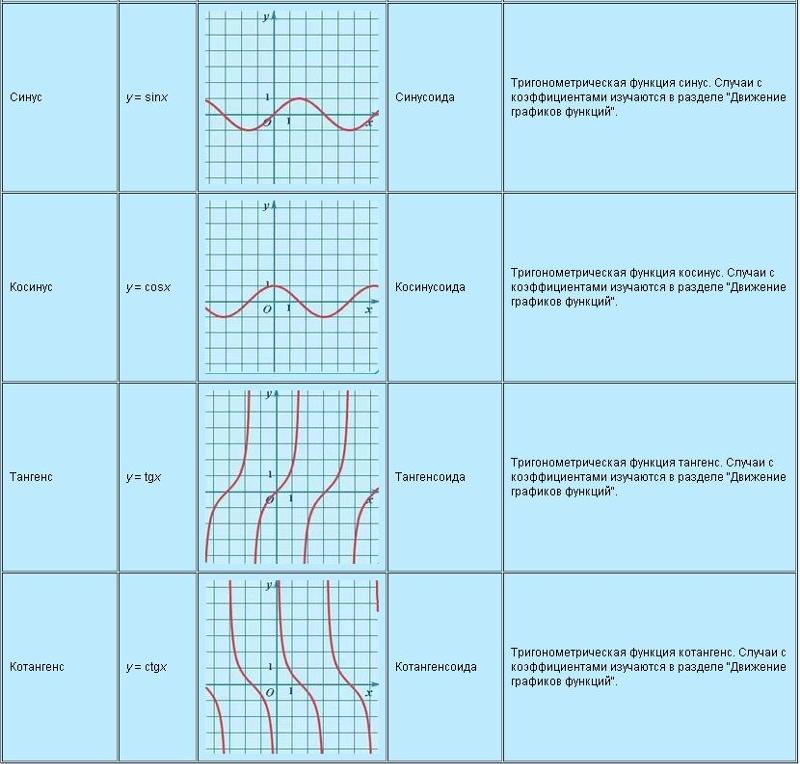
Но такие объекты все еще не хватает. Они распадаются, они могут быть уничтожены, но он также может быть хорошо спрятаны в храмах, пирамидах и других знаковых зданий, которые могут лежать неподвижно, должным образом обеспеченных против «охотников за сокровищами».
Великая пирамида в размер и дизайн точности никогда не было равных. Пирамида весит примерно шесть миллионов тонн. В своей позиции, как Эйфелева башня Великая пирамида была самым высоким зданием в мире. Для его строительства было использовано более двух миллионов камней. Ни один камень не весит меньше тонны.
В результате пятно контакта у внешнего колеса сильно уменьшается. А так как на внешнее колесо в повороте приходится основная нагрузка, вся ось сильно теряет в сцеплении. Это, конечно, можно частично компенсировать кастером и развалом. Тогда сцепление внешнего колеса будет хорошим, а у внутреннего — практически исчезнет.
Схождение колес автомобиля
Существует два вида схождения автомобиля: положительное и отрицательное.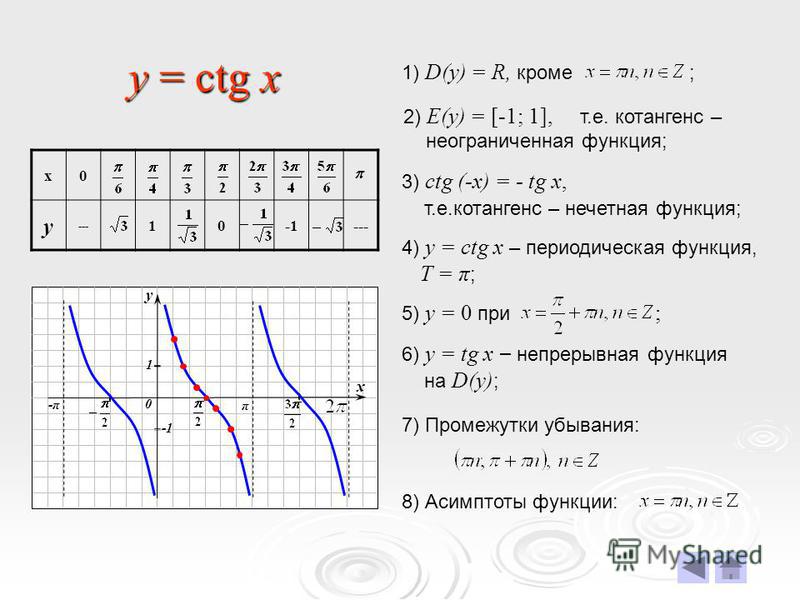 Определить тип схождения очень просто: нужно провести две прямые линии вдоль колес автомобиля. Если эти линии пересекутся спереди автомобиля, то схождение положительное, а если сзади — отрицательное. Если будет положительное схождение передних колес, то автомобиль будет легче заходить в поворот, а также приобретет дополнительную поворачиваемость.
Определить тип схождения очень просто: нужно провести две прямые линии вдоль колес автомобиля. Если эти линии пересекутся спереди автомобиля, то схождение положительное, а если сзади — отрицательное. Если будет положительное схождение передних колес, то автомобиль будет легче заходить в поворот, а также приобретет дополнительную поворачиваемость.На задней оси при положительном схождении колес, автомобиль при прямолинейном движении будет более устойчивым, а если будет отрицательное схождение — то автомобиль будет вести себя неадекватно, и рыскать из стороны в сторону.
И некоторые из более чем семидесяти тонн. Внутри камеры соединены коридорами. Сегодня, грубая каменная пирамида, но как только он был обработан до зеркального блеска кладки. Считается, что пик Великой пирамиды был украшен чистым золотом. Солнечные лучи слепили сотни километров. В течение многих столетий, эксперты предположили, о цели пирамид. Традиционная теория утверждает, что пирамиды были символическим воротами в загробный мир. Другие считают, что пирамида была астрономической обсерватории. Кто-то говорит, что помощь в географическом измерении.
Другие считают, что пирамида была астрономической обсерватории. Кто-то говорит, что помощь в географическом измерении.
Но следует помнить, что чрезмерное отклонение схождения автомобиля от нулевого значения увеличит сопротивление качению при прямолинейном движении, в поворотах это будет заметно в меньшей степени.
Развал колес
Развал колес, как и схождение, может быть как отрицательным, так и положительным.Если смотреть спереди автомобиля, и колеса будут наклоняться вовнутрь, то это отрицательный развал, а если будут отклоняться наружу автомобиля — то это уже положительный развал. Развал колеса необходим для сохранения сцепления колеса с дорожным полотном.
Одна причудливая теория утверждает, что Великая пирамида была на зернохранилищах. Тем не менее, эксперты сегодня в целом согласны, что пирамиды были гораздо больше, чем просто гигантская могила. Ученые утверждают, что массивная технология пирамида не может быть доступна для людей в этот момент истории человечества, когда были построены эти здания. Например, высота пирамиды соответствует расстоянию от Земли до Солнца. Пирамида была точно ориентирована на четыре мира с точностью, которая никогда не достигалась.
Например, высота пирамиды соответствует расстоянию от Земли до Солнца. Пирамида была точно ориентирована на четыре мира с точностью, которая никогда не достигалась.
И что удивительно, Великая Пирамида лежит в точном центре земли. Тот, кто построил Великую пирамиду, мог точно определить широту и долготу. Это удивительно, потому что технология определения долготы была открыта в наше время в шестнадцатом веке. Пирамиды были построены в точном центре Земли. Также высоту пирамиды — видно с огромной высоты, можно увидеть с Луны. Более того, форма пирамиды является одной из лучших для отражения радаров. Эти причины заставляют некоторых исследователей полагать, что египетские пирамиды были построены за пределами их других целей и для навигации потенциальными иностранными исследователями.
Изменение угла развала колес сказывается на поведении автомобиля на прямой, ведь колеса стоят не перпендикулярно дороге, а значит имеют не максимальное сцепление. Но это сказывается только на заднеприводных автомобилях при трогании с места с пробуксовкой.
Для тех, кто хочет понять, что означают Углы Установки Колес (Развал/Схождение) и досконально разобраться в вопросе, в этой статье есть ответы на все вопросы.
Пирамида Хеопса расположена чуть более чем в восьми километрах к западу от Каира. Он построен на искусственно созданной квартире площадью 1, 6 квадратных километра. Его основание простирается до 900 квадратных метров и почти миллиметровое в горизонтальном положении. Два и три четверти миллиона каменных блоков были использованы для строительства, причем самый тяжелый вес весом до 70 тонн. Они вписываются так, что этот факт является загадкой. Тем не менее, техническая сторона создания пирамиды остается загадкой, так как это будет серьезной проблемой для современных передовых технологий.
Экскурс в историю показывает, что мудреная установка колес применялась на различных средствах передвижения задолго до появления автомобиля. Вот несколько более или менее хорошо известных примеров.
Не секрет, что колеса некоторых карет и прочих колясок на конной тяге, предназначенных для «динамичной» езды, устанавливали с большим, хорошо заметным глазу положительным развалом . Делалось это для того, чтобы грязь, летевшая с колес, не попадала в экипаж и на важных седоков, а разбрасывалась по сторонам.У утилитарных повозок для неспешного передвижения все было с точностью до наоборот. Так, дореволюционные руководства о том, как построить хорошую телегу, рекомендовали ставить коле- са с отрицательным развалом . В этом случае при потере нагеля, стопорящего колесо, оно не сразу соскакивало с оси. У возницы было время, чтобы заметить повреждение «ходовой», чреватой особенно большими неприятностями при наличии в телеге нескольких десятков пудов муки и отсутствии домкрата. В конструкции орудийных лафетов (опять-таки наоборот) иногда применялся положительный развал колес. Понятно, что не с целью уберечь пушку от грязи. Так прислуге было удобно накатывать орудие за колеса руками сбоку, не опасаясь отдавить ноги. А вот у арбы ее огромные колеса, которые помогали запросто перебираться через арыки, были наклонены в другую сторону — к повозке. Достигавшееся при этом увеличение колеи способствовало повышению устойчивости среднеазиатского «мобиля», отличавшегося высоким расположением центра тяжести. Какое отношение эти исторические факты имеют к установке колес современных автомобилей ? Да, в общем, ни какого. Тем не менее, они позволяют сделать полезный вывод. Видно, что установка колес (в частности, их развал) не подчинена какой-либо единой закономерности.
А вот у арбы ее огромные колеса, которые помогали запросто перебираться через арыки, были наклонены в другую сторону — к повозке. Достигавшееся при этом увеличение колеи способствовало повышению устойчивости среднеазиатского «мобиля», отличавшегося высоким расположением центра тяжести. Какое отношение эти исторические факты имеют к установке колес современных автомобилей ? Да, в общем, ни какого. Тем не менее, они позволяют сделать полезный вывод. Видно, что установка колес (в частности, их развал) не подчинена какой-либо единой закономерности.
Поэтому нет никаких гипотез о том, что магические силы использовались при построении пирамиды — магические формулы, написанные на папирусе, позволяли перемещать тяжелые куски камня и с удивительной точностью ставить их друг на друга. Эдгар Кейси сказал, что эти пирамиды были построены десять тысяч лет назад, а другие полагают, что пирамиды построены жителями Атлантиды, которые до катаклизма, уничтожившего их континент, в основном искали убежище в Египте.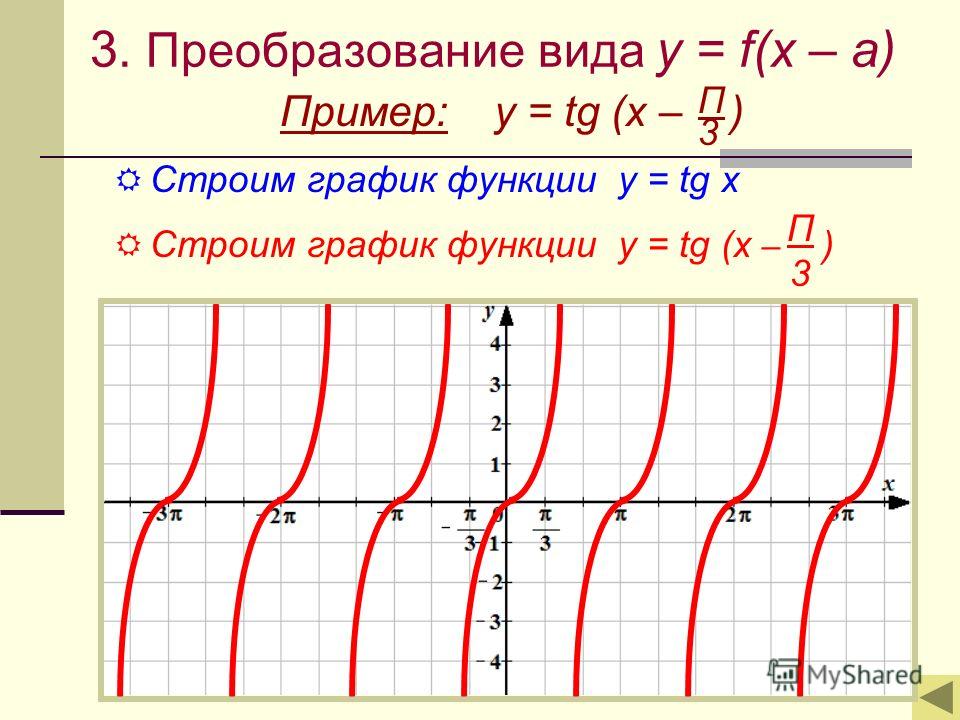 Он создает научные центры, они также создали пирамидальное убежище, где можно было бы скрыть большие тайны.
Он создает научные центры, они также создали пирамидальное убежище, где можно было бы скрыть большие тайны.
При выборе этого параметра «производитель» в каждом конкретном случае руководствовался разными соображениями, которые он считал приоритетными. Итак, к чему стремятся конструкторы автомобильных подвесок при выборе УУК? Конечно, к идеалу. Идеалом для автомобиля, который движется прямолинейно, считается такое положение колес, когда плоскости их вращения (плоскости качения) перпендикулярны поверхности дороги, параллельны друг другу, оси симметрии кузова и совпадают с траекторией движения. В этом случае потери мощности на трение и износ протектора шин минимальны, а сцепление колес с дорогой, наоборот, максимально. Естественно, возникает вопрос: что же заставляет преднамеренно отклоняться от идеала? Забегая вперед, можно привести несколько соображений. Во-первых, мы судим об углах установки колес на основании статической картины, когда автомобиль неподвижен. Кто сказал, что в движении, при ускорении, торможении и маневрировании автомобиля она не меняется? Во-вторых, сокращение потерь и продление срока службы шин не всегда является приоритетной задачей. Прежде чем рассказывать о том, какие факторы принимают в расчет разработчики подвесок, условимся, что из большого числа параметров, описывающих геометрию подвески автомобиля, мы ограничимся лишь теми, что входят в группу первичных (primary) или основных. Они называются так потому, что определяют настройку и свойства подвески, всегда контролируются при ее диагностике и регулируются, если таковая возможность предусмотрена. Это хорошо известные схождение, развал и углы наклона оси поворота управляемых колес. При рассмотрении этих важнейших параметров нам придется вспомнить и о других характеристиках подвески.
Прежде чем рассказывать о том, какие факторы принимают в расчет разработчики подвесок, условимся, что из большого числа параметров, описывающих геометрию подвески автомобиля, мы ограничимся лишь теми, что входят в группу первичных (primary) или основных. Они называются так потому, что определяют настройку и свойства подвески, всегда контролируются при ее диагностике и регулируются, если таковая возможность предусмотрена. Это хорошо известные схождение, развал и углы наклона оси поворота управляемых колес. При рассмотрении этих важнейших параметров нам придется вспомнить и о других характеристиках подвески.
Пирамида состоит из 203 слоев каменных блоков весом от 2, 5 до 15 тонн. Некоторые блоки на дне пирамиды у основания весит до 50 тонн. Первоначально вся пирамида была покрыта мелкой белой и полированной известняковой оболочкой, но камень использовался для строительства, Особенно после частых землетрясений в этом районе.
Вес пирамиды пропорционален весу Земли 1: 10. Пирамида — это максимум 280 египетских локтей, а площадь основания — 440 египетских локтей. Если базовая схема разделена двойной высотой пирамиды, мы получим номер Людольфа — 3. Отклонение от фигуры Людольфа составляет всего 0, 05%. Основание основания равно окружности круга с радиусом, равным высоте пирамиды.
Если базовая схема разделена двойной высотой пирамиды, мы получим номер Людольфа — 3. Отклонение от фигуры Людольфа составляет всего 0, 05%. Основание основания равно окружности круга с радиусом, равным высоте пирамиды.
Схождение (TOE) характеризует ориентацию колес относительно продольной оси автомобиля. Положение каждого колеса может быть определено отдельно от других, и тогда говорят об индивидуальном схождении. Оно представляет собой угол между плоскостью вращения колеса и осью автомобиля при его наблюдении сверху. Суммарное схождение (или просто схождение) колес одной оси. как и следует из названия, представляет собой сумму индивидуальных углов. Если плоскости вращения колес пересекаются впереди автомобиля, схождение положительное (toe-in), если сзади — отрицательное (toe-out). В последнем случае можно говорить о расхождении колес.
В регулировочных данных иногда схождение приводится не только в виде угловой, но и линейной величины. Это связано с тем. что о схождении колес также судят по разности расстояний между закраинами ободьев, замеренных на уровне их центров сзади и спереди оси.
Какой бы ни была истина, может быть, археологи, конечно, признать мастерство древних строителей, к примеру. Флиндерс Питри пришел к выводу, что ошибки в измерении были настолько малы, что он обложен палец. Стены, соединяющие коридоры, падающие 107 м в центр пирамиды, показали отклонение всего 0, 5 см от идеальной точности. Мы можем объяснить тайну пирамиды фараона педантизм архитекторов и строителей или неизвестной египетской магии или простой необходимости соблюдения размеров настолько близко, насколько это возможно, чтобы достичь максимальной выгоды пирамиды?
В различных источниках, в том числе и серьезной технической литературе, часто приводится версия о том, что схождение колес необходимо для компенсации побочного действия развала. Мол, из-за деформации шины в пятне контакта «разваленное» колесо можно представить как основание конуса. Если колеса установлены с положительным углом развала (почему — пока неважно), они стремятся «раскатиться» в разные стороны . Чтобы этому противодействовать, плоскости вращения колес сводят.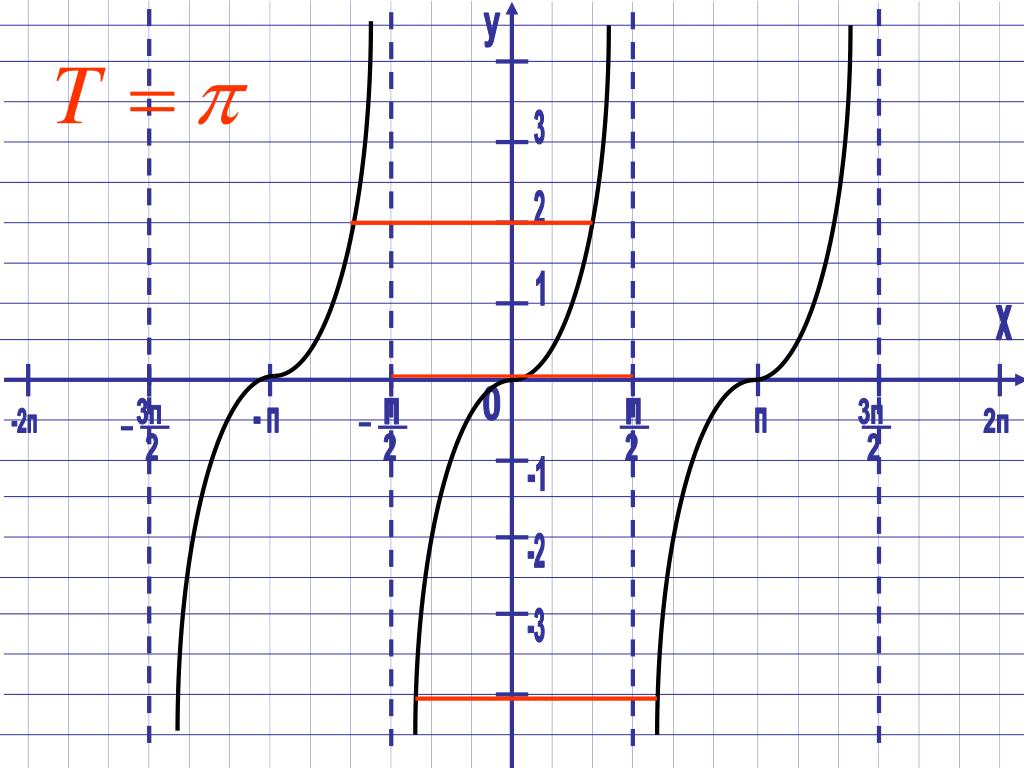 (рис.20)
(рис.20)
Это просто совпадение, что это число выражает расстояние от Солнца, которое сообщается в миллионах миль? Египетский локоть — это ровно один десятимиллиметровый радиус земли. Великая пирамида выражает отношение 2р между окружностью и радиусом Земли. Круг Квадратная площадь круга составляет 023 фута.
Он также обсуждает сходство между фигурами в Наска, Великой пирамиде и египетскими иероглифическими текстами. Боулз отмечает, что Великая пирамида и Плато Наска будут на экваторе, когда Северный полюс будет расположен на юго-востоке Аляски. Используя координаты и сферическую тригонометрию, книга демонстрирует замечательную связь между тремя моментами — древними местами.
Версия, надо сказать, не лишена изящества, но не выдерживает критики. Хотя бы потому, что предполагает однозначную взаимосвязь между развалом и схождением. Следуя предлагаемой логике, колеса, имеющие отрицательный угол развала, обязательно должны устанавливаться с расхождением, а если угол развала нулевой, то и схождения быть не должно.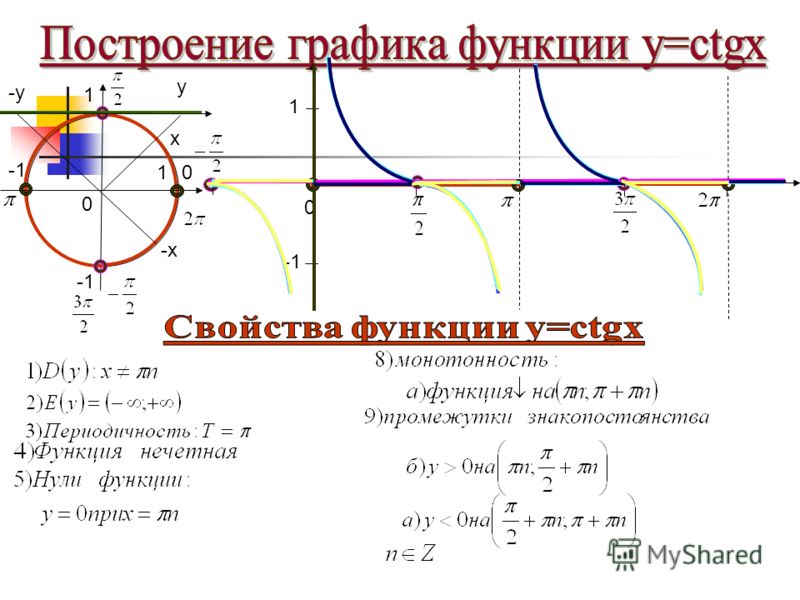 В действительности это совсем не так.
В действительности это совсем не так.
Конечно, эта связь существует также между Великой пирамидой, платформой Наска и осью «древней линии», независимо от того, где находится Северный полюс. Эта зависимость может использоваться для определения расстояний между тремя точками и плоскостью. В королевской камере диагональ 309 от восточной стены, расстояние от камеры 412, средняя диагональ — 515.
Расстояния между Ольянтайтамбо, Большой пирамидой и Точкой Оси на «Древней линии» выражают одно и то же геометрическое соотношение. 3-4 Расстояние Великой пирамиды от Оллантайтамбо составляет ровно 30% от периферии Земли. Расстояние от Великой Пирамиды до Мачу-Пикчу и Точка Оси на Аляске составляет 25% от земного периметра. Растянув этот равнобедренный треугольник по высоте, мы получим два прямоугольных треугольника со сторонами от 15% до 20% — 25%.
Действительность, как водится, подчиняется более сложным и неоднозначным закономерностям.При качении наклоненного колеса в пятне контакта действительно присутствует боковая сила, которую часто так и называют — тяга развала. Она возникает в результате упругой деформации шины в поперечном направлении и действует в сторону наклона. Чем больше угол наклона колеса, тем больше тяга развала. Именно ее используют водители двухколесной техники — мотоциклов и велосипедов — при прохождении поворотов. Им достаточно наклонить своего скакуна, чтобы заставить его «прописывать» криволинейную траекторию, которую остается лишь корректировать рулевым управлением. Тяга развала играет немаловажную роль и при маневрировании автомобилей, о чем будет сказано далее. Так что вряд ли ее стоит намеренно компенсировать схождением. Да и сам посыл, что из-за положительного угла развала колеса стремятся развернуться наружу, т.е. в сторону расхождения, неверен. Напротив, конструкция подвески управляемых колес в большинстве случаев такова, что при положительном развале его тяга стремится увеличить схождение. Так что «компенсация побочного действия развала» не причем.Известно несколько факторов, обусловливающих необходимость схождения колес.
Она возникает в результате упругой деформации шины в поперечном направлении и действует в сторону наклона. Чем больше угол наклона колеса, тем больше тяга развала. Именно ее используют водители двухколесной техники — мотоциклов и велосипедов — при прохождении поворотов. Им достаточно наклонить своего скакуна, чтобы заставить его «прописывать» криволинейную траекторию, которую остается лишь корректировать рулевым управлением. Тяга развала играет немаловажную роль и при маневрировании автомобилей, о чем будет сказано далее. Так что вряд ли ее стоит намеренно компенсировать схождением. Да и сам посыл, что из-за положительного угла развала колеса стремятся развернуться наружу, т.е. в сторону расхождения, неверен. Напротив, конструкция подвески управляемых колес в большинстве случаев такова, что при положительном развале его тяга стремится увеличить схождение. Так что «компенсация побочного действия развала» не причем.Известно несколько факторов, обусловливающих необходимость схождения колес. Первый состоит в том, что предварительно выставленным схождением компенсируется влияние продольных сил, действующих на колесо при движении автомобиля. Характер и глубина (а значит, и результат) влияния зависят от многих обстоятельств: ведущее колесо или свободно катящееся, управляемое, или нет, наконец, от кинематики и эластичности подвески. Так, на свободно катящееся колесо автомобиля в продольном направлении воздействует сила сопротивления качению. Она создает изгибающий момент, стремящийся развернуть колесо относительно узлов крепления подвески в направлении расхождения. Если подвеска автомобиля жесткая (например, не разрезная или торсионная балка), то эффект окажется не очень значительным. Тем не менее он обязательно будет, поскольку «абсолютная жесткость» — термин и явление сугубо теоретические. К тому же перемещение колеса определяется не только упругой деформацией элементов подвески, но и компенсацией конструктивных зазоров в их соединениях, колесных подшипниках и т.д.
Первый состоит в том, что предварительно выставленным схождением компенсируется влияние продольных сил, действующих на колесо при движении автомобиля. Характер и глубина (а значит, и результат) влияния зависят от многих обстоятельств: ведущее колесо или свободно катящееся, управляемое, или нет, наконец, от кинематики и эластичности подвески. Так, на свободно катящееся колесо автомобиля в продольном направлении воздействует сила сопротивления качению. Она создает изгибающий момент, стремящийся развернуть колесо относительно узлов крепления подвески в направлении расхождения. Если подвеска автомобиля жесткая (например, не разрезная или торсионная балка), то эффект окажется не очень значительным. Тем не менее он обязательно будет, поскольку «абсолютная жесткость» — термин и явление сугубо теоретические. К тому же перемещение колеса определяется не только упругой деформацией элементов подвески, но и компенсацией конструктивных зазоров в их соединениях, колесных подшипниках и т.д.
В случае подвески с большой податливостью (что характерно, например, для рычажных конструкций с эластичными втулками) результат многократно возрастет.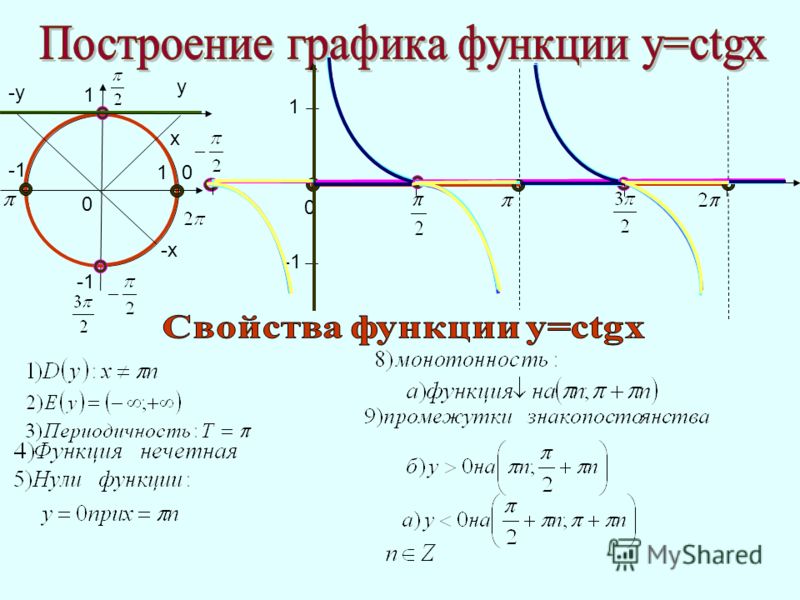 Если колесо не только свободно катящееся, но и управляемое, ситуация усложняется. За счет появления у колеса дополнительной степени свободы та же сила сопротивления оказывает двоякое воздействие. Момент, изгибающий переднюю подвеску, дополняется моментом, стремящимся развернуть колесо вокруг оси поворота. Разворачивающий момент, величина которого зависит от расположения оси поворота, воздействует на детали механизма рулевого управления и вследствие их податливости также вносит свою весомую лепту в изменение схождения колеса в движении. В зависимости от плеча обкатки вклад разворачивающего момента может быть со знаком «плюс» или «минус». То есть он может либо усиливать расхождение колес, либо противодействовать этому. Если не принять все это во внимание и установить изначально колеса с нулевым схождением, в движении они займут расходящееся положение. Из этого «вытекут» последствия, характерные для случаев нарушения регулировки схождения: повышенный расход топлива, пилообразный износ протектора и проблемы с управляемостью, о чем будет сказано далее.
Если колесо не только свободно катящееся, но и управляемое, ситуация усложняется. За счет появления у колеса дополнительной степени свободы та же сила сопротивления оказывает двоякое воздействие. Момент, изгибающий переднюю подвеску, дополняется моментом, стремящимся развернуть колесо вокруг оси поворота. Разворачивающий момент, величина которого зависит от расположения оси поворота, воздействует на детали механизма рулевого управления и вследствие их податливости также вносит свою весомую лепту в изменение схождения колеса в движении. В зависимости от плеча обкатки вклад разворачивающего момента может быть со знаком «плюс» или «минус». То есть он может либо усиливать расхождение колес, либо противодействовать этому. Если не принять все это во внимание и установить изначально колеса с нулевым схождением, в движении они займут расходящееся положение. Из этого «вытекут» последствия, характерные для случаев нарушения регулировки схождения: повышенный расход топлива, пилообразный износ протектора и проблемы с управляемостью, о чем будет сказано далее.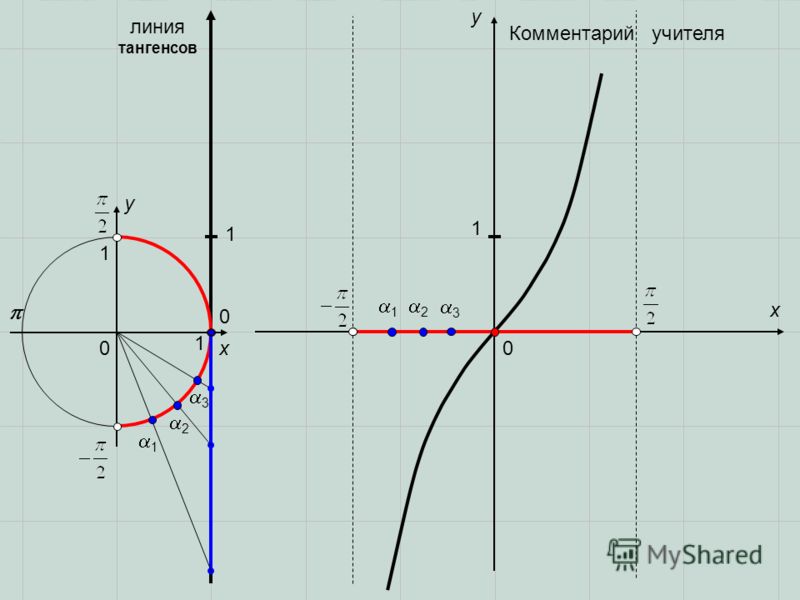
Сила сопротивления движению зависит от скорости автомобиля. Поэтому идеальным решением стало бы переменное схождение, обеспечивающее столь же идеальное положение колес на любых скоростях. Поскольку сделать это сложно, колесо предварительно «сводят» так, чтобы достичь минимального износа шин в режиме крейсерской скорости. Колесо, расположенное на ведущей оси, большую часть времени подвергается действию силы тяги. Она превышает силы сопротивления движению, поэтому равнодействующая сил будет направлена по ходу движения. Применив ту же логику, получим, что в этом случае колеса в статике нужно установить с расхождением. Аналогичный вывод можно сделать и в отношении управляемых ведущих колес.
Лучший критерий истины — практика. Если, памятуя об этом, посмотреть регулировочные данные для современных автомобилей, можно испытать разочарование, не обнаружив большой разницы в схождении управляемых колес задне- и переднеприводных моделей. В большинстве случаев и у тех, и у других этот параметр будет положительным.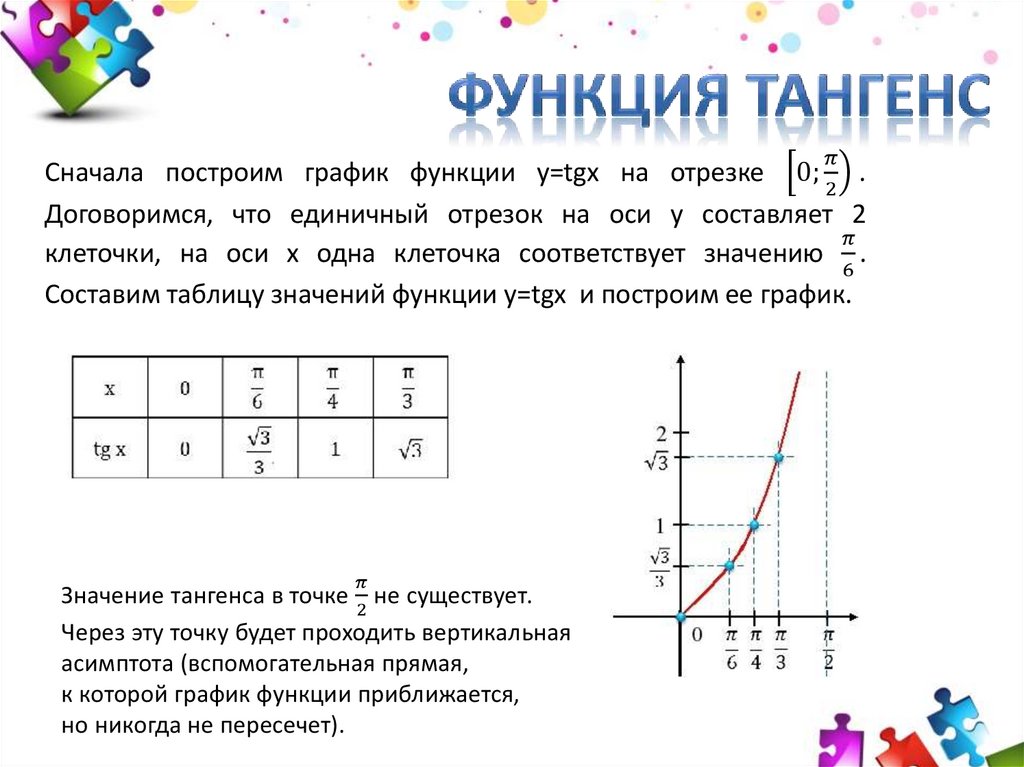 Разве что среди переднеприводных автомобилей чаще встречаются случаи «нейтральной» регулировки схождения. Причина не в том, что описанная выше логика не верна. Просто при выборе величины схождения наряду с компенсацией продольных сил учитывают и другие соображения, которые вносят поправки в конечный результат. Одно из наиболее важных — обеспечение оптимальной управляемости автомобиля. С ростом скоростей движения и динамичности автотехники этот фактор приобретает все большее значение.
Разве что среди переднеприводных автомобилей чаще встречаются случаи «нейтральной» регулировки схождения. Причина не в том, что описанная выше логика не верна. Просто при выборе величины схождения наряду с компенсацией продольных сил учитывают и другие соображения, которые вносят поправки в конечный результат. Одно из наиболее важных — обеспечение оптимальной управляемости автомобиля. С ростом скоростей движения и динамичности автотехники этот фактор приобретает все большее значение.
Управляемость — понятие многогранное, поэтому стоит уточнить, что схождение колес наиболее ощутимо влияет на стабилизацию прямолинейной траектории автомобиля и его поведение на входе в поворот. Наглядно это влияние можно пояснить на примере управляемых колес.
Допустим, в движении по прямой на одно из них оказывается случайное возмущающее воздействие от неровности дороги. Возросшая сила сопротивления поворачивает колесо в направлении уменьшения схождения. Через рулевой механизм воздействие передается на второе колесо, схождение которого, наоборот, увеличивается. Если изначально колеса имеют положительное схождение, сила сопротивления на первом уменьшается, а на втором — растет, что противодействует возмущению. Когда схождение равно нулю, противодействующий эффект отсутствует, а когда оно отрицательное — появляется дестабилизирующий момент, способствующий развитию возмущения. Автомобиль с такой регулировкой схождения будет рыскать по дороге, его придется постоянно ловить подруливанием, что недопустимо для обычного дорожного автомобиля.
Если изначально колеса имеют положительное схождение, сила сопротивления на первом уменьшается, а на втором — растет, что противодействует возмущению. Когда схождение равно нулю, противодействующий эффект отсутствует, а когда оно отрицательное — появляется дестабилизирующий момент, способствующий развитию возмущения. Автомобиль с такой регулировкой схождения будет рыскать по дороге, его придется постоянно ловить подруливанием, что недопустимо для обычного дорожного автомобиля.
У этой «монеты» есть и обратная, позитивная сторона — отрицательное схождение позволяет добиться от рулевого управления наиболее быстрой реакции. Малейшее действие водителя тут же провоцирует резкое изменение траектории — автомобиль охотно маневрирует, легко «соглашается» на поворот. Такая регулировка схождения сплошь и рядом используется в автоспорте.
Те, кто смотрят телепередачи о чемпионате WRC, наверняка обращали внимание на то, как активно приходится работать рулем тому же Лёбу или Гронхольму даже на относительно прямых участках трассы. Аналогичное воздействие на поведение автомобиля оказывает схождение колес задней оси — уменьшение схождения вплоть до небольшого расхождения увеличивает «подвижность» оси. Этот эффект часто используют для компенсации недостаточной поворачиваемости автомобилей, например, переднеприводных моделей с перегруженной передней осью.
Аналогичное воздействие на поведение автомобиля оказывает схождение колес задней оси — уменьшение схождения вплоть до небольшого расхождения увеличивает «подвижность» оси. Этот эффект часто используют для компенсации недостаточной поворачиваемости автомобилей, например, переднеприводных моделей с перегруженной передней осью.
Таким образом, статические параметры схождения, которые приведены в регулировочных данных, представляют собой некую суперпозицию, а иногда и компромисс между желанием сэкономить на топливе и резине и добиться оптимальных для автомобиля характеристик управляемости. Причем заметно, что в последние годы превалирует последнее.
Развал – параметр, который отвечает за ориентацию колеса относительно дорожного покрытия . Мы помним, что в идеале они должны быть перпендикулярны друг другу, т.е. развала быть не должно. Тем не менее у большинства дорожных автомобилей он есть. В чем фишка?
Справка.
Развал (camber) отражает ориентацию колеса относительно вертикали и определяется как угол между вертикалью и плоскостью вращения колеса. Если колесо на самом деле «развалено», т.е. его вершина наклонена наружу, развал считается положительным. Если колесо наклонено к кузову – развал отрицательный.
Если колесо на самом деле «развалено», т.е. его вершина наклонена наружу, развал считается положительным. Если колесо наклонено к кузову – развал отрицательный.
До недавнего времени наблюдалась тенденция именно разваливать колеса, т.е. придавать углам развала положительные значения. Многим, наверняка, памятны учебники по теории автомобиля, в которых установка колес с развалом объяснялась стремлением перераспределить нагрузку между внешним и внутренним ступичными подшипниками . Мол, при положительном угле развала большая ее часть приходится на внутренний подшипник , который проще выполнить более массивным и прочным. В результате выигрывает долговечность подшипникового узла. Тезис не очень убедительный, хотя бы потому, что он если и справедлив, то только для идеальной ситуации – прямолинейного движения автомобиля по абсолютно ровной дороге. Известно, что при маневрах и проезде неровностей, даже самых незначительных, подшипниковый узел испытывает динамические нагрузки , которые на порядок превышают статические силы. Да и распределяются они не совсем так, как «диктует» положительный развал колес.
Да и распределяются они не совсем так, как «диктует» положительный развал колес.
Иногда пытаются толковать положительный развал как дополнительную меру, направленную на уменьшение плеча обкатки. Когда у нас дойдет дело до знакомства с этим важным параметром подвески управляемых колес, станет понятно, что такой способ воздействия далеко не самый удачный. Он сопряжен с одновременным изменением ширины колеи и включенного угла наклона оси поворота колеса, что чревато нежелательными последствиями. Существуют более прямые и менее болезненные варианты изменения плеча обкатки. К тому же его минимизация не всегда является целью разработчиков подвески.
Более убедительно выглядит версия, что положительным развалом компенсируется смещение колес, происходящее при увеличении нагрузки на ось (в результате роста загрузки автомобиля или динамического перераспределения его массы при ускорении и торможении). Эласто-кинематические свойства большинства типов современных подвесок таковы, что с увеличением веса, приходящегося на колесо, угол развала уменьшается. Чтобы при этом обеспечить максимальное сцепление колес с дорогой, логично их предварительно чуть «развалить». Тем более что в умеренных дозах развал несильно отражается на сопротивлении качению и износе шин.
Чтобы при этом обеспечить максимальное сцепление колес с дорогой, логично их предварительно чуть «развалить». Тем более что в умеренных дозах развал несильно отражается на сопротивлении качению и износе шин.
Достоверно известно, что на выбор величины развала также оказывает влияние общепринятое профилирование дорожного полотна. В цивилизованных странах, где существуют дороги, а не направления, их поперечное сечение имеет выпуклый профиль. Чтобы в этом случае колесо оставалось перпендикулярным к опорной поверхности, ему нужно придать небольшой положительный угол развала.
Просматривая спецификации на УУК, можно заметить, что в последние годы превалирует противоположная «развальная тенденция». Колеса большинства серийных автомобилей в статике устанавливаются с отрицательным развалом. Дело в том, что, как уже упоминалось, на первый план выходит задача обеспечения их наилучшей устойчивости и управляемости. Развал – это параметр, который оказывает определяющее влияние на так называемую боковую реакцию колес.
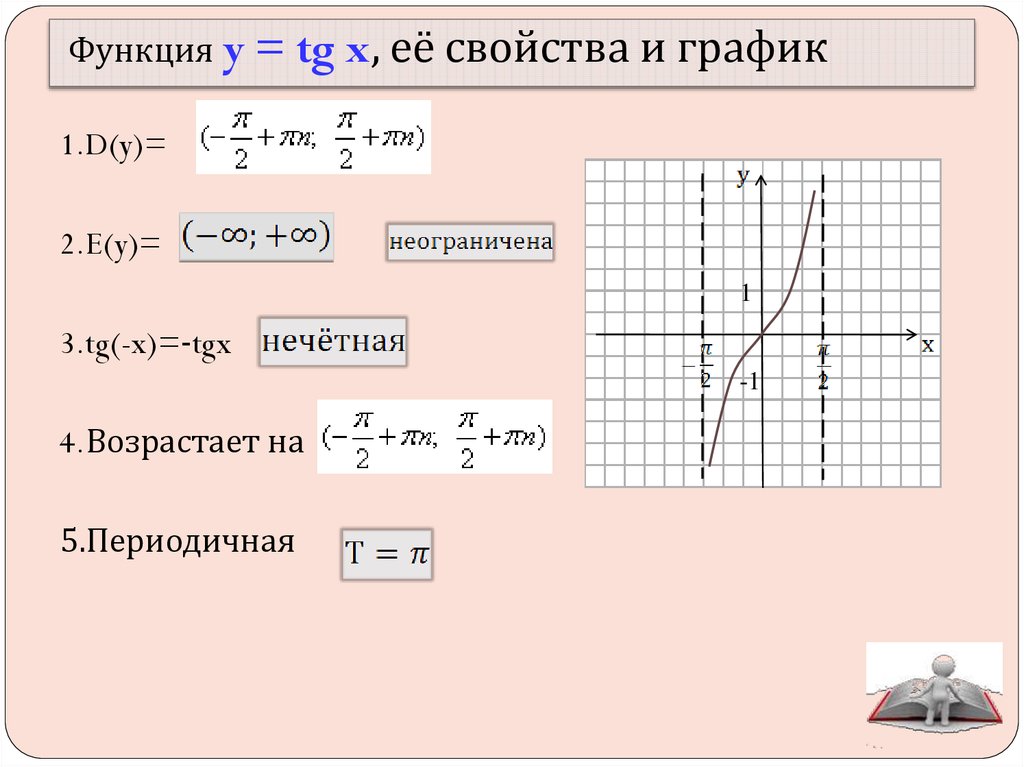 Именно она противодействует центробежным силам , действующим на автомобиль в повороте, и способствует его удержанию на криволинейной траектории. Из общих соображений следует, что сцепление колеса с дорогой (боковая реакция) будет максимальным при наибольшей площади пятна контакта, т.е. при вертикальном положении колеса. На самом деле у колеса стандартной конструкции она достигает пика при небольших отрицательных углах наклона, что обусловлено вкладом упоминавшейся тяги развала. Значит, чтобы сделать колеса автомобиля предельно цепкими в повороте, нужно их не разваливать, а, наоборот, «сваливать». Этот эффект известен давно и столь же давно используется в автоспорте. Если предметно взглянуть на «формульный» болид, хорошо заметно, что его передние колеса установлены с большим отрицательным развалом.
Именно она противодействует центробежным силам , действующим на автомобиль в повороте, и способствует его удержанию на криволинейной траектории. Из общих соображений следует, что сцепление колеса с дорогой (боковая реакция) будет максимальным при наибольшей площади пятна контакта, т.е. при вертикальном положении колеса. На самом деле у колеса стандартной конструкции она достигает пика при небольших отрицательных углах наклона, что обусловлено вкладом упоминавшейся тяги развала. Значит, чтобы сделать колеса автомобиля предельно цепкими в повороте, нужно их не разваливать, а, наоборот, «сваливать». Этот эффект известен давно и столь же давно используется в автоспорте. Если предметно взглянуть на «формульный» болид, хорошо заметно, что его передние колеса установлены с большим отрицательным развалом.Что хорошо для гоночных болидов , не совсем подходит для серийных автомобилей. Чрезмерный отрицательный развал вызывает повышенный износ внутренней зоны протектора. С увеличением наклона колеса сокращается площадь пятна контакта.
 Сцепление колес при прямолинейном движении уменьшается, в свою очередь снижается эффективность ускорения и торможения. На способность автомобиля удерживать прямолинейную траекторию избыточный отрицательный развал влияет так же, как и недостаточное схождение, автомобиль становится излишне нервозным. Виновна в этом все та же тяга развала. В идеальной ситуации вызванные развалом боковые силы действуют на оба колеса оси и уравновешивают друг друга. Но стоит одному из колес потерять сцепление с дорогой, как тяга развала другого оказывается некомпенсированной и заставляет автомобиль отклониться от прямолинейной траектории. Кстати, если припомнить, что величина тяги зависит от наклона колеса, нетрудно объяснить боковой увод автомобиля при неодинаковых углах развала правого и левого колес. Одним словом, при выборе величины развала также приходится искать «золотую середину».
Сцепление колес при прямолинейном движении уменьшается, в свою очередь снижается эффективность ускорения и торможения. На способность автомобиля удерживать прямолинейную траекторию избыточный отрицательный развал влияет так же, как и недостаточное схождение, автомобиль становится излишне нервозным. Виновна в этом все та же тяга развала. В идеальной ситуации вызванные развалом боковые силы действуют на оба колеса оси и уравновешивают друг друга. Но стоит одному из колес потерять сцепление с дорогой, как тяга развала другого оказывается некомпенсированной и заставляет автомобиль отклониться от прямолинейной траектории. Кстати, если припомнить, что величина тяги зависит от наклона колеса, нетрудно объяснить боковой увод автомобиля при неодинаковых углах развала правого и левого колес. Одним словом, при выборе величины развала также приходится искать «золотую середину».Чтобы обеспечить автомобилю хорошую устойчивость, недостаточно в статике сделать углы развала отрицательными. Конструкторы подвески должны добиться, чтобы колеса сохраняли оптимальную (или близкую к ней) ориентацию на всех режимах движения.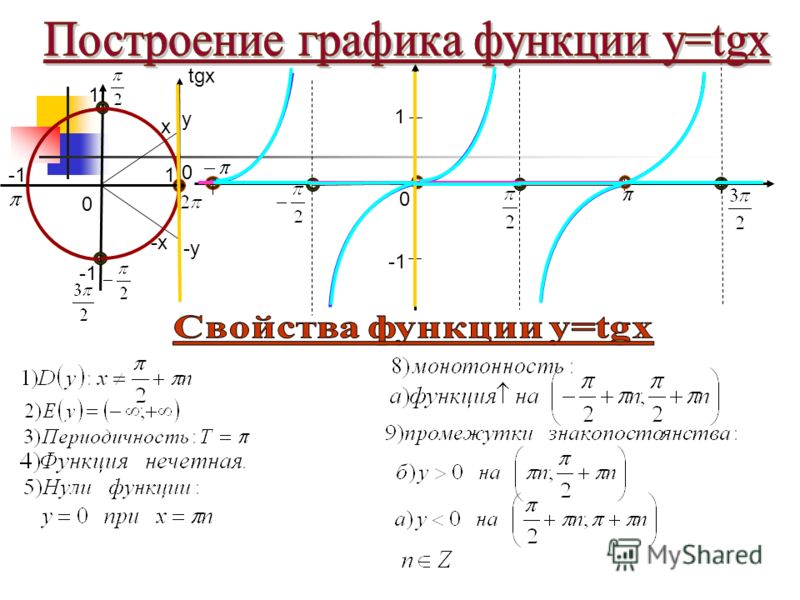 Выполнить это непросто, поскольку при маневрах любые изменения положения кузова, сопровождающиеся смещением элементов подвески (клевки, боковые крены и т.д.), приводят к существенному изменению развала колес. Как ни странно, эта задачка решается проще на спортивных автомобилях с их «зубодробительными» подвесками, отличающимися высокой угловой жесткостью и короткими ходами. Здесь статические величины развала (и схождения) меньше всего отличаются от того, как они выглядят в динамике.
Выполнить это непросто, поскольку при маневрах любые изменения положения кузова, сопровождающиеся смещением элементов подвески (клевки, боковые крены и т.д.), приводят к существенному изменению развала колес. Как ни странно, эта задачка решается проще на спортивных автомобилях с их «зубодробительными» подвесками, отличающимися высокой угловой жесткостью и короткими ходами. Здесь статические величины развала (и схождения) меньше всего отличаются от того, как они выглядят в динамике.
Чем больше диапазон ходов подвески, тем больше изменение развала в движении. Поэтому тяжелее всего приходится разработчикам обычных дорожных автомобилей с максимально эластичными (для наилучшего комфорта) подвесками. Им приходится поломать голову над тем, как «совместить несовместное» – комфорт и устойчивость. Обычно компромисс удается найти, «поколдовав» над кинематикой подвески.
Существуют решения, позволяющие свести к минимуму изменение углов развала и придать этим изменениям желательный «тренд». Например, желательно, чтобы в повороте наиболее нагруженное внешнее колесо оставалось бы в том самом оптимальном положении – с небольшим отрицательным развалом. Для этого при крене кузова колесо должно еще больше «заваливаться» на него, что достигают оптимизацией геометрии направляющих элементов подвески. Помимо этого, стараются уменьшить сами крены кузова, применяя стабилизаторы поперечной устойчивости.
Например, желательно, чтобы в повороте наиболее нагруженное внешнее колесо оставалось бы в том самом оптимальном положении – с небольшим отрицательным развалом. Для этого при крене кузова колесо должно еще больше «заваливаться» на него, что достигают оптимизацией геометрии направляющих элементов подвески. Помимо этого, стараются уменьшить сами крены кузова, применяя стабилизаторы поперечной устойчивости.
Справедливости ради стоит сказать, что эластичность подвески не всегда враг устойчивости и управляемости. В «хороших руках » эластичность, напротив, способствует им. Например, при умелом использовании эффекта «самоподруливания» колес задней оси. Возвращаясь к теме разговора, можно резюмировать, что углы развала, которые указываются в спецификациях для легковых автомобилей , будут значительно отличаться от того, какими они окажутся в повороте.
Завершая «разборку» со схождением и развалом, можно упомянуть еще об одном интересном аспекте, имеющем практическое значение.
 В регулировочных данных на УУК приводятся не абсолютные значения углов развала и схождения, а диапазоны допустимых величин. Допуски на схождение жестче и обычно не превышают ±10″, на развал – в несколько раз более свободные (в среднем ±30″). Это значит, что мастер, выполняющий регулировку УУК, может настроить подвеску, не выходя за пределы заводских спецификаций. Казалось бы, несколько десятков угловых минут – ерунда. Вогнал параметры в «зеленый коридор» – и порядок. Но давайте посмотрим, каков может быть результат. К примеру, в спецификациях для BMW 5-й серии в кузове Е39 указываются: схождение 0°5″±10″, развал –0°13″±30″. Это значит, что, оставаясь в «зеленом коридоре», схождение может принять значение от –0°5″ до 5″, а развал от –43″ до 7″. То есть и схождение, и развал могут быть отрицательными, нейтральными или положительными. Имея представление о влиянии схождения и развала на поведение автомобиля, можно намеренно «подшаманить» эти параметры так, чтобы получить желаемый результат.
В регулировочных данных на УУК приводятся не абсолютные значения углов развала и схождения, а диапазоны допустимых величин. Допуски на схождение жестче и обычно не превышают ±10″, на развал – в несколько раз более свободные (в среднем ±30″). Это значит, что мастер, выполняющий регулировку УУК, может настроить подвеску, не выходя за пределы заводских спецификаций. Казалось бы, несколько десятков угловых минут – ерунда. Вогнал параметры в «зеленый коридор» – и порядок. Но давайте посмотрим, каков может быть результат. К примеру, в спецификациях для BMW 5-й серии в кузове Е39 указываются: схождение 0°5″±10″, развал –0°13″±30″. Это значит, что, оставаясь в «зеленом коридоре», схождение может принять значение от –0°5″ до 5″, а развал от –43″ до 7″. То есть и схождение, и развал могут быть отрицательными, нейтральными или положительными. Имея представление о влиянии схождения и развала на поведение автомобиля, можно намеренно «подшаманить» эти параметры так, чтобы получить желаемый результат. Эффект не окажется разительным, но он обязательно будет.
Эффект не окажется разительным, но он обязательно будет.Рассмотренные нами развал и схождение – параметры, которые определяются для всех четырех колес автомобиля. Далее речь пойдет об угловых характеристиках, которые имеют отношение только к управляемым колесам и определяют пространственную ориентацию оси их поворота.
Известно, что положение оси поворота управляемого колеса автомобиля определяется двумя углами: продольным и поперечным. А почему бы не сделать ось поворота строго вертикальной? В отличие от случаев с развалом и схождением ответ на этот вопрос более однозначный. Здесь практически единодушны, по крайней мере в отношении продольного угла наклона – кастера.
Справедливо отмечают, что главная функция кастера – скоростная (или динамическая) стабилизация управляемых колес автомобиля. Стабилизацией в данном случае называют способность управляемых колес сопротивляться отклонению от нейтрального (соответствующего прямолинейному движению) положения и автоматически возвращаться к нему после прекращения действия внешних сил, вызвавших отклонение.
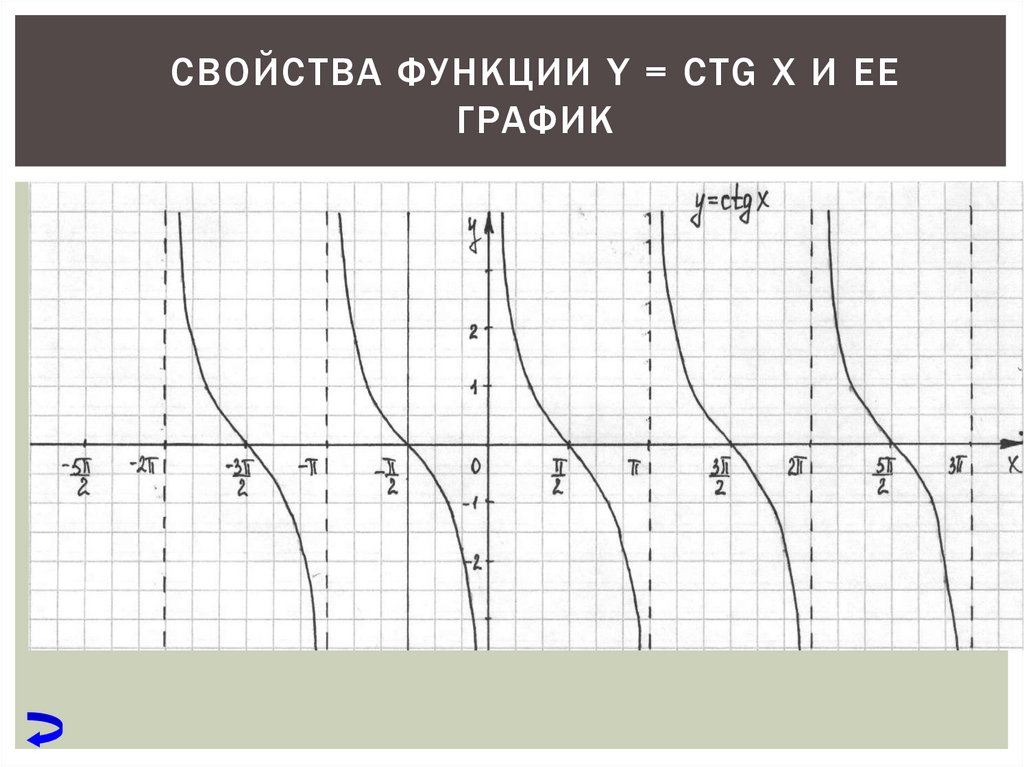 На движущееся автомобильное колесо постоянно действуют возмущающие силы, стремящиеся вывести его из нейтрального положения. Они могут быть следствием проезда неровностей дороги, неуравновешенности колес и т.д. Поскольку величина и направление возмущений постоянно меняются, их воздействие носит случайный колебательный характер. Не будь механизма стабилизации, парировать колебания пришлось бы водителю, что превратило бы управление автомобилем в мучение и наверняка увеличило износ шин. При грамотно выполненной стабилизации автомобиль устойчиво движется по прямой с минимальным вмешательством водителя и даже с отпущенным рулевым колесом.
На движущееся автомобильное колесо постоянно действуют возмущающие силы, стремящиеся вывести его из нейтрального положения. Они могут быть следствием проезда неровностей дороги, неуравновешенности колес и т.д. Поскольку величина и направление возмущений постоянно меняются, их воздействие носит случайный колебательный характер. Не будь механизма стабилизации, парировать колебания пришлось бы водителю, что превратило бы управление автомобилем в мучение и наверняка увеличило износ шин. При грамотно выполненной стабилизации автомобиль устойчиво движется по прямой с минимальным вмешательством водителя и даже с отпущенным рулевым колесом.Отклонение управляемых колес может быть вызвано намеренными действиями водителя, связанными с изменением направления движения. В этом случае стабилизирующий эффект содействует водителю на выходе из поворота, автоматически возвращая колеса в нейтральное положение. А вот на входе в поворот и в его апексе «драйверу», напротив, приходится преодолевать «сопротивление» колес, прикладывая к рулевому колесу определенное усилие.
 Возникающая на рулевом колесе реактивная сила создает то, что называют чувством руля или информативностью рулевого управления и чему уделяют много внимания и разработчики автомобилей, и автомобильные журналисты.
Возникающая на рулевом колесе реактивная сила создает то, что называют чувством руля или информативностью рулевого управления и чему уделяют много внимания и разработчики автомобилей, и автомобильные журналисты.Если вы уже знакомы с тригонометрическим кругом , и хотите лишь освежить в памяти отдельные элементы, или вы совсем нетерпеливы, – то вот он, :
Мы же здесь будем все подробно разбирать шаг за шагом.
Тригонометрический круг – не роскошь, а необходимость
Тригонометрия у многих ассоциируется с непроходимой чащей. Вдруг наваливается столько значений тригонометрических функций, столько формул… А оно ведь, как, – незаладилось вначале, и… пошло-поехало… сплошное непонимание…
Очень важно не махать рукой на значения тригонометрических функций , – мол, всегда можно посмотреть в шпору с таблицей значений.
Если вы постоянно смотрите в таблицу со значениями тригонометрических формул, давайте избавляться от этой привычки!
Нас выручит ! Вы несколько раз поработаете с ним, и далее он у вас сам будет всплывать в голове.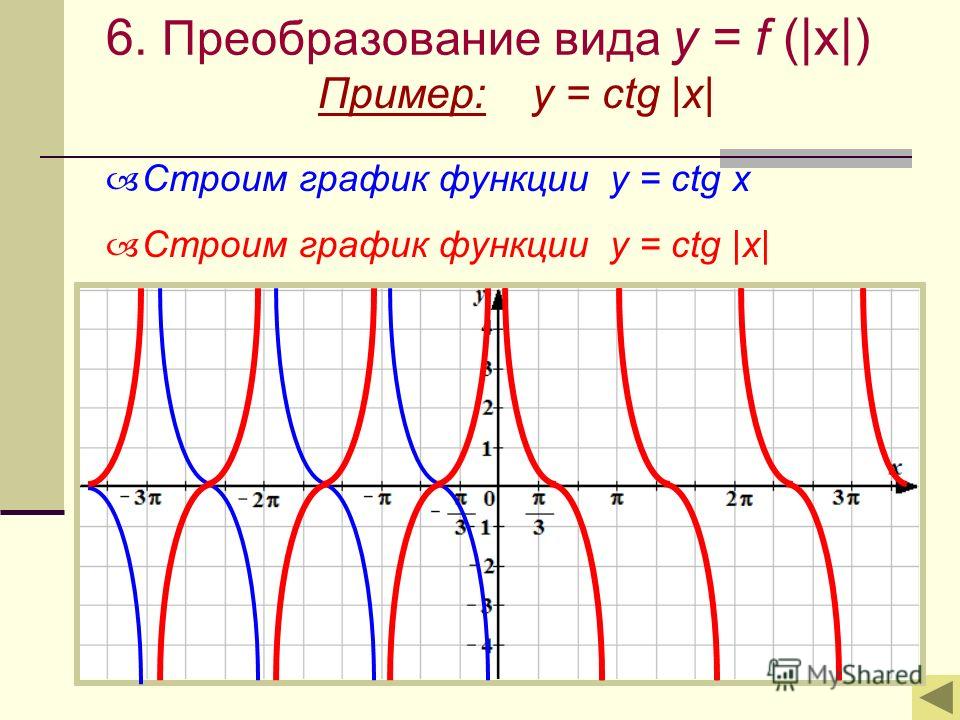 Чем он лучше таблицы? Да в таблице-то вы найдете ограниченное число значений, а на круге – ВСЕ!
Чем он лучше таблицы? Да в таблице-то вы найдете ограниченное число значений, а на круге – ВСЕ!
К примеру, скажите, глядя в стандартную таблицу значений тригонометрических формул , чему равен синус, скажем, 300 градусов, или -45.
Никак?.. можно, конечно, подключить формулы приведения … А глядя на тригонометрический круг, легко можно ответить на такие вопросы. И вы скоро будете знать как!
А при решении тригонометрических уравнений и неравенств без тригонометрического круга – вообще никуда.
Знакомство с тригонометрическим кругом
Давайте по порядку.
Сначала выпишем вот такой ряд чисел:
А теперь такой:
И, наконец, такой:
Конечно, понятно, что, на самом-то деле, на первом месте стоит , на втором месте стоит , а на последнем – . То есть нас будет больше интересовать цепочка .
Но как красиво она получилась! В случае чего – восстановим эту «лесенку-чудесенку».
И зачем оно нам?
Эта цепочка – и есть основные значения синуса и косинуса в первой четверти.
Начертим в прямоугольной системе координат круг единичного радиуса (то есть радиус-то по длине берем любой, а его длину объявляем единичной).
От луча «0-Старт» откладываем в направлении стрелки (см. рис.) углы .
Получаем соответствующие точки на круге. Так вот если спроецировать точки на каждую из осей, то мы выйдем как раз на значения из указанной выше цепочки.
Это почему же, спросите вы?
Не будем разбирать все. Рассмотрим принцип , который позволит справиться и с другими, аналогичными ситуациями.
Треугольник АОВ – прямоугольный, в нем . А мы знаем, что против угла в лежит катет вдвое меньший гипотенузы (гипотенуза у нас = радиусу круга, то есть 1).
Значит, АВ= (а следовательно, и ОМ=). А по теореме Пифагора
Надеюсь, уже что-то становится понятно?
Так вот точка В и будет соответствовать значению , а точка М – значению
Аналогично с остальными значениями первой четверти.
Как вы понимаете, привычная нам ось (ox) будет осью косинусов , а ось (oy) – осью синусов . позже.
позже.
Слева от нуля по оси косинусов (ниже нуля по оси синусов) будут, конечно, отрицательные значения.
Итак, вот он, ВСЕМОГУЩИЙ , без которого никуда в тригонометрии.
А вот как пользоваться тригонометрическим кругом, мы поговорим в .
Отсчёт углов на тригонометрическом круге.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
Он почти такой, как в предыдущем уроке. Есть оси, окружность, угол, всё чин-чинарём. Добавлены номера четвертей (в уголках большого квадрата) — от первой, до четвёртой. А то вдруг кто не знает? Как видите, четверти (их ещё называют красивым словом «квадранты») нумеруются против хода часовой стрелки. Добавлены значения угла на осях. Всё понятно, никаких заморочек.
И добавлена зелёная стрелка. С плюсом. Что она означает? Напомню, что неподвижная сторона угла всегда прибита к положительной полуоси ОХ. Так вот, если подвижную сторону угла мы будем крутить по стрелке с плюсом , т.е. по возрастанию номеров четвертей, угол будет считаться положительным. Для примера на картинке показан положительный угол +60°.
Так вот, если подвижную сторону угла мы будем крутить по стрелке с плюсом , т.е. по возрастанию номеров четвертей, угол будет считаться положительным. Для примера на картинке показан положительный угол +60°.
Если будем откладывать углы в обратную сторону, по ходу часовой стрелки, угол будет считаться отрицательным. Наведите курсор на картинку (или коснитесь картинки на планшете), увидите синюю стрелку с минусом. Это — направление отрицательного отсчёта углов. Для примера показан отрицательный угол (- 60°). А ещё вы увидите, как поменялись циферки на осях… Я их тоже перевёл в отрицательные углы. Нумерация квадрантов не меняется.
Вот тут, обычно, начинаются первые непонятки. Как так!? А если отрицательный угол на круге совпадёт с положительным!? Да и вообще, получается что, одно и то же положение подвижной стороны (или точки на числовой окружности) можно обозвать как отрицательным углом, так и положительным!?
Да. Именно так. Скажем, положительный угол 90 градусов занимает на круге точно такое же положение, что и отрицательный угол в минус 270 градусов.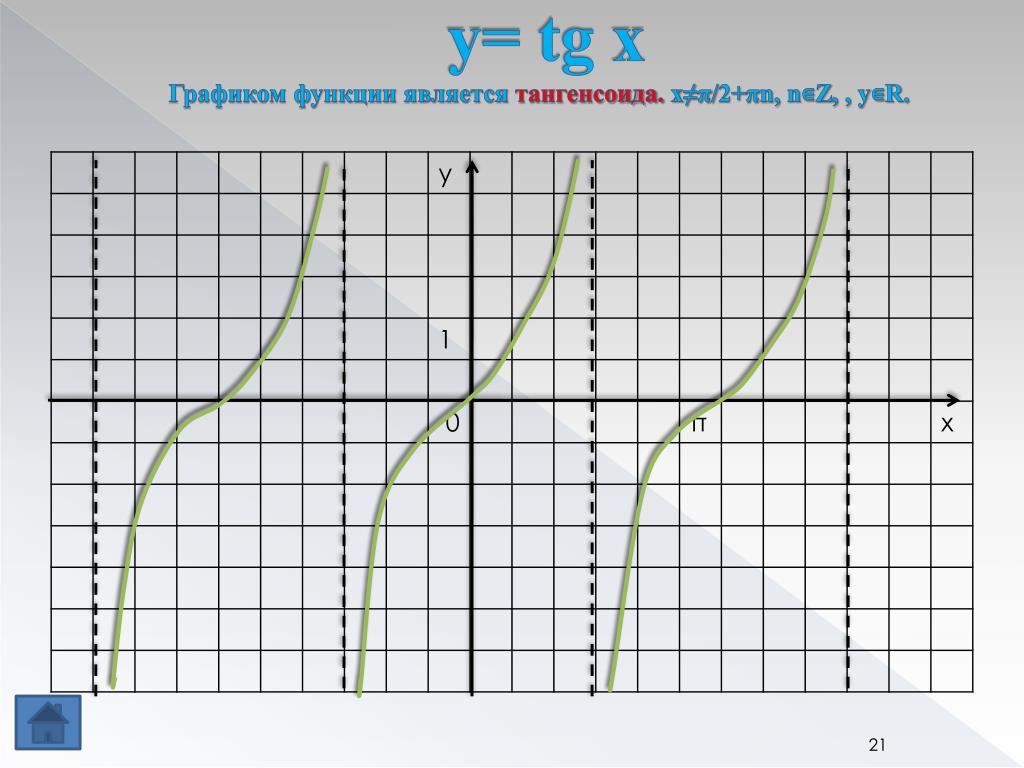 Положительный угол, к примеру, +110° градусов занимает точно такое же положение, что и отрицательный угол -250°.
Положительный угол, к примеру, +110° градусов занимает точно такое же положение, что и отрицательный угол -250°.
Не вопрос. Всяко правильно.) Выбор положительного или отрицательного исчисления угла зависит от условия задания. Если в условии ничего не сказано открытым текстом про знак угла, (типа «определить наименьший положительный угол» и т.д.), то работаем с удобными нам величинами.
Исключением (а как без них?!) являются тригонометрические неравенства, но там мы эту фишку освоим.
А теперь вопрос вам. Как я узнал, что положение угла 110° совпадает с положением угла -250°?
Намекну, что это связано с полным оборотом. В 360°… Непонятно? Тогда рисуем круг. Сами рисуем, на бумаге. Отмечаем угол примерно 110°. И считаем , сколько остается до полного оборота. Останется как раз 250°…
Уловили? А теперь — внимание! Если углы 110° и -250° занимают на круге одно и то же положение, то что? Да то, что у углов 110° и -250° совершенно одинаковые синус, косинус, тангенс и котангенс!
Т.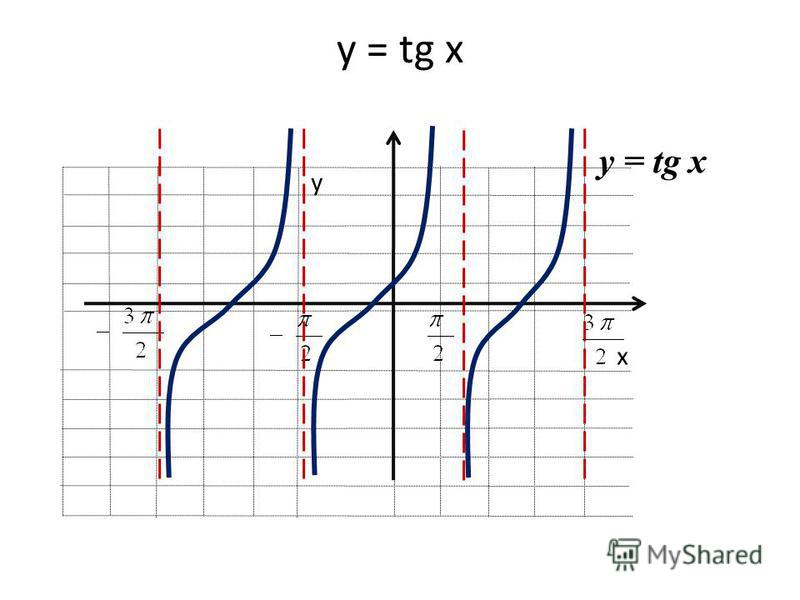 е. sin110° = sin(-250°), ctg110° = ctg(-250°) и так далее. Вот это уже действительно важно! И само по себе — есть масса заданий, где надо упростить выражения, и как база для последующего освоения формул приведения и прочих премудростей тригонометрии.
е. sin110° = sin(-250°), ctg110° = ctg(-250°) и так далее. Вот это уже действительно важно! И само по себе — есть масса заданий, где надо упростить выражения, и как база для последующего освоения формул приведения и прочих премудростей тригонометрии.
Понятное дело, 110° и -250° я взял наобум, чисто для примера. Всё эти равенства работают для любых углов, занимающих одно положение на круге. 60° и -300°, -75° и 285°, ну и так далее. Отмечу сразу, что углы в этих парочках — разные. А вот тригонометрические функции у них — одинаковые.
Думаю, что такое отрицательные углы вы поняли. Это совсем просто. Против хода часовой стрелки — положительный отсчёт. По ходу — отрицательный. Считать угол положительным, или отрицательным зависит от нас . От нашего желания. Ну, и ещё от задания, конечно… Надеюсь, вы поняли и как переходить в тригонометрических функциях от отрицательных углов к положительным и обратно. Нарисовать круг, примерный угол, да посмотреть, сколько недостаёт до полного оборота, т. е. до 360°.
е. до 360°.
Углы больше 360°.
Займемся углами которые больше 360°. А такие бывают? Бывают, конечно. Как их нарисовать на круге? Да не проблема! Допустим, нам надо понять, в какую четверть попадёт угол в 1000°? Легко! Делаем один полный оборот против хода часовой стрелки (угол-то нам дали положительный!). Отмотали 360°. Ну и мотаем дальше! Ещё оборот — уже получилось 720°. Сколько осталось? 280°. На полный оборот не хватает… Но угол больше 270° — а это граница между третьей и четвёртой четвертью. Стало быть наш угол в 1000° попадает в четвёртую четверть. Всё.
Как видите, это совсем просто. Ещё раз напомню, что угол 1000° и угол 280°, который мы получили путём отбрасывания «лишних» полных оборотов — это, строго говоря, разные углы. Но тригонометрические функции у этих углов совершенно одинаковые ! Т.е. sin1000° = sin280°, cos1000° = cos280° и т.д. Если бы я был синусом, я бы не заметил разницы между этими двумя углами…
Зачем всё это нужно? Зачем нам переводить углы из одного в другой? Да всё за тем же. ) С целью упрощения выражений. Упрощение выражений, собственно, главная задача школьной математики. Ну и, попутно, голова тренируется.)
) С целью упрощения выражений. Упрощение выражений, собственно, главная задача школьной математики. Ну и, попутно, голова тренируется.)
Ну что, потренируемся?)
Отвечаем на вопросы. Сначала простые.
1. В какую четверть попадает угол -325° ?
2. В какую четверть попадает угол 3000° ?
3. В какую четверть попадает угол -3000° ?
Есть проблемы? Или неуверенность? Идём в Раздел 555, Практическая работа с тригонометрическим кругом. Там, в первом уроке этой самой «Практической работы…» всё подробненько… В таких вопросах неуверенности быть не должно!
4. Какой знак имеет sin555° ?
5. Какой знак имеет tg555° ?
Определили? Отлично! Сомневаетесь? Надо в Раздел 555… Кстати, там научитесь рисовать тангенс и котангенс на тригонометрическом круге. Очень полезная штучка.
А теперь вопросы помудрёнее.
6. Привести выражение sin777° к синусу наименьшего положительного угла.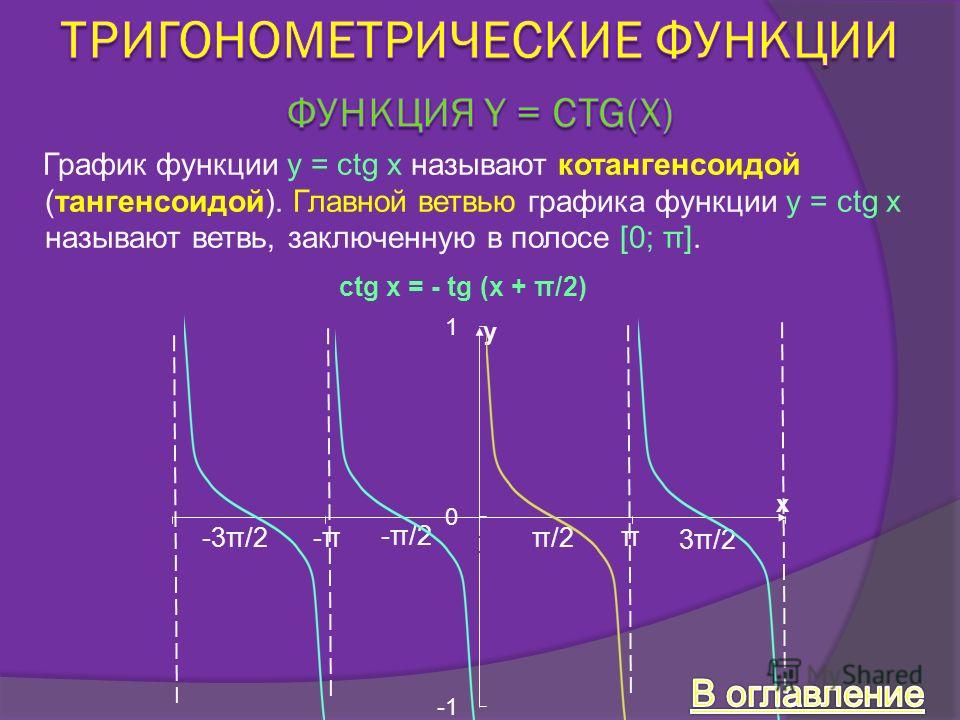
7. Привести выражение cos777° к косинусу наибольшего отрицательного угла.
8. Привести выражение cos(-777°) к косинусу наименьшего положительного угла.
9. Привести выражение sin777° к синусу наибольшего отрицательного угла.
Что, вопросы 6-9 озадачили? Привыкайте, на ЕГЭ и не такие формулировочки встречаются… Так и быть, переведу. Только для вас!
Слова «привести выражение к…» означают преобразовать выражение так, чтобы его значение не изменилось, а внешний вид поменялся в соответствии с заданием. Так, в задании 6 и 9 мы должны получить синус, внутри которого стоит наменьший положительный угол. Всё остальное — не имеет значения.
Ответы выдам по порядку (в нарушение наших правил). А что делать, знака всего два, а четверти всего четыре… Не разбежишься в вариантах.
6. sin57°.
7. cos(-57°).
8. cos57°.
9. -sin(-57°)
Предполагаю, что ответы на вопросы 6 -9 кое-кого смутили. Особенно -sin(-57°) , правда?) Действительно, в элементарных правилах отсчёта углов есть место для ошибок… Именно поэтому пришлось сделать урок: «Как определять знаки функций и приводить углы на тригонометрическом круге?» В Разделе 555. Там задания 4 — 9 разобраны. Хорошо разобраны, со всеми подводными камнями. А они тут есть.)
Особенно -sin(-57°) , правда?) Действительно, в элементарных правилах отсчёта углов есть место для ошибок… Именно поэтому пришлось сделать урок: «Как определять знаки функций и приводить углы на тригонометрическом круге?» В Разделе 555. Там задания 4 — 9 разобраны. Хорошо разобраны, со всеми подводными камнями. А они тут есть.)
В следующем уроке мы разберёмся с загадочными радианами и числом «Пи» . Научимся легко и правильно переводить градусы в радианы и обратно. И с удивлением обнаружим, что этой элементарной информации на сайте уже хватает , чтобы решать некоторые нестандартные задачки по тригонометрии!
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Касательная к окружности, значение, свойства, примеры
LearnPracticeDownload
Слово «касательная» означает «касаться». Латинское слово, обозначающее то же самое, — «tangere». В общем, мы можем сказать, что линия, которая пересекает окружность ровно в одной точке на ее окружности и никогда не входит внутрь окружности, является касательной . Окружность может иметь много касательных. Они перпендикулярны радиусу. Давайте узнаем больше о значении тангенса и теоремах в этой статье.
Латинское слово, обозначающее то же самое, — «tangere». В общем, мы можем сказать, что линия, которая пересекает окружность ровно в одной точке на ее окружности и никогда не входит внутрь окружности, является касательной . Окружность может иметь много касательных. Они перпендикулярны радиусу. Давайте узнаем больше о значении тангенса и теоремах в этой статье.
| 1. | Тангенс Значение |
| 2. | Касательная окружности |
| 3. | Свойства касательной |
| 4. | Теоремы касательной |
| 5. | Тангенс окружности Формула |
| 6. | Часто задаваемые вопросы по касательной |
Тангенс Значение
В геометрии касательная — это линия, проведенная из внешней точки и проходящая через точку на кривой. Один из реальных примеров касательной: когда вы едете на велосипеде, каждая точка окружности колеса касается дороги.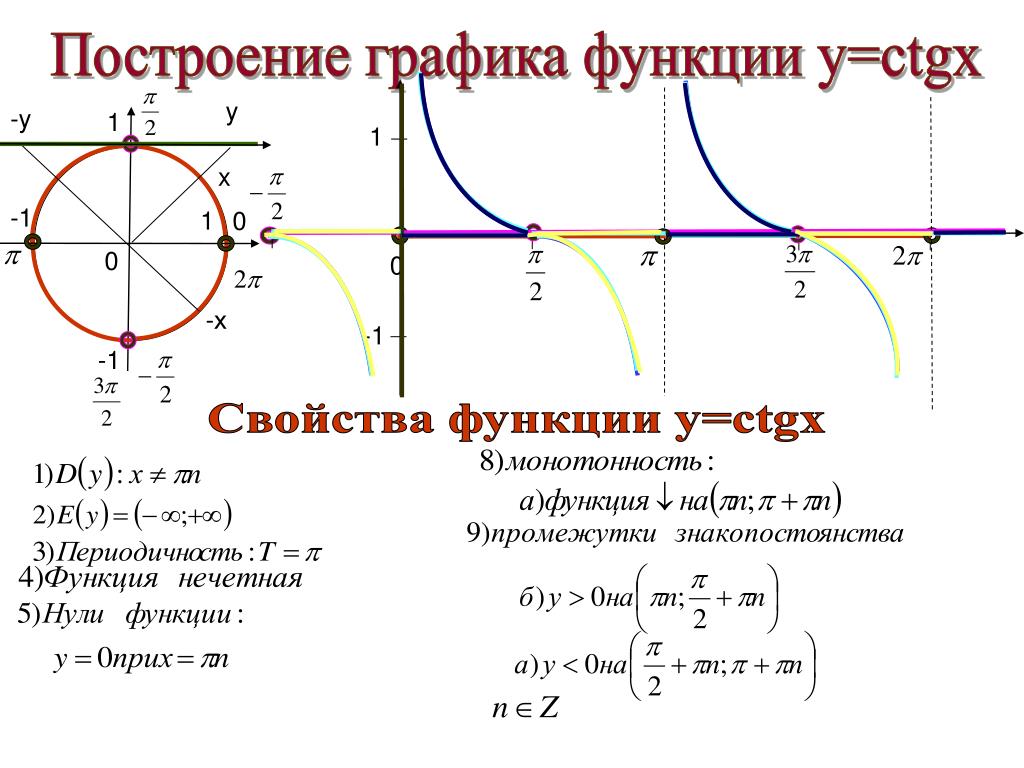 Давайте разберемся с понятием касательной на примере. На следующем рисунке показаны дуга S и точка P, внешняя по отношению к S. Касательная из P проведена к S. Это пример представления касательной.
Давайте разберемся с понятием касательной на примере. На следующем рисунке показаны дуга S и точка P, внешняя по отношению к S. Касательная из P проведена к S. Это пример представления касательной.
Касательная Определение: Касательная в геометрии определяется как линия, которая касается кривой или изогнутой поверхности ровно в одной точке.
Тангенс окружности
Касательная окружности определяется как прямая линия, которая касается или пересекает окружность только в одной точке. Касательная — это линия, которая никогда не входит внутрь круга. На следующем рисунке показана окружность с точкой P. Касательная L проходит через точку P. Это пример касательной к окружности.
Точка касания
Точка касания определяется как единственная точка пересечения, в которой прямая линия касается или пересекает окружность. На приведенном выше рисунке точка P представляет собой точку касания.
Свойства касательной
Касательная имеет два важных свойства:
- Касательная касается кривой только в одной точке.

- Касательная — это линия, которая никогда не входит внутрь окружности.
- Касательная касается радиуса окружности в точке касания под прямым углом.
Помимо вышеперечисленных свойств, касательная к окружности имеет связанные с ней математические теоремы, которые используются при выполнении основных расчетов в геометрии. Давайте подробно обсудим некоторые касательные к теоремам об окружности.
Теоремы касательной
Существуют две наиболее важные теоремы о касательной окружности. Это теорема о касательной к радиусу и теорема о двух касательных. Обсудим их утверждения и доказательства подробно.
Касательная Радиус Теорема: Касательная в любой точке окружности перпендикулярна радиусу через точку касания.
Дано: Касательная PL к окружности S (с центром окружности O) и точка касания A.
Доказать: OA перпендикулярна касательной PL.
Доказательство: Точка P лежит вне круга.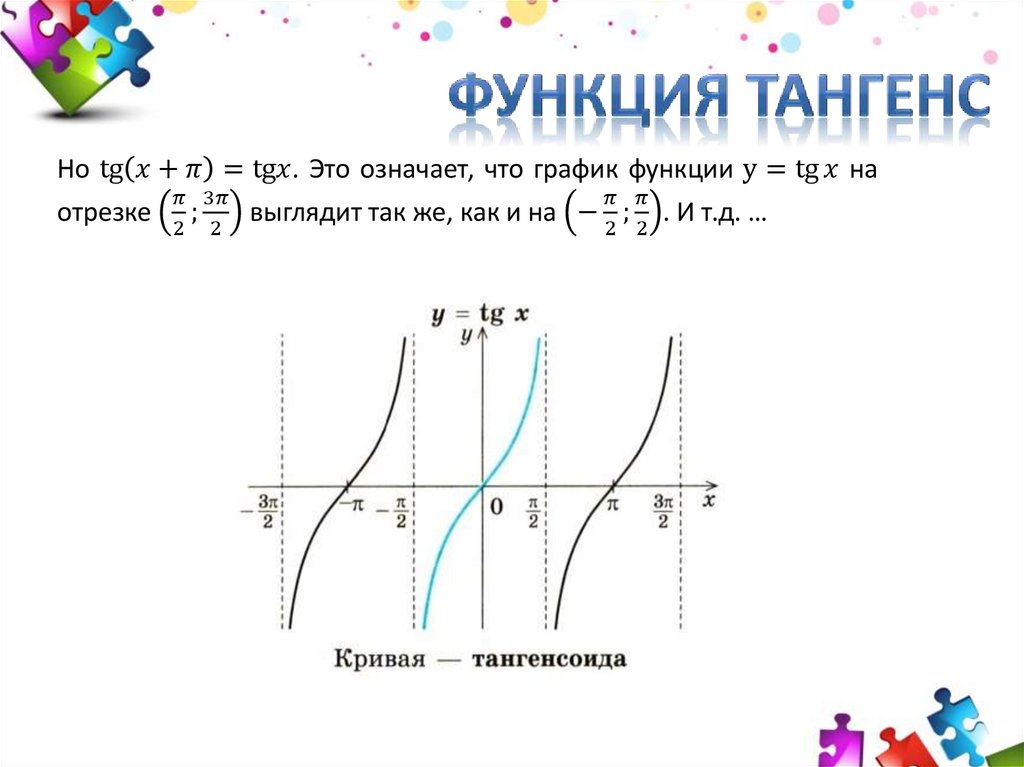 При присоединении к PO получаем PO > OA (радиус окружности). Это условие будет применяться ко всем точкам на линии PL, кроме точки A.
При присоединении к PO получаем PO > OA (радиус окружности). Это условие будет применяться ко всем точкам на линии PL, кроме точки A.
PO > OA доказывает, что OA — кратчайшее из всех расстояний от точки O до других точек на PL.
Отсюда доказано, что OA перпендикулярна PL.
Теорема о двух касательных: Предположим, что из внешней точки C к окружности проведены две касательные. Пусть точками касания будут A и B, как показано на рисунке ниже.
Теорема утверждает следующее:
- Длины этих двух касательных будут равны, то есть CA = CB.
- Две касательные образуют в центре равные углы, то есть ∠COA = ∠COB.
- Угол между касательными будет разделен пополам линией, соединяющей внешнюю точку и центр, то есть ∠ACO = ∠BCO.
Доказательство: Все три части будут доказаны, если мы покажем, что ΔCAO конгруэнтно ΔCBO. Сравнивая два треугольника, видим, что:
- ОА = ОВ (радиусы одной окружности)
- OC = OC (общая сторона)
- ∠OAC = ∠OBC = 90° (касательная, проведенная к окружности, перпендикулярна радиусу в точке касания)
- Таким образом, по критерию RHS ΔCAO конгруэнтно ΔCBO, откуда следует истинность всех трех утверждений.

Тангенс окружности Формула
Давайте теперь узнаем об уравнении касательной. Тангенс — это линия, и чтобы написать уравнение линии, нам нужны две вещи: наклон (м) и точка на линии. Общее уравнение касательной к окружности:
1) Уравнение касательной к окружности x 2 + y 2 = a 2 для прямой y = mx +c определяется уравнением y = mx ± a √[1+ m 2 ].
2) Касательная к уравнению окружности x 2 + y 2 = a 2 в точке (\(a_1, b_1)\) равна x\(a_1\)+y\(b _1\)= a 2
Таким образом, уравнение касательной можно представить как сделанный.
☛ Похожие темы
Проверьте эти интересные статьи, связанные с касательной и касательной к окружности.
- Калькулятор касательной
- Касательная линия
- Тангенциальная функция
Примеры касательной к окружности
Пример 1: TP и TQ — две касательные к окружности с центром O, такие, что ∠POQ = 130°, тогда угол ∠PTQ равен?
Решение:
Дано: TP и TQ касательные.

Используя теорему о касательном радиусе, если радиус провести к касательным TP и TQ, он будет перпендикулярен этим касательным.
Таким образом, OP перпендикулярна TP, а QO перпендикулярна TQ. Отсюда следует, что
∠OPT = 90°
∠OQT = 90°
Мы знаем, что сумма внутренних углов четырехугольника равна 360°.
Следовательно, ∠POQ + ∠PTQ + ∠OPT + ∠OQT = 360°
∠PTQ = 360° — (130° + 90° + 90°)
∠PTQ = 50°
Следовательно, значение ∠PTQ равно 50°.
Пример 2: Рассмотрим хорду AB длиной 10 см в окружности радиусом 6 см. Касательные в точках A и B пересекаются в точке C, как показано ниже:
Каковы длины этих касательных, CA и CB?
Решение:
Обратите внимание, что ∠ADC=90°. При сравнении ΔOAC с ΔODA:
- ∠OAC=∠ODA=90°
- ∠DOA=∠COA (общий)
Таким образом, два треугольника ΔOAC и ΔODA подобны по критерию подобия AA.

Следовательно, OD: OA = AD: AC.Мы знаем, что OA = 6 см, а AD составляет половину AB, что составляет 10 см, поэтому AD равно 10/2 = 5 см. Теперь нам нужно вычислить значение OD по теореме Пифагора:
OD 2 = OA 2 − AD 2 = 6 2 − (5) 2 = 36 – 90 = 1 3 1 9 00002 OD = √(11) = 3,316 см
Подставляем это значение в отношение подобия OD: OA = AD: AC, чтобы получить:
AC = (OA×AD)/OD = (6×5)/(3,316 ) ≈ 9,047 см
Согласно теореме о двух касательных, касательные, проведенные из внешней точки к окружности, имеют одинаковую меру. Таким образом, АС = СВ.
Таким образом, AC = BC = 9,047 см приблизительно.
Пример 3: Рассмотрим две концентрические окружности с радиусами 5 дюймов и 7 дюймов. Хорда AB большей окружности касается меньшей окружности в точке C. Какова длина AB?
Решение: Рассмотрим следующий рисунок:
Обратите внимание, что поскольку AB является касательной к меньшему кругу в точке C, OC должен быть перпендикулярен AB.
 Таким образом, ΔOAC прямоугольный в C. Кроме того, C является серединой AB, поэтому AC = BC = (1/2)AB. Using the Pythagoras theorem, we have:
Таким образом, ΔOAC прямоугольный в C. Кроме того, C является серединой AB, поэтому AC = BC = (1/2)AB. Using the Pythagoras theorem, we have:AC 2 = OA 2 − OC 2 = 7 2 − 5 2 = 24
AC = 4.9 inches approx
AB = 2 × AC = 9,8 дюйма
Следовательно, длина касательной AB приблизительно равна 9,8 дюйма.
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему стоит математика, с сертифицированными экспертами ourCuemath.
Записаться на бесплатный пробный урок
Практические вопросы по касательной
перейти к слайдуперейти к слайду
Часто задаваемые вопросы по Tangent
Что означает тангенс?
Термин «тангенс» происходит от латинского слова «tangere», что означает «прикасаться». Касательная в геометрии определяется как линия или плоскость, которая касается кривой или криволинейной поверхности ровно в одной точке на границе кривой.
Касательная в геометрии определяется как линия или плоскость, которая касается кривой или криволинейной поверхности ровно в одной точке на границе кривой.
Что такое касательная окружности?
Касательная — это линия, которая никогда не входит внутрь круга. Касательная к окружности может быть описана как прямая линия, проходящая через точку на окружности и перпендикулярная радиусу. Касательная окружности касается окружности в одной точке, но не входит внутрь окружности.
Каковы две основные теоремы касательной к окружности?
Ниже перечислены две основные теоремы касательной к окружности:
- Касательная в любой точке окружности перпендикулярна радиусу, проходящему через точку касания.
- Длины двух касательных, проведенных из внешней точки к окружности, равны.
Какова формула касательной окружности?
Общее уравнение касательной к окружности можно выразить следующим образом:
- Касательная к уравнению окружности x 2 + y 2 = a 2 для прямой y = mx +c задается уравнением y = mx ± a √[1+ m 2 ] .

- ТАНГАНСТВА КРУГКА Уравнения x 2 + Y 2 = A 2 AT (A 1 , B 1 ) IS XA 1 + YB 1 = A 1 + YB 1 = A .
Таким образом, уравнение касательной можно представить в виде xa 1 + yb 1 = a 2 , где (a 1 , b 1 ) — координаты, от которых проводится касательная.
Каковы четыре свойства касательных к окружности?
Ниже перечислены четыре основных свойства касательной к окружности:
- Касательная — это прямая линия, которая касается окружности только в одной точке.
- Перпендикулярно радиусу в точке касания.
- Никогда не входит внутрь круга.
- Длины двух касательных к окружности из одной и той же внешней точки равны.
Насколько важен тангенс в реальной жизни?
Изучение тангенсов необходимо, потому что это позволяет нам узнать наклон кривой функции в конкретной точке.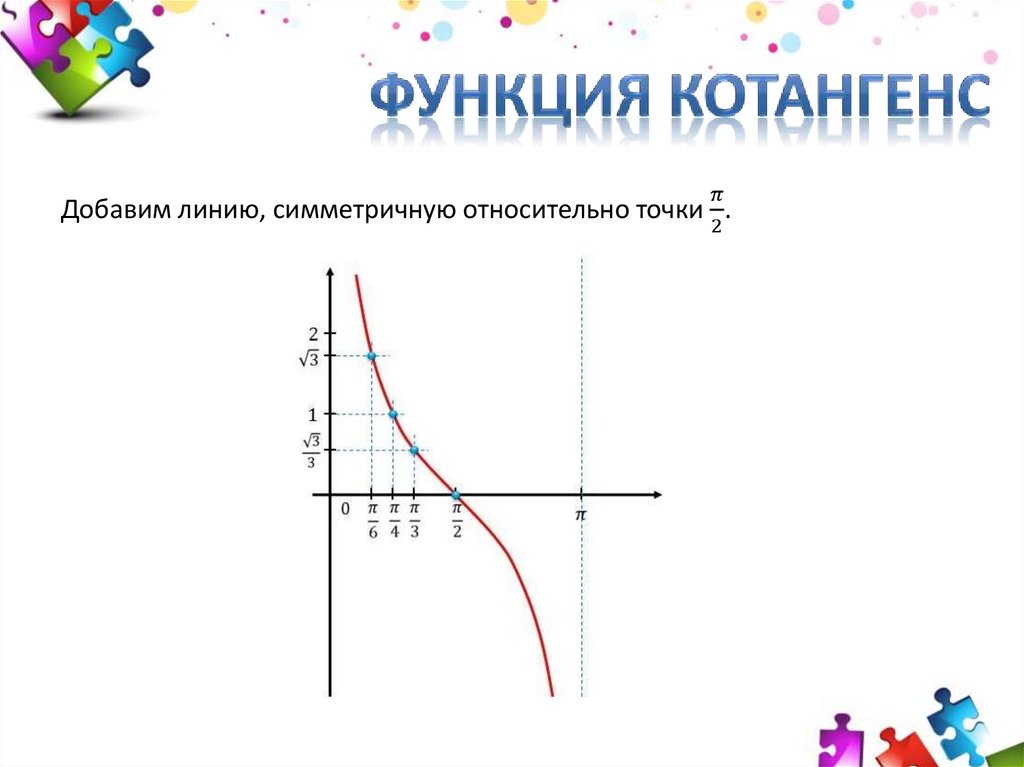 Легко найти наклон прямой, но чтобы узнать наклон кривой функции, необходимо изучить касательную к окружности. Тангенс может использоваться для различных приложений, таких как:
Легко найти наклон прямой, но чтобы узнать наклон кривой функции, необходимо изучить касательную к окружности. Тангенс может использоваться для различных приложений, таких как:
- В дифференциалах и приближениях
- Архитектура
- Машиностроение
- Конструкции
Как узнать, касаются ли две окружности?
Мы знаем, что прямая считается касательной к окружности, если она касается окружности ровно в одной точке. Точно так же одна окружность может касаться другой окружности, если окружности встречаются или касаются точно в одной точке.
Скачать БЕСПЛАТНЫЕ учебные материалы
Загрузить рабочие листы по окружностям и касательным
Рабочие листы по математике и
наглядный учебный план
Касательная к кругу – объяснение и примеры
Вы когда-нибудь строили или видели ограждение вокруг сада или какой-либо дороги из-за ситуации с правопорядком? Полиция не позволит вам приблизиться к забору. Некоторые могут получить шанс коснуться забора и уйти.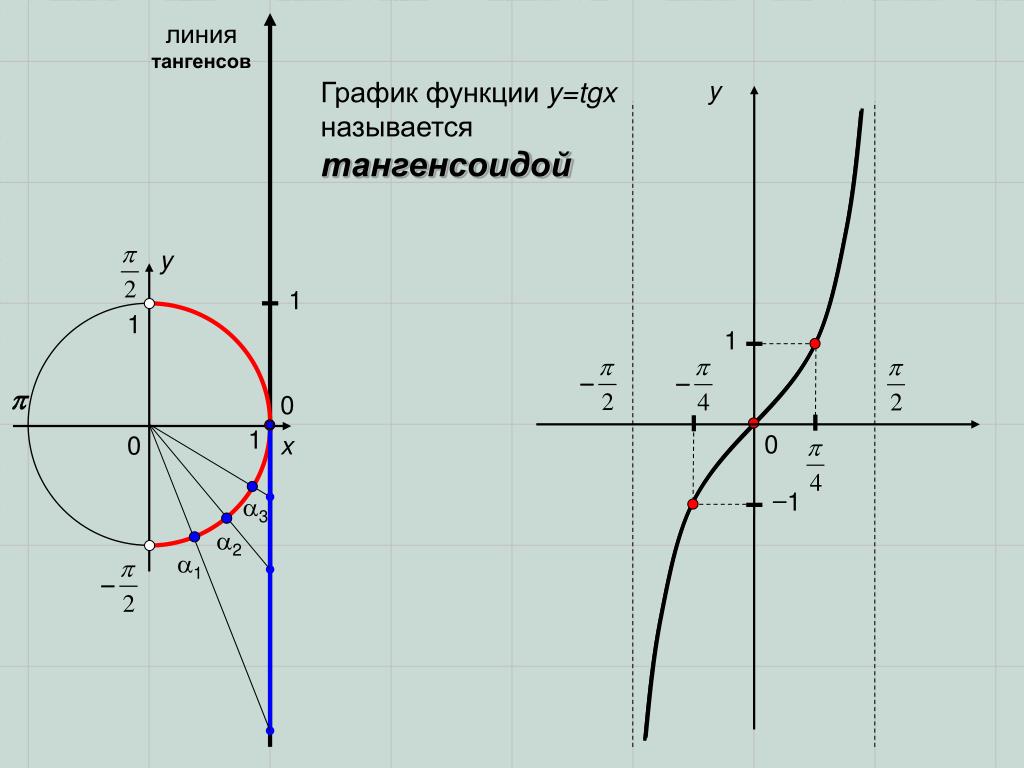 Если они идут по прямой линии, они в основном следуют по касательной к форме, сделанной внутри ограждения.
Если они идут по прямой линии, они в основном следуют по касательной к форме, сделанной внутри ограждения.
Это определение касательной , которая представляет собой линию, которая касается формы в любой точке и удаляется . И именно это означает латинское слово « тангенс », « коснуться ».
Касательные можно построить вокруг любой формы, но в этом уроке основное внимание будет уделено касательным к окружности.
Из этой статьи вы узнаете:
- Что такое касательная окружности; &
- Как найти касательную окружности.
Что такое касательная к окружности?
Касательная к окружности определяется как прямая линия, которая касается окружности в одной точке. Точка, в которой касательная касается окружности, называется точкой касания или точкой касания.
С другой стороны, секущая представляет собой удлиненную хорду или прямую линию , которая пересекает окружность в двух различных точках .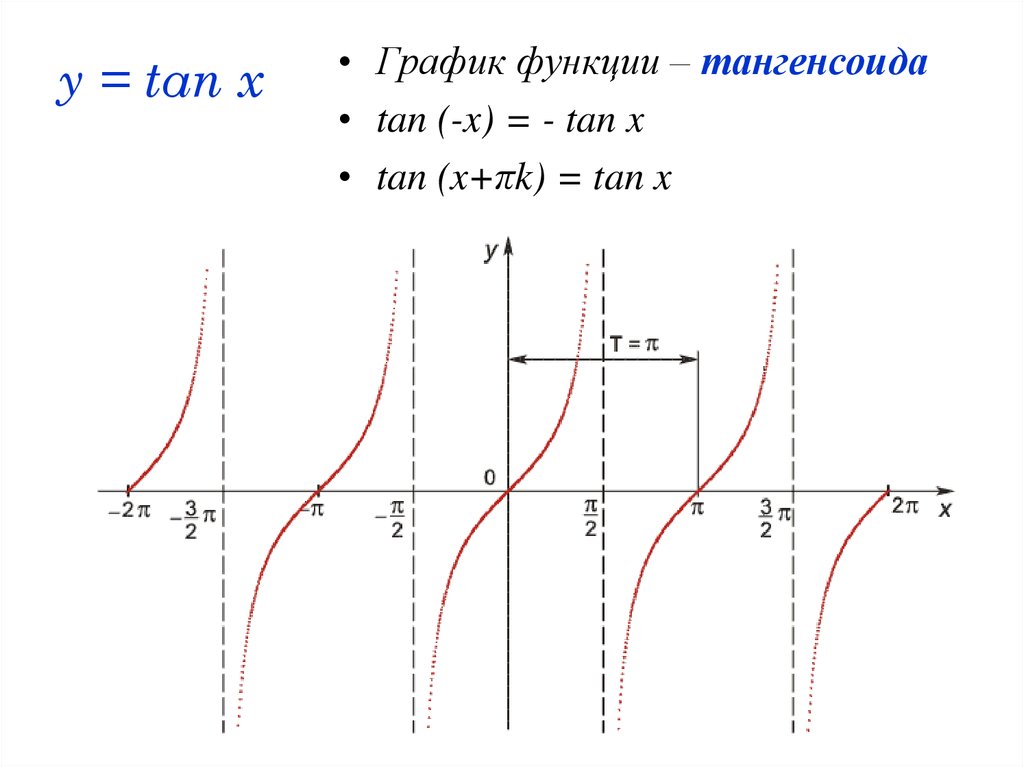
Теорема касательной к окружности
Теорема касательной утверждает что прямая является касательной к окружности тогда и только тогда, когда прямая перпендикулярна радиусу, проведенному к точке касания.
Свойства касательной
- Одна касательная может касаться окружности только в одной точке окружности.
- Касательная никогда не пересекает окружность, что означает, что она не может проходить через окружность.
- Касательная никогда не пересекает окружность в двух точках.
- Касательная перпендикулярна радиусу окружности.
Радиус окружности OP перпендикулярен касательной RS.
- Длина двух касательных из общей внешней точки к окружности равна.
Длина PR = Длина PQ
Как найти тангенс окружности?
Посмотрите на круг внизу.
Предположим, что линия DB — это секанс, а AB — тангенс окружности, тогда секанс и тангенс связаны следующим образом:
DB/AB = AB/CB
Умножение крестом дает уравнение.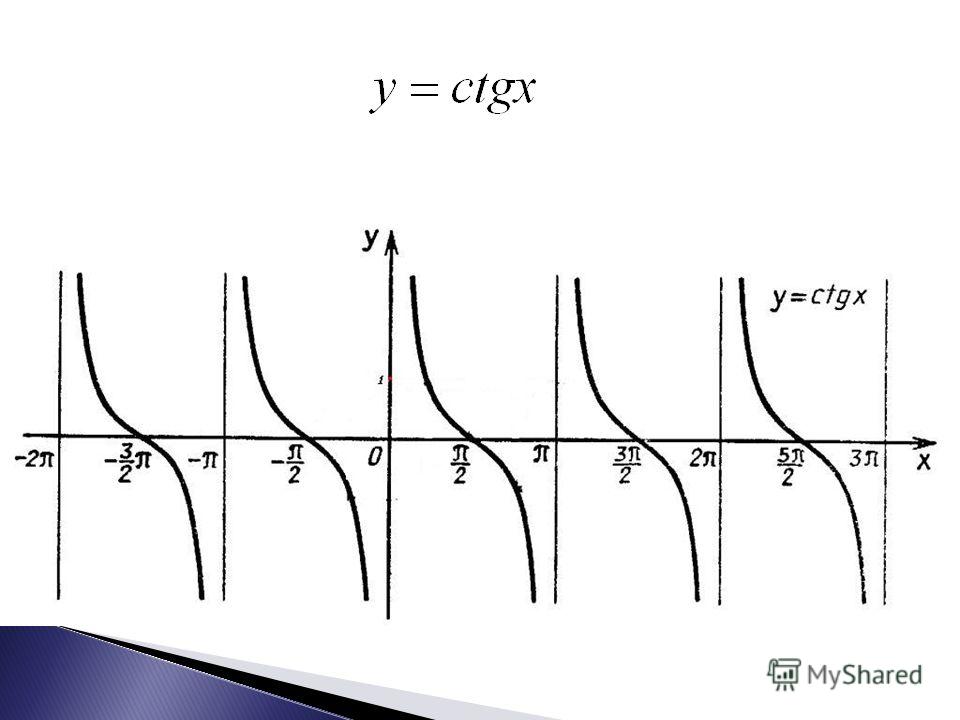
AB 2 = DB * CB ………… Это дает формулу для тангенса.
Давайте решим несколько примеров задач на касательную окружности.
Могут ли две окружности касаться друг друга?
Да!
Две окружности касаются друг друга, если они касаются друг друга ровно в одной точке. Согласно определению, касательная касается окружности ровно в одной точке.
Следующая диаграмма представляет собой пример двух касательных окружностей.
Пример 1
Найдите длину касательной в окружности, показанной ниже.
Решение
Диаграмма выше имеет одну касательную и одну секущую.
Даны следующие длины:
PQ = 10 см и QR = 18 см,
Следовательно, PR = PQ + QR = (10 + 18) см
= 28 см.
⇒ SR 2 = PR * RQ
⇒ SR 2 = 28 * 18
⇒ SR 2 = 504 cm
⇒ √ SR 2 = √504
⇒ SR = 22,4 см
Итак, длина касательной равна 22,4 см.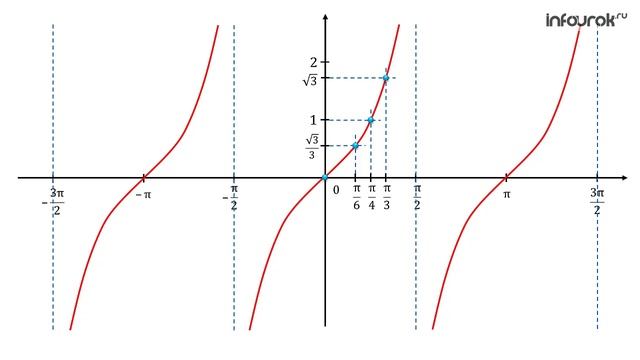
Пример 2
Найдите длину касательной на следующей диаграмме, учитывая, что AC = 6 м и СВ = 10 м.
Решение
Поскольку радиус окружности перпендикулярен касательной, треугольник ABC является прямоугольным (угол A = 90 градусов).
по теореме Pythagorean
⇒ AB 2 + AC 2 = CB 2
⇒ AB 2 + 6 2 = 10 2 + 6 2 = 10 2 + 6 2 = 10 2 + 2 = 10 2 + 6 2 = 10 2 + 2 = 10 2 .
Вычтите 36 с обеих сторон.
⇒ АБ 2 = 100 – 36
⇒ AB 2 = 64
√AB 2 = √64
AB = 8.
Следовательно, длина касательной равна 8 метрам.
Пример 3
Если DC = 20 дюймов и BC = 12 дюймов, рассчитайте радиус, показанный ниже.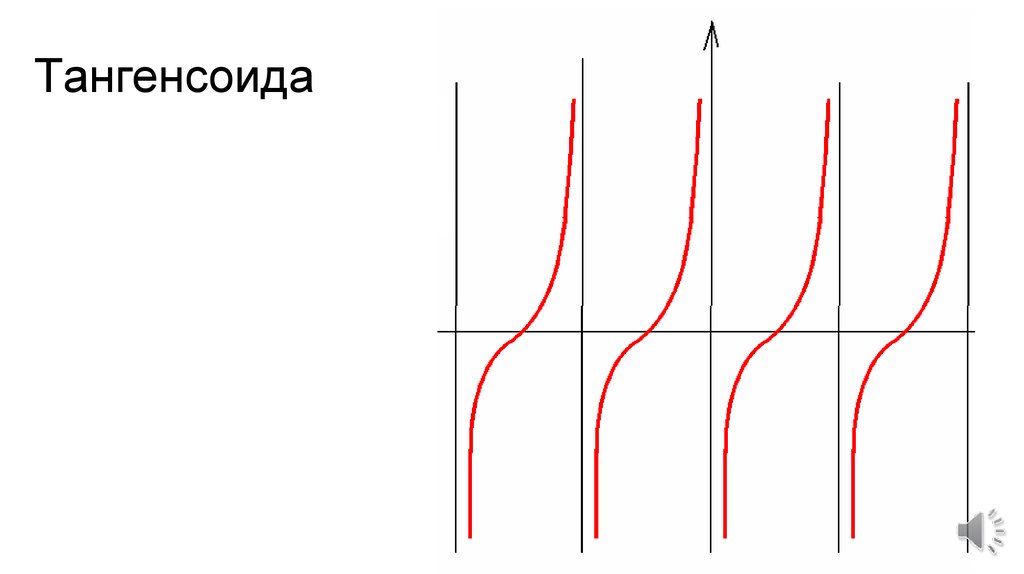
Решение
DC 2 = AC * BC
Но AC = AB + BC = R + 12
20 2 = 12 (R + 12
20 2 = 12 (R + 12)0002 400 = 12р +144
Вычесть 144 с обеих сторон.
256 = 12r
Разделите обе стороны на 12, чтобы получить
r = 21,3
Итак, радиус окружности равен 21,3 дюйма. Пример 4 Следовательно,
20 = х 2 + 4
Вычесть 4 с обеих сторон.
16 = x 2
√16 = √x 2
x = 8
Таким образом, значение x равно 8 см.
Пример 5
Вычислите длину касательной в окружности, показанной ниже.
Решение
DC 2 = 27 (10 + 27)
= 27 *37
DC 2 = 999
. Негативное значение, мы имеем 9 = 999
.0003
DC = 31,61
Таким образом, тангенс равен 31,61 см.
Solution
Let XY = x
x (x +14) = 56 2
x 2 + 14x = 3136
x 2 + 14x – 3136 = 0
Решите квадратное уравнение, чтобы получить
x = 63,4
Следовательно, длина XY равна 63,4 см.
Пример 7
Вычислите длину AB в круге ниже.
Раствор
по теореме Pythagorean,
40 2 + AB 2 = 100 2
9000. 160456 = 100 2 9000. 160456 + 3 2 9000. 160456 + 2 9000. 160456. = 8400АВ = 91.7
Отсюда длина АВ равна 91,7 мм
12.5: Тангенциальная и нормальная составляющие ускорения
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 5530
Цели обучения
- Описывать векторы скорости и ускорения частицы, движущейся в пространстве.

- Объясните тангенциальную и нормальную составляющие ускорения.
- Назовите законы движения планет Кеплера.
Теперь мы увидели, как описывать кривые на плоскости и в пространстве и как определять их свойства, такие как длина дуги и кривизна. Все это ведет к главной цели этой главы — описанию движения по плоским кривым и пространственным кривым. Теперь у нас есть все необходимые инструменты; в этом разделе мы объединим эти идеи и посмотрим, как их использовать.
Векторы движения на плоскости и в пространстве
Наша отправная точка — использование векторных функций для представления положения объекта как функции времени. Весь следующий материал может быть применен либо к кривым на плоскости, либо к пространственным кривым. Например, когда мы смотрим на орбиты планет, все кривые, определяющие эти орбиты, лежат в плоскости, потому что они эллиптические. Однако частица, движущаяся по спирали, движется по кривой в трех измерениях.
Определение: скорость, скорость и ускорение
Пусть \(\vecs r(t)\) — дважды дифференцируемая вектор-функция параметра \(t\), представляющая положение объекта как функцию время.
Вектор скорости \(\vecs v(t)\) объекта определяется как
\[\text{Скорость}\,=\vecs v(t)=\vecs r′(t). \label{Eq1} \]
Вектор ускорения \(\vecs a(t)\) определяется как
\[\text{Ускорение}\,=\vecs a(t)=\vecs v′( т)=\vecs г″(т). \label{Eq2} \]
Скорость определяется как
\[\mathrm{Скорость}\,=v(t)=‖\vecs v(t)‖=‖\vecs r′(t)‖=\dfrac{ds {дт}. \label{Eq3} \]
Поскольку \(\vecs{r}(t)\) может быть двух- или трехмерным, эти вектор-функции могут иметь два или три компонента. В двух измерениях мы определяем \(\vecs{r}(t)=x(t) \hat{\mathbf i}+y(t) \hat{\mathbf j}\), а в трех измерениях \(\vecs r (t) = x (t) \ hat {\ mathbf i} + y (t) \ hat {\ mathbf j} + z (t) \ hat {\ mathbf k} \). Тогда скорость, ускорение и скорость можно записать так, как показано в следующей таблице.
 Найдите скорость, ускорение и скорость как функции времени.
Найдите скорость, ускорение и скорость как функции времени.- Подсказка
Используйте уравнения \ref{Eq1}, \ref{Eq2} и \ref{Eq3}.
- Ответить
\[\begin{align*}\vecs v(t) &=\vecs{r}'(t) =(2t-3)\,\hat{\mathbf i}+2\,\hat{\mathbf j}+\,\hat{\mathbf k}\\[4pt] \vecs a(t) &=\vecs v′(t) =2\,\hat{\mathbf i} \end{align*}\ ] 92-12t+14} \номер\]
Единицами скорости и скорости являются футы в секунду, а единицами измерения ускорения являются футы в секунду в квадрате.
Чтобы лучше понять векторы скорости и ускорения, представьте, что вы едете по извилистой дороге. Если вы не повернете руль, вы продолжите движение по прямой и собьетесь с дороги. Скорость, с которой вы движетесь, когда сбегаете с дороги, вместе с направлением дает вектор, представляющий вашу скорость, как показано на рисунке \(\PageIndex{2}\).
Рисунок \(\PageIndex{2}\): В каждой точке дороги, по которой движется автомобиль, вектор скорости автомобиля касается пути, пройденного автомобилем.
Однако тот факт, что вы должны крутить руль, чтобы оставаться на дороге, указывает на то, что ваша скорость всегда меняется (даже если ваша скорость не меняется), потому что ваше направление постоянно меняется, чтобы удерживать вас на дороге. Когда вы поворачиваете направо, ваш вектор ускорения также указывает вправо. Когда вы поворачиваете налево, ваш вектор ускорения указывает налево. Это указывает на то, что ваши векторы скорости и ускорения постоянно меняются, независимо от того, изменяется ли ваша фактическая скорость (рис. \(\PageIndex{3}\)).
Рисунок \(\PageIndex{3}\): Пунктирная линия представляет собой траекторию движения объекта (например, автомобиля). Вектор ускорения всегда указывает внутрь поворота.Компоненты вектора ускорения
Мы можем объединить некоторые концепции, обсуждаемые в разделе «Длина дуги и кривизна», с вектором ускорения, чтобы глубже понять, как этот вектор связан с движением на плоскости и в пространстве. Напомним, что единичный касательный вектор \(\vecs T\) и единичный вектор нормали \(\vecs N\) образуют соприкасающуюся плоскость в любой точке \(P\) на кривой, определяемой векторнозначной функцией \(\ vecs{r}(t)\). Следующая теорема показывает, что вектор ускорения \(\vecs{a}(t)\) лежит в соприкасающейся плоскости и может быть записан как линейная комбинация единичного касательного и единичного нормального вектора. 92 \kappa \vecs{N}(t) \nonumber \]
Напомним, что единичный касательный вектор \(\vecs T\) и единичный вектор нормали \(\vecs N\) образуют соприкасающуюся плоскость в любой точке \(P\) на кривой, определяемой векторнозначной функцией \(\ vecs{r}(t)\). Следующая теорема показывает, что вектор ускорения \(\vecs{a}(t)\) лежит в соприкасающейся плоскости и может быть записан как линейная комбинация единичного касательного и единичного нормального вектора. 92 \kappa \vecs{N}(t) \nonumber \]
Здесь \(v(t) = \|\vecs v(t)\|\) — скорость объекта, а \(\kappa\ ) — это кривизна \(C\), описываемая \(\vecs{r}(t)\).
Доказательство
Поскольку \(\vecs{v}(t)=\vecs{r}′(t)\) и \(\vecs{T}(t)=\dfrac{\vecs{r}'( t)}{||\vecs{r}′(t)||}\), имеем \(\vecs v(t)=||\vecs{r}′(t)||\vecs{T} (t)=v(t)\vecs{T}(t)\).
Теперь продифференцируем это уравнение:
\[\vecs{a}(t)=\vecs{v}′(t)=\dfrac{d}{dt}\left(v(t)\vecs{T }(t)\right)=v′(t)\vecs{T}(t)+v(t)\vecs{T}′(t) \nonumber \] 92 \vecs{N}(t).\)
\(\square\)
Коэффициенты при \(\vecs{T}(t)\) и \(\vecs{N}(t)\) называются тангенциальной составляющей ускорения и нормальной составляющей ускорения соответственно. Мы пишем \(a_\vecs{T}\) для обозначения тангенциальной компоненты и \(a_\vecs{N}\) для обозначения нормальной компоненты.
Мы пишем \(a_\vecs{T}\) для обозначения тангенциальной компоненты и \(a_\vecs{N}\) для обозначения нормальной компоненты.
Теорема \(\PageIndex{2}\): тангенциальная и нормальная составляющие ускорения
Пусть \(\vecs{r}(t)\) — векторнозначная функция, которая обозначает положение объекта как функцию времени. Тогда \(\vecs{a}(t)=\vecs{r}′′(t)\) — вектор ускорения. Касательная и нормальная составляющие ускорения \(a_\vecs{T}\) и \(a_\vecs{N}\) определяются по формулам 92}}. \label{Eq2B} \]
Эти компоненты связаны формулой
\[\vecs{a}(t)=a_\vecs{T} \vecs{T}(t)+a_\vecs{N} \vecs{N}(t). \label{Eq3B} \]
Здесь \(\vecs{T}(t)\) — единичный касательный вектор к кривой, заданной \(\vecs{r}(t)\), а \(\vecs {N}(t)\) — единичный вектор нормали к кривой, заданной \(\vecs{r}(t)\).
Нормальная составляющая ускорения также называется центростремительной составляющей ускорения или иногда радиальной составляющей ускорения . Чтобы понять центростремительное ускорение, предположим, что вы едете в автомобиле по круговой трассе с постоянной скоростью. Затем, как мы видели ранее, вектор ускорения всегда направлен к центру пути. Как гонщик в машине, вы чувствуете притяжение к за пределами трассы, потому что вы постоянно поворачиваете. Это ощущение действует в направлении, противоположном центростремительному ускорению. То же самое верно и для некруговых путей. Причина в том, что ваше тело имеет тенденцию двигаться по прямой линии и сопротивляется силе, возникающей в результате ускорения, толкающей его в сторону. Обратите внимание, что в точке \(B\) на рисунке \(\PageIndex{4}\) вектор ускорения направлен назад. Это связано с тем, что автомобиль замедляется при входе в поворот.
Чтобы понять центростремительное ускорение, предположим, что вы едете в автомобиле по круговой трассе с постоянной скоростью. Затем, как мы видели ранее, вектор ускорения всегда направлен к центру пути. Как гонщик в машине, вы чувствуете притяжение к за пределами трассы, потому что вы постоянно поворачиваете. Это ощущение действует в направлении, противоположном центростремительному ускорению. То же самое верно и для некруговых путей. Причина в том, что ваше тело имеет тенденцию двигаться по прямой линии и сопротивляется силе, возникающей в результате ускорения, толкающей его в сторону. Обратите внимание, что в точке \(B\) на рисунке \(\PageIndex{4}\) вектор ускорения направлен назад. Это связано с тем, что автомобиль замедляется при входе в поворот.
Касательные и нормальные единичные векторы в любой заданной точке кривой обеспечивают систему отсчета в этой точке. 2−3t)\,\hat{\mathbf k}\), где \(t\) измеряет время в секундах а расстояние измеряется в футах.
2−3t)\,\hat{\mathbf k}\), где \(t\) измеряет время в секундах а расстояние измеряется в футах.
- Найти \(a_\vecs{T}\) и \(a_\vecs{N}\) как функции \(t\).
- Найти \(a_\vecs{T}\) и \(a_\vecs{N}\) в момент времени \(t=2\).
Решение
- Начнем вычислять функции скорости и ускорения:
\[\begin{align*} \vecs{v}(t) &= \vecs{r}'(t) \\[4pt] &= 2t\,\hat{\mathbf i}+2\,\ шляпа {\ mathbf j} + (6t-3) \, \ шляпа {\ mathbf k} \\ [4pt] \ vecs {a} (t) &= \ vecs {v} ‘(t) \\ [4pt] &=2\,\hat{\mathbf i}+6\,\hat{\mathbf k} \end{align*}\] Теперь применим уравнение \ref{Eq1B}: \[\begin{align*}a_ {\vecs{T}} &=\dfrac{\vecs{v}\cdot \vecs{a}}{||\vecs{v} ||} \\[4pt] &= \dfrac{ (2t \, \ шляпа {\ mathbf i} +2 \, \ шляпа {\ mathbf j} + (6t-3) \, \ шляпа {\ mathbf k}) \ cdot (2 \, \ шляпа {\ mathbf i} +6 \ , \ шляпа {\ mathbf k}) }{|| 2t\,\шляпа{\mathbf i} + 2\,\шляпа{\mathbf j} + (6t-3)\,\шляпа{\mathbf k} ||} \\[4pt] &= \dfrac{4t + 6(6t-3)}{\sqrt{(2t)^2 +2^2 + (6t-3)^2}} \\[4pt] &= \dfrac{40t-18}{40t^2 — 36t+13} \end{align*}\] Теперь мы можем применить уравнение \ref{Eq2B}: 92\,\hat{\mathbf j}\), где \(t\) измеряет время в секундах.
 2}} \end{align*}\ ] 92} } \\ = \sqrt{4- \dfrac{36}{11}} \\ = \sqrt{\dfrac{8}{11}}\\ =\dfrac{2\sqrt{2}}{\ sqrt{11}} \end{align*}\]
2}} \end{align*}\ ] 92} } \\ = \sqrt{4- \dfrac{36}{11}} \\ = \sqrt{\dfrac{8}{11}}\\ =\dfrac{2\sqrt{2}}{\ sqrt{11}} \end{align*}\]Движение снаряда
Теперь давайте рассмотрим применение векторных функций. В частности, давайте рассмотрим влияние силы тяжести на движение объекта при его перемещении по воздуху и то, как она определяет результирующую траекторию этого объекта. В дальнейшем мы пренебрегаем влиянием сопротивления воздуха. Эта ситуация, когда объект движется с начальной скоростью, но на него не действуют никакие другие силы, кроме силы тяжести, известна как движение снаряда. Он описывает движение объектов от мячей для гольфа до бейсбольных мячей и от стрел до пушечных ядер.
Сначала нам нужно выбрать систему координат. Если мы стоим в начале этой системы координат, то мы выбираем положительную ось \(y\) вверх, отрицательную ось \(y\) — вниз, а положительную \(x\). ) — ось должна быть направлена вперед (т.
Рисунок \(\PageIndex{5}\): Объект падает под действием силы тяжести. е. в сторону от метателя предмета). Действие гравитации направлено вниз, поэтому второй закон Ньютона говорит нам, что сила, действующая на объект в результате гравитации, равна массе объекта, умноженной на ускорение, вызванное гравитацией, или \(\vecs F_g=m\vecs a\), где \(\vecs F_g\) представляет собой силу гравитации, а \(\vecs a = -g\,\hat{\mathbf j}\) представляет собой ускорение, возникающее в результате действия силы тяжести на поверхности Земли. Значение \(г\) в английской системе измерений составляет примерно 32 фута/сек 2 и примерно 9,8 м/с 2 в метрической системе. Это единственная сила, действующая на объект. Поскольку гравитация действует вниз, мы можем записать силу, возникающую в результате гравитации, в виде \(\vecs F_g=−mg\,\hat{\mathbf j}\), как показано на рисунке \(\PageIndex{5} \).
е. в сторону от метателя предмета). Действие гравитации направлено вниз, поэтому второй закон Ньютона говорит нам, что сила, действующая на объект в результате гравитации, равна массе объекта, умноженной на ускорение, вызванное гравитацией, или \(\vecs F_g=m\vecs a\), где \(\vecs F_g\) представляет собой силу гравитации, а \(\vecs a = -g\,\hat{\mathbf j}\) представляет собой ускорение, возникающее в результате действия силы тяжести на поверхности Земли. Значение \(г\) в английской системе измерений составляет примерно 32 фута/сек 2 и примерно 9,8 м/с 2 в метрической системе. Это единственная сила, действующая на объект. Поскольку гравитация действует вниз, мы можем записать силу, возникающую в результате гравитации, в виде \(\vecs F_g=−mg\,\hat{\mathbf j}\), как показано на рисунке \(\PageIndex{5} \).Второй закон Ньютона также говорит нам, что \(F=m\vecs{a}\), где \(\vecs a\) представляет собой вектор ускорения объекта.
 Эта сила должна быть всегда равна силе тяжести, поэтому мы знаем, что
Эта сила должна быть всегда равна силе тяжести, поэтому мы знаем, что\[\begin{align*} \vecs F =\vecs F_g \\ m\vecs{a} = -mg \,\hat{\mathbf j} \\ \vecs{a} = -g\,\ шляпа {\ mathbf j}. \end{align*}\]
Теперь воспользуемся тем, что вектор ускорения является первой производной вектора скорости. Следовательно, мы можем переписать последнее уравнение в виде
\[\vecs v'(t) = -g\,\hat{\mathbf j} \nonumber \]
Взяв первообразную каждой части этого уравнения получаем
\[ \vecs v(t) = \int -g \,\hat{\mathbf j}\; dt = -gt\,\hat{\mathbf j} + \vecs C_1 \nonumber \]
для некоторого постоянного вектора \(\vecs C_1\). Чтобы определить значение этого вектора, мы можем использовать скорость объекта в фиксированный момент времени, скажем, в момент времени \(t=0\). Мы называем эту скорость начальной скоростью : \(\vecs v(0)=\vecs v_0\). Следовательно, \(\vecs v(0)=−g(0)\,\hat{\mathbf j}+\vecs C_1=\vecs v_0\) и \(\vecs C_1= \vecs v_0\).
 Это дает вектор скорости как \(\vecs v(t)=-gt\,\hat{\mathbf j}+\vecs v_0\).
Это дает вектор скорости как \(\vecs v(t)=-gt\,\hat{\mathbf j}+\vecs v_0\).Далее мы используем тот факт, что скорость \(\vecs{v}(t)\) является производной от положения \(\vecs{s}(t)\). Это дает уравнение 92 \,\hat{\mathbf j}+\vecs{v}_0 t+\vecs{s}_0. \nonumber \]
Рассмотрим подробнее начальную скорость и начальное положение. В частности, предположим, что объект брошен вверх из начала координат под углом \(\theta\) к горизонтали с начальной скоростью \(\vecs{v}_0\). Как мы можем изменить предыдущий результат, чтобы отразить этот сценарий? Во-первых, мы можем предположить, что он выброшен из источника. Если нет, то мы можем переместить начало координат в точку, откуда он был брошен. Следовательно, \(\vecs{s}_0=\vecs{0}\), как показано на рисунке \(\PageIndex{6}\). 92\справа)\,\шляпа{\mathbf j}. \end{align*}\]
Коэффициент \(\hat{\mathbf i}\) представляет собой горизонтальную составляющую \(\vecs{s}(t)\) и представляет собой горизонтальное расстояние объекта от начало координат во время \(t\) .
 Максимальное значение горизонтального расстояния (измеренное на одной и той же начальной и конечной высоте) называется дальностью \(R\). Коэффициент при \(\hat{\mathbf j}\) представляет вертикальную составляющую \(\vecs{s}(t)\) и представляет собой высоту объекта в момент \(t\) . Максимальное значение вертикального расстояния равно высоте \(H\).
Максимальное значение горизонтального расстояния (измеренное на одной и той же начальной и конечной высоте) называется дальностью \(R\). Коэффициент при \(\hat{\mathbf j}\) представляет вертикальную составляющую \(\vecs{s}(t)\) и представляет собой высоту объекта в момент \(t\) . Максимальное значение вертикального расстояния равно высоте \(H\).Пример \(\PageIndex{3}\): Движение пушечного ядра
Во время празднования Дня независимости пушечное ядро выпущено из пушки на скале в сторону воды. Пушка нацелена под углом 30° над горизонтом, а начальная скорость пушечного ядра составляет 600 футов/сек. Утес находится на высоте 100 футов над водой (рис. \(\PageIndex{7}\)).
- Найдите максимальную высоту пушечного ядра. 92 \right)\,\hat{\mathbf j} \end{align*}\]
- Пушечное ядро достигает максимальной высоты, когда вертикальная составляющая его скорости равна нулю, поскольку при этом пушечное ядро не поднимается и не падает.
 2}-4(4)(-25) }{2(4)} \\[4pt] &= \dfrac{75 \pm \sqrt{6025}}{ 8} \\[4pt] &= \dfrac{75 \pm 5\sqrt{241}}{8} \end{align*}\] 92\right)\,\hat{\mathbf j}\\[4pt] &=9914,26\,\hat{\mathbf i}−100,7424\,\hat{\mathbf j} \end{align*}\] Таким образом, мяч ударяется о воду примерно на расстоянии 9914,26 фута от основания утеса. Обратите внимание, что вертикальная составляющая вектора положения очень близка к −100, что говорит нам о том, что мяч только что ударился о воду. Обратите внимание, что 9914,26 фута не является истинным радиусом действия пушки, поскольку пушечное ядро приземляется в океане ниже пушки. Дальность действия пушки будет определяться путем определения того, как далеко находится пушечное ядро, когда его высота составляет 100 футов над водой (такая же, как высота пушки).
2}-4(4)(-25) }{2(4)} \\[4pt] &= \dfrac{75 \pm \sqrt{6025}}{ 8} \\[4pt] &= \dfrac{75 \pm 5\sqrt{241}}{8} \end{align*}\] 92\right)\,\hat{\mathbf j}\\[4pt] &=9914,26\,\hat{\mathbf i}−100,7424\,\hat{\mathbf j} \end{align*}\] Таким образом, мяч ударяется о воду примерно на расстоянии 9914,26 фута от основания утеса. Обратите внимание, что вертикальная составляющая вектора положения очень близка к −100, что говорит нам о том, что мяч только что ударился о воду. Обратите внимание, что 9914,26 фута не является истинным радиусом действия пушки, поскольку пушечное ядро приземляется в океане ниже пушки. Дальность действия пушки будет определяться путем определения того, как далеко находится пушечное ядро, когда его высота составляет 100 футов над водой (такая же, как высота пушки). - Путь любой планеты вокруг Солнца имеет форму эллипса, при этом центр Солнца находится в одном из фокусов эллипса (закон эллипсов).
- Линия, проведенная от центра Солнца к центру планеты, заметает равные площади за равные промежутки времени (закон равных площадей) (рисунок \(\PageIndex{8}\)).
- Отношение квадратов периодов любых двух планет равно отношению кубов длин их больших полуосей орбит (Закон Гармоний).

- Вес автомобиля;
- Трение между шинами и дорогой;
- Радиус окружности;
- «Крутизна» поворота.
Упражнение \(\PageIndex{3}\)
Лучник выпускает стрелу под углом 40° над горизонтом с начальной скоростью 98 м/сек. Рост лучника 171,5 см. Найдите горизонтальное расстояние, которое пролетит стрела до удара о землю.
 2\sin2\theta}{g}\,\hat{\mathbf i}. \end{выравнивание*}\] 92}{г}\) единиц.
2\sin2\theta}{g}\,\hat{\mathbf i}. \end{выравнивание*}\] 92}{г}\) единиц.Законы Кеплера
В начале 1600-х годов Иоганн Кеплер смог использовать удивительно точные данные своего наставника Тихо Браге, чтобы сформулировать свои три закона движения планет, теперь известные как законы движения планет Кеплера. Эти законы применимы и к другим объектам Солнечной системы, обращающимся вокруг Солнца, таким как кометы (например, комета Галлея) и астероиды. Варианты этих законов применяются к спутникам на орбите вокруг Земли.
Теорема \(\PageIndex{2}\): законы Кеплера о движении планет
Третий закон Кеплера особенно полезен при использовании соответствующих единиц измерения. В частности, 90 926 1 астрономическая единица 90 456 определяется как среднее расстояние от Земли до Солнца, и в настоящее время признано равным 149.3 \nonumber \]
для любой планеты Солнечной системы, где \(T_P\) — период жизни этой планеты, измеряемый в земных годах, а \(D_P\) — среднее расстояние от этой планеты до Солнца, измеряемое в астрономических единицы. Следовательно, если мы знаем среднее расстояние от планеты до Солнца (в астрономических единицах), то можем вычислить продолжительность ее года (в земных годах) и наоборот.
Законы Кеплера были сформулированы на основе наблюдений Браге; однако они не были официально доказаны, пока сэр Исаак Ньютон не смог применить исчисление.
 2} \) (Рисунок \(\PageIndex{93}\vecs{r}. \nonumber \]
2} \) (Рисунок \(\PageIndex{93}\vecs{r}. \nonumber \]Это уравнение показывает, что векторы \(d\vecs{v}/dt\) и \(\vecs r\) параллельны друг другу, поэтому \(d\vecs {v}/dt \ раз \vecs {r}=\vecs 0\). Далее продифференцируем \(\vecs{r} \times \vecs{v}\) по времени:
\[\dfrac{d}{dt}(\vecs{r}\times \vecs{v} )=\dfrac{d\vecs{r}}{dt}\times \vecs v+\vecs{r} \times \dfrac{d\vecs{v}}{dt}=\vecs{v}\times \vecs {v}+\vecs{0}=\vecs{0}. \label{Eq10} \]
Это доказывает, что \(\vecs{r}\times\vecs{v}\) является постоянным вектором, который мы называем \(\vecs C\). Поскольку \(\vecs r\) и \(\vecs v\) оба перпендикулярны \(\vecs C\) для всех значений \(t\), они должны лежать в плоскости, перпендикулярной \(\vecs C \). Следовательно, движение планеты лежит в плоскости. 93}[(\vecs{r} \cdot \vecs{v})\vecs{r} — (\vecs{r} \cdot \vecs{r})\vecs{v}]. \label{Eq11} \]
Последнее равенство в уравнении \ref{Eq10} взято из формулы тройного перекрестного произведения (Введение в векторы в пространстве).
 Нам нужно выражение для \(\vecs{r}\cdot \vecs{v}\). Чтобы вычислить это, мы дифференцируем \(\vecs{r}\cdot \vecs{r}\) по времени:
Нам нужно выражение для \(\vecs{r}\cdot \vecs{v}\). Чтобы вычислить это, мы дифференцируем \(\vecs{r}\cdot \vecs{r}\) по времени:\[ \dfrac{d}{dt}(\vecs{r}\cdot \vecs{ r})=\dfrac{d\vecs{r}}{dt}\cdot \vecs{r}+\vecs{r}\cdot \dfrac{d\vecs{r}}{dt}=2\vecs{ r}\cdot \dfrac{d\vecs{r}}{dt}=2\vecs{r}\cdot \vecs{v}. \label{Eq12} \] 92} \dfrac{d}{dt}||\vecs{r}||. \end{align*}\]
Следовательно, уравнение \ref{Eq15} принимает вид
\[\dfrac{d \vecs{v}}{dt}\times \vecs{C}=GM\left( \dfrac {d}{dt}\dfrac{ \vecs{r}}{ || \vecs{r} ||} \right).\nonumber \]
Так как \(\vecs{C}\) является постоянным вектором , мы можем проинтегрировать обе части и получить
\[ \vecs{v}\times\vecs{C} = GM \dfrac{ \vecs{r} }{|| \vecs{r} ||} + \vecs{D}, \nonumber \]
, где \(\vecs D\) — постоянный вектор. Наша цель — найти \(|| \vecs{r} ||\). Начнем с вычисления \( \vecs{r} \cdot ( \vecs{v}\times \vecs{C}\): 92}{GM}\left( \dfrac{1}{1+e\cos\theta} \right). \nonumber \]
, где \(e=||\vecs{D}||/GM\).
 Это полярное уравнение коники с фокусом в начале координат, которую мы установили как Солнце. Это гипербола, если \(e>1\), парабола, если \(e=1\), или эллипс, если \(e<1\). Поскольку планеты имеют замкнутые орбиты, единственной возможностью является эллипс. Однако здесь следует упомянуть, что гиперболические кометы существуют. Это объекты, которые просто проходят через Солнечную систему со скоростью, слишком большой, чтобы попасть на орбиту вокруг Солнца. Когда они проходят достаточно близко к Солнцу, гравитационное поле Солнца отклоняет траекторию настолько, что траектория становится гиперболической. 92\), а период обращения Луны равен 27,3 дня, найдем длину большой оси обращения Луны вокруг Земли.
Это полярное уравнение коники с фокусом в начале координат, которую мы установили как Солнце. Это гипербола, если \(e>1\), парабола, если \(e=1\), или эллипс, если \(e<1\). Поскольку планеты имеют замкнутые орбиты, единственной возможностью является эллипс. Однако здесь следует упомянуть, что гиперболические кометы существуют. Это объекты, которые просто проходят через Солнечную систему со скоростью, слишком большой, чтобы попасть на орбиту вокруг Солнца. Когда они проходят достаточно близко к Солнцу, гравитационное поле Солнца отклоняет траекторию настолько, что траектория становится гиперболической. 92\), а период обращения Луны равен 27,3 дня, найдем длину большой оси обращения Луны вокруг Земли.Решение
Важно соблюдать единицы измерения. Так как универсальная гравитационная постоянная содержит секунды в единицах, нам нужно использовать секунды и для периода Луны:
\[27,3\; \text{дни} \times \dfrac{24 \; \текст{ч}}{1 \; \text{день}} \times \dfrac{3600 \; \text{esc}}{1 \; \текст{час}} =2 358 720\; \text{сек}\номер \] 99 \text{м}= 1 224 000 \text{км} \номер\]
Пример \(\PageIndex{5}\): комета Галлея
Вернемся к началу главы, в котором обсуждается движение кометы Галлея вокруг Солнца.
 Первый закон Кеплера гласит, что комета Галлея следует по эллиптической траектории вокруг Солнца, причем Солнце является одним из фокусов эллипса. Период кометы Галлея составляет примерно 76,1 года, в зависимости от того, насколько близко она проходит мимо Юпитера и Сатурна, когда проходит через внешнюю часть Солнечной системы. Возьмем \(T=76,1\) лет. Каково среднее расстояние кометы Галлея от Солнца? 99\) миль.
Первый закон Кеплера гласит, что комета Галлея следует по эллиптической траектории вокруг Солнца, причем Солнце является одним из фокусов эллипса. Период кометы Галлея составляет примерно 76,1 года, в зависимости от того, насколько близко она проходит мимо Юпитера и Сатурна, когда проходит через внешнюю часть Солнечной системы. Возьмем \(T=76,1\) лет. Каково среднее расстояние кометы Галлея от Солнца? 99\) миль.Возникает естественный вопрос: каковы максимальное (афелий) и минимальное (перигелий) расстояния от кометы Галлея до Солнца? Эксцентриситет орбиты кометы Галлея составляет 0,967 (Источник: http://nssdc.gsfc.nasa.gov/planetary…cometfact.html). Напомним, что формула эксцентриситета эллипса имеет вид \(e=c/a\), где a — длина большой полуоси, а c — расстояние от центра до любого из фокусов. Следовательно, \(0,967=c/17,96\) и \(c\приблизительно 17,37\) а.е. Вычитая это из 99\) миль. Среднее расстояние от Плутона до Солнца составляет 39,5 а.
 е. (Источник: http://www.oarval.org/furthest.htm), поэтому кажется, что комета Галлея остается как раз в пределах орбиты Плутона.
е. (Источник: http://www.oarval.org/furthest.htm), поэтому кажется, что комета Галлея остается как раз в пределах орбиты Плутона.НАВИГАЦИЯ НА ПОВОРОТЕ В КРОН
Как быстро гоночный автомобиль может пройти круговой поворот без заноса и удара о стену? Ответ может зависеть от нескольких факторов:
В этом проекте мы исследуем этот вопрос для гоночных автомобилей NASCAR на гоночной трассе Bristol Motor Speedway в Теннесси. Прежде чем рассматривать этот трек в частности, мы используем векторные функции для развития математики и физики, необходимых для ответа на такие вопросы, как этот.
Автомобиль массой \(m\) движется с постоянной угловой скоростью \(\omega\) по окружности радиусом \(R\) (рисунок \(\PageIndex{9}\)). Кривая наклонена под углом \(\theta\). Если высота автомобиля над землей равна \(h\), то положение автомобиля в момент времени \(t\) определяется функцией \(\vecs r(t)=< R\cos(\omega t),R\sin(\omega t),h>\).
 2\). 92 \справа)/R\).
2\). 92 \справа)/R\).
При движении автомобиля по кривой на него действуют три силы: гравитация, сила со стороны дороги (эта сила перпендикулярна земле) и сила трения (рис. \(\PageIndex{10}\)) . Поскольку описать силу трения, создаваемую шинами и дорогой, сложно, мы используем стандартное приближение для силы трения. Предположим, что \(\vecs{f}=\mu \vecs{N}\) для некоторой положительной константы \(\mu \). Константа \(\mu\) называется коэффициентом трения .
Рисунок \(\PageIndex{10}\): На автомобиль действуют три силы: гравитация (обозначается \(m\vecs g\)) , сила трения \(\vecs f\) , а сила, действующая на дорогу \(\vecs N\) . Пусть \(v_{max}\) обозначает максимальную скорость, которую автомобиль может развить на повороте без заноса. Другими словами, \(v_{max}\) — это максимальная скорость, с которой автомобиль может пройти поворот. Когда автомобиль движется с этой скоростью, центростремительная сила равна 92}{Р}. \nonumber \]
\nonumber \]
Следующие три вопроса касаются разработки формулы, связывающей скорость \(v_{max}\) с углом крена \(\theta\).
- Покажите, что \(\vecs{N} \cos\theta=m\vecs g+\vecs{f} \sin\theta\). Сделайте вывод, что \(\vecs{N}=(m\vecs g)/(\cos\theta-\mu \sin\theta)\).
- Центростремительная сила представляет собой сумму сил в горизонтальном направлении, поскольку центростремительная сила направлена к центру круговой кривой. Покажи это
\[\vecs{F}_{cent}=\vecs{N} \sin\theta+\vecs{f}\cos\theta. \номер\] 92=((\sin\theta+\mu\cos\theta)/(\cos\theta-\mu\sin\theta))gR\). Сделать вывод, что максимальная скорость фактически не зависит от массы автомобиля.
Теперь, когда у нас есть формула, связывающая максимальную скорость автомобиля и угол крена, мы можем ответить на вопросы, аналогичные заданным в начале проекта.
Bristol Motor Speedway — шорт-трек NASCAR в Бристоле, штат Теннесси. Трек имеет приблизительную форму, показанную на рисунке \(\PageIndex{11}\). Каждый конец трассы примерно полукруглый, поэтому, когда автомобили поворачивают, они движутся примерно по круговой кривой. Если автомобиль выезжает на внутреннюю колею и движется со скоростью в нижней части поворота 1, он движется по полукругу радиусом примерно 211 футов с углом крена 24°. Если автомобиль решает пойти по внешнему пути и мчится по вершине поворота 1, то автомобиль движется по полукругу с углом крена 28°. (Трасса имеет вираж с переменным углом наклона.)
Каждый конец трассы примерно полукруглый, поэтому, когда автомобили поворачивают, они движутся примерно по круговой кривой. Если автомобиль выезжает на внутреннюю колею и движется со скоростью в нижней части поворота 1, он движется по полукругу радиусом примерно 211 футов с углом крена 24°. Если автомобиль решает пойти по внешнему пути и мчится по вершине поворота 1, то автомобиль движется по полукругу с углом крена 28°. (Трасса имеет вираж с переменным углом наклона.)
Коэффициент трения для обычной шины в сухих условиях составляет примерно 0,7. Поэтому мы предполагаем, что коэффициент для шины NASCAR в сухих условиях составляет примерно 0,98.
Прежде чем ответить на следующие вопросы, обратите внимание, что проще производить расчеты в футах и секундах, а затем перевести ответы в мили в час в качестве последнего шага.
- Как быстро автомобиль может пройти нижнюю часть поворота в сухую погоду без заноса?
- Как быстро автомобиль может пройти начало поворота в сухую погоду без заноса?
- Во влажных условиях коэффициент трения может достигать 0,1. Если это так, то как быстро автомобиль может пройти нижнюю часть поворота без заноса?
- Предположим, измеренная скорость автомобиля, движущегося по внешнему краю поворота, составляет 105 миль в час. Оцените коэффициент трения шин автомобиля.
Ключевые понятия
- Если \(\vecs{r}(t)\) представляет положение объекта в момент времени t , то \(\vecs{r}'(t)\) представляет скорость и \(\vecs{r}′′(t)\) представляет собой ускорение объекта в момент времени t.
 Величина вектора скорости равна скорости.
Величина вектора скорости равна скорости. - Вектор ускорения всегда указывает на вогнутую сторону кривой, определяемой \(\vecs{r}(t)\). Тангенциальная и нормальная составляющие ускорения \(a_\vecs{T}\) и \(a_\vecs{N}\) являются проекциями вектора ускорения на единичный касательный и единичный вектор нормали к кривой.
- Три закона движения планет Кеплера описывают движение объектов по орбите вокруг Солнца. Его третий закон можно изменить, чтобы описать движение объектов на орбите вокруг других небесных тел.
- Ньютон смог использовать свой закон всемирного тяготения в сочетании со своим вторым законом движения и исчислением, чтобы доказать три закона Кеплера.
Ключевые уравнения
- Скорость \[\vecs{v}(t)=\vecs{r}′(t) \nonumber \]
- Ускорение \[\vecs{a}(t)=\vecs{v}'(t)=\vecs{r}»(t) \nonumber \]
- Скорость \[v(t)=||\vecs{v}(t)||=||\vecs{r}′(t)||=\dfrac{ds}{dt} \nonumber \]
- Тангенциальная составляющая ускорения \[a_{\vecs{T}} =\vecs{a}\cdot \vecs{T}=\dfrac{\vecs{v}\cdot \vecs{a}}{|| \vecs v||} \номер\]
- Нормальная составляющая ускорения \[a_{\vecs{N}}=\vecs{a}\cdot \vecs{N} = \dfrac{|| \vecs{v} \times \vecs{a} ||}{||\vecs{v}||} = \sqrt{||\vecs{a}||^2 — a_{\vecs{T}} } \номер\]
Глоссарий
- вектор ускорения
- вторая производная вектора положения
- Законы Кеплера о движении планет
- три закона, управляющие движением планет, астероидов и комет на орбитах вокруг Солнца
- нормальная составляющая ускорения
- коэффициент единичного вектора нормали \(\vecs N\), когда вектор ускорения записан как линейная комбинация \(\vecs T\) и \(\vecs N\)
- движение снаряда
- движение объекта с начальной скоростью, но без действия другой силы, кроме силы тяжести
- тангенциальная составляющая ускорения
- коэффициент единичного касательного вектора \(\vecs T\), когда вектор ускорения записан как линейная комбинация \(\vecs T\) и \(\vecs N\)
- вектор скорости
- производная вектора положения
Авторы и авторство
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Показать страницу Содержание
- нет
- Метки

Свойства тангенциальных и радиальных углов мюонов в ШАЛ – arXiv Vanity
J. Zabirowski\addressSoltan Institute for Nuclear Research, Cosmic Ray Phys. отдел,
а/я 447, PL-90-950 Лодзь, Польша
,
K. Daumiller\addressInstitut für Experimentelle Kernphysik, Universität Karlsruhe,
а/я 3640, D-76021 Карлсруэ, Германия
а также
P. Doll\addressInstitut für Kernphysik, Forschungszentrum Karlsruhe,
Почтовый индекс Box 3640, D-76021 Карлсруэ, Германия
электронная почта:
Abstract
Тангенциальные и радиальные углы мюонов в ШАЛ — полезное понятие для исследования высоты рождения мюонов, может быть использован также для исследования мюонные импульсы. Параметр ζ, являющийся комбинацией тангенциального и радиальные углы, и его возможные приложения в исследовании мюонов в ливнях.
1 Введение
эксперимента ШАЛ, объединяющие массивы полевых детекторов, способные измерять
направление ливня — с детекторами слежения за мюонами, можно использовать для определения
средней высоты рождения мюонов (MPH), параметра, чувствительного к первичному
масса. Треки мюона в воздушном ливне, как правило, не компланарны ливню.
оси, которые привели к понятию тангенциального и радиального углов [1] .
Однако, как будет показано ниже, эти две независимые наблюдаемые
может дать возможность исследовать компоненты импульса мюона в ливнях.
Хороший пример эксперимента EAS, в котором идеи, представленные в этой статье,
можно использовать KASCADE [2] с его недавно представленным большим мюонным
Детектор слежения [3] . Мы используем данные, смоделированные с помощью CORSIKA [4] .
ver.5.644 и модель адронных взаимодействий QGSJet для всех обсуждений и примеров
приведен ниже.
Треки мюона в воздушном ливне, как правило, не компланарны ливню.
оси, которые привели к понятию тангенциального и радиального углов [1] .
Однако, как будет показано ниже, эти две независимые наблюдаемые
может дать возможность исследовать компоненты импульса мюона в ливнях.
Хороший пример эксперимента EAS, в котором идеи, представленные в этой статье,
можно использовать KASCADE [2] с его недавно представленным большим мюонным
Детектор слежения [3] . Мы используем данные, смоделированные с помощью CORSIKA [4] .
ver.5.644 и модель адронных взаимодействий QGSJet для всех обсуждений и примеров
приведен ниже.
2 Тангенциальные и радиальные углы
Как показано на рис. 1, направление ливня и расположение мюонный детектор определяют две перпендикулярные плоскости: тангенциальную и радиальные.
Тангенциальный угол τ и радиальный угол ρ являются углами между
направление ливня и ортогональные проекции мюонного трека на
тангенциальной и радиальной плоскостях соответственно.
Измеренное значение τ отражает величину рассеяния мюонов в атмосфере и любой соответствующий материал поглотителя/детектора вместе с возможное смещение места рождения мюона от оси ливня. Его распространение (рис. 2) симметрична относительно нуля и сужается с увеличением импульса мюона, чего можно было ожидать от величины, связанной с многократное рассеяние.
Рисунок 2: Зависимость тангенциального угла от импульса мюона. Рисунок 3: Распределение радиального угла.Типичное распределение радиального угла показано на рис. 3. Его значение зависит от поперечного импульса родителя мюона (мезона) и расстояния мюона к оси ливня на уровне наблюдения. В реальных экспериментальных условиях мюоны отбираются в определенном диапазоне расстояний от ядра. Заштрихованное распределение показано для типичного расстояния 20–180 м от основной. Большие значения ρ удаляются.
3 Параметр ζ
Как видно из рис. 1, используя простую тригонометрию и подставляя
тангенс угла, что верно в пределах 5% погрешности до 0. 4рад,
можно записать следующие выражения для τ и ρ:
4рад,
можно записать следующие выражения для τ и ρ:
τ≅PBPD=ptp∥×sin∠POB
ρ≅PAPD=ptp∥×cos∠POB
Определим новый параметр ζ следующим образом:
ς ≡√τ2+ρ2=ptp∥ ;
, который действителен для τ ≤ 0,4 рад и ρ ≤ 0,4 рад.
Итак, измеряя в эксперименте углы ливня и мюонов и вычисляя ρ и τ, с помощью ζ появляется возможность исследовать мюонные импульсное пространство. Точность ζ зависит от точности углового измерений в атмосферном ливне и, в частности, на точность слежения за мюонами. Известно, что точность слежения улучшается, когда только мюоны высоких энергий считается. Поэтому хотелось бы иметь как можно большее содержание мюонов высоких энергий в анализируемая выборка данных, насколько это возможно.
Рис. 4. Распределение мюонов по импульсу в ливнях, инициированных первичными потоками протонов с энергия E0=1015 эВ. Заштрихованная область показывает влияние эксперимента. порог 1 ГэВ/c и ограниченное расстояние до ядра ливня: 20 — 180 м. Типичное распределение мюонов по импульсу в ливнях, инициированных первичными потоками протонов с
E0=1015 эВ показано на рис. 4. Во всех моделируемых ливнях (твердых
линия) ≈ 30% составляют мюоны с импульсом более 10 ГэВ/c. В действительности
экспериментальные условия, где порог, например. 1 ГэВ/с, а мюоны
регистрируется в ограниченном диапазоне расстояний до ядра ливня, получается заштрихованная
распределения на рис. 4. В этом образце при значительно сниженном
статистики уже имеется ≈ 45 % мюонов с pµ ≥ 10 ГэВ/c.
Однако хотелось бы увеличить содержание мюонов высоких энергий в выборке данных даже
больше, и для этой цели можно использовать параметр ζ.
4. Во всех моделируемых ливнях (твердых
линия) ≈ 30% составляют мюоны с импульсом более 10 ГэВ/c. В действительности
экспериментальные условия, где порог, например. 1 ГэВ/с, а мюоны
регистрируется в ограниченном диапазоне расстояний до ядра ливня, получается заштрихованная
распределения на рис. 4. В этом образце при значительно сниженном
статистики уже имеется ≈ 45 % мюонов с pµ ≥ 10 ГэВ/c.
Однако хотелось бы увеличить содержание мюонов высоких энергий в выборке данных даже
больше, и для этой цели можно использовать параметр ζ.
Действительно, как видно из рис. 5, ζ сильно зависит от импульс. В то время как при малых импульсах наблюдается полный разброс значений ζ, его распределение становится более ограниченным низкими значениями с увеличением мюонного импульс.
Рисунок 5: Зависимость ζ от импульса мюона. На нижней панели среднее значение ζ нанесен на график. Среднее значение ζ экспоненциально убывает с импульсом, что показано на
нижняя панель рис. 5. Таким образом, при анализе можно использовать разрез
на значение ζ и, таким образом, увеличить содержание мюонов высоких энергий в
анализируемый образец.
На рис. 6 отношение мюонов с импульсом более 10 ГэВ/c ко всем мюонам в образце (выше порога 1 ГэВ/c) в зависимости от приложенного разреза на Значение ζ построено для двух первичных энергий протонов. Только мюоны в рассматривалось расстояние от 20 до 180 м до ядра ливня. Видно, что выбирая для анализа мюоны напр. с ζ < 0,02 приводит к значительным увеличение содержания высокоэнергетических мюонов в выборке данных.
Рис. 6. Относительное содержание мюонов с импульсом более 10 ГэВ/с во всех данных. образца (мюоны выше 1 ГэВ/c) в зависимости от приложенного ζ-разреза.Другое применение параметра ζ довольно прямолинейно. Его значение не что иное, как тангенс угла мюона относительно оси ливня. Итак, зная расстояние до ядра ливня простая триангуляция позволяет воспроизвести производственная высота. Конечно, предполагается, что мюоны исходят из оси ливня, что в общем-то не так. Но, оказывается, такое приближение работает хорошо.
Рисунок 7: Сравнение истинного (z0) и реконструированного с использованием параметра ζ (MPH) распределения высот рождения мюонов для двух основных компонентов, протона и железа, Е0=1015 эВ. Выборка данных была обогащена мюонами высоких энергий путем отбора мюонов.
с ζ < 0,02.
Выборка данных была обогащена мюонами высоких энергий путем отбора мюонов.
с ζ < 0,02.На рис. 7 сравниваются истинные распределения высот рождения мюонов (z0) с расчетными (MPH), используя только что упомянутую процедуру, для двух первичных виды, H и Fe с энергией E0=1015 эВ. В этих расчетах разрез на ζ < 0,02. Видно хорошее согласие обоих кривые. Средние значения высот добычи разнесены более чем на 2 километра для протон и железо. Таким образом, можно использовать эту процедуру расчета среднего образования мюонов высота для определения первичной массы.
Параметр ζ можно использовать для исследования быстрот мюонов в ливнях. Замена импульса для полной энергии, которая допускается выше 1 ГэВ без существенной ошибки, можно выразить быстроту y и псевдобыстроту η с помощью параметра ζ следующим образом:
y=12lnE+p∥E−p∥≈12ln(√ζ2+1)+1(√ζ2+1)−1
η=ln2×p∥pt≈−lnζ2
В качестве примера на рис. 8 показано псевдобыстрое распределение мюонов в ливнях, инициированных
первичным протоном с энергией E0=1016 эВ. Только мюоны с импульсом больше
1 ГэВ/с. Пунктирная линия показывает все значения псевдобыстроты для всех смоделированных мюонов.
Сплошная линия соответствует случаю, когда η можно вычислить по параметру ζ, т.е.
мюонов с абсолютными значениями τ и ρ менее 0,4 рад. Штриховая линия соответствует
случае, когда расстояние мюонов до ядра ливня находится в диапазоне 20 — 180 м. Большие значения,
самые интересные,
обрезаются из-за минимального расстояния 20 м, поэтому важно приходить с измерениями как можно ближе к
ядро, насколько это возможно.
Только мюоны с импульсом больше
1 ГэВ/с. Пунктирная линия показывает все значения псевдобыстроты для всех смоделированных мюонов.
Сплошная линия соответствует случаю, когда η можно вычислить по параметру ζ, т.е.
мюонов с абсолютными значениями τ и ρ менее 0,4 рад. Штриховая линия соответствует
случае, когда расстояние мюонов до ядра ливня находится в диапазоне 20 — 180 м. Большие значения,
самые интересные,
обрезаются из-за минимального расстояния 20 м, поэтому важно приходить с измерениями как можно ближе к
ядро, насколько это возможно.
Приведенный выше пример показывает, что с помощью ζ можно исследовать быстроты мюонов в душ. В общем, измерение направленных параметров мюонов в ливнях с помощью ζ параметра можно исследовать импульсное пространство мюона.
Авторы признательны за большую поддержку этой работы, полученную от Польской государственной
Комитет по научным исследованиям (грант
№ 5 P03B 133 20) и Федерального министерства исследований Германии (05 CU1VK1/9, ВТЗ ПОЛ 99/005).
Каталожные номера
- [1] К. Бернлёр, Astropart. физ. 5 (1996) 139.
- [2] Х.О. Klages et al.-KASCADE, Nucl. физ. B (Proc. Suppl.) 52B (1997) 92.
- [3] P. Doll и др., Nucl. Инстр. и мет. А488 (2002) 517.
- [4] D. Heck et al., FZKA report 6019, Forschungszentrum Karlsruhe (1998).
Касательный или описанный четырехугольник, теоремы и задачи. Электронное обучение.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Узнать о центростремительном и тангенциальном ускорении
центростремительное и тангенциальное ускорение Определение
Центростремительное ускорение определяется как движение объекта к центральной точке окружности, тогда как при тангенциальном ускорении объект движется к касательной окружности.
Обзор центростремительного и тангенциального ускорения
Ускорение можно определить как изменение скорости движущегося объекта. Любой объект, находящийся в движении, обладает ускорением. Когда объект движется равномерно по кругу, его направление постоянно меняется, поэтому с ним всегда связано некоторое ускорение. Слово «центростремительный» означает движение к центральной точке, поэтому при этом типе ускорения объект движется к центральной точке окружности.
Центростремительное ускорение прямо пропорционально скорости или скорости движущегося объекта и обратно пропорционально радиусу окружности. Тангенциальное ускорение можно определить по тому, насколько быстро изменяется скорость объекта, движущегося по кругу. Это тангенциальное ускорение всегда направлено перпендикулярно центростремительному ускорению объекта, движущегося по окружности. Итак, при тангенциальном ускорении объект движется по касательной к окружности.
Есть вопрос по этой теме?
Что вы выучите:
- Центрипетальный и тангенциальный определение ускорения
- Обзор центрипетального и тангенциального ускорения
- Центрипетальный ускорение. в скорости движущегося объекта и изменениях, происходящих в направлении движущегося объекта, даже если скорость этого движущегося объекта считается постоянной.
 Когда объект движется по равномерному круговому движению, его направление постоянно меняется, поэтому с ним всегда связано некоторое ускорение. Человек также может испытать этот тип ускорения во время вождения автомобиля. Это ускорение может стать гораздо более заметным, если скорость автомобиля будет больше. Слово центростремительный означает направление к центральной точке, поэтому этот тип ускорения указывает на центральную точку вращающегося тела. Центростремительное ускорение определяется как:
Когда объект движется по равномерному круговому движению, его направление постоянно меняется, поэтому с ним всегда связано некоторое ускорение. Человек также может испытать этот тип ускорения во время вождения автомобиля. Это ускорение может стать гораздо более заметным, если скорость автомобиля будет больше. Слово центростремительный означает направление к центральной точке, поэтому этот тип ускорения указывает на центральную точку вращающегося тела. Центростремительное ускорение определяется как: ac=ΔvΔt{a_c} = \frac{{\Delta v}}{{\Delta t}}ac=ΔtΔv
Δv=v2−v1\Delta v = {v_2} — {v_1}Δv= v2−v1
Где ac={a_c} =ac= центростремительное ускорение, Δv=\Delta v = Δv= изменение скорости, Δt=\Delta t = Δt= изменение во времени
Треугольник ABC который состоит из радиусов, обозначенных r, и длины хорды, обозначенной ∆s, показана на рисунке выше. Другой треугольник PQR, который состоит из векторов скорости, также показан на вышеприведенном рисунке.
 Оба эти треугольника, показанные выше, имеют две из трех равных сторон, поэтому называются равнобедренными треугольниками. Итак, v1=v2=v{v_1} = {v_2} = vv1=v2=v Поскольку эти оба треугольника называются подобными треугольниками, то в соответствии с их свойствами это дается как:
Оба эти треугольника, показанные выше, имеют две из трех равных сторон, поэтому называются равнобедренными треугольниками. Итак, v1=v2=v{v_1} = {v_2} = vv1=v2=v Поскольку эти оба треугольника называются подобными треугольниками, то в соответствии с их свойствами это дается как:Δvv=Δsr\frac{{\Delta v}}{v} = \frac{{\Delta s}}{r}vΔv=rΔs
Δv=vrΔs\Delta v = \frac{v}{ r}\Delta sΔv=rvΔs
Разделив Δt\Delta tΔt на обе стороны, получим:
ΔvΔt=vr×ΔsΔt\frac{{\Delta v}}{{\Delta t}} = \frac {v}{r} \times \frac{{\Delta s}}{{\Delta t}}ΔtΔv=rv×ΔtΔs
Где Δv=\Delta v = Δv= изменение скорости движущегося объекта , Δt\Delta tΔt изменение во времени, скорость или скорость движущегося объекта, r радиус окружности, Δs=\Delta s = Δs= изменение длины хорды 92}}}{r}ac=rv2
Где ac{a_c}ac= центростремительное ускорение, v = скорость или скорость движущегося объекта, r = радиус окружности
Таким образом, центростремительное ускорение прямо пропорциональна скорости или скорости движущегося объекта и обратно пропорциональна радиусу окружности.
 Следовательно, можно сказать, что центростремительное ускорение будет больше только в том случае, если скорость движущегося объекта больше, а радиус окружности, по которой он движется, меньше.
Следовательно, можно сказать, что центростремительное ускорение будет больше только в том случае, если скорость движущегося объекта больше, а радиус окружности, по которой он движется, меньше.Тангенциальное ускорение
Когда объект движется по кругу, тангенциальное ускорение можно определить по тому, насколько быстро изменяется скорость этого объекта. Это тангенциальное ускорение всегда направлено перпендикулярно центростремительному ускорению объекта, движущегося по окружности. Это ускорение будет наблюдаться только тогда, когда объект движется по кругу. Предположим, что автомобиль движется с некоторой скоростью по круговой кривой, пересекающей дорогу, что показывает, что автомобиль находится по касательной к этой кривой. Итак, наблюдая за движением автомобиля, мы сможем увидеть тангенциальное ускорение. Тангенциальное ускорение очень похоже на линейное ускорение, но единственная разница в том, что объект при линейном ускорении движется по прямой линии, тогда как при тангенциальном ускорении объект движется по кругу.

Тангенциальное ускорение = (радиус вращения) × (угловое ускорение) {\ rm {тангенциальное ускорение}} = ({\ rm {радиус вращения}}) \ times ({\ rm {угловое ускорение}}) Тангенциальное ускорение = (радиус вращения) × ( угловое ускорение)
at=ΔvΔt{a_t} = \frac{{\Delta v}}{{\Delta t}}at=ΔtΔv
здесь at={a_t} = at= тангенциальное ускорение, Δv=\ Delta v = Δv= изменение скорости тела, Δt=\Delta t = Δt= изменение во времени
Тангенциальное ускорение по отношению к расстоянию определяется как: 92}}}at=dt2d2s
Или
at=v⋅dvds{a_t} = v \cdot \frac{{dv}}{{ds}}at=v⋅dsdv
Где at= {a_t} = at= тангенциальное ускорение, ds={\rm{ds}} = ds=изменение пройденного расстояния, v={\rm{v}} = v= линейная скорость, t затраченное время, d v изменение скорости, d t изменение во времени
Различные возможные значения тангенциального ускорения
Существует три основных возможных диапазона значений, которые может иметь тангенциальное ускорение.


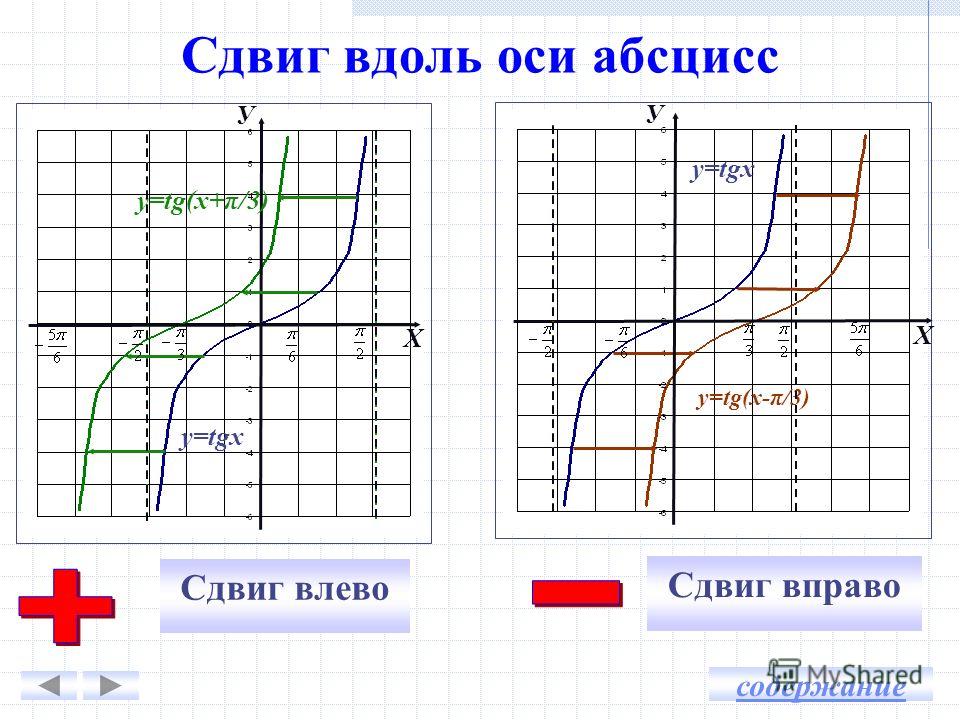 2x}$.
2x}$.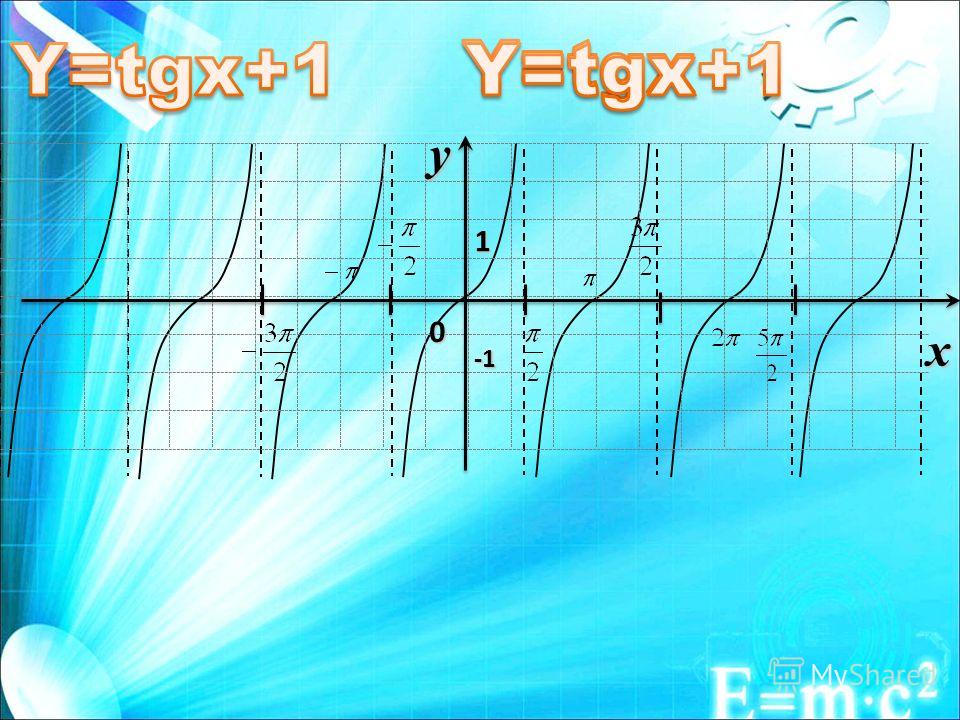

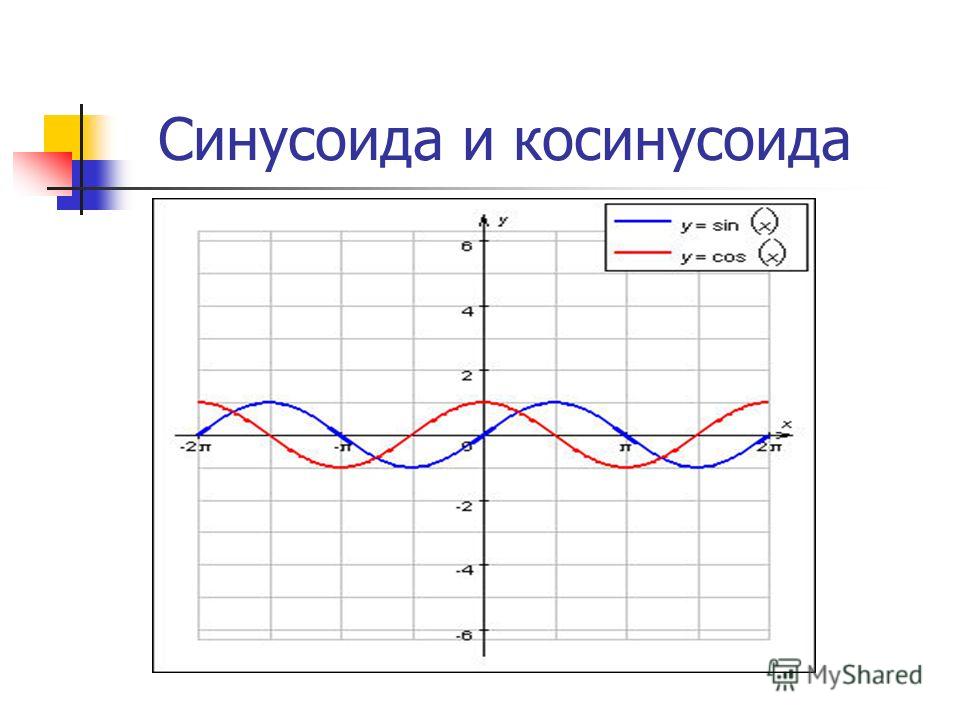
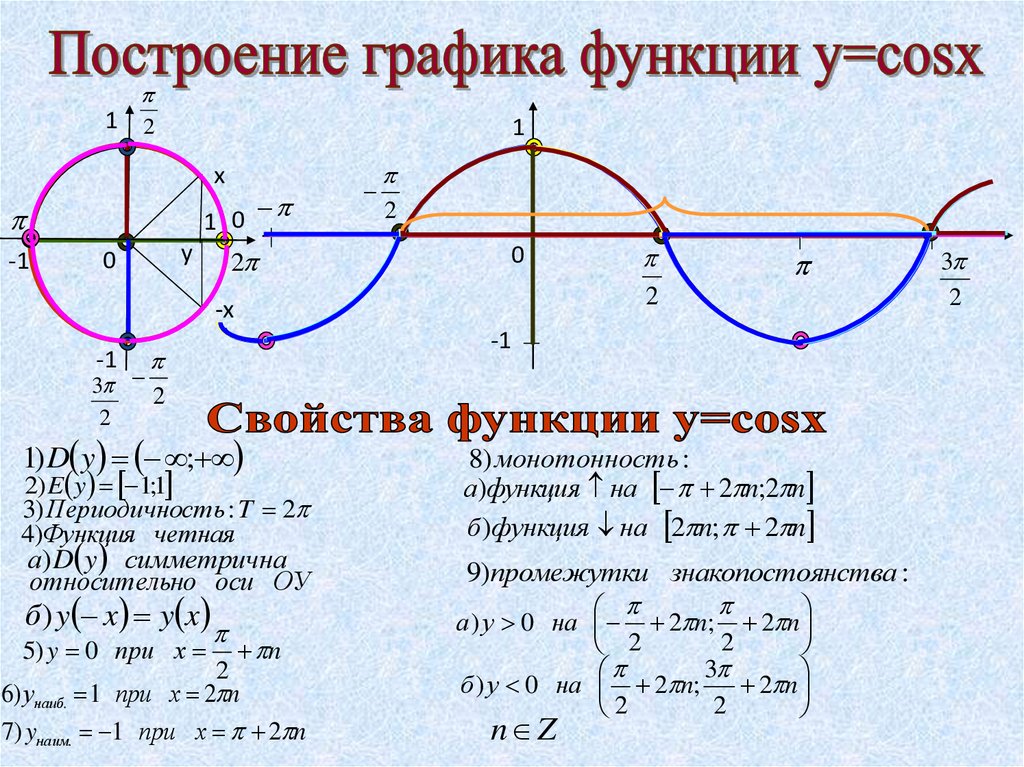 Определение промежутков знакопостоянства.
Определение промежутков знакопостоянства. Что называется областью определения функции?
Что называется областью определения функции?



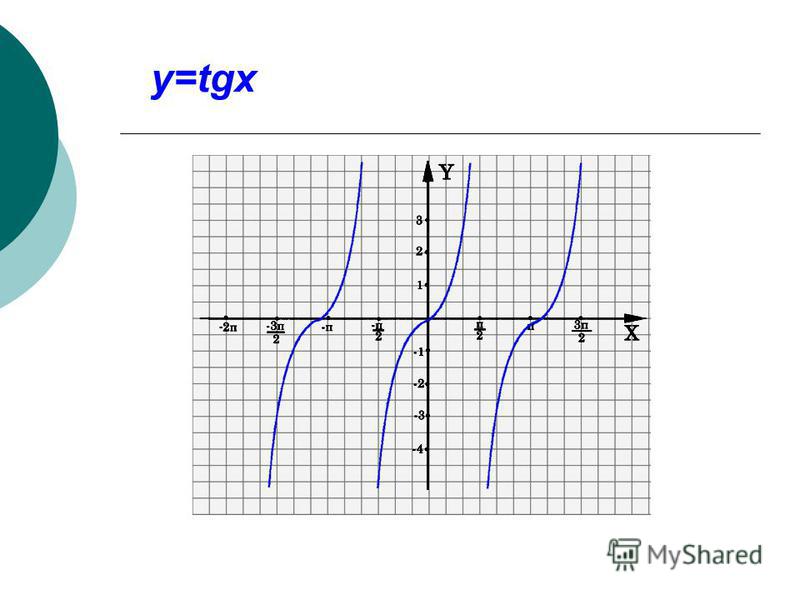
 2. Растяжение графика вдоль оси Оу с коэффициентом равным -2, растяжение вдоль оси Ох с коэффициентом равным 2.
2. Растяжение графика вдоль оси Оу с коэффициентом равным -2, растяжение вдоль оси Ох с коэффициентом равным 2.
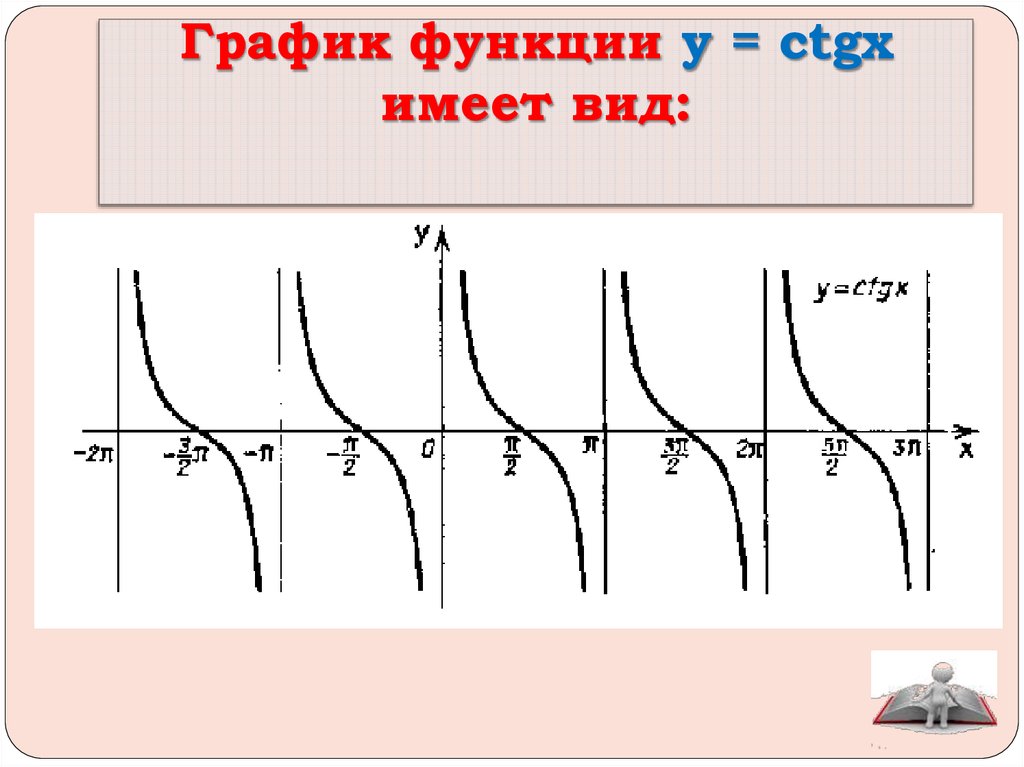

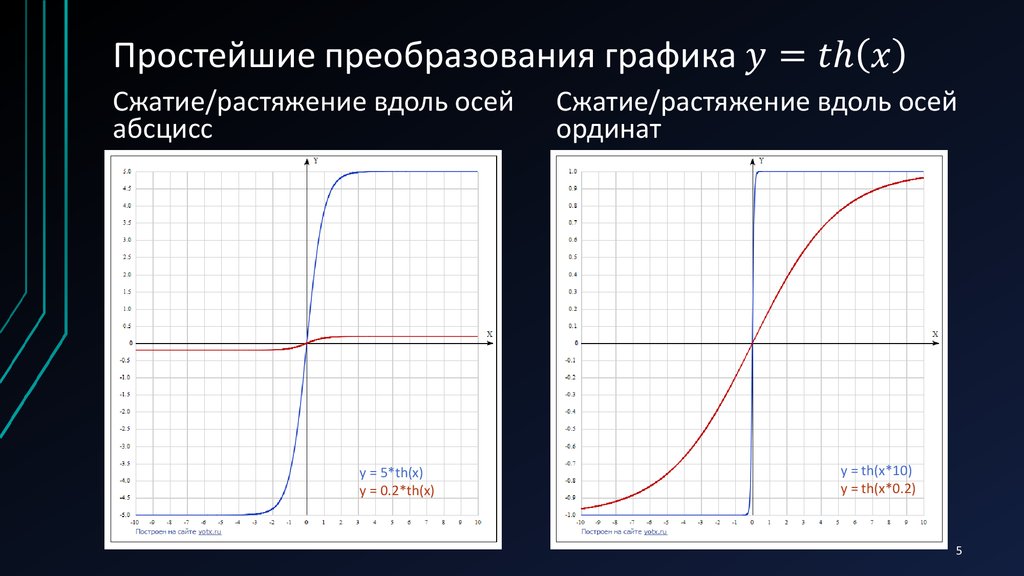

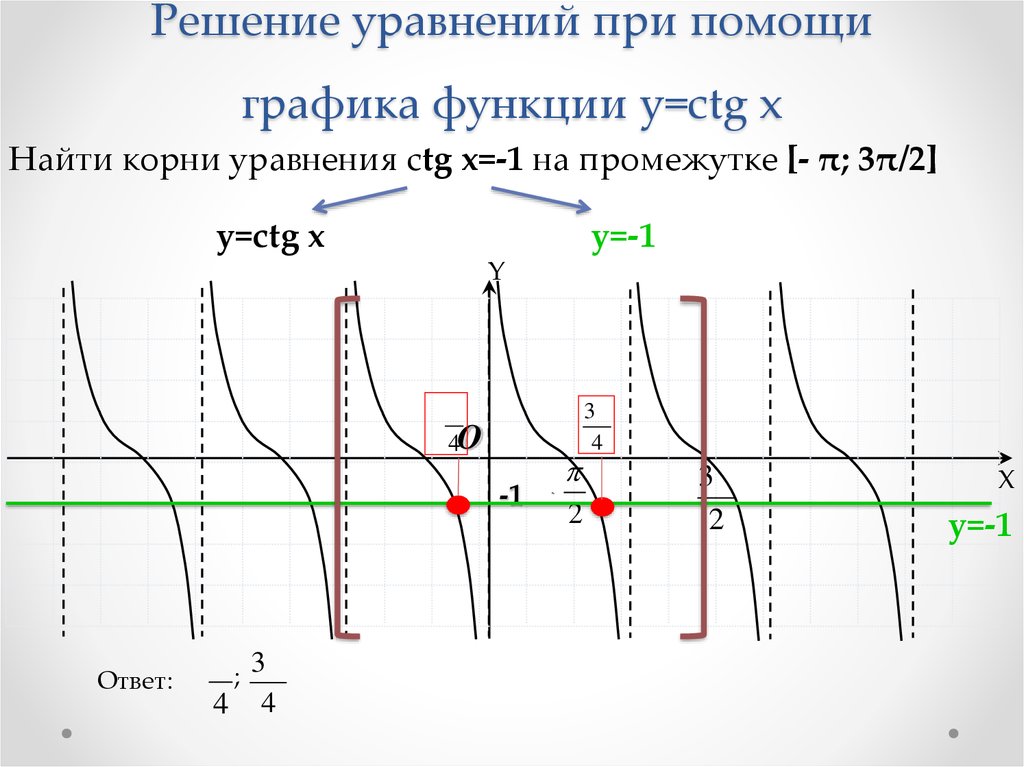

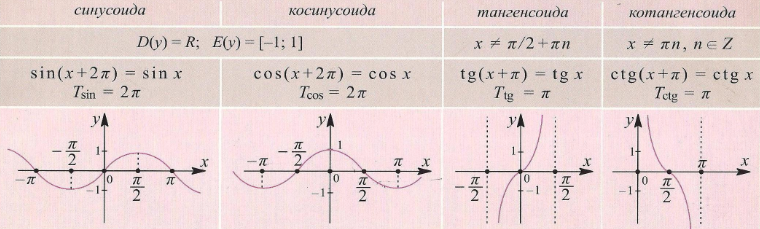
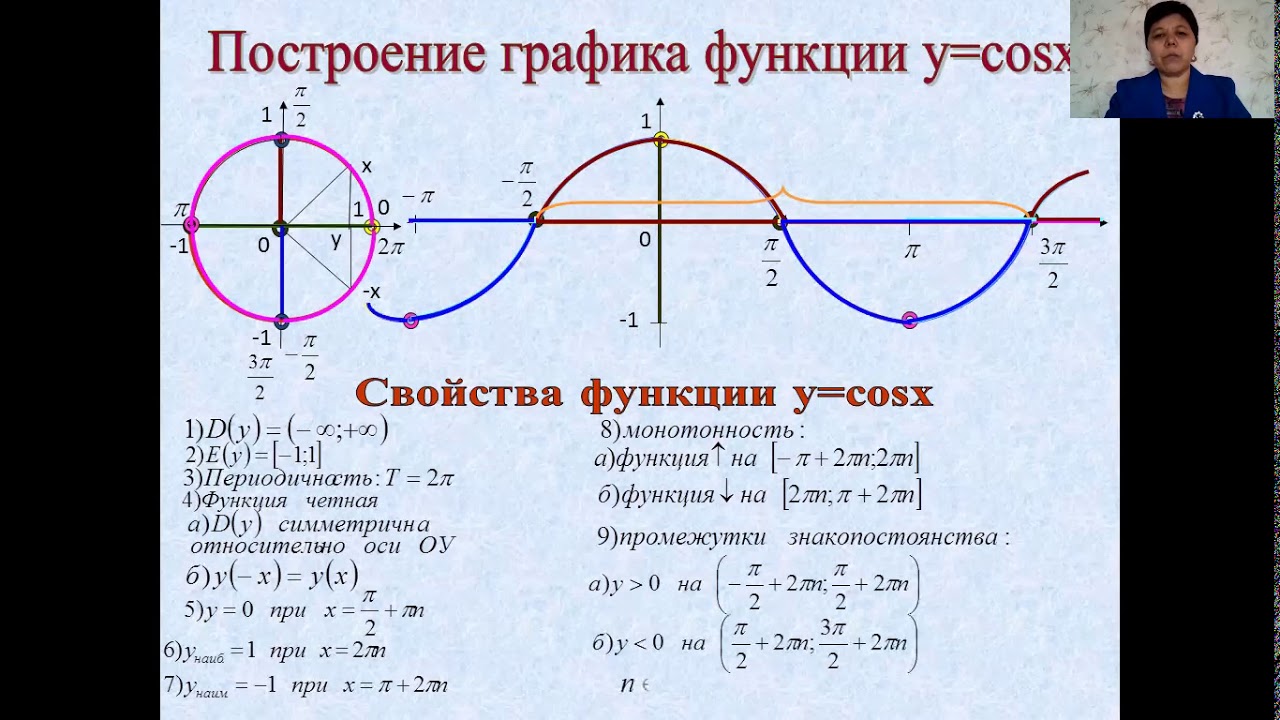
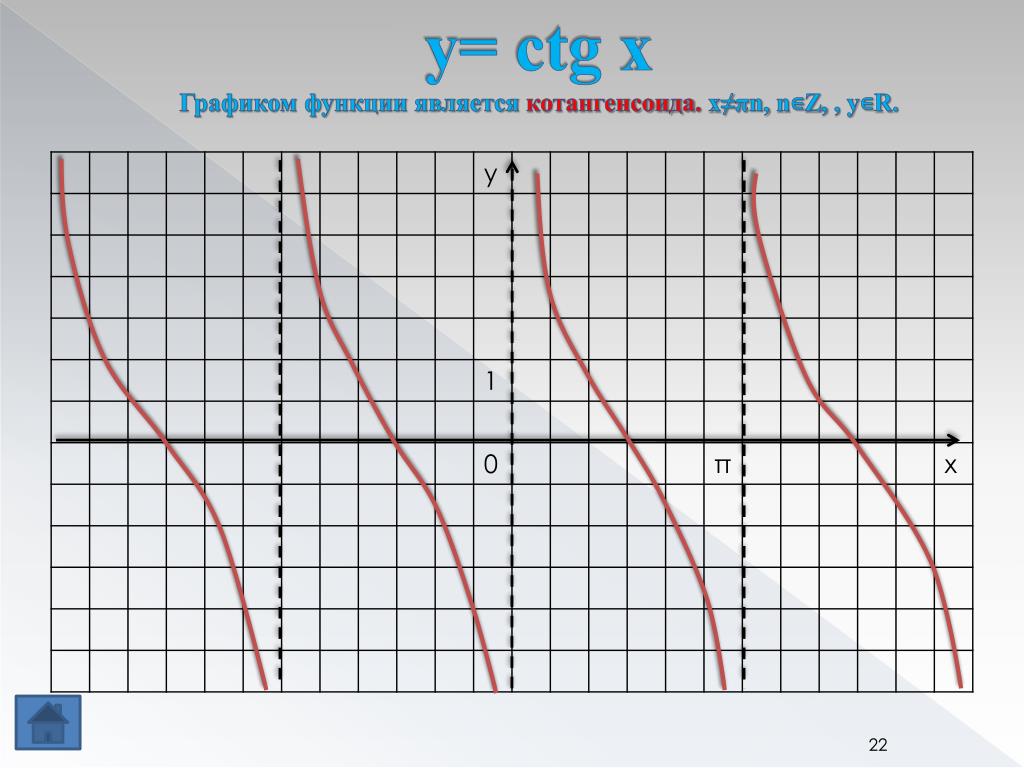

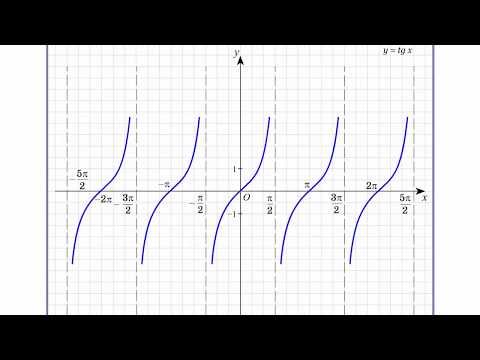 Таким образом, ΔOAC прямоугольный в C. Кроме того, C является серединой AB, поэтому AC = BC = (1/2)AB. Using the Pythagoras theorem, we have:
Таким образом, ΔOAC прямоугольный в C. Кроме того, C является серединой AB, поэтому AC = BC = (1/2)AB. Using the Pythagoras theorem, we have: