Math.ru
Владимир Григорьевич Шерватов
Гостехиздат, 1954. 58 с.
Тираж 25000 экз.
Серия Популярные лекции по математике, выпуск 16
| |||||||||||
Настоящая брошюра содержит элементарное изложение
теории так называемых «гиперболических функций», во многом аналогичных
обыкновенным тригонометрическим функциям. Гиперболические функции
часто встречаются в разнообразных физических и технических исследованиях;
весьма важную роль играют они также в неевклидовой геометрии
Лобачевского, участвуя во всех тригонометрических зависимостях этой
геометрии (см., например, книгу А. П. Нордена «Элементарное введение
в геометрию Лобачевского», М.
Брошюра состоит из трех глав. Первая глава посвящена гиперболическому повороту и его применению к изучению свойств гиперболы; она может представлять и известный самостоятельный интерес. Основное место занимает глава II, в которой излагаются элементы теории гиперболических функций. Глава III тесно связана с брошюрой А. И. Маркушевича «Площади и логарифмы», составляющей вып. 9 «Популярных лекций по математике»; она устанавливает связь теории гиперболических функций с теорией логарифмов.
Иное построение теории гиперболических функций, не
использующее гиперболического поворота, содержится в статье Д.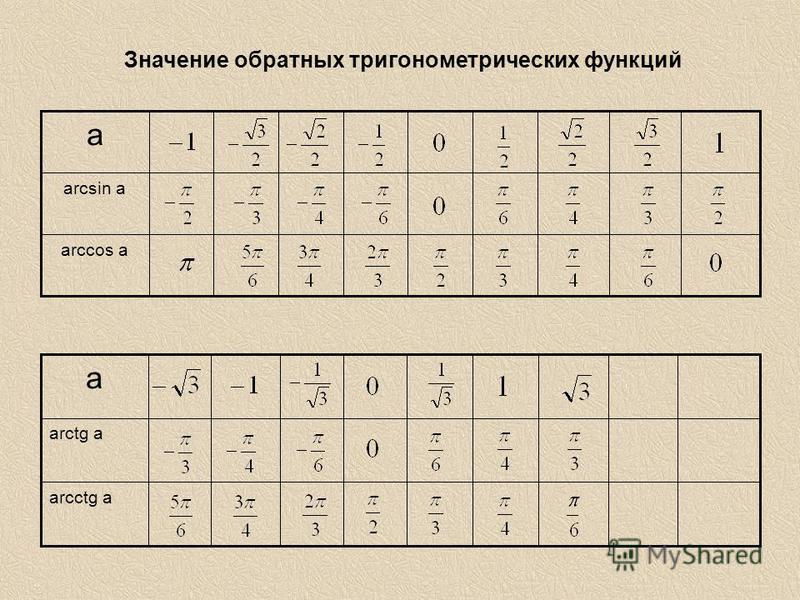 И.
Перепелкина «Геометрическая теория гиперболических функций»,
напечатанной в вып. 2 сборника «Математическое просвещение», ОНТИ,
М. — Л., 1934; к сожалению, в настоящее время этот сборник представляет
собой библиографическую редкость. Читателю брошюры можно порекомендовать
также книгу Б. Н. Делоне и Д. А. Райкова «Аналитическая геометрия»,: ч.
1, Гостехиздат, М. — Л., 1948, где содержится обширный материал,
примыкающий к изложенному в первой главе.
И.
Перепелкина «Геометрическая теория гиперболических функций»,
напечатанной в вып. 2 сборника «Математическое просвещение», ОНТИ,
М. — Л., 1934; к сожалению, в настоящее время этот сборник представляет
собой библиографическую редкость. Читателю брошюры можно порекомендовать
также книгу Б. Н. Делоне и Д. А. Райкова «Аналитическая геометрия»,: ч.
1, Гостехиздат, М. — Л., 1948, где содержится обширный материал,
примыкающий к изложенному в первой главе.
Брошюра рассчитана на участников и руководителей школьных математических кружков; она может быть также использована и в работе вузовских кружков по математике. Мелким шрифтом в главе III напечатан более трудный материал, не рассчитанный на школьника. Впрочем, нигде у читателя не предполагается никаких знаний, выходящих за пределы курса средней школы.
Автор выражает искреннюю признательность
И. М. Яглому, помощь и указания которого сыграли значительную роль при
написании брошюры.
В. Г. Шерватов.
Содержание
Предисловие
Глава I. Гиперболический поворот
   § 1. Сжатие к прямой
   § 2. Гиперболический поворот
   § 3. Несколько свойств гиперболы
Глава II. Гиперболические функции
   § 1. Уравнение гиперболы, отнесенной к осям
   § 2. Определение и основные свойства гиперболических функций
   § 3. Формулы сложения
Глава III. Связь с логарифмами
   § 1. Геометрическая теория логарифмов
   § 2. Аналитические выражения для гиперболических функций
   § 3. Формулы Эйлера
| |||||||||||
Постоянный адрес этой страницы: http://math.ru/lib/plm/16
Лекция Основные элементарные функции
Скачать с Depositfiles
Лекция 3. Основные элементарные функции
Контрольные вопросы
1. Показательная и логарифмическая функции и их свойства.
2. Степенная функция, тригонометрические функции и их свойства.
3. Гиперболические функции, обратные тригонометрические и гиперболические функции.
Показательная функция
Показательная функция определяется формулой:
, (1)
При действительных (при ) получим действительную функцию .
Свойства показательной функции
1) ;
2) ;
3) , т. к. ;
к. ;
4) ; ;
5) Функция периодическая с периодом : .
Логарифмическая функция
Определяется как обратная к показательной
Число называется логарифмом числа , если и обозначается , . Найдем выражение для действительной и мнимой частей показательной функции. Из определения следует:
т.е.
Итак, (2)
т.е. — многозначная (бесконечнозначная) функция.
При k=0 получаем функцию — главное значение логарифма
Свойства логарифмической функции
1) ;
2) ;
3) ;
4) .
Докажем первое свойство:
=.
Примеры Вычислить: .
а) ; , ; тогда ;
;
б) ; , ; , =
в) ; , , .
Степенная функция.
1) Если — натуральное число, то функция — однозначная:
2) Если , , то функция — т — значная:
, .
3) Если , то функция — q-значная:
.
4) Степенная функция с произвольным комплексным определяется равенством .
Пример .
При имеем — действительное число.
Тригонометрические функции
Определяются равенствами:
; ; ; .
При действительных получаем тригонометрические функции действительного аргумента .
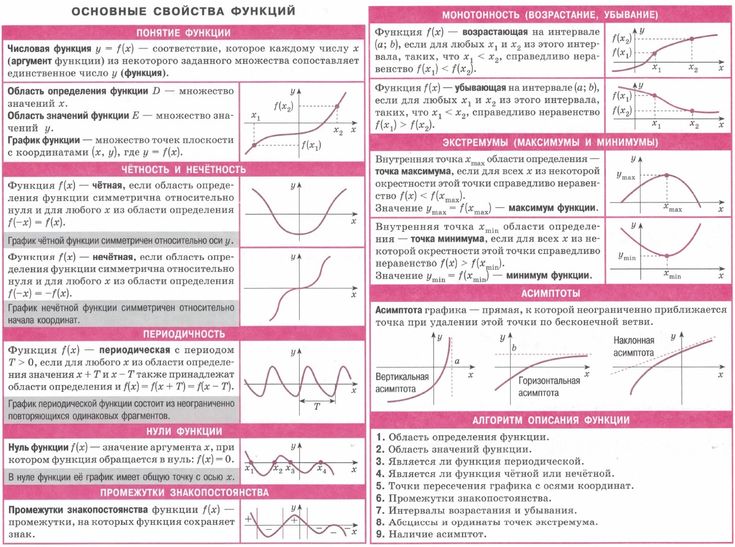
Свойства тригонометрических функций
1) ;
2) ;
3) ;
4) ;
5) ;
6) ;
7) ;
;
9) ;
10) ;
11) при ;
12) при ;
13) ;
14) и т.д.
Докажем, например, что .
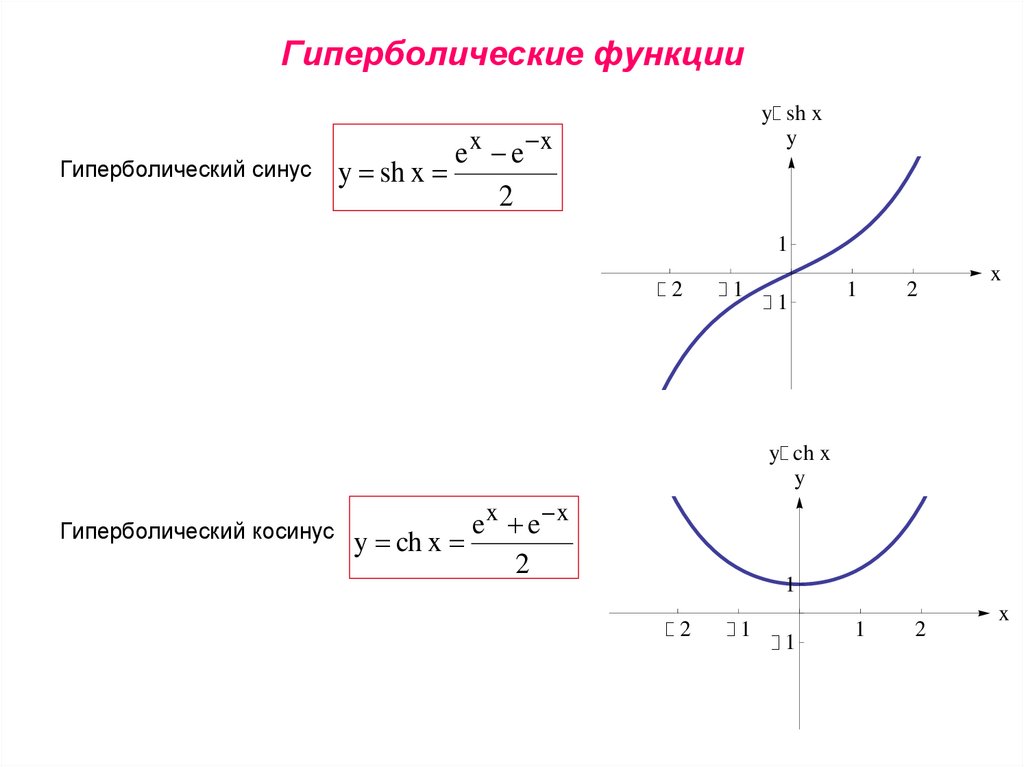
Гиперболические функции
Определяются равенствами:
; ; ; ;
Связь с тригонометрическими функциями:
; ;
; ;
Свойства гиперболических функций
1) ; 2) ; 3) ;
4) ; 5) ;
6) ; 7) .
Дома вывести формулу для .
Функции и имеют период , и .
Обратные тригонометрические функции
,если .
(здесь нет , т.е. корень имеет два значения).
-бесконечнозначная функция.
.
Итак, ;
;
;
.
Обратные гиперболические функции: (apea)
; ;
; — бесконечнозначные функции.
круговые и гиперболические триггерные функции
круговые и гиперболические триггерные функции| Путь: физические идеи > основы > |
Это в основном страница «просто для развлечения».
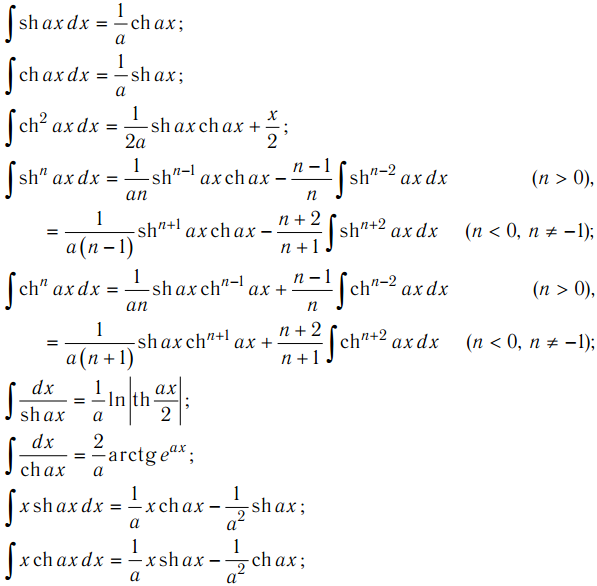 Это не добавляет многого к тому, что
уже обсуждалось где-то на сайте. Тем не менее, я нашел это
интересно пройти по пунктам круговой и гиперболический
функции, поэтому я решил написать это.
Это не добавляет многого к тому, что
уже обсуждалось где-то на сайте. Тем не менее, я нашел это
интересно пройти по пунктам круговой и гиперболический
функции, поэтому я решил написать это.Мы начнем с формульных определений функций и производные от некоторых их свойств, как для упрощения того, что будет позже и дать нам прочную основу для некоторых выводов. Хорошо развивать геометрические свойства функций, как мы идем. Потерпите нас; будет довольно большой кусок алгебры, прежде чем мы добраться до любых изображений.
В дополнение к тому, что мы делали в других местах, мы будем определение триггерных функций в терминах экспоненциальной функции, с с которого мы начнем. Это упрощает вывод (а много), а также делает сходство между круговым и гиперболическим работает немного яснее (или, по крайней мере, я надеюсь, что это так).
Напоследок, мы будем использовать x , y , u , v , t и θ как действительные переменные, и мы будем
используя z в качестве комплексной переменной.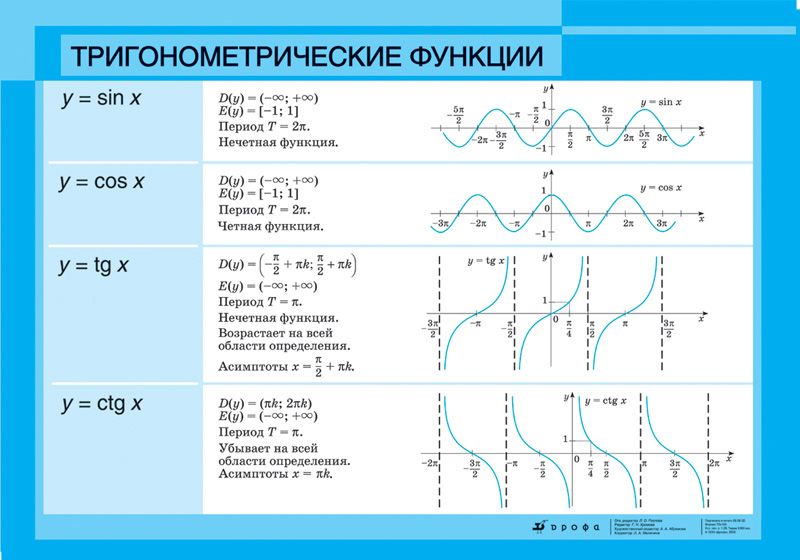 Обычно мы упоминаем, что каждый
значит, как мы идем, так что соглашение не критично.
Обычно мы упоминаем, что каждый
значит, как мы идем, так что соглашение не критично.
1. Экспоненциальная функция
Мы определяем экспоненциальную функцию e z как функция, которая имеет эти два свойства:
(1.1) 1.1 (a) говорит, что она ведет себя как экспоненциальная функция. (Много
так ведут себя и другие функции, например 10
Вместе эти два свойства полностью определяют его. Нам понадобится немного дополнительные (производные) свойства; мы поставили их производные, наряду с кратким обсуждением комплексных чисел, более здесь, чтобы немного уменьшить раздувание этой страницы.
Производное от e z само по себе:
(1.2)
Величина e iθ равна 1 для всех действительных θ;
следовательно, e iθ отображает реальную линию на единицу окружность в комплексной плоскости:
(1. 3)
3)
И, наконец,
(1,4) Если рассматривать комплексную плоскость как аналог R 2 , с реальной и мнимой частями, образующими x и y компоненты векторов, то угол между вектором положения e iθ а ось x — это θ.
В частности, из свойства (1.4) следует, что e iπ/2 = i и e iπ = -1.
2. Определения триггерных функций
Мы будем определять синус и косинус напрямую, а остальные функции с точки зрения них. Как для круговой, так и для гиперболической функций тангенс — это синус над косинусом, котангенс — это величина, обратная тангенс, секанс обратен косинусу, а косеканс равен инверсия синуса.
2.1 Круговой синус и косинус
Определим синус и косинус как мнимую и действительную части e iθ , соответственно:
(2.
(2.1.2)
Так как комплексное число есть сумма его действительной части и я раз его мнимой части имеем:
(2.1.3)
Поскольку мы уже знаем, что e iθ содержит R на единичную окружность (показана здесь), мы знаем, что точка (cos (θ), sin (θ) ) должна попасть на единичный круг, и из (1.4) мы знаем, что точка находится в угол θ с осью x . (Что мы и хотели найти, конечно!)
Уравнение (1.3) сразу приводит к знакомая личность,
(2.1.4)
Производные синуса и косинуса тоже выпадают из нашего
определения. Мы можем просто продифференцировать формулы (2.
В качестве альтернативы мы можем дифференцировать e iθ . Мы есть,
(2.1.5)
Но мы знаем, что e z является собственной производной, поэтому, используя цепное правило, мы также должны иметь:
(2.1.6)
Приравнивая соответствующие действительную и мнимую части из (2.1.5) и (2.1.6) мы получаем, куда шли, а именно:
(2.1.7)
2.2 Гиперболический синус и косинус
Определим гиперболический синус и косинус как нечетную и четную части e θ , соответственно, где θ переменная с действительным значением:
(2.2.1)
Разбиение функции на нечетные и четные части уникально, и это выглядит так:
(2.2.2)
Поскольку функция представляет собой сумму своих четных и нечетных частей, мы имеем:
(2. 2.3)
2.3)
Поскольку sinh нечетно, а cosh четно, мы также имеем:
(2.2.4)
Если мы умножим левую и правую части (2.2.3) на е −θ , подставляя в правую часть из (2.2.4), получаем основное идентификатор:
(2.2.5)
Это говорит нам о том, что точки (cosh θ, sh θ ) должны лежат на единичной гиперболе (которая является геометрическим местом уравнения x 2 — у 2 = 1 ).
Наконец, дифференцирование уравнений (2.2.2) приводит к производным для гиперболические функции:(2.2.6)
3. Геометрическая интерпретация синуса и косинуса
Мы показали единичную окружность и единичную гиперболу с центром в
источник. Мы нарисовали только одну ветвь единичной гиперболы (есть
другую ветку, симметрично расположенную слева), и мы не рисовали
«согипербола», представляющая собой единичную гиперболу, повернутую на 90 градусов.
| Рис. 1. Круговые функции | Рисунок 2: Гиперболические функции |
3.1 Круговые функции
Проведите линию от начала координат до пересечения с окружностью; хорошо назовите это «линия радиуса». Нарисуйте отрезок от этого пересечение с осью x . Длина этой линии сегментом является синус (показан оранжевым цветом на рис. 1).
Нарисуйте второй отрезок от пересечения до г ось. Длина этого отрезка равна косинусу.
Проведите касательную к окружности в точке пересечения окружности. ось x . Запустите этот сегмент линии до того места, где он попадает в линия радиуса. Длина этого отрезка является касательной.
Проведите еще одну линию от оси y , также касательной к окружности,
до пересечения с линией радиуса. Длина этой линии
отрезок – котангенс.
Длина этой линии
отрезок – котангенс.
И, наконец, рассмотрим угол — т. е. аргумент к триггерные функции. Рассмотрим область «Область u» , показанную на синий. Площадь всего единичного круга равна π, а «угол» весь круг равен 2π. Итак, если угол, образованный линией радиуса с осью x равна θ, то площадь u должна быть (θ/2π)⋅π = θ/2.
Другими словами, «угол» (который является аргументом триггерных функций) в два раза больше площади и .
3.2 Гиперболические функции
Проведите линию от начала координат до пересечения с гиперболой; хорошо назовите это «линия радиуса». Нарисуйте отрезок от этого пересечение с осью x . Длина этого сегмента линии — гиперболический синус (показан красным на рис. 2).Нарисуйте второй отрезок от пересечения до y ось. Длина этого отрезка равна гиперболическому косинусу.
Проведите касательную к гиперболе в точке (1,0), где она
пересекает ось x . Запустите этот сегмент линии до того места, где он
попадает на линию радиуса. Длина этого отрезка есть гипербола
касательная.
Запустите этот сегмент линии до того места, где он
попадает на линию радиуса. Длина этого отрезка есть гипербола
касательная.
Проведите еще одну линию от оси y в точке (0,1) до тех пор, пока она не пересекает линию радиуса. Длина этого отрезка равна гиперболический котангенс. (Если бы мы еще показали «согиперболу», которая вращается 90 градусов, то линия котангенса будет касательной к нему.)
И, наконец, рассмотрим угол — т. е. аргумент триггерные функции. Рассмотрим область «Область u» , показанную на синий. Это немного сложнее доказать, чем случай с циркуляром. функций, но на самом деле площадь u равна θ/2. Мы доказываем, что (через прямую интеграцию) здесь.
Другими словами, «угол» (который является аргументом триггерных функций) в два раза больше площади и .
4. Бонусный раздел: Формулы суммы углов
Определение функций как частей экспоненциальной функции делает
также легко вывести формулы суммы. Он также показывает
сходства между круговой и гиперболической функциями.
Он также показывает
сходства между круговой и гиперболической функциями.
4.1 Круговые триггерные функции суммы углов
Найдем формулу суммы углов синуса и суммы углов косинуса одновременно. Основное свойство (1.1(а)) показательной функции говорит нам, что
(4.1.1)
Отсюда и из уравнения (2.1.3) получаем почти готово:
(4.1.2)
Приравнивая действительную и мнимую части первой и последней формулы, получаем получить:
(4.1.3)
4.2 Гиперболические триггерные функции суммы углов
Мы будем действовать так же, как и в предыдущем разделе. Основное свойство (1.1(a)) экспоненциальной функции говорит нам, что
(4.2.1)
И с этим и уравнением (2.2.3) мы почти сделано:
(4.2.2)
Произведение двух четных функций четно, а произведение двух нечетных
функции четные.
Произведение нечетной функции на четную нечетно.
Итак, мы можем приравнять четную часть последнего выражения в (4.2.2) к четную часть первого выражения, а нечетные части приравняем, и мы получить:
(4.2.3)
и готово.
Страница создана 24.03.2018
Гиперболические функции — GeeksforGeeks
Гиперболическая функция косинуса определяется как: 2
А гиперболическая функция синуса определяется как:
sinh(x) = (e x - e -x )/2
Из приведенного выше определения мы можем видеть следующие свойства кош (x) и sh(x) функции:
ch(x) — четная функция:
ch(-x) = (e -x + e x )/2
= (е х + е -х )/2
= ch(x) Следовательно, функция четная.
Точно так же sinh(x) является нечетной функцией:
sinh(-x) = (e -x - e x )/2
= -((е х - е -х )/2)
= -sinh(x) Следовательно, функция sinh(x) является нечетной функцией.
Диапазон cosh(x):
кош(х) = (е -х + е х )/2 Пусть у = е х Так, ch(x) = (y + 1/y)/2 . Теперь (y + 1/y) ≥ 2 для y>0. Следовательно, ch(x) ≥ 1
. Следовательно, диапазон ch(x) равен [1, ∞).
Диапазон sin(x):
sh(x) = (e x - e -x )/2 Пусть sh(x) = y. Итак, у = (е 2 х - 1)/2е х . 2уе х = е 2х - 1 е 2x - 2уе х + 1 = 0 x = ln(y + √(y 2 + 1))
Очевидно, поскольку x находится в (-∞, ∞), y должен лежать в (-∞, ∞), так что приведенный выше журнал дает все действительные числа .
Аналогия гиперболических синусов и косинусов и нормальных тригонометрических синусов и косинусов .
Правило Осборна:
Это правило гласит, что нормальные тригонометрические тождества синусов и косинусов остаются теми же самыми даже с гиперболическими синусами и косинусами, т. е. cos(x) можно заменить на ch(x), а sin(x) можно заменить на sinh(x). Но следует помнить, что при умножении двух синусоидальных функций происходит изменение знака тождества.
е. cos(x) можно заменить на ch(x), а sin(x) можно заменить на sinh(x). Но следует помнить, что при умножении двух синусоидальных функций происходит изменение знака тождества.
Например,
sin(2A) = 2sin(A)cos(A)
В гиперболических функциях то же самое, т.е.
sin(2x) = 2sin(x)cosh(x) Но, cos(2A) = 1 - 2sin 2 (x)
, что становится
cosh(2x) = 1 + 2sinh 2 (x)
Аналогия есть и в геометрии. В то время как (cos(t), sin(t)) представляют точки на единичной окружности, (cosh(x), sinh(x)) представляют точки на гиперболе с точкой пересечения x = 1.
Идентичность:
шш 2 (х) - синх 2 (х) = 1
Доказательство: = LHS = ((e x + e -x )/2) 2 - ((e x - e -x )/2) 2 = ((e 2x + e -2x + 2)/4) - ((e 2x + e -2x - 2)/4) = 4/4 = 1
Другие гиперболические функции:
tanh(x) = sh(x)/cosh(x) coth(x) = ch(x)/sinh(x) cosech(x) = 1/sinh(x) sech(x) = 1/ch(x)
Производные гиперболических функций:
= д (кош (х)) / дх = d((e x + e -x )/2)/dx = 1/2(d(e x + e -x )/dx) = 1/2 (е х - е - х ) = sinh(x)
Аналогично,
d(sinh(x))/dx = ch(x)
Вы можете видеть разницу между производными sin(x) и cos(x) и sinh(x) и кош(х).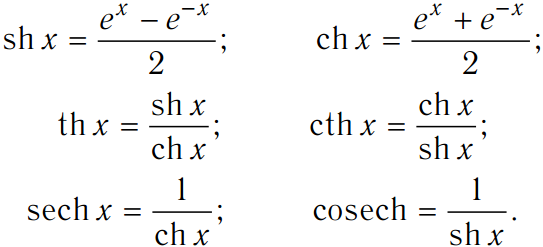

 48)
48)