Мини-тренажер табличных значений синуса, косинуса, тангенса углов | Материал по алгебре (10 класс) на тему:
Опубликовано 01.03.2015 — 8:56 — Киселева Ирина Владимировна
В тренажер включены примеры для проверки знаий таблицы значений синуса, косинуса,тангенса углов
Скачать:
Предварительный просмотр:
=
=
=
tg =
=
=
tg 0°=
=
=
=
=
=
=
tg =
=
=
tg 30°=
=
=
=
=
=
=
tg =
=
=
tg 0°=
=
=
=
=
=
=
tg =
=
=
tg 30°=
=
=
=
=
=
=
tg =
=
=
tg 0°=
=
=
=
=
=
=
tg =
=
=
tg 30°=
=
=
=
=
=
=
tg =
=
=
tg 0°=
=
=
=
=
=
=
tg =
=
=
tg 30°=
=
=
=
=
=
=
tg =
=
=
tg 0°=
=
=
=
=
=
=
tg =
=
=
tg 30°=
=
=
=
=
=
=
tg =
=
=
tg 0°=
=
=
=
=
=
=
tg =
=
=
tg 30°=
=
=
=
=
=
=
tg =
=
=
tg 0°=
=
=
=
=
=
=
tg =
=
=
tg 30°=
=
=
=
По теме: методические разработки, презентации и конспекты
Конспект урока по теме: Значения синуса, косинуса, тангенса для углов 30°, 45°, 60°.
Тип занятия: урок-практикумЗадачи занятия:Обучающие: -повторить теоретические знания по теме: «Синус, косинус, тангенс острого угла прямоугольного треугольника»-систематизировать знания по темеРазвива…
Презентация по теме » Значения синуса, косинуса, тангенса углов 30,45,60 градусов»
Презентация по теме » значения синуса,косинуса,тангенса углов 30,45,60 градусов»…
Конспект по теме » Значения синуса,косинуса, тангенса углов 30,45,60 градусов
Конспект по теме » Значения синуса,косинуса углов 30,45,60 градусов»…
Урок по теме»Значения синуса,косинуса, тангенса углов 30,45,60 градусов»
Значения синуса,косинуса, тангенса углов 30,45,60 градусов…
Презентация к уроку » Значения синуса,косинуса, тангенса углов 30,45,60 градусов»
Значения синуса,косинуса , тангенса углов 30,45,60 градусов…
Конспект урока по геометрии в 8 классе по теме: «Значения синуса, косинуса, тангенса некоторых углов».
конспект…
Урок геометрии в 8 классе «Значения синуса, косинуса, тангенса и котангенса для углов 30°, 45° и 60°»
Цель урока: Вывести значение тригонометрических функций для углов 30°, 45° и 60°; научить применять формулы соотношений между углами и сторонами прямоугольных треугольников при решении зада.
..
Поделиться:
Урок геометрии в 8 классе «Значения синуса, косинуса и тангенса стандартных углов»
Муниципальное бюджетное общеобразовательное учреждение
«Завет-Ленинская школа-детский сад»
Джанкойского района Республики Крым
Конспект урока геометрии
в 8 классе
«Значения синуса, косинуса и тангенса стандартных углов»
учитель математики
МБОУ «Завет-Ленинская школа-
детский сад»
Гординская Наталия Григорьевна
с. Завет-Ленинский, 2022
Тема урока: Значения синуса, косинуса и тангенса стандартных углов.
Цели урока:
Образовательные:
научить учащихся вычислять значения синуса, косинуса и тангенса для углов 30ᵒ, 45ᵒ, 60ᵒ;
формировать навыки решения прямоугольных треугольников, используя синус, косинус и тангенс острого угла;
научить использовать «Четырёхзначные таблицы» Брадиса, для нахождения значений синуса, косинуса и тангенса острых углов.
Развивающие:
развивать логическое мышление учащихся;
внимание, память, культуру математической речи и записей.
Воспитательные:
воспитывать интерес к математике, настойчивость, активность, трудолюбие.
Оборудование: учебник, четырёхзначные таблицы Брадиса, пректор, интерактивная доска.
Тип урока: усвоение новых знаний.
План урока.
Организационный момент.
Актуализация опорных знаний учащихся.
Изучение нового материала.
Физкультминутка.
Закрепление изученного материала.
Подведение итогов урока.
Рефлексия.
Домашнее задание.
Ход урока.
Организационный момент.
Проверить готовность к уроку, присутствующих. Сообщить тему урока, сформулировать цели.
Учитель. Ребята откройте свои тетради и запишите тему сегодняшнего урока «Значения синуса, косинуса, и тангенса стандартных углов.». Сегодня на уроке мы с вами заполним таблицу значений синуса, косинуса и тангенса углов 30ᵒ 45ᵒ и 60ᵒ и выясним почему именно такие значения имеют эти углы.
Актуализация опорных знаний учащихся.
Проверка домашнего задания.
Проверить устно домашние задачи № 591 (в, г), № 592 (в, г). Один из учащихся читает свое решение, остальные проверяют. Если возникли вопросы учитель на них отвечает.
Решение задачи по готовому чертежу.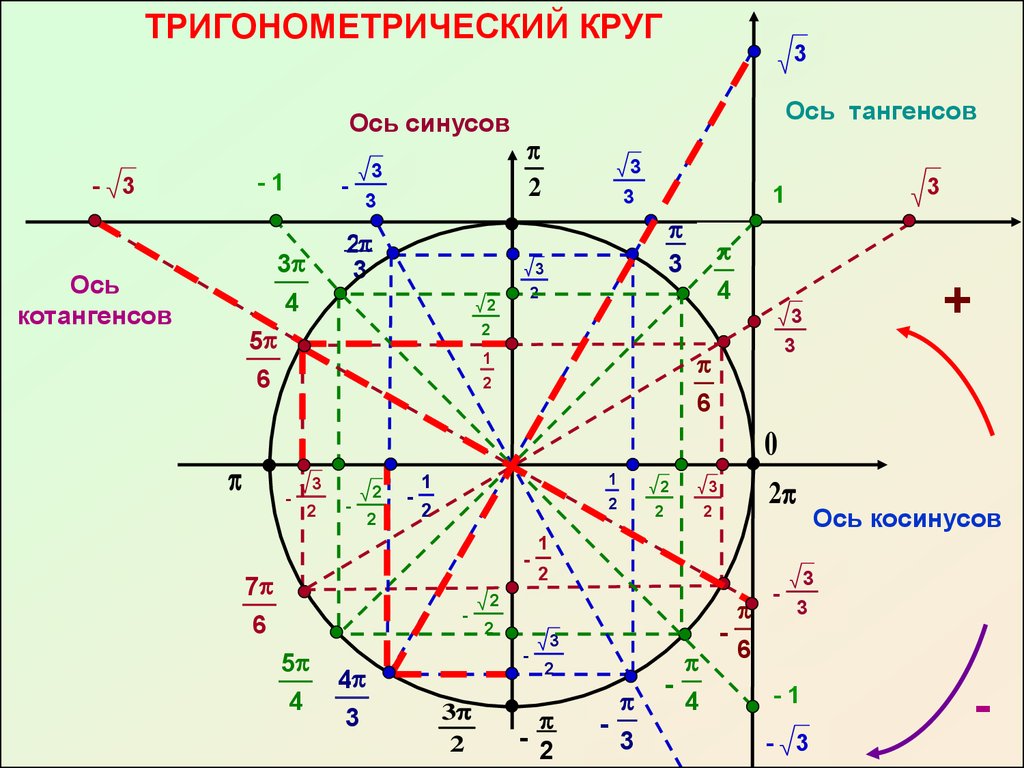
Найти sin A, cos A, tg A, sin B, cos B, tg B.
Фронтальный опрос.
Что называют синусом острого угла прямоугольного треугольника?
Что называют косинусом острого угла прямоугольного треугольника?
Что называют тангенсом острого угла прямоугольного треугольника?
Изучение нового материала.
Изобразите в тетради треугольник угол С=90ᵒ, угол А=30ᵒ, угол В=60ᵒ.
Приготовьте для заполнения таблицу:
α | 30ᵒ | 45ᵒ | 60ᵒ |
sin α | |||
cos α | |||
tg α | 1 |
Найдём сначала значения синуса, косинуса и тангенса для углов 30ᵒ и 60ᵒ.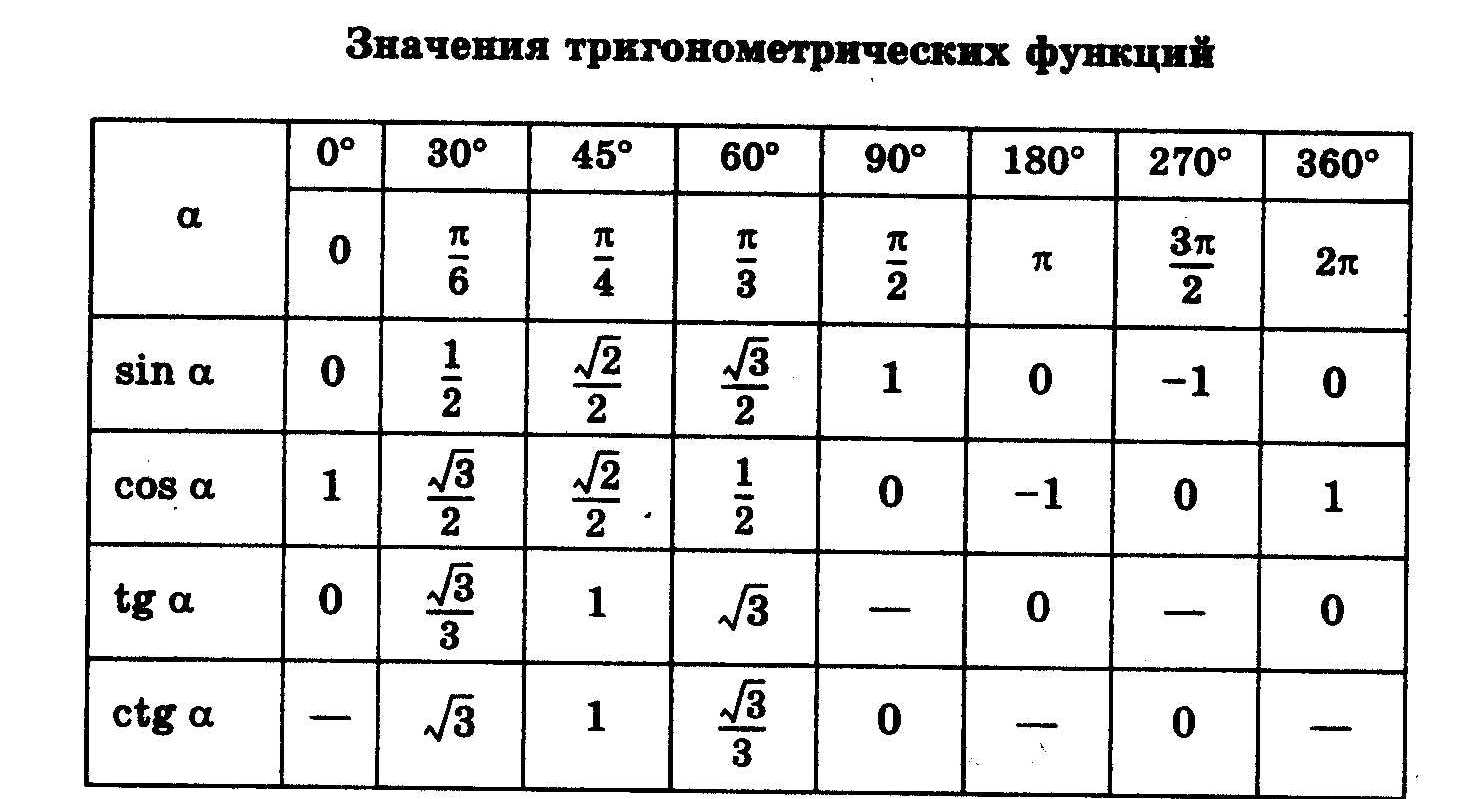
Для этого рассмотрим прямоугольный треугольник АВС. Так, как катет, лежащий против угла в 30ᵒ, равен половине гипотенузы, то = , но = sin A = sin 30ᵒ.
С другой стороны = cos B = cos 60ᵒ.
Итак sin 30ᵒ = , cos 60ᵒ = , занесём данные в таблицу.
Из основного тригонометрического тождества sin2 α + cos2 α = 1, найдём:
cos 30ᵒ = = =
sin 60ᵒ = = = , занесём значения в таблицу.
Найдём: tg 30ᵒ = = =
tg 60ᵒ = = , занесём значения углов в таблицу.
Найдём теперь sin 45ᵒ, cos 45ᵒ и tg45ᵒ. Для этого рассмотрим равнобедренный прямоугольный треугольник АВС, АС = ВС, угол А равен углу В и равен 45ᵒ.
По теореме Пифагора АВ2 = АС2 + ВС2 = 2 АС2 = 2 ВС2, откуда АС = ВС =
sin 45ᵒ = sin A = = =
cos 45ᵒ = cos A = = =
tg 45ᵒ = tg A = = 1, занесём данные в таблицу.
Мы с вами получили таблицу значений синуса, косинуса и тангенса стандартных углов. Эти значения ребята вам необходимо выучить, так как они будут встречаться чаще всего в задачах. Значения тех углов, которых нет в данной таблице вы найдёте в четырёхзначных таблицах Брадиса (рассказать учащимся, как использовать таблицы Брадиса для определения значений синуса, косинуса, тангенса и котангенса углов любой градусной меры.)
Дополнительная информация по теме.
Существует механическое правило вычисления значений синуса, косинуса и тангенса углов 0ᵒ, 30ᵒ, 45ᵒ, 60ᵒ, 90ᵒ.
1.В первой строчке таблицы записываются значения углов; во второй цифры от 0 до 4; в третьей цифры от 4 до 0.
2. У каждой цифры ставится знак квадратного корня.
3.Извлекается корень; ставится дробная черта и в знаменателях ставятся двойки
.
4.
Выполняется деление чисел и затем вычисляются значения тангенса.
Если у учащихся возникнут вопросы по поводу значений синуса, косинуса и тангенса углов 0ᵒ и 90ᵒ можно на примере единичной окружности объяснить почему именно такие значения имеют эти углы.
Физкультминутка.
«Мы ногами топ- топ,
Мы руками хлоп-хлоп!
Мы глазами миг-миг,
Мы плечами чик-чик.
Повернись вокруг себя
Влево, вправо – раз и два!
Раз – присели, два привстали
Руки вверх мы все подняли.»
Закрепление изученного материала.
Коллективное решение заданий из учебника под руководством учителя.
№ 594
Наводящие вопросы к задаче:
Как найти острый угол прямоугольного треугольника, если другой острый угол равен β?
Какая связь существует между катетом, противолежащим ему углом и гипотенузой?
Как взаимосвязаны два катета прямоугольного треугольника и один из его острых углов?
Как используя четырёхзначные таблицы Брадиса, найти sin 50ᵒ, tg 50ᵒ.
Самостоятельно выполнить № 596.
Подведение итогов урока.
В конце урока учащимся предлагается наклеить в тетради стикер: зелёный – понравилось всё; красный – не понравилось; жёлтый – понравились отдельные моменты.
Рефлексия.
Ребята! На полях в тетради после каждого задания нарисуйте:
Все понятно
Понятно частично
Ничего не понятно
Домашнее задание.
Пункт учебника 69 – изучить, табличные значения стандартных углов выучить, выполнить № 595
Дополнительная задача:
В прямоугольной трапеции основания равны 6 см и 11 см, меньшая боковая сторона равна 4 см. Найдите синус, косинус и тангенс острого угла трапеции.
Графики: другие тригонометрические функции
Тангенс является нечетной функцией, потому что
Тангенс имеет период π, потому что
Тангенс не определен, если cos x = 0.
Это происходит, когда x = q π/2, где q — нечетное целое число. В этих точках значение тангенса стремится к бесконечности и не определено. При графическом изображении касательной пунктирная линия используется, чтобы показать, где значение касательной не определено. Эти строки называются
График функции тангенса в интервале от 0 до π/2 показан на рисунке 1 .
Рис. 1
Часть функции касательной.
Тангенс является нечетной функцией и симметричен относительно начала координат. График касательной за несколько периодов показан на рисунке 2 . Обратите внимание, что асимптоты показаны пунктирными линиями, а значение касательной в этих точках не определено.
Рисунок 2
Несколько периодов функции тангенса.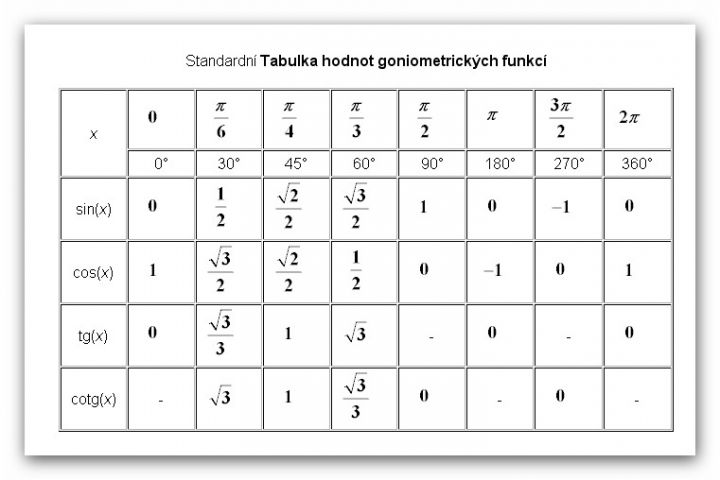
Котангенс является обратной величиной тангенса, и его график показан на рисунке 3. Обратите внимание на разницу между графиком тангенса и котангенса в интервале от 0 до π/2.
Рисунок 3
Часть функции котангенса.
Как показано на рис. 4, на графике котангенса асимптоты расположены на кратных π.
Рисунок 4
Несколько периодов функции котангенса.
Поскольку графики как тангенса, так и котангенса неограниченно простираются как выше, так и ниже оси x , амплитуда тангенса и котангенса не определена.
Общие формы функций тангенса и котангенса
Переменные C и D определяют период и фазовый сдвиг функции, как и в функциях синуса и косинуса. Период равен π/ C , а фазовый сдвиг равен |D/C|.
Пример 1: Определить период, фазовый сдвиг и расположение асимптот функции
и построить график не менее двух полных периодов функции.
Асимптоты можно найти, решив Cx + D = π/2 и Cx + D = −π/2 для X .
Период функции
Фазовый сдвиг функции равен
Поскольку фазовый сдвиг положительный, он находится влево (рис. 5).
Рисунок 5 Фазовый сдвиг функции касательной.
Амплитуда не определена для секанса или косеканса.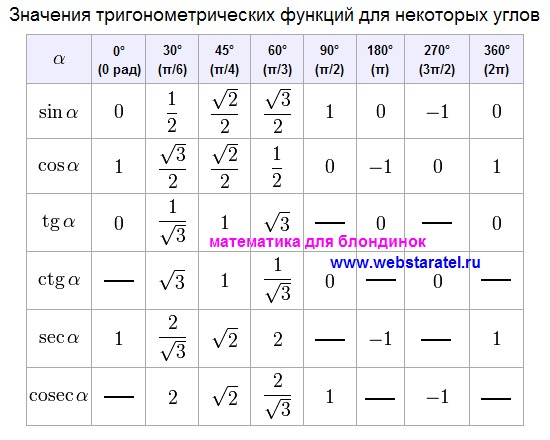
Пример 2: Определить период, фазовый сдвиг и расположение асимптот функции
и построить график не менее двух периодов функции.
Асимптоты можно найти, решая Cx + D = 0, Cx + D = π и Cx + D = 2π для x .
Период функции
Фазовый сдвиг функции равен
Поскольку фазовый сдвиг положителен, он находится влево.
График обратной функции
показан на рис. 6 . График синуса (или косинуса) может упростить построение графика косеканса (или секанса).
Рисунок 6
Несколько периодов функции косеканса и функции синуса.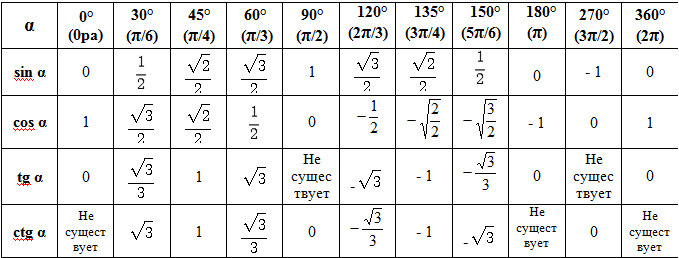
танкот.nb
tancot.nbГрафики тангенса, котангенса, косеканса и секанса
Мы собираемся найти графики этих функций, используя тот же метод, который мы использовали для sin(x) и cos(x). Мы будем использовать таблицу значений для построения некоторых точек, а затем «заполним» остальную часть графика. Это будет немного сложнее, чем раньше, потому что эти функции не везде непрерывны; это означает, что на графиках будут некоторые «разрывы» — каждый из них будет иметь вертикальные асимптоты. Подробнее об этом позже.
График Tan(x)
Начнем с таблицы значений. Еще раз напомню: вам не нужно запоминать эти значения; вы можете найти их все, используя наши определения единичного круга и вписав в круг треугольник 45°-45°-90° или 30°-60°-90°. Мы сделали это во время лекции по разделу 5.2.
| х | 0 | ||||||
| у=загар(х) | 0 | 1 |
Если мы нанесем эти точки на график, они будут выглядеть так:
Мы можем соединить точки с помощью плавной кривой, чтобы получить представление о том, как выглядит график, но это еще не все.
Мы знаем, что оно периодическое с периодом . Это означает, что график просто повторяется вечно и всегда слева и справа.
График детской кроватки (x)
Теперь проделаем то же самое с . Единственная реальная разница в нашем методе заключается в том, что он не определен, когда sin(x)=0, а НЕ когда cos(x)=0. Это означает, что вертикальные асимптоты будут в другом месте.
Сначала таблица значений:
| х | |||||||
| у=кроватка(х) | 1 | 0 |
Если мы нанесем эти точки на график, они будут выглядеть так:
Мы можем соединить точки с помощью плавной кривой, чтобы получить представление о том, как выглядит график, но это еще не все.
Как и в случае с , мы должны признать, что слева и справа от этого графика есть вертикальные асимптоты, где (помните, для кратных .)
Мы знаем, что оно периодическое с периодом . Это означает, что график просто повторяется вечно и всегда слева и справа.
Графики Csc(x) и Sec(x)
В книге не уделяется особого внимания графикам csc(x) и sec(x), и мы, вероятно, тоже не будем. Но вы должны хотя бы видеть графики. Как указано в книге, если вы знаете, каковы значения sin(x) и cos(x), вы можете по пунктам выяснить, каковы значения csc(x) и sec(x), потому что вы знать и . Сначала рассмотрим функцию косеканса.
Первое, что вы должны заметить, это то, что csc(x) равно undefined всякий раз, когда sin(x)=0, потому что тогда , и мы не можем делить на ноль. Поэтому неудивительно, что график csc(x) будет иметь вертикальные асимптоты в тех местах, где sin(x)=0. Кроме того, csc(x) положительна, когда sin(x) положительна, а csc(x) отрицательна, когда sin(x) отрицательна.