В параллелограмме углы: Параллелограмм — урок. Геометрия, 8 класс.

Параллелограмм и трапеция. Основные свойства и признаки. — Математика

На этом занятии рассмотрим параллелограмм, его свойства и признаки,  вспомним  формулы для вычисления площади параллелограмма и трапеции.   Разберем  задачи 3 и 6  из базы заданий ЕГЭ

Конспект занятия «Параллелограмм и трапеция. Основные свойства и признаки.»

Выпуклые четырехугольники

Выпуклый четырехугольник — четырехугольник, который расположен по одну сторону от любой из своих сторон.

Сумма углов выпуклого четырехугольника равна 360˚.

Средняя линия — отрезок прямой, соединяющий середины противоположных сторон.

Теоремы:

• Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, необходимо и достаточно, чтобы сумма длин противоположных сторон были равны друг другу. Центр окружности — точка пересечения биссектрис.

• Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, необходимо и достаточно, чтобы суммы противоположных углов были равны.

  Центр окружности — точка пересечения серединных перпендикуляров к сторонам четырехугольника.

Параллелограмм, его признаки и свойства

Параллелограмм — четырехугольник, у которого противоположные стороны попарно параллельны.

Теоремы (свойства параллелограмма):

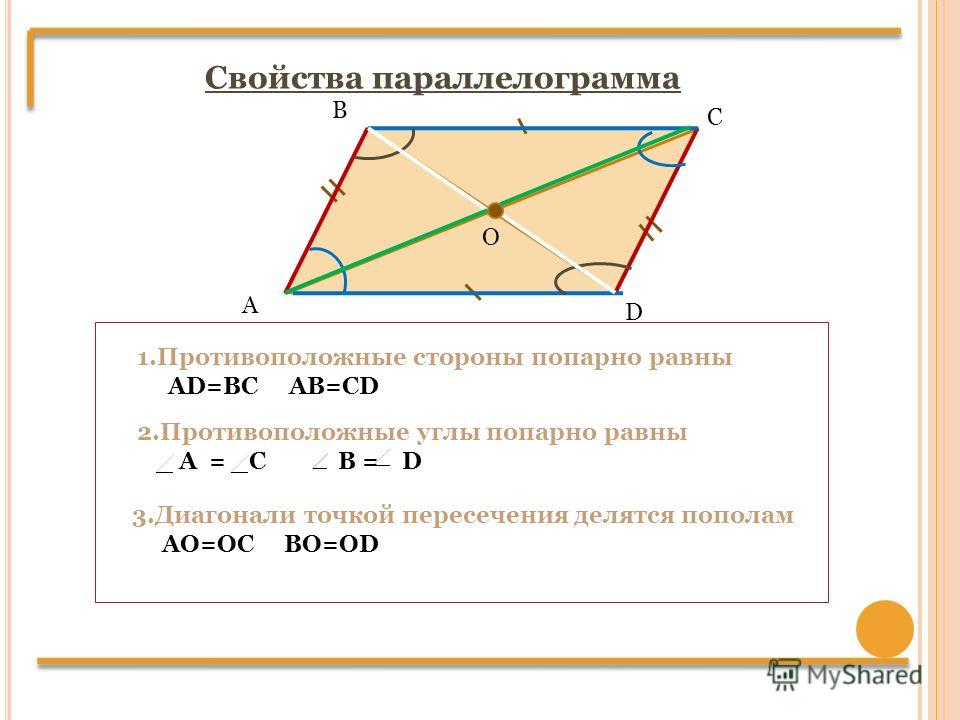
• В параллелограмме противоположные стороны равны и противоположные углы равны: AB=CD, BC=AD, ,.

• Диагонали параллелограмма точкой пересечения делятся пополам: AO=OC, OB=OD.

• Углы, прилежащие к любой стороне, в сумме равны 180˚.

• Диагонали параллелограмма делят его на два равных треугольника.

• Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон: AC² + BD² = 2AB² + 2BC .

Признаки параллелограмма:

• Если противоположные стороны четырехугольника попарно параллельны, то этот четырехугольник — параллелограмм.

• Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.

• Если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник — параллелограмм.

• Если в четырехугольнике диагонали, пересекаясь, точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.

Дополнительно:

• Середины сторон произвольного (в том числе невыпуклого или пространственного) четырехугольника K,L,M,N являются вершинами параллелограмма Вариньона.

• Стороны этого параллелограмма параллельны соответствующим диагоналям четырехугольника ABCD. Периметр параллелограмма Вариньона равен сумме длин диагоналей исходного четырехугольника, а площадь параллелограмма Вариньона равна половине площади исходного четырехугольника.

Прямоугольник, его признаки и свойства

Прямоугольником называется параллелограмм, у которого все углы прямые.

Свойства:

Признак прямоугольника: Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник.

Помним: Вокруг прямоугольника всегда можно описать окружность.

Ромб, его признаки и свойства

Ромб — параллелограмм, у которого все стороны равны.

Свойства:

• Все свойства параллелограмма.

• Диагонали ромба взаимно перпендикулярны.

• Диагонали ромба делят углы ромба пополам.

Признаки ромба:

• Если в параллелограмме диагонали взаимно перпендикулярны, то этот параллелограмм — ромб.

• Если в параллелограмме диагонали делят углы пополам, то этот параллелограмм — ромб.

Помним: В ромб всегда можно вписать окружность.

Квадрат, его признаки и свойства

Квадрат – параллелограмм, у которого все стороны равны и все углы — прямые; или прямоугольник, у которого все стороны равны; или ромб, у которого все углы — прямые.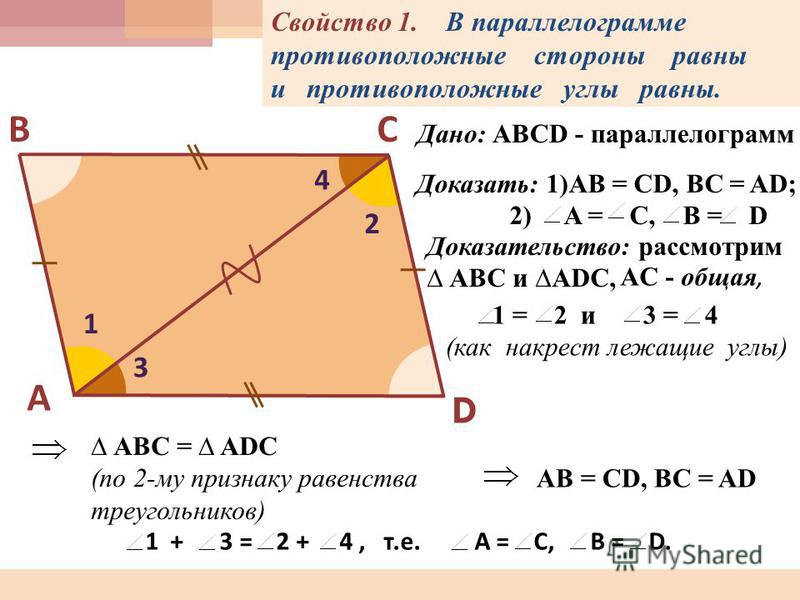

Свойства:

Трапеция, ее признаки и свойства

Трапеция — четырехугольник, у которого две стороны параллельны, а две стороны не параллельны. Параллельные стороны называются основаниями трапеции, две другие —боковыми сторонами.

Высота трапеции — расстояние между прямыми, на которых лежат основания трапеции, любой общий перпендикуляр этих прямых.

Средняя линия трапеции — отрезок, соединяющий середины боковых сторон. 

Свойство трапеции:

Если в трапецию вписана окружность, то сумма оснований равна сумме боковых сторон: a + b = c + d , а средняя линия равна полусумме боковых сторон: m = (c+d): 2 .

Равнобедренная трапеция — трапеция, у которой боковые стороны равны AB = CD. Тогда равны диагонали AC = BD и углы при основании  , .

Из всех трапеций только около равнобедренной трапеции можно описать окружность, так как окружность можно описать около четырехугольника, только если сумма противоположных углов равна 180˚.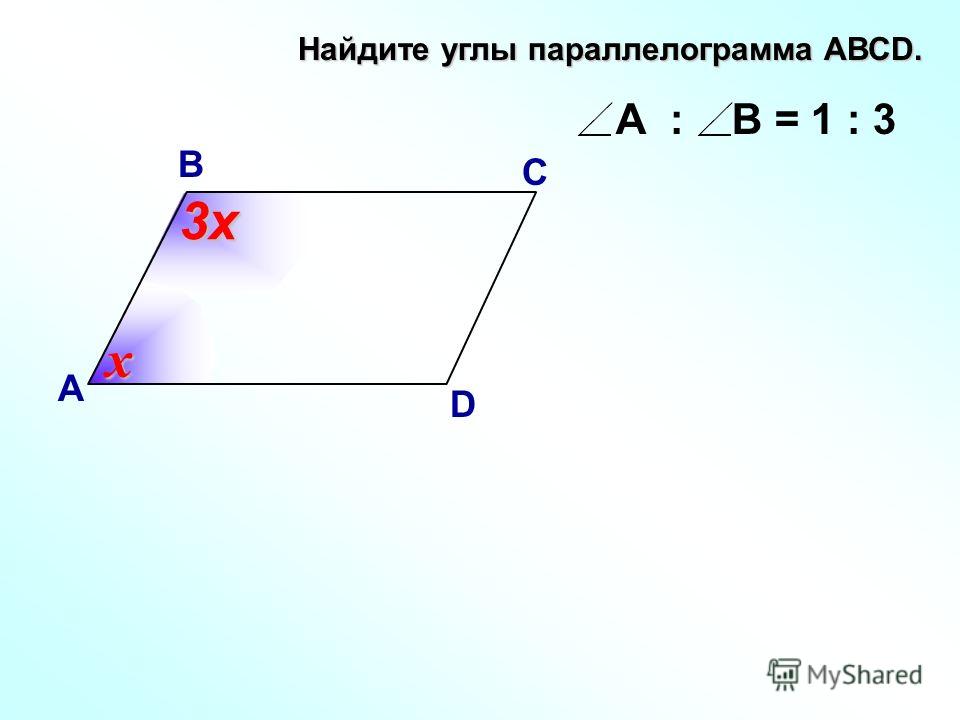

В равнобедренной трапеции расстояние от вершины одного основания, до проекции противоположной вершины на прямую, содержащую это основание равно средней линии.

Прямоугольная трапеция — трапеция, у которой один из углов при основании равен 90˚.

Теоремы о площади четырехугольника

• Любой четырехугольник можно разбить на треугольники, и его площадь будет равна сумме площадей треугольников.

• Если в четырехугольник можно вписать окружность, то его площадь равна: S=pr.

• Если четырехугольник вписан в окружность,то его площадь будет равна

.

Следствие: Площадь ромба равна: .

• Площадь квадрата: .

Задание 1

(4 балла)

В ромбе ABCD угол BCD равен 48°. Найдите угол DBA. Ответ дайте в градусах.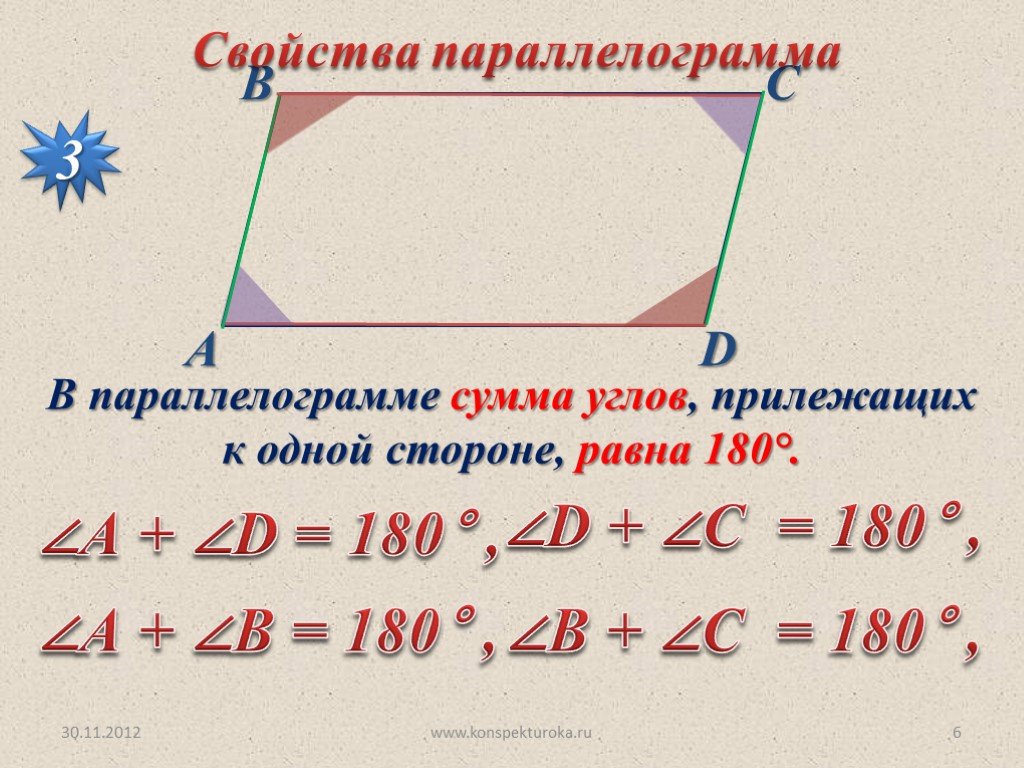

Задание 2

(4 балла)

Боковые стороны трапеции, описанной около окружности, равны 9 и 12. Найдите среднюю линию трапеции.

Задание 3

(4 балла)

В рав­но­бед­рен­ной тра­пе­ции диа­го­на­ли пер­пен­ди­ку­ляр­ны. Вы­со­та тра­пе­ции равна 9. Най­ди­те ее сред­нюю линию.

Проверить правильность выполнения заданий вы можете в автоматическом режиме в разделе домашние задания на странице с курсом «Математика Подготовка к ЕГЭ 2016»

Следующий урок на тему » Окружность. Круг. Углы в окружности. Хорды, секущие, касательные.»

Предыдущий урок на тему » Треугольник. Виды треугольников и их свойства.»

Параллелограммы — что это, определение и ответ

Параллелограмм – это четырехугольник, противоположные стороны которого попарно равны и параллельны. \circ}\)

4. Из параллельности сторон вытекает равенство частей углов. Например:

\(\angle DAC = \angle BCA\)

\(\angle CBD = \angle BDA\)

5. Две диагонали делят параллелограмм на две пары равных (по стороне и двум углам) треугольников:

\(\mathrm{\Delta}ABC = \mathrm{\Delta}BCD\)

\(\mathrm{\Delta}ABD = \mathrm{\Delta}ACD\)

6. Диагонали параллелограмма точкой пересечения делятся пополам:

\(AO = OC\)

\(BO = OD\)

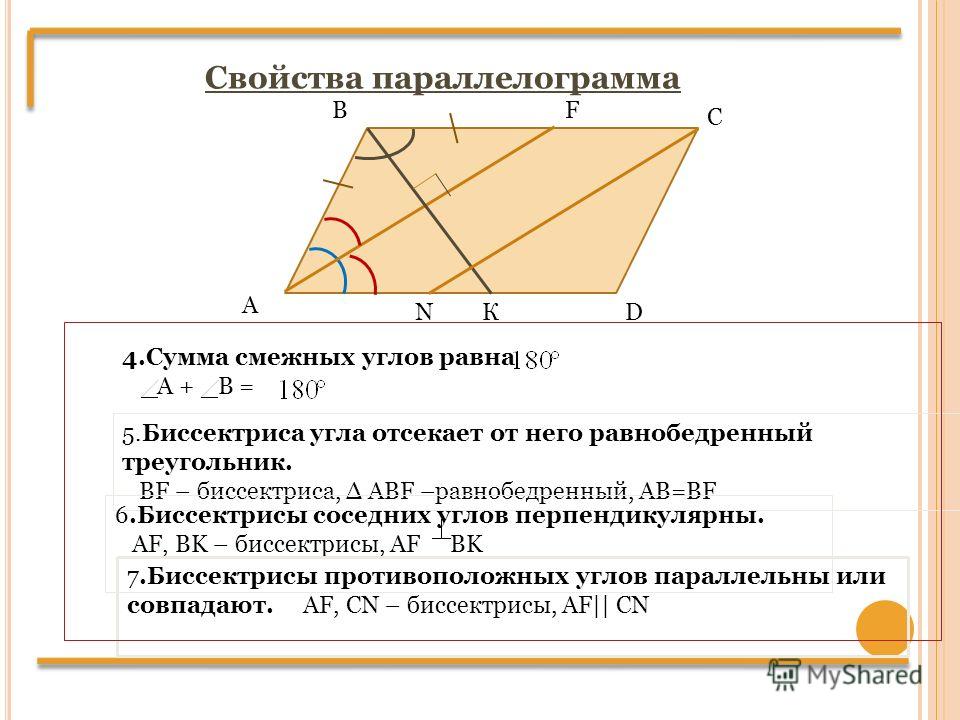
Также параллелограмм обладает необычными свойствами, связанные с биссектрисами:

Пусть AL и СК – биссектрисы противоположных углов, а ВМ – биссектриса смежного с ними угла.

Тогда:

1. Биссектрисы противоположных углов параллельны:

\(AL\ ||\ CK\)

2. Биссектрисы смежных углов перпендикулярны:

\(AL,\ CK\bot BM\)

3. Биссектриса параллелограмма отсекает от него два равных угла. Например:

\(\mathrm{\Delta}ABL\ — \ равнобедренный,\ т.к.\ \angle BAL = \angle BLA\)

\(\mathrm{\Delta}ABM\ — \ равнобедренный,\ т. к.\ \angle ABM = \angle AMB\)

ПРИЗНАКИ ПАРАЛЛЕЛОГРАММА:

Для того, чтобы доказать, что фигура действительно является параллелограммом, нужно знать, какими свойствами мы можем пользоваться. Четырехугольник ABCD будет параллелограммом, если выполняется хотя бы одно из следующих условий:

1. Четырехугольник имеет две пары параллельных сторон:

\(AB\ ||\ CD\)

\(BC\ ||\ AD\)

2. Четырехугольник имеет пару параллельных и равных сторон:

\(AB\ ||\ CD,\ AB = CD\)

\(или\)

\(BC\ ||\ AD,\ BC = AD\)

3. В четырехугольнике противоположные стороны попарно равны:

\(AB = CD\)

\(BC = AD\)

4. В четырехугольнике противоположные углы попарно равны:

\(\angle DAB = \angle BCD\)

\(\angle ABC = \angle CDA\)

5. В четырехугольнике диагонали точкой пересечения делятся пополам:

\(AO = OC\)

\(BO = OD\)

6. Сумма углов четырехугольника, прилегающих к любой стороне, равна 180°:

\(\angle ABC + \angle BCD = \angle BCD + \angle CDA = \angle CDA + \angle DAB = \angle DAB + \angle ABC = 180{^\circ}\)

ПЛОЩАДЬ ПАРАЛЕЛОГРАММА:

1. Через высоту и сторону

Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне.

\(S = ah_{1} = bh_{2}\)

2. Через две стороны и угол между ними

Площадь параллелограмма равна произведению его сторон на синус угла между ними.

\(S = ab \bullet \sin\alpha\)

3. Через диагонали и угол между ними

Площадь параллелограмма равна половине произведения его диагоналей на синус угла между ними.

\(S = \frac{1}{2}d_{1}d_{2} \bullet \sin\gamma\)

{\circ}$.

Параллелограмм — это особый тип четырехугольника, у которого обе пары противоположных сторон параллельны и равны. На данном рисунке изображен параллелограмм ABCD, у которого AB II CD и AD II BC. Кроме того, AD $=$ BC и AB $=$ CD.

Обратите внимание, что квадраты и прямоугольники являются особыми типами параллелограммов. В прямоугольнике все углы прямые.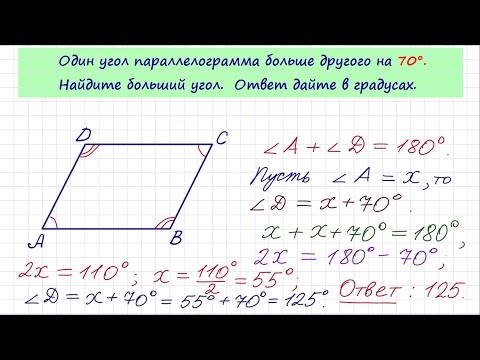 Квадрат бывает равносторонним и равноугольным.

Родственные игры

Углы параллелограмма

9{\circ}$

 Познакомимся с теоремами, связанными с углами параллелограмма:

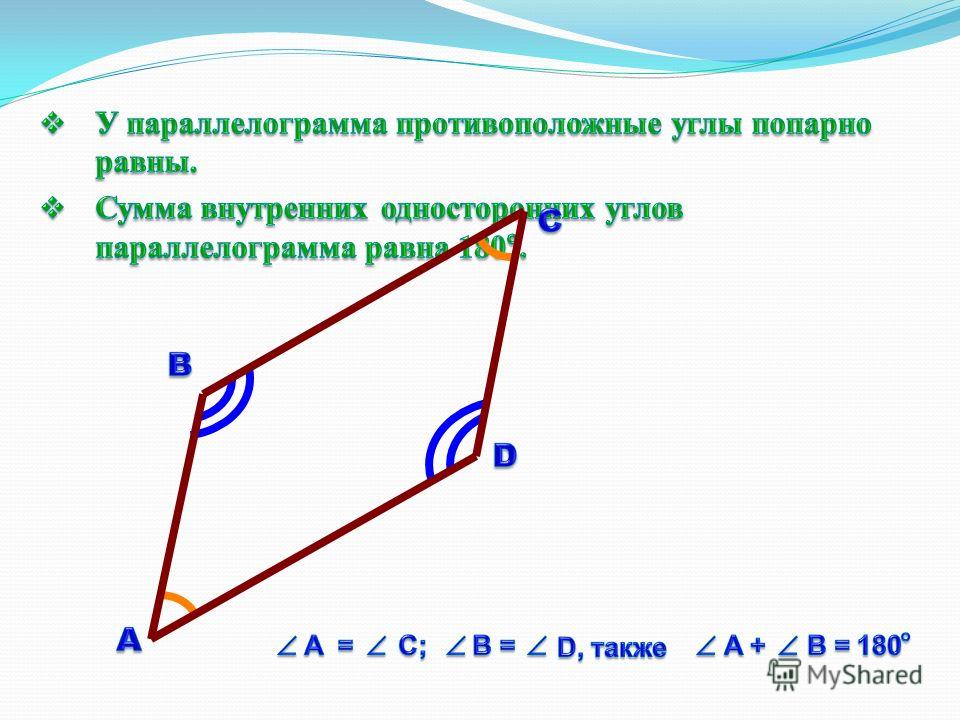
1. Противоположные углы параллелограмма равны.

2. Теорема о последовательных углах параллелограмма: последовательные углы параллелограмма являются дополнительными.

Теорема 1: Противоположные углы параллелограмма равны.

Дано: PQRS — параллелограмм.

Доказать: $\angle P = \angle R$ и $\angle Q = \angle S$

Доказательство: В параллелограмме PQRS диагональ PR делит параллелограмм на два треугольника.

Кроме того, PQ || СР и КР || PS

Таким образом, диагональ PR выступает в роли секущей.

При сравнении треугольников PQR и PSR имеем:

PR $=$ PR (общие стороны)

Мы знаем, что внутренние углы равны.

Таким образом,

 $\угол 1 = \угол 4$ (чередующиеся внутренние углы)

$\угол 2  = \угол 3$  (альтернативные внутренние углы)

Таким образом, два треугольника равны, $\Delta\; PQR \конг\Дельта\; PSR$

Следовательно, $\angle Q = \angle S$ по CPCTC (соответствующие части конгруэнтных треугольников конгруэнтны).

Аналогично можно показать, что $\angle P = \angle R$.

Противоположные углы параллелограмма равны.

Отсюда доказано.

Докажем и обратную теорему.

Теорема, обратная приведенной выше, выглядит следующим образом:

9{\circ}$.

 Это показывает, что последовательные углы являются дополнительными.

 Означает, что PS || QR.

 Аналогично можно показать, что PQ || РС.

 Следовательно, ПС || QR и PQ || РС.

PQRS — параллелограмм.

Отсюда доказано.

Теорема 2: Смежные углы параллелограмма являются дополнительными.

Дано: PQRS — параллелограмм, у которого четыре угла $\угол P \угол Q, \угол R, \угол S$ соответственно. 9{\circ}$.

Таким образом, последовательные углы параллелограмма являются дополнительными.

  Забавные факты!

• Параллелограмм — это особый тип четырехугольника, у которого обе пары противоположных сторон параллельны и равны.
  {\circ}$. 9{\circ}$

• Диагональ параллелограмма делит его на два равных треугольника.

• Прямоугольники и квадраты являются примерами параллелограммов с углами 90 градусов, также известными как прямые углы. Ромбы и квадраты являются примерами параллелограммов, у которых стороны одинаковой длины.

• Если один угол в параллелограмме прямой, то все углы прямые.

Заключение

Параллелограмм — это особый тип четырехугольника, у которого обе пары противоположных сторон параллельны и равны, а противоположные углы равны. Теперь, когда мы изучили теоремы, связанные с углами параллелограмма, давайте решим несколько примеров для лучшего понимания. 9{\circ}$

2. Два смежных угла параллелограмма относятся как 2:3. Найдите величину углов.

Решение: 

Пусть углы равны $2x$ и $3x$.

Мы знаем, что смежные углы параллелограмма являются дополнительными.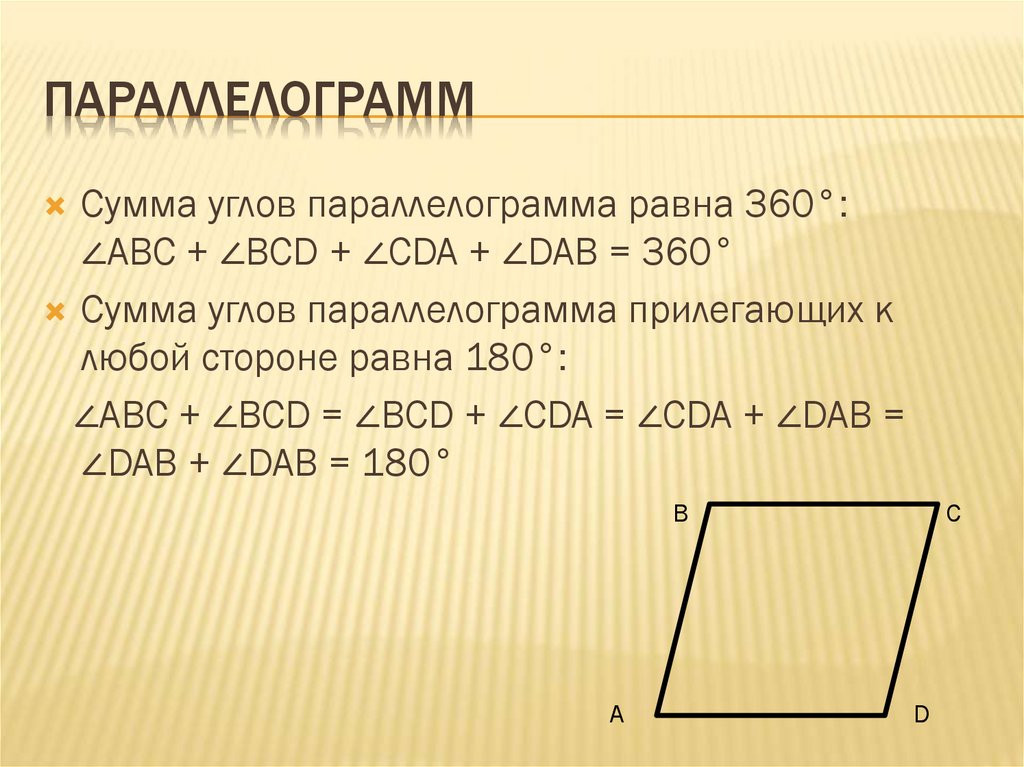

Таким образом,

$ 2x + 3x = 180 $

$ 5x = 180 $

$ x = x 36 $

СЕЙЧАС, 2x = 2 \ Times 36 = 72 $

и 3x = 3 \ умножить на 36 = 108$ 9{\circ}$

Мы знаем, что если в параллелограмме один угол равен 90 градусов, то и все остальные углы также равны 90 градусам.

Значит, данный параллелограмм называется прямоугольником с четырьмя прямыми углами.

5. В приведенном ниже параллелограмме ABCD найдите $\угол A, \угол B, \угол C$ и $\угол D$ .

Решение:

В параллелограмме смежные углы дополнительные.

В приведенном выше параллелограмме углы $\angle A$ и $\angle B$ являются смежными углами. 9\circ$.

2

В параллелограмме обе пары противоположных сторон ________.

равные

параллельные

конгруэнтные

Все вышеперечисленное

Правильный ответ: Все вышеперечисленное
Параллелограмм – это особый тип четырехугольника, у которого обе пары противоположных сторон параллельны и равны (конгруэнтны).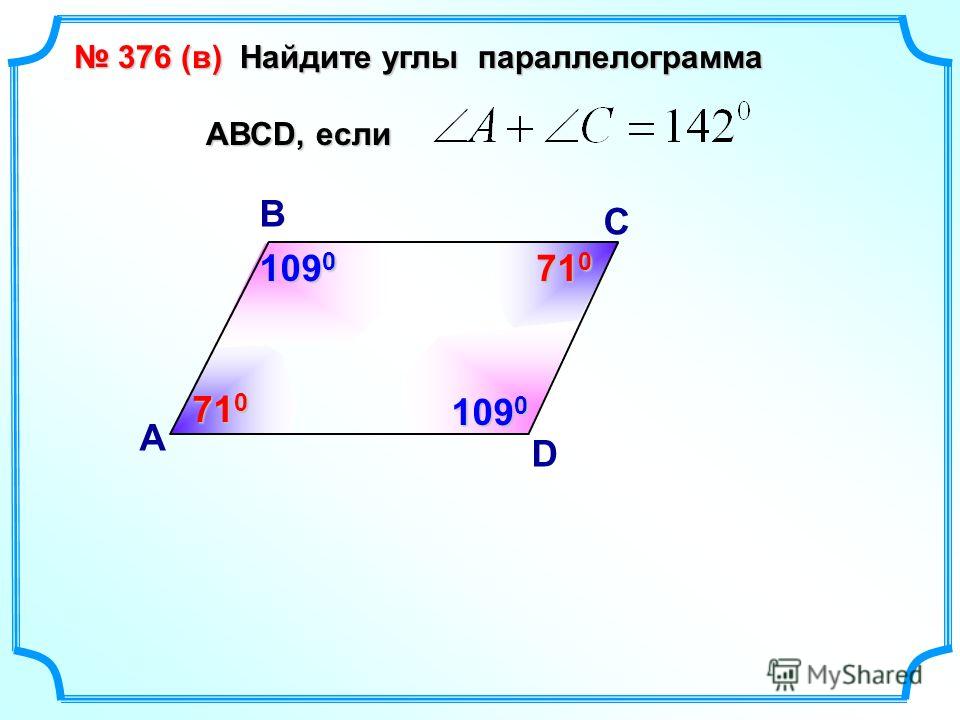

3

Какое из следующих утверждений НЕВЕРНО?

Смежные углы параллелограмма смежные. 9{\circ}$ и любые два соседних (последовательных) угла параллелограмма являются дополнительными.

Все ли параллелограммы прямоугольники?

Нет, параллелограмм не всегда является прямоугольником. В прямоугольнике все углы должны быть равны 90°. Но для параллелограмма внутренние углы должны быть равны 90°. Однако все прямоугольники являются параллелограммами, потому что прямоугольник имеет два набора параллельных сторон и две пары противоположных сторон, которые равны. Следовательно, он соблюдает все свойства параллелограмма.

Является ли параллелограмм четырехугольником?

Да, параллелограмм — это четырехугольник. Четырехугольник — это замкнутая форма и тип многоугольника, который имеет четыре стороны, четыре вершины и четыре угла. Параллелограмм также является замкнутой фигурой с четырьмя углами.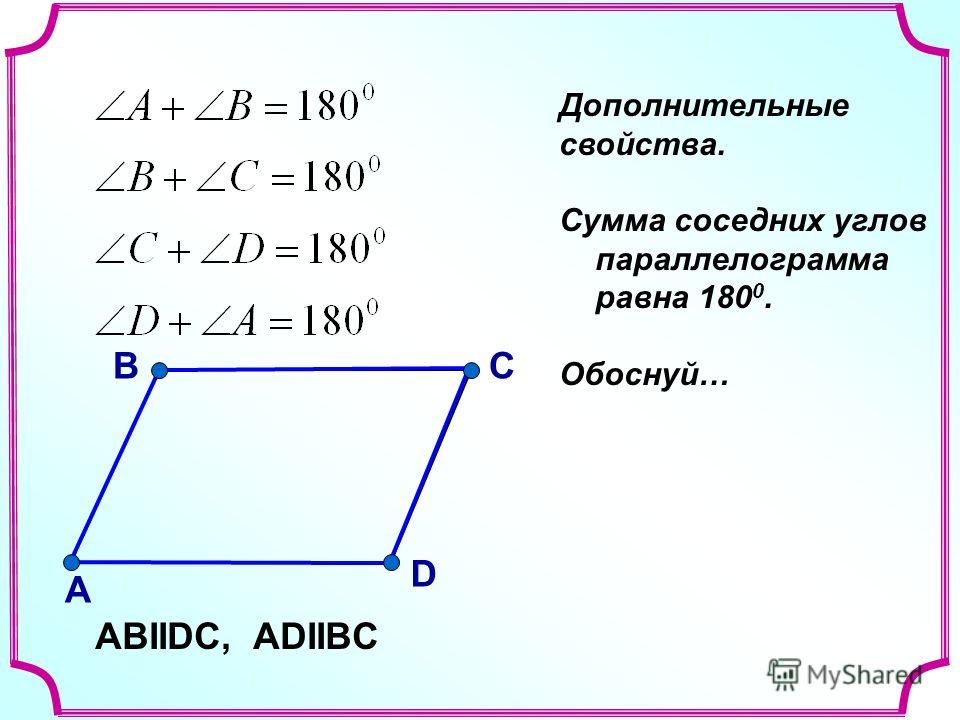 Следовательно, его можно назвать четырехугольником.

Могут ли параллелограмм иметь прямые углы?

Да, параллелограмм с четырьмя прямыми углами называется прямоугольником. В прямоугольнике каждая пара внутренних углов является дополнительной, потому что два прямых угла складываются с прямым углом, поэтому противоположные стороны прямоугольника параллельны. Это означает, что прямоугольник является параллелограммом. 9{\circ}$.

В параллелограмме противоположные углы равны, а в ромбе все четыре угла равны.

Углы параллелограмма

Параллелограмм — это четырехсторонняя фигура с двумя парами параллельных сторон. Противоположные стороны параллелограмма равны по длине, а противолежащие углы равны по размеру. В этом посте мы сосредоточимся на углах параллелограмма. А именно, мы обсудим, как вычислить внутренние углы параллелограмма, а также внешние углы.

 

Как рассчитать внутренние углы параллелограмма

Существует несколько способов вычисления внутренних углов параллелограмма.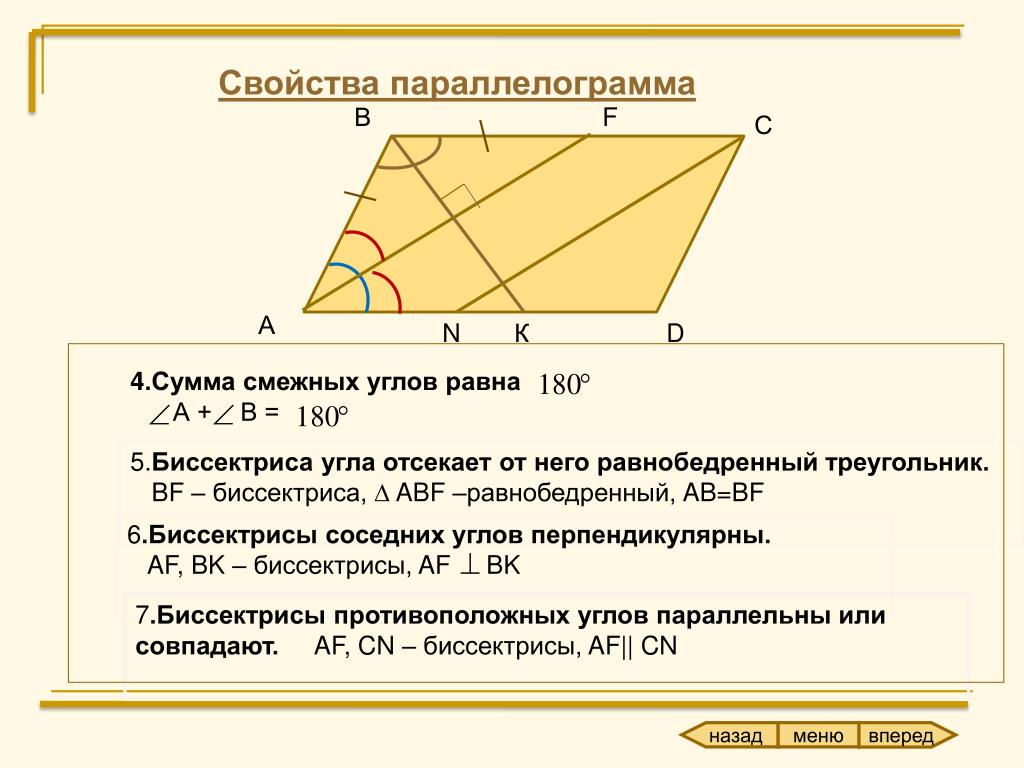 Один из способов — просто сложить измерения четырех углов и разделить на четыре. Это даст вам среднюю меру угла, которую вы затем можете использовать, чтобы найти меру каждого отдельного угла.

 

Другой метод нахождения внутренних углов параллелограмма состоит в том, чтобы разделить пополам обе пары противоположных сторон линиями (или отрезками). Это создаст четыре прямоугольных треугольника внутри параллелограмма. Затем вы можете использовать теорему Пифагора, чтобы найти длину сегментов, образованных линиями деления пополам, что позволит вам вычислить каждый угол, используя базовую тригонометрию.

 

Как только вы нашли внутренние углы, не так уж сложно найти внешние углы. Видите ли, сумма мер внутреннего и внешнего углов при любой вершине (угле) многоугольника всегда равна 360 градусам. Таким образом, если вы знаете две меры угла, вы можете легко вычислить третью.

Вычисление углов параллелограмма не так уж сложно, если знать несколько основных формул.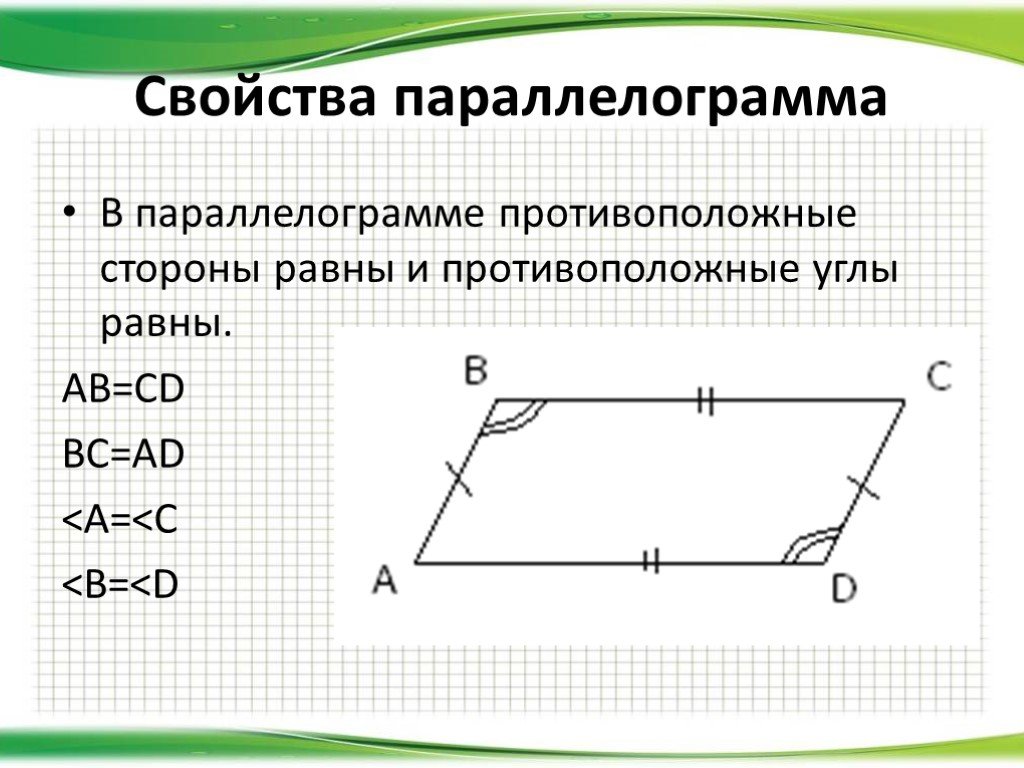 В этом сообщении блога мы рассмотрели два метода нахождения внутренних углов, а также то, как использовать эту информацию для вычисления внешних углов. Если вы когда-нибудь сталкивались с задачей по геометрии, которая включает в себя вычисление углов в параллелограмме, просто вернитесь к этому сообщению в блоге, чтобы освежить в памяти!

Как найти углы параллелограмма?

Чтобы найти углы параллелограмма, вам нужно будет использовать свойства параллелограмма. Углы в параллелограмме равны, поэтому, если вы можете найти один угол, вы будете знать все углы. Вы можете использовать следующие шаги, чтобы найти угол в параллелограмме:

1. Найдите две смежные стороны параллелограмма.

2. Используйте теорему Пифагора, чтобы найти длину гипотенузы треугольника, образованного этими двумя сторонами.

3. Используйте функцию арккосинуса, чтобы найти угол между этими двумя сторонами.

4. Найденный угол является одним из углов параллелограмма.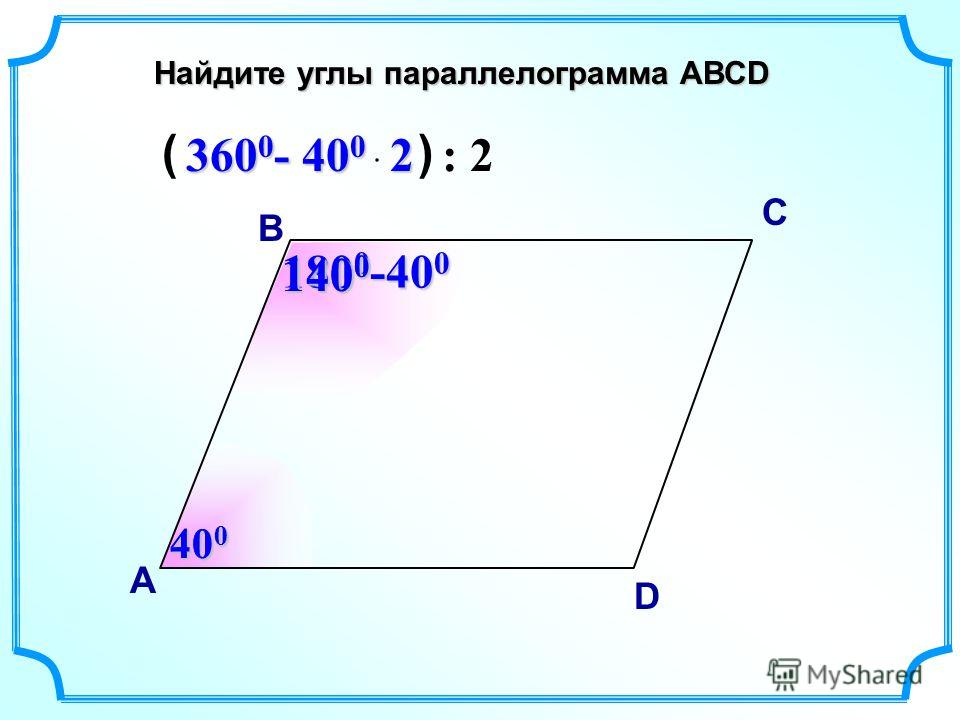 Остальные углы равны ему, поэтому вы знаете все углы параллелограмма.

 

Сумма углов параллелограмма равна 180?

Нет, сумма углов параллелограмма не равна 180. Сумма углов параллелограмма равна 360.

 

Равны ли углы параллелограмма?

Да, углы параллелограмма равны. Вы можете использовать следующие шаги, чтобы найти угол в параллелограмме:

1. Найдите две смежные стороны параллелограмма.

2. Используйте теорему Пифагора, чтобы найти длину гипотенузы треугольника, образованного этими двумя сторонами.

3. Используйте функцию арккосинуса, чтобы найти угол между этими двумя сторонами.

4. Найденный угол является одним из углов параллелограмма. Остальные углы равны ему, поэтому вы знаете все углы параллелограмма.

 

Все ли углы параллелограмма равны 90°?

Нет, все углы параллелограмма не равны 90. Сумма углов параллелограмма равна 360.

Вы можете использовать следующие шаги, чтобы найти угол в параллелограмме:

1.