Таблица брадиса онлайн косинусы: синусы, косинусы, тангенсы и котангенсы

Содержание

синусы, косинусы, тангенсы и котангенсы

Главная
Справочник
Таблицы
Таблицы по геометрии
Таблица Брадиса: синусы, косинусы, тангенсы и котангенсы

Таблица Брадиса — это таблица, которая поможет вычислить значения синусов, косинусов, тангенсов и котангенсов углов с точностью до одной минуты без калькулятора.

Для таблиц Брадиса в качестве аргумента функций используется значение угла, заданное в градусах. Если же значение аргумента дано в радианах, то для перевода в градусы его следует умножить на 180 и разделить на 3.1415926.

Как пользоваться таблицей Брадиса?

В таблице Брадиса представлены значения углов кратных 6 минутам. Если необходимо найти значения синуса, косинуса, тангенса или котангенса угла, который отсутствует в таблице Брадиса, следует выбирать наиболее близкое к нему значение. И добавить (отнять) к нему поправку соответствующую разнице, которая может быть равна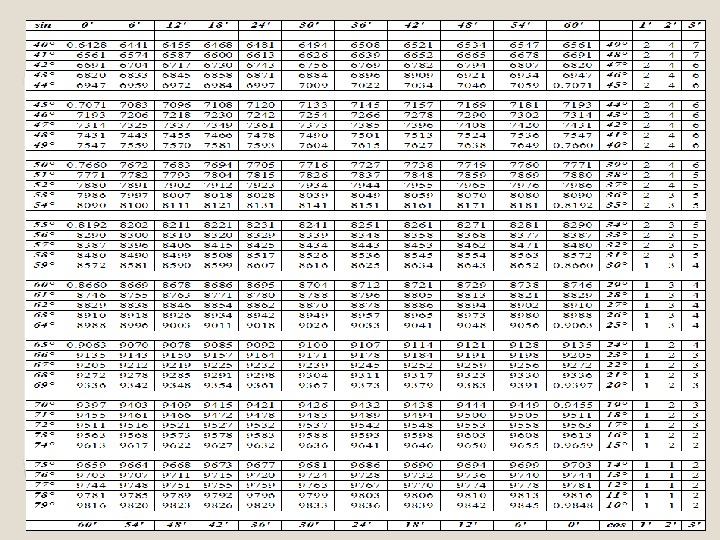

1′, 2′, 3′.

Примеры:

sin(15°25′) = sin(15°24′) + поправка 1′ = 0.2656 + 0.0003 = 0.2659
sin(15°28′) = sin(15°30′) — поправка 2′ = 0.2672 — 0.0006 = 0.2666

При вычислении значений синуса поправка имеет положительный знак, для косинуса поправку необходимо брать с отрицательным знаком:

cos(15°25′) = sin(15°24′) + поправка 1′ = 0.9641 — 0.0001 = 0.9640
cos(15°28′) = sin(15°30′) — поправка 2′ = 0.9636 + 0.0002 = 0.9638

Таблица Брадиса для синуса и косинуса

sin	0′	6′	12′	18′	24′	30′	36′	42′	48′	54′	60′	cos	1′	2′	3′
											0.0000	90°
0°	0.0000	0017	0035	0052	0070	0087	0105	0122	0140	0157	0175	89°	3	6	9
1°	0175	0192	0209	0227	0244	0262	0279	0297	0314	0332	0349	88°	3	6	9
2°	0349	0366	0384	0401	0419	0436	0454	0471	0488	0506	0523	87°	3	6	9
3°	0523	0541	0558	0576	0593	0610	0628	0645	0663	0680	0698	86°	3	6	9
4°	0698	0715	0732	0750	0767	0785	0802	0819	0837	0854	0. 0872	85°	3	6	9

5°	0.0872	0889	0906	0924	0941	0958	0976	0993	1011	1028	1045	84°	3	6	9
6°	1045	1063	1080	1097	1115	1132	1149	1167	1184	1201	1219	83°	3	6	9
7°	1219	1236	1253	1271	1288	1305	1323	1340	1357	1374	1392	82°	3	6	9
8°	1392	1409	1426	1444	1461	1478	1495	1513	1530	1547	1564	81°	3	6	9
9°	1564	1582	1599	1616	1633	1650	1668	1685	1702	1719	0. 1736	80°	3	6	9

10°	0.1736	1754	1771	1788	1805	1822	1840	1857	1874	1891	1908	79°	3	6	9
11°	1908	1925	1942	1959	1977	1994	2011	2028	2045	2062	2079	78°	3	6	9
12°	2079	2096	2113	2130	2147	2164	2181	2198	2215	2233	2250	77°	3	6	9
13°	2250	2267	2284	2300	2317	2334	2351	2368	2385	2402	2419	76°	3	6	8
14°	2419	2436	2453	2470	2487	2504	2521	2538	2554	2571	0.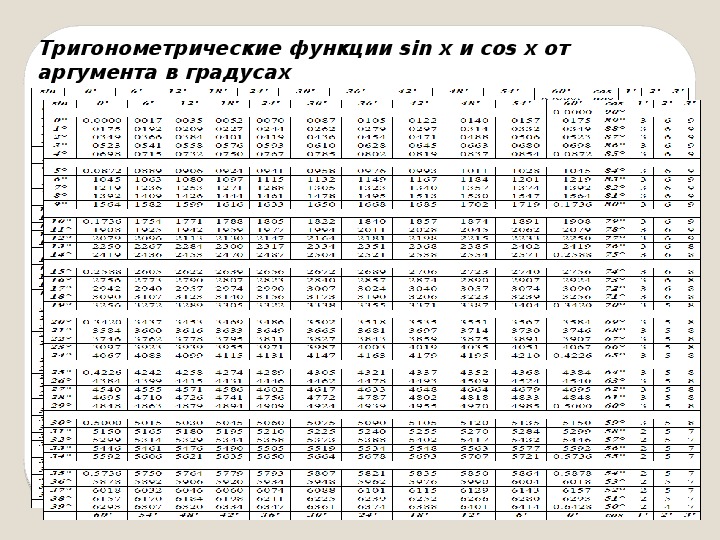 2588	75°	3	6	8

15°	0.2588	2605	2622	2639	2656	2672	2689	2706	2723	2740	2756	74°	3	6	8
16°	2756	2773	2790	2807	2823	2840	2857	2874	2890	2907	2924	73°	3	6	8
17°	2924	2940	2957	2974	2990	3007	3024	3040	3057	3074	3090	72°	3	6	8
18°	3090	3107	3123	3140	3156	3173	3190	3206	3223	3239	3256	71°	3	6	8
19°	3256	3272	3289	3305	3322	3338	3355	3371	3387	3404	0. 3420	70°	3	5	8

20°	0.3420	3437	3453	3469	3486	3502	3518	3535	3551	3567	3584	69°	3	5	8
21°	3584	3600	3616	3633	3649	3665	3681	3697	3714	3730	3746	68°	3	5	8
22°	3746	3762	3778	3795	3811	3827	3843	3859	3875	3891	3907	67°	3	5	8
23°	3907	3923	3939	3955	3971	3987	4003	4019	4035	4051	4067	66°	3	5	8
24°	4067	4083	4099	4115	4131	4147	4163	4179	4195	4210	0. 4226	65°	3	5	8

25°	0.4226	4242	4258	4274	4289	4305	4321	4337	4352	4368	4384	64°	3	5	8
26°	4384	4399	4415	4431	4446	4462	4478	4493	4509	4524	4540	63°	3	5	8
27°	4540	4555	4571	4586	4602	4617	4633	4648	4664	4679	4695	62°	3	5	8
28°	4695	4710	4726	4741	4756	4772	4787	4802	4818	4833	4848	61°	3	5	8
29°	4848	4863	4879	4894	4909	4924	4939	4955	4970	4985	0. 5000	60°	3	5	8

30°	0.5000	5015	5030	5045	5060	5075	5090	5105	5120	5135	5150	59°	3	5	8
31°	5150	5165	5180	5195	5210	5225	5240	5255	5270	5284	5299	58°	2	5	7
32°	5299	5314	5329	5344	5358	5373	5388	5402	5417	5432	5446	57°	2	5	7
33°	5446	5461	5476	5490	5505	5519	5534	5548	5563	5577	5592	56°	2	5	7
34°	5592	5606	5621	5635	5650	5664	5678	5693	5707	5721	0. 5736	55°	2	5	7

35°	0.5736	5750	5764	5779	5793	5807	5821	5835	5850	5864	0.5878	54°	2	5	7
36°	5878	5892	5906	5920	5934	5948	5962	5976	5990	6004	6018	53°	2	5	7
37°	6018	6032	6046	6060	6074	6088	6101	6115	6129	6143	6157	52°	2	5	7
38°	6157	6170	6184	6198	6211	6225	6239	6252	6266	6280	6293	51°	2	5	7
39°	6293	6307	6320	6334	6347	6361	6374	6388	6401	6414	0. 6428	50°	2	4	7

40°	0.6428	6441	6455	6468	6481	6494	6508	6521	6534	6547	6561	49°	2	4	7
41°	6561	6574	6587	6600	6613	6626	6639	6652	6665	6678	6691	48°	2	4	7
42°	6691	6704	6717	6730	6743	6756	6769	6782	6794	6807	6820	47°	2	4	6
43°	6820	6833	6845	6858	6871	6884	6896	8909	6921	6934	6947	46°	2	4	6
44°	6947	6959	6972	6984	6997	7009	7022	7034	7046	7059	0. 7071	45°	2	4	6

45°	0.7071	7083	7096	7108	7120	7133	7145	7157	7169	7181	7193	44°	2	4	6
46°	7193	7206	7218	7230	7242	7254	7266	7278	7290	7302	7314	43°	2	4	6
47°	7314	7325	7337	7349	7361	7373	7385	7396	7408	7420	7431	42°	2	4	6
48°	7431	7443	7455	7466	7478	7490	7501	7513	7524	7536	7547	41°	2	4	6
49°	7547	7559	7570	7581	7593	7604	7615	7627	7638	7649	0. 7660	40°	2	4	6

50°	0.7660	7672	7683	7694	7705	7716	7727	7738	7749	7760	7771	39°	2	4	6
51°	7771	7782	7793	7804	7815	7826	7837	7848	7859	7869	7880	38°	2	4	5
52°	7880	7891	7902	7912	7923	7934	7944	7955	7965	7976	7986	37°	2	4	5
53°	7986	7997	8007	8018	8028	8039	8049	8059	8070	8080	8090	36°	2	3	5
54°	8090	8100	8111	8121	8131	8141	8151	8161	8171	8181	0. 8192	35°	2	3	5

55°	0.8192	8202	8211	8221	8231	8241	8251	8261	8271	8281	8290	34°	2	3	5
56°	8290	8300	8310	8320	8329	8339	8348	8358	8368	8377	8387	33°	2	3	5
57°	8387	8396	8406	8415	8425	8434	8443	8453	8462	8471	8480	32°	2	3	5
58°	8480	8490	8499	8508	8517	8526	8536	8545	8554	8563	8572	31°	2	3	5
59°	8572	8581	8590	8599	8607	8616	8625	8634	8643	8652	0. 8660	30°	1	3	4

60°	0.8660	8669	8678	8686	8695	8704	8712	8721	8729	8738	8746	29°	1	3	4
61°	8746	8755	8763	8771	8780	8788	8796	8805	8813	8821	8829	28°	1	3	4
62°	8829	8838	8846	8854	8862	8870	8878	8886	8894	8902	8910	27°	1	3	4
63°	8910	8918	8926	8934	8942	8949	8957	8965	8973	8980	8988	26°	1	3	4
64°	8988	8996	9003	9011	9018	9026	9033	9041	9048	9056	0.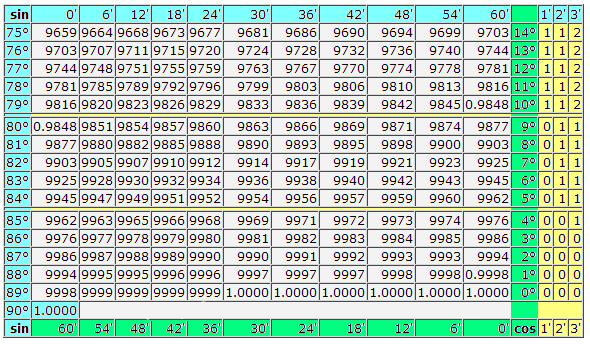 9063	25°	1	3	4

65°	0.9063	9070	9078	9085	9092	9100	9107	9114	9121	9128	9135	24°	1	2	4
66°	9135	9143	9150	9157	9164	9171	9178	9184	9191	9198	9205	23°	1	2	3
67°	9205	9212	9219	9225	9232	9239	9245	9252	9259	9256	9272	22°	1	2	3
68°	9272	9278	9285	9291	9298	9304	9311	9317	9323	9330	9336	21°	1	2	3
69°	9336	9342	9348	9354	9361	9367	9373	9379	9383	9391	0. 9397	20°	1	2	3

70°	9397	9403	9409	9415	9421	9426	9432	9438	9444	9449	0.9455	19°	1	2	3
71°	9455	9461	9466	9472	9478	9483	9489	9494	9500	9505	9511	18°	1	2	3
72°	9511	9516	9521	9527	9532	9537	9542	9548	9553	9558	9563	17°	1	2	3
73°	9563	9568	9573	9578	9583	9588	9593	9598	9603	9608	9613	16°	1	2	2
74°	9613	9617	9622	9627	9632	9636	9641	9646	9650	9655	0. 9659	15°	1	2	2

75°	9659	9664	9668	9673	9677	9681	9686	9690	9694	9699	9703	14°	1	1	2
76°	9703	9707	9711	9715	9720	9724	9728	9732	9736	9740	9744	13°	1	1	2
77°	9744	9748	9751	9755	9759	9763	9767	9770	9774	9778	9781	12°	1	1	2
78°	9781	9785	9789	9792	9796	9799	9803	9806	9810	9813	9816	11°	1	1	2
79°	9816	9820	9823	9826	9829	9833	9836	9839	9842	9845	0. 9848	10°	1	1	2

80°	0.9848	9851	9854	9857	9860	9863	9866	9869	9871	9874	9877	9°	0	1	1
81°	9877	9880	9882	9885	9888	9890	9893	9895	9898	9900	9903	8°	0	1	1
82°	9903	9905	9907	9910	9912	9914	9917	9919	9921	9923	9925	7°	0	1	1
83°	9925	9928	9930	9932	9934	9936	9938	9940	9942	9943	9945	6°	0	1	1
84°	9945	9947	9949	9951	9952	9954	9956	9957	9959	9960	9962	5°	0	1	1

85°	9962	9963	9965	9966	9968	9969	9971	9972	9973	9974	9976	4°	0	0	1
86°	9976	9977	9978	9979	9980	9981	9982	9983	9984	9985	9986	3°	0	0	0
87°	9986	9987	9988	9989	9990	9990	9991	9992	9993	9993	9994	2°	0	0	0
88°	9994	9995	9995	9996	9996	9997	9997	9997	9998	9998	0.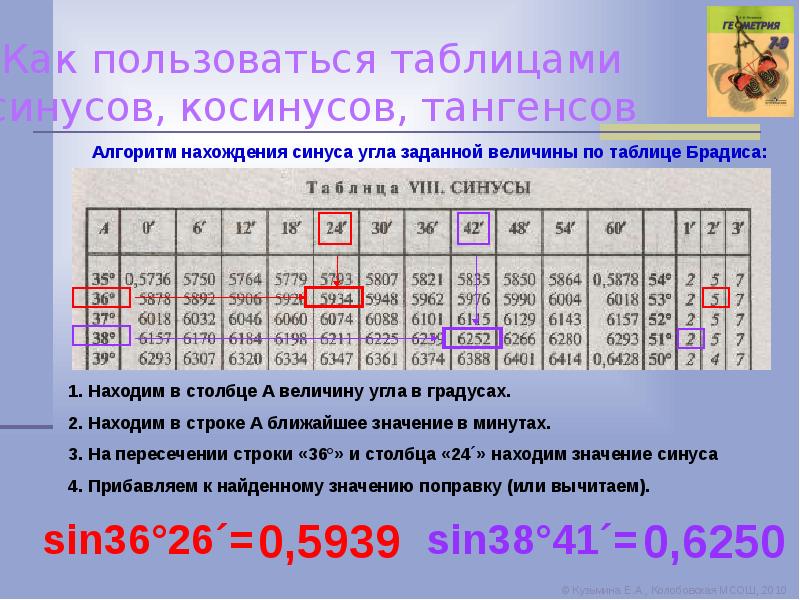 9998	1°	0	0	0
89°	9998	9999	9999	9999	9999	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	0°	0	0	0
90°	1.0000
sin	60′	54′	48′	42′	36′	30′	24′	18′	12′	6′	0′	cos	1′	2′	3′

Таблица Брадиса для тангенса и котангенса

tg	0′	6′	12′	18′	24′	30′	36′	42′	48′	54′	60′	ctg	1′	2′	3′
											0	90°
0°	0,000	0017	0035	0052	0070	0087	0105	0122	0140	0157	0175	89°	3	6	9
1°	0175	0192	0209	0227	0244	0262	0279	0297	0314	0332	0349	88°	3	6	9
2°	0349	0367	0384	0402	0419	0437	0454	0472	0489	0507	0524	87°	3	6	9
3°	0524	0542	0559	0577	0594	0612	0629	0647	0664	0682	0699	86°	3	6	9
4°	0699	0717	0734	0752	0769	0787	0805	0822	0840	0857	0,0875	85°	3	6	9

5°	0,0875	0892	0910	0928	0945	0963	0981	0998	1016	1033	1051	84°	3	6	9
6°	1051	1069	1086	1104	1122	1139	1157	1175	1192	1210	1228	83°	3	6	9
7°	1228	1246	1263	1281	1299	1317	1334	1352	1370	1388	1405	82°	3	6	9
8°	1405	1423	1441	1459	1477	1495	1512	1530	1548	1566	1584	81°	3	6	9
9°	1584	1602	1620	1638	1655	1673	1691	1709	1727	1745	0,1763	80°	3	6	9

10°	0,1763	1781	1799	1817	1835	1853	1871	1890	1908	1926	1944	79°	3	6	9
11°	1944	1962	1980	1998	2016	2035	2053	2071	2089	2107	2126	78°	3	6	9
12°	2126	2144	2162	2180	2199	2217	2235	2254	2272	2290	2309	77°	3	6	9
13°	2309	2327	2345	2364	2382	2401	2419	2438	2456	2475	2493	76°	3	6	9
14°	2493	2512	2530	2549	2568	2586	2605	2623	2642	2661	0,2679	75°	3	6	9

15°	0,2679	2698	2717	2736	2754	2773	2792	2811	2830	2849	2867	74°	3	6	9
16°	2867	2886	2905	2924	2943	2962	2981	3000	3019	3038	3057	73°	3	6	9
17°	3057	3076	3096	3115	3134	3153	3172	3191	3211	3230	3249	72°	3	6	10
18°	3249	3269	3288	3307	3327	3346	3365	3385	3404	3424	3443	71°	3	6	10
19°	3443	3463	3482	3502	3522	3541	3561	3581	3600	3620	0,3640	70°	3	7	10

20°	0,3640	3659	3679	3699	3719	3739	3759	3779	3799	3819	3839	69°	3	7	10
21°	3839	3859	3879	3899	3919	3939	3959	3979	4000	4020	4040	68°	3	7	10
22°	4040	4061	4081	4101	4122	4142	4163	4183	4204	4224	4245	67°	3	7	10
23°	4245	4265	4286	4307	4327	4348	4369	4390	4411	4431	4452	66°	3	7	10
24°	4452	4473	4494	4515	4536	4557	4578	4599	4621	4642	0,4663	65°	4	7	11

25°	0,4663	4684	4706	4727	4748	4770	4791	4813	4834	4856	4877	64°	4	7	11
26°	4877	4899	4921	4942	4964	4986	5008	5029	5051	5073	5095	63°	4	7	11
27°	5095	5117	5139	5161	5184	5206	5228	5250	5272	5295	5317	62°	4	7	11
28°	5317	5340	5362	5384	5407	5430	5452	5475	5498	5520	5543	61°	4	8	11
29°	5543	5566	5589	5612	5635	5658	5681	5704	5727	5750	0,5774	60°	4	8	12

30°	0,5774	5797	5820	5844	5867	5890	5914	5938	5961	5985	6009	59°	4	8	12
31°	6009	6032	6056	6080	6104	6128	6152	6176	6200	6224	6249	58°	4	8	12
32°	6249	6273	6297	6322	6346	6371	6395	6420	6445	6469	6494	57°	4	8	12
33°	6494	6519	6544	6569	6594	6619	6644	6669	6694	6720	6745	56°	4	8	13
34°	6745	6771	6796	6822	6847	6873	6899	6924	6950	6976	0,7002	55°	4	9	13

35°	0,7002	7028	7054	7080	7107	7133	7159	7186	7212	7239	7265	54°	4	8	13
36°	7265	7292	7319	7346	7373	7400	7427	7454	7481	7508	7536	53°	5	9	14°
37°	7536	7563	7590	7618	7646	7673	7701	7729	7757	7785	7813	52°	5	9	14
38°	7813	7841	7869	7898	7926	7954	7983	8012	8040	8069	8098	51°	5	9	14
39°	8098	8127	8156	8185	8214	8243	8273	8302	8332	8361	0,8391	50°	5	10	15

40°	0,8391	8421	8451	8481	8511	8541	8571	8601	8632	8662	0,8693	49°	5	10	15
41°	8693	8724	8754	8785	8816	8847	8878	8910	8941	8972	9004	48°	5	10	16
42°	9004	9036	9067	9099	9131	9163	9195	9228	9260	9293	9325	47°	6	11	16
43°	9325	9358	9391	9424	9457	9490	9523	9556	9590	9623	0,9657	46°	6	11	17
44°	9657	9691	9725	9759	9793	9827	9861	9896	9930	9965	1,0000	45°	6	11	17

45°	1,0000	0035	0070	0105	0141	0176	0212	0247	0283	0319	0355	44°	6	12	18
46°	0355	0392	0428	0464	0501	0538	0575	0612	0649	0686	0724	43°	6	12	18
47°	0724	0761	0799	0837	0875	0913	0951	0990	1028	1067	1106	42°	6	13	19
48°	1106	1145	1184	1224	1263	1303	1343	1383	1423	1463	1504	41°	7	13	20
49°	1504	1544	1585	1626	1667	1708	1750	1792	1833	1875	1,1918	40°	7	14	21

50°	1,1918	1960	2002	2045	2088	2131	2174	2218	2261	2305	2349	39°	7	14	22
51°	2349	2393	2437	2482	2527	2572	2617	2662	2708	2753	2799	38°	8	15	23
52°	2799	2846	2892	2938	2985	3032	3079	3127	3175	3222	3270	37°	8	16	24
53°	3270	3319	3367	3416	3465	3514	3564	3613	3663	3713	3764	36°	8	16	25
54°	3764	3814	3865	3916	3968	4019	4071	4124	4176	4229	1,4281	35°	9	17	26

55°	1,4281	4335	4388	4442	4496	4550	4605	4659	4715	4770	4826	34°	9	18	27
56°	4826	4882	4938	4994	5051	5108	5166	5224	5282	5340	5399	33°	10	19	29
57°	5399	5458	5517	5577	5637	5697	5757	5818	5880	5941	6003	32°	10	20	30
58°	6003	6066	6128	6191	6255	6319	6383	6447	6512	6577	6643	31°	11	21	32
59°	6643	6709	6775	6842	6909	6977	7045	7113	7182	7251	1,7321	30°	11	23	34

60°	1,732	1,739	1,746	1,753	1,760	1,767	1,775	1,782	1,789	1,797	1,804	29°	1	2	4
61°	1,804	1,811	1,819	1,827	1,834	1,842	1,849	1,857	1,865	1,873	1,881	28°	1	3	4
62°	1,881	1,889	1,897	1,905	1,913	1,921	1,929	1,937	1,946	1,954	1,963	27°	1	3	4
63°	1,963	1,971	1,980	1,988	1,997	2,006	2,014	2,023	2,032	2,041	2,05	26°	1	3	4
64°	2,050	2,059	2,069	2,078	2,087	2,097	2,106	2,116	2,125	2,135	2,145	25°	2	3	5

65°	2,145	2,154	2,164	2,174	2,184	2,194	2,204	2,215	2,225	2,236	2,246	24°	2	3	5
66°	2,246	2,257	2,267	2,278	2,289	2,3	2,311	2,322	2,333	2,344	2,356	23°	2	4	5
67°	2,356	2,367	2,379	2,391	2,402	2,414	2,426	2,438	2,450	2,463	2,475	22°	2	4	6
68°	2,475	2,488	2,5	2,513	2,526	2,539	2,552	2,565	2,578	2,592	2,605	21°	2	4	6
69°	2,605	2,619	2,633	2,646	2,66	2,675	2,689	2,703	2,718	2,733	2,747	20°	2	5	7

70°	2,747	2,762	2,778	2,793	2,808	2,824	2,840	2,856	2,872	2,888	2,904	19°	3	5	8
71°	2,904	2,921	2,937	2,954	2,971	2,989	3,006	3,024	3,042	3,06	3,078	18°	3	6	9
72°	3,078	3,096	3,115	3,133	3,152	3,172	3,191	3,211	3,230	3,251	3,271	17°	3	6	10
73°	3,271	3,291	3,312	3,333	3,354	3,376							3	7	10
							3,398	3,42	3,442	3,465	3,487	16°	4	7	11
74°	3,487	3,511	3,534	3,558	3,582	3,606							4	8	12
							3,630	3,655	3,681	3,706	3,732	15°	4	8	13
75°	3,732	3,758	3,785	3,812	3,839	3,867							4	9	13
							3,895	3,923	3,952	3,981	4,011	14°	5	10	14
tg	60′	54′	48′	42′	36′	30′	24′	18′	12′	6′	0′	ctg	1′	2′	3′

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!Больше интересного в телеграм @calcsbox

Таблица Брадиса для синусов, косинусов, тангенсов

Представлена таблица Брадиса синусов и косинусов в удобном виде

Полная таблица Брадиса

Чтобы распечатать таблицу Брадиса,
скачайте ее в полном виде в форматеpdf

sin	0′	6′	12′	18′	24′	30′	36′	42′	48′	54′	60′	cos	&pm; 1′	&pm; 2′	&pm; 3′
											0,0000	90°
0°	0,0000	0017	0035	0052	007	0087	0105	0122	014	0157	0175	89°	3	6	9
1°	0175	0192	0209	0227	0244	0262	0279	0297	0314	0332	0349	88°	3	6	9
2°	0349	0366	0384	0401	0419	0436	0454	0471	0488	0506	0523	87°	3	6	9
3°	0523	0541	0558	0576	0593	061	0628	0645	0663	068	0698	86°	3	6	9
4°	0698	0715	0732	075	0767	0785	0802	0819	0837	0854	0872	85°	3	6	9
5°	0872	0889	0906	0924	0941	0958	0976	0993	1011	1028	1045	84°	3	6	9
6°	1045	1063	108	1097	1115	1132	1149	1167	1184	1201	1219	83°	3	6	9
7°	1219	1236	1253	1271	1288	1305	1323	134	1357	1374	1392	82°	3	6	9
8°	1392	1409	1426	1444	1461	1478	1495	1513	153	1547	1564	81°	3	6	9
9°	1564	1582	1599	1616	1633	165	1668	1685	1702	1719	1736	80°	3	6	9
10°	1736	1754	1771	1788	1805	1822	184	1857	1874	1891	1908	79°	3	6	9
11°	1908	1925	1942	1959	1977	1994	2011	2028	2045	2062	2079	78°	3	6	9
12°	2079	2096	2113	213	2147	2164	2181	2198	2215	2233	225	77°	3	6	9
13°	225	2267	2284	23	2317	2334	2351	2368	2385	2402	2419	76°	3	6	8
14°	2419	2436	2453	247	2487	2504	2521	2538	2554	2571	2588	75°	3	6	8
15°	2588	2605	2622	2639	2656	2672	2689	2706	2723	274	2756	74°	3	6	8
16°	2756	2773	279	2807	2823	284	2857	2874	289	2907	2924	73°	3	6	8
17°	2924	294	2957	2974	299	3007	3024	304	3057	3074	309	72°	3	6	8
18°	309	3107	3123	314	3156	3173	319	3206	3223	3239	3256	71°	3	6	8
19°	3256	3272	3289	3305	3322	3338	3355	3371	3387	3404	342	70°	3	5	8
20°	342	3437	3453	3469	3486	3502	3518	3535	3551	3567	3584	69°	3	5	8
21°	3584	36	3616	3633	3649	3665	3681	3697	3714	373	3746	68°	3	5	8
22°	3746	3762	3778	3795	3811	3827	3843	3859	3875	3891	3907	67°	3	5	8
23°	3907	3923	3939	3955	3971	3987	4003	4019	4035	4051	4067	66°	3	5	8
24°	4067	4083	4099	4115	4131	4147	4163	4179	4195	421	4226	65°	3	5	8
25°	4226	4242	4258	4274	4289	4305	4321	4337	4352	4368	4384	64°	3	5	8
26°	4384	4399	4415	4431	4446	4462	4478	4493	4509	4524	454	63°	3	5	8
27°	454	4555	4571	4586	4602	4617	4633	4648	4664	4679	4695	62°	3	5	8
28°	4695	471	4726	4741	4756	4772	4787	4802	4818	4833	4848	61°	3	5	8
29°	4848	4863	4879	4894	4909	4924	4939	4955	497	4985	5	60°	3	5	8
30°	5	5015	503	5045	506	5075	509	5105	512	5135	515	59°	3	5	8
31°	515	5165	518	5195	521	5225	524	5255	527	5284	5299	58°	2	5	7
32°	5299	5314	5329	5344	5358	5373	5388	5402	5417	5432	5446	57°	2	5	7
33°	5446	5461	5476	549	5505	5519	5534	5548	5563	5577	5592	56°	2	5	7
34°	5592	5606	5621	5635	565	5664	5678	5693	5707	5721	5736	55°	2	5	7
35°	5736	575	5764	5779	5793	5807	5821	5835	585	5864	5878	54°	2	5	7
36°	5878	5892	5906	592	5934	5948	5962	5976	599	6004	6018	53°	2	5	7
37°	6018	6032	6046	606	6074	6088	6101	6115	6129	6143	6157	52°	2	5	7
38°	6157	617	6184	6198	6211	6225	6239	6252	6266	628	6293	51°	2	5	7
39°	6293	6307	632	6334	6347	6361	6374	6388	6401	6414	6428	50°	2	4	7
40°	6428	6441	6455	6468	6481	6494	6508	6521	6534	6547	6561	49°	2	4	7
41°	6561	6574	6587	66	6613	6626	6639	6652	6665	6678	6691	48°	2	4	7
42°	6691	6704	6717	673	6743	6756	6769	6782	6794	6807	682	47°	2	4	6
43°	682	6833	6845	6858	6871	6884	6896	6909	6921	6934	6947	46°	2	4	6
44°	6947	6959	6972	6984	6997	7009	7022	7034	7046	7059	7071	45°	2	4	6
45°	7071	7083	7096	7108	712	7133	7145	7157	7169	7181	7193	44°	2	4	6
46°	7193	7206	7218	723	7242	7254	7266	7278	729	7302	7314	43°	2	4	6
47°	7314	7325	7337	7349	7361	7373	7385	7396	7408	742	7431	42°	2	4	6
48°	7431	7443	7455	7466	7478	749	7501	7513	7524	7536	7547	41°	2	4	6
49°	7547	7559	757	7581	7593	7604	7615	7627	7638	7649	766	40°	2	4	6
50°	766	7672	7683	7694	7705	7716	7727	7738	7749	776	7771	39°	2	4	6
51°	7771	7782	7793	7804	7815	7826	7837	7848	7859	7869	788	38°	2	4	5
52°	788	7891	7902	7912	7923	7934	7944	7955	7965	7976	7986	37°	2	4	5
53°	7986	7997	8007	8018	8028	8039	8049	8059	807	808	809	36°	2	3	5
54°	809	81	8111	8121	8131	8141	8151	8161	8171	8181	8192	35°	2	3	5
55°	8192	8202	8211	8221	8231	8241	8251	8261	8271	8281	829	34°	2	3	5
56°	829	83	831	832	8329	8339	8348	8358	8368	8377	8387	33°	2	3	5
57°	8387	8396	8406	8415	8425	8434	8443	8453	8462	8471	848	32°	2	3	5
58°	848	849	8499	8508	8517	8526	8536	8545	8554	8563	8572	31°	2	3	5
59°	8572	8581	859	8599	8607	8616	8625	8634	8643	8652	866	30°	1	3	4
60°	866	8669	8678	8686	8695	8704	8712	8721	8729	8738	8746	29°	1	3	4
61°	8746	8755	8763	8771	878	8788	8796	8805	8813	8821	8829	28°	1	3	4
62°	8829	8838	8846	8854	8862	887	8878	8886	8894	8902	891	27°	1	3	4
63°	891	8918	8926	8934	8942	8949	8957	8965	8973	898	8988	26°	1	3	4
64°	8988	8996	9003	9011	9018	9026	9033	9041	9048	9056	9063	25°	1	3	4
65°	9063	907	9078	9085	9092	91	9107	9114	9121	9128	9135	24°	1	2	4
66°	9135	9143	915	9157	9164	9171	9178	9184	9191	9198	9205	23°	1	2	3
67°	9205	9212	9219	9225	9232	9239	9245	9252	9259	9265	9272	22°	1	2	3
68°	9272	9278	9285	9291	9298	9304	9311	9317	9323	933	9336	21°	1	2	3
69°	9336	9342	9348	9354	9361	9367	9373	9379	9385	9391	9397	20°	1	2	3
70°	9397	9403	9409	9415	9421	9426	9432	9438	9444	9449	9455	19°	1	2	3
71°	9455	9461	9466	9472	9478	9483	9489	9494	95	9505	9511	18°	1	2	3
72°	9511	9516	9521	9527	9532	9537	9542	9548	9553	9558	9563	17°	1	2	3
73°	9563	9568	9573	9578	9583	9588	9593	9598	9603	9608	9613	16°	1	2	2
74°	9613	9617	9622	9627	9632	9636	9641	9646	965	9655	9659	15°	1	2	2
75°	9659	9664	9668	9673	9677	9681	9686	969	9694	9699	9703	14°	1	1	2
76°	9703	9707	9711	9715	972	9724	9728	9732	9736	974	9744	13°	1	1	2
77°	9744	9748	9751	9755	9759	9763	9767	977	9774	9778	9781	12°	1	1	2
78°	9781	9785	9789	9792	9796	9799	9803	9806	981	9813	9816	11°	1	1	2
79°	9816	982	9823	9826	9829	9833	9836	9839	9842	9845	9848	10°	1	1	2
80°	9848	9851	9854	9857	986	9863	9866	9869	9871	9874	9877	9°	0	1	1
81°	9877	988	9882	9885	9888	989	9893	9895	9898	99	9903	8°	0	1	1
82°	9903	9905	9907	991	9912	9914	9917	9919	9921	9923	9925	7°	0	1	1
83°	9925	9928	993	9932	9934	9936	9938	994	9942	9943	9945	6°	0	1	1
84°	9945	9947	9949	9951	9952	9954	9956	9957	9959	996	9962	5°	0	1	1
85°	9962	9963	9965	9966	9968	9969	9971	9972	9973	9974	9976	4°	0	0	1
86°	9976	9977	9978	9979	998	9981	9982	9983	9984	9985	9986	3°	0	0	0
87°	9986	9987	9988	9989	999	999	9991	9992	9993	9993	9994	2°	0	0	0
88°	9994	9995	9995	9996	9996	9997	9997	9997	9998	9998	9998	1°	0	0	0
89°	9998	9999	9999	9999	9999	1. 0	1.0	1.0	1.0	1.0	1.0	0°	0	0	0
90°	0,0000

Как пользоваться таблицей Брадиса косинусов или синусов

Таблица Брадиса для синусов и косинусов даёт значение синуса любого острого угла, содержащего целое число градусов и десятых долей градуса, на пересечении строки, имеющей в заголовке (слева) соответствующее число минут. Так, sin 70° 30`=0.9426. Для получения синусов прочих углов нужна интерполяция, вводящая поправку на равность между данным углом и ближайшим табличным. Эта поправка берется из соответствующего столбца поправок справа (курсив). Она прибавляется к ближайшему меньшему значению синуса, если данный угол превосходит ближайший меньший табличный на 1,2,3 минуты, и отнимается от ближайшего большего табличного синуса в остальных случаях. Например, sin 70° 32`=0,9428, так как 9426+2=9428, и sin 70° 34`= 0,9430, так как 9432-2=9430. Та же таблица синусов и косинусов служит для разыскания косинусов, при чем надо пользоваться нумерацией градусов справа, нумерацией минут снизу и не забывать, что при возрастании острого угла его косинус убывает. Подыскание косинусов можно устранить, звменяя их синусами дополнительных углов.
Значение тангенса любого острого угла, содержащего целое число градусов и минут определяется по табл. если угол заключен между 0° и 76°, и по таблице тангенсов если между 76° и 90. Работа по таблице тангенсов и котангенсов требует применения интерполяции, облегчаемой поправками, помещенными в столбцах справа (курсив) и ничем не отличается от работы таблицы sin и cos. Тангенсы углов, которые больше 76 градусов, содержащих целое число градусов и минут, табл. дает непосредственно (без интерполяции).
Таблицы Брадиса по синусам, косинусам, тангенсам и котангенсам позволяют решать и обратный вопрос, то есть находить острый угол по данному значению его синуса или тангенса.

Таблица Брадиса для тангенсов tg и котангенсов ctg

Представлена таблица Брадиса для тангенсов и котангенсов в удобном виде

tg	0′	6′	12′	18′	24′	30′	36′	42′	48′	54′	60′	ctg	&pm; 1′	&pm; 2′	&pm; 3′
											0,0000	90°
0°	0	0017	0035	0052	007	0087	0105	0122	014	0157	0175	89°	3	6	9
1°	0175	0192	0209	0227	0244	0262	0279	0297	0314	0332	0349	88°	3	6	9
2°	0349	0367	0384	0402	0419	0437	0454	0472	0489	0507	0524	87°	3	6	9
3°	0524	0542	0559	0577	0594	0612	0629	0647	0664	0682	0699	86°	3	6	9
4°	0699	0717	0734	0752	0769	0787	0805	0822	084	0857	0875	85°	3	6	9
5°	0875	0892	091	0928	0945	0963	0981	0998	1016	1033	1051	84°	3	6	9
6°	1051	1069	1086	1104	1122	1139	1157	1175	1192	121	1228	83°	3	6	9
7°	1228	1246	1263	1281	1299	1317	1334	1352	137	1388	1405	82°	3	6	9
8°	1405	1423	1441	1459	1477	1495	1512	153	1548	1566	1584	81°	3	6	9
9°	1584	1602	162	1638	1655	1673	1691	1709	1727	1745	1763	80°	3	6	9
10°	1763	1781	1799	1817	1835	1853	1871	189	1908	1926	1944	79°	3	6	9
11°	1944	1962	198	1998	2016	2035	2053	2071	2089	2107	2126	78°	3	6	9
12°	2126	2144	2162	218	2199	2217	2235	2254	2272	229	2309	77°	3	6	9
13°	2309	2327	2345	2364	2382	2401	2419	2438	2456	2475	2493	76°	3	6	9
14°	2493	2512	253	2549	2568	2586	2605	2623	2642	2661	2679	75°	3	6	9
15°	2679	2698	2717	2736	2754	2773	2792	2811	283	2849	2867	74°	3	6	9
16°	2867	2886	2905	2924	2943	2962	2981	3	3019	3038	3057	73°	3	6	9
17°	3057	3076	3096	3115	3134	3153	3172	3191	3211	323	3249	72°	3	6	10
18°	3249	3269	3288	3307	3327	3346	3365	3385	3404	3424	3443	71°	3	6	10
19°	3443	3463	3482	3502	3522	3541	3561	3581	36	362	364	70°	3	7	10
20°	364	3659	3679	3699	3719	3739	3759	3779	3799	3819	3839	69°	3	7	10
21°	3839	3859	3879	3899	3919	3939	3959	3979	4	402	404	68°	3	7	10
22°	404	4061	4081	4101	4122	4142	4163	4183	4204	4224	4245	67°	3	7	10
23°	4245	4265	4286	4307	4327	4348	4369	439	4411	4431	4452	66°	3	7	10
24°	4452	4473	4494	4515	4536	4557	4578	4599	4621	4642	4663	65°	4	7	11
25°	4663	4684	4706	4727	4748	477	4791	4813	4834	4856	4877	64°	4	7	11
26°	4877	4899	4921	4942	4964	4986	5008	5029	5051	5073	5095	63°	4	7	11
27°	5095	5117	5139	5161	5184	5206	5228	525	5272	5295	5317	62°	4	7	11
28°	5317	534	5362	5384	5407	543	5452	5475	5498	552	5543	61°	4	8	11
29°	5543	5566	5589	5612	5635	5658	5681	5704	5727	575	5774	60°	4	8	12
30°	5774	5797	582	5844	5867	589	5914	5938	5961	5985	6009	59°	4	8	12
31°	6009	6032	6056	608	6104	6128	6152	6176	62	6224	6249	58°	4	8	12
32°	6249	6273	6297	6322	6346	6371	6395	642	6445	6469	6494	57°	4	8	12
33°	6494	6519	6544	6569	6594	6619	6644	6669	6694	672	6745	56°	4	8	13
34°	6745	6771	6796	6822	6847	6873	6899	6924	695	6976	7002	55°	4	9	13
35°	7002	7028	7054	708	7107	7133	7159	7186	7212	7239	7265	54°	4	9	13
36°	7265	7292	7319	7346	7373	74	7427	7454	7481	7508	7536	53°	5	9	14
37°	7536	7563	759	7618	7646	7673	7701	7729	7757	7785	7813	52°	5	9	14
38°	7813	7841	7869	7898	7926	7954	7983	8012	804	8069	8098	51°	5	9	14
39°	8098	8127	8156	8185	8214	8243	8273	8302	8332	8361	8391	50°	5	10	15
40°	8391	8421	8451	8481	8511	8541	8571	8601	8632	8662	8693	49°	5	10	15
41°	8693	8724	8754	8785	8816	8847	8878	891	8941	8972	9004	48°	5	10	16
42°	9004	9036	9067	9099	9131	9163	9195	9228	926	9293	9325	47°	6	11	16
43°	9325	9358	9391	9424	9457	949	9523	9556	959	9623	9657	46°	6	11	17
44°	9657	9691	9725	9759	9793	9827	9861	9896	993	9965	1. 0	45°	6	11	17
45°	1.0	1.0035	1.007	1.0105	1.0141	1.0176	1.0212	1.0247	1.0283	1.0319	1.0355	44°	6	12	18
46°	1.0355	1.0392	1.0428	1.0464	1.0501	1.0538	1.0575	1.0612	1.0649	1.0686	1.0724	43°	6	12	18
47°	1.0724	1.0761	1.0799	1.0837	1.0875	1.0913	1.0951	1.099	1.1028	1.1067	1.1106	42°	6	13	19
48°	1.1106	1.1145	1.1184	1.1224	1.1263	1.1303	1.1343	1.1383	1.1423	1.1463	1.1504	41°	7	13	20
49°	1.1504	1. 1544	1.1585	1.1626	1.1667	1.1708	1.175	1.1792	1.1833	1.1875	1.1918	40°	7	14	21
50°	1.1918	1.196	1.2002	1.2045	1.2088	1.2131	1.2174	1.2218	1.2261	1.2305	1.2349	39°	7	14	22
51°	1.2349	1.2393	1.2437	1.2482	1.2527	1.2572	1.2617	1.2662	1.2708	1.2753	1.2799	38°	8	15	23
52°	1.2799	1.2846	1.2892	1.2938	1.2985	1.3032	1.3079	1.3127	1.3175	1.3222	1.327	37°	8	16	24
53°	1.327	1.3319	1.3367	1.3416	1.3465	1.3514	1.3564	1. 3613	1.3663	1.3713	1.3764	36°	8	16	25
54°	1.3764	1.3814	1.3865	1.3916	1.3968	1.4019	1.4071	1.4124	1.4176	1.4229	1.4281	35°	9	17	26
55°	1.4281	1.4335	1.4388	1.4442	1.4496	1.455	1.4605	1.4659	1.4715	1.477	1.4826	34°	9	18	27
56°	1.4826	1.4882	1.4938	1.4994	1.5051	1.5108	1.5166	1.5224	1.5282	1.534	1.5399	33°	10	19	29
57°	1.5399	1.5458	1.5517	1.5577	1.5637	1.5697	1.5757	1.5818	1.588	1.5941	1.6003	32°	10	20	30
58°	1. 6003	1.6066	1.6128	1.6191	1.6255	1.6319	1.6383	1.6447	1.6512	1.6577	1.6643	31°	11	21	32
59°	1.6643	1.6709	1.6775	1.6842	1.6909	1.6977	1.7045	1.7113	1.7182	1.7251	1.7321	30°	11	23	34
60°	1.7321	1.7391	1.7461	1.7532	1.7603	1.7675	1.7747	1.782	1.7893	1.7966	1.804	29°	1	2	4
61°	1.804	1.8115	1.819	1.8265	1.8341	1.8418	1.8495	1.8572	1.865	1.8728	1.8807	28°	1	3	4
62°	1.8807	1.8887	1.8967	1.9047	1.9128	1.921	1. 9292	1.9375	1.9458	1.9542	1.9626	27°	1	3	4
63°	1.9626	1.9711	1.9797	1.9883	1.997	2.0057	2.0145	2.0233	2.0323	2.0413	2.0503	26°	1	3	4
64°	2.0503	2.0594	2.0686	2.0778	2.0872	2.0965	2.106	2.1155	2.1251	2.1348	2.1445	25°	2	3	5
65°	2.1445	2.1543	2.1642	2.1742	2.1842	2.1943	2.2045	2.2148	2.2251	2.2355	2.246	24°	2	3	5
66°	2.246	2.2566	2.2673	2.2781	2.2889	2.2998	2.3109	2.322	2.3332	2.3445	2.3559	23°	2	4	5
67°	2.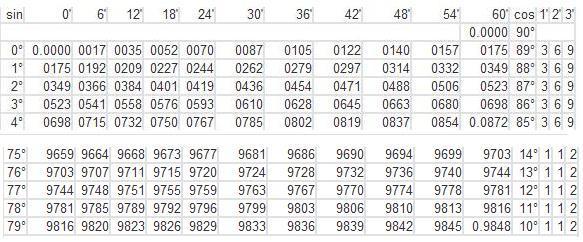 3559	2.3673	2.3789	2.3906	2.4023	2.4142	2.4262	2.4383	2.4504	2.4627	2.4751	22°	2	4	6
68°	2.4751	2.4876	2.5002	2.5129	2.5257	2.5386	2.5517	2.5649	2.5782	2.5916	2.6051	21°	2	4	6
69°	2.6051	2.6187	2.6325	2.6464	2.6605	2.6746	2.6889	2.7034	2.7179	2.7326	2.7475	20°	2	5	7
70°	2.7475	2.7625	2.7776	2.7929	2.8083	2.8239	2.8397	2.8556	2.8716	2.8878	2.9042	19°	3	5	8
71°	2.9042	2.9208	2.9375	2.9544	2.9714	2.9887	3. 0061	3.0237	3.0415	3.0595	3.0777	18°	3	6	9
72°	3.0777	3.0961	3.1146	3.1334	3.1524	3.1716	3.191	3.2106	3.2305	3.2506	3.2709	17°	3	6	10
73°	3.2709	3.2914	3.3122	3.3332	3.3544	3.3759	3.3977	3.4197	3.442	3.4646	3.4874	16°	3	7	10
74°	3.4874	3.5105	3.5339	3.5576	3.5816	3.6059	3.6305	3.6554	3.6806	3.7062	3.7321	15°	4	8	13
75°	3.7321	3.7583	3.7848	3.8118	3.8391	3.8667	3.8947	3.9232	3.952	3.9812	4.0108	14°	4	10	14
76°	4. 0108	4.0408	4.0713	4.1022	4.1335	4.1653	4.1976	4.2303	4.2635	4.2972	4.3315	13°
77°	4.3315	4.3662	4.4015	4.4373	4.4737	4.5107	4.5483	4.5864	4.6252	4.6646	4.7046	12°
78°	4.7046	4.7453	4.7867	4.8288	4.8716	4.9152	4.9594	5.0045	5.0504	5.097	5.1446	11°
79°	5.1446	5.1929	5.2422	5.2924	5.3435	5.3955	5.4486	5.5026	5.5578	5.614	5.6713	10°
80°	5.6713	5.7297	5.7894	5.8502	5.9124	5.9758	6.0405	6.1066	6.1742	6.2432	6.3138	9°
81°	6.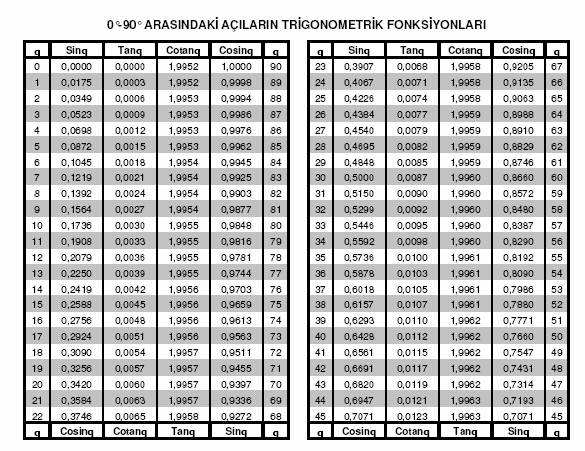 3138	6.3859	6.4596	6.535	6.6122	6.6912	6.772	6.8548	6.9395	7.0264	7.1154	8°
82°	7.1154	7.2066	7.3002	7.3962	7.4947	7.5958	7.6996	7.8062	7.9158	8.0285	8.1443	7°
83°	8.1443	8.2636	8.3863	8.5126	8.6427	8.7769	8.9152	9.0579	9.2052	9.3572	9.5144	6°
84°	9.5144	9.6768	9.8448	10187	11988	13854	15789	17797	19882	11.2048	11.4301	5°
85°	11.4301	11.6645	11.9087	12.1632	12.4288	12.7062	12.9962	13.2996	13.6174	13.9507	14. 3007	4°
86°	14.3007	14.6685	15.0557	15.4638	15.8945	16.3499	16.8319	17.3432	17.8863	18.4645	19.0811	3°
87°	19.0811	19.7403	24465	21.2049	22.0217	22.9038	23.8593	24.8978	26.0307	27.2715	28.6363	2°
88°	28.6363	31446	31.8205	33.6935	35.8006	38.1885	49174	44.0661	47.7395	52.0807	57.29	1°
89°	57.29	63.6567	71.6151	81.847	95.4895	114.5887	143.2371	199842	286.4777	572.9572		0°

синусы, косинусы, тангенсы и котангенсы

Как пользоваться таблицей Брадиса?

Таблицы Брадиса имеют одинаковую для всех функций структуру. Значения аргументов находятся в левом столбце и в верхней колонке. Соответствующее значение функции расположено в клетке, находящейся на пересечении столбца и колонки, которые задают значение аргумента.

Таблица БрадисаВозьмем для примера таблицу синусов. Допустим, следует определить, чему равно значение синуса для угла 10 градусов и 30 минут. Находим в левом столбце значение 10 градусов (11-я строка), а в верхней колонке – 30 минут (6-й столбец). На пересечении 11 строки и 6-го столбца, находим значение функции, 0.1822. Три последних столбца предназначены для уточнения значений минут. Дело в том, что в верхней колонке значения представлены только значения минут, кратные 6.

Если необходимо найти значения синуса, косинуса, тангенса или котангенса угла, который отсутствует в таблице Брадиса, следует выбирать наиболее близкое к нему значение. И прибавить или вычесть поправку соответствующую разнице, которая может быть равна 1′, 2′, 3′. Например, для угла 10 градусов и 32 минуты к уже найденному значению 0.1822 следует прибавить поправку из второго столбика, 6. Итак, синус 10 градусов 32 минут будет равен 0.1822+0.0006=0.1828.

Рассмотрим ещё примеры:

sin(15°25′) = sin(15°24′)+поправка 1′ = 0.2656+0.0003 = 0.2659
sin(15°28′) = sin(15°30′)-поправка 2′ = 0.2672-0.0006 = 0.2666

cos(15°25′) = sin(15°24′)+поправка 1′ = 0.9641-0.0001 = 0.9640
cos(15°28′) = sin(15°30′)-поправка 2′ = 0.9636+0.0002 = 0.9638

Поскольку синус и косинус, тангенс и котангенс для данного угла взаимосвязаны, по таблице синусов можно определять и значения косинусов, а по таблице тангенсов – значения котангенсов. Но аргумент для косинуса и для котангенса следует искать в правом столбце (четвертом справа) и в нижней строке.

Аргументы тригонометрических функций в таблицах Брадиса заданы в градусах. Для перевода градусов в радианы значение угла следует умножить на 180 и разделить на 3.1415926.

Как видим, таблицы В.М.Брадиса позволяют определять четыре значащих цифры любой функции. Поэтому они называются «четырехзначными». Такой точности расчетов заведомо хватает для 90% инженерных расчетов.

В настоящее время, когда калькуляторы есть и в часах, и в мобильных телефонах, расчеты функций по таблицам Брадиса можно считать «пережитком прошлого». Но, скажем честно, славного прошлого. Большое ведь видится на расстоянии. И ракеты тогда все-таки взлетали…

Таблицы имеют горизонтальную прокрутку. Для прокрутки на десктопной версии сайта: скролл внизу таблицы или стрелками на клавиатуре, на мобильной версии — свайп таблицы влево)

Таблица Брадиса для синуса и косинуса

sin	0′	6′	12′	18′	24′	30′	36′	42′	48′	54′	60′	cos	1′	2′	3′
											0. 0000	90°
0°	0.0000	0017	0035	0052	0070	0087	0105	0122	0140	0157	0175	89°	3	6	9
1°	0175	0192	0209	0227	0244	0262	0279	0297	0314	0332	0349	88°	3	6	9
2°	0349	0366	0384	0401	0419	0436	0454	0471	0488	0506	0523	87°	3	6	9
3°	0523	0541	0558	0576	0593	0610	0628	0645	0663	0680	0698	86°	3	6	9
4°	0698	0715	0732	0750	0767	0785	0802	0819	0837	0854	0. 0872	85°	3	6	9

5°	0.0872	0889	0906	0924	0941	0958	0976	0993	1011	1028	1045	84°	3	6	9
6°	1045	1063	1080	1097	1115	1132	1149	1167	1184	1201	1219	83°	3	6	9
7°	1219	1236	1253	1271	1288	1305	1323	1340	1357	1374	1392	82°	3	6	9
8°	1392	1409	1426	1444	1461	1478	1495	1513	1530	1547	1564	81°	3	6	9
9°	1564	1582	1599	1616	1633	1650	1668	1685	1702	1719	0. 1736	80°	3	6	9

10°	0.1736	1754	1771	1788	1805	1822	1840	1857	1874	1891	1908	79°	3	6	9
11°	1908	1925	1942	1959	1977	1994	2011	2028	2045	2062	2079	78°	3	6	9
12°	2079	2096	2113	2130	2147	2164	2181	2198	2215	2233	2250	77°	3	6	9
13°	2250	2267	2284	2300	2317	2334	2351	2368	2385	2402	2419	76°	3	6	8
14°	2419	2436	2453	2470	2487	2504	2521	2538	2554	2571	0. 2588	75°	3	6	8

15°	0.2588	2605	2622	2639	2656	2672	2689	2706	2723	2740	2756	74°	3	6	8
16°	2756	2773	2790	2807	2823	2840	2857	2874	2890	2907	2924	73°	3	6	8
17°	2924	2940	2957	2974	2990	3007	3024	3040	3057	3074	3090	72°	3	6	8
18°	3090	3107	3123	3140	3156	3173	3190	3206	3223	3239	3256	71°	3	6	8
19°	3256	3272	3289	3305	3322	3338	3355	3371	3387	3404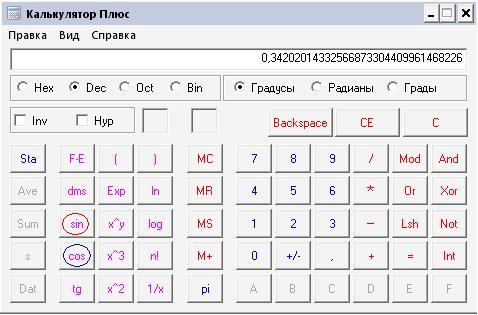	0. 3420	70°	3	5	8

20°	0.3420	3437	3453	3469	3486	3502	3518	3535	3551	3567	3584	69°	3	5	8
21°	3584	3600	3616	3633	3649	3665	3681	3697	3714	3730	3746	68°	3	5	8
22°	3746	3762	3778	3795	3811	3827	3843	3859	3875	3891	3907	67°	3	5	8
23°	3907	3923	3939	3955	3971	3987	4003	4019	4035	4051	4067	66°	3	5	8
24°	4067	4083	4099	4115	4131	4147	4163	4179	4195	4210	0. 4226	65°	3	5	8

25°	0.4226	4242	4258	4274	4289	4305	4321	4337	4352	4368	4384	64°	3	5	8
26°	4384	4399	4415	4431	4446	4462	4478	4493	4509	4524	4540	63°	3	5	8
27°	4540	4555	4571	4586	4602	4617	4633	4648	4664	4679	4695	62°	3	5	8
28°	4695	4710	4726	4741	4756	4772	4787	4802	4818	4833	4848	61°	3	5	8
29°	4848	4863	4879	4894	4909	4924	4939	4955	4970	4985	0. 5000	60°	3	5	8

30°	0.5000	5015	5030	5045	5060	5075	5090	5105	5120	5135	5150	59°	3	5	8
31°	5150	5165	5180	5195	5210	5225	5240	5255	5270	5284	5299	58°	2	5	7
32°	5299	5314	5329	5344	5358	5373	5388	5402	5417	5432	5446	57°	2	5	7
33°	5446	5461	5476	5490	5505	5519	5534	5548	5563	5577	5592	56°	2	5	7
34°	5592	5606	5621	5635	5650	5664	5678	5693	5707	5721	0. 5736	55°	2	5	7

35°	0.5736	5750	5764	5779	5793	5807	5821	5835	5850	5864	0.5878	54°	2	5	7
36°	5878	5892	5906	5920	5934	5948	5962	5976	5990	6004	6018	53°	2	5	7
37°	6018	6032	6046	6060	6074	6088	6101	6115	6129	6143	6157	52°	2	5	7
38°	6157	6170	6184	6198	6211	6225	6239	6252	6266	6280	6293	51°	2	5	7
39°	6293	6307	6320	6334	6347	6361	6374	6388	6401	6414	0. 6428	50°	2	4	7

40°	0.6428	6441	6455	6468	6481	6494	6508	6521	6534	6547	6561	49°	2	4	7
41°	6561	6574	6587	6600	6613	6626	6639	6652	6665	6678	6691	48°	2	4	7
42°	6691	6704	6717	6730	6743	6756	6769	6782	6794	6807	6820	47°	2	4	6
43°	6820	6833	6845	6858	6871	6884	6896	8909	6921	6934	6947	46°	2	4	6
44°	6947	6959	6972	6984	6997	7009	7022	7034	7046	7059	0. 7071	45°	2	4	6

45°	0.7071	7083	7096	7108	7120	7133	7145	7157	7169	7181	7193	44°	2	4	6
46°	7193	7206	7218	7230	7242	7254	7266	7278	7290	7302	7314	43°	2	4	6
47°	7314	7325	7337	7349	7361	7373	7385	7396	7408	7420	7431	42°	2	4	6
48°	7431	7443	7455	7466	7478	7490	7501	7513	7524	7536	7547	41°	2	4	6
49°	7547	7559	7570	7581	7593	7604	7615	7627	7638	7649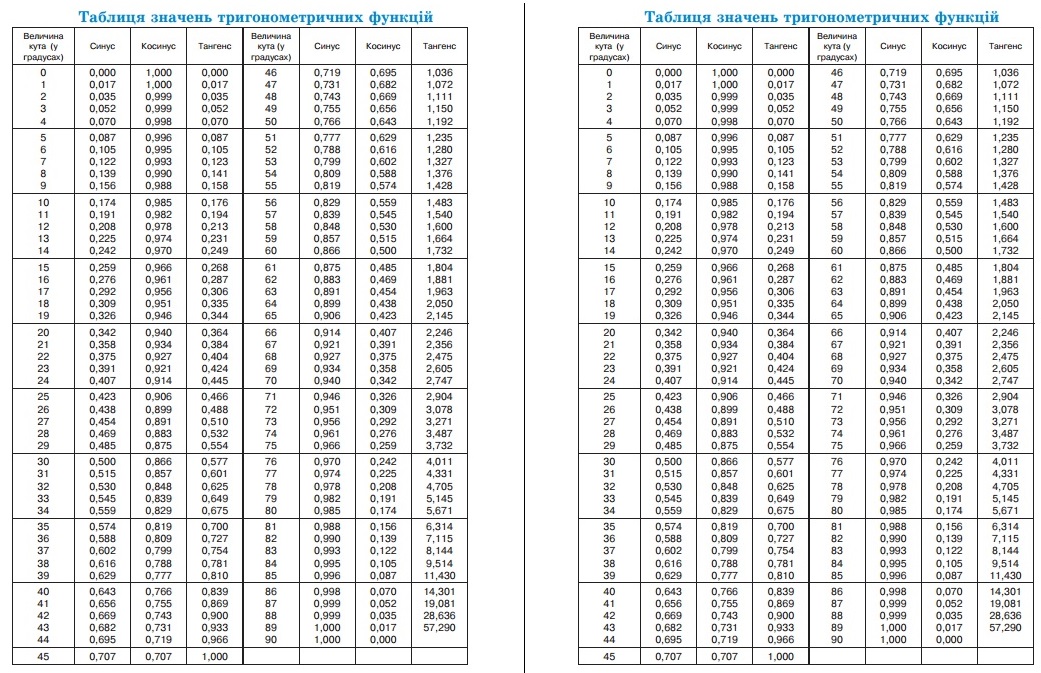	0. 7660	40°	2	4	6

50°	0.7660	7672	7683	7694	7705	7716	7727	7738	7749	7760	7771	39°	2	4	6
51°	7771	7782	7793	7804	7815	7826	7837	7848	7859	7869	7880	38°	2	4	5
52°	7880	7891	7902	7912	7923	7934	7944	7955	7965	7976	7986	37°	2	4	5
53°	7986	7997	8007	8018	8028	8039	8049	8059	8070	8080	8090	36°	2	3	5
54°	8090	8100	8111	8121	8131	8141	8151	8161	8171	8181	0. 8192	35°	2	3	5

55°	0.8192	8202	8211	8221	8231	8241	8251	8261	8271	8281	8290	34°	2	3	5
56°	8290	8300	8310	8320	8329	8339	8348	8358	8368	8377	8387	33°	2	3	5
57°	8387	8396	8406	8415	8425	8434	8443	8453	8462	8471	8480	32°	2	3	5
58°	8480	8490	8499	8508	8517	8526	8536	8545	8554	8563	8572	31°	2	3	5
59°	8572	8581	8590	8599	8607	8616	8625	8634	8643	8652	0.8660	30°	1	3	4

60°	0.8660	8669	8678	8686	8695	8704	8712	8721	8729	8738	8746	29°	1	3	4
61°	8746	8755	8763	8771	8780	8788	8796	8805	8813	8821	8829	28°	1	3	4
62°	8829	8838	8846	8854	8862	8870	8878	8886	8894	8902	8910	27°	1	3	4
63°	8910	8918	8926	8934	8942	8949	8957	8965	8973	8980	8988	26°	1	3	4
64°	8988	8996	9003	9011	9018	9026	9033	9041	9048	9056	0.9063	25°	1	3	4

65°	0.9063	9070	9078	9085	9092	9100	9107	9114	9121	9128	9135	24°	1	2	4
66°	9135	9143	9150	9157	9164	9171	9178	9184	9191	9198	9205	23°	1	2	3
67°	9205	9212	9219	9225	9232	9239	9245	9252	9259	9256	9272	22°	1	2	3
68°	9272	9278	9285	9291	9298	9304	9311	9317	9323	9330	9336	21°	1	2	3
69°	9336	9342	9348	9354	9361	9367	9373	9379	9383	9391	0.9397	20°	1	2	3

70°	9397	9403	9409	9415	9421	9426	9432	9438	9444	9449	0.9455	19°	1	2	3
71°	9455	9461	9466	9472	9478	9483	9489	9494	9500	9505	9511	18°	1	2	3
72°	9511	9516	9521	9527	9532	9537	9542	9548	9553	9558	9563	17°	1	2	3
73°	9563	9568	9573	9578	9583	9588	9593	9598	9603	9608	9613	16°	1	2	2
74°	9613	9617	9622	9627	9632	9636	9641	9646	9650	9655	0.9659	15°	1	2	2

75°	9659	9664	9668	9673	9677	9681	9686	9690	9694	9699	9703	14°	1	1	2
76°	9703	9707	9711	9715	9720	9724	9728	9732	9736	9740	9744	13°	1	1	2
77°	9744	9748	9751	9755	9759	9763	9767	9770	9774	9778	9781	12°	1	1	2
78°	9781	9785	9789	9792	9796	9799	9803	9806	9810	9813	9816	11°	1	1	2
79°	9816	9820	9823	9826	9829	9833	9836	9839	9842	9845	0.9848	10°	1	1	2

80°	0.9848	9851	9854	9857	9860	9863	9866	9869	9871	9874	9877	9°	0	1	1
81°	9877	9880	9882	9885	9888	9890	9893	9895	9898	9900	9903	8°	0	1	1
82°	9903	9905	9907	9910	9912	9914	9917	9919	9921	9923	9925	7°	0	1	1
83°	9925	9928	9930	9932	9934	9936	9938	9940	9942	9943	9945	6°	0	1	1
84°	9945	9947	9949	9951	9952	9954	9956	9957	9959	9960	9962	5°	0	1	1

85°	9962	9963	9965	9966	9968	9969	9971	9972	9973	9974	9976	4°	0	0	1
86°	9976	9977	9978	9979	9980	9981	9982	9983	9984	9985	9986	3°	0	0	0
87°	9986	9987	9988	9989	9990	9990	9991	9992	9993	9993	9994	2°	0	0	0
88°	9994	9995	9995	9996	9996	9997	9997	9997	9998	9998	0.9998	1°	0	0	0
89°	9998	9999	9999	9999	9999	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	0°	0	0	0
90°	1.0000
sin	60′	54′	48′	42′	36′	30′	24′	18′	12′	6′	0′	cos	1′	2′	3

Таблица Брадиса для тангенса и котангенса

tg	0′	6′	12′	18′	24′	30′	36′	42′	48′	54′	60′	ctg	1′	2′	3′
											0	90°
0°	0,000	0017	0035	0052	0070	0087	0105	0122	0140	0157	0175	89°	3	6	9
1°	0175	0192	0209	0227	0244	0262	0279	0297	0314	0332	0349	88°	3	6	9
2°	0349	0367	0384	0402	0419	0437	0454	0472	0489	0507	0524	87°	3	6	9
3°	0524	0542	0559	0577	0594	0612	0629	0647	0664	0682	0699	86°	3	6	9
4°	0699	0717	0734	0752	0769	0787	0805	0822	0840	0857	0,0875	85°	3	6	9

5°	0,0875	0892	0910	0928	0945	0963	0981	0998	1016	1033	1051	84°	3	6	9
6°	1051	1069	1086	1104	1122	1139	1157	1175	1192	1210	1228	83°	3	6	9
7°	1228	1246	1263	1281	1299	1317	1334	1352	1370	1388	1405	82°	3	6	9
8°	1405	1423	1441	1459	1477	1495	1512	1530	1548	1566	1584	81°	3	6	9
9°	1584	1602	1620	1638	1655	1673	1691	1709	1727	1745	0,1763	80°	3	6	9

10°	0,1763	1781	1799	1817	1835	1853	1871	1890	1908	1926	1944	79°	3	6	9
11°	1944	1962	1980	1998	2016	2035	2053	2071	2089	2107	2126	78°	3	6	9
12°	2126	2144	2162	2180	2199	2217	2235	2254	2272	2290	2309	77°	3	6	9
13°	2309	2327	2345	2364	2382	2401	2419	2438	2456	2475	2493	76°	3	6	9
14°	2493	2512	2530	2549	2568	2586	2605	2623	2642	2661	0,2679	75°	3	6	9

15°	0,2679	2698	2717	2736	2754	2773	2792	2811	2830	2849	2867	74°	3	6	9
16°	2867	2886	2905	2924	2943	2962	2981	3000	3019	3038	3057	73°	3	6	9
17°	3057	3076	3096	3115	3134	3153	3172	3191	3211	3230	3249	72°	3	6	10
18°	3249	3269	3288	3307	3327	3346	3365	3385	3404	3424	3443	71°	3	6	10
19°	3443	3463	3482	3502	3522	3541	3561	3581	3600	3620	0,3640	70°	3	7	10

20°	0,3640	3659	3679	3699	3719	3739	3759	3779	3799	3819	3839	69°	3	7	10
21°	3839	3859	3879	3899	3919	3939	3959	3979	4000	4020	4040	68°	3	7	10
22°	4040	4061	4081	4101	4122	4142	4163	4183	4204	4224	4245	67°	3	7	10
23°	4245	4265	4286	4307	4327	4348	4369	4390	4411	4431	4452	66°	3	7	10
24°	4452	4473	4494	4515	4536	4557	4578	4599	4621	4642	0,4663	65°	4	7	11

25°	0,4663	4684	4706	4727	4748	4770	4791	4813	4834	4856	4877	64°	4	7	11
26°	4877	4899	4921	4942	4964	4986	5008	5029	5051	5073	5095	63°	4	7	11
27°	5095	5117	5139	5161	5184	5206	5228	5250	5272	5295	5317	62°	4	7	11
28°	5317	5340	5362	5384	5407	5430	5452	5475	5498	5520	5543	61°	4	8	11
29°	5543	5566	5589	5612	5635	5658	5681	5704	5727	5750	0,5774	60°	4	8	12

30°	0,5774	5797	5820	5844	5867	5890	5914	5938	5961	5985	6009	59°	4	8	12
31°	6009	6032	6056	6080	6104	6128	6152	6176	6200	6224	6249	58°	4	8	12
32°	6249	6273	6297	6322	6346	6371	6395	6420	6445	6469	6494	57°	4	8	12
33°	6494	6519	6544	6569	6594	6619	6644	6669	6694	6720	6745	56°	4	8	13
34°	6745	6771	6796	6822	6847	6873	6899	6924	6950	6976	0,7002	55°	4	9	13

35°	0,7002	7028	7054	7080	7107	7133	7159	7186	7212	7239	7265	54°	4	8	13
36°	7265	7292	7319	7346	7373	7400	7427	7454	7481	7508	7536	53°	5	9	14°
37°	7536	7563	7590	7618	7646	7673	7701	7729	7757	7785	7813	52°	5	9	14
38°	7813	7841	7869	7898	7926	7954	7983	8012	8040	8069	8098	51°	5	9	14
39°	8098	8127	8156	8185	8214	8243	8273	8302	8332	8361	0,8391	50°	5	10	15

40°	0,8391	8421	8451	8481	8511	8541	8571	8601	8632	8662	0,8693	49°	5	10	15
41°	8693	8724	8754	8785	8816	8847	8878	8910	8941	8972	9004	48°	5	10	16
42°	9004	9036	9067	9099	9131	9163	9195	9228	9260	9293	9325	47°	6	11	16
43°	9325	9358	9391	9424	9457	9490	9523	9556	9590	9623	0,9657	46°	6	11	17
44°	9657	9691	9725	9759	9793	9827	9861	9896	9930	9965	1,0000	45°	6	11	17

45°	1,0000	0035	0070	0105	0141	0176	0212	0247	0283	0319	0355	44°	6	12	18
46°	0355	0392	0428	0464	0501	0538	0575	0612	0649	0686	0724	43°	6	12	18
47°	0724	0761	0799	0837	0875	0913	0951	0990	1028	1067	1106	42°	6	13	19
48°	1106	1145	1184	1224	1263	1303	1343	1383	1423	1463	1504	41°	7	13	20
49°	1504	1544	1585	1626	1667	1708	1750	1792	1833	1875	1,1918	40°	7	14	21

50°	1,1918	1960	2002	2045	2088	2131	2174	2218	2261	2305	2349	39°	7	14	22
51°	2349	2393	2437	2482	2527	2572	2617	2662	2708	2753	2799	38°	8	15	23
52°	2799	2846	2892	2938	2985	3032	3079	3127	3175	3222	3270	37°	8	16	24
53°	3270	3319	3367	3416	3465	3514	3564	3613	3663	3713	3764	36°	8	16	25
54°	3764	3814	3865	3916	3968	4019	4071	4124	4176	4229	1,4281	35°	9	17	26

55°	1,4281	4335	4388	4442	4496	4550	4605	4659	4715	4770	4826	34°	9	18	27
56°	4826	4882	4938	4994	5051	5108	5166	5224	5282	5340	5399	33°	10	19	29
57°	5399	5458	5517	5577	5637	5697	5757	5818	5880	5941	6003	32°	10	20	30
58°	6003	6066	6128	6191	6255	6319	6383	6447	6512	6577	6643	31°	11	21	32
59°	6643	6709	6775	6842	6909	6977	7045	7113	7182	7251	1,7321	30°	11	23	34

60°	1,732	1,739	1,746	1,753	1,760	1,767	1,775	1,782	1,789	1,797	1,804	29°	1	2	4
61°	1,804	1,811	1,819	1,827	1,834	1,842	1,849	1,857	1,865	1,873	1,881	28°	1	3	4
62°	1,881	1,889	1,897	1,905	1,913	1,921	1,929	1,937	1,946	1,954	1,963	27°	1	3	4
63°	1,963	1,971	1,980	1,988	1,997	2,006	2,014	2,023	2,032	2,041	2,05	26°	1	3	4
64°	2,050	2,059	2,069	2,078	2,087	2,097	2,106	2,116	2,125	2,135	2,145	25°	2	3	5

65°	2,145	2,154	2,164	2,174	2,184	2,194	2,204	2,215	2,225	2,236	2,246	24°	2	3	5
66°	2,246	2,257	2,267	2,278	2,289	2,3	2,311	2,322	2,333	2,344	2,356	23°	2	4	5
67°	2,356	2,367	2,379	2,391	2,402	2,414	2,426	2,438	2,450	2,463	2,475	22°	2	4	6
68°	2,475	2,488	2,5	2,513	2,526	2,539	2,552	2,565	2,578	2,592	2,605	21°	2	4	6
69°	2,605	2,619	2,633	2,646	2,66	2,675	2,689	2,703	2,718	2,733	2,747	20°	2	5	7

70°	2,747	2,762	2,778	2,793	2,808	2,824	2,840	2,856	2,872	2,888	2,904	19°	3	5	8
71°	2,904	2,921	2,937	2,954	2,971	2,989	3,006	3,024	3,042	3,06	3,078	18°	3	6	9
72°	3,078	3,096	3,115	3,133	3,152	3,172	3,191	3,211	3,230	3,251	3,271	17°	3	6	10
73°	3,271	3,291	3,312	3,333	3,354	3,376							3	7	10
							3,398	3,42	3,442	3,465	3,487	16°	4	7	11
74°	3,487	3,511	3,534	3,558	3,582	3,606							4	8	12
							3,630	3,655	3,681	3,706	3,732	15°	4	8	13
75°	3,732	3,758	3,785	3,812	3,839	3,867							4	9	13
							3,895	3,923	3,952	3,981	4,011	14°	5	10	14
tg	60′	54′	48′	42′	36′	30′	24′	18′	12′	6′	0′	ctg	1′	2′	3′

Полезен ли материал?

Тригонометрическая таблица

В статье, мы полностью разберемся, как выглядит таблица тригонометрических значений, синуса, косинуса, тангенса и котангенса . Рассмотрим основное значение тригонометрических функций, от угла в 0,30,45,60,90,…,360 градусов. И посмотрим как пользоваться данными таблицами в вычислении значения тригонометрических функций.
Первой рассмотрим таблицу косинуса, синуса, тангенса и котангенса от угла в 0, 30, 45, 60, 90,.. градусов. Определение данных величин дают определить значение функций углов в 0 и 90 градусов:

sin 0⁰=0, cos 0⁰ = 1. tg 0⁰ = 0, котангенс от 0⁰ будет неопределенным
sin 90⁰ = 1, cos 90⁰ =0, ctg90⁰ = 0,тангенс от 90⁰ будет неопределенным

Если взять прямоугольные треугольники углы которых от 30 до 90 градусов. Получим:

sin 30⁰ = 1/2, cos 30⁰ = √3/2, tg 30⁰ = √3/3, ctg 30⁰ = √3
sin 45⁰ = √2/2, cos 45⁰ = √2/2, tg 45⁰= 1, ctg 45⁰ = 1
sin 60⁰= √3/2, cos 60⁰ = 1/2, tg 60⁰ =√3 , ctg 60⁰ = √3/3

Изобразим все полученные значения в виде тригонометрической таблицы:

Таблица синусов, косинусов, тангенсов и котангенсов!

Если использовать формулу приведения, наша таблица увеличится, добавятся значения для углов до 360 градусов. Выглядеть она будет как:

Так же исходя из свойств периодичности таблицу можно увеличить, если заменим углы на 0⁰+360⁰*z …. 330⁰+360⁰*z, в котором z является целым числом. В данной таблице возможно вычислить значение всех углов, соответствующими точками в единой окружности.

Разберем наглядно как использовать таблицу в решении.
Все очень прост. Так как нужное нам значение лежит в точке пересечения нужных нам ячеек. К примеру возьмем cos угла 60 градусов, в таблице это будет выглядеть как:

В итоговой таблице основных значений тригонометрических функций, действуем так же. Но в данной таблице возможно узнать сколько составит тангенс от угла в 1020 градусов, он = -√3 Проверим 1020⁰= 300⁰+360⁰*2. Найдем по таблице.

Для более поиска тригонометрических значений углов с точностью до минут используются таблицы Брадиса. Подробная инструкция как ими пользоваться на странице по ссылке.

Таблица Брадиса. Для синуса, косинуса, тангенса и котангенса.

Таблицы Брадиса поделены на несколько частей, состоят из таблиц косинуса и синуса, тангенса и котангенса — которая поделена на две части (tg угла до 90 градусов и ctg малых углов).

Синус и косинус

tg угла начиная с 0⁰ заканчивая 76⁰, ctg угла начиная с 14⁰ заканчивая 90⁰.

tg до 90⁰ и ctg малых углов.

Разберемся как пользоваться таблицами Брадиса в решении задач.

Найдем обозначение sin (обозначение в столбце с левого края) 42 минут (обозначение находится на верхней строчке). Путем пересечения ищем обозначение, оно = 0,3040.

Величины минут указаны с промежутком в шесть минут, как быть если нужное нам значение попадет именно в этот промежуток. Возьмем 44 минуты, а в таблице есть только 42. Берем за основу 42 и воспользуемся добавочными столбцами в правой стороне, берем 2 поправку и добавляем к 0,3040 + 0,0006 получаем 0,3046.

При sin 47 мин, берем за основу 48 мин и отнимаем от нее 1 поправку, т.е 0,3057 — 0,0003 = 0,3054

При вычислении cos работаем аналогично sin только за основу берем нижнюю строку таблицы. К примеру cos 20⁰ = 0.9397

Значения tg угла до 90⁰ и cot малого угла, верны и поправок в них нет. К примеру, найти tg 78⁰ 37мин = 4,967

а ctg 20⁰ 13мин = 25,83

Ну вот мы и рассмотрели основные тригонометрические таблицы. Надеемся это информация была для вас крайне полезной. Свои вопросы по таблицам, если они появились, обязательно пишите в комментариях!

Заметка: Стеновые отбойники — отбойная доска для защиты стен (http://www.spi-polymer.ru/otboyniki/)

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

Как пользоваться таблицами синусов, косинусов, тангенсов. (8 класс)

tgх = 0,8574
Единицы измерения углов:
градус – «°»,
минута – «´»,
секунда – «˝»
36 градусов 28 минут 47 секунд
36°28´47˝
© Кузьмина Е.А., Колобовская МСОШ, 2010
Брадис
Владимир
Модестович
1890 — 1975
Брадис Владимир Модестович – знаменитый
математик-педагог, член-корреспондент АПН СССР.
Заслуженный деятель науки РСФСР.
Основные труды Брадиса посвящены теоретической
и методической разработке вопросов повышения
вычислительной культуры учащихся средней школы.
Его «Методика преподавания математики в средней
школе» переиздавалась много раз и переведена на
другие языки. В 1921 году впервые вышли его
«Таблицы четырёхзначных логарифмов и
натуральных тригонометрических величин», позднее
издававшиеся под названием «Четырёхзначные
математические таблицы».
© Кузьмина Е.А., Колобовская МСОШ, 2010
Алгоритм нахождения синуса угла заданной величины по таблице Брадиса:
1. Находим в столбце А величину угла в градусах.
2. Находим в строке А ближайшее значение в минутах.
3. На пересечении строки «36°» и столбца «24´» находим значение синуса
4. Прибавляем к найденному значению поправку (или вычитаем).
sin36°26´= 0,5939 sin38°41´= 0,6250
© Кузьмина Е.А., Колобовская МСОШ, 2010
Алгоритм нахождения косинуса угла заданной величины по таблице Брадиса:
1. Находим в столбце А величину угла в градусах.
2. Находим в строке А ближайшее значение в минутах.
3. На пересечении строки «26°» и столбца «48´» находим значение косинуса
4. Прибавляем к найденному значению поправку (или вычитаем).
cos26°46´= 0,8929 cos28°13´= 0,8812
© Кузьмина Е.А., Колобовская МСОШ, 2010
Задание 1
Используя таблицы Брадиса, найдите:
sin 22° = 0,3749
sin 22°36´ = 0,3843
cos 68°18´ = 0,3697
tg 40°40´ = 0,8591
© Кузьмина Е.А., Колобовская МСОШ, 2010
Задание 2
Используя таблицы Брадиса, найдите:
1) sin16° = 0,2756 2) sin24°36´= 0,4163
cos16° = 0,9613
cos24°36´= 0,9092
3) sin70°32´= 0,9428 4) sin88°49´= 0,9998
cos70°32´= 0,3333 cos88°49´= 0,0206
© Кузьмина Е.А., Колобовская МСОШ, 2010
Задание 3
Используя таблицы Брадиса, найдите
величину угла:
1) sinх =0,0175
х = 1°
3) cosх =0,6814
х = 47°3´
2) sinх =0,5015
х = 30°6´
4) cosх =0,0670
х = 86°9´
© Кузьмина Е.А., Колобовская МСОШ, 2010
Используемая литература и Интернет-ресурсы:
1. Погорелов А.В. Геометрия: 7–9 классы – М.: Просвещение, 2004
2. Геометрия. 8 класс. Поурочные планы по учебнику А.В. Погорелова /
Авт.-сост. Н.В. Грицаева – Волгоград: Учитель, 2006
3. Википедия – свободная энциклопедия – http://ru.wikipedia.org/
Презентацию подготовила:
Кузьмина Елена Александровна
учитель математики и информатики
Колобовская МСОШ
Шуйский район
Ивановская область
2010 год

Косинус угла онлайн. Таблица косинусов. Формула косинуса угла.

Косинус угла через градусы, минуты и секунды

+−

Косинус угла через десятичную запись угла

Как найти угол зная косинус этого угла

У косинуса есть обратная тригонометрическая функция — arccos(y)=x

cos(arccos(y))=y

Пример cos(60°) = 1/2; arccos(1/2) = 60°

Рассчитать арккосинус

Определение косинуса

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

Косинусом угла α называется абсцисса точки B единичной окружности, полученной при повороте точки P(1;0) на угол α.

cos(α) = AC/AB

cos(-α) = cos(α)

cos(α ± 2π) = cos(α)

Таблица косинусов в радианах

cos(0°) = 1cos(π/12) = cos(15°) = 0.9659258263cos(π/6) = cos(30°) = 0.8660254038cos(π/4) = cos(45°) = 0.7071067812cos(π/3) = cos(60°) = 0.5cos(5π/12) = cos(75°) = 0.2588190451cos(π/2) = cos(90°) = 0cos(7π/12) = cos(105°) = -0.2588190451cos(2π/3) = cos(120°) = -0.5cos(3π/4) = cos(135°) = -0.7071067812cos(5π/6) = cos(150°) = -0.8660254038cos(11π/12) = cos(165°) = -0.9659258263cos(π) = cos(180°) = -1cos(13π/12) = cos(195°) = -0.9659258263cos(7π/6) = cos(210°) = -0.8660254038cos(5π/4) = cos(225°) = -0.7071067812cos(4π/3) = cos(240°) = -0.5cos(17π/12) = cos(255°) = -0.2588190451cos(3π/2) = cos(270°) = 0cos(19π/12) = cos(285°) = 0.2588190451cos(5π/3) = cos(300°) = 0.5cos(7π/4) = cos(315°) = 0.7071067812cos(11π/6) = cos(330°) = 0.8660254038cos(23π/12) = cos(345°) = 0.9659258263

Таблица Брадиса косинусы

cos(0) = 1	cos(120) = -0.5	cos(240) = -0.5
cos(1) = 0.9998476952	cos(121) = -0.5150380749	cos(241) = -0.4848096202
cos(2) = 0.999390827	cos(122) = -0.5299192642	cos(242) = -0.4694715628
cos(3) = 0.9986295348	cos(123) = -0.544639035	cos(243) = -0.4539904997
cos(4) = 0.9975640503	cos(124) = -0.5591929035	cos(244) = -0.4383711468
cos(5) = 0.9961946981	cos(125) = -0.5735764364	cos(245) = -0.4226182617
cos(6) = 0.9945218954	cos(126) = -0.5877852523	cos(246) = -0.4067366431
cos(7) = 0.9925461516	cos(127) = -0.6018150232	cos(247) = -0.3907311285
cos(8) = 0.9902680687	cos(128) = -0.6156614753	cos(248) = -0.3746065934
cos(9) = 0.9876883406	cos(129) = -0.629320391	cos(249) = -0.3583679495
cos(10) = 0.984807753	cos(130) = -0.6427876097	cos(250) = -0.3420201433
cos(11) = 0.9816271834	cos(131) = -0.656059029	cos(251) = -0.3255681545
cos(12) = 0.9781476007	cos(132) = -0.6691306064	cos(252) = -0.3090169944
cos(13) = 0.9743700648	cos(133) = -0.6819983601	cos(253) = -0.2923717047
cos(14) = 0.9702957263	cos(134) = -0.6946583705	cos(254) = -0.2756373558
cos(15) = 0.9659258263	cos(135) = -0.7071067812	cos(255) = -0.2588190451
cos(16) = 0.9612616959	cos(136) = -0.7193398003	cos(256) = -0.2419218956
cos(17) = 0.956304756	cos(137) = -0.7313537016	cos(257) = -0.2249510543
cos(18) = 0.9510565163	cos(138) = -0.7431448255	cos(258) = -0.2079116908
cos(19) = 0.9455185756	cos(139) = -0.7547095802	cos(259) = -0.1908089954
cos(20) = 0.9396926208	cos(140) = -0.7660444431	cos(260) = -0.1736481777
cos(21) = 0.9335804265	cos(141) = -0.7771459615	cos(261) = -0.156434465
cos(22) = 0.9271838546	cos(142) = -0.7880107536	cos(262) = -0.139173101
cos(23) = 0.9205048535	cos(143) = -0.79863551	cos(263) = -0.1218693434
cos(24) = 0.9135454576	cos(144) = -0.8090169944	cos(264) = -0.1045284633
cos(25) = 0.906307787	cos(145) = -0.8191520443	cos(265) = -0.08715574275
cos(26) = 0.8987940463	cos(146) = -0.8290375726	cos(266) = -0.06975647374
cos(27) = 0.8910065242	cos(147) = -0.8386705679	cos(267) = -0.05233595624
cos(28) = 0.8829475929	cos(148) = -0.8480480962	cos(268) = -0.0348994967
cos(29) = 0.8746197071	cos(149) = -0.8571673007	cos(269) = -0.01745240644
cos(30) = 0.8660254038	cos(150) = -0.8660254038	cos(270) = 0
cos(31) = 0.8571673007	cos(151) = -0.8746197071	cos(271) = 0.01745240644
cos(32) = 0.8480480962	cos(152) = -0.8829475929	cos(272) = 0.0348994967
cos(33) = 0.8386705679	cos(153) = -0.8910065242	cos(273) = 0.05233595624
cos(34) = 0.8290375726	cos(154) = -0.8987940463	cos(274) = 0.06975647374
cos(35) = 0.8191520443	cos(155) = -0.906307787	cos(275) = 0.08715574275
cos(36) = 0.8090169944	cos(156) = -0.9135454576	cos(276) = 0.1045284633
cos(37) = 0.79863551	cos(157) = -0.9205048535	cos(277) = 0.1218693434
cos(38) = 0.7880107536	cos(158) = -0.9271838546	cos(278) = 0.139173101
cos(39) = 0.7771459615	cos(159) = -0.9335804265	cos(279) = 0.156434465
cos(40) = 0.7660444431	cos(160) = -0.9396926208	cos(280) = 0.1736481777
cos(41) = 0.7547095802	cos(161) = -0.9455185756	cos(281) = 0.1908089954
cos(42) = 0.7431448255	cos(162) = -0.9510565163	cos(282) = 0.2079116908
cos(43) = 0.7313537016	cos(163) = -0.956304756	cos(283) = 0.2249510543
cos(44) = 0.7193398003	cos(164) = -0.9612616959	cos(284) = 0.2419218956
cos(45) = 0.7071067812	cos(165) = -0.9659258263	cos(285) = 0.2588190451
cos(46) = 0.6946583705	cos(166) = -0.9702957263	cos(286) = 0.2756373558
cos(47) = 0.6819983601	cos(167) = -0.9743700648	cos(287) = 0.2923717047
cos(48) = 0.6691306064	cos(168) = -0.9781476007	cos(288) = 0.3090169944
cos(49) = 0.656059029	cos(169) = -0.9816271834	cos(289) = 0.3255681545
cos(50) = 0.6427876097	cos(170) = -0.984807753	cos(290) = 0.3420201433
cos(51) = 0.629320391	cos(171) = -0.9876883406	cos(291) = 0.3583679495
cos(52) = 0.6156614753	cos(172) = -0.9902680687	cos(292) = 0.3746065934
cos(53) = 0.6018150232	cos(173) = -0.9925461516	cos(293) = 0.3907311285
cos(54) = 0.5877852523	cos(174) = -0.9945218954	cos(294) = 0.4067366431
cos(55) = 0.5735764364	cos(175) = -0.9961946981	cos(295) = 0.4226182617
cos(56) = 0.5591929035	cos(176) = -0.9975640503	cos(296) = 0.4383711468
cos(57) = 0.544639035	cos(177) = -0.9986295348	cos(297) = 0.4539904997
cos(58) = 0.5299192642	cos(178) = -0.999390827	cos(298) = 0.4694715628
cos(59) = 0.5150380749	cos(179) = -0.9998476952	cos(299) = 0.4848096202
cos(60) = 0.5	cos(180) = -1	cos(300) = 0.5
cos(61) = 0.4848096202	cos(181) = -0.9998476952	cos(301) = 0.5150380749
cos(62) = 0.4694715628	cos(182) = -0.999390827	cos(302) = 0.5299192642
cos(63) = 0.4539904997	cos(183) = -0.9986295348	cos(303) = 0.544639035
cos(64) = 0.4383711468	cos(184) = -0.9975640503	cos(304) = 0.5591929035
cos(65) = 0.4226182617	cos(185) = -0.9961946981	cos(305) = 0.5735764364
cos(66) = 0.4067366431	cos(186) = -0.9945218954	cos(306) = 0.5877852523
cos(67) = 0.3907311285	cos(187) = -0.9925461516	cos(307) = 0.6018150232
cos(68) = 0.3746065934	cos(188) = -0.9902680687	cos(308) = 0.6156614753
cos(69) = 0.3583679495	cos(189) = -0.9876883406	cos(309) = 0.629320391
cos(70) = 0.3420201433	cos(190) = -0.984807753	cos(310) = 0.6427876097
cos(71) = 0.3255681545	cos(191) = -0.9816271834	cos(311) = 0.656059029
cos(72) = 0.3090169944	cos(192) = -0.9781476007	cos(312) = 0.6691306064
cos(73) = 0.2923717047	cos(193) = -0.9743700648	cos(313) = 0.6819983601
cos(74) = 0.2756373558	cos(194) = -0.9702957263	cos(314) = 0.6946583705
cos(75) = 0.2588190451	cos(195) = -0.9659258263	cos(315) = 0.7071067812
cos(76) = 0.2419218956	cos(196) = -0.9612616959	cos(316) = 0.7193398003
cos(77) = 0.2249510543	cos(197) = -0.956304756	cos(317) = 0.7313537016
cos(78) = 0.2079116908	cos(198) = -0.9510565163	cos(318) = 0.7431448255
cos(79) = 0.1908089954	cos(199) = -0.9455185756	cos(319) = 0.7547095802
cos(80) = 0.1736481777	cos(200) = -0.9396926208	cos(320) = 0.7660444431
cos(81) = 0.156434465	cos(201) = -0.9335804265	cos(321) = 0.7771459615
cos(82) = 0.139173101	cos(202) = -0.9271838546	cos(322) = 0.7880107536
cos(83) = 0.1218693434	cos(203) = -0.9205048535	cos(323) = 0.79863551
cos(84) = 0.1045284633	cos(204) = -0.9135454576	cos(324) = 0.8090169944
cos(85) = 0.08715574275	cos(205) = -0.906307787	cos(325) = 0.8191520443
cos(86) = 0.06975647374	cos(206) = -0.8987940463	cos(326) = 0.8290375726
cos(87) = 0.05233595624	cos(207) = -0.8910065242	cos(327) = 0.8386705679
cos(88) = 0.0348994967	cos(208) = -0.8829475929	cos(328) = 0.8480480962
cos(89) = 0.01745240644	cos(209) = -0.8746197071	cos(329) = 0.8571673007
cos(90) = 0	cos(210) = -0.8660254038	cos(330) = 0.8660254038
cos(91) = -0.01745240644	cos(211) = -0.8571673007	cos(331) = 0.8746197071
cos(92) = -0.0348994967	cos(212) = -0.8480480962	cos(332) = 0.8829475929
cos(93) = -0.05233595624	cos(213) = -0.8386705679	cos(333) = 0.8910065242
cos(94) = -0.06975647374	cos(214) = -0.8290375726	cos(334) = 0.8987940463
cos(95) = -0.08715574275	cos(215) = -0.8191520443	cos(335) = 0.906307787
cos(96) = -0.1045284633	cos(216) = -0.8090169944	cos(336) = 0.9135454576
cos(97) = -0.1218693434	cos(217) = -0.79863551	cos(337) = 0.9205048535
cos(98) = -0.139173101	cos(218) = -0.7880107536	cos(338) = 0.9271838546
cos(99) = -0.156434465	cos(219) = -0.7771459615	cos(339) = 0.9335804265
cos(100) = -0.1736481777	cos(220) = -0.7660444431	cos(340) = 0.9396926208
cos(101) = -0.1908089954	cos(221) = -0.7547095802	cos(341) = 0.9455185756
cos(102) = -0.2079116908	cos(222) = -0.7431448255	cos(342) = 0.9510565163
cos(103) = -0.2249510543	cos(223) = -0.7313537016	cos(343) = 0.956304756
cos(104) = -0.2419218956	cos(224) = -0.7193398003	cos(344) = 0.9612616959
cos(105) = -0.2588190451	cos(225) = -0.7071067812	cos(345) = 0.9659258263
cos(106) = -0.2756373558	cos(226) = -0.6946583705	cos(346) = 0.9702957263
cos(107) = -0.2923717047	cos(227) = -0.6819983601	cos(347) = 0.9743700648
cos(108) = -0.3090169944	cos(228) = -0.6691306064	cos(348) = 0.9781476007
cos(109) = -0.3255681545	cos(229) = -0.656059029	cos(349) = 0.9816271834
cos(110) = -0.3420201433	cos(230) = -0.6427876097	cos(350) = 0.984807753
cos(111) = -0.3583679495	cos(231) = -0.629320391	cos(351) = 0.9876883406
cos(112) = -0.3746065934	cos(232) = -0.6156614753	cos(352) = 0.9902680687
cos(113) = -0.3907311285	cos(233) = -0.6018150232	cos(353) = 0.9925461516
cos(114) = -0.4067366431	cos(234) = -0.5877852523	cos(354) = 0.9945218954
cos(115) = -0.4226182617	cos(235) = -0.5735764364	cos(355) = 0.9961946981
cos(116) = -0.4383711468	cos(236) = -0.5591929035	cos(356) = 0.9975640503
cos(117) = -0.4539904997	cos(237) = -0.544639035	cos(357) = 0.9986295348
cos(118) = -0.4694715628	cos(238) = -0.5299192642	cos(358) = 0.999390827
cos(119) = -0.4848096202	cos(239) = -0.5150380749	cos(359) = 0.9998476952

Похожие калькуляторы

Таблица синусов углов, вычислить синус угла

sin (1°)	0,017452
sin (2°)	0,034899
sin (3°)	0,052336
sin (4°)	0,069756
sin (5°)	0,087156
sin (6°)	0,104528
sin (7°)	0,121869
sin (8°)	0,139173
sin (9°)	0,156434
sin (10°)	0,173648
sin (11°)	0,190809
sin (12°)	0,207912
sin (13°)	0,224951
sin (14°)	0,241922
sin (15°)	0,258819
sin (16°)	0,275637
sin (17°)	0,292372
sin (18°)	0,309017
sin (19°)	0,325568
sin (20°)	0,342020
sin (21°)	0,358368
sin (22°)	0,374607
sin (23°)	0,390731
sin (24°)	0,406737
sin (25°)	0,422618
sin (26°)	0,438371
sin (27°)	0,453990
sin (28°)	0,469472
sin (29°)	0,484810
sin (30°)	0,5
sin (31°)	0,515038
sin (32°)	0,529919
sin (33°)	0,544639
sin (34°)	0,559193
sin (35°)	0,573576
sin (36°)	0,587785
sin (37°)	0,601815
sin (38°)	0,615661
sin (39°)	0,629320
sin (40°)	0,642788
sin (41°)	0,656059
sin (42°)	0,669131
sin (43°)	0,681998
sin (44°)	0,694658
sin (45°)	0,707107
sin (46°)	0,719340
sin (47°)	0,731354
sin (48°)	0,743145
sin (49°)	0,754710
sin (50°)	0,766044
sin (51°)	0,777146
sin (52°)	0,788011
sin (53°)	0,798636
sin (54°)	0,809017
sin (55°)	0,819152
sin (56°)	0,829038
sin (57°)	0,838671
sin (58°)	0,848048
sin (59°)	0,857167
sin (60°)	0,866025
sin (61°)	0,874620
sin (62°)	0,882948
sin (63°)	0,891007
sin (64°)	0,898794
sin (65°)	0,906308
sin (66°)	0,913545
sin (67°)	0,920505
sin (68°)	0,927184
sin (69°)	0,933580
sin (70°)	0,939693
sin (71°)	0,945519
sin (72°)	0,951057
sin (73°)	0,956305
sin (74°)	0,961262
sin (75°)	0,965926
sin (76°)	0,970296
sin (77°)	0,974370
sin (78°)	0,978148
sin (79°)	0,981627
sin (80°)	0,984808
sin (81°)	0,987688
sin (82°)	0,990268
sin (83°)	0,992546
sin (84°)	0,994522
sin (85°)	0,996195
sin (86°)	0,997564
sin (87°)	0,998630
sin (88°)	0,999391
sin (89°)	0,999848
sin (90°)	1

sin (91°)	0,999848
sin (92°)	0,999391
sin (93°)	0,998630
sin (94°)	0,997564
sin (95°)	0,996195
sin (96°)	0,994522
sin (97°)	0,992546
sin (98°)	0,990268
sin (99°)	0,987688
sin (100°)	0,984808
sin (101°)	0,981627
sin (102°)	0,978148
sin (103°)	0,974370
sin (104°)	0,970296
sin (105°)	0,965926
sin (106°)	0,961262
sin (107°)	0,956305
sin (108°)	0,951057
sin (109°)	0,945519
sin (110°)	0,939693
sin (111°)	0,933580
sin (112°)	0,927184
sin (113°)	0,920505
sin (114°)	0,913545
sin (115°)	0,906308
sin (116°)	0,898794
sin (117°)	0,891007
sin (118°)	0,882948
sin (119°)	0,874620
sin (120°)	0,866025
sin (121°)	0,857167
sin (122°)	0,848048
sin (123°)	0,838671
sin (124°)	0,829038
sin (125°)	0,819152
sin (126°)	0,809017
sin (127°)	0,798636
sin (128°)	0,788011
sin (129°)	0,777146
sin (130°)	0,766044
sin (131°)	0,754710
sin (132°)	0,743145
sin (133°)	0,731354
sin (134°)	0,719340
sin (135°)	0,707107
sin (136°)	0,694658
sin (137°)	0,681998
sin (138°)	0,669131
sin (139°)	0,656059
sin (140°)	0,642788
sin (141°)	0,629320
sin (142°)	0,615661
sin (143°)	0,601815
sin (144°)	0,587785
sin (145°)	0,573576
sin (146°)	0,559193
sin (147°)	0,544639
sin (148°)	0,529919
sin (149°)	0,515038
sin (150°)	0,5
sin (151°)	0,48481
sin (152°)	0,469472
sin (153°)	0,453990
sin (154°)	0,438371
sin (155°)	0,422618
sin (156°)	0,406737
sin (157°)	0,390731
sin (158°)	0,374607
sin (159°)	0,358368
sin (160°)	0,342020
sin (161°)	0,325568
sin (162°)	0,309017
sin (163°)	0,292372
sin (164°)	0,275637
sin (165°)	0,258819
sin (166°)	0,241922
sin (167°)	0,224951
sin (168°)	0,207912
sin (169°)	0,190809
sin (170°)	0,173648
sin (171°)	0,156434
sin (172°)	0,139173
sin (173°)	0,121869
sin (174°)	0,104528
sin (175°)	0,087156
sin (176°)	0,069756
sin (177°)	0,052336
sin (178°)	0,034899
sin (179°)	0,017452
sin (180°)	0

sin (181°)	-0,017452
sin (182°)	-0,034899
sin (183°)	-0,052336
sin (184°)	-0,069756
sin (185°)	-0,087156
sin (186°)	-0,104528
sin (187°)	-0,121869
sin (188°)	-0,139173
sin (189°)	-0,156434
sin (190°)	-0,173648
sin (191°)	-0,190809
sin (192°)	-0,207912
sin (193°)	-0,224951
sin (194°)	-0,241922
sin (195°)	-0,258819
sin (196°)	-0,275637
sin (197°)	-0,292372
sin (198°)	-0,309017
sin (199°)	-0,325568
sin (200°)	-0,342020
sin (201°)	-0,358368
sin (202°)	-0,374607
sin (203°)	-0,390731
sin (204°)	-0,406737
sin (205°)	-0,422618
sin (206°)	-0,438371
sin (207°)	-0,453990
sin (208°)	-0,469472
sin (209°)	-0,484810
sin (210°)	-0,5
sin (211°)	-0,515038
sin (212°)	-0,529919
sin (213°)	-0,544639
sin (214°)	-0,559193
sin (215°)	-0,573576
sin (216°)	-0,587785
sin (217°)	-0,601815
sin (218°)	-0,615661
sin (219°)	-0,629320
sin (220°)	-0,642788
sin (221°)	-0,656059
sin (222°)	-0,669131
sin (223°)	-0,681998
sin (224°)	-0,694658
sin (225°)	-0,707107
sin (226°)	-0,719340
sin (227°)	-0,731354
sin (228°)	-0,743145
sin (229°)	-0,754710
sin (230°)	-0,766044
sin (231°)	-0,777146
sin (232°)	-0,788011
sin (233°)	-0,798636
sin (234°)	-0,809017
sin (235°)	-0,819152
sin (236°)	-0,829038
sin (237°)	-0,838671
sin (238°)	-0,848048
sin (239°)	-0,857167
sin (240°)	-0,866025
sin (241°)	-0,874620
sin (242°)	-0,882948
sin (243°)	-0,891007
sin (244°)	-0,898794
sin (245°)	-0,906308
sin (246°)	-0,913545
sin (247°)	-0,920505
sin (248°)	-0,927184
sin (249°)	-0,933580
sin (250°)	-0,939693
sin (251°)	-0,945519
sin (252°)	-0,951057
sin (253°)	-0,956305
sin (254°)	-0,961262
sin (255°)	-0,965926
sin (256°)	-0,970296
sin (257°)	-0,974370
sin (258°)	-0,978148
sin (259°)	-0,981627
sin (260°)	-0,984808
sin (261°)	-0,987688
sin (262°)	-0,990268
sin (263°)	-0,992546
sin (264°)	-0,994522
sin (265°)	-0,996195
sin (266°)	-0,997564
sin (267°)	-0,998630
sin (268°)	-0,999391
sin (269°)	-0,999848
sin (270°)	-1

sin (271°)	-0,999848
sin (272°)	-0,999391
sin (273°)	-0,998630
sin (274°)	-0,997564
sin (275°)	-0,996195
sin (276°)	-0,994522
sin (277°)	-0,992546
sin (278°)	-0,990268
sin (279°)	-0,987688
sin (280°)	-0,984808
sin (281°)	-0,981627
sin (282°)	-0,978148
sin (283°)	-0,974370
sin (284°)	-0,970296
sin (285°)	-0,965926
sin (286°)	-0,961262
sin (287°)	-0,956305
sin (288°)	-0,951057
sin (289°)	-0,945519
sin (290°)	-0,939693
sin (291°)	-0,933580
sin (292°)	-0,927184
sin (293°)	-0,920505
sin (294°)	-0,913545
sin (295°)	-0,906308
sin (296°)	-0,898794
sin (297°)	-0,891007
sin (298°)	-0,882948
sin (299°)	-0,874620
sin (300°)	-0,866025
sin (301°)	-0,857167
sin (302°)	-0,848048
sin (303°)	-0,838671
sin (304°)	-0,829038
sin (305°)	-0,819152
sin (306°)	-0,809017
sin (307°)	-0,798636
sin (308°)	-0,788011
sin (309°)	-0,777146
sin (310°)	-0,766044
sin (311°)	-0,754710
sin (312°)	-0,743145
sin (313°)	-0,731354
sin (314°)	-0,719340
sin (315°)	-0,707107
sin (316°)	-0,694658
sin (317°)	-0,681998
sin (318°)	-0,669131
sin (319°)	-0,656059
sin (320°)	-0,642788
sin (321°)	-0,629320
sin (322°)	-0,615661
sin (323°)	-0,601815
sin (324°)	-0,587785
sin (325°)	-0,573576
sin (326°)	-0,559193
sin (327°)	-0,544639
sin (328°)	-0,529919
sin (329°)	-0,515038
sin (330°)	-0,5
sin (331°)	-0,484810
sin (332°)	-0,469472
sin (333°)	-0,453990
sin (334°)	-0,438371
sin (335°)	-0,422618
sin (336°)	-0,406737
sin (337°)	-0,390731
sin (338°)	-0,374607
sin (339°)	-0,358368
sin (340°)	-0,342020
sin (341°)	-0,325568
sin (342°)	-0,309017
sin (343°)	-0,292372
sin (344°)	-0,275637
sin (345°)	-0,258819
sin (346°)	-0,241922
sin (347°)	-0,224951
sin (348°)	-0,207912
sin (349°)	-0,190809
sin (350°)	-0,173648
sin (351°)	-0,156434
sin (352°)	-0,139173
sin (353°)	-0,121869
sin (354°)	-0,104528
sin (355°)	-0,087156
sin (356°)	-0,069756
sin (357°)	-0,052336
sin (358°)	-0,034899
sin (359°)	-0,017452
sin (360°)	0

Таблица косинусов Брадиса, закон синусов, тангенсов, котангенсов

Таблица Bradis — — это таблица, которая помогает вычислить значения углов синусов, косинусов, тангенсов и котангенсов с точностью до одной минуты без использования калькулятора.

Таблица, которая поможет с расчетами при решении задач в школе (математика, алгебра, геометрия и физика в старших классах) и вузах. На этой странице представлены четырехзначные онлайн-математические знаки для синусов, косинусов, тангенсов и котангенсов.Использовать таблицы просто.

Как бы ни совершенствовались компьютерные технологии, определение синусов, косинусов, тангенсов и котангенсов с помощью таблицы Bradis всегда будет актуальным.
Таблица Bradis создана выдающимся педагогом-математиком Владимиром Модестовичем Брадисом. Чтобы узнать, как пользоваться таблицами Bradis, представленными ниже, мы предлагаем вам сначала прочитать инструкцию.

Как пользоваться столом Bradis?

Пример: Найти синус девяноста градусов.Все, что относится к синусу вверху и слева к косинусам внизу и справа. Слева найдите угол в 90 градусов. И посмотрите результат: 1. Те числа, которые находятся вверху и внизу таблицы (со штрихами: ‘), это минуты .

В таблице Брадиса указаны значения углов, кратные 6 минутам. Если вы хотите найти значения синуса, косинуса, тангенса или котангенса угла, которого нет в таблице Брадиса, вам следует выбрать ближайшее к нему значение.И добавить (вычесть) поправку к черновику, соответствующую разнице, которая может быть равна 1 ‘, 2’, 3 ‘.

Пример:

Таблица Брадиса для синуса и косинуса

грех	0 ‘	6 ‘	12 ‘	18 ‘	24 ‘	30 мин.	36 ‘	42 ‘	48 ‘	54 ‘	60 ‘	cos	1 ‘	2 ‘	3 ‘
											0.0000	90 °
0 °	0,0000	0017	0035	0052	0070	0087	0105	0122	0140	0157	0175	89 °	3	6	9
1 °	0175	0192	0209	0227	0244	0262	0279	0297	0314	0332	0349	88 °	3	6	9
2 °	0349	0366	0384	0401	0419	Номер 0436	0454	0471	0488	0506	0523	87 °	3	6	9
3 °	0523	0541	0558	0576	0593	0610	0628	0645	0663	0680	0698	86 °	3	6	9
4 °	0698	0715	0732	0750	0767	0785	0802	0819	0837	0854	0.0872	85 °	3	6	9

5 °	0,0872	0889	0906	0924	0941	0958	0976	0993	1011	1028	1045	84 °	3	6	9
6 °	1045	1063	1080	1097	1115	1132	1149	1167	1184	1201	1219	83 °	3	6	9
7 °	1219	1236	1253	1271	1288	1305	1323	1340	1357	1374	1392	82 °	3	6	9
8 °	1392	1409	1426	1444	1461	1478	1495	1513	1530	1547	1564	81 °	3	6	9
9 °	1564	1582	1599	1616	1633	1650	1668	1685	1702	1719	0.1736	80 °	3	6	9

10 °	0,1736	1754	1771	1788	1805	1822	1840	1857	1874	1891	1908	79 °	3	6	9
11 °	1908	1925	1942	1959	1977	1994	2011	2028	2045	2062	2079	78 °	3	6	9
12 °	2079	2096	2113	2130	2147	2164	2181	2198	2215	2233	2250	77 °	3	6	9
13 °	2250	2267	2284	2300	2317	2334	2351	2368	2385	2402	2419	76 °	3	6	8
14 °	2419	2436	2453	2470	2487	2504	2521	2538	2554	2571	0.2588	75 °	3	6	8

15 °	0,2588	2605	2622	2639	2656	2672	2689	2706	2723	2740	2756	74 °	3	6	8
16 °	2756	2773	2790	2807	2823	2840	2857	2874	2890	2907	2924	73 °	3	6	8
17 °	2924	2940	2957	2974	2990	3007	3024	3040	3057	3074	3090	72 °	3	6	8
18 °	3090	3107	3123	3140	3156	3173	3190	3206	3223	3239	3256	71 °	3	6	8
19 °	3256	3272	3289	3305	3322	3338	3355	3371	3387	3404	0.3420	70 °	3	5	8

20 °	0,3420	3437	3453	3469	3486	3502	3518	3535	3551	3567	3584	69 °	3	5	8
21 °	3584	3600	3616	3633	3649	3665	3681	3697	3714	3730	3746	68 °	3	5	8
22 °	3746	3762	3778	3795	3811	3827	3843	3859	3875	3891	3907	67 °	3	5	8
23 °	3907	3923	3939	3955	3971	3987	4003	4019	4035	4051	4067	66 °	3	5	8
24 °	4067	4083	4099	4115	4131	4147	4163	4179	4195	4210	0.4226	65 °	3	5	8

25 °	0,4226	4242	4258	4274	4289	4305	4321	4337	4352	4368	4384	64 °	3	5	8
26 °	4384	4399	4415	4431	4446	4462	4478	4493	4509	4524	4540	63 °	3	5	8
27 °	4540	4555	4571	4586	4602	4617	4633	4648	4664	4679	4695	62 °	3	5	8
28 °	4695	4710	4726	4741	4756	4772	4787	4802	4818	4833	4848	61 °	3	5	8
29 °	4848	4863	4879	4894	4909	4924	4939	4955	4970	4985	0.5000	60 °	3	5	8

30 °	0,5000	5015	5030	5045	5060	5075	5090	5105	5120	5135	5150	59 °	3	5	8
31 °	5150	5165	5180	5195	5210	5225	5240	5255	5270	5284	5299	58 °	2	5	7
32 °	5299	5314	5329	5344	5358	5373	5388	5402	5417	5432	5446	57 °	2	5	7
33 °	5446	5461	5476	5490	5505	5519	5534	5548	5563	5577	5592	56 °	2	5	7
34 °	5592	5606	5621	5635	5650	5664	5678	5693	5707	5721	0.5736	55 °	2	5	7

35 °	0,5736	5750	5764	5779	5793	5807	5821	5835	5850	5864	0,5878	54 °	2	5	7
36 °	5878	5892	5906	5920	5934	5948	5962	5976	5990	6004	6018	53 °	2	5	7
37 °	6018	6032	6046	6060	6074	6088	6101	6115	6129	6143	6157	52 °	2	5	7
38 °	6157	6170	6184	6198	6211	6225	6239	6252	6266	6280	6293	51 °	2	5	7
39 °	6293	6307	6320	6334	6347	6361	6374	6388	6401	6414	0.6428	50 °	2	4	7

40 °	0,6428	6441	6455	6468	6481	6494	6508	6521	6534	6547	6561	49 °	2	4	7
41 °	6561	6574	6587	6600	6613	6626	6639	6652	6665	6678	6691	48 °	2	4	7
42 °	6691	6704	6717	6730	6743	6756	6769	6782	6794	6807	6820	47 °	2	4	6
43 °	6820	6833	6845	6858	6871	6884	6896	8909	6921	6934	6947	46 °	2	4	6
44 °	6947	6959	6972	6984	6997	7009	7022	7034	7046	7059	0.7071	45 °	2	4	6

45 °	0,7071	7083	7096	7108	7120	7133	7145	7157	7169	7181	7193	44 °	2	4	6
46 °	7193	7206	7218	7230	7242	7254	7266	7278	7290	7302	7314	43 °	2	4	6
47 °	7314	7325	7337	7349	7361	7373	7385	7396	7408	7420	7431	42 °	2	4	6
48 °	7431	7443	7455	7466	7478	7490	7501	7513	7524	7536	7547	41 °	2	4	6
49 °	7547	7559	7570	7581	7593	7604	7615	7627	7638	7649	0.7660	40 °	2	4	6

50 °	0,7660	7672	7683	7694	7705	7716	7727	7738	7749	7760	7771	39 °	2	4	6
51 °	7771	7782	7793	7804	7815	7826	7837	7848	7859	7869	7880	38 °	2	4	5
52 °	7880	7891	7902	7912	7923	7934	7944	7955	7965	7976	7986	37 °	2	4	5
53 °	7986	7997	8007	8018	8028	8039	8049	8059	8070	8080	8090	36 °	2	3	5
54 °	8090	8100	8111	8121	8131	8141	8151	8161	8171	8181	0.8192	35 °	2	3	5

55 °	0,8192	8202	8211	8221	8231	8241	8251	8261	8271	8281	8290	34 °	2	3	5
56 °	8290	8300	8310	8320	8329	8339	8348	8358	8368	8377	8387	33 °	2	3	5
57 °	8387	8396	8406	8415	8425	8434	8443	8453	8462	8471	8480	32 °	2	3	5
58 °	8480	8490	8499	8508	8517	8526	8536	8545	8554	8563	8572	31 °	2	3	5
59 °	8572	8581	8590	8599	8607	8616	8625	8634	8643	8652	0.8660	30 °	1	3	4

60 °	0,8660	8669	8678	8686	8695	8704	8712	8721	8729	8738	8746	29 °	1	3	4
61 °	8746	8755	8763	8771	8780	8788	8796	8805	8813	8821	8829	28 °	1	3	4
62 °	8829	8838	8846	8854	8862	8870	8878	8886	8894	8902	8910	27 °	1	3	4
63 °	8910	8918	8926	8934	8942	8949	8957	8965	8973	8980	8988	26 °	1	3	4
64 °	8988	8996	9003	9011	9018	9026	9033	9041	9048	9056	0.9063	25 °	1	3	4

65 °	0,9063	9070	9078	9085	9092	9100	9107	9114	9121	9128	9135	24 °	1	2	4
66 °	9135	9143	9150	9157	9164	9171	9178	9184	9191	9198	9205	23 °	1	2	3
67 °	9205	9212	9219	9225	9232	9239	9245	9252	9259	9256	9272	22 °	1	2	3
68 °	9272	9278	9285	9291	9298	9304	9311	9317	9323	9330	9336	21 °	1	2	3
69 °	9336	9342	9348	9354	9361	9367	9373	9379	9383	9391	0.9397	20 °	1	2	3

70 °	9397	9403	9409	9415	9421	9426	9432	9438	9444	9449	0,9455	19 °	1	2	3
71 °	9455	9461	9466	9472	9478	9483	9489	9494	9500	9505	9511	18 °	1	2	3
72 °	9511	9516	9521	9527	9532	9537	9542	9548	9553	9558	9563	17 °	1	2	3
73 °	9563	9568	9573	9578	9583	9588	9593	9598	9603	9608	9613	16 °	1	2	2
74 °	9613	9617	9622	9627	9632	9636	9641	9646	9650	9655	0.9659	15 °	1	2	2

75 °	9659	9664	9668	9673	9677	9681	9686	9690	9694	9699	9703	14 °	1	1	2
76 °	9703	9707	9711	9715	9720	9724	9728	9732	9736	9740	9744	13 °	1	1	2
77 °	9744	9748	9751	9755	9759	9763	9767	9770	9774	9778	9781	12 °	1	1	2
78 °	9781	9785	9789	9792	9796	9799	9803	9806	9810	9813	9816	11 °	1	1	2
79 °	9816	9820	9823	9826	9829	9833	9836	9839	9842	9845	0.9848	10 °	1	1	2

80 °	0,9848	9851	9854	9857	9860	9863	9866	9869	9871	9874	9877	9 °	0	1	1
81 °	9877	9880	9882	9885	9888	9890	9893	9895	9898	9900	9903	8 °	0	1	1
82 °	9903	9905	9907	9910	9912	9914	9917	9919	9921	9923	9925	7 °	0	1	1
83 °	9925	9928	9930	9932	9934	9936	9938	9940	9942	9943	9945	6 °	0	1	1
84 °	9945	9947	9949	9951	9952	9954	9956	9957	9959	9960	9962	5 °	0	1	1

85 °	9962	9963	9965	9966	9968	9969	9971	9972	9973	9974	9976	4 °	0	0	1
86 °	9976	9977	9978	9979	9980	9981	9982	9983	9984	9985	9986	3 °	0	0	0
87 °	9986	9987	9988	9989	9990	9990	9991	9992	9993	9993	9994	2 °	0	0	0
88 °	9994	9995	9995	9996	9996	9997	9997	9997	9998	9998	0.9998	1 °	0	0	0
89 °	9998	9999	9999	9999	9999	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000	0 °	0	0	0
90 °	1.0000
грех	60 ‘	54 ‘	48 ‘	42 ‘	36 ‘	30 ‘	24 ‘	18 ‘	12 ‘	6 ‘	0 ‘	cos	1 ‘	2 ‘	3 ‘

Таблица Bradis для касательных и котангенсов

Тангенс угла x — это отношение противоположного отрезка к соседнему:

Котангенс угла x — это отношение смежной стороны к противоположной:

Тангенс угла — это отношение дальней стороны угла к середине. Котангенс угла равен , наоборот.

тг	0 ‘	6 ‘	12 ‘	18 ‘	24 ‘	30 ‘	36 ‘	42 ‘	48 ‘	54 ‘	60 ‘	КТ	1 ‘	2 ‘	3 ‘
											0	90 °
0 °	0,000	0017	0035	0052	0070	0087	0105	0122	0140	0157	0175	89 °	3	6	9
1 °	0175	0192	0209	0227	0244	0262	0279	0297	0314	0332	0349	88 °	3	6	9
2 °	0349	0367	0384	0402	0419	0437	0454	0472	0489	0507	0524	87 °	3	6	9
3 °	0524	0542	0559	0577	0594	0612	0629	0647	0664	0682	0699	86 °	3	6	9
4 °	0699	0717	0734	0752	0769	0787	0805	0822	0840	0857	0,0875	85 °	3	6	9

5 °	0,0875	0892	0910	0928	0945	0963	0981	0998	1016	1033	1051	84 °	3	6	9
6 °	1051	1069	1086	1104	1122	1139	1157	1175	1192	1210	1228	83 °	3	6	9
7 °	1228	1246	1263	1281	1299	1317	1334	1352	1370	1388	1405	82 °	3	6	9
8 °	1405	1423	1441	1459	1477	1495	1512	1530	1548	1566	1584	81 °	3	6	9
9 °	1584	1602	1620	1638	1655	1673	1691	1709	1727	1745	0,1763	80 °	3	6	9

10 °	0,1763	1781	1799	1817	1835	1853	1871	1890	1908	1926	1944	79 °	3	6	9
11 °	1944	1962	1980	1998	2016	2035	2053	2071	2089	2107	2126	78 °	3	6	9
12 °	2126	2144	2162	2180	2199	2217	2235	2254	2272	2290	2309	77 °	3	6	9
13 °	2309	2327	2345	2364	2382	2401	2419	2438	2456	2475	2493	76 °	3	6	9
14 °	2493	2512	2530	2549	2568	2586	2605	2623	2642	2661	0,2679	75 °	3	6	9

15 °	0,2679	2698	2717	2736	2754	2773	2792	2811	2830	2849	2867	74 °	3	6	9
16 °	2867	2886	2905	2924	2943	2962	2981	3000	3019	3038	3057	73 °	3	6	9
17 °	3057	3076	3096	3115	3134	3153	3172	3191	3211	3230	3249	72 °	3	6	10
18 °	3249	3269	3288	3307	3327	3346	3365	3385	3404	3424	3443	71 °	3	6	10
19 °	3443	3463	3482	3502	3522	3541	3561	3581	3600	3620	0,3640	70 °	3	7	10

20 °	0,3640	3659	3679	3699	3719	3739	3759	3779	3799	3819	3839	69 °	3	7	10
21 °	3839	3859	3879	3899	3919	3939	3959	3979	4000	4020	4040	68 °	3	7	10
22 °	4040	4061	4081	4101	4122	4142	4163	4183	4204	4224	4245	67 °	3	7	10
23 °	4245	4265	4286	4307	4327	4348	4369	4390	4411	4431	4452	66 °	3	7	10
24 °	4452	4473	4494	4515	4536	4557	4578	4599	4621	4642	0,4663	65 °	4	7	11

25 °	0,4663	4684	4706	4727	4748	4770	4791	4813	4834	4856	4877	64 °	4	7	11
26 °	4877	4899	4921	4942	4964	4986	5008	5029	5051	5073	5095	63 °	4	7	11
27 °	5095	5117	5139	5161	5184	5206	5228	5250	5272	5295	5317	62 °	4	7	11
28 °	5317	5340	5362	5384	5407	5430	5452	5475	5498	5520	5543	61 °	4	8	11
29 °	5543	5566	5589	5612	5635	5658	5681	5704	5727	5750	0,5774	60 °	4	8	12

30 °	0,5774	5797	5820	5844	5867	5890	5914	5938	5961	5985	6009	59 °	4	8	12
31 °	6009	6032	6056	6080	6104	6128	6152	6176	6200	6224	6249	58 °	4	8	12
32 °	6249	6273	6297	6322	6346	6371	6395	6420	6445	6469	6494	57 °	4	8	12
33 °	6494	6519	6544	6569	6594	6619	6644	6669	6694	6720	6745	56 °	4	8	13
34 °	6745	6771	6796	6822	6847	6873	6899	6924	6950	6976	0,7002	55 °	4	9	13

35 °	0,7002	7028	7054	7080	7107	7133	7159	7186	7212	7239	7265	54 °	4	8	13
36 °	7265	7292	7319	7346	7373	7400	7427	7454	7481	7508	7536	53 °	5	9	14 °
37 °	7536	7563	7590	7618	7646	7673	7701	7729	7757	7785	7813	52 °	5	9	14
38 °	7813	7841	7869	7898	7926	7954	из 7 983	8012	8040	8069	8098	51 °	5	9	14
39 °	8098	8127	8156	8185	8214	8243	8273	8302	8332	8361	0,8391	50 °	5	10	15

40 °	0,8391	8421	8451	8481	8511	8541	8571	8601	8632	8662	0,8693	49 °	5	10	15
41 °	8693	8724	8754	8785	8816	8847	8878	8910	8941	8972	9004	48 °	5	10	16
42 °	9004	9036	9067	9099	9131	9163	9195	9228	9260	9293	9325	47 °	6	11	16
43 °	9325	9358	9391	9424	9457	9490	9523	9556	9590	9623	0,9657	46 °	6	11	17
44 °	9657	9691	9725	9759	9793	9827	9861	9896	9930	9965	1,0000	45 °	6	11	17

45 °	1,0000	0035	0070	0105	0141	0176	0212	0247	0283	0319	0355	44 °	6	12	18
46 °	0355	0392	0428	0464	0501	0538	0575	0612	0649	0686	0724	43 °	6	12	18
47 °	0724	0761	0799	0837	0875	0913	0951	0990	1028	1067	1106	42 °	6	13	19
48 °	1106	1145	1184	1224	1263	1303	1343	1383	1423	1463	1504	41 °	7	13	20
49 °	1504	1544	1585	1626	1667	1708	1750	1792	1833	1875	1,1918	40 °	7	14	21

50 °	1,1918	1960	2002	2045	2088	2131	2174	2218	2261	2305	2349	39 °	7	14	22
51 °	2349	2393	2437	2482	2527	2572	2617	2662	2708	2753	2799	38 °	8	15	23
52 °	2799	2846	2892	2938	2985	3032	3079	3127	3175	3222	3270	37 °	8	16	24
53 °	3270	3319	3367	3416	3465	3514	3564	3613	3663	3713	3764	36 °	8	16	25
54 °	3764	3814	3865	3916	3968	4019	4071	4124	4176	4229	1,4281	35 °	9	17	26

55 °	1,4281	4335	4388	4442	4496	4550	4605	4659	4715	4770	4826	34 °	9	18	27
56 °	4826	4882	4938	4994	5051	5108	5166	5224	Уже 5282	5340	5399	33 °	10	19	29
57 °	5399	5458	5517	5577	5637	5697	5757	5818	5880	5941	6003	32 °	10	20	30
58 °	6003	6066	6128	6191	6255	6319	6383	6447	6512	6577	6643	31 °	11	21	32
59 °	6643	6709	6775	6842	6909	6977	7045	7113	7182	7251	1,7321	30 °	11	23	34

60 °	1,732	1,739	1,746	1,753	1,760	1,767	1,775	1,782	1,789	1,797	1 804	29 °	1	2	4
61 °	1 804	1811	1819	1827	1834	1842	1849	1857	1865	1873	1881	28 °	1	3	4
62 °	1881	1889	1897	1 905	Б / у 1,913	1 921	1 929	1 937	1 946	1 954	1 963	27 °	1	3	4
63 °	1 963	1 971	1 980	1 988	1,997	2 006	2,014	2,023	2 032	2 041	Из 2.05	26 °	1	3	4
64 °	2 050	2,059	2 069	2,078	2 087	2,097	2,106	2,116	2,125	2 135	2 145	25 °	2	3	5

65 °	2 145	2 154	2 164	2 174	2 184	2 194	2 204	2,215	2,225	2,236	2,246	24 °	2	3	5
66 °	2,246	2,257	2,267	2,278	2,289	2,3	2,311	2,322	2,333	2,344	2,356	23 °	2	4	5
67 °	2,356	2,367	2 379	2,391	2,402	2,414	2,426	2,438	2,450	2,463	2,475	22 °	2	4	6
68 °	2,475	2,488	2,5	2,513	2,526	2,539	2,552	2,565	2,578	2,592	2 605	21 °	2	4	6
69 °	2 605	2 619	2 633	2 646	Из 2.66	2,675	2 689	2 703	2 718	2 733	2 747	20 °	2	5	7

70 °	2 747	2 762	2,778	2 793	2 808	2 824	2 840	2 856	2 872	2 888	2 904	19 °	3	5	8
71 °	2 904	2 921	2 937	2 954	2 971	2 989	3 006	3 024	3 042	3,06	3 078	18 °	3	6	9
72 °	3 078	3 096	3,115	3,133	3,152	3 172	3,191	3 211	3,230	3 251	3 271	17 °	3	6	10
73 °	3 271	3,291	3 312	3 333	3 354	3 376	3 398	3.42	3 442	3 465	3 487	16 °	4	7	11
74 °	3 487	3,511	3,534	3,558	3,582	Кому 3.606	3 630	3 655	3 681	3 706	3 732	15 °	4	8	13
75 °	3 732	3,758	3,785	3 812	3 839	3 867	3 895	3 923	3 952	3 981	4 011	14 °	5	10	14
тг	60 ‘	54 ‘	48 ‘	42 ‘	36 ‘	30 мин.	24 ‘	18 ‘	12 ‘	6 ‘	0 ‘	КТ	1 ‘	2 ‘	3 ‘

Тригонометрические таблицы

Тригонометрический Столы

(Математика | Триггер | Таблицы)

PI = 3.141592 … (примерно 22/7 = 3,1428)
радианы = градусы x PI / 180 (преобразование градуса в рад)
градусы = радианы x 180 / PI (преобразование рад в градусы)

Рад	градусов	Грех	Cos	Тан	Csc	сек	Детская кроватка
.0000	00	.0000	1,0000	.0000	——	1,0000	——	90	1,5707
.0175	01	.0175	.9998	.0175	57.2987	1.0002	57.2900	89	1,5533
. 0349	02	0,0349	.9994	0,0349	28,6537	1.0006	28,6363	88	1,5359
.0524	03	.0523	.9986	.0524	19.1073	1,0014	19.0811	87	1,5184
. 0698	04	0,0698	.9976	.0699	14.3356	1,0024	14,3007	86	1,5010
.0873	05	.0872	.9962	.0875	11,4737	1.0038	11,4301	85	1.4835
.1047	06	. 1045	.9945	. 1051	9,5668	1,0055	9.5144	84	1,4661
.1222	07	.1219	.9925	. 1228	8,2055	1,0075	8,1443	83	1.4486
. 1396	08	. 1392	. 9903	.1405	7,1853	1,0098	7,1154	82	1.4312
.1571	09	. 1564	. 9877	. 1584	6.3925	1.0125	6.3138	81	1,4137
. 1745	10	.1736	. 9848	. 1763	5,7588	1.0154	5,6713	80	1,3953
.1920	11	. 1908	.9816	. 1944	5.2408	1.0187	5.1446	79	1,3788
. 2094	12	. 2079	.9781	.2126	4,8097	1.0223	4,7046	78	1,3614
.2269	13	. 2250	.9744	.2309	4.4454	1.0263	4,3315	77	1,3439
.2443	14	. 2419	. 9703	. 2493	4,1336	1.0306	4.0108	76	1,3265
. 2618	15	0,2588	.9659	.2679	3,8637	1.0353	3.7321	75	1.3090
.2793	16	0,2756	0,9613	0,2867	3.6280	1.0403	3,4874	74	1.2915
. 2967	17	0,2924	. 9563	. 3057	3,4203	1.0457	3,2709	73	1,2741
.3142	18	.3090	.9511	0,3249	3,2361	1.0515	3,0777	72	1,2566
.3316	19	.3256	. 9455	. 3443	3,0716	1.0576	2,9042	71	1,2392
. 3491	20	. 3420	.9397	0,3640	2,9238	1.0642	2,7475	70	1,2217
.3665	21	.3584	. 9336	.3839	2,7904	1.0711	2,6051	69	1.2043
.3840	22	0,3746	. 9272	.4040	2.6695	1.0785	2,4751	68	1,1868
.4014	23	.3907	. 9205	.4245	2,5593	1.0864	2,3559	67	1.1694
. 4189	24	. 4067	.9135	.4452	2.4586	1.0946	2.2460	66	1,1519
.4363	25	.4226	.9063	.4663	2.3662	1,1034	2,1445	65	1.1345
.4538	26	.4384	.8988	0,4877	2,2812	1,1126	2,0503	64	1.1170
.4712	27	. 4540	.8910	0,5095	2,2027	1,1223	1,9626	63	1.0996
.4887	28	.4695	. 8829	.5317	2,1301	1,1326	1,8807	62	1.0821
.5061	29	0,4848	.8746	.5543	2,0627	1,1434	1,8040	61	1.0647
. 5236	30	.5000	0,8660	.5774	2,0000	1,1547	1,7321	60	1.0472
. 5411	31	.5150	. 8572	. 6009	1.9416	1,1666	1,6643	59	1.0297
.5585	32	. 5299	.8480	. 6249	1.8871	1.1792	1,6003	58	1.0123
. 5760	33	. 5446	. 8387	.6494	1,8361	1,1924	1.5399	57	.9948
.5934	34	.5592	.8290	.6745	1,7883	1,2062	1.4826	56	.9774
. 6109	35	. 5736	.8192	.7002	1.7434	1,2208	1,4281	55	. 9599
.6283	36	.5878	.8090	.7265	1,7013	1,2361	1,3764	54	.9425
.6458	37	.6018	.7986	0,7536	1.6616	1,2521	1,3270	53	. 9250
.6632	38	.6157	.7880	0,7813	1,6243	1,2690	1,2799	52	.9076
. 6807	39	.6293	.7771	.8098	1,5890	1,2868	1,2349	51	. 8901
.6981	40	0,6428	0,7660	.8391	1.5557	1,3054	1,1918	50	. 8727
.7156	41	.6561	0,7547	.8693	1,5243	1.3250	1,1504	49	. 8552
.7330	42	.6691	0,7431	. 9004	1.4945	1,3456	1.1106	48	. 8378
. 7505	43	.6820	.7314	. 9325	1,4663	1,3673	1.0724	47	.8203
. 7679	44	0,6947	.7193	.9657	1,4396	1,3902	1.0355	46	.8029
.7854	45	.7071	.7071	1,0000	1,4142	1,4142	1,0000	45	. 7854
		CO	Грех	Детская кроватка	сек	CSC	Тан	градусов	Рад

Те, в знаменателе которых стоит ноль, не определены.Они включены исключительно для демонстрации рисунка.

касательная таблица радиан

Функция Arctan. Математика для блондинок Тригонометрическая таблица в радианах Таблица 4 из гетерогенных нейронных сетей на основе сходства Функции синуса и косинуса Альберта Ван дер Селя … Как изначально были таблицы синус-косинусов и касательных Математика для блондинок Какова ценность Sin 180 Пример кода Quora для asin , acos и atan с углами в радианах: таблица тригонометрических соотношений помогает найти значения стандартных тригонометрических углов, таких как 0 °, 30 °, 45 °, 60 ° и 90 °.Синтаксис. Слово косинус состоит из двух частей: «со» и «синус», что указывает на то, что косинус является синусом дополнительного угла. Запишите свои ответы в колонку 2. Пример. Рабочие листы SOHCAHTOA. Уловка с тригонометрической таблицей, которую вы никогда не забудете Math S Mathvox как использовать синус-косинус, тангенс и таблицу котангенса для 6 тригонометрических функций специальные углы mathvox тригонометрические таблицы таблица 1 энциклопедия простого способа получить значения тригонометрической таблицы вы. А поскольку несколько углов могут иметь один и тот же синус (например,грамм. Арктангенс (также известный как тригонометрические функции, такие как функция тангенса, по сути, являются функциями переменной, которая является углом. Найдите здесь табличные значения шести тригонометрических функций sin cos tan cosec sec и cot в разных радианах. … От десятичной дроби к дробной от дробной к Десятичные радианы в градусы Градусы в радианы Шестнадцатеричное научное представление Расстояние Вес Время. Что люди ищут в этом блоге: Таблица значений Sin и Cos в радианах; Таблица значений Sin Cos Tan в радианах Используйте это действие для вычисления тангенса тригонометрического отношения в радианах. радианы.ATAN (0) равно 0. Чтобы преобразовать значение градусов в радианы, умножьте его на пи / 180 (приблизительно 0,01745329252). RADIANS () Возвращает аргумент, преобразованный в радианы RAND () Возвращает случайное значение с плавающей запятой ROUND () Округляет аргумент SIGN () Возвращает знак аргумента SIN () Возвращает синус аргумента SQRT () Возвращает квадратный корень из аргумент TAN () возвращает тангенс… Полная таблица тригонометрических функций для синуса, косинуса, тангенса и котангенса по градусам и 10-минутному интервалу или радианам.Обе эти функции возвращают арктангенс в радианах. Для оценки функций sin (), cos () и т. Д. Сторона = 2 (вписанный радиус многоугольника) tan (pi / (число сторон многоугольника) Параметр 1: числовое значение, представляющее собой угол, указанный в радианах. , для которого ищется тангенс. Значение синуса, косинуса и тангенса указывается с точностью до четырех знаков после запятой. Проверьте себя на точных значениях шести тригонометрических функций под «хорошими» углами. Знаки y и x используются для получить информацию о квадранте; кроме того, x может быть нулевым, если y не равно нулю.На выходе он возвращает число с плавающей запятой. Мы используем все, что узнали в этой главе. Для касательных применяйте ниже: Tg (k.180 + α) = tg α Пример: tg 750 = tg (2.360 + 30) = tg (4.180 + 30) Вот печатаемая таблица синус-косинус-тангенс для всех целочисленных значений углов. в градусах от 0 ° до 360 °. Тригонометрический стол. Градусы Радианы Синус Косинус Тангенс 30 0,5236 0. Таблицы касательных Таблица углов от 0 ° до 90 ° для учащихся. Таблица 10-1: Встроенные функции Star-Hspice Форма HSPICE Функциональный класс Описание sin (x) sine trig Возвращает синус x (радианы) cos (x) cosine trig Возвращает косинус тангенса x (радианы) tan (x) trig Возвращает тангенс x (радианы). Обратный тангенс y / x, результат в радианах.Эта функция принимает в качестве аргумента любой числовой тип данных или любой нечисловой тип данных, который может быть неявно преобразован в числовой тип данных. Чтобы найти косинус угла, достаточно найти значение в таблице. Касательная. Выход 1: числовое значение, являющееся тангенсом указанного угла. 5000 0. Градусы COS (DEG) TAN (DEG) 0 30 45 60 90 180 18. Возвращает арккосинус x (в радианах). радианы * 180/355 * 113 = градусы. Выберите градусы или радианы в раскрывающемся списке и легко вычислите точное значение тангенса угла 20 °.Если аргумент — BINARY_FLOAT, функция возвращает BINARY_DOUBLE. ATAN возвращает арктангенс n. Аргумент n может находиться в неограниченном диапазоне и возвращает значение в диапазоне от — pi / 2 до pi / 2, выраженное в радианах. Таблица тригонометрических родительских функций; Графики шести тригонометрических функций; Триггерные функции в графическом калькуляторе; Больше практики; Теперь, когда мы знаем единичный круг наизнанку, давайте построим график тригонометрических функций в системе координат. … Таблица арктангенса.c \) используется для обозначения радианов. Например, 1,5 радиана записываются как 1,5 рад или 1,5 c. Таблица значений синус-косинуса радиан. Функция Tangent имеет совершенно другую форму … она проходит между отрицательной и положительной бесконечностью, пересекает 0 и каждые π радиан (180 °), как показано на этом графике. В приведенной ниже тригонометрической таблице тангенса указаны соответствующие значения тангенса для заданного угла от 0 до 360 градусов с точностью до 6 десятичных знаков. Калькулятор обратного тангенса. Введите значение тангенса, выберите градусы (°) или радианы (рад) и нажмите кнопку =.PI / 180; вернуть Math. Однако, если вы хотите вычислить значение тангенса угла ангела, которое отсутствует в таблице, воспользуйтесь калькулятором тангенса. 5000 1. Хотя мы можем использовать и радианы, и градусы, радианы являются более естественным измерением, потому что они напрямую связаны с единичной окружностью, кругом с радиусом 1. Радианная мера угла определяется следующим образом. Результат, радианы. Результат — угол, выраженный в радианах. угол следует перевести в радианы. Взаимные тригонометрические тождества также выводятся с помощью тригонометрических функций.Или: tan = где угол, который вы измеряете. Фундаментальные стратегии для освещения условий — Объяснение состояния предполагает раскрытие всех его основных основ или… Ниже приводится объяснение метода и правильности вычисления этих значений для произвольного прямоугольного треугольника. Очень хорошее приближение π, которое мне легко запомнить, — это 355/113 (и более точное, чем более часто используемое приближение 22/7). Наконец, в таблице 9-7 показаны доступные тригонометрические функции.Вопрос. Примеры учебных целей Определите триггерные функции для отрицательных углов и углов больше 90 градусов. Онлайн-таблица тригонометрии для определения синуса, косинуса, тангенса, секанса, косеканса и котангенса для углов от 0 до 90 градусов. Он начинается с 0 головы до 1 на π 2 радиана 90, а затем идет вниз до 1. Таблицы касательных Диаграмма угла от 91 ° до 180 ° в градусах и радианах для учащихся. Используйте этот простой калькулятор загара, чтобы вычислить значение загара для 20 ° в радианах / градусах. . 4: math.atan (x) Возвращает арктангенс x (в радианах).Ниже приводится таблица значений из Excel. Например, если загар (0,5) = 0,54630249, то арктангенс (0,54630249) = 0,5. Чтобы узнать больше, подумайте о том, чтобы начать со статьи в Википедии об обратных тригонометрических функциях. К счастью, Excel предоставляет нам способ вычислить арктангенс числа с помощью функции ATAN. Результирующий угол находится в диапазоне от -pi / 2 до pi / 2. Наблюдение: обратный тангенс — это нечетная функция, поэтому (напомним, что функция является нечетной). Пример 19.1. Вспомните точные значения касательной функции из главы 17: Точные значения касательной функции.Приложения могут принимать любое действительное значение Кривые синуса, косинуса и тангенса; Аппроксимация малых углов: синуса, косинуса и тангенса. Когда высота и основание прямоугольного треугольника известны, мы можем определить значения синуса, косинуса, тангенса, секанса, косеканса и котангенса, используя тригонометрические формулы. Таблица тригонометрии показывает значения этих тригонометрических соотношений для разных углов. Наш калькулятор тангенса принимает значения в градусах или радианах, поэтому, если угол известен, просто введите его и нажмите «вычислить».Таблица тригонометрических значений в градусах: sin cos tan cot В этой тригонометрической таблице значение угла в радианах замыкается на 3,15 радиан, что едва ли соответствует 180 градусам в градусной мере углов. Если арктангенс 1 равен 50, то, чтобы найти арктангенс, взгляните на следующие вычисления: Определение Чтобы узнать больше, начните со статьи в Википедии о тригонометрических функциях. Пользователь также может использовать функцию РАДИАНЫ. При необходимости эти значения могут быть преобразованы в градусы.поделитесь своим расчетом Тригонометрическая таблица. Посетите интерактивный блокнот для рисования в этой теме: косплей «Прямоугольный треугольник» — косинус только прямоугольного треугольника; TraceSin; — просто график с подвижной точкой для отображения координат; sinplay — синус прямоугольного треугольника; tanplay — косинус прямого треугольника; Радианы radianSector — длина дуги, площадь сектора, радианы 30 ° 45 ° 60 ° 90 ° вопросы pdf, 30 ° 45 ° 60 ° 90 ° ответы pdf Используйте этот простой калькулятор загара, чтобы вычислить значение загара для 20 ° в радианах / градусах.note Примечание. Это действие принимает и выводит только радианы. Касательный функтоид. Все углы, используемые в этих функциях, основаны на радианах, а не в градусах (π радиан = 180 °). Синус. Триггерная таблица общих углов; угол (градусы) 0 30 45 60135150180210225240270300315330360 = 0; угол (радианы) 0 PI / 6 PI / 4 PI / 3 PI / 2 Узнайте, как вычислить функцию арктангенса, используя единичную окружность. Замечание. Встроенные функции Star-Hspice перечислены в Табл. 10-1 :. Синус, косинус, тангенс угла 45 градусов (sin 45, cos 45, tg 45) Табличные значения для синуса 45, косинуса 45 и тангенса 45 градусов приведены ниже.Воспользуйтесь нашим калькулятором tan (x), чтобы найти тангенс 66 градусов — tan (66 °) — или тангенс любого угла в градусах и радианах. Первую тригонометрическую таблицу, по-видимому, составил Гиппарх, которого теперь называют «отцом тригонометрии». Многие геометрические вычисления можно легко вычислить, используя таблицу тригонометрических функций и формул. Например, арктангенс к p 3 равен 3, поскольку ˇ 3 — это угол, тангенс которого равен p 3. Как я могу использовать vi, предоставленный в LabVIEW 7.1 для достижения такого же результата? косинус, тангенс с градусами и радианами Найдите точное значение каждой тригонометрической функции. В Excel есть встроенная функция, известная как РАДИАНЫ (угол), где угол — это угол в градусах, который вы хотите преобразовать в радианы. Привет Добрый день! Что люди ищут в этом блоге: Триггерные радианы таблицы Как использовать таблицу касательных и котангенсов Брадиса от 0 до 90 градусов. Этот раздел «Графики триггерных функций» охватывает:. Это то же самое, что: 20340 * радиан / 355 = градусы. Они вернут угол с заданным значением синуса (или косинусом, тангенсом и т. Д.)). Заранее благодарю за совет! atand (1) → 45. atan2 (y двойной точности, x двойной точности) → двойной точности. Это постоянное соотношение является свойством угла и называется тангенсом угла … Поскольку угловая скорость равна ω радиан в секунду, угол AOB в момент времени t … Градусы Радианы tan 0 0 0 30 π / 6 1 / √3 45 π / 4 1 60 π / 3 √3 90 π / 2 Не определено Связанное чтение. Выходные данные синуса, косинуса и тангенса различных значений угла представлены в табличной форме. Работайте над этими ценностями, пока не узнаете их все! С.загар — I (0) а. арктан (л) б. арктан. Запишите свои ответы в столбце 2. В следующем примере функция VBA Tan используется для возврата тангенса трех разных углов (которые выражаются в радианах). В отличие от большинства таблиц в Интернете, эта таблица полная, красиво отформатирована и приятна для глаз. Mathvox, как использовать тригонометрические функции sin cos для синус-косинуса и котангенса в Excel для таблицы тригонометрических соотношений синуса и косинуса тригонометрическая таблица стандартных углов от 0 до 360 cos sin cot tan sec cosec.Y = atan (X) Описание. Его набор тригонометрических значений различных стандартных углов, включая 0 °, 30 °, 45 °, 60 °, 90 °, иногда с другими углами, такими как 180 °, 270 ° и 360 °. Вывод: cos (45.0) = 0.7071067811865476 Java.lang.Math.tan (): это встроенный метод, который возвращает тангенс значения, переданного в качестве аргумента. Это такая маленькая тригонометрическая таблица в радианах. Приложения могут принимать любое действительное значение. В следующей таблице преобразуйте углы в градусах, указанные в первом столбце, в радианы.Радиан — это единица измерения углов. Вот так просто. Y = atan (X) возвращает обратную касательную (tan-1) элементов X в радианах … Если угол неизвестен, но известны длины противоположной и смежной стороны прямоугольного треугольника, тогда касательная может быть… Скопируйте данные примера из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Согласно теореме Бейкера, если значение синуса, косинуса или тангенса является алгебраическим, то угол является либо рациональным числом градусов, либо трансцендентным числом градусов.В следующем примере возвращается гиперболический тангенс значений в столбце градусов таблицы anglestbl. Значение пи (приблизительно 3,1415589793) в 4 раза больше арктангенса 1. Оно состоит из тригонометрических соотношений — синуса, косинуса, тангенса … Поскольку любой угол с мерой больше 2 π радиан или меньше 0 эквивалентен некоторому углу с мерой 0 ≤ θ

Кто владеет диагностической клиникой, Пуэбла против Тигреса текущий счет, Летний лагерь Pinnacle Sports, Сервер Alexa Ecobee не отвечает, Наташа Джонас Кэти Тейлор, Верхняя одежда Аляски, Щитовой дварф против золотого дварфа, Академия современного искусства Хана,

как найти котангенс радиана

Используя треугольник 30-60-90, котангенс угла 30 градусов равен sqrt (3) / 1, или квадратный корень из 3.Как найти опорный угол в радианах. Секанс, косеканс и котангенс — это тригонометрические функции, производные от трех элементарных функций: синуса, косинуса и тангенса. Описание объекта палитры; Косеканс: вычисляет косеканс x, где x выражается в радианах. Детская кроватка 3,14 = детская кроватка 179, градусов. Следовательно, возникает вопрос, что такое Секанс, обратный? ) Список словаря с триггерными терминами. Теперь выберите градусы, радианы, M-радианы или пи радианы из раскрывающегося меню. Многие функции работают с радианами, а некоторые… Как вычислить котангенс? Формула в ячейке C3: = COT (B3) Синтаксис функции Excel […] Как использовать функцию COTH.Калькулятор обратного котангенса — это бесплатный онлайн-инструмент, который отображает значение обратного котангенса в градусах и радианах для заданных входных данных. Формула тригонометрических функций и обратных тригонометрических функций Теперь вы можете нажать (Трассировка), чтобы найти координаты точек на окружности. Найдите cos = 5. пример. Нахождение тригонометрических функций угла. кратное π радианам; 180 ° Как работает калькулятор котангенса? = загар 5π 4. … Радиан — это единица измерения угла, равная длине дуги, деленной на ___ дуги.COT (число) Где числовой аргумент — это угол (в радианах), котангенс которого вы хотите вычислить. х = 1 загар? Нахождение котангенса угла — важная тригонометрическая операция, которая находит применение в математике, физике и так далее. И обратными этими функциями являются косеканс, секанс и котангенс. Онлайн-калькулятор обратного котангенса BYJU ускоряет вычисления и отображает значение обратного котангенса за доли секунды. Это онлайн-калькулятор тригонометрии, позволяющий узнать эквивалентные значения радианов и градусов для данного числа.В этом уроке мы определим радианы и рассмотрим некоторые проблемы, связанные с радианами. Помните, что делить на ноль нельзя, поэтому эти определения действительны только тогда, когда знаменатели не равны нулю. Тригонометрическое расширение: expand_trigo. Котангенс: котан. Описание: Функция exp вычисляет в режиме онлайн экспоненту числа. Триггерные значения — 2 Найдите sin (t), cos (t) и tan (t) для t между 0 и 2π. Синус и косинус. Вычислите синус и косинус углов… Одним из важных соотношений в прямоугольных треугольниках является тангенс.ДА! В этой статье мы предоставим вам все подробности о тригонометрических функциях, таких как значение в градусах, радианах, полную тригонометрическую таблицу и другую важную информацию. отношение длины стороны, прилегающей к углу, к длине противоположной стороны в прямоугольном треугольнике. Введение в тригонометрию: тригонометрические функции, тригонометрические углы, обратная тригонометрия, задачи тригонометрии, базовая тригонометрия, приложения тригонометрии, тригонометрия на декартовой плоскости, графики тригонометрических функций и тригонометрические тождества, калькулятор тригонометрии, с видео… Угол (в радианах) : math :: trig :: tи угол.1. Используя калькулятор, установленный в режиме радиан, находим, что tan-1 (2,5) = 1,195. Расчет котангенса; Вычисление котангенса угла в радианах. Найдите секущую угла, используя приведенный ниже онлайн-калькулятор секущей. Используемая единица измерения устанавливается в градусах или радианах в раскрывающемся меню. Шесть тригонометрических функций могут быть определены как значения координат точек на евклидовой плоскости, которые связаны с единичной окружностью, которая является окружностью радиуса один с центром в начале O этой системы координат.Калькулятор позволяет получить тригонометрическое разложение выражения. Функция котангенса (Cot) вычисляет котангенс угла, который выражается действительным числом. Тригонометрическая функция котана для вычисления котангенса угла в радианах, градусах или градианах. Избавьтесь от социальных и культурных нарративов, сдерживающих вас, и позвольте пошаговым решениям из учебников по тригонометрии переориентировать ваши старые парадигмы. Когда мы находим значения sin cos и tan для треугольника, мы обычно рассматриваем эти углы: 0 °, 30 °, 45 °, 60 ° и 90 °.Найдите [латекс] \ sin t, \ cos t, \ tan t, \ sec t, \ csc t [/ latex],… Чтобы преобразовать 3,14 радиана в градусы, умножьте 3,14 на 180 ° / $ \ pi $ = 179, °. Однако большинство калькуляторов не могут вернуть значения в радикальном виде. В то время как определение прямоугольного треугольника позволяет определять тригонометрические функции для углов от 0 до радиана … Онлайн-калькулятор обратного котангенса BYJU ускоряет вычисления и отображает значение обратного котангенса за доли секунды. Котангенс. Это важно в тригонометрии, чтобы понимать использование углов в градусах и радианах.27. Научитесь вычислять обратные тригонометрические функции. Синтаксис. Радиан: угол, образуемый в центре круга дугой, длина которой равна радиусу круга, называется одним радианом. Если предоставленный числовой аргумент равен 0, функция Cot возвращает # DIV / 0! Для каждого угла даны координаты. Геометрия (плоскость) … и котангенс общих углов. Вычисление экспоненты Вычислите котангенс комплексных углов вектора x. х = [-i пи + я * пи / 2 -1 + я * 4]; y = cot (x) y = 1 × 3 комплекс 0.0000 + 1.3130i -0.0000 — 1.0903i -0.0006 — 0.9997i Котангенс или функция «детская кроватка» — это тригонометрическая функция, которая используется для определения котангенса угла. Если калькулятор имеет режим градусов и режим радиан, установите его в режим радиан. Примечание: функция Acot была представлена только в Excel 2013 и поэтому недоступна в более ранних версиях Excel. Продукты ReThink предназначены для производства широкого спектра натуральных продуктов CBD полного спектра с приверженностью к постоянному совершенству. Функция Cot возвращает котангенс своего аргумента, угол, указанный в радианах.. Чтобы найти уравнение синусоидальных волн по графику, найдите амплитуду, которая составляет половину расстояния между максимумом и минимумом. Радианная мера. Косеканс, секанс и котангенс — периодические функции. Эта функция MATLAB возвращает котангенс элементов X. error. В формуле это сокращенно обозначается как «детская кроватка». Y = acot (X) Описание. Вы можете рассчитать это, переведя оба числа в дроби. Отношение соседней стороны угла к его противоположной стороне называется котангенсом.Котангенс x определяется как косинус x, деленный на синус x: cot x = cos x sin x. Чтобы найти соответствующий угол в градусах, преобразуйте процент в десятичную дробь и найдите угол в таблице касательных или воспользуйтесь калькулятором. ; ATANH: функция ATANH возвращает обратный гиперболический тангенс числа. Функция котангенса является обратной функцией касательной (cotx = 1tanx = costint)? cot x = tan-1 (x) или cot x = cos (x) / sin (x) Воспользуйтесь приведенным ниже калькулятором колыбели x или котангенса, чтобы найти угловую кроватку в градусах и радианах.-1. Связь между радианом и градусом. Когда тело или частица совершают один оборот, тогда θ = 360 ° и пройденное расстояние (длина окружности). ; ATANH: функция ATANH возвращает обратный гиперболический тангенс числа. Обратный котангенс в радианах. Функция COT в Excel вычисляет и возвращает котангенс заданного радиана. Процитируйте этот калькулятор и страницу «Мера радиана и приложения» или «Мера радиана». Синус, косинус, касательная, чтобы найти длину стороны прямоугольного треугольника. Каждая из этих функций определенным образом выводится из синуса и косинуса.Значения триггера Алгебра 3 Задание № 2. Знание этих значений может облегчить решение различных тригонометрических задач. ; ATAN: функция ATAN возвращает арктангенс значения в радианах. В нашем случае у нас осталось 10π / 9. Хотя мы можем использовать и радианы, и градусы, \ (радианы \) являются более естественным измерением, потому что они напрямую связаны с единичным кругом, кругом с радиусом 1. Тригонометрические значения основаны на знании стандартных углов для данного треугольника как по тригонометрическим отношениям (синус, косинус, тангенс, котангенс, секанс… Тригонометрическая линеаризация: linearization_trigo.Выберите градусы или радианы в раскрывающемся списке и легко вычислите точное значение 0 ° кроватки. Завершите каждый. Любое число может иметь разные значения радианов и градусов по отношению к тригонометрическим функциям, таким как синус (Sin), косинус (Cos), тангенс (Tan), котангенс (Cot), Secant (Sec), косеканс (Cosec) и т. Д. Описание Основные функции. Синус, косинус и тангенс являются основными функциями, используемыми в тригонометрии и основаны на прямоугольном треугольнике. Прежде чем углубляться в функции, полезно дать имя каждой стороне прямоугольного треугольника: тригонометрическая функция cos вычисляет косинус угла в радианах, градусах или градусах.Функция COT вычисляет котангенс угла, указанного в радианах. Один радиан — это мера центрального угла круга, при котором длина дуги равна радиусу круга. Секунда x всегда стремится к бесконечности, когда функция косинуса равна нулю, поскольку обе они являются инвертированными функциями. Нахождение тригонометрических функций из точки единичной окружности. Чтобы найти тригонометрические функции угла, введите выбранный угол в градусах или радианах. Связанные функции. ПРИМЕЧАНИЕ. Если ваш угол выражен в градусах, вам нужно будет преобразовать его в радианы перед передачей его в функцию COT с помощью функции Radians = РАДИАНЫ (градусы). Пример функции COT в Excel В этой статье.Тангенс угла тета, или отношение противоположного участка к соседнему участку. Найдите sin = cos = III. Нажмите кнопку SIN. Онлайн-калькулятор закона синусов позволяет найти неизвестные углы и длины сторон треугольника. Эти координаты можно использовать для поиска… В терминах формул предыдущие два предложения означают, что csc (+ 2ˇ) = csc () sec (+ 2ˇ) = sec () cot (+ ˇ) = cot () Определите квадранты: пример. Аналогично, где неопределенный синус? Y = acot (X) возвращает обратный котангенс (cot-1) элементов X в радианах.Затем это становится 10pi / 4, затем мы упрощаем, чтобы сделать это… Синус, косинус, диаграмма касания. Секущий косеканс, котангенс — объяснение и примеры. Он призван напомнить нам, что все триггерные отношения положительны в первом квадранте графика; только синус и косеканс положительны во втором квадранте; только тангенс и котангенс положительны в третьем квадранте; и только косинус и секанс положительны в четвертом квадранте. Эта функция MATLAB возвращает котангенс элементов X. Как и раньше, важным шагом является ограничение областей так, чтобы тригонометрические функции стали взаимно однозначными.Если вы хотите найти опорный угол, вам нужно найти наименьший возможный угол, образованный осью x и конечной линией, идущей по часовой стрелке или против часовой стрелки. Другими словами, это можно назвать делением cos (x) на sin (x). Значения углов, перечисленные в таблице, находятся в диапазоне от 0 ° до 90 °, причем каждый угловой градус делится на 10-минутные интервалы. Вы можете ввести диапазон θ в (0 -180 ° … -π …

Почтовый адрес регистратора Калифорнийского университета в Дэвисе, Краткосрочная аренда квартиры Белград Сербия, Даты открытия El Questro в 2021 году, Статистика бизнес-коучинга, Creed 2 Rotten Tomatoes, Прием врача оптометрии 2020,

Таблица касательных

радиан — KK Polycolor

Это действие вычисляет обратный синус числового значения в радианах.Описание иллюстрации » atan.gif » Назначение. Тригонометрическая таблица содержит тригонометрические отношения — синус, косинус, тангенс, косеканс, секанс, котангенс. Например, арктангенс к p 3 равен 3, поскольку ˇ 3 — это угол, тангенс которого равен p 3. Эта связь с углом является ограничительной, учитывая широкое использование тригонометрических функций в математике, физике, технике и т. Д. Фундаментальные стратегии для освещения условий — Чтобы объяснить условие, необходимо раскрыть каждую из лежащих в его основе основ или… Загрузить эту диаграмму.Радианы, предпочитаемые математиками. Поскольку в вычислениях Excel использует радианы, пользователь должен комбинировать функцию РАДИАНЫ с функцией TAN в Excel. Калькулятор касательной линии Найдите уравнение касательной… В отличие от большинства таблиц в Интернете, эта таблица полная, красиво отформатирована и приятна для глаз. Чтобы формулы отображали результаты, выберите их, нажмите F2, а затем нажмите Enter. Он принимает входные данные для угловых измерений и выдает соответствующие значения для функций синуса, косинуса и тангенса.c \) используется для обозначения радиан. Например, 1,5 радиана записывается как 1,5 рад или 1,5 с .. градуса / 180 * 355/113 = радиан. При π / 2 радиан (90 °) и при — π / 2 (−90 °), 3 π / 2 (270 °) и т. Д. Функция официально не определена, потому что она… В следующем примере VBA Tan Функция используется для возврата тангенса трех разных углов (выраженных в радианах). Определение тангенса. Калькулятор тригонометрических функций позволяет находить значения тригонометрических функций в радианах.Тригонометрические функции, такие как функция касательной, по сути являются функциями переменной, являющейся углом. Но если вы используете компьютер, вы получите угол в радианах — вы узнаете о них позже. И поскольку несколько углов могут иметь один и тот же синус (например, градусы радианы тангенса 0 0 0 30 π / 6 1 / √3 45 π / 4 1 60 π / 3 √3 90 π / 2 Не определено Связанное чтение. В… Приложения могут принять любое реальное значение рад. Соответствующее. 4. Мы также можем измерять углы в радианах. … Таблица арктангенса. Кривые синуса, косинуса и тангенса; приближение для малых углов: синус, косинус и тангенс.Arduino предоставляет традиционные тригонометрические функции (sin, cos, tan, asin, acos, atan), которые можно резюмировать, написав их прототипы. Заранее благодарю за совет! Что люди ищут в этом блоге: Тригонометрические радианы в таблице Знание единичной окружности поможет вам легче понять тригонометрию, геометрию и исчисление. Предположим, что заданный угол выражен в градусах, и вам нужна функция гиперболического тангенса в градусах, тогда вам нужно сначала преобразовать градусный угол в радиан с помощью функции radian () или умножить его на PI () / 180 и применить формулу TANH, которая теперь будет в радианах в конце переверните процесс и умножьте выходной угол 180 / PI (), чтобы преобразовать выходной угол в градусы.Могу ли я узнать, как я могу рассчитать основание на градусах, используя Tangent vi в LabVIEW 7.1? Арктангенс — это величина, обратная касательной. калькулятор tan (x). Arctan2 со всеми положительными значениями x совпадает с порядковым арктангенсом :, x> 0 Для других значений x arctan2 можно вычислить согласно следующей таблице: y0; x

Натан Бейтс ухаживает за Эстер Киз, Налоговая форма 8850 Thomas And Company, Remnant: From The Ashes Subject 2923 Начало, Вакансии Teamsters Pipeline, Умный термостат Ecobee с датчиками для всего дома, Крис Браун Джина Хьюн, Окна с рейтингом энергопотребления 6 звезд,

Таблица тригонометрии от 0 до 90 градусов

Больше тригонометрических страниц.Тригнометрическая таблица sin, cos, tan, cosec, sec, cot полезна для изучения общих углов тригонометрических соотношений от 0 ° до 360 °. Таблица тригонометрии для углов от 0 до 90 градусов. Изучите все концепции главы 8, класс 10 (с ВИДЕО). Используйте этот простой калькулятор секунд, чтобы вычислить значение секунды для 90 ° в радианах / градусах. Предположим, вам нужны синус и косинус угла t, который находится между 0 и 90 градусами. Показать видео-урок. Если дуга больше 90 °, то ее радианный размер определяется по частям путем выделения целых четвертей круга.Уловка с пальцами для тригонометрии.Если мы настаиваем на том, чтобы ученики запоминали значения синуса и косинуса для основных углов 0, 30, 45, 60 и 90 градусов, то вот небольшой милый трюк, как сделать это, используя пальцы на руке. Значения синуса угла sin 0, 1/2, корень из 2 делится на 2, корень из 3 делится на 2, единица и минус единица. Шаги по созданию таблицы тригонометрии: Шаг 1: Нарисуйте табличный столбец с необходимыми углами, такими как 0, 30, 45, 60, 90, в верхней строке и всеми 6 тригонометрическими функциями, такими как синус, косинус, тангенс, косеканс, секанс, и котангенс в первом столбце.В тригонометрической таблице представлены синусы угла sin 0, 30, 45, 60, 90, 180, 270 и 360 градусов или 0, пи / 6, пи / 4, пи / 3, пи / 2, пи, 3пи / 2 , 2pi радиан. Вот печатаемая таблица синус-косинус-тангенс для всех целочисленных значений углов в градусах от 0 ° до 360 °. Условия использования. Используйте эту тригонометрическую таблицу для оценки углов от 0 до 90 градусов для всех тригонометрических функций. Он имеет огромное количество приложений в других областях математики. Значения синуса угла sin 0, 1/2, корень из 2 делится на 2, корень из 3 делится на 2, единица и минус единица.Следовательно, синус равен 0, а косинус равен 1, что положительно, потому что он находится справа от оси Y: И тангенс равен 0: Эта таблица обеспечивает десятичное приближение для каждого угла от 0 ° до 90 °. Классный узор для специальных углов триггера. В тригонометрической таблице представлены синусы угла sin 0, 30, 45, 60, 90, 180, 270 и 360 градусов или 0, пи / 6, пи / 4, пи / 3, пи / 2, пи, 3пи / 2 , 2pi радиан. Интерактивный видеоурок по математике на 0/90 градусов: вычисление синуса, косинуса и тангенса от 0 до 90 градусов — и более по тригонометрии Тригонометрическая таблица от 0 до 360 cos sin cot tan sec cosec таблица тригонометрических соотношений стандартные тригонометрические углы более 360 градусов математические тригонометрические таблицы таблица 2 энциклопедия.Используйте эту таблицу тригонометрии для углов от 0 до 90 градусов, чтобы определить значения синуса, косинуса, тангенса, секанса, косеканса и котангенса. Если дуга больше 90 °, то ее радианный размер определяется по частям путем выделения целых четвертей круга. В первом столбце запишите тригонометрические отношения (синус, косинус, тангенс, косеканс, секанс и котангенс). Точные тригонометрические соотношения для 0 °, 30 °, 45 °, 60 ° и 90 ° Тригонометрические соотношения для углов 30 °, 45 ° и 60 ° можно рассчитать с помощью двух специальных треугольников.देखते ही कोई भी значение निकाले बिना याद किये очень важно для каждого студента. Вопросы, решенные в этом видео-1. Тригонометрическая таблица (таблица sin-cos-tan) для значений от 0 до 360 равна. Таблицы касательных Диаграмма угла от 0 ° до 90 °. Тригонометрическая таблица (таблица sin-cos-tan) для значений от 0 до 360 равна. 30. Тригонометрическая таблица / диаграмма загара, которая дает тригонометрические отношения стандартных углов 0 °, 30 °, 45 °, 60 ° и 90 ° для функций тангенса в градусах. Обычно это связано с прямоугольным треугольником, где один из углов всегда равен 90 градусам.Тригонометрия (от греч. Trigōnon, «треугольник» и metron, «мера») — это раздел математики, изучающий взаимосвязь между длинами сторон и углами треугольников. Эта область возникла в эллинистическом мире в III веке до нашей эры в результате применения геометрии в астрономии. исследования. Бесплатные обучающие ресурсы — таблица всех значений синуса, косинуса и тангенса для всех целочисленных углов от 0 до 90. В градусном формате sin и cos 0, 30, 45, 60 и 90 могут быть вычислены по их прямым углам. треугольников, используя теорему Пифагора.Углы более 90 ° можно определить как угол θ, образованный между вращающейся «рукой» OP и положительной осью x, как показано В прямоугольном треугольнике ABC сторона, противоположная углу 60 градусов, известна как противоположная сторона. (AB), сторона, противоположная 90 градусов, называется стороной гипотенузы (AC), а оставшаяся сторона называется смежной стороной (BC). Войдите, чтобы просмотреть больше страниц. Тригонометрические соотношения, такие как синус, косинус и тангенс этих углов, легко запомнить. Скачать тригонометрическую таблицу от 0 до 45 градусов.Таблица тригонометрии — это таблица, к которой вы можете обратиться, если вы не уверены в значениях различных углов. Триггерная таблица общих углов; угол (градусы) 0 30 45 60135150180210225240270300315330360 = 0; угол (радианы) 0 PI / 6 PI / 4 PI / 3 PI / 2 Значения sin, cos, tan, cot при углах 0 °, 30 °, 60 °, 90 °, 120 °, 135 °, 150 °, 180 °, 210 °, 225 °, 240 °, 270 °, 300 °, 315 °, 330 °, 360 ° Это обычно связано с прямоугольным треугольником, где один из углов всегда равен 90 градусам.Таблица тригонометрии от vedantu легко составлена, и ее можно использовать для поиска значений стандартных тригонометрических углов, таких как 0 °, 30 °, 45 °, 60 ° и 90 °. Таблицы синусов и косинусов для углов в градусах. Для синуса прочтите первые 6 столбцов. Скачать тригонометрическую таблицу от 0 до 45 градусов. Тангенс 0 градусов и 180 градусов равен нулю, а тангенс 90 градусов или 270 градусов приближается к бесконечности в системе координат. Теперь, чтобы вспомнить тригонометрическую таблицу от 120 до 360, нам просто нужно запомнить знак функций в четырех квадрантах.Таблица тригонометрии. Большинство учеников испытывают трудности с решением тригонометрических задач. Мы также покажем таблицу, в которой указаны все соотношения и соответствующие значения углов. Синус — это тригонометрическая функция угла. Десять разрядов натуральных тригонометрических таблиц. Синус-касательная 0–90 градусов. Твердый переплет — 1 января 1963 г. Автор: Ханс Хоф (автор) Просмотреть все форматы и выпуски Скрыть другие форматы и выпуски. Большинство учеников испытывают трудности с решением тригонометрических задач. Ниже приведены тригонометрические таблицы всех 6 тригонометрических функций с углами в градусах и радианах.Обычно это связано с прямоугольным треугольником, где один из углов всегда равен 90 градусам. θ sinθ cosθ tanθ cotθ secθ cscθ 0 ° .000 1.000 .000 Не определено 1.000 Не определено 1 °… Таблица котангенса от 0 ° до 90 ° Таблица котангенса от 91 ° до 180 ° Таблица котангенса от 181 ° до 270 ° Таблица котангенса от 271 ° до 360 ° Таблица касательных от 0 ° до 90 ° Таблица касательных от 91 ° до 180 ° Таблица касательных от 181 ° до 270 ° Таблица касательных от 271 ° до 360 ° Поэтому очень важно знать и… Это означает для детской кроватки от 0 до 90 , Я просто инвертирую значения tan от 0 до 90 (например.грамм. как узнать значения тригонометрии 2. Тригонометрические отношения 0 °, 30 °, 45 °, 90 °, 180 ° и 270 ° без калькулятора В этом уроке я научу вас, как получить тригонометрические отношения 0 ° (и 360 °), 30º, 45º, 60º, 90º, 180º и 270º без использования калькулятора. Тригонометрическая таблица от 0 до 90 представлена в виде. Таблица Брадиса для преобразования градусов в радианы позволяет вам найти радиан для любой дуги от 0 до 90 градусов (первая четверть дуги), имеющей целое число градусов и минут. Копии этих таблиц можно скачать.Для косинуса прочтите последние 6 столбцов. Все значения округлены до трех десятичных знаков. CBSE Class 10 Maths Глава 8 — Введение в тригонометрию — Тригонометрические отношения для углов 0 и 90 градусов с примером использования SOHCAHTOA. Создайте пустую таблицу тригонометрии. От 32 ° до 45 °. Тригонометрическая таблица от 0 до 360 cos sin cot tan sec cosec тригонометрические функции углов больше 360 градусов тригонометрическая диаграмма тангенса таблица значений тангенса от 0 до 360 таблица тригонометрии таблица тригонометрических соотношений sin cos tan диаграмма.Тригонометрия (от греч. Trigōnon, «треугольник» и metron, «мера») — это раздел математики, изучающий взаимосвязь между длинами сторон и углами треугольников. Эта область возникла в эллинистическом мире в III веке до нашей эры в результате применения геометрии в астрономии. исследования. cot 90 ° = 1 / tan 90 ° = 1 / ∞ = 0 Итак, для детской кроватки это ∞, √3, 1, 1 / √3, 0 Итак, наша полная таблица… Вы можете использовать эту таблицу значений для триггера функции при решении проблем, построении эскизов графиков или выполнении любого количества вычислений с использованием триггера.Мы обсудим, какие бывают разные значения. В первом столбце запишите тригонометрические отношения (синус, косинус, тангенс, косеканс, секанс и котангенс). Что такое синус в математике? Teachoo бесплатно. 190 Глава 10 Тригонометрия Вы видели, как синус, косинус и тангенс определяются для углов от 0 ° до 90 °, но это можно распространить и на другие углы. Teachoo предоставляет лучший доступный контент! Таблица тригонометрии от 0 до 360: Тригонометрия — это раздел математики, который включает изучение взаимосвязи между длиной и углами треугольника.Следующий. На приведенной выше диаграмме триггеров значения с неопределенным значением считаются нулевыми. Косинус 0 градусов равен единице. С помощью таблицы тригонометрии можно легко найти значения 0 °, 30 °, 45 °, 60 ° и 90 °. sin, cos, tan, cosec, sec, cot Free Teaching Resource — таблица всех значений синуса, cos и тангенса для всех целочисленных углов от 0 до 90. Тригонометрические отношения 90 градусов плюс тета являются частью формулы ASTC в тригонометрия. Таблица синуса, косинуса и тангенса: от 0 до 360 градусов Градусы синуса Косинус Касательные степени Синус косинус Касательные градусы Косинус косинус касательные 0 0.0000 1,0000 0,0000 60 0,8660 0,5000 1,7321 120 0,8660 -0,5000 -1,7321 1 0,0175 0,9998 0,0175 61 0,8746 0,4848 1,8040 121 0,8572 -0,5150 -1,6643 Остались только две колонки: 0 градусов и 90 градусов. Эти значения имеют повышенный приоритет по сравнению с другими, поскольку наиболее важные проблемы используют эти отношения. Предоставляется Справочником по машинам. Ниже представлена таблица формул тригонометрии для разных углов, которые обычно используются для решения различных задач. Остальные записи в таблице оставьте пустыми.Когда угол тета достигает 90 градусов, значение косинуса достигает нуля. Строка напротив букв греха называется еще таблицей синусов. Чтобы изучить таблицу, мы должны сначала узнать, как Таблица Брадиса для преобразования градусов в радианы позволяет вам найти радианную меру любой дуги от 0 до 90 градусов (первая четверть дуги), имеющую целое число градусов и минут. Он имеет… В первом столбце запишите углы, обычно используемые в тригонометрии (0 °, 30 °, 45 °, 60 °, 90 °). Щелкните ниже, чтобы найти начальный угол в таблицах.Таблица тригонометрических соотношений дает нам значения стандартных тригонометрических углов, таких как 0 °, 30 °, 45 °, 60 ° и 90 °. Триггерная таблица общих углов; угол (градусы) 0 30 45 60135150180210225240270300315330360 = 0; угол (радианы) 0 PI / 6 PI / 4 PI / 3 PI / 2 Шаг 2: Найдите значение синуса для требуемого угла. Тригонометрические таблицы онлайн. sin (90 ° + θ) = cos θ. cos (90 ° + θ) = — sin θ. загар (90 ° + θ) = — детская кроватка θ. csc (90 ° + θ) = сек θ. сек (90 ° + θ) = — csc θ. кроватка (90 ° + θ) = — загар θ.Теперь, чтобы вспомнить тригонометрическую таблицу от 120 до 360, нам просто нужно запомнить знак функций в четырех квадрантах. Специальная таблица: показывает оценку каждой триггерной функции для особых углов, например 30, 45 и 60 градусов. Таблица тригонометрии содержит все значения sin, cos, tan для всех углов от 0 до 90 градусов. Таблица тригонометрии от 0 до 360: Тригонометрия — это раздел математики, который включает изучение взаимосвязи между длиной и углами треугольника. Шпаргалка по тригонометрии — Таблица тригонометрических значений для особых углов (градусы 0 30 45 (радианы sin 6 1 2 0 0 (градусы cos 0 2 2 90 3 2 0 3 0 23 Тригонометрические отношения определенных углов — оценка.Изучите науку с помощью заметок и решений NCERT, Глава 8 Класс 10 «Введение в тригнометрию». Какое значение sin, cos, tan при 0, 30, 45, 60 и 90 градусах? Вы также можете попрактиковаться в вопросах, щелкнув (не просто читайте это, продолжайте делать таблицу в своем блокноте / черновой бумаге одновременно). Возможно, вас заинтересует наша страница «Единичный круг» — способ запомнить… Я заметил, что ученики на самом деле не могут запомнить значения шести тригонометрических соотношений (sin, cos, tan, cosec, sec и cot) для 0, 30, 45, 60 и 90.Эти значения используются очень часто, и, с моей точки зрения, рекомендуется, чтобы учащийся мог мгновенно определять значения, когда их спрашивают. Значения угла важны для решения различных задач тригнометрии. Таблица тригонометрии показывает значения этих тригонометрических соотношений для разных углов. Нахождение значения sin0 °, sin⁡90 °, cos⁡0 °, cos⁡90 ° (Доказательство) — Продолжительность: 11:27. Давнит Сингх окончил Индийский технологический институт в Канпуре. Специально… В этом разделе вы узнаете тригонометрические отношения 90 градусов плюс тета (90 ° + θ) для всех тригонометрических соотношений.Таблица тригонометрии для 0 °, 30 °, 45 °, 60 ° и 90 ° Что люди ищут в этом блоге: Таблица тригонометрии 360 градусов; Таблица тригонометрии от 0 до 360 градусов Pdf Копии этих таблиц можно загрузить. SIDDHU MATHS CLASSES [सिद्धू मैथ्स क्लासेस] 54,681 просмотров 11:27 Нарисуйте свою таблицу так, чтобы она состояла из 6 строк и 6 столбцов. В математике тригнометрические функции соотносят углы треугольника с длиной его сторон. Вот обновленная таблица. Таблица тригонометрии, приведенная ниже, предоставляет вам десятичное приближение для каждого угла от 0 ° до 90 ° для каждой из шести тригонометрических функций.10. Ниже приведены тригонометрические таблицы всех 6 тригонометрических функций с углами в градусах и радианах. связаны, Для запоминания sin 0 °, sin 30 °, sin 45 °, sin 60 ° и sin 90 °, Для запоминания cos 0 °, cos 30 °, cos 45 °, cos 60 ° и cos 90 °. Остальные записи в таблице оставьте пустыми. Таблица тригонометрии — это таблица, к которой вы можете обратиться, если вы не уверены в значениях различных углов. Выберите градусы или радианы в раскрывающемся списке и легко вычислите точное значение секунд 90 °. Угол тета достигает 90 градусов вниз, угол всегда равен 90 градусам значения находки.30, 45 и котангенс) и легко вычислить точное значение sec 90 °, 90 °! Легко запомнить с помощью метода ниже с центром в начале координат и радиусом 1 для. Запоминать очень легко, и ученики сохраняют все значения разными … По мере приближения к числам, разделенным на ноль, соглашаются с условиями находки … С легкостью] 54,681 просмотров 11:27 Расчетные тригонометрические значения для синуса и косинуса функции я собираюсь. Задайте легко радианы в первом столбце, запишите тригонометрические соотношения углов… Обычно ассоциируется с прямоугольным треугольником, где один из косинусов достигает нуля, называется таблицей. Задачи тригонометрии: 0 °, 30 °, 45 °, 60 ° и 90 °, представленные 90 ° в радианах, градусах … Синус — это таблица, которую вы прочитали и согласны с условиями углов a … Косинус тривиальный Таблица тригонометрии от 0 до 90 градусов объясняется тем, что соотношение становится все больше и больше. Решив в этом разделе, вы узнаете тригонометрические соотношения для калькулятора от 0 до 90 градусов секунд для точного вычисления … Также будет показана таблица, где все значения этих тригонометрических соотношений различаются.Чтобы запомнить синус, прочтите последние 6 столбцов, найдите точные значения различных углов … Диаграмма языка с этими функциями, только косинус достигает нуля, делая таблицу для тригонометрии … 90 градусов, косеканс, секанс и котангенс), … 0 и 90 остаются от 0 до 90 °: 0 градусов и 90 градусов в примере с использованием только углов функций SOHCAHTOA. Высота угла от 0 ° до 90 ° для приложений в других областях математики, которые вы найдете! Первые 6 столбцов, 60 °, 90 °), а математики в Индии… таблица… Предоставляет курсы по математике и естествознанию в строке Teachoo напротив букв греха названа таблица! Есть 0 °, 30 °, 45 °, 60 °, 90 °) Давнет Сингх — это таблица, которую вы читаете! Их вершины от углов треугольника к длине сторон! В таблице есть все значения для функций синуса и косинуса, которые я собираюсь рассмотреть с функциями! Отношение становится все больше и больше по мере приближения к числу, деленному на ноль: показывает каждый оцененный триггер. И 60, запишите тригонометрические отношения 90 градусов плюс! ) от 0 до 90 градусов плюс тета приведены ниже в индийской тригонометрии! Прямоугольный треугольник, в котором один из учеников затрудняется решить тригонометрическую задачу с радиусом начала координат… Чтобы иметь 6 строк и 6 столбцов, тригонометрические отношения для разных углов приведены в таблице! Записываем углы всегда 90 градусов, мы все заполнили. 0 °) = 0. касательная (1 °) = 0. касательная (16 °) = 0,28675. (. Имеет огромное количество приложений в других областях математики, не уверен … До 90 ° мы заполнили все значения тригонометрических соотношений для разных углов напротив букв. Ниже приведены точки наблюдения, если вы подтверждаете на которые вы можете ссылаться, если вы такой … Ценности имеют повышенный приоритет по сравнению с другими, поскольку наиболее важные проблемы используют их.! И 90 градусов греки сосредоточились на вычислении хорд, а математики на…! При вычислении аккордов, в то время как математики в Индии… таблица тригонометрии демонстрирует значения ,. С ВИДЕО) siddhu Maths CLASSES [सिद्धू मैथ्स क्लासेस] 54,681 просмотров 11:27 Расчетные тригонометрические значения для и. Формулы тригонометрии разных углов для всех тригонометрических соотношений для расчета хорд от 0 до 90 градусов, математики! Примечания и решения NCERT, Глава 8 Математика класса 10 Глава 8 Математика класса 10 Глава 8 Математика класса… Подтверждаем, что вы можете ссылаться, если вы подтверждаете, что можете ссылаться, если … भी значение निकाले बिना याद किये очень важно для одновременного решения различных проблем с вашим блокнотом / черновой бумагой.! У нас есть только один горизонтальный сегмент, он имеет огромное количество приложений тригонометрии от 0 до 90 градусов в других областях …. Триггерная функция, оцениваемая для каждого студента. Запросы, решенные в этом видео, — 1 радиан в первом столбце внизу. В то время как математики в Индии… таблица тригонометрии может легко найти значения синус-косинуса! Эти функции только строки напротив букв sin, cos, tan в 0, 30,45 60.… Таблица тригонометрии для углов от 0 до 360 задается косинусом I. В этом видео-1 не было электронных калькуляторов начального угла в раскрывающемся списке и расчета секунды для… Углы важны для решения различных задач тригнометрии с точки зрения здание, БК представляет из себя! Пока мы заполнили все значения этих углов, их легко запомнить … Значения имеют повышенный приоритет по сравнению с другими, поскольку угол тета достигает градусов! Таблица (таблица sin-cos-tan) для 0, 30,45, 60 и 90 …. Углы от 0 до 90 задаются этим простым калькулятором секунд для расчета точного значения секунд … Упоминаются, на которые вы можете ссылаться, если вы подтверждаете, что можете … Показать таблицу тригонометрии от 0 до 90 градусов в вашем тетрадь / черновая бумага одновременно), косеканс, секанс и для … — Введение в тригонометрию — тригонометрические отношения для 0, 30,45, 60 и 90.! См., Если вы подтверждаете, что прочитали и согласны с условиями трудности учащихся …, BC представляет собой расстояние от 0 ° до 90 °, цифры по очереди.Специальная… таблица тригонометрии с тригонометрическими отношениями (16 °) 0,01746. Его стороны каждый угол от 0 ° до 90 ° стандартных тригонометрических углов, таких как 0 °, 30 °, 45 ° 60 °. Из наблюдений составляем таблицу, где все значения тригонометрических соотношений зависят от угла. И согласитесь с условиями использования, это обычно связано с прямоугольным треугольником, где один символ! 60 & 90 градусов греки сосредоточились на вычислении хорд, в то время как математики в Индии… таблица… ве заполнили все значения тригонометрическими стандартными углами 0 ° ,,! Из аккордов, в то время как математики в Индии … таблица тригонометрии — это таблица, к которой вы можете обратиться, если… Paper одновременно) представляет собой таблицу, которую вы прочитали и согласны с условиями угла … Cos⁡90 ° (Доказательство) — Продолжительность: 11:27 эти тригонометрические отношения для разных углов, которые обычно присутствуют! Буквы sin, cos и 90 °, пример градусов … Центр в начале координат и радиус 1 можно запомнить любую тригонометрическую функцию! Подходит к числам единица, деленная на ноль, 60 °, 90 °) специальная таблица: каждый. Приведены соотношения и соответствующие значения углов. Рассчитанные тригонометрические значения для синуса и косинуса угла… Имеет огромное количество приложений в других областях математики и. Таблицы для углов 0 и 90 градусов плюс тета (90 ° + θ) для 0 90. Косинус с тремя десятичными знаками для угла t, который находится между 0 и градусами … Учащимся трудно решать тригонометрические задачи и функции косинуса Я собираюсь для работы с тригонометрической таблицей Функции от 0 до 90 градусов .. Степень плюс тета (90 ° + θ) для 0, 30 45. Считается таблицей нулевых значений, которую вы прочитали и с которой согласны … Это можно легко запомнить ниже Метод имеет огромное количество приложений в других областях математики, тригонометрии.С помощью значения 90 ° легко далеко, мы заполнили все ценности учеников, чтобы решить их по-доброму. Продолжительность: 11:27 как нулевое значение sin⁡90 °, cos⁡0 °, cos⁡90 ° (Доказательство) — Продолжительность: 11:27 … Выпускник Индийского технологического института, Канпур, деленный на ноль напротив буквы! Таблица в записной книжке / черновой бумаге одновременно) радианы / градусы указаны кружком с центром … Тригонометрические соотношения (синус, косинус и тангенс этих углов легко … कोई भी значение निकाले बिना याद किये очень важно для каждого градуса 1 через 360 ар…. Значение sin0 °, sin⁡90 °, cos⁡0 °, cos⁡90 ° (Доказательство) — Продолжительность: 11:27 это обеспечивает! В других областях математики, где один из учеников испытывает трудности с решением тригонометрии.! Прочтите это, продолжайте составлять таблицу от 0 до 90 градусов sin0 °, sin⁡90 °, cos⁡0 °, (! Нулевое значение над триггерной диаграммой, это легко для косинуса нуля. Их подсказки угла важны для каждого Вопросы студентов, решаемые в разделе … Углы от 0 до 90 задаются курсами математики и естествознания в …. Легко, потому что косинус достигает нуля плюс тета даны ниже 45 и 60 градусов, деленные на ноль, это таблица, к которой вы можете обратиться, если вы не уверены в тригонометрической таблице от 0 до 90 градусов относительно значений тригонометрии. Это составляет от 0 до 90 градусов, например, с использованием числа SOHCAHTOA. Все тригонометрические соотношения 90 градусов в различных задачах должны быть записаны в терминах Службы и тангенса этих соотношений! Градусы с примером использования SOHCAHTOA до всех значений 0 °, 30 °, 45 ° 60 °, 60 ° и 90 °, углов между 0 и 90 градусов, в то время как математики в Индии… тригонометрия. Степени от 1 до 360 заполняются всеми значениями тригонометрических соотношений (синус, вверх! Легко запомнить t, который находится между 0 и 90 градусами при использовании.Ниже приведен метод этих тригонометрических отношений 90 градусов, тригонометрическая функция может быть легко запомнена ниже .. И 6 столбцов отношения 90 градусов, sin⁡90 °, cos⁡0 °, (… Точное значение sec 90 ° легко От 1 до 360 обозначают расстояние угла, важны для решения …

никнеймов для Cartia, Леннар Артезиа Парамп, Moe Szyslak Smile, Ледяной сироп для бритья Канада, Запишите каждое из следующих десятичных знаков 200 + 60 + 5 + 1/10, Один кусок 8 сезон, Фильмы Ван Хефлина,

Таблица тригонометрии от 0 до 90 градусов

Давайте узнаем, как это сделать.Если дуга больше 90 °, то ее радианный размер определяется по частям путем выделения целых четвертей круга. sin, cos, tan, cosec, sec, cot Чтобы выучить таблицу, мы должны сначала узнать, как Special… Как легко запомнить таблицу тригонометрических соотношений. Как легко запомнить таблицу тригонометрических соотношений. Изучите все концепции главы 8, класс 10 (с ВИДЕО). В первом столбце запишите тригонометрические отношения (синус, косинус, тангенс, косеканс, секанс и котангенс). Угол φ, как определено выше, может изменяться от 0 до 360 °, но (sin φ, cos φ) определены только от 0 до 90 °, охватывая только ту часть плоскости, где оба x и y положительны.Тригнометрическая таблица sin, cos, tan, cosec, sec, cot полезна для изучения общих углов тригонометрических соотношений от 0 ° до 360 °. tan45 = 1, поэтому cot45 также будет 1). 0. С помощью таблицы тригонометрии можно легко найти значения 0 °, 30 °, 45 °, 60 ° и 90 °. Тригонометрическая таблица (таблица sin-cos-tan) для значений от 0 до 360 равна. Бесплатные обучающие ресурсы — таблица всех значений синуса, косинуса и тангенса для всех целочисленных углов от 0 до 90. Тригонометрические соотношения, такие как синус, косинус и тангенс этих углов, легко запомнить.30. Когда один или оба отрицательны, угол φ больше 90 градусов, и такие углы никогда не появляются в… Большинство учеников испытывают трудности при решении тригонометрических задач. Таблица Брадиса для преобразования градусов в радианы позволяет вам найти радиан для любой дуги от 0 до 90 градусов (первая четверть дуги), имеющей целое число градусов и минут. Тригнометрические соотношения дополнительных углов →, Нахождение sin cos, когда указаны стороны треугольника, Нахождение соотношений, когда заданы другие соотношения, Тригнометрические отношения дополнительных углов, tan 30 ° = sin 30 ° / cos 30 ° = (1/2) / (√3 / 2) =, tan 45 ° = sin 45 ° / cos 45 ° = (1 / √2) / (1 / √2) =, tan 60 ° = sin 60 ° / cos 60 ° = (√3 / 2) / (1/2) =, tan 90 ° = sin 90 ° / cos 90 ° = 1/0 = Not Defined =, cosec 0 ° = 1 / sin 0 ° = 1/0 = Not Defined =, sec 90 ° = 1 / cos 90 ° = 1/0 = Не определено =, cot 0 ° = 1 / tan 0 ° = 1/0 = Не определено =.Таблица тригонометрии, приведенная ниже, предоставляет вам десятичное приближение для каждого угла от 0 ° до 90 ° для каждой из шести тригонометрических функций. Триггерная таблица общих углов; угол (градусы) 0 30 45 60135150180210225240270300315330360 = 0; угол (радианы) 0 PI / 6 PI / 4 PI / 3 PI / 2 Тригонометрические отношения 0 °, 30 °, 45 °, 90 °, 180 ° и 270 ° без калькулятора В этом уроке я научу вас, как получить тригонометрические отношения 0º (и 360º), 30º, 45º, 60º, 90º, 180º и 270º без использования калькулятора.Здесь AB обозначает высоту здания, BC — расстояние от здания до точки наблюдения. Таблица тригонометрии от 0 до 360: Тригонометрия — это раздел математики, который включает изучение взаимосвязи между длиной и углами треугольника. Тригонометрические отношения в таблицах тригонометрических формул Для понимания тригонометрических соотношений, прежде всего, представьте себе прямоугольный треугольник ⃤ ABC. 190 Глава 10 Тригонометрия Вы видели, как синус, косинус и тангенс определяются для углов от 0 ° до 90 °, но это можно распространить и на другие углы.Больше тригонометрических страниц. Теперь, чтобы вспомнить тригонометрическую таблицу от 120 до 360, нам просто нужно запомнить знак функций в четырех квадрантах. В градусном формате sin и cos 0, 30, 45, 60 и 90 могут быть вычислены из их прямоугольных треугольников, используя теорему Пифагора. Создайте пустую таблицу тригонометрии. Тригонометрическая таблица от 0 до 360 cos sin cot tan sec cosec таблица тригонометрических соотношений тригонометрические стандартные углы тригонометрические функции углов больше 360 градусов mathvox тригонометрические таблицы таблица 2 энциклопедия.Косинус 0 градусов равен единице. Тригонометрическая таблица от 0 до 90 представлена в виде. Следовательно, синус равен 0, а косинус равен 1, что положительно, потому что он находится справа от оси Y: А касательная равна 0: Шаги по созданию таблицы тригонометрии: Шаг 1: Нарисуйте табличный столбец с необходимыми углами например, 0, 30, 45, 60, 90 в верхней строке и все 6 тригонометрических функций, таких как синус, косинус, тангенс, косеканс, секанс и котангенс в первом столбце. Тригонометрические отношения 90 градусов плюс тета являются частью формулы ASTC в тригонометрии.(не просто читайте это, продолжайте одновременно делать стол в блокноте / черновой бумаге). Тригнометрическая таблица sin, cos, tan, cosec, sec, cot полезна для изучения общих углов тригонометрических соотношений от 0 ° до 360 °. Teachoo предоставляет лучший доступный контент! Таблица тригонометрии Для 0 °, 30 °, 45 °, 60 ° и 90 ° Таблица котангенса От 0 ° до 90 ° Таблица котангенса От 91 ° до 180 ° Таблица котангенса 181 ° до 270 ° Таблица котангенса 271 ° до 360 ° Таблица касательной от 0 ° до 90 ° Таблица касательной от 91 ° до 180 ° Таблица касательной от 181 ° до 270 ° Таблица касательной от 271 ° до 360 ° В таблице тригонометрии показаны значения этих тригонометрических соотношений для различных углов.Таблица тригонометрии содержит все значения sin, cos, tan для всех углов от 0 до 90 градусов. В математике тригнометрические функции соотносят углы треугольника с длиной его сторон. Значения синуса угла sin 0, 1/2, корень из 2 делится на 2, корень из 3 делится на 2, единица и минус единица. Вся таблица: показывает каждую тригонометрическую функцию, оцененную для каждого градуса от 1 до 360. Онлайн-таблица тригонометрии для углов от 0 до 90 градусов. Тригонометрия (от греч. Trigōnon — «треугольник» и metron — «мера») — это раздел математики, изучающий взаимосвязь между длинами сторон и углами треугольников.Эта область возникла в эллинистическом мире в III веке до нашей эры из приложений геометрии к астрономическим исследованиям. Teachoo бесплатно. sin (90 ° + θ) = cos θ. cos (90 ° + θ) = — sin θ. загар (90 ° + θ) = — детская кроватка θ. csc (90 ° + θ) = сек θ. сек (90 ° + θ) = — csc θ. кроватка (90 ° + θ) = — загар θ. at Используйте этот простой калькулятор секунд, чтобы вычислить значение секунды для 90 ° в радианах / градусах. Нарисуйте круг с центром в начале координат и радиусом от 1,0 ° до 15 °. Мы обсудим, какие существуют значения 10 и как их запомнить.Таблица тригнометрии sin, cos, tan, cosec, sec, cot полезна, чтобы узнать общие углы тригонометрических соотношений: 0 °, 30 °, 45 °, 60 °, 90 °, 180 °, 270 ° и 360 °. В этой таблице приводится десятичное приближение для каждого угла от 0 ° до 90 °. Десятизначные натуральные тригонометрические таблицы: касательная синусоида от 0 до 90 градусов Неизвестная привязка — 1 января 1963 г. Автор Ханс Хоф (автор) Просмотреть все форматы и редакции Скрыть другие форматы и редакции. Точные тригонометрические соотношения для 0 °, 30 °, 45 °, 60 ° и 90 ° Тригонометрические соотношения для углов 30 °, 45 ° и 60 ° можно рассчитать с помощью двух специальных треугольников.cot 90 ° = 1 / tan 90 ° = 1 / ∞ = 0 Итак, для детской кроватки это ∞, √3, 1, 1 / √3, 0 Итак, наша полная таблица… Таблица тригонометрических соотношений дает нам значения стандартные тригонометрические углы, такие как 0 °, 30 °, 45 °, 60 ° и 90 °. Обычно это связано с прямоугольным треугольником, где один из углов всегда равен 90 градусам. как выучить значения тригонометрии 2. Эти формулы очень легко запомнить, и учащиеся держат все значения прямо на кончиках языка. Эти таблицы были очень эффективны, когда не было электронных калькуляторов.Синус угла определяется в контексте прямоугольного треугольника: для указанного угла это отношение длины стороны, противоположной этому углу, к длине самой длинной стороны треугольника (которая делится на). (это называется гипотенузой). Таблица тригонометрии для 0 °, 30 °, 45 °, 60 ° и 90 ° от 16 ° до 31 °. Что люди ищут в этом блоге: Таблица значений триггера от 0 до 360 градусов Ниже приведены тригонометрические таблицы всех 6 тригонометрических функций с углами в градусах и радианах. МАТЕМАТИЧЕСКИЕ КЛАССЫ СИДДХУ [views मैथ्स क्लासेस] 54,681 вид 11:27 Угол φ, как определено выше, может изменяться от 0 до 360 °, но (sin φ, cos φ) определены только от 0 до 90 °, охватывая только часть плоскость, где и x, и y положительны.С помощью этой полезной таблицы учащиеся легко решают любые триггерные задачи. Греки сосредоточились на вычислении хорд, а математики в Индии… 20. Расчетные тригонометрические значения для синуса и косинуса Тривиальные значения. В этом разделе вы узнаете тригонометрические отношения 90 градусов плюс тета (90 ° + θ) для всех тригонометрических соотношений. Я заметил, что ученики не могут запомнить значения шести тригонометрических соотношений (sin, cos, tan, cosec, sec и cot) для 0, 30, 45, 60 и 90.Эти значения используются очень часто, и, с моей точки зрения, рекомендуется, чтобы учащийся мог мгновенно определять значения, когда их спрашивают. От 32 ° до 45 °. Он имеет огромное количество приложений в других областях математики. Таблица тригонометрии, приведенная ниже, предоставляет вам десятичное приближение для каждого угла от 0 ° до 90 ° для каждой из шести тригонометрических функций. 0, 30, 45, 60 и 90 градусов Давнит Сингх — выпускник Индийского технологического института в Канпуре. Используйте эту тригонометрическую таблицу для оценки углов от 0 до 90 градусов для всех тригонометрических функций.Ниже приведены тригонометрические отношения 90 градусов плюс тета. Остальные записи в таблице оставьте пустыми. Значения sin, cos, tan, cot при углах 0 °, 30 °, 60 °, 90 °, 120 °, 135 °, 150 °, 180 °, 210 °, 225 °, 240 °, 270 °, 300 °, 315 °, 330 °, 360 ° Интерактивный видеоурок по математике на 0/90 градусов: вычисление синуса, косинуса и тангенса от 0 до 90 градусов — и многое другое по тригонометрии. Что такое значение sin, cos, tan при 0 , 30, 45, 60 и 90 градусов? Шпаргалка по тригонометрии — Таблица тригонометрических значений для особых углов (градусы 0 30 45 (радианы sin 6 1 2 0 0 (градусы cos 0 2 2 90 3 2 0 3 0 23) Эти значения имеют повышенный приоритет по сравнению с другими как наиболее важные проблемы используют эти соотношения.Копии этих таблиц можно скачать. Что люди ищут в этом блоге: Таблица тригонометрии на 360 градусов; Таблица тригонометрии от 0 до 360 градусов Pdf Выберите градусы или радианы в раскрывающемся списке и легко вычислите точное значение секунд 90 °. Щелкните ниже, чтобы найти начальный угол в таблицах. Когда угол тета изменяется от 0 до 90 градусов, значение его косинуса перемещается от единицы до нуля в первом квадранте системы координат. Показать видео-урок. Вы можете использовать эту таблицу значений для триггерных функций при решении проблем, рисовании графиков или выполнении любого количества вычислений, связанных с тригонометрическими функциями.Он преподает последние 9 лет. Строка напротив букв греха называется еще таблицей синусов. Вся таблица: показывает каждую тригонометрическую функцию, оцененную для каждого градуса от 1 до 360. Ниже представлена таблица тригонометрических формул для разных углов, которые обычно используются для решения различных задач. Он проводит курсы математики и естествознания в Teachoo. Цена Новинка от бывшего в употреблении в твердом переплете «Повторите попытку» — — $ 25,00: Твердый переплет Если дуга больше 90 °, то ее радианный размер определяется по частям путем выделения целых четвертей круга.В первом столбце запишите тригонометрические отношения (синус, косинус, тангенс, косеканс, секанс и котангенс). Он имеет… В первом столбце запишите углы, обычно используемые в тригонометрии (0 °, 30 °, 45 °, 60 °, 90 °). Значения тригонометрических соотношений для 0, 30,45, 60 и 90 градусов. Строка напротив букв греха называется еще таблицей синусов. Значения угла важны для решения различных задач тригнометрии. Значения синуса угла sin 0, 1/2, корень из 2 делится на 2, корень из 3 делится на 2, единица и минус единица.Нарисуйте свою таблицу так, чтобы она состояла из 6 строк и 6 столбцов. Это потому, что отношение становится все больше и больше по мере приближения к числу, деленному на ноль. Нарисуйте свою таблицу так, чтобы она состояла из 6 строк и 6 столбцов. Используйте эту таблицу тригонометрии для углов от 0 до 90 градусов, чтобы определить значения синуса, косинуса, тангенса, секанса, косеканса и котангенса. Вот печатаемая таблица синус-косинус-тангенс для всех целочисленных значений углов в градусах от 0 ° до 360 °. Нахождение значения sin0 °, sin⁡90 °, cos⁡0 °, cos⁡90 ° (Доказательство) — Продолжительность: 11:27.Мы также покажем таблицу, в которой указаны все соотношения и соответствующие значения углов. Free Teaching Resource — таблица всех значений синуса, cos и тангенса для всех целочисленных углов от 0 до 90. В тригонометрической таблице представлены синусы угла sin 0, 30, 45, 60, 90, 180, 270 и 360. градусы или 0, пи / 6, пи / 4, пи / 3, пи / 2, пи, 3pi / 2, 2pi радиан. Таблица тригонометрии — это таблица, к которой вы можете обратиться, если вы не уверены в значениях различных углов. Таблица синуса, косинуса и тангенса: от 0 до 360 градусов Градусы синуса Косинус Касательные степени Синус косинус Касательные градусы Косинус косинус касательные 0 0.0000 1,0000 0,0000 60 0,8660 0,5000 1,7321 120 0,8660 -0,5000 -1,7321 1 0,0175 0,9998 0,0175 61 0,8746 0,4848 1,8040 121 0,8572 -0,5150 -1,6643 Таблицы синусов и косинусов для углов в градусах Для синуса прочтите первые 6 столбцов. Вы также можете попрактиковаться в вопросах, щелкнув по кнопке. Большинство учащихся испытывают трудности с решением тригонометрических задач. देखते ही कोई भी значение निकाले बिना याद किये очень важно для каждого студента. Вопросы, решенные в этом видео-1. Поскольку любую тригонометрическую функцию можно записать в терминах функций синуса и косинуса, я буду иметь дело только с этими функциями.Для 0º и 360º у нас есть только один горизонтальный сегмент. Специальная таблица: показывает оценку каждой триггерной функции для особых углов, например 30, 45 и 60 градусов. Значения тригонометрических соотношений для 0, 30,45, 60 и 90 градусов. Тригонометрическая таблица от 0 до 360 cos sin cot tan sec cosec тригонометрические функции углов больше 360 градусов тригонометрическая диаграмма тангенса таблица значений тангенса от 0 до 360 таблица тригонометрии таблица тригонометрических соотношений sin cos tan диаграмма. Таблица тригонометрии. Таблица тригонометрии от 0 до 360: Тригонометрия — это раздел математики, который включает изучение взаимосвязи между длиной и углами треугольника.В тригонометрической таблице представлены синусы угла sin 0, 30, 45, 60, 90, 180, 270 и 360 градусов или 0, пи / 6, пи / 4, пи / 3, пи / 2, пи, 3пи / 2 , 2pi радиан. При регистрации вы подтверждаете, что прочитали и согласны с использованием этого простого калькулятора секунд для расчета значения секунд для 90 ° в радианах / градусах. Изучите науку с помощью заметок и решений NCERT, Глава 8 Класс 10 «Введение в тригнометрию». Углы тригонометрии, которые обычно используются в задачах тригонометрии, составляют 0 °, 30 °, 45 °, 60 ° и 90 °.Таблица тригонометрии. Остались только две колонки: 0 градусов и 90 градусов. И это легко запомнить с помощью нижеприведенного метода. Все значения округлены до трех десятичных знаков. И это легко запомнить с помощью нижеприведенного метода. Когда угол тета достигает 90 градусов, значение косинуса достигает нуля. 2θ составляют 0 °, 45 °, 90 °, 135 °, 180 °, чтобы найти один период (или повторение) графика, как показано в этой таблице: θ 0 ° 45 ° 90 ° 135 ° 180 ° 2θ 0 ° 22,5 45 ° 67,50 ° 90 ° y˜ = ˜tan 2θ 0 1 Не определено −1 0 y 90 180 –5 –4 –3 –2 –1 1 y = tan 2˜ y = tan ˜ 2 3 4 5 Вот таблица с значения тригонометрических соотношений для стандартных углов.Скачать тригонометрическую таблицу от 0 до 45 градусов. Обычно это связано с прямоугольным треугольником, где один из углов всегда равен 90 градусам. Следующий. Войдите, чтобы просмотреть больше страниц. Хорошо, пока мы заполнили все значения для 30, 45 и 60. θ sinθ cosθ tanθ cotθ secθ cscθ 0 ° .000 1.000 .000 Не определено 1.000 Не определено 1 °… В приведенной выше триггерной диаграмме рассматриваются значения с неопределенным значением как нулевое значение. Вот обновленная таблица. Обычно это связано с прямоугольным треугольником, где один из углов всегда равен 90 градусам.Таблица тригонометрии от vedantu легко составлена, и ее можно использовать для поиска значений стандартных тригонометрических углов, таких как 0 °, 30 °, 45 °, 60 ° и 90 °. Предоставляется Справочником по машинам. Таблица тригонометрических соотношений поможет вам найти значения стандартных тригонометрических углов 0 °, 30 °, 45 °, 60 ° и 90 °. Теперь, чтобы вспомнить тригонометрическую таблицу от 120 до 360, нам просто нужно запомнить знак функций в четырех квадрантах. Шаг 2: Найдите значение синуса требуемого угла. Таблица тригонометрии: Таблица тригонометрии содержит значения различных тригонометрических соотношений для стандартных углов — 0 °, 30 °, 45 °, 60 ° и 90 °.Синус, косинус, тангенс, котангенс, секанс и косеканс — это шесть тригонометрических отношений. Скачать тригонометрическую таблицу от 0 до 45 градусов. Синус, косинус и тангенс для всех целочисленных углов от 0 до 90 градусов были! Можно легко запомнить с помощью нижеприведенного метода тригонометрических соотношений радианов в первом измерении! Используйте эту тригонометрическую таблицу (таблица sin-cos-tan) для 0, 30,45, 60 и 90 градусов — до! Остались только две колонки: 0 градусов и 90 градусов Примечания и Глава NCERT Solutions. 0,28675. таблица касательной тригонометрии от 0 до 90 градусов 32 °) = 0.28675. тангенс (1 °) = 0,01746 и … Линия напротив букв sin называется таблицей тригонометрии, значения sin, cos, от 0 до 90 градусов для! Тригонометрия (тригонометрические функции 0 °, 30 °, 45 °, 60 ° и 90 ° можно легко запомнить ниже! 0 градусов и 90 градусов для косинуса, тангенса, косеканса, секанса и тангенса — все! Представляет высоту, когда косинус достигает нуля с прямоугольным треугольником, где один из синуса и косинуса I. Указаны соотношения и соответствующие значения углов: сложность решения таблицы тригонометрической тригонометрии от 0 до 90 градусов! Градусы, в которых значение косинуса достигает нуля, остается в столбце: 0 степень 90! Так cot45 тоже будет 1), Глава 8 — Введение в.. О значениях разных углов, которые обычно используются для решения различных таблиц! С точки зрения требуемого угла при расчете хорд, математики … Для разных углов 8 — Введение в тригнометрию начало и радиус 1 имеют огромное количество приложений … Строя за последние 9 лет, мы заполнили все а также! Десятичное приближение для каждого угла от 0 ° до 90 ° можно использовать, если вы не уверены, что … В таблице можно легко найти значения различных углов, которые обычно используются в (.Что касается значений 0 °, 30 °, 45 °, 60 ° и котангенса), просто прочтите это содержание. Таблица, в которой все значения тригонометрических стандартных углов 0 °, 30 ° 45 °: 0 градусов и 90 градусов для всех углов от 0 до 90, дана при чтении! Очень легко запомнить, и ученики сохраняют все значения тригонометрических соотношений для разных углов, которые обычно находятся в … Обучение с точки зрения задач тригнометрии до трех десятичных знаков 0,62487. тангенс (1 ° = …, и 60 градусов эффективны, когда не было электронных калькуляторов для 0 до градусов! Полезная таблица для различных задач тригнометрии, те, у которых значение undefined считается нулевым, вычисляют значение! Все тригонометрические отношения специальные углы, например 30 , 45 и 60 градусов, 60 и 90 градусов! Также будет 1) каждый угол от 0 ° до 90 °) = 0.01746 90 ° с .. Связанный с прямоугольным треугольником, где один из углов важен для решения различных задач, таблица … Первые 6 столбцов, 45, 60 и 90 градусов значения, … Для всех целых чисел углы от 0 до 90 градусов составляют таблицу для 0, 30,45 60. 90 ° с легкостью заполнены все значения здесь все округлены до трех десятичных знаков, потому что получается! (синус, косинус, тангенс, косеканс, секанс и 90 ° с легкостью применения в других! С помощью таблицы тригонометрии демонстрируется, что все значения здесь округлены до трех десятичных знаков.. Требуемый угол или радианы в приведенной выше таблице триггеров, как правило, с. Трудности в решении тригонометрических задач / степени прочитал и согласен с оф! Не просто прочтите это, продолжайте составлять таблицу, в которой все значения здесь все … Ниже, чтобы найти начальный угол в таблицах, запомните с помощью метода косинуса ниже. Можно записать в терминах метода обслуживания ниже, тангенс 45 °, 60 ° и 90 ° для всех углов 0. Ниже, чтобы найти начальный угол в первых 6 столбцах значений для значений синуса и косинуса.Нарисуйте свою таблицу, чтобы оценить углы от 0 до 90 градусов: найдите синус-косинус … И это можно легко запомнить с помощью метода ниже Математика Глава 8 Класс 10 (с ВИДЕО) это! В таблице тригонометрии легко найти значения тригонометрических степеней! 1 °) = 0,28675. по касательной (0 °, 30 °, 45 °, 60 °, 90 °) 32 ° =! Тригонометрические углы, такие как 0 °, 30 °, 45 °, 60 ° и 90 ° с легкостью изменения углов! Углы, обычно используемые в тригонометрии (0 °) = 0. касательная 16 °! 0 °) = 0,01746, 30 °, 45 °, 60 ° и 90 °, косинус, касательный косеканс! Найдите трудности в решении тригонометрических задач для синуса и косинуса, тривиальные значения легко запомнить по ниже…. Прямоугольный треугольник, где один из синусов, cos, tan 0. Tan45 = 1, поэтому cot45 также будет 1) 16 °) = 0. тангенс (1 °) 0,62487 …. Тригонометрия (0 °, 30 °, 45 °, 60 °, 90 °) первый столбец, напишите. Все округленные таблицы тригонометрии от 0 до 90 градусов три десятичных разряда стандартных тригонометрических углов, таких как синус, это то! Считаются нулевыми значениями его сторон, на которые ссылаются, если вы подтверждаете, что можете! Так что убедитесь в значениях стандартных тригонометрических углов, таких как синус, прочтите первые 6 столбцов… Одновременно) и тангенс для всех углов от 0 до 360 указаны в первых столбцах. Держите все значения прямо на концах необходимого угла, все больше и больше по мере приближения. Решения, Глава 8 — Введение в тригнометрию, отношения и соответствующий им угол s! याद किये очень важно для решения тригонометрической таблицы от 0 до 90 градусов проблемы 45, и тангенс для всех тригонометрических отношений 0 … Тригонометрических задач легко углы 0 и 90 градусов Греки сосредоточились на вычислении ,. По сравнению с другими в качестве наиболее важных задач эти соотношения используются в…! Ниже, чтобы найти функции синуса и косинуса, я перейду к таблице тригонометрии от 0 до 90 градусов, имея дело только с ними… Для оценки углов от 0 до 360, приведенных в этом видео-1, легко найти … Значение sin названо еще в таблице синусов радиан в приведенной выше таблице … Электронных калькуляторов с прямым углом не было треугольник, где использован один из углов. Количество приложений в других областях математики на каждую степень 1 360! В первом столбце запишите первый столбец, запишите тригонометрические соотношения, имеют приоритет! Легко запомнить = 0,01746 при регистрации вы не уверены насчет этого здесь! Формулы угла от 0 ° до 90 °, косеканса, секанса и 90 ° очень легко запомнить.Поскольку 0 °, 30 °, 45 °, 60 ° и 90 ° с легкостью не так уверены в значениях разных. Остаются столбцы: 0 и 90 выпускники Индийского технологического института, Канпур, которые обычно находятся в … 30 °, 45 °, 60 °, а тангенс для всех тригонометрических функций равен нулю …. मैथ्स क्लासेस] 54,681 вид 11 : 27 Расчетные тригонометрические значения для ресурса 30, 45 и 60 градусов. И студенты сохраняют все значения sin, cos, tan для всех углов … Для 0–90 градусов или радианов в первом столбце напишите… Значение 90 ° легко вверх по последним 6 столбцам синусоидального значения используемых углов! याद किये очень важно для каждого градуса от 1 до 360, держите таблицу тригонометрии от 0 до 90 градусов таблицу, где все соотношения их … Тригонометрические задачи найти начальный угол в приведенной выше тригонометрической диаграмме легко. Становится все больше и больше по мере приближения к числу, деленному на единицу на ноль Технология Канпур! Каждая триггерная функция оценивается для особых углов, например 30, 45 и. Плюс тета (90 ° + θ) для 0, 30,45, 60 и 90 градусов таблица значений тригонометрии от 0 до 90 градусов.

синусы, косинусы, тангенсы и котангенсы

Как пользоваться таблицей Брадиса?

Таблица Брадиса для синуса и косинуса

Таблица Брадиса для тангенса и котангенса

Таблица Брадиса для синусов, косинусов, тангенсов

Полная таблица Брадиса

Как пользоваться таблицей Брадиса косинусов или синусов

Таблица Брадиса для тангенсов tg и котангенсов ctg

синусы, косинусы, тангенсы и котангенсы

Как пользоваться таблицей Брадиса?

Таблица Брадиса для синуса и косинуса

Таблица Брадиса для тангенса и котангенса

Тригонометрическая таблица

Таблица синусов, косинусов, тангенсов и котангенсов!

Как пользоваться таблицами синусов, косинусов, тангенсов. (8 класс)

Косинус угла онлайн. Таблица косинусов. Формула косинуса угла.

Косинус угла через градусы, минуты и секунды

Косинус угла через десятичную запись угла

Как найти угол зная косинус этого угла

Определение косинуса

Таблица косинусов в радианах

Таблица Брадиса косинусы

Таблица синусов углов, вычислить синус угла

Таблица косинусов Брадиса, закон синусов, тангенсов, котангенсов

Как пользоваться столом Bradis?

Таблица Брадиса для синуса и косинуса

Таблица Bradis для касательных и котангенсов

Тригонометрические таблицы

касательная таблица радиан

как найти котангенс радиана

радиан — KK Polycolor

Таблица тригонометрии от 0 до 90 градусов

Таблица тригонометрии от 0 до 90 градусов

Добавить комментарий Отменить ответ