Раздел недели: Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Математический справочник / / Интегральное и дифференциальное исчисление. Табличные производные и интегралы. Поделиться:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Поиск в инженерном справочнике DPVA. Введите свой запрос:
Дополнительная информация от Инженерного cправочника DPVA, а именно — другие подразделы данного раздела: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста.
Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.
Коды баннеров проекта DPVA.ru
Начинка: KJR Publisiers
Консультации и техническая
поддержка сайта: Zavarka Team

Физика
166
Реклама и PR
31
Педагогика
80
Психология
72
Социология
7
Астрономия
9
Биология
30
Культурология
86
Экология
8
Право и юриспруденция
36
Политология
13
Экономика
49
Финансы
9
История
16
Философия
8
Информатика20
Право
35
Информационные технологии
6
Экономическая теория
7
Менеджент
719
Математика
338
Химия
20
Микро- и макроэкономика
1
Медицина
5
Государственное и муниципальное управление
2
География
542
Информационная безопасность
2
Аудит
11
Безопасность жизнедеятельности
3
Архитектура и строительство
1
Банковское дело
1
Рынок ценных бумаг
6
Менеджмент организации
2
Маркетинг
238
Кредит
3
Инвестиции
2
Журналистика
1
Конфликтология
15
Этика
9
Формулы дифференцирования Частные дифференциалы Дифференциал параметрической функции Производная функции определения и понятия
Узнать цену работы
Узнай цену
своей работы
Имя
Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругое Принимаю Политику конфиденциальностиПодпишись на рассылку, чтобы не пропустить информацию об акциях
таблица производных и интегралов
|
| Таблица производных |
|
|
|
|
|
|
|
|
|
| Таблица интегралов | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1. |
|
|
|
|
|
|
|
|
| 1. | ∫dx = x +C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||
| 2. (xa )’ = αxα−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 2. | ∫xkdx = |
|
| xk +1 | +C |
| , (k ≠ −1 ) |
|
| |||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| k +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||
|
|
| 1 |
|
|
|
|
|
|
|
|
|
| 1 | ‘ |
|
| 1 |
|
|
|
|
| dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| dx |
|
|
|
|
| ||||||||||||||
3. | ( x )’ = |
|
|
|
|
|
| , |
|
|
|
|
|
|
|
|
|
|
| = − |
|
|
|
| 3. | ∫ x | = 2 |
|
| x | +C , |
|
| ∫ |
| x |
|
| = ln | x | +C | ||||||||||||||||||||||||||||
|
| 2 x |
|
|
|
|
|
|
|
| x 2 |
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||
| 4. |
|
|
|
|
| (ex )’ = ex | 4. | ∫axdx = |
|
| ax |
|
| +C , |
|
| ∫exdx = ex +C | |||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
| ln a |
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||
|
| (loga x ) |
|
|
|
|
| 1 |
|
|
|
|
|
|
|
|
| (ln x ) | 1 |
|
|
| ∫ |
| dx |
|
| = ln |
|
|
|
|
|
| x |
|
|
| +C |
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||
5. | ‘ = |
|
|
|
|
|
|
|
| , |
|
| ‘ = x | 5. |
|
| tg | 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||||
x ln a |
|
|
| sin x |
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
6. | (sin x )’ = cos x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 6. |
|
| dx |
|
|
| = ln |
| tg | x | + | π |
|
| x +C |
|
| |||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ∫cos x |
| 4 |
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 2 |
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||
7. | (cos x )’ = −sin x |
|
|
|
|
|
|
|
|
|
|
|
|
| 7. | ∫sin xdx = −cos x +C |
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||
8. | (tgx )’ = |
| 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 8. | ∫cos xdx = sin x +C |
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||
2 |
| x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||
|
|
|
|
| cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
9. | (ctgx )’ = − |
| 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 9. | ∫ |
| dx |
|
|
| = tgx +C |
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||||
sin2 x |
|
|
|
|
|
|
|
|
|
|
|
|
| cos2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||
| 10. |
|
|
|
|
|
| 1 |
|
|
|
|
|
|
|
|
|
|
| 10. ∫ | dx | = −ctgx +C |
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||
|
|
| 1 − x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
| sin2 x |
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||
| 11. |
|
| 1 |
|
|
|
|
|
|
|
|
| 11. ∫ |
| dx |
|
|
|
|
|
|
|
| = arcsin x |
| +C |
|
|
|
| ||||||||||||||||||||||||||||||||||||||
|
|
| 1 − x | 2 |
|
|
|
|
|
|
| 2 |
|
|
|
| 2 |
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| a |
|
| − x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| a |
|
|
|
|
|
|
|
|
|
| ||||||||||||
| 12. |
|
|
|
| 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 12. ∫ |
| dx |
|
|
|
|
|
|
|
| = ln |
| x + |
| x | 2 | ±a | 2 |
| +C | |||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| x 2 ±a2 |
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||
| 1 + x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||
| 13. |
|
|
| 1 |
|
|
|
|
|
|
|
|
|
| 13. ∫ | dx |
|
|
|
|
| = |
|
| 1 |
| ln |
| x −a |
|
| +C |
|
|
|
| ||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||
| 1 + x 2 |
|
|
|
|
|
|
|
| x 2 | −a2 |
|
|
|
|
|
| 2a |
| x +a |
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 14. | dx |
|
|
|
|
|
|
|
|
| 1 |
|
|
|
|
|
|
|
| x |
|
|
|
|
|
|
|
|
|
|
| ||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| = a arctg a |
| +C |
|
|
|
| |||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| x 2 | +a2 |
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||
Правила дифференцирования и |
| Некоторые тригонометрические | |||||||||||||||
|
|
|
|
|
|
|
| интегрирования |
|
|
| формулы: | |||||
|
|
|
|
|
|
|
|
|
| ||||||||
а) |
|
|
| Правила дифференцирования | 1 | sin2 x + cos2 x = 1; 1 − sin2 x = cos2 x; | |||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 − cos2 x = sin2 x. |
|
1 |
| Производная суммы: |
|
| 2 | sin2 x = 1 − cos 2x , cos2 | x = 1 + cos 2x , | ||||||||||
|
| (u ± v )’ = u ‘± v ‘ |
|
|
|
|
| 2 | 2 | ||||||||
2 |
| Производная произведения: |
|
| 3 | 1 |
| ||||||||||
|
| (u v )’ | = u ‘ v + u v ‘ |
|
|
| sin α sin β = 2 (cos(α | − β) − cos(α + β)) | |||||||||
3 | ( |
|
|
|
| ) | ‘ | = c u ‘ |
|
|
|
| 4 | 1 |
| ||
| c u |
|
|
|
|
| sin α cos β = 2 (sin(α − β) + sin(α + β)) | ||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
| Производная частного: |
|
| 5 | 1 |
| ||||||||||
|
| u l | = | u ‘ v −u v ‘ |
|
|
|
| cos α cos β = 2 (cos(α | + β) + cos(α − β)) | |||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
| v2 |
|
|
|
|
|
|
| ||||
|
| v |
|
|
|
|
|
|
|
|
|
| |||||
5 |
| Сложная функция: |
|
|
|
|
| Формулы сокращённого умножения | |||||||||
|
| ((f (ϕ(x)))’ = f ‘ϕ ϕ ‘(x) |
|
|
|
|
| ||||||||||
б) |
|
|
|
|
| Правила интегрирования |
|
| 1 | (a ±b)2 = a2 ± 2ab +b2 |
| ||||||
1 |
| ∫( | f (x) ± g(x) dx = | ∫ | f (x)dx ± | ∫ | g(x |
|
|
| |||||||
|
|
|
|
|
| ) |
|
|
|
|
| ||||||
2 |
| ∫k f (x)dx = k ∫f (x)dx |
|
| 2 | a2 −b2 = (a −b)(a +b) |
| ||||||||||
3 |
| ∫f (ax +b)dx = |
|
|
|
|
|
|
| ||||||||
| = | 1 ∫f (ax +b)d(ax +b) |
|
|
|
|
| ||||||||||
|
|
|
| a |
|
|
|
|
|
|
|
|
|
|
| ||
4 |
| ∫f (ϕ(x)) ϕ ‘(x)dx ± ∫f (ϕ(x))dϕ(x | 3 | (a ±b)3 = a3 ± 3a2b + 3ab2 ±b3 | |||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| a3 ±b3 = (a ±b)(a2 ab +b2 ) | |
5 |
|
|
|
|
| Интегрирование по частям |
|
|
|
| |||||||
|
|
|
|
|
|
| ∫u dv = u v − ∫v du |
|
|
|
|
| |||||
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
13.
 04.20151.47 Mб21стихи о лете.pdf
04.20151.47 Mб21стихи о лете.pdf - #
13.04.201563.67 Кб2Стихи.docx
- #
13.04.201562.46 Кб15структура статьи.doc
- #
13.04.2015376.56 Кб70таблица Гаусса.pdf
- #
13.04.2015357.21 Кб29таблица Лапласа.pdf
- #
13.04.2015133.44 Кб1445таблица производных и интегралов.pdf
- #
19.11.2018192.51 Кб0Тат яз. в русс. гр 9 класс.doc
- #
13.04.201518.7 Кб38ТАТАР ТЕЛЕННӘН ДИАГНОСТИК ТЕСТ.docx
- #
13.04.201516.56 Кб7ТАТРСКИЙ.docx
- #
13.04.2015105.98 Кб18Тезаурус КСЕ.doc
- #
13.04.201592.06 Кб7тем план 11 правильная.docx
Таблица ⚠️ полная и формулы интегралов для студентов
Содержание:
- Основные формулы интегралов
- Правила интегрирования функций
-
Интегралы элементарных функций
- Первообразные рациональных функций
- Логарифмы
- Экспоненциальные функции
- Иррациональные функции
- Тригонометрические функции
- Гиперболические функции
- Специальные функции
Содержание
- Основные формулы интегралов
- Правила интегрирования функций
-
Интегралы элементарных функций
- Первообразные рациональных функций
- Логарифмы
- Экспоненциальные функции
- Иррациональные функции
- Тригонометрические функции
- Гиперболические функции
- Специальные функции
Основные формулы интегралов
Интегрирование — это процесс нахождения интеграла, что является одной из основных операций математического анализа.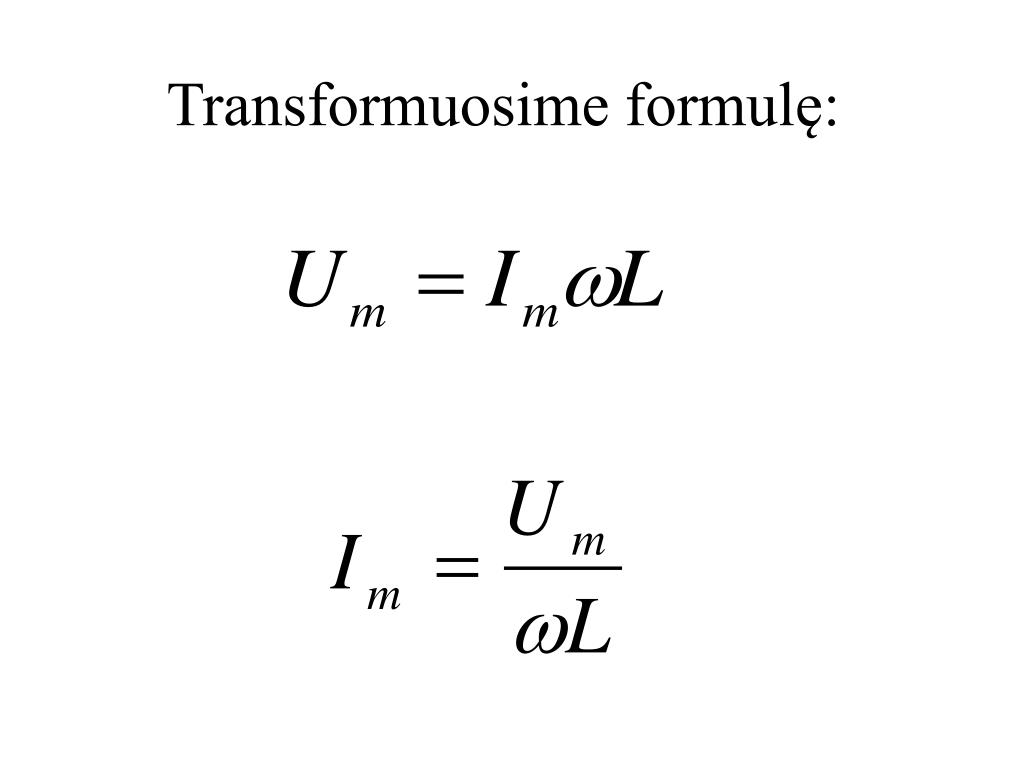 При вычислении определенного интеграла определяется площадь криволинейной трапеции, которая ограничивается сверху кривой (графиком заданной функции), снизу осью х, справа и слева вертикальными прямыми, которые параллельны оси y в заданных точках.
При вычислении определенного интеграла определяется площадь криволинейной трапеции, которая ограничивается сверху кривой (графиком заданной функции), снизу осью х, справа и слева вертикальными прямыми, которые параллельны оси y в заданных точках.
Знания основных формул интегрирования помогут взять неопределенный и вычислить определенный интегралы. Решение задач, где используются интегралы всегда начинается с взятия неопределенного интеграла, поэтому в этом разделе представлены основные формулы неопределенных интегралов, где С — это произвольная константа интегрирования, то есть число, которое можно задать, если нам будет известны дополнительные условия, например, значения функции в конкретной точке.
Ниже представлена таблица основных интегралов.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- \(\int0\times\operatorname dx=C\\ \)
- \(\int\operatorname dx=\int1\times\operatorname dx=x+C\;\\\)
- \(\int x^n\operatorname dx=\frac{x^{n+1}}{n+1}+C\;,\;при\;n\neq-1,\;x>0\\\)
- \(dx=\ln\left|\left.
 2}\right|\right.\right)+C\\\)
2}\right|\right.\right)+C\\\)
Правила интегрирования функций
Для того чтобы взять интеграл, не всегда хватает знания таблицы основных формул, также необходимо знать свойства интегралов и правила интегрирования различных функций.
- \(\int c\;f(x)\operatorname dx=c\int\;f(x)\operatorname dx\;\)постоянный множитель (константу) можно вынести за знак интеграла
- \(\int\lbrack\;f(x)+g(x)\rbrack\operatorname dx=\int\;f(x)\operatorname dx\;+\int\;g(x)\operatorname dx\) интеграл от суммы функций равен сумме интегралов этих функций
- \(\int\lbrack\;f(x)-g(x)\rbrack\operatorname dx=\int\;f(x)\operatorname dx\;-\int\;g(x)\operatorname dx\) интеграл от разности функций равен разности интегралов этих функций
- \(\int\;u\operatorname dv\;=uv-\int v\operatorname du\) правило интегрирования по частям, где u=f(x), v=g(x)
Метод замены переменной помогает упростить сложные интегралы и свести их либо к более простым, либо к табличным значениям, которые можно сразу проинтегрировать и вычислить значения, если нам известны пределы интегрирования (для определенного интеграла). x\;+C\)
x\;+C\)
Насколько полезной была для вас статья?
Рейтинг: 5.00 (Голосов: 2)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
Таблица основных неопределенных интегралов. Правила интегрирования. Интегралы от степенной, показательной, тригонометрических функций
Интегрирование степенной функции
Интегралы от показательной функции и гиперболических функций
Интегралы от тригонометрических функций
Интегралы, сводящиеся к обратным тригонометрическим функциям
Более сложные интегралы
Общие законы интегрирования
Несложный пример
Сводная таблица интегралов
Скачайте таблицу интегралов (часть I) по этой ссылке
Скачайте таблицу интегралов (часть II) по этой ссылке
Перечисленные интегралы — это базис, основа основ. Данные формулы, безусловно, следует запомнить. При вычислении более сложных интегралов вам придется постоянно ими пользоваться.
Данные формулы, безусловно, следует запомнить. При вычислении более сложных интегралов вам придется постоянно ими пользоваться.
Обратите особое внимание на формулы (5), (7), (9), (12), (13), (17) и (19). Не забывайте при интегрировании добавлять к ответу произвольную постоянную С!
Интеграл от константы
∫Adx=Ax+C (1)
Интегрирование степенной функции
В действительности, можно было ограничиться только формулами (5) и (7), но остальные интегралы из этой группы встречаются настолько часто, что стоит уделить им немного внимания.
∫xdx=x22+C (2)
∫x2dx=x33+C (3)
∫1xdx=2x+C (4)
∫1xdx=ln|x|+C (5)
∫1x2dx=−1x+C (6)
∫xndx=xn+1n+1+C(n≠−1) (7)
Интегралы от показательной функции и от гиперболических функций
Разумеется, формулу (8) (пожалуй, самую удобную для запоминания) можно рассматривать как частный случай формулы (9). Формулы (10) и (11) для интегралов от гиперболического синуса и гиперболического косинуса легко выводятся из формулы (8), но лучше просто запомнить эти соотношения.
∫exdx=ex+C (8)
∫axdx=axlna+C(a>0,a≠1) (9)
∫shxdx=chx+C (10)
∫chxdx=shx+C (11)
Базовые интегралы от тригонометрических функций
Ошибка, которую часто делают студенты: путают знаки в формулах (12) и (13). Запомнив, что производная синуса равна косинусу, многие почему-то считают, что интеграл от функции sinx равен сosx. Это неверно! Интеграл от синуса равен «минус косинусу», а вот интеграл от cosx равен «просто синусу»:
∫sinxdx=−cosx+C (12)
∫cosxdx=sinx+C (13)
∫1cos2xdx=tgx+C (14)
∫1sin2xdx=−ctgx+C (15)
Сводная таблица интегралов
Скачайте таблицу интегралов (часть I) по этой ссылке
Скачайте таблицу интегралов (часть II) по этой ссылке
Интегралы, сводящиеся к обратным тригонометрическим функциям
Формула (16), приводящая к арктангенсу, естественно, является частным случаем формулы (17) при a=1. Аналогично, (18) — частный случай (19).
Аналогично, (18) — частный случай (19).
∫11+x2dx=arctgx+C=−arcctgx+C (16)
∫1×2+a2=1aarctgxa+C(a≠0) (17)
∫11−x2dx=arcsinx+C=−arccosx+C (18)
∫1a2−x2dx=arcsinxa+C=−arccosxa+C(a>0) (19)
Репетитор по математическому анализу
Более сложные интегралы
Данные формулы тоже желательно запомнить. Они также используются достаточно часто, а их вывод довольно утомителен.
∫1×2+a2dx=ln|x+x2+a2|+C (20)
∫1×2−a2dx=ln|x+x2−a2|+C (21)
∫a2−x2dx=x2a2−x2+a22arcsinxa+C(a>0) (22)
∫x2+a2dx=x2x2+a2+a22ln|x+x2+a2|+C(a>0) (23)
∫x2−a2dx=x2x2−a2−a22ln|x+x2−a2|+C(a>0) (24)
1) Интеграл от суммы двух функций равен сумме соответствующих интегралов: ∫(f(x)+g(x))dx=∫f(x)dx+∫g(x)dx (25)
2) Интеграл от разности двух функций равен разности соответствующих интегралов: ∫(f(x)−g(x))dx=∫f(x)dx−∫g(x)dx (26)
3) Константу можно выносить за знак интеграла: ∫Cf(x)dx=C∫f(x)dx (27)
Легко заметить, что свойство (26) — это просто комбинация свойств (25) и (27).
4) Интеграл от сложной функции, если внутренняя функция является линейной: ∫f(Ax+B)dx=1AF(Ax+B)+C(A≠0) (28)
Здесь F(x) — первообразная для функции f(x). Обратите внимание: эта формула подходит только для случая, когда внутренняя функция имеет вид Ax + B.
Важно: не существует универсальной формулы для интеграла от произведения двух функций, а также для интеграла от дроби:
∫f(x)g(x)dx=?∫f(x)g(x)dx=? (30)
Это не означает, конечно, что дробь или произведение нельзя проинтегрировать. Просто каждый раз, увидев интеграл типа (30), вам придется изобретать способ «борьбы» с ним. В каких-то случаях вам поможет интегрирование по частям, где-то придется сделать замену переменной, а иногда помощь могут оказать даже «школьные» формулы алгебры или тригонометрии.
Простой пример на вычисление неопределенного интеграла
Пример 1. Найти интеграл: ∫(3×2+2sinx−7ex+12)dx
Воспользуемся формулами (25) и (26) (интеграл от суммы или разности функций равен сумме или разности соответствующих интегралов. Получаем:
∫3x2dx+∫2sinxdx−∫7exdx+∫12dx
Получаем:
∫3x2dx+∫2sinxdx−∫7exdx+∫12dx
Вспомним, что константу можно выносить за знак интеграла (формула (27)). Выражение преобразуется к виду
3∫x2dx+2∫sinxdx−7∫exdx+12∫1dx
А теперь просто воспользуемся таблицей основных интегралов. Нам потребуется применить формулы (3), (12), (8) и (1). Проинтегрируем степенную функцию, синус, экспоненту и константу 1. Не забудем добавить в конце произвольную постоянную С:
3×33−2cosx−7ex+12x+C
После элементарных преобразований получаем окончательный ответ:
x3−2cosx−7ex+12x+C
Проверьте себя дифференцированием: возьмите производную от полученной функции и убедитесь, что она равна исходному подинтегральному выражению.
Сводная таблица интегралов
| ∫Adx=Ax+C |
| ∫xdx=x22+C |
| ∫x2dx=x33+C |
| ∫1xdx=2x+C |
| ∫1xdx=ln|x|+C |
| ∫1x2dx=−1x+C |
| ∫xndx=xn+1n+1+C(n≠−1) |
| ∫exdx=ex+C |
| ∫axdx=axlna+C(a>0,a≠1) |
| ∫shxdx=chx+C |
| ∫chxdx=shx+C |
| ∫sinxdx=−cosx+C |
| ∫cosxdx=sinx+C |
| ∫1cos2xdx=tgx+C |
| ∫1sin2xdx=−ctgx+C |
| ∫11+x2dx=arctgx+C=−arcctgx+C |
| ∫1×2+a2=1aarctgxa+C(a≠0) |
| ∫11−x2dx=arcsinx+C=−arccosx+C |
| ∫1a2−x2dx=arcsinxa+C=−arccosxa+C(a>0) |
| ∫1×2+a2dx=ln|x+x2+a2|+C |
| ∫1×2−a2dx=ln|x+x2−a2|+C |
| ∫a2−x2dx=x2a2−x2+a22arcsinxa+C(a>0) |
| ∫x2+a2dx=x2x2+a2+a22ln|x+x2+a2|+C(a>0) |
| ∫x2−a2dx=x2x2−a2−a22ln|x+x2−a2|+C(a>0) |
Скачайте таблицу интегралов (часть I) по этой ссылке
Скачайте таблицу интегралов (часть II) по этой ссылке
Если Вы учитесь в ВУЗе, если у Вас возникли сложности с высшей математикой (математический анализ, линейная алгебра, теория вероятностей, статистика), если Вам нужны услуги квалифицированного преподавателя, зайдите на страничку репетитора по высшей математике.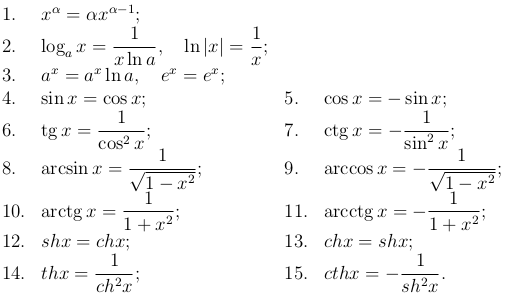 Будем решать Ваши проблемы вместе!
Будем решать Ваши проблемы вместе!
Возможно, вас заинтересуют также
Таблица производных элементарных функций
или другие разделы онлайн — справочника по математике.
Рекомендуемая литература для подготовки к экзамену по высшей математике.
Интегралы для чайников — что это, как решать, примеры
О чем статья
Почему вы не знаете, как решать интегралы
А для чего нужны интегралы? Попробуйте сами себе ответить на этот вопрос.
Объясняя тему интегралов, учителя перечисляют малополезные школьным умам области применения. Среди них:
- вычисление площади фигуры.
- вычисление массы тела с неравномерной плотностью.
- определение пройденного пути при движении с непостоянной скоростью.
- и др.
Связать все эти процессы не всегда получается, поэтому многие ученики путаются, даже при наличии всех базовых знаний для понимания интеграла.
Главная причина незнания – отсутствие понимания практической значимости интегралов.
Нужна помощь в написании работы?
Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Заказать работу
Интеграл – что это?
Предпосылки. Потребность в интегрировании возникла в Древней Греции. В то время Архимед начал применять для нахождения площади окружности методы, похожие по сути на современные интегральные исчисления. Основным подходом для определения площади неровных фигур тогда был «Метод исчерпывания», который достаточно лёгок для понимания.
Суть метода. В данную фигуру вписывается монотонная последовательность других фигур, а затем вычисляется предел последовательности их площадей. Этот предел и принимался за площадь данной фигуры.
Метод исчерпывания для определения площади круга
В этом методе легко прослеживается идея интегрального исчисления, которая заключается в нахождении предела бесконечной суммы. В дальнейшем эта идея применялась учёными для решения прикладных задач астронавтики, экономики, механики и др.
В дальнейшем эта идея применялась учёными для решения прикладных задач астронавтики, экономики, механики и др.
Современный интеграл. Классическая теория интегрирования была сформулирована в общем виде Ньютоном и Лейбницем. Она опиралась на существовавшие тогда законы дифференциального исчисления. Для её понимания, необходимо иметь некоторые базовые знания, которые помогут математическим языком описать визуальные и интуитивные представления об интегралах.
Объясняем понятие «Интеграл»
Процесс нахождения производной называется дифференцированием, а нахождение первообразной – интегрированием.
Интеграл математическим языком – это первообразная функции (то, что было до производной) + константа «C».
Интеграл простыми словами – это площадь криволинейной фигуры. Неопределенный интеграл – вся площадь. Определенный интеграл – площадь в заданном участке.
Интеграл записывается так:
Каждая подынтегральная функция умножается на компонент «dx». Он показывает, по какой переменной осуществляется интегрирование. «dx» – это приращение аргумента. Вместо X может быть любой другой аргумент, например t (время).
Неопределённый интеграл
Неопределенный интеграл не имеет границ интегрирования.
Для решения неопределённых интегралов достаточно найти первообразную подынтегральной функции и прибавить к ней «C».
Пример решения неопределенного интеграла.
Определённый интеграл
В определенном интеграле на знаке интегрирования пишут ограничения «a» и «b». Они указаны на оси X в графике ниже.
Точки A и B на оси X – есть ограничение зоны определения интеграла
Для вычисления определенного интеграла необходимо найти первообразную, подставить в неё значения «a» и «b» и найти разность. В математике это называется формулой Ньютона-Лейбница:
Пример решения определенного интеграла
Таблица интегралов для студентов (основные формулы)
Скачайте формулы интегралов, они вам еще пригодятся
Как вычислять интеграл правильно
Существует несколько простейших операций для преобразования интегралов. Вот основные из них:
Вот основные из них:
Вынесение константы из-под знака интеграла
Разложение интеграла суммы на сумму интегралов
Если поменять местами a и b, знак изменится
Можно разбить интеграл на промежутки следующим образом
Это простейшие свойства, на основе которых потом будут формулироваться более сложные теоремы и методы исчисления.
Примеры вычисления интегралов
Решение неопределенного интеграла
Решение определенного интеграла
Базовые понятия для понимания темы
Чтобы вы поняли суть интегрирования и не закрыли страницу от непонимания, мы объясним ряд базовых понятий. Что такое функция, производная, предел и первообразная.
Функция – правило, по которому все элементы из одного множества соотносятся со всеми элементами из другого.
Производная – функция, описывающая скорость изменения другой функции в каждой конкретной точке. Если говорить строгим языком, – это предел отношения приращения функции к приращению аргумента. Он вычисляется вручную, но проще использовать таблицу производных, в которой собрано большинство стандартных функций.
Он вычисляется вручную, но проще использовать таблицу производных, в которой собрано большинство стандартных функций.
Приращение – количественное изменение функции при некотором изменении аргумента.
Предел – величина, к которой стремиться значение функции, при стремлении аргумента к определённому значению.
Пример предела: допустим при X равном 1, Y будет равно 2. Но что, если X не равен 1, а стремится к 1, то есть никогда её не достигает? В этом случае y никогда не достигнет 2, а будет только стремиться к этой величине. На математическом языке это записывается так: limY(X), при X –> 1 = 2. Читается: предел функции Y(X), при x стремящемся к 1, равен 2.
Как уже было сказано, производная – это функция, описывающая другую функцию. Изначальная функция может быть производной для какой-либо другой функции. Эта другая функция называется первообразной.
Заключение
Найти интегралы не трудно. Если вы не поняли, как это делать, прочитайте статью еще раз. Со второго раза становится понятнее. Запомните! Решение интегралов сводится к простым преобразованиям подынтегральной функции и поиска её в таблице интегралов.
Со второго раза становится понятнее. Запомните! Решение интегралов сводится к простым преобразованиям подынтегральной функции и поиска её в таблице интегралов.
Обучение и сборы | Портлендский государственный университет
Доступность в действии
Штат Портленд стремится предоставить отличное образование по доступной цене, а также возможности и связи, связанные с пребыванием в одном из самых интересных городов страны.
Свяжитесь с нашими сотрудниками по приему или финансовой помощи, чтобы разработать план оплаты обучения в колледже. Затем узнайте, как первоклассное образование в одном из самых доступных государственных исследовательских университетов страны может определить ваш путь к успеху.
Стоимость обучения может изменяться каждый год и подлежит утверждению Советом попечителей. Плата за посещение PSU определяется на основе количества полученных кредитов, статуса резидента и успеваемости в классе бакалавриата / магистратуры. Чтобы рассчитать, сколько вы можете рассчитывать на плату за обучение и сборы, просмотрите график оплаты за соответствующий учебный год.
Плата за посещение PSU определяется на основе количества полученных кредитов, статуса резидента и успеваемости в классе бакалавриата / магистратуры. Чтобы рассчитать, сколько вы можете рассчитывать на плату за обучение и сборы, просмотрите график оплаты за соответствующий учебный год.
Рассчитайте стоимость обучения и сборы
Стоимость обучения и сборы будут варьироваться в зависимости от вашей программы, количества кредитов, которые вы берете, вашего статуса резидента, вашего класса и многих других факторов. Вы также можете использовать наш инструмент оценки стоимости, чтобы примерно определить, сколько вы будете платить, или использовать таблицы сборов ниже.
- Таблицы платы за обучение и сборы на 2022–2023 учебный год
- Загрузить Таблицы стоимости обучения на 2022-2023 учебный год, PDF, 257 КБ
- Таблицы стоимости обучения и оплаты на 2021-2022 учебный год
- Скачать Таблицы стоимости обучения на 2021-2022 учебный год, PDF, 937 КБ
- Таблицы стоимости обучения и оплаты на 2020-2021 учебный год
- Скачать Таблицы стоимости обучения на 2020-2021 учебный год, PDF, 6,2 МБ
- Таблицы стоимости обучения и оплаты за 2019-2020 учебный год, PDF, 5,8 МБ
- Таблицы стоимости обучения и оплаты за 2018-2019 учебный год, PDF, 612 КБ
Postbaccalaureate
Студенты, получившие степень бакалавра, оцениваются по ставке за обучение в бакалавриате для всех курсов, которые они изучают под номером 499 или ниже, и оцениваются по ставке за обучение для выпускников для всех курсов, которые они изучают под номером 500 или выше. Право на получение финансовой помощи для студентов после бакалавриата зависит от программы. Кроме того, обратите внимание, что учащиеся, зачисленные в классы дифференцированного обучения, будут получать более высокие ставки за эти конкретные курсы. Свяжитесь с отделом финансовой помощи студентам для получения дополнительной информации.
Право на получение финансовой помощи для студентов после бакалавриата зависит от программы. Кроме того, обратите внимание, что учащиеся, зачисленные в классы дифференцированного обучения, будут получать более высокие ставки за эти конкретные курсы. Свяжитесь с отделом финансовой помощи студентам для получения дополнительной информации.
Резиденция для целей обучения
Студенты со статусом резидента оцениваются за обучение в штате, а для студентов-нерезидентов оценивается более высокий уровень платы за обучение, который более точно соответствует фактической стоимости обучения. Руководство и процедуры по проживанию разработаны, чтобы помочь учащимся понять критерии классификации и процесс, с помощью которого определяется класс проживания. Переведенные учащиеся, которые были классифицированы как жители штата Орегон в своей предыдущей школе, не должны предполагать, что они будут классифицированы как жители штата PSU. Узнайте больше о резидентуре в Портлендском государственном университете.
Обязательные сборы за 2022–2023 академический год
Указанные ниже расходы рассчитаны на основе зачисления на полный рабочий день (12 или более кредитов за семестр для студентов и 9 или более кредитов за семестр для аспирантов). Ваши расходы могут варьироваться в зависимости от того, сколько кредитов вы берете каждый семестр.
| Плата | Описание | Сумма |
|---|---|---|
| Здание | Этот сбор предназначен для оплаты обслуживания долга, связанного с прошлыми проектами строительства и реконструкции в кампусе ПГУ. Любые дополнительные собранные средства помещаются в резерв или используются для небольших строительных проектов. Сумма варьируется в зависимости от количества кредитов, на которые зачислен студент. Комитет по студенческим взносам несет ответственность за рекомендацию суммы и распределения платы за здание для ASPSU и президента. | 45,00 $ |
| Случайно | Эта плата покрывает такие услуги, как студенческие мероприятия и программы лидерства, ресурсные центры, услуги по уходу за детьми и спортивные мероприятия. Сумма варьируется в зависимости от количества кредитов, на которые зачислен студент. Комитет по студенческим взносам несет ответственность за рекомендацию суммы и распределение непредвиденных расходов для ASPSU и президента. | 323,00 $ |
| Служба здравоохранения | Плата за студенческий медицинский центр является обязательной платой, начисляемой всем учащимся, получающим 5 или более зачетных часов без ограничений по дифференцированному обучению. Плата взимается за поддержку всех услуг, предлагаемых Центром здоровья и консультирования студентов (SHAC), как дистанционно, так и лично. Ознакомьтесь с полным перечнем услуг, покрываемых оплатой услуг Студенческого медицинского центра. | 190,00 $ |
| Академический студенческий оздоровительный центр | Плата, начисляемая каждый семестр для покрытия расходов на строительство, техническое обслуживание и эксплуатацию, а также для приобретения и технического обслуживания оборудования для здания Центра академического и студенческого отдыха. | 44,00 $ |
Онлайн-курсы имеют дополнительную плату в размере 22 долларов США за кредит
Вступительный взнос в размере 450 долларов США для всех новых студентов выставляется в начале первого семестра. Единовременная плата, взимаемая с вновь поступивших студентов и аспирантов для покрытия расходов, связанных с приемом, ориентацией студентов, транскриптами, информационными технологиями и другими услугами, связанными с зачислением новых студентов.
Медицинское страхование PSU страховой взнос в размере 1 108 долларов США за триместр; однако у студентов есть возможность отказаться от взноса по медицинскому страхованию при наличии страхового полиса.
Утвержденные штрафы и сборы
- Полный список штрафов и сборов за 2022–2023 гг., PDF, 175 КБ
- Полный список штрафов и сборов за 2021–2022 годы, PDF, 177 КБ
- Полный список штрафов и сборов за 2020–2021 годы, PDF, 173 КБ
- Полный список штрафов и сборов за 2019–2020 годы, PDF, 183 КБ
- Полный список штрафов и сборов за 2018–2019 годы, PDF, 138 КБ
Ограниченное дифференцированное обучение
Плата за обучение и плата за курсы Ограниченно-дифференциальное обучение оцениваются отдельно от расходов, связанных с обычными курсами. Стоимость обучения для разделов курса с ограниченным дифференцированным обучением указана в столбце сборов в расписании занятий. Кредиты, связанные с курсами ограниченного дифференцированного обучения, не учитываются при определении статуса зачисления учащегося. Таким образом, студент бакалавриата, зачисленный на 8 кредитов обычных классов и на курс ограниченного дифференцированного обучения с 4 кредитами, оценивается как обычное обучение в размере 8 кредитов плюс дополнительная плата за курс ограниченного дифференцированного обучения. В стоимость курсов с ограниченным дифференцированным обучением не входят непредвиденные расходы, плата за медицинское обслуживание студентов или план медицинского страхования студентов. Таким образом, учащиеся, зарегистрированные только для курсов с ограниченным дифференцированным обучением, не имеют права пользоваться услугами, поддерживаемыми за счет дополнительных сборов, платы за медицинское обслуживание учащихся или плана медицинского страхования учащихся.
Стоимость обучения для разделов курса с ограниченным дифференцированным обучением указана в столбце сборов в расписании занятий. Кредиты, связанные с курсами ограниченного дифференцированного обучения, не учитываются при определении статуса зачисления учащегося. Таким образом, студент бакалавриата, зачисленный на 8 кредитов обычных классов и на курс ограниченного дифференцированного обучения с 4 кредитами, оценивается как обычное обучение в размере 8 кредитов плюс дополнительная плата за курс ограниченного дифференцированного обучения. В стоимость курсов с ограниченным дифференцированным обучением не входят непредвиденные расходы, плата за медицинское обслуживание студентов или план медицинского страхования студентов. Таким образом, учащиеся, зарегистрированные только для курсов с ограниченным дифференцированным обучением, не имеют права пользоваться услугами, поддерживаемыми за счет дополнительных сборов, платы за медицинское обслуживание учащихся или плана медицинского страхования учащихся.
Со студентов, зачисленных на курсы с ограниченным дифференцированным обучением, взимается плата в размере 44 долларов США за семестр в Центре отдыха студентов, и они будут иметь полный доступ к Центру отдыха и связанным с ним услугам. Учащиеся, отказавшиеся от курса с ограниченным дифференцированным обучением после истечения крайнего срока 100% возврата, будут нести ответственность за оплату. Чтобы подать петицию, перейдите на страницу петиций.
Поддержка студентов: Центр финансового благополучия
Центр финансового благополучия PSU может помочь вам сделать правильный финансовый выбор. Мы предлагаем инструменты, которые помогут вам понять управление капиталом. Вы можете посетить одно из наших образовательных мероприятий в кампусе или записаться на прием и встретиться один на один с наставником или финансовым тренером.
Информация о Центре финансового благополучия
Обследование пациентов с болью в колене: Часть II.
 Дифференциальный диагноз
Дифференциальный диагнозУОЛТЕР Л. КАЛМБАХ, доктор медицины, и МАРК ХАТЧЕНС, доктор медицины.
Семейный врач. 2003;68(5):917-922
Это вторая часть статьи о боли в колене, состоящей из двух частей. Часть I, «История, физикальное обследование, рентгенограммы и лабораторные тесты», опубликована на странице 907 в этом выпуске .
Доступна более поздняя статья об оценке боли в колене у взрослых.
Боль в колене — частая жалоба, имеющая множество возможных причин. Осведомленность об определенных закономерностях может помочь семейному врачу более эффективно определить основную причину. У девочек-подростков и молодых женщин чаще возникают проблемы с отслеживанием надколенника, такие как подвывих надколенника и пателлофеморальный болевой синдром, тогда как у мальчиков-подростков и молодых мужчин чаще возникают проблемы с механизмом разгибания колена, такие как апофизит большеберцовой кости (поражение Осгуда-Шлаттера) и тендинит надколенника. . Отраженная боль, возникающая в результате патологии тазобедренного сустава, такой как смещение эпифиза головки бедренной кости, также может вызывать боль в колене. Активные пациенты чаще имеют острые растяжения связок и травмы от чрезмерной нагрузки, такие как бурсит гусиной лапки и синдром медиальной складки. Травма может привести к острому разрыву или перелому связок, что приводит к острому отеку коленного сустава и гемартрозу. Септический артрит может развиться у пациентов любого возраста, но воспалительная артропатия, вызванная кристаллами, более вероятна у взрослых. Остеоартроз коленного сустава часто встречается у пожилых людей.
. Отраженная боль, возникающая в результате патологии тазобедренного сустава, такой как смещение эпифиза головки бедренной кости, также может вызывать боль в колене. Активные пациенты чаще имеют острые растяжения связок и травмы от чрезмерной нагрузки, такие как бурсит гусиной лапки и синдром медиальной складки. Травма может привести к острому разрыву или перелому связок, что приводит к острому отеку коленного сустава и гемартрозу. Септический артрит может развиться у пациентов любого возраста, но воспалительная артропатия, вызванная кристаллами, более вероятна у взрослых. Остеоартроз коленного сустава часто встречается у пожилых людей.
Определение основной причины боли в колене может быть затруднено, отчасти из-за обширной дифференциальной диагностики. Как обсуждалось в части I этой статьи, состоящей из двух частей, 1 семейный врач должен быть знаком с анатомией коленного сустава и распространенными механизмами травм, а подробный анамнез и целенаправленное медицинское обследование могут сузить круг возможных причин. Возраст пациента и анатомическая локализация боли — два фактора, которые могут иметь значение для постановки точного диагноза (таблицы 1 и 2) .
Возраст пациента и анатомическая локализация боли — два фактора, которые могут иметь значение для постановки точного диагноза (таблицы 1 и 2) .
| Children and adolescents Patellar subluxation Tibial apophysitis (Osgood-Schlatter lesion) Jumper’s knee (patellar tendonitis) Referred pain: slipped capital femoral epiphysis, others Osteochondritis dissecans | Adults Patellofemoral pain syndrome (хондромаляция надколенника) Синдром медиальной складки Бурсит гусиной лапки Травма: растяжение связок (передняя крестообразная, медиальная коллатеральная, латеральная коллатеральная), разрыв мениска Воспалительная артропатия: ревматоидный артрит, синдром Рейтера Септический артрит | Пожилые люди Остеоартрит Индуцированная кристаллами воспалительная артропатия: подагра, псевдоподагра Подколенная киста (киста Бейкера) |
| Боль в передней части колена |
| Подвывих или вывих надколенника |
| Апофизит большеберцовой кости (поражение Осгуда-Шлаттера) |
| Jumper’s knee (patellar tendonitis) |
| Patellofemoral pain syndrome (chondromalacia patellae) |
| Medial knee pain |
| Medial collateral ligament sprain |
| Medial meniscal tear |
| Pes гусиный бурсит |
| Синдром медиальной складки |
| Боль в латеральном колене |
| Растяжение латеральной коллатеральной связки |
| Lateral meniscal tear |
| Iliotibial band tendonitis |
| Posterior knee pain |
| Popliteal cyst (Baker’s cyst) |
| Posterior cruciate ligament injury |
Дети и подростки
Дети и подростки с болью в колене, вероятно, имеют одно из трех распространенных состояний: подвывих надколенника, апофизит большеберцовой кости или тендинит надколенника. Дополнительные диагнозы, которые следует учитывать у детей, включают соскальзывание эпифиза головки бедренной кости и септический артрит.
Дополнительные диагнозы, которые следует учитывать у детей, включают соскальзывание эпифиза головки бедренной кости и септический артрит.
Подвывих надколенника
Подвывих надколенника является наиболее вероятным диагнозом у девочки-подростка, у которой наблюдаются эпизоды деформации коленного сустава. 2 Эта травма чаще возникает у девочек и молодых женщин из-за увеличения угла четырехглавой мышцы бедра (угла Q), обычно превышающего 15 градусов.
Защемление надколенника вызывается латеральным подвывихом надколенника, обычно присутствует умеренный выпот. Умеренный или сильный отек колена может указывать на гемартроз, который предполагает вывих надколенника с костно-хрящевым переломом и кровотечением.
АПОФИЗИТ ГОЛЕНИ
У мальчика-подростка с болью в передней части колена, локализованной в бугристости большеберцовой кости, вероятно, имеется апофизит большеберцовой кости или поражение Осгуда-Шлаттера 3,4 (рис. 1) . 5 Типичным пациентом является 13- или 14-летний мальчик (или 10- или 11-летняя девочка), который недавно пережил всплеск роста.
5 Типичным пациентом является 13- или 14-летний мальчик (или 10- или 11-летняя девочка), который недавно пережил всплеск роста.
Пациенты с апофизитом большеберцовой кости обычно сообщают о нарастающей и ослабевающей боли в колене в течение нескольких месяцев. Боль усиливается при сидении на корточках, ходьбе вверх или вниз по лестнице или при сильных сокращениях четырехглавой мышцы. Этот апофизит чрезмерного использования усугубляется прыжками и преодолением барьеров, потому что повторяющиеся жесткие приземления создают чрезмерную нагрузку на место прикрепления сухожилия надколенника.
При физикальном осмотре бугристость большеберцовой кости болезненна и опухла, может ощущаться тепло. Боль в колене воспроизводится при активном разгибании или пассивном гиперфлексии колена с сопротивлением. Выпота нет. Рентгенограммы обычно отрицательны; редко они показывают отрыв апофиза бугристости большеберцовой кости. Однако врач не должен ошибочно принимать нормальный вид апофиза большеберцовой кости за отрывной перелом.
ТЕНДОНИТ ПАТЕЛЛАРА
Колено прыгуна (раздражение и воспаление сухожилия надколенника) чаще всего возникает у мальчиков-подростков, особенно во время скачка роста 2 (рис. 1) . 5 Пациент сообщает о неопределенной боли в передней части колена, которая сохраняется в течение нескольких месяцев и усиливается после таких действий, как ходьба по лестнице или бег.
При физикальном осмотре сухожилие надколенника болезненно, и боль воспроизводится при разгибании колена с сопротивлением. Выпота обычно нет. Рентгенограммы не указаны.
ЭПИФИЗ ГОЛОВКИ БЕДРА С СКОЛЬЗЕНИЕМ
Ряд патологических состояний приводит к отдаче боли в колено. Например, у детей и подростков с болью в колене необходимо учитывать возможность соскальзывания эпифиза головки бедренной кости. 6 Пациенты с этим заболеванием обычно жалуются на плохо локализованную боль в колене и отсутствие травм колена в анамнезе.
Типичный пациент со смещением эпифиза головки бедренной кости имеет избыточный вес и сидит на диагностическом столе, при этом пораженное бедро слегка согнуто и ротировано наружу. Осмотр колена нормальный, но боль в тазобедренном суставе возникает при пассивной внутренней ротации или разгибании пораженного бедра.
Осмотр колена нормальный, но боль в тазобедренном суставе возникает при пассивной внутренней ротации или разгибании пораженного бедра.
Рентгенограммы обычно показывают смещение эпифиза головки бедренной кости. Однако отрицательные рентгенограммы не исключают диагноз у пациентов с типичными клиническими проявлениями. Таким пациентам показана компьютерная томография (КТ).
РАССЕКАЮЩИЙ ОСТЕОХОНДРИТ
Рассекающий остеохондрит представляет собой внутрисуставной остеохондроз неизвестной этиологии, характеризующийся дегенерацией и рекальцинозом суставного хряща и подлежащей кости. В колене чаще всего поражается медиальный мыщелок бедренной кости. 7
Пациент жалуется на неопределенную, плохо локализованную боль в колене, а также на утреннюю скованность или рецидивирующий выпот. Если присутствует свободное тело, также могут быть зарегистрированы механические симптомы блокировки или захвата коленного сустава. При физикальном обследовании у пациента может наблюдаться атрофия четырехглавой мышцы или болезненность вдоль пораженной хрящевой поверхности. Может присутствовать легкий суставной выпот. 7
Может присутствовать легкий суставной выпот. 7
Рентгенограммы на обычной пленке могут показать костно-хрящевое поражение или свободное тело в коленном суставе. При подозрении на расслаивающий остеохондрит рекомендуемые рентгенограммы включают переднезаднюю, заднепереднюю туннельную, боковую проекцию и проекцию Мерчанта. Остеохондральные поражения в латеральной части медиального мыщелка бедренной кости могут быть видны только в задне-передней проекции туннеля. Магнитно-резонансная томография (МРТ) обладает высокой чувствительностью при выявлении этих аномалий и показана пациентам с подозрением на костно-хрящевое поражение. 7
Взрослые
СИНДРОМ ПЕРЕГРУЗКИ
Боль в переднем колене
сидя (так называемый «театральный знак»). 8 Пателло-феморальный болевой синдром является частой причиной болей в передней части коленного сустава у женщин.
При физикальном обследовании может быть обнаружен небольшой выпот вместе с крепитацией надколенника при движении. Боль пациента можно воспроизвести, применяя прямое давление на переднюю часть надколенника. Болезненность надколенника можно выявить путем медиального или латерального подвывиха надколенника и пальпации верхней и нижней фасеток надколенника. Рентгенограммы обычно не показаны.
Боль пациента можно воспроизвести, применяя прямое давление на переднюю часть надколенника. Болезненность надколенника можно выявить путем медиального или латерального подвывиха надколенника и пальпации верхней и нижней фасеток надколенника. Рентгенограммы обычно не показаны.
Медиальная боль в колене
Одним из часто игнорируемых диагнозов является синдром медиальной складки . Складка, избыточная медиальная синовиальная оболочка сустава, может воспаляться при повторяющихся чрезмерных нагрузках. 4,9 У пациента остро началась медиальная боль в колене после заметного увеличения обычной активности. При физикальном осмотре в медиальной части колена, непосредственно перед линией сустава, выявляется болезненное подвижное узелковое образование. Выпота в суставах нет, остальная часть коленного сустава в норме. Рентгенограммы не указаны.
Гусиный бурсит — еще одна возможная причина медиальной боли в колене. Сухожильное место прикрепления портняжной, тонкой и полусухожильной мышц в переднемедиальной части проксимального отдела большеберцовой кости образует бурсу гусиной стопы. 9 Бурса может воспалиться в результате чрезмерного использования или прямого ушиба. Бурсит гусиной лапки можно легко спутать с растяжением медиальной коллатеральной связки или, реже, с остеоартритом медиального отдела коленного сустава.
9 Бурса может воспалиться в результате чрезмерного использования или прямого ушиба. Бурсит гусиной лапки можно легко спутать с растяжением медиальной коллатеральной связки или, реже, с остеоартритом медиального отдела коленного сустава.
Пациент с бурситом гусиной лапки жалуется на боль в медиальной части колена. Эта боль может усиливаться при повторяющемся сгибании и разгибании. При физикальном обследовании отмечается болезненность в медиальной части колена, сразу кзади и дистальнее медиальной линии сустава. Выпота в коленном суставе нет, но может быть небольшой отек в месте прикрепления медиальных мышц задней поверхности бедра. Вальгусное стресс-тестирование в положении лежа на спине или сгибание колена с сопротивлением в положении лежа может воспроизвести боль. Рентгенограммы обычно не показаны.
Боль в латеральном колене
Чрезмерное трение между подвздошно-большеберцовой связкой и латеральным мыщелком бедра может привести к тендиниту подвздошно-большеберцовой связки . 9 Этот синдром перенапряжения обычно возникает у бегунов и велосипедистов, хотя он может развиться у любого человека после деятельности, связанной с повторяющимся сгибанием колена. Напряженность подвздошно-большеберцового тракта, чрезмерная пронация стопы, варусная деформация коленного сустава и скручивание большеберцовой кости являются предрасполагающими факторами.
9 Этот синдром перенапряжения обычно возникает у бегунов и велосипедистов, хотя он может развиться у любого человека после деятельности, связанной с повторяющимся сгибанием колена. Напряженность подвздошно-большеберцового тракта, чрезмерная пронация стопы, варусная деформация коленного сустава и скручивание большеберцовой кости являются предрасполагающими факторами.
Пациент с тендинитом подвздошно-большеберцового тракта жалуется на боль в латеральной части коленного сустава. Боль усиливается при физической активности, особенно при беге с горы и подъеме по лестнице. При физикальном осмотре отмечается болезненность в области латерального надмыщелка бедренной кости, примерно на 3 см проксимальнее линии сустава. Также могут присутствовать отек мягких тканей и крепитация, но выпота в суставах нет. Рентгенограммы не указаны.
Реакция Ноубла используется для воспроизведения боли при тендините подвздошно-большеберцового тракта. Когда пациент лежит на спине, врач кладет большой палец на латеральный надмыщелок бедра, в то время как пациент неоднократно сгибает и разгибает колено. Болевые симптомы обычно наиболее выражены при сгибании колена на 30 градусов.
Болевые симптомы обычно наиболее выражены при сгибании колена на 30 градусов.
Тендинит подколенной мышцы — еще одна возможная причина болей в колене сбоку. Однако это состояние встречается довольно редко. 10
ТРАВМА
Растяжение передней крестообразной связки
Повреждение передней крестообразной связки обычно происходит из-за бесконтактных сил торможения, например, когда бегун ставит одну ногу и резко поворачивает в противоположном направлении. Результирующая вальгусная нагрузка на колено приводит к смещению большеберцовой кости вперед и растяжению или разрыву связки. 11 Пациент обычно сообщает о том, что слышит или чувствует «хлопок» во время травмы и должен немедленно прекратить деятельность или соревнование. Отек колена в течение двух часов после травмы свидетельствует о разрыве связки и последующем гемартрозе.
При физикальном обследовании у пациента выявляется выпот в суставах от умеренного до тяжелого, который ограничивает диапазон движений. Тест переднего выдвижного ящика может быть положительным, но может быть и отрицательным из-за гемартроза и защиты мышцами подколенного сухожилия. Тест Лахмана должен быть положительным и более надежным, чем тест переднего выдвижного ящика (см. текст и рисунок 3 в части I этой статьи 1 ).
Тест переднего выдвижного ящика может быть положительным, но может быть и отрицательным из-за гемартроза и защиты мышцами подколенного сухожилия. Тест Лахмана должен быть положительным и более надежным, чем тест переднего выдвижного ящика (см. текст и рисунок 3 в части I этой статьи 1 ).
Рентгенограммы показаны для выявления возможного отрывного перелома большеберцовой кости. МРТ коленного сустава показана как часть предоперационной оценки.
Растяжение медиальной коллатеральной связки
Повреждение медиальной коллатеральной связки встречается довольно часто и обычно является результатом острой травмы. Пациент сообщает о неправильном шаге или столкновении, которое вызывает вальгусную нагрузку на колено, за которой следует немедленное появление боли и отека в медиальной части колена. 11
При физикальном обследовании у пациента с повреждением медиальной коллатеральной связки выявлена точечная болезненность по медиальной линии сустава. Вальгусное стресс-тестирование колена, согнутого на 30 градусов, воспроизводит боль (см. текст и 9).0149 Рисунок 4 в части I настоящего артикула 1 ). Четко определенная конечная точка вальгусного стресс-теста указывает на растяжение связок 1 или 2 степени, тогда как полная медиальная нестабильность указывает на полный разрыв связки (растяжение 3 степени).
Вальгусное стресс-тестирование колена, согнутого на 30 градусов, воспроизводит боль (см. текст и 9).0149 Рисунок 4 в части I настоящего артикула 1 ). Четко определенная конечная точка вальгусного стресс-теста указывает на растяжение связок 1 или 2 степени, тогда как полная медиальная нестабильность указывает на полный разрыв связки (растяжение 3 степени).
Растяжение латеральной коллатеральной связки
Повреждение латеральной коллатеральной связки встречается гораздо реже, чем повреждение медиальной коллатеральной связки. Растяжение боковой коллатеральной связки обычно возникает в результате варусной нагрузки на колено, как это происходит, когда бегун ставит одну ногу, а затем поворачивается к ипсилатеральному колену. 2 Пациент сообщает об остром появлении боли в латеральном колене, требующей немедленного прекращения активности.
При осмотре: точечная болезненность по латеральной линии сустава. Нестабильность или боль возникают при варусном нагрузочном тестировании колена, согнутого на 30 градусов (см. текст и рисунок 4 в части I этой статьи 1 ). Рентгенограммы обычно не показаны.
текст и рисунок 4 в части I этой статьи 1 ). Рентгенограммы обычно не показаны.
Разрыв мениска
Мениск может быть остро разорван при внезапном скручивании колена, например, когда бегун внезапно меняет направление. 11,12 Разрыв мениска также может возникать в связи с длительным дегенеративным процессом, особенно у пациентов с недостаточностью передней крестообразной связки коленного сустава. Пациент обычно сообщает о повторяющихся болях в коленях и эпизодах захвата или блокировки коленного сустава, особенно при приседании или скручивании колена.
При физикальном обследовании обычно выявляют умеренный выпот и болезненность по медиальной или латеральной линии сустава. Также может быть заметна атрофия медиальной косой широкой мышцы бедра. Тест Мак-Мюррея может быть положительным (см. 9).0149 Рисунок 5 в части I этой статьи 1 ), но отрицательный результат теста не исключает возможности разрыва мениска.
Рентгенограммы на обычной пленке обычно отрицательны и редко показаны. МРТ является радиологическим тестом выбора, потому что он демонстрирует наиболее значительные разрывы мениска.
МРТ является радиологическим тестом выбора, потому что он демонстрирует наиболее значительные разрывы мениска.
ИНФЕКЦИЯ
Инфекция коленного сустава может возникнуть у пациентов любого возраста, но чаще встречается у тех, чья иммунная система ослаблена раком, сахарным диабетом, алкоголизмом, синдромом приобретенного иммунодефицита или терапией кортикостероидами. Пациент с септическим артритом сообщает о внезапном появлении боли и припухлости колена без предшествующей травмы. 13
При осмотре колено теплое, опухшее и очень болезненное. Даже легкое движение коленного сустава вызывает сильную боль.
Артроцентез показывает мутную синовиальную жидкость. Анализ жидкости показывает количество лейкоцитов (WBC) выше 50 000 на мм 90 161 3 90 162 (50 × 10 90 161 9 90 162 на л), более 75 процентов (0,75) полиморфноядерных клеток, повышенное содержание белка (более 3 г на дл [30 г на л]) и низкой концентрации глюкозы (более чем на 50 процентов ниже, чем концентрация глюкозы в сыворотке). 14 Окраска жидкости по Граму может выявить возбудитель. Общие патогены включают Staphylococcus aureus , виды Streptococcus, Haemophilus influenzae и Neisseria gonorrhoeae .
14 Окраска жидкости по Граму может выявить возбудитель. Общие патогены включают Staphylococcus aureus , виды Streptococcus, Haemophilus influenzae и Neisseria gonorrhoeae .
Гематологические исследования показывают повышенный уровень лейкоцитов, повышенное количество незрелых полиморфноядерных клеток (т. е. сдвиг влево) и повышенную скорость оседания эритроцитов (обычно более 50 мм в час).
Пожилые люди
ОСТЕОАРТРИТ
Остеоартроз коленного сустава является распространенной проблемой после 60 лет. Пациента беспокоят боли в коленях, которые усиливаются при физической нагрузке и уменьшаются в покое. 15 У пациента нет системных симптомов, но обычно он просыпается с утренней скованностью, которая несколько исчезает при активности. В дополнение к хронической тугоподвижности и боли в суставах пациент может сообщать об эпизодах острого синовита.
Выводы при физикальном обследовании включают уменьшение диапазона движений, крепитацию, умеренный суставной выпот и пальпируемые остеофитные изменения в коленном суставе.
При подозрении на остеоартрит рекомендуемые рентгенограммы включают передне-заднюю и задне-переднюю туннельные проекции с нагрузкой, а также проекцию Мерчанта без нагрузки и боковую проекцию. Рентгенограммы показывают сужение суставной щели, склероз субхондральной кости, кистозные изменения и образование гипертрофических остеофитов.
ВОСПАЛИТЕЛЬНАЯ АРТРОПАТИЯ, ИНДУЦИРОВАННАЯ КРИСТАЛЛАМИ
Острое воспаление, боль и отек при отсутствии травмы предполагают возможность воспалительной артропатии, вызванной кристаллами, такой как подагра или псевдоподагра. 16,17 Подагра обычно поражает колено. При этой артропатии кристаллы урата натрия осаждаются в коленном суставе и вызывают интенсивную воспалительную реакцию. При псевдоподагре возбудителем являются кристаллы пирофосфата кальция.
При осмотре: коленный сустав гиперемирован, теплый, болезненный и опухший. Даже минимальный диапазон движений чрезвычайно болезненный.
Артроцентез показывает прозрачную или слегка мутную синовиальную жидкость. Анализ жидкости дает количество лейкоцитов от 2000 до 75000 на мм 9 .0161 3 (от 2 до 75 × 10 9 на л), высоким содержанием белка (более 32 г на дл [320 г на л]) и концентрацией глюкозы, которая составляет примерно 75 процентов от концентрации глюкозы в сыворотке. 14 При микроскопии синовиальной жидкости в поляризованном свете выявляются палочки с отрицательным двулучепреломлением у пациента с подагрой и ромбы с положительным двойным лучепреломлением у пациента с псевдоподагрой.
Анализ жидкости дает количество лейкоцитов от 2000 до 75000 на мм 9 .0161 3 (от 2 до 75 × 10 9 на л), высоким содержанием белка (более 32 г на дл [320 г на л]) и концентрацией глюкозы, которая составляет примерно 75 процентов от концентрации глюкозы в сыворотке. 14 При микроскопии синовиальной жидкости в поляризованном свете выявляются палочки с отрицательным двулучепреломлением у пациента с подагрой и ромбы с положительным двойным лучепреломлением у пациента с псевдоподагрой.
ПОДКОЛЕННАЯ КИСТА
Подколенная киста (киста Бейкера) является наиболее распространенной синовиальной кистой коленного сустава. Начинается с задне-медиальной стороны коленного сустава на уровне икроножно-полуперепончатой сумки. Пациент сообщает о постепенном появлении слабой или умеренной боли в подколенной области колена.
При физикальном осмотре пальпируется пальпируемая полнота в медиальной части подколенной области, в месте отхождения медиальной головки икроножной мышцы или вблизи нее. Тест Мак-Мюррея может быть положительным при повреждении медиального мениска. Окончательный диагноз подколенной кисты можно поставить с помощью артрографии, УЗИ, КТ или, реже, МРТ.
Тест Мак-Мюррея может быть положительным при повреждении медиального мениска. Окончательный диагноз подколенной кисты можно поставить с помощью артрографии, УЗИ, КТ или, реже, МРТ.
Курсы — Knewton
Как получить курсы alta
Для пользовательских ISBN alta: обращайтесь в службу поддержки по вопросам о партнерстве и пользовательских продуктах Alta.
- Все
- Биология
- Химия
- Экономика
- Математика
- Физика
- Психология
- Статистика
Алгебра и тригонометрия
Альта-Алгебра и Тригонометрия объединяет материалы обоих курсов, чтобы обеспечить более гибкие учебные планы в различных математических программах. Этот курс также можно использовать в модели Just-in-Time Corequisite.
Этот курс также можно использовать в модели Just-in-Time Corequisite.
Содержание
Деловой расчет
Alta Business Calculus предназначен для односеместрового настраиваемого курса бизнес-исчисления, включающего такие темы, как пределы и производная, интеграция, многомерное исчисление и полиномы Тейлора. Этот курс также можно использовать в модели Just-in-Time Corequisite.
Содержание
Бизнес-статистика
Alta Business Statistics предназначен для вводного курса статистики продолжительностью один семестр, ориентированного на бизнес, включая такие темы, как выборка и данные, описательная статистика и доверительные интервалы. Этот курс также можно использовать в модели Just-in-Time Corequisite.
Содержание
Раннее трансцендентальное исчисление с обзором предварительного исчисления
Knewton Alta Calculus Early Transcendentals with Precalculus Review был разработан, чтобы включать в себя всесторонний обзорный материал Precalculus, чтобы помочь лучше подготовить студентов к исчислению. В курс также были добавлены цели дополнительного обучения, чтобы дать инструкторам больше контроля и детализации.
В курс также были добавлены цели дополнительного обучения, чтобы дать инструкторам больше контроля и детализации.
Содержание
Исчисление, Ранние Трансцендентальные
Альта-исчисление предназначено для типичного трехсеместрового курса общего исчисления с такими темами, как пределы, дифференцирование, интегрирование, последовательности и ряды, векторы, исчисление с несколькими переменными и дифференциальные уравнения второго порядка. Этот курс также можно использовать в модели Just-in-Time Corequisite.
Содержание
Высшая алгебра
Alta College Algebra предназначен для типичного курса алгебры колледжа продолжительностью один семестр и включает такие темы, как уравнения и неравенства, полиномиальные и рациональные функции, экспоненциальные и логарифмические функции, а также системы уравнений и неравенств. Этот курс также можно использовать в модели Just-in-Time Corequisite.
Содержание
Алгебра колледжа с необходимой поддержкой: целевой обзор
Alta College Algebra with Corequisite Support: A Targeted Review — это односеместровый курс, который зависит от результатов на уровне колледжа по алгебре колледжа, но также предлагает возможность целевых дискретных повторных заданий на более низком уровне, чтобы помочь некоторым учащимся подготовиться к материал уровня колледжа, который составляет их конечную цель в алгебре колледжа.
Содержание
Колледж физики
Alta for College Physics предназначен для двухсеместрового вводного курса физики на основе алгебры и обеспечивает среду, которая формирует необходимые навыки и уверенность учащихся, устраняя пробелы в знаниях с помощью своевременных инструкций, бесплатных диаграмм тела на основе Desmos и базовые курсы повышения квалификации и математические бустеры.
Содержание
Концепции биологии
Курс «Концепции биологии» рассчитан на один семестр неспециального курса биологии и включает такие темы, как структура и функции клеток, фотосинтез, деление клеток и генетика, молекулярная биология и биотехнология, эволюция, строение и функции животных и экология.
Содержание
Элементарная алгебра
Элементарная алгебра Alta предназначена для типичного односеместрового курса начальной алгебры, включая такие темы, как действительные числа и их действия, графические линии и квадратные уравнения.
Содержание
Элементарная и средняя алгебра
Alta Элементарная и промежуточная алгебра объединяет материалы обоих курсов, что позволяет использовать более гибкие учебные программы в различных математических программах.
Содержание
Конечная математика
Alta Finite Mathematics рассчитан на односеместровый курс по математике, применимый для студентов, изучающих бизнес, социальные науки, науки о жизни или экономику. Этот курс также можно использовать в модели Just-in-Time Corequisite.
Содержание
Конечная математика с бизнес-исчислением
Alta Finite Mathematics with Business Calculus рассчитан на двухсеместровый курс, охватывающий такие темы, как системы линейных уравнений и матриц, финансовая математика, логика, статистика и многомерное исчисление. Этот курс также можно использовать в модели Just-in-Time Corequisite.
Этот курс также можно использовать в модели Just-in-Time Corequisite.
Содержание
Основы математики
Alta Foundations of Mathematics сочетает в себе материал из предварительной алгебры, элементарной алгебры и промежуточной алгебры, что позволяет гибко комбинировать содержание в различных типах программ по математике для раннего или развивающего обучения.
Содержание
Общая, органическая и биологическая химия (GOB)
Alta Общая, органическая и биохимия — это курс продолжительностью один или два семестра, предназначенный для студентов, чьи профессиональные цели требуют понимания химии, но не овладения ею. Этот курс могут пройти многие студенты, изучающие специальности, связанные со здоровьем.
Содержание
Алгебра среднего уровня
Alta Intermediate Algebra предназначен для типичного односеместрового курса алгебры среднего уровня, включая такие темы, как построение графиков функций, решение линейных уравнений, радикальные функции и уравнения и биномиальная теорема.
Содержание
Введение в химию
Альта Введение в химию направлен на развитие основных химических принципов, таких как атомная структура, химическая классификация, связь, химические реакции, газовые законы и термодинамика. Курс был разработан, чтобы соответствовать объему и последовательности типичного односеместрового вводного курса химии.
Содержание
Курс повышения математической грамотности
КурсAlta Math Literacy был разработан, чтобы соответствовать объему и последовательности типичного односеместрового курса математической грамотности.
Содержание
Преалгебра
Предварительная алгебра Alta разработана для типичного односеместрового курса предварительной алгебры с такими темами, как целые числа, дроби, геометрия и графики.
Содержание
Преалгебра и элементарная алгебра
Предварительная алгебра Альта и Элементарная алгебра объединяют материалы обоих курсов, чтобы обеспечить более гибкие учебные программы в программах начальной математики и развития.
Содержание
Предварительный расчет
Alta Precalculus предназначен для типичного односеместрового курса предварительного исчисления с такими темами, как периодические функции, тригонометрические тождества и уравнения, а также пределы и непрерывность. Этот курс также можно использовать в модели Just-in-Time Corequisite.
Содержание
Основы экономики
Alta Principles of Economics предназначен для настраиваемого вводного курса микроэкономики и макроэкономики продолжительностью один или два семестра, включая такие темы, как спрос и предложение, денежно-кредитная политика, международная торговля и эластичность.
Содержание
Основы общей химии
Alta Principles of General Chemistry предназначен для типичного двухсеместрового введения в курс химии, включая такие темы, как атомы, молекулы и ионы, вещества и растворы, кинетика и электрохимия.
Содержание
Основы общей химии (Atoms First)
Alta Principles of General Chemistry (Atoms First) предназначен для типичного двухсеместрового введения в курс химии, включая такие темы, как атомы, молекулы и ионы, вещества и растворы, кинетика и электрохимия.
Содержание
Принципы макроэкономики
Альта Макроэкономика предназначена для типичного односеместрового введения в курс макроэкономики, включая такие темы, как ВВП, инфляция, совокупный спрос и совокупное предложение, денежно-кредитная политика и международная торговля.
Содержание
Принципы микроэкономики
Альта Микроэкономика предназначена для типичного односеместрового введения в курс микроэкономики, включая такие темы, как спрос и предложение, эластичность и потребительский выбор.
Содержание
Психология
Alta Psychology предназначен для вводного или общего курса психологии и легко адаптируется к любой программе. Он развивает понимание основ психологии и психологических исследований, биопсихологии, состояний сознания, ощущений и восприятия, обучения, мышления и интеллекта, памяти, психологии развития, эмоций и мотивации, личности, социальной психологии, производственной/организационной психологии, стресса и здоровья, психологии. расстройства, а также терапия и лечение.
Он развивает понимание основ психологии и психологических исследований, биопсихологии, состояний сознания, ощущений и восприятия, обучения, мышления и интеллекта, памяти, психологии развития, эмоций и мотивации, личности, социальной психологии, производственной/организационной психологии, стресса и здоровья, психологии. расстройства, а также терапия и лечение.
Содержание
Количественное мышление
Alta Quantitative Reasoning — курс продолжительностью один или два семестра, предназначенный для студентов, которым требуются навыки количественной грамотности. Многие студенты, получающие степень, требующую общего образования по математике, будут проходить этот курс. Этот курс также можно использовать в модели Just-in-Time Corequisite.
Содержание
Количественное мышление с соответствующей поддержкой: целевой обзор
Alta Quantitative Reasoning with Corequisite Support: A Targeted Review — это курс продолжительностью один семестр, который основан на результатах колледжа по Quantitative Reasoning, но также предлагает возможность для целевых дискретных обзорных заданий на более низком уровне (или на вспомогательном уровне). область), чтобы помочь подготовить некоторых студентов к материалу уровня колледжа, который составляет их конечную цель.
область), чтобы помочь подготовить некоторых студентов к материалу уровня колледжа, который составляет их конечную цель.
Содержание
Исчисление одной переменной, ранние трансцендентальные
Alta Single Variable Calculus предназначен для типичного двухсеместрового общего курса исчисления, включая такие темы, как пределы, дифференцирование, интегрирование, а также последовательности и ряды. Этот курс также можно использовать в модели Just-in-Time Corequisite.
Содержание
Статистическое мышление
Alta Statistical Reasoning — курс продолжительностью один или два семестра, знакомящий с основными понятиями логики и приложениями статистики. Многие студенты, получающие степень, требующую общего образования по математике, будут проходить этот курс. Этот курс также можно использовать в модели Just-in-Time Corequisite.
Содержание
Статистика
Alta Statistics предназначен для типичного курса статистики, рассчитанного на один семестр, с такими темами, как выборка и данные, вероятность, нормальное распределение и доверительные интервалы. Этот курс также можно использовать в модели Just-in-Time Corequisite.
Этот курс также можно использовать в модели Just-in-Time Corequisite.
Содержание
Статистика с соответствующей поддержкой: Целевой обзор
Alta Statistics with Corequisite Support: A Targeted Review — это курс продолжительностью один семестр, который зависит от результатов на уровне колледжа по статистике, но также предлагает возможность для целевых дискретных обзорных заданий от Preалгебры, чтобы помочь подготовить некоторых студентов к поступлению в колледж. уровень материала, который составляет их конечную цель.
Содержание
Обзор экономики
Alta Survey of Economics предназначен для настраиваемого вводного курса микроэкономики и макроэкономики продолжительностью один семестр, включая такие темы, как спрос и предложение, денежно-кредитная политика, международная торговля и эластичность.
Содержание
Обзор математики
Alta Survey of Mathematics предназначен для односеместрового курса, охватывающего математику, с которой вы можете столкнуться в повседневной жизни. Темы, затронутые в этом курсе, включают критическое мышление, множества и логику и потребительскую математику. Этот курс также можно использовать в модели Just-in-Time Corequisite.
Темы, затронутые в этом курсе, включают критическое мышление, множества и логику и потребительскую математику. Этот курс также можно использовать в модели Just-in-Time Corequisite.
Содержание
Тригонометрия
Альта-тригонометрия предназначена для типичного односеместрового курса тригонометрии, включая такие темы, как радианные меры и их применение, графики тригонометрических функций, тригонометрические уравнения и векторы.
Содержание
Тригонометрия с соответствующей поддержкой: целевой подход
Альта-тригонометрия с соответствующей поддержкой была разработана для соответствия объему и последовательности типичного односеместрового курса тригонометрии в сочетании с материалом, который можно использовать для целевых, дискретных заданий, чтобы помочь некоторым студентам подготовиться к материалу, который составляет их конечные цели в тригонометрии. .
Содержание
Готовы к альте?
Запросить доступГотовы к альте в вашем курсе?
Заполните форму, чтобы рассказать о себе больше, и вскоре кнерд свяжется с вами.
Инструмент корректировки дифференциации
Стратегии корректировки дифференциации, представленные на этой странице, являются рекомендациями для удовлетворения особых потребностей в обучении высокопотенциальных и одаренных учащихся.
Примеры каждой корректировки дифференциации приведены в соответствие с ресурсами из Digital Learning Selector (DLS). Профессиональное обучение для поддержки использования приложений DLS для настройки дифференциации можно найти на MyPL.
Регулировка: Сложность
| Стратегии | Примеры применения |
|---|---|
|
|
Регулировка: Вызов
| Стратегии | Примеры применения |
|---|---|
|
|
| Стратегии | Примеры применения |
|---|---|
|
|
Настройка: Абстракция
| Стратегии | Примеры применения |
|---|---|
|
|
Адаптация: творческое и критическое мышление
| Стратегии | Примеры применения |
|---|---|
|
|
Приспособление: мышление высшего порядка
| Стратегии | Примеры применения |
|---|---|
|
|
| Стратегии | Примеры применения |
|---|---|
|
|
Настройка: Подлинность
| Стратегии | Примеры применения |
|---|---|
|
|
Адаптация: среда обучения
| Стратегии | Примеры применения |
|---|---|
|
|
Обучение и сборы | Единая регистрация и финансовые услуги
Плата за обучение
Ищи:- Этот сайт
- Все UWM
Быстрые ссылки
Тенденции и события
Контактная информация
Суммы, указанные в следующих таблицах сборов, не включают плату за специальные курсы, плату за дистанционное обучение или дифференцированное обучение, которое будет взиматься в дополнение к обычной плате за обучение. Полный список см. в соответствующем Расписании занятий.
Полный список см. в соответствующем Расписании занятий.
Осень 2022
Лето 2022
Spring 2022
Winterim 2022
Осень 2021
Summer 2021
Spring 2021
Winterim 2021
Осень 20209
0004 Summer 2020
Spring 2020
Uwinterim 2020
Осень 2019
Лето 2019
Лето 2019
Таблица вознаграждений магистров бизнеса
Таблица вознаграждений магистров медицинских наук
Таблица вознаграждений за аудит
Обязательные / отдельные (сегментные) сборы
Дополнительные / дифференцированные сборы за кредит
Весна 2019
Весна 2019 г. Срок службы обучения и платы — 22 января 2019 г.
График платы за комиссионные по сборе бакалавриата
График платы за платную плату
График платы за комиссию по диссертаторам
. / Раздельные (Seg) студенческие сборы
Дополнительные / дифференцированные сборы за кредит
UWinteriM 2019
UWinterIM 2019 Плата за обучение и оплата Срок оплаты — 2 января 2019 г.
Расценки для бакалавров
Расценки для выпускников
Расценки для диссертаций
Расценки для магистров бизнеса
Расценки для магистров медицинских наук
Расценки для аудиторов
Дополнительные / дифференцированные сборы за кредит
Осень 2018 г.
Осень 2018 г. Срок обучения и оплаты — 4 сентября 2018 г.
График оплаты бакалавриата
График оплаты магистратуры
График оплаты диссертации
График оплаты магистратуры по бизнесу
График оплаты магистра наук о здоровье
Перечень сборов за аудит
Обязательные / отдельные (сегментные) студенческие сборы
Дополнительные / дифференцированные сборы за кредит
Оценки/возвраты для снижения кредитной нагрузки. Процентные оценки устанавливаются системой Университета Висконсина. Пожалуйста, посетите административную политику системы UW 805. Политика обучения и комиссий для кредитных инструкций, раздел C.4 Возврат/снятие средств/снятие средств для возмещения и Графики платежей для снятия или списания средств.
Интерактивный календарь добавления/удаления UWM позволяет просматривать крайние сроки добавления, исключения или отказа от занятий. Вы также можете просмотреть любые связанные сборы или оценки за обучение для внесения изменений в свое расписание после начала семестра.
Уровень оплаты: уровень оплаты (выпускник или бакалавриат) определяет карьеру студента. Студенты, принятые в качестве аспирантов со степенью или без степени, платят за все пройденные курсы.
Миннесота-Висконсин Взаимная плата за обучение: Соглашение о взаимности за обучение между Миннесотой и Висконсином позволяет жителям Миннесоты, посещающим Висконсинские учебные заведения, получать специальную ставку. Если вы хотите воспользоваться Соглашением о взаимности в оплате обучения между Миннесотой и Висконсином, подайте заявку на сертификацию в качестве резидента Миннесоты.
Программа студенческого обмена Среднего Запада (MSEP): Программа студенческого обмена Среднего Запада (MSEP) — это программа взаимного обучения для нескольких штатов. Студенты, которые являются законными жителями определенных штатов и соответствуют всем критериям приемлемости и срокам для конкретного учебного заведения, могут претендовать на скидку на обучение MSEP. Чтобы узнать больше об этой программе в UWM, позвоните в отдел набора и информационно-пропагандистской деятельности по телефону 414/229-2222.
Студенты, которые являются законными жителями определенных штатов и соответствуют всем критериям приемлемости и срокам для конкретного учебного заведения, могут претендовать на скидку на обучение MSEP. Чтобы узнать больше об этой программе в UWM, позвоните в отдел набора и информационно-пропагандистской деятельности по телефону 414/229-2222.
Обязательные/отдельные платежи: Отдельный взнос является частью общей суммы, выплачиваемой Университету студентами, посещающими кредитные курсы. Студенты, набравшие менее восьми кредитов в осеннем и весеннем семестре (шесть кредитов в летнем семестре), платят пропорциональную плату. Сумма, подлежащая оценке, определяется частично Студенческой ассоциацией и частично ректором. Эти средства предназначены для поддержки определенных студенческих услуг (см. Таблицу обязательных/раздельных сборов, расположенную под соответствующим графиком обучения и оплаты выше). Студенты, записавшиеся исключительно на курсы с оплатой вместо обучения (FILT), не оплачивают отдельные сборы и не смогут пользоваться некоторыми объектами кампуса или получить проездной на университетский автобус. Если вы попадаете в эту категорию, но хотите иметь полный доступ ко всем объектам кампуса, вы можете заплатить дополнительную плату в зависимости от количества взятых кредитов. Обратитесь в кассу МТИ 285 (414/229-4914) для получения дополнительной информации.
Если вы попадаете в эту категорию, но хотите иметь полный доступ ко всем объектам кампуса, вы можете заплатить дополнительную плату в зависимости от количества взятых кредитов. Обратитесь в кассу МТИ 285 (414/229-4914) для получения дополнительной информации.
Некредитные курсы: Плата за некредитные курсы оценивается так же, как и за обычные кредитные курсы.
UPASS: UPASS — это абонемент на семестр/лето для неограниченного бесплатного пользования местными пригородными автобусами. Осенний UPASS также действует во время UWinterIM.
Справочник персонала офиса Bursar
Тенденции и события
Быстрые ссылки
Навигация
Набор инструментов для учащихся
Магазин учебников
Контактная информация
Мы:
Офис регистратора UWM
Mellencamp Hall Room 274
Свяжитесь с нами по поводу зачисления, планирования получения степени, вашей личной информации или других вопросов. >>
>>
Финансовая помощь UWM, пособия по трудоустройству студентов и военному образованию
Mellencamp Hall Room 162
Свяжитесь с нами по вопросам финансов, льгот на образование для ветеранов, студенческих кредитов или по другим финансовым вопросам. >>
Офис UWM Bursar’s
Mitchell Hall Room 285
Свяжитесь с нами по поводу осуществления платежей, планов рассрочки или других вопросов по оплате. >>
Найдите нас
3 способа планирования для разных учеников: что делают учителя
В Волшебник страны Оз Дороти и команда настолько напуганы загадочной личностью Волшебника, что им трудно говорить с ним на равных. Страх и разочарование переполняют их, когда они слепо соглашаются на самоубийственную миссию, чтобы убить Ведьму Запада. Взамен каждый из них получает ценный приз: сердце, мозг, мужество и дорогу домой. По иронии судьбы, у них уже есть эти дары, которые они обнаруживают только после того, как раскрывают человека за занавеской, изображающего из себя сварливого волшебника.
Дифференцированное обучение (DI) завораживает педагогов тем, насколько оно отвечает потребностям всех учащихся. Набор навыков, необходимых для дифференциации, кажется мистическим для некоторых и непостижимым для других в этой среде государственных стандартов и тестов с высокими ставками. Где найти время? Реальность такова, что у каждого учителя уже есть инструменты, позволяющие эффективно дифференцировать всех учащихся. Я обращаюсь к некоторым из этих элементов, таких как туман оценок, в других сообщениях Edutopia.
Элементы DI впервые были представлены мне в Как дифференцировать обучение в классах для смешанных способностей Кэрол Томлинсон, и мое понимание позже углубилось благодаря моему другу и наставнику доктору Сьюзан Аллан. Ядром дифференциации являются отношения между учителями и учениками. Ответственность учителя заключается в том, чтобы соединить содержание, процесс и продукт. Учащиеся реагируют на обучение на основе готовности, интересов и профиля обучения. В этом посте мы рассмотрим роль учителя в эффективном планировании DI, а в следующих трех постах посмотрим, как реагируют ученики.
В этом посте мы рассмотрим роль учителя в эффективном планировании DI, а в следующих трех постах посмотрим, как реагируют ученики.
Изображение предоставлено: John McCarthy
Содержание, процесс и результат — это то, к чему учителя постоянно обращаются во время планирования урока и обучения. Это области, в которых учителя имеют огромный опыт во всем, от планирования урока до оценивания. Как только убрана завеса, отделяющая эти три области, удовлетворение разнообразных потребностей учащихся становится очевидным и легким, потому что оно присутствовало всегда.
Дифференциальный контент
Контент включает знания, концепции и навыки, которые учащиеся должны усвоить в соответствии с учебной программой. Дифференциация контента включает в себя использование различных форматов доставки, таких как видео, чтение, лекции или аудио. Контент может быть разбит на части, разделен через графические органайзеры, адресован через группы-головоломки или использован для предоставления различных методов решения уравнений. Студенты могут иметь возможность выбирать содержание, исходя из своих интересов.
Студенты могут иметь возможность выбирать содержание, исходя из своих интересов.
Например, на уроке дробей учащиеся могли:
- Посмотрите обзорное видео Академии Хана.
- Завершите модель Фрайера для академической лексики, такой как знаменатель и числитель.
- Посмотрите и обсудите демонстрацию дробей через разрезание торта.
- Съешь торт.
Этот пример должен убедить учителей в том, что дифференциация может происходить в целых группах. Если мы предоставляем различные способы изучения результатов контента, учащиеся находят разные способы подключения.
Процесс дифференциации
Процесс – это то, как учащиеся понимают содержание. Им нужно время, чтобы обдумать и переварить учебные действия, прежде чем перейти к следующему сегменту урока. Подумайте о семинаре или курсе, где к концу сеанса вы чувствовали себя переполненным информацией, возможно, даже ошеломленным. Обработка помогает учащимся оценить, что они делают и чего не понимают. Это также возможность формативной оценки для учителей, позволяющая следить за успеваемостью учащихся.
Это также возможность формативной оценки для учителей, позволяющая следить за успеваемостью учащихся.
Например, один или два сеанса обработки за каждые 30 минут обучения уменьшают чувство насыщения содержанием. Рефлексия — мощный навык, который развивается во время обработки переживаний. Некоторые стратегии включают в себя:
- Think-Pair-Share
- Ведение журнала
- Партнерский разговор
- Сохранить последнее слово (PDF)
- Литературные кружки (которые также поддерживают дифференциацию контента)
Из этих трех элементов DI меньше всего используется процессный опыт. Начните с любой из общих стратегий и убедитесь в долгосрочном положительном влиянии на обучение.
Дифференциация продукта
Дифференциация продукта, вероятно, является наиболее распространенной формой дифференциации.
- Учителя предоставляют выбор, а учащиеся выбирают один из форматов.
- Студенты предлагают свои варианты.

Продукты могут различаться по сложности, чтобы соответствовать уважительному уровню для каждого учащегося. (Я обсуждаю готовность в другом посте.) Ключом к выбору продукта является наличие четких академических критериев, понятных учащимся. Когда продукты четко согласованы с целями обучения, голос и выбор учащихся процветают, а также обеспечивается внимание к важному содержанию.
Например, одна из моих любимых практик — предлагать три или четыре варианта товаров. Все варианты, кроме последнего, разработаны заранее для учащихся, которые хотят получить полную картину того, что необходимо сделать. Последний вариант бессрочный, карт-бланш. Учащиеся придумывают другую идею продукта и предлагают ее учителю. Они должны показать, как вариант их продукта будет соответствовать академическим критериям. Учитель может одобрить предложение как есть или попросить внести изменения. Если предложение слишком расфокусировано, учащиеся работают над развитием новой идеи. Если они не могут представить утвержденное предложение к установленному сроку, они должны выбрать один из заранее определенных продуктов.

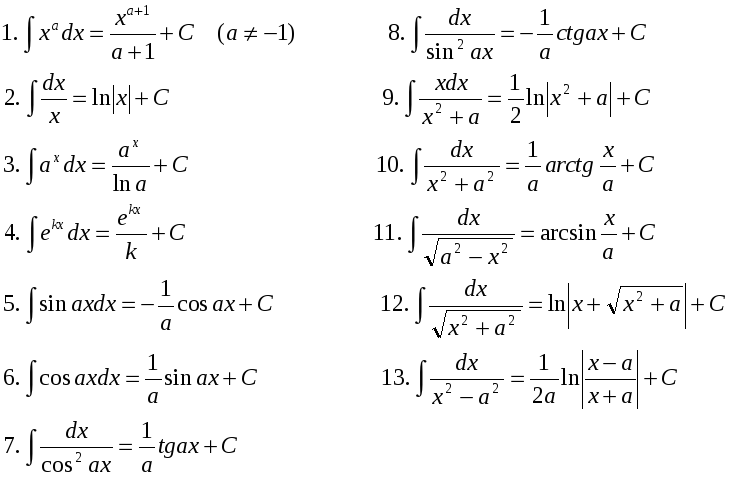

 (C )’ = 1, (x )’ = 1
(C )’ = 1, (x )’ = 1

 (ax )’ = ax ln a ,
(ax )’ = ax ln a ,

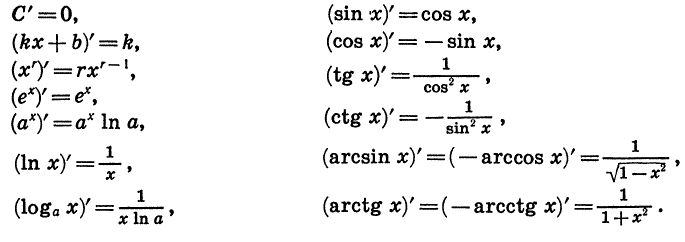


 (arcsin x )’ =
(arcsin x )’ = (arccos x )’ = −
(arccos x )’ = −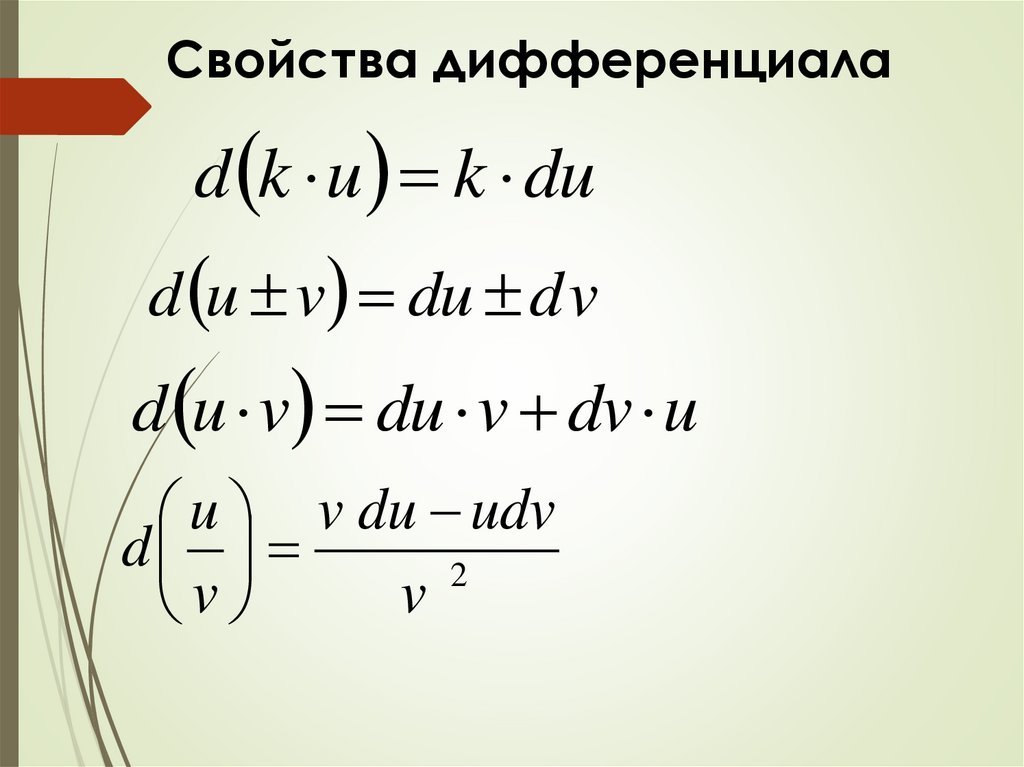 (arctgx )’ =
(arctgx )’ = (arcctgx )’ = −
(arcctgx )’ = − ∫
∫
 04.20151.47 Mб21стихи о лете.pdf
04.20151.47 Mб21стихи о лете.pdf 2}\right|\right.\right)+C\\\)
2}\right|\right.\right)+C\\\)