Таблица для параболы: Построение графика квадратичной функции — урок. Алгебра, 8 класс.

Урок алгебры в 9-м классе по теме «Сдвиг графика квадратичной функции вдоль осей координат «

Цели:

• интерпретировать графическую запись с аналитической для графиков функций вида у = ах² , у = ах² + q, у = а(х + p)²;
• обобщить выводы для функции  вида у = а(х + p)² + q;
• развивать графические навыки.

Учащиеся должны:

знать:
– с помощью каких сдвигов вдоль координатных осей из графиков функции у = ах2 можно получить параболу, задаваемую уравнением  у = ах² + q, у = а(х + p)², у = а(х + p)² + q;
уметь:
– в конкретных случаях построить параболы у = ах² + q, у = а(х + p)²; у = а(х + p

)² + q;
– изображать параболы (отмечать вершину, проводить ось симметрии, показывать – направление ветвей).

Тип урока: урок ознакомления с новым материалом.

Оборудование: компьютер,  проектор.

Дидактическое обеспечение урока: презентация Power Point.

ХОД УРОКА

I. Организационный момент

Сообщение темы и постановка целей урока. (Слайды 1-3).

II. Актуализация знаний учащихся

Устная работа.

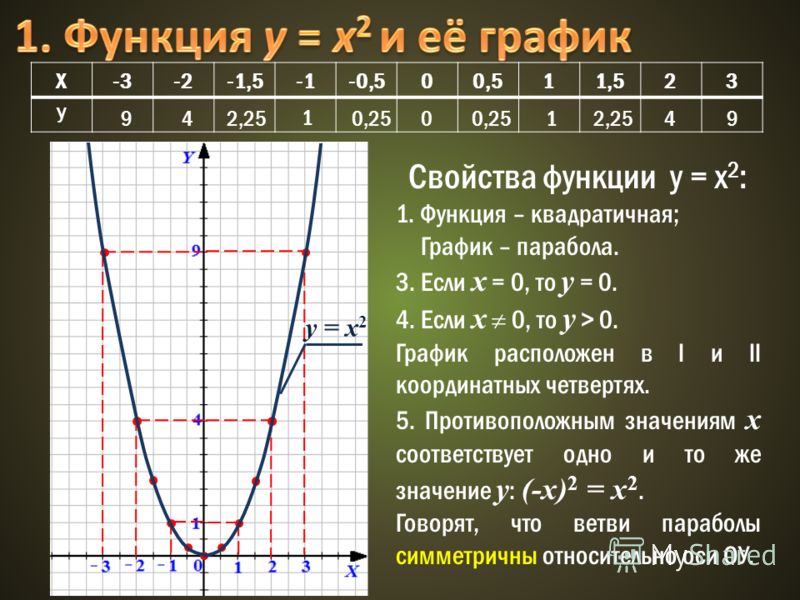
• Опишите свойства функции, используя график  
• Установите соответствие между графиками функций и  формулами. (Слайды 4-5).

III. Изучение нового материала

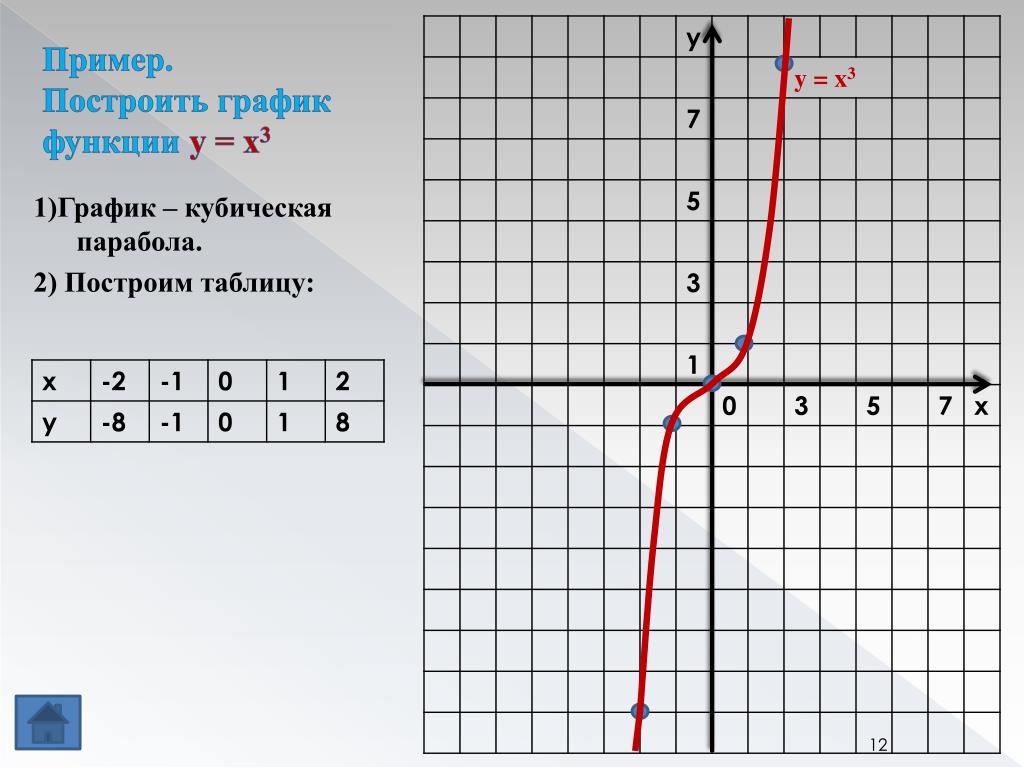
1. Учитель: Постройте  график функции вида

(Слайд 6)

На слайде заготовлена таблица значений

х. Учащиеся переносят таблицу в тетрадь,  им дается время посчитать соответствующие значения y и  занести их в таблицу, а затем идет проверка. На координатной плоскости в тетрадях учащиеся по точкам строят график.

2. Учитель: Постройте график функциу = ах² + q:

1-й. вариант:  

2-й вариант:

(Слайд 7. Анимация сдвигов графиков на слайде помогает сделать вывод.)

На слайде заготовлены таблицы значений х. Учащиеся переносят таблицу в тетрадь,  им дается время посчитать соответствующие значения y и  занести их в таблицу, а затем идет проверка. На координатной плоскости в тетрадях учащиеся по точкам строят графики своих функций. После построения графика в первом варианте он сравнивается с исходным. Ребята проводят анализ и делают вывод, а затем аналогично для второго варианта.

3. Обобщение полученных выводов:

График функции у = ах² + q может быть получен из графика функции у = ах² путем переноса его вдоль оси Оу вверх на отрезок длины q, если q > 0, или вниз на отрезок длины | q |, если q < 0. При этом вершина параболы окажется в точке (0; q).

(Слайд 8. Анимация сдвигов графиков на слайде помогает лучшему восприятию правила.)

4. Учитель: Постройте график функции у  =  а(х + p)²:

1-й вариант:

2-й вариант:

(Слайд 9. Анимация сдвигов графиков на слайде помогает сделать вывод.)

На  слайде заготовлены таблицы значений х. Учащиеся переносят таблицу в тетрадь,  им дается время посчитать соответствующие значения y и  занести их в таблицу, а затем идет проверка. На координатной плоскости в тетрадях учащиеся по точкам строят графики своих функций. После построения графика в первом варианте он сравнивается с исходным. Ребята проводят анализ и делают вывод, а затем аналогично для второго варианта.

5. Обобщение полученных выводов:

График функции у = а(х + p)² может быть получен из графика функции у = ах² путем переноса его вдоль оси Ох влево на отрезок длины p, если p > 0,
или вправо на отрезок длины | p |, если p < 0.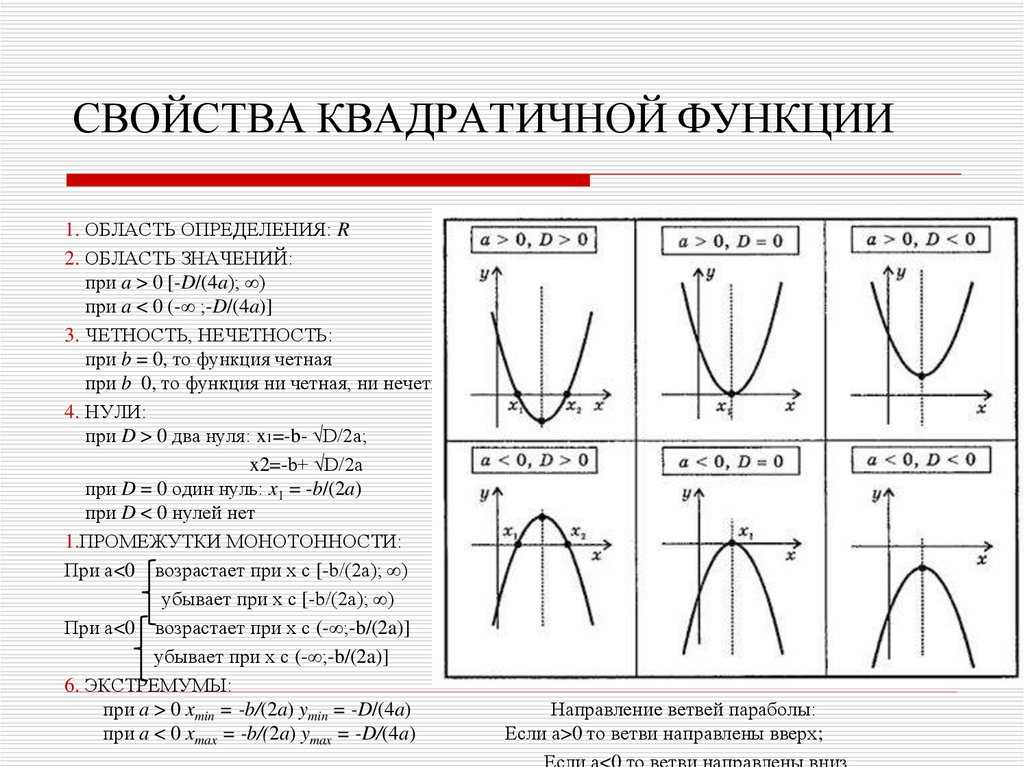 При этом вершина параболы окажется в точке (–

p; 0).

(Слайд 10. Анимация сдвигов графиков на слайде помогает лучшему восприятию правила.)

6. Задайте формулой функцию, если исходная у = 2х2 и запишите координаты вершины.

(Слайды 11-12).

7. Обобщение для графиков функций вида: у = а(х + p)² + q.

(Слайд 13).

График функции у = а(х + p)² + q может быть получен из графика функции у = ах²  с помощью двух параллельных переносов: вдоль оси Оу на | q | единиц – вверх или вниз в зависимости от знака числа q, и вдоль оси Ох на  | p | единиц – влево или вправо в зависимости от знака числа p. Вершиной параболы у = а(х + p)² + q

будет точка   (– p; q).

IV. Закрепление нового материала

1. Задайте формулой функцию и запишите координаты вершины параболы.

(Слайд 14).

2. Установите соответствие между графиком функции, формулой и координатами вершины параболы.

(Слайды 15-16.)

3. Решение упражнений: № 234, 244, 257. (Слайд 17).

V. Подведение итогов

– Как из параболы  получить параболу

– Как из параболы получить параболу

(Слайд 18.)

VI. Домашнее задание

П. 2.3., № 233 (б, г), 235 (б, г), 243(б, г),245 (б, г),  249 (б, г), 256 (б, г). (Слайд 19).

Расчетная таблица для определения параметров линейного тренда, описывающего тенденцию изменения числа зарегистрированных разбоев за период 2004-2013 гг.

Годы	yt	t	ty	t2
2004 2005 2006 2007 2008 2009 2010 2011 2012 2013	16,5 18,5 30,4 34,2 37,9 37,7 34,6 34,3 38,5 41,1	-9 -7 -5 -3 -1 1 3 5 7 9	-148,5 -129,5 -152,0 -102,6 -37,9 37,7 103,8 171,5 269,5 369,9	81 49 25 9 1 1 9 25 49 81	21,93 24,25 26,57 28,89 31,21 33,53 35,85 38,17 40,49 42,81
Итого	323,7	0	381,9	330	323,7

Таким образом, уравнение линейного тренда имеет вид:

.

Рассчитаем отклонения эмпирических значений числа зарегистрированных разбоев от выровненных по тренду (таблица 2.16, гр. 4).

Проранжируем полученные отклонения в порядке убывания (таблица 2.16, гр. 5).

Определим медиану отклонений :

Cравним значения отклонений с:

Получили ряд плюсов и минусов. Отразим результаты в таблице 2.16.

Таблица 2.16

Расчетная таблица для определения параметров критерия серий, основанного на медиане выборки числа зарегистрированных разбоев за период 2004-2013 гг.

Год	yt	t			ранжированные	Знаки сравнения
А	1	2	3	4	5	6
2004 2005 2006 2007 2008 2009 2010 2011 2012 2013	16,5 18,5 30,4 34,2 37,9 37,7 34,6 34,3 38,5 41,1	-9 -7 -5 -3 -1 1 3 5 7 9	21,93 24,25 26,57 28,89 31,21 33,53 35,85 38,17 40,49 42,81	-5,43 -5,75 3,83 5,31 6,69 4,17 -1,25 -3,87 -1,99 -1,71	6,69 5,31 4,17 3,83 -1,25 -1,71 -1,99 -3,87 -5,43 -5,75	— — + + + + + — — —

Выдвигается гипотеза H₀: если отклонения от тренда случайны, то и их чередование должно быть случайным.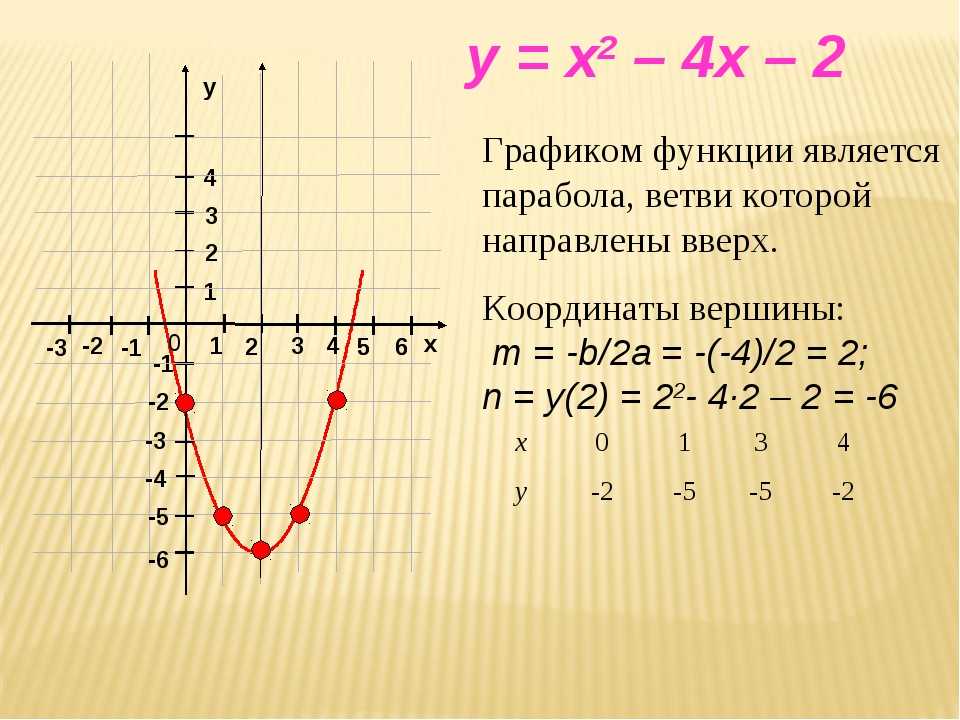

Для проверки выдвинутой гипотезы определим длину наибольшей серии:

и число серий V(n)=3; n=10.

Гипотеза не отвергается, если справедлива следующая система неравенств.

Оба неравенства выполняются, гипотеза о случайности отклонений уровней временного ряда от тренда в виде прямой не отвергается.

Произведем оценку случайности отклонений эмпирических значений числа зарегистрированных разбоев от теоретических, полученных по уравнению параболы второго порядка:

Для нахождения неизвестных параметров используем метод наименьших квадратов.

Параметры данного уравнения определим из следующей системы:

Промежуточные вычисления приведены в таблице 2.17.

Таблица 2.17

Расчетная таблица для определения параметров параболы второго порядка, описывающей тенденцию изменения числа зарегистрированных разбоев за период 2004-2013 гг.

Годы	yt	t	ty	t2	t4	t2y
2004 2005 2006 2007 2008 2009 2010 2011 2012 2013	16,5 18,5 30,4 34,2 37,9 37,7 34,6 34,3 38,5 41,1	-9 -7 -5 -3 -1 1 3 5 7 9	-148,5 -129,5 -152 -102,6 -37,9 37,7 103,8 171,5 269,5 369,9	81 49 25 9 1 1 9 25 49 81	6561 2401 625 81 1 1 81 625 2401 6561	1336,5 906,5 760 307,8 37,9 37,7 311,4 857,5 1886,5 3329,1	16,65 22,49 27,45 31,53 34,73 37,05 38,49 39,05 38,73 37,53
Итого	323,7	0	381,9	330	19338	9770,90	323,7

Подставив в данную систему вычисленные значения, получим следующие значения параметров уравнения параболы.

Полученное уравнение параболы второго порядка выглядит следующим образом:

Рассчитаем отклонения эмпирических значений признака от выровненных по тренду (таблица 2.18, гр. 4).

Проранжируем полученные отклонения в порядке убывания (графа 5).

Определим медиану отклонений :=.

Сравним значения отклонений с:

Получили ряд плюсов и минусов (графа 6).

Отразим результаты в таблице.

Таблица 2.18

Использование таблиц параболы | Parabola

Обзор продукта   ->

Изучение данных в таблицах Parabola

Таблицы Parabola отображаются в интерактивном представлении потока. Любой, у кого есть доступ к вашему Flow, сможет взаимодействовать с выходными данными вашего Flow.

Данные, которые экспортируются в таблицы Parabola, будут вашими базовыми данными set , которые можно настроить с помощью табличных представлений, которые можно использовать для:

• Фильтр
• Сортировка
• Группа
• Агрегат
• Визуальный стиль

Табличные представления могут быть названы и доступны для вашей команды.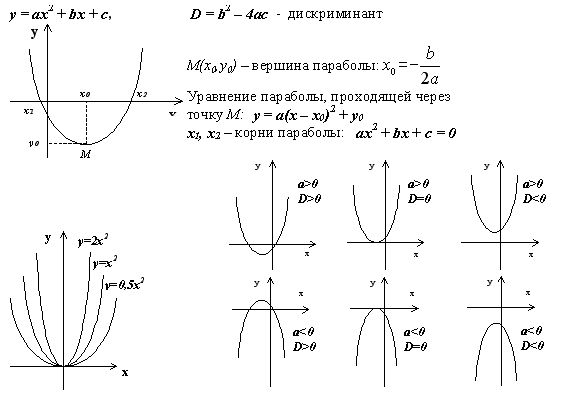

Любой товарищ по команде с доступом к редактору потока может создавать новые представления, дублировать существующие представления или сохранять свои изменения в качестве нового представления.

‍

При создании нового представления таблицы или редактировании существующего представления любые изменения будут черновыми и видны только редактору, внесшему эти изменения. Черновые представления можно сохранять, что делает их видимыми для всех, у кого есть доступ к потоку, или отбрасывать.

‍

Табличные представления будут обновлять свои результаты, если: выполняется поток, обновляются базовые данные и/или изменяются настройки.

Шаг Отправить в таблицу Parabola всегда будет обновлять базовые данные таблицы, которые представления будут использовать для расчета своих результатов.

Параметры просмотра

Табличные представления можно переименовывать, дублировать, переупорядочивать и применять фильтры, сортировку и визуальное форматирование:

Управление представлениями

Перетащите представления, чтобы изменить их порядок.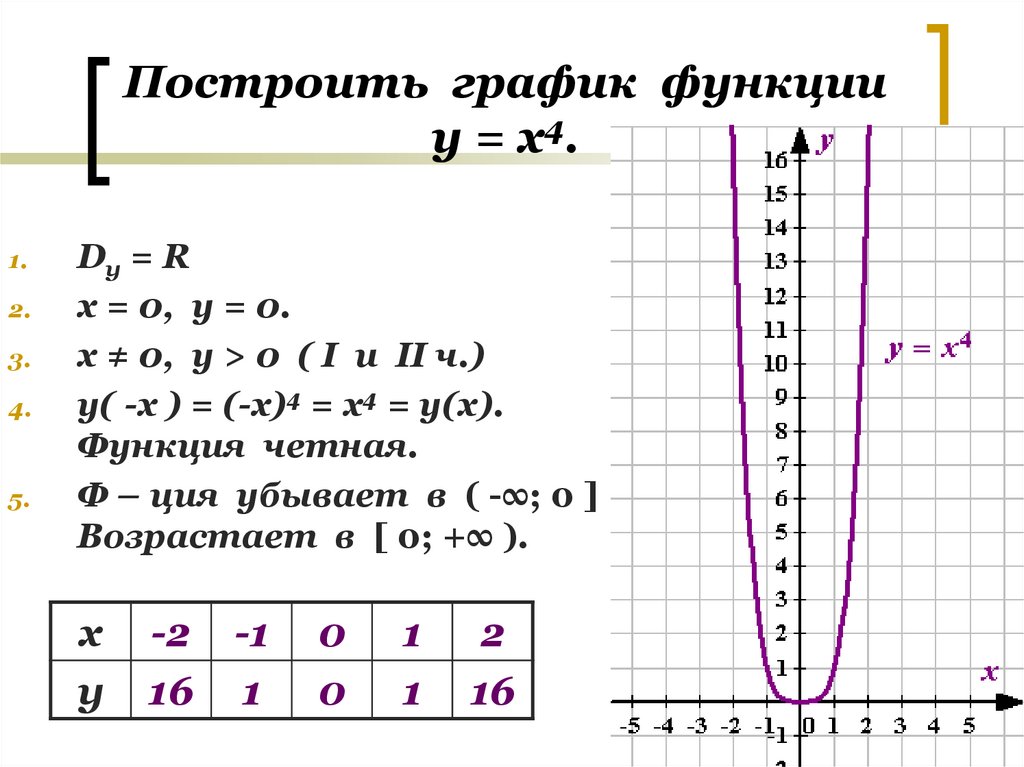

Нажмите дополнительное меню рядом с названием представления, чтобы переименовать, дублировать или удалить его

‍

Фильтры

Нажмите кнопку «Фильтр», чтобы быстро добавить новое правило фильтрации, или используйте параметры представления меню для доступа к тем же элементам управления фильтром. Эти фильтры определяют, какие строки сохраняются в представлении.

‍

Сортировка

Нажмите кнопку «Сортировка», чтобы быстро добавить новое правило сортировки, или используйте меню параметров просмотра, чтобы получить доступ к тем же элементам управления сортировкой. Эти сортировки определяют, какие строки сохраняются в представлении.

‍

Стили таблиц

Используйте меню параметров просмотра, чтобы получить доступ к параметрам отображения, чтобы выбрать один из 4 вариантов цветовой темы для представления.

‍

Выделение столбца

Используйте меню параметров просмотра для доступа к параметрам столбца, чтобы выбрать любое количество столбцов, чтобы выделить их более ярким цветом.

‍

Опции агрегирования

Операции подсчета

Подсчитать все

Подсчитывает число или строки во всей таблице и для любых групп.

Подсчет уникальных

Подсчитывает количество уникальных значений в указанном столбце для всей таблицы и для любых групп. Уникальные значения чувствительны к регистру и пробелам

Подсчет пустых

Подсчитывает количество пустых ячеек в указанном столбце для всей таблицы и для любых групп. Ячейки, содержащие только пробел или другие невидимые символы, не считаются пустыми.

Математические операции

Сумма

Суммирует все числовые значения в указанном столбце для всей таблицы и для любых групп. Ячейки, которые пусты или содержат нечисловые значения, пропускаются. Если результат не может быть получен, будет показано значение — -.

Среднее

Создает среднее значение путем суммирования всех числовых значений в указанном столбце для всей таблицы и для любых групп и деления суммы на общее количество использованных значений.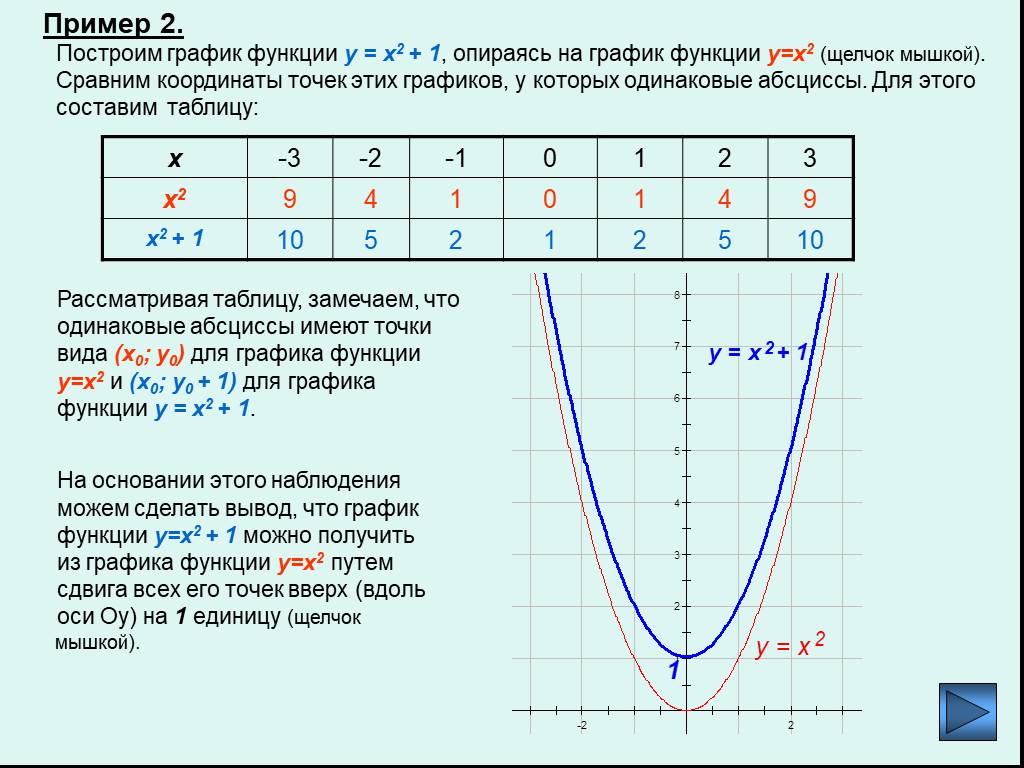 Ячейки, которые пусты или содержат нечисловые значения, пропускаются. Если результат не может быть получен, будет показано значение — -.

Медиана

Находит значение, при котором половина значений больше и половина меньше в указанном столбце для всей таблицы и для любых групп. Ячейки, которые пусты или содержат нечисловые значения, пропускаются. Если результат не может быть получен, будет показано значение — -.

Минимум (мин.)

Находит наименьшее значение в указанном столбце для всей таблицы и для любых групп. Ячейки, которые пусты или содержат нечисловые значения, пропускаются. Если результат не может быть получен, будет показано значение — -.

Максимум (Max)

Находит наибольшее значение в указанном столбце для всей таблицы и для любых групп. Ячейки, которые пусты или содержат нечисловые значения, пропускаются. Если результат не может быть получен, будет показано значение — -.

‍

Полезные советы для групп и агрегаций

• Если агрегацию невозможно обработать, Parabola будет отображать два тире (- -) в качестве значения. Если вы столкнулись с этим, мы рекомендуем использовать шаг «Очистить текст» или шаг «Заполнить пустое место», чтобы очистить данные перед отправкой в ​​таблицу Parabola 9.0016
• Таблицы можно группировать до 4 раз. После 4 групп параметр +Добавить группу будет отключен
• Группы применяются во вложенном порядке, начиная с первой группы и создавая подгруппы с каждым последующим правилом
• Используйте параметры сортировки в правилах групп, чтобы определить, в каком порядке группы показаны в. Обычные правила сортировки будут использоваться для сортировки строк внутри групп.

‍

Совместное использование таблиц с товарищами по команде

Любой, у кого есть доступ (просмотрщик или редактор) к вашему потоку, сможет увидеть результаты в любом табличном представлении без необходимости доступа к другому инструменту.

Чтобы поделиться столом, вы можете либо поделиться Flow со своим товарищем по команде (см. инструкции здесь)*, либо нажать «Поделиться» в определенном представлении таблицы.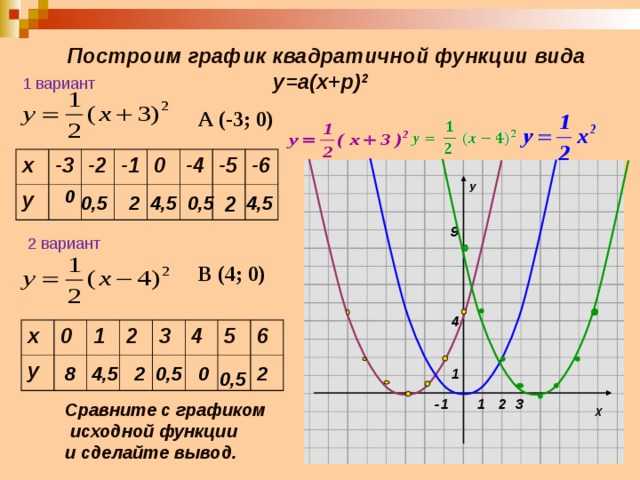 Совместное использование стола даст вашему товарищу по команде доступ к потоку и напрямую свяжет их со столом.

*Примечание: если ваш товарищ по команде еще не является членом вашей команды Parabola, вы можете добавить его, нажав «Пригласить кого-то нового в свою команду» в нижней части окна обмена.

‍

Данные, экспортированные в таблицу Parabola, можно просматривать, фильтровать, сортировать и совместно использовать, но нельзя изменять вручную. Это гарантирует, что ваша команда каждый раз просматривает согласованные данные.

Как находить квадратные уравнения в таблице

••• AndreyCherkasov/iStock/GettyImages

Обновлено 26 апреля 2018 г. которые описывают точки на параболе. Однако некоторые могут не осознавать, что вы также можете выполнить обратную операцию, чтобы вывести уравнение из точек. Эта операция более сложная, но жизненно необходима ученым и математикам, которым необходимо сформулировать уравнение, описывающее график экспериментальных значений.