Длина дуги окружности калькулятор и формулы
{L = \dfrac{\pi R \alpha}{180\degree}}
Найти длину дуги
через радиус и уголпо формуле Гюйгенса
Радиус окружности R
ммсмдммкмдюймы (in)футы (ft)
Угол α
градусы (°)радианы (рад)грады (град)обороты (об)минуты (′)секунды (″)миллирадианымикрорадианы
Результат в
ммсмдммкмдюймы (in)футы (ft)
Виджет
Ссылка на расчет
Сообщить об ошибке
Сохранить расчет
Печатать
Длина дуги окружности — важный параметр, который используется в геометрии и математике для решения различных задач. На этой странице приведены две формулы для расчета длины дуги окружности — через радиус и угол между радиусами и по формуле Гюйгенса.
Дуга — одно из двух подмножеств окружности, на которые её разбивают любые две различные принадлежащие ей точки. Любые две точки окружности разбивают её на две части, при этом каждая из частей является дугой.
Содержание:
- калькулятор длины дуги окружности
- формула длины дуги окружности через радиус и угол
- формула длины дуги окружности по формуле Гюйгенса
- примеры задач
Если обобщить, то дуга окружности — это часть окружности, ограниченная двумя ее точками. Ниже приведены несколько примеров дуг окружностей:
-
Полная окружность — это дуга, которая охватывает всю окружность. Угол, определяющий полную окружность, равен 360° или 2π радиан. Длина дуги полной окружности равна общей длине окружности, которая может быть вычислена по формуле L = 2πr, где r — радиус окружности.

-
Полуокружность — это дуга, которая охватывает половину окружности. Угол, определяющий полуокружность, равен 180° или π радиан. Длина дуги полуокружности равна половине общей длины окружности и может быть вычислена по формуле L = πr.
-
Сектор окружности — это область, ограниченная дугой окружности и двумя ее радиусами.
Это только несколько примеров дуг окружности. Дуги могут быть разных размеров и форм, в зависимости от угла, определяющего их, и расположения на окружности.
Формула длины дуги окружности через радиус и угол
{L = \dfrac{\pi R \alpha}{180\degree}}
R — радиус окружности
α
{L = R \alpha}
R — радиус окружности
α — центральный угол (угол между радиусами) в радианах
Формула длины дуги окружности по формуле Гюйгенса
{L \approxeq 2m + \dfrac{2m-M}{3}}
m — длина хорды m
M — длина хорды M
Обратите внимание, что в данной формуле используется не привычный знак равно «=», а знак «равно или почти равно», который записывается так — «\approxeq». Это связано с тем, что формула Гюйгенса дает погрешность при вычислении. Хоть величина погрешности невелика, знать об этом надо.
Это связано с тем, что формула Гюйгенса дает погрешность при вычислении. Хоть величина погрешности невелика, знать об этом надо.
Относительная погрешность формулы Гюйгенса составляет порядка 0,5% когда угол дуги равен 60°. Если же угловая мера дуги уменьшается, то уменьшается и погрешность. Например, для дуги в 45° относительная погрешность будет равна примерно 0,02%.
Примеры задач на нахождение длины дуги
Задача 1
Найдите длину дуги окружности радиуса 6см, если ее градусная мера равна 30.
Решение
Для решения этой задачи нам подойдет первая формула. Подставим в нее значение радиуса и угла и произведем вычисления:
L = \dfrac{\pi R \alpha}{180\degree} = \dfrac{\pi \cdot 6 \cdot 30\degree}{180\degree} = \dfrac{\pi \cdot 180\degree}{180\degree} = \pi \: см \approx 3.14 \: см.
Ответ: {\pi \: см \approx 3.14 \: см.}
Введем известные значения в калькулятор для проверки полученного ответа.
Задача 2
Найдите длину дуги окружности радиуса 3см, если ее градусная мера равна 150 градусов.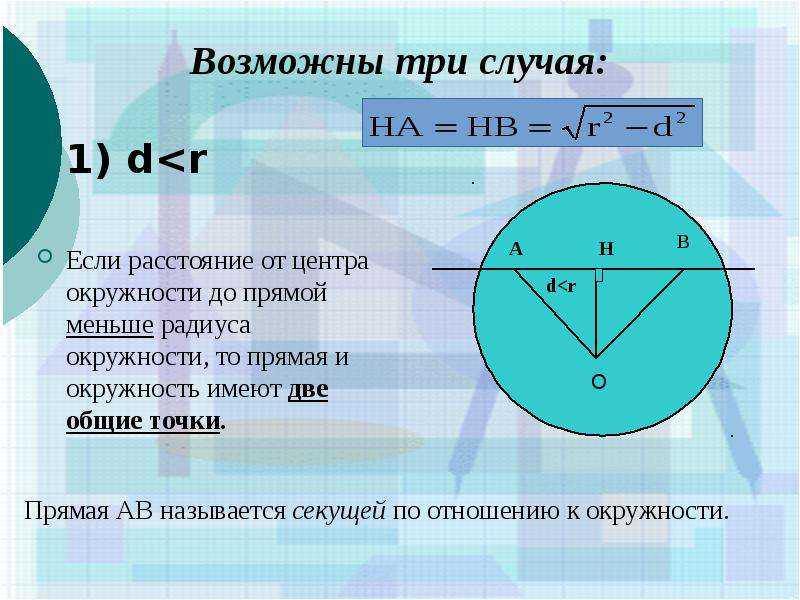
Решение
Задача аналогична предыдущей. Также воспользуемся первой формулой.
L = \dfrac{\pi R \alpha}{180\degree} = \dfrac{\pi \cdot 3 \cdot 150\degree}{180\degree} = \dfrac{\pi \cdot 3 \cdot 5}{6} = \dfrac{\pi \cdot 5}{2} = \dfrac{5}{2} \pi \: см = 2.5 \pi \: см \approx 7.85398 \: см.
Ответ: {2.5 \pi \: см \approx 7.85398 \: см.}
В проверке ответа нам снова поможет калькулятор .
Длина дуги окружности имеет множество применений в математике и ее приложениях. Например, она используется для вычисления длины дуги графика функции, заданной в полярных координатах. Также длина дуги окружности используется при вычислении пути, пройденного телом при движении по окружности, а также для вычисления объема тела, полученного путем вращения дуги окружности вокруг ее диаметра.
Длина хорды окружности при заданной длине перпендикуляра Калькулятор
✖Радиус окружности — это длина любого отрезка, соединяющего центр и любую точку окружности. | створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр | +10% -10% | |
✖Длина перпендикуляра к хорде окружности — это кратчайшее расстояние от центра до середины хорды окружности. | створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр | +10% -10% |
|
✖Длина хорды окружности — это длина отрезка, соединяющего любые две точки на окружности окружности. |
|
⎘ копия |
👎
Формула
сбросить
👍
Длина хорды окружности при заданной длине перпендикуляра Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. 2))
2))
Что такое Круг?
Окружность — это базовая двухмерная геометрическая фигура, которая определяется как совокупность всех точек на плоскости, находящихся на фиксированном расстоянии от фиксированной точки. Фиксированная точка называется центром круга, а фиксированное расстояние называется радиусом круга. Когда два радиуса становятся коллинеарными, эта общая длина называется диаметром круга. То есть диаметр — это длина отрезка внутри круга, проходящего через центр, и он будет в два раза больше радиуса.
Каковы свойства аккордов?
Если хорды параллельны друг другу, то длина дуги между ними будет одинаковой. Хорды одинаковой длины равноудалены от центра окружности. Чем больше длина хорды, тем ближе она к центру окружности.
Share
Copied!
Формула для определения длины дуги, длины хорды и площади сегмента окружности
Содержание
- 1 Онлайн-калькулятор для расчета площади сегмента окружности, длины дуги (длины кривой), длины хорды
- 1.
 1 Данные, необходимые для расчета:
1 Данные, необходимые для расчета: - 1.2 Формулы для расчета площади части или части окружности:
- 1.2.1 Пример для лучшего понимания
- 1.
- 2 Онлайн калькулятор для расчета площади сегмента окружности
Онлайн-калькулятор для расчета площади сегмента круга, длины дуги (длины кривой), расчета длины хорды
В этой статье рассмотрены формулы на примере расчета площади сегмента круга (часть площади круга или часть площади круга). ) , длина дуги, а также длина хорды, а также предоставлен хороший онлайн-калькулятор.
Данные, необходимые для расчета:
- Диаметр круга = D (м)
- Перпендикулярная длина от хорды окружности до края окружности = ч (метры)
Формулы для расчета площади части круга или части круга:
- Общая площадь круга = π r 2
- Радиус окружности = r= D/2 = диаметр / 2
- Угол сектора = θ = 2 cos -1 (( r – h) / r )
- Длина хорды сегмента окружности = c = 2 SQRT[ ч (2р – ч ) ]
- Дуга Длина сегмента окружности = l = 0,01745 x r x θ
- Площадь сегмента = As = 1/2 ( rl – c ( r – h ))
- Площадь круга, кроме площади сегмента A = π r 2 – As
Пример для лучшего понимания
Данные:
- Диаметр круга = 1,6 (м)
- Перпендикулярная длина от хорды окружности до края окружности = 0,76 (метры)
Расчет :
- Радиус окружности = 1,6/2 = 0,8 м
- Общая площадь круга = 3,141 x 0,8 x 0,8 = 2,0102 м 2
- г – h = 0,04
- (отн.
 ч) /r = 0,05
ч) /r = 0,05 - cos -1 (( r – h) / r = 87,13
- Угол сектора = θ = 2 cos -1 (( r – h) / r ) = 174,27 град.
- Дуга Длина сегмента окружности = l = 0,01745 x r x θ = 0,01745 x 0,8 x 174,27 = 2,432 м
- ч(2р – ч) = 0,6384
- Длина хорды сегмента окружности = c = 2 SQRT[ h (2r – h ) ] = 1,597 м
- с ( г – ч ) = 0,6392
- рл = 1,94623
- Площадь сегмента круга = As = 1/2 ( rl – c ( r – h )) = 0,9412 м 2
- Площадь круга, кроме площади сегмента A = π r 2 – As = 1,069 м 2
Онлайн-калькулятор для расчета площади сегмента круга
Щелкните здесь
Похожие темы
Формула для оценки объема горизонтального цилиндра на разных уровнях (вакуумный кристаллизатор на разных объемах).
Расчет NPSH, Формулы NPSHa, NPSHr, Кавитация насоса, Потеря напора всасывающей и напорной линии насоса с онлайн-калькулятором.
Калькулятор для определения объема жидкости для вертикально установленного цилиндрического объема, а также для определения объема в разделенной части цилиндрического резервуара.
Принципы Рийе и расчет перепадов давления для корпусов многокорпусных испарителей, таких как четырехкратный и пятикратный эффект, с помощью онлайн-калькулятора.
Привет, друзья! Спасибо, что читаете и пользуетесь нашим онлайн-калькулятором. Надеюсь, вам понравилось. Дайте обратную связь, комментарии и, пожалуйста, не забудьте поделиться этим
Сообщение Автор: siva alluri
Целью этого блога «sugarprocesstech» является предоставление базовых знаний в области сахарной промышленности и обеспечение максимальных расчетов в отношении производительности и проектирования оборудования онлайн-калькуляторы .
Формула измерения дуги | Как найти меру угла дуги (Видео)0024
Дуга — это сегмент окружности по окружности. градусная мера – это угол, образуемый дугой в центре окружности, а длина дуги — это отрезок вдоль дуги. Эта мера угла может быть выражена в радианах или градусах, и мы можем легко преобразовать их по формуле π\pi π радианы = 180°
градусная мера – это угол, образуемый дугой в центре окружности, а длина дуги — это отрезок вдоль дуги. Эта мера угла может быть выражена в радианах или градусах, и мы можем легко преобразовать их по формуле π\pi π радианы = 180°
Вы также можете измерить длину окружности или расстояние вокруг окружности. Если вы возьмете меньше, чем полная длина вокруг круга, ограниченного двумя радиусами, у вас будет дуга . Эта изогнутая часть круга и внутреннее пространство называется сектором , как кусок пиццы. Когда вы разрезаете круглую пиццу, корка делится на дуги.
Дуга окружности
Если мы разрезаем вкусную, свежую пиццу, у нас есть две половинки, и каждая половина представляет собой дугу , измеряющую 180° . Если мы сделаем три дополнительных надреза с одной стороны только (то есть мы разрежем половину сначала на две четверти, а затем каждую четверть на две восьмых), у нас будет одна сторона пиццы с одним большим, 180° дуга и другая сторона пиццы с четырьмя, 45° дуги, подобные этой:
Малая и большая дуги Половина пиццы, состоящая из одного гигантского куска, представляет собой большую дугу поскольку ее размеры 180 ° (или больше). На другой стороне пиццы есть четыре малых дуг , поскольку каждая из них меньше 180° .
На другой стороне пиццы есть четыре малых дуг , поскольку каждая из них меньше 180° .
Размер дуги в зависимости от длины дуги
Дуга является частью длины окружности, которая лежит между двумя точками на окружности. Дуга имеет два измерения:
Размер дуги в зависимости от длины дугиДлина дуги — это расстояние по окружности, измеренное в тех же единицах, что и радиус, диаметр или длина окружности; эти единицы будут линейными мерами, такими как дюймы, см, м, ярды и т. д.
Измерение угла дуги , снятое в центре окружности, частью которой является дуга, измеряется в градусах (или радианах)
Не путайте измерение дуги (длины или угла) с прямым -линейное расстояние хорда , соединяющая две точки дуги на окружности. Длина хорды будет всегда короче длины дуги.
Градусы и радианы
Чтобы иметь возможность вычислять меру дуги, вы должны понимать измерения углов как в градусах, так и в радианах. Угол измеряется либо в градусах, либо в радианах. Окружность имеет размер 360 градусов, или 2π2\pi 2π радиан, тогда как 90 241 один радиан равен 180 градусам 90 242 . Итак, градусы и радианы связаны следующими уравнениями:
Угол измеряется либо в градусах, либо в радианах. Окружность имеет размер 360 градусов, или 2π2\pi 2π радиан, тогда как 90 241 один радиан равен 180 градусам 90 242 . Итак, градусы и радианы связаны следующими уравнениями:
180°=πрадиан180°=\pi радиан180°=πрадиан
Соотношение между радианами и градусами позволяет нам преобразовать их друг в друга с помощью простых формул. Чтобы преобразовать градусы в радианы, мы берем градусную меру, умноженную на пи, деленную на 180.
Давайте преобразуем 90 градусов в радианы, например:
Теперь давайте преобразуем π3\frac{\pi }{3}3π градусы:
Формула измерения дуги
Как только вы освоите радианы, мы можем использовать формулу измерения дуги, для которой требуется длина дуги, s и радиус окружности r для расчета.
Как найти меру дуги
Давайте рассмотрим пример, где длина дуги 3 см, а радиус 4 см, как показано на рисунке:
Как найти меру дугиНачните с нашей формулы , и подставим все, что знаем:
Теперь мы можем преобразовать 34\frac{3}{4}43 радиан в градусы, умножив на 180 и разделив на π\pi π.
Как найти длину дуги
Чтобы рассчитать длину дуги, необходимо знать значение центрального угла, образующего дугу (угол двух радиусов). Длина дуги — это дробная часть длины окружности круга. Длина окружности любого круга находится с помощью 2πr2\pi r2πr, где r = радиус. Если у вас есть диаметр, вы также можете использовать πd\pi dπd, где d = диаметр.
Формула для определения длины дуги:
Давайте попробуем пример с этой пиццей:
Как измерить длину дугиНаш круг имеет диаметр 16 дюймов , что дает радиус 8 дюймов . Мы знаем, что срез равен 60° . Таким образом, формула для этого конкретного куска пиццы выглядит следующим образом:
Идентификация указанного угла дуги
Измерение угла дуги показано как mAB⌢m\overset\frown{AB}mAB⌢, где A и B равны две точки на окружности, образующие дугу. Мм означает размер, а короткая изогнутая линия над AB⌢\overset\frown{AB}AB⌢ указывает, что мы имеем в виду дугу.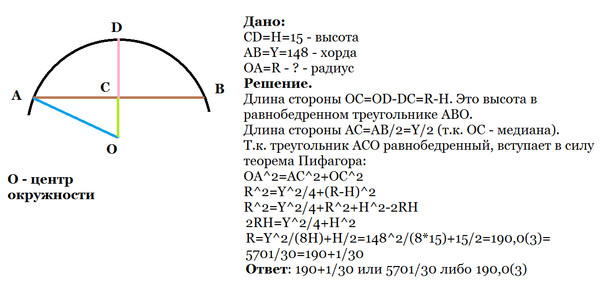

 ⓘ Радиус круга [r]
ⓘ Радиус круга [r] ⓘ Длина перпендикуляра к хорде окружности [lPerpendicular]
ⓘ Длина перпендикуляра к хорде окружности [lPerpendicular]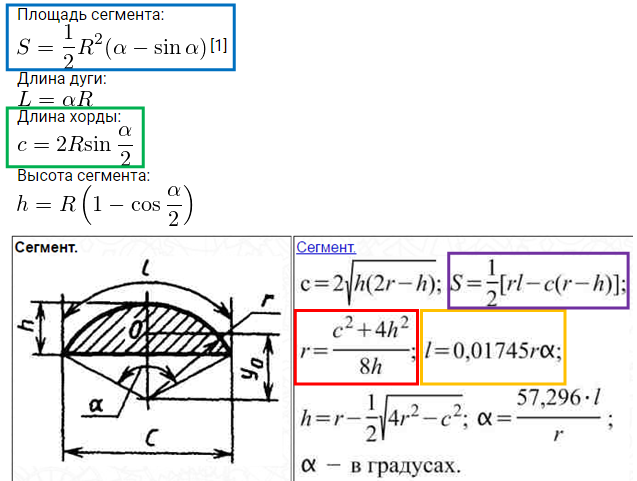 ⓘ Длина хорды окружности при заданной длине перпендикуляра [lc]
ⓘ Длина хорды окружности при заданной длине перпендикуляра [lc]
 1 Данные, необходимые для расчета:
1 Данные, необходимые для расчета: ч) /r = 0,05
ч) /r = 0,05