Таблица до 20 на минус и на плюс: Таблица сложения в пределах 20 – наглядное пособие – Корпорация Российский учебник (издательство Дрофа – Вентана)

море полезной информации о питании для автозвука

1. Главное — питание. С него надо начинать аудиосистему.

2. Лучшее питание должно быть у самого мощного усилителя — как правило у усилителя сабвуфера

3. Как выбрать толщину провода?
Очень просто — прочитайте 100500 статей про выбор толщины провода, закончите курсы «школоты автозвука», сделайте сложные расчеты на логарифмической линейке и обязательно закончите курс «теоретические основы электротехники» в каком-нибудь вузе.

 Ну или выбирайте так:

• до 800 Ватт — 4Ga (25кв),
• 800+ Вт — 2 Ga (35кв),
• 1,5 кВт и больше — 0ga (50 кв)

Речь о суммарной мощности системы. Если вы выберете провод слишком толстый — ничего страшного, если слишком тонкий — будет потеря вольтажа от начала провода до конца. То есть под капотом будет 12.5 Вольт, на моноблоке 11. 5 Вольт — это очень и очень … нехорошо, так как при этом вы не только рискуете спалить усилители, но и прогреваете провод. И чем он тоньше — тем сильнее будет прогреваться.

Для наглядности — если запитать усилитель тонкой проволокой — она накалится до красна. Если при этом она будет в силиконовой оплетке… ну вы поняли. 

4. Вольтметр должен стоять обязательно. В любом виде, но вы должны знать что происходит в системе на каких треках. Как минимум вы должны померить вольтаж после запуска аудиосистемы в двух местах:
 

• под капотом
• и на самом большом потребителе (как правило моноблоке) —

вольтаж должен быть одинаковый ине просаживаться ниже 12 Вольт.

5. Забудьте про конденсаторы (накопители).
Единственная польза от конденсатора — это вольтметр, если он на нем есть, если же нет — польза от конденсатора только продавцу конденсаторов.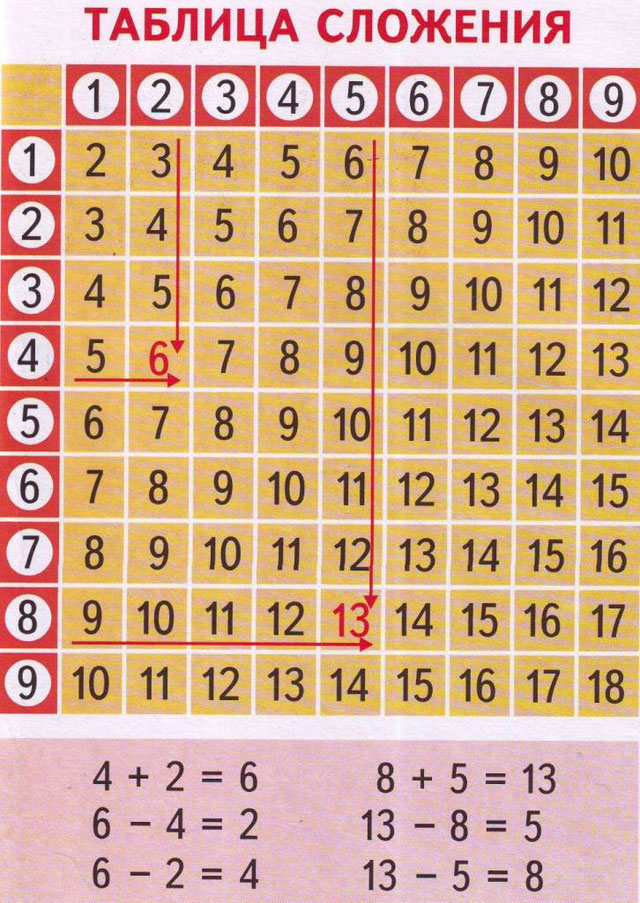

Конденсатор стоит не дешево — купите лучше провод потолще или дополнительный АКБ

6. Как выбрать дополнительный АКБ?

В идеале — он должен быть точно такой же как и под капотом, еще лучше — если они будут оба новые.

Если нет возможности поставить такой же — пусть они будут одного типа:

• оба АГМ,
• либо оба литий.

Вы можете поставить АГМ вместе с кислотой или даже АГМ вместе с литием — но АКБ с большим вольтажем будет постоянно находиться в состоянии разряда, пока общий вольтаж не выровняется. На практике — я использовал много раз АГМ и кислоту и ничего за год и больше эксплуатации не происходило.

7. Как подключать доп АКБ? Реле, переходники — на… все это — просто соедините плюс с плюсом и минус с минусом.

8. Помимо сильных потребителей — не забывайте про самый слабый — ГУ (магнитолу) — не запитывайте ее от прикуривателя или от рандомной проводки, на которой найдете плюс и минус.

Не ленитесь — тащите и плюс и минус от туда же, откуда взяли питание на усилки. Так будет ниже риск получить наводки и магнитола не будет выключаться, когда вы заводите автомобиль.

9. Генератор очень важен. Если опустить кучу теории — генератор нужно выбирать так — на каждый киловатт мощности нужен генератор 80 А + АКБ 69-70 Ач.

Это конечно идеальная картина и часто в системах потребляющих 4 кВт стоят штатные гены на 100А и пара АКБ.
Но если генератора будет не достаточно — АКБ будут постоянно разряжаться, пока играет музыка и в конце концов вольтаж начнет падать.

Короче, что бы не париться — люксовая приора с родным геной и родным не дохлым АКБ может иметь стабильную аудиосистему около 2 кВт. Еще проще — кикс тысячник и пару сабов в 1Ом = гена 115-120 А + АКБ 70 Ач. Играть будет 🙂

10. Никогда не покупайте алюминиевый провод. Даже объяснять не буду — просто не покупайте! Только медь!

11. Чем промышленный кабель отличается от брендовых автомобильных?

Во-первых сечением — он будет тоньше, но благодаря цене — выгоднее будет купить две протяжки промышленного, чем одну автомобильного и в итоге получить большее сечение за меньшие деньги.
Во-вторых — гибкостью — автомобильный будет более гибкий, с ним будет проще работать.
В третьих — презентабельностью.
В четвертых — лужением. Автомобильные луженые провода

дольше не окисляются. На что это влияет? Ни на что 🙂

12. Предохранители. Выбрать предохранитель очень просто — прилагаю таблицу выбора предохранителей

13. Минус нужно тянуть от АКБ, не тащить одну протяжку плюса, а минус брать с кузова, а тащить ОБА провода от АКБ. Если система не мощная — можно и с кузова, но лучше делать все по уму, ведь если система не мощная, то и провода не дорогие, а значит не нужно экономить пять метров провода — лучше сразу сделать как надо.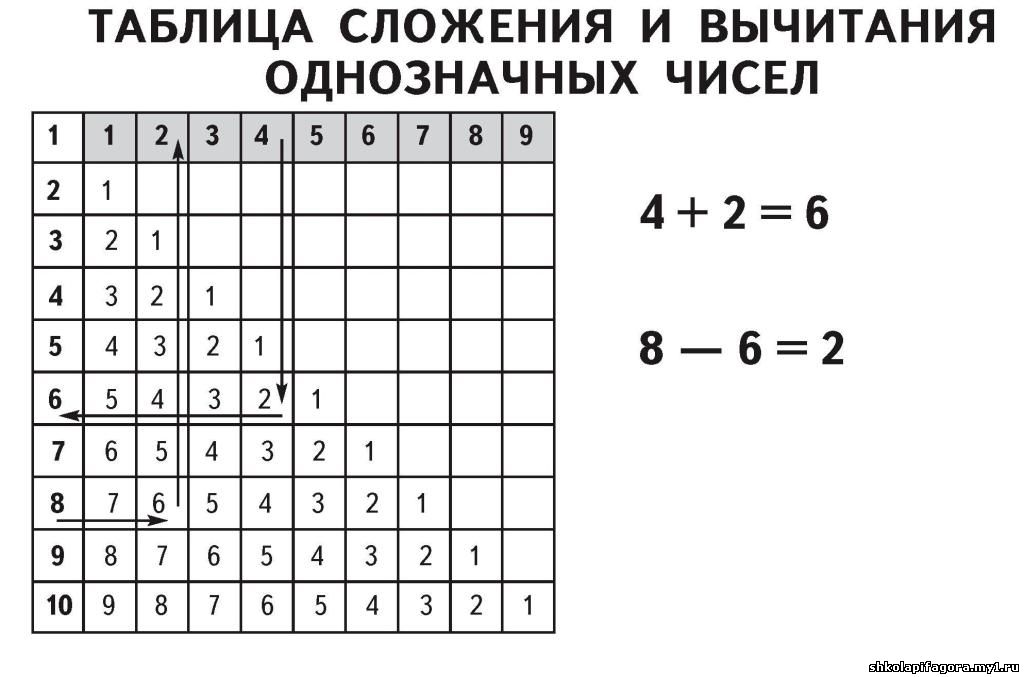

Минус должен быть такого же или большего сечения чем плюс, не меньше!

14. Где располагать предохранители?

Предохранитель должен стоять на каждом плюсовом силовом проводе как можно ближе к плюсовой клемме АКБ.

Если АКБ два — то на проводе должно быть два предохранителя — возле каждой плюсовой клеммы.

Не ставьте преды возле усилителей — это бесполезно. Предохранитель в случае короткого замыкания (КЗ) должен обесточивать весь провод. Пример — произошло КЗ где то по центру кузова, предохранитель возле усилителя сгорел и усилитель и кусок провода от него до преда — обесточен, но весь остальной провод под напряжением! Если пред сгорает возле АКБ — провод по всей длине кузова обесточен!

15. Главное — питание. С него надо начинать аудиосистему.

Если рубрика полезная и вы хотите еще советы — подписывайтесь!

Сложение и вычитание рациональных чисел

В данном уроке рассматривается сложение и вычитание рациональных чисел.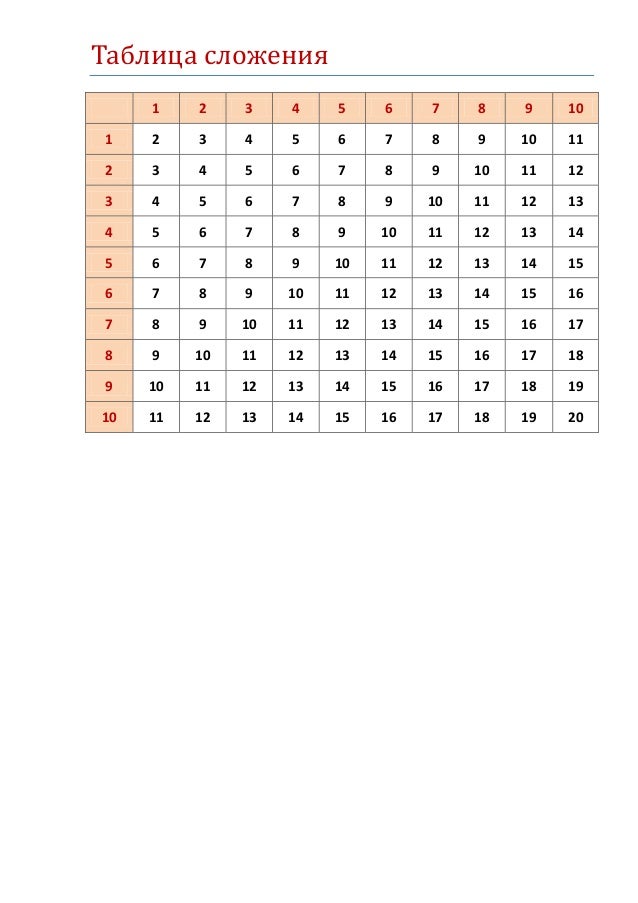 Тема относится к категории сложных. Здесь необходимо использовать весь арсенал полученных ранее знаний.

Правила сложения и вычитания целых чисел справедливы и для рациональных чисел. Напомним, что рациональными называют числа, которые могут быть представлены в виде дроби  ,  где

a – это числитель дроби, b – знаменатель дроби. При этом, b не должно быть нулём.

В данном уроке дроби и смешанные числа мы всё чаще будем называть одним общим словосочетанием — рациональные числа.

 

Пример 1. Найти значение выражения: 

Заключим каждое рациональное число в скобки вместе со своими знаками. Учитываем, что плюс который дан в выражении, является знаком операции и не относится к дроби . У этой дроби свой знак плюса, который невидим по причине того, что его не записывают. Но мы запишем его для наглядности:

Это сложение рациональных чисел с разными знаками. Чтобы сложить рациональные числа с разными знаками, нужно из большего модуля вычесть меньший модуль, и перед полученным ответом поставить знак того рационального числа, модуль которого больше.

А чтобы понять какой модуль больше, а какой меньше, нужно суметь сравнить модули этих дробей до их вычисления:

Модуль рационального числа   больше, чем модуль рационального числа . Поэтому мы из  вычли . Получили ответ . Затем сократив эту дробь на 2, получили окончательный ответ .

Некоторые примитивные действия, такие как заключение чисел в скобки и проставление модулей, можно пропустить. Данный пример вполне можно записать покороче:

---

Пример 2. Найти значение выражения: 

Заключим каждое рациональное число в скобки вместе со своими знаками. Учитываем, что минус, стоящий между рациональными числами  и  является знаком операции и не относится к дроби . У этой дроби свой знак плюса, который невидим по причине того, что его не записывают. Но мы запишем его для наглядности:

Заменим вычитание сложением. Напомним, что для этого нужно к уменьшаемому прибавить число, противоположное вычитаемому:

Получили сложение отрицательных рациональных чисел.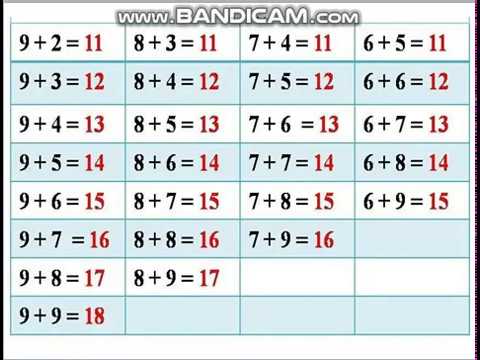 Чтобы сложить отрицательные рациональные числа, нужно сложить их модули и перед полученным ответом поставить минус:

Запишем решение данного примера покороче:

Примечание. Заключать в скобки каждое рациональное число вовсе необязательно. Делается это для удобства, чтобы хорошо видеть какие знаки имеют рациональные числа.

---

Пример 3. Найти значение выражения: 

В этом выражении у дробей разные знаменатели. Чтобы облегчить себе задачу, приведём эти дроби к общему знаменателю. Не будем подробно останавливаться на том как это сделать. Если испытываете с этим затруднения, обязательно повторите урок действия с дробями.

После приведения дробей к общему знаменателю выражение примет следующий вид:

Заключим каждое рациональное число в скобки вместе своими знаками:

Это сложение рациональных чисел с разными знаками. Вычитаем из большего модуля меньший модуль, и перед полученным ответом ставим знак того рационального числа, модуль которого больше:

Запишем решение данного примера покороче:

---

Пример 4. Найти значение выражения  

Заключим каждое рациональное число в скобки вместе со своими знаками:

Вычислим данное выражение в следующем порядке: слóжим рациональные числа  и , затем из полученного результата вычтем рациональное число . 

Первое действие:

Второе действие:

Таким образом, значение выражения  равно 

---

Пример 5. Найти значение выражения: 

Представим целое число −1 в виде дроби , а смешанное число  переведём в неправильную дробь:

Приведём данные дроби к общему знаменателю. После их приведения к общему знаменателю, они примут следующий вид:

Заключим каждое рациональное число в скобки вместе со своими знаками:

Получили сложение рациональных чисел с разными знаками. Вычитаем из большего модуля меньший модуль, и перед полученным ответом ставим знак того рационального числа, модуль которого больше:

Получили ответ .

Есть и второй способ решения. Он заключается в том, чтобы сложить отдельно целые части.

Итак, вернёмся к изначальному выражению:

Заключим каждое число в скобки. Для этого смешанное число  временно развернём:

Вычислим целые части:

(−1) + (+2) = 1

В главном выражении вместо (−1) + (+2) запишем полученную единицу:

Полученное выражение  свернём. Для этого запишем единицу и дробь вместе:

Запишем решение этим способом покороче:

---

Пример 6. Найти значение выражения

Переведём смешанное число  в неправильную дробь. Остальную часть перепишем без изменения:

Заключим каждое рациональное число в скобки вместе со своими знаками:

Заменим вычитание сложением:

Получили сложение отрицательных рациональных чисел. Слóжим модули этих чисел и перед полученным ответом поставим минус:

Запишем решение данного примера покороче:

---

Пример 7. Найти значение выражение

Представим целое число −5 в виде дроби , а смешанное число  переведём в неправильную дробь:

Приведём данные дроби к общему знаменателю. После их приведения к общему знаменателю, они примут следующий вид:

Заключим каждое рациональное число в скобки вместе со своими знаками:

Заменим вычитание сложением:

Получили сложение отрицательных рациональных чисел. Слóжим модули этих чисел и перед полученным ответом поставим минус:

Таким образом, значение выражения   равно .

Решим данный пример вторым способом. Вернемся к изначальному выражению:

Запишем смешанное число в развёрнутом виде. Остальное перепишем без изменений:

Заключим каждое рациональное число в скобки вместе своими знаками:

Заменим вычитание сложением там, где это можно:

Вычислим целые части:

В главном выражении вместо запишем полученное число −7

Выражение   является развёрнутой формой записи смешанного числа .   Запишем число −7 и дробь  вместе, образуя окончательный ответ:

Запишем это решение покороче:

---

Пример 8. Найти значение выражения

Переведём смешанные числа в неправильные дроби:

Заключим каждое рациональное число в скобки вместе своими знаками:

Заменим вычитание сложением:

Получили сложение отрицательных рациональных чисел. Слóжим модули этих чисел и перед полученным ответом поставим минус:

Таким образом, значение выражения   равно 

Данный пример можно решить и вторым способом. Он заключается в том, чтобы сложить целые и дробные части по отдельности. Вернёмся к изначальному выражению:

Заключим каждое рациональное число в скобки вместе со своими знаками:

Заменим вычитание сложением:

Получили сложение отрицательных рациональных чисел. Слóжим модули этих чисел и перед полученным ответом поставим минус. Но в этот раз слóжим по отдельности целые части (−1 и −2), и дробные  и 

Запишем это решение покороче:

---

Пример 9. Найти выражения выражения

Переведём смешанные числа в неправильные дроби:

Заключим рациональное число  в скобки вместе своим знаком. Рациональное число  в скобки заключать не нужно, поскольку оно уже в скобках:

Приведём данные дроби в общему знаменателю. После их приведения к общему знаменателю, они примут следующий вид:

Получили сложение отрицательных рациональных чисел. Слóжим модули этих чисел и перед полученным ответом поставим минус:

Таким образом, значение выражения  равно 

Теперь попробуем решить этот же пример вторым способом, а именно сложением целых и дробных частей по отдельности.

В этот раз, в целях получения короткого решения, попробуем пропустить некоторые действия, такие как: запись смешанного числа в развёрнутом виде и замена вычитания сложением:

Обратите внимание, что дробные части были приведены к общему знаменателю.

---

Пример 10. Найти значение выражения

Заменим вычитание сложением:

В получившемся выражении нет отрицательных чисел, которые являются основной причиной допущения ошибок. А поскольку нет отрицательных чисел, мы можем убрать плюс перед вычитаемым, а также убрать скобки:

Получилось простейшее выражение, которое вычисляется легко. Вычислим его любым удобным для нас способом:

---

Пример 11. Найти значение выражения

Это сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший модуль, и перед полученными ответом поставим знак того рационального числа, модуль которого больше:

---

Пример 12. Найти значение выражения

Выражение состоит из нескольких рациональных чисел. Согласно порядку действий, в первую очередь необходимо выполнить действия в скобках.

Сначала вычислим выражение , затем выражение Полученные результаты слóжим .

Первое действие:

Второе действие:

Третье действие:

Ответ: значение выражения  равно 

---

Пример 13. Найти значение выражения

Переведём смешанные числа в неправильные дроби:

Заключим рациональное число  в скобки вместе со своим знаком. Рациональное число  заключать в скобки не нужно, поскольку оно уже в скобках:

Приведём данные дроби в общему знаменателю. После их приведения к общему знаменателю, они примут следующий вид:

Заменим вычитание сложением:

Получили сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший модуль, и перед полученными ответом поставим знак того рационального числа, модуль которого больше:

Таким образом, значение выражения равно

---

Рассмотрим сложение и вычитание десятичных дробей, которые тоже относятся к рациональным числам и которые могут быть как положительными, так и отрицательными.

Пример 14. Найти значение выражения −3,2 + 4,3

Заключим каждое рациональное число в скобки вместе со своими знаками. Учитываем, что плюс который дан в выражении, является знаком операции и не относится к десятичной дроби 4,3. У этой десятичной дроби свой знак плюса, который невидим по причине того, что его не записывают. Но мы его запишем для наглядности:

(−3,2) + (+4,3)

Это сложение рациональных чисел с разными знаками. Чтобы сложить рациональные числа с разными знаками, нужно из большего модуля вычесть меньший модуль, и перед полученным ответом поставить знак того рационального числа, модуль которого больше. А чтобы понять какой модуль больше, а какой меньше, нужно суметь сравнить модули этих десятичных дробей до их вычисления:

(−3,2) + (+4,3) = |+4,3| − |−3,2| = 1,1

Модуль числа 4,3 больше, чем модуль числа −3,2 поэтому мы из 4,3 вычли 3,2. Получили ответ 1,1. Ответ положителен, поскольку перед ответом должен стоять знак того рационального числа, модуль которого больше. А модуль числа 4,3 больше, чем модуль числа −3,2

Таким образом, значение выражения −3,2 + (+4,3) равно 1,1

Этот пример можно записать покороче:

−3,2 + (+4,3) = 1,1

---

Пример 15. Найти значение выражения 3,5 + (−8,3)

Это сложение рациональных чисел с разными знаками. Как и в прошлом примере из большего модуля вычитаем меньший и перед ответом ставим знак того рационального числа, модуль которого больше:

3,5 + (−8,3) = −(|−8,3| − |3,5|) = −(8,3 − 3,5) = −(4,8) = −4,8

Таким образом, значение выражения 3,5 + (−8,3) равно −4,8

Этот пример можно записать покороче:

 3,5 + (−8,3) = −4,8

---

Пример 16. Найти значение выражения −7,2 + (−3,11)

Это сложение отрицательных рациональных чисел. Чтобы сложить отрицательные рациональные числа, нужно сложить их модули и перед полученным ответом поставить минус.

Запись с модулями можно пропустить, чтобы не загромождать выражение:

−7,2 + (−3,11) = −7,20 + (−3,11) = −(7,20 + 3,11) = −(10,31) = −10,31

Таким образом, значение выражения −7,2 + (−3,11) равно −10,31

Этот пример можно записать покороче:

−7,2 + (−3,11) = −10,31

---

Пример 17. Найти значение выражения −0,48 + (−2,7)

Это сложение отрицательных рациональных чисел. Слóжим их модули и перед полученным ответом поставим минус. Запись с модулями можно пропустить, чтобы не загромождать выражение:

−0,48 + (−2,7) = (−0,48) + (−2,70) = −(0,48 + 2,70) = −(3,18) = −3,18

---

Пример 18. Найти значение выражения −4,9 − 5,9

Заключим каждое рациональное число в скобки вместе со своими знаками. Учитываем, что минус который располагается между рациональными числами −4,9 и 5,9 является знаком операции и не относится к числу 5,9. У этого рационального числа свой знак плюса, который невидим по причине того, что он не записывается. Но мы запишем его для наглядности:

(−4,9) − (+5,9)

Заменим вычитание сложением:

(−4,9) + (−5,9)

Получили  сложение отрицательных рациональных чисел. Слóжим их модули и перед полученным ответом поставим минус:

(−4,9) + (−5,9) = −(4,9 + 5,9) = −(10,8) = −10,8

Таким образом, значение выражения −4,9 − 5,9 равно −10,8

Запишем решение этого примера покороче:

−4,9 − 5,9 = −10,8

---

Пример 19.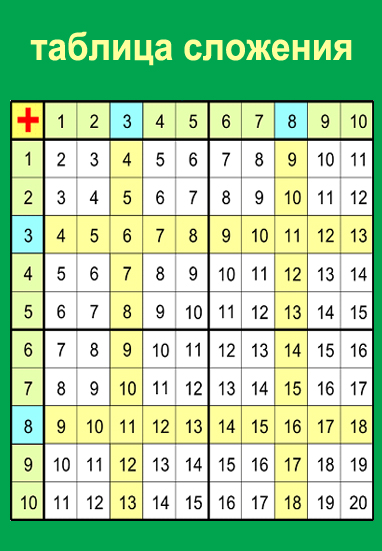 Найти значение выражения 7 − 9,3

Заключим в скобки каждое число вместе со своими знаками

(+7) − (+9,3)

Заменим вычитание сложением

(+7) + (−9,3)

Получили сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший модуль, и перед ответом поставим знак того числа, модуль которого больше:

(+7) + (−9,3) = −(9,3 − 7) = −(2,3) = −2,3

Таким образом, значение выражения 7 − 9,3 равно −2,3

Запишем решение этого примера покороче:

7 − 9,3 = −2,3

---

Пример 20. Найти значение выражения −0,25 − (−1,2)

Заменим вычитание сложением:

−0,25 + (+1,2)

Получили сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший модуль, и перед ответом поставим знак того числа, модуль которого больше:

−0,25 + (+1,2) = 1,2 − 0,25 = 0,95

Запишем решение этого примера покороче:

−0,25 − (−1,2) = 0,95

---

Пример 21. Найти значение выражения −3,5 + (4,1 − 7,1)

Выполним действия в скобках, затем слóжим полученный ответ с числом −3,5

Первое действие:

4,1 − 7,1 = (+4,1) − (+7,1) = (+4,1) + (−7,1) = −(7,1 − 4,1) = −(3,0) = −3,0

Второе действие:

−3,5 + (−3,0) = −(3,5 + 3,0) = −(6,5) = −6,5

Ответ: значение выражения −3,5 + (4,1 − 7,1) равно −6,5.

---

Пример 22. Найти значение выражения (3,5 − 2,9) − (3,7 − 9,1)

Выполним действия в скобках. Затем из числа, которое получилось в результате выполнения первых скобок, вычтем число, которое получилось в результате выполнения вторых скобок:

Первое действие:

3,5 − 2,9 = (+3,5) − (+2,9) = (+3,5) + (−2,9) = 3,5 − 2,9 = 0,6

Второе действие:

3,7 − 9,1 = (+3,7) − (+9,1) = (+3,7) + (−9,1) = −(9,1 − 3,7) = −(5,4) = −5,4

Третье действие

0,6 − (−5,4) = (+0,6) + (+5,4) = 0,6 + 5,4 = 6,0 = 6

Ответ: значение выражения (3,5 − 2,9) − (3,7 − 9,1) равно 6.

---

Пример 23. Найти значение выражения −3,8 + 17,15 − 6,2 − 6,15

Заключим в скобки каждое рациональное число вместе со своими знаками

(−3,8) + (+17,15) − (+6,2) − (+6,15)

Заменим вычитание сложением там, где это можно:

(−3,8) + (+17,15) + (−6,2) + (−6,15)

Выражение состоит из нескольких слагаемых. Согласно сочетательному закону сложения, если выражение состоит из нескольких слагаемых, то сумма не будет зависеть от порядка действий. Это значит, что слагаемые можно складывать в любом порядке.

Не будем изобретать велосипед, а слóжим все слагаемые слева направо в порядке их следования:

Первое действие:

(−3,8) + (+17,15) = 17,15 − 3,80 = 13,35

Второе действие:

13,35 + (−6,2) = 13,35 − 6,20 = 7,15

Третье действие:

7,15 + (−6,15) = 7,15 − 6,15 = 1,00 = 1

Ответ: значение выражения −3,8 + 17,15 − 6,2 − 6,15 равно 1.

---

Пример 24. Найти значение выражения

Переведём десятичную дробь −1,8 в смешанное число. Остальное перепишем без изменения:

Далее вычисляем данное выражение, применяя ранее изученные правила:

---

Пример 25. Найти значение выражения

Заменим вычитание сложением. Попутно переведём десятичную дробь (−4,4) в неправильную дробь

В получившемся выражении нет отрицательных чисел. А поскольку нет отрицательных чисел, мы можем убрать плюс перед вторым числом, и убрать скобки. Тогда получим простое выражение на сложение, которое решается легко

---

Пример 26. Найти значение выражения

Переведём смешанное число в неправильную дробь, а десятичную дробь −0,85 в обыкновенную дробь. Получим следующее выражение:

Получили  сложение отрицательных рациональных чисел. Слóжим их модули и перед полученным ответом поставим минус:

---

Пример 27. Найти значение выражения

Переведём обе дроби в неправильные дроби. Чтобы перевести десятичную дробь 2,05 в неправильную дробь, можно перевести ее сначала в смешанное число, а затем в неправильную дробь:

После перевода обеих дробей в неправильные дроби, получим следующее выражение:

Получили сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший модуль и перед полученным ответом поставим знак того числа, модуль которого больше:

---

Пример 28. Найти значение выражения 

Заменим вычитание сложением. Далее переведём десятичную дробь в обыкновенную дробь. Затем вычислим получившееся выражение, применяя ранее изученные правила:

---

Пример 29. Найти значение выражения

Переведём десятичные дроби −0,25 и −1,25 в обыкновенные дроби, остальное перепишем без изменения. Получим следующее выражение:

Можно сначала заменить вычитание сложением там, где это можно и сложить рациональные числа одно за другим.

Есть и второй вариант: сначала сложить рациональные числа и , а затем из полученного результата вычесть . Этим вариантом и воспользуемся.

Первое действие:

Второе действие:

Ответ: значение выражения  равно −2.

---

Пример 30. Найти значение выражения

Переведём десятичные дроби в обыкновенные. Остальное перепишем без изменения:

Получили сумму из нескольких слагаемых. Если сумма состоит из нескольких слагаемых, то выражение можно вычислять в любом порядке. Это следует из сочетательного закона сложения.

Поэтому мы можем организовать наиболее удобный для нас вариант. В первую очередь можно сложить первое и последнее слагаемое, а именно рациональные числа   и  . У этих чисел одинаковые знаменатели, а значит это освободит нас от необходимости приводить их к нему.

Первое действие:

Полученное число можно сложить со вторым слагаемым, а именно с рациональным числом . У рациональных чисел и   одинаковые знаменатели в дробных частях, что опять же является преимуществом для нас

Второе действие:

Ну и слóжим полученное число −7 с последним слагаемым, а именно с рациональным числом . Удобно то, что при вычислении данного выражения, семёрки исчезнут, поскольку их сумма будет равна нулю:

Третье действие:

Ответ: значение выражения  равно

Задание 1. Найдите значение выражения:

Решение:

Показать решение

Задание 2. Найдите значение выражения:

Решение:

Показать решение

Задание 3. Найдите значение выражения:

Решение:

Показать решение

Задание 4. Найдите значение выражения:

Решение:

Показать решение

Задание 5. Найдите значение выражения:

Решение:

Показать решение

Задание 6. Найдите значение выражения:

Решение:

Показать решение

Задание 7. Найдите значение выражения:

Решение:

Показать решение

Задание 8. Найдите значение выражения:

Решение:

Показать решение

Задание 9. Найдите значение выражения:

Решение:

Показать решение

Задание 10. Найдите значение выражения:

Решение:

Показать решение

---

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Опубликовано Автор

Дополнительные советы и рекомендации

T46WUOHXSHk

 

Вот множество «мыслительных трюков», которые вы можете использовать, чтобы упростить сложение.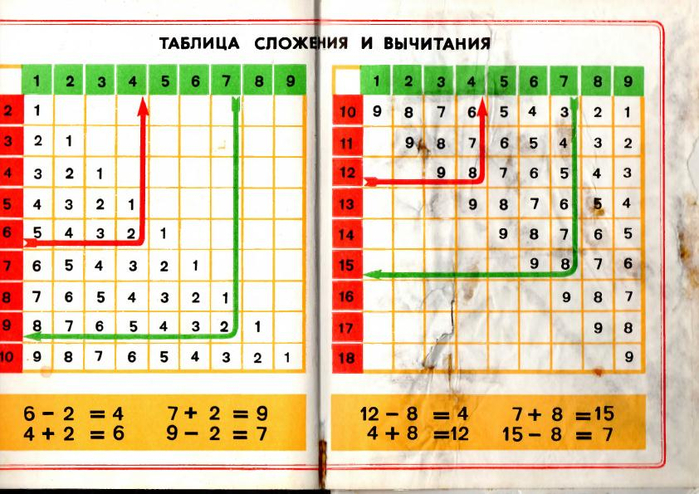

Используйте те, которые вам понятны!

Считать от числа вверх

Пример: 6 + 3

Подумай «6 … 7, 8, 9»

Подсказка: начните с большего числа.

Пример: 2 + 6

2 + 6 Сложнее: «2 … 3, 4, 5, 6, 7, 8»

6 + 2 Проще: «6 … 7, 8»

Вместо этого сделайте 6 + 2 (вы получите тот же ответ).

Стратегия прыжка

Мы также можем считать 2 или 10 секунд или делать любые «прыжки», которые мы хотим, чтобы помочь нам решить вычисление.

Пример: 4 + 12

Подумайте «4 … 14 … 15, 16»

Добавление до десяти

Посмотрите, есть ли какие-либо числа в сумме с 10. Они не обязательно должны стоять рядом друг с другом.

Пример: 7 + 8 + 3 + 2 + 5

7+3 равно 10,

8+2 еще 10, что дает 20,

Плюс 5 равно 25

Сделай десятки последними

Разбейте большие числа на десятки и единицы, добавьте единицы, затем добавьте десятки.

Пример: 14+5

Разбейте «14» на десятки и единицы: 10 + 4

Сложите единицы: 4 + 5 = 9

Теперь сложите десятки: 10 + 9 = 19

Подумайте » 4 плюс 5 равно 9, плюс 10 равно 19″

Другой пример: 14 + 12

Разбиваем на десятки и единицы: 10 + 4 + 10 + 2

Складываем единицы: 4 + 2 = 6

Теперь добавляем десятки: 6 + 10 + 10 = 26

Стремитесь к десятке

nYGXYJqN2pQ

Когда число близко к десяти, мы можем «позаимствовать» у другого числа, чтобы оно достигло десяти.

изображения/add-aim-10.js	Пример: 9 + 7 9 всего на 1 меньше 10
, поэтому возьмите 1 из 7: 9 + 1 + 6 и отдайте его 9: 10 + 6 = 16 Подумайте: «9 плюс 1 равно 10… 7 меньше 1 равно 6… вместе это 16″

Пример: 8 + 5

8+2=10, поэтому возьмем 2 из числа 5: 8 + 2 + 3
и добавим его в число 8: 10 + 3 = 13

Мы также можем переместить назад от до десяти, увеличив при необходимости другое число:

Пример: 12 + 7

Уменьшить 12 на 2: 12 − 2 = 10
Увеличить 7 на 2: 7 + 2 = 9

12 + 7 = 10 + 9 = 19

Метод компенсации

«Компенсация» — это когда вы округляете число (чтобы упростить добавление), а затем убираете лишнее после добавления.

Пример 19+16

Легче сделать 20 + 16 = 36

Затем уберите лишнюю 1 (из 19 получилось 20), чтобы получить: 35

Пример 395 + 126

Легче сделать 400 + 126 = 526

Затем уберите лишние 5 (из 395 получилось 400), чтобы получить: 521

Двойной, когда числа совпадают

Пример 5 + 5 = 2 x 5 = 10

Удвоить, если цифры близки, то исправить

Пример: 5 + 6 почти две пятерки, но 6 на 1 больше, чем 5, поэтому:

5 + 6 = две пятерки + 1 = 10 + 1 = 11

Пример: 7 + 9 похоже на две восьмерки, но 7 на 1 меньше 8, а 9 на 1 больше 8.

Таким образом, равно двум восьмерам , потому что 1 меньшая и 1 большая компенсируют друг друга:

7 + 9 = «8 минус 1» + «8 добавить 1» = две восьмерки = 16

Таблица дополнений

Мы также можем использовать дополнительную таблицу, чтобы помочь нам.

 

6591, 6592, 6593, 6597, 6598, 6584, 6585, 6586, 6587, 6588

Таблица умножения на 1–5

Попробуйте использовать эту таблицу Таблицы умножения на 1–5 , когда вы начнете учить своего ребенка умножению. Таблица охватывает первые пять таблиц умножения и содержит все числа, кратные от 1 до 12.

Таблица ярко окрашена, чтобы родителям и учителям было легко обсуждать ее с детьми. Крупные буквы позволяют практиковаться в чтении таблицы умножения и играть в викторины с диаграммой.

Скачать бесплатно Таблицу умножения на 1-5 >>

Таблица умножения – таблицы умножения 1-5

В дополнение к приведенной выше таблице вы также можете использовать эту таблицу умножения . Диаграмма организована так, что факторы 1–5 перечислены в верхней строке, а факторы 1–12 — в первом столбце. Произведение факторов находится там, где два фактора пересекаются на графике.

Например, вы можете видеть, что там, где пересекаются множители 2 и 8, появляется ответ 16.

Эта таблица также идеально подходит для обучения пропуску счета (подробности см. ниже).

Посетите нашу таблицу умножения 1-100 для получения дополнительной информации об этих типах таблиц >>.

Загрузить бесплатную Таблицу умножения – Таблицы умножения 1-5 >>

 

Использование таблицы умножения

Многие взрослые испытывают трудности с таблицей умножения, так что вы можете себе представить, насколько сложной может быть таблица умножения для детей. Чтобы помочь вашему ребенку запомнить таблицу умножения, вам нужно быть готовым тратить много времени, создавать веселье и интерес и повторять упражнения снова и снова.

Вот несколько советов о том, что вы можете сделать:

• Практика делает совершенным – при изучении новой таблицы умножения попросите ребенка повторить таблицу умножения по таблице.
• Сосредоточьтесь на одном факторе за раз – Придерживайтесь одного фактора и «играйте» с ним, пока ваш ребенок не познакомится с ним и его продуктами. Помните — запоминание всех продуктов займет время, это не произойдет за один присест!
• Работа по секциям – Начните с таблиц умножения на два и три, а затем доведите до четырех и пяти, когда ваш ребенок будет готов.
• Найдите ответ – вызовите случайные вопросы на умножение, и пусть ваш ребенок найдет ответ в таблице.
• Видео по таблице умножения – в Интернете есть много замечательных видео, которые вы можете использовать, чтобы научить своего ребенка таблице умножения. Смотрите нашу страницу видео таблицы умножения для наших рекомендаций.
• Таблица сотен – используйте таблицу сотен, чтобы показать ребенку, как работает умножение. Вы можете использовать диаграмму сотен, чтобы продемонстрировать шаблоны умножения, которые создает каждая таблица умножения. Ниже приведен пример шаблона умножения на 3 таблицы.

• Пропустить счет — попробуйте научить ребенка пропускать счет. Счет с пропуском — это когда вы считаете с шагом, отличным от единицы. Например, счет с пропуском на два выглядит следующим образом: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20. Счет с пропуском — это хороший математический навык для дети учатся — это улучшает их способность понимать умножение, а также дает детям возможность быстрее считать предметы (счет предметов на два намного быстрее, чем счет на один).
• Гонка на время – по секундомеру сколько времени нужно, чтобы прочитать таблицу умножения по таблице или по памяти. Запишите время, чтобы ваш ребенок мог попытаться побить свой лучший результат.
• Помните — не имеет значения, в каком порядке вы умножаете 2 числа; результат будет тот же. Например, 4 х 6 и 6 х 4 равны 24. Многие дети знают, что 6 х 4 = 24, но если вы спросите их 4 х 6, они почесают в затылке.

  No related posts.