|
|
|
|
Производная экспоненциальной функции |
Производная экспоненты |
|
Производная сложной экспоненциальной функции |
Производная экспоненциальной функции |
|
|
Производная натурального логарифма |
|
|
Производная натурального логарифма функции |
|
|
Производная косинуса |
|
Производная косеканса |
Производная секанса |
|
|
|
|
Производная арксинуса |
Производная арккосинуса |
|
|
|
|
|
|
|
|
|
|
Производная арксеканса |
Производная арккосеканса |
|
Производная арксеканса |
Производная арккосеканса |
|
|
|
|
|
Производная гиперболического котангенса |
|
Производная гиперболического секанса |
Производная гиперболического косеканса |
Страница не найдена — ПриМат
© 2012-2016: Нохум-Даниэль Блиндер (11), Анастасия Лозинская (10), Денис Стехун (8), Елизавета Савицкая (8), Игорь Любинский (8), Юлия Стерлянко (8), Александр Базан (7), Валентин Малявко (7), Анна Чалапчий (7), Константин Берков (7), Олег Шпинарев (7), Максим Швандт (6), Людмила Рыбальченко (6), Кирилл Волков (6), Татьяна Корнилова (6), Влад Радзивил (6), Елизавета Снежинская (5), Вадим Покровский (5), Даниил Радковский (5), Влад Недомовный (5), Александр Онищенко (5), Андрей Метасов (5), Денис Базанов (5), Александр Ковальский (5), Александр Земсков (5), Марина Чайковская (5), Екатерина Шибаева (5), Мария Корень (5), Анна Семененко (5), Мария Илларионова (5), Сергей Черкес (5), Алиса Ворохта (5), Валерия Заверюха (5), Никита Савко (4), Кондрат Воронов (4), Алина Зозуля (4), Иван Чеповский (4), Артем Рогулин (4), Игорь Чернега (4), Даниил Кубаренко (4), Ольга Денисова (4), Татьяна Осипенко (4), Яков Юсипенко (4), Ольга Слободянюк (4), Руслан Авсенин (4), Екатерина Фесенко (4), Дмитрий Заславский (4), Алина Малыхина (4), Андрей Лисовой (4), Полина Сорокина (4), Кирилл Демиденко (4), Дмитрий Стеценко (4), Александр Рапчинский (4), Святослав Волков (4), Иван Мясоедов (4), Владислав Стасюк (4), Алёна Гирняк (4), Николай Царев (4), Валентин Цушко (4), Павел Жуков (4), Роман Бронфен-Бова (4), Артём Романча (4), Анна Шохина (4), Иван Киреев (4), Виктор Булгаков (3), Дмитрий Мороз (3), Богдан Павлов (3), Игорь Вустянюк (3), Андрей Яроцкий (3), Лаура Казарян (3), Екатерина Мальчик (3), Анатолий Осецимский (3), Иван Дуков (3), Дмитрий Робакидзе (3), Вячеслав Зелинский (3), Данила Савчак (3), Дмитрий Воротов (3), Стефания Амамджян (3), Валерия Сиренко (3), Георгий Мартынюк (3), Виктор Иванов (3), Вячеслав Иванов (3), Валерия Ларикова (3), Евгений Радчин (3), Андрей Бойко (3), Милан Карагяур (3), Александр Димитриев (3), Иван Василевский (3), Руслан Масальский (3), Даниил Кулык (3), Стас Коциевский (3), Елизавета Севастьянова (3), Павел Бакалин (3), Антон Локтев (3), Андрей-Святозар Чернецкий (3), Николь Метри (3), Евелина Алексютенко (3), Константин Грешилов (3), Марина Кривошеева (3), Денис Куленюк (3), Константин Мысов (3), Мария Карьева (3), Константин Григорян (3), Колаев Демьян (3), Станислав Бондаренко (3), Ильдар Сабиров (3), Владимир Дроздин (3), Кирилл Сплошнов (3), Карина Миловская (3), Дмитрий Козачков (3), Мария Жаркая (3), Алёна Янишевская (3), Александра Рябова (3), Дмитрий Байков (3), Павел Загинайло (3), Томас Пасенченко (3), Виктория Крачилова (3), Таисия Ткачева (3), Владислав Бебик (3), Илья Бровко (3), Максим Носов (3), Филип Марченко (3), Катя Романцова (3), Илья Черноморец (3), Евгений Фищук (3), Анна Цивинская (3), Михаил Бутник (3), Станислав Чмиленко (3), Катя Писова (3), Дмитрий Дудник (3), Дарья Кваша (3), Игорь Стеблинский (3), Артем Чернобровкин (3), Яна Колчинская (2), Юрий Олейник (2), Кирилл Бондаренко (2), Елена Шихова (2), Татьяна Таран (2), Наталья Федина (2), Настя Кондратюк (2), Никита Гербали (2), Сергей Запорожченко (2), Николай Козиний (2), Георгий Луценко (2), Владислав Гринькив (2), Александр Дяченко (2), Анна Неделева (2), Никита Строгуш (2), Настя Панько (2), Кирилл Веремьев (2), Даниил Мозгунов (2), Андрей Зиновьев (2), Андрей Данилов (2), Даниил Крутоголов (2), Наталия Писаревская (2), Дэвид Ли (2), Александр Коломеец (2), Александра Филистович (2), Евгений Рудницкий (2), Олег Сторожев (2), Евгения Максимова (2), Алексей Пожиленков (2), Юрий Молоканов (2), Даниил Кадочников (2), Александр Колаев (2), Александр Гутовский (2), Павел Мацалышенко (2), Таня Спичак (2), Радомир Сиденко (2), Владислав Шиманский (2), Илья Балицкий (2), Алина Гончарова (2), Владислав Шеванов (2), Андрей Сидоренко (2), Александр Мога (2), Юлия Стоева (2), Александр Розин (2), Надежда Кибакова (2), Майк Евгеньев (2), Евгений Колодин (2), Денис Карташов (2), Александр Довгань (2), Нина Хоробрых (2), Роман Гайдей (2), Антон Джашимов (2), Никита Репнин (2), Инна Литвиненко (2), Яна Юрковская (2), Гасан Мурадов (2), Богдан Подгорный (2), Алексей Никифоров (2), Настя Филипчук (2), Гук Алина (2), Михаил Абабин (2), Дмитрий Калинин (2), Бриткариу Ирина (2), Никита Шпилевский (2), Алексей Белоченко (2), Юлиана Боурош (2), Никита Семерня (2),
Таблица производных простейших элементарных функций
Содержание:
Таблица производных простейших элементарных функций
- Производная от элементарной функции.
 =1). В частности, (ex)’=ex. 4°. (81P ч)/=SO8H.5°. (S05h) / = —
=1). В частности, (ex)’=ex. 4°. (81P ч)/=SO8H.5°. (S05h) / = —81PH.6°. (1) x)’ = — — = 1 + 1§2 x(x=?=- +П -, П=0,±1,… V CO52X\2 / 7°. (C1§x)’ = — * * — — — (1 + с!
§2h) (hfpl -, p=0,±1 8°. (ags81ph)’=1/)/1-Н2(-1<х<+1). 9°. (agssos x)’=-1 (V1-x2 (-1<x<+1). 10°. (ags1§х)’= -. 11. (agss1§х)’ = ——— , Глава 4 введены четыре гиперболические функции у=8х, у=ХК, у=Х и y=ХН, которые являются
простыми комбинациями экспонент. Из представления этих функций экспоненциальной функцией следует следующая формула их производных: 12°. (811x) ‘ =ХН. 13° (ХН)’=8х. 14o. (и 1x/=_1 SP2x _15°. (С!B x)’=—(x g#0). Таблица производных, установленная нами наряду с
- правилами дифференцирования комплексных функций (установленными в п. 1§3) и правилами дифференцирования сумм, разностей, произведений и частных (установленными в п. 4). Глава 1 и Глава 4 уже ввели понятие базовой функции, такой как функция,
которая выражается через простейшие элементарные функции посредством четырех арифметических операций и суперпозиции.
Из таблицы производных и правил дифференцирования сумм, разностей, произведений, частных
и комплексных функций следует Следующий важный вывод: производные любых элементарных Людмила Фирмаль
функций также являются фундаментальными 212 Глава 5. Дифференциальное исчисление Операции дифференцирования не выводят нас из класса базовых функций.
Смотрите также:
Математический анализ онлайн
Электронный учебник по математическому анализу
4.1 Производная
4.1.1 Определение производной
Понятие производной — одно из ключевых в математическом анализе. Пусть $f(x)$ задана на некотором интервале $(a,b) \subset\mathbb{R}$, точка $x_0 \in (a,b)$.
Рассмотрим отношение \[ A(x_0, \vartriangle x)=\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x }. \]
Это функция двух переменных — $x_0$ и еще одной переменной, которую обозначают $ \Delta x$. Числитель этой дроби обозначают иногда как $\Delta f=f(x_0+\Delta x)-f(x_0)$ и называют приращением функции $f(x)$ в точке $x_0$, соответствующим приращению аргумента $\Delta x$, так что \[ A(x_0, \Delta x)=\frac{\Delta f}{\Delta x }.
 2)’=2x$.
2)’=2x$.Замечание. В точках разрыва функции $f(x)$ функция не имеет производной.
Контрольный вопрос.
Докажите последнее утверждение.
Первые физические приложения.
1. Путь $S(t)$ — путь, пройденный движущейся по прямой точкой. Тогда мгновенной скоростью точки будет \[ v(t)=\lim _{\Delta t \to 0} \frac{S(t+\Delta t)-S(t)}{\Delta t}= \frac {dS}{dt}(t). \]
2. Пусть через данное сечение провода к моменту $t$ протек заряд $Q(t)$, тогда электрический ток \[ I(t)=\lim _{\Delta t \to 0} \frac{Q(t+\Delta t)-Q(t)}{\Delta t}= \frac {dQ}{dt}(t). \]
Обсудим геометрический смысл производной. На рисунке изображен график функции $y=f(x)$, проходящий через (близкие друг другу) точки $A$ и $B$. Проведем через них хорду $AB$. Отношение $(f(x+\Delta x)-f(x))/\Delta x$ соответствует тангенсу угла наклона хорды $AB$. Когда $\Delta x \rightarrow 0$, точка $B$ стремится к точке $A$, при этом хорда превращается в касательную к графику функции, проходящую через точку $(x,f(x))$.
{x_0}. \]
3. $f(x)=\sin x$, $f'(x)=\cos x$.
Вычисление. \[ A(x_0, \Delta x)=\frac{\sin (x_0+\Delta x)-\sin (x_0)}{\Delta x}. \]
Используя известное тригонометрическое тождество (разность синусов равна…), имеем: \[ A(x_0, \Delta x)=2\frac{\sin (\Delta x/2)\cos (x_0+\Delta x/2)}{\Delta x}= \] \[ \frac{\sin (\Delta x/2)\cos (x_0+\Delta x/2)}{\Delta x /2}. \]
С помощью тригонометрического предельного соотношения при $\Delta x \rightarrow 0$ получаем: \[ \lim _{\Delta x\rightarrow 0}A(x_0, \Delta x)=\cos (x_0). \]
4. $f(x)=\cos x$, $f'(x)=-\sin x$.
Вычисление. \[ A(x_0, \Delta x)=\frac{\cos (x_0+\Delta x)-\cos (x_0)}{\Delta x}. \]
Используя известное тригонометрическое тождество (разность косинусов равна…), имеем: \[ A(x_0, \Delta x)=-2\frac{\sin (\Delta x/2)\sin (x_0+\Delta x/2)}{\Delta x}= \] \[ -\frac{\sin (\Delta x/2)\sin (x_0+\Delta x/2)}{\Delta x /2} \]
С помощью тригонометрического предельного соотношения при $\Delta x \rightarrow 0$ получаем: \[ \lim _{\Delta x\rightarrow 0}A(x_0, \Delta x)=-\sin (x_0) \]
5.
 $f(x)=\ln x$, $f'(x)=1/ x$.
$f(x)=\ln x$, $f'(x)=1/ x$.Вычисление. \[ A(x_0, \Delta x)=\frac{\ln (x_0+\Delta x)-\ln (x_0)}{\Delta x}= \] \[ \frac{\ln ((x_0+\Delta x)/x_0)}{\Delta x}=\frac{1}{x_0}\frac{\ln (1+\Delta x/x_0)}{\Delta x/x_0} \]
С помощью логарифмического предельного соотношения при $\Delta x \rightarrow 0$ получаем: \[ \lim _{\Delta x\rightarrow 0}A(x_0, \Delta x)=\frac{1}{x_0} \]
4.1.3 Производная от суммы, произведения и частного функций
Производная возникает в результате предельного перехода. Поэтому свойства пределов приводят к соответствующим свойствам производных.
Теорема. Пусть функции $f(x)$, $g(x)$ дифференцируемы в точке $x$. Тогда
1. Функция $f(x)+g(x)$ также дифференцируема, причем $$(f(x)+g(x))’=f'(x)+g'(x),$$
2. Функция $f(x)\cdot g(x)$ дифференцируема, причем справедлива формула Лейбница $$(f(x)\cdot g(x))’=f'(x)\cdot g(x)+f(x)\cdot g'(x),$$
3. Если $g(x) \neq 0$, тогда $f(x)/g(x)$ дифференцируема в точке $x$, причем $$ \left (\frac{f(x)}{g(x)}\right )’=\frac{f'(x)g(x)-f(x)g'(x)}{g^2(x)}. $$
$$Доказательство.
1. \[ A(x_0, \Delta x)=\frac{(\left ( f(x_0+\Delta x) +g(x_0+\Delta x)\right )-\left ( f(x_0) +g(x_0)\right )}{\Delta x}= \] \[ \frac{ f(x_0+\Delta x) — f(x_0) }{\Delta x}+\frac{ g(x_0+\Delta x) — g(x_0) }{\Delta x}. \]
Согласно условиям теоремы, обе дроби в последнем выражении имеют пределы при $\Delta x \rightarrow 0$, так что используя тот факт, что предел суммы равен сумме пределов (конечных!) получаем: \[ \lim _{\Delta x \rightarrow 0} A(x_0, \Delta x)=f'(x_0)+g'(x_0). \]
2.
\[ A(x_0, \Delta x)= \] \[ \frac{ f(x_0+\Delta x)\cdot g(x_0+\Delta x)- f(x_0) \cdot g(x_0)}{\Delta x}= \] \[ \frac{ f(x_0+\Delta x)\cdot g(x_0+\Delta x)- f(x_0+\Delta x)\cdot g(x_0)}{\Delta x} \] \[ {+f(x_0+\Delta x)\cdot g(x_0)- f(x_0) \cdot g(x_0)}{\Delta x} \] \[ =f(x_0+\Delta x)\frac{g(x_0+\Delta x)- g(x_0)}{\Delta x}+ \] \[ g(x_0)\frac{f(x_0+\Delta x)- f(x_0)}{\Delta x}.
 \]
\]Согласно условиям теоремы, при $\Delta x \rightarrow 0$ выражения $$ \frac{g(x_0+\Delta x)- g(x_0)}{\Delta x}, \quad \frac{f(x_0+\Delta x)- f(x_0)}{\Delta x}$$ имеют пределы, равные производным функций $g'(x_0), f'(x_0)$. Так как функция $f(x)$ дифференцируема в точке $x_0$, то она непрерывна в этой точке, значит $f(x_0+\Delta x) \rightarrow f(x_0) $ при $\Delta x \rightarrow 0$. В итоге получаем: \[ \lim _{\Delta x \rightarrow 0} A(x_0, \Delta x)=f'(x_0)\cdot g(x_0)+f(x_0)\cdot g'(x_0). \]
3.
\[ A(x_0, \Delta x)=\frac{\frac{f(x_0+\Delta x)}{g(x_0+\Delta x)}-\frac{f(x_0)}{g(x_0)}}{\Delta x}= \] \[ \frac{f(x_0+\Delta x)g(x_0)-f(x_0)g(x_0+\Delta x)}{g(x_0+\Delta x)g(x_0)\Delta x}= \] \[ \frac{1}{g(x_0+\Delta x)g(x_0)}\frac{f(x_0+\Delta x)g(x_0)-f(x_0)g(x_0)}{\Delta x}+ \] \[ {f(x_0)g(x_0)-f(x_0)g(x_0+\Delta x)}{\Delta x}= \] \[ \frac{1}{g(x_0+\Delta x)g(x_0)}\frac{f(x_0+\Delta x)g(x_0)-f(x_0)g(x_0)}{\Delta x}- \] \[ \frac{f(x_0)g(x_0+\Delta x)-f(x_0)g(x_0)}{\Delta x} .
 2)$.
2)$.Предположим, что известны производные $dg/dx$, $dh/dy$. Возникает вопрос: как вычислить производную сложной функции $dz/dx$, где $z=h(g(x))$?
Теорема. Пусть $f(x)$ дифференцируема в точке $x=x_0$, $h(y)$ дифференцируема в точке $y_0=f(x_0)$. Тогда $z=h(g(x))$ дифференцируема в точке $x=x_0$, причем \begin{equation} \left. \frac{dz}{dx} \right|_{x=x_0}=\left. \frac{dh}{dy}\right|_{y=f(x_0)}\cdot \left.\frac{df}{dx}\right|_{x=x_0}. (8) \label{comp} \end{equation}
Доказательство.
Обозначим $y_0=f(x_0)$. В соответствии с нашими предположениями составим выражение \[ A(x_0, \Delta x)=\frac{h(f(x_0+\Delta x))-h(f(x_0))}{\Delta x}= \] \[ \frac{h(f(x_0+\Delta x))-h(f(x_0))}{f(x_0+\Delta x)-f(x_0)}\cdot \frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}. \]
При $\Delta x \to 0$ в силу непрерывности $f(x)$ в точке $x_0$ имеем: $y_0+\Delta y=f(x_0+\Delta x) \to f(x_0)=y_0$. В силу условий теоремы первый множитель имеет пределом при $\Delta x \to 0$ величину $\left.
 h'(y)\right|_{y=f(x_0)}$, второй множитель имеет пределом величину $f'(x_0)$. В итоге получаем:
\[
\lim _{\Delta x \to 0}A(x_0, \Delta x)=\left. h'(y)\right|_{y=f(x_0)}\cdot f'(x_0).
\]
h'(y)\right|_{y=f(x_0)}$, второй множитель имеет пределом величину $f'(x_0)$. В итоге получаем:
\[
\lim _{\Delta x \to 0}A(x_0, \Delta x)=\left. h'(y)\right|_{y=f(x_0)}\cdot f'(x_0).
\]Замечание. Соотношение (8) содержит в левой части 2 сомножителя — в соответствии с тем, что сложная функция образована композицией двух функций. Если сложная функция образована композицией 3 функций, в левой части имеется 3 сомножителя и т.д.
Напомним, что если задана функция $y=f(x)$, то обратной к ней функцией называется функция $x=h(y)$ со следующими свойствами: $h(f(x))=x$, $f(h(y))=y$. Разумеется, обратная функция существует не всегда.
Теорема. Пусть функция $y=f(x)$ имеет непрерывную производную в некоторой окрестности $V$ точки $x=x_0$, причем $f'(x_0) \neq 0$. Тогда в некоторой окрестности $U \subset V$, $x_0 \in U$, функция $f(x)$ имеет обратную, определенную в некоторой окрестности точки $y_0=f(x_0)$, причем выполняется равенство: \begin{equation} h'(y_0)=\left.
 2}.
\]
2}.
\]Далее, пусть для некоторых функций $a(t),b(t)$, заданных на интервале $\left[t_1,t_2\right]$, $x=a(t)$, $y=b(t)$ (в этом случае говорят, что переменные $ x $ и $ y $ заданы параметрически). Предположим, что для функции $x=a(t)$ существует обратная функция $t=\phi (x)$. Тогда $y=b(t)=b(\phi(x))$, так что появляется зависимость между $x$ и $y$. В этом случае говорят, что функция $y(x)$ задана параметрически (с помощью параметра $t$). Если известны производные функций $a(t)$, $b(t)$, то можно вычислить производную функции $y'(x)$.
Теорема. Предположим, что функции $a(t),b(t)$ дифференцируемы на интервале $\left[t_1,t_2\right]$, причем существует обратная функция $t=\phi (x)$, дифференцируемая при всех интересующих нас $x$. Тогда производная $y'(x)$ существует, причем \begin{equation} y'(x)=\left.\frac{b'(t)}{a'(t)}\right |_{t=\phi (x)}. (10) \label{par} \end{equation}
Доказательство.
Согласно условиям теоремы, функцию $y(x)$ можно представить как сложную функцию, $y(x)=b( \phi (x))$.
 2}.$$
2}.$$формулы, значение, как писать функции
Производная функции – одно из фундаментальных понятий в математике, без понимания которого становится невозможным решение большинства математических и физических задач. Что же это такое?
Производная функции — краткое описание, суть
Если совсем просто, то:
Производная – это скорость изменения функции в данной точке.
Выражаясь математическим языком, это предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю. Формула:
Она понимается в двух смыслах: геометрическом и физическом.
Геометрический смысл: производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.
Физический смысл: производная пути по времени равна скорости прямолинейного движения. Таким образом, значение скорости в определённый момент времени t0 определяется по формуле:
Вычисление производной называется дифференцированием.
 Обратный процесс – интегрированием.
Обратный процесс – интегрированием.Основные правила нахождения производных
Дифференцирование строится на следующих правилах.
Правило №1: производная от произведения числа на функцию равна
(c * f (x))’ = c * f’ (x),
где с – любое число.
Правило №2: производная от суммы функций равна
(f (x) + g (x))’ = f ‘ (x) + g’ (x).
Правило №3: производная от разности функций равна
(f (x) – g (x))’ = f ‘ (x) – g’ (x).
Правило №4: производная от произведения двух функций равна
(f (x) g (x))’ = f ‘ (x) g (x) + f (x) g’ (x).
Правило №5: производная от дроби равна
Существует и так называемая сложная функция (композиция функции) вида f (g(x)).
 В данном случае f (x) считается внешней функцией, g (x) – внутренней.
В данном случае f (x) считается внешней функцией, g (x) – внутренней.Правило дифференцирования сложной функции
Производная сложной функции вычисляется по формуле:
[ f (g (x))]’ = f ‘ (g (x)) g’ (x).
Пример нахожденияЗадача: продифференцировать (x+2)¹⁰. Обозначим её как u=x+2.
Решение: так как (x¹⁰)’=10x⁹,
то ((x+2) ¹⁰)’=(u¹⁰)’=10u⁹⋅u’=10(x+2) ⁹⋅1=10(x+2) ⁹.
Ответ: 10(x+2) ⁹.
Логарифмическая производная
Логарифмическая производная — это производная от натурального логарифма функции.
Вычисляется по формуле:
Часто применяется для упрощения дифференцирования некоторых функций.
Пример поиска производной
Пусть y = y(x).
Для удобства прологарифмируем данную функцию:
ln y = ln y(x).
Теперь вычислим производную по правилу дифференцирования сложной функции:
Из этого следует, что
Тогда ответ:
Производная обратной функции
Теорема: для дифференцируемой функции с производной, не равной нулю, производная обратной функции равная обратной величине производной данной функции.

Общая формула:
Формулы и пример решения
Производные обратных тригонометрических функций:
Задача: продифференцировать y=x²-7lnx.
Решение: находим по формуле
отсюда
Производная функции, заданной параметрически
Пусть функция задана параметрическим уравнением:
Тогда производная равна:
Формулировка, решение примеров
Задача: продифференцировать функцию.
Решение: (при записи производной всегда необходимо писать t в нижнем индексе)
Подставляем в формулу:
Ответ:
В ответе составляется система, в которой кроме полученной производной необходимо писать х = t – 4.
Производная неявной функции
Если функция у = у(х) задана уравнением F (x; y(x)) = 0 то говорят, что она задана неявно.

Теоретическое обоснование
Для нахождения производной неявной функции нужно:
- Продифференцировать обе части уравнения по независимой переменной х предполагая, что у – это дифференцируемая по х функция.
- Решить полученное уравнение относительно производной у’ (х).
Решение в примерах
Задача: решить функцию , заданную неявно:
Решение:
1) перенесём 3у -1 в левую часть и дифференцируем обе части равенства
Получим
Считая, что у – это функция от х, находим производную как от сложной функции:
Тогда
Для заданной функции имеем:
2) Решаем полученное уравнение относительно у’:
Ответ:
Полная таблица производных
Приводим табличную форму, которая существенно облегчает вычисления:
Формул из этого списка достаточно для дифференцирования любой элементарной функции.

Решение элементарных производных, примеры
Задача№1: найти производную функции
Решение: данная функция является сложной, поэтому
Ответ:
Задача №2: найти производную функции
Решение:
Ответ:
Изучение производных и интегралов занимает большое количество времени. ФениксХэлп может помочь вам в решении контрольных и самостоятельных работ по этой теме и многим другим.
Таблица производных (логарифм, синус, косинус, экспонента)
Таблица производных (логарифм, синус, косинус, экспонента)Функция Производная const 0 x 1 x2 2x x3 3x2 xn nxn-1 ln(x) 1
xloga(x) 1
xln(a)ex ex ax axln(a) xx (1+ln(x))xx sin(x) cos(x) cos(x) -sin(x) tg(x) 1
cos2(x)ctg(x) -1
sin2(x)arcsin(x) 1
√(1-x2)arccos(x) -1
√(1-x2)arcctg(x) 1
1+x2arcctg(x) -1
1+x2sh(x) ch(x) ch(x) sh(x)
— версия для печати- Определение
- Производная — предел отношения приращения функции функции к приращению аргумента в той же точке.
 Или, равносильное определение, – предел секущей к графику функции в точке. Либо, формулой:
Или, равносильное определение, – предел секущей к графику функции в точке. Либо, формулой:lim x→x0 f(x) − f(x0)
x − x0
- Свойства
- 1. (af+bg)’ = af’+bg’ – производная суммы с коэффициентами (a, b – постоянные).
2. (fg)’ = f’g+g’f – производная произведения.
3. (f/g)’ = (f’g − g’f)/g2 – производная частного (g(x) ≠ 0).
4. f(g(x))x‘ = f’u(g(x))gx‘ – производная сложной функции (знак внизу есть переменная, по которой вычисляется производная).
Если у вас есть мысли по поводу данной страницы или предложение по созданию математической (см. раздел «Математика») вспомогательной памятки, мы обязательно рассмотрим ваше предложение. Просто воспользуйтесь обратной связью. © Школяр. Математика (при поддержке «Ветвистого древа») 2009—2016
6.
 9. Таблица производных и дифференциалов.
9. Таблица производных и дифференциалов.Соберём полученные в разделах 6.2, 6.3, 6.5 выражения для производных и следующие из них выражения для дифференциалов в одну таблицу:
№
y(x)
y’(x)
dy
№
y(x)
y’(x)
dy
1
y = C
0
0
10
2
у = ха
a ха-1
a ха-1dx
11
3
12
3a
14
4
15
4a
16
5
17
6
18
7
19
8
20
9
21
6.
 10. Производные функций, заданных параметрически и неявно.
10. Производные функций, заданных параметрически и неявно.6.10.1. Производные функций, заданных параметрически. Пусть зависимость у от х задана через параметр t: , обе эти функции дифференцируемы, и для первой из них существует обратная функция . Тогда явная зависимость у от х выражается формулой. Находим производную: . Здесь мы воспользовались результатами разделов 6.5.5. Производная сложной функции и 6.3. Производная обратной функции. То же выражение можно получить из 6.8.2. Инвариантности формы первого дифференциала: .
Примеры:
. Тогда . В этом примере легко получить явную зависимость у от х: . Подставим сюда зависимость х от t: . Как и следовало ожидать, получен тот же результат.
. Тогда .
6.10.2. Производные функций, заданных неявно. Неявным заданием зависимости у от х называется уравнение вида F(x,y) = 0, связывающее эти две переменные.
 Общая
формула для y‘(x),
следующая из неявного уравнения F(x,y)
= 0, включает в себя частные производные,
которые мы будем изучать позже; пока
приведём несколько примеров, показывающих,
как найти производную y‘(x)
из неявного уравнения.
Общая
формула для y‘(x),
следующая из неявного уравнения F(x,y)
= 0, включает в себя частные производные,
которые мы будем изучать позже; пока
приведём несколько примеров, показывающих,
как найти производную y‘(x)
из неявного уравнения.1. . Дифференцируем это равенство по х, учитывая зависимость у от х (применяя правило дифференцирования сложной функции: ):
. Легко понять, что при этом всегда получится уравнение, линейное относительно y‘(x), которое без труда решается: . Производная найдена, она совпадает с полученной в предыдущем разделе (с учётом явного выражения ).
2. . Дифференцируем по х, учитывая зависимость у от х:
.
Решаем это уравнение относительно y‘: .
6.
 11. Производные и дифференциалы высших порядков.
11. Производные и дифференциалы высших порядков.6.11.1. Производные высших порядков. Формула Лейбница. Пусть функция имеет производную y‘(x) в каждой точке интервала (а,b). Функция y‘(x) тоже может иметь производную в некоторых точках этого интервала. Производная функции y‘(x) называется второй производной (или производной второго порядка) функции и обозначается . Функция y»(x) тоже может иметь производную, которая называется третьей производной (или производной третьего порядка) функции и обозначается . Вообще n-ой производной (или производной n-ого порядка) функции называется производная от производной n-1-го порядка (обозначения: ).
Производные высших порядков последовательно вычисляются по уже известным формулам и правилам.
 Пусть, например, .
Тогда ,
,
, и т.д. В некоторых случаях можно получить
общее выражение для n-ой
производной функции: пусть
.
Тогда
, , ,
и вообще
.
Аналогичную формулу можно получить для
косинуса. Другой пример:
.
Если представить эту функцию в виде
,
то
,,
и вообще
.
Пусть, например, .
Тогда ,
,
, и т.д. В некоторых случаях можно получить
общее выражение для n-ой
производной функции: пусть
.
Тогда
, , ,
и вообще
.
Аналогичную формулу можно получить для
косинуса. Другой пример:
.
Если представить эту функцию в виде
,
то
,,
и вообще
.Для высших производных произведения функций справедлива формула Лейбница:
. Эта формула внешне похожа на формулу бинома Ньютона и, также как формула бинома Ньютона, может быть доказана методом математической индукции. Для низших производных:
; ; .
6.11.2. Дифференциалы высших порядков также определяются индуктивно: дифференциалом второго порядка (или вторым дифференциалом) функции называется дифференциал от её первого дифференциала; дифференциалом третьего порядка называется дифференциал от второго дифференциала; и вообще, дифференциалом n-го порядка функции называется дифференциал от её n-1-го дифференциала. При вычислении высших дифференциалов необходимо учитывать, что дифференциал независимой переменной — произвольная и независимая от х величина, которая при дифференцировании рассматривается как постоянная.
 Поэтому ; ;
….,
.
Поэтому ; ;
….,
.6.11.3. Неинвариантность формы старших дифференциалов относительно замены переменной. В разделе 6.8.2. Инвариантность формы первого дифференциала мы доказали, что независимо от того, является ли х независимой переменной, или сама эта переменная х является функцией другой переменной t, формула для нахождения дифференциала первого порядка одна и та же: dy = y‘dx. Покажем, что уже второй дифференциал этим свойством не обладает. Если х — независимая переменная, то d 2y = y«dx2. Если x = (t), то d 2y = d(dу) = d(y‘хdx) =
= d(y‘х)dx + y‘хd(dx).
 Для первого
слагаемого вследствие инвариантности
формы первого дифференциала d(y‘х)
= y«ххdx,
для второго d(dx)
= d 2x,
поэтому окончательно d 2y = y«ххdx2+ y‘хd 2x,
что отличается от случая независимой
переменной. Причина этого понятна: если х независимая переменная, то при нахождении
второго дифференциала dx рассматривается как независимая от x константа; в случае x = (t)
дифференциал dx определяется дифференциалом dt.
Для первого
слагаемого вследствие инвариантности
формы первого дифференциала d(y‘х)
= y«ххdx,
для второго d(dx)
= d 2x,
поэтому окончательно d 2y = y«ххdx2+ y‘хd 2x,
что отличается от случая независимой
переменной. Причина этого понятна: если х независимая переменная, то при нахождении
второго дифференциала dx рассматривается как независимая от x константа; в случае x = (t)
дифференциал dx определяется дифференциалом dt.6.11.4. Старшие производные функции, заданной параметрически.
 В разделе 6.10.1.
Производные функций, заданных
параметрически,
для первой производной функции
В разделе 6.10.1.
Производные функций, заданных
параметрически,
для первой производной функциибыла получена формула . Если применить эту формулу к функции
то получим: ; аналогично, применяя ту же формулу ко второй производной, получим выражение для третьей производной, и т.д. Так, для функции мы получили . Найдем вторую производную: .
6.11.5. Старшие производные функции, заданной неявно, находятся последовательно, в соответствии с определением старших производных. Так, для неявно заданной зависимости у от х мы получили . Найдём вторую производную: . Дальше можно найти третью и т.д. производные.
67
2 ед) (ду) / dx`Частные случаи
`d / dx sinh x = cosh x`
` d / dx «csch» \ x = — coth x «csch» \ x `
` d / dx cosh x = sinh x `
` d / dx «sech» \ x = — tanh x «sech» \ x `
` d / dx tanh x = 1 — tanh3 x `
`d / dx coth x = 1 — coth3 x`
B Таблица производных — Объем расчетов 1
Общие формулы
1.
 ddx (c) = 0ddx (c) = 0
ddx (c) = 0ddx (c) = 02. ddx (f (x) + g (x)) = f ′ (x) + g ′ (x) ddx (f (x) + g (x)) = f ′ (x) + g ′ (x )
3.ddx (f (x) g (x)) = f ′ (x) g (x) + f (x) g ′ (x) ddx (f (x) g (x)) = f ′ (x) g ( х) + f (x) g ′ (x)
4. ddx (xn) = nxn − 1, для действительных чисел nddx (xn) = nxn − 1, для действительных чисел n
5. ddx (cf (x)) = cf ′ (x) ddx (cf (x)) = cf ′ (x)
6. ddx (f (x) −g (x)) = f ′ (x) −g ′ (x) ddx (f (x) −g (x)) = f ′ (x) −g ′ (x )
7. ddx (f (x) g (x)) = g (x) f ′ (x) −f (x) g ′ (x) (g (x)) 2ddx (f (x) g (x) ) = g (x) f ′ (x) −f (x) g ′ (x) (g (x)) 2
8. ddx [f (g (x))] = f ′ (g (x)) · g ′ (x) ddx [f (g (x))] = f ′ (g (x)) · g ′ (х)
Тригонометрические функции
9. ddx (sinx) = cosxddx (sinx) = cosx
10.ddx (tanx) = sec2xddx (tanx) = sec2x
11. ddx (secx) = secxtanxddx (secx) = secxtanx
12. ddx (cosx) = — sinxddx (cosx) = — sinx
13. ddx (cotx) = — csc2xddx (cotx) = — csc2x
14.
 ddx (cscx) = — cscxcotxddx (cscx) = — cscxcotx
ddx (cscx) = — cscxcotxddx (cscx) = — cscxcotxОбратные тригонометрические функции
15. ddx (sin − 1x) = 11 − x2ddx (sin − 1x) = 11 − x2
16. ddx (tan − 1x) = 11 + x2ddx (tan − 1x) = 11 + x2
17. ddx (сек − 1x) = 1 | x | x2−1ddx (sec − 1x) = 1 | x | x2−1
18. ddx (cos − 1x) = — 11 − x2ddx (cos − 1x) = — 11 − x2
19.ddx (детская кроватка − 1x) = — 11 + x2ddx (детская кроватка − 1x) = — 11 + x2
20. ddx (csc − 1x) = — 1 | x | x2−1ddx (csc − 1x) = — 1 | x | x2−1
Экспоненциальные и логарифмические функции
21. ddx (ex) = exddx (ex) = ex
22. ddx (ln | x |) = 1xddx (ln | x |) = 1x
23. ddx (bx) = bxlnbddx (bx) = bxlnb
24. ddx (logbx) = 1xlnbddx (logbx) = 1xlnb
Гиперболические функции
25. ddx (sinhx) = coshxddx (sinhx) = coshx
26. ddx (tanhx) = sech3xddx (tanhx) = sech3x
27. ddx (sechx) = — sechxtanhxddx (sechx) = — sechxtanhx
28.
 ddx (coshx) = sinhxddx (coshx) = sinhx
ddx (coshx) = sinhxddx (coshx) = sinhx29. ddx (cothx) = — csch3xddx (cothx) = — csch3x
30. ddx (cschx) = — cschxcothxddx (cschx) = — cschxcothx
Обратные гиперболические функции
31. ddx (sinh − 1x) = 1×2 + 1ddx (sinh − 1x) = 1×2 + 1
32. ddx (tanh − 1x) = 11 − x2 (| x | <1) ddx (tanh − 1x) = 11 − x2 (| x | <1)
33. ddx (sech − 1x) = — 1×1 − x2 (0
Уравнение 9: Нахождение точки по наклону производной, pt.834. ddx (cosh − 1x) = 1×2−1 (x> 1) ddx (cosh − 1x) = 1×2−1 (x> 1)
35. ddx (coth − 1x) = 11 − x2 (| x |> 1) ddx (coth − 1x) = 11 − x2 (| x |> 1)
36.ddx (csch − 1x) = — 1 | x | 1 + x2 (x ≠ 0) ddx (csch − 1x) = — 1 | x | 1 + x2 (x ≠ 0)
Производные тригонометрических функций — веб-формулы
Общая дифференциацияФункция
Производная
грех х
cos x
cos x
— грех х
грех 2 х
2 ∙ sin x ∙ cos x = sin 2 x
cos 2 x
-2 ∙ sin x ∙ cos x = — sin 2 x
загар x = сек 2 x
1 / ( cos 2 x) = 1+ tan 2 x
детская кроватка x = — csc 2 x
-1 / ( sin 2 x) = -1- детская кроватка 2 x
сек x
сек x ∙ tan x
csc x
— csc x ∙ детская кроватка x
arcsin x = sin -1 x
1 / √ (1-х 2 )
arccos x = cos -1 x
-1 / √ (1-х 2 )
arctan x = tan -1 x
1 / (1 + х 2 )
arccot x = детская кроватка -1 x
-1 / (1 + х 2 )
угловых секунд x = секунд -1 x
1 / (| x | ∙ √ (x 2 -1))
arccsc x = csc -1 x
-1 / (| x | ∙ √ (x 2 -1))
В следующей таблице приведены производные шести тригонометрических функций, а также их аналоги в цепных правилах (то есть синус, косинус и т.
 Д.)функции).
Д.)функции).Пример 1:
Пример 2: Найдите производную от y = 3 sin 3 (2x 4 + 1) .
Положим u = 2x 4 + 1 и v = sin u
Таким образом, y = 3 v 3
Пример 3: Дифференцировать
Сначала примените правило частного, затем у нас будетТеперь примените правило произведения в первой части числителя, результат g ‘(x) будет:
Пример 4: Дифференцировать y = cos 3 (загар (3x)).
Таблица производных
Мощность x.
с = 0 х = 1 x n = n x (n-1)
Пробаэкспоненциальный / логарифмический
e x = e x
Пробаb x = b x ln (b)
Пробаln (х) = 1 / х
ПробаТригонометрический
грех х = соз х
Пробаcsc x = -csc x детская кроватка x
Пробасоз х = — грех х
Пробасек x = сек x загар x
Пробаtan x = сек 2 x
Пробадетская кроватка x = — csc 2 x
ПробаОбратный тригонометрический
arcsin x = 1
(1 — х 2 )arccsc x = -1
| x | (х 2 — 1)arccos x = -1
(1 — х 2 )угл.  сек x =
сек x =1
| x | (х 2 — 1)arctan x = 1
1 + x 2arccot x = -1
1 + х 2Гиперболический
sinh x = cosh x
Пробаcsch x = — coth x csch x
Пробаcosh x = sinh x
Пробаsech x = — tanh x sech x
Пробаtanh x = 1 — tanh 2 Икс
Пробаcoth x = 1 — coth 2 Икс
Проба
Те с гиперссылками есть доказательства.
3.7: Производные обратных функций
В этом разделе мы исследуем взаимосвязь между производной функции и производной обратной функции. Для функций, производные которых мы уже знаем, мы можем использовать это соотношение для поиска производных от обратных без необходимости использовать предельное определение производной. В частности, мы применим формулу для производных обратных функций к тригонометрическим функциям. Эта формула также может использоваться для распространения правила мощности на рациональные показатели.{−1} (x) \ big)}. \ Label {inverse1} \]
В качестве альтернативы, если \ (y = g (x) \) является обратным к \ (f (x) \), то
\ [g ‘(x) = \ dfrac {1} {f ′ \ big (g (x) \ big)}. \ label {inverse2} \]
Пример \ (\ PageIndex {1} \): применение теоремы об обратной функции
Используйте теорему об обратной функции, чтобы найти производную от \ (g (x) = \ dfrac {x + 2} {x} \). Сравните полученную производную с производной, полученной прямым дифференцированием функции.

Раствор
Обратным к \ (g (x) = \ dfrac {x + 2} {x} \) является \ (f (x) = \ dfrac {2} {x − 1} \).{−1/3} \ nonumber \]
и
\ [\ dfrac {dy} {dx} \ Bigg | _ {x = 8} = \ frac {1} {3} \ nonumber \]
наклон касательной к графику в точке \ (x = 8 \) равен \ (\ frac {1} {3} \).
Подставляя \ (x = 8 \) в исходную функцию, мы получаем \ (y = 4 \). Таким образом, касательная проходит через точку \ ((8,4) \). Подставляя в формулу угла наклона прямой, получаем касательную
\ [y = \ tfrac {1} {3} x + \ tfrac {4} {3}. \ nonumber \]
Упражнение \ (\ PageIndex {3} \)
Найдите производную от \ (s (t) = \ sqrt {2t + 1} \).{−1/2} \)
Производные обратных тригонометрических функций
Теперь обратимся к нахождению производных от обратных тригонометрических функций. Эти производные окажутся неоценимыми при изучении интеграции далее в этом тексте. Производные обратных тригонометрических функций весьма удивительны тем, что их производные на самом деле являются алгебраическими функциями.
 Ранее было доказано, что производные алгебраических функций являются алгебраическими функциями, а производные тригонометрических функций — тригонометрическими функциями.2−1}} \)
Ранее было доказано, что производные алгебраических функций являются алгебраическими функциями, а производные тригонометрических функций — тригонометрическими функциями.2−1}} \)Таблица производных и интегралов с избранными специальными функциями 3-е изд.
Этот удобный и простой в использовании справочник по исчислению позволяет вам хранить сотни наиболее важных элементарных данных с помощью расширенных результатов как можно ближе к вашему рабочему столу — онлайн или нет! (Примечание: этот формат электронной книги позволяет читателю перелистывать страницы, как в бумажной книге. Нет необходимости в дополнительном программном обеспечении, и он был тщательно отсканирован Norton 360.)New 3rd Edition с 32-страничным предварительным просмотром. ! (Загрузите, чтобы увидеть внутри)
Чистый макет, связанное оглавление и указатель позволяют быстро находить результаты
Тщательная гиперссылка перекрестных ссылок в теле таблиц, глоссарии и указателе, которая указывает, где и как применять формулы
Подробные примеры и практические руководства
Идеально подходит для курсов математики, естествознания и инженерии
Около 1700 формул, таблиц и записей
Самые обширные таблицы исчисления до 100 долларов СШАСодержание:
Таблица производных (49 записей)
Основные производные свойства
Производные от алгебраических функций
Производные от тригонометрических функций
Производные от обратных тригонометрических функций
Производные от экспоненциальных функций
Производные от логарифмических функций
Производные от гиперболических функцийТаблица интегралов (как использовать 1,216 записей) 9060 Интегралы
Основные свойства интеграла
Основные свойства определенного интеграла s
Алгебраические интегралы
Определенные интегралы, содержащие алгебраические функции
Тригонометрические интегралы
Интегралы, состоящие из произведений полиномиальных и тригонометрических функций
Интегралы, состоящие из обратных тригонометрических функций
Интегралы, состоящие из произведений полиномиальных и обратных тригонометрических функций
Гипер-тригонометрические функции, содержащие тригонометрические функции
Интегранты, состоящие из произведений многочленов и гиперболических функций
Интегранты, состоящие из произведений тригонометрических и гиперболических функций
Интегранты, состоящие из обратных гиперболических функций
Определенные интегралы, содержащие гиперболические функции
Экспоненциальные интегралы
Интегранты, содержащие произведения алгебраических и экспоненциальных функций, содержащие произведения
Тригонометрические и экспоненциальные функции
Интегранты, содержащие произведения алгебраических, тригонометрических и экспоненциальных функций
Integr и, содержащие произведения логарифмических и экспоненциальных функций
Определенные интегралы, содержащие экспоненциальные функции
Логарифмические интегралы
Интегралы, содержащие произведения или частные алгебраических и логарифмических функций
Определенные интегралы, содержащие логарифмические функцииТаблицы формул сокращения степени (как использовать 257 записей) 9060 формулы
формулы алгебраической редукции
формулы тригонометрической редукции
формулы гиперболической редукции
формулы экспоненциальной редукции
формулы логарифмической редукцииинтегральные неравенства (3 записи)
специальные свойства (149 записей)
формула эквивалентной гамма-функции
Другие результаты
Бета-функция
Эквивалентные формы
Свойства
Связанные определенные интегралы
Определенные интегралы, относящиеся как к бета-, так и к гамма-функциям
Другие результаты
Маска Эйлера Константа Херони
Эквивалентные формы
Связи между константой Эйлера-Маскерони и гамма-функцией
Числа Бернулли
Альтернативные определения
Некоторые числа Бернулли
Свойства
Представление серий
Асимптотическое представление
Числа Эйлера
Некоторые определения свойств ряда
60 Некоторые определения чисел Эйлера
60 Числа Бернулли и Эйлера
Функция полилогарифма
Свойства
Функции ошибок и дополнительных ошибок
Эквивалентные формы
Свойства
Асимптотические представления
Экспоненциальный интеграл
Эквивалентные формы
Свойства
Асимптотическое представление
Табличные свойства ссылок
Табличные функции к специальным функциямГлоссарий
Неправильные интегральные и бесконечные серии тестов, теоремы
После покупки и загрузки отправьте мне электронное письмо, чтобы получить файл регистрации.

NB: Это электронная книга с файлом .exe, которая будет работать ТОЛЬКО на компьютере WINDOWS, который вы используете для ее регистрации.
Производные тригонометрических функций | StudyPug
Производная триггерной функции
Прежде чем мы начнем изучать, как получать производные от триггерных функций, почему бы нам не вернуться к основам? Возвращение назад и изучение основ — это всегда хорошо. Это потому, что многие люди склонны забывать о свойствах тригонометрических функций.Кроме того, если забыть об определенных триггерных свойствах, идентификаторах и триггерных правилах, решение некоторых вопросов в Calculus станет еще сложнее. Давайте сначала взглянем на шесть тригонометрических функций.
Шесть тригонометрических функцийПервая тригонометрическая функция, которую мы рассмотрим, — это f (x) = sinxf (x) = \ sin xf (x) = sinx . Если построить график функции, мы получим:
График 1: sinxОбратите внимание, что функция непрерывна из [-∞, ∞ \ infty, \ infty∞, ∞], и это красивая гладкая кривая без резких поворотов.
 Это означает, что sinx \ sin xsinx дифференцируем в каждой точке, и поэтому нам не придется беспокоиться о получении чего-то неопределенного. Кроме того, мы знаем, что наклон при x = π2 ± πn, n∈Ix = \ frac {\ pi} {2} \ pm \ pi n, n \ in Ix = 2π ± πn, n∈I равен 000. Следовательно, производная sinx \ sin xsinx всегда будет равна нулю в этих точках.
Это означает, что sinx \ sin xsinx дифференцируем в каждой точке, и поэтому нам не придется беспокоиться о получении чего-то неопределенного. Кроме того, мы знаем, что наклон при x = π2 ± πn, n∈Ix = \ frac {\ pi} {2} \ pm \ pi n, n \ in Ix = 2π ± πn, n∈I равен 000. Следовательно, производная sinx \ sin xsinx всегда будет равна нулю в этих точках.Далее идет функция f (x) = cosxf (x) = \ cos xf (x) = cosx . Если бы мы построили график функции, мы получим:
График 2: cosxСнова отметим, что функция непрерывна из [-∞, ∞ \ infty, \ infty∞, ∞] и имеет красивую гладкую кривую.Таким образом, cosx \ cos xcosx также дифференцируем в каждой точке. Кроме того, наклон равен 0 при xxx = 0 ± πn, n∈I \ pm \ pi n, n \ in I ± πn, n∈I. Следовательно, производная cosx \ cos xcosx будет равна 0 в этих точках.
Теперь функция y = tanxy = \ tan xy = tanx немного интереснее. Его можно переписать как y = sinxcosxy = \ frac {\ sin x} {\ cos x} y = cosxsinx, график этой функции выглядит так:
График 3: танксОбратите внимание, что значения xxx при x = π2 ± πn, n∈Ix = \ frac {\ pi} {2} \ pm \ pi n, n \ in Ix = 2π ± πn, n∈I не определены и имеют вертикальную асимптоты.
 Это означает, что производная tanx \ tan xtanx не будет дифференцируемой в этих точках. Здесь следует отметить одну интересную вещь: наклон tanx \ tan xtanx никогда не бывает отрицательным или 0. Следовательно, мы должны ожидать, что производная tanx \ tan xtanx всегда будет положительной.
Это означает, что производная tanx \ tan xtanx не будет дифференцируемой в этих точках. Здесь следует отметить одну интересную вещь: наклон tanx \ tan xtanx никогда не бывает отрицательным или 0. Следовательно, мы должны ожидать, что производная tanx \ tan xtanx всегда будет положительной.Далее следуют функции, обратные sin cos tan. Во-первых, величина, обратная sinx \ sin xsinx, равна cscx \ csc xcscx. Мы видим, что график f (x) = cscxf (x) = \ csc xf (x) = cscx выглядит так:
График 4: cscxОпять же, существуют вертикальные асимптоты в xxx = 0 ± πn, n∈I \ pm \ pi n, n \ in I ± πn, n∈I.Таким образом, они не дифференцируются в этих точках. Кроме того, наклон функции при x = π2 ± πn, n∈Ix = \ frac {\ pi} {2} \ pm \ pi n, n \ in Ix = 2π ± πn, n∈I равен 0. Таким образом, производные в этих точках всегда равны 0.
Теперь следующая функция — f (x) = secxf (x) = \ sec xf (x) = secx, что является обратной величиной cosx \ cos xcosx. График дает:
График 5: secxЭто очень похоже на cscx \ csc xcscx, но разница в том, что роли значений xxx были изменены.
 Теперь значения xxx при x = π2 ± πn, n∈Ix = \ frac {\ pi} {2} \ pm \ pi n, n \ in Ix = 2π ± πn, n∈I являются вертикальными асимптотами, а xxx значение при x = 0 ± πn, n∈Ix = 0 \ pm \ pi n, n \ in Ix = 0 ± πn, n∈I, когда касательные наклоны функции равны 0.Следовательно, производная функции не дифференцируема в точках x = π2 ± πn, n∈Ix = \ frac {\ pi} {2} \ pm \ pi n, n \ in Ix = 2π ± πn, n∈I и производная равна 0 при x = 0 ± πn, n∈Ix = 0 \ pm \ pi n, n \ in Ix = 0 ± πn, n∈I.
Теперь значения xxx при x = π2 ± πn, n∈Ix = \ frac {\ pi} {2} \ pm \ pi n, n \ in Ix = 2π ± πn, n∈I являются вертикальными асимптотами, а xxx значение при x = 0 ± πn, n∈Ix = 0 \ pm \ pi n, n \ in Ix = 0 ± πn, n∈I, когда касательные наклоны функции равны 0.Следовательно, производная функции не дифференцируема в точках x = π2 ± πn, n∈Ix = \ frac {\ pi} {2} \ pm \ pi n, n \ in Ix = 2π ± πn, n∈I и производная равна 0 при x = 0 ± πn, n∈Ix = 0 \ pm \ pi n, n \ in Ix = 0 ± πn, n∈I.Последняя функция — y = cotxy = \ cot xy = cotx.
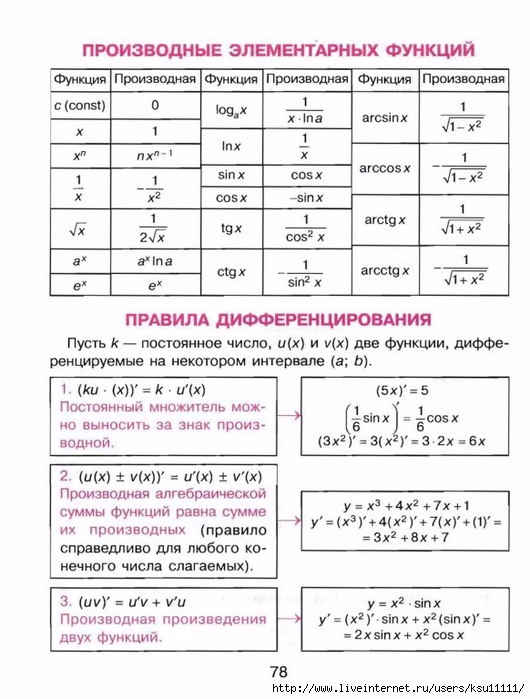
График 6: cotxОбратите внимание, что вертикальные асимптоты находятся в точках x = 0 ± πn, n∈Ix = 0 \ pm \ pi n, n \ in Ix = 0 ± πn, n∈I и наклон этой асимптоты никогда не бывает положительным или 0. Следовательно, производная этой функции всегда положительна и не дифференцируема в точках x = 0 ± πn, n∈Ix = 0 \ pm \ pi n, n \ in Ix = 0 ± πn, n∈I.
Теперь, когда мы закончили рассматривать 6 тригонометрических функций, давайте рассмотрим некоторые тригонометрические тождества, которые пригодятся при взятии производных.
Тригонометрические идентификаторы
Первые шесть идентификаторов — это взаимные идентификаторы, которые могут пригодиться, когда вам нужны производные в определенной форме.
Формула 1: взаимные идентичностиТеперь самые важные личности — это эти трое.
Формула 2: тригонометрические тождестваОни очень полезны, когда дело доходит до упрощения производных.Теперь, когда у нас есть основы, давайте продолжим и фактически посмотрим на производную от триггерных функций.
Триггерные производныеШесть производных триггерной функции следующие:
1. Производная sinx \ sin xsinx:
Формула 3: производная sinx2. Производная cosx \ cos xcosx равна:
Формула 4: производная от cosx3. Производная tanx \ tan xtanx:
Формула 5: производное tanx4.Производная от cscx \ csc xcscx равна:
Формула 6: производная от cscx5. Производная secx \ sec xsecx:
Формула 7: производная от secx6.
Формула 8: производная от cotx Производная от cotx \ cot xcotx:
Производная от cotx \ cot xcotx:Если вы действительно хотите знать, как мы получаем деривативы, то посмотрите эту статью ниже:
Производная обратных триггерных функций
В статье показано, что производную sin и косинус можно найти, используя определение производной, а остальное можно найти с помощью правила частного.{2} cotx2 тоже будет. Если вы хотите узнать больше о выводе тригонометрических функций, я предлагаю вам взглянуть на эту ссылку.
http://tutorial.math.lamar.edu/Classes/CalcI/DiffTrigFcns.aspx
Теперь пора перейти к рассмотрению некоторых вопросов, которые имеют приложение к наклону функции.
Наклон тригонометрической функцииПредположим, мы хотим найти наклон функции:
Уравнение 8: Наклон производной функции pt.1В точке x = 0. Как бы мы это сделали? Что ж, поймите, найти наклон функции — это то же самое, что взять производную. Это потребует использования правила частного, поскольку функция является частным.

Напомним, что правило частного говорит следующее:
Если у вас есть функция
Уравнение 8: Наклон производной функции pt.2Тогда производная этой функции будет:
Уравнение 8: Наклон производной функции pt.3Итак, если бы мы установили
Уравнение 8: Наклон производной функции pt.4Тогда их производные будут:
Уравнение 8: Наклон производной функции pt.5Следовательно, использование правила частного дает производную:
Уравнение 8: Наклон производной функции pt.6Упрощение этого уравнения дает:
Уравнение 8: Наклон производной функции pt.7Чтобы упростить это уравнение, мы хотели бы использовать тригонометрическое тождество:
Уравнение 8: Наклон производной функции pt.8Таким образом, наше уравнение принимает вид:
Уравнение 8: Наклон производной функции pt.9Теперь, когда у нас есть производная, все, что нам нужно сделать, это вставить точку x = 0, чтобы получить наклон. Следовательно,
Уравнение 8: Наклон производной функции pt. 10
10Таким образом, наклон функции в точке x = 0 равен 12 \ frac {1} {2} 21. Однако что, если бы нам дали касательный наклон функции в определенной точке, и нам нужно найти эту точку?
Нахождение точек по наклонуПредположим, вам дана функция:
Уравнение 9: Нахождение точки с учетом наклона производной pt.{2} sin2 сам по себе в уравнении, так что:Подставляя это в наше уравнение, получаем:
Уравнение 9: Нахождение точки с учетом наклона производной, pt.9Теперь нам нужно рассмотреть положительный случай, а затем отрицательный. В положительном случае имеем:
Уравнение 9: Нахождение точки с учетом наклона производной, pt.10Видите, что, поскольку x не ограничено, было бесконечно много решений. На самом деле, мы знаем, что решения следующие:
Уравнение 9: Нахождение точки с учетом наклона производной pt.11Теперь, если мы посмотрим на отрицательный случай, то у нас будет:
Уравнение 9: Нахождение точки с учетом наклона производной, pt.

 =1). В частности, (ex)’=ex. 4°. (81P ч)/=SO8H.5°. (S05h) / = —
=1). В частности, (ex)’=ex. 4°. (81P ч)/=SO8H.5°. (S05h) / = —


 $f(x)=\ln x$, $f'(x)=1/ x$.
$f(x)=\ln x$, $f'(x)=1/ x$. $$
$$ \]
\]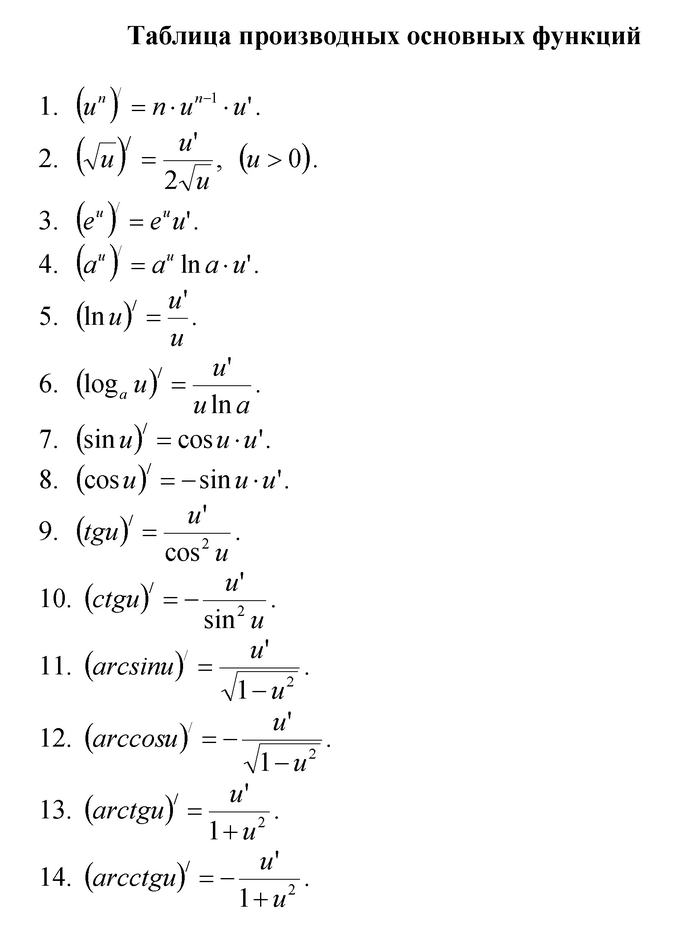 2)$.
2)$. h'(y)\right|_{y=f(x_0)}$, второй множитель имеет пределом величину $f'(x_0)$. В итоге получаем:
\[
\lim _{\Delta x \to 0}A(x_0, \Delta x)=\left. h'(y)\right|_{y=f(x_0)}\cdot f'(x_0).
\]
h'(y)\right|_{y=f(x_0)}$, второй множитель имеет пределом величину $f'(x_0)$. В итоге получаем:
\[
\lim _{\Delta x \to 0}A(x_0, \Delta x)=\left. h'(y)\right|_{y=f(x_0)}\cdot f'(x_0).
\] 2}.
\]
2}.
\] 2}.$$
2}.$$ Обратный процесс – интегрированием.
Обратный процесс – интегрированием. В данном случае f (x) считается внешней функцией, g (x) – внутренней.
В данном случае f (x) считается внешней функцией, g (x) – внутренней.


 Или, равносильное определение, – предел секущей к графику функции в точке. Либо, формулой:
Или, равносильное определение, – предел секущей к графику функции в точке. Либо, формулой: 9. Таблица производных и дифференциалов.
9. Таблица производных и дифференциалов. 10. Производные функций, заданных параметрически и неявно.
10. Производные функций, заданных параметрически и неявно. Общая
формула для y‘(x),
следующая из неявного уравнения F(x,y)
= 0, включает в себя частные производные,
которые мы будем изучать позже; пока
приведём несколько примеров, показывающих,
как найти производную y‘(x)
из неявного уравнения.
Общая
формула для y‘(x),
следующая из неявного уравнения F(x,y)
= 0, включает в себя частные производные,
которые мы будем изучать позже; пока
приведём несколько примеров, показывающих,
как найти производную y‘(x)
из неявного уравнения. 11. Производные и дифференциалы высших порядков.
11. Производные и дифференциалы высших порядков. Пусть, например, .
Тогда ,
,
, и т.д. В некоторых случаях можно получить
общее выражение для n-ой
производной функции: пусть
.
Тогда
, , ,
и вообще
.
Аналогичную формулу можно получить для
косинуса. Другой пример:
.
Если представить эту функцию в виде
,
то
,,
и вообще
.
Пусть, например, .
Тогда ,
,
, и т.д. В некоторых случаях можно получить
общее выражение для n-ой
производной функции: пусть
.
Тогда
, , ,
и вообще
.
Аналогичную формулу можно получить для
косинуса. Другой пример:
.
Если представить эту функцию в виде
,
то
,,
и вообще
. Поэтому ; ;
….,
.
Поэтому ; ;
….,
. Для первого
слагаемого вследствие инвариантности
формы первого дифференциала d(y‘х)
= y«ххdx,
для второго d(dx)
= d 2x,
поэтому окончательно d 2y = y«ххdx2+ y‘хd 2x,
что отличается от случая независимой
переменной. Причина этого понятна: если х независимая переменная, то при нахождении
второго дифференциала dx рассматривается как независимая от x константа; в случае x = (t)
дифференциал dx определяется дифференциалом dt.
Для первого
слагаемого вследствие инвариантности
формы первого дифференциала d(y‘х)
= y«ххdx,
для второго d(dx)
= d 2x,
поэтому окончательно d 2y = y«ххdx2+ y‘хd 2x,
что отличается от случая независимой
переменной. Причина этого понятна: если х независимая переменная, то при нахождении
второго дифференциала dx рассматривается как независимая от x константа; в случае x = (t)
дифференциал dx определяется дифференциалом dt.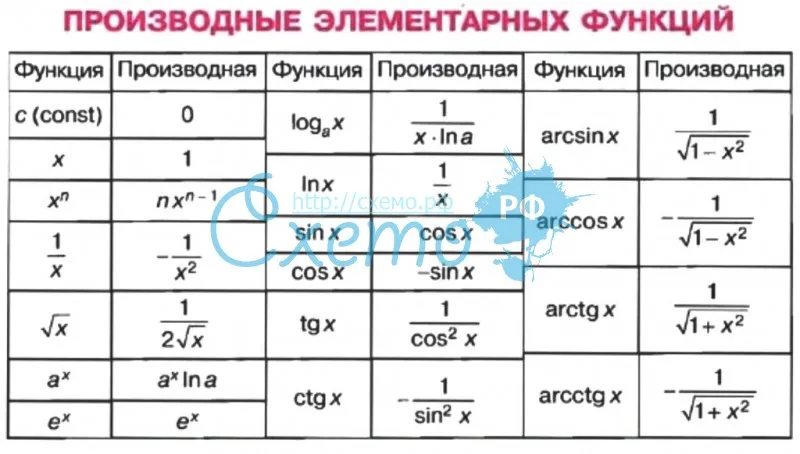 В разделе 6.10.1.
Производные функций, заданных
параметрически,
для первой производной функции
В разделе 6.10.1.
Производные функций, заданных
параметрически,
для первой производной функции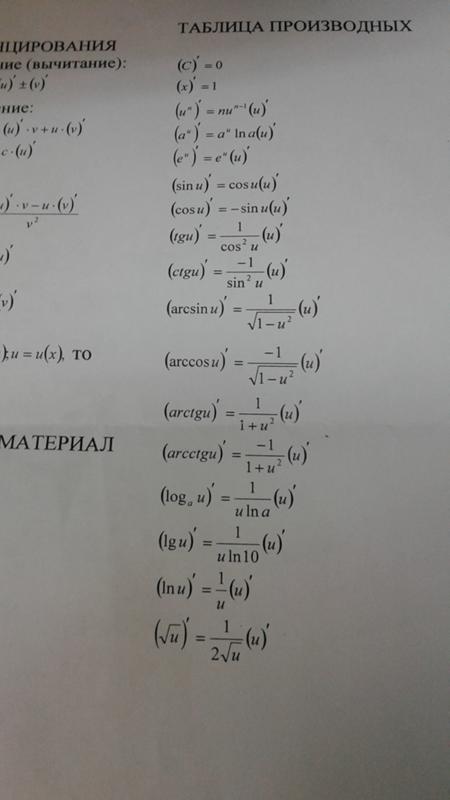 ddx (c) = 0ddx (c) = 0
ddx (c) = 0ddx (c) = 0 ddx (cscx) = — cscxcotxddx (cscx) = — cscxcotx
ddx (cscx) = — cscxcotxddx (cscx) = — cscxcotx ddx (coshx) = sinhxddx (coshx) = sinhx
ddx (coshx) = sinhxddx (coshx) = sinhx Д.)функции).
Д.)функции). сек x =
сек x =
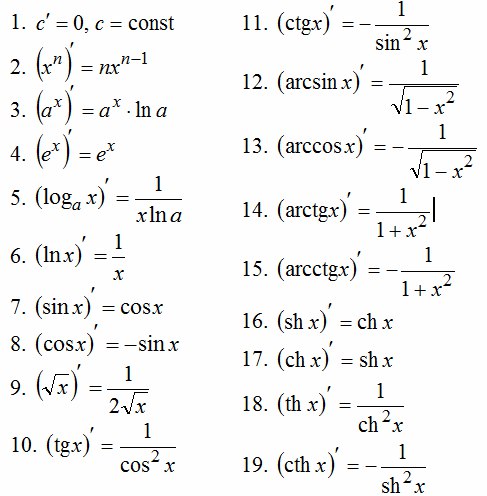
 Ранее было доказано, что производные алгебраических функций являются алгебраическими функциями, а производные тригонометрических функций — тригонометрическими функциями.2−1}} \)
Ранее было доказано, что производные алгебраических функций являются алгебраическими функциями, а производные тригонометрических функций — тригонометрическими функциями.2−1}} \)
 Это означает, что sinx \ sin xsinx дифференцируем в каждой точке, и поэтому нам не придется беспокоиться о получении чего-то неопределенного. Кроме того, мы знаем, что наклон при x = π2 ± πn, n∈Ix = \ frac {\ pi} {2} \ pm \ pi n, n \ in Ix = 2π ± πn, n∈I равен 000. Следовательно, производная sinx \ sin xsinx всегда будет равна нулю в этих точках.
Это означает, что sinx \ sin xsinx дифференцируем в каждой точке, и поэтому нам не придется беспокоиться о получении чего-то неопределенного. Кроме того, мы знаем, что наклон при x = π2 ± πn, n∈Ix = \ frac {\ pi} {2} \ pm \ pi n, n \ in Ix = 2π ± πn, n∈I равен 000. Следовательно, производная sinx \ sin xsinx всегда будет равна нулю в этих точках.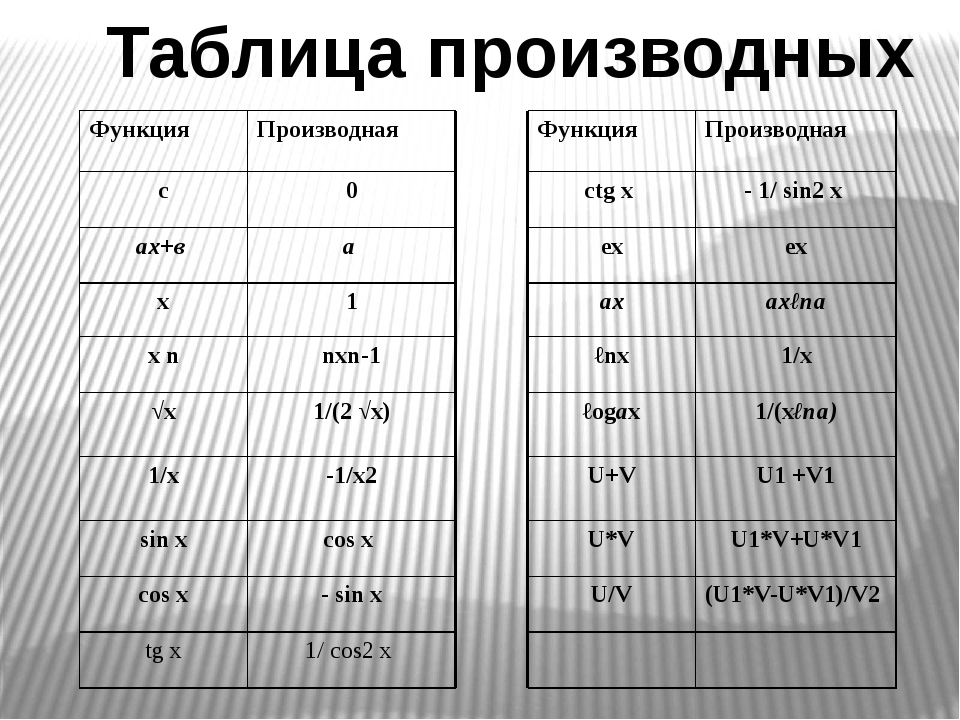 Это означает, что производная tanx \ tan xtanx не будет дифференцируемой в этих точках. Здесь следует отметить одну интересную вещь: наклон tanx \ tan xtanx никогда не бывает отрицательным или 0. Следовательно, мы должны ожидать, что производная tanx \ tan xtanx всегда будет положительной.
Это означает, что производная tanx \ tan xtanx не будет дифференцируемой в этих точках. Здесь следует отметить одну интересную вещь: наклон tanx \ tan xtanx никогда не бывает отрицательным или 0. Следовательно, мы должны ожидать, что производная tanx \ tan xtanx всегда будет положительной. Теперь значения xxx при x = π2 ± πn, n∈Ix = \ frac {\ pi} {2} \ pm \ pi n, n \ in Ix = 2π ± πn, n∈I являются вертикальными асимптотами, а xxx значение при x = 0 ± πn, n∈Ix = 0 \ pm \ pi n, n \ in Ix = 0 ± πn, n∈I, когда касательные наклоны функции равны 0.Следовательно, производная функции не дифференцируема в точках x = π2 ± πn, n∈Ix = \ frac {\ pi} {2} \ pm \ pi n, n \ in Ix = 2π ± πn, n∈I и производная равна 0 при x = 0 ± πn, n∈Ix = 0 \ pm \ pi n, n \ in Ix = 0 ± πn, n∈I.
Теперь значения xxx при x = π2 ± πn, n∈Ix = \ frac {\ pi} {2} \ pm \ pi n, n \ in Ix = 2π ± πn, n∈I являются вертикальными асимптотами, а xxx значение при x = 0 ± πn, n∈Ix = 0 \ pm \ pi n, n \ in Ix = 0 ± πn, n∈I, когда касательные наклоны функции равны 0.Следовательно, производная функции не дифференцируема в точках x = π2 ± πn, n∈Ix = \ frac {\ pi} {2} \ pm \ pi n, n \ in Ix = 2π ± πn, n∈I и производная равна 0 при x = 0 ± πn, n∈Ix = 0 \ pm \ pi n, n \ in Ix = 0 ± πn, n∈I.
 Производная от cotx \ cot xcotx:
Производная от cotx \ cot xcotx:
 10
10