О корнях кубического уравнения | Статья в журнале «Молодой ученый»
Известно, что решение некоторых теоретических и практических задач, а также моделирование некоторых физических процессов требует определение границ отрезков (интервалов) в которых находятся корни кубического уравнения с действительными коэффициентами.
В данной статье предлагается способ, с помощью которого можно определить аналитический вид вершин таких границ.
Ключевые слова: кубическое уравнение, действительные корни, многочлен, конечные промежутки, аналитический, границы.
It is known that the solution of some theoretical and practical problems, as well as the modeling of certain physical processes, requires the determination of the boundaries of segments (intervals) in which the roots of a cubic equation with real coefficients are located.
In this article, we propose a method by which we can determine the analytical form of the vertices of such boundaries.
Keywords: cubic equation, real roots, polynomial, finite intervals, analytic, boundaries.
Нахождение конечных отрезков, в которых может находиться каждый из действительных корней, имеет большое практическое значение для инженеров.
Существуют различные методы решения кубических уравнений. Эти методы разделяются на аналитические (точные) и численные. Аналитическим методам относятся метод Карно, тригонометрический способ Виета, использование возвратных уравнений и т. д. [1,2,3].
Численным методам можно отнести методы Ньютона (касательных, хорд и их совместное применение) [1,2], метод Горнера, Лобачевского, метод итерации, деления отрезка пополам, метод скоростного спуска и т. д. Каждый из этих методов имеют свои плюсы и минусы.
Предложенный мною способ находится как бы между точным и численным методами. Так что если кубическое уравнение имеет два или три одинаковых корня, то этот способ позволяет точно аналитическими формулами найти эти корни. Однако если кубическое уравнение имеет три различных действительных корней, то устанавливаются три интервала вершины которых задаются аналитически.
Аналитическое задании вершин интервалов в которых находятся действительные корни кубических уравнений позволяют установить пределы изменения физических параметров входящих в эти уравнения.
Как известно [1], для нахождения критических точек и интервалов возрастания и убывания мы поступаем следующим образом. Сначала делаем подстановку . Тогда получаем:
.
Пусть . Подставляяполучаем:
Следовательно, еслито
Другими словами прифункция возрастающая. А если возможно три случая:
1) в промежутке функция возрастающая;
2) в промежутке функция убывающая;
3) в промежутке функция возрастающая.
С другой стороны если подставитьито прифункция возрастающая, а при
а) в промежутке функция возрастающая;
б) в промежутке функция убывающая;
с) в промежутке функция возрастающая.
Таким образом понятно, что второй корень находится в промежутке.Предположим, что одним из корней уравненияявляется xo.
Тогда,
или ,
Сравнивая последнее уравнение с уравнением , получаем:
Таким образом, одним из корней является, другие две корня являются решением уравнения или .Для этого. Тогда
Определим промежуток, в котором находятся корни xo:Тогда
Как видно эти корни находятся в промежутке.
Пусть. Здесь.
Условие равенство возможно при.
Следовательно, при
при
А теперь предположим, чтоТогда . Здесь Следовательно
, здесь
.
Так как,то
Таким образом в этом случае получается
То есть
Аналогично можно показать чтo при
.
Если все три корни равны, тоЗдесь получаем
Так как , то В этом случаеКак видим, если два или все три корня равны, то они совпадают с одной из точек .Можно показать, что в этом случае график функции касается оси абсцисс.
Действительно, если функция имеет вид ,, тогдаиТаким образом в точке уравнение касательной будет. А это и есть уравнение абсциссы.
В этом случае график функции при
А при
Таким образом, если нам дано уравнение в виде , то вычисляются значение выражений,D=и определяется знак D. Если Dто уравнение имеет три действительных корня. При этом если , то один из корней отрицательный, а если , то уравнение не имеет отрицательных корней. В случае когда , то график функции в одной точке пересекает, а в другой касается оси абсцисс то есть два корня совпадают. Если все три корня равны, то . А теперь рассмотрим случайВ этом случаеи график функции с осью абсцисс имеет всего одну точку пересечения. Найдем абсциссу этой точки.
Пусть . Тогда
Отсюда получаемили.
Здесь, если ,то. В этом случае все три корня совпадают.
Это точка является точкой перехода. Действительно приполучаем , и в этой точке .
С другой стороны, так как
,то при получаеми. То есть в этой точке касательная совпадает с осью абсцисс и график функции является кубической параболой.
Рассуждая аналогическим образом, можно показать, что при и
1) если , то ;
2) если , то
здесь . А при и
1) единственный корень уравнения находится в промежутке ;
2) а при единственный корень уравнения находится в промежутке .
Таким образом, в данной статье предлагается способ, с помощью которого можно определить аналитический вид вершин границ отрезков (интервалов), в которых могут находиться корни кубических уравнений.
Литература:
- Бронштейн И. Н., Семендяев К. А. Справочник по математике — Изд 7-е стереотипное. – М: Государственное издательство технико-теоретической литературы, — с.138–139.
- Демидович Б. П., Марон И. А., Шувалова Э. З. Численные методы анализа — М.: Наука, 1968.
- Копченова Н. В., Марон И. А. Вычислительная математика в примерах и задачах. — M.: Наука 1972.
Основные термины (генерируются автоматически): корень, кубическое уравнение, ось абсцисс, промежуток, график функции, уравнение, единственный корень уравнения, случай график функции, функция, образ.
moluch.ru
Решения кубических уравнений с вещественными коэффициентами. Универсальные методы.
Решения кубических уравнений с вещественными коэффициентами. Универсальные методы.
Кубическим уравнением называется уравнение вида
ax3 + bx2 + cx +d = 0 , (1)
где a, b,c ,d — постоянные коэффициенты, а х — переменная.
Мы рассмотрим случай, когда коэффициенты являются веществеными числами.
Корни кубического уравнения.
Число х называется корнем кубического уравнения (1), если при его подстановке уравнение (1) обращается в верное равенство.
Кубическое уравнение имеет не более трех корней (над комплексным полем всегда три корня, с учетом кратности) . И всегда имеет хотя бы 1 (вещественный) корень. Все возможные случаи состава корней легко определить с помощью знака
Δ= -4b3d + b2c2 — 4ac3 + 18abcd — 27a2d2.
Итак, возможны только 3 следующих случая:
- Δ > 0 — тогда уравнение имеет 3 различных корня. (Для продвинутых — три различных вещественных корня)
- Δ < 0 — уравнение имеет лишь 1 корень. (1 вещественный и пару комплексно сопряженных корней)
- Δ = 0 — хотя бы 2 корня уравнения совпадают. Т.е. мы имеем дело либо с уравнением с 2умя совпадающими корнями, и еще 1ним отличным от них, либо с уравнением с 3емя совпадающими корнями. (В любом случае все корни вещественные. И уравнение имеет 3 совпадающих корня, тогда и только тогда, когда результант его и его второй производной равен нулю)
На практике часто , решение кубических уравнений упирается в разложении их на множители. Т.е. алгоритм приблизительно следующий: угадываем один корень, пусть это будет корень α. Затем делим многочлен на (х- α), (если α корень, то он должен поделиться без остатка). Ну а дальше мы имеем дело с обычным квадратным уравнением. Но угадать можно только рациональный корень, и то, если коэффициенты подобраны удачным образом, так что этот корень просто угадывается. Мы же рассмотрим универсальные методы решения кубичесих уравнений.
Формула Кардано.
Это формула для нахождения корней канонической формы кубического уравнения. (Над полем комлексных чисел).
Канонической формой кубического уравнения называется уравнение вида
y3 + py + q = 0 (2)
К такому виду можно привести любое кубическое уравнение вида (1) с помощью следующей замены:
x= y — b/3a (3)
p= — b2/3a2 + c/a
q= 2b3/27a3 — bc/3a2 + d/a
Итак, приступим к вычислению корней. Найдем следующие величины:
Q=(p/3)3 + (q/2)2
α = (-q/2 + Q1/2)1/3
β = (-q/2 — Q1/2)1/3
Дискриминант уравнения (2) в этом случае равен
Δ = — 108Q
Дискриминант исходного уравнения (1) будет иметь тот же знак , что и вышеуказанный дискриминант. Корни уравнения (2) выражаются следующим образом:
y1= α + β
y2= — (α + β)/2 + (31/2(α — β)/2)i
y3 =- (α + β)/2 — (31/2(α — β)/2)i
Соответственно, если Q>0, то уравнения (2) и (1) будут иметь лишь 1 (вещественный) корень, y1. Подставим его в (3) и найдем х для уравнения (1). (если вас интересуют также мнимые корни, то просто вычислите еще и y2, y3 и подставьте их в (3).
Если Q<0, то уравнение (2), как и уравнение (1) имеет три различных вещественных корня, но для их вычисления нужно уметь извлекать квадратный корень из отрицательного числа. Если вы это умеете, то проделайте расчеты, получите три корня y1, y2, y3 и подставьте их в (3).
Если же Q =0, то все корни уравнений (1) и (2) вещественные, причем как минимум 2 корня каждого из уравнений совпадают. При этом имеем
α = β, и
y1=2α,
y2= y3 = — α. Аналогично подставляем в (3) и получаем ответ.
Тригонометрическая формула Виета.
Эта формула находит решения приведенного кубического уравнения, то есть уравнения вида
x3 + ax2 + bx +c = 0 (4)
Очевидно, любое уравнение вида (1) можно привести к виду (4), просто поделив его на коэффициент а.
Итак, алгоритм применения этой формулы:
1. Вычисляем
Q=(a2— 3b)/9
R=(2a3 — 9ab + 27c)/54
2. Вычисляем
S = Q3 — R2
3. a) Если S>0, то вычисляем
φ=(arccos(R/Q3/2))/3
И наше уравнение имеет 3 корня (вещественных):
x1= — 2(Q)1/2cos(φ) — a/3
x2= — 2(Q)1/2cos(φ+2π/3) — a/3
x3= — 2(Q)1/2cos(φ-2π/3) — a/3
б) Если S<0, то заменим тригонометрические функции гиперболическими.
Вычисляем
φ=(Arch( |R|/|Q|3/2)/3
Тогда
единственный корень (вещественный): x1= -2sgn(R)*|Q|1/2*ch(φ) — a/3
Для тех, кого интересуют также и мнимые корни:
x2= sgn(R)*|Q|1/2*ch(φ) — a/3 +(3|Q|)1/2 sh(φ)i
x3= sgn(R)*|Q|1/2*ch(φ) — a/3 -(3|Q|)1/2sh(φ)i
ГДЕ:
ch(x)=(ex+e-x)/2
Arch(x) = ln(x + (x2-1)1/2)
sh(x)=(ex-e-x)/2
sgn(x) — знак х
в) Если S=0,то уравнение имеет меньше трех различных решений:
x1= -2*R1/3 — a/3
x2=x3=R1/3 — a/3
tehtab.ru
Примеры решений кубических уравнений
Обзор методов решения кубических уравнений приведен на странице “Решение кубических уравнений”. Здесь мы приводим два примера, используя формулы Кардано и Виета.
Пример решения кубического уравнения с комплексными корнями
Решить кубическое уравнение:
(1.1) .
Решение
Поиск целых корней
Уравнение (1.1) имеет целые коэффициенты. Проверим, не содержит ли это уравнение целых корней. Член без – это 1. У числа 1 есть два делителя: 1 и – 1. Подставим в уравнение (1.1) и . Ни для одного из этих чисел уравнение не выполняется. Следовательно, целых корней нет.
Сведение уравнения к приведенному виду
Пусть обозначают коэффициенты при , и свободный член. Делаем подстановку
(1.2) .
В результате получаем уравнение приведенного вида:
(1.3) ,
где
;
.
Определение вида корней
Определяем, имеет ли уравнение комплексные корни. Для этого находим дискриминант:
.
Дискриминант положителен. Следовательно, уравнение имеет один действительный корень и два комплексно сопряженных.
Нахождение корней по формуле Кардано
Поскольку дискриминант положителен, то находим корни по формуле Кардано:
, ,
где
; ; .
При , для величин и , можно взять действительные значения корней. Тогда соотношение выполняется автоматически.
В нашем случае:
;
;
;
;
;
;
;
;
.
Итак, мы нашли корни неполного кубического уравнения. По формуле (1.2) находим корни исходного уравнения:
.
Ответ
;
;
.
Пример с действительными корнями
Решить кубическое уравнение:
(2.1) .
Решение
Поиск целых корней
Уравнение (2.1) имеет целые коэффициенты. Проверим, нет ли у этого уравнения целых корней. Свободный член – это 1. У него есть два делителя: 1 и – 1. Подставим в уравнение (2.1) и . Уравнение не выполняется ни для одного из этих чисел. Следовательно, целых корней нет.
Сведение уравнения к приведенному виду
В исходном уравнении (2.1),
.
Делаем подстановку
(2.2)
и приводим уравнение (2.1) к приведенному (неполному) виду:
(2.3) ,
где
;
.
Определение вида корней
Определяем, имеет ли уравнение комплексные корни. Находим дискриминант:
.
Дискриминант отрицателен. Следовательно, уравнение имеет три действительных корня.
Нахождение корней по формуле Виета
Поскольку дискриминант отрицателен, то находим корни по формуле Виета:
;
;
;
;
.
Итак, мы нашли корни приведенного кубического уравнения. По формуле (2.2) находим корни исходного уравнения:
.
Ответ
;
;
.
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Г. Корн, Справочник по математике для научных работников и инженеров, 2012.
Автор: Олег Одинцов. Опубликовано:
1cov-edu.ru
Кубические уравнения, формулы и примеры
Определение и формула кубического уравнения
Решение таких уравнений всегда можно найти с помощью формул Кардано (Джероламо (Джироламо, Иероним) Кардано (1501-1576) — итальянский математик, инженер, философ, медик и астролог).
Формулы Кардано — формулы для нахождения корней приведенного кубического уравнения
К такому виду может быть приведено любое кубическое уравнение общего вида (1) заменой . Коэффициенты уравнений (1) и (2) после такой замены связаны соотношениями:
Решение приведенного кубического уравнения (2) ищем в виде
После подстановки уравнение сводится к виду
Функции и выбираются так, чтобы слагаемое
Для нахождения функций и нужно решить систему
которая после замены , приводится к системе
Согласно теореме Виета, значения и являются корнями квадратного уравнения
Откуда
Выполняя обратную замену, находим три такие пары и , удовлетворяющие условию . А тогда находим три корня уравнения (2) , откуда .
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Кубическое уравнение, Корни кубического уравнения, Дискриминант кубического уравнения, формула Кардане
Кубическим называется уравнение:
Это уравнение с помощью формулы x = z — а/3 можно привести к виду: Корни кубического уравнения вычисляются по формуле z = u+v (формула Кардане) Все три корня уравнения определяются следующими формулами: где u1 — любое из трех значений и, определяемых первой из формул, v1 — то из трех значений v, которое соответствует u на основании равенстваДискриминантом кубического уравнения называется выражение
Из уравнения при D 0 — три различных действительных корня.Замечание. Третий случай ( D > 0 ) называется неприводимым. В этом случае все корни уравнения с действительными коэффициентами являются действительными, однако для нахождения их по формуле z = … следует извлекать кубические корни из комплексных чисел.
Формула называется формулой Кардане. Правило, соответствующее этой формуле, впервые опубликовано в книге итальянского ученого Д. Кардане «Великое искусство или о правилах алгебры» (1545). Это правило решения кубического уравнения было получено ранее (1535) другим итальянским математиком Н. Тартальей.
Пример решения кубического уравнения смотрите ниже
Примеры работ
Материалы сайта
Обращаем Ваше внимание на то, что все материалы опубликованы для образовательных целей.
univer-nn.ru
Формулы квадратного и кубического уравнения
Квадратным уравнением называется уравнение вида
$ax^2 + bx + c = 0 $
Оно может иметь один корень, два или ни одного (в поле вещественных чисел).
Сначала нужно вычислить дискриминант $D=b^2-4ac $, если:
- $D > 0$, уравнения имеет два корня;
- $D = 0$, уравнение имеет один корень;
- $D
Корни ищем по формулах:
$x_1=\frac{-b-\sqrt{D}}{2a}$;
$x_2=\frac{-b+\sqrt{D}}{2a}$.
Вы можете посмотреть, как данные формулы применяется на практике на странице онлайн решения квадратного уравнения уравнения или же в специальном видео-уроке!
Кубическим уравнением называется уравнение вида
$ax^3 + bx^2 + cx +d = 0 $, (1)
где $a, b,c ,d$ — постоянные коэффициенты, а $ x $ — переменная.
Мы рассмотрим случай, когда коэффициенты являются вещественными числами.
Кубическое уравнение имеет не более трех корней (над комплексным полем всегда три корня, с учетом кратности) . И всегда имеет хотя бы 1 (вещественный) корень. Все возможные случаи состава корней легко определить с помощью знака дискриминанта кубического уравнения, т.е.:
$ \delta= -4b^3d + b^2c^2 — 4ac^3 + 18abcd — 27a^2d^2$.
Итак, возможны только 3 следующих случая:
- $ \delta>0 $- тогда уравнение имеет 3 различных корня. (Для продвинутых — три различных вещественных корня)
- $ \delta
- $ \delta=0 $ — хотя бы 2 корня уравнения совпадают. Т.е. мы имеем дело либо с уравнением с 2-умя совпадающими корнями, и еще 1-ним отличным от них, либо с уравнением с 3-емя совпадающими корнями. (В любом случае все корни вещественные. И уравнение имеет 3 совпадающих корня, тогда и только тогда, когда результат его и его второй производной равен нулю).
На практике часто, решение кубических уравнений упирается в разложении их на множители. Т.е. алгоритм приблизительно следующий: угадываем один корень, пусть это будет корень $ \alpha $. Затем делим многочлен на $ (x- \alpha),$ (если $ \alpha $ корень, то он должен поделиться без остатка). Ну а дальше мы имеем дело с обычным квадратным уравнением. Но угадать можно только рациональный корень, и то, если коэффициенты подобраны удачным образом, так что этот корень просто угадывается. Мы же рассмотрим универсальные методы решения кубичесих уравнений.
Формула Кардано.
Это формула для нахождения корней канонической формы кубического уравнения. (Над полем комплексных чисел).
Канонической формой кубического уравнения называется уравнение вида
$y^3 + py + q = 0$ (2)
К такому виду можно привести любое кубическое уравнение вида (1) с помощью следующей замены:
$x= y -\frac {b}{3a}$ (3)
$p= — \frac{b^2}{3a^2} + \frac{c}{a} $
$q= \frac{2b^3}{27a^3} — \frac{bc}{3a^2} + \frac{d}{a}$
Итак, приступим к вычислению корней. Найдем следующие величины:
$Q=(\frac{p}{3})^3 + (\frac{q}{2})^2$
$\alpha = (-\frac{q} {2} + Q^{\frac{1}{2}})^{\frac{1}{3}}$
$\beta = (-\frac{q} {2} — Q^{\frac{1}{2}})^{\frac{1}{3}}$
Дискриминант уравнения (2) в этом случае равен
$\delta = — 108Q $
Дискриминант исходного уравнения (1) будет иметь тот же знак , что и вышеуказанный дискриминант. Корни уравнения (2) выражаются следующим образом:
$y_1= \alpha + \beta$;
$y_2= — \frac{\alpha + \beta}{2} + 3^{\frac{1}{2}}\frac{\alpha — \beta}{2}i$;
$y_3 = — \frac{\alpha + \beta}{2} — 3^{\frac{1}{2}}\frac{\alpha — \beta}{2}i$.
Вы можете посмотреть, как описанный метод применяется на практике на странице онлайн решения кубического уравнения!
Материалы по теме:
Поделиться с друзьями:
Загрузка…matemonline.com
Решение кубических уравнений, формулы и примеры
Запишем поэтапный ход деления. Делим старший элемент делимого (слагаемое со старшей степенью) на старший элемент делителя. То есть надо подобрать такой одночлен, что его произведение со старшим элементом делителя, то есть , будет равно старшему элементу делимого, то есть . Искомый одночлен равен , записываем его в поле для частного:Далее делитель умножаем на полученное частное (для этого каждое слагаемое делителя умножаем на ), записываем результат под делимым так, чтобы каждая степень полученного после умножения выражения была записана под соответствующей степенью делимого:
Отнимаем многочлены:
Поскольку степень полученного остатка больше степени делителя, то деление продолжаем. Теперь подбираем одночлен, на который нужно умножить делитель , чтобы получить в результате старшее слагаемое остатка . Таким одночленом является , его записываем в поле для частного к записанному уже там значению :
Умножаем делитель на указанный одночлен, результат записываем под остатком и вычитаем от него:
Степень полученного остатка равна степени делителя (а должна быть строго меньше, чтобы процесс деления закончился), поэтому деление продолжаем.
Чтобы получить выражение , делитель нужно умножить на 2 (записываем это слагаемое в частное со знаком плюс), а результат этого умножения записываем под последним остатком и вычитаем от него. В результате получаем остаток, равный нулю. Деление закончено.
Итак, полное оформление деления многочлена на многочлен столбиком имеет следующий вид:
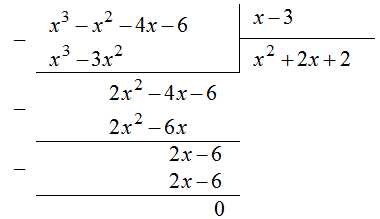
В результате деления можем сделать следующие выводы:
1) поскольку остаток равен нулю, то значение — корень многочлена ;
2) многочлен можно записать в виде:
ru.solverbook.com
