Таблица истинности a bvc: Таблицы истинности — Информатика — Презентации

Содержание

Построение таблиц истинности и логических функций

Похожие презентации:

Пиксельная картинка

Информационная безопасность. Методы защиты информации

Электронная цифровая подпись (ЭЦП)

Этапы доказательной медицины в работе с Pico. Первый этап

История развития компьютерной техники

От печатной книги до интернет-книги

Краткая инструкция по CIS – 10 шагов

Информационные технологии в медицине

Информационные войны

Моя будущая профессия. Программист

1. Построение таблиц истинности и логических функций

Автор: Воронова Светлана Аркадьевна,
преподаватель ГБПОУ ВО «ВАМК»

2. Алгоритм построения таблиц истинности для сложных выражений

1. Определить количество строк:
количество строк = 2n + строка для заголовка
n — количество простых высказываний
2. Определить количество столбцов:
количество столбцов = количество переменных +
количество логических операций
3.

Заполнить столбцы результатами
выполнения логических операций в
обозначенной последовательности с
учетом таблиц истинности основных
логических операций.

3. ПРИМЕР

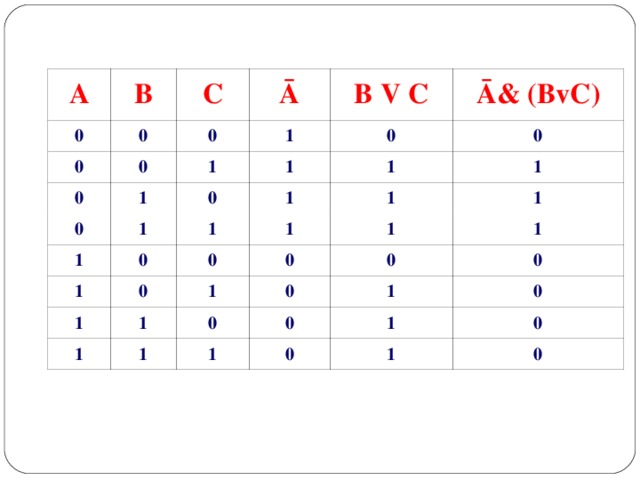
Составить таблицу истинности логического
выражения: D = ¬ А & (B V C)
1. Определить количество строк: на входе три
простых высказывания: А, В, С поэтому n=3 и
количество строк = 23 +1 = 9
9 строк
2. Определить количество столбцов:
А, В, С, ¬ А, B V C, D
6 столбцов
3. Заполнить столбцы с учетом таблиц истинности
логических операций
A
B
C
¬А
BVC
¬ А & (B V C)
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
1
1
1
1
0
0
0
0
0
1
1
1
0
1
1
1
0
1
1
1
0
0
0
0

5. Алгоритм построения логической функции по таблице истинности

1. Выделить в таблице истинности те строки, в
которых значение функции равно 1
2.

Выписать искомую формулу в виде дизъюнкции
нескольких логических элементов. Число этих
элементов равно числу выделенных строк.
3. Каждый логический элемент в этой дизъюнкции
записать в виде конъюнкции аргументов
функции.
4. Если значение какого-либо аргумента функции в
соответствующей строке таблице равно 0, то этот
аргумент взять с отрицанием.
Пусть дана таблица истинности для некоторой
логической функции Z(X,Y)
X
Y
Z
0
0
1
0
1
0
1
0
1
1
1
0
В первой и третьей строках таблицы истинности
значение функции равно 1.
1. В первой и третьей строках таблицы истинности
значение функции равно 1.
2. Так как строки две, получаем дизъюнкцию двух
элементов: ( ) V ( ).
3. Каждый логический элемент в этой дизъюнкции
запишем в виде конъюнкции аргументов
функции X и Y: (X & Y) V (X & Y).
4. Берем аргумент с отрицанием если его значение в
соответствующей строке таблицы равно 0 и
получаем искомую функцию:
Z (X, Y) =(¬ X & ¬Y) V (X & ¬Y).

English Русский Правила

Таблицы истинности | Презентация к уроку на тему:

Опубликовано 23.11.2017 — 21:28 — Сальникова Юлия Анатольевна

Понятие таблица истинности, алгорит составления таблиц истинности

Скачать:

Предварительный просмотр:

Подписи к слайдам:

Слайд 1

Таблицы истинности Информатика для студентов 2 курса

Слайд 2

Таблица истинности — это таблица, устанавливающая соответствие между возможными наборами значений логических переменных и значениями функций. Таблица состоит из строк и столбцов

Слайд 3

Алгоритм построения таблиц истинности Определить количество строк в таблице истинности Количество строк равно 2 n , где n — количество логических переменных. 2. Определить количество столбцов в таблице истинности Количество столбцов равно количеству логических переменных плюс количество логических операций.

Слайд 4

Построить таблицу истинности с указанным количеством строк и столбцов Ввести названия столбцов таблицы в соответствии с последовательностью выполнения логических операций с учетом скобок и приоритетов; Заполнить столбцы входных переменных наборами значений; Заполнить таблицу истинности по столбцам, выполняя логические операции в соответствии с установленной последовательностью.

Слайд 5

Порядок выполнения логических операций Действия в скобках Инверсия Конъюнкция Дизъюнкция

Слайд 6

построить таблицу истинности для следующего сложного (составного) логического выражения : А & (B V C)

Слайд 7

Алгоритм выполнения Простые выражения (логические переменные): А, В, С ; (3) Количество логических операций: ¬ А — инверсия; B  C — операция дизъюнкции; ¬ А & (B  C) . операция конъюнкции. Всего: 3 Количество строк: на входе три простых высказывания: А, В, С , поэтому a=3 и количество строк = 2 ³ +1 = 9. Количество столбцов: 3+3=6 Заполняем столбцы с учетом таблиц истинности логических операций.

Слайд 8

А B C A B V C А & (B V C) 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 1 1 1 1 1 0 0 0 0 0 1 1 1 0 1 1 1 0 1 1 1 0 0 0 0 Таблица истинности :

Слайд 9

Задание для самостоятельной работы Постройте таблицу истинности для логического выражения: D=А V B & C

По теме: методические разработки, презентации и конспекты

Элементы математической логики — Практическое занятие №2 — Составление таблиц истинности

Цель работы: закрепить основные понятия алгебры высказываний, отработать навыки составления таблицы истинности для высказываний, сформировать умения определять равносильность формул. …

Построение таблиц истинности

закрепить умение строить истинные сложные высказывания из простых с использованием логических операций, сформировать навыки построения таблиц истинности…

Проверочная работа по теме «Таблицы истинности»

Проверочная работа по теме «Основы логики» предназначена для использования на уроках информатики для студентов 1 курса. Работа состоит из 8 вопросов разного характера. Разработан в программе MS Word….

Контрольная работа на тему: Проектирование логических схем, построение таблиц истинности.

Контрольная работа на тему: Проектирование логических схем, построение таблиц истинности.Контрольная работа содержит задания 24 варианта по 2 задания.Есть ответы….

4 раздел — итоговая таблица, таблица для графической части

4 раздел — итоговая таблица, таблица для графической части…

Основные логические операции, таблицы истинности

презентация основные логические операции, таблицы истинности…

Технологическая карта. Основные логические операции, построение таблиц истинности простых высказываний.

ТЕХНОЛОГИЧЕСКАЯ КАРТАФ. И. О. преподавателя: Денисенко Яна СергеевнаДата проведения занятия: __.__.2018 г.Тема занятия: Основные логические операции, построение таблиц истинности простых высказываний…

как составить таблицу истинности из логического выражения

A, B, C и D являются булевыми переменными, что означает, что каждая из них принимает значение «правда или ложь». Более сложные выражения имеют значение «истина» или «ложь». в зависимости от значений этих переменных, так, например, A’BD’ истинно, если А ложно, В истинно, D ложно, С либо истинно, либо ложно.

Сказать, что F = G, где F и G комплексные выражения, означает, что нет независимо от того, какие значения имеют логические переменные, значение F одинаково как значение G (то есть F и G либо оба истинны, либо оба ложны). Так, например, у нас есть

 АВ + АС = А(В+С)

, потому что если А истинно и либо В, либо С истинно, то обе стороны верны, а в любом другом случае обе стороны ложны—нет возможности присвоить значения для A, B, C так, чтобы две стороны вышли по-разному.

Как упоминалось в предыдущих постах, вы всегда можете доказать (или опровергнуть!) равенство, перебирая все возможные присваивания «true» и «false» переменные. Цель, кажется, состоит в том, чтобы доказать «теоремами», то есть используя операции, ранее подтвержденные. Как вы говорите, мы можем либо манипулировать одну сторону уравнения, пока она не примет вид другой стороны, или мы мог манипулировать обеими сторонами и привести их в общую форму.

В этом случае первое, на что следует обратить внимание, это то, что правая сторона (RHS) является копией LHS с некоторыми дополнительными элементами, прикрепленными к концу. Для этого причина, по которой проще всего манипулировать только RHS, чтобы избавиться от избыток! Мы можем начать с этой основной теоремы:

, если Q истинно всякий раз, когда истинно P, то Q = Q + P

Мы можем доказать эту теорему, систематически рассматривая все возможности для P и Q. Или посмотрите на это так: если Q истинно, то обе части уравнение верно. А если Q ложно, то и P должно быть ложно (поскольку по предположение, если бы P было истинным, Q было бы истинным), следовательно, обе стороны ложны.

Учитывая эту теорему, мы доказываем:

 XY + X'Z = XY + X'Z + YZ

Доказательство: пусть P будет YZ, а Q будет XY+X’Z. Предположим, что P истинно, то есть Y и Z оба верны. Но если Y и Z оба истинны, то XY+X’Z должны быть истинны. (Причина: если X истинно, то, поскольку Y истинно, XY истинно. И если X истинно ложно, тогда, поскольку Z истинно, X’Z истинно. Таким образом, в любом случае XY+X’Z равно верно.) Итак, мы показали, что Q истинно всякий раз, когда истинно P, следовательно, предыдущую теорему Q = Q + P, которую в данном случае мы и хотели доказать.

Теперь мы можем доказать

 A'D' + AC' = A'D' + AC' + C'D'

Это то же самое, что и предыдущая теорема, полагая A вместо X, D’ вместо Y, и C’ вместо Z.

Из последней теоремы следует, что

 B(A'D' + AC') = B(A'D' + AC' + C'D')

то же, что и

 A'BD' + ABC' = A'BD' + ABC' + BC'D'

Учитывая это, мы можем взять правую часть оригинала и заменить A’BD’ + ABC’ для A’BD’ + ABC’ + BC’D’, то есть мы можем опустить термин BC’D’.

Шагами, аналогичными описанным выше, мы можем доказать эти две теоремы:

 A'BD' + BCD = A'BD' + BCD + A'BC
 BCD + ABC' = BCD + ABC' + ABD

, которые позволяют нам опустить последние два члена RHS оригинала, завершение доказательства.

truetable — Таблица истинности для функций переключения

спросил

8 лет, 1 месяц назад

Изменено 8 лет, 1 месяц назад

Просмотрено 771 раз

Кто-нибудь может объяснить, как работает эта концепция?

У меня 1 вопрос. Но я не знаю, есть ли идеи по построению таблицы истинности.

f(A,B,C) = AB + A’C

Ответ был ABC + ABC’ + A’BC + A’B’C

И я понятия не имею, как он туда попал. 🙁

правдивость

1. Создайте столбец для каждого входа, каждой промежуточной функции и конечной функции:

 A B C | АБ | А' | А'С | АВ + А'С
--------------------------------
      | | | |
      | | | |
      | | | |
      | | | |
      | | | |
      | | | |
      | | | |
      | | | |

2. Перечислите все возможности ввода и начните заполнять промежуточные значения функции, а затем конечное значение функции:

 А Б В | АБ | А' | А'С | АВ + А'С
--------------------------------
0 0 0 | 0 | 1 | 0 | 0
0 0 1 | | | |
0 1 0 | | | |
0 1 1 | | | |
1 0 0 | | | |
1 0 1 | | | |
1 1 0 | | | |
1 1 1 | | | |

3. Теперь вы закончите таблицу истинности.

Обновление в соответствии с редактированием вопроса OP:

«данный ответ» можно уменьшить следующим образом с помощью булевой алгебры:

 ABC + ABC' + A'BC + A'B'C
АВ(С + С') + А'С(В + В')
АВ + А'С

…что совпадает с данным f(A,B,C). Не уверен, почему ABC + ABC' + A'BC + A'B'C можно считать «ответом», но это показывает эквивалентность между двумя формулами.